Distributional Analysis in Educational Evaluation: A Case Study from the New York City Voucher Program

Abstract

We use quantile treatment effects estimation to examine the consequences of the random-assignment New York City School Choice Scholarship Program (NYCSCSP) across the distribution of student achievement. Our analyses suggest that the program had negligible and statistically insignificant effects across the skill distribution. In addition to contributing to the literature on school choice, the paper illustrates several ways in which distributional effects estimation can enrich educational research: First, we demonstrate that moving beyond a focus on mean effects estimation makes it possible to generate and test new hypotheses about the heterogeneity of educational treatment effects that speak to the justification for many interventions. Second, we demonstrate that distributional effects can uncover issues even with well-studied datasets by forcing analysts to view their data in new ways. Finally, such estimates highlight where in the overall national achievement distribution test scores of children exposed to particular interventions lie; this is important for exploring the external validity of the intervention’s effects.

Introduction

Excellence and equity goals motivate much of American educational policy. These two goals are not always mutually reinforcing. Some educational policies and practices boost average academic achievement even as they broaden educational inequalities (c.f. Arygs, Rees, & Brewer 1996). Others have little effect on average achievement but narrow inequalities (c.f. Hong, et al. 2012). The twin goals of excellence and equity should lead policy-makers to be interested in both the average effects of educational policies and their distributional consequences. But although developmental science suggests that many interventions may have heterogeneous effects (e.g., Duncan & Vandell 2012), much educational evaluation research focuses on the estimation of mean treatment effects either for the population at large or for particular subgroups of interest.

In this paper we demonstrate distributional effects estimation by re-evaluating data from the New York City School Choice Scholarship Program (NYCSCSP). This random-assignment experiment, in which low-income elementary school students in New York City applied for a $1,400 private school voucher, strongly influenced student school choices. Nearly 80 percent of the students who were randomly selected from the pool of eligible applicants to receive the voucher used their vouchers to enroll in private schools (Mayer et al. 2002). In addition, the experiment provides a continuous and nationally-normed measure with which to analyze the effects of choice on the distribution of student achievement. While data from the NYCSCP have been studied extensively, there is very little evidence to suggest that this voucher offer influenced mean student achievement. Nonetheless, both theory and prior studies suggest that the program’s effects may be heterogeneous, indicating that mean effects analyses may obscure theoretically and practically important effects across the distribution of achievement.

Our findings are largely consistent with the hypothesis that vouchers have no meaningful effects at any point in the distribution. We find some evidence to suggest that the New York City voucher offer had a small negative effect on math achievement in the first year for a small share of the top of the distribution. However, this effect fades out rapidly and is not precisely estimated. Furthermore, the measured effect of the New York City voucher offer is close to zero for the bulk of the study sample’s math and reading achievement distributions.

In addition to contributing to the literature on school choice and vouchers, this demonstration illustrates three ways in which distributional effects estimation can enrich educational research more broadly. First, we demonstrate that moving beyond a focus on mean effects estimation makes it possible to generate and test new hypotheses about the heterogeneity of educational treatment effects that can speak to the justification for many interventions. Given the fact that educators and policy-makers are interested in narrowing educational inequality, we argue that distributional effects estimators should be central tools used in evaluation of many educational interventions. Second, we demonstrate that distributional effects can uncover issues even with well-studied datasets by forcing analysts to view their data in new ways. Our distributional re-evaluation of NYCSCP data has revealed several issues related to missing data, attrition, and non-response weights in the New York City voucher data that earlier analyses had not addressed. Finally, such estimators highlight where in the overall national achievement distribution test scores of children exposed to particular interventions lie in a way that simple means miss, making more explicit where external validity claims can be made. Here, we show that the sample of baseline achievement in the New York City voucher experiment is predominately limited to the bottom half of the national public school test score distribution, shedding new light on the external validity of this study’s findings.

School choice and the distribution of achievement

Arguing that traditional public schools are monopolistic and inefficient, school voucher proponents aim to create more vibrant educational marketplaces. By broadening the educational choices available to parents and students and creating incentives for schools to improve, vouchers and other school choice programs aim to boost educational outcomes for students who might otherwise have no choice but to enroll in low-quality public schools (Chubb & Moe 1990; Friedman & Friedman 1980).

School reformers have launched a handful of voucher programs across the U.S. over the past two decades in an attempt to demonstrate the effectiveness of this approach. In 1997, the School Choice Scholarships Foundation initiated one such program in New York City, offering three-year scholarships worth $1,400 a year to a randomly selected group of low income children in grades K–4. This program’s random assignment design makes it possible to generate unbiased estimates of the effects of a voucher offer for families who apply for vouchers. This is unlike observational comparisons of voucher recipients with other public school children which likely suffer from bias due to the potentially confounding characteristics of families who self-select into voucher programs.¹ Mathematica Policy Research (MPR) and the Harvard University Program on Education Policy collected enrollment and achievement data from students in the treatment and control groups.

Analyses of the New York City voucher experiment data clearly indicate that vouchers influence school choice. Students randomly selected to receive a voucher were several times more likely than their peers in the control group to attend private schools. More than three-fourths of voucher recipients used their vouchers to enroll in private schools at some point in the program, and more than half enrolled in private schools for the entire three-year scholarship period. 85 percent of the students who used the voucher enrolled in Catholic schools, where tuition estimates ranged from $1,200 – $2,500 in 1997 (Hartocollis 1997; Steinberg 1997a, 1997b). Parent surveys clearly indicate that parents whose children received an offer of a voucher had higher levels of satisfaction with their children’s schools, compared to parents in the control group. Voucher lottery winners – and in particular, those who actually used their vouchers to attend private schools – enrolled in smaller schools with smaller classrooms, more computer labs, and more after-school programs than did their peers in the control group (Mayer et al. 2002).

But to date there is little evidence to suggest that these school resources translated to higher levels of achievement for voucher recipients. While the New York voucher experiment has inspired a vigorous debate about appropriate methods for analyzing experimental data (Barnard et al. 2003; Krueger & Zhu 2004a; Krueger & Zhu 2004b; Peterson & Howell 2004), the results of various analyses of the program’s mean effect on student achievement are strikingly consistent. Voucher recipients score no higher, on average, than do students in the control group on standardized measures of math and reading achievement (Krueger & Zhu 2004a; Mayer et al. 2002; Howell et al. 2002). Voucher programs implemented in other contexts yield somewhat more mixed results. Evaluations of voucher offers in Charlotte, NC (Cowen 2008; Greene 2001), Milwaukee, WI (Rouse 1998), Washington, DC (Howell et al. 2002; Wolf et al. 2013), and Chile (Lara et al. 2011) provide evidence of modest positive average effects on student achievement. (Cowen 2012 provides a comprehensive review of the existing literature on voucher program achievement effects.)

The evidence that the NYC voucher experiment had no average effect does not mean, however, that it had no effect at all. In fact, some evidence suggests that voucher receipt and private school enrollment had positive effects on African American students’ achievement (Barnard et al. 2003; Howell et al. 2002; Mayer et al. 2002; Peterson & Howell 2004). While these findings are highly sensitive to how student race is measured (Krueger & Zhu 2004a, Krueger & Zhu 2004b),² they suggest that small average effects of voucher programs mask larger heterogeneous voucher program effects for particular types of students. In fact, this is one of the possibilities that motivated our use of distributional estimators. Furthermore, recent studies indicate that both the New York City and the Washington DC voucher program have larger long-run effects on student attainment than one might expect given their short-term achievement effects (Chingos & Peterson 2012; Wolf et al. 2013). Distributional analyses may provide one potential avenue to make sense of some of these contradictory findings, if, for example, voucher receipt helps students at the bottom of the skills distribution acquire a baseline level of skills and successfully progress through their educational career to high school graduation.

Furthermore, distributional analyses provide a tool to evaluate claims that are central to the policy debates surrounding educational choice. One of the most prominent arguments for school choice plans holds that choice provides a mechanism to narrow educational inequality by giving poor students access to the same high-quality schooling that affluent students enjoy, thus shrinking ex-post achievement gaps. However, these equity-enhancing effects may not occur if high-quality schools of choice target admissions offers and tuition discounts exclusively to the low-income students they expect will benefit most from attendance. That is, if schools of choice only take the highest performing voucher recipients, ex-post inequality in achievement may be relatively unaffected.

Most mean effect estimates provide little insight into the validity of these arguments about the effects of choice on the distribution of ex-post student achievement for two reasons. First, they only look at averages and may miss offsetting effects. Second, to the extent they look at effects by level of achievement, it is by level of achievement ex ante, which need not be the same as the ex-post achievement about which much of the rhetoric is aimed. Thus, we maintain that distributional effects estimates based on differences in post-voucher offer scores provide an essential parameter for fully evaluating school choice.

In this paper, we investigate the possibility that weak average effects of vouchers disguise larger (and possibly contradictory) voucher program effects for high or low achieving students. We test three competing hypotheses regarding the effects of voucher programs on student achievement for students in the sample of voucher seekers.

(1) Common School Hypothesis: Vouchers mitigate inequality by boosting achievement primarily at the bottom of the distribution

The U.S. school choice movement was inspired in part by research indicating that Catholic and other private schools are particularly beneficial for poor, minority, low-performing and otherwise at-risk students (Coleman & Hoffer 1987; Evans & Schwab 1995; Greeley 1982; Hoffer, Greeley & Coleman 1995; Neal 1997; Morgan 2001). Catholic and other private schools are typically smaller than competing public schools, their curricula are often relatively undifferentiated, and they are frequently situated in social networks that allow parents and teachers to more closely monitor student achievement and behavior than is possible in public schools. In part as a result of these school characteristics, schools of choice may produce more equal educational outcomes than traditional public schools which are less well-equipped to support low-performing students who they must by law serve. By providing a mechanism for students to opt out of neighborhood public schools and into Catholic and other private schools, voucher experiments attempt to make the positive achievement effects thought to be associated with Catholic schools more broadly available. Nearly all of the students in the New York City experiment who used a voucher to attend a private school enrolled in a school with a religious affiliation, and 85 percent enrolled in Catholic schools (Howell, Wolf, Campbell, and Peterson 2002). Assuming that previously estimated Catholic school effects are causal and generalize to the schools that these voucher recipients chose, the “common school hypothesis” suggests that voucher school programs will have positive effects at the bottom of the program sample’s academic achievement distribution, but not at the middle or the top of the distribution.³

(2) Stratifying Hypothesis: Vouchers exacerbate inequality among applicants by boosting achievement primarily at the top of the distribution of applicants

In contrast, one might imagine several mechanisms through which voucher programs might magnify educational inequalities. Assuming that peers have an independent effect on student achievement, schools have strong incentives to prefer enrolling higher-achieving students over lower-achieving students. Epple, Figlio, & Romano (2008) provide suggestive empirical evidence indicating that U.S. private high schools act on these incentives, using tuition discounts to attract relatively high-achieving students. This “cream-skimming” phenomenon may benefit high-achieving voucher recipients, who gain access to high-quality selective private schools.

Many of New York City’s elite private schools have competitive admissions, and most of the city’s private schools charged tuition levels that were higher than the $1,400 stipend that the voucher provided, even among the predominately Catholic schools the voucher winners selected. If higher-quality private schools restrict admissions and tuition discounts to relatively high-achieving students or to students with high levels of socio-emotional skills ex-ante, the voucher treatment may buy high-achieving students access to a more effective private school treatment than that available to lower-achieving students. In such a scenario, voucher programs may boost achievement at the top of the achievement distribution for applicants, but not at the bottom of the achievement distribution, by sending these children to different types of private schools.⁴

(3) No-Effects Hypothesis: Vouchers have no effect across the distribution

While each of the prior two hypotheses are theoretically viable, perhaps the most common-sense hypothesis based on the results of earlier analyses of New York City voucher data is that vouchers simply do not influence the distribution of achievement. For many students, the voucher program may have amounted to a weak treatment. It did little to change students’ home or neighborhood life. Furthermore, the extent to which it influenced the quality of schools to which students were exposed is debatable. Although many voucher recipients used their vouchers to enroll in private schools, they likely attended inexpensive private schools in their own neighborhoods. If these schools do not differ substantially from the neighborhood public schools that students would have otherwise attended, or if family and neighborhood factors trump the effects of schools on achievement for these students, voucher receipt may have had no effect on either the mean or the distribution of student achievement for students in the program sample.

In this paper, we use quantile treatment effect (QTE) estimation to test these competing hypotheses. This technique, which is not widely used in educational research, provides unique insights into the ways in which the treatment influences the distribution of student achievement, making it possible to explicitly investigate this intervention’s consequences for educational inequality.

Data: The New York City School Choice Scholarship Program

The New York City School Choice Scholarship Program (NYCSCSP) was a three year private school choice randomized experiment. Randomization procedures are described in detail in Hill, Rubin, and Thomas (2000). As noted above, low income students (students qualified for free school lunch) in grades K–4 at the time of application were eligible to apply for vouchers of $1,400 to be used towards private school tuition for subsequent school years. Initial applications were received in the spring of 1997 from 5,000 students who met the eligibility requirements. Of these, approximately 2,600 students were randomized at the family level to treatment and control using two methods of random assignment from separate lottery rounds.

Students from 1,000 families were randomized using a Propensity Matched Pairs Design (PMPD) in the first lottery and a Stratified Block design was used for students from an additional 960 families from a second series of lotteries. As described in Krueger and Zhu (2004a), from these two sampling methods, 30 mutually exclusive “random assignment strata” were created from: 5 lottery blocks (1 PMPD block plus 4 stratified blocks) times 2 school types (above- or below-median test scores) times 3 family size groups (1, 2, or 3 or more students per family). Within these original strata, assignment was random. Krueger and Zhu (2004a) detail the discovery by Mathematica that some families misreported their family size and were placed in the wrong strata. While revised strata were created and used by Howell and Peterson (2002) and Mayer, Peterson, et al. (2002), because assignment was random within the original strata, we follow Krueger and Zhu’s use of the original, rather than the revised strata. Krueger and Zhu note that differences in results between the two sets of strata are very minor.

Krueger and Zhu also identified two issues with sample weights that were subsequently revised by Mathematica in 2003 (as a result only the revised weights are available to us).⁵ When we attempt to replicate others’ findings, we are constrained to either use these revised sample weights, which adjust for non-response, or use no weights. The combined effect of using the original strata and having only the revised weights makes it so that we are unable to exactly replicate any work published prior to Krueger and Zhu (2004a), including Mayer, Peterson, et al. (2002). Thus, replication attempts are primarily concentrated on Krueger and Zhu (2004a) and Jin and Rubin (2009), both of which use the original strata and revised weights.

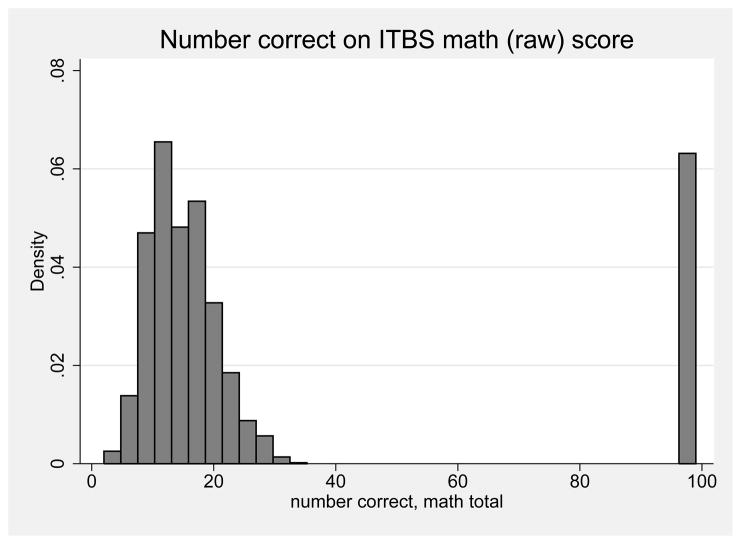
Baseline student achievement in reading and math was collected for nearly all students, except for applicants in kindergarten, using the Iowa Test of Basic Skills (ITBS). Prior to our analysis of the effects of voucher assignment on the distribution of achievement, we compare distributions of students in the treatment and control group on pretest National Percentile Rankings (NPR).⁶ Initial examinations of the distribution of these baseline ITBS scores reveal unexpected differences between treatment and control at the top of the raw ITBS score distribution and at the bottom of the ITBS percentile score distribution. Taken at face value, these findings seem to indicate that the randomization procedure failed to generate balanced treatment and control groups.

However, Figure 1 indicates that the problem involves the coding of missing data, rather than the treatment assignment process. This histogram for baseline scores on the raw ITBS mathematics exam reveals that a large number of students scored 99 on baseline tests in reading and math with the next highest score not exceeding 50.⁷ The distribution of all other baseline and post-tests in reading and math throughout the voucher study show a similar pattern (not shown). Furthermore, participants with a raw score of 99 have NPR scores and normal curve equivalent (NCE) scores of 0. Communications with the ITBS’s publisher indicate that these scores are not valid. While analyses reported below indicate that Krueger and Zhu (2004a) and Jin and Rubin (2009) do not set these cases to missing, we do so in our analyses.⁸

Figure 1.

Histogram of raw ITBS math items correct at baseline.

Notes: Figure shows histogram of raw number of math items correct on baseline ITBS test as reported in the public-use version of the data. The large point mass at 99 represents those individuals with ITBS raw math scores of 99 and associated National Percentile Ranking scores of 0, and represents a missing data code. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research. Baseline scores unavailable for kindergarten students.

We create inverse propensity score weights to adjust for nonresponse (including both non-response because the observation is missing any test score in the data and non-response from our treating the invalid 99 raw scores as missing data). First, we predict treatment status as a function of demographics, baseline scores when available, and whether the student has a missing math or reading test score or an invalid 99 math or reading raw test score, using a logistic regression. We calculate a predicted probability of being in the treatment group p̂, and then construct weights of 1/p̂ for those in the treatment group and 1/(1−p̂) for the control group. These weights balance the treatment and control group on these observable dimensions such as demographics and baseline scores (Table 2) and also balance the incidence of a missing or invalid score across the years (Table 1).

Table 2.

Balance in Xs and test scores at baseline across treatment and control groups, our inverse propensity-score weights

	Control mean	T-C difference	SE	P-value
Child characteristics
Male	0.496	0.001	0.019	0.951
African-American	0.438	−0.002	0.019	0.932
Hispanic	0.489	−0.0001	0.019	0.994
Labeled gifted	0.109	−0.0007	0.012	0.958
Labeled special education	0.110	0.0007	0.012	0.958
Speaks English at home	0.764	−0.003	0.017	0.854
Mother/family characteristics
Mother’s years of schooling	12.977	−0.006	0.069	0.932
Mother works full time	0.215	0.0002	0.017	0.989
Mother born in the US (not PR)	0.600	0.001	0.020	0.960
Family gets some welfare	0.779	0.001	0.016	0.947
Mother in same house 1 year ago	0.914	0.0005	0.011	0.965
Mother is Catholic	0.539	−0.00031	0.020	0.988
Probability income ≤ $15, 000	0.502	−0.001	0.025	0.958
Baseline test scores (no K scores)
Math score	19.79	0.012	1.004	0.990
Reading score	25.57	−0.111	1.067	0.917

Notes: Table reports treatment control differences for baseline demographics and baseline test scores, treating the invalid 99 scores as missing. Column 1 reports the control group mean, column 2 the T-C difference, column 3 the SE on this difference, and column 4 the p-value. The inverse p-score weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. SEs clustered by family. Mother born in the US denotes born in one of the 50 states and Washington DC< and not Puerto Rico, and family welfare use denotes use of Food Stamps, AFDC/public assistance, Social Security, or Medicaid. The probability that income is less than or equal to $15,000 is reported in the table, the specifications (following others) control for the natural log of the midpoint of income ranges. A small number of observations are missing demographics. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Table 1.

Imbalance in incidence of “missing data” values across treatment and control groups

	Control mean	T-C difference	SE	P-value	N
Panel A: Differences in missing scores, Mathematica weights
Missing score, baseline, math/reading	0.310	−0.015	0.020	0.444	2666
Panel B: Differences in invalid (99) scores, Mathematica weights
Invalid (99) score, baseline, math	0.120	0.012	0.015	0.425	2666
Invalid (99) score, baseline, reading	0.066	0.021	0.012	0.089*	2666
Invalid (99) score, year 1, math	0.067	−0.039	0.010	0.000***	2080
Invalid (99) score, year 1, reading	0.036	0.001	0.008	0.944	2080
Invalid (99) score, year 2, math	0.068	0.016	0.015	0.301	1754
Invalid (99) score, year 2, reading	0.027	0.008	0.009	0.379	1754
Invalid (99) score, year 3, math	0.046	−0.013	0.010	0.226	1801
Invalid (99) score, year 3, reading	0.022	0.019	0.010	0.054*	1801
Panel C: Differences in missing scores, authors’ inverse p-score weights
Missing score, baseline, math/reading	0.309	0.002	0.019	0.929	2662
Missing score, year 1, math/reading	0.219	0.002	0.020	0.915	2662
Missing score, year 2, math/reading	0.343	0.003	0.024	0.895	2662
Missing score, year 3, math/reading	0.329	0.003	0.024	0.883	2662
Panel D: Differences in invalid (99) scores, authors’ inverse p-score weights
Invalid (99) score, baseline, math	0.122	−0.001	0.014	0.936	2662
Invalid (99) score, baseline, reading	0.075	−0.0004	0.011	0.973	2662
Invalid (99) score, year 1, math	0.039	−0.0004	0.008	0.964	2662
Invalid (99) score, year 1, reading	0.032	0.0006	0.007	0.937	2662
Invalid (99) score, year 2, math	0.050	−0.001	0.009	0.910	2662
Invalid (99) score, year 2, reading	0.022	−0.0005	0.006	0.934	2662
Invalid (99) score, year 3, math	0.025	−0.001	0.006	0.867	2662
Invalid (99) score, year 3, reading	0.021	0.0006	0.007	0.921	2662

Notes: Table reports treatment control differences for baseline and year 1–3 missing test scores and the invalid 99 raw/0 percentile test scores. Panels A and B report the differences with the MPR non-response weights, and Panels C and D with our inverse propensity score weights. Column 1 reports the control group mean, column 2 the T-C difference, column 3 the SE on this difference, and column 4 the p-value. The inverse p-score weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. SEs clustered by family. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

After accounting for the miscoded nonresponse by treating it as a missing value, roughly 31 percent of the New York City voucher respondents are missing tests in reading or math at baseline. Table 1 provides a detailed description of differences between treatment and control groups in various types of missing data/attrition using both our own and the Mathematica weights. In Panel A, we use the Mathematica weights and show the T-C difference in the probability of no score being present. In Panel B, we show the differences by year in the probability of getting an invalid 99 raw score using the same Mathematica weights; these differences are significantly different from 0 at the 10% level for 3 measures out of 8 and at the 5% level 1 time out of 8. Panel C estimates use our inverse propensity score weights to see if the presence of a missing score is balanced with our weights, and shows it is. Finally, Panel D shows that our weights, unlike the Mathematica weights, also balance the probability that a test score is an invalid 99 across the treatment and control groups.⁹ Thus, as the table indicates, there are small but statistically significant differences in the prevalence of missing data mistakenly included as valid for the treatment and control groups using the Mathematica weights (which were constructed while treating the miscoded 99 cases as valid data). In particular, students in the treatment group are nearly one-third or 2.1 percentage points more likely to have 99 values on the baseline reading test (although this difference is not statistically significant at the 5 percent level, p=0.089). Students in the treatment group were less than half as likely or 3.9 percentage points less likely to have 99 values on the year 1 math test (p<0.01). Finally, treatment group students were 1.9 percentage points more likely to have invalid 99 reading scores in year 3 (p=0.054). As Panels C and D in Table 1 make clear, our inverse propensity score weights thoroughly account for these differences.

Table 2 indicates that our inverse propensity score weighted data (which both exclude the 99s and use our weights) are well balanced across the treatment and control groups. They are balanced on the following measures: child’s gender, race/ethnicity, gifted or special education status, the family’s annual income being low, whether the family speaks English at home, maternal years of schooling, whether the mother works full time, whether the mother was born in the U.S., whether the family receives some form of public assistance, whether the family has lived in their house for at least one year, and whether the mother is Catholic. Non-response to these questions was quite low, and the only variable with more than 10 percent of the observations missing information was whether the mother was U.S. born (in the 50 states or DC, but not Puerto Rico), with 13.2 percent missing. Checks for whether the share of observations missing this demographic information differed between the treatment and control groups show that the shares were not significantly different.

There are no significant differences between treatment and control observations on either the raw or percentile ITBS scores at baseline, further evidence of balance when our inverse propensity score weights are utilized. These preliminary analyses point to an unintended benefit of our distributional analytic approach. Although similarly detailed preliminary data analyses should arguably be routine standard practice regardless of the analytic method, evaluators who are interested exclusively in mean treatment effect estimation may inadvertently overlook such out of range scores, if they simply compare of means and standard deviations to demonstrate balance between treatment and control groups.

Methods

The analyses that follow take advantage of randomized assignment into the treatment and control groups in the New York City voucher experiment to estimate the mean effect of the voucher offer as well as its effect on the distribution of student achievement. The potential outcomes model provides a framework for estimation of the effects of a treatment. Each individual i has two potential outcomes, Y_1i and Y_0i (for our purposes, a test score). Person i has outcome Y_1i if assigned to the treatment group and outcome Y_0i if assigned to the control group. D(i) denotes the group that person i is assigned to in a randomized experiment. If person i is assigned to the treatment group, then D(i) = 1, and if person i is assigned to the control group, D(i) = 0; the treatment effect on person i is defined as d_i=Y_1i − Y_0i.

Quantiles, Average Treatment Effects, and Quantile Treatment Effects

Let Y be a random variable with a cumulative distribution function (CDF) F(y), where F(y) = Pr[Y ≤ y]. Then, the qth quantile of the distribution F(y) is defined as the smallest value y_q such that F(y_q) is at least as large as q (e.g., y_0.5 is the median). Now consider two (marginal) distributions F₁ (the CDF for the potential outcomes if D = 1), and F₀ (the CDF for the potential outcomes if D = 0). We define the difference between the qth quantiles of these two distributions as y_q = y_q1 − y_q0, where y_qd is the qth quantile of distribution F_d.

The joint distribution of (Y_0i,Y_1i) is not identified without assumptions. However, if program assignment is independent of the potential outcomes, the difference in means, or average treatment effect, d = E[d_i] = E[Y₁] − E[Y₀], is identified because each expectation requires only observations from one of the two marginal distributions. Similarly, identification of the marginal distributions implies identification of the quantiles y_qd, and thus identification of the differences in their quantiles, y_q = y_q1 − y_q0. In this experimental setting, the quantile treatment effect (QTE) is the estimate of this difference in a particular quantile of the two marginal distributions. For example, we consistently estimate the QTE at the 0.50 quantile by subtracting the control group’s sample median from the treatment group’s sample median. Graphically, QTE estimates are the horizontal differences in the CDFs of the outcome for the treatment and control groups at various percentiles.

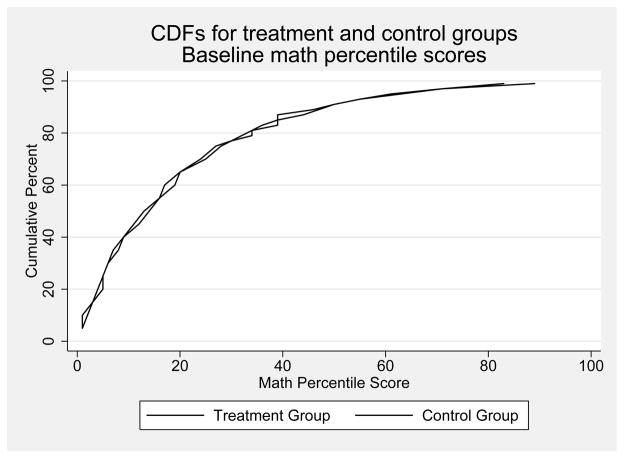
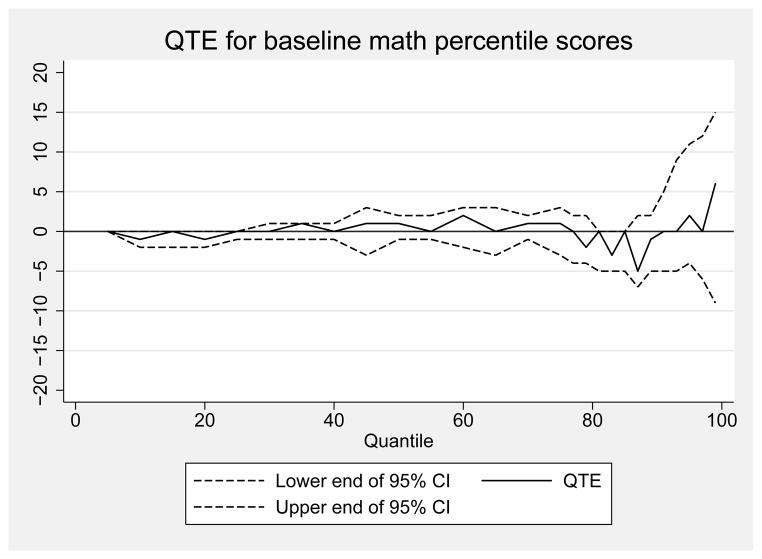
As an example, we show the CDFs and QTE for the baseline math NPR scores in Figures 2 and 3. Figure 2 shows the CDFs for the baseline math scores in the treatment and control groups. The horizontal distance between these CDFs at each point in the distribution is the quantile treatment effect (QTE) at that point or quantile. Figure 3 translates the horizontal differences in the CDFs to a QTE plot, showing the QTE (y-axis) for baseline math NPR scores at each percentile (x-axis), along with 95% confidence intervals (dashed lines), calculated by bootstrapping families with replacement within strata. Figure 3 shows that the bulk of the QTE point estimates are zero or close to zero for the baseline scores, and even when they are not, the pointwise confidence intervals clearly include zero. These QTE estimates indicate that the New York City voucher data are well balanced on baseline achievement after addressing weighting and missing data issues.

Figure 2.

Cumulative distribution functions (CDFs) of math National Percentile Rankings for the treatment and control groups for the baseline year

Notes: Figure shows cumulative distribution functions for baseline math National Percentile Ranking scores from the Iowa Test of Basic Skills separately for the treatment (voucher offer) and control (no voucher offer) groups. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Figure 3.

Quantile treatment effect estimates of the impact of a voucher offer on math National Percentile Rankings at baseline

Notes: Figure shows QTE for the effect of being offered a voucher for private school on baseline math National Percentile Ranking scores from the Iowa Test of Basic Skills. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research. Baseline scores unavailable for kindergarten students.

Findings/Results

Revisions to previous mean treatment effect estimates

Since our preliminary analyses indicate that previous analyses using data from the New York City voucher experiment included a substantial amount of miscoded missing data, we begin by reconsidering the mean effect of the New York City voucher experiment. The first column of Table 3 summarizes results drawn from Table 3b Panel 3 of the Krueger and Zhu (2004a) mean effect analyses, which includes students who scored zero on the ITBS National Percentile Ranking/99 on the raw test as non-missing cases. Their analysis indicated that the New York City voucher offer had no effect on average on student mathematics or reading achievement in any of the study’s three years. In the second column of Table 3, we report our replication of the Krueger and Zhu analyses, again including students with zero percentile scores on the ITBS as non-missing cases. We are able to replicate the Krueger and Zhu coefficients precisely, with only minor differences in the standard errors that do not affect the (lack of) significance of the coefficients (these occur because we are constructing standard errors after bootstrapping families within strata while they use another method).

Table 3.

Effect of excluding “missing data” values on mean treatment effects reported in Krueger and Zhu (2004a)

		Using Mathematica weights	Using our inverse p-score weights
	K&Z estimates	Our replication	Our estimates
	0s included	0s included	0s excluded
Panel A: Effects for full sample, math National Percentile Rankings
Year 1	0.17 (1.34)	0.17 (1.38)	−0.88 (1.05)
Year 2	−0.69 (1.40	−0.69 (1.37)	−1.29 (1.15)
Year 3	0.23 (1.35)	0.23 (1.28)	−0.004 (1.18)
Panel B: Effects for full sample, reading National Percentile Rankings
Year 1	−0.84 (1.25)	−0.84 (1.32)	−1.79 (1.09)
Year 2	0.41 (1.30)	0.41 (1.26)	0.22 (1.16)
Year 3	−0.73 (1.26)	−0.73 (1.32)	0.52 (1.13)

Notes: Table reports original results from panel 3 of Table 3B of Krueger and Zhu (2004a), our replication of these results, and then shows the impact of excluding the 0 percentile values (which are invalid percentiles corresponding to the 99 raw scores) and using inverse propensity score weights as an alternative to the non-response adjusted weights provided with the Mathematica data. Dependent variable is the math (Panel A) or reading (Panel B) National Percentile Ranking scores from the Iowa Test of Basic Skills in the spring for years 1–3 of voucher distribution. Regressions also control for dummies for the strata in the initial sampling. Estimates in column 2 use the Mathematica provided non-response weights, while those in 3 use our inverse propensity score weights. The p-score weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, dummies for missing demographics, dummies for invalid scores or missing scores, dummies for strata (sample design) and grade at baseline, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

In the third column of Table 3, we report our estimates of the mean effects of the New York City voucher offer, estimated with out of-range values set to missing and using our inverse propensity-score weights. The results reported in the third column of Table 3 are similar to the results in the prior two columns, indicating that the New York City voucher program had no mean effect on math or reading achievement in any of its three years. This finding suggests that the inclusion of data from students who were actually missing data on the ITBS due to 99s but had a National Percentile Ranking score of 0 changed point estimates but did not lead to substantively different conclusions about the lack of a statistically significant mean effect of receiving a voucher in the New York City experiment. This third column most accurately captures the true effect of the New York City voucher offer, since these Column 3 results do not assume that students who were missing ITBS scores but were coded as 99s would have scored that the very bottom of the test’s distribution, and the relevant weights balance attrition between the treatment and control groups.

Previous work by Mayer et al. (2002) is not replicable with our restricted use data given that weights have been changed since Krueger and Zhu discovered they were being calculated incorrectly. However, given Krueger and Zhu’s ability to replicate Mayer et al.’s results and our ability to replicate the Krueger and Zhu results only while including the zeros, it seems very likely that results from Mayer and colleagues in their 2002 paper and in their 2003 reply to Krueger and Zhu also include respondents with out-of-range zero ITBS scores in their analyses.

Finally, an additional set of papers, Jin and Rubin (2009) and Jin, Barnard, and Rubin (2010) also use the NYC voucher data in their analyses. Jin, Barnard, and Rubin do not present any basic descriptive statistics that reveal how they handled the missing data, but Jin and Rubin do. Their Figure 1 presents box-and-whisker plots of pre-test scores and year 3 post-test scores of “complete cases” [their term] using the sum of the normal curve equivalent (NCE) math and reading scores. Near replication of these plots is only possible if the NCE scores of zero are treated as valid scores. Once excluded, the mean NCE score increases from 28.7 to 32.2 in reading and 22.7 to 27.6 in math at baseline and 32.6 to 33.7 in reading and 32.5 to 33.8 in math on the year 3 post-test. This suggests that results from Jin and Rubin, and possibly also Jin, Barnard, and Rubin, include out-of-range test scores as valid data.

In sum, while our re-analysis corrects a data problem with earlier analysis of NYCSCP data, our findings are substantively consistent with earlier findings: the NYCSCSP had no mean effect on student math achievement overall (Howell et al. 2002; Krueger & Zhu 2004a, 2004b).¹⁰ In supplementary analyses, we consider the consequences of our corrections for the debate about whether the New York City voucher experiment has a disproportionately positive effect for African-American students. While these analyses, reported in Appendix Table 3 and discussed in Appendix A, do not resolve this dispute, they do draw attention to the considerable skills overlap between racial categories and across various codings of African American in this sample.

Quantile treatment effect estimates

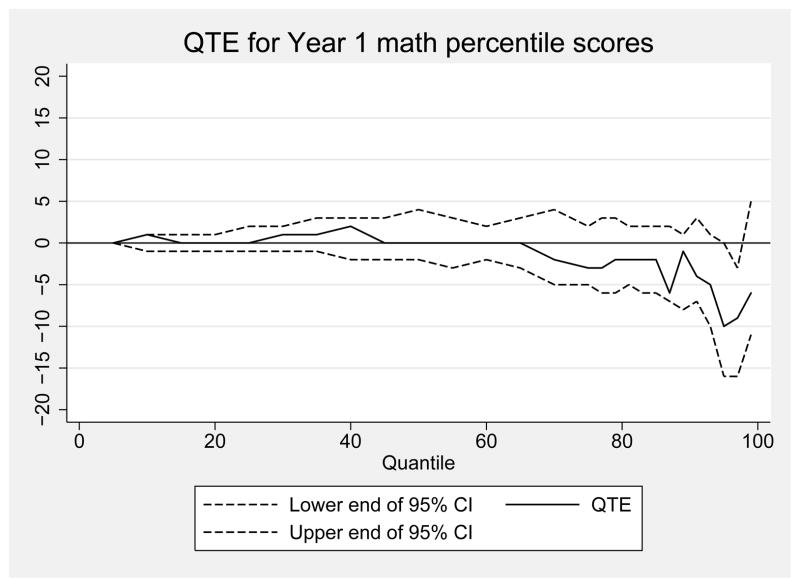
Having established that the voucher program had no mean effect on student achievement, we next turn to the QTE, which provides an estimate of the effect of voucher receipt on the distribution of student achievement. Figure 4 shows the QTE for NPR math scores as of spring of the first year, Figure 5 shows NPR math scores for the spring of the second year, and Figure 6 shows NPR math scores for the spring of the third year. In each of these QTE plots, the horizontal differences between the cumulative distributions of math NPR scores (y-axis) are plotted as a function of the percentile of the distribution at which this difference is calculated (x-axis). Thus, the x-axis ranges from 1–99 (measuring percentiles), and the y-value at each percentile q from 1–99 is the difference between the qth quantiles of the treatment and control groups. This difference represents the horizontal distance between the two CDFs for treatment and control.

Figure 4.

Quantile treatment effect estimates of the impact of a voucher offer on math National Percentile Rankings for the first year after random assignment

Notes: Figure shows QTE for the effect of being offered a voucher for private school on math National Percentile Ranking scores from the Iowa Test of Basic Skills in the spring after the first year of voucher distribution. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Figure 5.

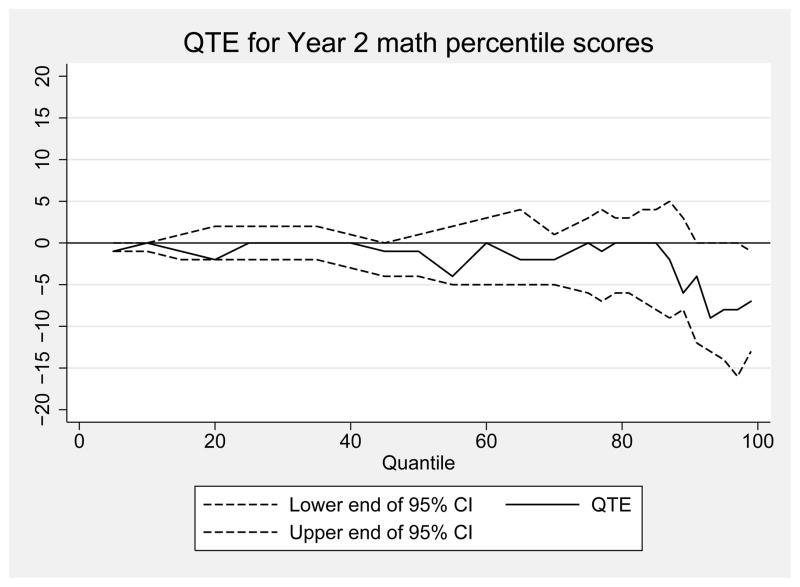
Quantile treatment effect estimates of the impact of a voucher offer on math National Percentile Rankings for the second year after random assignment

Notes: Figure shows QTE for the effect of being offered a voucher for private school on math National Percentile Ranking scores from the Iowa Test of Basic Skills in the spring after the second year of voucher distribution. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Figure 6.

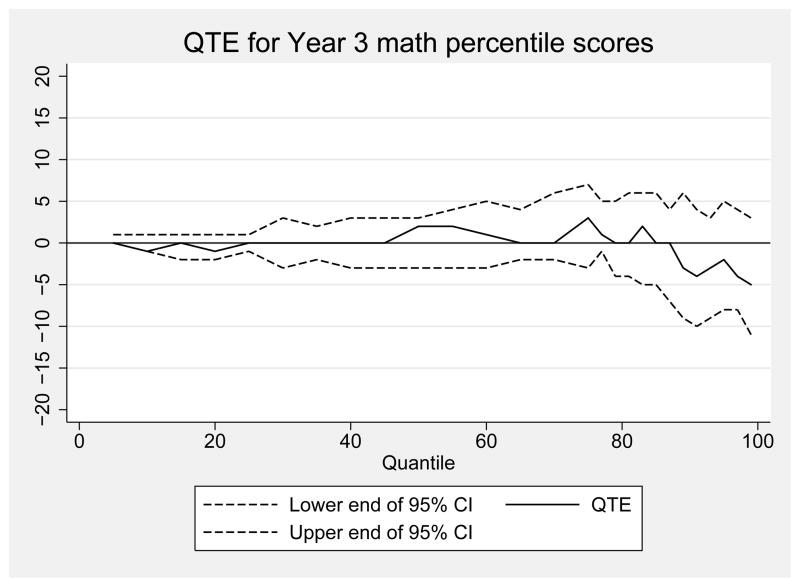
Quantile treatment effect estimates of the impact of a voucher offer on math National Percentile Rankings for the third year after random assignment

Notes: Figure shows QTE for the effect of being offered a voucher for private school on math National Percentile Ranking scores from the Iowa Test of Basic Skills in the spring after the third year of voucher distribution. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Figure 4 shows the QTE for differences in math outcomes in year 1. For most of the distribution, there are few test score differences between the percentiles of the test scores of the voucher-offer group and the control students, as the solid line rarely deviates from the zero. This solid line shows the difference between the math scores of the treatment and control children at each percentile. For example, the 25^th percentile treatment score is 6 and the 25^th percentile control score is 6, leading to a difference of zero NPR points, and the 75^th percentile treatment score is 34 and the 75^th percentile control score is 37, leading to a difference of −3 NPR points. Figure 4 shows that the difference between the percentiles of the treatment and control students’ math score distributions remains fairly consistently close to zero. However, at the very top of the distribution, the difference between the treatment and control students’ test distributions becomes larger and negative. For example, the 91^st percentile treatment score is 56 and the 91^st percentile control score is 60, leading to a difference of −4 NPR points, and the 97^th percentile treatment score is 75, the 97^th percentile control score is 84, and the difference is −9 NPR points. This difference is significant at the 5 percent level at the 97^th percentile, where the confidence interval falls below the zero line, but it is not significant at even the 10 percent level for any other percentile, even though the treatment control difference indicated by the solid line is as low as −10 at the 95^th percentile. Thus, for the bulk of the distribution of achievement in math, effects are zero, and we can rule out effects larger than 5 percentile points at the 10 percent level for all but a small share of the distributions.

Figure 5 shows the QTE for math NPR scores at the end of year 2. As in year 1, there are few differences between the distribution of math scores for treatment and control students in year 2. The solid line showing the treatment and control differences is at or near zero, or negative but not significant at even the 10 percent level, for most of the distribution. At the 93^rd percentile, the difference between the quantiles of the treatment and control distributions is the largest, at −9, but it is not significant at the 5 percent level as the confidence interval includes zero.

Figure 6 shows the QTE for math NPR scores at the end of year 3. Differences in year 3 math scores are even less pronounced than in years 1 and 2. For most of the distribution, the solid line displaying these differences is very near to the zero line--the difference between treatment and control scores is −1, 0, or 1 percentile point for most of the distribution. Unlike estimates from earlier years, the point estimates in year 3 are positive at several points in the middle of the distribution. Furthermore, there are some larger treatment and control differences above the 89^th percentile, with the largest, negative difference of −5 occurring at the 99^th percentile. However, none of these differences is statistically significant, and overall Figure 6 suggests that whatever negative effect emerged in the first two years has reverted to zero by the third year.

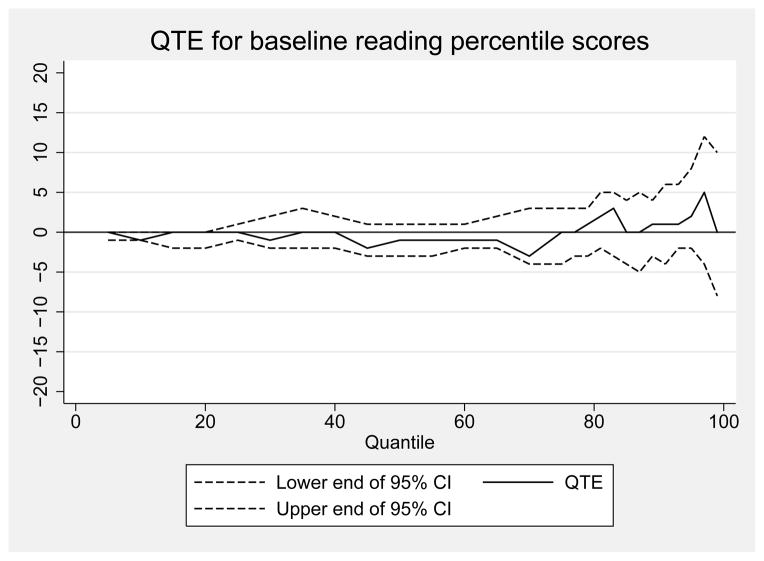
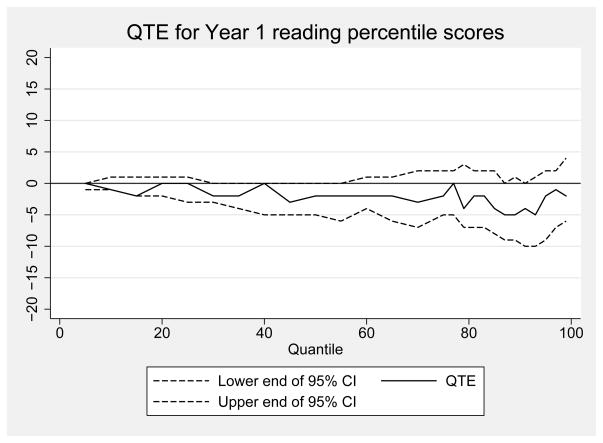
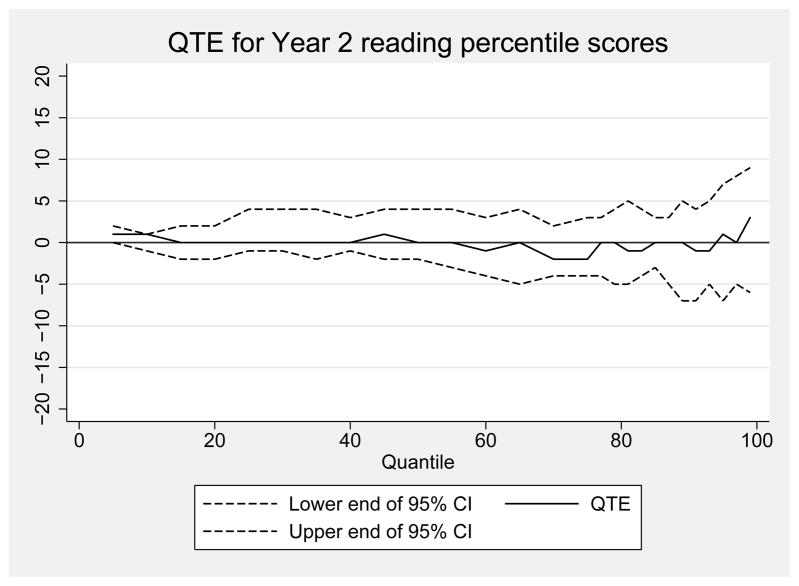
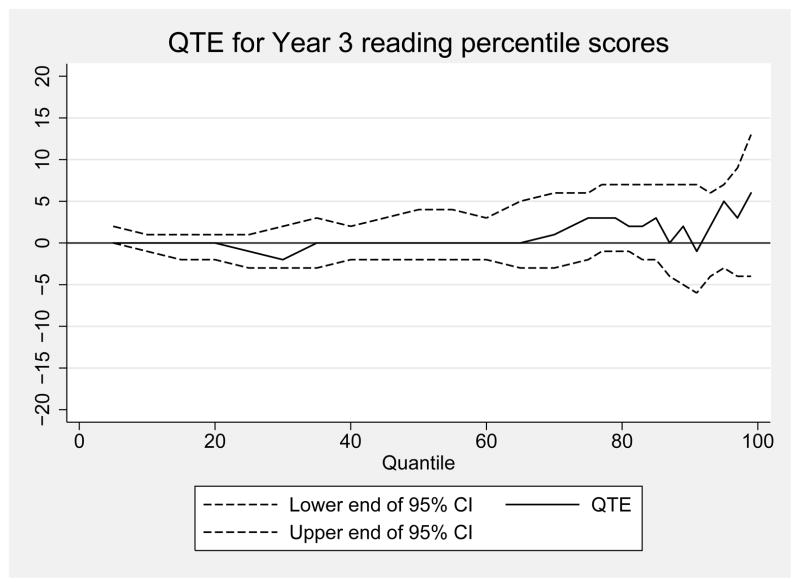
We also estimated QTE using the same approach for reading at baseline and in years 1 through 3. These results are reported in Appendix Figures 1 through 4. In each of the three treatment years, the test score differences between treatment and control were at or near zero for the entire distribution. At no point in any year were these differences larger than three percentage points and at no point were the differences statistically significant. Visual inspection of these figures indicates that the voucher effect on the distribution of student reading achievement grows more positive over time, particularly at the top of the distribution. However, none of these point estimates are statistically significant.

One might be interested in supplemental instrumental variables QTE analyses that consider the effect of enrolling in private schools on the distribution of achievement, but we note that the reduced form QTE estimates above for this analysis are small and statistically indistinguishable from 0 across the distribution, which implies the IVQTE should also be zero.

External validity: Considering the NYC Voucher Recipients in Context

These findings suggest that the NYC voucher experiment had no mean effect as well as no effect on the distribution of student achievement. At first glance, these findings seem to align closely with the predictions of the no-effects hypothesis. Before making this conclusion, however, it is important to consider the extent to which the distribution of achievement for students in the NYC voucher experiment reflects the distribution of students who might be eligible for vouchers if a similar school choice policy were implemented nationwide. Figure 7 places the NYC voucher program participants in the broader context of elementary school achievement across the United States by comparing the frequency of scores at various percentiles of the national distribution for baseline math for students in both the treatment and the control groups of the NYC voucher experiment with the frequency of math achievement scores for all students in the nationally representative Early Childhood Longitudinal Study, Kindergarten Cohort (ECLS-K) who attend Catholic schools as well as all ECLS-K students who come from low-income homes.¹¹ This comparison illustrates in part the stark educational disadvantage that students who were eligible and applied for the NYC voucher experiment and other poor youth face. While the achievement distribution for the NYC voucher students at baseline is skewed to the left relative to that of poor youth nationwide, it is skewed even more sharply to the left compared to Catholic school students nationwide. This fact has potentially important implications for interpreting the results of the NYC voucher experiment. While our analyses clearly indicate that this treatment had no effect for this set of students in the lower part of the skill distribution, it provides little grounds for inference regarding the effects of voucher programs on a more nationally representative student population of possible applicants for vouchers. Since the NYC voucher study includes few students above the middle of a broader test score distribution, we cannot make strong statements about the likely effects of vouchers on students at the top of a broader distribution although one also wonders the extent to which such a group would respond and apply for a $1400 per year voucher. Distributional analyses of less strictly means-tested voucher programs, such as the statewide programs operating in Indiana, Florida, and Georgia, may thus produce very different findings higher up in the achievement distribution.

Figure 7.

Histogram of scores falling at various points in the overall national distribution for a national sample of low-income children in public schools (ECLS-K Spring 1st and 3rd), all children in Catholic schools (ECLS-K Spring 1st and 3rd), and New York City School Choice Scholarships Program children at baseline in 1st, 2nd, 3rd and 4th

Notes: Figure shows histogram of percentiles of from the ELCS-K overall public school distribution among poor kids (income low enough for free lunch or on welfare) and for all Catholic school attendees in Spring of first and third grades and well as percentiles of the National Percentile Ranking from the ITBS for the pre-tests for grades 1, 2, 3, and 4 from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research. Baseline scores unavailable for kindergarten students in NYCSCSP and scores for end of second grade unavailable in the ECLS K. Statistics weighted to reflect non-response and complex sampling.

Discussion

Our findings suggest that the NYC voucher experiment had little effect across the distribution of student achievement, with the possible exception of small negative effects in math in a small region near the top of the distribution of students who sought vouchers, which fade out over time. This may not be so surprising given the size of the intervention, although the offer had a very large effect on take-up of private school.

These small distributional findings mostly disconfirm both the Common School and Stratifying hypotheses. To the extent that vouchers are used to attend schools with a common curriculum, this seems to have had none of the anticipated positive effects for low-achievers. Similarly, our analyses provide little evidence to suggest that voucher receipt had a stratifying effect on the distribution of student achievement among voucher applicants by boosting achievement at the top of the distribution in the experiment. Indeed, we find some evidence that high-achievers (relative to the average achievement in the experimental sample) may have experienced some small penalties in mathematics from the voucher offer. Overall, the distributional findings are most consistent with our third hypothesis, that vouchers (at least of this magnitude) have no positive or negative effect for the vast majority of students to whom they were offered.

Put in the context of other interventions, such as KIPP or charter schools, perhaps these null-effects findings are not surprising. These interventions have significant impacts, but at much greater expense. For example, evaluations of KIPP Lynn in Massachusetts found that a year of enrollment in KIPP resulted in average effects of 0.35 SD in math and 0.12 SD in reading, with the students entering KIPP with the lowest baseline scores experiencing the largest effects (Angrist et al. 2010). Experimental evaluations of New York City and Boston charter schools found more modest effects on student achievement. In New York, the average effects were 0.09 SD in math and 0.065 SD in reading (Hoxby, Murarka, and Kang 2009). In Boston, the average effects were 0.18 SD in math and 0.09 SD in reading (Abdulkadiroglu et al. 2011). These results, which come from programs that were considerably more comprehensive than the vouchers we evaluate, likely serve as an upper bound on the possible achievement impacts that we might have observed. While the vouchers cost $1,400 per child, a year of enrollment at KIPP costs approximately $13,000 per student at some of the east coast KIPP schools (Angrist, Dynarski, Kane, Pathak, and Walters 2012). Unfortunately, we lack data on the quality of schools that treatment and control students attended, but given the size of the voucher, it seems unlikely that many voucher recipients attended resource-rich, high-quality private schools. Thus, perhaps it would take a much larger financial investment to see effects that are comparable to a program like KIPP.

Furthermore, temporary negative effects associated with moving schools may depress short-term effects of voucher experiments. We also lack the data to test this possibility over the long run, since the NYC voucher experiment only provides us with three years’ worth of post-test data. However, we note that our point estimates of voucher effects tend to be more positive in the third year after voucher receipt than in the first two years, especially at the top of the distribution. While not statistically significant, these later year positive results are interesting in light of recent evidence suggesting that vouchers have positive long-term effects on educational attainment (Chingos & Peterson 2013; Wolf et al. 2013).

Despite these nearly null distributional findings, examining the New York voucher data with a distributional lens yielded other important information that would not have otherwise been discovered. We uncovered unusually large concentrations of test score responses with a raw score of 99 and an NPR or NCE score of 0 when early results returned unbelievably large group differences at the tails of the distribution. Only when we included the observations with these missing data codes in our analyses were we able to replicate previously published analyses of these data. While excluding these codes does not change the substantive conclusions from previous results, it reduces the magnitude of even the most favorable previous findings.

Similarly, our analyses draw attention to the unique challenges faced by the students who qualified for and entered into the NYC voucher lottery. While the 20,000 students who entered into the NYC voucher lottery represent a non-trivial proportion of the age- and income-eligible youth in the New York City public schools, the distribution of achievement for these students is truncated and skewed to the left compared to the distribution of achievement for all students nationwide. This is in part by design: The NYC voucher experiment (like many other similar social interventions) was explicitly targeted at highly disadvantaged youth in low-achieving schools. Since many arguments both in favor of and against vouchers relate to their presumed effects for similar inner-city low-income students (Peterson 2000; Schmoke 1999), this focus is appropriate. Our finding that the voucher offer has no achievement effect for students at any point of this sample’s truncated achievement distribution is highly policy relevant since it speaks directly to these arguments.

However, viewing this sample’s achievement distribution against the achievement distribution for all U.S. youth makes it clear the somewhat limited extent to which results from this study generalize. Since the students in the New York City voucher experiment sample are clustered predominantly in the lower half of the national test score distribution, this study provides little information about potential voucher effects on higher-achieving students who would apply for vouchers. It also raises a broader point, that if no one in a given test score range would take-up an offer of a voucher of a particular size, no voucher experiment can be informative about effects in that range. This limitation applied to earlier analyses of the voucher intervention’s mean effects and its effects on subgroups, as well as evaluations of other interventions that are targeted at high-poverty inner-city populations (i.e., Angrist et al.’s evaluation of KIPP schools and Dobbie, Fryer and Fryer’s evaluation of the Harlem Children’s Zone). However, this is not always well recognized, in part because many of these evaluations typically focus on mean effects in standard deviation terms. In addition to taking the compressed achievement distribution into account when analyzing data from highly targeted social experiments, it will be important for future researchers to apply distributional analysis techniques to evaluations of educational interventions in more representative contexts.

In sum, this paper seeks to familiarize researchers with distributional analytic techniques. Given the importance of equity considerations in educational policy discussions, we argue that QTE are essential parameters for the evaluation of virtually any educational intervention. While these parameters do not substitute for mean effect analyses or analyses that look for heterogeneous effects on observable subgroups, they provide a new way for thinking about the effects of intervention on the distribution of educational achievement. Our distributional analysis of the New York City voucher experiment shows that the offer of a small voucher did little to influence student achievement. The possible exception is a small negative effect for a small group of high-performing students after the first two years of the program, but not after the third. The distributional approach taken here provides additional evidence suggesting that vouchers have a limited impact on student achievement. In addition, this distribution approach provides new insights into the data quality and context, which promise to enrich a broad range of educational evaluations.

Appendix A

One important point of contention in prior analyses of the NYC voucher experiment involves variation in the effect of the voucher offer by race and ethnicity. Several studies find that the voucher offer had a small positive effect on the academic achievement of African-American recipients (Barnard, Frangakis, Hill, & Rubin, 2003; Howell, Wolf, Campbell, & Peterson 2002; Peterson and Howell, 2004). However, subsequent analyses suggest that the observed effects for African Americans are sensitive to the definition of racial and ethnic categories and hold only when controlling for students’ initial characteristics while omitting students without baseline scores (Krueger & Zhu, 2004a, 2004b).

This debate is potentially consequential in two regards: first, evidence of a unique positive voucher effect for African-Americans may point toward a strategy to mitigate persistent and troublesome black-white test score gaps. Second, several analysts have suggested that evidence of a unique positive voucher effect for African-Americans is consistent with the idea embedded in the “common school” hypothesis that vouchers may be particularly beneficial for students at the bottom of the skills distribution.

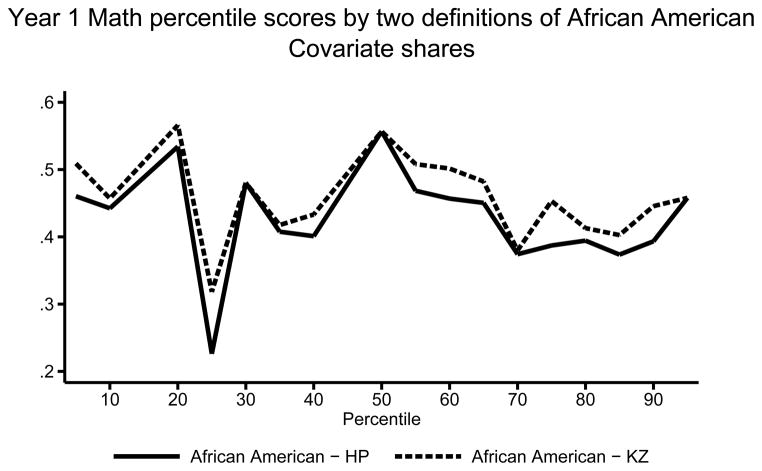
In this appendix, we reconsider the evidence regarding the extent to which NYC voucher offer effects vary by student race and ethnicity in light of the invalidly coded as 99 missing data we found and associated weighting corrections that we have implemented. In doing so, we note that it is important to consider several distinctive characteristics of the NYC voucher experiment sample. By design, all of the students who participated in the NYC voucher experiment were from low-income families in New York City. As Table 2 makes clear, the vast majority of these students were black or Hispanic. Within these racial categories, however, lies a great deal of ethnic heterogeneity. 15 percent of students identified as African-American come from immigrant families, with origins primarily in the Caribbean. Similarly, the Hispanic category includes Puerto Rican and Dominican students (many of which may be phenotypically black). This heterogeneity helps to explain the debates concerning the definition of African Americans in these data. While Howell and Peterson categorize only students whose mother indicated her race at baseline as African American as African-Americans, Krueger and Zhu additionally categorize children as African American if their mother indicated her race was African American in a subsequent data collection wave, if the mother indicated her race was other but wrote in some combination of Black/African American and something else as her race (e.g., Black/Hispanic), or if the father indicated his race was African American in the baseline wave. Our analyses indicate that these definitions likely yield common racial categorizations for 90 percent of students in the sample, but disagree for 10 percent of students in the sample.

Appendix Table 3 summarizes the consequences of these questions of racial categorization for estimating the effect of the NYC voucher experiment on African-American students’ mathematics achievement. In the first model of Panel 1 (column 1), we replicate Howell & Peterson’s estimates of the treatment effect for African-Americans (point estimates are identical, SEs nearly so, differing due to our use of bootstrapping by family within strata for SEs). This analysis indicates that the voucher offer significantly improved black student math achievement in the study’s first and third years. (This analysis yields a positive, but not statistically significant, treatment effect for black students in Year 2.) Similarly, in the first model of Panel 2 (column 1), we attempt to replicate Krueger and Zhu’s racial categorization scheme to estimate of the effects of the voucher offer for African-Americans. While this replication is not perfect (our sample sizes are 1 observation off from their reported sample sizes),¹² it returns an estimate of the African-American treatment effect that is very close to Krueger and Zhu’s published findings. Using the Krueger and Zhu definition of African-American and also treating the 99s as valid percentile scores of 0, we find a positive and significant treatment effect on Math scores in Year 1, but no effects in subsequent years.

The subsequent models (columns) in Appendix Table 3 consider the extent to which these findings are sensitive to corrections for out-of-range values on the ITBS and associated non-response weighting. Model 2 replicates both analyses with a sample that excludes students who have out-of-range values on the ITBS but uses the original MPR weights; Model 3 replicates the Howell and Peterson and Krueger and Zhu analyses on the original sample (including students who have out-of-range values on the ITBS as non-missing zeros) with our inverse propensity score weights (which ensure the incidence of missing data and invalid 99s is balanced as well as adjust for other non-response); and model 4 replicates both analyses with a sample that excludes students who have out-of-range values on the ITBS and uses our inverse propensity score weights.

We focus particular attention on the results reported in Model 4, since we believe that this model most thoroughly accounts for missing data and attrition by both excluding the invalid 99 scores and balancing attrition due to missing or invalid scores across the treatment and control groups using our inverse propensity-score weights. In most cases, these analyses return estimates of the effect of the NYC voucher offer for African-Americans that are between 36 and 99% of the magnitude of the Howell & Peterson estimates and between 41 and 74% of the magnitude of our replication of the Krueger and Zhu estimates. Using the Howell & Peterson definition, the Model 4 analysis returns a significant positive treatment effect for African-Americans for math in Year 3, but not in other years. Using the Krueger and Zhu definition, Models 2, 3, and 4 return no significant treatment effects for African-Americans for math.

Elsewhere, analysts have viewed this evidence pointing to a unique positive and significant voucher effect for African-Americans as an indication that vouchers may have unique positive consequences for students at the bottom of the skill distribution. However, a distributional analysis suggests that this interpretation may be misleading in the context of the NYC voucher data. In Appendix Figure 5, we show that the blacks (and because the sample is nearly entirely blacks and Hispanics, also Hispanics) are relatively evenly located across the overall baseline test score distribution. The x-axis in Appendix Figure 5 represents the percentiles of the overall baseline test score distribution for the control group. The y-axis denotes the share of the observations that are black that are located between the qth percentile and the q+1^st percentile at which we calculated the QTE, using either the Howell and Peterson or the Krueger and Zhu definitions of African American. So, if these lines were horizontal, it would be equivalent to the statement that the blacks are uniformly distributed across the baseline score distribution for both definitions. As Appendix Figure 5 indicates, black students are distributed approximately evenly across the overall test score distribution in the NYC voucher data. This finding may not be particularly surprising, given the fact that all participants in this study are low-income New York City youth. However, it represents an important piece of context to consider in interpreting evidence of heterogeneous effects in this experiment.

Appendix Figure 1.

Quantile treatment effect estimates of the impact of a voucher offer on reading National Percentile Rankings at baseline

Notes: Figure shows QTE for the effect of being offered a voucher for private school on baseline reading National Percentile Ranking scoress from the Iowa Test of Basic Skills. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research. Baseline scores unavailable for kindergarten students.

Appendix Figure 2.

Quantile treatment effect estimates of the impact of a voucher offer on reading National Percentile Rankings for the first year after random assignment

Notes: Figure shows QTE for the effect of being offered a voucher for private school on reading National Percentile Ranking scores from the Iowa Test of Basic Skills in the spring after the first year. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Appendix Figure 3.

Quantile treatment effect estimates of the impact of a voucher offer on reading National Percentile Rankings for the second year after random assignment

Notes: Figure shows QTE for the effect of being offered a voucher for private school on reading National Percentile Ranking scores from the Iowa Test of Basic Skills in the spring after the second year. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Appendix Figure 4.

Quantile treatment effect estimates of the impact of a voucher offer on reading National Percentile Rankings for the third year after random assignment

Notes: Figure shows QTE for the effect of being offered a voucher for private school on reading National Percentile Ranking scores from the Iowa Test of Basic Skills in the spring after the third year. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Appendix Figure 5.

Share of each one percentile range of control group test distribution that is made up of African American using either the definition of the Mathematica reports or the definition in Krueger and Zhu

Notes: Figure shows the share of each percentile range of the overall control group pre-random assignment math National Percentile Ranking scores from the Iowa Test of Basic Skills at baseline that is made up of African Americans using the Krueger and Zhu and Mathematica report definitions. For example, the value for the 5th percentile is the weighted share of the observations with test scores larger than the 4th percentile of scores but less than or equal to the 5th percentile of scores that is made of African Americans. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Appendix Table 1.

Attrition in the New York City School Choice Scholarships Program

	Math scores			Reading scores
	Year 1	Year 2	Year 3	Year 1	Year 2	Year 3
Panel A: Full sample, T and C
Number randomized	2666	2666	2666	2666	2666	2666
Number with missing test score	586	912	865	586	912	865
Number with valid test score	1977	1626	1734	1995	1697	1743
Number with invalid 99 test score	103	128	67	85	57	58
Panel B: Control group, no offer of scholarship
Number randomized	1292	1292	1292	1292	1292	1292
Number with missing test score	319	504	445	319	504	445
Number with valid test score	904	739	811	929	766	830
Number with invalid 99 test score	69	49	36	44	22	17
Panel C: Treatment group, received offer of scholarship
Number randomized	1374	1374	1374	1374	1374	1374
Number with missing test score	267	408	420	267	408	420
Number with valid test score	1073	887	923	1066	931	913
Number with invalid 99 test score	34	79	31	41	35	41

Notes: Table reports number of observations with valid scores or invalid scores of the total number randomized for whom data are present in the Mathematica restricted use data. Top panel presents total N in data, along with counts of those missing test scores, with valid test scores, and with invalid (99) test scores. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Appendix Table 2.

Private School Attendance in the New York City School Choice Scholarships Program

	Year 1	Year 2	Year 3
Panel A: Control group, no offer of scholarship
Number randomized	1292	1292	1292
Number attending public school	963	846	828
Number attending private school	66	74	98
Number not reporting whether attended private school	263	372	366
Panel B: Treatment group, received offer of scholarship
Number randomized	1292	1292	1292
Number attending public school	352	482	616
Number attending private school	1022	892	758
Number not reporting whether attended private school	0	0	0

Notes: Table reports number of observations reporting whether attended private school by year after random assignment in the Mathematica restricted use data. Panel A reports numbers for the treatment group, and Panel B for the control group. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.

Appendix Table 3.

Effect of excluding “missing data” values on mean treatment effects for African Americans reported in Krueger and Zhu (2004a) using Peterson and Howell or Krueger and Zhu definition of African American

	Using Mathematica weights		Using our inverse p-score weights
	Our replication, K&Z	Our estimates	Our estimates	Our estimates
	0s included	0s excluded	0s included	0s excluded
Panel A: Effects for Peterson & Howell sample of African Americans, math NPRs
Year 1	4.54*** (1.53)	3.65** (1.59)	2.64 (1.42)	2.37 (1.46)
Year 2	2.59 (2.06)	3.03 (2.09)	2.01 (1.67)	2.02 (1.73)
Year 3	4.00** (1.86)	3.38* (1.92)	4.22** (1.73)	3.94** (1.78)
Panel B: Effects for Krueger & Zhu sample of African Americans, math NPRs
Year 1	3.18** (1.53)	2.21 (1.57)	1.41 (1.38)	1.31 (1.41)
Year 2	1.33 (1.97)	1.74 (2.01)	0.48 (1.65)	0.43 (1.72)
Year 3	2.83 (1.76)	2.32 (1.81)	2.33 (1.66)	2.10 (1.70)

Notes: Table reports original results from panel 3 of Table 3B of Krueger and Zhu (2004a), our replication of these results, and then shows the impact of excluding the 0 percentile values (which are invalid percentiles), as well as the impact of using inverse propensity score weights as an alternative to the non-response adjusted weights in the data. Dependent variable is the math (Panel A) or reading (Panel B) National Percentile Ranking scores from the Iowa Test of Basic Skills in the spring for years 1–3 of voucher distribution. Estimates in columns 1 and 2 use the MPR provided weights, while those in 3 and 4 use inverse propensity score weights. The p-score weights are 1/p̂ for treatment observations and 1/(1 − p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test scores. 95% CIs are obtained by bootstrapping families with replacement. Data from the New York City School Choice Scholarships Program evaluation conducted by Mathematica Policy Research.