Classification of pallidal oscillations with increasing parkinsonian severity

Abstract

The firing patterns of neurons in the basal ganglia are known to become more oscillatory and synchronized from healthy to parkinsonian conditions. Similar changes have been observed with local field potentials (LFPs). In this study, we used an unbiased machine learning approach to investigate the utility of pallidal LFPs for discriminating the stages of a progressive parkinsonian model. A feature selection algorithm was used to identify subsets of LFP features that provided the most discriminatory information for severity of parkinsonian motor signs. Prediction errors <20% were achievable using 28 of the possible 206 features tested. For all subjects, a spectral feature within the beta band was chosen through the feature selection algorithm, but a combination of features, including alpha-band power and phase-amplitude coupling, was necessary to achieve minimal prediction errors. There was large variability between the discriminatory features for individual subjects, and testing of classifiers between subjects yielded prediction errors >50%. These results suggest that pallidal oscillations can be predictive biomarkers of parkinsonian severity, but the features are more complex than spectral power in individual frequency bands, such as the beta band. Additionally, the best feature set was subject specific, which highlights the pathophysiological heterogeneity of parkinsonism and the importance of subject specificity when designing closed-loop system controllers dependent on such features.

the pathophysiology of Parkinson's disease (PD) has been associated with a diverse set of changes in firing rate and pattern of individual neurons throughout the basal ganglia (Bergman et al. 1994; Filion and Tremblay 1991; Miller and DeLong 1987). Spectral features of local field potential (LFP) activity have also been associated with PD (Avila et al. 2010; George et al. 2013; Kuhn et al. 2009; Weinberger et al. 2006) and provide a signal modality for translation to chronic human recordings (Rosa et al. 2011) given the signal's relative robustness to changes in the neural interface around the implanted electrodes (Buzsaki et al. 2012). Such LFP-based biomarkers have gained recent attention in the context of aiding the targeting of deep brain stimulation (DBS) implants (Priori et al. 2003; Wong et al. 2009), assisting in the titration of medication (Priori et al. 2004), programming DBS therapies (Yoshida et al. 2010), and diagnosing disease phenotype, monitoring progression of disease, or providing internal feedback for the implementation of adaptive DBS systems (Little et al. 2013; Priori et al. 2013).

Several theories have emerged that suggest changes in individual frequency bands are correlated with severity levels of specific parkinsonian motor signs. Increased activity in the beta band (13–30 Hz) in the subthalamic nucleus (STN) has been correlated with bradykinesia levels (Ray et al. 2008) and in some cases with rigidity (Little et al. 2012). Similar patterns have been found in clinical studies of globus pallidus (GP) (Brown et al. 2004; Silberstein et al. 2003). Tremor activity has been associated with oscillations at the tremor frequency (3–6 Hz) (Reck et al. 2009), in the theta (∼5 Hz) and beta bands (Tass et al. 2010), or in the gamma band (35–55 Hz) (Weinberger et al. 2009) of subthalamic LFPs.

However, other human studies and animal models of PD have challenged these theories through confounding or inconsistent results. For example, the presence of large beta-band oscillations was observed in 100% of one cohort of STN-DBS lead implants (Little et al. 2012), while others showed robust beta peaks in ∼70% of cases (Bronte-Stewart et al. 2009) and other studies have reported beta-band peaks in less than half of all cases (Rosa et al. 2011). In a primate study, Devergnas found increased power below the beta band and decreased power in the beta band in the pallidum and cortex with increasingly more severe parkinsonism in nonhuman primates, but STN beta activity was unchanged (Devergnas et al. 2014). In a similar primate study, Leblois et al. did not see changes in oscillatory activity of pallidal neurons with initial induction of a parkinsonian state, indicating that these beta oscillations may not be causal to the emergence of parkinsonian motor signs (Leblois et al. 2007).

These results among human and animal studies should not be overly surprising given the wide variety of symptomatology within the PD population. In the search for a biomarker of the disease, however, this variability indicates that such an oscillatory feature would not be robust across patients or potentially also over time, rendering it inadequate for clinical applications such as assisted DBS programming or closed-loop DBS therapies. In this study, we used supervised machine learning algorithms to classify parkinsonian severity based on LFP recordings from the pallidum of three nonhuman primates rendered progressively parkinsonian through staged treatments of the dopaminergic cell neurotoxin 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP). We then used feature selection techniques to identify a subset of LFP features whose combination would better classify parkinsonian severity for individual subjects and across the small cohort of subjects.

MATERIALS AND METHODS

Subjects.

The data set was collected from three adult rhesus monkeys [Macaca mulatta; P1 (female, 5.2 kg, 11 yr old), P2 (male, 9.4 kg, 12 yr old), and P3 (female, 8.4 kg, 23 yr old)]. All procedures were performed in compliance with the US Public Health Service policy on the humane care and use of laboratory animals. Study protocols were approved by the Institutional Animal Care and Use Committees at the Cleveland Clinic and the University of Minnesota. Animals were implanted with titanium cephalic recording chambers (Crist Instruments, Bethesda, MD) oriented toward the pallidum and a stainless steel headpost for head fixation (Elder et al. 2005). Animals were rendered progressively parkinsonian through intracarotid (0.2–0.6 mg/kg in 20 ml of solution, ∼15-min infusion) and intramuscular (0.2–0.6 mg/kg, 1–2 mg/ml solution) injections of MPTP. Parkinsonian motor signs were evaluated with a modified Unified Parkinson's Disease Rating Scale (mUPDRS), which was used to rate joint rigidity, akinesia, bradykinesia, tremor, and other parkinsonian signs individually on a scale of 0–3 (Vitek et al. 2012). Subscale scores for the arm and leg contralateral to the cephalic recording chamber were averaged to form the composite score that defined the parkinsonian state (mild: 3–13, moderate: 18–28, and severe: 32–42).

Electrophysiology.

Two epoxy-coated tungsten microelectrodes (impedance 0.8–1.2 MΩ measured at 1 kHz; FHC, Bowdoin, ME) were advanced into the brain with a chamber-mounted multichannel microdrive system (AlphaEPS, AlphaOmega). The pallidum was identified by characteristic firing rates and patterns (Boraud et al. 2002; Filion and Tremblay 1991) and by cross-referencing the electrode location with monkey Cicerone (Miocinovic et al. 2007). Spontaneous neural activity through each microelectrode was band-pass filtered into a LFP channel (0.075–390 Hz), which was sampled at 781.3 Hz and referenced to the recording chamber. In total, 669 paired recordings were made across the three subjects in the naive, mild, moderate, and severe parkinsonian states with at least one microelectrode in the GP (Table 1). The data set was also used in a previous report (Connolly et al. 2015).

Table 1.

Count of pallidal LFP recordings across subjects and parkinsonian states

	P1	P2	P3	Total
Naive	103	118	55	276
Mild	71	51	27	149
Moderate	39	43	75	157
Severe	47	40		87
Total	260	252	157	669

LFP, local field potential.

To justify combining all pallidal recordings for a given subject in a given state, we first tested for differences among power spectra among three groups, globus pallidus externus (GPe; GPe/GPe and GPe/other), globus pallidus internus (GPi; GPi/GPi and GPi/other), and GPe/GPi, based on jackknifing U-statistics (Arvesen 1969) with a Bonferroni-corrected α = 0.05/3 = 0.0167. This method produced a test statistic that was normally distributed with mean of 0 and standard deviation of 1, which means that a statistic with absolute value exceeding 2.128 would indicate that the two populations had different power spectra. For all three comparisons across all subjects and parkinsonian states, the test statistic did not exceed significance at any frequency value. Therefore, we combined the recordings for the analysis.

Feature extraction.

Data processing was performed in MATLAB 2014a (MathWorks, Natick, MA) with custom scripts and the machine learning toolbox. Each 30- to 120-s paired recording was converted into a single bipolar LFP by subtracting the two individual LFPs, removing the common far-field signal contributed by the chamber reference electrode. The multitaper method was used to calculate a spectrogram of the LFP using a 2-s window with 10% window steps, resulting in a 1-Hz frequency resolution (Bokil et al. 2010). Time windows containing movement artifacts were visually identified and removed. The spectrogram was averaged over the remaining windows to produce a single power spectral density (PSD) for each paired recording. This PSD was normalized by the power in the frequencies above 5 Hz and excluding 55–65 Hz to account for variability in signal amplitude between recordings. The primary spectral feature set was comprised of the average power in 1-Hz bands from 1 to 58 Hz, 2-Hz bands from 62 to 100 Hz, and 5-Hz bands from 100 to 390 Hz.

An additional feature set was created with phase-amplitude coupling (PAC) in order to capture modulations across frequency bands with parkinsonian severity (Tort et al. 2008). The bipolar LFP was filtered into frequency bands and was Hilbert transformed into the signal

$$H\left(t\right)$$

. The continuous phase was calculated by taking the angle of signal

$$H\left(t\right)$$

,

$$\varphi \left(t\right)={\tan }^{\text{−}1}\left(\mathfrak{J}\left(H\left(t\right)\right)/\text{ℜ}\left(H\left(t\right)\right)\right)$$

and the continuous amplitude was calculated by taking the magnitude of the signal

$$H\left(t\right)$$

,

$$A\left(t\right)={\left|H\left(t\right)\right|}^{\text{2}}$$

Phase signals spanned frequency bands of base

$$\sqrt{2}$$

from 2 to 2.8 Hz, from 2.8 to 4 Hz, … from 64 to 91 Hz, and from 91 to 128 Hz, and amplitude signals spanned frequency bands from 64 to 91 Hz, from 91 to 128 Hz, … from 256 to 362 Hz, and from 362 to 390 Hz. A modulation index (MI) was calculated for each phase-amplitude pair by parsing the phase signal into 20 bins of 18° width from 0 to 360° and taking the average of the amplitude signal over all time points with corresponding phase in that bin, denoted Ā(ϕ). This distribution of average amplitudes across phase bins was normalized to

$$p=\raisebox{1ex}{$\overline{A}\left(\varphi \right)$}\!\left/ \!\raisebox{-1ex}{${\displaystyle {\sum }_{\varphi }\overline{A}\left(\varphi \right)}$}\right.$$

and the entropy of the distribution was calculated as

$$H=-{\displaystyle \sum _{\varphi }p\hspace{0.17em}\ln \hspace{0.17em}p}$$

The entropy was compared to that of 200 time-shuffled surrogates to calculate a z score. The magnitudes of these z scores were used as a secondary feature set.

Classification.

An unbiased machine learning classifier was used to identify discriminant features of GP LFPs consistent with parkinsonian state. Parkinsonian severity, determined by the mUPDRS on or near the day of each recording, was used to train three classifiers and determine the accuracy of classification results. Linear discriminant analysis (LDA) (Duda et al. 2001), support vector machine (SVM) using a linear kernel (Cristianini and Shawe-Taylor 2000), and SVM using a radial basis function kernel (RBF) were considered as classifiers (Vapnik 2000). SVMs perform binary classification by projecting the feature set into a high-dimensional space in which there exists a linear separation between the two groups. In the space of the original feature set, this separation is called the hyperplane. The classification problem proposed here involves four groups: naive, mild, moderate, and severe. To generalize the binary SVM for this problem, four classifiers were trained to discriminate recordings that were “in” versus those that were “out” of each group (i.e., naive vs. mild, moderate, and severe combined). To use the four SVMs to predict the group of an observation, the score was calculated for each of the four classifiers as the weighted sum of the dot product between the features and the support vectors (positive indicates in group, negative indicates out of group). The observation was predicted to be from the group with the highest score.

Preliminary analysis was done to select the best-performing machine learning algorithm for the pallidal LFP data set. The classifiers were trained to discriminate the parkinsonian state based on the spectral features for all subjects pooled together. The three classifiers were statistically compared with the 5 × 2 cross-validated paired t-test (Dietterich 1998) with a Bonferroni-corrected significance level of α = 0.05/3 = 0.01667. We found that the SVM using an RBF kernel performed significantly better than the SVM using a linear kernel and the LDA. The RBF SVM was used for the remainder of the study.

Classifiers were evaluated with 10-fold cross-validation, where 90% of the data was used for training and the remaining 10% was used for testing, and this was repeated on all ten 10% subsets of data. In addition, the cross-validation was performed 10 times to account for variability in the random selection of the cross-validation subsets. The prediction error was calculated as the number of observations that were classified into the wrong group by the algorithm. The error was summed across the 10 subsets for each cross-validation run, divided by the total number of observations, and then averaged across the 10 repeats. In addition, the sensitivity of the classifier in categorizing each group was calculated as

$$Se=\frac{\text{true}\hspace{0.17em}\text{positive}}{\text{true}\hspace{0.17em}\text{positive}+\text{false}\hspace{0.17em}\text{negative}}$$

and this value was averaged across the 10 cross-validation repeats. Similarly, the specificity was calculated as

$$Sp=\frac{\text{true}\hspace{0.17em}\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{a}\text{tive}}{\text{true}\hspace{0.17em}\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{a}\text{tive}+\text{false}\hspace{0.17em}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\text{tive}}$$

The entire feature set including both spectral and PAC components contained 206 features. Having a large number of features in comparison to the size of the data set can lead to overfitting of the algorithm and nongeneralizable results. Feature selection was performed to 1) reduce the number of features used for the classification to avoid overfitting and yield a more robust algorithm and 2) identify which particular features were necessary to discriminate parkinsonian severity. The lasso regularization technique with 10-fold cross-validation was used to perform feature selection through least-squares regression with a penalty on the size of the estimated coefficients (Tibshirani 1996). This procedure finds the combination of features that produces the minimum mean-square error (MSE). Lasso regularization was performed separately for the spectral and PAC feature sets. For this study, we selected the feature set containing the minimum number of features with a MSE within one standard error of the minimum possible MSE. New SVMs were trained with the minimum feature set and were compared to the SVMs trained on the entire feature set. Finally, the intersubject variability was probed by training classifiers and testing classifiers on different subjects.

RESULTS

Changes in spectral and PAC features in globus pallidus were inconsistent across subjects.

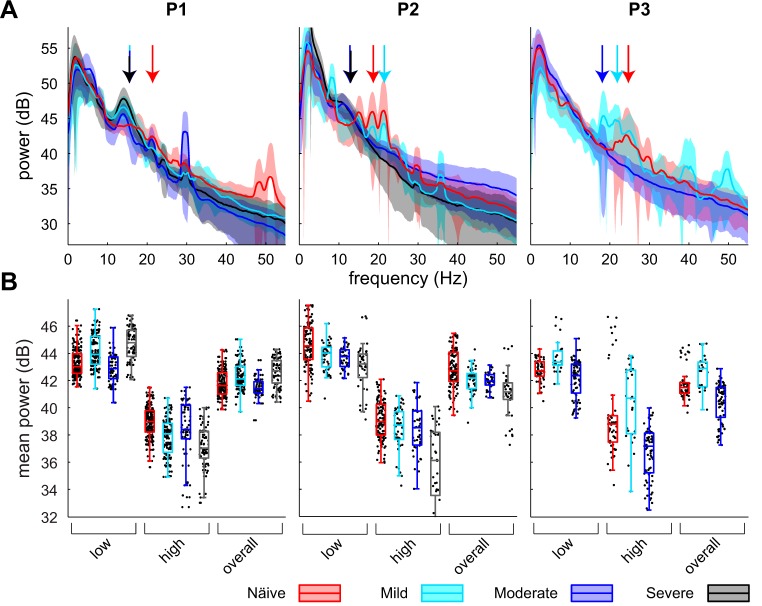
A total of 669 LFPs within the sensorimotor GP were recorded across three nonhuman primates in the naive state and at three levels of parkinsonian severity (Table 1). Beta oscillations were present in the naive state and did not change in amplitude as parkinsonism progressed (Fig. 1). While the amplitude was stable in the overall beta band (11–32 Hz) as well as the low (11–22 Hz) and high (22–32 Hz) beta bands, the peak oscillatory frequency within the beta band shifted to lower frequencies in all subjects as parkinsonian severity increased, and the time point of this change and the median frequency of beta oscillations were found to vary among subjects (Fig. 1, arrows). In subject P1 the median frequency of oscillations in the beta band shifted between the naive and mild states, while in subject P2 the median frequency shifted between the mild and moderate states. Subject P3 demonstrated a shift toward a lower median frequency between the naive and mild states, but the LFPs in the moderate state contained very little beta oscillatory activity. Subject P3 was not carried through to the severe state because of confounding medical complications.

Fig. 1.

A: power spectral densities (PSDs) for each subject across the naive, mild, moderate, and severe parkinsonian states. Solid lines show population means, and shaded areas represent ±1 SD. Arrows indicate median frequency of oscillations in the beta band for the naive, mild, moderate, and severe states. B: boxplots of average power in the low (11–22 Hz), high (22–32 Hz), and overall (11–32 Hz) beta bands across observations for a given subject and parkinsonian state. Black dots represent values for individual observations and are displayed with a jitter on the x-axis for improved visualization.

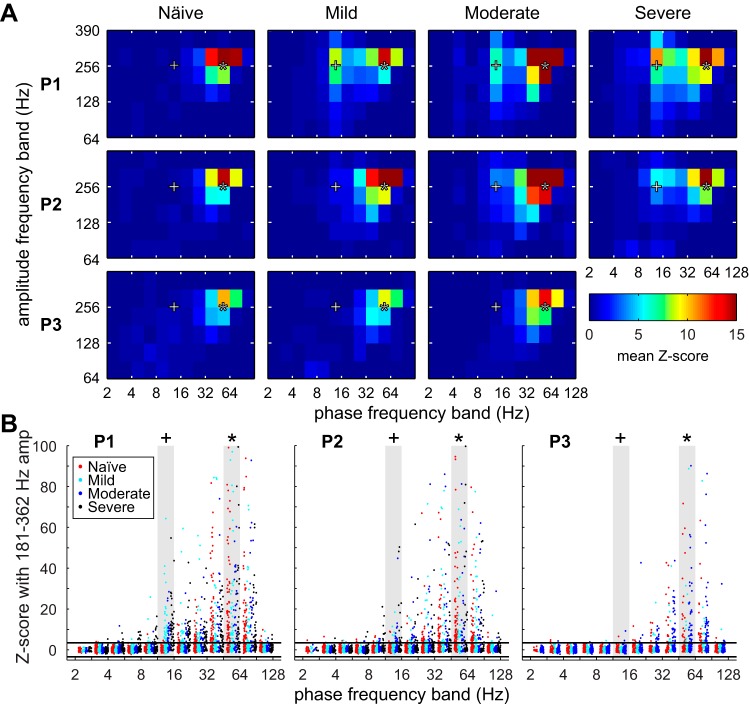
Spontaneous coupling between the gamma phase (45–64 Hz) and high-frequency oscillation (HFO) amplitude (256–362 Hz) existed in all three subjects in the naive state and did not change with severity (Fig. 2A). In two of the three subjects, aberrant coupling between the beta phase (11–16 Hz) and HFO amplitude developed in the mild (subject P1) and moderate (subject P2) states and persisted as severity increased. As parkinsonian severity worsened, the number of recordings with significant beta-HFO coupling increased, but there was still a large proportion of recordings with no significant beta-HFO coupling (Fig. 2B). Subject P3 did not demonstrate strong coupling between the beta phase and HFO amplitude in any state. Neither the spectral nor the PAC analysis revealed a set of biomarkers that obviously discriminated LFPs by parkinsonian severity and was consistent with the features from the other two subjects. Therefore, machine learning algorithms were used to identify the combination of features that best discriminated LFPs by parkinsonian severity on an individual-subject basis in an unbiased manner.

Fig. 2.

Phase-amplitude coupling (PAC) between 12 phase bands and 6 frequency bands. A: z scores were averaged across observations for individual subjects separated by parkinsonian state. z Scores above 3.197 were considered significant at α = 0.05 with Bonferroni correction for the 6 × 12 frequency band pairs. B: scatterplots show the PAC z scores for individual recordings between all phase bands and averaged between 2 high-frequency oscillation (HFO) bands (181–256 Hz and 256–362 Hz). Two phase-amplitude pairs of interest are highlighted, beta phase (11–16 Hz) to HFO amplitude (+) and gamma phase (48–64 Hz) to HFO amplitude (*). Horizontal lines represent a confidence threshold of α < 0.05 with Bonferroni correction.

Support vector machine using a radial basis kernel outperformed other classifiers.

Before investigation of the influence of feature sets and intersubject variability on classification, the proposed machine learning algorithms were tested against each other to choose the best one for this application. The algorithms were trained to discriminate parkinsonian severity based on the spectral features from recordings from all subjects. The LDA performed the worst with 38.47% error, the linear SVM was second with 29.34% error, and the SVM using the RBF kernel performed the best with 24.25% error. With the 5 × 2 cross-validated t-test, the linear SVM did not outperform the LDA after Bonferroni correction (t₅ = 2.8328, P < 0.021475). The RBF SVM outperformed both the LDA (t₅ = 4.8031, P = 0.002145) and the linear SVM (t₅ = 4.3091, P = 0.003625). The linear boundaries in the LDA and linear SVM were not able to discriminate parkinsonian severity as well as the nonlinear hyperplane of the RBF SVM.

Spectral features were more informative than PAC features in globus pallidus.

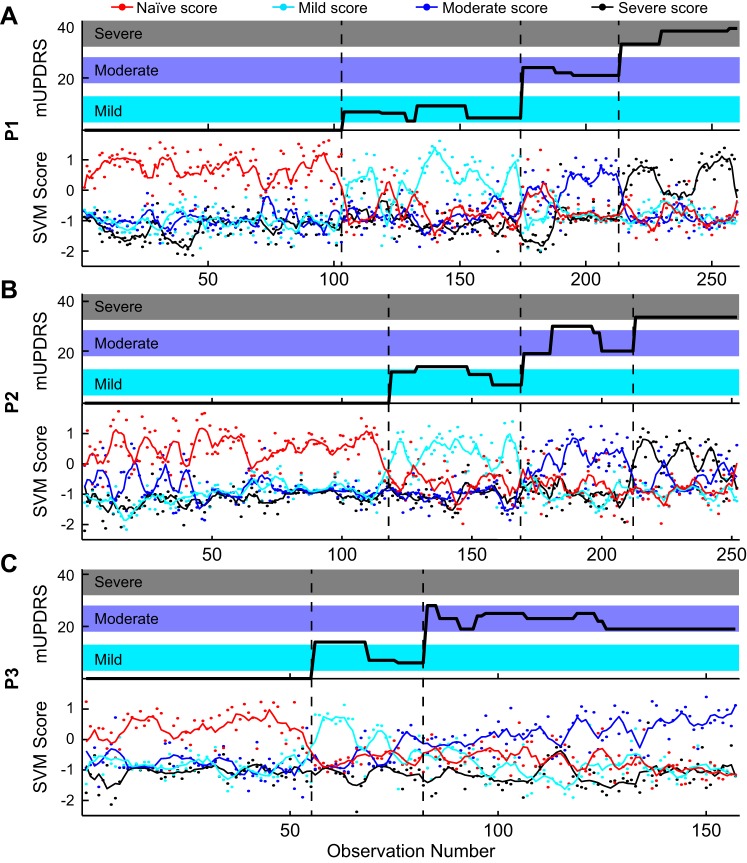
RBF SVMs were trained to discriminate parkinsonian severity for each subject individually and for the pooled data (Fig. 3, Table 2). When only spectral features were used the prediction error was 19% for the pooled population, whereas the use of only PAC features resulted in 61% errors. For subjects P1 and P2 and pooled data, the PAC sensitivity was high for the naive state but low for the mild and moderate states, indicating that many mild and moderate observations were incorrectly predicted as being naive. The spectral feature set was nearly twice as large as the PAC feature set (134 compared with 72 features), and larger numbers of features may lead to more accurate fitting of the classifier. However, when the two feature sets were combined (206 features), the prediction error was 28% for the pooled data, larger than the error rate with only spectral features. Again, the sensitivity for the naive state was larger compared with the mild, moderate, and severe cases. Adding more features to the spectral feature set did not improve the overall prediction. Instead, the inclusion of PAC features added variability that contradicted the spectral features and reduced the accuracy of the classifier. This trend was consistent when the SVM was trained and tested on LFPs from individual subjects. Prediction errors were between 9% and 14% for individual subjects with only spectral features, and the error rate was the lowest for subject P1.

Fig. 3.

Top: modified Unified Parkinson's Disease Rating Scale (mUPDRS) for subjects P1 (A), P2 (B), and P3 (C) associated with each observation. Bottom: each observation was given an in-versus-out score for the naive (red dot), mild (cyan dot), moderate (blue dot), and severe (black dot) support vector machine (SVM) classifiers. The predicted class was assigned based on the highest score. The lines show smoothed trends for classifier scores. Dashed black lines show the change from one parkinsonian state to another.

Table 2.

Performance of SVM classifiers using only PSD, only PAC, or both PSD and PAC features

		Sensitivity/Specificity
	Error	Naive	Mild	Moderate	Severe
	PSD (134 features)
P1	0.11	0.96/0.94	0.83/0.95	0.81/0.97	0.92/0.97
P2	0.14	0.94/0.88	0.84/0.99	0.70/0.95	0.85/0.96
P3	0.14	0.89/0.94	0.69/0.97	0.91/0.84
All	0.19	0.90/0.85	0.76/0.96	0.73/0.91	0.79/0.98
	PAC (72 features)
P1	0.52	0.77/0.40	0.26/0.74	0.10/0.89	0.47/0.85
P2	0.59	0.72/0.16	0.11/0.78	0.17/0.84	0.12/0.87
P3	0.57	0.35/0.59	0.08/0.88	0.61/0.31
All	0.61	0.66/0.29	0.16/0.74	0.19/0.69	0.27/0.90
	PSD + PAC (206 features)
P1	0.19	0.96/0.82	0.76/0.93	0.66/0.97	0.71/0.97
P2	0.21	0.92/0.73	0.73/0.97	0.53/0.95	0.76/0.96
P3	0.22	0.79/0.86	0.59/0.99	0.85/0.76
All	0.28	0.87/0.74	0.67/0.92	0.58/0.89	0.62/0.96

SVM, support vector machine; PSD, power spectral density; PAC, phase-amplitude coupling.

Features spanning multiple frequency bands were relevant for classification.

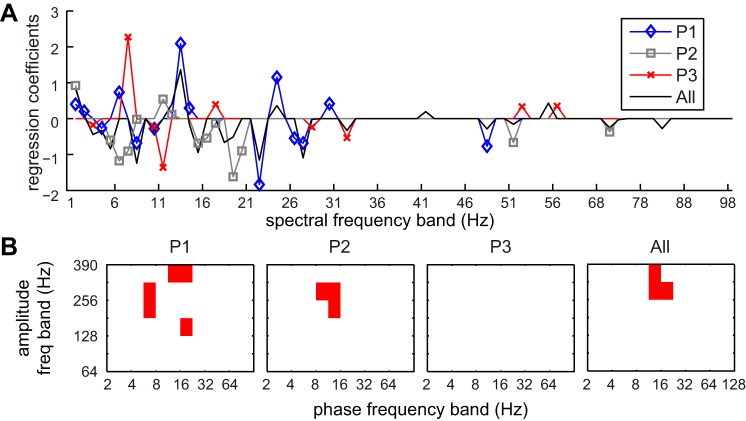
The lasso feature selection revealed that different combinations of spectral and PAC features were discriminatory for individual subjects and for the pooled data. Mean spectral power above 100 Hz was never included in the lasso results, but power in bands from 1 to 35 Hz and from 47 to 57 Hz did have nonzero regression coefficients across multiple subjects (Fig. 4A). For subject P1, the regression coefficient for 22–23 Hz was −1.84, indicating that the mean power in this band decreased as parkinsonism increased, while the regression coefficient for 13–14 Hz was 2.09, indicating that power in this band increased with parkinsonian severity. This aligns with the observation that the median oscillatory frequency in the beta band decreased with increased severity. For subject P2, the regression coefficient for 19–20 Hz was −1.62 and the coefficient for 11–12 Hz was 0.54. The coefficients in the beta range were smaller for subject P3 except for a coefficient of −1.36 in the 11–12 Hz band. A coefficient in the theta-alpha range 7–8 Hz was 2.27, indicating an increase power at this frequency with parkinsonian severity. While gamma-HFO PAC was present in subject P3, there were no changes in any phase-amplitude pairs across parkinsonian states, and this was reflected in the lack of nonzero regression coefficients for PAC features for this subject (Fig. 4B). Five PAC features had nonzero coefficients for P1 and three had nonzero coefficients for P2, but they did not directly overlap. For the pooled data, three features had nonzero coefficients, involving the beta phase (8–11 Hz and 11–16 Hz) and the HFO amplitude (256–362 Hz and 362–390 Hz).

Fig. 4.

Lasso regularization was used to select the smallest subset of features yielding a mean-square error (MSE) within 1 SE of the minimum possible MSE. A: regularization coefficients for the PSD feature set for individual subjects (P1, blue; P2, gray; P3, red) and pooled data (All, black). B: red squares show the PAC features with nonzero regularization coefficients for individual subjects and pooled data.

The reduced feature sets were used to train new RBF SVMs. First, the 28 lasso-selected features based on the pooled data were used to train and test RBF SVMs with data from individual subjects and pooled data (Table 3). Prediction errors were improved over the classifier that used all 206 features for subjects P1 (10% compared with 19%) and P2 (13% compared with 21%) and were similar for subject P3 (21% compared with 22%). The prediction error for the pooled data was also improved (18% compared with 28%). When the subset of features selected by subject-specific lasso analyses was used to train a classifier for that subject, the prediction error improved for subject P3 (17%), stayed the same for P2 (12%), and worsened for P1 (15%).

Table 3.

Classifier performance using a subset of features selected by lasso regularization

	All-Subject Features (28 features)					Subject-Specific Features (20, 18, 11 features)
		Sensitivity/Specificity					Sensitivity/Specificity
	Error	Naive	Mild	Moderate	Severe	Error	Naive	Mild	Moderate	Severe
P1	0.10	0.97/0.96	0.85/0.95	0.82/0.99	0.92/0.96	0.15	0.97/0.94	0.77/0.93	0.82/0.97	0.79/0.95
P2	0.13	0.97/0.88	0.79/1.00	0.77/0.97	0.87/0.96	0.12	0.93/0.88	0.82/0.98	0.77/0.96	0.88/0.97
P3	0.21	0.75/0.88	0.64/0.95	0.87/0.77		0.17	0.85/0.92	0.59/0.93	0.87/0.82
All	0.18	0.90/0.86	0.72/0.95	0.74/0.92	0.85/0.97

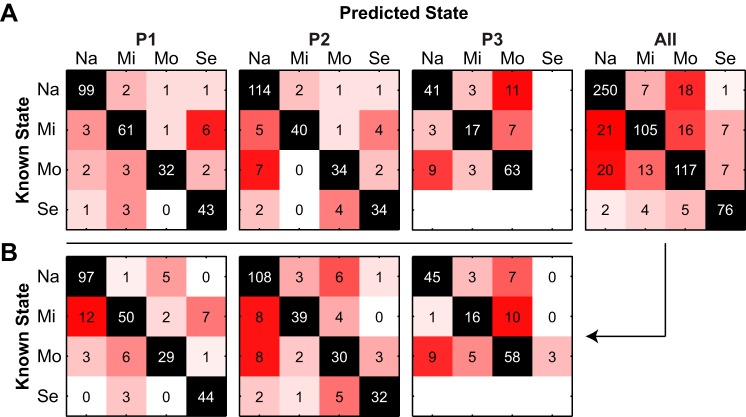
Figure 5 shows confusion matrices that display the counts of observations that were known for each group (rows) against the counts of observations that were predicted to be in each group (columns) from a single run using 10-fold cross-validation. Counts along the diagonal were correctly classified, whereas counts off the diagonal were incorrectly classified. These confusion matrices display the results from individual subjects and pooled data (Fig. 5A) using RBF SVMs that were trained with the 28 lasso-selected features based on the pooled data. For subject P1, six observations from the mild state were misclassified as being in the severe state. The remaining errors were distributed across the other known-predicted group pairs. For subject P2, most errors occurred when mild (5) or moderate (7) observations were mistakenly classified as naive. For subject P3, the most errors occurred when naive or mild observations were classified as being from the moderate state or moderate observations were misclassified as being from the naive state. This indicates that the features from the naive and moderate states were similar to each other and different from the mild state.

Fig. 5.

Confusion matrices for radial basis function (RBF)-SVMs using the 28 lasso-selected features based on pooled data. A: classifiers were trained and tested on data from individual subjects (P1, P2, P3) or on the pooled data (All). B: the confusion matrix results from classification of pooled data were split up by individual subject. x- and y-axis labels indicate naive (Na), mild (Mi), moderate (Mo), and severe (Se) states.

The prediction results from the pooled data were separated into individual subjects (Fig. 5B). The pooled data classifier mistakenly classified 12 mild observations from subject P1 as being from the naive state but successfully separated the naive and severe states. As in subject P1, the classifier mistakenly classified subject P2 observations from the mild and moderate states as being from the naive state but only made three errors between the naive and severe states. For subject P3, the pattern of prediction errors mirrored those from the SVM trained only with features from P3. Because the classifier was trained on the pooled data, there was a chance that some P3 observations could be classified as being from a severe state even though there were no severe observations in this animal. Surprisingly, only three moderate observations were misclassified as being from the severe state.

Individual subject classifiers could not predict severity for other subjects.

RBF SVMs were trained on the 28 lasso-selected features based on the pooled data from one or two subjects and tested on data from another subject to investigate intersubject variability, resulting in large prediction errors (Table 4). The smallest error (51%) occurred when the SVM was trained with observations from P1 and tested on observations from P2. The largest errors occurred when P3 was involved, and 83% of the observations from P3 were incorrectly classified when using a SVM trained on data from P1. When data from two subjects were used to train the algorithm and it was tested on the third subject, the errors were reduced slightly but not to the levels seen when pooled data were used for training or when individual subject classifiers were used.

Table 4.

Classification performance when testing on subjects not included in training data

	Test
	P1	P2	P3
Train on 1, test on 1
P1		0.51	0.83
P2	0.61		0.63
P3	0.78	0.73
Train on 2, test on 1	0.56	0.59	0.71

DISCUSSION

In this study, machine learning algorithms were able to predict naive, mild, moderate, and severe parkinsonian severity from LFP spectral and PAC features. Single-subject classifiers could predict the degree of severity with ∼20% errors, while classification of pooled data achieved 28% error. Reducing the number of features used by the classifier through lasso regularization yielded smaller prediction errors of 9–21%. When no data from a subject were used in the training of a classifier but were used for testing, error rates were very high at 56–83%. Algorithms could be used to predict parkinsonian severity based on sample LFPs from the same subject. Otherwise, we anticipate that a large number of subjects in a diverse training set would be necessary to train a robust classifier because training on two nontesting subjects was better than training on one.

Application of classifiers to Parkinson's disease.

Machine learning algorithms have become a popular tool for studying PD. Behavioral measures have been characterized in order to quantify the severity of gait abnormalities (Muniz et al. 2010; Tahir and Manap 2012) or to predict onset of tremor in order to initiate DBS (Basu et al. 2013). SVMs and Bayesian classifiers have been trained on structural MR images to discriminate between essential tremor and PD patients (Cherubini et al. 2014) and identify PD patients who are at risk for developing dementia (Morales et al. 2013), both of which are useful diagnostic measures for DBS patient selection. Both unsupervised (Wong et al. 2009) and supervised (Guillen et al. 2011; Rajpurohit et al. 2015) learning techniques have been used to identify the optimal DBS implant location from intraoperative microelectrode recordings. Sanders et al. used 29 features of single-neuron activity recorded from the internal or external segments of the GP or from the STN to train binary classifiers to discriminate baseline from parkinsonian recordings in nonhuman primates (Sanders et al. 2013). The authors found variability in feature selection across the different nuclei and achieved binary prediction errors of 18–29%, which were slightly higher than those found in our study, which classified LFP features based on four states.

Unbiased biomarker identification using machine learning algorithms.

The lasso regularization procedure identified different spectral and PAC features as being discriminant for different subjects. Without prior preference for particular frequency ranges such as the beta band, the algorithm identified features between 11 and 32 Hz as having nonzero coefficients for all three subjects individually and for the pooled data (Fig. 4A). However, the addition of other spectral features was necessary to produce minimum prediction errors. For all individual subjects and for the pooled data, there was a spectral feature in the beta range with a negative regression coefficient and a spectral feature at a lower frequency band with a positive regression coefficient, indicating that the frequency of spectral peaks was decreasing from the higher to the lower band as parkinsonian severity increased.

Despite the apparent increase in beta-HFO PAC after the onset of parkinsonism in two of three subjects, the use of PAC features alone produced prediction errors above 52% (Table 2), even with subject-specific classifiers. Most errors occurred because parkinsonian observations were being classified into the naive group. The PAC analysis showed an increase in the average strength of the MI between beta phase and HFO amplitude as severity increased, but this was not associated with an increasing strength at the level of individual recordings. Instead, the proportion of recordings having a significantly strong MI increased as severity increased. Therefore, some recordings in the mild, moderate, and severe states had MIs close to 0, which the classifier would otherwise identify as being from the naive state. It is worth noting that because the PAC varied across different locations within the sensorimotor GP, it remains unclear how well classification with PAC features would do when recording oscillatory activity from a bipolar pair of electrodes in a fixed location within the brain across states.

If spectral power in certain frequency bands was linearly correlated with parkinsonian motor signs, then one would expect more errors to occur between neighboring parkinsonian states (i.e., mild to moderate) than between nonneighboring (i.e., naive to severe). However, this was not the case (Fig. 5). Most often, observations were incorrectly classified as being in the naive state, lacking parkinsonian features. This further points to parkinsonian motor signs emerging and increasing in severity according to a population change across the sensorimotor GP that may not necessarily be reflected at the location of a single recording.

Between-subject variability.

Prediction errors were extremely high when no data from the testing subject were used to train the classifier. Subject P1 was more similar to subject P2 than to subject P3 because the cross-testing errors were smaller when trained on P1 and tested on P2 or vice versa than when P3 was used for training or testing. When data from two subjects were used to train a classifier the prediction errors were slightly improved in some cases, but the accuracy was not close to that achieved when the same subject was used to train and test the classifiers. The variability in classification of LFP features across subjects could be explained in part by slight temporal differences in the progression of specific motor signs, but in general all three developed bradykinesia, akinesia, and rigidity gradually over the study and had little to no tremor. The recordings were categorized into parkinsonian states based on mUPDRS measurements taken at one point in time, but motor signs can vary on the order of minutes to hours and with behavioral state. These fluctuations could cause variability within a subject and increase the noise in the data. The addition of more subjects would incorporate more samples of the symptomatology to understand whether the motor signs were the cause of the cross-subject errors or whether individual subjects were prone to developing different neural correlates of disease. Both prior studies using a progressive model of parkinsonism in nonhuman primates saw differences in the timing, frequency content, and direction of changes in neural activity with increasing parkinsonian severity across subjects (Devergnas et al. 2014; Leblois et al. 2006). Addition of more subjects may be expected to support the variability seen in this data set.

Limitations.

While the MPTP model has been widely used to investigate the mechanisms of PD, there are several proposed mechanisms for the slow, progressive induction of parkinsonian symptoms that need to be compared (Braak et al. 2005). While the rhesus macaque develops akinetic-rigid parkinsonism, which prior studies have associated with beta oscillations (Brown 2007), this species does not develop the dominant tremor that is seen in some PD patients. Beta in the naive state is believed to be linked with intention to move (Riehle et al. 1997), but we could not control for intention in this study and have included only spontaneous recordings during which the animal was at rest. Previous studies show that LFP content in the basal ganglia-thalamo-cortical loop is significantly modulated by movement in the parkinsonian state (Brazhnik et al. 2012), suggesting that additional changes in pallidal oscillatory activity are likely to be elucidated during movement in this progressive model of parkinsonism.

LFPs from humans are often recorded as a bipolar signal between two clinical DBS macroelectrodes. For this reason, we chose to analyze bipolar instead of unipolar LFPs. While recording differentially between two electrodes in close proximity removes far-field noise or extraneous cortical information from the recording, if neuronal ensembles surrounding the two electrodes were oscillating strongly and at the same frequency and phase this information would be removed with the bipolar recording technique. We examined the power spectra, median frequency of beta oscillations, and amplitude of beta oscillations in the unipolar recordings and did not find results different from those presented here.

The data should also be considered in terms of the recording approach. Microelectrodes (1-kHz impedance of 0.8–1.2 MΩ) were used to acquire LFPs, whereas DBS lead macroelectrode contacts whose impedance is on the order of 1–10 kΩ are more often used in a clinical setting,. The LFPs were also acquired at a sampling rate of 781.3 Hz, which limits the information content of the LFPs to below the Nyquist frequency at 390 Hz. It is possible that the significant PAC extended above the 256–362 Hz band that was found to be significant in our study, but the low sampling rate prohibited the detection of significant coupling in this range. For this reason, we cannot conclude the upper frequency limit of significant coupling but can only conclude that significant couplings occurred in the band > 256 Hz.

Conclusions.

The results of this study provide evidence that LFPs in the pallidum could be used to determine the severity of bradykinetic and rigid parkinsonian motor signs. However, the power in the beta band would be insufficient for providing robust prediction, and a complex combination of LFP features would be necessary. As few as 10–28 features of the LFP were needed to discriminate between disease states, but results were unique to individual subjects. Ultimately, if specific features of the LFP were to be used as a biomarker of parkinsonian motor signs, those features would need to be tuned on a subject-specific, behavior-specific, and therapy-specific basis.

GRANTS

This material is based upon work supported by the National Institute of Neurological Disorders and Stroke under Grants R01 NS-058945 and R01 NS-081118, by the Michael J. Fox Foundation, and by the National Science Foundation Graduate Research Fellowship under Grant 00006595.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.T.C. analyzed data; A.T.C., A.L.J., K.B.B., J.L.V., and M.D.J. interpreted results of experiments; A.T.C. prepared figures; A.T.C., K.B.B., J.L.V., and M.D.J. drafted manuscript; A.T.C., K.B.B., J.L.V., and M.D.J. edited and revised manuscript; A.T.C., A.L.J., K.B.B., J.L.V., and M.D.J. approved final version of manuscript; A.L.J., K.B.B., and J.L.V. conception and design of research; A.L.J. performed experiments.