Abstract
When vision of the hand is unavailable, movements drift systematically away from their targets. It is unclear, however, why this drift occurs. We investigated whether drift is an active process, in which people deliberately modify their movements based on biased position estimates, causing the real hand to move away from the real target location, or a passive process, in which execution error accumulates because people have diminished sensory feedback and fail to adequately compensate for the execution error. In our study participants reached back and forth between two targets when vision of the hand, targets, or both the hand and targets was occluded. We observed the most drift when hand vision and target vision were occluded and equivalent amounts of drift when either hand vision or target vision was occluded. In a second experiment, we observed movement drift even when no visual target was ever present, providing evidence that drift is not driven by a visual-proprioceptive discrepancy. The observed drift in both experiments was consistent with a model of passive error accumulation in which the amount of drift is determined by the precision of the sensory estimate of movement error.
Keywords: movement drift, proprioception, vision
when people make multiple reaches without visual feedback, the reaches gradually drift away from their intended targets (Brown et al. 2003a, 2003b; Cameron et al. 2011; Smeets et al. 2006). This drift goes undetected by participants and can be substantial, such that the hand may start landing several centimeters from the target within 5–10 reaches without vision. Plausible explanations for this phenomenon include error accumulation via separate controllers for movement versus position (Brown et al. 2003a, 2003b), drifting proprioceptive estimates of hand location in the absence of vision (Paillard and Brouchon 1968; Wann and Ibrahim 1992), and shifting integrated estimates of the unseen hand and the visual target (Smeets et al. 2006). The first of these explanations implies that drift is a passive process: the estimate of the hand's position deteriorates, and error accumulates because participants do not detect their failure to hit the target. The second two explanations imply that drift is an active process: participants sense that the hand is missing the target, so motor corrections are applied that bring the felt hand closer to the target while moving the real hand away from it. In the present study we examined whether movement drift is more likely to be passively or actively driven. The answer to this question has important implications for the reliability and role of proprioception in movement control.
We examined the independent effects of target vision and hand vision on movement drift, and we compared the results with the predictions of two models of movement drift, an active model proposed by Smeets et al. (2006) and a passive model proposed in the present study. According to Smeets et al.'s (2006) model, movement drift is caused by active compensation for a growing discrepancy between the integrated estimates of the hand and the target. Their model is based on two key ideas. The first is that people optimally integrate vision and proprioception to localize both the hand (Ernst and Banks 2002) and the target. The second is that vision and proprioception are not aligned with each other. Smeets et al. (2006) propose that neither of the individual sensory estimates (visual or proprioceptive) drifts; only the integrated estimates of the hand and the target drift. When the target is visible and the hand is invisible, the target and hand estimates will drift away from each other, for vision will contribute more to the integrated target estimate and proprioception will contribute more to the integrated hand estimate. To overcome the resulting sensed error between the hand and target, participants will move their real hand away from the target. It is this attempt to overcome perceived error that causes drifting reaching movements, according to Smeets et al. (2006).
Our passive model, in contrast, is based on the idea that people are poor at detecting error between their unseen hand and a visible target (or vice versa). Studies of goal-directed reaching have shown that performance is poorer and there tends to be less online correction when people reach without visual feedback of their hand (see Khan et al. 2006 for a review). Furthermore, people rely heavily on visual feedback of the hand when it is available for online correction, even if the feedback is incorrect (Saunders and Knill 2003). These findings suggest that visual hand-to-visual target feedback is a more reliable source of error feedback than intersensory error, and that participants rely minimally on proprioception for error correction to visual targets. We suggest, accordingly, that when vision of the hand is absent movement error will need to be comparatively large before it is detected, and this will allow drift to occur.
We suggest that drift accumulates passively, via motor bias (a small but consistent error in the specification of the direction and/or amplitude of a reach), until sufficient separation between hand and target estimates has occurred for error correction to counter the accumulating drift. In other words, Smeets et al.'s model proposes that error correction causes drift, whereas our model proposes that error correction contains it.
METHODS
Participants
A total of 15 participants (3 women, 12 men; ages 19–48 yr) from the University of Barcelona took part in the experiments after providing informed consent (8 in experiment 1 and 7 in experiment 2). Two participants completed both experiments. Two participants were left-handed by self-report. B. D. Cameron and J. López-Moliner participated in experiment 2. All participants had normal or corrected-to-normal vision except for one who reported an uncorrected +2.0 diopter prescription for the right eye (but reported no difficulty perceiving the visual stimuli). The study was approved by the local research ethics board and was conducted in accordance with the Declaration of Helsinki.
Apparatus
Experiments were conducted in a dark room. Participants sat in front of a digitizing tablet (Calcomp DrawingTablet III 24240) that recorded the position of a handheld stylus. Stimuli were presented on an inverted LED LCD monitor at a frame rate of 120 Hz positioned above the tablet. A half-silvered mirror was positioned halfway between the monitor and the tablet, hiding subjects' hand from view and reflecting the stimuli presented on the monitor, giving participants the illusion that the stimuli were in the same plane as the tablet. A Macintosh Pro 2.6 GHz Quad-Core computer controlled the presentation of the stimuli and registered the position of the stylus at a frequency of 125 Hz. The setup was calibrated by aligning the position of the stylus with dots presented on the screen.
Participants were allowed to adjust the height of their chair for comfort. The distance between the eyes and the tablet surface differed across participants, but the approximate distance was 50 cm. Participants were allowed to move their eyes freely, and these movements were not monitored.
Procedure
Experiment 1.
Our design was inspired by Brown et al. (2003a), and we have adopted several of that study's procedures. In experiment 1, every trial began with two visible target locations (circles of 1-cm diameter) and the cursor representing the stylus position (circle of 1-cm diameter). On a given trial, only two visual targets would be presented, separated by 15 cm and positioned at one of three configurations: center vertical (angle of imaginary intertarget line: 90°), left of center and tilted (angle: 126°), or right of center and tilted (angle: 41°). The target layout is shown in Fig. 1. Participants had to move the stylus (represented by the cursor) to the farther of the two targets, and then a tone was played. The tone repeated every 1.5 s, and the task was to move the stylus back and forth between the targets, returning the stylus to the original target prior to each tone (1 movement cycle). In different blocks participants either had or did not have proprioceptive information about the target locations. Proprioceptive targets consisted of tactile stimuli (metal nuts 0.5 cm tall and 1 cm in diameter) fixed to the upper surface of the table below the digitizing tablet, such that these tactile markers were 8 cm below the visual target locations. The tactile markers provided proprioceptive target locations when the nondominant arm was placed on them. That is, these markers provided additional sensory information about target location that could theoretically be used to assist performance when the participant reached to targets with his/her dominant arm (van Beers et al. 1996). However, there is the possibility that the coordinate frames for the proprioceptively sensed dominant and nondominant hands are not aligned (Jones et al. 2012; Wilson et al. 2010), an issue that we return to below.
Fig. 1.
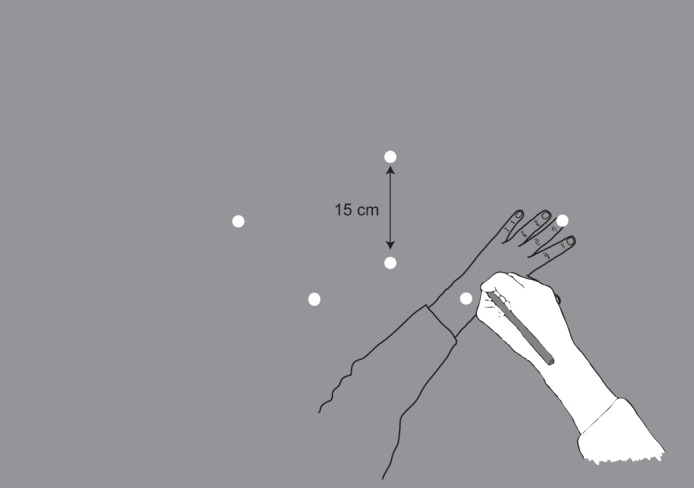
Schematic of the stimulus display and the positioning of the dominant (white) and nondominant (gray) hands. The nondominant hand was positioned below the reaching surface only on the Proprioceptive Target trials. Only 2 of the target locations (white circles, 15 cm apart) were used on any given trial, and the participant reached back and forth between them with the dominant hand.
In both kinds of block participants saw the targets and the cursor for the first 6.0 s of every trial. Thus full vision was available for the completion of four movement cycles at the start of every trial. After that, target vision, cursor vision (which we will refer to as “effector vision”), or both were occluded for the remainder of the trial (NoTarget, NoEffector, and NoVision, respectively), making nine unique combinations of target location and visual manipulation, which were randomized.
Participants completed two blocks of trials, one of which involved proprioceptive targets (i.e., the nondominant arm positioned on the tactile markers) and one of which did not. The order of blocks was counterbalanced across participants. Prior to each block, participants completed a practice session of nine trials with the corresponding target type (proprioceptive targets or no proprioceptive targets). Each practice trial lasted 15 s and included the full-vision part of each trial (6.0 s) plus the subsequent removal of some or all visual information. After the practice trials, participants completed nine experimental trials, each of which lasted 65 s. This time period was sufficient to collect four full-vision movement cycles and at least 36 vision-manipulated movement cycles.
Accordingly, participants completed nine trials in each block. In the Proprioceptive Target block, participants were reminded at the start of each trial to position their nondominant arm on the tactile markers that corresponded to the visual targets for that trial, placing the tip of their middle finger on the far marker and resting their arm such that the near tactile marker contacted the arm at a location between the wrist and the elbow. Participants were also told to use the tactile markers to assist their performance; the purpose of this instruction was to encourage the use of proprioceptive information about the target's location.
Experiment 2.
In experiment 2 we implemented a further test of the active and passive models of movement drift. Smeets et al.'s model is based on the premise that there is a discrepancy between vision and proprioception. We reasoned, therefore, that if participants exhibit movement drift in the absence of any visual representation of the hand or target, it would imply that drift can be caused by something other than an intersensory discrepancy. In experiment 2, we asked participants to close their eyes and position their hand at a self-chosen location in the workspace, move to a second location of their choosing, and then continue moving back and forth between those two locations as accurately as possible. In other words, target locations were specified by the same hand that was doing the moving. This meant that target and hand were represented in the same modality (proprioception) and that there was no interlimb discrepancy to worry about (unlike the Proprioceptive Target condition in experiment 1, where participants were reaching to the opposite hand). Moreover, by having participants close their eyes for the duration of the trial, eye movements were eliminated as a potential contributor to movement drift.
In experiment 2 no visual stimuli were presented and the reaching hand was occluded at all times by the mirror. Participants closed their eyes prior to the start of each trial, positioned the stylus at any location on the tablet surface, and then indicated to the experimenter that they were ready to begin. At that point, the experimenter started the trial and the metronome began to beep. Participants moved to a second location, in any direction they liked, and then back to the initial location in time for the next beep (every 1.5 s). Each trial lasted for 60 s, allowing for 40 movement cycles. Participants were asked to keep their eyes closed throughout the trial and to be as accurate as possible while adhering to the timing imposed by the metronome. Each participant completed 13 trials.
Participants were told that they could choose any two locations they liked on each trial, and the only guideline the experimenter provided was that the movement should be ∼10–20 cm long (but this was not measured or enforced during the experiment).
Data Analysis
Displacement data were filtered with a fourth-order Butterworth filter (low-pass cutoff: 10 Hz). To analyze drift over the course of each trial, we first located the reversal points in the continuous movement trace (i.e., the end points of each targeted movement). Because participants were producing movement cycles timed to a metronome, these reversal points were easy to locate with an algorithm that searched for the maximal point of excursion within a moving time window. The success of the algorithm was confirmed visually. We then calculated the Euclidean distance of each end point from the corresponding target location. A mean Euclidean distance was calculated for each movement cycle, and values were collapsed across target location. Thus for each participant we had a series of 40 Euclidean distance values (1 for each movement cycle) for each visual condition.
Analysis of variance was conducted with the ezANOVA package (Lawrence 2013) in R (R Core Team 2013). Post hoc comparisons were carried out in base R, using pairwise t-tests with the Holm-Bonferroni correction to control familywise error rate (the reported P values are the corrected values).
We carried out a cross-validation procedure for the active and passive drift models (described in next section), using a “leave one out” method, in which we trained the model on the mean drift of seven of the eight participants and then applied the obtained parameter values to the remaining participant. This procedure was repeated eight times for each visual condition, such that each participant served as the test participant once in each visual condition. The error value obtained for each condition was, then, the mean of the eight error values for that condition.
Modeling
Smeets et al.'s (2006) model of drift.
We used Smeets et al.'s (2006) equations to generate predictions of their model for our three visual conditions. For these equations and their descriptions we refer to the “hand” rather than the “effector” (to be consistent with Smeets et al. 2006), but the meanings of the terms are the same for our purposes. Their model proposes that sensory estimates decay as a function of the number of movements (n). For instance, the visual estimate of the unseen hand will deteriorate with each movement that is made without vision, and this will depend on how much variability there is in movement execution (σex2). Below are the equations for the integrated hand estimate (x̂h) and for the integrated target estimate (x̂t) from Smeets et al. (2006) when vision of the target is available and the hand is occluded (NoEffector):
| (1) |
| (2) |
Here σv2 is the variance of the visual estimate, σp2 is the variance of the proprioceptive estimate, σex2 is the variance of the execution error, n is the number of movements, xh,p is the proprioceptive estimate of hand position, xh,v is the visual estimate of hand position, xt,p is the proprioceptive estimate of target position, and xt,v is the visual estimate of target position. In Eqs. 1 and 2 execution error affects only the proprioceptive estimate of the target and the visual estimate of the hand, because real-time proprioceptive information about the hand is available and real-time visual information about the target is available.
To arrive at the predictions of the Smeets et al. (2006) model for the other visual conditions in our study (NoTarget and NoVision), we changed whether the execution error (the component of the model that determines the rate of sensory estimate decay) affects the visual estimate of the hand, the visual estimate of the target, and/or the proprioceptive estimate of the target. First, we consider the case in which vision of the targets is removed, but vision of the hand is available (NoTarget):
| (3) |
| (4) |
Note that for the hand the integrated estimate is not affected by execution error, because real-time visual information and real-time proprioceptive information are available when the hand is visible. Therefore, the integrated hand estimate should not change as a function of movement. For the target the absence of both real-time visual and real-time proprioceptive information means that both sensory estimates of the target are decaying as a function of movement, but because they are both changing at the same rate the integrated target estimate should not change as a function of movement. Accordingly, the integrated hand and target estimates are not expected to move away from each other, so there should be no movement drift. It is possible that proprioceptive and visual estimates of the target do not decay at the same rate. However, we have treated it that way here because according to Smeets et al.'s (2006) model the rate of decay for both sensory estimates is determined entirely by the variability in movement execution (see Eqs. 1 and 2). In other words, the predictions we have presented here are consistent with their model.
Next, we consider the case in which neither target vision nor hand vision is available (NoVision):
| (5) |
| (6) |
In this case, the visual and proprioceptive estimates of the unseen target should both decay (as in NoTarget), meaning that the integrated estimate of the target location should be minimally biased toward either sensory estimate. The integrated estimate of the unseen hand, which still has real-time access to proprioception, should become biased toward the proprioceptive estimate (as in NoEffector). Accordingly, if Smeets et al.'s (2006) model is correct, we should see some drift caused by the biased integrated estimate of the hand, but it should be less drift than we see in NoEffector, where the target estimate is strongly biased toward vision. These predictions are presented in Fig. 2.
Fig. 2.
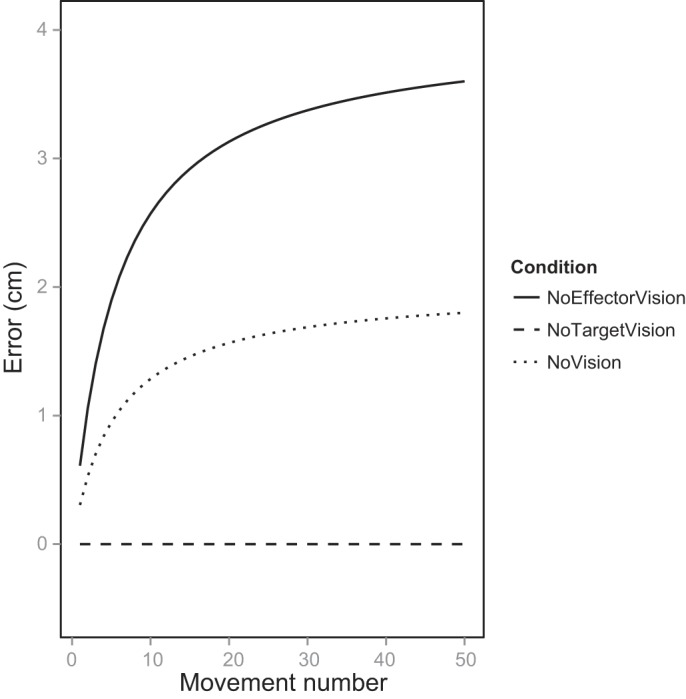
Predicted movement drift based on Smeets et al.'s (2006) active-drift model for each of the visual conditions. The magnitude of error depends on the assumed bias between vision and proprioception, and we have used a value of 4 cm based on data from Smeets et al. (2006), but this value does not impact the relative amounts of drift among conditions. We have shown predictions only for the No Proprioceptive Target trials (see text).
The rate of drift predicted by the model is affected by the size of the execution variance (faster drift for larger execution variance), and the total amount of drift is affected by the visual-proprioceptive discrepancy. For the predictions we present in Fig. 2, we used the execution variance obtained from the full-vision movements in our experiment (0.3 cm) and an intersensory discrepancy of 4 cm (Smeets et al. 2006). At this point we are more interested in the relative amounts of drift across visual conditions than the actual rates of drift, so the accuracy of these parameter values is not important.
Although we also made predictions for Proprioceptive Target trials (i.e., when the nondominant hand was below the tablet) based on Smeets et al.'s (2006) model, those predictions are not presented here. Our rationale for including proprioceptive targets in experiment 1 was that they would reduce or eliminate the decay in the proprioceptive estimate of the target as a function of movement. However, our predictions relied on the assumption that the bias in the proprioceptive estimate of the nondominant arm relative to vision is the same as the bias in the proprioceptive estimate of the dominant arm relative to vision. We assumed that only the variability—and not the location—of the proprioceptive estimate of the target would be influenced by the presence of the real-time proprioceptive target. In retrospect, this assumption is probably incorrect (Jones et al. 2012; Wilson et al. 2010), and so the drift pattern with proprioceptive targets is unlikely to present a valid test of Smeets et al.'s (2006) model. Therefore, we do not carry out any modeling for the Proprioceptive Target trials from experiment 1.
Passive model of drift.
Our passive model of drift is based on the idea that participants optimally combine their prior belief about the quality of their motor command with their sensory estimate of movement error. We propose that a person's everyday movement success gives him or her a relatively robust (low variability) and unbiased (mean error = 0) prior. That is, in the complete absence of conflicting or confirmatory sensory information, people will tend to think that they hit the target they reached for. If they have to repeat the task, their best strategy will be to execute the same movement that they did on the previous trial.
When participants have impoverished error information (e.g., no vision of the hand, no vision of the target, or no vision of either one), we would expect them to rely more on their prior than they would when they have robust error information (such as full vision of the hand and the target). In other words, the effect of the prior on a subsequent movement will depend on the quality of the error information. If the sensory information about movement error is unreliable, the hand will have to land relatively far from the target for a correction to be applied to the subsequent movement.
If there is any bias present in the movements that people produce, such as a tendency to aim a little left or right or short or long when a target is at a given location in the workspace, this bias would be expected to propagate over the course of multiple movements when the sensory error is unreliable. People would keep producing bias until their sensory error estimate offsets their confidence in their motor command. That is, movement end point would be expected to stabilize at a position where the best estimate of the movement error (an optimal combination of the sensory error and the prior error) is equal to the magnitude of the motor bias. A pictorial representation of this error estimation process is presented in Fig. 3.
Fig. 3.
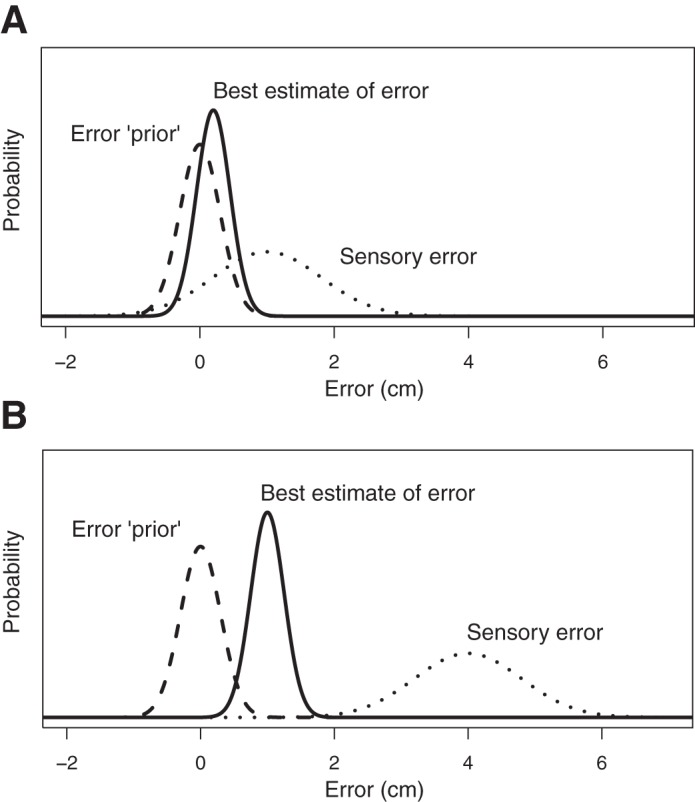
Proposed error processing for our passive drift model during early drift (A) and late drift (B). The best estimate of error grows as the hand moves farther from the target, and drift would plateau when the magnitude of the best estimate of error is equivalent to the magnitude of the motor bias.
In mathematical terms (Eq. 7), our model states that the position of the hand at the end of a movement (xi) is equal to the position of the hand at the end of the previous movement (xi−1) plus a constant motor bias (m) minus a correction (ci). The magnitude of the correction is determined by the sum of the weighted true error [the distance between the real hand (xi−1) and the true target (xt)] and the weighted prior, according to maximum likelihood estimation (Ernst and Banks 2002). Equation 8 shows the simplified version of the equation for the magnitude of the correction, where the weighted prior is not present because the mean of the error prior is assumed to be zero.
| (7) |
| (8) |
Here, σsens2 is the variance of the sensory error and σprior2 is the variance of the error prior. One can see that the smaller the variance of the error prior, the smaller the correction, while the smaller the variance of the sensory error, the larger the correction. If the prior is constant across all visual conditions in our study (and we assume that it is), then the smallest corrections should occur in the NoVision condition, when the sensory error is the least reliable (largest variance). Accordingly, our passive model predicts the most drift in NoVision.
Model fitting.
For the Smeets et al. model, we used the appropriate version of the model (Eqs. 1–6 above) for each visual condition. In each case we used a constant value of execution error, and we obtained a value for this parameter from participant performance in full vision (Smeets et al. 2006). We also applied Smeets et al.'s (2006) assumption that vision and proprioception have equal precision, so we used a single sensory variability parameter, which was allowed to vary during fitting. Visual estimates of the hand and target were assumed to be equivalent, as were proprioceptive estimates of the hand and target (Smeets et al. 2006). This meant that there were only two position estimates in the model, xv and xp, the latter of which is equal to xv + b, where b is the intersensory bias, which was allowed to vary during fitting. The actual value of the position estimate xv does not affect the fitting; only the difference between xv and xp (i.e., b) matters (Smeets et al. 2006). In summary, the parameters used during fitting were σex = 0.3 cm (from full vision), xp = xv + b, σp = σv = σ (free to vary), and b (free to vary).
For our passive model, two parameters (σsens, m) were free to vary during the fitting to the end-point data. We used the execution error from full-vision movements (0.3 cm) as a fixed estimate of the standard deviation of the error prior (σprior), based on the assumption that participants estimate it correctly (Smeets et al. 2006), and the mean of the error prior (xprior) was set to zero. Fitting was initiated from the first movement end point after removal of visual information. Starting the fit from this point ensured that all movements used for the fit were from the same visual exposure, and it also minimized the effect of the initial rapid increase in error potentially caused by the sudden offset of full vision (Brown et al. 2003a, 2003b; Smeets et al. 2006), and so it should provide better parameter estimates. This approach is also consistent with Brown et al.'s (2003a) analysis of drift, where they analyzed rate of drift after the first trial without vision. However, because this approach mitigates the effects of early error on the fit, it may put the Smeets et al. (2006) model at a slight disadvantage compared with ours.1 This should be kept in mind when comparing the quality of the fits for the competing models.
To carry out the fits, we applied the “optim” function in R (R Core Team 2013), which uses a Nelder-Mead simplex algorithm, to minimize the sum of squared differences between the model prediction and the data points. All visual conditions were fit, and we obtained parameter estimates from each, which are reported in results.
RESULTS
Experiment 1
Total error accumulation as a function of visual condition and target type.
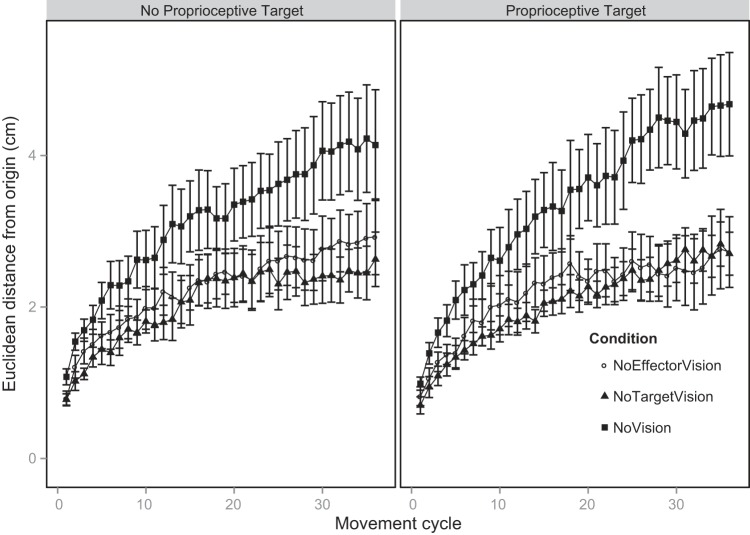
In Fig. 4 we show the accumulation of end-point error for each visual condition and for each target type. The pattern of drift is similar across target types, suggesting that the proprioceptive targets had little to no effect on the rate and magnitude of error accumulation. This observation is supported by an absence of any statistical effect of target type on the total drift [F(1,7) = 0.15, P = 0.70]. There was, however, an effect of visual condition on the total drift [F(2,14) = 18.11, P = 0.0001]. The post hoc analysis of the visual condition means showed that participants drifted more when they had no vision compared with when they had no target vision (P = 0.007) and they drifted more when they had no vision compared with when they had no effector vision (P = 0.002). The amount of drift did not significantly differ between NoTarget and NoEffector conditions (P = 0.56). [There was no interaction between target type and visual condition, F(2,14) = 0.81, P = 0.46, so we collapsed across target type prior to the post hoc analysis of the visual condition means.]
Fig. 4.
Group mean drift as a function of target type (No Proprioceptive Target, Proprioceptive Target) and visual condition (NoEffector, NoTarget, NoVision). Error bars represent SE (between-subject variability).
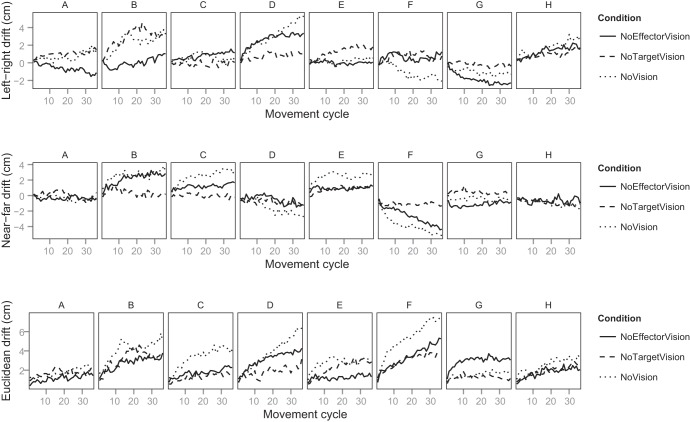
Figure 5 shows the drift for each participant in the No Proprioceptive Target condition. Drift is shown for the left-right dimension and the near-far dimension, and one can see that participants exhibit different directions and amounts of drift, a finding that is consistent with previous research on movement drift (Brown et al. 2003a; Smeets et al. 2006). The overall drift for each participant is shown in Fig. 5, bottom. While several participants show a pattern that is consistent with the mean pattern of drift (Fig. 4), there is variability among the participants. One participant (participant G), for instance, exhibits the most drift in NoEffector rather than NoVision. We can only speculate about the cause of this variability, but we suggest that part of it is due to motor noise (a parameter that we do not include in our model). In the absence of visual error feedback, there may be a random walk component to movement error (van Beers et al. 2013), and this effect may lead to larger drift accumulation on some trials than others, independent of visual condition. Accordingly, given enough trials for each participant in each visual condition, we would expect a reduction in the interparticipant variability. An alternative is that control strategies varied across participants, leading to a failure of our model in some cases. Ultimately, because we compare our model's ability and that of the Smeets et al. model to fit each participant's data in our cross-validation procedure (next section), the interparticipant variability does not compromise our ability to compare the two models.
Fig. 5.
Directional and Euclidean drift for all participants in experiment 1 for the No Proprioceptive Target condition. For left-right drift (top), positive indicates rightward and negative indicates leftward with respect to the target location. This is equivalent to constant error in the x-dimension. For near-far drift (middle), positive indicates farther from the participant and negative indicates nearer to the participant than the target. This is equivalent to constant error in the y-dimension. Euclidean drift (bottom) is the dimensionless distance of the effector from the target. Participants are indicated by letters A–H. For each participant, data were collapsed across the 3 target locations.
Comparison of drift data with active and passive drift models.
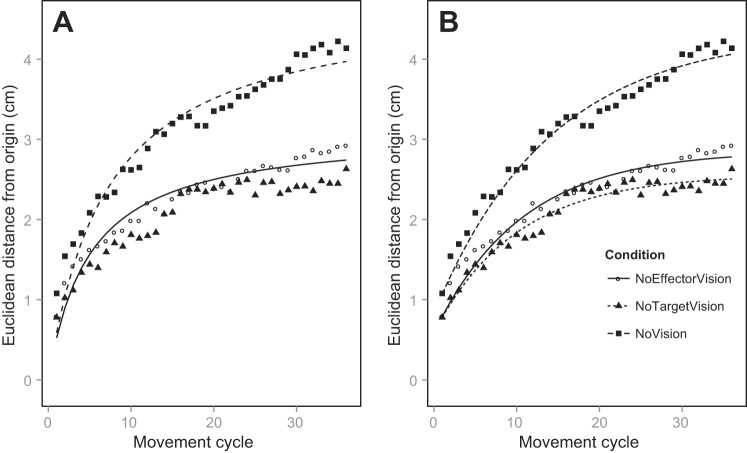
In Fig. 6 we show the fits of both models (the active Smeets et al. model and our passive model) to the drift data for the No Proprioceptive Target condition. For the Smeets et al. model, good fits are achieved for NoEffector and NoVision but not for NoTarget, where the modeled drift is essentially locked at zero. We expected a good fit for the NoEffector condition, as this is the condition for which Smeets et al.'s model was designed; parameter values that we observed (σ = 0.47 cm, b = 3.12 cm) were comparable to those from Smeets et al. (2006), and the error of the fit (the sum of squared residuals) was 0.62. For the NoVision condition, the fit produced a value of the intersensory bias parameter that is less plausible (σ = 0.56 cm, b = 9.5 cm), for it implies that participants have six more centimeters of intersensory bias in NoVision than they do in NoHand, but the error of the fit was reasonably low (1.35). No fitting was possible for the NoTarget condition, so the error was high (160.82). No fitting occurs for NoTarget because the model specifies that both the visual and proprioceptive estimates of the target decay as a function of the number of movements, and because the variances of vision and proprioception are assumed to be equal (Smeets et al. 2006), no drift can occur, no matter what values of σ and b are used.
Fig. 6.
Drift data (symbols) for the No Proprioceptive Target condition, along with least-squares fits (lines) for the active Smeets et al. (2006) model (A) and our passive model (B). The NoTarget condition fit is not presented for the active model, as the drift for that model is mathematically locked at zero.
For our passive model, we found good fits for all three visual conditions. In NoEffector we obtained parameter values of σsens = 0.96 cm and m = 0.26 cm and an error of 0.45 for the fit. In NoTarget we obtained parameter values of σsens = 0.92 cm and m = 0.24 cm and an error of 0.32 for the fit. In NoVision we obtained parameter values of σsens = 1.10 cm and m = 0.30 cm and an error of 0.66 for the fit.
Cross-validation (see methods) provided error values for Smeets et al.'s model of 38.47, 182.50, and 81.50 for NoEffector, NoTarget, and NoVision, respectively. The error values for our passive model were 35.00, 26.20, and 79.49 for NoHand, NoTarget, and NoVision, respectively. Except for the NoTarget condition, both models performed about equally well. Note, however, that for the fitting of Smeets et al.'s model to work in NoVision, the intersensory discrepancy (b) had to increase dramatically relative to the value in NoHand (see parameter values in previous paragraph), a physiologically implausible scenario.
Experiment 2
In Fig. 7 we show the effector's distance from the target as a function of movement cycle. As the figure shows, participants drifted substantially, by an amount that is comparable to NoVision in experiment 1; however, a direct comparison between experiments is probably not warranted, as different target locations and distances (which were self-selected in experiment 2) are involved in the two cases.
Fig. 7.

Movement drift for experiment 2. The solid line represents the least-squares fit of our passive model to the group mean drift (open circles). Drift for individual participants is shown by the dashed lines.
Figure 7 also shows the fit of our passive model to the data, which provided parameter estimates of σsens = 1.09 and m = 0.38. The quality of the fit was also very good, with a sum of squared residuals of 0.09 cm2.
DISCUSSION
The drift that we observed does not appear to support the model proposed by Smeets et al. (2006). Whereas their model predicts the most drift when the effector is occluded and the least drift when the target is occluded, we observed the most drift when both the effector and target were occluded, and we observed roughly equivalent amounts of drift when the effector or the target was occluded (experiment 1). Furthermore, our passive model was able to account for the drift in all three conditions, and it provided plausible parameter values for sensory error and motor bias. Smeets et al.'s model was also able to provide good fits to the NoEffector and NoVision conditions, but the parameter values needed to obtain these fits were not consistent with each other: a large modification in the intersensory discrepancy parameter was required.
In experiment 2, in which participants reached without vision to remembered proprioceptive locations, we observed substantial drift, even though the target of the movement was never visually specified. The data are difficult to reconcile with a drift model based on intersensory discrepancy, such as the Smeets et al. (2006) model. Our passive model, on the other hand, is not only conceptually consistent with the presence of drift in experiment 2 but was able to provide a good fit to the data, with parameter values that were comparable to those obtained in experiment 1. We believe that the results of both experiments provide strong support for our passive model of movement drift.
Causes of Movement Drift
The two models that we have compared in this study invoke very different mechanisms for movement drift. The Smeets et al. (2006) model relies on active error correction driven by an inherent discrepancy between vision and proprioception, whereas our model relies on a passive accumulation of error driven by an inherent motor bias. In Smeets et al.'s model, the error signal that causes the drift decreases the farther the hand moves from the target. In our model, the error signal that counteracts the drift increases the farther the hand moves from the target. Both models predict stabilization of drift as the hand moves farther from the target location.
Currently we can only speculate about the nature of the motor bias that we have proposed as driving movement drift. The motor bias appears to vary across participants and across locations in the workspace, and we suspect that it may be caused by error in the sensorimotor transformation phase of movement planning. To execute a reach to a visual target, for instance, the retinal coordinates of the target are thought to be transformed into body-centered coordinates; those coordinates are then integrated with the sensed position of the effector, after which a motor command can be generated (Andersen et al. 1993). Sensorimotor transformation is thought to involve a parieto-frontal network, with the posterior parietal cortex (PPC) playing an important role in the coding of both visual and proprioceptive target locations for reaching (Bernier and Grafton 2010). While much of the error that might occur during sensorimotor transformation is probably random, there is evidence that some of the error is systematic, and the systematic error appears to vary across participants (Soechting and Flanders 1989a, 1989b).
Soechting and Flanders (1989b) suggest that the systematic error arises at the stage of sensorimotor transformation when the target estimate relative to the body (an “extrinsic” coordinate frame) is converted to a change in the relative positions of the segments of the arm (an “intrinsic” coordinate frame). This transformation from extrinsic to intrinsic has been proposed to occur between the ventral premotor cortex and primary motor cortex (Kakei et al. 2003). In the context of our study, we are suggesting that this transformation error would arise in all conditions (NoVision, NoTarget, NoEffector) and that the differences in drift that emerge across the conditions are a function of the quality of the sensory feedback in each condition. That is, we would expect the neural underpinnings of the sensorimotor transformation to be consistent across the conditions of our study, and what would differ across conditions is the amount of correction applied subsequent to the accumulation of movement error. The error computation would likely involve the integration of visual, proprioceptive, and efferent information. The PPC has been implicated in both sensory integration and error correction (Desmurget et al. 1999; Mulliken et al. 2008; Pisella et al. 2000), so it is a plausible candidate for estimating the movement error. The finding that drift accumulates when sensory feedback is impoverished might imply that integration in the PPC weights motor expectation heavily, and that performance deteriorates if the motor expectation is uncalibrated.
The coding of target location can be influenced by gaze direction, and systematic errors in reaching can be caused by where the eyes are fixated relative to a remembered target (Henriques et al. 1998). Gaze direction is also related to hand localization during reaching (Bedard and Sanes 2009; DeSouza et al. 2000). Accordingly, some of the error in reaching that we observed in the present study may be caused by the position of the eyes during each trial. However, given that we observed comparable patterns of drift across visual conditions [when there was a real-time visual target (experiment 1), when there was no real-time target (experiment 1), and when the eyes were closed for the duration of the trial (experiment 2)] we do not think that gaze direction accounts for the majority of drift that we observed. To our knowledge, no study has yet examined the effect of gaze direction on movement drift, though there is indirect evidence that gaze behavior does not affect motor bias when the hand is seen versus unseen (Soechting and Flanders 1989a).
In Soechting and Flanders (1989a), participants reached to remembered visual targets with or without vision of their hand. Participants exhibited roughly equivalent amounts of end-point bias in the two cases despite the fact that gaze position was not controlled. This leaves three possibilities for their study and for ours (neither study recorded eye position): eye behavior did not differ between hand vision and no hand vision conditions; eye position differed between conditions but did not affect end-point bias; or eye position did differ and did impact error, but the combined effects of the eye-driven error and the motor error produced the same amount of bias in the two visual conditions. If either of the first two possibilities is true, and if we assume that eye behavior in our study was comparable to eye behavior in Soechting and Flanders (1989a), then gaze position does not confound our interpretation of the results from experiment 1. However, if the last possibility is true, then it means that the bias term in our model has a different source in each of our visual conditions. The absence of gaze recording in our study means that we cannot rule out this possibility. However, we would argue that the last possibility is the least likely, for it relies on the coincidence that different mechanisms led to equivalent amounts of error. Furthermore, Soechting and Flanders (1989a) found that participants could accurately locate the remembered target position with a visible pointer (as opposed to the reaching hand), suggesting that unrestricted gaze did not affect target localization and that end-point bias arose, rather, from a sensorimotor transformation error.
The previous paragraph argues against a significant role for gaze in the generation of error on each movement, but it does not directly address the role of gaze in the estimation of error at the end of each movement. Under normal reaching conditions, people tend to fixate the target they are reaching for (Land and Hayhoe 2001), but we know less about how the eyes behave when the target is unseen and/or the hand is unseen. A reasonable assumption is that, without visual targets, the eye position is more variable, and so we might expect more gaze variability in NoTarget and NoVision than in NoEffector of experiment 1. More eye movements would lead to more remapping of the remembered target locations, which might increase bias in the target position estimates and, accordingly, error estimation. That said, the comparable patterns of drift that we observed in NoVision (experiment 1), in which the eyes were open, and experiment 2, in which the eyes were closed, lead us to believe that the effect of more variable eye position was not large.
Finally, we note that our passive model of movement drift is consistent with the drift mechanism proposed by Brown et al. (2003a). They suggested that drift accumulates because proprioception for position sense is poor while proprioception for movement control is robust. After observing substantial drift in limb position following movement but relatively preserved trajectory formation, Brown et al. (2003a) proposed that “[t]he position control system relies more heavily on visually-specified limb position information and is fairly indifferent to small [proprioceptive] position errors, although it triggers corrections when larger, more categorical changes in limb position are sensed [via proprioception].” The results from the present study provide support for the idea that proprioceptive position sense is relatively poor and that error can therefore passively accumulate when visual error information is missing. Our results do not, however, allow us to comment on the relative reliability of proprioception for movement control, and so we remain neutral with respect to Brown et al.'s (2003a) suggestion that proprioception is used differently for position sense versus movement control.
Movement Drift When Effector Is Visible but Target Is Not
It may seem counterintuitive for the hand to drift when it is visible but the target is not (NoTarget). An alternative way of thinking about our model, a way that may be more appropriate for the NoTarget case, is that the aim point for the current movement is the aim point of the previous movement plus some motor bias and minus some correction. Viewed this way, the aim -point is updated for each movement based on the participant's belief about the quality of the preceding movement and the estimate of the separation between the aim point and the initial/remembered target location. (If the sensory estimate of the initial target location is poor, as would be expected when the target has disappeared, the new aim point will be strongly influenced by the end point of the previous movement.) As the separation between the aim point and the initial target location grows, the aim point will drift less and less. Computationally, this view of the model does not differ from the one outlined above (see Modeling). Conceptually, though, this view may be more in line with our intuition about performance when the hand is visible but the target is not: the effective target location drifts because it is an optimal combination of the remembered target location and the previous end point of the visible hand.
Challenges for Our Model
One challenge for our model is accounting for the absence of drift that occurs when people have full vision of their hand and the target. The sensory error based on combining independent estimates of the hand and target would be smallest in this condition (relative to NoEffector, NoTarget, and NoVision), but our model would still predict some drift if the error were calculated in this way. We think, however, that full vision presents a special case, because error between the visible hand and target can be coded retinotopically. No transformation of target location into the same coordinate system as the hand would be necessary. Error processing would not rely on egocentric localization of the target, and therefore the sensory acuity for the error could be extremely high (i.e., Vernier acuity). This is quite different from the kind of error processing that we assume underlies the drift pattern in experiments 1 and 2. Accordingly, we think that the failure of our model to account for full-vision performance does not undermine its validity for other feedback conditions.
Another important challenge for our model is explaining why people tend to drift in the same direction over multiple testing sessions (Smeets et al. 2006). A stable person-specific visual-proprioceptive discrepancy can account for this phenomenon quite nicely and appears to be supported by evidence that people have stable but idiosyncratic biases in their proprioceptive estimates of limb position (Rincon-Gonzalez et al. 2011; Vindras et al. 1998). [The applicability, however, of perceptually assessed estimates of proprioceptive bias to action-based use of proprioception is still not clear (Dijkerman and de Haan 2007; Jones et al. 2012).] We, on the other hand, have attributed drift consistency to a person-specific motor bias, an hypothesis we have not tested here but one that is consistent with evidence from Soechting and Flanders (1989a, 1989b) that errors in sensorimotor transformation produce biased reaching. These types of errors in sensorimotor transformation could be just as stable over time as the intersensory bias proposed by Smeets et al. (2006). Furthermore, the substantial drift that we observed in experiment 2, where there was no visual target (and thus no obvious source of intersensory bias), seems to weigh strongly in favor of our account.
It is possible that the drift we observed across different conditions is caused by different mechanisms. That is, the cause of drift in NoTarget may be different from the cause of drift in NoEffector. However, given the consistent patterns of drift that we observed across the three conditions of experiment 1 and the single condition of experiment 2—and in light of a single model's ability to account for all of these—we think that a single (passive) mechanism is the most parsimonious explanation. At the very least, we have outlined a compelling alternative to Smeets et al.'s (2006) model.
GRANTS
The research group is supported by Grant 2014SGR79 from the Catalan government. B. D. Cameron was supported by a Juan de la Cierva fellowship from the Spanish Government and Marie Curie Fellowship PCIG13-GA-2013-618407. J. López-Moliner was supported by an ICREA Academic Distinguished Professorship award and grant PSI2013-41568-P from MINECO.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: B.D.C. and J.L.-M. conception and design of research; B.D.C. performed experiments; B.D.C. analyzed data; B.D.C., C.d.l.M., and J.L.-M. interpreted results of experiments; B.D.C. and C.d.l.M. prepared figures; B.D.C. drafted manuscript; B.D.C., C.d.l.M., and J.L.-M. edited and revised manuscript; B.D.C., C.d.l.M., and J.L.-M. approved final version of manuscript.
Footnotes
We attempted to compensate for this by subtracting the first drift point from all values (to eliminate the early error) prior to fitting with the Smeets et al. model; however, the model was unable to accommodate the new slower rate of drift, and the fit deteriorated as a result. Accordingly, we do not report the fits for the modified data.
REFERENCES
- Andersen RA, Syder LH, Li CS, Stricanne B. Coordinate transformations in the representation of spatial information. Curr Opin Neurobiol 3: 171–176, 1993. [DOI] [PubMed] [Google Scholar]
- Bedard P, Sanes JN. Gaze and hand position effects on finger-movement-related human brain activation. J Neurophysiol 101: 834–842, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beers RJ, Sittig AC, Denier JJ. How humans combine simultaneous proprioceptive and visual position information. Exp Brain Res 111: 253–261, 1996. [DOI] [PubMed] [Google Scholar]
- Bernier PM, Grafton ST. Human posterior parietal cortex flexibly determines reference frames for reaching based on sensory context. Neuron 68: 776–788, 2010. [DOI] [PubMed] [Google Scholar]
- Brown LE, Rosenbaum DA, Sainburg RL. Limb position drift: implications for control of posture and movement. J Neurophysiol 90: 3105–3118, 2003a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown LE, Rosenbaum DA, Sainburg RL. Movement speed effects on limb position drift. Exp Brain Res 153: 266–274, 2003b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cameron BD, Franks IM, Inglis JT, Chua R. Reach adaptation to online target error. Exp Brain Res 209: 171–180, 2011. [DOI] [PubMed] [Google Scholar]
- Desmurget M, Epstein CM, Turner RS, Prablanc C, Alexander GE, Grafton ST. Role of the posterior parietal cortex in updating reaching movements to a visual target. Nat Neurosci 2: 563–567, 1999. [DOI] [PubMed] [Google Scholar]
- DeSouza JF, Dukelow SP, Gati JS, Menon RS, Andersen RA, Vilis T. Eye position signal modulates a human parietal pointing region during memory-guided movements. J Neurosci 20: 5835–5840, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dijkerman HC, de Haan EH. Somatosensory processes subserving perception and action. Behav Brain Sci 30: 189–201, 2007. [DOI] [PubMed] [Google Scholar]
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415: 429–433, 2002. [DOI] [PubMed] [Google Scholar]
- Henriques DY, Klier EM, Smith MA, Lowy D, Crawford JD. Gaze-centered remapping of remembered visual space in an open-loop pointing task. J Neurosci 18: 1583–1594, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones SA, Cressman EK, Henriques DY. Proprioceptive localization of the left and right hands. Exp Brain Res 204: 373–383, 2009. [DOI] [PubMed] [Google Scholar]
- Jones SA, Fiehler K, Henriques DY. A task-dependent effect of memory and hand-target on proprioceptive localization. Neuropsychologia 50: 1462–1470, 2012. [DOI] [PubMed] [Google Scholar]
- Kakei S, Hoffman DS, Strick PL. Sensorimotor transformations in cortical motor areas. Neurosci Res 46: 1–10, 2003. [DOI] [PubMed] [Google Scholar]
- Khan MA, Franks IM, Elliott D, Lawrence GP, Chua R, Bernier PM, Hansen S, Weeks DJ. Inferring online and offline processing of visual feedback in target-directed movements from kinematic data. Neurosci Biobehav Rev 30: 1106–1121, 2006. [DOI] [PubMed] [Google Scholar]
- Land MF, Hayhoe M. In what ways do eye movements contribute to everyday activities? Vision Res 41: 3559–3565, 2001. [DOI] [PubMed] [Google Scholar]
- Lawrence MA. ez: Easy analysis and visualization of factorial experiments. R package version 4.2-2: http://CRAN.R-project.org/package=ez, 2013. [Google Scholar]
- Mulliken GH, Musallam S, Andersen RA. Forward estimation of movement state in posterior parietal cortex. Proc Natl Acad Sci USA 105: 8170–8177, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paillard J, Brouchon M. Active and passive movements in the calibration of position sense. In: The Neuropsychology of Spatially Oriented Behavior, edited by Freedman SI. Homewood, IL: Dorsey, 1968, p. 37–55. [Google Scholar]
- Pisella L, Gréa H, Tilikete C, Vighetto A, Desmurget M, Rode G, Boisson D, Rossetti Y. An “automatic pilot” for the hand in human posterior parietal cortex: toward reinterpreting optic ataxia. Nat Neurosci 3: 729–736, 2000. [DOI] [PubMed] [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing, http://www.R-project.org/, 2013. [Google Scholar]
- Rincon-Gonzalez L, Buneo CA, Helms Tillery SI. The proprioceptive map of the arm is systematic and stable, but idiosyncratic. PLoS One 6: e25214, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossetti Y, Desmurget M, Prablanc C. Vectorial coding of movement: vision, proprioception, or both? J Neurophysiol 74: 457–463, 1995. [DOI] [PubMed] [Google Scholar]
- Saunders JA, Knill DC. Humans use continuous visual feedback from the hand to control fast reaching movements. Exp Brain Res 152: 341–352, 2003. [DOI] [PubMed] [Google Scholar]
- Smeets JB, Van Den Dobbelsteen JJ, de Grave DD, van Beers RJ, Brenner E. Sensory integration does not lead to sensory calibration. Proc Natl Acad Sci USA 103: 18781–18786, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soechting JF, Flanders M. Sensorimotor representations for pointing to targets in three-dimensional space. J Neurophysiol 62: 582–594, 1989a. [DOI] [PubMed] [Google Scholar]
- Soechting JF, Flanders M. Errors in pointing are due to approximations in sensorimotor transformations. J Neurophysiol 62: 595–608, 1989b. [DOI] [PubMed] [Google Scholar]
- van Beers RJ, Brenner E, Smeets JB. Random walk of motor planning in task-irrelevant dimensions. J Neurophysiol 109: 969–977, 2013. [DOI] [PubMed] [Google Scholar]
- van Beers RJ, Sittig AC, Denier van der Gon JJ. The precision of proprioceptive position sense. Exp Brain Res 122: 367–377, 1998. [DOI] [PubMed] [Google Scholar]
- Vindras P, Desmurget M, Prablanc C, Viviani P. Pointing errors reflect biases in the perception of the initial hand position. J Neurophysiol 79: 3290–3294, 1998. [DOI] [PubMed] [Google Scholar]
- Wann J, Ibrahim S. Does limb proprioception drift? Exp Brain Res 91: 162–166, 1992. [DOI] [PubMed] [Google Scholar]
- Wilson ET, Wong J, Gribble PL. Mapping proprioception across a 2D horizontal workspace. PLoS One 5: e11851, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]