A moving blocker-based strategy for simultaneous megavoltage and kilovoltage scatter correction in cone-beam computed tomography image acquired during volumetric modulated arc therapy

Abstract

Purpose

To evaluate a moving blocker-based approach in estimating and correcting megavoltage (MV) and kilovoltage (kV) scatter contamination in kV cone-beam computed tomography (CBCT) acquired during volumetric modulated arc therapy (VMAT).

Methods and materials

During the concurrent CBCT/VMAT acquisition, a physical attenuator (i.e., "blocker") consisting of equally spaced lead strips was mounted and moved constantly between the CBCT source and patient. Both kV and MV scatter signals were estimated from the blocked region of the imaging panel, and interpolated into the unblocked region. A scatter corrected CBCT was then reconstructed from the unblocked projections after scatter subtraction using an iterative image reconstruction algorithm based on constraint optimization. Experimental studies were performed on a Catphan^® phantom and an anthropomorphic pelvis phantom to demonstrate the feasibility of using a moving blocker for kV-MV scatter correction.

Results

Scatter induced cupping artifacts were substantially reduced in the moving blocker corrected CBCT images. Quantitatively, the root mean square error of Hounsfield unites (HU) in seven density inserts of the Catphan phantom was reduced from 395 to 40.

Conclusions

The proposed moving blocker strategy greatly improves the image quality of CBCT acquired with concurrent VMAT by reducing the kV-MV scatter induced HU inaccuracy and cupping artifacts.

Gantry-mounted cone-beam computed tomography (CBCT) has become a valuable tool in image-guided radiation therapy [1, 2]. Currently, it is widely used for patient positioning before daily treatment [3, 4]. It is also used frequently for verification imaging after beam delivery to quantify intrafraction motion [3, 4], which is important for continuous quality assurance in treatment procedures such as lung stereotactic body radiotherapy (SBRT) [5] and prostate intensity modulated radiotherapy (IMRT) [6]. However, CBCT acquired either before or after treatment does not provide "true" anatomical information during beam delivery. As rotational radiation therapy techniques such as volumetric modulated arc therapy (VMAT) [7] gain popularity in IMRT and SBRT, efforts have been made to acquire kilovoltage (kV) CBCT during beam delivery [8, 9], in order to provide 3D anatomy in real time for more accurate plan verification and adaptive radiation therapy (ART) [10, 11]. However, during concurrent CBCT/VMAT acquisition a large amount of scattered photons from the MV beam can reach the kV imaging detector panel [12, 13], along with scattered photons from the kV imaging source. Similar to the effect of kV scatter, the MV scattered photons further degrade the image quality by aggravating the cupping artifact, which manifests as decreased image intensity in the reconstructed CBCT images. This hinders the potential application of CBCT for quantitative tasks such as plan verification and ART. Therefore, it is important to correct kV-MV scatter contamination in CBCT images.

In our previous studies [14, 15], a moving blocker-based approach was proposed to estimate the kV scatter signal and reconstruct the complete volume within the field of view (FOV) from a single CBCT scan. In that approach, a beam attenuation blocker was inserted between an X-ray source and a patient, and was moved constantly during CBCT acquisition. The signal measured in the blocked region on the detector panel was assumed to be contributed by scatter only and was used to estimate the scatter in the unblocked region through interpolation. The primary signal in the unblocked region was then obtained via subtracting the estimated scatter signal, and then used for CBCT reconstruction. With a proper design of the moving blocker, the acquired CBCT projection can provide needed information to reconstruct the whole object within FOV. Essentially, the missing information at one projection is effectively compensated by measurements from other projections. In this work, we propose to use the moving blocker scatter correction strategy to simultaneously estimate and correct the on-treatment MV and kV scatter in CBCT projections acquired with concurrent VMAT without interrupting the MV radiation delivery. During concurrent CBCT/VMAT acquisition, distribution of MV scatter on the kV CBCT detector is undisturbed by the moving blocker. Therefore, the detected signal in the blocked regions of the kV detector is assumed to be contributed by scattered photons from both the MV VMAT treatment beam and kV imaging photons. As both scatter signals are smooth, low-frequency signals [12, 13, 16, 17], scatter in the unblocked regions can be estimated through interpolation and corrected afterwards.

Materials and Methods

Moving blocker-based scatter correction scheme

In the proposed moving blocker system, a lead blocker is inserted between the CBCT source and the patient and moves back and forth along the gantry rotation axis during image acquisition. Motion of blocker was simulated to test the feasibility of the system for kV-MV scatter correction. Scatter signal detected in the blocked region was used to estimate the scatter fluence of the unblocked region through cubic B-spline interpolation. Primary signal in the unblocked region was obtained by subtracting the estimated scatter signal. A line integral of each ray in the unblocked region was then calculated by logarithmic transformation. In this study, an iterative image reconstruction algorithm based on constrained optimization and total variation minimization (CO-TV) [18] was adopted to reconstruct CBCT from the partially blocked projection data [15]. Details of the blocker design, motion simulation and scatter estimation are described in the ‘Supplement material’.

CBCT acquisitions

Both a Catphan^® 600 phantom (The Phantom Laboratory Inc., Salem, NY) and an anthropomorphic pelvis phantom CIRS 801-P (Computerized Imaging Reference Systems Inc., Norfolk, VA) (see ‘Supplement material’ for phantom detail) were used for the concurrent CBCT/VMAT acquisition. The acquisitions were performed on a TrueBeam LINAC system (Varian Medical Systems, Inc, Palo Alto, CA) in its Developer Mode. XML code was developed to enable acquisition of kV projection images during the delivery of VMAT. Concurrently acquired CBCT scans with moving-blocker-scatter-correction (mb-kVMV-CBCT) and without moving-blocker or scatter correction (kVMV-CBCT) were both performed and reconstructed with CO-TV. Details of the VMAT plan and CBCT acquisition were summarized in ‘Supplement material’. KV CBCT scans without blocker or scatter correction (kV-CBCT) were also performed and reconstructed with CO-TV for comparison. In addition, standard clinic kV CBCTs (cCBCT) with adaptive deconvolution scatter correction [19] and Feldkamp-Davis-Kress (FDK) reconstruction, as provided by the manufacturer, were also included. It is noted that concurrent kV-MV acquisition is not currently supported in the clinical mode. Therefore, the benchmark image provided by the manufacturer software was acquired under ordinary conditions, where only kV scatter was measured and corrected thereafter. Fan-beam multi-detector CTs (MDCT) were acquired with a GE Discovery ST CT scanner (GE Medical System, Milwaukee, WI) to serve as the benchmark. Evaluations of the CBCTs, such as HU accuracy, contrast-to-noise ratios (CNRs), image resolution and non-uniformity, were performed, as described in ‘Supplement material’.

Results

Figure 1 shows reconstruction results of the Catphan phantom. Cupping artifacts are observed in the scatter contaminated images (Figs. 1(a) and 1(b)) with lowered image intensity and contrast as compared with the MDCT (Fig. 1(d)). It can also be observed that cupping artifacts in the kVMV-CBCT are more severe than that in the kV-CBCT. In contrast, image intensity and contrast are better retained and cupping artifacts are greatly suppressed in the mb-kVMV-CBCT (Fig. 1(c)) after scatter correction with the moving blocker system. Quantitative measurements of image intensity/HU accuracy, as represented by the root-mean-square-error (RMSE) of density insert HUs and the 25%–75% HU error range, are summarized in Tab. 1. With cupping artifacts, the RMSE is 136HU in the kV-CBCT image. MV scatter in concurrent CBCT/VMAT further degrades the image quality, with a RMSE of 395HU in the reconstructed kVMV-CBCT image. After applying the proposed scatter correction strategy, the RMSE is reduced to 40HU. The 25%–75% HU error range shows similar results.

Fig. 1.

One axial slice of the Catphan® 600 phantom sensitometry module: (a) CO-TV reconstruction from kV scatter-contaminated projection data (kV-CBCT); (b) CO-TV reconstruction from kV-MV scatter-contaminated CBCT/VAMT projection data (kVMV-CBCT); (c) CO-TV reconstructed from kV-MV scatter-corrected moving blocker CBCT/VMAT projection data (mb-kVMV-CBCT); (d) benchmark fan-beam MDCT image; (e) standard clinic kV CBCT image (cCBCT). Density inserts labeled in (a) were used for evaluating HU accuracy. Display widow [−600, 600] HU.

Table 1.

Comparison of the HUs between CBCTs and MDCT with the Catphan® 600 phantom sensitometry module. RMSE was calculated within 6 density inserts delineated in Fig. 1(a) and the 25~75% absolute HU difference was measured within the slice shown in Fig. 1.

	Delrin	Teflon	Air	PMP	LDPE	Polyst -yrene	RMSE	25~75% diff
MDCT	368	972	−975	−163	−73	−16	-	-
kV-CBCT	242	726	−790	−145	−57	−25	136	35~73
kVMV-CBCT	27	242	−530	−248	−284	−211	395	209~362
mb-kVMV-CBCT	423	1052	−958	−154	−77	−13	40	14~37
cCBCT	342	935	−996	−192	−105	−49	33	13~36

CNRs of the density inserts are summarized in Tab. 2. It shows that the image contrast of the concurrent VMAT/CBCT improved as the kV-MV scatter was corrected by the moving blocker strategy. Image non-uniformity measurements are summarized in Tab. 2. Non-uniformity measurements in CO-TV reconstructed kV-CBCT, mb-kVMV-CBCT and MDCT are all very low as compared to the kVMV-CBCT images, which suggest that these images are extremely uniform. At this level of uniformity, there is no visible difference among them, as shown in both Fig. 1 and 3. Higher uniformity in CO-TV reconstructed images could be caused by the regularization of the TV term, which strongly encourages the smoothness of a piece-wise region such as the region used in the non-uniformity calculation. The high uniformity of kV-CBCT may also due to a built-in collimator on the Varian flat-panel detector, which eliminates large-angle scatter photons. Nevertheless, uniformity in kVMV-CBCTs improved after employing the proposed moving blocker strategy.

Table 2.

Comparison of the image non-uniformity and CNR of 6 density inserts of the Catphan® 600 phantom sensitometry module.

	Non- uniformity	CNR
		Delrin	Teflon	Air	PMP	LDPE	Polyst -yrene
MDCT	0.009	34.2	120.8	157.6	41.8	28.5	20.5
kV-CBCT	0.002	31.9	123.3	162.7	40.9	24.4	18.3
kVMV-CBCT	0.036	30.0	70.6	74.2	21.3	28.2	14.4
mb-kVMV-CBCT	0.001	37.6	125.3	155.3	41.8	30.3	21.9
cCBCT	0.027	39.0	120.1	144.2	34.1	22.2	14.5

Fig. 3.

One axial slice of the anthropomorphic pelvis phantom: (a) CO-TV reconstruction of kV-CBCT; (b) CO-TV reconstruction of kVMV-CBCT; (c) CO-TV reconstructed of mb-kVMV-CBCT; (d) benchmark fan-beam MDCT image; (e) standard cCBCT image. Display widow [− 500, 1000] HU. Phantom dimension shown in this slice is 355×218 mm².

Figure 2(b) shows the MTF measurement of each CBCT of a point-like structure in the Catphan phantom shown in Fig. 2(a). It shows that the image resolution of CBCTs reconstructed by CO-TV is enhanced as compared to the cCBCT reconstructed by the standard FDK algorithm.

Fig. 2.

(a) a point-like structure in Catphan phantom used for MTF measurement. (b) MTF of each reconstructed CBCT image.

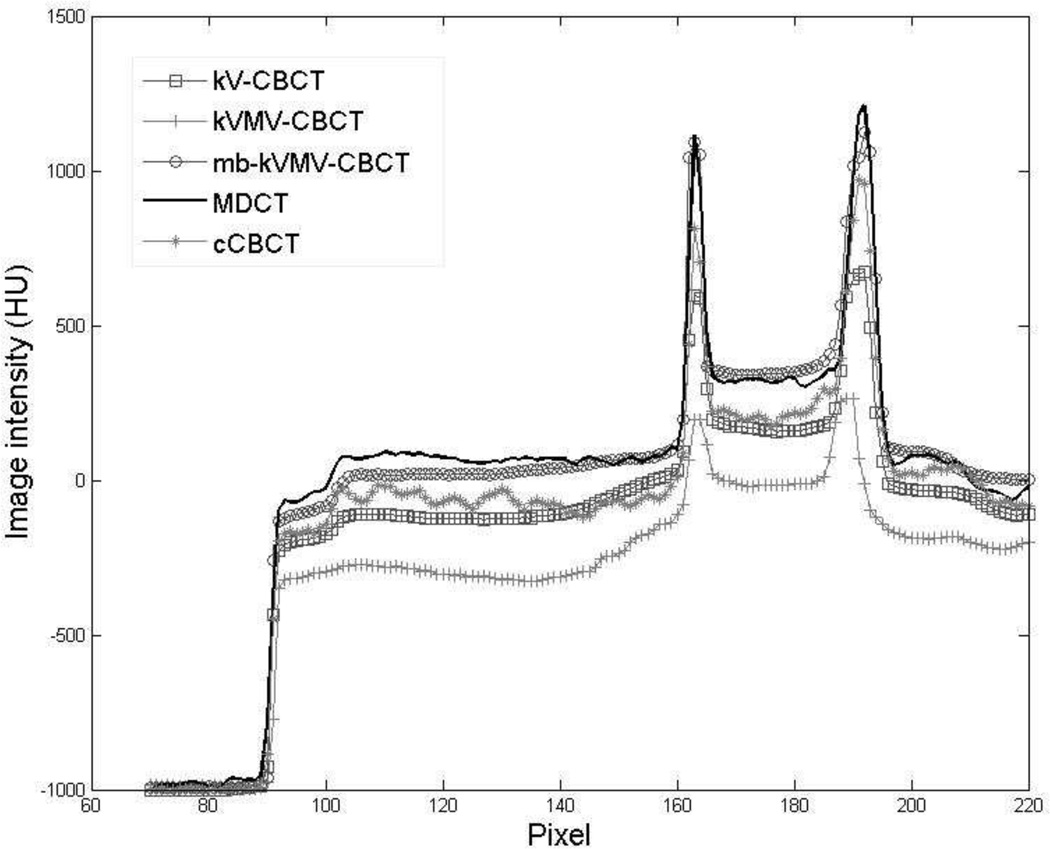
Figure 3 shows the reconstruction results of the pelvis phantom. The images acquired without the blocker or scatter correction, as shown in Fig. 3(a) and (b), are degraded by severe cupping/streaking artifacts caused by either the kV scatter alone or both the kV-MV scatter contamination. The image intensity of both soft tissues and bony structures decreases dramatically, especially in the kV-MV scatter contaminated CBCT (Fig. 3(b)). In contrast, cupping artifacts are greatly suppressed in mb-kVMV-CBCT (Fig. 3(c)). A horizontal profile of each image in Fig. 3(a)–(e) was plotted in Fig. 4, to further illustrate the effectiveness of the proposed moving blocker scatter correction strategy.

Fig. 4.

Comparison of the horizontal profiles in Fig. 3(a)–(e), as indicated by a white dashed line in Fig. 3(d).

Discussion

In this study, a moving blocker-based scatter correction strategy is proposed to correct MV and kV scatter simultaneously in a CBCT acquired with concurrent rotational radiation therapy, i.e., VMAT. In contrast to previously proposed kV scatter correction methods [14, 15], the scattered photons of the MV treatment beams which reached the kV detector panel were corrected together with kV scatter. In such acquisition geometry, the MV scatter distribution is not affected by the blocker. Therefore, the partial distribution of the MV scatter is able to be detected in the blocker shadow, although it cannot be distinguished from the kV scatter. Experimental studies were performed on a Catphan phantom and an anthropomorphic pelvis phantom. Results of both phantom studies have shown that the MV scatter further degrades the CBCT image quality by increasing the HU inaccuracy and decreasing the image contrast, in addition to the artifacts caused by kV scatter. The proposed moving blocker strategy greatly improves the image quality of CBCT acquired concurrently with radiation therapy by reducing the kV-MV scatter induced HU inaccuracy.

It is noted that the cCBCT provided by the manufacturer with analytical scatter correction showed much improved HU accuracy and image quality in the Catphan phantom study (Fig. 1(e)). However, since concurrent VMAT/CBCT delivery isn’t in current clinical use, no standard MV scatter correction tool is provided by the manufacturer. In addition, the same algorithm didn’t perform equally well on the pelvis phantom. Significant cupping artifacts are observed in Fig. 3(e). Blocky noise shown in CO-TV reconstructed Catphan CBCTs (Fig. 1 (a)–(c)) is caused by the TV penalty as it leads to a piecewise constant solution. One potential solution is to incorporate a higher-order penalty such as the Hessian penalty [20]. The round structure shown in non-scatter-corrected pelvis phantom CBCTs (Fig. 3(a) and 3(b)) was caused by data inconsistency at the boundary of half-fan CBCT FOV [21]. KV and/or MV scatter induced inconsistencies in different projection angles would aggravate this artifact, which can be corrected by a strategy proposed by Yan et al [21]. On the other hand, the scatter corrected image showed improved data consistency and thereafter a less pronounced ring in the reconstructed image (Fig. 3(c) and 3(e)).

It is also noted that the HU values of “air” inserts in the Catphan phantom increased in the scatter contaminated CBCT images. This inconsistency is introduced by the reconstruction algorithm, which enforces positive line integrals during preprocessing. For example, when a line from an X-ray source to a detector passes through the air cavity, the line integral L is calculated as log(I₀/I), where I is the photon received by the detector and I₀ is the emitted photon from the source. In the presence of scatter, it is possible that I=I_prim+I_scatter>I₀, where I_prim is the attenuated primary photon through the line and I_scatter is the scattered photons received by the same detector. Therefore, the line integral will be smaller than 0, which violates the physical meaning of the line integral. In this case, L is enforced to be 0 during the preprocessing step, which introduces a positive bias in the system. Eventually, the bias accumulates in the air cavity region of the reconstructed phantom CBCT, which makes the HU value of air larger than −1000.

Compared to the kV scatter, estimation of the MV scatter is much more complicated. It depends not only on the geometry of the imaging object and MV beam energy, but also on the field shape and dose rate of the MV beam, which keep changing in a dynamic VMAT plan to obtain an optimized dose distribution. Therefore, it is challenging to use model-based algorithms to estimate MV scatter, such as kernel-based scatter estimation [22, 23] and Monte Carlo simulation [24]. On the other hand, measurement-based scatter correction strategies provide practical solutions. Recently, two studies [12, 13] proposed MV scatter estimation methods to correct MV scatter contamination in a kV CBCT acquired with concurrent rotational radiation therapy. Both of these methods are based on the MV scatter measured during kV-unexposed frames. One suggested alternating the kV pulse sequence to disable the kV source in every other frame [13]. During the kV-unexposed frames, only MV scatters, noise and artifacts will be measured and subsequently subtracted from the neighboring kV-exposed frames. The other study [12] measured the MV scatter by acquiring a set of kV-off projection images taken during one VMAT treatment fraction. Then the MV-scatter-only images were used to correct the corresponding kV-MV projections acquired in the following VMAT fractions [12]. The MV scatter estimation accuracy of the former method [13] is limited by the dynamically updating field shape and dose rate of the MV beam. The latter one has limited applications in hypofractionated treatment. Its accuracy may not be guaranteed due to patient geometry change over a treatment course. In addition to the methods based on MV scatter measurements, an effort has also been made to acquire MV-scatter-free kV CBCT images by alternating the MV beam delivery and kV projection data acquisition [25]. However, interruption of the MV irradiation increases treatment time and complicates the LINAC control system. Furthermore, all the above-mentioned methods deal with the MV scatter only but not the kV scatter. In addition, higher CNR results of the current study, as compared to the above-mentioned strategies [13, 25], also suggest that kV scatter can affect the image quality, although the difference is partially due to the noise suppression enforced by TV regularization. Therefore, an extra step of kV scatter correction is still needed to further enhance the image quality of kV CBCT. In contrast, our proposed moving blocker-based scatter correction strategy doesn’t interfere with VMAT delivery, nor is it limited by dynamic MV delivery or patient geometry. More importantly, the proposed strategy simultaneously corrects both the MV and kV scatter. Other measurement-based algorithms proposed for kV CBCT scatter correction, such as a synchronized-moving-grid system [26, 27], may also be translated for kV-MV scatter correction in the concurrent CBCT/VMAT acquisition.

In our previous studies, two reconstruction algorithms, CO-TV [15] and PWLS-TV [14], were proposed for partial projection reconstruction. Both algorithms showed comparable performance on noise/artifacts suppression, while the CO-TV costs much less computation time than PWLS-TV. Therefore we switched back to CO-TV for image reconstruction in this study. Currently, the reconstruction algorithm is coded to run sequentially with C++. It takes about 5.5 hours for the CO-TV to reconstruct a CBCT of the pelvis phantom with a 3.07Hz Intel Core i7 CPU. However, it is feasible to implement the reconstruction algorithm in a parallel fashion for graphic processing units (GPU) [28] or GUP clusters [21] application, which will make the proposed reconstruction algorithm fast enough for clinic implementation. Based on a multi-GPU study of a similar CBCT reconstruction via total variation by Yan et al, reconstruction of our pelvis data could be finished within 1 min.

The MV VMAT beams used in this work were all 360° full arcs, which was essential for half-fan CBCT reconstruction. In circumstances where the treatment arc doesn’t rotate through a full circle, the arc can be padded to 360° with kV acquisition only. On the other hand, a full-fan CBCT scan needs only 200° of kV acquisition, which can be scheduled during any portion of the 200° gantry rotation. In future applications, acquisition of X-ray projections could be scheduled at angles with equal intervals to eliminate angle-wise over- or under-sampling. In the situation of comparable number of projections and identical X-ray energy and tube current-time, dose to patient from the mb-kVMV-CBCT scans were half of the kV-CBCT scans, due to the attenuation blocker between the CBCT source and patient, where half of the incidental photons of the kV X-ray beam were blocked by the attenuator. These simple modifications to the concurrent acquisition won’t significantly increase the complexity of the plan nor prolong the delivery time.

In contrast to our previous experimental study on an Elekta Synergy XVI system [14], the motor-controlled blocker system cannot be mounted on the Varian TrueBeam system used in this work at this moment. Therefore, experiments were performed using multiple scans with a manually shifted stationary blocker and afterwards data sorting. This work can be considered as a "proof-of-concept" study. Similar simulation was used in our first moving blocker study [15]. In another previous study [14], a real moving blocker system was implemented and evaluated, and the system performed similarly to the earlier “proof-of-concept” experiment on kV scatter correction. Hence, it is reasonable to conclude from the current results of this ‘moving’ blocker experiment that a moving blocker-based scatter correction strategy can successfully correct the kV-MV scatter in a CBCT acquired concurrently with VMAT. We plan to modify the design of the blocker system so that it can be mounted on the Varian TrueBeam system. An experimental study with a true moving blocker system will be performed in a future study.

In this work, we performed the moving blocker scatter correction on a virtually human male pelvis phantom that mimicked the tissue/organ density and attenuation precisely, in addition to a standard quality assurance phantom. All anatomical dimensions of the phantom are based on The Visible Human Project (VHP) data sets that serve as a reference for the study of human anatomy. Since the size and heterogeneity of the phantom are equivalent to human beings, we expect that similar results of the pelvis phantom study could be obtained in a pelvic patient study. A patient study could be performed in the future when concurrent CBCT/VMAT delivery is available in ‘Clinic Mode’, as well as when the aforementioned moving blocker system becomes available.

In summary, the moving blocker-based scatter correction strategy has been proved to provide a simple solution to correct kV-MV scatter simultaneously in CBCTs acquired with concurrent rotational radiation therapy. High-quality CBCT acquired concurrently with VMAT treatment provides true anatomical information during radiation treatment. This provides a valuable tool for plan verification and ART applications [29].