Single-Parent Households and Children’s Educational Achievement: A State-Level Analysis

Abstract

Although many studies have examined associations between family structure and children’s educational achievement at the individual level, few studies have considered how the increase in single-parent households may have affected children’s educational achievement at the population level. We examined changes in the percentage of children living with single parents between 1990 and 2011 and state mathematics and reading scores on the National Assessment of Educational Progress. Regression models with state and year fixed effects revealed that changes in the percentage of children living with single parents were not associated with test scores. Increases in maternal education, however, were associated with improvements in children’s test scores during this period. These results do not support the notion that increases in single parenthood have had serious consequences for U.S. children’s school achievement.

1. Introduction

Two well-known facts provide a rationale for the current study. First, the percentage of children living with single parents increased substantially in the United States during the second half of the 20^th century. Only 9 percent of children lived with single parents in the 1960s—a figure that increased to 28 percent in 2012 (Child Trends, 2013). Given current trends, about of half of all children will spend some time living with single parents before reaching adulthood (McLanahan and Percheski, 2008). Second, research shows that children in single-parent households score below children in two-parent households, on average, on measures of educational achievement (Amato, 2005; Brown, 2010; McLanahan and Sandefur, 1994). The combination of these two observations suggests that the rise in single parenthood has lowered (or slowed improvements in) the educational achievement of children in the United States.

Some observers have claimed that the rise of single-parent families (as reflected in high rates of divorce and nonmarital childbearing) is the primary cause of school failure and related problems of delinquency, drug use, teenage pregnancies, poverty, and welfare dependency in American society (Blankenhorn, 1995; Fagan, 1999; Pearlstein, 2011; Popenoe, 2009; Whitehead, 1997). Consider the following statements:

Very high rates of family fragmentation in the United States are subtracting from what very large numbers of students are learning in school and holding them back in other ways. This in turn is damaging the country economically by making us less hospitable to innovation while also making millions of Americans less competitive in an increasingly demanding worldwide marketplace

(Perstein, 2011, p. xiii)

Fatherlessness is the most harmful demographic trend of this generation. It is the leading cause of declining child well-being in our society. It is also the engine driving our most urgent social problems, from crime to adolescent pregnancy to child sexual abuse to domestic violence against women

(Blankenhorn, 1995, p. 1).

Marital and family stability is undeniably linked to economic prosperity for American families… The effects of marital breakdown on national prosperity and the well-being of individual children are like the action of termites on the beams in a home’s foundation: They are weakening, quietly but seriously, the structural underpinnings of society

(Fagan, 1999).

How strong is the evidence to support these claims? Although dozens (perhaps hundreds) of studies have examined associations between family structure and children’s educational achievement at the individual level, few studies have considered whether single parenthood is linked to declines in children’s educational achievement (or other forms of well-being) at the aggregate level. The purpose of the current study is to assess whether changes in the percentage of children living with single parents were related to changes in children’s scores on the National Assessment of Educational Progress (NAEP) between 1990 and 2011. To address this question, we conducted a state-level analysis of NAEP data using statistical models with state and year fixed-effects.

2. Background

A small number of studies have suggested that single parenthood has problematic consequences for children’s school performance at the aggregate or societal level. Using multilevel modeling, Pong (1997, 1998) found that U.S. students performed more poorly on math and reading achievement tests in schools with high proportions of children from single-parent families, even after controlling for school socioeconomic status and other school characteristics. Bankston and Caldas (1998) obtained comparable results with aggregate data on general academic achievement from students in Louisiana. In a cross-national study, Pong, Dronkers, and Hampden-Thompson (2003) found that single-parent family status was negatively associated with math and science achievement scores in nine out of 11 countries. Moreover, the gap in achievement between children with one rather than two parents was smaller in countries with more supportive social policies, such as family and child allowances and parental leave. These four studies are useful in showing that single parenthood and academic performance are associated within schools and countries. None of these studies, however, used longitudinal data to see if increases in single parenthood are accompanied by declines in the aggregate level of student performance.

Several studies have shown that the rise in the percentage of children living with single parents since the 1960s was related to an increase in child poverty in the U.S., although the strength of this association varies with the particular years studied (Eggebeen and Lichter, 1991; Iceland, 2003; Martin, 2006; Thomas and Sawhill, 2005). Given that single parents (usually mothers) are more likely than married mothers to be poor, this result is not surprising. Nevertheless, the rise in child poverty associated with single parenthood since the 1960s may have had negative consequences for children’s educational outcomes.

Several good reasons exist for assuming that the number of parents in a household affects children’s academic achievement (for reviews, see Amato, 2010; Brown 2010; McLanahan and Percheski 2008). First, children in single-parent households have a lower standard of living than do children in two-parent households. Family income, in turn, is a good predictor of children’s school grades and test scores. Second, parents are important sources of social capital and provide many resources to children, including emotional support, encouragement, everyday assistance, and help with homework. Parents’ provision of social capital, in turn, is positively associated with children’s school success. Children who live with single parents, however, have less access to these social resources, in general, than do children with two parents in the household. Finally, most children with single parents have experienced the disruption of their parents’ unions, and many of these children endure additional parental transitions before reaching adulthood. The cumulative amount of household instability or “turbulence” in children’s lives is associated with a variety of problematic outcomes, including school performance and educational attainment.

Selection provides an alternative explanation. Growing up in poverty increases the risk of becoming a single parent as well as the risk of academic failure for one’s children. In addition, some parents have personal traits that predict poor academic outcomes for children, such as low cognitive ability, personality disorders, alcohol or substance use problems, and poor social and parenting skills. These traits also increase the risk of relationship disruptions and the formation of single-parent households. Because these traits can be causes of single parenthood as well as problematic child outcomes, the association between family structure and children’s academic achievement is likely to be at least partly spurious.

Researchers have adopted a variety of strategies to assess whether the links between family structure and child outcomes are causal or spurious, including the use of fixed effects models to control for unmeasured time-invariant variables. Results from studies using fixed effects models are mixed, however, with some suggesting that associations between family structure and child outcomes are spurious (Aughinbaugh, Pierret, and Rothstein, 2005; Bjorklund and Sundstrom, 2006; Bjorklund, Ginther, and Sundstrom, 2007), and others supporting a causal interpretation (Amato and Anthony, 2014; Cherlin, Chase-Lansdale, and McRae, 1998; Ermisch and Francesconi, 2000; Gennetian, 2005). After reviewing studies that used fixed effects models and other methods to adjust for unobserved heterogeneity, McLanahan, Tach, and Schneider (2013) concluded that father absence probably increases children’s antisocial behavior but may not affect children’s cognitive outcomes and academic performance. This debate in the literature is unlikely to be resolved in the near future, and most reviewers have concluded that a combination of selection and causal factors are responsible for the links between family structure and children’s well-being (e.g., Amato 2010; McLanahan and Percheski, 2008; McLanahan et al., 2013).

2. The Current Study

The current study examines associations between the percentage of children living in single-parent households and children’s test scores on the NAEP. Because mathematical and reading skills are central to children’s school success, we focus on trends in math and reading scores in grades 4 and 8. State level data on these outcomes have been available since the early 1990s.

Analyzing data at the state level makes it possible to determine if the increase in single parenthood in the United States since 1990 was associated with declines in children’s test scores in the general population. This goal differs from most previous studies in this literature, which have examined links between family structure and school achievement among individual children. The current study attempts to answer the question, “Has the increase in single parenthood lowered the educational achievement of children in the U.S.?” rather than, “Do children living with single parents have lower levels of educational achievements than children living with two parents?”

A disadvantage of using population-level data involves the well-known ecological fallacy, or the possibility that associations observed at the aggregate level do not hold at the individual level. An offsetting advantage, however, is that population-level data are less susceptible to selection effects than are individual-level data. If associations observed at the individual level are due mainly to the self-selection of troubled adults into single parenthood, then children’s aggregate-level test scores will not necessarily decline. Because the children of troubled parents will be disadvantaged irrespective of what type of families they reside in, increases in the proportion of single-parent households would have few consequences for children’s aggregate test scores. Of course, traits such as low cognitive ability, personalities problems, and mental health disorders change slowly at the population level. For this reason, the increase in single parenthood since the 1960s almost certainly was due to structural factors rather to than genes or personalities. This being the case, a decline in children’s mean test scores concomitant with an increase in single parenthood would suggest a causal interpretation, assuming that relevant third variables are controlled.

4. Methods

4.1. Demographic Variables

Data on children’s living arrangements between 1990–2011 came from the American Community Survey, the U.S. Decennial Census, and the Current Population Survey (CPS), depending on the year. These data were downloaded through the Integrated Public Use Microdata Series USA (Ruggles et al., 2010). We relied on constructed variables to describe children’s living arrangements. MOMLOC and POPLOC indicated whether a child’s mother and father resided in the same household, respectively. We classified children into single-parent households if they lived with a mother or a father (either biological or adoptive) but not both. We also included a variable to reflect the percentage of children living with neither parent. Children in all households with two parents (two biological parents, two adoptive parents, one biological parent and a step-parent) served as a combined reference category. We did not distinguish between cases in which children lived with married and unmarried parents in the main analysis, given our focus on the number of parents in the household rather than parents’ marital status. (We considered parents’ marital status in supplementary analyses, however, as described later.) Children were between the ages of 8 and 11 for the analysis of 4^th grade achievement and between the ages of 12 and 15 for the analysis of 8^th grade achievement.

Although children living with stepparents are of interest, it is not possible to identify all stepparents from the available information (Minnesota Population Center, 2011). As a result, an unknown number of children classified as living with two parents are living with a parent and a stepparent. This ambiguity precluded the use of stepfamilies as a separate analytic category in the main analysis, although we attempted to deal with this issue in supplementary analyses, as noted below. In addition, it is difficult to identify children living with same-sex parents. Although this is a limitation, the percentage of children living with same-sex parents is relatively small and should not distort the results appreciably.

As discussed below, our fixed effects models controlled for all stable state-level variables and period effects that influenced all states similarly. It was necessary, however, to control for variables that might be causes of single parenthood as well as children’s academic achievement to reduce the possibility of observing spurious associations. To control for race-ethnicity, we included the percentage of children in each age group who were Black or Hispanic. To control for parental education, we included three variables: the percentage of mothers (of children in each age group) with high school degrees, with some college or postsecondary education, and with college degrees. The percentage of mothers without high school degrees was omitted because it was perfectly correlated with the sum of the other three variables. Finally, we included the percentage of children living below the federal poverty line. We used these variables as controls because children’s race/ethnicity, parents’ education, and poverty status are related to the likelihood of living with a single parent (Kreider and Elliot, 2009) as well as children’s academic test scores (Cheadle, 2008). All of the variables described in this section were weighted and aggregated to the state level in each year (1990–2011).

4.2. Student Achievement Variables

The NAEP surveys were congressionally mandated to track the academic skills of students over time, with the first national assessment occurring in 1969. The implementation of the No Child Left Behind Act of 2001 increased the importance of the NAEP by requiring states to participate in biennial mathematics and reading assessments (National Center for Educational Statistics, 2009).

The NAEP uses a multi-stage sampling method to select students for assessment. All eligible schools within a state are grouped according to location, racial/ethnic composition, and student achievement to ensure an accurate representation of the student population. Within these groups, selected schools are assigned weights based on the school population relative to the state’s student population for that grade, with larger schools receiving larger weights. Within sampled schools, students in the target grades were randomly selected and then randomly assigned to a single subject area in which they were tested (Allen et al. 2001). Approximately 3000 students per subject and per grade are assessed in each state, though this varies somewhat by state size.

The National Assessment Governing Board oversees the construction of questions with input from teachers, researchers, measurement experts, policymakers and the general public.

A great deal of attention is paid to ensure that tests are comparable between states and across time. To ensure comparability across states, for example, the same set of test booklets is used across the nation. Assessments are generally consistent from year to year and any changes are carefully documented and investigated. In 2004, for example, accommodations were allowed for children with disabilities and limited English language abilities. Although national estimates include both public and private schools, the state level data (used in the current analysis) includes test scores from public schools only. (Enrollment in private schools declined slightly since the mid 1990s, from 11.7% to 10% of all children [National Center for Education Statistics, 2013]. This trend should not have major implications for our analysis.)

Although data are collected on a range of subjects, we focused on mathematics and reading scores because these were available for the largest number of years. The NAEP mathematics survey was administered in 1992, 1996, 2000, 2003, 2005, 2007, 2009 and 2011 for grades 4 and 8, with grade 8 also being tested in 1990. The mathematics test is designed to measure ability in five core areas: number properties and operations, measurement, geometry, data analysis and statistics, and algebra. These core areas are measured through a combination of multiple choice and constructed response questions. The NAEP reading survey was administered in 1998, 2002, 2003, 2005, 2007, 2009 and 2011 for grades 4 and 8, with grade 4 also being tested in 1992 and 1994. This test assesses comprehension of both literary and informational texts using a combination of multiple choice and constructed response questions.

State NAEP scores are available in two forms. The first is a mean score based on Item Response Theory (IRT), with individual scores ranging from 0 to 500. Depending on the year, standard deviations for the tests ranged from 29–32 for 4^th grade mathematics, from 35–42 for 4^th grade reading, from 36–38 for 8^th grade mathematics, and from 34–36 for 8^th grade reading. The second score is based on achievement levels and involves the percentage of students in four groups: below basic proficiency, basic proficiency, proficient, and advanced proficiency. Our first analysis was based on the mean (overall) state scores on each test for each year. Because the percentage of children living with single parents might disproportionately affect children at the bottom or top of the test distributions, we supplemented the analysis of mean scores with state data on the percentage of children scoring at below basic and advanced proficiency levels. Across all states and years, the percentage of students who scored at the below basic level was 26% for 4^th grade mathematics, 36% for 4^th grade reading, 34% for 8^th grade mathematics, and 26% for 8^th grade reading. The percentage of students who scored at advanced levels was 4% for 4^th grade mathematics, 7% for 4^th grade reading, 5% for 8^th grade mathematics, and 2% for 8^th grade reading.

4.3. Plan of Analysis

We used pooled time series regression analysis with fixed state and year effects to estimate the statistical models. The data file included one observation for each state in each year beginning in 1990 and concluding in 2011. Because state NAEP scores were not available in every year, the total number of observations was 382 for 4^th grade math, 421 for 4^th grade reading, 404 for 8^th grade math, and 322 for 8^th grade reading. We included a series of dummy variables (one for each state minus one) to capture state fixed effects and a second series of dummy variables (one for each year minus one) to capture year fixed effects.

The formula for the first model (without control variables) is

$${\mathrm{Y}}_{it}=\mathrm{\alpha }+\mathrm{\beta }\text{Percentage}\text{Single}{\text{Parent}}_{it}+\sum _1^{\text{i-}1}{\text{State}}_i+\sum _1^{\text{t-}1}{\text{Year}}_t+{\mathrm{\epsilon }}_{it}$$

where Y_it is the mean NAEP score in state i in year t; α is a constant, β is a regression coefficient, State_i refers to state fixed effects, Year_t refers to year fixed effects, and ε_it is the error term. State fixed effects control for all unmeasured state variables that are time invariant. Examples include region of the country, state government policies that did not change during the period of observation, and relatively stable cultural factors such as religiosity and political party support (consistently red or blue states). Year fixed effects control for all period effects (such as elections, changes in federal policies, and economic recessions) that affect all states similarly. Because the statistical models included only within-state change, the regression coefficients can be interpreted as the estimated effect of changes in the independent variables on changes in the dependent variables. (See Allison, 2009, for a discussion of fixed effects models. For a recent study that used state and year fixed effects, see Amato and Beattie, 2011.)

The regression analyses involve four models. The first model shows the association between changes in single parenthood and changes in state NAEP scores controlling for state and year fixed effects. The second model included controls for the percentage of Black and Hispanic children (in the appropriate age range) in each state. Controlling for these variables is necessary because race-ethnicity might affect the likelihood of becoming a single parent, but becoming a single parent cannot affect one’s race-ethnicity. The third model added controls for mothers’ education. Although maternal education can affect the likelihood of becoming a single parent, it also is possible that having a child outside of marriage affects a mothers’ likelihood of completing high school or attending college. For this reason, adding maternal education yields a slightly conservative estimate of the effects of single parenthood. (In preliminary models we also used paternal education and a variable reflecting the average education of mothers and fathers. Because maternal and paternal variables are positively correlated, these models yielded results that did not differ substantively from those presented in the main analysis.) In the fourth and final model, we included the percentage of children in poverty. Because poverty can be a cause as well as a consequence of single parenthood, this model was the most conservative with respect to estimating family structure effects. Specifically, the final model indicates whether single parenthood has an estimated effect that is independent of poverty.

5. Results

5.1. Descriptive Trends

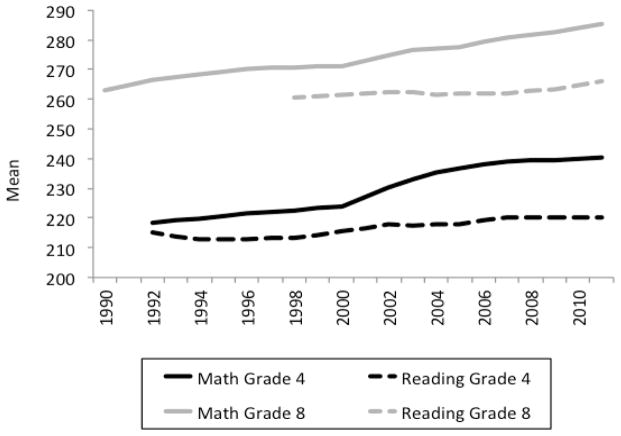
Figure 1 shows the state means for the NAEP tests. In this figure and the one that follows, each state is weighted equally, although weighting by population size produces similar trends.

Figure 1.

Mean State Scores on Math and Reading Tests (National Assessment of Educational Progress) by Year.

Mean 4^th grade math scores increased from 218 in 1992 to 240 in 2011. This 22-point improvement represents a gain of about two-thirds of a standard deviation. Although mean math scores improved in all states, some states improved more than others, with increases ranging from +12 to +30 points. Scores on the 4^th grade reading test increased modestly, rising from 215 to 220 overall, or about one-eighth of a standard deviation. Not all states showed improvements, with changes for individual states ranging from −5 to +16 points.

Figure 1 also shows that mean 8^th grade math scores increased from 263 in 1990 to 285 in 2011. This 22-point improvement represents a gain of about two-thirds of a standard deviation. States varied a great deal, however, with the amount of change ranging from −5 to +57 points. Between 1998 and 2011, mean 8^th grade reading scores increased from 261 to 266—a change of about one-seventh of a standard deviation. The amount of change across states ranged from −17 to +35 points. (The overall trends for 4^th and 8^th graders were similar, although this similarity would be less striking if different starting and ending years had been selected.)

Despite a good deal of variability across states, bivariate fixed effects regression analyses (not shown) revealed that the year of observation was positively and significantly associated with the state means of all four tests (all p < .01). Although not shown in the figure, the percentage of children scoring at below basic and advanced proficiency levels mirrored the trends for the means. That is, between the early 1990s and 2011, the percentage of children at both grade levels scoring at the below basic level declined and the percentage of children scoring at the advanced level increased, although these trends were stronger for mathematics than for reading. All of these time trends were statistically significant (p < .01).

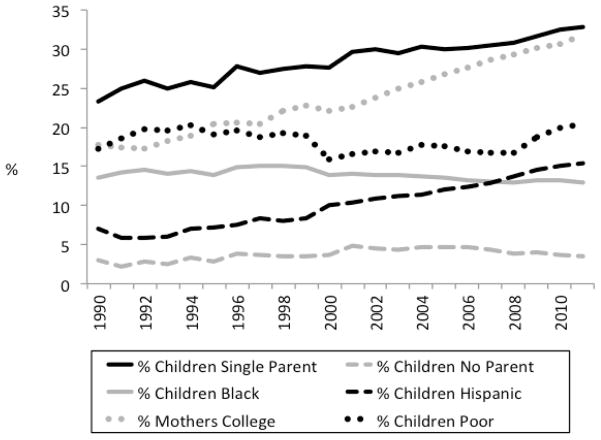
The demographic variables also changed over time. Figure 2 shows that the mean percentage of 4th grade children living with single parents increased from 23% in 1990 to 33% in 2011. This 10 percentage point change represents an increase of about half of a percentage point per year. Variation existed across states, however, with increases ranging from 3% to 19%. A regression analysis (not shown) revealed that the overall increase was statistically significant (p < .001). The percentage of children living with neither parent also rose slightly during this period, from about 3% in the early 1990s to 4% in the late 2000’s. Although small, this increase was statistically significant (p < .001). The figure also shows that the percentage of Black children changed relatively little during this time (a decline of one half of a percent). In contrast, the percentage of Hispanic children increased substantially from 7 percent in the early 1990s to 15 percent in 2011 (p < .001). Maternal education also increased. The percentage of mothers with college degrees, for example, increased from 18 percent to 32 percent (p < .001). Finally, the percentage of children living in poverty fluctuated a good deal during this period, although it rose after the Great Recession in 2007. The trends for 8^th grade children were nearly identical to those of 4^th grade children and never differed by more than a percentage point across years. For this reason, only the 4^th grade trends are shown in a figure.

Figure 2.

Mean Percentage of 4^th Grade Children Living with Single Parents, No Parents, and Other Demographic Variables by Year.

Taken together, Figures 1 and 2 demonstrate that children’s performance on the NAEP exams improved during the same period that the percentage of children living with single parents increased. Although a more detailed analysis is necessary to reach firm conclusions, these contrary trends suggest that the increase in single parenthood did not have catastrophic effects on children’s school achievement. Nevertheless, as noted earlier, not all states showed improvements in NAEP scores. And even in the case of 4^th grade math (in which all states showed improvements), the two variables could be negatively associated in a fixed effects framework if test scores increased more slowly in states that had the largest increases in single parenthood.

Preliminary analysis revealed a high correlation of .71 (p < .001) between the percentage of children living with single parents and the percentage of Black children across all states and years. Between-state correlations for single years were similar in magnitude. Given that single parenthood is more common among African Americans than among whites, this finding is not surprising. Although correlations of this magnitude can produce multicollinearity problems, state fixed effects models rely entirely on within-state variation and exclude between-state variation. With only within-state variation modeled, the correlation between the two variables was only .37 (p < .001). Although statistically significant, the moderate within-state correlation was unlikely to cause estimation problems. All other correlations between independent variables were low or moderate in magnitude (below .40).

5.2. Regression Analysis

We estimated fixed effects and random effects models for the same outcomes in preliminary analyses. In each case, Hausman tests (Worrall, 2008) indicated that fixed effects models provided a better fit to the data than did random effects models (all p < .05). In other words, using random effects models with these data (and failing to take unmeasured differences between states into account) would have provided misleading results.

Preliminary analyses without fixed effects revealed that the percentage of children living with single parents was negatively associated with mean NAEP scores. In other words, scores tended to be lower in states with relatively large proportions of single-parent households. States with large proportions of single-parent households differ from other states in many other ways, however. When state fixed effects (which control for all stable state characteristics) were added to the models, the percentage of children living with single parents and mean NAEP scores were positively associated. This is because the percentage of children living with single parents increased at the same time that children’s test scores also increased (see Figures 1 and 2)—another potentially misleading association. To control for secular trends in both variables, it was necessary to add dummy variables for years in the statistical models to capture year fixed effects.

The state and year fixed effects accounted for most of the variance in test scores. For example, the fixed effects accounted for 95% of the variance in 4^th grade mathematics and 88% of the variance in 8^th grade mathematics. Nevertheless, after accounting for the state and year fixed effects, the independent variables (family structure, race-ethnicity, maternal education, and poverty) accounted for significant increments in variance for all of the mathematics outcomes (mean scores, % below basic, and % advanced) at both grade levels. For example, with the variance due to the fixed effects removed from the data, the independent variables accounted for 9% of the remaining variance in 4^th grade mathematics scores and 14% of the remaining variance in 8^th grade mathematics scores. The independent variables, however, did not account for significant increments in variance for the reading outcomes at either grade level. For this reason, we focus on the results for mathematics in the remainder of this paper.

Table 1 shows the regression results for state mean NAEP scores for the 4^th grade (top panel) and 8^th grade (bottom panel). For ease of presentation, the dummy variables for states and years are not shown. The constants also are excluded from the table because they reflect the excluded states and years and do not have a substantive interpretation. Model 1 reveals that the association between the percentage of children with single parents and 4^th grade math scores was negative but close to zero (−.051) and not statistically significant. The corresponding coefficient for the percentage of children living with no parents (−.272), in contrast, was negative and statistically significant. The regression coefficient indicated that a 1-point increase in the percentage of children living with neither parent was associated with a decline in test scores equivalent one-fourth of a point—a small effect. In Model 2, which included children’s race-ethnicity, the percentage of Black children was negatively and significantly associated with test scores, whereas the coefficient for the percentage of Hispanic children was not statistically significant. With race-ethnicity controlled, the coefficient for the percentage of children living with neither parent declined and no longer was significant. In Model 3, the variables reflecting maternal education (high school graduate, some college, and college graduate) were positive and statistically significant. These results indicate that increases in maternal educational attainment were linked with improvements in children’s test scores. Finally in Model 4, the percentage of children living at or below the poverty line was not significant, and adding this variable to the equation did not change the coefficients for race and maternal education appreciably.

Table 1.

Fixed Effects Regression of Mean Math Scores (National Assessment of Educational Progress) on the Percentage of Children Living with Single Parents or No Parents: State Data, 1990–2011.

	Model 1	Model 2	Model 3	Model 4
Grade 4
% Single parent	−.051 (.048)	−.014 (.047)	−.013 (.049)	−.022 (.054)
% No parent	−.272** (.138)	−.142 (.121)	−.149 (.111)	−.152 (.113)
% Black		−.180* (.077)	−.158* (.074)	−.162* (.077)
% Hispanic		−.020 (.062)	.040 (.068)	.036 (.067)
% Mom high school			.200** (.071)	.208** (.073)
% Mom some college			.207** (.071)	.217** (.072)
% Mom college grad			.166* (.078)	.177* (.079)
% Poverty				.029 (.071)
Grade 8
% Single parent	−.017 (.080)	.082 (.093)	.041 (.090)	−.050 (.093)
% No parent	−.449 (.289)	−.346 (.258)	−.278 (.235)	−.391 (.252)
% Black		−.435* (.200)	−.340 (.182)	−.380* (.183)
% Hispanic		−.011 (.130)	.145 (.141)	.121 (.137)
% Mom high school			.652*** (.153)	.699*** (.156)
% Mom some college			.538*** (.129)	.603*** (.132)
% Mom college grad			.375** (.146)	.459** (.155)
% Poverty				.268* (.110)

Table values are unstandardized regression coefficients with robust standard errors in parentheses. Results are based on 12 separate regression analyses with dummy variables for states and years. Total observations (states x years) = 382 for 4^th grade and 404 for 8^th grade.

^*p < .05.

^**p < .01.

^***p < .001 (two-tailed).

With respect to the 8^th grade, the regression coefficients for the percentage of children living with single parents and no parents failed to attain statistical significance in any model. In Model 2, the coefficient for Black children was negative and significant, and in Model 3, the variables reflecting maternal education all achieved significance. The coefficient for poverty was positive and statistically significant in Model 4 (a counter-intuitive finding). This result indicates that states with high levels of child poverty tended to have higher mathematics test scores, controlling for family structure, race-ethnicity, and maternal education. Overall, the results from Table 1 do not support the notion that the increase in the percentage of children living with single parents reduced children’s test scores.

The next set of analyses, shown in Table 2, focused on the percentage of children scoring at a below basic level of proficiency on the NAEP mathematics test. The percentage of children living with single parents was not a significant predictor of this outcome in any model at either grade level. The coefficient for no parents, however, was positive and significant in two of the four models for 8^th grade students. The regression coefficient for the percentage of Black children was positive and significant for 4^th grade students in all models, although the corresponding coefficient for 8^th grade students was significant only in Model 2. For students at both grade levels, maternal education was negatively and significantly related to the outcome. Finally, increases in child poverty were not associated with math scores at either grade level.

Table 2.

Fixed Effects Regression of the Percentage of Children Scoring at a Below Basic Level of Math Proficiency (National Assessment of Educational Progress) on the Percentage of Children Living with Single Parents or No Parents: State Data, 1990–2011.

	Model 1	Model 2	Model 3	Model 4
Grade 4
% Single parent	.032 (.064)	−.045 (.061)	−.041 (.061)	−.024 (.068)
% No parent	.291 (.173)	.022 (.144)	.047 (.130)	.054 (.133)
% Black		.372** (.107)	.335** (.104)	.343** (.107)
% Hispanic		.076 (.085)	−.022 (.094)	−.014 (.092)
% Mom high school			−.335*** (.093)	−.353*** (.010)
% Mom some college			−.376*** (.088)	−.400*** (.091)
% Mom college grad			−.227* (.102)	−.251* (.107)
% Poverty				−.062 (.137)
Grade 8
% Single parent	.026 (.064)	−.027 (.069)	.005 (.069)	.023 (.073)
% No parent	.386* (.161)	.321 (.157)	.294 (.151)	.316* (.116)
% Black		.249* (.124)	.154 (.122)	.160 (.121)
% Hispanic		.053 (.091)	−.102 (.100)	−.098 (.100)
% Mom high school			−.553*** (.090)	−.562*** (.090)
% Mom some college			−.519*** (.097)	−.531*** (.097)
% Mom college grad			−.359*** (.107)	−.375*** (.110)
% Poverty				−.052 (.076)

Table values are unstandardized regression coefficients with robust standard errors in parentheses. Results are based on 12 separate regression analyses with dummy variables for states and years. Total observations (states x years) = 382 for 4^th grade math and 404 for 8^th grade.

^*p < .05.

^**p < .01.

^***p < .001 (two-tailed).

The final analyses, involving the percentage of children scoring at an advanced level of proficiency, are summarized in Table 3. In contrast to previous results, the percentage of children living with single parents was negatively and significantly associated with 4^th grade math achievement, but only with control variables in the models (models 2, 3, and 4). A comparable result appeared for 8^th grade math in Models 1 through 3. Although the results are not entirely consistent across grade levels, they suggest that increases in the percentage of children living with single parents were related to declines in the percentage of children scoring at the top of the mathematics distribution. In addition, the coefficient for not living with either parent in the 8^th grade was negative and significant in Models 3 and 4.

Table 3.

Fixed Effects Regression of the Percentage of Children Scoring at an Advanced Level of Math Proficiency (National Assessment of Educational Progress) on the Percentage of Children Living with Single Parents or No Parents: State Data, 1990–2011

	Model 1	Model 2	Model 3	Model 4
Grade 4
% single parent	−.031 (.016)	−.045** (.017)	−.045** (.015)	−.042* (.017)
% no parent	−.006 (.040)	−.057 (.042)	−.048 (.040)	−.047 (.040)
% Black		.070** (.025)	.073** (.025)	.074** (.025)
% Hispanic		.003 (.026)	.006 (.026)	.007 (.031)
% Mom high school			−.050* (.023)	−.052* (.023)
% Mom some college			−.053* (.024)	−.056* (.026)
% Mom college grad			.022 (.026)	.020 (.027)
% Poverty				−.009 (.020)
Grade 8
% single parent	−.061** (.022)	−.070** (.024)	−.050* (.023)	−.050 (.026)
% no parent	−.066 (.044)	−.078 (.046)	−.105* (.044)	−.105* (.069)
% Black		.042 (.035)	.046 (.034)	.046 (.034)
% Hispanic		.026 (.029)	.044 (.030)	.044 (.030)
% Mom high school			−.029 (.028)	−.029 (.030)
% Mom some college			.007 (.029)	.007 (.029)
% Mom college grad			.062 (.033)	.062 (.034)
% Poverty				−.001 (.027)

Table values are unstandardized regression coefficients with robust standard errors in parentheses. Results are based on 12 separate regression analyses with dummy variables for states and years. Total observations (years x states) = 382 for 4^th grade math and 404 for 8^th grade math.

^*p < .05.

^**p < .01.

^***p < .001 (two-tailed).

With respect to the control variables, the percentage of Black children was positively related to 4^th grade outcomes (but not 8^th grade outcomes)—a result that appears to contradict the earlier results for this variable. Combined with the results from Table 2, this outcome suggests that increases in the percentage of Black children within states resulted in more children scoring in both tails of the distribution of 4^th grade math scores. Maternal education (although not necessarily having a college degree in this case) was positively related to advanced scores on the 4^th grade test but not to advanced scores on the 8^th grade test. Poverty was not related to advanced test scores in any model.

5.3. Alternative Specifications

Alternative specifications of the models yielded few new findings. First, weighting the data by state populations (so that larger states contributed more to the analysis than smaller states) yielded results nearly identical to those reported in Tables 1–3. Second, following Friedberg (1998), we included a series of state x time interaction terms in the models to control for state-level trends that may have been distinct from the national trend. None of the coefficients for single-parent households were significant in these models, although most of the coefficients for maternal education continued to be significant. Third, we conducted analyses in which the percentage of children living in single-parent households was lagged by 1 through 5 years. This procedure did not produce findings that differed substantively from those reported in Tables 1–3. Fourth, Washington D.C. consistently had low mean scores on the achievement tests as well as the highest proportions of children living with single parents. Because this was an influential case, we ran the analyses with Washington D.C. excluded, but the results were nearly identical. Fifth, Bertrand, Duflo, and Mullainathan (2004) suggested using bootstrapped standard errors to deal with potential problems with serial correlation in fixed effects models. Following this suggestion, we conducted new analysis with bootstrapped errors, and although the standard errors increased modestly, the results were essentially the same as those reported earlier.

Fifth, although our data set undercounts stepparents, we created a dummy variable for stepparent households that we were able to identify. This step effectively removed identified stepfamilies from the omitted comparison group of two-parent households. With the new stepparent variable in the model, the results mirrored those in Table 1–3, and the pattern of largely non-significant results for the single-parent household variable was replicated. The stepparent variable yielded one significant finding: a positive association between the percentage of 4^th grade children living with a stepparent and the percentage of children scoring at a below basic level of proficiency (b = .33, p < .05). Finally, we conducted additional analyses with a dummy variable for two-parent households in which parents were unmarried. With this variable in the model, the omitted comparison group consisted of two-parent married couple households. The new variable was never significant, however, suggesting that the increase in unmarried parent households was not associated with children’s test scores. Moreover, the results for single parenthood variable did not change with this new variable in the model.

6. Discussion

The percentage of children living with single parents in the United States has increased steadily in recent decades. Moreover, research consistently demonstrates that children living with single parents score lower on measures of academic ability and achievement than do children with two continuously married parents (Amato 2005; Brown, 2010; McLanahan and Sandefur, 1994). Given these findings, many observers have assumed that the increase in single parenthood has placed downward pressure on children’s school performance and educational achievement. Few studies, however, have attempted to establish whether the increase in single parenthood was linked with declines in children’s test scores (or with other aspects of children’s well-being) at the population level. The purpose of the present study was to assess whether the increase in single parenthood between 1990 and 2011 had consequences for state scores on the National Assessment of Educational Progress.

Did the rise in the percentage of single-parent households lower the academic performance of American children? Since 1990 the percentage of children living in single-parent households increased, as did children’s mean NAEP scores. Nevertheless, these two variables could be negatively associated if test scores rose more slowly in states with the largest increases in single parenthood. A statistical model with state and year fixed effects is necessary to determine whether this is the case. The current analysis indicates, however, that the percentage of children living with single parents was not associated with children’s mathematics scores. We did not focus on children’s reading scores, because they increased only modest during the last few decades and were not related significantly to our independent variables. Nevertheless, the results for reading scores also support the conclusion that increases in single parenthood did not lower children’s aggregate-level school performance. These findings contradict the claim that single parenthood has produced widespread school failure, a pervasive decline in the academic ability of American children, and a general weakening of American economic competitiveness (Blankenhorn, 1995; Fagan, 1999; Pearlstein, 2011; Popenoe, 2009; Whitehead, 1997).

Despite the null results for mean state test scores, the present study suggests that the increase in single-parent households since 1990 reduced the percentage of children who scored at the top of the test score distributions (advanced NAEP levels). How big are these estimated effects? The regression coefficient for single-parent households in Model 3 of Table 1 (which included controls for race-ethnicity and maternal education but not poverty) was −.045 for 4^th grade math. Between 1990 and 2011, the percentage of children in this age group living with single parents increased by 9.48 points. This means that the rise in single parenthood was associated with a .43 decline in the percentage of 4^th grade children scoring at an advanced level (9.48 × −.045). For 8^th grade students, the corresponding coefficient in Model 3 of Table 3 was −.05, and our estimate of the total effect of the rise in single parenthood amounts to .48 of a percentage point (9.51 × −.05). A decline of approximately one-half of a percentage point is not trivial, especially when the percentage of children scoring at advanced levels ranged from only 2% to 8% during this period. Moreover, single parenthood increased a good deal between 1960 and 1990, and NAEP scores are not available for this period. If we were to extrapolate the current results to the 1960s, the cumulative effects of single parenthood on children’s advanced math scores would be larger. Nevertheless, these modest declines are not consistent with the strong claims made by many observers about single parenthood and the declining academic achievement of American children.

Given strong claims about the negative effects of single parenthood on American children, the current findings are surprisingly mild. These findings are consistent with the assumption that most of the associations between single parenthood and children’s academic performance (previously observed at the individual level) are due to selection. This interpretation is consistent with McLanahan, Tach, and Schneider (2013), who concluded that the evidence for a causal effect of family structure on children’s educational achievement is weak. We suspect that not all of the association is spurious, however. In a recent study based on fixed effects regression models, Amato (2014) found that the average estimated effects of divorce on children’s standardized math and reading scores were statistically significant but weak: slightly below one tenth of a standard deviation for primary school students and slightly above one tenth of a standard deviation for high school students. With effect sizes in this range, even large increases in the percentage of children living with single parents would result in exceedingly small aggregate-level changes. This conclusion is consistent with Amato (2005), who argued that changes in family structure have had only modest effects on child outcomes at the societal level. For example, he estimated that the percentage of children who have repeated a grade would be only 3 percentage points lower (21% rather than 24%) if children’s family structures had not changed between 1960 and 1995.

Although the increase in single-parent households does not appear to have affected children’s test scores appreciably, it is possible that family structure has had stronger effects on behavior than on cognitive ability, as suggested by McLanahan, Tach, and Schneider (2013). If this is true, then the increase in single-parent households may have negatively affected children’s school grades and the probability of high school graduation, despite having few measureable consequences for test scores. It is also possible that the increase in single parenthood affected trends in other child outcomes, such as delinquency, behavior disorders, accidents, or mental health problems. Additional research that focuses on other aggregate-level outcomes would be a useful supplement to existing individual-level studies.

Although not the main focus of the current study, the percentage of children living without either parent was associated with some outcomes, such as the percentage of 8^th grade students scoring at a below basic level of proficiency. Comparatively little attention has been given to children living with neither parent, presumably because their numbers are relatively small and have not increased much in recent decades. Despite this lack of attention, however, children living without parents have worse educational outcomes, on average, than do children living with one or two parents, not only in the United States but also in other countries (Scott, DeRose, Lippman, and Cook, 2013). How big is this effect in the current study? Our data indicate that the percentage of children living without parents increased by only about 1 percentage point between 1990 and 2011, and the regression coefficient from Table 2 (8^th grade, Model 2) was .321. Consequently, the increase in children living without parents may have been responsible for an increase of one-third of a percentage point in below basic achievement. Given the minimal changes in this household type, its effects at the aggregate level are necessarily modest.

Other findings from the current study are worthy of comment. The percentage of Black children was negatively associated with mean mathematics scores in the 4^th and 8^th grades (Table 1). These findings are consistent with earlier research (e.g., Cheadle 2008) and speak to the continuing educational disadvantages associated with race in the United States. The current study also yielded an unexpected finding: a positive association between the percentage of Black children and the percentage of 4^th children scoring at an advanced level of proficiency. This suggests that an increase in the size of the Black population increases the variance in outcomes, with more scores in the bottom and the top of the distribution. Although this is an intriguing possibility, more research is needed to explore this finding. In contrast to the findings for Black children, the percentage of Hispanic children in the population was not related to any educational outcomes. In other words, the relatively large increase in the size of the Hispanic population in the United States during the last two decades does not appear to have had any negative consequences for children’s educational performance on the NAEP—a finding that may be relevant to current debates about immigration.

Increases in the educational attainment of mothers were associated positively with most of the educational outcomes. Tables 1–3 included coefficients for three levels of maternal education (high school graduate, some college, and college graduate), with the percentage of mothers without high school degrees serving as the omitted category. For most outcomes and grade levels, all of the education coefficients were significant, although the coefficients for the Mom High School and Mom Some College categories were sometimes larger than the coefficients for the Mom College Grad category. Although these coefficients appear to be in the “wrong” order, their confidence intervals overlapped considerably. For example, for 4^th grade mathematics scores, the coefficients (and 95% confidence intervals) were .208 (.064–.352) for high school, .217 (.074–.359) for some college, and .178 (.022–.333) for college graduate. Even though the pattern of coefficients was not always in the expected rank order, the overriding conclusion is that increases in maternal educational were related to improvements in mathematics achievement among American children. This positive change occurred despite the growth of single-parents households during the same period. This conclusion is consistent with Western, Bloome, and Percheski (2008), who found that income inequality in the U.S. was exacerbated by increases in single-parent families but cushioned by corresponding increases in women’s educational attainment and employment. Many observers have focused on the potentially troubling consequences of the increase in single-parent households and failed to note the substantial and beneficial increase in maternal education in recent decades. A balanced assessment of children’s changing well-being in the U.S. should take both trends into account.

The current study is limited in several respects. Reading and math scores were not available in every year due to the structure of the NAEP. Moreover, we were unable to examine student achievement prior to 1990, a period in which single parenthood increased a great deal. Furthermore, the focus on reading and math achievement excluded other potentially informative educational outcomes, such as the percentage of children each year who are held back or drop out of school. And we could not distinguish clearly between children living with two biological parents and children living with one biological parent and a stepparent.

Moreover, variables not included in our model may have affected the percentage of children living with single parents as well as children’s test scores during this period. One possibility involves welfare reform. Our model (with year fixed effects) captured aspects of the national welfare reform legislation of 1996 that affected all states similarly. Nevertheless, many states were experimenting with welfare reform prior to the passage of the federal legislation, and states were given discretion on how to implement some aspects of the legislation. Including all of these state variations in the statistical model was beyond the limits of the current study. Of course, because our results for single parenthood were not statistically significant, there is no risk that omitted variables produced a spurious association in the current study. It is possible, of course, that one or more omitted variables masked a negative association between single parenthood and children’s test scores. For a suppression effect to occur, however, the omitted variable would need to have a positive effect on single parenthood as well as a positive effect on children’s test scores (or a negative effect on each variable). It is difficult to think of omitted variables that might be related to our independent and dependent variable in this manner.

Despite these limitations, the current study is one of the few to consider how changes in family structure affected child outcomes at the societal rather than the individual level. Additional studies that examine a broader range of child outcomes, as well as a longer time periods, would make useful contributions to our understanding of a topic of great public concern.

Highlights.

• We used the CPS, the decennial U.S. Census, and the American Community Survey for data on single-parent households, and the National Assessment of Educational Progress for data on children’s math and reading scores.

• We used regression models with state and year fixed effects to estimate the effects of changes in the percentage of children living with single parents on changes in children’s 4^th and 8^th grade test scores between 1990 and 2010.

• Single parenthood was not associated with mean mathematics and reading scores, although it was weakly but negatively associated with the percentage of children who scored at an “advanced” level of proficiency in mathematics.

• Increases in maternal education were generally related to improvements in children’s math scores.