Heat conductivity of DNA double helix

Abstract

Thermal conductivity of isolated single molecule DNA fragments is of importance for nanotechnology, but has not yet been measured experimentally. Theoretical estimates based on simplified (1D) models predict anomalously high thermal conductivity. To investigate thermal properties of single molecule DNA we have developed a 3D coarse-grained (CG) model that retains the realism of the full all-atom description, but is significantly more efficient. Within the proposed model each nucleotide is represented by 6 particles or grains; the grains interact via effective potentials inferred from classical molecular dynamics (MD) trajectories based on a well-established all-atom potential function. Comparisons of 10 ns long MD trajectories between the CG and the corresponding all-atom model show similar root-mean-square deviations from the canonical B-form DNA, and similar structural fluctuations. At the same time, the CG model is 10 to 100 times faster depending on the length of the DNA fragment in the simulation. Analysis of dispersion curves derived from the CG model yields longitudinal sound velocity and torsional stiffness in close agreement with existing experiments. The computational efficiency of the CG model makes it possible to calculate thermal conductivity of a single DNA molecule not yet available experimentally. For a uniform (polyG-polyC) DNA, the estimated conductivity coefficient is 0.3 W/mK which is half the value of thermal conductivity for water. This result is in stark contrast with estimates of thermal conductivity for simplified, effectively 1D chains (”beads on a spring”) that predict anomalous (infinite) thermal conductivity. Thus, full 3D character of DNA double-helix retained in the proposed model appears to be essential for describing its thermal properties at a single molecule level.

I. Introduction

Heat conductivity of nanostructures is of great importance both from fundamental and applied points of view. For example, superior thermal conductivity has been observed in graphene^1,2 and carbon nanotubes³, which has raised an exciting prospect of using these materials in thermal devices^4–8. Generally, one can not expect that bulk thermal properties of a material will remain unchanged at the nanoscale: in some nano materials such as silicon thermal conductivity is about two orders of magnitude smaller than that of bulk crystals⁹, with the reduction in conductivity attributed to strong inelastic surface scattering. Furthermore, some familiar physical laws such as Fourier's law of heat transfer that work in bulk materials are no longer valid on the nanoscale^10–13.

Deoxyribonucleic acid (DNA) is one of the most promising nanowire materials due to the relative ease of modifications combined with the self-assembly capability which make it possible to construct a great variety of DNA-based nanostructures^14,15. While electrical conductivity of single DNA molecules has been extensively studied, the corresponding thermal properties remain largely unexplored. The first, and to the best of our knowledge the only published work so far that attempted to measure thermal conductivity of single molecule DNA – DNA-gold composite¹⁶ – gave an estimate of 150 W/mK for the coefficient of thermal conductivity, which was conspicuously close to that of pure gold. The study concluded that molecular vibrations play a key role in thermal conduction process in DNA molecule, but thermal conductivity of single molecule DNA remained unknown.

At the same time, theoretical approaches to the problem have met with their own difficulties. Numerical modeling of heat transfer along carbon nanotubes and nanoribbons showed that thermal conductivity increases steadily with the length of the specimen^10–13. If one makes an analogy with 1D anharmonic chains that always have infinite thermal conductivity^17,18, one might interpret these results as suggesting anomalously high thermal conductivity for quasi one-dimensional nanosystems. Since at some level the DNA double helix may also be considered as a quasi 1D system, one wonders if the corresponding thermal conductivity is also anomalously high, increasing with the length of the DNA molecule? It is possible that over-simplified “beads-on-spring” models of DNA are inappropriate in this context, and thermal properties of the real double helix do not exhibit the low dimensional anomaly in heat conductivity.

The goal of this work is to investigate heat conductivity of single molecule DNA by direct modeling of heat transfer along the double helix via classical molecular dynamics of the DNA. To accomplish this goal we will have to choose a level of detail that is computationally feasible but at the same time retains key properties of the fully atomistic picture of the molecule.

Classical molecular dynamics (MD) simulations based on fully atomistic (all-atom) representations^19–21 (see Fig. 1) are among the most widely used tools currently employed to study dynamics of the DNA double helix²². In these simulations the dynamics of the atoms is governed by semi-empirical potentials, or force-fields; CHARMM27^20,21 or AMBER²³ are the most common force-fields that accurately reproduce a variety of structural and dynamical properties of small fragments of canonical and non-canonical nucleic acids in water, at least on time-scales of up to one microsecond^22,24–32. Importantly, classical force-fields such as AMBER³³ can reproduce high-level quantum mechanical calculations for hydrogen bonding and base stacking interactions^34,35. However, accuracy of these all-atom models in which every atom of the DNA fragment and all of the surrounding solvent molecules are represented explicitly comes at a price of substantial computational expense that limits the range of applicability of the models.

Fig. 1.

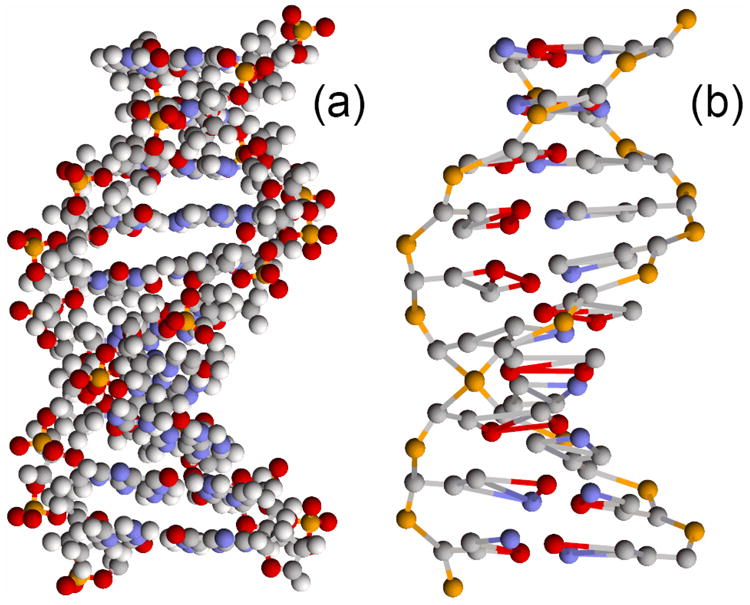
View of a DNA fragment (CGTTTAAAGC) for (a) standard all-atom representation of the double helix and (b) the proposed coarse-grained model (12CG) based on 12 united atom particles (grains) per base pair.

The so-called implicit solvent approach^36–40 reduces the computational expense by replacing the discrete water environment with a continuum with dielectric and “hydrophobic” properties of water. The solvent degrees of freedom are “integrated out” and the corresponding free energy term is added to the Hamiltonian of the system. However, even in this case all-atom simulations may be computationally expensive. For example, a single 5 ns long simulation of a 147 base pair DNA fragment reported in Ref.⁴¹ took 115 hours on 128 processors. This example suggests that all-atom models may not be suitable for the program set out in this work, in which heat transfer along long fragments of DNA will have to be examined. We therefore resort to yet another level of approximation – coarse-graining (CG), where sets of original atoms are grouped into single “united atoms” particles or grains.

The remainder of this work is organized as follows. We begin with an outline of the coarse-graining procedure leading to the proposed model, followed by a description of the potential function. Details are provided in the Appendix. We validate the model by comparing its dynamics with that of the corresponding all-atom model. Small amplitude vibrations and dispersion curves are analyzed next, leading to an addition verification of the model by comparison of several predicted characteristics (speed of sound, torsional rigidity) with the experiment. Then, we describe in detail the formalism used to model the heat transfer along a single DNA molecule. In “Conclusion” we provide a summary of the results and a brief discussion.

II. The Coarse-Grained Model of Double Helical DNA

Naturally, there is no unique prescription for subdividing a macromolecule into grains. The grouping of individual atoms into grains aims to achieve a balance between faithful representation of the underlying dynamics and the associated computational expense which is directly related to the number of grains retained in the CG description. A fairly large number of coarse-grain DNA models has been developed^42–61. Many of these models are phenomenological – each nucleotide is represented by 1 to 3 grains interacting via relatively simple pair potentials designed to reproduce either certain set of experimental properties or the results of numerical simulations based on the corresponding all-atom models. However, the oversimplified description of the nitrogen bases carries the risk of losing some key details of the base-base interactions, particularly their stacking part, that affects intramolecular rearrangements. The latter plays a very important role in heat transfer along the DNA molecule⁶². To make sure the nitrogen bases are treated as accurately as possible within the CG description, we follow a strategy in which each base is modeled by three grains; the interaction between the bases is modeled at the all-atom level via a computationally effective strategy described below.

Within the coarse-grain model each nucleotide is represented by 6 coarse-grained particles, or grains: 1 for the phosphate group, 2 for the sugar ring, and 3 for the nitrogen base. The mass of each coarse grain equals the net mass of the original atoms that make up that grain; for the 3 base grains the original mass is distributed between them as described in the Appendix. The fine-level to coarse-grain reduction employed by our model is shown in Fig. 2. Following Bruant et al.⁴², where all-atom molecular simulations were used to identify a set of relatively rigid groups of atoms in the DNA, all of the original atoms of the phosphate and C5′ groups [atoms P, O1P, O2P, O3′, O5′, C5′, H5′1, H5′2, see Fig. 2] are combined into a single [P] grain which is placed at the position of the original P atom.

Fig. 2.

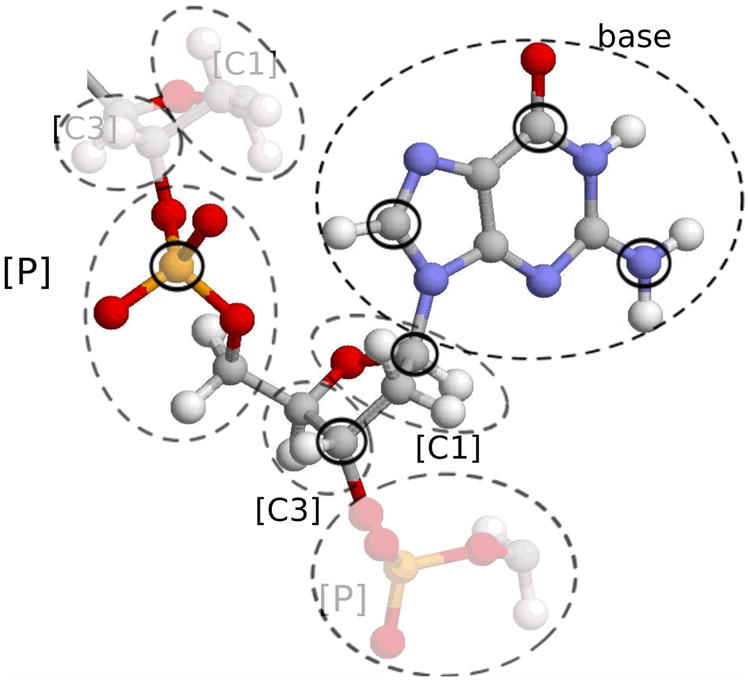
Combining original atoms into coarse grains on the DNA backbone. Dashed lines indicate atoms that are included in the corresponding grain, solid circles mark the atoms on which the grain is centered.

The sugar groups are described by two grains which are placed on the original C3′ and C1′ atoms; they will be denoted as [C3] and [C1]. The grain [C3] includes C3′, H3′, C4′ and H4′ original atoms, the grain [C1] includes original C1′, H1′, C2′, H2′1, H2′2 and O4′ atoms. Thus, within our coarse-grain model the backbone of the double helix is represented by a chain of 3 particles (grains) [P], [C3] and [C1] (see Fig. 2).

Nitrogen bases (A, T, G and C) are rather rigid, planar structures; spatial position and orientation of each base can be uniquely determined from positions of any three atoms that belong to that base. Therefore, bases A, T, G, C will be described in terms of three grains. For the A base, we identify the three grains with the original C8, N6, C2 atoms; for the T base, the three atoms are C7, O4, O2; for the G they are C8, O6, N2 atoms; and for the C base, they are C6, N4, and O2 original atoms. Thus within the suggested model one base-pair (bp) of the DNA double helix consists of 12 grains – we call the model “12CG” [see Fig. 1 (b)]. For N base-pair double helix, our system will consist of 12N particles. Note that within our terminology the simplest possible “beads-on-spring” model would be called “1CG” (one grain per base pair), and the all-atom representation would be “40CG”, although in this case the exact number would depend slightly on the base sequence e.

Interactions between neighboring base pairs are obviously very important for heat transfer along the DNA molecule. So within the framework of our coarse-grained model the stacking of neighboring base pairs should be taken into account as accurately as possible. We take advantage of the planar structure of the bases to bring the accuracy of the stacking interactions close to the all-atom level, but with little additional computational expense: from the known grain coordinates of each coarse-grain base, one can trivially restore coordinates of all of the original atoms in the base with virtually no additional computational expense. We then uses these coordinates to calculate the stacking energy using accurate all-atom potentials, see Appendix for details.

III. The Potential Function

To describe interactions between the grains, we employ a potential function that contains all of the “standard” terms used in classical molecular dynamics simulations^63,64. These terms include internal energy contributions such as bond stretching and angle bending, short-range van der Waals (vdW) interactions, and long-range electrostatic interactions in the presence of water and ions. The latter are modeled implicitly, at the continuum dielectric, linear response level. The detailed term by term description of the potential is given in the Appendix.

The total energy of the system consists of nine terms:

$$H=E_k+E_v+E_b+E_a+E_t+E_{\mathit{\text{hb}}}+E_{\mathit{\text{st}}}+E_{\mathit{\text{el}}}+E_{\mathit{\text{vdW}}}.$$ (1)

The first term E_k stands for kinetic energy of the system, the terms E_v, E_a, E_t describe respectively bond, angle and torsion deformation energy of the backbone. The term E_b stands for base deformation energy and was introduced to hold four points – C1′ and three points on a nitrogen base – near one plane. Last two terms E_el, E_vdW describe electrostatic and van der Waals interactions between grains on the backbone. Interaction between nitrogen bases, including interactions along the same chain (stacking) as well as interactions across the complementary chains (including hydrogen bonds between complementary bases), are described by two terms E_st and E_hb. These two potentials depend on coordinates of all of the original atoms of the base. These coordinates are uniquely calculated from positions of the three grains that form each base; the reader is referred to Appendix for details. A fortran implementation of the model is freely available at http://people.cs.vt.edu/onufriev/software

IV. Validation of the Model

We begin validating the proposed coarse-grain model by comparing the resulting DNA dynamics with that produced by the corresponding well-established all-atom model. Later in this work we will also discuss direct comparisons with the experiment (estimated sound velocities).

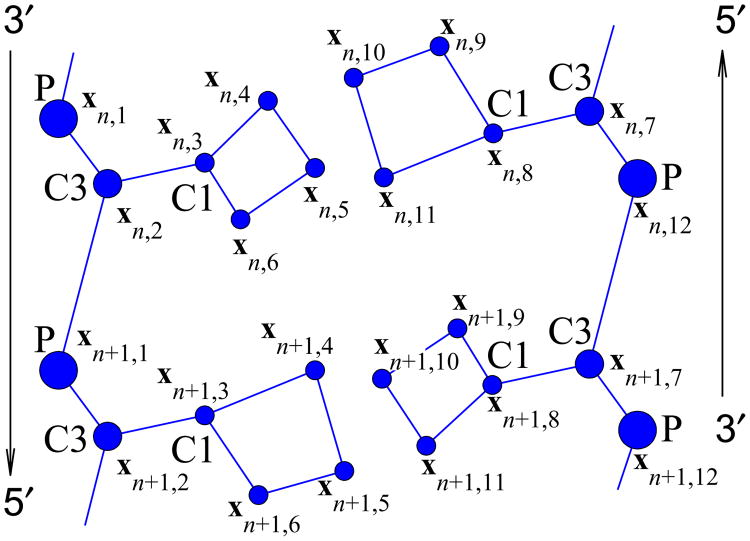
In what follows we use following notation for convenience: x_n,j, j = 1,⋯, 12 are coordinates of 12 grains on the n-th base-pair of the double helix (see Fig. 3). Therefore, the configuration of n-th base-pair is given by a 36-dimensional coordinate vector ${\mathbf{u}}_n={\{{\mathbf{x}}_{n,j}\}}_{j=1}^{12}$. The constant temperature dynamics of the double helix is obtained by integrating numerically the following system of Langevin's equations:

Fig. 3.

Fragment of the DNA double helix in the coarsegrained representation. Base-pairs n and n + 1 are shown.

$${\mathbf{M}}_n{\ddot{\mathbf{u}}}_n=-\partial H/\partial {\mathbf{u}}_n-\mathrm{\Gamma }{\mathbf{M}}_n{\dot{\mathbf{u}}}_n+{\mathrm{\Xi }}_n,$$ (2)

where n = 1,2,…, N, Γ = 1/t_r is the Langevin collision frequency with t_r = 1 ps being the corresponding particle relaxation time, M_n is a diagonal matrix of grain masses of n-th base-pair, and ${\mathrm{\Xi }}_n={\{{\mathrm{\xi }}_{n,k}\}}_{k=1}^{36}$ is a 36-dimensional vector of Gaussian distributed stochastic forces describing the interaction of n-th base-pair grains with the thermostat with correlation functions

$$\langle {\xi }_{n,i}(t_1){\xi }_{m,j}(t_2)\rangle =2M\mathrm{\Gamma }{k}_{B}T{\delta }_{nm}{\delta }_{ij}\delta (t_2-t_1),$$

where the mass M = M_k, if i = 3(k−1) + l, k = 1,…, 12, l = 1, 2, 3.

To bring the temperature of the molecule to the desired value T = 300K, we integrate the system (2) over time t = 20t_r starting from the following initial conditions

$${\{{\mathbf{u}}_n(0)={\mathbf{u}}_n^0,{\dot{\mathbf{u}}}_n(0)=\mathbf{0}\}}_{n=1}^N$$ (3)

that correspond to the equilibrium state of the double helix ${\{{\mathbf{u}}_n^0\}}_{n=1}^N$. Once the system is thermalized, the temperature is maintained at T = 300K and the trajectory continues for 10 ns.

The first step in the validation procedure is to estimate root-mean-square deviation (RMSd) of the end point (t=10 ns) of the trajectory from a reference DNA structure, and compare the RMSd values between the CG and the reference all-atom trajectory (AMBER). Given two structures, the RMSd can be computed as:

$$d={\left[\frac{1}{12N}\underset{\mathbf{S}\in SO(3),\mathbf{1}\in {\mathbb{R}}^3}{min}\sum _{i=1}^{12N}{({\mathbf{r}}_i-(\mathbf{S}{\mathbf{r}}_i^{\prime }+\mathbf{1}))}^2\right]}^{1/2},$$

where r_i,i = 1,…, 12N is the reference (e.g., initial), and ${\mathbf{r}}_i^{\prime }$ is the final set of coordinates of the structure. The expression is minimized over a translation (vector l) and a rotation around a fixed point (operator S). The details of the algorithm are described in the Ref.⁸⁰. Analysis of RMS deviations from reference structures as a function of simulation time is commonly used as initial check of stability of the system and quality of the underlying models^66,68.

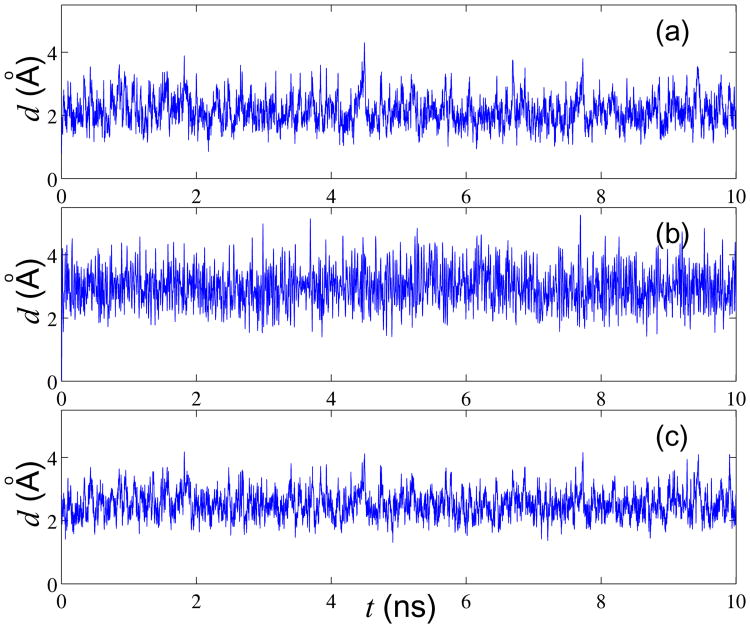
As is common in the field, the following sequence of 12 base pairs d(CGCGAATTGCGC)₂ (Dickerson's dodecamer) was used for this test; experimental X-ray structure of this B-DNA fragment is available. A constant temperature (T = 300K) simulation was performed for 10 ns. As one can see from the Fig. 4 the various RMSd metrics fluctuate around their equilibrium values, which suggests that the system remains stable in dynamics, on the time scale of the simulation. A comparison with the corresponding all-atom simulation is shown in Fig. 4 (b). This all-atom simulation uses the same 12 base-pair fragment, and is based on the latest nucleic acid force-field (parmbsc0²³) from AMBER. The solvent was represented via the generalized Born implicit solvent approximation; all other parameters such as Langevin collision frequency, ambient salt concentration, etc. were the same as in the CG simulation shown in Fig. 4 (a). Comparing Figs. 4 (a) and (b) we can see that the all-atom RMSd is slightly larger than that of the 12CG models. We can conclude that the 12CG model is somewhat more rigid as compared with all-atom one. Finally, we note that the equilibrium RMS deviation from the experimental (X-ray) B-form DNA is about 2.5Å, Fig. 4 (c), which is similar to what was observed earlier in all-atom implicit solvent simulations⁶⁸.

Fig. 4.

Comparison of time dependence of RMS deviation relative to various reference structures in coarse-grained and all-atom molecular dynamics simulations of a 12 base-pair DNA fragment at T=300K. (a) 12CG model simulation. RMSd is relative to the first frame. (b) All-atom model simulation. RMSd is relative to the first frame, (c) 12CG model simulation. RMSd is relative to B-DNA X-ray structure⁸¹. For all-atom structures the RMSd is computed only for the subset of atoms that define grain centers in the corresponding CG model.

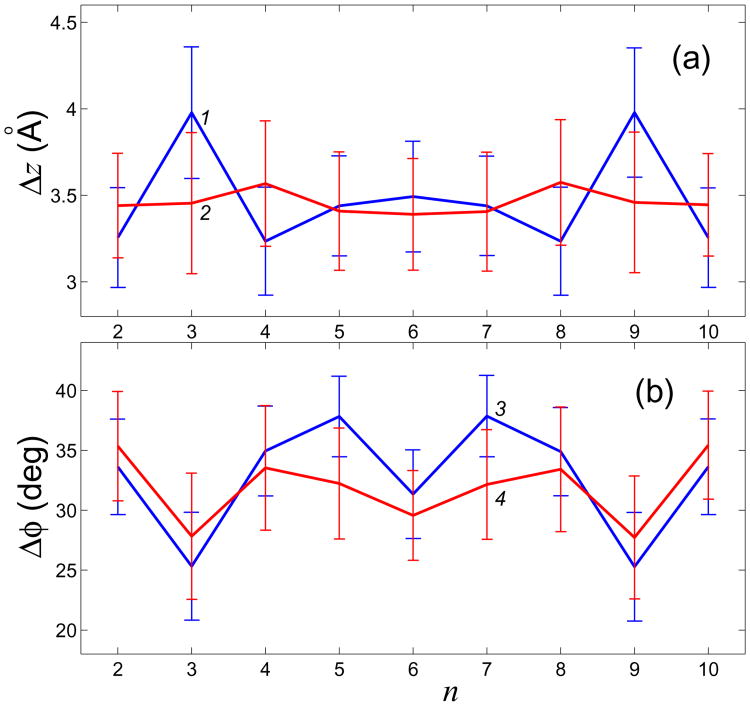
Another common set of structural parameters used in validation of DNA models is helical parameters. These parameters determine the interaction between neighboring base pairs, hence they are significant for heat transfer processes. Let's choose, for simplicity, two of them which are the most relevant ones for describing the overall structure of the double helix. The first of these parameters is the angle ϕ, called twist, through which each successive base pair is rotated around the helical axis relative to its (nearest neighbor) predecessor. The second one, rise, is the distance between such two neighboring base pairs. Given the structure of a single nucleotide and the values of the twist and rise, one can re-construct the whole molecule assuming that it is a “one-dimensional” uniform crystal. Exact algorithm of calculating these parameters is described in⁸². We used X3DNA⁸² package and in-house software for computing these parameters in our all-atom and CG models. With regards to twist and rise, the validation of our 12CG model was performed in the same manner as previously described in the context of an all-atom model⁶⁶. The results are presented in Fig. 5, where the averages of the 10ns simulation trajectories and the standard deviations (indicated by error bars) for each base pair step are shown. One can see that the twist and rise values for 12CG model are rather close to those of the all-atom model. A small difference is comparable with that seen between DNA simulations in explicit vs. implicit solvent⁶⁶.

Fig. 5.

Comparison of two common helical parameters (a) Δz (rise) and (b) Δϕ (twist) between the CG model (curves 1, 3) and the corresponding all-atom model (curves 2, 4) (n – number of base pair step). Shown are averages over the corresponding 10ns molecular dynamics trajectories at T=300K.

V. The Dispersion Curves and Small-Amplitude Oscillations

The proposed 12CG model enables one to compute dynamical evolution of a DNA molecule with any base sequence. However, for homogeneous molecules, that is if all base pairs are identical, the molecule can be considered as quasi-one-dimensional crystal with the elementary cell being one nucleotide pair of the double helix. This is a very useful simplification that will be employed here; it is also a very reasonable one as long as the focus is on the over-all physics of the structure, not on sequence dependent effects. The main advantage of the homogeneity assumption is that linear oscillations can be analyzed by standard techniques of solid state physics. To be specific, let's consider a poly-G double helical chain, assumed to extend along the z-axis. In the ground state of the double helix, each successive nucleotide pair is obtained from its predecessor by translation along the z-axis by step Δz and by rotation around the same axis through helical step Δϕ These are the rise and twist parameters introduced in the previous section.

$$\begin{array}{c}{x}_{n,j,1}=x_{n-1,j,1}cos(\mathrm{\Delta }\varphi )-x_{n-1,j,2}sin(\mathrm{\Delta }\varphi ),\\ x_{n,j,2}=x_{n-1,j,1}sin(\mathrm{\Delta }\varphi )-x_{n-1,j,2}cos(\mathrm{\Delta }\varphi ),\\ x_{n,j,3}=x_{n-1,j,3}+\mathrm{\Delta }z\end{array}$$ (4)

Thus, the energy of the ground state is a function of 38 variables: ${\{{\mathbf{x}}_{1,j}\}}_{j=1}^{12}$, Δϕ, Δz, where x_1,j = (x_1,j,1,x_1,j,2,x_1,j,3) is the vector position of j-th grain of the first nucleotide pair.

Finding the ground state amounts to the following minimization problem:

$$E_0=E_v+\dots +E_{\mathit{\text{vdW}}}\to min:{\{{\mathbf{x}}_{1,j}\}}_{j=1}^{12},\mathrm{\Delta }\varphi ,\mathrm{\Delta }z,$$ (5)

where the sum extends over one nucleotide pair n = 1, and the relation (4) holds for calculation of the energies E_v,…,E_vdW.

Numerical solution of the problem (5) has shown that the ground state of poly-G DNA corresponds to the twist value of Δϕ₀ = 38.30°, and the rise value (z-step) of Δz₀ = 3.339Å. It should be noticed that if all of the long-range interaction were omitted, i.e., without two last terms E_q and E_vdW in the Hamiltonian (B1), the helical step values would change only slightly, by about 1 per cent: Δϕ₀ = 38.03°, Δz₀ = 3.309Å. Thus, long-range electrostatic interactions between the charged group result in the relative elongation of the chain by only about 1 per cent. Parameters of the double helix computed within our model differ only slightly from the “canonical” parameters of the B-conformation of a (heterogeneous) DNA double helix in the crystal form⁸³, for which the average twist angle is Δϕ = 34° ÷ 36°, and average rise per base pair is Δz = 3.4Å.

To find the ground state of the homogeneous double helix under tension, it is necessary to minimize (5) under the fixed value of longitudinal step Δz. As a result, one can obtain the dependence of the homogeneous state energy on the longitudinal step. This function E₀(Δz) has a minimum when Δz = Δz₀, which corresponds to the B-conformation of the double helix. Longitudinal stiffness of the helix K_z = d²E₀/dΔz²|_Δz0. Specifically, within our model we estimate K_z = 16 N/m. Since the energy E₀ which is being derived is normalized to one nucleotide pair one can calculate the stretching modulus S = K_zΔz₀ = 16 N/m × 3.4 Å= 5440pN. This estimate is somewhat higher than the corresponding estimates of 1530 ⋯ 3760 pN obtained from fluctuations of distances between base pairs observed in MD simulations⁴². The relatively larger value of K_z from our CG model is consistent with the model's over-all larger stiffness relative to the all-atom description, see a discussion above. Some of the difference between the two estimates may also be due to methodological differences in estimating longitudinal stiffness. Values of the stretching modulus derived from experiments are of the order 1000 pN^84–86, i.e., about 5 times smaller than our estimate based on the CG model. One should keep in mind, however, that we have obtained only an upper estimate for the stretching modulus: temperature was assumed to be zero, the calculations were based on a homogeneous poly-G–poly-C sequence that was reported to be more rigid than inhomogeneous and poly-A–poly-T sequences used in experiments^87,88, and the entropy component was not considered in our calculations.

To obtain E₀(Δϕ), that is the dependence of the helix energy on the helical step Δϕ, we set Δz = Δz₀ in (5) and perform the minimization with respect to the remaining 36 parameters. Then, torsion stiffness of the double helix K_ϕ = Δz₀d²E₀/dΔϕ²|_Δφ0. Our estimate, K_ϕ = 5.8 × 10⁻²⁸ J·m, is in good agreement with the experimental value of K_ϕ = 4.1 ± 0.3 × 10⁻²⁸ J·m, obtained for DNA macromolecule in B-conformation⁸⁹.

For analysis of small-amplitude oscillations of the double helix it is convenient to use local cylindrical coordinates v_{n, j} = (v_n,j,1,v_n,j,2,v_n,j,3), given by the following expressions:

$$\begin{array}{c}{x}_{n,j,1}=x_{n,j,1}^0-v_{n,j,1}sin{\varphi }_{n,j}+v_{n,j,2}cos{\varphi }_{n,j},\\ x_{n,j,2}=x_{n,j,2}^0+v_{n,j,1}cos{\varphi }_{n,j}+v_{n,j,2}sin{\varphi }_{n,j},\\ x_{n,j,3}=x_{n,j,3}^0+v_{n,j,3},\end{array}$$ (6)

with ${\mathbf{x}}_{n,j}^0$, (n = 0, ±1, ±2,…; j = 1,2,…,12) being coordinates of the grains in the ground state of the double helix, and ϕ_n,j being angular coordinate of the grain (n,j). Within these new coordinates the molecule's Hamiltonian (B1) has the following form:

$$H=\sum _n[\frac{1}{2}(\mathbf{M}{\dot{\mathbf{v}}}_n,{\dot{\mathbf{v}}}_n)+P({\mathbf{v}}_{n-1},{\mathbf{v}}_n,{\mathbf{v}}_{n+1})],$$ (7)

where v_n = (u_n,1, u_n,2,…, u_n,12) is a 36-dimensional vector, M is 36-dimensional diagonal mass matrix. Note that the last two terms E_q and E_vdW, responsible for long-range interaction, have been omitted. This simplification is critical from the methodological point of view, but has very little impact on the accuracy of the estimates of DNA thermal conductivity. The point will be discussed below.

Hamiltonian (7) corresponds to the following system of equations of motion:

$$-\mathbf{M}{\ddot{\mathbf{v}}}_n=P_1({\mathbf{v}}_n,{\mathbf{v}}_{n+1},{\mathbf{v}}_{n+2})+P_2({\mathbf{v}}_{n-1},{\mathbf{v}}_n,{\mathbf{v}}_{n+1})+P_3({\mathbf{v}}_{n-2},{\mathbf{v}}_{n-1},{\mathbf{v}}_n),$$ (8)

where P_i(v₁, v₂, v₃) = ∂P/∂v_i, i = 1,2,3. Within the linear approximation, the system (8) has the form

$$-\mathbf{M}{\ddot{\mathbf{v}}}_n=B_1{\mathbf{v}}_n+B_2{\mathbf{v}}_{n+1}+B_2^{\ast }{\mathbf{v}}_{n-1}+B_3{\mathbf{v}}_{n+2}+B_3^{\ast }{\mathbf{v}}_{n-2},$$ (9)

where matrix elements are given by

$$B_1=P_{11}+P_{22}+P_{33},B_2=P_{12}+P_{23},B_3=P_{13},$$

and partial derivative matrix is given by

$$P_{ij}=\frac{{\partial }^{2}P}{\partial {\mathbf{v}}_i\partial {\mathbf{v}}_j}(\mathbf{0},\mathbf{0},\mathbf{0}),i,j=1,2,3.$$

Solution of the system of linear equations (9) can be found in the standard form

$${\mathbf{v}}_n=A\mathbf{e}exp[i(qn-\omega t)],$$ (10)

where A is linear mode amplitude, e is unit vector (|e| = 1), q ∈ [0,π] is dimensionless wave number. Substituting the expression (10) into the system (9), we arrive at the following 36-dimensional eigenvalue problem:

$${\omega }^2\mathbf{M}\mathbf{e}=[B_1+B_{2}exp(iq)+B_2^{\ast }exp(-iq)+B_{3}exp(2iq)+B_3^{\ast }exp(-2iq)]\mathbf{e}.$$ (11)

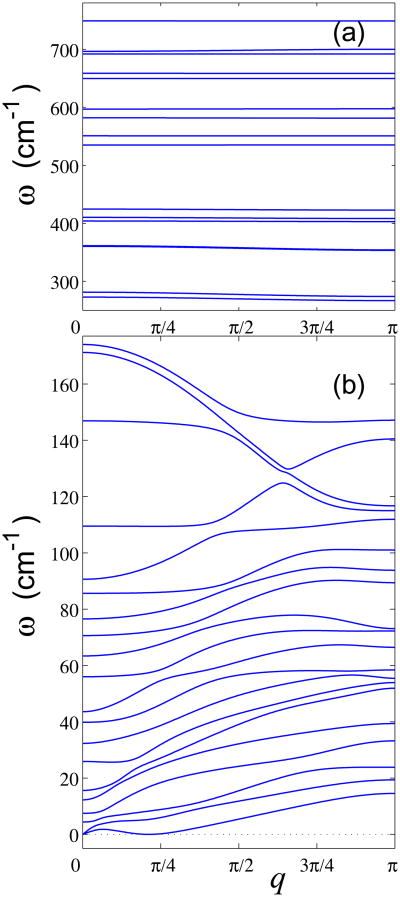
Thus, to obtain dispersion relations which characterize eigenmodes of the DNA double helix, one has to find all eigenvalues of the problem (11) for each value of wave number 0 ≤ q ≤ π. The calculated dispersion curve includes 36 branches ${\{{\omega }_j(q)\}}_{j=1}^{36}$ and is shown on the Fig. 6.

Fig. 6.

36 branches of the dispersion curve of homogeneous poly-G DNA: (a) high-frequency and (b) low-frequency branches.

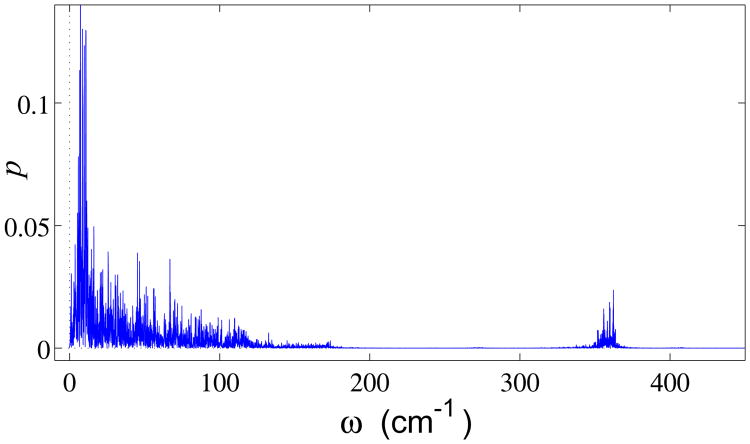
It can be seen from Fig. 6 that frequency spectrum consists of low-frequency 0 ≤ ω ≤ 175cm⁻¹ and high-frequency ω ∈ [267,749]cm⁻¹ domains. The high-frequency domain describes internal oscillations of the bases. As shown in Fig. 6 (a), corresponding dispersion curves have very small slope, meaning that the high-frequency oscillations have a small dispersion. The low-frequency oscillations have larger dispersion – see Fig. 6 (b). There are two acoustic dispersion curves which include zero point (q = 0, ω = 0). The first curve ω₁(q) describes torsional acoustic oscillations, the second one ω₂(q) describes longitudinal acoustic oscillations of the double helix. Thus we can obtain the two sound velocities

$$v_t=\mathrm{\Delta }z\underset{q\to 0}{lim}\frac{{\omega }_1(q)}{q},v_l=\mathrm{\Delta }z\underset{q\to 0}{lim}\frac{{\omega }_2(q)}{q},$$

with Δz being z-step of a double helix. The value of the torsional sound velocity is v_t = 850 m/s, and the value of the longitudinal sound velocity is v_l = 1790 m/s. One of these dispersion curves includes the special point (q = Δϕ,ω = 0) (Δϕ is the angular helix step). This curve describes bending oscillations of the double helix which we do not analyze in detail because we have so far neglected the long-range interactions that are known to have strong effect on bending rigidity of the DNA.

The estimated longitudinal sound velocity is in agreement with experimental value of the sound velocity in DNA fibers⁹⁰: v_l = 1900 m/s. Another experimental estimate⁹¹ of the same quantity is higher, v_l = 2840 m/s, and was obtained from inelastic X-ray scattering. The same work reports torsional sound velocity v_t = 600 m/s; the 20 % discrepancy with our estimate of v_t = 850 m/s appears acceptable given similar margin of error seen between different experimental estimates for the longitudinal velocity.

VI. Frequency Spectrum of the Thermal Oscillations

Let's again consider a homogenous poly-G DNA chain consisting of N = 200 base pairs and calculate its frequency spectrum density. We begin by simulating dynamics of the helix without taking into account long-range interactions. Later, we will turn them on to analyze the effect of making this approximation.

To obtain thermalized state of the double helix, the system of Langevin's equations (2) should be numerically integrated. For thermalization of the double helix let's consider initial conditions corresponding to the ground state (3), and integrate the system (2) over time t = 20t_r. After the equilibration period, the coupling with the thermostat is switched off, and the frequency density p(ω) of the kinetic energy distribution is obtained. To increase precision, distribution density was calculated as an average over all grains of the helix.

The computed frequency spectrum density at T = 300K is shown in the Fig. 7. The spectrum is clearly divided into a low-frequency 0 ≤ ω ≤ 175 cm^–1 and a high-frequency 267 < ω < 749 cm⁻¹ domain, consistent with the dispersion curves of Fig. 6.

Fig. 7.

Frequency spectrum density of the DNA double helix thermal fluctuations at T = 300K.

Simulating the double helix dynamics with account for all interactions, including long-range ones, (results not shown) yields almost the same frequency spectrum. Only the density of oscillations in the interval 0 ≤ ω < 10 cm⁻¹ increases somewhat.

VII. Heat Conductivity of the Double Helix

For numerical modeling of the heat transfer along the DNA double helix, we consider a chain of a fixed length with the ends placed in two separate thermostats each with its own temperature. To calculate the coefficient of thermal conductivity, we have to calculate numerically the heat flux through any cross section of the double helix. Therefore, first we need to obtain a formula for the longitudinal local heat flux.

Let us consider the homogeneous double helix poly-G DNA. (The method below is also applicable to any sequences of bases).

If long-range interactions (electrostatic and van der Waals) are not taken into account we can present the Hamiltonian of the helix (B1) in the form

$$H=\sum _n\frac{1}{2}(\mathbf{M}{\dot{\mathbf{u}}}_n,{\dot{\mathbf{u}}}_n)+P({\mathbf{u}}_{n-1},{\mathbf{u}}_n,{\mathbf{u}}_{n+1}),$$ (12)

where the first term describes the kinetic energy of atoms in a given cell and the second term describes the energy of interaction between the atoms within the cell and with the atoms of neighboring cells. The corresponding equations of motion can be written in the form

$$\mathbf{M}{\ddot{\mathbf{u}}}_n=-P_1({\mathbf{u}}_n,{\mathbf{u}}_{n+1},{\mathbf{u}}_{n+2})-P_2({\mathbf{u}}_{n-1},{\mathbf{u}}_n,{\mathbf{u}}_{n+1})-P_3({\mathbf{u}}_{n-2},{\mathbf{u}}_{n-1},{\mathbf{u}}_n),$$ (13)

where the function P_j is defined as

$$P_j=\frac{\partial }{\partial {\mathbf{u}}_j}P({\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3),j=1,2,3.$$

To determine the energy flux through the double helix cross section, we re-write formula (12) in a compact form, H = Σ_n h_n, where h_n is the energy density,

$$h_n=\frac{1}{2}(\mathbf{M}{\dot{\mathbf{u}}}_n,{\dot{\mathbf{u}}}_n)+P({\mathbf{u}}_{n-1},{\mathbf{u}}_n,{\mathbf{u}}_{n+1}).$$ (14)

Local longitudinal heat flux j_n is defined through local energy density h_n by the discrete version of the continuity equation,

$$\frac{d}{dt}{h}_n=j_n-j_{n+1}.$$ (15)

Using the energy density (14) and the equations of motion (13), we can derive the following relations:

$$\frac{d}{dt}{h}_n=(\mathbf{M}{\ddot{\mathbf{u}}}_n,{\dot{\mathbf{u}}}_n)+(P_{1,n},{\dot{\mathbf{u}}}_{n-1})+(P_{2,n},{\dot{\mathbf{u}}}_n)+(P_{3,n},{\dot{\mathbf{u}}}_{n+1})=-(P_{1,n+1},{\dot{\mathbf{u}}}_n)-(P_{3,n-1},{\dot{\mathbf{u}}}_n)+(P_{1,n},{\dot{\mathbf{u}}}_{n-1})+(P_{3,n},{\dot{\mathbf{u}}}_{n+1}),$$

Where

$$P_{j,n}=P_j({\mathbf{u}}_{n-1},{\mathbf{u}}_n,{\mathbf{u}}_{n+1}),j=1,2,3.$$

From this and (15) it follows that the energy flux through the n-th cross section has the following simple form:

$$j_n=(P_{1,n},{\dot{\mathbf{u}}}_{n-1})-(P_{3,n-1},{\dot{\mathbf{u}}}_n).$$ (16)

Let us note that taking into account long-range interactions would complicate this formula considerably, making the calculations virtually intractable. This is why the approximation we have made is critical.

For a direct numerical modeling of the heat transfer along the double helix, we consider a finite structure of the length NΔz with fixed ends. We assume that the first N₊ = 20 segments are placed in the thermostat at temperature T₊ = 310 K and the last N₋ = 20 segments are placed in the other thermostat at T₋ = 290 K. The helix dynamics is described by the following equations of motion:

$$\begin{array}{c}\mathbf{M}{\ddot{\mathbf{u}}}_n=-{\mathbf{F}}_n-\mathrm{\Gamma }\mathbf{M}{\dot{\mathbf{u}}}_n+{\mathrm{\Xi }}_n^{+},n=1,\dots ,N_{+},\\ \mathbf{M}{\ddot{\mathbf{u}}}_n=-{\mathbf{F}}_n,n=N_{+}+1,\dots ,N-N_{-},\\ \mathbf{M}{\ddot{\mathbf{u}}}_n=-{\mathbf{F}}_n-\mathrm{\Gamma }\mathbf{M}{\dot{\mathbf{u}}}_n+{\mathrm{\Xi }}_n^{-},n=N-N_{-}+1,\dots ,N,\end{array}$$ (17)

where F_n =∂H/∂u_n, Γ = 1/t_r, is the damping coefficient (relaxation time t_r = 1 ps, and ${\mathrm{\Xi }}_n^{\pm }=({\xi }_1^{\pm },\dots ,{\xi }_{36}^{\pm })$ is a 36-dimensional vector of normally distributed random forces normalized by the condition

$$\langle {\xi }_{n,i}^{\pm }(t_1){\xi }_{m,j}^{\pm }(t_2)\rangle =2M{k}_B{T}_{\pm }{\delta }_{nm}{\delta }_{ij}\delta (t_2-t_1),$$

where the mass M = M_k, if i = 3(k − 1) + l, k = 1,…, 12, l = 1,2, 3.

We take the initial conditions (3) corresponding to the equilibrium state of the helix. With these initial conditions, we integrate the equations of motion (17) numerically, by employing the velocity Verlet method with step Δt = 0.0005 ps. After integration time t₀ [this value depends on the helix length between the thermostats, ΔL = (N − N₊ − N₋)Δz], we observe the formation of a temperature gradient and a constant heat energy flux in the central part of the helix. It is important to notice that the time t₀ can be reduced by modifying the initial distribution of the energy, e.g., by taking the initial condition for the system (17) as homogeneously thermalized state with the mean temperature T = (T₊ + T₋)/2 = 300 K.

After the stationary heat flux is established, the temperature distribution can be found using the formula

$$T_n=\underset{t\to \infty }{lim}\frac{1}{36k_{B}t}{\mathit{\int }}_0^t(\mathbf{M}{\dot{\mathbf{u}}}_n(\tau ),{\dot{\mathbf{u}}}_n(\tau ))d\tau$$

and the averaged value of the energy flux along the helix

$$J_n=\underset{t\to \infty }{lim}\frac{\mathrm{\Delta }z}{t}{\mathit{\int }}_0^t{j}_n(\tau )d\tau .$$

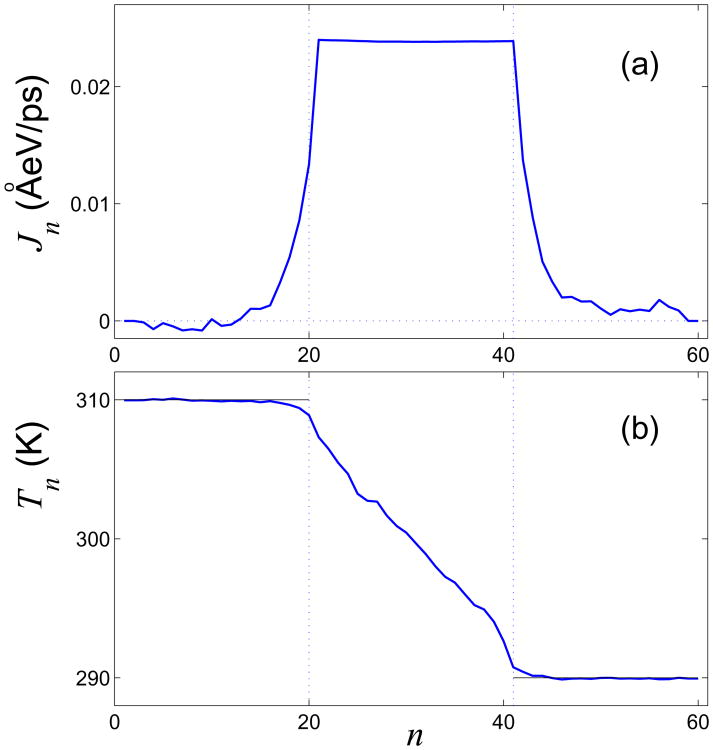
Distributions of the local energy flux and temperature along the helix are shown in Figs. 8 (a) and (b). In the steady-state regime, the heat flux through each of the cross section at the central part of the helix should remain the same, i.e. J_n ≡ J, N₊ < n ≤ N − N₋. This property can be employed as a criterion for the accuracy of numerical modeling and can also be used to determine the characteristic time for achieving the steady-state regime and calculation of J_n and T_n. Figure 8 (a) suggests that the flux is constant along the central part of the helix indicating that we have reached the required regime.

Fig. 8.

Distributions of (a) local heat flux J_n and (b) local temperature T_n in the double helix with length NΔz. The input parameters are N = 60, temperatures T₊ = 310 K and T₋ = 290 K, and the number of cells in the thermostats, N_± = 20.

At the central part of the helix, we observe a linear gradient of the temperature distribution, so that we can define the coefficient of thermal conductivity as

$$\kappa (N-N_{+}-N_{-})=\frac{(N-N_{-}-N_{+}-1)J}{(T_{N_{+}+1}-T_{{N-N}_{-}})S},$$ (18)

where S = πR² is the area of the cross section of the double helix (R = 8 Å is the radius of helix on phosphorus atoms). In this way, the calculation of thermal conductivity is reduced to the calculation of the limiting value,

$$\kappa =\underset{N\to \infty }{lim}\kappa (N).$$

In order to determine the coefficient of thermal conductivity, we need to know only the dependence of the temperature from base-pair number in the central part of the helix. However, a change of the temperature distribution at the edges of the helix can also provide some useful information. If the helix is placed into a Langevin thermostat at temperature T, each segment of the helix should have the temperature T_n = T due to the energy balance of the input energy from random forces and the energy lost to dissipation. Then, an averaged energy flow from the n-th segment of the helix can be presented as

$$\mathrm{\Gamma }(\mathbf{M}{\dot{\mathbf{u}}}_n,{\dot{\mathbf{u}}}_n)=36k_B{T}_n/t_r.$$

If only the edges of the helix are placed into thermostat, there appears an additional energy exchange with its central part, so the energy from the right edge will flow to the left one. As a result, the temperature of the left edge is reduced (T_n ≤ T₊, n = 1, 2,…, N₊), whereas the temperature at the right edge increases (T_n ≥ T₋, n = N − N₋ + 1, …, N) – see Fig. 8 (b). This information allows us to find the energy flux in the central part of the double helix using only the energy imbalance at the edges,

$$\frac{J{t}_r}{\mathrm{\Delta }z36k_B}=\sum _{n=1}^{N_{+}}(T_{+}-T_n)=\sum _{n=N-N_{-}+1}^N(T_n-T_{-}).$$ (19)

If the lengths of the edges placed into thermostat coincide, i.e., N₊ = N₋ = N_±, we can rewrite this formula in the following simplified form:

$$J=\frac{\mathrm{\Delta }z18k_B}{t_r}\sum _{n=1}^{N_{\pm }}(T_{+}-T_{-}-T_n+T_{N+1-n}).$$ (20)

Equation (19) gives an alternative way to calculate thermal energy flux J; the equation can be employed to verify results obtained via Eq. (16). Let us note that although (16) is obtained under the assumption of no long-range interactions, formula (20) remains valid also if these interactions are taken into account.

Numerical modeling of the heat transfer shows that both formulas lead to the same value of the heat-conductivity coefficient if long-range interactions are absent. When N=80 (the number of internal links N_i = N − N₊ − N₋ = 20), the heat-conductivity coefficient κ = 0.26 W/mK. When N = 80 (N_i = 40) − conductivity κ = 0.29 W/mK, when N = 120 (N_i = 80) − κ = 0.27 W/mK, and when N = 200 (N_i = 160) − κ = 0.28 W/mK. The same values are obtained also if the long-range interactions are taken into account (and the heat flow is calculated by formula (20) only). These considerations help us reach the conclusion that the contribution of the long-range interactions to the heat transfer along the double helix is very minor.

It is worth noting that the use of formula (20) for calculating the value of heat transfer requires more time-consuming calculations. Therefore, it is preferable to use formula (16). Also, equation (16) allows one to estimate relative contributions of various interactions into the process of heat transfer. We find that interaction between neighboring base pairs contributes 32% to the net energy flow, with the rest of the heat transfer occurring along the two sugar-phosphate chains.

As one can see from the results, the value of heat conductivity κ in the DNA macromolecule does not depend on the length of the molecule. This is normal thermal conductivity for which Fourier's law is valid at nano-level as well, at least as far as the DNA is concerned. This is in contrast to earlier models of heat conduction along carbon nanotubes and nanoribbons that predicted anomalous thermal conductivity – divergence of the coefficient of thermal conductivity with sample length^10–13. Compared to nanotubes, the DNA double helix is much which leads to strongly nonlinear behavior at T = 300 K (in contrast, a nanotube is a rigid quasi-one-dimensional structure, with only weak nonlinear dynamics). Contribution of nonlinearity to the DNA dynamics will be explored in more detail in the following section.

VIII. Dependence of the Thermal Conductivity On Temperature

At T = 300 K the DNA double helix exhibits high- amplitude vibrations (the amplitudes can be estimated from Fig. 4 and 5). The contribution of nonlinearity to the DNA dynamics can be estimated from the temperature dependence of dimensionless heat capacity

$$c(T)=\frac{1}{36N{k}_{B}T}\frac{d}{dT}E(T),$$ (21)

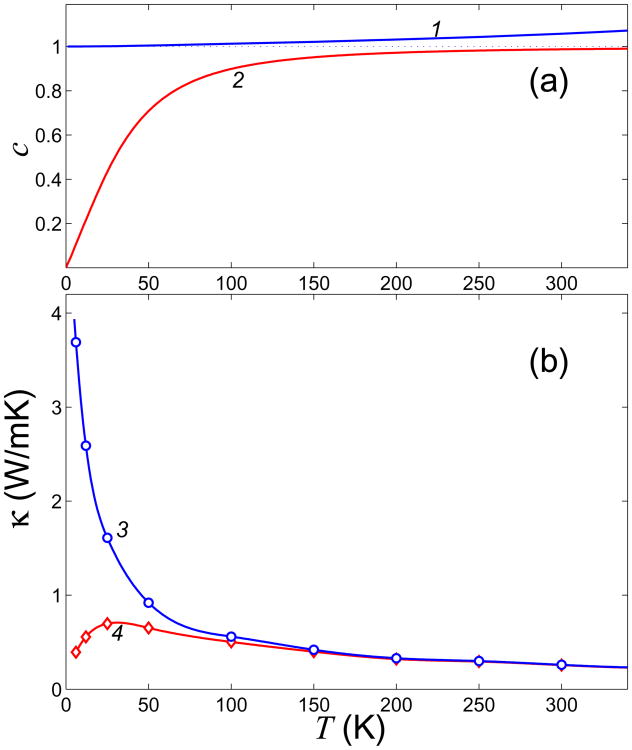
where E(T) = 〈H〉 is average double helix energy at temperature T. For a harmonic system, dimensionless heat capacity c(T) ≡ 1; for a system with strong anharmonism c(T) < 1, and c(T) > 1 for weakly anharmonic systems. As seen from Fig. 9, heat capacity of the double helix equals to 1 for low temperatures (T < 10 K) and increases monotonously when the temperature grows. The heat capacity c = 1.05 at T = 300 K, implying weak anharmonism.

Fig. 9.

(a) Temperature dependence of dimensionless specific heat c(T) and c_q(T) (curves 1 and 2, respectively); b) heat conductivity κ(T) and κ_q(T) (curves 3 and 4, respectively) of the DNA double helix. The dependencies c(T) and κ(T) are obtained in the framework of classical molecular dynamics model, while c_q(T) and κ_q(T) are computed within the quantum framework.

The role of nonlinearity decreases monotonously as the temperature decreases. In the limiting case T → 0 the double helix becomes harmonic. Therefore, classical thermal conductivity has to increase monotonously as the temperature decreases, and diverge when T → 0. The results of our numerical modeling confirm this conclusion – see Fig. 9 (b), curve 3. At T ↘ 0 the heat conductivity κ ↗∞.

We should mention that the temperature dependence of the DNA thermal conductivity found above is obtained with the framework of classical molecular-dynamics model, which does not take into account quantum effects of “frozen” high-frequency oscillations (to take those into account requires substantial modifications to the model^92,93). In crystals at low temperatures, thermal conductivity decays monotonically when T → 0. This is explained by the fact that at low temperatures the temperature dependence of thermal conductivity is defined mainly by the temperature dependence of heat capacity.

In classical mechanics, heat capacity of phonons does not depend on temperature, whereas in quantum mechanics such a dependence is defined by the formula c(ω,T) = k_BF_E(ω,T), where the Einstein function

$$F_E(\omega ,T)={\left(\frac{ħ\omega }{k_{B}T}\right)}^2\frac{exp(ħ\omega /k_{B}T)}{{[exp(ħ\omega /k_{B}T)-1]}^2},$$

where ω is the phonon frequency (0 ≤ F_E ≤ 1, function F_E ↘ 0 for T ↘ 0 and F_E ↗ 1 for T ↗ ∞).

As seen from the DNA dispersion curves ${\{{\omega }_j(q)\}}_{i=1}^{36}$, the main contribution in the heat conductivity is determined by the 20 low-frequencies phonons (16 high-frequencies phonons have very small group velocities, and therefore can not be efficient energy carriers). The temperature dependence of dimensionless heat capacity of low frequencies phonons can be found using formula

$$c_q(T)=\frac{1}{20\pi }\sum _{i=1}^{20}{\mathit{\int }}_0^{\pi }{F}_E({\omega }_i(q),T)dq.$$ (22)

One can see from Fig. 9 that the heat capacity c_q does not noticeably depend on temperature if T > 150 K, and tends monotonously to zero as the temperatures decrease below T < 150 K.

Thus, thermal vibrations of the double helix can be described classically for T > 150 K only. For lower temperatures, quantum effect caused by “freezing out” of high-frequency vibrations must be taken into account. Due to these effects the DNA heat capacity (22) tends monotonously to zero as the temperature decreases. The double helix thermal conductivity κ_q(T) ≈ c_q(T)κ(T), (where the temperature dependence κ(T) is calculated classically) because the phonon energy is proportional to heat capacity. As it seen form Fig. 9 (b) at T > 30 K the thermal conductivity κ_q grows monotonously as the temperature decreases, reaching its maximum at T ≈ 30 K, and then decreases monotonously as T → 0.

These calculations show that heat transfer in the DNA occurs mainly due to propagation of low-frequency phonons (frequencies ω < 175 cm⁻¹), i.e., by “soft” low-frequencies waves. Such oscillations are strongly coupled to deformation of orientation angles. This fact clearly distinguishes the DNA double helix from the essentially rigid carbon nanotubes and nanoribbons. The simplest model of a one-dimensional system with orientational interaction is one-dimensional chain of interacting rotators. This chain has a finite thermal conductivity^94,95. On the other hand, nanotubes and nanoribbons are commonly described in the one-dimensional approximation as anharmonic Fermi Pasta Ulam (FPU) chains that lead to infinite heat conductivity^17,18.

Thus, the double helix of a homogeneous poly-G DNA has a finite thermal conductivity κ = 0.3 W/mK. The double helix with a nonhomogeneous (arbitrary) base sequence may be expected to have a smaller value of the heat conductivity coefficient since the presence of inhomogeneities leads to additional phonon scattering. Therefore, thermal conductivity of a generic DNA double helix, κ ≤ 0.3 W/mK, may be expected to be less than half of that of water heat conductivity which is 0.6 W/mK. This means that DNA macromolecule is a thermal insulator relative to its surrounding solution. It should be noted that experimentally measured thermal conductivity of the DNA-gold composite structure (DNA is a matrix for gold nano-particles)¹⁶ gives the coefficient of thermal conductivity 150 W/mK, which is 500 times higher than the predicted thermal conductivity of pure DNA. Thus, we conclude that the measured thermal conductivity of the DNA-gold composite is completely determined by the metal component, not the DNA.

IX. Conclusions

A coarse-grain (12CG) model of DNA double helix is proposed in which each nucleotide is represented by 6 “grains”. The corresponding effective pair potentials are inferred from correlation functions obtained from classical all-atom molecular dynamics (MD) trajectories and potentials (AMBER). The computed structural characteristics and fluctuations of the double helix at T = 300 K are in reasonable agreement with available experimental data and earlier computations based on all-atom models. An analysis of dispersion curves derived from the coarsegrained model yields longitudinal and torsional sound velocities in close agreement with experiment.

The numerical modeling of heat conductivity along a single DNA molecule shows that double DNA helix has a finite (normal) thermal conductivity. This means that Fourier's law is valid at nano-level for the DNA, i.e., coefficient of thermal conductivity does not depend on the length of the DNA fragment. Single molecule DNA thermal conductivity does not exceed 0.3 W/mK, which is two times smaller than thermal conductivity of water. Thus, DNA double helix is a poor heat conductor. At the same time, it is known from modeling of heat transfer along carbon nanotubes and nanoribbons that the coefficient of thermal conductivity in these systems diverges as the specimen length grows^10–13. The anomalous behavior of thermal conductivity in long nano-objects is caused by their rigid structure as well as by their weakly nonlinear quasi one-dimensional dynamics, mostly due to rigid covalent interactions. In contrast, the DNA double-helix is a soft 3D structure with strongly nonlinear dynamics. Based on the results of our coarse-grained simulations we conjecture that heat conduction along the double helix is due predominantly to weak non-valent orientational interactions.

Appendix A: Masses of the Coarse Grains

The mass of each of the backbone grains [P],[C3] and [C1] is calculated as a sum of the masses of the original atoms included in the grain, Fig. 2. So m_[P] = 109 a.e., m_[C3] = 26 a.e., m_[C1] = 43 a.e. The distribution of the total mass of base X (X = A, T, G, C) between its three defining grains, m₁, m₂, m₃, can be found from the condition of preserving the total mass and preserving the position of the center of mass of the base. Values of the grain masses are shown in table I.

Table I.

Masses of the three coarse grains (m₁,m₂,m₃) for each of the base X=A, T, G, C. In units of proton mass m_p

X	m1	m2	m3
A	52.230	28.139	53.632
T	51.822	16.204	56.974
G	61.731	34.357	53.912
C	39.254	35.492	35.254

Appendix B: The Potential Function

For convenience let's re-write the Hamiltonian of the system:

$$H=E_k+E_v+E_b+E_a+E_t+E_{\mathit{\text{hb}}}+E_{\mathit{\text{st}}}+E_{\mathit{\text{el}}}+E_{\mathit{\text{vdW}}}.$$ (B1)

The first term is the kinetic energy of the systems:

$$E_k=\sum _{n=1}^{12N}\frac{1}{2}{M}_i{\dot{\mathbf{r}}}_i^2,$$ (B2)

where the summation is over all 12N coarse-grain particles (grains) in the system.

The second term E_v in the Hamiltonian (B1) stands for deformation energy of “valence” (pair) bonds. pair potentials have the standard form

$$U_{\alpha \beta }({\mathbf{x}}_1,{\mathbf{x}}_2)=\frac{1}{2}{K}_{\alpha \beta }{(|{\mathbf{x}}_2-{\mathbf{x}}_1|-R_{\alpha \beta })}^2,$$ (B3)

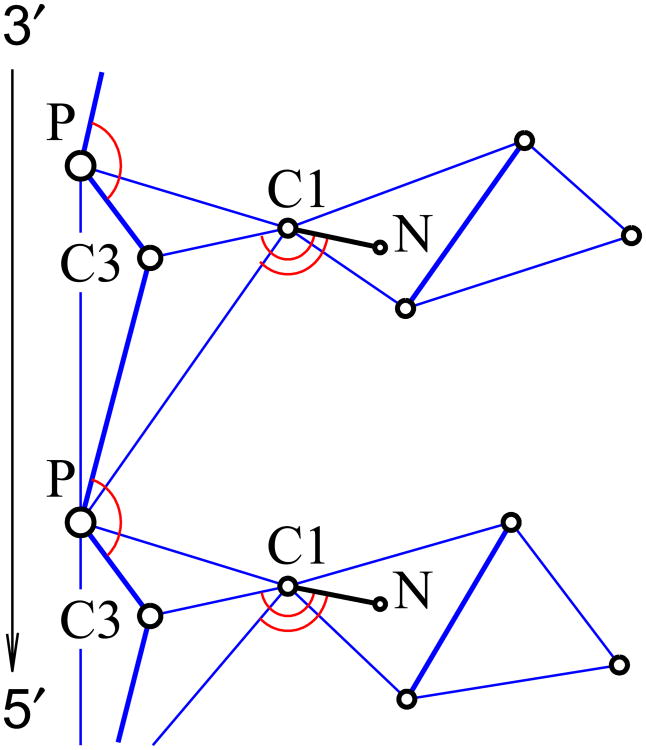
where αβ denotes types of bonded particles (for example, P and C3), parameter R_αβ is the equilibrium length, parameter K_αβ is the bond stiffness. values of these parameters were obtained by analysis of all-atomic MD trajectories. These potentials are calculated for the following pairs: P and C3, C3 and C1, C3 and P,P and C1, C1 and P, P and P (from neighbouring sites). Order in a pair corresponds to direction from 3′-end to 5′-end (see Fig. 10). The parameter values are given in the table II.

Fig. 10.

Grains involved in valent interactions. Blue lines denote valent (harmonic) bonds, red arcs mark valent angles, bold blue lines are axes of rotation in the torsion potentials. The circles marked as N stand for original atoms N9 on A,G bases and N1 on T,C bases (no coarse grains are centered on these atoms, their coordinates are calculated from the positions of the three grains that define the base plane).

Table II.

Values of the stiffness coefficients K_αβ lengths R_αβ for pair interaction potentials U_αβ(X₁,X₂).

αβ	PC3	C3C1	C3P	PC1	C1P	PP
Kαβ (eV / Å2)	9.11	8.33	0.694	0.66	0.781	0.20
Rαβ(Å)	2.6092	2.3657	4.0735	3.6745	4.8938	6.4612

The third term E_b in the Hamiltonian (B1) describes base deformation energy. This term was introduced to keep all four points near one plane and serves to mimic valent interaction in nitrogen bases. Let's denote the position of C1 particle by x₁ and positions of the three particles on a base by x₂, x₃, x₄. The deformation energy includes harmonic constraints on pair distances and a constraint on the bending angle of the rectangle {x₁ x₂,x₃,x₄} around its diagonal. Thus base γ(γ=A, T, G, C) deformation energy is give by the following formula:

$$\begin{gathered} U_{\mathrm{\gamma }}({\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3,{\mathbf{x}}_4)=\frac{1}{2}{K}_{\mathrm{\gamma }}[{(|{\mathbf{x}}_1-{\mathbf{x}}_2|-R_{\mathrm{\gamma }12})}^2+{(|{\mathbf{x}}_1-{\mathbf{x}}_4|-R_{\mathrm{\gamma }14})}^2+{(|{\mathbf{x}}_2-{\mathbf{x}}_3|-R_{\mathrm{\gamma }23})}^2 \\ +{(|{\mathbf{x}}_2-{\mathbf{x}}_4|-R_{\mathrm{\gamma }24})}^2+{(|{\mathbf{x}}_3-{\mathbf{x}}_4|-R_{\mathrm{\gamma }34})}^2]+{\epsilon }_{\gamma }(1+cos\theta ), \end{gathered}$$ (B4)

where θ is the angle between the two planes x₁x₂x₄ and x₂x₃x₄ (equilibrium corresponds to all four points lying on one plane and θ = π). The values of potential parameters can be found in table III. Parameters R_γ14,…,R_γ34 were defined as equilibrium distances between corresponding points on bases, values of parameters K_γ and ε_γ were determined from analysis of frequency spectrum of base oscillations in all atomic DNA molecular dynamics¹⁹.

Table III.

Values of parameters for potential U_X describing deformation of the base X=A, T, G, C.

γ	A	T	G	C
Rγ12 (Å)	2.6326	5.0291	2.5932	2.4826
Rγ14 (Å)	4.3195	2.7007	5.2651	2.6896
Rγ23 (Å)	4.2794	2.8651	4.2912	3.5882
Rγ24 (Å)	4.3111	5.5150	5.6654	3.5014
Rγ34 (Å)	3.5187	4.5399	4.5807	4.5523
Kγ (eV/Å2)	30	30	30	20
εγ (eV)	100	100	150	70

The fourth term E_a in the Hamiltonian B1 describes the energy of angle deformation and has following form:

$$U_a(\theta )={\epsilon }_a{(cos\theta -cos{\theta }_a)}^2,$$

This energy is calculated for following angles: C3-P-C3, C3-C1-N, N-C1-P. Here N denotes a specific nitrogen atom atom on the base: atom N9 for bases A and G, and atom N1 for bases T and C. Equilibrium angle and deformation energy are summarized in the table IV.

Table IV.

Values of deformation energy ε_X and equilibrium angle θ_X for angle potentials.

type	C3-P-C3	C3-C1-N	N-C1-P
εa (eV)	0.5	3.	0.3
θa	130.15°	141.63°	87.17°

The fifth term E_t in the Hamiltonian (B1) describes torsional deformation energy. It has the form:

$$U_t={\epsilon }_t(1-cos(\varphi -{\varphi }_0))$$

The first type of potential is for the torsion C3-C1-N9-C8 (C3-C1-N1-C6) – i.e., rotations of base A, G (T, C) around the bond C1—N9 (C1–N1). The second type of potential is for the torsion C3-P-C3-C1, the third one for the torsion C1-C3-P-C3. Parameters of these potentials are summarized in table V.

Table V.

Deformation energy ε_t and equilibrium values ϕ₀ for the torsional potentials.

Potential	C3-C1-N-C	C3-P-C3-C1	C1-C3-P-C3
εt (eV)	0.5	0.5	0.5
ϕ0	0	−26.21°	48.58°

The sixth term E_hb in the Hamiltonian (B1) describes the energy of interaction between complementary bases. Since each nitrogen base is a rigid planar structure, one can restore positions of all of its original atoms from positions of the three coarse-grain atoms, as outlined in the previous section. Let's denote the set of coordinates of three coarse-grain atoms by X_n with n being a number of the base-pair. One can calculate coordinates of all of the original atoms on the base: r₁(X_n), r₂(X_n),…,. Hence we can use the proven all-atom AMBER (van der Waals and electrostatics) potentials¹⁹ for hydrogen bonds and stacking interactions. Thus

$$E_{\mathit{\text{hb}}}=\sum _n{V}_{XY}(X_n,Y_n)=\sum _n{U}_{\mathit{\text{AMBER}}}(r_1(X_n),r_2(X_n),\dots ,r_1(Y_n),r_2(Y_n),\dots ).$$

where V_XY (X_n, Y_n) is a potential of interaction between X (X=A,T,G,C) base and complementary Y (Y=A,T,G,C) base.

The main part of the hydrogen bond energy is interactions between atoms near the hydrogen bond – see Fig. 11 (a) and (b). Hence the number of interacting atoms can be reduced. Let's denote this “reduced” potential by $V_{XY}^{\ast }(X_n,Y_n)$. Then

Fig. 11.

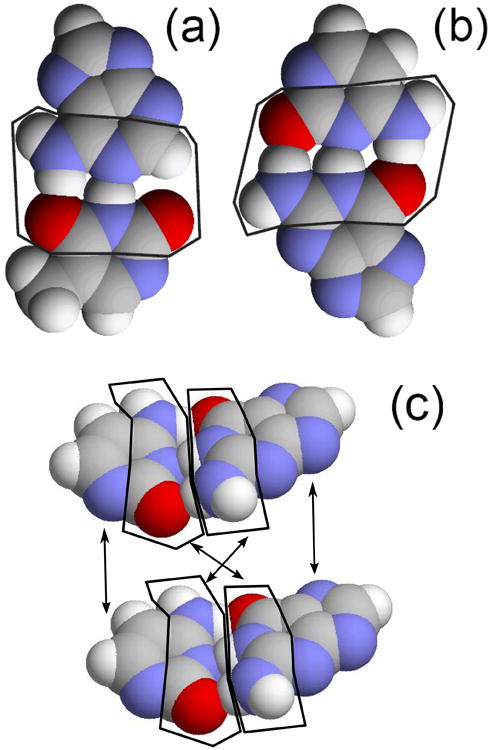
View of (a) AT base pair, (b) GC base pair (highlighted are atoms which contribute most to base-base interaction energy) and (c) two neighboring base-pairs (AT and GC). Arrows indicate parts of nitrogen bases whose interaction is taken into account: for bases on the complementary strands only those atoms that face another contribute to the interaction, while for neighboring bases on the same strand all of the atoms contribute.

$$E_{\mathit{\text{hb}}}=\sum _n{V}_{XY}^{\ast }(X_n,Y_n).$$

The interaction energy between neighboring bases is given by

$$E_{\mathit{\text{st}}}=\sum _n{V}_{XY}(X_n,X_{n+1})+V_{XY}^{\ast }(X_n,Y_{n+1})+V_{XY}(Y_n,Y_{n+1})+V_{XY}^{\ast }(Y_n,X_{n+1}).$$

Atoms whose interactions are taken into account in calculation of the interaction energy between neighbor bases are shown in Fig. 11 (c).

The eighth term E_el of the Hamiltonian (B1) describes the charge-charge interactions within the double helix. Within our model, only the phosphate groups interact via long-range electrostatic forces. We assume that each [P] grain carries charge equal to the electron charge q_P = −1e, while all other particles are neutral. The total electrostatic energy of the DNA in aqueous environment (including ions) is written as E_el = E_vac +ΔG_solv, where E_vac represents the Coulomb interaction energy in vacuum, and ΔG_solv is defined as the free energy of transferring the molecule from vacuum into solvent, i.e., solvation free energy. The above decomposition is an approximation made by most classical (non-polarizable) potential. Within our model we further assume that ΔG_solv contains only the electrostatic part; this is a reasonable assumption as long as the shape of the DNA double-helix does not change drastically during dynamics (e.g., the strands do not separate), and thus changes in the “hydrophobic” part of ΔG_solv can be neglected. While computation of the Coulomb part of the interaction is trivial, estimation of ΔG_solv is not, due to non-trivial shape of the biomolecule. Within the framework of the continuum dielectric, linear response theory the principle way of estimating ΔG_solv is by solving the Poisson-Boltzmann (PB) equation with the boundary conditions determined by the molecular surface that separates the high dielectric solvent from the low dielectric interior of the molecule. However, the corresponding procedures are expensive, and currently of limited practical use in dynamical simulations. We therefore resort to the so-called generalized Born model^65–67 (GB), which is the most widely used alternative to the PB treatment when speed of computation is a concern, particularly in molecular dynamics³⁶, including simulations of nucleic acids^41,68–77.

The GB model approximates ΔG_solv by the following formula proposed by Still et al.⁶⁵

$$\mathrm{\Delta }{G}_{\mathit{\text{solv}}}\approx -\frac{1}{2}(1-\frac{1}{{\epsilon }_{\mathit{\text{out}}}})\sum _{ij}\frac{q_i{q}_j}{f(r_{ij},R_i,R_j)},$$ (B5)

where ε_out is the dielectric constant of water, r_ij is the distance between atoms i and j, q_i is the partial charge of atom i, R_i is the so-called effective Born radius of atom i, and $f={[r_{ij}^2+R_i{R}_{j}exp(-r_{ij}^2/4R_i{R}_j)]}^{\frac{1}{2}}$. The empirical function is designed to interpolate between the limits of large $r_{ij}\gg \sqrt{R_i{R}_j}$ where the Coulomb law applies, and the opposite limit where the two atomic spheres fuse into one, restoring the famous Born formula for solvation energy of a single ion. The effective Born radius of an atom represents its degree of burial within the low dielectric interior of the molecule: the further away is the atom from the solvent, the larger is its effective radius. In our model, we assume constant effective Born radii which we calculate once from the first principles⁷⁸. The screening effects of monovalent salt are introduced approximately, at the Debye-Huckel level by substitution

$$1-{{\epsilon }_{\mathit{\text{out}}}}^{-1}\to -{{\epsilon }_{\mathit{\text{out}}}}^{-1}exp(-0.73\kappa f).$$

The 0.73 pre-factor was found empirically to give the best agreement with the numerical PB treatment⁷⁹. Here κ is the Debye-Huckel screening parameter $\kappa [{\mathring{\mathrm{A}}}^{-1}]\approx 0.316\sqrt{[\text{salt}][\text{mol}/L]}$.

Further simplifications come from the fact that we have only one non-zero charge species in our model, the [P] grain. Then, the total electrostatics energy is given by

$$E_{\mathit{\text{el}}}=C_0+\sum _{i,j=1}^{N_P}{V}_q(r_{ij})$$

where the summation is performed over all different [P]-grains pairs where

$$V_q(r)=C_1[\frac{1}{r}-\frac{1}{f(r)}(1-{\epsilon }_{\mathit{\text{out}}}^{-1}{e}^{-0.73\kappa f(r)}\left)\right]$$ (B6)

Here r denotes the distance between coarse-grain [P] particles, R_i = R_j = R_P = 2.104 Å is the effective Born radius of phosphate particle. The coefficient C₁ = 14.400611ÅeV, ε_out = 78, κ = 0.1 what corresponds to physiological conditions. Parameter

$$C_0=-\frac{1}{2}{C}_1(1-\frac{1}{{\epsilon }_{\mathit{\text{out}}}})\sum _{i=0}^N\frac{1}{R_P}$$

describes self-energy (solvation energy) of phosphate groups.

The resulting total electrostatic potential due to a single [P] particle as a function of distance is shown in Fig. 12. One can see that for small distances r < 80Å potential decreases with increasing distance r as r⁻³. For long distances the fall-off is exponential. Thus we can introduce a cut-off distance R_Q = 100Å for the electrostatics interactions. For r > R_Q interaction between particles is set to zero: V_q = 0.

Fig. 12.

Electrostatics potential V_q(r), equation (B6).

The last term E_vdW in the Hamiltonian (B1) describes van der Waals interaction between different side chain [P] and [C3] grains. The potential depends on the distance r between two grains and is given by

$$U_{ij}(r)={\epsilon }_{ij}{[{\left(\frac{{\sigma }_{ij}}{r-d_{ij}}\right)}^6-1]}^2-{\epsilon }_{ij},i,j=P,C3,$$

where ${\epsilon }_{ij}=\sqrt{{\epsilon }_i{\epsilon }_j},d_{ij}=d_i+d_j,{\sigma }_{ij}={\sigma }_i+{\sigma }_j$, energy parameters are ε_P = 0.01eV, ε_C3 = 0.005eV, diameters are d_P = 2.4Å, d_C3 = 2Å, parameter σ_P = 1.6Å, σ_C3 = 1.9Å.

In practical applications of the 12CG model one should keep in mind that the model was designed to describe only the double helical form of DNA, so it may not be appropriate to situation when melting or base openings are expected. This limitation is the price one pays for computational efficiency: within our model van der Waals interactions are calculated only for backbone grains that belong to separate DNA strands, and only nearest neighbor base pairs interact.