Radiostratigraphy and age structure of the Greenland Ice Sheet

Abstract

Several decades of ice-penetrating radar surveys of the Greenland and Antarctic ice sheets have observed numerous widespread internal reflections. Analysis of this radiostratigraphy has produced valuable insights into ice sheet dynamics and motivates additional mapping of these reflections. Here we present a comprehensive deep radiostratigraphy of the Greenland Ice Sheet from airborne deep ice-penetrating radar data collected over Greenland by The University of Kansas between 1993 and 2013. To map this radiostratigraphy efficiently, we developed new techniques for predicting reflection slope from the phase recorded by coherent radars. When integrated along track, these slope fields predict the radiostratigraphy and simplify semiautomatic reflection tracing. Core-intersecting reflections were dated using synchronized depth-age relationships for six deep ice cores. Additional reflections were dated by matching reflections between transects and by extending reflection-inferred depth-age relationships using the local effective vertical strain rate. The oldest reflections, dating to the Eemian period, are found mostly in the northern part of the ice sheet. Within the onset regions of several fast-flowing outlet glaciers and ice streams, reflections typically do not conform to the bed topography. Disrupted radiostratigraphy is also observed in a region north of the Northeast Greenland Ice Stream that is not presently flowing rapidly. Dated reflections are used to generate a gridded age volume for most of the ice sheet and also to determine the depths of key climate transitions that were not observed directly. This radiostratigraphy provides a new constraint on the dynamics and history of the Greenland Ice Sheet.

Key Points

• Phase information predicts reflection slope and simplifies reflection tracing

• Reflections can be dated away from ice cores using a simple ice flow model

• Radiostratigraphy is often disrupted near the onset of fast ice flow

1. Introduction

The Greenland and Antarctic ice sheets have both been surveyed extensively using ice-penetrating radar, and these surveys have detected numerous internal reflections. Analysis of these reflections has illuminated many aspects of ice sheet dynamics, including their strain history and their response to climatic and subglacial forcings [e.g., Whillans, ¹⁹⁷⁶; Nereson et al., ¹⁹⁹⁸; Siegert, ¹⁹⁹⁹; Fahnestock et al., ^{2001a, 2001b}; Conway et al., ²⁰⁰²; Wang et al., ²⁰⁰²; Matsuoka et al., ²⁰⁰³; Arcone et al., ²⁰⁰⁵; Jacobel and Welch, ²⁰⁰⁵; Siegert et al., ²⁰⁰⁵; Catania et al., ²⁰⁰⁶; Waddington et al., ²⁰⁰⁷; Corr and Vaughan, ²⁰⁰⁸; Buchardt, ²⁰⁰⁹; Carter et al., ²⁰⁰⁹; Drews et al., ²⁰⁰⁹; MacGregor et al., ^{2009a, 2009b}; Catania and Neumann, ²⁰¹⁰; Leysinger Vieli et al., ²⁰¹¹; Christianson et al., ²⁰¹³; Medley et al., ²⁰¹³; Keisling et al., ²⁰¹⁴]. Similar studies of the radiostratigraphy of ice masses on Mars have proven equally valuable in understanding their formation history [e.g., Smith and Holt, ²⁰¹⁰; Karlsson et al., ²⁰¹¹; Brothers et al., ²⁰¹³].

By virtue of its accessibility and smaller size relative to the East and West Antarctic ice sheets, the Greenland Ice Sheet (GrIS) has been more comprehensively surveyed by ice-penetrating radar than those Antarctic ice masses. Multiple institutions have regularly collected and analyzed radar data from the GrIS since the 1960s [Gudmandsen, ¹⁹⁷⁵; Jacobel and Hodge, ¹⁹⁹⁵; Dahl-Jensen et al., ^{1997, 2003}; Fahnestock et al., ^{2001a, 2001b}; Nixdorf and Göktas, ²⁰⁰¹; Baldwin et al., ²⁰⁰³; Legarsky and Gao, ²⁰⁰⁶; Buchardt, ²⁰⁰⁹; Catania and Neumann, ²⁰¹⁰; Bamber et al., ²⁰¹³; Christianson et al., ²⁰¹⁴; Vallelonga et al., ²⁰¹⁴; Keisling et al., ²⁰¹⁴]. Despite these advantages, previous efforts to directly map and interpret the radiostratigraphy of the GrIS are limited with respect to the data now available. This situation has arisen because tracing reflections in ice-penetrating radar data is laborious and also challenging in regions of complex ice flow [Sime et al., ²⁰¹¹]. As a result, numerous such data sets collected across Greenland and Antarctica now exist for which few or no internal reflections have been mapped, let alone interpreted glaciologically. This situation has motivated the development of alternate ways of describing and mapping observed radiostratigraphy that do not require direct tracing of reflections [Karlsson et al., ^{2009, 2012, 2013}; Sime et al., ^{2011, 2014}; Ferro and Bruzzone, ²⁰¹²]. However, directly traced reflections are generally preferred, as they are often assumed to be isochronal and thus more easily related to known reflection mechanisms. If dated, traced reflections can be readily incorporated into ice flow models [e.g., Fahnestock et al., ^2001b; Baldwin et al., ²⁰⁰³; Waddington et al., ²⁰⁰⁷; Buchardt, ²⁰⁰⁹; Koutnik, ²⁰⁰⁹].

Here we present the first comprehensive and dated radiostratigraphy of the GrIS from deep ice-penetrating radar data collected by The University of Kansas (KU) over the past two decades. In this context, “deep” refers to radar systems designed to both sound the entire ice thickness and detect internal reflections close to the bed [e.g., Gogineni et al., ¹⁹⁹⁸]. We first describe the methods we developed both to trace this radiostratigraphy efficiently and to verify it, as they are widely applicable to the study of both deep and shallow ice sheet radiostratigraphy. We describe the age structure of the GrIS and present several straightforward inferences of the ice sheet's history and dynamics from this new data set, including the present location of Eemian ice and disrupted radiostratigraphy. These results demonstrate the value of ice sheet-wide maps of radiostratigraphy, both undated and dated, for glaciological studies.

2. Ice-Penetrating Radar Data

We examined the 479,595 km of 150 and 195 MHz ice-penetrating radar data collected over the GrIS using several airborne platforms by KU between 1993 and 2013 (Table 1 and Figure 1). These data include 512 transects of varying lengths (6–3965 km; median 530 km). Note that many sorties (individual flights) are split into multiple transects (also known as segments). The system designs, acquisition parameters, and processing techniques applied to these data are described in detail elsewhere (Table 1). The nominal vertical range resolution in ice of these data is 2.5–4.4 m and their along-track horizontal resolution varies between 15 and 150 m, depending on the system used and whether the data were focused using synthetic aperture radar (SAR) techniques [Leuschen et al., ²⁰⁰⁰; Legarsky et al., ²⁰⁰¹].

Table 1.

Airborne Ice-Penetrating Radar Campaigns Collected Across the GrIS by KU Between 1993 and 2013

Campaigna	Radar Systemb	Total Length Acquiredc (km)	Total Length Tracedc,d (km)
1993 P3	ICORDS	21,773	4,209
1995 P3	ICORDS	19,720	6,652
1996 P3	ICORDS	5,673	2,995
1997 P3	ICORDS	18,459	5,953
1998 P3	ICORDS v2	23,473	9,160
1999 P3	ICORDS v2	35,607	24,438
2001 P3	ICORDS v2	12,210	2,624
2002 P3	ICORDS v2	20,348	10,644
2003 P3	ACORDS	14,889	6,026
2005 TO	ACORDS	6,971	759
2006 TO	MCRDS	10,430	1,800
2007 P3	MCRDS	12,838	2,194
2008 TO	MCRDS	22,758	7,467
2009 TO	MCRDS	8,753	341
2010 DC8	MCoRDS	11,047	3,687
2010 P3	MCoRDS	27,921	2,853
2011 P3	MCoRDS v2	73,623	25,879
2011 TO	MCoRDS v2	6,270	658
2012 P3	MCoRDS v2	85,162	23,244
2013 P3	MCoRDS v2	41,670	16,508
Total		479,595	158,091

^aAirborne platform abbreviations are as follows: P3: P3-B Orion; TO: DHC-6 Twin Otter; DC8: Douglas DC-8.

^bRadar-system abbreviations are as follows: ICORDS: Improved Coherent Radar Depth Sounder; ACORDS: Advanced Coherent Radar Depth Sounder; MCRDS: Multi-Channel Radar Depth Sounder; MCoRDS: Multi-Channel Coherent Radar Depth Sounder. The suffix “v2” means that an upgraded version of the original system was used. See Gogineni et al. [1998, 2001] for descriptions of the ICORDS systems, Namburi [2003] for ACORDS, Lohoefener [2006] for MCRDS, Shi et al. [2010] for MCoRDS v1, and Rodríguez-Morales et al. [2014] for MCoRDS v2.

^cOccasional gaps in along-transect data acquisition, which are more common during earlier campaigns, will tend to cause our estimates of the total transect lengths acquired and traced to be overestimated. Note that these values do not include transects that mapped Arctic ice caps exclusively.

^dNumber of 1 km segments where at least one reflection was traced.

Figure 1.

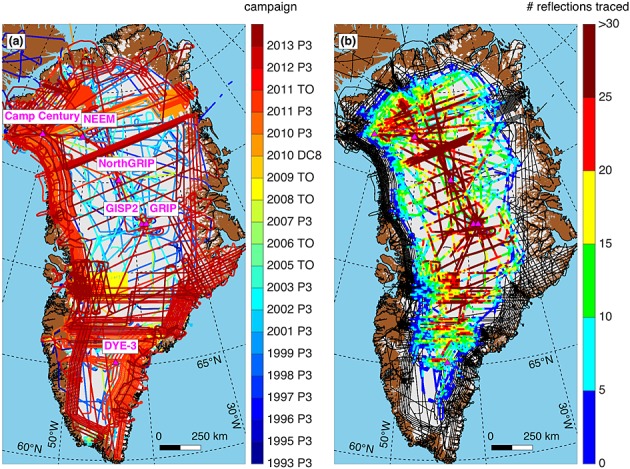
Airborne ice-penetrating radar surveys collected over the GrIS by KU between 1993 and 2013. Transects are color-coded by (a) campaign and (b) maximum number of reflections traced within 1 km segments along track. Portions of transects shown as black lines indicate no reflections were traced in those segments. Triangle denotes deep ice core sites. Ice, land, and ocean masks are from Bamber et al. [2013].

The radiostratigraphy recorded within these radar data varies in quality depending on the system used and the area of the ice sheet surveyed. The overall quality of these radar data has improved over time as newer radar systems were developed and deployed. However, from the perspective of mapping radiostratigraphy, this improvement is not necessarily continuous. This situation arises because the primary goal of these surveys is to measure ice thickness, with the observation of internal reflections considered an important but secondary goal. As the radar systems deployed by KU improved, the focus of such surveys often turned to regions where ice thickness is harder to measure (e.g., Jakobshavn Isbræ). In such regions, ice tends to be warmer, flow faster, and flow in more complex ways than in the ice sheet interior. Surface clutter due to crevasses and volume scattering due to englacial water storage present additional challenges to the detection of deep internal reflections [e.g., Forster et al., ²⁰¹⁴]. The combination of these factors means that relatively weak internal reflections are often difficult to detect and map near the ice sheet margin [e.g., Legarsky and Gao, ²⁰⁰⁶]. Many recent surveys have been understandably focused in these challenging areas and in the southernmost portion of the GrIS, due to large changes in ice dynamics there [e.g., Moon et al., ²⁰¹²]. Despite these challenges, continuous reflections are often observed within 100 km of the ice sheet margin and also within the earliest radar data acquired by KU over the GrIS (Table 1 and Figure 1).

The two-way traveltimes of the air-ice and ice-bed reflections were measured by KU personnel throughout the acquisition period [e.g., Gogineni et al., ²⁰⁰¹], and we use these traveltimes without further modification. To infer the absolute elevation of any observed reflection from such measurements, the aircraft elevation must be known. Unfortunately, the radar system time delay is not recorded in the data product of the earlier radar systems, so the recorded two-way traveltime is biased by an unknown constant that may vary between campaigns. As a result, when matching internal reflections observed in transects from different campaigns as described below, we sometimes observed intersections where all matching reflections (including air-ice and ice-bed) had a consistent and large absolute bias in the difference between their elevations (>25 m). The KU radar data used in this study were collected over two decades, which encompasses an extended period of dramatic thinning of the GrIS margins and inherently variable rates of firn densification [e.g., Csatho et al., ²⁰¹⁴]. However, these biases were also observed within the interior, where measured rates of elevation change are much smaller. We chose to correct radar-reported aircraft elevations so that the surface elevation inferred from the air-ice reflection traveltime matches that of the Greenland Ice Mapping Project (GIMP) digital elevation model (DEM) [Howat et al., ²⁰¹⁴], similar to the approach of Bamber et al. [2013]. We forgo the more challenging first step also undertaken by Bamber et al. [2013] of correcting the radar-reported aircraft elevations using concurrently collected airborne laser altimetry data. In taking this approach, the radiostratigraphy we mapped explicitly cannot be used to detect evidence of change in the internal structure of the GrIS during the period that the data were collected. Furthermore, because the vast majority of reflections that we traced are at least several hundred meters deep, we do not correct for the cumulative effect of two decades of snowfall, melting, and flow upon the depths of the observed reflections, as these effects are smaller than or comparable to the range resolutions of the radar systems we used.

To correct two-way traveltimes through ice to ice-equivalent depth, we assume that the real part of the complex relative permittivity of ice (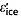, hereafter permittivity) is 3.15, equivalent to a radio-wave velocity in ice of 168.9 m µs⁻¹. (This notation and all other notation used in this study are tabulated in the notation section.) This velocity is somewhat higher than that reported by Hempel et al. [2000] at −32°C (168.1 m µs⁻¹). However, our chosen value has proven suitable for the GrIS based on ground-truth comparison of radar-measured ice thickness at multiple ice core sites [Gogineni et al., ²⁰⁰¹]. We explicitly do not include a firn correction, but note that the spatial pattern of this firn correction is generally predicted to change slowly across the dry snow zone of the GrIS [Reeh et al., ²⁰⁰⁵], where we principally mapped reflections. This lack of an explicit firn correction introduces a true depth uncertainty 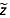for all traced reflections of the order of 10 m, but which is likely less than that. In highly dynamic regions of the GrIS, densification rates may change across short distances (∼10 km) [e.g., Christianson et al., ²⁰¹⁴], altering the depth-averaged value of 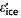and suggesting that depth uncertainties are greater there. However, for simplicity here we assume a uniform value of 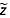across the GrIS.

We project all radar data used in this study using the National Snow and Ice Data Center Sea Ice Polar Stereographic North projection (EPSG:3413; http://nsidc.org/data/atlas/epsg_3413.html). This projection is the same as that used by the GIMP DEM; it uses the WGS84 ellipsoid, a standard parallel of 70°N, and a false central meridian of 45°W and sets both the northing and easting origin as the North Pole. Other Greenland data sets also used in this study are reprojected onto EPSG:3413.

3. Methods

We describe below the methods that we use to predict, trace, date, normalize, and grid the GrIS radiostratigraphy. Figure 2 presents three flowcharts illustrating this sequence.

Figure 2.

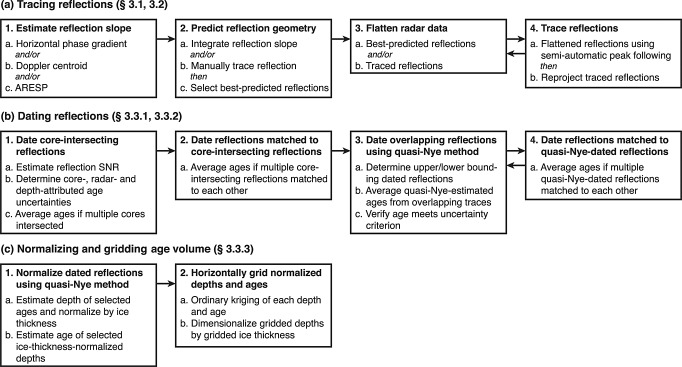
Flowcharts illustrating the key steps and order of operations for (a) tracing, (b) dating, and (c) normalizing the radiostratigraphy.

In tracing the GrIS radiostratigraphy, our strategy was to trace as many reflections as possible, irrespective of whether they were continuous throughout an entire transection or identifiable within other transects. In general, we only traced a reflection if it was distinct across a horizontal distance greater than ∼5 km. In these KU radar data, relatively few reflections shallower than ∼200 m were traceable, generally due to receiver saturation associated with the air-surface reflection, although this situation improved with later radar systems.

We focused on distinct reflections (narrowly peaked in traveltime) that were easily traced using semiautomatic peak following, e.g., Fahnestock et al. [2001a]. Distinct reflections in meteoric ice are often attributed to thin conductivity contrasts, which are correlated with volcanic eruptions and are widely considered to be isochronal [e.g., Hempel et al., ²⁰⁰⁰]. Density contrasts can cause permittivity contrasts and are also considered isochronal, but because we mostly traced reflections deeper than the firn column, it is unlikely that many of the reflections we traced are due to density contrasts. Changes in crystal-orientation fabric can also cause radar reflections [e.g., Matsuoka et al., ²⁰⁰³; Eisen et al., ²⁰⁰⁷]. If such fabric contrasts are unrelated to a distinct climate event, then they may not be isochronal. A basal layer that contains both distinct reflections and diffuse reflectivity was regularly observed. This layer may include boundaries between meteoric and accreted ice [e.g., Bell et al., ²⁰¹⁴], possibly due to fabric contrasts [Horgan et al., ²⁰⁰⁸; MacGregor et al., ^2009a] that are unlikely to be isochronal. In some regions, distinct and continuous reflections were observed both above and within this layer, and where possible, we traced these reflections.

3.1. Radiostratigraphy Prediction Using Phase Information

To address the challenge of tracing radiostratigraphy efficiently, here we introduce and apply two new methods for predicting radiostratigraphy in ice sheets using the phase information recorded by coherent radar sounders. In terms of their ultimate goal of predicting radiostratigraphy, these new methods are related to those developed by Sime et al. [2011] and Panton [2014]. Specifically, all these methods measure reflection slopes. The motivation for developing such approaches is twofold. First, when integrated along track, these measurements of reflection slope represent predictions of the radiostratigraphy. These predictions can then be used to vertically rescale each radar trace relative to a reference position, simplifying both the tracing of discontinuous reflections using semiautomatic methods and also their interpretation [Fahnestock et al., ^2001b]. Second, a formalism now exists for studies of ice sheet dynamics using reflection slope, rather than morphology [Parrenin et al., ²⁰⁰⁶; Parrenin and Hindmarsh, ²⁰⁰⁷]. Automated methods of measuring reflection slope can thus accelerate studies of ice sheets using this formalism [Sime et al., ^{2011, 2014}].

Sime et al. [2011] used image-processing techniques to analyze the structure of processed radargrams after converting them into binary images (“automated radio-echo-sounding processing” or ARESP), whereas our methods use information recorded naturally by coherent radars and are rooted in SAR techniques [e.g., Raney, ¹⁹⁹⁸; Legarsky et al., ²⁰⁰¹]. Our phase-based methods require radar data that have been pulse compressed but for which phase information is preserved. The latter limitation currently necessitates the use of minimally stacked coherent data that have not been SAR focused (coherently migrated). For the Greenland radar-sounding data collected by KU, our methods are only applicable to airborne campaigns from 2006 or later. For campaigns prior to 2006, we use ARESP to predict the radiostratigraphy following the algorithm presented by Sime et al. [2011] or we manually trace observed reflections (Figure 2a). Below we describe two distinct methods for using phase information to predict radiostratigraphy, starting with the conceptually simpler method.

3.1.1. Horizontal Gradient of Phase

The received radar signal from englacial reflections above the basal layer is typically horizontally coherent, i.e., their phase changes smoothly along track (Figure 3) [Holschuh et al., ²⁰¹⁴]. We exploit this phenomenon by recognizing that the along-track gradient of the recorded phase is equivalent to the along-track rate of change of the range from the aircraft to a given reflection, i.e., the reflection's along-track slope.

Figure 3.

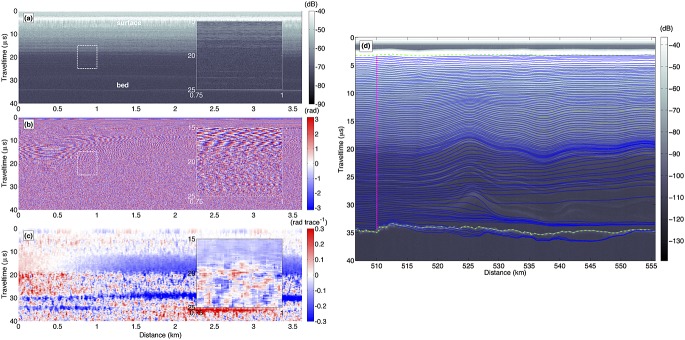
Example sequence for prediction of radiostratigraphy using horizontal differencing of phase. (a) Returned amplitude and (b) phase of a range-compressed but otherwise unfiltered complex radargram from a single receiver channel collected on 6 May 2011 (2011 P3 campaign; Table 1) (c) Unwrapped, horizontally differenced, and median-filtered phase of the complex radargram. Insets show zoomed-in portion of radargram as white dashed boxes. (d) Δϕ/Δx-predicted radiostratigraphy (blue lines) overlain on the SAR-focused returned amplitude for a larger segment of the same transect that includes the portion shown in Figures3a–3c. Magenta dots represent the points from which the Δϕ/Δx-predicted reflection slope is followed to then predict the radiostratigraphy.

The distance Δz (assumed to be vertical) that a radio wave travels through ice during a single (fast) time-sampling interval Δt is

(1)

where v_ice is the radio-wave velocity in ice,

(2)

where c is the speed of light in the vacuum. Any change in phase Δϕ of a radio wave across Δz is related to its wavelength λ_ice in ice as

(3)

Because λ_ice = v_ice/f_c, where f_c is the radar's center frequency, equation (3) reduces to

(4)

The along-track horizontal gradient of the recorded phase Δϕ/Δx, where Δx is the horizontal posting, is therefore related to the along-track change in traveltime Δt/Δx to a given reflection as

(5)

In practice, we calculate Δϕ/Δx by horizontally differencing the horizontally unwrapped phase trace by trace and then applying a two-dimensional median filter to reduce noise (typically 25–50 samples or ∼300–600 m in both the along-track direction x and two-way traveltime t; Figure 3c). We then choose a single trace from which to propagate the phase-predicted radiostratigraphy. Following equation (5), the predicted change in traveltime at successive adjacent traces is then integrated to predict reflection morphology (Figure 3d). Note that steeply dipped reflections are sometimes aliased in phase, resulting in negligible horizontal phase gradients that bias the phase-predicted reflection slope.

3.1.2. Doppler Centroid

An alternative method for calculating the phase-predicted reflection slope is to derive this information from the wavenumber of the Doppler centroid. This approach is similar in concept to some SAR methods [e.g., Raney, 1988] and frequency-wavenumber (f − k) migration in seismology.

We apply a Fourier transform in the along-track direction to short overlapping segments (<250 m) of the complex radar data (Figure 4). These segments must be sufficiently short that reflection slopes within them can be assumed to be uniform; otherwise, signal aliasing may occur [Holschuh et al., ²⁰¹⁴]. The amplitude of englacial reflections in this two-dimensional traveltime-wavenumber space, i.e., their Doppler spectrum, is often narrowly peaked. This observation further indicates that such reflections are highly specular. We take the Doppler centroid wavenumber k_D to be the wavenumber of this peak, which can be converted directly to Δϕ/Δx and again related to Δt/Δx following equation (5).

Figure 4.

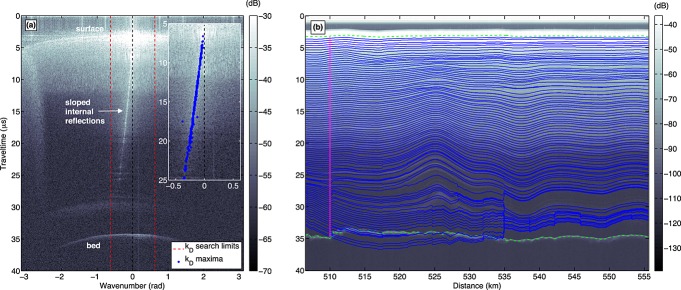
Example sequence for prediction of radiostratigraphy using the Doppler centroid wavenumber (k_D). (a) Amplitude of the along-track Fourier transform of a short segment (<250 m) of the same transection as shown in Figure 3. Vertical red dashed lines represent the edges of the search region for a k_D maxima and the vertical white dashed line is zero wavenumber. Blue dots in the inset panel represent distinct k_D maxima. (b) The k_D-predicted radiostratigraphy overlain on the SAR-focused returned amplitude. The format follows Figure 3d.

In practice, we assign a value to k_D in a traveltime bin only if the maximum amplitude of the Doppler centroid for that bin rises clearly above the noise floor, i.e., it is greater than five times the median amplitude within the bin in a narrow region centered around zero wavenumber (Figure 4a), which corresponds to a zero-slope reflection. We smooth the assigned values of k_D and interpolate between them to produce vertical profiles of k_D and then apply the same approach to predicting radiostratigraphy as described above (Figure 4b). This second method of using phase information tends to predict radiostratigraphy more accurately than the first method in deeper ice, where the signal-to-noise ratio is lower, but not always (compare Figures3d and 4b). The second method is also more efficient computationally, so it is our preferred method for predicting radiostratigraphy using phase information.

3.2. Flattening Radar Data and Reflections

Once the radiostratigraphy is predicted using any of the methods described above (Figure 2a), both this and the radar data can then be “flattened” relative to these predictions. A “flattened” radargram is one in which the original data are resampled (geometrically distorted) to match the depth relationship of predicted (or traced) reflections at a chosen reference location. This rescaling results in an adjusted radargram with reduced reflection slope. Fahnestock et al. [2001b] first flattened ice-penetrating radar data to illustrate both the continuity and accuracy of traced reflections and the amount of ice lost due to basal melt at the onset of the Northeast Greenland Ice Stream (NEGIS). Conceptually similar methods are sometimes applied to seismic data [e.g., Parks, ²⁰¹⁰].

The value of flattening radar data is threefold. First, flat reflections are easier to trace using conventional semiautomatic methods, as it is then possible to narrow the vertical window around which such algorithms follow reflections [e.g., Fahnestock et al., ^2001a]. Second, matching discontinuous reflections in a transection is easier if they can be assumed to be flat and they overlap horizontally with other reflections that are continuous. In such cases, the dominant pattern of radar reflectivity through the ice column permits identification of matching reflections across long distances (>100 km). Third, large-scale quality control of mapped reflections is also easier, following the same reasoning as for matching discontinuous flattened reflections.

Here we describe the algorithm used to vertically rescale the radar data so that they are implicitly flat with respect to the predicted or traced radiostratigraphy. This operation can be repeated multiple times and can be expressed in terms of dimensionless matrix indices, traveltime, or depth z to predicted or traced reflections. Expressed below in terms of depth, the along-transect depths z_j(x) of a set of reflections (predicted or traced) are first related to their depths at a reference position x₀ as

(6)

where the four values of p_i(x) are the best fit coefficients (in a least squares sense) for a third-order polynomial relationship between z_j(x) and z_j(x₀) for all reflections present at both locations. This polynomial need not necessarily be third order, and we also experimented with a second-order polynomial. We chose this particular flattening approach because a higher-order polynomial is qualitatively similar to models of the depth-age relationship in ice sheets, in that age typically increases nonlinearly with increasing depth [e.g., Nye, ¹⁹⁵⁷; Dansgaard and Johnsen, ¹⁹⁶⁹]. When flattening using a third-order polynomial, this approach requires at least four reflections and preferably more, but it is parallelizable and computationally efficient. The reference position is typically chosen as that where the predicted radiostratigraphy best matches the observed radiostratigraphy or, if the radiostratigraphy has already been traced, the trace with the most reflections. In the latter case, this choice increases the chances that the flattening operation will succeed at points along the transect where fewer reflections are available than at x₀.

We horizontally smooth the values of p_i(x) over along-transect distances of 1 km to prevent abrupt changes in the flattening due to the along-transect termination of reflections that are traced at x₀ but not throughout the transect. The polynomial coefficients are then used to rescale both the radar received power profile P_r at all sampled depths as

(7)

where P_r′(x, z) is the rescaled/flattened received power as a function of along-transect distance and depth, and the rescaled/flattened depth of each reflection 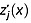is

(8)

This approach depends critically on the choice of x₀. In many cases, reflections are radar bright and spatially extensive but not present at x₀. In such cases, we repeat the flattening procedure by estimating the depth of such reflections at x₀ as if they had been traced there. This iteration is accomplished by calculating the mean value of 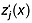for such reflections within regions of horizontal overlap with traces for which p_i(x) was determined. The p_i(x) values are then recalculated using equation (6). This approach can significantly extend the portion of the transect that can be flattened.

Figure 5 illustrates the value of flattening radar data using one of the most densely traced transects from the KU data set from central northern Greenland. When displayed in terms of elevation, it is difficult to verify continuity between the traced reflections, particularly those that are discontinuous. After flattening, it is easier to verify that discontinuous reflections are matched self-consistently. After dating the radiostratigraphy, the entire data set can be evaluated in a similar manner (Animation S1 in the supporting information).

Figure 5.

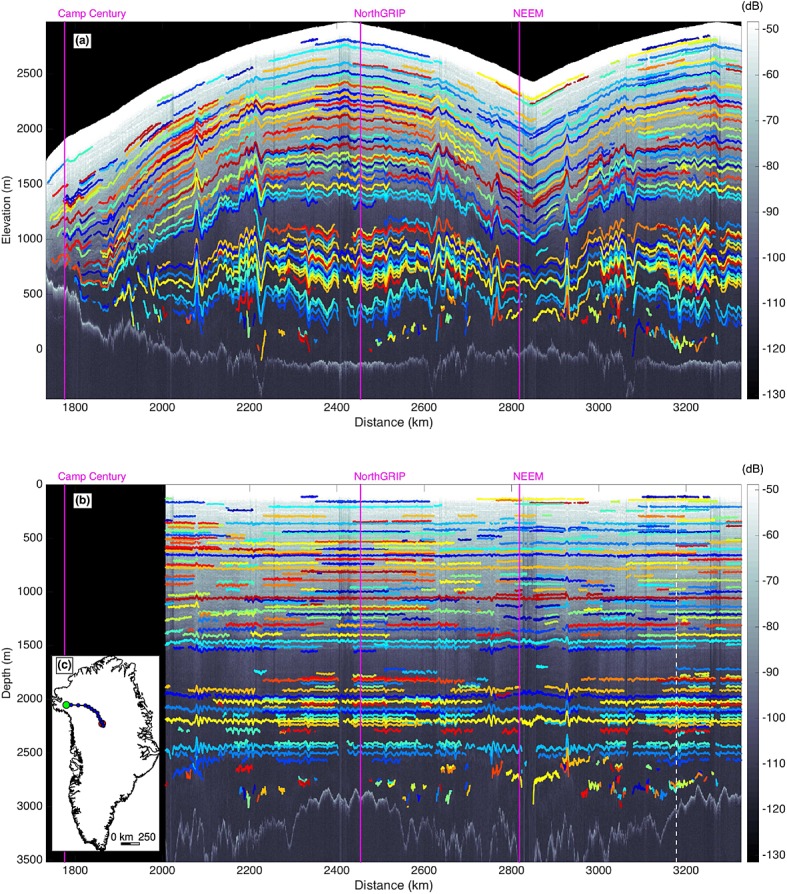
Example traced radargram (same transection as Figures3 and 4 from 6 May 2011). Radiostratigraphy is color coded using a set of 15 distinct colors that have no physical meaning. This transect's closest intersections with three ice cores are shown as vertical magenta dashed lines. Radar traces are displayed vertically in terms of (a) elevation and (b) a self-consistent flattened projection, i.e., depth at the reference trace. Vertical white dashed line is the trace with the most reflections, to which the flattening is referenced. The region where flattening was not possible is blanked out. (c) Map showing transect location in Greenland. Green (red) dot represents the start (end) of the transect as shown in Figures5a and 5b. Blue dots represent 100 km intervals. This transect ascends the central ice divide and then reverses course, following a parallel track.

3.3. Dating the Radiostratigraphy

Having traced the radiostratigraphy using the methods described above, we then seek to date these observed reflections. While inferences regarding ice sheet dynamics from reflection morphology alone are valuable [e.g., Conway et al., ²⁰⁰²; Catania et al., ²⁰⁰⁶; Hindmarsh et al., ²⁰⁰⁶; Rippin et al., ²⁰⁰⁶; Catania and Neumann, ²⁰¹⁰; Campbell et al., ²⁰¹³; Christianson et al., ²⁰¹³; Sime et al., ²⁰¹⁴], the value of traced reflections can increase substantially if they are also dated [e.g., Whillans, ¹⁹⁷⁶; Fahnestock et al., ^2001b; Baldwin et al., ²⁰⁰³; Dahl-Jensen et al., ²⁰⁰³; Buchardt, ²⁰⁰⁹; Medley et al., ²⁰¹³]. Hence, we seek to date as many traced reflections as possible, even those that do not intersect an ice core and are not continuous. This approach diverges somewhat from most previous studies, which often required reflections to be continuous and to intersect an ice core in order to be dated [e.g., Cavitte et al., ²⁰¹³] and sometimes also forward modeling to identify the cause of observed reflections [e.g., Eisen et al., ^{2006, 2007}]. The methods presented below are applicable to any set of traced reflections, although they may be less useful for very shallow reflections where simpler assumptions regarding ice flow may be permissible [Waddington et al., ²⁰⁰⁷; Medley et al., ²⁰¹³]. We separate reflection dating into four distinct steps, performed in order of decreasing confidence in the inferred reflection age (Figure 2b).

3.3.1. Sequential Reflection Dating Procedure

The first step is to date reflections in transects that intersected one or more of the six deep ice cores recovered from the GrIS, using their synchronized depth-age relationships a_c(z) (Table 2). We consider a transect to have intersected an ice core site if it passed within a 3 km radius of the site. Reflection age is estimated using the mean reflection depth within a horizontal distance of ±250 m along transect from the trace that is closest to the ice core site. For most ice cores, the depth of the deepest dated ice is less than the ice thickness (Table 2). We only date reflections that are observed within the dated depth range of those ice cores.

Table 2.

Ice-Core Depth–Age Relationships Used to Date GrIS Radiostratigraphy

Ice Core	Ice Thickness (m)	Maximum Dated Depth (m)	Maximum Dated Age (ka)	Depth–Age Relationship Reference(s)
Camp Century	1380	1136	11.7	Vinther et al. [2009]
DYE-3	2037	1786	11.7	Rasmussen et al. [2006]; Vinther et al. [2006]
GISP2	3053	2789	104.0	Seierstadt et al. [2014]
GRIP	3029	2751	104.0	Seierstadt et al. [2014]
NEEM	2561	2203	108.2	Rasmussen et al. [2013]
NorthGRIP	3085	3085	122.3	Seierstadt et al. [2014]

The assigned reflection age 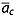is the unweighted mean of the reflection ages observed at each intersected core. The total age uncertainty 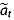of each core-intersecting reflection is

(9)

where 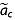is reported age uncertainty of the ice core at the appropriate depth, 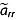is the age uncertainty due to the range resolution of the radar, and 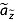is the age uncertainty due to the depth uncertainty 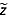of the core-intersecting reflections, which we assume is 10 m.

The age uncertainties from all intersected cores are averaged together. Reported age uncertainties (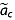) associated with the ice core-derived depth-age relationships are available for Greenland Ice Sheet Project 2 (GISP2), Greenland Ice Core Project (GRIP), North Greenland Eemian Ice Drilling (NEEM), and NorthGRIP. For the two oldest ice cores without reported values of 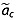(Camp Century and DYE-3) and for the deeper portions of the GISP2 and GRIP ice cores that also lack reported values of 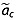, we assign them the mean value 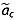from all cores that reported 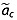at the equivalent age. We experimented with weighting 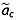by its uncertainty but found poor agreement between uncertainty-weighted means at ice core sites.

To estimate the age uncertainty due to the range resolution of the radar (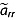), we follow Cavitte et al. [2013]:

(10)

where Δr is the range resolution of the radar system, which varies as a function of which airborne campaign is considered, and SNR is the manually measured signal-to-noise ratio of the reflection in the vicinity of its intersection with the ice core. Following equation (10), 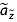is

(11)

Of the portions of the 232 transects we traced (512 total evaluated), only 42 met our 3 km radius criterion for core intersection. Of the 58 core intersections by these 42 transects (several transects intersected multiple ice core sites), 32 of these intersections were with Camp Century, while DYE-3, NEEM, and NorthGRIP were intersected only three times each. While an ice core intersection within a given transect is always valuable, it is preferable that it intersect an ice core as well dated as possible due to favorable glaciological conditions (e.g., NorthGRIP). This uneven distribution of ice core intersections presents multiple challenges.

To date an ice sheet-wide radiostratigraphy, we must also match reflections between transects collected by ever-evolving radar systems and date reflections away from ice cores. The second step in our sequential reflection dating procedure includes matching reflections between transects, quality controlling those matches, and assigning reflection ages based on those matches. We matched reflections between transects using manual identification at transect intersections only. This approach was selected over automatic matching (e.g., based on depths at intersections) because our tracing strategy was to map as many reflections as possible, rather than a few continuous reflections only. Thus, matching reflections were sometimes present near a transect intersection but not continuous across it. Also, significant operator judgment was sometimes required to identify a matching reflection pair, based on common patterns of observed englacial reflectivity.

As the bandwidth of the radar systems used increased and Δt decreased, the nature of the observed reflections sometimes changed. This change is most apparent in the upper half of the ice sheet, which is typically composed of ice from the Holocene epoch. There, reflections are numerous and often less distinct than deeper in the ice column [Karlsson et al., ²⁰¹³]. These Holocene reflections sometimes split in two or merge and constitute a key challenge in the matching process. Reflections are typically distinguishable and identifiable between transects collected by all generations of KU radar systems, but we disallow direct reflection matches between the oldest system (Improved Coherent Radar Depth Sounder (ICORDS), not v2) and any system newer than ICORDS v2 (Table 1).

Reflection matches are quality controlled by binning matching reflections and evaluating each bin's matches using network graphs. Specifically, within each bin (set of reflections matched to each other) we determine whether any reflection overlapped horizontally with another reflection from the same transect, which would violate loop continuity. Where such overlaps occur, network graphs are used to determine which matches to disallow and least disrupt the overall network of the bin's matched reflections.

We next assign ages from core-intersecting reflections to matched reflections in other transects. When assigning reflection ages in this second step, no additional age uncertainty is added to the matched reflection. Where a reflection is dated at multiple ice cores, or where multiple reflections are dated separately and also matched to each other, we average their ages and uncertainties and assign them the same mean age and uncertainty.

The third step in the dating procedure is to date reflections that cannot be matched to core-dated reflections by determining where undated reflections overlap horizontally with dated reflections, and then vertically interpolating and extrapolating the depth-age relationship within this overlap. The physical basis for this method is described in the following subsection. For each transect, we apply this method first to the undated reflection that overlaps horizontally with at least two core-dated reflections for the most traces, assuming that this reflection is observed within the best dated portions of the transect. Once dated, we consider the reflection with the second most horizontal overlap with dated reflections, now including the previously dated reflection. This process continues until all reflections are either dated or discarded as unable to be dated using this method.

This method produces semi-independent estimates of the reflection age at each overlapping trace (a_overlap). The mean age ā_overlap of the overlapping reflection is simply the unweighted mean value of a_overlap. Its uncertainty ã_overlap is estimated as

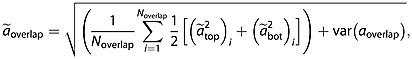(12)

where 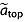and 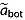are the total age uncertainties of the upper/top and lower/bottom dated reflections, respectively, N_overlap is the number of overlapping traces, and var(a_overlap) is the variance of a_overlap. The latter term accounts for the uncertainty in reflection age induced by the age interpolation/extrapolation, discussed below. If 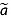_overlap > 0.25 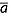_overlap, then the reflection age is rejected. In this manner, the depth-age relationship from an ice core can be propagated farther along transect than is possible using continuous, core-intersecting reflections only. This approach is particularly valuable in regions where the radiostratigraphy is disturbed, due to either ice flow or survey characteristics (e.g., aircraft maneuvers).

In the fourth step of the dating procedure, we again assign reflection ages based on intertransect matches, but using reflections dated during the third step only. Finally, we repeat the third and fourth steps in sequence until no new reflections are dated. This iterative approach can potentially date reflections that do not overlap horizontally with core-dated reflections.

3.3.2. Vertical Extension of Depth-Age Relationships Using the Effective Vertical Strain Rate

3.3.2.1. Method

MacGregor et al. [2012] described a method for inferring the effective intralayer vertical strain rate 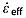between a bounding pair of dated radar reflections at depths z and ages a. Here we extend this method to date reflections that do not intersect ice cores and cannot be matched with core-intersecting reflections, i.e., the third step in the dating procedure discussed above. The 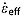is assumed to be uniform within the reflection-bounded layer and it places the bounding reflections at their observed depths within the ice column. It is related to the effective accumulation rate 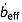and effective ice thickness H_eff as

(13)

where H_eff is

(14)

The 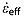is conceptually similar to the Nye model of a uniform vertical strain rate [Nye, ¹⁹⁵⁷], except that 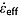is appropriate only within and presumably also near the bounded layer. Our initial guess for 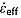is the apparent Nye vertical strain rate for the bounding reflection pair, calculated following Leysinger Vieli et al. [2011] as

(15)

where H is the radar-measured ice thickness. The best fit value of 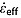is that which minimizes the depth residual 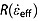between the predicted values of H_eff (equation (14)) at both bounding reflections/isochrones:

(16)

In practice, prior to solving equation (16) iteratively using Newton's method, we calculate 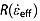for a range of 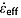values that is evenly spaced logarithmically between two orders of magnitude above and below 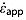. The preferred initial value of 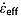within this range is 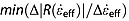, as this value tends to ensure a non-trivial solution (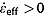). The cutoff tolerance for 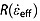is 1 cm and must occur within 100 iterations. Note that although H is used to determine 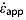, 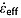is found by minimizing the difference in H_eff at the bounding reflections, rendering it independent of H.

Having determined 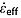, the age of an observed reflection at depth z within or near the layer is

(17)

Equivalently, following equation (17) and MacGregor et al. [2012], the depth of a reflection at age a is

(18)

Using equation (17), we calculate the ages of reflections either sandwiched by a pair of dated reflections or vertically near them (within both ±(z_bot − z_top) and ±0.2H). Both the depths of the upper and lower bounding reflections vary along-transect (and often which bounding reflections are used), so numerous (in some cases >10⁴) semi-independent estimates of a(z) are possible.

A disadvantage of the above approach is that the subaerial ice sheet surface (z_top, a_top = 0) cannot be used in conjunction with equation (16) because its use results in a trivial solution. For reflections in the top fifth of the ice column (z ≤ 0.2H) that cannot be dated using the iterative method and constraints described above, we again assume a uniform vertical strain rate between the surface and a deeper dated reflection (z_bot, a_bot) that is also in the top fifth of the ice column. The age of the shallower reflection is thus

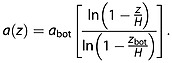(19)

We apply equation (19) only to shallow undated reflections that are not overlain by any dated reflections and are greater than 0.03H in depth, to avoid complications associated with the firn column.

The above dating method represents a simple but physically reasonable way of inferring the depth-age relationship between (and near) pairs of dated reflections in the absence of detailed information at ice core sites [e.g., Fudge et al., ²⁰¹⁴]. This physical model is subject to assumptions similar to those used by the Nye model, most critically that ice within the bounded layer is deforming in pure shear. We note that this method does not require that past accumulation and present vertical strain rates be balanced throughout the ice column. By relaxing this constraint and requiring only such a balance between the surface and the bottom of the bounded layer, this method provides a means of inferring the depth-age relationship in the neighborhood of the bounded layer. We term this method “quasi-Nye dating,” but note that it is conceptually similar to other ice flow models that assume a uniform vertical strain rate for part of the ice column [Dansgaard and Johnsen, ¹⁹⁶⁹; Whillans, ¹⁹⁷⁶].

3.3.2.2. Uncertainty Analysis

The potential accuracy of quasi-Nye dating depends on multiple factors related to local ice flow and the bounding reflections used. We evaluate these effects at the sites of the six deep ice cores recovered from the GrIS by simulating errors that are directly attributable to quasi-Nye dating. First, we assume that 10 reflections are observed in the vicinity of each ice core within 5–85% of the local ice thickness and whose depths are drawn from a uniform random distribution. Second, we date these reflections using the ice core depth-age relationships. Third, we add an uncertainty in their depths drawn from a normal random distribution whose standard deviation is 10 m, equivalent to our assumed value of 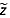. Finally, we use these 10 core-dated reflections and the quasi-Nye method to date the ice column at 1% intervals in thickness-normalized depth 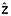( 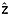= z/H), following the restrictions on vertically extrapolating the depth-age relationship described above. This process is repeated 1000 times.

Figure 6a shows that, for the above scenario, quasi-Nye dating of these ice cores can deviate substantially from the reported depth-age scales. However, Figure 6b shows that these deviations are generally relatively small. Based on best fit Gaussian curves to the distributions of these deviations, the relative age uncertainty typically due to quasi-Nye dating is <3%. Quasi-Nye dating tends to underestimate the age of ice from the Last Glacial Period (LGP; 11.7–115 ka). For ice of this age, which is generally found deeper within the GrIS, flow may also result from simple shear, leading to decreasing vertical strain rates there and hence older ice relative to a Nye model [Dansgaard and Johnsen, ¹⁹⁶⁹]. Conversely, where basal melting is known to occur (e.g., NorthGRIP), quasi-Nye dating overestimates ice age in a manner similar to that of a Nye model relative to a model that includes basal melting [Fahnestock et al., ^2001b; Dahl-Jensen et al., ²⁰⁰³].

Figure 6.

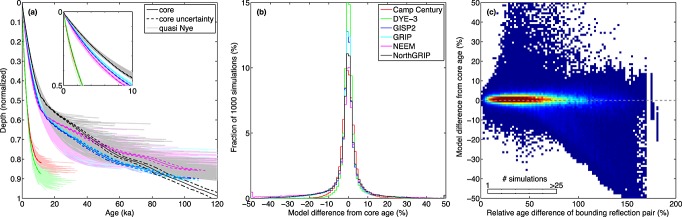
(a) Observed and 1000 quasi-Nye-modeled depth-age relationships for each of six deep ice cores recovered from the GrIS. Depth is normalized by the local ice thickness. (b) Distribution of relative differences between quasi-Nye-modeled and observed depth-age relationships (relative difference from core age). (c) Relationship between the relative age difference of the bounding reflections (age difference of bounding reflection pair divided by their mean age) and the relative difference from core age.

As an alternative to the quasi-Nye assumption of ice flow due to pure shear only, we could instead assume that ice flow is due entirely to simple shear. This alternative assumption is equivalent to setting the thickness of the “basal” shear layer in a Dansgaard and Johnsen [1969] depth-age model to H. However, we found that this alternative approach has a much stronger tendency to underestimate age at the ice core sites, as compared to the above quasi-Nye dating exercise, so we disregard it as a suitable method for dating reflections away from ice cores within the GrIS.

The above error simulation informs both suitable limits upon the use of quasi-Nye dating within the GrIS and the additional age uncertainty resulting from its use. Relative errors in quasi-Nye-modeled ages are significantly correlated with the depth, age and relative age differences between the bounding reflections (e.g., Figure 6c), but these relationships have limited predictive ability (linear correlation coefficients r < 0.5); therefore, we limit only extrapolation of the depth-age relationship, as described above. For each normalized depth and each core, the variance in the quasi-Nye-modeled age from the 1000 simulations is well correlated with the absolute mean relative error in age (r ≈ 0.65). Based on this relationship, we assume that the additional uncertainty attributable to quasi-Nye dating of any given reflection is well represented by var(a_overlap) (equation (12)).

3.3.3. Normalizing and Gridding Reflection-Inferred Depth-Age Relationships

Once the radiostratigraphy is dated following the sequence described above, we then seek to normalize this information into an age volume for the ice sheet, projected onto a regular grid. This approach simplifies visualizations of the data volume and it is rooted in the mapping of individual reflections matched across several transects [e.g., Fahnestock et al., ^2001b] and the corresponding value of subsequent gridding [e.g., Tikku et al., ²⁰⁰⁴]. Using quasi-Nye dating, we can infer the depth at a specified age or, conversely, the age at a specified depth. This approach is particularly valuable for ice sheet-wide mapping of the age at a particular normalized depth a(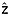_i) or the depth of a particular isochrone z(a_i). In the latter case, this isochrone can be synthetic, in the sense that its age does not need to be the same as that of an observed isochrone, although the accuracy of the depth of a synthetic isochrone will increase with proximity to observed reflections of similar ages.

In practice, these steps are first performed vertically for each separate transect and then gridded horizontally (Figure 2c). Because the along-track horizontal posting of these radar data is small (<20 m) and often varies, prior to vertical normalization, we horizontally average the observed reflection depths to a larger regular interval (1 km) that is consistent with recent horizontal grid intervals for the GrIS [e.g., Bamber et al., ²⁰¹³].

The ages and depths at preselected values of 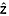and a are calculated using the quasi-Nye method, i.e., equations (18) and (17), respectively. To map the data volume effectively, we permit the dating of unbounded values of 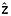that are within both ±(z_bot − z_top) and ±0.2H of a dated reflection, i.e., the same limits on vertical extrapolation of age when dating overlapping reflections. For unbounded values of a, the permissible age range is within both ±(a_bot − a_top) and ±5 ka, which primarily limits extrapolation of depth-age relationships in deep ice. As applied to this data set, we calculated the age at 25 evenly spaced normalized depths (Δ 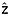= 0.04) and the depth of multiple isochrones of broad interest, specifically boundaries between key climate transitions. Age uncertainty ã(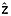_i) and depth uncertainty 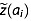are interpolated and extrapolated linearly. We estimate 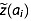using the NorthGRIP depth-age relationship and the depths, ages, and age uncertainties of traced reflections.

Following this 1-D process, the reflection-inferred depth-age relationships are normalized along track and can then be gridded horizontally, for which we use ordinary kriging at a resolution of 1 km [Deutsch and Journel, ¹⁹⁹⁷]. The spatial covariance of the age at each normalized depth is inferred from the least squares best fit between its semivariance and a zero-nugget exponential model, which was found empirically to represent these data well. For isochrone depths, a Gaussian model better represented the observed semivariance. A single mean semivariogram model is used for all values of 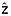_i and another for a_i, as we found that this approach produced smoother results and better constrained the gridded fields deeper within the ice sheet. Independent semivariogram models are used for ã(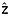_i) and 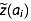. Kriging predictions are limited to grid points within 50 km of observations.

To grid isochrone depths, we first normalize these depths by the radar-measured along-track ice thickness, krige these normalized depths, and then re-dimensionalize the gridded result using an existing ice-thickness grid [Morlighem et al., ²⁰¹⁴]. This approach tends to produce a smoother result as compared to kriging the isochrone depth directly.

Because we use mean semivariogram models for kriging a(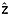_i) and z(a_i), the kriging-predicted variance cannot be incorporated directly into estimates of uncertainties in these values. Hence, we treat the kriged uncertainty fields 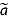(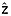_i) and 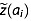as sufficiently representative of the uncertainties in their respective fields, while recognizing that they may underestimate this uncertainty.

3.4. Mapping Disrupted Radiostratigraphy

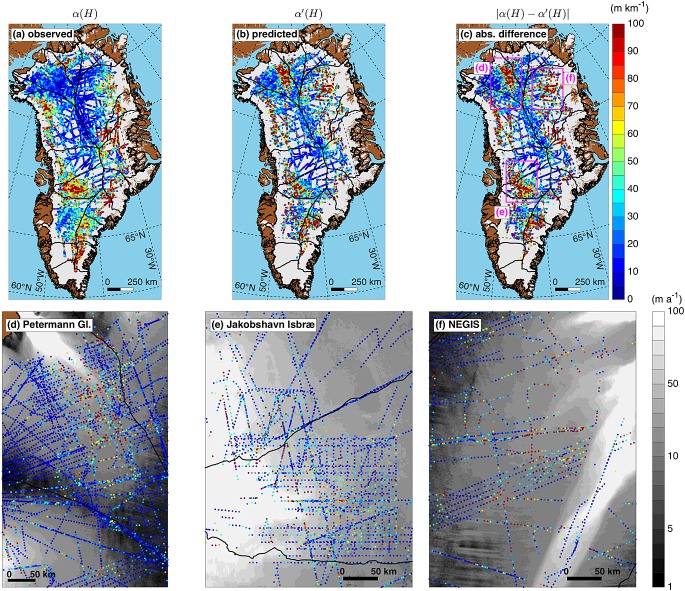
Once a horizontally and vertically extensive radiostratigraphy is traced, it is possible to develop a simple metric describing the extent of radiostratigraphy that does not clearly conform to the local bed topography, i.e., the degree to which this radiostratigraphy is “disrupted.” Within the regions of slower flow in the ice sheet interior (< ∼100 m a⁻¹), the observed radiostratigraphy may conform to the bed if several conditions are met: (1) A transect is aligned in the direction of ice flow; (2) the degree of basal sliding is uniform over a distance of several ice thicknesses and the dominant horizontal wavelength of the bed topography is sufficiently large that the overlying radiostratigraphy drapes over the bed, rather than overriding it [Hindmarsh et al., ²⁰⁰⁶]; (3) the ice column has not experienced any significant perturbations in flow during a period comparable to the maximum age of the ice column; and (4) the ice column is not and was not recently an ice divide, which could otherwise lead to a Raymond bump and distort the radiostratigraphy irrespective of the bed topography [e.g., Nereson et al., ¹⁹⁹⁸]. All of these conditions may not be met across large portions of the GrIS, particularly since relatively few transects within the region that we traced are aligned in the direction of present ice flow (C. Panton, personal communication, 2013). However, analysis of reflection and bed slopes can still reveal the presence of ice whose age structure is not locally bed conformable and guide further investigation. This analysis is also relevant to the validity of the local-layer approximation [Waddington et al., ²⁰⁰⁷], which assumes that the vertical velocity field inferred from dated reflections is represented adequately by local (rather than horizontally inherited) glaciological conditions.

We determine the extent of non-bed-conformable ice by first measuring the bed slope α(H) along track within 5 km intervals. We also measure the slopes of all observed reflections within the same 5 km intervals and fit the depth profile of these slopes α(x, z) to a second-order polynomial that best fits the following relationship in a least squares sense:

(20)

where α(x, z) is the reflection slope at any point in the ice column and the polynomials q_i(x) are the best fit polynomial coefficients for equation (20). The predicted bed slope α′(x, H(x)) is thus

(21)

and the difference between the observed and predicted bed slopes is

(22)

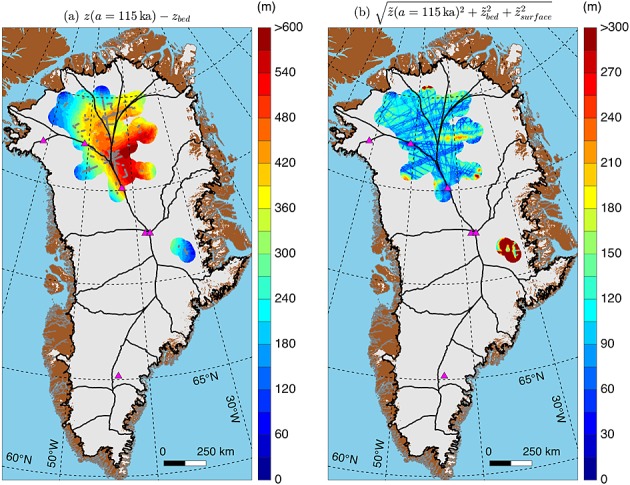
This simple metric describes the degree to which the radiostratigraphy is disrupted relative its local underlying bed topography. Another metric that can also indicate locally disrupted radiostratigraphy is the continuity index ψ developed by Karlsson et al. [2012]. We also calculate ψ across the GrIS in a manner similar to Sime et al. [2014] but done here using a majority of the KU data collected over the GrIS.

The continuity index is a measure of the variability in returned power within a given trace, calculated as the sum of the vertical gradient in returned power ΔP_r/Δz:

(23)

where N_ψ is the number of samples analyzed from the trace, as determined by the depth cutoffs discussed below (z_min and z_max). We modify the calculation of ψ, as compared to Karlsson et al. [2012], in several ways:

1. We require a minimum ice thickness of 1000 m for ψ to be calculated, similar to the minimum ice thickness within which the radiostratigraphy was generally traceable.

2. We analyze only the portion of the radar trace that is deeper than both 250 m and 0.1H (z_min). This cutoff prevents the surface multiple reflection from distorting ψ. Similarly, we analyze only the portion of the radar trace that is at least 100 m and 0.1H above the bed (z_max). This cutoff prevents diffuse reflectivity from within the basal layer from biasing ψ.

3. We linearly detrend P_r between z_min and z_max prior to calculating ψ to avoid biasing its calculation.

4. We do not report ψ values where the 5 km averaged azimuth of the transect changes by more than 10°, because aircraft maneuvers tend to artificially increase ψ.

5. Later campaigns are typically focused along the ice sheet margin (Figure 1a) but returned higher ψ values. This behavior is contrary to expectations and likely due to progressively improved radar system characteristics (e.g., bandwidth). Because we seek to merge ψ values measured by different campaigns and different radar systems (Table 1), we adjusted ψ from different campaigns with respect to each other, based on a comparison of their values where they intersected each other. For simplicity, we use only the P3 campaigns (Table 1), as these campaigns typically contained the highest quality radiostratigraphy.

Traces that recorded more and larger variations in returned power are considered indicative of good continuity in the radiostratigraphy and should return high ψ values. Traces with buckled or absent radiostratigraphy result in lower values of ψ. In terms of spatial extent, the continuity index has an advantage relative to Δα in that the former does not require that any reflections be traced, so it can be applied to all KU radar data rather than the subset that we ultimately traced.

4. Results

4.1. Radiostratigraphy Mapping and Dating

In total, we traced at least one reflection in 158,091 of the 479,595 km (33%) of ice-penetrating radar data collected by KU between 1993 and 2013 (Table 1). The maximum number of distinct reflections traced within a single 1 km segment is 66. Following a layer-continuity analysis of these same KU radar data [Sime et al., ²⁰¹⁴], these statistics suggest that we traced the majority of the continuous reflections contained within these data. We traced a total of 29,997 distinct reflections across all transects and manually identified 29,524 matches between these reflections at transect intersections. These matches resulted in 1849 unique sets of reflections matched to each other. Of these sets, 136 contained at least 10 reflections and 20 contained at least 100 reflections. Following the dating sequence described above, we dated 77% of the observed reflections. Of those dated reflections, 28% were dated by matching to core-intersecting reflections and the remainder by quasi-Nye dating. This radiostratigraphic data set is at least an order of magnitude larger than the most extensive known mappings of internal radiostratigraphy from any ice-penetrating radar data set [Hodgkins et al., ²⁰⁰⁰; Fahnestock et al., ^2001b; Tikku et al., ²⁰⁰⁴; Siegert et al., ²⁰⁰⁵; Legarsky and Gao, ²⁰⁰⁶; Carter et al., ²⁰⁰⁹; Leysinger Vieli et al., ²⁰¹¹].

The suitability of dating part of this radiostratigraphy using the quasi-Nye method is evaluated using two approaches. First, we compare quasi-Nye-inferred reflection ages to those inferred by 1-D (vertical) linear interpolation and extrapolation of depth-age relationships (Figure 7). In this evaluation, we use only the depth-age relationship from NorthGRIP to infer the depth-age relationship at the other ice core sites. Linear reflection dating tends to overestimate the age of reflections as compared to the logarithmic depth-age relationship predicted by equation (17) and is generally inadequate, a result similar to that of Lhomme et al. [2005] and Fudge et al. [2014]. Reflection ages calculated using quasi-Nye dating tend to better match ice core depth-age relationships and are more self-consistent, particularly at shallower depths and especially at Camp Century. This behavior is consistent with expectations. Vertical strain rates are generally predicted to be uniform in the upper portion of the ice sheet and are more likely to decrease closer to the bed, e.g., within the basal shear layer [Dansgaard and Johnsen, ¹⁹⁶⁹]. Quasi-Nye dating tends to perform better in the upper portion of the ice sheet and worse closer to the bed, because it may assume a uniform vertical strain rate over a larger depth than is physically reasonable (e.g., Figure 5).

Figure 7.

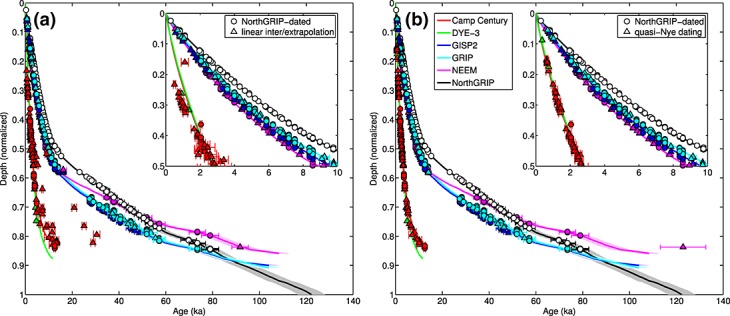
Depth-age relationships for the six deep ice cores recovered from the GrIS. Depth is normalized by the local ice thickness. Solid lines are the ice core-derived depth-age relationships (Table 2) and surrounding fill is the assigned age uncertainty. Circles are reflection depths/ages that were dated at NorthGRIP only. Triangles are non-core-intersecting reflections whose ages were estimated using regions where they overlapped with NorthGRIP-dated reflections. (a) Non-core-intersecting reflections (triangles) dated using 1-D (vertical) linear interpolation and extrapolation of depth-age relationships. (b) Non-core-intersecting reflections dated using quasi-Nye dating. Note that when dating the entire radiostratigraphy, all the ice core depth-age relationships are used.

Second, we verify the overall continuity of observed reflections and the quality of their inferred ages by flattening the traced radargrams to match their inferred depth at a reference ice core (Animation S1). In this case, we chose NorthGRIP as the reference ice core as it is generally considered the best dated of the GrIS's deep ice cores, due to basal melting there [Dahl-Jensen et al., ²⁰⁰³]. We adjust equations 6–8 so that the reference “trace” is the depth-age relationship at NorthGRIP. In this manner, a radar trace from any location within the ice sheet can be rescaled to approximate its expression had it been recorded at NorthGRIP instead. A minimum of four dated reflections is needed for a trace to be included in this analysis.

We observe a consistent pattern of very high frequency (VHF) radar reflectivity throughout the GrIS, regardless of the radar system used. This observation is qualitatively consistent with that of Karlsson et al. [2013], who examined the same radar data. As the radar system's bandwidth increased, as Δt decreased, and as SAR focusing was applied (Table 1), we observe the depth pattern of englacial reflectivity in finer detail. These improvements allowed us to trace an increasing number of reflections, although distinct reflections were observed even using the first iteration of ICORDS, which was deployed during the first four campaigns used in this study (1993–1997 P3; Table 1). For example, a trio of bright reflections dated to the LGP (colloquially known as the “triplet” or “three sisters”) dated to between 35 and 55 ka [Fahnestock et al., ^2001a] are observed by all radar systems (Animation S1).

The above tests suggest that our application of quasi-Nye dating to the GrIS is both self-consistent and sufficiently accurate to justify gridding of the ice sheet's age structure. Furthermore, based on both Figure 7 and Animation S1, we conclude that the majority of reflections that we mapped from within the GrIS are isochronal to within our ability to observe them with ice-penetrating radar. This result is consistent with numerous studies that have assumed that similar reflections are isochronal and produced physically self-consistent analyses based on that assumption [e.g., Fahnestock et al., ^2001b]. This result does not negate the possibility of non-isochronal or loosely isochronal reflections (e.g., those due to crystal-orientation-fabric contrasts) within the GrIS. However, it does suggest that within the GrIS and above its basal shear layer, few reflections are clearly non-isochronal.

4.2. Age Structure

Throughout the ice sheet, we observe a pattern of age that is consistent with what is already known of the age structure of the GrIS [Fahnestock et al., ^2001a; Karlsson et al., ²⁰¹³; Sime et al., ²⁰¹⁴] and its long-term and modern patterns of accumulation rate [Fahnestock et al., ^2001b; Ettema et al., ²⁰⁰⁹]. Shallower Holocene-aged ice, whose present depth is more strongly influenced by the long-term pattern of accumulation rate, is more downwarped west of the central ice divide, toward the south, and toward the ice sheet margins (Figures8 and 9 and Animation S2). Although our ability to map the age structure within the southern reaches of the ice sheet is limited, our results suggest that most of the ice sheet south of Jakobshavn Isbræ (∼69°N) is Holocene aged. The effect of NEGIS upon the age structure is evident as a prominent northeast trending change in the depth-age relationship that originates north of GRIP and GISP2.

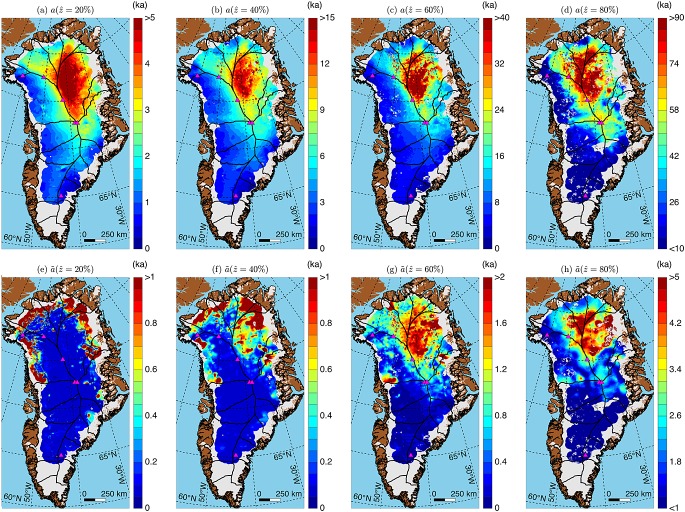
Figure 8.

Age of the GrIS at depths equal to (a) 20%, (b) 40%, (c) 60%, and (d) 80% of its ice thickness. Thick black lines denote ice-drainage basins [Zwally et al., ²⁰¹²]. (e–h) Uncertainty in ice age at depths equal to 20%, 40%, 60%, and 80% of the GrIS ice thickness, respectively.

Figure 9.

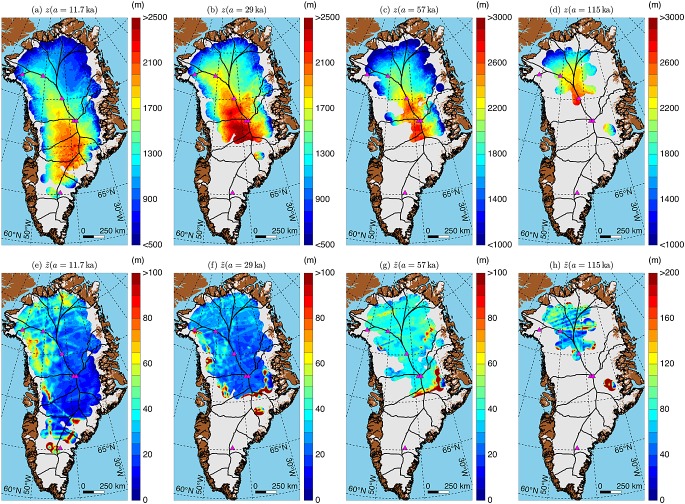
Depth of synthetic isochrones of ages (a) 11.7 ka (beginning of the Holocene epoch), (b) 29 ka (approximately the Last Glacial Maximum; end of Marine Isotope Stage (MIS) 3) [Lisiecki and Raymo, ²⁰⁰⁵], (c) 57 ka (beginning of MIS 3), and (d) 115 ka (end of the Eemian period) across the GrIS. (e–h) Uncertainty in the depth of the 11.7, 29, 57, and 115 ka isochrones, respectively.

The combination of the deep radar data used and our tracing strategy results in an age structure that is best constrained at midrange depths (∼10–80% of ice thickness) and farther north (> ∼70°N). The pattern of age at normalized depths (Figure 8) is more closely aligned with the modern pattern of ice drainage than the depth of specific isochrones (Figure 9), even that of the Holocene-LGP transition. These patterns diverge further with increasing depth/age, emphasizing the importance of both horizontal ice flow and likely changes in the past configuration of the GrIS in producing its present age structure.

To provide further context for the observed age structure, we compare it to that predicted by the Nye model in Animation S3 using modern values of accumulation rate and ice thickness. In this “modern” Nye model, the vertical strain rate for the full ice column is [Nye, ¹⁹⁵⁷]

(24)

where 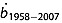is the modeled mean accumulation rate of ice between 1958 and 2007 for the GrIS [Ettema et al., ²⁰⁰⁹; Nowicki et al., ²⁰¹³]. The 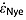and H then replace their equivalent effective values in equation (17).

Spatial variation in the depth-age relationship predicted by the Nye model depends on the local accumulation rate and ice thickness only. We consider this model to be the simplest possible model of the age structure of the GrIS. It assumes that all horizontal ice motion is due to basal sliding, no melting or freezing is occurring at the bed, and that only local conditions have influenced the depth-age relationship. In general, we find that deeper ice is significantly older than predicted by the Nye model. For shallower ice, which is more easily interpreted in terms of recent accumulation rates, most of ice sheet interior is younger than predicted by the Nye model, especially at high elevations and farther north. These differences indicate that, unsurprisingly, the assumptions that underpin the “modern” Nye age model are not valid for the whole of the GrIS. The clearest implication is that accumulation rates during the Holocene epoch were, on average, higher than the modeled modern values. Ice age also tends to deviate more clearly and more abruptly from the Nye model with increasing distance from ice divides, implying increased spatial variation in past accumulation rates, internal deformation, and basal sliding there. The Nye model is not valid in the ablation zone near the ice sheet margin, so any inference of age difference there is not clearly meaningful.

4.3. Extent of Eemian Ice

Animations S1 and S2 show that ice from the earlier part of the LGP (> ∼50 ka) is absent in several regions of the ice sheet, implying that it has either melted away at the bed or thinned significantly [Fahnestock et al., ^2001b]. Conversely, in other regions, the age of the ice likely exceeds that at NorthGRIP, raising the possibility that stratigraphically conformable (i.e., undisturbed) ice from the Eemian period (130–115 ka) still exists within the GrIS. Such ice has been long sought [e.g., Dahl-Jensen et al., ¹⁹⁹⁷] and was recently found in a disturbed state and successfully reconstructed [NEEM community members, ²⁰¹³].

The spatial extent of Eemian-aged reflections and the apparent thickness of Eemian ice are shown in Figure 10. Similarly, Animation S2 suggests the presence of Eemian ice mostly along or near the central ice divide. Close to the bed, where fewer reflections were traced, our estimate of Eemian ice thickness depends partly on the quality of quasi-Nye dating there. The vertical strain rate inferred between reflection pairs shallower in the ice column will tend to overestimate the vertical strain rate closer to the bed [Dansgaard and Johnsen, ¹⁹⁶⁹], suggesting that our approach will tend to overestimate the thickness of Eemian or older ice. Furthermore, in the process of normalizing the age structure, we cannot easily account for occasional overturning, as observed at NEEM [NEEM community members, ²⁰¹³]. Hence, we qualify as “apparent” the thickness of Eemian ice reported here and reemphasize both the inherent challenge of dating deep ice and the specific challenge of locating Eemian ice with the GrIS. Based on the success of the flattening of most of the reflections (Animation S1), particularly of the higher-quality data from later P3 campaigns, there are several portions of the GrIS interior with relatively simple depth-age relationships. Near the bed, some of this ice is probably Eemian aged, and such locations should be evaluated further as potential sites for future deep ice cores.

Figure 10.

(a) Apparent thickness of Eemian ice (≥115 ka) within the GrIS. Gray dots represent all mapped and dated internal reflections inferred to be 115 ka (the end of the Eemian period) or older. (b) Uncertainty in thickness of Eemian ice, expressed as the combination of the uncertainty in the depth of the 115 ka isochrone (Figure 9d) and the uncertainty in the gridded ice thickness [Bamber et al., ²⁰¹³].

4.4. Extent of Disrupted Radiostratigraphy

In numerous locations within Greenland's interior, the deepest radiostratigraphy does not drape smoothly over the observed along-track bed topography. Instead, it is deflected upward across horizontal scales of several kilometers or more, distorting the depth-age relationship of the ice column by up to several hundred meters. These features are most prominent in the onset region of Petermann Glacier in northwestern Greenland (Animation S2). Bell et al. [2014] mapped the larger instances of these features. The precise cause of this disruption/deflection is unknown, but it is unlikely to be due to flow over undetected highs in the bed topography, as previously hypothesized [Legarsky et al., ¹⁹⁹⁸], because extensive radar surveying of the GrIS has generally failed to reveal such highs. This disruption may be due to buckling associated with spatially or temporally varying basal friction [e.g., Hindmarsh et al., ²⁰⁰⁶; Wolovick et al., ²⁰¹⁴], basal freeze-on, as inferred for East Antarctica [Bell et al., ²⁰¹¹], or rheological variability within the basal shear layer [NEEM community members, ²⁰¹³]. Given the variability in magnitude of these radiostratigraphic disruptions, a combination of the above phenomena is also possible, or another as-of-yet unknown process. At least for Petermann Glacier, a plausible scenario is that recently described by Bell et al. [2014] and modeled by Wolovick et al. [2014]: basal freeze-on uplifts and overturns the overlying strata, generating complex units that include both accreted and distorted meteoric ice.

These features can contain unusually bright, indistinct, or overturned reflections that do not resemble the monotonous radiostratigraphy of the overlying ice sheet. Unusually bright reflections may be due to a large fabric contrast between meteoric and accreted ice, as hypothesized to occur over Lake Vostok [MacGregor et al., ^2009a]. It is possible that some of these coherent reflections and diffuse reflectivity are not isochronal, although they likely remain useful indicators of past flow [e.g., NEEM community members, ²⁰¹³]. Because we evaluated the isochronal nature of mapped reflections at ice core sites only, which are typically not near such features (excepting NEEM), we cannot presently further evaluate the nature of the complex reflectivity within these basal layers.

We find several regions with large differences between the observed and predicted bed slopes (equation (22)). These regions are typically located at the onset of fast ice flow, such as within and upstream of Petermann Glacier and Jakobshavn Isbræ (Figure 11). Low bed slopes in these regions are qualitatively consistent with observations of lower bed roughness there, particularly for Petermann Glacier [Rippin, ²⁰¹³]. The lack of bed-conforming radiostratigraphy in these regions suggests strong and long-term organization of ice flow that is consistent with pattern of surface velocity [Joughin et al., ²⁰¹⁰] and may be further modulated by spatiotemporal variation in basal friction [e.g., Hindmarsh et al., ²⁰⁰⁶; Christianson et al., ^{2013, 2014}]. This pattern is distinct from observations of some Antarctic glaciers that contain disrupted radiostratigraphy, which has been interpreted as evidence of fast ice flow in the past [e.g., Catania et al., ²⁰⁰⁵; Rippin et al., ²⁰⁰⁶].

Figure 11.

(a) Observed along-track bed slope (α(H)) within 5 km intervals across the GrIS. (b) Along-track bed slope predicted by the depth profile of the slope of internal reflections (α′(H)) within the same 5 km intervals. (c) Absolute value of the residual between the observed and predicted bed slopes (|α(H) − α′(H)|). (d–f) |α(H) − α′(H)| within selected regions outlined by magenta dashed lines in Figure 11c. Background shading is the satellite-measured surface speed [Joughin et al., ²⁰¹⁰]. For all panels, bed slopes and differences are plotted in ascending order to better resolve larger values.

A region north of NEGIS shows an unusual pattern for the difference between observed and predicted bed slope (Figure 11f). This region has low observed bed slope but is predicted to have a much higher bed slope. However, it is less clearly associated with a downstream outlet glacier, as is the case for Petermann Glacier. This pattern suggests that this region has experienced faster ice flow in the past, which could be recorded as buckling of internal radiostratigraphy [e.g., Rippin et al., ²⁰⁰⁶; Wolovick et al., ²⁰¹⁴]. Recent dynamic thinning of outlet glaciers downstream of this region [Khan et al., ²⁰¹⁴] suggests that past changes in ice flow there are possible.

Figure 12 shows the continuity index for the KU data collected across the GrIS. There is a steep dropoff in radiostratigraphic continuity in the ablation zone, as also observed by Sime et al. [2014]. A few transects have abnormally low or high continuity compared to other nearby transects, indicating variability in radar system performance both within and between survey campaigns. Overall, there is good agreement between the portions of the GrIS that we traced (Figure 1b) and the continuity index, further suggesting that we traced the majority of the well-resolved radiostratigraphy within the KU radar data.

Figure 12.

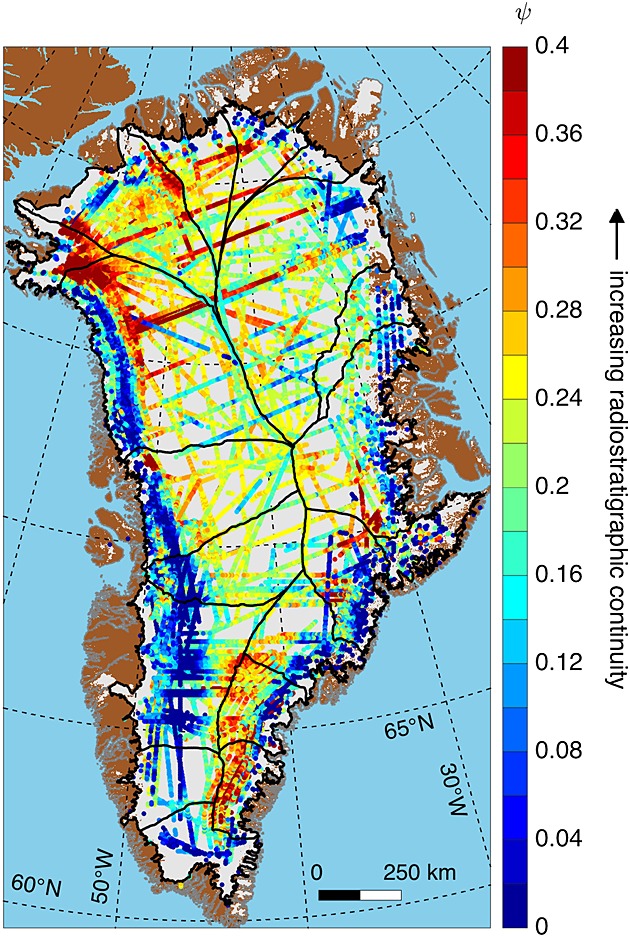
Continuity index (ψ) across the GrIS calculated from all KU P3 campaigns collected between 1993 and 2013 (Table 1).

For some parts of the GrIS, the pattern of the continuity index is remarkably different from that of Δα(H). For example, higher layer continuity is observed in southeastern Greenland and in the onset region of Petermann Glacier. This pattern suggests that disrupted radiostratigraphy that does not conform to the bed topography (higher Δα(H)) can be sufficiently well resolved so that there is no commensurate decrease in the continuity index. However, the region north of NEGIS discussed above also has a variable continuity index, further suggesting that this region has experienced faster ice flow in the past.

5. Discussion

5.1. Dating Observed Reflections

Our approach to dating the radiostratigraphy that we mapped diverges from earlier efforts, which generally focused on ice core synchronization [e.g., Buchardt, ²⁰⁰⁹; Cavitte et al., ²⁰¹³] or the nature of observed reflections [e.g., Eisen et al., ²⁰⁰⁶]. Due to challenges in navigation and system design, along with uncertainty in the radio-wave velocity, it is unlikely that airborne ice-penetrating radar can ever match ice core drilling in terms of the precision and accuracy of depth-age relationships. However, we need not expect nor require ice core levels of precision and accuracy in these radar observations to reasonably conclude that most deep radar reflections are isochronal and that other observed reflections sandwiched between them are also isochronal. Quasi-Nye dating can reasonably date reflections away from ice cores and the overwhelming majority of distinct reflections from within the GrIS are isochronal to within our ability to resolve them with ice-penetrating radar (Figure 7 and Animation S1).

Although quasi-Nye dating is less reliable deep in the ice column (Figure 6) or in regions of complex flow, our approach is also relevant to the search for million-year-old ice in East Antarctica [Fischer et al., ²⁰¹³; Van Liefferinge and Pattyn, ²⁰¹³], which would likely benefit from isochrone-constrained modeling of the depth-age relationship of basal ice. Any reflection, whether core dated or not, is often challenging to trace continuously to a specific, distant region of interest. By dating non-core-intersecting reflections observed between ice cores and a region of interest using the quasi-Nye method, the depth-age relationship can be better constrained deeper in the ice column independent of more sophisticated—and inherently more complex—ice flow models.

The modeling study of Lhomme et al. [2005] also demonstrated the general unsuitability of linear vertical interpolation and extrapolation of depth-age relationships in ice sheets and the need for a physically based interpolation method. Their alternative approach for inferring such relationships requires modeling of the surface mass-balance history of the GrIS and commensurate additional assumptions. Quasi-Nye dating accounts locally for the integrated effect of that history within a reflection-bounded layer, but it cannot account for any intralayer change in the vertical strain rate, as is possible using the balance-flux interpolation method described by Lhomme et al. [2005]. In our application of quasi-Nye dating, suitable values of are determined independently for each trace and reflection-bounded layer. Therefore, these vertical strain rates may not be smoothly varying, as is expected based on analysis of ice core depth-age relationships [Fudge et al., ²⁰¹⁴]. As such, there is presently a tradeoff between potential dating accuracy and simplicity of approach. Future work should aim to reconcile these methods.

5.2. Evaluation of Ice Sheet Models

Substantial challenges remain in the evaluation of models of the flow of ice sheets, particularly in their parameterization of basal processes [e.g., Aschwanden et al., ^{2012, 2013}]. The inclusion of non-diffusive tracers in numerical models of ice sheet flow enables prediction of internal stratigraphy and hence of age structure [Clarke et al., ²⁰⁰⁵]. At least two predictions of the present-age structure of the GrIS already exist [Huybrechts, ¹⁹⁹⁴; Clarke et al., ²⁰⁰⁵], and numerous studies of its past extent and marginal dynamics now exist [e.g., Young et al., ²⁰¹¹; Lane et al., ²⁰¹³]. Numerous localized paleoclimatic records suggest that, at centennial-to-millennial timescales, the GrIS in aggregate retreats in response to climatic warming and advances in response to cooling [Alley et al., ²⁰¹⁰]. Using the radiostratigraphy described here, the spatial variation of this dynamic response can now be evaluated at the scale of most of the ice sheet. However, this radiostratigraphy does not typically extend all the way to the ice sheet margin and would likely be difficult to reconcile directly with periglacial inferences of past ice sheet extent. It is thus likely to be of most value in further unraveling the spatial variation of ice sheet response within the interior [e.g., Vinther et al., ²⁰⁰⁹]. The rheology of the GrIS is age dependent, due to past climate changes and their influence upon ice crystal size [e.g., Paterson, ¹⁹⁹¹; NEEM community members, ²⁰¹³]. Thus, the age structure presented here can also indirectly constrain the rheology of the GrIS in models aiming to reproduce its present pattern of ice flow.

Unraveling past ice sheet states and boundary conditions from radiostratigraphy sometimes requires formal geophysical inverse methods [e.g., Waddington et al., ²⁰⁰⁷; MacGregor et al., ^2009b; Koutnik, ²⁰⁰⁹]. The number of degrees of freedom in a realistic model of the flow of an entire ice sheet is sufficiently large that it is not presently possible to invert the radiostratigraphy of an entire ice sheet to elucidate its past. However, it is important to recognize that this past was recorded and integrated by the radiostratigraphy.

While the age structure of models aiming to represent the present state of the GrIS can be evaluated directly using our data, future studies are also warranted to determine what history can be extracted independently from these data across large spatial scales. So far, direct inversions of ice sheet radiostratigraphy have used flowline or flowband ice flow models only. This new radiostratigraphic data set contains relatively few along-flow transects with radiostratigraphic data suitable for direct evaluation with such models. However, the possibility of a three-dimensional inversion of radiostratigraphy now exists. Higher-order or full-Stokes ice flow models are presently too computationally intensive to use as forward models in a geophysical inverse problem constrained by radiostratigraphy for the relevant glacial-interglacial timescales. However, in the GrIS interior, simplified or limited-domain ice flow models may be acceptable [e.g., Koutnik and Waddington, ²⁰¹²]. We note that the increased age uncertainty associated with our dating approach will also affect interpretation of ice sheet history from specific reflections and the age volume.

As an initial example of the value of this data set to the evaluation of ice sheet models, here we briefly consider the long-standing question of the extent and volume of the GrIS during the Eemian period. Numerous modeling efforts have considered this problem, motivated by the desire to constrain the contribution of the GrIS to sea level rise during a period of warmth similar to the present [e.g., Cuffey and Marshall, ²⁰⁰⁰; Tarasov and Peltier, ²⁰⁰³; Robinson et al., ²⁰¹¹; Born and Nisancioglu, ²⁰¹²; Helsen et al., ²⁰¹³]. While recent work suggests that the Eemian period is not an ideal analog for present and future warming [van de Berg et al., ²⁰¹¹], constraining the extent and volume of the GrIS in the past remains valuable for apportioning sea level contributions between the multiple ice sheets that were present during the Pleistocene.

Our mapped age volume shows no evidence of Eemian ice in southern Greenland and little to no ice from the LGP there (Figure 10 and Animation S2). Thus, at face value, our data do not support the hypothesis that a “southern dome” persisted during the Eemian period, favoring estimates of GrIS mass loss during the Eemian at the higher end of the reported range [e.g., Cuffey and Marshall, ²⁰⁰⁰]. Critically, this simple interpretation ignores past ice flow, which favors the preservation and detection of older ice in regions where the basal temperature, accumulation rate, and horizontal ice flow speed are all low. Indeed, we observe and infer the presence of Eemian-aged ice primarily near the central ice divide and in regions where the above mentioned parameters are generally low [Ettema et al., ²⁰⁰⁹; Joughin et al., ²⁰¹⁰] but not uniformly so [Fahnestock et al., ^2001b; Dahl-Jensen et al., ²⁰⁰³; Petrunin et al., ²⁰¹³]. Higher accumulation rates in southern Greenland could easily have thinned older ice to the degree that we cannot yet detect or resolve it using ice-penetrating radar, as appears to have occurred at DYE-3.

5.3. Sheath Folds in Basal Ice?

For several radargrams, the structure of the basal layer qualitatively resembles that of sheath folds in rock, which can form due to flow in the vicinity of rheologically weak layers or slip surfaces [e.g., Reber et al., ²⁰¹²]. These folds are three-dimensional structures whose vertical cross section (as they would be observed by ice-penetrating radar) varies depending on the cross section's orientation with respect to the main axis of the fold. Sheath folds can generate characteristic “eye” structures, which are observed occasionally near the base of the GrIS (Figure 13). If these features are indeed sheath folds, then these observations appear to support the hypothesis presented by NEEM community members [2013] explaining the formation of disrupted basal ice. They hypothesized that the interface between rheologically weaker ice from the LGP and stiffer ice from the Eemian period leads to the development of a slip surface there. This slip surface is equivalent to a false bed, which has also been identified in the West Antarctic Ice Sheet at Siple Dome [Pettit, ²⁰⁰³]. Reflections within and bounding these structures are often indistinct and difficult to trace except by purely manual methods, so we did not map them exhaustively. The apparent slopes of these reflections sometimes exceed that which can be imaged by airborne radar sounding [Holschuh et al., ²⁰¹⁴], so their resemblance to sheath folds may be partly due to aliasing of backscatter from these complex features.

Figure 13.

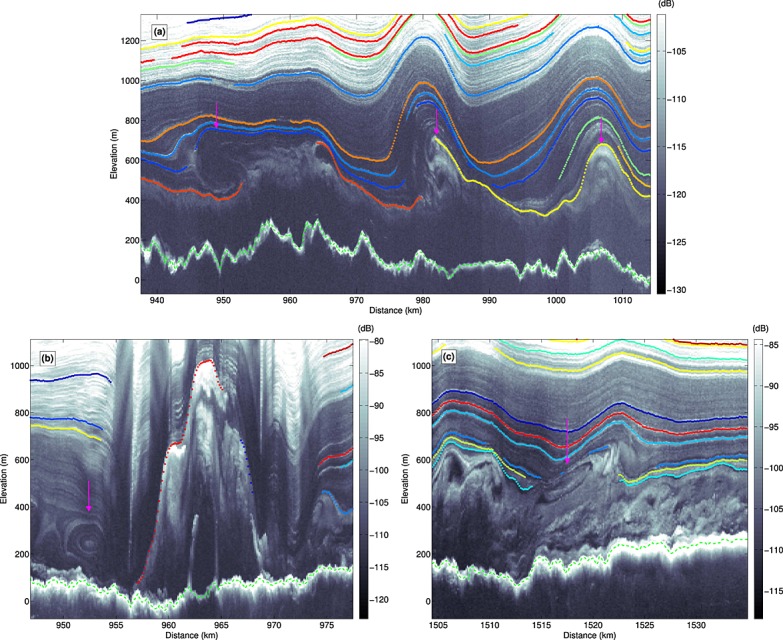
Example radargrams showing patterns qualitatively similar to sheath folds in rock from transects collected on (a) 29 March 2011 (76.4°N, 50.1°W) and (b, c) 29 April 2011 (79.5°N, 51.6°W; and 79.6°N, 50.2°W, respectively). Both transects were collected during the 2011 P3 campaign (Table 1). Magenta arrows point to “eye”-like features. The color of the traced reflections has no physical meaning.

The possibility of sheath folds within the GrIS does not exclude the possibility of widespread basal freeze-on beneath the GrIS, inferred from these same radar data by Bell et al. [2014], but these preliminary observations do suggest that multiple phenomena can disrupt basal ice. More study is warranted to further evaluate the possibility of sheath folds within the GrIS, which should include both more extensive reflection mapping and ice flow modeling.

6. Conclusions

We produced the first comprehensive deep radiostratigraphy of the GrIS using a suite of established and new methods to trace reflections and date them. The value of this holistic approach is evident in the spatial scale of data set that we mapped at sufficient density to then be gridded and further interpreted. This dated radiostratigraphy reveals the essential age structure of the GrIS. This age structure is monotonous across large sectors of the ice sheet, particularly within its upper layers, but the base of the ice sheet contains numerous complex features and, in several onset regions, disrupted ice is evident.

This radiostratigraphy constitutes a novel and potentially powerful constraint on both the internal dynamics of the GrIS and its integrated millennial-scale response to oceanographic, atmospheric, and subglacial forcings. In particular, large-scale ice flow models should assimilate these data, so that they may better reproduce not only the modern state of the GrIS [e.g., Price et al., ²⁰¹¹; Brinkerhoff and Johnson, ²⁰¹³] but also its thermodynamic history [Aschwanden et al., ²⁰¹³], which likely contains clues as to its future dynamic response to ongoing climate change [Nowicki et al., ²⁰¹³; Vaughan et al., ²⁰¹³]. Numerous other avenues exist for further analysis of this radiostratigraphy, including but not limited to searching for evidence of changes in flow direction [e.g., Conway et al., ²⁰⁰²], reproducing the geometry of observed reflections to constrain accumulation rates and basal melt rates [e.g., Fahnestock et al., ^{2001a, 2001b}; Waddington et al., ²⁰⁰⁷; Leysinger Vieli et al., ²⁰¹¹], and further analysis of the relationships between radiostratigraphy, bed topography, and basal conditions [e.g., Hindmarsh et al., ²⁰⁰⁶]. While not discussed in this study, we also recorded the echo intensity of the mapped reflections, which could constrain englacial radar attenuation rates across the GrIS [e.g., Matsuoka et al., ²⁰¹⁰].

We note that this first radiostratigraphic data set for the whole of the GrIS could be improved upon in several ways. First, advances in processing and/or re-processing of older KU data could reveal additional reflections, particularly in regions of disrupted radiostratigraphy. In this regard, advances in surface-clutter mitigation will be especially valuable near the ice sheet margin. Second, improved methods for predicting, flattening, and tracing observed reflections could motivate a more thorough evaluation of GrIS radiostratigraphy. Our implementation of phase-based slope prediction could likely also be improved. Again, such advances would be of greatest value for the ice sheet margins, where we encountered more difficulty in mapping reflections. Third, additional ice-penetrating radar data collected over the GrIS exist, including several spatially extensive airborne campaigns that have recorded deep internal reflections [e.g., Nixdorf and Göktas, ²⁰⁰¹] and more recent surveys of near-surface radiostratigraphy [e.g., Rodríguez-Morales et al., ²⁰¹⁴]. Ice thicknesses measured by other airborne campaigns were included in the recent compilations of the bed topography beneath the GrIS [Bamber et al., ²⁰¹³; Morlighem et al., ²⁰¹⁴]. However, none of these other surveys are as spatially extensive as the KU data set. Furthermore, the compilation of radiostratigraphy recorded by different radar systems with widely varying center frequencies, bandwidths, and other survey parameters is likely to be more challenging than the compilation of their ice-thickness measurements only. These systems ultimately all sound the same ice sheet, so the dominant pattern of radar reflectivity within the GrIS that others and we have observed (Animation S1) [Karlsson et al., ²⁰¹³] could ameliorate that challenge. Finally, additional measurements and models of the firn air content of the GrIS would better constrain the firn correction and ultimately reduce depth-induced age uncertainty when dating internal reflections.

This traced and gridded radiostratigraphy will be archived with the National Snow and Ice Data Center.

Notation

• real part of the complex relative permittivity of pure ice

• depth uncertainty

• Δz depth traveled by a radio wave through ice during Δt

• v_ice radio-wave velocity in ice

• Δt traveltime-sampling interval

• c speed of light in the vacuum

• Δϕ change in phase of radio wave across Δz

• λ_ice wavelength of radio wave in ice

• f_c radar center frequency

• Δϕ/Δx horizontal (along-track) gradient of phase

• x along-transect position

• t two-way traveltime

• Δt/Δx horizontal (along-track) gradient of two-way traveltime to a reflection

• k_D Doppler centroid wavenumber

• z ice-equivalent depth

• x₀ reference position for flattening

• p_i polynomial coefficients describing the least squares best fit between z_j(x) and z_j(x₀)

• P_r radar received power

• rescaled/flattened radar received power

• z′ rescaled/flattened reflection depth

• a ice age

• a_c(z) ice core depth-age relationship

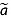• _c, a_overlap, 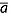_overlap mean ice core, overlapping, and mean overlapping reflection age

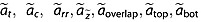• total core-intersecting, ice core-attributed, radar-attributed, depth-attributed, total overlapping upper/top and lower/bottom reflection age uncertainty

• Δr radar range resolution

• SNR signal-to-noise ratio of internal reflection echo intensity to local background

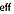• , H_eff, effective intralayer steady state accumulation rate, ice thickness, and strain rate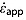

• apparent Nye vertical strain rate

• H ice thickness

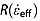• depth residual between 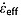-predicted values of H_eff at top and bottom isochrones

• z_top, z_bot depth of top and bottom isochrones bounding a layer

• a_top, a_bot age of top and bottom isochrones bounding a layer

• depth normalized by ice thickness

• α reflection slope

• α′ predicted reflection slope

• q_i polynomial coefficients describing the least squares fit between α(z) and z

• ψ continuity index

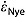• Nye uniform steady state vertical strain rate

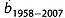• mean modeled accumulation rate of ice across Greenland between 1958 and 2007

Supporting Information

Readme

Animation S1

Animation S2

Animation S3