Sound frequency-invariant neural coding of a frequency-dependent cue to sound source location

Abstract

The century-old duplex theory of sound localization posits that low- and high-frequency sounds are localized with two different acoustical cues, interaural time and level differences (ITDs and ILDs), respectively. While behavioral studies in humans and behavioral and neurophysiological studies in a variety of animal models have largely supported the duplex theory, behavioral sensitivity to ILD is curiously invariant across the audible spectrum. Here we demonstrate that auditory midbrain neurons in the chinchilla (Chinchilla lanigera) also encode ILDs in a frequency-invariant manner, efficiently representing the full range of acoustical ILDs experienced as a joint function of sound source frequency, azimuth, and distance. We further show, using Fisher information, that nominal “low-frequency” and “high-frequency” ILD-sensitive neural populations can discriminate ILD with similar acuity, yielding neural ILD discrimination thresholds for near-midline sources comparable to behavioral discrimination thresholds estimated for chinchillas. These findings thus suggest a revision to the duplex theory and reinforce ecological and efficiency principles that hold that neural systems have evolved to encode the spectrum of biologically relevant sensory signals to which they are naturally exposed.

the capacity for sound localization is phylogenetically ubiquitous and basic to communication and environmental awareness in many species including humans. The century-old duplex theory of sound localization holds that low-frequency signals are localized on the basis of submillisecond interaural time differences (ITDs) whereas high-frequency signals are localized on the basis of interaural level differences (ILDs) attributable primarily to acoustic “shadowing” of the ear farther from the sound source by the head (Strutt 1907). While the magnitude of ITD cues depends almost exclusively on source azimuth and only slightly on frequency (e.g., Kuhn 1977; Kuwada et al. 2010), ILD cues (measured in the acoustic free field) are heavily frequency dependent (e.g., Feddersen et al. 1957; Koka et al. 2011). At low frequencies, for which ITD cues are most useful (<1–2 kHz, depending on species), ILDs (as measured in anechoic space) are generally small. ILDs gradually increase with frequency up to ∼3–4 kHz (again depending on species), beyond which ILD magnitudes increase rapidly and are dramatically affected by source azimuth. Two parallel and anatomically separate neural pathways have evolved in the mammalian brain stem to encode ITD and ILD cues, with the neurons that comprise the associated nuclei (the medial and lateral superior olive, respectively) exhibiting low- and high-frequency biases consistent with the duplex theory (for recent review, see Grothe et al. 2010; Tollin 2003).

Although the duplex theory has been largely supported by free-field localization studies using “far-field” sources >1 m from the head (e.g., Macpherson and Middlebrooks 2002), conditions under which the duplex theory may not account for empirical data have also been noted (e.g., Hafter 1983). For example, despite the clear and strong frequency dependence of acoustic ILDs under free-field conditions, human (e.g., Mills 1960) and animal (Wakeford and Robinson 1974; cf. Keating et al. 2014) psychophysical sensitivity to ILD is perplexingly invariant across frequency, with detection thresholds ∼1–4 dB for tones from 200 Hz to 10 kHz. Concordant with this finding, physiological studies have characterized ILD-coding neurons sensitive to frequencies spanning the entire tonotopic axis, including low frequencies (e.g., auditory brain stem: Caird and Klinke 1983; Finlayson and Caspary 1991; Sanes and Rubel 1988; Siveke et al. 2006; Tollin et al. 2008; Tollin and Yin 2005; midbrain: Brückner and Rübsamen 1995; Irvine and Gago 1990; Moore et al. 1983; Semple and Aitkin 1979; Semple and Kitzes 1987; cortex: Benson and Teas 1976). Nonetheless, the duplex theory view of ILD as an exclusively high-frequency cue has persisted.

According to ecological and efficiency principles (Attneave 1954; Barlow 1961), neural systems evolve to faithfully encode the spectrum of biologically relevant sensory signals to which they are naturally exposed. That is, the limited operating ranges of neurons are tuned, intrinsically or during ontogeny, to the range of salient stimuli in the environment. On these grounds, robust behavioral and neural sensitivity to ILDs carried by low-frequency signals—which are negligibly attenuated by the head—must seem peculiar. However, this view is predicated on classic measurements of ILD cues (e.g., Feddersen et al. 1957), which were conducted in the acoustic far field and in unnatural, noise- and reflection-free environments. In contrast, it has recently been demonstrated that relatively large ILDs can be produced by low-frequency sound sources under a variety of ecological conditions. For example, low-frequency sources near the head (especially at distances <1 m) can generate large ILDs (>10 dB) due to distance-dependent sound dispersion rather than frequency-dependent head-shadowing (Brungart et al. 1999; Kim et al. 2010). Large low-frequency ILDs can also occur in multisource, reverberant environments (Gourevitch and Brette 2012; Młynarski and Jost 2014). Animals that routinely inhabit enclosed spaces and interact with conspecifics in close proximity—including humans and a great variety of other mammals—are thus regularly exposed to large low-frequency ILDs. Given these conditions, ecological and efficiency principles hold that the auditory system should have the capacity to encode low-frequency ILD cues, in opposition to the duplex theory.

Toward an improved understanding of the occurrence of low-frequency ILDs acoustically, their encoding by neurons, and the peculiar frequency invariance of behavioral ILD sensitivity, we conducted acoustical and neurophysiological experiments using chinchillas (Chinchilla lanigera), a robust auditory model with good behavioral sound localization ability (Heffner et al. 1994). Specifically, we tested the hypothesis that ILD-sensitive neurons in the inferior colliculus (IC) of the chinchilla encode, with frequency-invariant acuity, the full range of acoustically available ILDs occurring as a joint function of source azimuth, frequency, and distance. We report that 1) like high-frequency neurons, low-frequency ILD-sensitive neurons successfully encode the large range of ILDs to which they are naturally exposed as a function of source azimuth and distance and, moreover, that 2) there are no differences in the ILD coding capabilities of low- and “traditional” high-frequency ILD-sensitive neurons. Taken together, these data offer the first clear evidence for a neural substrate of frequency-invariant behavioral ILD sensitivity (Mills 1960).

MATERIALS AND METHODS

General

Procedures were reviewed and approved by the University of Colorado Animal Care and Use Committees and complied with National Institutes of Health guidelines. Detailed methods are described in prior publications (Jones et al. 2011a; Koka et al. 2011). Briefly, adult chinchillas (10 males and 14 females, weight 450–700 g) were anesthetized with an intramuscular (im) injection of ketamine hydrochloride (KetaVed, 30 mg/kg im) and xylazine hydrochloride (TranquiVed, 5 mg/kg im); supplementary injections were administered to maintain an adequate level of anesthesia. Core body temperature was monitored and maintained with a heating pad at 37°C. Both electrophysiological recordings and acoustical measurements were acute experiments.

Acoustical Measurements of ILD

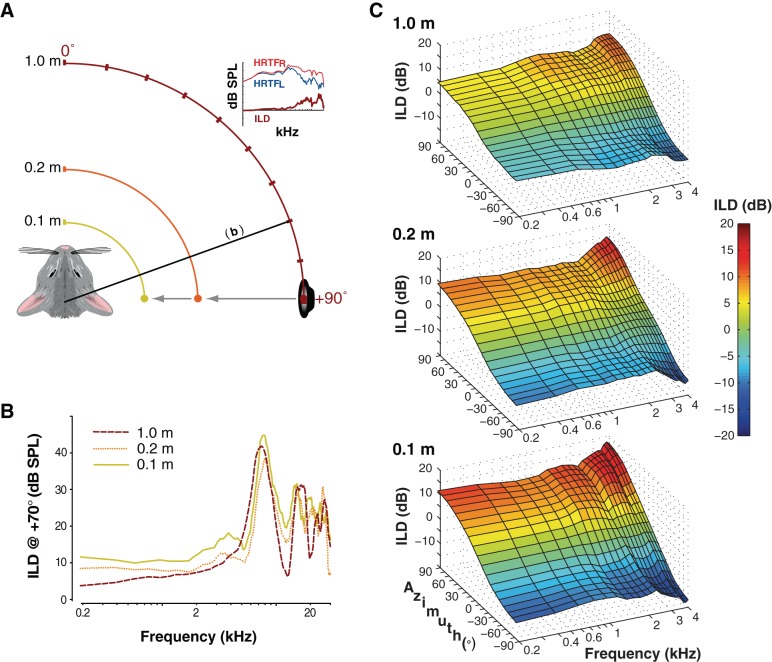
ILDs were calculated from acoustical measurements made at different sound source-to-observer distances (0.1, 0.2, and 1.0 m). Recordings took place in a double-walled semianechoic chamber (see Koka et al. 2011). Measurements made previously (e.g., Lupo et al. 2011) demonstrate that the chamber is effectively anechoic for frequencies > 250 Hz; moreover, contributions of any reflections across frequency are removed prior to analysis by time-windowing of recorded waveforms, as discussed in Koka et al. (2011). A cone-shaped speaker [MF1-M, Tucker-Davis Technologies (TDT), Alachua, FL], creating an acoustic point source, was attached to an industrial sliding camera tripod so that the source could be placed precisely at the required distances from the animal. The animal was positioned on a platform such that it could be rotated around its interaural axis through ±90° in 10° steps. The free field-to-eardrum acoustic impulse response for each ear and each location was measured, from which head-related transfer functions (HRTFs) were computed (Koka et al. 2011). The acoustic ILDs at each position were calculated by subtracting left ear HRTFs from right ear HRTFs (see also Fig. 1A).

Fig. 1.

Measurement of naturally occurring interaural level difference (ILD) cues to sound location across frequency, azimuth, and distance. A: adult chinchillas were positioned 0.1, 0.2, or 1.0 m from a point source loudspeaker. For each distance, a calibrated broadband stimulus (Koka et al. 2011) was presented from the speaker at each of 19 locations. “Head-related transfer functions” (HRTFs), giving sound pressure level across frequency after filtering by the torso, head, and pinnae, were measured for the left (HRTF_L) and right (HRTF_R) ears with probe microphones inserted deep into each ear canal. ILDs were computed at each azimuth-distance combination by subtracting the left HRTF from the right HRTF. B: for lateral source azimuths, ILDs increased markedly with decreasing source distance, particularly at low frequencies. Data are shown for a single animal. C: for frequencies below 4 kHz, increases in ILD with decreasing source distance are highly systematic and consistent across both azimuth and frequency. Data are shown for the same animal depicted in B.

Neurophysiological Methods

Extracellular single-unit recordings were made within the central nucleus of the inferior colliculus (ICC) of adult chinchillas. Recordings took place in a double-walled, sound-attenuating room (Industrial Acoustics, Bronx, NY). Prior to recordings, the animal was positioned in a custom stereotaxic head holder, both pinnae were removed, and tight-fitting hollow earpieces were fitted snugly into the external auditory meati to facilitate the presentation of acoustic stimuli (Jones et al. 2011b; Koka et al. 2010).

Extracellular electrical activity was measured with Parylene-coated tungsten microelectrodes (1–2 MΩ; Microprobe, Clarksburg, MD). Electrical activity was amplified (ISO-80, WPI, Sarasota, FL; Stanford Research Systems SRS 560, Sunnyvale, CA) and filtered (300-3,000 Hz). Candidate extracellular responses were isolated with a BAK amplitude-time window discriminator (model DDIS-1, Mount Airy, MD), and spike times were stored at a precision of 1 μs via a TDT RV8. Neurons were studied if their single-unit spike waveforms exhibited good signal-to-noise ratio along with amplitude and temporal action potential morphology that was consistent from spike to spike.

Acoustic calibration and stimulation.

All acoustic stimuli were generated in MATLAB (v7.1, The MathWorks, Natick, MA) and presented with Tucker Davis Technologies System III hardware with a sampling rate of 97,656.25 Hz at full 24-bit resolution. Sound was delivered via closed-field speakers (CF1, TDT) connected to tightly fitting custom insert earphones. Sound levels were calibrated with probe microphones (Brüel and Kjær type 4182, Norcross, GA) with probe tubes placed 2 mm from each tympanum. Output levels for tones from 0.1 to 30 kHz (0.1-kHz interval) were used to compute 256-tap digital finite impulse response filters, providing a virtually flat acoustic response at the tympanic membrane (±2 dB) and maximum compensated output levels of ∼95 dB SPL. All stimulus presentation, acquisition, and processing were done with custom MATLAB scripts.

Neuronal response classification.

For each isolated unit, the characteristic frequency (CF), spontaneous activity, and threshold were obtained by measuring a frequency-intensity response area. Pure tones of 50-ms duration with varying frequencies and SPLs were presented contralaterally (i.e., to the left ear) every 200 ms, and neural responses (spike/s) were recorded to generate response area curves. Neuronal CF was defined as the frequency corresponding to the lowest SPL that elicited a response greater (+2 SD) than the spontaneous activity. Neuronal ILD sensitivity was then examined with 50-ms-duration CF tones by holding the signal level to the contralateral (left) ear constant (approximately +20–30 dB re: threshold) and varying the level at the ipsilateral (right) ear from at least 30 dB below to 30 dB above the contralateral level in 5-dB increments. Neurons that exhibited increased firing for contralateral-favoring ILDs and decreased firing for ipsilateral-favoring ILDs were selected for further study. Each such neuron was presented with 50 repetitions of each ILD in random order (13–15 ILDs in total).

To quantify the neural ILD sensitivity within each neuron, the discharge rate as a function of ILD was fitted with a four-parameter logistic function of the form

$$rate\left(ILD\right)=y_0+\alpha /\left\{1+\exp \left[-\left(ILD-IL{D}_0\right)/\beta \right]\right\}$$ ((1)

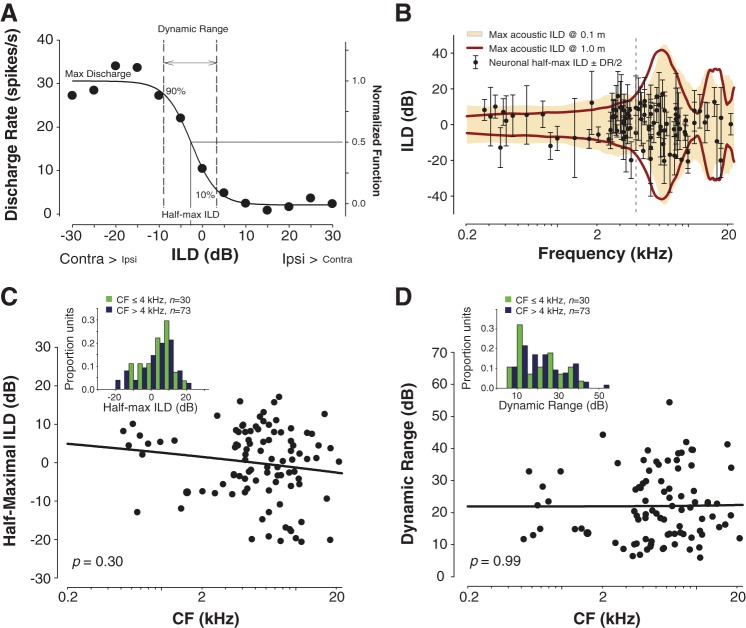
where ILD is the ILD presented, rate(ILD) is the predicted neural discharge rate, and y_o, α, β, and ILD_o are free parameters. The fitted functions accurately described the rate-ILD data (R > 0.9 in 96/103 neurons, R > 0.75 in remainder) and were used for all subsequent analyses (Fig. 2). Half-maximal ILD values were taken as the ILD at 50% of the normalized function (i.e., the inflection point; see Fig. 2A) that was fit to the discharge rate vs. ILD data for each neuron. The ILD dynamic range was taken as the difference between the ILD eliciting 90% of the maximum discharge rate and the ILD eliciting 10% of the maximum discharge rate. Note that this definition only represents 80% of the maximum discharge rate and that the range of ILDs that the neurons can actually code is even larger if the total range of discharge rates is considered (e.g., 0–100%); however, 10–90% characterizes the range of ILDs over which discharge rate is modulated nearly linearly and represents the discharge rate range over which the neuron carries the most information about ILD. The rate-ILD slope effectively gives the rate of change in firing as a function of ILD across the dynamic range (spikes·s⁻¹·dB ILD⁻¹). Collectively, the half-maximal ILD, ILD dynamic range, and rate-ILD slope capture the attributes of a neuron's response that, together with spike variance, determine its capacity to encode ILD (Tollin et al. 2008; Tsai et al. 2010; see also Fig. 3). It is important to note that the descriptive functions and parameters of interest reported here simply allow for the computation of a discharge rate and associated variance for each neuron throughout the range of ILDs tested here.

Fig. 2.

Neural sensitivity to ILDs is frequency invariant and subsumes the physiological range of acoustical ILDs. A: typical discharge rate vs. ILD neural tuning function. Raw spike rate data were fitted with a 4-parameter logistic function from which key tuning parameters were computed including half-maximal ILD—the ILD producing 50% of maximal firing—and ILD dynamic range—the range of ILDs producing 10–90% of maximal firing. For population-level analyses, firing rates were normalized. B: half-maximal ILDs and ILD dynamic ranges generally fall within the range of acoustic ILD experienced by adult chinchillas when source distance is taken into account. Bold crimson line and golden shaded region give the full range of acoustical ILD occurring across frequency for source distances of 1.0 and 0.1 m, respectively. Dashed vertical line at 4 kHz demarcates the boundary used to define nominal “low-frequency” and “high-frequency” populations of neurons (see text). C: scatterplot and power function regression of half-maximal ILD vs. frequency (bold line). Inset: histogram of half-maximal ILDs for units with characteristic frequencies (CFs) < or > 4 kHz. D: as in C, but for ILD dynamic range.

Fig. 3.

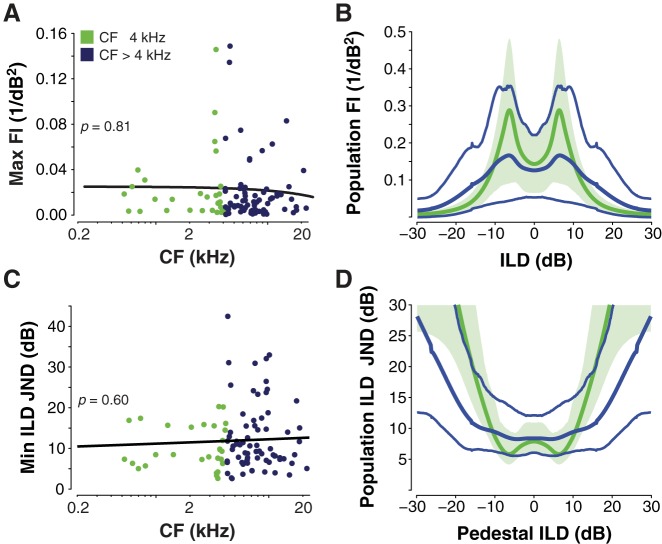
Low- and high-frequency ILD-sensitive neurons carry similar Fisher information (FI) and discriminate ILD with similar acuity. A: scatterplot and power function regression (bold line) of maximum FI across neuronal CF (see text). B: mean population FI (thick lines) for bootstrapped populations of 15 neurons; thin lines and shaded area indicate the 95% confidence intervals for FI for the high- and low-frequency neurons, respectively. Population FI is computed as the sum of FI for all neurons in the population. C: scatterplot and power function regression of neural ILD discrimination thresholds across CF (see text). JND, just-noticeable difference. D: mean population JNDs for the populations depicted by lines and shading, as in B.

Statistical Analyses

Cross-frequency analysis of neuronal ILD tuning properties.

Using the parameters obtained from Eq. 1, we assessed the relationships between neuronal ILD tuning properties and CF using 1) ordinary least-squares regression to obtain regression slopes and statistical significance (P values) for linear fits to each parameter × CF data set and 2) t-tests on the same properties for groups of “low” (≤4 kHz, n = 30) vs. “high” (>4 kHz, n = 73) CF neurons. A cutoff of 4 kHz was chosen for two reasons, both of which are motivated by studies using traditional far-field stimuli: First, Heffner et al. (1994) demonstrated in a series of psychophysical studies that chinchillas likely use ILDs for free-field sound localization only for frequencies above 4 kHz (and use ITDs below 4 kHz). Second, maximum acoustic ILDs available to the chinchilla for far-field sources are generally small (<5 dB) and relatively frequency invariant for frequencies below 4 kHz but become quite large (approaching 35 dB) and highly frequency dependent for frequencies above 4 kHz (Fig. 1; Jones et al. 2011b; Koka et al. 2011).

Fisher information computation.

We computed the Fisher information (FI) for each neuron in our sample. FI is a measure of the amount of information that neural spike count gives about a particular stimulus value, such as a single ILD, and thus quantifies the accuracy with which a stimulus is encoded via spike count (Seung and Sompolinsky 1993). Higher FI implies higher coding accuracy. Practically, this translates to a higher capacity for a neuron to discriminate, for example, two nearby values of ILD. Unlike information theoretic measures such as mutual information, which quantify information in bits, the unit of FI is simply the reciprocal of the variance of the units of interest, in this case dB ILD (i.e., 1/dB²). Thus as variance decreases (toward 0), FI increases (toward infinity). Here we used a common continuous-value approximation to FI given by

$$\text{FI}\left(ILD\right)=y\prime {\left(ILD\right)}^2/\sigma {\left(ILD\right)}^2$$ ((2)

where y′(ILD) is the derivative of the spike count with respect to the ILD and σ(ILD)² is the count variance. To facilitate analysis over a broad range of continuously varying ILDs, the fitted sigmoid function relating spike count to ILD (see above) was used to compute y′(ILD) for each neuron. Then, the ILD-dependent variance [σ(ILD)²] for each neuron was approximated by fitting a two-parameter power function of the form y = ax^b, where x is spike count and a and b are free parameters (Tsai et al. 2010). Across the ILD-sensitive neurons (n = 103), the variance vs. spike count data were well described by the power function (mean R² = 0.89 ± 0.1). The across-neuron mean exponent of the power function (parameter b) was 0.89 ± 0.22 with a mean constant (parameter a) value of 0.82 ± 0.3; these values were used for the computation of FI for all neurons. For each neuron, the count variance for any arbitrary ILD was computed by simply inputting the fitted sigmoid function into the power function relating count variance to spike count. Although we used particular parameter values for the power function, the FI results did not differ materially if a simple Poisson process was assumed for all neurons (i.e., power function parameters both equal 1.0).

RESULTS

Acoustic ILDs Depend on Sound Source Azimuth, Frequency, and Distance

Acoustic measurements were first made to characterize ILDs across source azimuth and frequency at three different source distances (1.0, 0.2, and 0.1 m; see Fig. 1A). As expected, ILDs generally increased with source azimuth and frequency, consistent with prior measurements in chinchillas (von Bismark 1967; Koka et al. 2011; Lupo et al. 2011). For a given source location and frequency, ILDs also increased with decreasing source distance; whereas ILDs were negligible at 1.0 m for frequencies <2 kHz, ILDs approached 10 dB even at 0.2 kHz for a source distance of 0.1 m (at lateral source azimuths; see Fig. 1, B and C). The acoustic ILD dynamic range for frequencies <2 kHz increased from 4–8 dB (±2–4 dB) ILD at 1.0 m to 18–24 dB (±9–12 dB) ILD at 0.1 m (i.e., a 3- to 4-fold increase). These data confirmed, consistent with measurements in other species (Brungart et al. 1999; Kim et al. 2010) and predictions from modeling (Duda and Martens 1998), that even very low-frequency sources near the head can generate large ILDs in small mammals like the chinchilla. We note, as an aside, that ILDs were only measured along the horizontal plane; near-field ILDs for lateral elevated locations (along the acoustic axis of either pinna) should be even larger than those reported here (see Koka et al. 2011). Signals originating nearer than 0.1 m from the head (e.g., reflections from the ground) would also be expected to produce even larger ILDs. Finally, ITDs varied as expected with source azimuth (e.g., Koka et al. 2011) but varied minimally with source distance (not shown; see also Kim et al. 2010).

Neural Sensitivity to ILD Covers the Full Physiological Range of ILD

To assess the extent to which low-frequency ILD information is encoded by the central auditory system, we next conducted in vivo neurophysiological experiments. A total of 359 well-isolated ICC neurons were studied in 24 adult animals, of which 103 (∼30%) were sensitive to ILD; of the total sample, 44% of high-CF (>4 kHz) and 16% of low-CF (<4 kHz) neurons were ILD sensitive. For each ILD-sensitive neuron (n = 103), ILD tuning parameters including the half-maximal ILD and ILD dynamic range were assessed (Fig. 2A; see materials and methods). Figure 2B plots these parameters for each neuron as a function of neuronal “characteristic frequency” (CF), the acoustic frequency to which each neuron was most sensitive. The ILD dynamic range indicates the ILDs over which a neuron's response was maximally modulated by the ILD cue, while the half-maximal ILD gives the midpoint ILD about which the response was modulated maximally. For comparison, the frequency-dependent ranges of maximum naturally occurring acoustic ILDs at 1.0 m and 0.1 m source distances are plotted on the same axes in Fig. 2B. A joint consideration of the half-maximal ILDs (Fig. 2C) and ILD dynamic ranges (Fig. 2D) (bold points and error bars in Fig. 2B) indicates that the coding of ILD by a population of ICC neurons generally spans the complete physiological range of ILDs. While very large ILDs (>30 dB) occurring at high frequencies appear to fall outside even the largest neuronal dynamic ranges, the illustrated dynamic ranges cover only 80% of the range over which each neuron is modulated (where the relationship between ILD and firing rate is nearly linear; see materials and methods). When a more complete range of ILDs over which each neuron is modulated (1–99%) is taken into consideration, dynamic ranges increase by an average of ∼20 dB ILD (19.1 ± 6.6 dB for CFs < 4 kHz, 19.3 ± 5.5 dB for CFs > 4 kHz; Student's unpaired t₁₀₁ = −0.1, P = 0.92). Thus some neurons are capable of encoding ILDs over a ±40 dB range.

Notably, the proportion of half-maximal ILDs falling within the acoustic range of ILDs depends on the source distance under consideration. For neurons with high (>4 kHz) CFs virtually all half-maximal ILD values fell within the range of acoustic ILDs produced at the given CF by a traditional far-field sound source (69/73, 95%; 1.0 m source distance; Fig. 2B), while for neurons with low (≤4 kHz) CFs a majority of half-maximal ILDs (18/30; ∼60%) fell at the edge (within 1 dB) or outside of this range of ILDs produced by a traditional far-field source. However, when a more ecologically comprehensive range of ILDs was considered, i.e., a range including ILDs produced by sources near the head (0.1 m; Fig. 2B), virtually all of the half-maximal ILDs fell within the range of ILDs for not only high-CF neurons (72/73; 99%) but also low-CF neurons (28/30; 93%). Two low-frequency half-maximal ILD values (2/30) fell just outside the acoustic ILD range measured at 0.1 m; it is expected that for sound source distances <0.1 m, the maximum ILDs available would be considerably larger, up to 20 dB or more (Duda and Martens 1998). Finally, we note that the acoustic ranges depicted in Fig. 2B are derived from anechoic measurements. Reflections and reverberation can introduce large ILDs at low frequencies and can also produce greater uniformity in ILDs across frequency (Młynarski and Jost 2014).

Frequency Invariance of ILD Neural Tuning Parameters

To assess the frequency dependence of neuronal ILD sensitivity, fitted tuning parameters were regressed on neuronal CF. Neither neuronal half-maximal ILD (Fig. 2C; regression slope P = 0.30) nor ILD dynamic range (Fig. 2D; P = 0.99) varied with CF. Statistical comparison of nominal “low” (<4 kHz)- and “high” (>4 kHz)-CF distributions of half-maximal ILDs (Fig. 2C, inset; Student's unpaired t₁₀₁ = 1.5, P = 0.14) and ILD dynamic ranges (Fig. 2D, inset; t₁₀₁ = −0.42, P = 0.68) further supported this conclusion. The same held true for firing rate slope, which describes the rate of change in firing across ILD (regression slope P = 0.98, low vs. high t₁₀₁ = 0.21, P = 0.83; data not shown). In other words, despite the strong frequency dependence of the magnitude of acoustic ILD cues for far-field sources, the neural coding of ILD by low- and high-frequency populations of ICC neurons appears to be frequency invariant.

Fisher Information Reveals Frequency-Invariant ILD Coding Acuity of ICC Neurons

Collectively, neural and acoustic data suggest that auditory midbrain neurons efficiently encode the full range of ILDs experienced ecologically as a function of source azimuth and distance across sound frequency. To more directly quantify the capacity of low- and high-frequency neurons to encode ecological ILD information, we next computed the FI carried by each neuron in our sample (see materials and methods; Dayan and Abbott 2001; Seung and Sompolinsky 1993). Figure 3A plots maximum FI for each unit as a function of unit CF. Maximum FI generally occurs where the spike variance is relatively low and the slope of modulation is relatively high, i.e., near the half-maximal ILD, but at a slightly lower point on the fitted spike-ILD function (see Tollin et al. 2008; a similar pattern emerges for ITD-based FI; see Shackleton et al., 2003). Consistent with the frequency invariance of the ILD-tuning parameters (Fig. 2), the maximum FI did not vary with CF (regression slope P = 0.81).

To obtain an estimate of FI carried by low- and high-frequency populations, we next computed total FI for 1,000 populations of 15 low- and high-frequency neurons, computed via 1,000-repeat bootstrapping with replacement. Figure 3B plots obtained means, representing the average of summed FI across all 15 neurons in each population, with 95% confidence bounds for low- and high-frequency populations as a function of ILD (note: neural data were obtained from the right IC; mirror symmetrical data representing the left IC are assumed). Consistent with Fig. 3A, confidence bounds for low- and high-CF populations overlap at all ILDs, indicating comparable transmission of ILD-coding FI across the ecologically relevant range of ILDs.

As a final assessment of neural ILD coding acuity across frequency, and to provide a more intuitive metric of neural ILD sensitivity, we computed single-unit ILD discrimination thresholds over the range of 30 to −30 dB ILD. Thresholds were calculated directly from the FI with the equation

$$JND\left(ILD\right)=d\prime /\surd FI\left(ILD\right)$$ (3)

where d′ is the discrimination index (Green and Swets 1966), FI(ILD) gives the Fisher information at a given ILD, and JND(ILD) defines the resultant just-noticeable difference (JND) in ILD (see Seung and Sompilinsky 1993; Tollin et al. 2008). In the present analysis, d′ was set to 1, a standard criterion in psychophysical experiments that yields 75% discrimination accuracy (Green and Swets 1966). Figure 3C plots minimum ILD JNDs for each unit as a function of unit CF, giving the best discrimination performance [which occurs across a range of reference (“pedestal”) ILDs] for each neuron. Regression analysis on these values revealed no relationship between the ILD JNDs and CF (P = 0.60), expected from the frequency invariance of FI.

Finally, Fig. 3D plots population ILD JNDs as a function of pedestal ILD for the 1,000 bootstrapped 15-neuron populations illustrated in in Fig. 3C. Mean minimum JNDs were ∼6 dB for the low-frequency population and ∼8 dB for the high-frequency population, with 95% confidence bounds overlapping at all pedestal ILDs. Minimum JNDs for both populations occurred at pedestal values near 0 dB, increasing significantly for larger pedestal values, consistent with psychophysical observations (e.g., Yost and Dye 1988). It is important to note that the value of estimated JNDs depends on the number of neurons in the sampled population: Assuming a symmetrical, unimodal distribution of FI across neurons in the total population, doubling the size of the sampled population also doubles the FI of sample population, thus decreasing JNDs by a factor of 1/√2 (see Eq. 3). For example, given bootstrapped populations of 60 neurons (4 times the 15-neuron populations considered), we would expect low- and high-frequency JNDs to decrease to 3–4 dB. Although there were not enough low-frequency neurons (n = 30) to test this prediction, repeating the bootstrapping procedure for the high-frequency population with 60-neuron populations yielded minimum population JNDs of ∼3.8 dB. The estimated ILD JND for chinchillas is ∼4 dB (see Koka et al. 2011). Collectively, our analysis of FI and FI-based neural JNDs suggests equal ILD coding acuity in low- and high-frequency populations with population JNDs on the same order as those expected behaviorally.

DISCUSSION

This study systematically compared the ILD sensitivity of auditory midbrain neurons to the physiological range of ILDs acoustically available across source azimuth, frequency, and distance in a robust auditory model, the chinchilla. The significant findings of this study are that 1) low-frequency ILD-sensitive ICC neurons, like high-frequency ILD-sensitive neurons, are sensitive to and accurately encode the large range of ILDs available ecologically as a joint function of source frequency, azimuth, and distance and that 2) low- and high-frequency ICC neurons encode ILD over comparable ranges of ILD and do so with the same acuity. In fact, the information carrying capacity of ILD-sensitive neurons, quantified via FI and derived neural ILD discrimination thresholds, was found to be frequency invariant, providing the first evidence for a neural substrate of frequency-invariant behavioral sensitivity to ILD (Grantham 1984; Mills 1960; Wakeford and Robinson 1974; Yost and Dye 1988; cf. Keating et al. 2014).

Comparison to Earlier Studies of Neural ILD Coding

In light of our findings, it is interesting to note that many studies of neural ILD coding have purposely biased their sampling of neurons to only high frequencies (typically >3–4 kHz), because these higher frequencies are where significant ILD cues are expected (Campbell et al. 2006; Irvine and Gago 1990; Nakamoto et al. 2004; Semple and Kitzes 1987, 1993; Stillman 1972; Zhang et al. 2004). Nonetheless, we are certainly not the first to report low-CF ILD-sensitive neurons, and such neurons are not rare. In fact, existing reports collectively suggest that low-frequency ILD-sensitive neurons represent a significant population across the auditory neuraxis. For example, a majority of the 168 ILD-sensitive lateral superior olive (LSO) neurons in the gerbil studied by Sanes and Rubel (1988) had CFs < 4 kHz, which prompted the authors to remark that the “. . .gerbil LSO presents a rather puzzling characteristic, containing numerous low-frequency EI neurons.” Caird and Klinke (1983) found six low-CF (<3 kHz) ILD-sensitive neurons in the LSO of cat, one of which was also sensitive to ITDs. Tollin and Yin (2005) and Tollin et al. (2008) also found low-CF LSO neurons that were sensitive to ILDs, and some of these were also sensitive to ITDs (see below). Finlayson and Caspary (1991) found that 100% of low-CF (<1.2 kHz) neurons they studied in the LSO of chinchilla were ILD sensitive. While 51% of neurons were also sensitive to interaural phase (similar to neurons described by Tollin and Yin 2005), 34% (21/61) were sensitive only to ILD. Siveke et al. (2006) found that 46/106 (43%) of low-CF (<5.4 kHz) neurons in the dorsal nucleus of the lateral lemniscus (DNLL) were sensitive to ILDs; 61% of these ILD-sensitive neurons had “best frequencies” (BFs) <2 kHz. They further reported that there were no significant differences in the ILD-coding characteristics of these low-BF and the higher-BF ILD-sensitive neurons, although 80% of low-BF neurons had their half-maximal ILDs falling outside of the physiological range of ILDs for the gerbil, according to far-field measurements (cf. Maki and Furukawa 2005).

At the level of the ICC, Brückner and Rübsamen (1995) found that nearly 30% of neurons with CFs <3 kHz in the gerbil were ILD sensitive. They further reported that the 21 neurons with CFs between 1 and 2 kHz had distributions of ILD coding characteristics (e.g., half-maximal ILD, ILD dynamic range, etc.) similar to those of the 40 neurons studied with CFs between 23 and 27 kHz. The 21 low-CF neurons had a median ILD dynamic range of 26.6 dB, slightly less than the 32.5-dB dynamic range for the high-CF neurons. The low-CF neurons had a median half-maximal ILD of −3 dB (e.g., 3 dB toward the contralateral ear). Thus, on average, the low-CF neurons in the gerbil IC would be capable of encoding ILDs of approximately ±13.3 dB. Brückner and Rübsamen (1995) stated that only 33% of the low-CF ILD-sensitive neurons had their half-maximal ILDs within a “. . .biologically relevant range of about ±5 dB. . .” and that the remaining 67% of low-CF neurons had half-maximal ILDs outside that range. Semple and Aitkin (1979) reported that ∼11% of low-CF neurons in the cat ICC were ILD sensitive. Perplexed, they stated that while one might expect ILD units to have high BFs, “. . .this argument cannot explain why EI units are found in larger proportion. . .” in the rostral portion of the ICC where low-CF neurons predominate. Chase and Young (2005) reported 21 low-CF (<4 kHz) neurons in the cat ICC that were sensitive to ITD and/or ILD. They went on to note specifically that some of these neurons were “. . .sensitive to ILD cues in the absence of ITD sensitivity, despite the small size of physical ILD cues at low frequencies.” Finally, at the level of the auditory cortex, Benson and Teas (1976) reported that 34 of 72 ILD-sensitive neurons (47%) in the chinchilla had a CF ≤4 kHz and that these neurons could encode ILDs of up to ±20 dB. Benson and Teas further showed that slopes of the rate vs. ILD functions, their so-called “discrimination index,” were invariant with sound frequency (correlation coefficient r = 0.08) and went on to state that “. . .when units were categorized according to their sensitivity to ΔI parameters, units with low best frequencies were just as sensitive as those with high best frequencies.”

Finally, many studies of ILD coding have demonstrated that neural sensitivity to ILD can depend on the overall sound level. While ILD coding by neurons in the LSO is highly dependent on overall sound level, neurons in the ICC have been shown to be more robust (invariant in their response) to changes in sound level (see Tsai et al. 2010 for review). Since we did not manipulate overall sound level in these experiments, we cannot speculate how our results would change across a range of overall levels. However, based on prior studies we would expect ILD coding to persist in many ICC neurons across a range of sound levels (see Tsai et al. 2010).

Accounting for the Paradox of Low-Frequency ILD Sensitivity

The existence of robust low-frequency ILD sensitivity in the auditory brain stem, midbrain, and cortex, and indeed in behavior (e.g., Mills 1960), is no longer paradoxical when data are examined with respect to more comprehensive measurements of acoustical ILDs. Indeed, the duplex theory view of ILD as an exclusively high-frequency cue, and the consequent bias in the study of ILD throughout the literature (e.g., in sampling of binaural neurons across frequency or in psychophysical stimulus design), is based on acoustic measurements of ILD for far-field sound sources in unnatural, noise- and reflection-free environments. In fact, large low-frequency ILDs can be produced under a number of different ecological conditions. For example, our acoustic data (Fig. 1) and existing data from other species (e.g., human: Brungart et al. 1999; rabbit: Kim et al. 2010) demonstrate that low-frequency ILDs increase substantially as the source-to-observer distance decreases. For sources near the head (e.g., 0.1 m), the range of ILDs experienced by the chinchilla can be >20 dB. Moreover, even for far-field sources, large low-frequency ILDs can be produced in reverberant or multisource environments, or by acoustic reflections from the ground (e.g., Młynarski and Jost 2014; Gourevitch and Brette 2012).

In a recent study, Młynarski and Jost (2014) analyzed the statistics of binaural cues in long-duration recordings from natural environments that included multiple, overlapping sound sources, reverberation, etc. and found that the auditory system is exposed to a similar distribution of ILDs across all frequencies, including relatively large values (>10 dB) in the lower frequencies. Thus, whereas a traditional understanding of sound localization based in the duplex theory (Strutt 1907) holds that there should be very few low-frequency ILD-sensitive neurons, and that any such neurons should have receptive fields constrained to the small range of ILDs generated by distal low-frequency sources, a modern understanding of sound localization should take into account the occurrence of large low-frequency ILDs that are regularly experienced in real-world environments and the high acuity with which such ILDs are encoded by auditory neurons. In fact, recognizing the prevalence of low-frequency ILDs suggested by recent measurements, ecological and efficiency principles (Attneave 1954) also predict the existence of low-frequency ILD-sensitive neurons, in opposition to the duplex theory.

While some of the studies discussed above have speculated on possible roles for low-frequency ILD-sensitive neurons in spatial hearing, none has systematically explored their functional significance in the context of the physiologically relevant acoustical cues available. At the same time, low-frequency ILDs and their encoding are assumed by many models of predominantly low-frequency binaural psychophysical phenomena. For example, models of the binaural-masking-level difference assume a subtractive process, including the equalization-cancellation model (Breebaart et al. 2001; Durlach 1963; Green 1966). Models of binaural speech segregation (Culling and Summerfield 1995) and the illusory binaural pitches (Huggins, binaural edge, and Fourcin) require subtractive mechanisms (Akeroyd and Summerfield 2000; Culling et al. 1998a, 1998b; Fourcin 1970). Models incorporating subtraction from the two ears have been able to account for phenomena not easily explained by Jeffress-like EE interaction (de Cheveigné 1993; Hartmann and Zhang 2003; Tollin and Henning 1999).

Possible Interactions Between ILD and Other Spatial Cues

Importantly, although we did not manipulate ITD cues during neural recordings, many low-frequency ILD-sensitive neurons in both the brain stem and midbrain are also sensitive to ITD (Chase and Young 2005, 2006; Finlayson and Caspary 1991; Siveke et al. 2006; Tollin and Yin 2005). It is thus conceivable that some of these units' ILD tuning could be altered by concomitant ITD. However, not all low-frequency ILD-sensitive neurons are influenced by ITDs, as demonstrated by Finlayson and Caspary (1991) (see above) in the LSO and by Chase and Young (2005) in the ICC. Multiple studies have demonstrated ILD sensitivity at the level of the ICC that originates via multiple pathways, some of which bypass the LSO entirely (e.g., Pollak 2012), where joint ITD and ILD sensitivity first arises (Tollin and Yin 2005). Psychophysical studies have also demonstrated low-frequency ILD sensitivity that does not depend on ITD. For example, Hartmann and Constan (2002) demonstrated that ILD discrimination thresholds in humans were comparable (and <1 dB) whether low-pass filtered (<1 kHz) noise presented to the two ears was correlated or uncorrelated. In some cases, large ILDs (like those present for near-field low-frequency sources) can significantly modulate neural ITD sensitivity, shifting ITD tuning toward more contralateral leading values with increasing intensities in the contralateral ear (Kuwada and Yin 1983; Smith and Delgutte 2008; see Palmer et al. 2007 for review). In neurons sensitive to both ITD and ILD, changes in source distance at a fixed azimuth, e.g., as would occur for a directly approaching source, could lead to significant modulation of firing. Such joint ITD-ILD coding could, in combination with traditional distance cues such as intensity and direct-to-reverberant energy ratio, provide robust coding of source location (Zahorik 2002).

Finally, low-frequency ILD sensitivity may also be useful in reverberant environments, wherein behavioral and neural sensitivity to ITD is significantly degraded (Devore and Delgutte 2010; Rakerd and Hartmann 1985). Kuwada et al. (2014) recently characterized effects of reverberation on virtual spatial sensitivity and envelope synchronization in neurons of the rabbit ICC for virtual source distances from 0.1 m to 1.6 m. The spatial tuning of low-frequency neurons was less degraded by reverberation for smaller source distances, where the direct-to-reverberant ratio was higher and larger ILDs were ostensibly available, but tuning to individual spatial cues (ITD and ILD) was not measured. Indeed, a comprehensive understanding of the cues that enable robust coding of sound location across sound frequency, azimuth, and distance will require measurement of both ITD and ILD sensitivity, along with HRTF-based spatial sensitivity, in large populations of neurons, and likely in multiple species, given cross-species variations in ITD and ILD neural and behavioral sensitivity (e.g., Grothe et al. 2010). Nonetheless, the present findings, together with existing psychophysical data (Mills 1960), predict a significant role for low-frequency ILDs in spatial hearing, and invite further reconsideration of the duplex theory.

GRANTS

This research was supported by National Institutes of Health Grants R01-DC-011555 (D. J. Tollin), T32-HD-041697 (H. G. Jones), F31-DC-011198 (J. L. Thornton), and F32-DC-013927 (A. D. Brown).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: H.G.J., K.K., and D.J.T. conception and design of research; H.G.J., K.K., and J.L.T. performed experiments; H.G.J., A.D.B., and K.K. analyzed data; H.G.J., A.D.B., and D.J.T. interpreted results of experiments; H.G.J. and A.D.B. prepared figures; H.G.J. drafted manuscript; H.G.J., A.D.B., and D.J.T. edited and revised manuscript; H.G.J., A.D.B., K.K., J.L.T., and D.J.T. approved final version of manuscript.