Simulating the Distance Distribution between Spin-Labels Attached to Proteins

Abstract

EPR/DEER spectroscopy is playing an increasingly important role in the characterization of the conformational states of proteins. In this study, force field parameters for the bifunctional spin-label (RX) used in EPR/DEER are parametrized and tested with molecular dynamics (MD) simulations. The dihedral angles connecting the C_α atom of the backbone to the nitroxide ring moiety of the RX spin-label attached to i and i + 4 positions in a polyalanine α-helix agree very well with those observed in the X-ray crystallography. Both RX_i,i+4 and RX_i,i+3 are more rigid than the monofunctional spin-label (R1) commonly used in EPR/DEER, while RX_i,i+4 is more rigid and causes less distortion in a protein backbone than RX_i,i+3. Simplified dummy spin-label models with a single effective particle representing the RX_i,i+3 and RX_i,i+4 are also developed and parametrized from the all-atom simulations. MD simulations with dummy spin-labels (MDDS) provide distance distributions that can be directly compared to distance distributions obtained from EPR/DEER to rapidly assess if a hypothetical three-dimensional (3D) structural model is consistent with experiment. The dummy spin-labels can also be used in the restrained-ensemble MD (re-MD) simulations to carry out structural refinement of 3D models. Applications of this methodology to T4 lysozyme, KCNE1, and LeuT are shown to provide important insights about their conformational dynamics.

Introduction

Accurate structural information about the accessible conformations of proteins is key to understanding their function. This information is typically best obtained from high resolution X-ray crystallography or nuclear magnetic resonance (NMR) spectroscopy. X-ray crystallography relies on the successful crystallization of proteins, while NMR yields structural information for small proteins only. As an alternative, experimental biophysicists have been increasingly relying on electron paramagnetic resonance (EPR) spectroscopy, which provides structural information for large and complex protein systems in their native like environment. EPR spectroscopy requires the introduction of spectroscopic probes into the system via site-directed spin-labeling (SDSL)¹ techniques. The EPR technique along with spin-labeling probes has proved to be a very useful technique in characterizing the structure–function relationship of membrane proteins, such as ion channels and transporter proteins, as well as enzymes and receptors. Double electron–electron resonance (DEER) is a powerful-pulsed EPR technique that reports the distance distribution between a pair of spin-labels. DEER can detect spin-labels that are separated by distances as large as 80 Å. Since the spin-pair distance distribution may change with the change in conformational states, information about the three-dimensional (3D) structure and function of a protein in its native environment can be obtained from EPR/DEER spectroscopy.

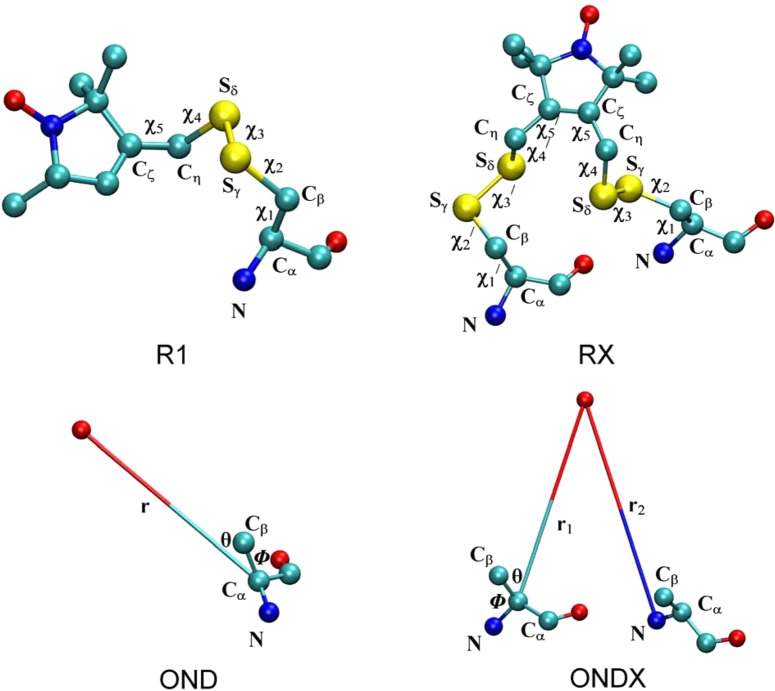
Although EPR/DEER is a very powerful technique, interpretation of the spin-label distributions is complicated by several factors. One of the main problems is the extremely flexible nature of the spin-label probes used in most EPR/DEER experiments. The commonly used nitroxide spin-label is MTSSL (1-oxyl-2,2,5,5-tetramethylpyrroline-3-methylmethanethiosulfonate) which is typically linked to a cysteine residue in the protein through a disulfide bond (R1 in Figure 1). The R1 spin-label possesses five dihedral angles denoted by χ₁, χ₂, χ₃, χ₄, and χ₅ along the flexible bonds, C_α–C_β–Sγ–Sδ−Cη–Cζ, and each of these dihedral angles has multiple rotameric states. The dihedral angles χ₁ and χ₂ can adopt 3-fold conformations, +60° (or gauche+), 180° (or trans), and −60° (or gauche), which are denoted by p, t, and m, respectively, and the dihedral angle χ₃ can adopt two stable conformations, p (+90°) and m (−90°). Computational analysis and spectroscopic measurements indicate that χ₄ and χ₅ are very flexible, which is also consistent with the fact that no reliable X-ray crystallographic information is available for these dihedral angles. One advantage of the flexibility of R1, however, is that it can be introduced at any site within a protein including buried regions. Often the EPR/DEER histograms are broad and bimodal with multiple peaks, which also make it difficult to interpret the experimental histograms in terms of protein structure refinement. Hubble and co-workers recently introduced MTSSL linked through two disulfide bonds (RX in Figure 1).² The bifunctional RX spin-label can be introduced at pairs of cysteine residues at i, i + 3 and i, i + 4 positions in an α-helix and i, i + 1 and i, i + 2 positions in a β-strand. The RX spin-label side chain has a total of 10 dihedral angles with five dihedrals, denoted by χ₁, χ₂, χ₃, χ₄, and χ₅, in one of the cysteine linkers and the remaining five dihedrals, denoted by χ₁′, χ₂′, χ₃′, χ₄′, and χ₅′, belonging to the second cysteine linker. Only one crystal structure of the RX side chain attached to positions 115 and 119 in an α-helix of T4 lysozyme is available, which displayed all 10 dihedral angle values suggesting the RX is more rigid than the R1.² The EPR/DEER spin-pair distance distributions obtained from RX are also found to be narrower than R1, even in various reaction mediums such as the micelles, proteo-liposomes, and lipodisq.³ Therefore, the analysis of the spin-pair distributions from the RX spin-label is expected to be easier than those obtained from the R1, suggesting the RX could be an important alternative to the R1 in the EPR/DEER spectroscopy. However, RX may introduce unwanted perturbations in the system due to the necessity to introduce two nearby cysteines. There remains not only a scarcity of reliable experimental data, but there also has been no computational study to understand the accessible rotameric states and the distance distributions of the RX spin-pairs in various sites in protein. Interpreting the EPR/DEER distance histogram data obtained from the RX inserted at various positions in proteins requires careful characterization of the dynamical properties of this spin-label. Computational methodologies can provide valuable insights about the dynamical properties of these spin-labels. In the case of R1, quantum mechanical ab initio methods offered very accurate energetics for various conformational states of R1.⁴⁻⁶ However, these methods are generally computationally too demanding for large protein systems and they ignore thermal fluctuations. Molecular dynamics (MD) simulations based on classical force fields offered a realistic alternative strategy to understand the conformational dynamics of the R1 spin-labels.^7,8 The results obtained from the MD simulations were consistent with the available information from X-ray crystallography.⁹ It is expected that MD simulations will also provide valuable information about the conformational dynamics of RX spin-labels inserted at various positions in a protein.

Figure 1.

Spin-label side chains, R1 and RX, resulting from linking MTSSL to cysteine through a disulfide bond, and dummy spin-labels, OND and ONDX, which mimics the dynamics of the R1 and RX, respectively. In the case of ONDX, X = 3 or 4 depending on the position of the second cysteine residue to which it is attached. The dihedral angles connecting the C_α atom of the protein backbone to the nitroxide ring are shown for both R1 and RX. OND is parametrized by using the C_α–ON distance, C_β–C_α–ON angle, and N–C_α–C_β–ON dihedral angle, while one more variable, the ON–N_i+3/i+4 distance from the second residue, is used to parametrize ONDX.

Accurate structural information on a protein is obtained from its 3D structure, which is not possible to obtain directly from EPR/DEER observations. However, computational tools can provide a “virtual route” to link the atomic 3D structures of proteins to the experimental EPR observations. Recently, a novel computational method, the restrained-ensemble (re-MD) method,^9,10 was developed following a maximum entropy principle¹¹ to help refine the 3D structural model on the basis of DEER histrograms. The re-MD simulations were used to refine the outer vestibule of the KcsA ion channel protein¹² and the LeuT transporter protein.¹³ The elastic network model in combination with MD simulation was also used to obtain structural models that satisfy EPR/DEER distance data.^14,15 There are also computational modeling methods, such as the multiscale modeling of macromolecular systems (MMM) software package of Yevhen Polyhach and Gunnar Jeschke^16,17 and the PRONOX algorithm of Hatmal et al.¹⁸ The MtsslWizard computational program of Hagelueken et al.¹⁹ provides interlabel distance distributions based on the analysis of spin-label rotamers inserted in a model protein structure.

In the present study, MD simulations were performed to characterize the conformational dynamics of spin-labels RX_i,i+3 and RX_i,i+4 in a polyalanine α-helix. Force field parameters for the RX spin-labels have been developed, and the results from the simulations were compared to available X-ray crystallographic structures. Using the vast amount of information obtained from the simulations of RX_i,i+3 and RX_i,i+4, simplified nitroxide dummy spin-labels, OND3 and OND4, respectively, are parametrized for the purpose of structural refinement. A simplified computational approach based on MD simulation of the dummy spin-labels (MDDS) has been presented which is demonstrated to provide better spin-pair distance distributions than the existing computational methods.¹⁶⁻¹⁹ The MDDS simulations have been conducted on spin-labeled T4 lysozyme,²⁰ KCNE1,²¹ and LeuT^22,23 protein systems. The results of the simulation suggest that MDDS simulations offer an effective strategy for obtaining important insights about the structure and function of various protein systems.

Methods

All molecular dynamic simulations of the spin-labeled polyalanine α-helix, T4 lysozyme, KCNE1, and LeuT were carried out with the CHARMM²⁴ and program package using the all-atom CHARMM36 protein force field²⁵ with the CMAP corrections and the force field parameters of R1 developed by Sezer et al.,⁷ the OND developed by Islam et al.,⁹ and the RX and ONDX developed in this study.

Molecular Dynamics Simulations of the Polyalanine α-Helix Labeled with RX

Two different systems of the polyalanine α-helix, which has a total of 18 alanine residues, is labeled at positions 8, 12 and 8, 11 with the RX spin-label, where 8, 12 and 8, 11 represent residues at positions i, i + 4 and i, i + 3, respectively. Both of the systems have a total of 232 atoms which are solvated by 7155 TIP3P water molecules within a 40 × 40 × 40 ų cubic box, and the salt concentration was maintained at 0.15 mM/mol by adding 7 potassium and 7 chloride ions. A weak positional harmonic restraint with a force constant of 0.5 (kcal/mol)/Ų was used on residues 1–5 and 15–18 for the system labeled with 8-12RX and on residues 1–5 and 14–18 for the system labeled with 8-11RX to avoid any large displacement. A 1 ns equilibration simulation and a 10 ns production MD simulation were performed with an integration time step of 1 fs. Both equilibration and production simulations were performed under NPT conditions where the temperature was kept at 300 K and the pressure at 1 atm. The simulations were performed with a Langevin thermostat to control the temperature of the simulation box. A collision frequency, γ, of 5.0 ps^–1 was used for the Langevin thermostat. A dielectric constant of 1.0 was used during the simulation. Bonds involving hydrogen atoms in water were constrained to their equilibrium values using the SHAKE algorithm. Periodic boundary conditions (PBCs) were imposed, and the nonbonded interactions were smoothly switched off from 10 to 12 Å using an atom-based cutoff. Long-range electrostatic behavior was controlled with the particle mesh Ewald (PME) method. A spherical harmonic restraint with a force constant of 1 kcal/mol was used to keep the center of mass of the backbone atoms of the systems near the origin of the box. From the two all-atom simulations, the force field parameters for the OND3 and OND4 are developed which are subsequently attached at positions 8, 12 and 8, 11 in the polyalanine α-helix. 500 ps equilibration and 5 ns MD production simulations were then carried out on these two systems using the same simulation parameters used in the all-atom simulations, and the statistics for various degrees of freedom involving the dummy spin-labels were compared with those obtained from the all-atom simulation.

Molecular Dynamics with Dummy Spin-Labels (MDDS)

To predict the spin-pair distance distributions of various labeled sites in T4 lysozyme, KCNE1, and LeuT, MD simulation with dummy spin-labels (MDDS) were carried out by attaching the mono- and bifunctional spin-labels, OND and OND4, respectively, in various sites in these proteins for which EPR/DEER data is available. Crystal structures of T4 lysozyme (2LZM),²⁰ KCNE1 (2K21),²¹ and LeuT (2A65,²²3TT1,²³ and 3TT3(23)) were used to construct the geometries of the T4 lysozyme, KCNE1, and LeuT systems for simulation. For all the simulations, the dummy spin-labels were attached directly with the C_α atom of the protein backbone and long side chain residues were truncated after the C_β atom to avoid steric clashes with the ON labels. Truncating long side chains will not cause any drastic change in the distance distribution, since the dummy spin-label force field has a nonbond term that accounts for the influence of nearby side chains. First, two systems of T4 lysozyme are constructed each labeled with OND and OND4 at positions 109/131 and 109–113/127–131, respectively, and two systems of KCNE1 are constructed each labeled with OND and OND4 at positions 47/66 and 46–50/66–70, respectively. Since the dummy spin-labels do not interact with each other, multiple dummy atoms can be introduced to a single protein structure. Since 37 sites in total were experimentally labeled in T4 lysozyme, all of these sites were labeled with OND into a single T4 lysozyme. Similarly, the dummy OND spin-labels were linked directly to the C_α atoms of the three PDB structures of LeuT at all residues included in the EPR/DEER mutant data set. All of the simulations were performed in a vacuum under NVT at 300 K using the Langevin thermostat with a collision frequency of 10.0 ps^–1. To begin, an adopted basis Newton–Raphson (ABNR) energy minimization (100 steps) and a short (10 ps) molecular dynamics simulation of the dummy ON spin-labels were performed with a time step of 0.5 fs by fixing the coordinates of all other atoms of the protein to its X-ray crystallographic structure. Finally, a 1 ns equilibration simulation and a 4 ns production MD simulation were performed by fixing the protein and using a time step of 1 fs from which the spin-pair distance distributions were calculated.

Restrained-Ensemble (re-MD) Simulation

The restrained-ensemble (re-MD) simulation^9,10 is used to match the distance distribution obtained from multiple copy spin-labels to match with those obtained from EPR/DEER distance distribution data. In this study, the dummy bifunctional spin-label OND4 was attached to positions 109–113 and 127–131 in T4 lysozyme. An ensemble of 25 replicas of OND4 was created for each of 109–113OND4 and 127–131OND4 (Figure S7, Supporting Information), which yield a total of 625 distances. An energy restraint was imposed via a large force constant, 10000 (kcal/mol)/Ų, at every step of the MD simulation so that the histogram obtained from the 625 spin–spin distances would match the experimental distance histogram obtained from the EPR/DEER. Large displacements of the protein backbone atoms were prevented by applying positional restraints with a harmonic force constant of 1 (kcal/mol)/Ų relative to the X-ray structure. To reduce the size of the simulated system, only the water molecules within 35 Å from the center of mass of the T4L system were kept, for a total of 19410. A spherical half-harmonic containing restraint with a force constant of 0.5 (kcal/mol)/Ų was used to keep the waters near the proteins. Both equilibration and production simulations were performed under NVT conditions where the temperatures for both replica OND4 atoms and normal atoms were kept at 300 K. The rest of the simulation parameters were kept the same as those used in the MDDS simulations. The dummy spin-labels were minimized using steepest decent and subsequently conjugate gradient algorithms. Finally, 1 ns equilibration and 5 ns re-MD simulation was performed.

Results and Discussion

Force Field Parameterization of the RX Spin-Label Side Chain

Sezer et al.⁷ previously developed force field parameters for the nitroxide ring moiety and the spin-label linker of the R1 spin-label side chain (Figure 1, R1). Force field parameters for the RX spin-label side chain were developed as an extension of the previous work. RX is linked to the protein with an additional linker, which has the same atom types as the first linker. Therefore, modification and duplication of several atom types and a patch command, which links the second linker of RX with the protein, were only required to develop the force field parameters of the RX spin-label side chain. All the force field parameters for RX and the corresponding patch command are uploaded in CHARMM-GUI (http://www.charmm-gui.org),²⁶ which can readily build a system with the RX in i, i + 2, i, i + 3, and i, i + 4 or custom positions in a protein for a molecular dynamics simulation. The performance of the RX force field parameters was then evaluated by comparing the X-ray crystal structures of the RX with those obtained from a long MD simulation.

Comparison with X-ray Structure

The dihedral angles connecting the C_α atom of the backbone with the nitroxide ring of the RX_i,i+3 and RX_i,i+4 spin-labels were calculated from the MD simulation of the labeled polyalanine α-helix. The time dependence of all the dihedral angles is provided in Figures S1 and S2 (Supporting Information). The dihedral angles in RX_i,i+4 obtained from the simulation are found to be very similar to those observed in the X-ray crystal structure of 115–119RX attached with T4 lysozyme (Table 1). The information reported in Table 1 for RX_i,i+4 remains unchanged when the trajectory is extended to 100 ns (see Figure S9 in the Supporting Information).

Table 1. Comparison of the Dihedral Angles (in Degrees) Connecting the C_α Atom of the Backbone with the Nitroxide Spin of the RX_i,i+4 and RX_i,i+3 Obtained from the X-ray Crystallography and the MD Simulation.

	χ1	χ2	χ3	χ4	χ5	χ1′	χ2′	χ3′	χ4′	χ5′
X-raya (RXi,i+4)	–94	–61	–81	–160	105	–70	–56	106	122	–90
MD (RXi,i+4)	–80	–65	–85	177	97	–60	–50	92	142	–97
MD (RXi,i+3)	–60	–70	90	170	–110	–70, −170	144	80	165	72

^aFleissner et al.²⁷

To be consistent with the convention used to represent rotamers in R1 (see R1 and RX in Figure 1), the conformations of the dihedral angles χ₁, χ₁′, χ₂, χ₂′, χ₄, and χ₄′ are denoted with p, t, and m to represent +60° (or gauche⁺), 180° (or trans), and −60° (or gauche^–), respectively, and the conformations of dihedral angles χ₃, χ₃′, χ₅, and χ₅′ are denoted with p and m around +90 and −90° (=270°), respectively. Both X-ray²⁷ and MD simulations show that spin-label linker i has the mmmtp rotamer along the dihedral angles χ₁, χ₂, χ₃, χ₄, and χ₅, respectively, while the dihedral angles χ₁′, χ₂′, χ₃′, χ₄′, and χ₅′ accommodate the mmptm rotamer at linker i + 4 of RX_i,i+4. There is no crystal structure for RX_i,i+3. MD simulation of the RX_i,i+3 reveals that the linker i has the mmptm rotamer along the χ₁, χ₂, χ₃, χ₄, and χ₅, respectively, while the linker i + 3 has mtptm and ttptm rotamers along the χ₁′, χ₂′, χ₃′, χ₄′, and χ₅′, respectively. χ₁′ has two rotameric states, m and t, with percent rotamer populations of 74 and 26, respectively. Comparison of the rotameric states of RX_i,i+3 and RX_i,i+4 shows a difference in rotameric states at χ₃, χ₅, χ₁′, and χ₅′. The helical shape of the backbone to which the RX_i,i+4 is attached shows very little change compared to the wild type; however, deviation from the helical geometry is observed for the RX_i,i+3 near residue i. The greatest difference is found along the N–C_α–C–N dihedral angle (ψ_i), with the average value of ψ_i differing by about 37° from that of the wild type (see Figure S3, Supporting Information). These observations suggest that the structure of protein will be less disrupted by labeling with RX_i,i+4 than RX_i,i+3 and therefore RX_i,i+4 is a better choice than RX_i,i+3.

Comparison of the Dynamics of R1 and RX

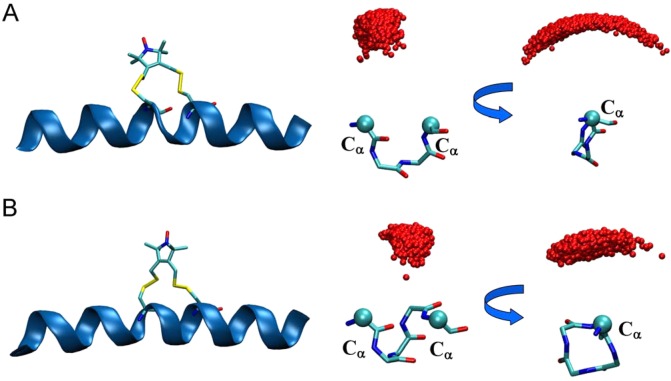
In reality, the EPR/DEER signal originates from the unpaired electrons of the nitroxide atoms (ON) of the R1 and RX. Only a detailed understanding of the position and dynamics of the ON atom would be able to provide important structural insights and function of various conformational states of the protein. Due to the existence of five dihedral angles connecting the nitroxide ring moiety with the C_α atom of the protein backbone, the exact position of the ON with respect to the backbone of the protein is difficult to predict. Small changes in the rotamer population could also cause the position of the ON to change substantially. Long MD and restrained-ensemble (re-MD) simulations of R1 labeled at various sites in T4 lysozyme displayed that the ON atoms with respect to the N, C_α, and C_β atoms of the labeled residues are distributed within a half-sphere around the C_α atom of the backbone (see Figure S4, Supporting Information).⁹ The configurations of the ON atoms of the RX_i,i+4 and RX_i,i+3 obtained from the MD simulation of the polyalanine α-helix show that the distribution of ON atoms for both of the RX spin-labels is very constrained (Figure 2 A and B). Interestingly, the configuration of ON atoms of the RX_i,i+3 is more distributed in the phase space than that of the RX_i,i+4. This again illustrates that the labeling with RX_i,i+4 would be a better choice than RX_i,i+3 to interpret the EPR/DEER experimental data.

Figure 2.

Polyalanine α-helix with (A) RX_i,i+3 and (B) RX_i,i+4 (left panel) and the corresponding dynamics of the nitroxide oxygen of the respective RX with respect to their C_α atoms obtained from MD simulation (right panel).

Simplified Representation of the Spin-Labels for Structural Refinement

While the detailed atomic models of the spin-labels R1 and RX provide valuable information, their utilization in the context of structural refinement of proteins is somewhat difficult. Fairly long MD simulations may be required to allow for the conformational transitions to adequately sample all the accessible rotameric states of the spin-labels attached to a protein. This can become a cumbersome task that detracts from the central goal of computations carried out in the context where one tries to make the best use of EPR/DEER data. To circumvent this issue, a simplified spin-label side chain, OND (OND in Figure 1), was designed to reproduce the 3D spatial distribution of the nitroxide oxygen of R1 relative to the protein backbone in all-atom RE-MD simulations of T4 lysozyme based on experimental EPR/DEER data.⁹ Optimal Lennard-Jones parameters of R_min = 4 Å and E_min = −0.05 kcal/mol were determined for R1 on the basis of the observed radial distribution of the ON atom relative to any protein atom.⁹ It should be emphasized that, although force field parameters are involved in defining the simplified dummy spin-labels, the latter are not true atomic models. Conceptually, the dummy particle attached to the backbone is only a statistical construct. Its purpose is to represent the average 3D spatial distribution of the nitroxide atom as it was extracted from the all-atom simulations restrained by 51 EPR/DEER distance histogram data from spin-labels inserted at 37 different positions in T4 lysozyme.⁹ Thus, the resulting simplified model incorporates a great amount of detailed information about atomic spin-labels, though in a statistical average way. For example, the notion of rotameric states is no longer relevant, and specific interactions with nearby side chains are not taken into account directly (apart from the single Lennard-Jones center ascribed to the ON atom). While various subtle effects may have some importance for the configuration of the nitroxide spin-labels at specific sites in a given protein, comparison with EPR/DEER data demonstrates that the simplified spin-label models are generally able to capture the dominant features needed for the purpose of structural refinement based on EPR/DEER data.

In the present study, force field parameters for simplified dummy spin-labels, OND3 and OND4 (ONDX in Figure 1), representing the all-atom RX attached to i, i + 3 and i, i + 4, respectively, were developed from five potential energy functions

1

where V_r1, V_r2, V_θ, V_ϕ, and V_nonbonded are the C_α–ON bond (r1), the ON–N_i+3/4 bond (r2), the C_β–C_α–ON angle (θ), the N–C_α–C_β–ON dihedral angle (ϕ), and the Lennard-Jones 6-12 potential representing the interactions between the ON particle and the rest of the protein, respectively. The force constants for the r1, r2, θ, and ϕ are calculated from the all-atom simulations of RX_i,i+3 and RX_i,i+4 attached to the polyalanine α-helix.

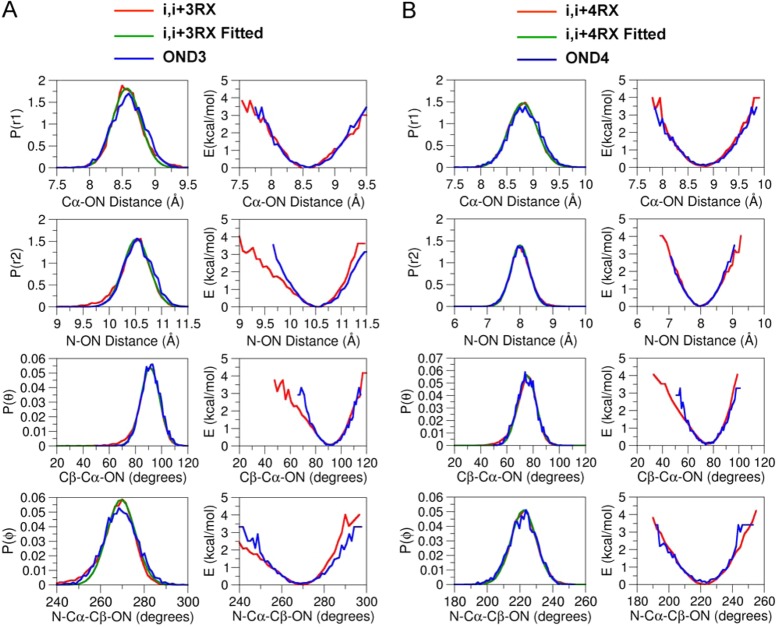
The distributions over r1, r2, θ, and ϕ for both RX_i,i+3 and RX_i,i+4 extracted from the MD simulation are shown in Figure 3 (red line). For the RX_i,i+3 and RX_i,i+4, the probability of finding the ON is maximum at a distance of about 8.5 and 8.8 Å, respectively, from the C_α and the widths for both of the distributions are about 1.5 Å. The probability of finding the ON is maximum at a distance of about 10.5 Å from N_i+3 in RX_i,i+3, while it is about 7.9 Å from N_i+4 in RX_i,i+4. The widths for both of the distributions are about 1 Å. The distributions for the θ for both the RX_i,i+3 and RX_i,i+4 range from 50 to 120°, but they peak at around 91 and 72°, respectively. There is one predominant rotameric state for the dihedral angle ϕ, positioned around 240–300 and 180–260° for both RX_i,i+3 and RX_i,i+4, respectively, which peak around 267 and 222°, respectively.

Figure 3.

Comparison of distribution and the potential of mean force of the distances, angle, and dihedral angle obtained from MD simulations with RX and dummy nitroxide atoms at positions (A) i, i + 3 and (B) i, i + 4 of the polyalanine α-helix.

The probability distribution functions are then modeled on the basis of four simple energy terms, V_r1 = k_r1(r₁ – r₀)², V_r2 = k_r2(r₂ – r₀)², V_θ = k_θ(θ – θ₀)², and V_ϕ = k_ϕ(1 + cos(nϕ – ϕ₀)), where k_r1, k_r2, k_θ, and k_ϕ are the force constants for the r₁ distance, the r₂ distance, the θ angle, and ϕ dihedral potentials and n represents the dihedral multiplicity. In addition, a Lennard-Jones 6-12 potential was used to account for the excluded-volume interactions between the ON particle and the rest of the protein. The nonbond parameters previously determined for R1 are used for the OND3 and OND4 particles in the simplified representation of the double-link RX spin-label.⁹ As for R1, the models can only account for interactions with neighboring protein groups in a highly simplified manner. Nevertheless, this is not a concern here, since the double-linked spin-label is highly constrained by the two disulfide (S–S) bonds. Nonbonded interactions between the ON particles and the water molecules are switched off by using the keyword NBFIX in the parameter file, which can be read by both the NAMD²⁸ and CHARMM²⁴ program packages. The probability distributions obtained from the MD simulation of the dummy and all-atom spin-labels agree very well (Figure 3). The optimal force constants for k_r1, k_r2, k_θ, and k_ϕ are 4.8 (kcal/mol)/Ų, 3.78 (kcal/mol)/Ų, 13.9 (kcal/mol)/rad², and 29.6 (kcal/mol)/rad², respectively, for the OND3 and 3.35 (kcal/mol)/Ų, 3.5 (kcal/mol)/Ų, 15.21 (kcal/mol)/rad², and 21.0 (kcal/mol)/rad², respectively, for the OND4.

Both OND3 and OND4 force field parameters could be attached directly to the C_α atom of any wild-type residue except glycine, since glycine does not have the C_β atom. To tackle this problem, the concept of the dummy C_β atom (CBD) is used only in the case of glycine. The CBD atom only connects to the C_α atom and does not interact with any other atom of the protein. The CBD is defined with three variables—the C_α–CBD bond, the N–C_α–CBD angle, and the H–N–C_α–CBD dihedral angle (see Figure S5 in the Supporting Information). The parameters for these three variables were taken from the parameters that define the C_β atom in the CHARMM36 protein force field.²⁵ All of the force field parameters for the OND3, OND4, and CBD are available in the CHARMM-GUI webpage. The simplified spin-labels can be inserted in all of the sites in a protein for the calculation of spin-pair distance distributions. The simplified representation of the all-atom spin-labels avoids the burdensome task of accounting for a large ensemble of Boltzmann-weighted spin-label rotamers of the all-atom spin-labels.

Molecular Dynamics of Dummy Spin-Labels (MDDS)

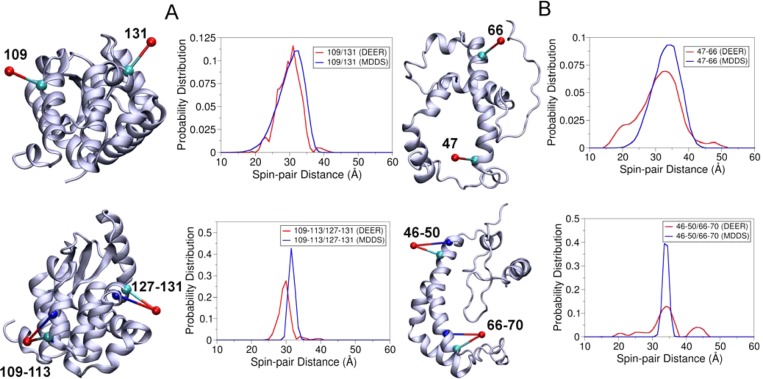
Having parametrized the OND and ONDX dummy spin-labels, it was necessary to check their performance in predicting the spin-pair distance distributions. EPR/DEER spin-pair distance distributions involving both the R1 and RX are available only for two protein systems, the T4 lysozyme^9,27 and the integral membrane protein KCNE1.³ In the case of T4 lysozyme, spin-pair distance distributions are available between 109R1 and 131R1, represented here with 109/131R1, and between 109 and 113RX and 127–131RX, represented here with 109–113/127–131RX. T4 lysozyme has been labeled with OND at positions 109 and 131 and with OND4 at positions 109–113 and 127–131. MDDS simulations were carried out for 5 ns by keeping the protein fixed. The calculated spin-pair distance distributions obtained from the MDDS simulations are compared with those obtained from the EPR/DEER (Figure 4A). The 109/131OND distance distribution obtained from the MDDS is found to agree very well with those obtained from the EPR/DEER. This agreement suggests that the force field parameters for OND produce very reliable spin-pair distance distributions. The 109–113/127–131OND4 distance distribution obtained from the MDDS is found to be slightly narrower, with the width of the distribution ranging from 29 to 35 Å, than the EPR/DEER distance distribution, which ranges from 26 to 33 Å. However, there is a difference of only 1.5 Å between the maximum peaks of the MDDS and EPR/DEER distance distributions.

Figure 4.

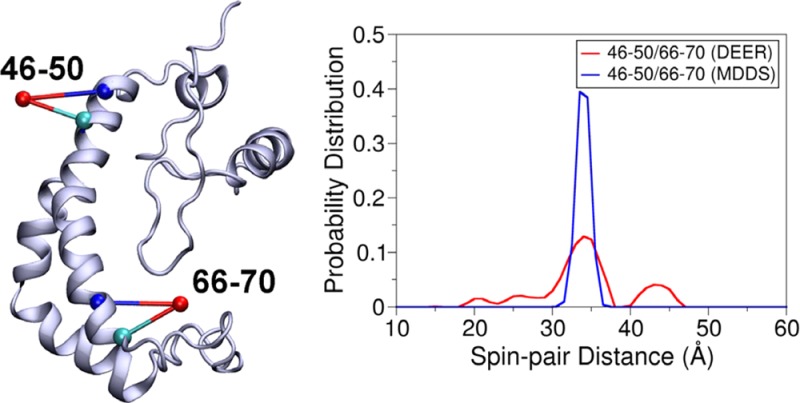
(A) Cartoon representation of T4 lysozyme with the OND at positions 109 and 131 and the OND4 at positions 109–113 and 127–131 and corresponding distance distributions obtained from MDDS and EPR/DEER. (B) Cartoon representation of KCNE1 with the OND at positions 47 and 66 and the OND4 at positions 46–50 and 66–70 and corresponding distance distributions obtained from MDDS and EPR/DEER.

The structure of the integral membrane protein KCNE1 (PDB 2K21) was obtained from NMR.²¹ Recently, the EPR/DEER distance distribution data has been reported for the 47/66R1 and 46–50/66–70RX spin-labels in this protein.³ The 47/66OND and 46–50/66–70OND4 distance distributions obtained from the simulation agree very well with those obtained from the EPR/DEER (Figure 4B), suggesting the structure of KCNE1 obtained from NMR is quite accurate. The spin-pair distance distribution obtained from the OND4 is again found narrower than the EPR/DEER, but the maximum peaks of the two distributions are almost the same. The broader distance distributions in the EPR/DEER may be due to the dynamics of the protein and/or due to the influence from the membrane environment, since RX attached to membrane proteins could provide broader distance distributions, poorer signal-to-noise, and poor DEER modulation for longer distances as compared to water-soluble proteins.³ Overall, OND and OND4 in conjunction with the MDDS simulations have been proved to provide very reliable distance distributions, which could be used to check the reliability or correctness of an already existing 3D structure of protein.

Application of MDDS to T4 Lysozyme

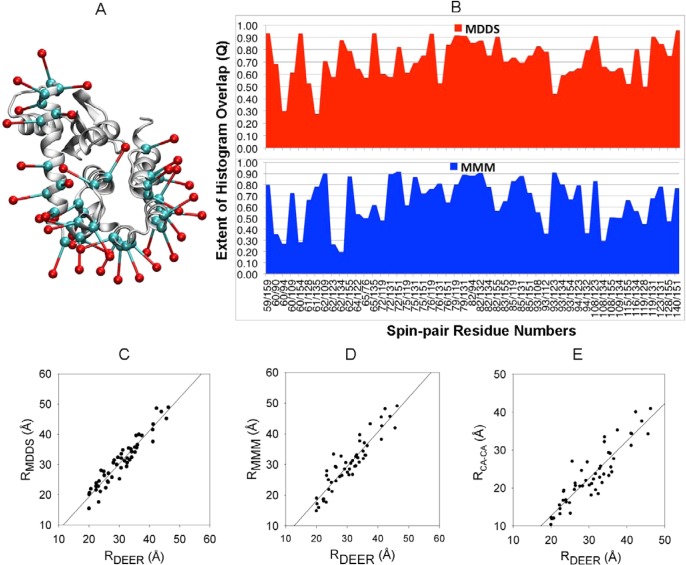
T4 lysozyme is the protein of known 3D structure for which the largest number of DEER histograms have been determined from EPR/DEER spectroscopy: 51 pairs from the insertion of the spin-label R1 at 37 positions.⁹ Here, the simplified R1 spin-label (OND) is used to examine the performance of MDDS simulations. The OND is attached to 37 positions in T4 lysozyme (Figure 5A). Overall, the simulated distributions are found to agree very well with those obtained from the EPR/DEER, although the calculated distance distributions for some spin-pairs are found to be slightly broader (see Figure S6 in the Supporting Information). It is possible to quantify the similarity between the calculated and experimental distance distributions by finding the probability of their overlap, which is defined as

where P^exp(n) and P^calc(n) are the histograms obtained from experiment and calculation, respectively. The value of the overlap factor Q ranges from 0 to 1 by definition. A value of 1 implies a complete overlap between the two distributions. In the present case, P^exp(n) are the histograms obtained from the EPR/DEER and P^calc(n) are the histograms obtained either from MDDS or MMM.¹⁶ MMM is a very commonly used computational technique to predict spin-pair distance distributions. We find that the overlap factor Q is higher than 0.5 for all but 3 spin-label pairs using MDDS (60/94, 61/135, and 93/123). In contrast, Q is lower than 0.5 for 14 spin-label pairs with MMM (Figure 5B). This comparison suggests that the distance histograms from MDDS are in better agreement with the experimental distributions than those from MMM. The average distances extracted from MDDS are also in better agreement with the average distances extracted from the EPR/DEER distributions than those from MMM (Figure 5 C and D) (see Table S1 in the Supporting Information for the average distances). A linear regression analysis of the average spin-pair distances obtained from the EPR/DEER data and the simulations yields a correlation coefficient of about 0.91 for MDDS and a correlation coefficient of 0.85 for MMM. Using this system, it is also possible to assess the accuracy of a common and seductive simplification that uses C_α–C_α distances as surrogate spin-labels to interpret the structural changes reported by the EPR/DEER spin-pair distributions. The correlation coefficient for the average spin-pair distances obtained from EPR/DEER and the C_α–C_α distances is only 0.80. As shown in Figure 5C and E, MDDS is clearly a better representation than simply using C_α–C_α distances. This analysis shows that modeling the spin-label is important to accurately represent the distance distribution from EPR/DEER data and correctly interpret the structural changes in proteins.

Figure 5.

Cartoon representation of (A) T4 lysozyme with 37 OND dummy spin-labels at positions 59, 60, 61, 62, 64, 65, 72, 75, 76, 79, 82, 83, 85, 86, 89, 90, 93, 94, 108, 109, 112, 115, 116, 119, 122, 123, 127, 128, 131, 132, 134, 135, 140, 151, 154, 155, and 159. OND dummy atoms and the C_α atoms are shown in red and cyan colors, respectively. (B) Comparison of the extent of spin-pair histogram overlap, Q, between the MDDS and MMM in T4 lysozyme. (C) 51 average interlabel experimental (R_DEER) vs MDDS (R_MDDS) distances in T4 lysozyme; the correlation coefficient is found to be 0.91. (D) 51 average interlabel experimental (R_DEER) vs MMM (R_MMM) distances in T4 lysozyme; the correlation coefficient is 0.85. (E) 51 average interlabel experimental (R_DEER) vs inter-residue C_α–C_α distances in the crystallographic structure of T4 lysozyme; the correlation coefficient is 0.80.

Application of MDDS to Understand Conformational States of LeuT

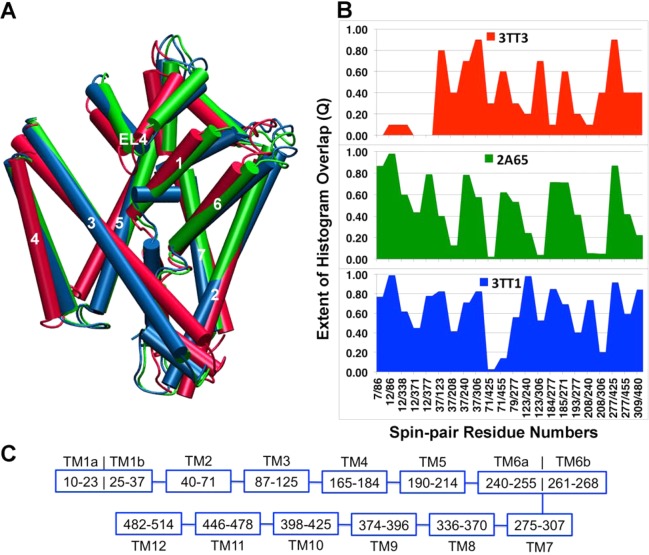
The leucine transporter (LeuT) is a bacterial homologue of the mammalian neurotransmitter:sodium symporter (NSS). The NSS includes biogenic amine transporters that terminate synaptic signaling through selective reuptake of neurotransmitter molecules.^22,29 These NSSs are targets of widely prescribed therapeutic drugs (e.g., selective serotonin reuptake inhibitors (SSRIs) and tricyclic antidepressants (TCAs)) and drugs of abuse (e.g., cocaine, amphetamine).³⁰ LeuT has emerged as a model for NSS transporters due to its sequence, structural, and functional similarities. There have been intensive efforts to understand the dynamics of ion-coupled substrate translocation in LeuT by means of both computational and experimental techniques including the X-ray crystallography and EPR spectroscopy.^{13,23,31−38} Three crystal structures of LeuT, PDB 2A65,²² PDB 3TT1,²³ and PDB 3TT3,²³ have been classified as being in the outward-facing, inward-facing, and substrate-occluded states, respectively. The inward- and outward-facing states of LeuT were crystallized by mutation of some highly conserved residues and subsequent conformational selection with antibodies.²³ Recently, Karmier et al.¹³ proposed an alternating access mechanism of LeuT through the use of EPR/DEER spin-pair distance distribution and subsequent structural refinement with the re-MD simulations. 3D structures obtained from the re-MD simulations were found very different in several sites of the inward-facing and substrate-occluded states when compared with the X-ray crystal structures, 3TT3 and 2A65, respectively. The study showed movements at the TMs 1b, 7b, 6a, and EL4 in the extracellular site and TMs 6b and 7a, N terminus in the intracellular ends during the alternating access of LeuT. Here, MDDS simulations are performed to cross-validate the three X-ray crystallographic structures in representing the outward-facing, inward-facing, and substrate-occluded states of LeuT. Three sets of EPR/DEER distance distribution data from 22 labeled sites are available that correspond to the three states of LeuT.¹³ Overall, the agreement between the distance distributions obtained from the MDDS and EPR/DEER decreases with the use of 3TT1, 2A65, and 3TT3 in the MDDS simulation (see Figure S7 in the Supporting Information). Figure 6 represents the extent of MDDS and DEER histogram overlap (Q) vs the spin-pair numbers for all three states of LeuT. All the spin-pairs have been found to have high Q (>0.5) for the 3TT1, except for spin-pairs 12/371, 37/208, 71/425, 71/455, 193/277, and 208/306, suggesting the 3TT1 most likely corresponds to the outward-facing conformation of LeuT. Eleven spin-pairs have Q lower than 0.5 in the 2A65, suggesting the crystal structure initially classified as a substrate-occluded state does not correspond to the structure of the actual substrate-occluded state in solution. Spin-pairs 37/123 and 37/208 have spin-label 37 in TM1b, 123/240 and 208/240 have spin-label 240 in TM6a, 37/208, 208/240, and 208/306 have spin-label 208 in TM5, and 208/306 and 123/306 have spin-label 306 in TM7. All of these spin-pairs have very low Q (<0.4), suggesting the TMs 1b, 6a, 5, and 7 are different in the actual substrate-occluded state in LeuT. Fourteen out of 22 spin-pairs have Q values less than 0.5 in 3TT3, implying that the structure is very wrong and it does not represent the inward-facing conformation of LeuT. Spin-pairs 7/86, 12/86, 12/338, 12/371, and 12/377, which have spin-labels 7 and 12 in TM1a, have very low Q (<0.2), suggesting that the actual conformation of the TM1 in the inward-facing apo state is very different than that observed in the crystallographic structure 3TT3. 123/240 and 208/240 have spin-label 240 in TM6 and 79/277, 184/277, 193/277, 208/306, 277/455, and 309/480 have spin-labels 277 and 309 in TM7. All of these spin-pairs have very low Q (<0.4) in the apo state, suggesting the actual conformations of the TM6 and TM7 are different in the apo state than those in the 3TT3. These results are in agreement with the structures obtained from the re-MD simulations which show that the actual substrate-occluded state of LeuT is more inward-facing than that reported in the 2A65 and the actual inward-facing conformation is very different in the TMs 6b, 7a, N terminus in the intracellular ends of the LeuT.¹³

Figure 6.

(A) Cartoon representation of the PDB structures of LeuT, 3TT1 (blue), 2A65 (green), and 3TT3 (red) which shows changes in some important TMs. (B) Comparison of the extent of overlap, Q, of the spin-pair distance distributions obtained from a MDDS simulation and EPR/DEER for three states of LeuT. Twenty-two distance distributions are available from labeled positions in 7, 12, 37, 71, 79, 86, 123, 184, 185, 193, 208, 240, 271, 277, 306, 309, 338, 371, 377, 425, 455, and 480 in LeuT. (C) The TMs and the corresponding residue numbers in LeuT are also shown for the sake of discussion.

Conclusion

In this study, force field parameters for atomic models of the bifunctional spin-labels (RX) have been developed and were tested in explicit-solvent MD simulations to understand their conformational dynamics. It was observed that RX_i,i+4 induces less distortion in a protein backbone than RX_i,i+3, and is thus a better choice to study protein conformations. For the purpose of aiding structural refinement, simplified dummy spin-labels were also developed to match the 3D spatial distribution of the nitroxide oxygen atom relative to the protein backbone observed in all-atom simulations of the RX_i,i+3 and RX_i,i+4 spin-labels. The dummy spin-labels called OND3 and OND4 are meant to simulate the RX_i,i+3 and RX_i,i+4, respectively. These models are designed to carry out MDDS and restrained-ensemble (re-MD) simulations. The results presented here highlight the usefulness of simplified spin-labels and MDDS simulations in predicting the EPR/DEER spin-pair distance distribution data. The distance distributions between spin-labels from MDDS simulations are in very good agreement with those obtained experimentally from EPR/DEER when the conformation of the protein is already known. The MDDS simulations perform better than the widely used MMM computational method. This suggests that MDDS simulation is a useful method to rapidly assess if a putative 3D model structure of the system is consistent with available EPR/DEER data. As the dummy spin-labels do not interact with one another, they can be introduced simultaneously to all the sites in a single MDDS simulation of the model structure. A system with dummy labels on all sites can be built by the web based CHARMM-GUI webpage. In the near future, one will be able to conduct the MDDS simulations using the spin-label descriptor module in charm-gui.org. A refinement of protein model structure is possible via the re-MD simulation by introducing noninteracting multiple copies of the dummy spin-labels inserted in various positions of the protein for which EPR/DEER data is available. The re-MD simulations of T4 lysozyme labeled with multiple copies (25) of 109–113OND4 and 127–131OND4 were able to match the calculated 109–113/127–131OND4 distance distribution with that obtained from the EPR/DEER (see Figure S8 in the Supporting Information). This result suggests that, if a sufficient number of EPR/DEER distance distributions are available, the re-MD simulation along with the simplified spin-labels can drive the conformation of a protein toward an accurate refined structure.

Supporting Information Available

Time dependence of the dihedral angles of RX_i,i+4 and RX_i,i+3 attached to a polyalanine α-helix, time dependence of the N–C_α–C–N dihedral angle (ψ) at position i when RX_i,i+3 is attached to a polyalanine α-helix, the dynamics of the nitroxide oxygen of R1 with respect to the C_α atom, simplified dummy OND and dummy CBD is attached to C_α atom of glycine, comparison of spin–spin distance histograms obtained from MDDS simulations of T4 lysozyme and experiment, average spin-pair distances obtained from DEER, MDDS and MMM and the C_α–C_α distances obtained from the T4 lysozyme X-ray crystal structure, comparison of distance distributions obtained from MDDS and DEER based on the outward-facing (3TT1), substrate-occluded (2A65), and inward-facing (3TT3) crystal structures of LeuT, and comparison of DEER, MDDS, and re-MD distance distributions between the 109–113RX and 127–131RX attached to T4 lysozyme. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States