Using Nonlinear Stochastic Evolutionary Game Strategy to Model an Evolutionary Biological Network of Organ Carcinogenesis Under a Natural Selection Scheme

Abstract

Molecular biologists have long recognized carcinogenesis as an evolutionary process that involves natural selection. Cancer is driven by the somatic evolution of cell lineages. In this study, the evolution of somatic cancer cell lineages during carcinogenesis was modeled as an equilibrium point (ie, phenotype of attractor) shifting, the process of a nonlinear stochastic evolutionary biological network. This process is subject to intrinsic random fluctuations because of somatic genetic and epigenetic variations, as well as extrinsic disturbances because of carcinogens and stressors. In order to maintain the normal function (ie, phenotype) of an evolutionary biological network subjected to random intrinsic fluctuations and extrinsic disturbances, a network robustness scheme that incorporates natural selection needs to be developed. This can be accomplished by selecting certain genetic and epigenetic variations to modify the network structure to attenuate intrinsic fluctuations efficiently and to resist extrinsic disturbances in order to maintain the phenotype of the evolutionary biological network at an equilibrium point (attractor). However, during carcinogenesis, the remaining (or neutral) genetic and epigenetic variations accumulate, and the extrinsic disturbances become too large to maintain the normal phenotype at the desired equilibrium point for the nonlinear evolutionary biological network. Thus, the network is shifted to a cancer phenotype at a new equilibrium point that begins a new evolutionary process. In this study, the natural selection scheme of an evolutionary biological network of carcinogenesis was derived from a robust negative feedback scheme based on the nonlinear stochastic Nash game strategy. The evolvability and phenotypic robustness criteria of the evolutionary cancer network were also estimated by solving a Hamilton–Jacobi inequality – constrained optimization problem. The simulation revealed that the phenotypic shift of the lung cancer-associated cell network takes 54.5 years from a normal state to stage I cancer, 1.5 years from stage I to stage II cancer, and 2.5 years from stage II to stage III cancer, with a reasonable match for the statistical result of the average age of lung cancer. These results suggest that a robust negative feedback scheme, based on a stochastic evolutionary game strategy, plays a critical role in an evolutionary biological network of carcinogenesis under a natural selection scheme.

Introduction

Biological systems are subject to intrinsic random genetic mutations, epigenetic alterations, and noises arising from internal and external stochastic fluctuations.^1,2 However, it is very important that the potential perturbative effects of stochastic noise,³ genetic mutations, and epigenetic alterations are buffered at the systemic phenotypic level. Indeed, biological systems are expected to display phenotypes that are robust to these genetic and epigenetic variations and noise.^4–8 However, phenotypic changes in evolutionary fitness pressure require that biological systems are able to adapt by producing heritable phenotypic variants. This ability has been termed as evolvability. Recently, a paradoxical question about the intuitively expected trade-off between robustness and evolvability has attracted much attention^9–12: how can biological systems generate phenotypes that are resistant to genetic mutations, epigenetic alterations, and noise, yet also retain their ability to evolve as a result of these effects? One answer is that the ability of a phenotype to resist mutations might enable genetic diversity, which could then be translated to phenotypic diversity as a result of subsequent genetic and epigenetic alterations, or environmental changes in selection pressure¹³ through what has been termed the neutral network.^8,14–16

The onset of cancer is characterized by an accumulation of genetic mutations and epigenetic alterations that are caused by different stresses, including tobacco, chemical agents, radiation, and viruses. These mutations and alterations typically modify the structures of DNA and chromatin, and consequently alter the gene products or the regulation of gene expression.¹⁷ Molecular biologists have long recognized carcinogenesis as an evolutionary process that involves natural selection. Indeed, cancer is driven by the somatic evolution of cell lineages.^18–31 In this work, the somatic evolution of cell lineages in an organ was modeled as a nonlinear stochastic biological network to study natural selection in evolutionary carcinogenesis. The evolutionary biological network of an organ is driven by intrinsic random fluctuations because of genetic and epigenetic variations and external disturbances attributed to carcinogens and other stressors. Therefore, we modeled the intrinsic random fluctuations because of genetic and epigenetic variations as a Poisson counting process, and the external disturbances were described by an uncertain signal. Therefore, an organ with different cell species undergoing carcinogenesis was modeled by a nonlinear stochastic system with an intrinsic Poisson counting process and external random disturbances.^32,33

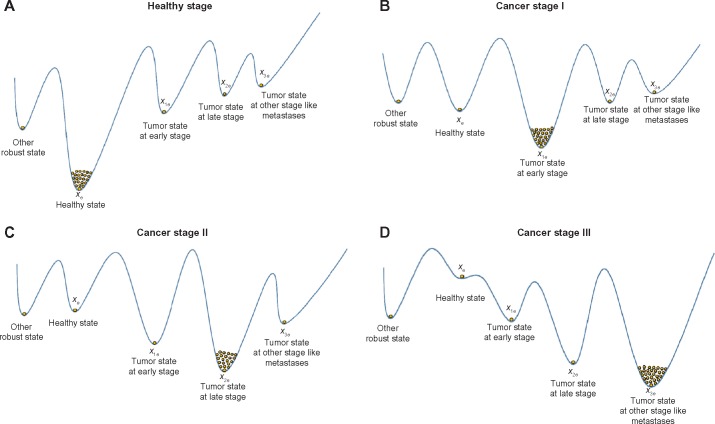
A natural selection scheme develops a robust property to efficiently attenuate intrinsic fluctuations and withstand external disturbances at the beginning of carcinogenesis. This maintains the normal function (ie, phenotype) of an evolutionary biological network under intrinsic random fluctuations because of genetic and epigenetic variations and external disturbances attributed to environmental stresses. A robust feedback scheme^9–11 may exist in natural selection to maintain the healthy phenotype of a biological network at the desired equilibrium point x_e (attractor; Fig. 1). Because the environmental disturbances and the intrinsic random Poisson fluctuations are unpredictable, the minimax evolution game strategy was employed. This strategy utilized a robust optimal feedback scheme that minimized the worst-case effects of external disturbances and intrinsic fluctuations on the robust stability of the phenotype at an equilibrium point favored by natural selection. Therefore, the strategy of natural selection on the evolutionary biological network during carcinogenesis was formulated as a nonlinear stochastic evolutionary game problem. Based on the stochastic Nash game strategy, effective feedback loops could be developed by natural selection for a cancer-associated biological network. This strategy can significantly improve the network’s robustness to genetic and epigenetic variations and extrinsic disturbances, as well as maintain the organ’s normal phenotype. However, neutral genetic mutations and epigenetic alterations gradually accumulated, and eventually overrode the network’s robustness developed through natural selection. The robust stability of the biological network thereby deteriorated, which leads to a shift from the healthy phenotypic state at the equilibrium point x_e to the cancerous phenotypic state at another equilibrium point x_1e. Hence, cancer initiated another new evolutionary process (Fig. 1). As time increased, the abovementioned shift of phenotypic state always occurred when the accumulated genetic mutations and epigenetic alterations were large enough. Therefore, cancer can be considered an aging disease.

Figure 1.

Four equilibrium points in the phenotypic landscape of the nonlinear stochastic biological network of an organ in (10) or (11) in carcinogenesis. The dots in the basin of the equilibrium points denote the accumulation of Poisson phenotypic fluctuations (population) of biological networks because of genetic and epigenetic changes in carcinogenesis. The vertical states illustrate the relative stability of robust states, healthy state, and tumor state of different stages at different equilibrium points, in the multiple dimensional state space. (A) At the beginning, the phenotypic trait of biological network is near the equilibrium point x_e at healthy state. (B) By suffering the accumulation of neutral phenotypic variations and the influence of environmental stresses in carcinogenesis, the robust stability of healthy state cannot be maintained through the evolutionary strategy u(t) with the effect of natural selection, and then, the phenotypic trait may be shifted from x_e to x_1e of tumor state at the early stage to start another evolutionary process (carcinogenesis). (C) Similarly, if the accumulated neutral phenotypic variations are large enough and environmental disturbances v(t) are strong enough, the evolutionary strategy u(t) cannot confer enough robust network stability to maintain the network local stability at x_1e. Then, the phenotypic trait of biological network is shifted from cancer stage I at the equilibrium point x_1e to cancer stage II at the equilibrium point x_2e to begin another stage of evolutionary process (carcinogenesis). (D) Finally, if the accumulation of neutral phenotypic variations is large enough to violate the phenotypic robustness criterion at x_2e, cancer is transited from cancer stage II to cancer stage III. Since the equilibrium points x_e in (B) and (C) are still locally stable, they are curable (treatable), ie, the curable stages in (B) and (C) may be reversible to (A) by adequate surgical or medical treatment (one kind of enhanced negative feedback). If the healthy state x_e is incurable (saddle point) as shown in (D), then it is impossible that this process is revertible to (A).

In this study, based on the stochastic Nash game strategy for the robust stabilization of evolutionary nonlinear biological networks in carcinogenesis,^34–39 both natural selection and external disturbances affected network evolution. Natural selection minimized network evolution (or maximized network fitness), while external disturbances, including genetic mutations and epigenetic alterations, maximized network evolution (or minimized network fitness). We solved a Hamilton–Jacobi inequality (HJI)-constrained optimization problem using the stochastic Nash game strategy to obtain a robust evolutionary feedback scheme for natural selection during carcinogenesis. Furthermore, the phenotype robustness criterion was also derived from the stochastic Nash game strategy to obtain insights into the evolvability of the cancer biological network. In order to simplify the procedure, the global linearization method was employed to interpolate several local linear stochastic systems and to approximate the nonlinear stochastic system of an organ undergoing carcinogenesis. Therefore, the HJI-constrained optimization problem could be replaced by a linear matrix inequality (LMI)-constrained optimization problem, which was solved easily using the LMI Control Toolbox in MATLAB.^40–42

Finally, an in silico example of evolutionary oncogenesis in lung cancer has been provided to illustrate natural selection based on the stochastic Nash game strategy. The nonlinear stochastic biological network of lung cancer-related tissue contains parenchymal cells, stromal cells, immature vascular endothelial cells (VECs), and VECs. The network was constructed using Poisson genetic and epigenetic variations and environmental disturbances. By using a robust feedback scheme with the natural selection property based on the proposed nonlinear stochastic Nash game strategy, we found that the tissue maintained a normal phenotype for ∼54.5 years in the aging process under genetic and epigenetic variations and environmental disturbances. When the robustness of the tissue network was violated by the accumulated neutral genetic and epigenetic variations and environmental disturbances, the normal phenotype of the tissue shifted from its original equilibrium point to another equilibrium point with a new, cancerous phenotype. This new phenotype^24,43 took ∼1.5 years to progress from stage I to stage II cancer, and about 2.5 years to progress from stage II to stage III cancer.

Stochastic Biological Network of Organ in Carcinogenesis

First, we considered a simplified analysis by using the linear biological network of a tissue or organ in carcinogenesis as the following random dynamic process.

$$\frac{dx(t)}{dt}=\left(A+{\displaystyle \sum _{k=1}^{N(t)}{A}_{k}p(t-t_k)}\right)x(t)+Bv(t)$$ (1)

where x(t) = [x₁(t) x₂(t) x₃(t),…,x_n(t)]^T denotes the masses at time t of n cell species in the biological network of a tissue or organ (in the liquid tumor case, ie, lymphomas and leukemias, the masses of cell species are changed to the densities of cancer cells in blood or lymph), v(t) denotes the environmental disturbances (signals or mutagens) because of different kinds of damages or carcinogens. p(t) is a Poisson point process and A_k denotes the effects of random genetic mutations and epigenetic alterations at t = t_k on the phenotype of the tissue. N(t) denotes a Poisson counting process of phenotypic variations in the tissue level because of random cellular genetic and epigenetic variations¹⁷ in carcinogenesis as follows:

$$N(t)={\displaystyle \sum _{k=1}^{N(t)}p(t-t_k)={\displaystyle \sum _{k=1}^{N(t)}1}}$$ (2)

with mean λt and variance λt,³³ and the weighting Poisson counting process

$${\displaystyle \sum _{k=1}^{N(t)}{A}_{k}p(t-t_k)}={\displaystyle \sum _{k=1}^{N(t)}{A}_k,\text{for}t\ge 0}$$ (3)

denotes the total phenotype effect of random genetic and epigenetic variations on the system matrix A. Poisson point processes are useful for modeling a wide range of event-driven phenomena involving the occurrence of events at random points in time, such as emission of subatomic particles from radioactive material, the detection of photons by the receiver of a weak optical signal, genetic mutations, neural discharges, lightning discharges, seismic events, and the arrival of customers always used to model a dynamic system exposed to sudden, infrequent, highly localized changes.^33,44 Therefore, it is suitable to model discontinuous genetic and epigenetic variations of biological network in the carcinogenesis process. The system matrix A denotes the interactions among these n cell species in the tissue or organ, and B denotes the coupling matrix between environmental disturbances (signals) and cell species in the organ, ie, it denotes the effect of environmental signals on the biological network of the organ, where

$$\begin{array}{l}A=\left[\begin{array}{llll}{a}_{11}\hfill & a_{12}\hfill & \cdots \hfill & a_{1n}\hfill \\ a_{21}\hfill & a_{22}\hfill & \cdots \hfill & a_{2n}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ a_{n1}\hfill & a_{n2}\hfill & \cdots \hfill & a_{nn}\hfill \end{array}\right];A_k=\left[\begin{array}{llll}{a}_{k11}\hfill & a_{k12}\hfill & \cdots \hfill & a_{k1n}\hfill \\ a_{k21}\hfill & a_{k22}\hfill & \cdots \hfill & a_{k2n}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ a_{kn1}\hfill & a_{kn2}\hfill & \cdots \hfill & a_{knn}\hfill \end{array}\right];\\ B=\left[\begin{array}{llll}{b}_{11}\hfill & b_{12}\hfill & \cdots \hfill & b_{1m}\hfill \\ b_{21}\hfill & b_{22}\hfill & \cdots \hfill & b_{2m}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ b_{n1}\hfill & b_{n2}\hfill & \cdots \hfill & b_{nm}\hfill \end{array}\right];v(t)=\left[\begin{array}{c}{v}_1(t)\\ v_2(t)\\ ⋮\\ v_m(t)\end{array}\right];\end{array}$$ (4)

a_ij = 0 if there exists no interaction between cell species i and cell species j; a_kij = 0 if the kth genetic or epigenetic variation has no phenotype effect on a_ij; and b_ij = 0 if the disturbance v_j(t) has no effect on the cell species i.

In general, the biological processes in the cancer are time-varying, ie, A(t) and B(t) in (1). In this study, because of discontinuous time-varying parameter variations, A(t) is replaced by $A+{\displaystyle \sum _{k=1}^{N(t)}{A}_{k}p(t-t_k)}$in (1). B(t) is replaced by time-invariant B but with varying part merged to uncertain disturbance v(t). In this study, v(t) is any bounded environmental stress. Therefore, in this study, we are with time-invariant system models A and B, but with random process to represent the time-varying process across time.

In order to operate successfully in the organ within the context of the organism, all the cells in the organ must be integrated into an architecture as system matrix A in the biological network of the organ in (1).

From (1), we get a linear stochastic evolutionary biological network in carcinogenesis as

$$\frac{dx(t)}{dt}=Ax(t)+{\displaystyle \sum _{k=1}^{N(t)}{A}_{k}x(t)p(t-t_k)}+Bv(t)$$ (5)

Since the weighted Poisson counting process ${\displaystyle \sum _{k=1}^{N(t)}{A}_{k}p(t-t_k)}$ in (1) or (5) is an accumulating process of phenotypic changes of biological network in the tissue level because of random genetic and epigenetic variations in the cellular level, the stochastic biological network in (5) can represent a population of biological networks over all possible Poisson genetic and epigenetic variations in the cancer evolutionary process, ie, one possible Poisson genetic or epigenetic variation represents one possible biological network in a population of the organs in carcinogenesis. The accumulated phenotypic variations ${\displaystyle \sum _{k=1}^{N(t)}{A}_{k}x(t)}p(t-t_k)$ in (5) may lead to permanent changes in the phenotypic trait of the organ. v(t) denotes the environmental stresses because of environmental changes or any agent capable of causing cancer. Therefore, the phenotypic trait x(t) of biological network will be perturbed away from the equilibrium point x_e = 0. Recently,⁴⁵ the lifetime risk of cancers of many different types is shown to be strongly correlated (0.81) with the total number of divisions of the normal self-renewing cells maintaining that tissue’s homeostasis, ie, to be strongly related to the accumulated Poisson phenotypic changes ${\displaystyle \sum _{k=1}^{N(t)}{A}_{k}x\left(t\right)p\left(t-t_k\right)}$ in the aging process.

Under the phenotypic variations and environmental disturbances in (5), in order to maintain its normal function and homeostasis, ie, to operate successfully around the equilibrium point x_e, the natural selection strategy of biological network in (5) needs to select some adequate phenotypic variations to improve the biological network robustness to resist the effects of genetic and epigenetic variations and environmental changes in carcinogenesis.

Suppose that the natural selection strategy of evolutionary biological network in the organ is to select the following phenotypic variations to improve the network robustness in carcinogenesis

$$u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}x(t)p(t-{t^{\prime }}_k)}$$ (6)

and the remaining (or neutral) phenotype variations are

$$\begin{array}{l}R(t)={\displaystyle \sum _{k=1}^{N_2(t)}{A}_{k}x}(t)p(t-t_k^{*})\\ ={\displaystyle \sum _{k=1}^{N(t)}{A}_{k}x(t)p(t-t_k)-{\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}x(t)}p(t-{t^{\prime }}_k)}\end{array}$$ (7)

which have not been selected by natural selection and are accumulated in the biological network. The temporal parameters ${t^{\prime }}_k$ and $t_k^{*}$ were defined as ${t^{\prime }}_{N_1(t)}\ge ,\dots ,\ge {t^{\prime }}_1$ and $t_{N_2(t)}^{*}\ge ,\dots ,\ge t_1^{*}$, respectively. It is worth noting that the ${t^{\prime }}_k$ is not equal to $t_k^{*}$. From (5)–(7), it is seen that

$$N(t)=N_1(t)+N_2(t),{\displaystyle \sum _{k=1}^{N(t)}{A}_{k}x(t)p(t-t_k)=u(t)+R(t)}$$ (8)

where the Poisson counting processes 1 ∼ N₁(t) and 1 ∼ N₂(t) have means λ₁t and λ₂t, respectively, and λ = λ₁ + λ₂.

Therefore, the stochastic evolutionary biological network of an organ under somatic genetic and epigenetic variations, environmental disturbances, and natural selection in (5) can be represented as follows:

$$\begin{array}{l}\frac{dx(t)}{dt}=Ax(t)+{\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}x(t)p(t-{t^{\prime }}_k)}+{\displaystyle \sum _{k=1}^{N_2(t)}{A}_{k}x(t)p}(t-t_k^{*})+Bv(t)\\ =Ax(t)+u(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{A}_{k}x(t)p(t-t_k^{*})+Bv(t)}\end{array}$$ (9)

where $u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}x(t)p(t-{t^{\prime }}_k)}$ denotes the evolutionary strategy of biological network by natural selection, ie, how to select adequate phenotypic variations to improve the network robustness to phenotypic variations and environmental disturbance v(t) and to finally maintain the normal function of biological network (or organ) in the network evolutionary process (carcinogenesis) was considered.

In the real organ, the stochastic evolutionary biological networks for n cell species, x₁,…,x_n, in carcinogenesis are always nonlinear, and the linear stochastic evolution network in (5) is thus modified as

$$\frac{dx(t)}{dt}=f(x)+{\displaystyle \sum _{k=1}^{N(t)}{f}_k(x)p(t-t_k)}+Bv(t)$$ (10)

where f(x) denotes the nonlinear interactive vector among n different cell species in the biological network, and f_k(x), for k = 1,…,N(t), denotes the nonlinear phenotypic variations because of Poisson genetic and epigenetic variations in carcinogenesis.

Suppose that the phenotypic variations in (10) could be separated into the part of evolutionary strategy $u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(x)p(t-{t^{\prime }}_k)}$ by natural selection and the remaining neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(x)p(t-t_k^{*})}$, which are accumulated as random dots in the basin of healthy state x_e in Figure 1A. The above nonlinear stochastic evolutionary biological network in carcinogenesis was then modified as

$$\frac{dx(t)}{dt}=f(x)+u(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(x)p(t-t_k^{*})+Bv(t)}$$ (11)

where

$$\begin{array}{c}{\displaystyle \sum _{k=1}^{N(t)}{f}_k(x)p(t-t_k)}={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(x)p(t-{t^{\prime }}_k)+{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(x)p(t-t_k^{*})}}\\ =u(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k}(x)p(t-t_k^{*})\end{array}$$ (12)

The nonlinear stochastic biological system in (11) represents an evolutionary organ under evolutionary strategy $u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(x)p(t-{t^{\prime }}_k)}$ by natural selection, and the neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(x)p(t-t_k^{*})}$ and environmental disturbance Bv(t) are accumulated in the basin of the healthy state at the equilibrium point x_e in Figure 1A during the carcinogenesis.

The nonlinear stochastic biological network in (10) and (11) has many equilibrium points (phenotypic traits) (Fig. 1). Suppose that the phenotypic trait of the biological network near the stable equilibrium point x_e is the healthy state, which is the phenotypic trait with normal function of interest by natural selection. For the convenience of analysis, the origin of nonlinear stochastic biological network in (11) is shifted to the equilibrium point (phenotypic trait) x_e. In this case, if the shifted nonlinear stochastic network is robustly stable at the origin, the equilibrium point (phenotype trait) x_e of interest is also robustly stable. Let us denote the phenotypic deviation around the phenotype at x_e as $\tilde{x}\left(t\right)=x\left(t\right)-x_e$ so that the following shifted nonlinear stochastic biological network of an organ is obtained as

$$\begin{array}{l}\frac{d\tilde{x}(t)}{dt}=f(\tilde{x})+{\displaystyle \sum _{k=1}^{N(t)}{f}_k(\tilde{x})p(t-t_k)+Bv(t)}\\ =f(\tilde{x})+u(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k^{*})+Bv(t)}\end{array}$$ (13)

where the notations $f(\tilde{x}+x_e)$ and $f_k(\tilde{x}+x_e)$ are, respectively, simplified by $f(\tilde{x})$ and $f_k(\tilde{x})\cdot u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}$ denotes the evolutionary strategy of nonlinear stochastic biological network by considering natural selection to maintain the normal function of evolutionary biological network.

In this situation, the origin $\tilde{x}\left(t\right)=0$ of the shifted nonlinear stochastic biological network in (13) is the equilibrium point x_e of the original biological network in (11).

Remark 1

1. The linear stochastic biological network of an organ in (9) was considered as the linearized system of (13) at the equilibrium point $\tilde{x}=0$ [or at equilibrium point x_e in the nonlinear stochastic biological network in (11)] with ${A=\frac{\partial f(\tilde{x})}{\partial \tilde{x}}|}_{\tilde{x}=0}$ and ${A_k=\frac{\partial f_k(\tilde{x})}{\partial \tilde{x}}|}_{\tilde{x}=0}$ since $x(t)=x_e[\text{ie},\tilde{x}(t)=x(t)-x_e=0]$ is the only equilibrium point in the linear biological system in (5) or (9).

2. The nonlinear stochastic system in (13) was considered as a Darwinian dynamic equation that satisfies Darwin’s conditions of variability, heritability, and the strategy to survive.³⁷ However, the heritability in this study implies the heritability of somatic cell evolution in carcinogenesis.

Natural Selection in Carcinogenesis

In carcinogenesis, the evolutionary biological network of an organ was modeled as the nonlinear stochastic system in (13). Under the effects of random genetic and epigenetic variations and environmental disturbance v(t), in order to maintain the normal function of evolutionary biological network to be in the healthy state at the equilibrium point x_e in Figure 1, an evolutionary strategy $u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}$ must be selected by natural selection to improve the robust stability of the healthy state or the equilibrium point at $x(t)=x_e(\text{or}\tilde{x}(t)=0)$ of evolutionary biological network. According to the robust stochastic stabilization strategy, the evolutionary strategy needs to make the system state (phenotype) of evolutionary biological network deviate from the healthy state as small as possible with a parsimonious effort of evolutionary strategy u(t) selected by natural selection in response to environmental disturbances, genetic and epigenetic variations, and initial state. Because the environmental disturbance v(t) and neutral somatic genetic and epigenetic variations are unpredictable, the evolution level e of the biological network because of the worst case of all possible bounded disturbances, neutral somatic genetic and epigenetic variations, and initial conditions was defined as,^14,16

$$\begin{array}{l}e=v(t)\in \stackrel{\max }{L_2}[0,t_p]\\ R(t)={\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k^{*})}\\ \frac{E{\displaystyle {\int }_0^{t_{\mathrm{P}}}\left\{{\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)\right\}dt}}{E\left\{{\tilde{x}}^T(0)\tilde{x}(0)\right\}+E{\displaystyle {\int }_0^{t_{\mathrm{P}}}\left\{{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})+v^T(t)v(t)}\right\}dt}}\end{array}$$ (14)

where L₂[0, t_p] denotes the set of all possible bounded environmental disturbances, ie, v(t) ∈ L²[0,t_p], if ${\displaystyle {\int }_0^{t_p}{v}^{\mathrm{T}}}(t)v(t)dt<\infty .E\{*\}$ denotes the expectation of *. The integration $E{\displaystyle {\int }_0^{t_p}\{{\tilde{x}}^{\mathrm{T}}(t)Q\tilde{x}(t)+u^{\mathrm{T}}(t)u(t)\}dt}$ in the numerator denotes the performance index of natural selection strategy of biological network in carcinogenesis. The positive symmetric weighting matrix Q is a trade-off between the state deviation $\tilde{x}(t)$ and the effort u(t), ie, a large Q will lead to a small state deviation in $\tilde{x}(t)$ but with large effort u(t), and vice versa. If Q is selected as the diagonal matrix, Q = diag[q₁,…, q_i,…, q_n], in the situation, the selection of a larger q_i will make the corresponding ith state x_i(t) be not easier to deviate from the equilibrium point, ie, a less $\tilde{x}(t)$ in carcinogenesis, and vice versa.

The physical meaning of evolution performance in (14) is that the worst-case effect of the initial condition, all possible environmental disturbance v(t), neutral genetic and epigenetic variations on the robust stability performance of $\tilde{x}(t)$ and control strategy effort of u(t) were considered as the evolution level of the biological network because the environmental disturbances and neutral genetic and epigenetic variations are unpredictable in carcinogenesis. The deviation $\tilde{x}(t)$ and evolutionary strategy u(t) are simultaneously considered in the evolutionary performance in (14) because natural selection employs a parsimonious strategy to achieve the robust stability with a less effort.

The phenotypic fitness (or phenotypic robustness) of the biologic network around the healthy phenotypic trait at the equilibrium point x_e is inversed to the evolution level of biological network,³⁹ ie,

$$f\alpha \frac{1}{e}$$ (15)

In other words, a biological network with a low evolution level e in carcinogenesis will lead to a high fitness. Therefore, the maximization of the biological network fitness to the phenotypic trait at equilibrium point x_e under the effect of genetic and epigenetic variations and environmental disturbances is equivalent to the minimization of the evolution level as

$$\max f\sim \min e$$ (16)

Therefore, by combining (14) and (16), the evolutionary strategy u(t) for the biological network suffers from the effect of natural selection to tolerate neutral phenotypic variations, to resist environmental disturbances, and to finally maintain the normal phenotype of biological network in carcinogenesis. It was to maximize the fitness of the biological network to the healthy state x_e as the following minimax evolutionary game problem

$$\begin{array}{l}{e}_0=\stackrel{\min }{u(t)\in {{\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}}^e}\\ =\stackrel{\min }{u(t)\in {\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}}\left[\underset{v(t)\in L_2[0,t_{\mathrm{p}}]}{\max }\left(\frac{E{\displaystyle {\int }_0^{t_{\mathrm{p}}}\{{\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)\}dt}}{E\{{\tilde{x}}^T(0)\tilde{x}(0)\}+E{\displaystyle {\int }_0^{t_{\mathrm{p}}}\left\{{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})}\right\}dt+E{\displaystyle {\int }_0^{t_{\mathrm{p}}}\{v^T(t)v(t)}}\}dt}\right)\right]\end{array}$$ (17)

where u(t) was selected as $u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}$ from the total phenotypic variations ${\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-t_k)}$ to maximize the fitness (or minimize the evolution level) of biological network in carcinogenesis. Since the initial phenotypic deviation $\tilde{x}(0)$ also affects $\tilde{x}(t)$ and u(t), its effect on the evolution level was also considered in the denominator of (17). e₀ in (17) was called the network evolvability of biological network with the minimax (game) strategy u(t) by considering natural selection, ie, the Nash stochastic game is performed for biological network of the organ by natural selection to resist the unpredictable environmental disturbances and tolerate the neutral phenotypic variations because of somatic genetic and epigenetic variations in carcinogenesis. Therefore, the maximum phenotypic robustness (fitness maximization) strategy of biological network by natural selection in carcinogenesis was formulated as a stochastic Nash game problem in (17) for nonlinear stochastic biological network of (13), ie, how to select $u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}$ from the total phenotypic variations ${\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-t_k)}$ because of the genetic and epigenetic variations in carcinogenesis to solve the minimum evolution (or maximum fitness) problem of the biological network at the healthy state x_e was considered.

The evolution game in (17) has two players u(t) and v(t). The environmental disturbance v(t) and neutral phenotype variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k^{*})}$ will maximize their effect on the deviation of phenotype $\tilde{x}(t)$ and the evolution strategy effort u(t) of the biological network from its equilibrium point x_e (ie, the worst-case effect of all possible disturbances v(t)∈L [0,t_p] and neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k^{*})}$ were considered in the evolution game) and the other player u(t) selected phenotypic variations to significantly improve the network robustness (fitness) of the phenotype x_e by minimizing the worst effect of all possible neutral phenotypic variations, environmental disturbances, and initial conditions on the phenotype deviation and evolution strategy effort in carcinogenesis.

In general, it is very difficult to solve the stochastic Nash game problem in (17) directly for the evolutionary strategy of nonlinear stochastic biological network of organs in carcinogenesis. In this study, a suboptimal method was introduced to solve the stochastic Nash game problem by minimizing the upper bound e of e₀ indirectly as follows:

$$\stackrel{\min }{u(t)\in {\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}}\left[\underset{v(t)\in L_2[0,t_{\mathrm{p}}]}{\max }\left(\frac{E{\displaystyle {\int }_0^{t_{\mathrm{p}}}\{{\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)\}dt}}{E\{{\tilde{x}}^T(0)\tilde{x}(0)\}+E{\displaystyle {\int }_0^{t_{\mathrm{p}}}{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})}\}dt+E{\displaystyle {\int }_0^{t_{\mathrm{p}}}\{v^T(t)v(t)}}\}dt}\right)\right]\le e$$ (18)

The upper bound e will be given beforehand to solve the suboptimal Nash game problem in (18) at first and e will be decreased as small as possible to approach to the solution e₀ of the stochastic Nash game problem in (17).

The suboptimal stochastic Nash game problem in (18) is equivalent to the following constrained stochastic Nash game problem^34,35,38

$$\begin{array}{l}\underset{u(t)\in {\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}}{\min }\underset{v(t)\in L_2[0,t_{\mathrm{p}}]E{\displaystyle {\int }_0^{t_{\mathrm{p}}}\{{\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)\}}}{\max }\\ -e{v}^T(t)v(t)-e{\displaystyle \sum _{k=1}^{N_2(2)}{f}_k{}^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})\}dt\le eE\{{\tilde{x}}^T(0)\tilde{x}(0)\}}\end{array}$$ (19)

Let us denote

$$\begin{array}{c}J=E{\displaystyle {\int }_0^{t_{\mathrm{p}}}\{{\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)-e{v}^T(t)v(t)\}}\\ -e{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k{}^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})\}dt}\end{array}$$ (20)

Therefore, we developed two steps to solve the constrained Nash stochastic game in (18) or (19). The first step was to solve the folla

$$\begin{array}{l}{J}_0=\underset{u(t)\in {\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}}{\min }\underset{v(x)\in L_2[0,t_p]}{\max }J\\ =\underset{u(t)\in {\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}}{\min }\underset{v(x)\in L_2[0,t_p]}{\max }E{\displaystyle {\int }_0^{t_p}\{{\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)}\\ -e{v}^T(t)v(t)-e{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k{}^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})\}dt}\end{array}$$ (21)

The second step is to solve the following constraint problem

$$J_0\le eE\{{\tilde{x}}^T(0)\tilde{x}(0)\}$$ (22)

Minimax nash game strategy of linear evolutionary biological network in carcinogenesis

For the convenience of illustration, we first solve the evolutionary game strategy of linear biological network in carcinogenesis. By solving the constrained stochastic Nash game problem in (21) and (22) [or (19)] for the natural selection strategy of the linear evolutionary stochastic biological network in (9) with the effect of the natural selection in carcinogenesis, we get the following result.

Proposition 1

For the linear stochastic evolutionary biological network (9) in carcinogenesis, the constrained stochastic Nash game problem in (18) or (19) can be solved by the following evolutionary game strategy u^*(t) and worst-case environmental disturbance v^*(t)

$$u^{*}(t)={\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}x(t)p(t-{t^{\prime }}_k)=-Px(t)}$$ (23)

$$v^{*}(t)=\frac{1}{e}{B}^{T}Px(t)$$ (24)

where the positive-definite matrix P > 0 is the solution of the following Riccati-like inequalities

$$\begin{array}{l}PA+A^{T}P-PP+Q\\ +{\displaystyle \sum _{k=1}^{N_{2\mathrm{p}}}{\lambda }_2}\left(P{A}_k+A_k^{T}P+A_k{}^{T}P{A}_k-e{A}_k{}^T{A}_k\right)+\frac{1}{e}PB{B}^{T}P\le 0\end{array}$$ (25)

and

$$P\le eI$$ (26)

where N_2p ≜ N₂(t_p), and 1 ∼ N_2p represent the total number of selected phenotypic variations and neutral phenotypic variations to the present time t_p, respectively.

Proof: see Appendix A

The Proposition 1 is the solution of the suboptimal Nash stochastic game in (18) or (19). We need to minimize the upper bound e to approach the network evolvability e₀ in (17) of the linear biological network (9) in carcinogenesis. The stochastic Nash game in (17) for network evolvability e₀ of the biological network in (9) needs to solve the following constrained optimization problem.

$$\begin{array}{l}{e}_0=\underset{P>0}{\min }e\\ \text{subject to}(25)\text{and}(26)\end{array}$$ (27)

Remark 2

1. The solution of the above network evolvability e₀ of linear biological network (9) in carcinogenesis can be obtained by decreasing e until no positive solution P in (25) within 0 < P ≤ eI in (27).

2. After solving e₀ from (27), the Riccati-like inequality in (25) becomes

$$\begin{array}{l}PA+A^{T}P-PP+Q\\ +{\displaystyle \sum _{k=1}^{N_{2\mathrm{p}}}{\lambda }_2}\left(P{A}_k+A_k{}^{T}P+A_k{}^{T}P{A}_k-e_0{A}_k{}^T{A}_k\right)+\frac{1}{e_0}PB{B}^{T}P\le 0\end{array}$$ (28)

which can be considered as the phenotypic robustness criterion of stochastic evolutionary biological network in (9) because the inequality in (28) is required for the robust stability of the evolutionary biological network under genetic and epigenetic variations and environmental disturbances in carcinogenesis.

1. The term ${\displaystyle \sum _{k=1}^{N_{2\mathrm{p}}}{\lambda }_2}\left(P{A}_k+A_k{}^{T}P+A_k{}^{T}P{A}_k-e_0{A}_k{}^T{A}_k\right)$ in the phenotypic robustness criterion (28) is the effect of neutral phenotypic variations that are not selected by natural selection but are accumulated randomly at the biological network in carcinogenesis.

2. After solving e₀ and P > 0 from the constrained optimization problem in (27), the solution of stochastic Nash game strategy in (17) for biological network of an organ by natural selection in carcinogenesis is obtained by modifying (23) and (24) as

$$u^{*}(t)={\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}x(t)p(t-{t^{\prime }}_k)}=-Px(t)$$ (29)

$$v^{*}(t)=\frac{1}{e_0}{B}^{T}Px(t)$$ (30)

where P > 0 is the solution of (28). The minimax strategy u^*(t) by considering natural selection is to select an adequate amount of phenotypic variations ${\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}p(t-{t^{\prime }}_k)}={\displaystyle \sum _{k=1}^{N_1(t)}{A}_k}$ to approach –P to enhance the robust stability of the biological system and minimize the evolution level e (or maximize the phenotypic fitness of the biological network of an organ via $f_0=\frac{1}{e_0}$). With the negative feedback –Px because of Nash game evolution strategy by natural selection, the phenotypic robustness criterion in (28) was rearranged as

$$\begin{array}{l}P\left(A-\frac{1}{2}P\right)+{\left(A-\frac{1}{2}P\right)}^{T}P+Q\\ +{\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2}\left(P{A}_k+A_k{}^{T}P+A_k{}^{T}P{A}_k-e{A}_k{}^T{A}_k\right)+\frac{1}{e_0}PB{B}^{T}P\le 0\end{array}$$ (31)

The eigenvalues of $\left(A-\frac{1}{2}P\right)$ are farther to the left-hand side of the complex s-domain than those of A, such that the network robustness of biological network is improved by negative feedback loops of the minimax Nash game strategy $u^{*}(t){\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}x(t)}p(t-{t^{\prime }}_k)=-Px(t)$ in carcinogenesis.

Further, the phenotypic robustness criterion in (31) of evolutionary biological network in carcinogenesis was reformulated as

$$\begin{array}{l}\underset{environmentalrobustness}{\underbrace{Q+\frac{1}{e_0}PB{B}^{T}P}}+\underset{phenotypicrobustness}{\underbrace{{\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2\left(P{A}_k+A_k{}^{T}P+A_k{}^{T}P{A}_k-e_0{A}_k{}^T{A}_k\right)}}}\\ \le \underset{enhancednetworkrobustness}{\underbrace{-\left[P\left(A-\frac{1}{2}P\right)+{\left(A-\frac{1}{2}P\right)}^{T}P\right]}}\end{array}$$ (32)

The physical meaning of network phenotypic robustness criterion in (32) is that if the enhanced network robustness of the biological network through negative feedback loops of the minimax evolutionary strategy in (17) can confer the environmental robustness to resist the environmental disturbances and phenotypic robustness and tolerate the neutral Poisson phenotypic variations, the phenotypic trait of biological network of an organ is maintained in carcinogenesis. Otherwise, the phenotypic trait of biological network of an organ may not be maintained under environmental disturbances and random Poisson genetic and epigenetic variations in carcinogenesis.³⁶ According to the statistical results,⁴⁵ the lifetime risk of many different cancers is strongly correlated (0.81) with the total number of divisions of the normal self-renewing cells maintaining that tissue’s homeostasis. Also, the violation of phenotypic robustness criterion in (32) can be explained by the number of cell divisions, and a third of cancer risk among tissues is attributable to environmental factors. Namely, the cause of the violation of phenotypic robustness criterion in (32) during carcinogenesis is attributed 1/3 risk (ie, $Q+\frac{1}{e_0}PB{B}^{T}P$) to environmental factor and 2/3 risk to intrinsic phenotypic factor (ie, ${\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2}\left(P{A}_k+A_k{}^{T}P+A_k{}^{T}P{A}_k-e_0{A}_k{}^T{A}_k\right)$) in (32).

1. Through the minimax game strategy of biological network of an organ in carcinogenesis, the accumulated phenotypic variations ${\displaystyle \sum _{k=1}^{N_1(t)}{A}_{k}p\left(t-{t^{\prime }}_k\right)=}{\displaystyle \sum _{k=1}^{N_1(t_p)}{A}_{k}p\left(t_p-{t^{\prime }}_k\right)=}{\displaystyle \sum _{k=1}^{N_{1p}}{A}_k}$, where N_1p ≜ N₁(tp), are chosen by natural selection to the amount of –P to construct negative feedback loops –Px(t) in (29). This is why many feedback loops, and the epigenetic methylations and miRNA regulations in cancer are always found to be with negative feedback (inhibition). The stochastic biological network of an organ in (9) was thus of the following form

$$\frac{dx(t)}{dt}=(A-P)x(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{A}_{k}x(t)p(t-t_k^{*})+Bv(t)}$$ (33)

Because the eigenvalues of (A − P) of biological network are in the far left-hand side of the complex s-domain, the biological network of an organ is more robust by the minimax game strategy of natural selection to resist environmental disturbances and to tolerate neutral phenotypic variations.

1. The minimax game strategy by natural selection can provide negative feedback loop –Px(t) for a greater network stability robustness improvement to buffer more neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{A}_{k}x(t)p(t-t_k^{*})}$ in carcinogenesis. However, when the neutral phenotypic variations because of Poisson genetic and epigenetic variations are accumulated in carcinogenesis, ie, the term ${\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2\left(P{A}_k+A_k{}^{T}P+A_k{}^{T}P{A}_k-e{A}_k{}^T{A}_k\right)}$ is large enough, and the network phenotypic robustness criterion of biological network in (32) is violated eventually, the biological network will become unstable at the healthy state, x(t) = x_e. Finally, the organ will become cancer.

Minimax game strategy of nonlinear biological network in carcinogenesis

After solving the minimax game strategy of linear biological network of an organ by natural selection in carcinogenesis, we will solve the minimax game problem in (17) for the evolutionary strategy of nonlinear biological network in (13) by natural selection in carcinogenesis. First, we solved the suboptimal Nash game problem in (18), or equivalently in (21) and (22), for nonlinear stochastic biological network in (17) operating near the healthy state x_e in Figure 1A.

Proposition 2

For the nonlinear stochastic biological network (13) in carcinogenesis, the suboptimal stochastic Nash game problem in (18) or (21) and (22) can be solved by the following evolutionary game strategy u^*(t) and worst-case environmental disturbance v^*(t)

$$u^{*}(t){\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x}(t))p(t-t_k)=-\frac{1}{2}\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}}$$ (34)

$$v^{*}(t)=\frac{1}{2e}{B}^T\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}$$ (35)

where the Lyapunov function $V(\tilde{x}(t))>0$ is the solution of the following constrained HJI

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^{T}f(\tilde{x})+{\displaystyle \sum _{k=1}^{N_2(t)}(V(\tilde{x}+f_k(\tilde{x})p(t-t_k^{*}))-V(\tilde{x}))}\\ -\frac{1}{4}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)+\frac{1}{4e}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T{B}^{T}B\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\\ +{\tilde{x}}^T(t)Q\tilde{x}(t)-e{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})\le 0}\end{array}$$ (36)

with

$$E\{V(\tilde{x}(t))\}\le eE\{{\tilde{x}}^T(0)\tilde{x}(0)\}$$ (37)

Proof: see Appendix B

After solving the above suboptimal Nash game problem in (18) or (21) and (22), for the stochastic biological network in (13), the minimax evolutionary strategy by natural selection in (17) was solved by minimizing the upper bound e as follows:

$$\begin{array}{l}{e}_0=\underset{V(\tilde{x}(t))>0^e}{\min }\\ subjectto(36)and(37)\end{array}$$ (38)

If $V(\tilde{x})$ and e₀ are obtained by solving the HJI-constrained optimization in (38), the network robust stability criterion in (36) and (37) in carcinogenesis was modified as

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^{T}f(\tilde{x}(t))+{\displaystyle \sum _{k=1}^{N_2(t)}(V(\tilde{x}(t)+f_k(\tilde{x}(t))p(t-t_k^{*}))-V(\tilde{x}(t)))}\\ -\frac{1}{4}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)+\frac{1}{4e_0}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T{B}^{T}B\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\\ +{\tilde{x}}^T(t)Q\tilde{x}(t)-e_0{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k{}^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})\le 0}\end{array}$$ (39)

with $V(\tilde{x}(t))\le e_0{\tilde{x}}^T(0)\tilde{x}(0)$. Since the HJI in (39) is necessary for the phenotype at $\tilde{x}(t)=0$ or x(t) = x_e to be robust, it can be considered as the phenotypic trait robustness criterion of nonlinear stochastic network in (13) at the phenotypic state x_e in carcinogenesis.

In this situation, the evolutional game strategy u^*(t) in (34) and the worst-case environmental disturbance v^*(t) in (35) were modified, respectively, as follows:

$$u^{*}(t)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k}(\tilde{x}(t))p(t-{t^{\prime }}_k)=-\frac{1}{2}\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}$$ (40)

$$v^{*}(t)=\frac{1}{2e_0}{B}^T\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}$$ (41)

where the Lyapunov function $V(\tilde{x}(t))$ is the solution of the network robust stability criterion in (39). The minimax strategy of u^*(t) is to select ${\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x}(t))p(t-t_k^{*})}$ to approach the nonlinear negative feedback − $\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}$ to minimize the evolution level e, and v^* denotes the worst-case disturbance to maximize evolution level e.

The robust stability criterion in (39) was rewritten as the following phenotypic robustness criterion in carcinogenesis.

$$\begin{array}{c}\underset{phenotypicrobustness}{\underbrace{{\displaystyle \sum _{k=1}^{N_2(t)}\left(V(\tilde{x}(t)+f_x(\tilde{x}(t))p(t-{t^{\prime }}_k))-V(\tilde{x}(t))\right)}-e_0{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k{}^T}(\tilde{x})f_k(\tilde{x})p(t-{t^{\prime }}_k)}}\\ \underset{enviromentalrobustness}{\underbrace{+{\tilde{x}}^T(t)Q\tilde{x}(t)+\frac{1}{4e_0}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T{B}^{T}B\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}}\\ \le \underset{enhancednetworkrobustness}{\underbrace{-\frac{1}{2}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T\left(f(\tilde{x}(t))-\frac{1}{4}\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\right)}}\\ \underset{enhancednetworkrobustness}{\underbrace{-\frac{1}{2}{\left(f(\tilde{x}(t))-\frac{1}{4}\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}}\end{array}$$ (42)

The first two terms are because of neutral phenotypic variations from the genetic and epigenetic variations in carcinogenesis, the last two terms on the left-hand side of (42) are by the worst-case environmental disturbance, and the terms on the right-hand side of (42) are because of the negative feedback through evolutionary minimax game strategy $u^{*}(t)=\frac{1}{2}\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}$. The biological meaning of phenotypic robustness criterion in (42) is that if the enhanced network robustness by evolutionary minimax strategy u^*(t) can confer phenotypic robustness to tolerate the neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(\tilde{x}(t))p(t-t_k^{*})}$ and environmental disturbances, the healthy state (or phenotypic trait) x_e was maintained in carcinogenesis. By substituting the minimax game evolutionary strategy u^*(t) in (40) into the nonlinear stochastic biological network in (13), we get

$$\frac{d\tilde{x}(t)}{dt}=\left(f(\tilde{x}(t))-\frac{1}{2}\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\right)+{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(\tilde{x}(t))p(t-t_k^{*})}+Bv(t)$$ (43)

Form (43), it is seen that $\left(f(\tilde{x}(t))-\frac{1}{2}\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\right)$ can make the nonlinear stochastic biological network of an organ more robustly stable than $f(\tilde{x}(t))$ because of the negative feedback loops of minimax game evolutionary strategy by considering natural selection in carcinogenesis.

If the network robustness on the right-hand side of (42) is improved by the minimax game evolutionary strategy, from the landscape of phenotype in Figure 1A, the healthy phenotypic trait is with deeper basin and steep cliff at the equilibrium point x_e, and the nonlinear biological network can harbor much more neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(\tilde{x}(t))p(t-t_k^{*})}$ ie, much more dots in the basin of x_e. However, as time increases, the neutral phenotypic variations are accumulated to a sufficiently large amount in carcinogenesis that the enhanced network robustness on the right-hand side of (42) cannot provide enough phenotypic robustness to tolerate these accumulated neutral phenotypic variations and resist environmental disturbances, and eventually the phenotypic robustness criterion in (42) is violated. This is why cancer is an aging-associated disease and the accumulating process of network phenotypic variations can be considered as an aging process of the tissue. In this situation, these accumulated neutral phenotypic variations may provide raw materials for biological network evolution to cause a possible phenotypic transition to the early stage of tumor state at the equilibrium point x_e1, ie, a phenotypic transition may occur from the basin x_e to another basin x_e1 in Figure 1B to start another cancer phenotypic evolutionary process at the equilibrium point x_e1 in carcinogenesis.

Remark 3

For the early stage of tumor at the equilibrium point x_e1 of stage I in Figure 1B, by a similar analysis as above, we could shift the origin of nonlinear stochastic biological network of an organ to x_e1 as follows:

$$\frac{d\tilde{x}(t)}{dt}=f({\tilde{x}}^{\prime }(t))+u(t)+{\displaystyle \sum _{k=1}^{{N^{\prime }}_2(t)}{f}_k({\tilde{x}}^{\prime }(t))p(t-t_k^{*})}+B{v}^{\prime }(t)$$ (44)

where ${\tilde{x}}^{\prime }(t)=x(t)-x_{e1}$.

As the minimax game evolutionary strategy in (40) is chosen for nonlinear stochastic network in (43) by natural selection in the healthy stage of carcinogenesis, the biological network of an organ with early cancer stage is of the following form through the evolutionary game strategy at x_e1:

$$\begin{array}{l}\frac{d{\tilde{x}}^{\prime }(t)}{dt}=\left(f({\tilde{x}}^{\prime }(t))-\frac{1}{2}\left(\frac{\partial V({\tilde{x}}^{\prime }(t))}{\partial {\tilde{x}}^{\prime }}\right)\right)\\ +{\displaystyle \sum _{k=1}^{N_2{}^{\prime }(t)}{f}_k({\tilde{x}}^{\prime }(t))p(t-t_k^{*})}+Bv(t)\end{array}$$ (45)

As the neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2{}^{\prime }(t)}{f}_k({\tilde{x}}^{\prime }(t))p(t-t_k^{*})}$ are accumulated to a sufficient large amount in the early stage of carcinogenesis so that the basin of x_e1 could not tolerate these neutral phenotypic variations and has not enough ability to resist environmental disturbances simultaneously, the biological network transits from the equilibrium point x_e1 to the equilibrium point x_e2 of another phenotype of cancer to begin the second stage of carcinogenesis in Figure 1C. Finally, the phenotype of cancer stage II will be transited to the phenotype of cancer stage III in Figure 1D when the phenotypic robustness criterion at x_2e is violated by Poisson random genetic and epigenetic variations in carcinogenesis. In the late stage of carcinogenesis, the network evolutionary strategy that maintains network robustness can be hijacked by cancer biological network to maintain dysfunction at the other equilibrium point in Figure 1, as that occurs in cancer drug resistance.^25,26

Remark 4

1. The feedback loop $-\frac{1}{2}\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x}(t))p(t-{t^{\prime }}_k)}$ provides the orderly tissue structure of organ by considering natural selection. However, the accumulated neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(\tilde{x}(t))p(t-t_k^{*})}$ are the source of random and complex tissue structures of cancer and provide raw materials to increase the heterogeneity of tumor cells for a new evolutionary possibility to cause a transition from one cancer state to another cancer state in carcinogenesis.

2. In Figure 1B and C, the cancer states at x_1e and x_2e are still curable, ie, the carcinogenesis is still reversible to Figure 1A by an adequate surgical or medical treatment (one kind of enhanced negative feedback). If the healthy state is incurable (saddle point) as shown in Figure 1D, then it is impossible that this process is reversible to the healthy state in Figure 1A.

The stochastic evolutionary game of nonlinear cancer-associated network in carcinogenesis

In general, it is very difficult to solve the HJI-constrained optimization problem in (38) for the evolution game strategy u^*(t) of the evolutionary biological network in (11) in carcinogenesis. At present, there is no efficient method to solve the nonlinear partial differential HJI in (39) either analytically or numerically. Therefore, in order to simplify the stochastic evolutionary game strategy, the global linearization technique⁴⁰ is employed to interpolate the nonlinear stochastic biological network in (13) with a set of local stochastic linearized biological networks like (9) at different operation points. Using the global linearization technique,⁴⁰ we suppose that all the global linearization of the nonlinear stochastic biological network in (13) are bounded by the following L vertices as⁴⁰

$$\left[\begin{array}{c}\frac{\partial f(\tilde{x})}{\partial \tilde{x}}\\ \frac{\partial f_1(\tilde{x})}{\partial \tilde{x}}\\ ⋮\\ \frac{\partial f_{N(t)}(\tilde{x})}{\partial \tilde{x}}\end{array}\right]=C_0[\left[\begin{array}{c}{A}_1\\ A_{11}\\ ⋮\\ A_{N(t)1}\end{array}\right]\cdots \left[\begin{array}{c}{A}_i\\ A_{1i}\\ ⋮\\ A_{N(t)i}\end{array}\right]\cdots \left[\begin{array}{c}{A}_L\\ A_{1L}\\ ⋮\\ A_{N(t)L}\end{array}\right]],\forall \tilde{x}(t)$$ (46)

where C₀ denotes the convex hull of the polytope with L vertices. That is, if the local linearized biological systems at all $\tilde{x}(t)$are inside the convex hull C₀, the trajectory of the nonlinear evolutionary biological network in (13) can be represented by the convex combination of the stable trajectories of the following L local linearized biological networks at L vertices of the polytope in (46)

$$\begin{array}{l}\frac{d\tilde{x}(t)}{dt}=A_i\tilde{x}(t)+Bv(t)+u(t)\\ +{\displaystyle \sum _{k=1}^{N_2(t)}{A}_{ki}p(t-t_k^{*})\tilde{x}(t)},\text{for}i=1,\dots ,L\end{array}$$ (47)

Based on the global linearization theory,⁴⁰ if (46) holds, every trajectory of nonlinear stochastic evolutionary biological network in (13) can be represented by a convex combination of L local linear biological networks in (47), ie,

$$\frac{d\tilde{x}(t)}{dt}={\displaystyle \sum _{i=1}^L{\alpha }_i(\tilde{x})}(A_i\tilde{x}(t)+Bv(t)+u(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{A}_{ki}p(t-t_k^{*})\tilde{x}(t)})$$ (48)

where the interpolation functions ${\alpha }_i(\tilde{x})$ satisfy the following constraints: $0\le {\alpha }_i(\tilde{x})\le 1$ and ${\displaystyle \sum _{i=1}^L{\alpha }_i}(\tilde{x})=1$. The physical meaning of (48) is that the evolutionary trajectory of the nonlinear stochastic biological network in (13) can be represented by the evolutionary trajectory of the interpolated biological network in (48). In (48), the evolutionary trajectory $u(t)={\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-{t^{\prime }}_k)}$in (13) can be represented as $u(t)={\displaystyle \sum _{i=1}^L{\displaystyle \sum _{k=1}^{N_1(t)}{\alpha }_i(\tilde{x})A_{ki}p(t-{t^{\prime }}_k)}\tilde{x}(t)}$ by the global linearization technique. For the Nash game evolutionary strategy problem in (17) in the carcinogenesis of the nonlinear stochastic network in (48), we get the following results for Nash game problem in (19), (21), or (22).

Proposition 3

For the interpolated evolutionary biological network (48) in carcinogenesis, the stochastic evolutionary Nash game problem in (19) is solved by the following evolutionary strategy u^*(t) and the worst-case environmental disturbance v^*(t)

$$u^{*}(t)={\displaystyle \sum _{i=1}^L{\displaystyle \sum _{k=1}^{N_1(t)}{\alpha }_i(\tilde{x})A_{ki}p(t-{t^{\prime }}_k)}\tilde{x}(t)=-P\tilde{x}}$$ (49)

$$v^{*}(t)=\frac{1}{e}{B}^{T}P\tilde{x}(t)$$ (50)

where the positive-definite matrix P is the solution of the following Riccati-like inequalities

$$\begin{array}{l}P{A}_i+A_i{}^{T}P-PP+Q\\ +{\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2}\left(P{A}_{ki}+A_{ki}{}^{T}P+A_{ki}{}^{T}P{A}_{ki}-e{A}_{ki}{}^T{A}_{ki}\right)\\ +\frac{1}{e}PB{B}^{T}P\le 0,i=1,\dots ,L\end{array}$$ (51)

$$0<P<eI$$ (52)

Proof: see Appendix C.

Remark 5

1. In comparison with Proposition 1 of a stochastic linear biological network in carcinogenesis in (9), the Riccati-like inequality in (25) is based on the local linearized network at $\tilde{x}(t)$ while the L Riccati-like inequalities in (51) are based on L local linearized biological networks in (48). Hence, the result of the Nash evolutionary game strategy in Proposition 3 is more suitable for nonlinear stochastic biological system in carcinogenesis.

2. The Riccati-like inequalities in (51) can be considered as the local linearization of HJI in (36) at the L vertices of polytope in (46).

3. For solving P in (51), the L Riccati-like inequalities in (52) can be transformed to the following equivalent LMIs by the Schur complement transformation method⁴⁰

$$\left[\begin{array}{cc}P{A}_i+A_i{}^{T}P+Q+{\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2}\left(P{A}_{ki}+A_{ki}{}^{T}P+A_{ki}{}^{T}P{A}_{ki}-e{A}_{ki}{}^T{A}_{ki}\right)& P\\ P& -{\left(\frac{1}{e}B{B}^T-I\right)}^{-1}\end{array}\right]\le 0$$ (53)

for i = 1,2,…,L.

These LMIs in (53) can be easily solved by using the LMI toolbox in MATLAB. However, e in (51) and (52) is only the upper bound of the network evolvability e₀. The network evolvability e₀ of the nonlinear biological network under evolutionary game strategy can be obtained by solving the following LMI-constrained optimization problem

$$\begin{array}{l}{e}_0=\underset{P>0}{\min }e\\ \text{subject}\text{to}(52)\text{and}(53)\end{array}$$ (54)

Remark 6

1. The e₀ in (54) could be solved by decreasing e until (53) has no positive solution for 0 < P ≤ eI with the help of LMI toolbox in MATLAB.

2. After solving e₀ in (54), the Riccati-like inequalities for the network robustness criteria of local linearized biological networks in (51) become

$$\begin{array}{l}P{A}_i+A_i{}^{T}P-PP+Q+{\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2}(P{A}_{ki}+A_{ki}{}^{T}P+A_{ki}{}^{T}P+A_{ki}{}^{T}P{A}_{ki}\\ -e_0{A}_{ki}{}^T{A}_{ki})+\frac{1}{e_0}PB{B}^{T}P\le 0,i=1,2,\dots ,L\end{array}$$ (55)

1. After solving P and e₀ from (54), the evolutionary game strategy $u^{*}(t)=-P\tilde{x}(t)$ and the worst-case disturbance $v^{*}(t)=\frac{1}{e_0}{B}^{T}P\tilde{x}(t)$ are solved for the nonlinear stochastic network in (13).

2. The Riccati-like inequalities for local network robustness criteria in (51) can be rearranged as

$$\begin{array}{l}P\left(A_i-\frac{1}{2}P\right)+{\left(A_i-\frac{1}{2}P\right)}^{T}P+Q\\ +{\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2}\left(P{A}_{ki}+A_{ki}{}^{T}P+A_{ki}{}^{T}P{A}_{ki}-e_0{A}_{ki}{}^T{A}_{ki}\right)\\ +\frac{1}{e_0}PB{B}^{T}P\le 0,i=1,2,\dots ,L\end{array}$$ (56)

Obviously, every interaction matrix A_i of local linearized biological networks is shifted by $-\frac{1}{2}$ so that the eigenvalues of $\left(A_i-\frac{1}{2}P\right)$ are on the farther left-hand side of the s-complex domain, and thus the evolutionary biological network is with more network robustness to tolerate local genetic and epigenetic variations and resist environmental disturbances in carcinogenesis.

1. The minimax game evolutionary strategy u^*(t) is to select the total amount of phenotypic variations ${\displaystyle \sum _{i=1}^L{\displaystyle \sum _{k=1}^{N_1(t)}{\alpha }_i(\tilde{x}(t))A_{ki}p(t-{t^{\prime }}_k)}=-P}$. This is so as to select adequate genetic and epigenetic variations to form negative feedback loops $-P\tilde{x}(t)$ in the nonlinear biological network, which can resist environmental disturbances and buffer neutral genetic and epigenetic variations in carcinogenesis. Therefore, the increase of inhibitive epigenetic methylation and miRNA regulation can be observed¹⁷ in carcinogenesis.⁴⁶

2. The phenotypic robustness criterion in (56) can be rearranged as

$$\begin{array}{l}\underset{localenvironmentalrobustness}{\underbrace{Q+\frac{1}{e_0}PB{B}^{T}P}}+\underset{localphenotypicrobustness}{\underbrace{{\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2}\left(P{A}_{ki}+A_{ki}{}^{T}P+A_{ki}{}^{T}P{A}_{ki}-e_0{A}_{ki}{}^T{A}_{ki}\right)}}\\ \le \underset{enhancedlocalnetworkrobustness}{\underbrace{-\left[P\left(A_i-\frac{1}{2}P\right)+{\left(A_i-\frac{1}{2}P\right)}^{T}P\right]}},\text{for}i=1,\dots ,L\end{array}$$ (57)

The biological meaning in (57) is that if the enhanced local network robustness of each local linearized biological network by using evolutionary game strategy u^*(t) under natural selection can confer both local phenotypic robustness to buffer neutral local genetic and epigenetic variations and local environmental robustness and to resist the local environmental disturbances in carcinogenesis, the phenotype of nonlinear stochastic network with Nash game evolutionary strategy can be maintained in the basin of the equilibrium point in carcinogenesis.

1. From the phenotype robustness criterion in (57) in the cancer evolutionary process, it is more appealing to make the left-hand side of (57) as small as possible and to make the right-hand side of (57) as large as possible. In this situation, the coupling matrix B between biological network, environmental disturbances, and phenotypic effects A_ki (because of genetic mutations and epigenetic alterations) should be as small as possible. In order to maintain network robustness, there always exists some membrane or transparent membrane to make B smaller to isolate the biological network from environmental disturbance, and some redundant and modular structures make the phenotypic effect A_ki of genetic mutations and epigenetic alterations as small as possible. Further, the negative feedback loop $P\tilde{x}(t)$ mediated by evolutionary strategy u^*(t) makes the right-hand side of (57) as large as possible. These networks are also hijacked by cancer to maintain dysfunction in the late stage of carcinogenesis. This always occurs in cancer drug resistance.^25,26

2. Because the Nash game evolutionary strategy can improve significantly the local network robustness of each local linearized biological network, the nonlinear stochastic biological network will harbor more neutral genetic and epigenetic variations. However, as the harbored neutral genetic and epigenetic variations are accumulated to the extent that the third term in (57) becomes very large and the phenotypic robustness criterion of biological network in (57) cannot be guaranteed in carcinogenesis, the phenotype of biological network might be shifted to cancer state at another equilibrium point in Figure 1 with the help of the environmental disturbances and start another period of cancer network evolution at the other equilibrium point favored by natural selection.

In Silico Example

Considering the dynamic evolutionary game strategy in the oncogenesis of lung cancer, some cell lineages related to lung cancer are described as follows. The tissue contains paren-chymal cells and stromal cells. The stroma typically contains VECs, pericytes, and smooth muscle cells in its blood vessels.^27,28,30,31 Along with fibroblasts and other cell types, parenchymal cells tend to exhibit considerable phenotypic variations because of genetic and epigenetic variations during oncogenesis.²⁴

Let x₁(t) and x₂(t) be the mass of parenchymal cells with phenotypes 1 and 2, respectively. Further, let y(t) be the mass of immature VECs within the tumor and z(t) be the mass of VECs, which can be represented by the length of existing microvessel in 1 g of undiseased tissue (ie, one unit is equal to microvessel length in 1 g of undiseased tissue). The dynamic system of cells related to lung cancer is thus described as follows²⁴:

$$\begin{array}{l}\frac{d{x}_1(t)}{dt}={\mathrm{\Phi }}_1(v)x_1(t)-0.01x_1(t)\\ \frac{d{x}_2(t)}{dt}={\mathrm{\Phi }}_2(v)x_2(t)-0.01x_2(t)\\ \frac{dy(t)}{dt}=(0.06H(x_{1,}{x}_{2,}z)-0.04)y(t)\\ \frac{dy(t)}{dt}=3y(t)-0.004m(t)z(t)\end{array}$$ (58)

where h₁(m) = 0.28c(m)e^–0.06c(m), h₂(m) = 0.4c(m)e^–0.06c(m), m(t) = z(t)/[x₁(t) + x₂(t)], c(m) = 95m(t)/[1.375 + m(t)], and H(x₁,x₂,z) = [x₁(t)h₁(m) + x₂(t)h₂(m)]/[x₁(t) + x₂(t)].

The variable m(t) represents tumor vascularization (perfusion) in microvessel units per gram of parenchyma [m(t), to a physiologist, is proportional to tumor microvessel length density]. The functions Φ_i(m) express per capita growth rate of cell type i as a function of blood supply and are represented by the following equations, respectively,^24,31

$${\mathrm{\Phi }}_1(m)=\frac{0.05c^2(m)}{{0.76}^2+c^2(m)}-0.05\left(1-\frac{c^2(m)}{{0.4}^2+c^2(m)}\right)$$ (59)

and

$${\mathrm{\Phi }}_2(m)=\frac{0.05c^2(m)}{{0.53}^2+c^2(m)}-0.03\left(1-\frac{c^2(m)}{{0.1}^2+c^2(m)}\right)$$ (60)

In carcinogenesis, the tissue dynamic system in (58) suffers from phenotypic variations because of genetic and epigenetic variations and environmental disturbances as the following nonlinear stochastic Poisson system

$$\left[\begin{array}{c}\frac{d{x}_1(t)}{dt}\\ \frac{d{x}_2(t)}{dt}\\ \frac{dy(t)}{dt}\\ \frac{dz(t)}{dt}\end{array}\right]=f(x)+{\displaystyle \sum _{k=1}^{N_1(t)}{f}_k(x)}p(t-{t^{\prime }}_k)+{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k(x)}p(t-{t^{\prime }}_k)+v(t)$$ (61)

where $x(t)=\left[\begin{array}{c}{x}_1(t)\\ x_2(t)\\ y(t)\\ z(t)\end{array}\right],f(x)=\left[\begin{array}{c}{\mathrm{\Phi }}_1(m)x_1(t)-0.01x_1(t)\\ {\mathrm{\Phi }}_2(m)x_2(t)-0.01x_2(t)\\ (0.06H(x_1,x_2,z)-0.04)y(t)\\ 3y(t)-0.004m(t)z(t)\end{array}\right],f_k(x)=0.5f(x)$ and the mean of Poisson process is imposed as λ₂ = 0.05.

The equilibrium point x of the nominal lung tissue system is at x_e = [x_e1,x_e2,x_e3,x_e4]^T = [6.19 × 10^–11 2.20 × 10^–3 0 9.88 × 10^–6]^T of the nominal system in (58) simulated from the initial condition x(0) ≜ [10⁻² −1.20 ×10⁻² 0 1.16 ×10⁻⁷]^T. For the simplicity, the state of the lung tissue in (61) is shifted to the form $\tilde{x}(t)=x(t)-x_e$. Thus, the new equilibrium point of the phenotype concerned is at ${\tilde{x}}_e=O_{4\times 1}$, through the following in silico example.

Based on the above evolutionary game strategy, the phenotypic variations ${\displaystyle \sum _{k=1}^{N_1(t)}{f}_k}(\tilde{x})p(t-{t^{\prime }}_k)$ are selected by considering natural selection to construct negative feedback loops to modify the lung cancer-associated cell system in (58), in order to resist environmental disturbances and to tolerate the effect because of the neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k}(\tilde{x})p(t-t_k^{*})$. According to the global linearization scheme in (46)–(48), the nonlinear stochastic Poisson system in (61) can be approximated by interpolating the following l local linear stochastic Poisson systems

$$\left[\begin{array}{c}\frac{d{\tilde{x}}_1(t)}{dt}\\ \frac{d{\tilde{x}}_2(t)}{dt}\\ \frac{d{\tilde{x}}_3(t)}{dt}\\ \frac{d{\tilde{x}}_4(t)}{dt}\end{array}\right]={\displaystyle \sum _{i=1}^l{\varphi }_i}(\tilde{x})\left(A_i\tilde{x}(t)+{\displaystyle \sum _{k=1}^{N_1(t)}{A}_{ki}}\tilde{x}(t)p(t-{t^{\prime }}_k)+{\displaystyle \sum _{k=1}^{N_2(t)}{A}_{ki}}\tilde{x}(t)p(t-t_k^{*})\right)+v(t)$$ (62)

where A_i are given in Appendix D,A_ki = 0.5A_i and l = 5.

Based on the evolutionary game strategy in Proposition 3, natural selection is to select the phenotypic variations to construct the following negative feedback loops to improve the system robustness

$$u^{*}(t)={\displaystyle \sum _{i=1}^l{\displaystyle \sum _{k=1}^{N_1(t)}{\varphi }_i}(\tilde{x}(t))A_{ki}\tilde{x}(t)p(t-{t^{\prime }}_k)=-P\tilde{x}(t)}$$

where P is the solution of the constrained optimization problem in (54) as follows:

$$P={10}^{-4}\times \left[\begin{array}{cccc}1.59& -0.07& -0.69& -0.86\\ *& 23.34& 7.37& -4.55\\ *& *& 191.87& -41.90\\ *& *& *& 11.97\end{array}\right]$$

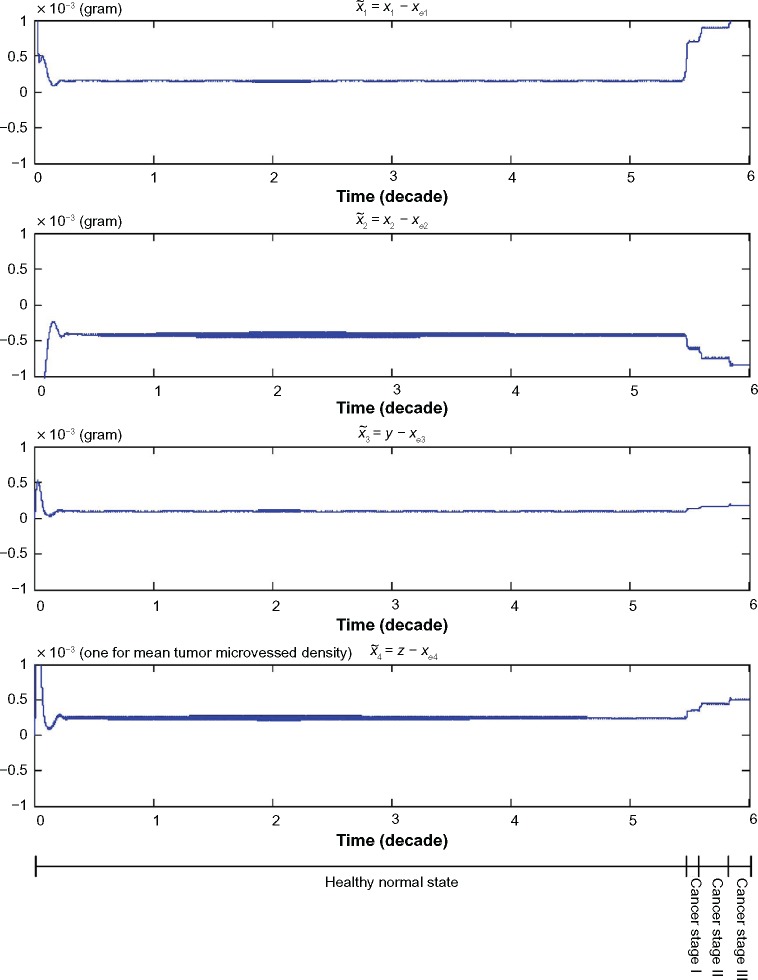
We also find the evolvability e₀ = 0.4688 and fitness f₀ = 2.1331 for the lung tissue system with the phenotype at the equilibrium point x_e = [6.19 × 10^–11 2.20 × 10^–3 0 9.88 × 10^–6]^T in (61). From the computer simulation in Figure 2, it is seen that the phenotype of the lung tissue is maintained at equilibrium point x_e under the Poisson genetic and epigenetic variations and environmental disturbances in the period of time t = 0 ∼ 19,906 (days) ≈ 54.5 (years).

Figure 2.

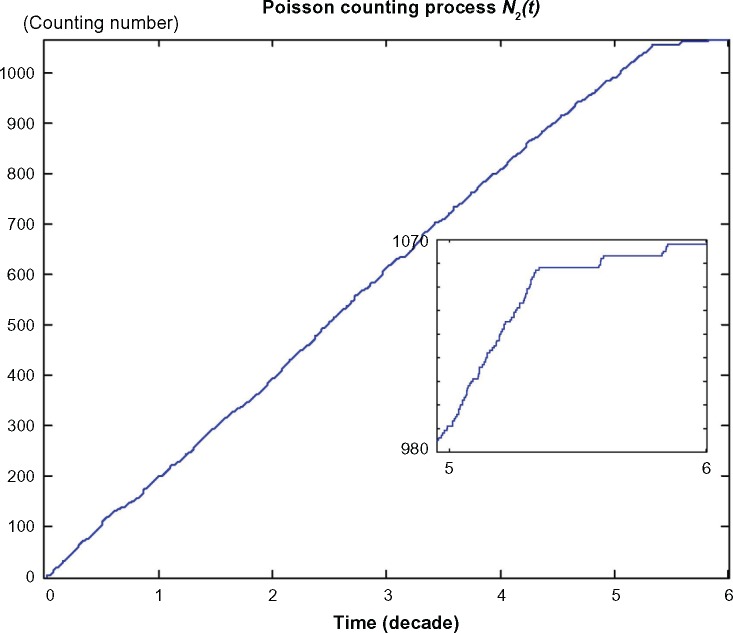
The trajectories of the nonlinear stochastic biological network of lung cancer cells in carcinogenesis with states $\tilde{x}={\left[x_1-x_e{}_1,x_2-x_{e2},y–x_{e3},z-x_{e4}\right]}^T$, suffering from Poisson genetic and epigenetic variations with Poisson counting process as shown in Figure 3 and environmental disturbance v(t). Even the network robustness is enhanced by evolutionary game strategy; however, it is seen that the phenotype will shift to another phenotype when the neutral phenotype variations are accumulated to a sufficiently large amount such that the phenotypic robustness criterion in (42) or (57) is violated (ie, the normal phenotype of the lung cancer-associated network is shifted from the equilibrium point at x_e = [6.19 × 10⁻¹¹ 2.20 × 10⁻³ 0 9.88 × 10⁻⁶]^T to the phenotype of first stage lung cancer state at the equilibrium point $x_{1e}={\tilde{x}}_{1e}+x_e={\left[1{.46\times 10}^{-4}1{.80\times 10}^{-3}1{.02\times 10}^{-4}2{.75\times 10}^{-4}\right]}^T$ at 54.5 years of age, and then the second stage lung cancer state at the equilibrium point $x_{2e}={\tilde{x}}_{2e}+x_e={\left[7.09\times 10^{-4}1.60\times 10^{-3}1.30\times 10^{-4}3.60\times 10^{-4}\right]}^T$ at 58.5 years of age and so on). Obviously, the cancer network evolution seems to increase its step in the late stages of carcinogenesis. From the literature in Ref. 47, lung cancer occurs mostly in men over 50 years, often at age of 60–75 years. Moreover, the units of state x₁, x₂, and y are grams, and the unit of state z represents the length of existing microvessel in 1 g of undiseased tissue (ie, one unit is equal to microvessel length in 1 g of undiseased tissue).

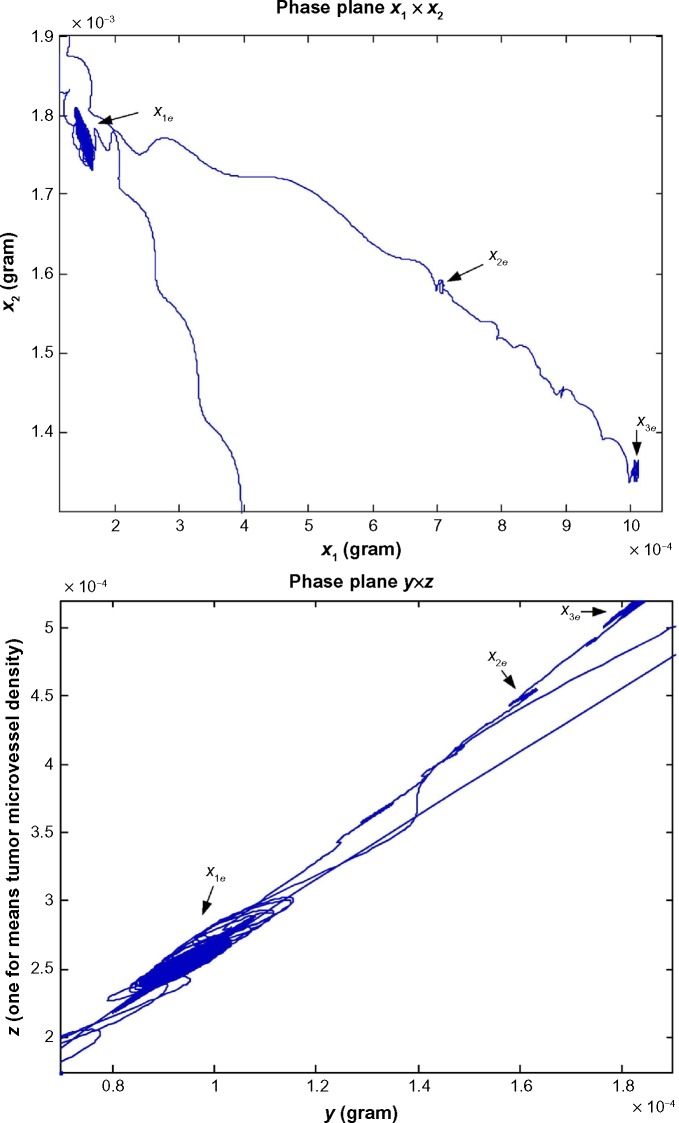
The neutral phenotypic variations ${\displaystyle \sum _{k=1}^{N_2(t)}{f}_k}(\tilde{x})p(t-t_k^{*})$ are accumulated large enough as shown in Figure 3 so that the phenotypic robustness criterion in (42) or (57) of nonlinear stochastic biological system in (61) or (62) is eventually violated in carcinogenesis. The network robust stability is thus broken down and the phenotypic trait of the lung tissue is shifted to another equilibrium point $x_{2e}={\tilde{x}}_{2e}+x_e={[7.09\times {10}^{-4}1.60\times {10}^{-3}1.30\times {10}^{-4}3.60\times {10}^{-4}]}^T$ which can be considered as the phenotype at the first stage of lung cancer, to start another evolutionary process in carcinogenesis. The simulation result in Figure 2 indicates that the phenotypic shift of the lung cancer-associated cell network takes 54.5 years from the normal state to stage I cancer, 1.5 years from stage I to stage II cancer, and 2.5 years from stage II to stage III cancer. For clarity, the evolutionary simulation in the phase plane is given in Figure 4 to illustrate the transition of lung cancer from the healthy state at x_e = [6.19 × 10^–11 2.20 × 10^–3 0 9.88 × 10^–6]^T to stage cancer at x_1e = [1.46 × 10^–4 1.80 × 10^–3 1.02 × 10^–4 2.75 × 10^–4]^T, then to stage II cancer at x_2e = [7.09 × 10^–4 1.60 × 10^–3 1.30 × 10^–4 3.60 × 10^–4]^T, and finally to stage III cancer at x_3e = [1.01 × 10^–3 1.35 × 10^–3 1.80 × 10^–4 5.12 × 10^–4]^T. Based on the results of simulation, we found that the average age of lung cancer is more than 50 years, the transition from stage I cancer to stage II cancer is about 1.5 years, and the period from stage II to stage III lung cancer is about 2.5 years. The literature⁴⁷ seems to give a statistical support to these results.

Figure 3.

The Poisson counting process of the neutral genetic and epigenetic variations N₂(t) that are accumulated in carcinogenesis of lung cancer cell lineages in the example. The vertical axis denotes the counting number of phenotypic changes of Poisson counting process N₂(t) in carcinogenesis.

Figure 4.

The evolutionary simulation in phase plane for the biological network of in silico example in carcinogenesis. This evolutionary simulation in phase plane could support the phenotypic transition of lung cancer from the healthy state at the equilibrium point x_e = [6.19 × 10⁻¹¹ 2.20 × 10⁻³ 0 9.88 × 10⁻⁶]^T, to the cancer stage I state at the equilibrium point x_1e = [1.46 × 10^–4 1.80 × 10^–3 1.02 × 10^–4 2.75 × 10^–4]^T, then to the cancer stage II state at the equilibrium point x_2e = [7.09 × 10^–4 1.60 × 10^–3 1.30 × 10^–4 3.60 × 10^–4]^T, and finally to the cancer stage III state at the equilibrium point x_3e = [1.01 × 10^–3 1.35 × 10^–3 1.80 × 10^–4 5.12 × 10^–4]^T. Moreover, the units of state x₁, x₂, and y are grams, and the unit of state z represents the length of existing microvessel in 1 g of undiseased tissue (ie, one unit is equal to microvessel length in 1 g of undiseased tissue).

Discussion

For ecologists and evolutionary biologists, natural selection and evolution are usually viewed as the domains of peppered moths and finches, driven to adapt by predators and competition. A long time ago, few evolutionary biologists could conceive that their field of biology would have a pivotal role in the understanding and combat of complex diseases such as cancer.⁴⁸ Recently, molecular biologists have acknowledged carcinogenesis as an evolutionary process involving natural selection that buffers neutral phenotypic variations and withstands environmental disturbances in the aging process.⁴⁹ In order to maintain the phenotypic stability of interest by natural selection, a stochastic Nash game strategy was developed using natural selection to improve the stability of a cancer-associated biological network. This strategy minimized the worst-case effects of uncertain neutral genetic and epigenetic variations and environmental disturbances on the variations from its normal carcinogenic phenotype. With the stochastic Nash game strategy, the robust phenotypic stability criterion for evolutionary biological networks in carcinogenesis is found in (42) or (57). This criterion states that the phenotypic robustness plus the environmental robustness should be less than or equal to the enhanced network robustness. Essentially, if the enhanced network robustness by the stochastic Nash game strategy can confer both phenotypic robustness to buffer neutral Poisson and epigenetic and genetic variations, and environmental robustness to withstand environmental disturbances in carcinogenesis, by considering natural selection, the network phenotype of the cancer-associated biological network can be robustly stable in the basin around the equilibrium point x_e. In the evolutionary period, the linear network interaction matrix A is modified by $\left(A-\frac{1}{2}P\right)$ in (31) [or $f(\tilde{x}(t))$ is modified by $f(\tilde{x}(t))-\frac{1}{4}\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}$ in (42) for a non-linear network case] through negative feedback loops of the stochastic Nash game strategy. This could then decrease the evolvability e₀ of the biological network in carcinogenesis or increase the fitness f₀ of the biological network in (15). In this situation, the phenotype is more robust because of the larger and deeper basin in the phenotypic landscape, as presented in Figure 1. However, when large amounts of neutral genetic and epigenetic variations are continuously accumulated in a larger and deep basin in a period of carcinogenesis, they may provide more raw material for new evolutionary heterogenic possibilities through random genetic drift.^24,25,50 Therefore, the stochastic Nash game strategy may improve the network robustness in order to maintain the phenotypic trait in an evolutionary period and may eventually improve the evolution of the cancer biological network, with a phenotypic shift from the normal phenotype at the equilibrium point x_e to the cancer phenotype at the equilibrium point x_1e. This evolutionary phenomenon has been illustrated by the in silico example of the evolutionary network of lung cancer cells in Figure 2.

From the phenotypic robustness criterion in (42) or (57), the results reveal two ways to improve the phenotypic robustness of the evolutionary biological network in carcinogenesis. One way is to improve the stability and robustness of the network by making the right-hand side of (42) or (57) as large a value as possible so that the phenotypic robustness criterion always holds. The other way to improve the stability and robustness of the network is to reduce the effect of neutral genetic variations A_ki and the coupling B of environmental disturbances v(t) on the biological network. This has the effect of making the left-hand side of (42) or (57) as small as possible. The evolutionary game strategy involves selecting certain somatic phenotypic variations to develop negative feedback loop $-\frac{1}{2}\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}$ in (40) as the first way to improve the robustness of nonlinear biological networks and thus maintain their normal phenotypic function. This is why many negative feedback loops and inhibitive epigenetic methylations and miRNA regulations in biological networks have been found to improve the robustness of the network and prevent a phenotypic shift to the cancerous state. Furthermore, there are numerous redundant, membranous, modular, and complex structures in cancer biological networks, which are helpful in attenuating the effect of intrinsic neutral genetic and epigenetic variations and environmental disturbances on the left-hand side of (42) or (57). This is the second way to maintain the phenotype of the biological network in carcinogenesis. After enduring several evolutionary stages, the biological network phenotype is shifted to late-stage cancer at certain equilibrium points. These robust network strategies are always hijacked by cancer in order to resist anticancer drugs. This is why many anticancer treatments have limited success and cures remain elusive.^25,26 Therefore, based on the phenotype robustness criterion of the evolutionary network in (42) or (57), we could gain deep insight into the development of complex negative feedback, and redundant, modular, membranous, and scale-free structures of cancer tissue by natural selection during carcinogenesis.

Recently, it has been reported that the phenotype of a synthetic gene network always evolves because of genetic mutations from one generation to another generation, thus making it difficult to properly design a robust synthetic gene network.^43,50–53 Therefore, the robust phenotypic criterion in (42) and (57), based on the proposed stochastic Nash game strategy, may be a suitable remedy for the limitations of conventional synthetic design methods.

Conclusion

In this study, evolutionary biological networks with unpredictable somatic genetic variations and uncertain environmental disturbances in carcinogenesis were modeled as nonlinear Poisson dynamic systems. An evolutionary Nash game strategy was developed to select certain phenotypic somatic variations to construct negative feedback loops. This strategy buffered neutral genetic and epigenetic variations and unpredictable environmental disturbances to efficiently improve network robustness and to avoid shifting to the cancerous state, thus maintaining the phenotype favored by natural selection during carcinogenesis. The phenotypic robustness criterion for each cancer-related state at an equilibrium point of the evolutionary biological network during carcinogenesis was also derived from this study. We determined that the evolutionary Nash game strategy was able to select certain phenotypic variations because of somatic Poisson genetic and epigenetic variations. Negative feedback loops were constructed to make the basin of the phenotype equilibrium point significantly deeper and wider in the phenotypic landscape (Fig. 1), so that the biological network could buffer more neutral genetic and epigenetic variations and withstand additional environmental disturbances during carcinogenesis. However, as enough random neutral genetic and epigenetic variations accumulated over a long period of time, they provided the raw heterogenic material for new adaptation and evolutionary innovation. This enabled the shift to a new phenotype at a neighboring equilibrium point to commence another period of network evolution during carcinogenesis. Taken together, our results demonstrate why cancer is a disease associated with aging.

The global linearization technique was also employed to simplify the solution procedure for the nonlinear biological network in carcinogenesis. In this manner, a difficult HJI-constrained optimization problem for the evolutionary Nash game strategy could be simplified to an equivalent LMI-constrained optimization problem. Therefore, the trade-off between evolvability, genetic and epigenetic robustness, and network phenotypic robustness can be easily discussed in terms of the local stability robustness and local environmental disturbance-filtering ability of a set of local linear evolutionary biological networks. In the example of a dynamic system of cells related to lung cancer, the results of the simulation support the proposed game strategy of an evolutionary biological network during carcinogenesis.

Appendix

Appendix A: Proof of Proposition 1

For the linear stochastic biological network in (9), since x_e=0, $\tilde{x}(t)=x(t)-x_e=x(t)$. From (20), we get

$$\begin{array}{l}J=E{\displaystyle {\int }_0^{t_p}\{x^T(t)Qx(t)+u^T(t)u(t)-e{v}^T(t)v(t)-e{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k^T{A}_{k}x(t)p(t-t_k^{*})}\}dt}\\ =E\{x^T(0)Px(0)\}-E\{x^T(t_p)Px(t_p)\}+E{\displaystyle {\int }_0^{t_p}\{x^T(t)Qx(t)+u^T(t)u(t)-e{v}^T(t)v(t)}\\ -e{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k^T{A}_{k}x(t)p(t-t_k^{*})+\frac{d}{dt}x}{(t)}^{T}Px(t)\}dt\end{array}$$

$$\begin{array}{l}=E\{x^T(0)Px(0)\}-E\{x^T(t_p)Px(t_p)\}+E{\displaystyle {\int }_0^{t_p}\{x^T(t)Qx(t)+u^T(t)u(t)-e{v}^T(t)v(t)}\\ +(x^T(t)A^T+u^T(t)+v^T(t)B^T)(P(x(t)+x^T(t)P(Ax(t)+u(t)+Bv(t))\\ +\left({\displaystyle \sum _{k=1}^{N_2(t)}((x^T(t)+x^T(t)A_k^{T}p(t-t_k^{*}))P}(x(t)+A_{k}x(t)p(t-t_k^{*}))-x^T(t)Px(t))\right)\\ -e{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k^T{A}_{k}x(t)p(t-t_k^{*})\}dt}\end{array}$$

$$\begin{array}{l}=E\{x^T(0)Px(0)\}-E\{x^T(t_p)Px(t_p)\}+E{\displaystyle {\int }_0^{t_p}\{x^T(t)Qx(t)+u^T(t)u(t)-e{v}^T(t)v(t)}\\ +(x^T(t)A^{T}Px(t)+u^T(t)Px(t)+v^T(t)B^{T}Px(t)+x^T(t)PAx(t)+x^T(t)Pu(t)\\ +x^T(t)PAv(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)Px(t){\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k^{T}Px(t)p(t-t_k^{*})}}\\ +{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)P{A}_{k}x(t)p(t-t_k^{*})+{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k^{T}P{A}_{k}x(t)p(t-t_k^{*})-}{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)Px(t)}}\\ -e{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k^T{A}_{k}x(t)p(t-t_k^{*})\}}dt\end{array}$$

$$\begin{array}{l}=E\{x^T(0)Px(0)\}-E\{x^T(t_p)Px(t_p)\}+E{\displaystyle {\int }_0^{t_p}\{x^T(t)Qx(t)+u^T(t)u(t)}\\ -e{v}^T(t)v(t)+x^T(t)A^{T}Px(t)+u^T(t)Px(t)+v^T(t)B^{T}Px(t)+x^T(t)PAx(t)\\ +x^T(t)Pu(t)+x^T(t)PBv(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A^T{}_{k}Px(t)p(t-t_k^{*})}\\ +{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)P{A}_{k}x(t)p(t-t_k^{*})+{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k{}^{T}P{A}_{k}x(t)p(t-t_k^{*})}}\\ -e{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k{}^T{A}_{k}x(t)p(t-t_k^{*})\}}dt\end{array}$$

$$\begin{array}{l}=E\{x^T(0)Px(0)\}-E\{x^T(t_p)Px(t_p)\}+E{\displaystyle {\int }_0^{t_p}\{x^T(t)Qx(t)+x^T(t)A^{T}Px(t)}\\ +x^T(t)PAx(t)+{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k{}^{T}Px(t)p(t-t_k^{*})+}{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)P{A}_{k}x(t)p(t-t_k^{*})}\\ +{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k{}^{T}P{A}_{k}x(t)p(t-t_k^{*})-e{\displaystyle \sum _{k=1}^{N_2(t)}{x}^T(t)A_k{}^T{A}_{k}x(t)p(t-t_k^{*})}}\\ +{\left(u(t)+Px(t)\right)}^T\left(u(t)+Px(t)\right)-x^T(t)PPx(t)\\ -{\left(\sqrt{ev}(t)-\frac{1}{\sqrt{e}}{B}^{T}Px(t)\right)}^T\left(\sqrt{ev}(t)-\frac{1}{\sqrt{e}}{B}^{T}Px(t)\right)+\frac{1}{e}{x}^T(t)PB{B}^{T}Px(t)\}dt\end{array}$$

Then, the stochastic Nash game in (21) becomes

$$\begin{array}{l}{J}_0=\underset{u\in {\displaystyle \sum _{k=1}^{N_{1(t)}}{A}_{k}x(t)p(t-{t^{\prime }}_k)}}{\min }\underset{v(t)}{\max }J\\ =E\{x{\left(0\right)}^{T}Px(0)\}-E\{x{\left(t_p\right)}^{T}Px(t_p)\}+E{\displaystyle {\int }_0^{t_p}\{x{\left(t\right)}^T(PA+A^{T}P-PP+Q}\\ +{\displaystyle \sum _{k=1}^{N_2(t)}{\lambda }_2(P{A}_k+A_k{}^{T}P+A_k{}^{T}P{A}_k-e{A}_k{}^T{A}_k)+\frac{1}{e}PB{B}^{T}P})x(t)\}dt\end{array}$$

By the Riccati-like inequality in (25), we get J0 has the upper bound as follows

$$J_0\le E\{x^T(0)Px(0)\}$$

By the second step of stochastic Nash game in (22), we get

$$P\le eI$$

which is the inequality in (26).

Appendix B: Proof of Proposition 2

For the nonlinear stochastic biological network in (13), we get

$$J=E{\displaystyle {\int }_0^{t_p}\{{\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)-e{v}^T(t)v(t)-}e{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})f_k{}^{(\tilde{x})}p(t-t_k^{*}})\}dt$$ (B.1)

For some Lyapunov positive $V(\tilde{x}(t))$, get the following equivalent equation

$$\begin{array}{l}J=E\{V(\tilde{x}(0))\}-E\{V(\tilde{x}(t_p))\}\\ +E{\displaystyle {\int }_0^{t_p}\{{\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)-e{v}^T(t)v(t)}\\ -e{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})f_k{}^{(\tilde{x})}p(t-t_k^{*}})\}dt+E{\displaystyle {\int }_0^{t_p}\{dV(\tilde{x}(t))\}}\end{array}$$ (B.2)

By the Itô’s formula of Poisson process in (13), we get

$$\begin{array}{l}E{\displaystyle {\int }_0^{t_p}\{dV(\tilde{x}(t))\}}\\ =E{\displaystyle {\int }_0^{t_p}\{{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T(f(\tilde{x})+u(t)+Bv(t)}\\ +{\displaystyle \sum _{k=1}^{N_2(t)}(V(\tilde{x}+f_k(\tilde{x})p(t-t_k^{*}}))-V(\tilde{x})))\}dt\end{array}$$ (B.3)

Substituting (B.3) into (B.2), we get

$$\begin{array}{l}J=E\{V(\tilde{x}(0))\}-E\{V(\tilde{x}(t_p))\}\\ +E{\displaystyle {\int }_0^{t_p}\{({\tilde{x}}^T(t)Q\tilde{x}(t)+u^T(t)u(t)}\\ -e{v}^T(t)v(t)-e{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})p(t-t_k^{*}}))\\ +{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T(f(\tilde{x})+u(t)+Bv(t))\\ +{\displaystyle \sum _{k=1}^{N_2(t)}(V(\tilde{x}+f_k(\tilde{x})p(t-t_k^{*}))-V(\tilde{x})))\}dt}\end{array}$$ (B.4)

By the fact that

$$\begin{array}{l}{u}^T(t)u(t)+{\left(\frac{\left(\partial V(\tilde{x}(t))\right)}{\partial \tilde{x}}\right)}^{T}u(t)\\ ={\left(u(t)+\frac{1}{2}\left(\frac{\left(\partial V\left(\tilde{x}\left(t\right)\right)\right)}{\partial \tilde{x}}\right)\right)}^T\left(u(t)+\frac{1}{2}\left(\frac{\partial V\left(\tilde{x}\right)\left(t\right)}{\partial \tilde{x}}\right)\right)-\frac{1}{4}{\left(\frac{\left(\partial V\left(\tilde{x}\left(t\right)\right)\right)}{\partial \tilde{x}}\right)}^T\left(\frac{\left(\partial V\left(\tilde{x}\left(t\right)\right)\right)}{\partial \tilde{x}}\right)\\ -ev(t)v(t)+{\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)}^{T}Bv\left(t\right)\\ =-{\left(\sqrt{e}v(t)-\frac{1}{2\sqrt{e}}{B}^T\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)\right)}^T\left(\sqrt{e}v(t)-\frac{1}{2\sqrt{e}}{B}^T\left(\frac{\partial V\left(\tilde{x}\right)\left(t\right)}{\partial \tilde{x}}\right)\right)\\ +\frac{1}{4e}{\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)\end{array}$$ (B.5)

Substituting (B.5) into (B.4), we get

$$\begin{array}{l}J=E\left\{V\left(\tilde{x}\left(0\right)\right)\right\}-E\left\{V\left(\tilde{x}\left(t_p\right)\right)\right\}\\ +E{\displaystyle {\int }_0^{t_p}\{{\tilde{x}}^T\left(t\right)Q\tilde{x}\left(t\right)+{\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)}^{T}f\left(\tilde{x}\right)}\\ +{\displaystyle \sum _{k=1}^{N_2\left(t\right)}\left(V\left(\tilde{x}+f_k\left(\tilde{x}\right)p\left(t-t_k^{*}\right)\right)-V\left(\tilde{x}\right)\right)-\frac{1}{4}{\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)}\\ +{\left(u\left(t\right)+\frac{1}{2}\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)\right)}^T\left(u\left(t\right)+\frac{1}{2}\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)\right)\\ -{\left(\sqrt{e}v\left(t\right))-\frac{1}{2\sqrt{e}}{B}^T\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)\right)}^T\left(\sqrt{e}v\left(t\right))-\frac{1}{2\sqrt{e}}{B}^T\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)\right)\\ +\frac{1}{4e}{\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V\left(\tilde{x}\left(t\right)\right)}{\partial \tilde{x}}\right)-e{\displaystyle \sum _{k=1}^{N_2\left(t\right)}{f}_k^T\left(\tilde{x}\right)f_k^T\left(\tilde{x}\right)f_k\left(\tilde{x}\right)p\left(t-t_k^{*}\right)\}dt}\end{array}$$ (B.6)

Then,

$$\begin{array}{l}\underset{u(t)}{\min }\underset{v(t)}{\max }J\\ =E\{V(\tilde{x}(0))\}-E\{V(\tilde{x}(t))\}+\underset{u(t)}{\min }\underset{v(t)}{\max }E{\displaystyle {\int }_0^{t_p}\{{\tilde{x}}^T(t)Q\tilde{x}(t)}\\ +{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^{T}f(\tilde{x})+{\displaystyle \sum _{k=1}^{N_2(t)}\left(V\left(\tilde{x}+f_k(\tilde{x})p(t-t_k^{*})\right)-V(\tilde{x})\right)}\\ -\frac{1}{4}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\\ +{\left(u(t)-\frac{1}{2}\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\right)}^T\left(u(t)-\frac{1}{2}\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\right)\\ -{\left(\sqrt{e}v(t)-\frac{1}{2\sqrt{e}}{B}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\right)}^T\left(\sqrt{e}v(t)-\frac{1}{2\sqrt{e}}{B}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\right)\\ +\frac{1}{4e}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)-e{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})\}dt}\\ E\{V(\tilde{x}(0))\}-E\{V(\tilde{x}(t))\}\\ +E{\displaystyle {\int }_0^{t_p}({\tilde{x}}^T(t)Q\tilde{x}(t)+}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^{T}f(\tilde{x})\\ +{\displaystyle \sum _{k=1}^{N_2(t)}(V\left(\tilde{x}+f_k(\tilde{x})p(t-t_k^{*})\right)-V(\tilde{x}))-\frac{1}{4}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}\\ +\frac{1}{4e}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)-e{\displaystyle \sum _{k=1}^{N_2(t)}{f}_k^T(\tilde{x})f_k(\tilde{x})p(t-t_k^{*})\}dt}\end{array}$$ (B.7)

By the HJI in (36) and the fact $E\{V(\tilde{x}(t_p))\}\ge 0$, we get

$$\underset{u(t)}{\min }\underset{v(t)}{\max }J\le E\{V(\tilde{x}(0))\}\le eE\{{\tilde{x}}^T(0)\tilde{x}(0)\}$$ (B.8)

which is the inequality (37)

Q.E.D.

Appendix C: Proof of Proposition 3

Since we replace the nonlinear stochastic network in (13) by the interpolated local linear biological network in (48), the HJI in Proposition 2 can be replaced by

$$\begin{array}{l}\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\left({\displaystyle \sum _{i=1}^L{\alpha }_i(\tilde{x})A_i\tilde{x}(t)}\right)+{\tilde{x}}^T(t)Q\tilde{x}(t)\\ -\frac{1}{4}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)+\frac{1}{4e}{\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}\right)\\ +{\displaystyle \sum _{k=1}^{N_2(t)}\left(V\left(\tilde{x}+{\displaystyle \sum _{i=1}^L{\alpha }_i(\tilde{x})A_{ki}\tilde{x}(t)p(t-t_k^{*})}\right)-V(\tilde{x})\right)}\\ -e{\displaystyle \sum _{k=1}^{N_2(t)}{\displaystyle \sum _{i=1}^L{\displaystyle \sum _{j=1}^L{\alpha }_i(\tilde{x}){\alpha }_j(\tilde{x})A_{ki}{A}_{kj}p(t-t_k^{*})\le 0}}}\end{array}$$ (C.1)

with $V(\tilde{x}(0))\le e{\tilde{x}}^T(0)\tilde{x}(0)$. If we choose $V(\tilde{x}(t))\le {\tilde{x}}^T(t)P\tilde{x}(t)$, by the fact ${\displaystyle \sum _{i=1}^L{\alpha }_i(\tilde{x})=1}$ and $\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}=2P\tilde{x}(t)$, we get

$$\begin{array}{l}{\displaystyle \sum _{i=1}^L{\alpha }_i(\tilde{x}){\tilde{x}}^T(t)(P{A}_i+A_i^{T}P-PP+Q+\frac{1}{e}PB{B}^{T}P}\\ +{\displaystyle \sum _{k=1}^{N_{2p}}{\lambda }_2\left(P{A}_{ki}+A_{ki}^{T}P+A_{ki}^{T}P{A}_{ki}-e{A}_{ki}^T{A}_{ki}\right))\tilde{x}}(t)\le 0\end{array}$$ (C.2)

The above inequality hold if the Riccati-like inequalities in (51) hold. Further,

$$u^{*}(t)=-\frac{1}{2}\frac{\partial V(\tilde{x}(t))}{\partial \tilde{x}}=-P\tilde{x}(t),v^{*}(t)=\frac{1}{e}{B}^{T}Px(t)$$ (C.3)

which are the solutions of Nash game evolutionary strategy

$$u^{*}(t)={\displaystyle \sum _{i=1}^L{\displaystyle \sum _{k=1}^{N_1(t)}{\alpha }_i(\tilde{x})A_{i}p(t-{t^{\prime }}_k)=}}-P\tilde{x}(t),v^{*}(t)=\frac{1}{e}{B}^{T}P\tilde{x}(t)$$ (C.4)

Q.E.D.

Appendix D: Parameters A_i of global linearization scheme in silico example

$$\begin{array}{c}{A}_1\left[\begin{array}{cccc}-0.0534782& -0.0254467& 0.0520144& 0.0003126\\ 0.0005168& -0.0038916& -0.0135070& -0.0001828\\ 0.0000006& 0.0000004& -0.0237363& -4.9803948\times {10}^{-9}\\ -0.0000367& -0.0000331& -0.0000629& -0.0237372\end{array}\right]\\ A_2=\left[\begin{array}{cccc}-0.0596919& 0.0036681& 0.0000219& 0.5821825\\ -0.0001722& -0.0417919& -0.0003613& -0.2061930\\ -0.0003118& -0.0006342& -0.0395600& 0.6118400\\ 1.2427067\times {10}^{-9}& -2.6932285\times {10}^{-9}& 3.0000000& -0.0000029\end{array}\right]\\ A_3=\left[\begin{array}{cccc}-0.0599859& 0.0000641& 0.0001830& 0.3217975\\ -0.0000170& -0.0395879& -0.0000082& -0.0324759\\ -0.0000328& 0.0001248& -0.0398643& 0.1280925\\ 2.0485833\times {10}^{-10}& -2.7951458\times {10}^{-10}& 3.0000000& -0.0000008\end{array}\right]\\ A_4=\left[\begin{array}{cccc}-0.0599820& 0.0004016& -0.0000326& 0.2173435\\ -0.0000171& -0.0400054& 0.0000678& -0.0178187\\ -0.0000197& 0.0000895& -0.0398498& 0.0719197\\ 1.1501642\times {10}^{-10}& -1.9750672\times {10}^{-9}& 3.0000000& -0.0000005\end{array}\right]\\ A_5=\left[\begin{array}{cccc}-0.0600004& 0.0005292& 0.0002048& 0.1781146\\ -0.0000175& -0.0401022& 0.0000980& -0.0078165\\ -0.0000255& 0.0000218& -0.0397513& 0.0722756\\ 1.7267656\times {10}^{-10}& -1.3279752\times {10}^{-9}& 3.0000000& -0.0000005\end{array}\right]\end{array}$$