Abstract
Proteins operate and interact with partners by dynamically exchanging between functional substates of a conformational ensemble on a rugged free energy landscape. Understanding how these substates are linked by coordinated, collective motions requires exploring a high-dimensional space, which remains a tremendous challenge. While molecular dynamics simulations can provide atomically detailed insight into the dynamics, computational demands to adequately sample conformational ensembles of large biomolecules and their complexes often require tremendous resources. Kinematic models can provide high-level insights into conformational ensembles and molecular rigidity beyond the reach of molecular dynamics by reducing the dimensionality of the search space. Here, we model a protein as a kinematic linkage and present a new geometric method to characterize molecular rigidity from the constraint manifold Q and its tangent space
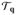 Q at the current configuration q. In contrast to methods based on combinatorial constraint counting, our method is valid for both generic and non-generic, e.g., singular configurations. Importantly, our geometric approach provides an explicit basis for collective motions along floppy modes, resulting in an efficient procedure to probe conformational space. An atomically detailed structural characterization of coordinated, collective motions would allow us to engineer or allosterically modulate biomolecules by selectively stabilizing conformations that enhance or inhibit function with broad implications for human health.
Q at the current configuration q. In contrast to methods based on combinatorial constraint counting, our method is valid for both generic and non-generic, e.g., singular configurations. Importantly, our geometric approach provides an explicit basis for collective motions along floppy modes, resulting in an efficient procedure to probe conformational space. An atomically detailed structural characterization of coordinated, collective motions would allow us to engineer or allosterically modulate biomolecules by selectively stabilizing conformations that enhance or inhibit function with broad implications for human health.
Keywords: Protein, Rigidity, Nullspace, Singular configuration, Protein collective motions, Conformational sampling
1. Introduction
A protein is a linear sequence of amino acids or residues, synthesized into a polypeptide chain by the ribosome (Figure 1a,b). The function of a protein is largely dictated by its folded, three-dimensional structure, which determines its ability to bind to other molecules, such as small ligands, other proteins, or nucleic acids [6]. Advances in imaging technology such as X-ray crystallography, nuclear magnetic resonance spectroscopy or cryo-electron microscopy increasingly enable rapid characterization of biological macromolecules in atomic detail. The Protein Data Bank (PDB), an international repository of the three-dimensional coordinates of protein, RNA, and DNA, now contains over 100, 000 structures [2]. However, proteins fluctuate between conformational substates spanning a wide range of spatiotemporal scales to perform their cellular function and engage with partners (Figure 1c). These motions range from pico-second timescale atomic vibrations to diffusive, collective motion at millisecond or longer timescales often associated with biological activity [35]. Despite enormous advances in experimental techniques, we cannot directly observe biomolecular, spatiotemporal ensembles. Characterizing these exchanges and understanding how different parts of proteins are dynamically coupled through collective motions can tremendously benefit human health: It would allow us to engineer or allosterically modulate biomolecules by selectively stabilizing conformations that enhance or inhibit function.
Figure 1.
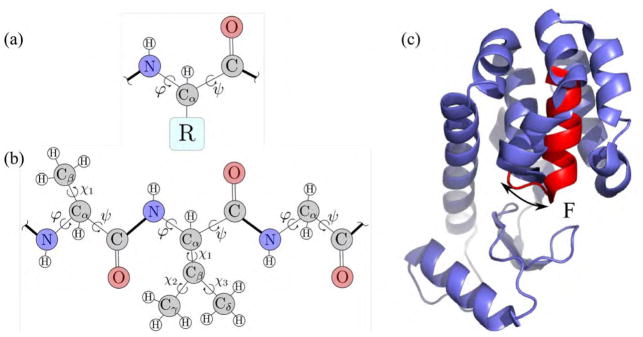
A protein is a polypeptide chain folded into a three-dimensional shape. (a) An amino acid or residue consists of a fixed backbone, and one of 20 side-chains, indicated by R, covalently bound to the Cα backbone atom. (b) A polypeptide chain is a kinematic linkage, with groups of atoms as rigid bodies and covalent, rotatable bonds as joints with a revolute degree of freedom (φ, ψ, χ). (c) A mutant T4 lysozyme can exchange between a low energy ground state, and a sparsely populated excited state [4]. Helix F collectively rearranges between the ground state (blue) and the excited state (red).
Experimental techniques have significant potential to uncover a molecular basis for protein conformational dynamics. While X-ray crystallography experiments mostly yield a single, low-energy ground state of the molecule, nuclear magnetic resonance relaxation dispersion experiments can provide insight into functionally relevant excited states, but lack a structural basis for collective motions. Computationally integrating these data sources has proved challenging [8, 9]. Molecular dynamics simulations can yield atomically detailed trajectories, but rely on imperfect force-fields and often demand specialized hardware [17] and algorithms to examine long, biologically relevant time scales or larger molecules [25]. By contrast, non-deterministic conformational sampling-based algorithms, such as kinematics-based methods, can provide high-level insights into conformational ensembles at spatiotemporal scales beyond the reach of molecular dynamics simulations [9, 10, 29].
Kinematics-based methods exploit that the linear, branched topology of a biomolecule closely resembles kinematic truss structures. These methods represent a protein or nucleic acid as a kinematic linkage with groups of atoms as rigid bodies and covalent, rotatable bonds as joints with a revolute degree of freedom (Figure 1a,b). Hydrogen bonds and other non-covalent interactions are encoded as holonomic constraints, resulting in nested, interdependent cycles that require coordinated changes of the degrees of freedom, effectively reducing the dimensionality of configuration space. The remaining motions are known as floppy modes and yield collective motion of the degrees of freedom in a lower-dimensional constraint manifold Q [5, 34, 36, 41]. The constraints reduce conformational flexibility or can even completely rigidify larger substructures of biomolecules by merging rigid bodies through rotationally locked degrees of freedom or hydrogen bonds. Configuration space, i.e., the set of all degrees of freedom, is sometimes denoted as conformation space when applied to proteins.
In generic, e.g., non-singular configurations rigidity is a topological property, which is characterized completely by combinatorial, explicit constraint counting using an exact, graph theoretical ‘pebble game’ algorithm [21, 22]. However, the pebble game fails to recognize additional flexibility resulting from special geometries like singular or symmetric configurations. In these non-generic situations, rigidity is a geometric property that cannot be characterized by combinatorial methods. While singularities form a non-dense subset of configuration space [18], biomolecules could exploit specific characteristics of non-genericity such as increased instantaneous mobility [42], a change of motion pattern [38] or large motions along emerging hinge axes to control accessibility of substates. Many biomolecules possess structural symmetries that allow geometrically concerted motions [30, 23].
We present a new, geometric method that extends characterization of biomolecular rigidity to non-generic configurations. Our method recognizes that admissible infinitesimal joint velocities lie in the null space of the Jacobian of the constraint function. In generic configurations, the tangent space
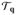 Q to the configuration manifold Q at the current configuration q coincides with the nullspace of the constraint Jacobian matrix [27]. We formulate our Jacobian in the minimum coordinates of the unconstrained linkage, leading to manageable system sizes even for very large molecules. We identify rigid substructures in the protein directly and exactly from analysis of the null space. In addition to characterizing substructures as rigid or flexible, our geometric approach provides an explicit basis for coordinated motions along floppy modes. We furthermore demonstrate how singularities affect biomolecular rigidity and identify non-generic motions that went undetected using combinatorial constraint counting.
Q to the configuration manifold Q at the current configuration q coincides with the nullspace of the constraint Jacobian matrix [27]. We formulate our Jacobian in the minimum coordinates of the unconstrained linkage, leading to manageable system sizes even for very large molecules. We identify rigid substructures in the protein directly and exactly from analysis of the null space. In addition to characterizing substructures as rigid or flexible, our geometric approach provides an explicit basis for coordinated motions along floppy modes. We furthermore demonstrate how singularities affect biomolecular rigidity and identify non-generic motions that went undetected using combinatorial constraint counting.
Characterizing rigidity and reducing the dimensionality to represent proteins with fewer degrees of freedom is important for several reasons. It can reveal conformationally coupled subunits in biomolecules, leading to efficient exploration of their conformation space. Together with a fast sampling procedure our rigidity analysis can lead to an efficient, multi-scale procedure to probe conformational space. Reducing dimensionality also reduces the risk of overfitting in analyzing sparse, experimental data. Furthermore, linking distance constraints to rigidity can lead to fast estimates of conformational entropy without resorting to simulations [37]. Recent studies have suggested a linear relationship between conformational entropy and binding entropy measured from calorimetry [12, 24].
The remainder of this study is organized as follows: Section 2 introduces state of the art methods for rigidity analysis. We present our new method in Section 3 and validate it on synthetic examples in Section 4. Section 5 contains results from real proteins, and Section 6 is the conclusion.
2. Background
We lay out a few principles from graph and rigidity theory in the context of proteins.
2.1. Modeling proteins using graph theory
Graph theory provides an abstract representation of a kinematic linkage. We start by introducing basic terminology and refer to [33, 16, 19, 40] for a more comprehensive review. A framework (G, p) in ℝ3 is a graph G = (V, E), with a set of edges E connecting the vertices V, and a map p: V ↦ ℝ3. Let a configuration p ∈ ℝ3|V| represent the position of each vertex v ∈ V. Edges e ∈ E represent distance constraints between vertices and constrain the motion of the framework. For an edge ei, j, adjacent vertices vi and vj define the constraint equation
| (1) |
with li, j the constant length of the connecting edge. Two frameworks (G, p) and (G, q) are equivalent if their edges are the same length. (G, p) and (G, q) are congruent if |p(u) − p(v)| = |q(u) − q(v)| for all u, v ∈ V. A motion of the framework is a continuous sequence p(t), 0 ≤ t < T of configurations with T > 0 such that p(t) satisfies all constraint equations for 0 < t ≤ T. Proteins can be described by body-bar graphs [32], where bodies or vertices correspond to individual atoms and bars or edges to distance constraints between the atoms. Body-bar-and-hinge graphs [20] have hinge constraints, a class of edges that constrain two adjacent bodies to rotate about a connecting hinge [39]. Equivalent frameworks represent different possible protein configurations for the same set of constraints.
2.2. Mobility analysis using rigidity matrices
Admissible deformations of a framework result from vertex velocities that are in agreement with all constraints. Differentiating the geometric condition (1) yields
| (2) |
with R(p) the so-called rigidity matrix and v the instantaneous velocities of the vertices. Solutions to this matrix equation correspond to infinitesimal motions in the tangent space
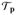 Q to the constraint manifold Q ⊂ ℝ3|V| that satisfy the constraints. We disregard rigid-body motions and only consider deformations, i.e., motions such that p(t) is not congruent to the initial configuration. A framework is called infinitesimally flexible if a deformation exists, and it is flexible, if the infinitesimal motion translates into finite motion. The same holds in reverse for rigidity, i.e., the framework is rigid if it does not admit finite motion and infinitesimally rigid if (2) has only trivial solutions (i.e. either ν = 0 or it represents only rigid body motions of the complete framework). In general, if a framework is flexible it is also infinitesimally flexible and if it is infinitesimally rigid, it also is rigid [39]. The rank of R(p) equals the number of independent rows in (2), which is at most the number of columns minus the number of trivial solutions. If the rank of the rigidity matrix is maximal, i.e. 3|V| – 6 in 3D, the framework is infinitesimally rigid. The rank also characterizes genericity: a configuration is generic if the rigidity matrix achieves maximum possible rank on all subgraphs [39, 16]. In a generic configuration, infinitesimal rigidity is equivalent to finite rigidity [13]. It follows that the rigidity matrix similarly characterizes infinitesimal and finite rigidity for generic configurations, i.e., rigidity becomes a topological property. This is not necessarily the case for non-generic or singular configurations: there, rigidity is encoded in the geometry and infinitesimal motions do not always translate to finite motions. We focus on infinitesimal rigidity and drop the term ‘infinitesimal’ for convenience.
Q to the constraint manifold Q ⊂ ℝ3|V| that satisfy the constraints. We disregard rigid-body motions and only consider deformations, i.e., motions such that p(t) is not congruent to the initial configuration. A framework is called infinitesimally flexible if a deformation exists, and it is flexible, if the infinitesimal motion translates into finite motion. The same holds in reverse for rigidity, i.e., the framework is rigid if it does not admit finite motion and infinitesimally rigid if (2) has only trivial solutions (i.e. either ν = 0 or it represents only rigid body motions of the complete framework). In general, if a framework is flexible it is also infinitesimally flexible and if it is infinitesimally rigid, it also is rigid [39]. The rank of R(p) equals the number of independent rows in (2), which is at most the number of columns minus the number of trivial solutions. If the rank of the rigidity matrix is maximal, i.e. 3|V| – 6 in 3D, the framework is infinitesimally rigid. The rank also characterizes genericity: a configuration is generic if the rigidity matrix achieves maximum possible rank on all subgraphs [39, 16]. In a generic configuration, infinitesimal rigidity is equivalent to finite rigidity [13]. It follows that the rigidity matrix similarly characterizes infinitesimal and finite rigidity for generic configurations, i.e., rigidity becomes a topological property. This is not necessarily the case for non-generic or singular configurations: there, rigidity is encoded in the geometry and infinitesimal motions do not always translate to finite motions. We focus on infinitesimal rigidity and drop the term ‘infinitesimal’ for convenience.
2.3. Mobility analysis using the pebble game
Instead of using the full rigidity matrix to determine mobility, there exist fast integer methods called pebble game algorithms. The pebble game [21, 22] is an efficient combinatorial constraint counting algorithm to determine rigidity of body-bar, bar-joint or mixed constraint graphs at generic configurations[31], with application to mechanisms and macromolecules. For body-bar or body-bar-hinge graphs that represent macromolecules, the algorithm identifies the set of linear independent and redundant constraints (bars or edges) as well as remaining degrees of freedom (pebbles) by iteratively shifting pebbles through the graph. We use the pebble game to validate our new method on generic configurations [34, 11].
3. Methods
3.1. Kinematic modeling and constraint enforcement
In contrast to graph-theoretical approaches where each molecular bond is modeled as a constraint, our method distinguishes between dihedral angles, i.e., degrees of freedom of the open loop configuration, and cycle-closing hydrogen bond constraints. We represent a protein by a rooted, directed spanning tree, i.e., an acyclic graph G = (V, E) that connects all vertices v ∈ V such that each one, except the root, has only one incoming, directed edge e ∈ E. Vertices vi, i = 1, …, |V| represent rigid bodies, and edges e j, j = 1, …, d represent degrees of freedom.
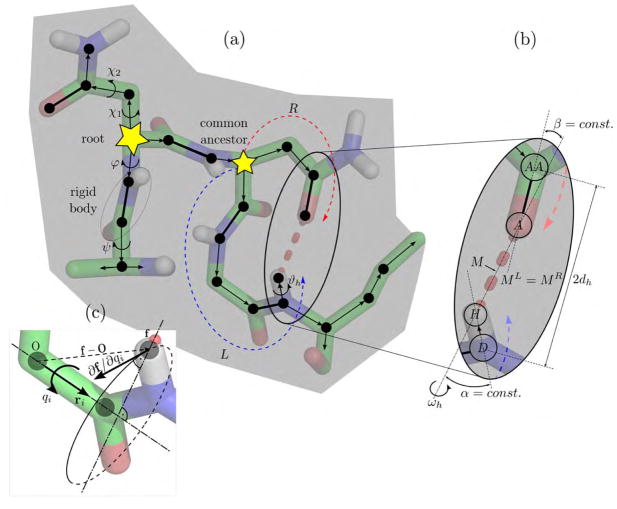
Figure 2(a) shows a protein fragment and part of the superimposed spanning tree that propagates through the molecule starting from the root. Atoms, shown as filled circles, are either connected via edges (thin arrows), i.e., the dihedral angles φ, ψ, χ, and ϑh of rotatable, single-covalent bonds, or non-rotatable double covalent bonds (thick lines) that merge adjacent atoms into a single rigid body vertex. A hydrogen bond, shown as a thick dashed red line, forms a closed kinematic cycle imposing constraints on the edges in the left (L) and right (R) branch leaving from a common ancestor. Figure 2(b) highlights the geometry of the hydrogen bond between hydrogen atom H and acceptor atom A. Each hydrogen bond only allows a rotation about angle ωh about the bond axis, restraining the position of the midpoint M and the angles α and β. This rotation affects the distance 2dh between donor atom D and base atom AA. Figure 2(c) shows the circular path of an atom with forward endpoint map f upon a rotation about the axis with unit vector ri about angle qi.
Figure 2.
Kinematic representation of a protein, green represents carbon atoms, red oxygen, blue nitrogen, and white hydrogen. (a) Directed kinematic spanning tree of a protein fragment. Edges (thin arrows) represent rotatable bonds, and vertices represent rigid groups of atoms. Individual atoms (black dots) that are connected via non-rotatable double covalent bonds (thick lines) are merged into a single rigid body. Starting from the root, each vertex is visited by a directed edge from its parent vertex. Hydrogen bonds constrain two branches leaving from a common ancestor at their end effectors. (b) Constraint parameterization. Changes in position of the hydrogen bond midpoint M along the left and the right branches have to match. The angles α and β are fixed, allowing a rotation ωh only around the hydrogen bond axis. (c) The partial derivative ∂f/∂qi required for the constraint Jacobian matrix is the cross-product ri × (f – O) and can be efficiently calculated.
Bond lengths, bond angles and the peptide torsion angle ω are assumed fixed at their initial values. Rigid bodies are the largest sets of atoms in a protein, without any degree of freedom in their interior. We initially set each atom or group of double-bonded atoms as a rigid body. The rigid bodies of atoms connected by a non-rotatable covalent bond are merged. Hydrogen atoms are explicitly included in the model. A vector qd ∈
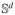 , q = (q1, …, qd)T completely specifies a conformation for a molecule with d dihedral degrees of freedom. Hydrogen bonds are encoded as holonomic constraints, resulting in closed loops or so-called kinematic cycles in G. A cycle-closing hydrogen bond connects two subtrees propagating from a common ancestor rigid body in V (Figure 2(a)). To avoid hydrogen bond dissociation, a perturbation Δq should leave the relative positions of the hydrogen bond atom H and acceptor atom A unchanged. Our model permits a rotation ωh about the hydrogen bond axis, but all other relative motion is prevented (Figure 2(b)).
, q = (q1, …, qd)T completely specifies a conformation for a molecule with d dihedral degrees of freedom. Hydrogen bonds are encoded as holonomic constraints, resulting in closed loops or so-called kinematic cycles in G. A cycle-closing hydrogen bond connects two subtrees propagating from a common ancestor rigid body in V (Figure 2(a)). To avoid hydrogen bond dissociation, a perturbation Δq should leave the relative positions of the hydrogen bond atom H and acceptor atom A unchanged. Our model permits a rotation ωh about the hydrogen bond axis, but all other relative motion is prevented (Figure 2(b)).
We distinguish between free degrees of freedom qf, which are not subject to constraints, and cycle degrees of freedom q in qd. Clearly q is the complement of qf in qd. Since free degrees of freedom are not affected by cycles, we limit our analysis to q ∈
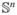 , n ≤ d. The m cycle-closing hydrogen bonds introduce 5m holonomic constraints Φ = Φ(q), which define a constraint manifold
, n ≤ d. The m cycle-closing hydrogen bonds introduce 5m holonomic constraints Φ = Φ(q), which define a constraint manifold
| (3) |
If f = f(q) ∈ ℝ3 is the forward endpoint map for the hydrogen atom H and the acceptor atom A with respect to the left (L) and right (R) branch of the cycle from their common ancestor rigid body (Figure 2b), then
| (4) |
enforces the cycle-closing constraint, where 1/2(fH + fA) denotes the mid-point M along the hydrogen bond. Note that (4) corresponds to three constraints for the Cartesian coordinates x, y, z of M. We further constrain the relative orientation of coordinate frames at H and A by keeping angles α and β between the bond axis and adjacent covalent bonds constant. If fD and fAA denote the forward maps for the donor atom D and the base atom AA, then
| (5) |
| (6) |
where
| (7) |
| (8) |
are constants determined by the initial configuration. Note that formulating the loop closure explicitly in terms of dihedral angles leads to complicated and highly non-linear expressions [14]. Since the holonomic constraints are required to hold at all times, the angular velocities q̇ satisfy the instantaneous consistency condition dΦ/dt = 0, thus
| (9) |
where J is the Jacobian matrix of the constraints. Taking the derivative of the geometric constraints from (4) – (6) with respect to dihedral angles qL in the left and qR in the right branch we obtain
| (10) |
i.e., a set of five constraint equations per cycle. These partial derivatives are efficiently calculated with cross-products
| (11) |
where ri is a unit vector along the rotation axis of qi, and O is a point on the rotation axis (Figure 2c). Overall, we obtain a 5m × n Jacobian matrix. In contrast to most mechanical linkages, proteins can feature a large number of redundant hydrogen bond constraints such that both cases, 5m > n and n > 5m are possible.
Admissible velocities {q̇ ∈ ℝn: Jq̇ = 0} span a subspace ker (J(q)) of dimension n – r, with r ≤ min(n, 5m), i.e., the rank of the Jacobian matrix. We compute a basis for the nullspace ker (J(q)) from the singular value decomposition [15]. The singular value decomposition uniquely decomposes the Jacobian matrix J = UΣVT, U ∈ ℝ5m×5m, Σ ∈ ℝ5m×n, V ∈ ℝn×n. The 5m × n diagonal matrix Σ contains the singular values and the columns of U and V are known as the left- and right-singular vectors. Right-singular vectors corresponding to vanishing singular values form an orthonormal basis of the nullspace.
If N(q) ∈ ℝn×(n–r) denotes a matrix whose columns form an orthonormal basis for the nullspace, we obtain a direct mapping consistent with (9) from generalized velocities u̇ ∈ ℝn–r onto admissible velocities q̇ N ∈ ker (J(q)) via
| (12) |
see, e.g., [3]. The motions u̇ are sometimes called floppy modes [34]. Note that (12) yields admissible, coordinated velocities, i.e. velocities that are consistent with the velocity constraint equations (9), for any u̇ ∈ ℝn–r. Perturbing a molecular conformation with a vector selected from a sufficiently small neighborhood of the origin in the nullspace of J, i.e., {ΔqN ∈ ℝn | |ΔqN| ≪ 1, JΔqN = 0} maintains hydrogen-bond distances in linear approximation and can be used to efficiently probe conformational space [41, 9, 29].
3.2. Geometric rigidity analysis
We identify necessary and sufficient conditions for dihedral angles or hydrogen bonds to lock, which lead to larger rigid substructures in proteins. First, we directly identify locked dihedral angles in q, before we extend our analysis to also identify locked hydrogen bonds that are not contained in q, as locked hydrogen bonds rigidly connect adjacent rigid substructures. Finally, we clarify how our geometric method correctly determines rigid substructures in non-generic configurations.
3.2.1. Identifying locked dihedral angles
Rigidified torsion angles qi have zero angular velocity, i.e., , for any vector u̇ ∈ ℝn–r. From (12) it follows, iff Nij = 0 for all j = 1 … n – r, i.e., the i-th row of N is zero.
3.2.2. Identifying locked hydrogen bonds
Next, we derive conditions to identify locked hydrogen bonds. We first relate admissible torsion angle velocities to rotations about the hydrogen bonds. Recalling the geometry of a hydrogen bond i in Figure 2(b), the distance between its donor atom D and its base atom AA changes only if there is a rotation about the hydrogen bond. The case α = β = 0 can be excluded for hydrogen bonds. Starting from the quadratic equation
| (13) |
we follow our previous approach to obtain
| (14) |
as the change of the squared distance dh,i in terms of q and q̇N. Additionally, velocities have to satisfy the constraints and are restricted to admissible velocities. We obtain the scalar expression ḋh,i for each hydrogen bond and can arrange them in matrix form. Substituting admissible velocities from (12) and introducing
| (15) |
we obtain a vector of distance changes
| (16) |
We argue, as before, that a locked hydrogen bond leaves the distance invariant for any vector u̇ ∈ ℝn–r. It follows that hydrogen bond i is locked if and only if the i-th row of JhN is zero.
The additional computational effort to identify locked hydrogen bonds is negligible. All partial derivatives and the nullspace matrix have been previously computed in (10) and the singular value decomposition.
3.2.3. Non-generic configurations
Non-genericity in a closed chain is manifested by two or more linearly dependent constraints or degrees of freedom, which evokes a drop in rank of the constraint Jacobian. Consequently, the dimension of the nullspace increases, leading to an increased instantaneous mobility [42, 1]. This is reflected in an additional column of the nullspace matrix N, corresponding to a non-generic motion or floppy mode. The changes in mobility and rigid substructures are predicted with our geometric method but remains undetected with combinatorial constraint counting. Note that non-generic configurations in the free serial-chain degrees of freedom, previously introduced as qf, might occur as well. However, they can only reduce mobility at the end-effector [28], but can not rigidify rotational bonds and thus, the limitation to q holds.
4. Validation on generic and non-generic configurations
We validate our approach with the pebble game on a regular configuration and examine differences in rigidity that occur in non-generic configurations using a synthetic example implemented in Matlab, with similar bond lengths, angles and constraints as a regular protein.
4.1. Rigidity in generic configurations
Figure 3(a) shows a graph representation of our synthetic example, with the final assignment of pebbles from the pebble game algorithm. Each vertex, represented by a large circle, is a rigid body with six degrees of freedom. Double-headed arrows correspond to five-bar links, and two single-headed arrows correspond to rigid six-bar links. Dashed arrows represent the additional constraints, which also have five bars. The numbers on either side of the arrows show how many edges are covered by pebbles of the adjacent vertex. The total number of assigned (small numbers) and remaining (large numbers inside the circles) pebbles always equal six for each vertex. We recover six pebbles at the root of the spanning tree, representing the six trivial rigid body motions. Dashed lines without arrows in the overconstrained areas indicate redundant bars that are not covered by pebbles. The top area corresponds to an isostatic region where degrees of freedom exactly match the number of constraints. One free pebble remains, implying a single floppy mode shared between the links labeled with a star.
Figure 3.
Example structure with protein backbone inspired geometry. (a) Body-bar graph representation. Double-headed (two single-headed) arrows indicate a five (six) bar connection with small accompanying numbers representing bars that are occupied with pebbles of the adjacent body. Free pebbles are shown as large numbers within the circular bodies. Apart from the six trivial rigid body motions collected at the root, we find one more free pebble that represents a floppy mode shared between star-tagged connections. (b) Tree representation of the structure, with dots as atoms and thick (thin, numbered) lines as locked (rotatable) bonds. Four dotted constraints partly rigidify the structure. The same dihedral angles are identified as flexible, producing the indicated motion pattern upon sampling of other configurations. Numbers correspond to associated rows in the nullspace matrix. (c) Nullspace matrix with one column and 18 rows obtained with our analysis. The red colored entries indicate the moveable, star-tagged dihedral angles, while vanishingly small entries belong to rigidified links. The matrix is an explicit basis for the resulting motion in (b).
Figure 3(b) shows the same synthetic example as a three-dimensional kinematic linkage model. Here, filled circles correspond to atoms, thick solid lines to locked degrees of freedom and thinner solid lines with numbers to rotatable degrees of freedom. Dashed lines represent the constraints. Figure 3(c) is the 18 × 1 nullspace matrix obtained from our analysis. The red, non-zero entries represent the coordinated degrees of freedom (labeled with stars). The remaining entries correspond to locked degrees of freedom. The pebble game and our analysis yield the same result. The pebble game, however, only identifies the potential of motion, whereas our nullspace method provides an explicit basis for the motion. Sampling the constraint manifold leads to the motion pattern shown in Figure 3(b).
4.2. Rigidity in non-generic configurations
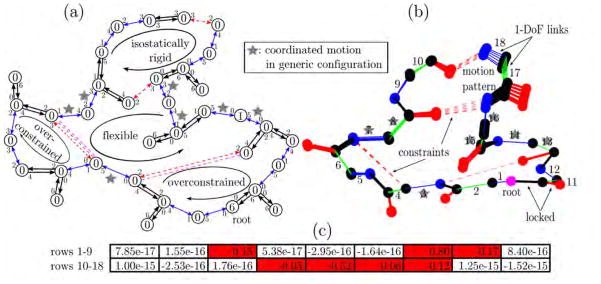
We slightly modify our example to examine collective motions in a non-generic configuration (Figure 4). Links seven and fourteen are now collinear, forming a hinge around which the two parts of the structure can rotate. We also modified the constraint configuration in the lower right with respect to the previous example. Figure 4(a) shows that an additional independent link turns the cycle into an isostatic region instead of an overconstrained region. It removes the previously remaining free pebble such that the pebble game now predicts complete rigidity for the entire graph. The pebble game fails to recognize motion around the hinge resulting from the particular geometry; it overestimates structural rigidity. Our nullspace method recognizes collinearity of the two links. The corresponding hinge motion (Figure 4(b)) leads to two non-zero entries in the nullspace matrix (Figure 4(c)).
Figure 4.
Example structure in non-generic configuration. (a) Body-bar graph representation and pebble game. A change in the constraints with respect to the previous example leads to complete rigidity with the pebble game. As geometry is not considered, the algorithm does not account for the collinearity of the two indicated bonds. (b) Tree representation and kinematic sampling along the constraint compliant rotation about the hinge axis. The geometric method realizes the collinearity and correctly predicts the admissible motion. (c) Corresponding nullspace matrix. We identify the two red-colored non-zero entries describing the possible rotation of angle seven and fourteen. This explicit basis describes the sampled motion pattern.
5. Nullspace and rigidity of proteins
5.1. Numerical analysis of the nullspace
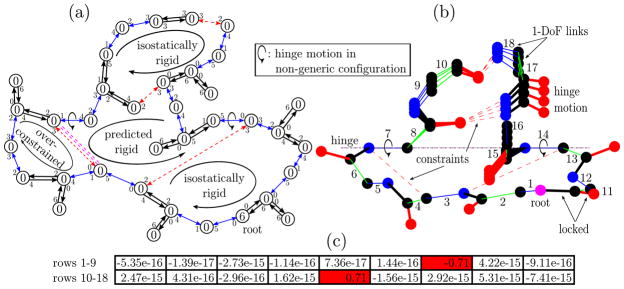
We examined the distribution of the magnitudes of singular values to determine numerical thresholds for vanishingly small ones [7]. The left panel of Figure 5 shows the empirical cumulative distribution function (CDF) for the normalized singular values from the Jacobian matrices of three test proteins (Protein Data Bank codes 3msw, 1hhp and 2lao). Graphical representations of the proteins follow in Section 5.2, Figures 6 and 7. Each protein was randomly perturbed to obtain ten distinct conformations for each. The cumulative distribution functions are nearly identical for the ten distinct conformations and have similar shape for all three proteins. The distributions show that a gap in the eigen spectrum, where the dimension of the nullspace is constant, overlaps for the three proteins. Selecting a threshold value τ within this gap separates non-vanishing singular values and correctly identifies the physical nullspace. For the two smaller proteins with codes 1hhp and 3msw, the gap is larger than for LAO-binding protein (2lao). LAO-binding protein limits overlap between the gaps owing to a small singular value shown in the enlarged area where the dimension of the nullspace changes. This suggests proximity to a non-generic conformation. Choosing a threshold above this value allows more flexibility and can lead to a different set of rigid clusters.
Figure 5.
Left: Cumulative distribution function (CDF) of normalized singular values for three different test proteins and ten samples each. A common margin of several orders of magnitude in the spectral gap clearly separates the vanishing singular values. The biggest protein, LAO binding protein (2lao), has the smallest the margin. It is bound by a very small singular value, shown in the enlarged area, suggests proximity to a non-generic configuration. Overall, the cumulative distribution function and its implications for the nullspace codimension is similar for all test proteins. Right: Cumulative distribution function for the largest entry in magnitude of each row of the nullspace matrix. It represents the ratio of coordinated and rigidified angles. A common margin indicates a region where the number of rigidified and coordinated angles is constant for all test proteins, separating the rigidified degrees of freedom. Torsion angles whose corresponding row has a maximum value above (to the left of) the margin are considered moveable. Again, 2lao has the smallest individual margin. The cumulative distribution functions are highly variable between the different proteins, which implies distinct distributions of floppy modes over the rotational angles.
Figure 6.
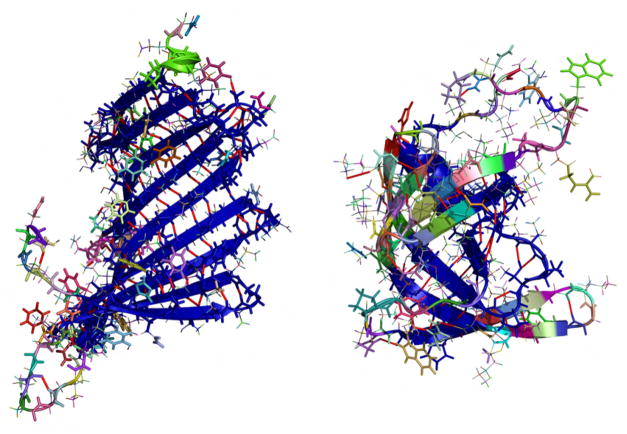
Rigid cluster decomposition with individual coloring. Clusters containing four or more atoms are shown in thick lines, the biggest cluster is dark blue. Hydrogen bond constraints are marked as red lines. Left: Protein Data Bank code 3msw. The dominant β-meander motif forms a single rigid cluster, while loops on the lower left remain flexible, consisting of multiple smaller rigid clusters. Right: Protein Data Bank code 1hhp. The central β-meander motif rigidly connects to the α-helix in the background. The rainbow appearance of other motifs like the loops and the three β-hairpins indicates flexibility.
Figure 7.
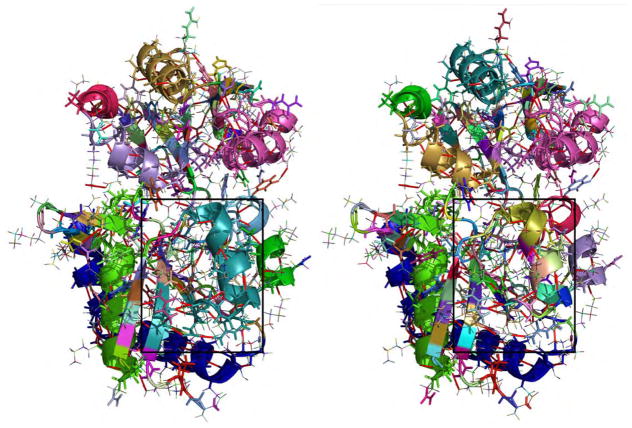
Rigid cluster decomposition of LAO binding protein (2lao) with individual coloring. Clusters containing four or more atoms are shown in thick lines, hydrogen bond constraints are marked as red lines. Left: Set of rigid clusters identical to generic rigidity analysis, obtained with threshold parameters in the determined common margin region. The large turquois cluster in the highlighted rectangle links the α-helix to part of the adjacent β-strand. Right: Rigidity analysis with slightly relaxed threshold parameters. We find very similar results, but identify the highlighted area where a previously large rigid cluster is now composed of multiple small clusters, as a singular motion is possible.
We determined rigidified and moveable degrees of freedom from the nullspace matrix. For τ within the identified common margin, the right panel of Figure 5 shows the empirical cumulative distribution function for the largest entry in magnitude of each row of the nullspace matrix. We introduce a second threshold parameter ν, which selects locked hydrogen bonds. The parameter ν defines another common margin, uniquely separating rigidified from coordinatedly moving degrees of freedom. Rows with entries of maximum absolute values above the threshold ν, i.e., to the left of the common margin, identify coordinatedly moving degrees of freedom. Again, 2lao mostly limits the common margin, while individual margins are significantly larger. This protein features many small singular values between 1e – 2 and 1e – 8, which correspond to small scale rotations, indicated by the increasing ratio of coordinated angles (blue lines). 3msw has the largest margin between moveable and rigidified degrees of freedom, but features a very different transmission of floppy modes to motion. They yield coordinated motions of only 16% of all dihedral angles, while the other 84% are completely rigidified. For the two other proteins, approximately half of the rotation angles are part of coordinated motions. The rigidified angles in 1hhp, in contrast to both other proteins, have slightly larger entries, which is related to the small number of constraints compared to the number of dihedral angles (see Table 1). Numerically identifying rigid substructures is a robust method depending only on two parameters. Protein size influences the method, as absolute distributions of the examined values spread out in bigger systems. This also means that close-to-non-generic configurations as in the 2lao example are more likely to occur. Our method features a dynamic approach: the two parameters can be seen as adjustable sliders tuning the degree of constraint enforcement. This can be used to identify regions that become flexible when constraints are relaxed and regions that are almost always rigid, similar to overconstrained, isostatic and flexible region [34]. Taken together, we obtain a robust numerical procedure for a complete rigidity analysis solely based on the nullspace matrix.
Table 1.
Descriptive statistics for rigidity analysis of three protein structures.
| PDB code | # atoms | # h-bonds | d | n | nrigid | n – r | # rigid clusters | | biggest cluster (atoms)| |
|---|---|---|---|---|---|---|---|---|
| 1hhp | 1563 | 58 | 558 | 321 | 144 | 39 | 412 | 335 |
| 3msw | 2203 | 109 | 841 | 520 | 437 | 21 | 403 | 900 |
| 2lao | 3608 | 188 | 1404 | 934 | 470 | 68 | 929 | 215 |
| 2lao* | 3608 | 188 | 1404 | 934 | 416 | 69 | 982 | 215 |
more flexible cutoff
5.2. Rigid cluster identification in proteins
We applied our method to the three example proteins from Section 5.1 to identify all rigidified dihedral angles together with the set of rigid substructures. We used the KINARI webserver [11], which implements the pebble game algorithm, for comparison. We identified hydrogen bonds with the software HBPLUS [26], using an energy threshold of −1.0kcal/mol. Other non-covalent interactions were ignored. We chose threshold parameters in agreement with the previous numerical analysis and found rigid substructures for the proteins identical to those from KINARI. Table 1 shows descriptive statistics for the three example proteins, where d and n are the dimensions of the overall and constrained set of torsion angles and n – r is the number of floppy modes (see Section 3.1).
The number of hydrogen bond constraints in 1hhp is too small to fully constrain its dihedral angles in q, as 5·58 < 321. Motion in the two other structures is possible only due to linear dependence of the constraints. In agreement with the ratio of coordinatedly moving angles from Figure 5, 3msw has the biggest rigid cluster with 900 atoms, distributing the remaining floppy modes over just a few dihedral angles participating in coordinated motion. The left panel in Figure 6 shows the 3msw rigid cluster decomposition with each color representing an individual rigid body. Clusters with four and more atoms are shown. The large, dark blue β-meander motif is completely rigidified and forms the biggest cluster. Similarly, the smaller β-meander motif in 1hhp is rigidly connected with the α-helix in the background. The rainbow appearance of the three β-hairpins indicates multiple small clusters and thus, more flexibility than in 3msw (see Figure 6 right).
Figure 7 shows the set of rigid clusters in 2lao, with the generic rigidity result that is equally obtained with our method and KINARI on the left side, and a slightly loosened threshold τ on the right. We identify the change as a more flexible partition of the α-helix in the marked rectangle, i.e. the additional floppy mode yields a coordinated flex of the helix. Line four in Table 1 reveals that 54 previously rigid dihedral angles are part of this floppy mode. All other rigid clusters are identical, although the color pattern changes with the new ‘by size’ order of the clusters.
Overall, both methods give identical, correct results in generic configurations. The pebble game’s explicit, combinatorial constraint counting procedure results in a very fast integer algorithm, independent of numerical problems related to precision in the structure files or ill-conditioned matrix operations. However, it fails to recognize when non-generic configurations occur, overestimating rigidity by missing non-generic, admissible motions.
While our Jacobian-based method is subject to numerical precision, we demonstrated that a wide range of threshold parameters identify the same set of rigid bodies as the pebble game. Interestingly, threshold parameter selection provides an additional feature, which allows fine-tuning of constraint flexibility without the need to explicitly re-model hydrogen bonds. Vanishingly small singular values indicate proximity to a non-generic configuration. Parameter tuning can show how motions close to singularities affect rigidity and flexibility, providing geometric mobility information for generic and non-generic configurations alike. Large rotations about new hinges that emerge in non-generic configurations could open previously inaccessible, functionally important substates. Additionally, non-generic configurations can block certain directions for motion, which allows the structure to withstand high forces when, for instance, it interacts with binding partners. While the pebble game only provides combinatorial rigidity information, our geometric approach explicitly shows what remaining coordinated motions look like and allows direct sampling without cycle break-up.
6. Conclusion
We characterized rigidity in proteins using geometric tools that kinematically describe the molecular structure. We showed that rigidity is explicitly encoded in the nullspace of the Jacobian matrix of the constraints. The Jacobian matrix defines a constraint manifold Q, which coincides with the tangent space
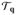 Q at regular configurations q. Our numerical analysis revealed a robust method to obtain rigid substructures, in which constraint enforcement can be tuned by selecting appropriate values for two parameters τ and ν. Results from our algorithm coincide with those obtained from combinatorial constraint counting methods at generic configurations. In addition, the encoded geometry provides specific information on the proximity to non-generic configurations, and yields valid results at non-generic configurations. Our method circumvents the need of a numerically expensive dynamic simulation. Advanced utilization of the information contained in the singular values and the nullspace, e.g., local curvature and global appearance of the constraint manifold, will be the focus of future work.
Q at regular configurations q. Our numerical analysis revealed a robust method to obtain rigid substructures, in which constraint enforcement can be tuned by selecting appropriate values for two parameters τ and ν. Results from our algorithm coincide with those obtained from combinatorial constraint counting methods at generic configurations. In addition, the encoded geometry provides specific information on the proximity to non-generic configurations, and yields valid results at non-generic configurations. Our method circumvents the need of a numerically expensive dynamic simulation. Advanced utilization of the information contained in the singular values and the nullspace, e.g., local curvature and global appearance of the constraint manifold, will be the focus of future work.
We further showed that the nullspace constitutes an explicit basis for the floppy modes that can be used to efficiently probe conformational space. Floppy modes are a set of minimal coordinates for the closed cycles, which significantly reduce system size and encode collective, functional motions of proteins. The dual use of the nullspace matrix to predict rigidity and sample new configurations puts the numerical cost compared to the fast pebble game algorithm into a more favorable perspective. Once the nullspace matrix is available, explicit rigidity information can be obtained at virtually no additional expense. In terms of a comprehensive analysis of protein rigidity and conformational space, our method combines the two formerly separate tasks into an elegant and efficient one-step procedure. Our rigidity analysis and conformational exploration can provide high-level insights into dynamic processes beyond the reach of MD simulations, with broad implications for drug design and protein engineering.
Acknowledgments
We gratefully acknowledge financial support by the Bavaria California Technology Center under project number 7, 2014 – 1 and the Deutsche Telekom Stiftung. H.v.d.B. is supported by the US National Institute of General Medical Sciences Protein Structure Initiative (U54GM094586) at the Joint Center for Structural Genomics and a SLAC National Accelerator Laboratory LDRD (Laboratory Directed Research and Development) grant SLAC-LDRD-0014-13-2.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Dominik Budday, Email: dominik.budday@fau.de.
Sigrid Leyendecker, Email: sigrid.leyendecker@ltd.uni-erlangen.de.
References
- 1.Arponen T, Müller A, Piipponen S, Tuomela J. Kinematical analysis of overconstrained and underconstrained mechanisms by means of computational algebraic geometry. Meccanica. 2014;49 (4):843–862. [Google Scholar]
- 2.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat T, Weissig H, Shindyalov IN, Bourne PE. The protein data bank. Nucleic acids research. 2000;28 (1):235–242. doi: 10.1093/nar/28.1.235. http://www.rcsb.org/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Betsch P, Leyendecker S. The discrete null space method for the energy consistent integration of constrained mechanical systems. Part II: Multibody dynamics. International journal for numerical methods in engineering. 2006;67 (4):499–552. [Google Scholar]
- 4.Bouvignies G, Vallurupalli P, Hansen DF, Correia BE, Lange O, Bah A, Vernon RM, Dahlquist FW, Baker D, Kay LE. Solution structure of a minor and transiently formed state of a T4 lysozyme mutant. Nature. 2011;477 (7362):111–4. doi: 10.1038/nature10349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Burdick JW. Advanced Robotics. Vol. 1989. Springer; 1989. On the inverse kinematics of redundant manipulators: Characterization of the self-motion manifolds; pp. 25–34. [Google Scholar]
- 6.Coleman W. Biology in the nineteenth century: problems of form, function and transformation. Vol. 1. Cambridge University Press; 1971. [Google Scholar]
- 7.Edelman A. Eigenvalues and condition numbers of random matrices. SIAM Journal on Matrix Analysis and Applications. 1988;9 (4):543–560. [Google Scholar]
- 8.Fenwick RB, van den Bedem H, Fraser JS, Wright PE. Integrated description of protein dynamics from room-temperature X-ray crystallography and NMR. Proc Natl Acad Sci USA. 2014;111:E445–54. doi: 10.1073/pnas.1323440111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fonseca R, Pachov DV, Bernauer J, van den Bedem H. Characterizing RNA ensembles from NMR data with kinematic models. Nucl Acids Res. 2014;42:9562–9572. doi: 10.1093/nar/gku707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fonseca R, van den Bedem H, Bernauer J. KGSrna: Efficient 3D kinematics-based sampling for nucleic acids. In: Przytycka TM, editor. Research in Computational Molecular Biology. Vol. 9029 of Lecture Notes in Computer Science. Springer International Publishing; 2015. pp. 80–95. [Google Scholar]
- 11.Fox N, Jagodzinski F, Li Y, Streinu I. Kinari-web: A server for protein rigidity analysis. Nucleic Acids Research. 2011;39 (Web Server Issue):W177–W183. doi: 10.1093/nar/gkr482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Frederick KK, Marlow MS, Valentine KG, Wand AJ. Conformational entropy in molecular recognition by proteins. Nature. 2007;448 (7151):325–9. doi: 10.1038/nature05959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gluck H. Geometric topology. Springer; 1975. Almost all simply connected closed surfaces are rigid; pp. 225–239. [Google Scholar]
- 14.Go N, Scheraga HA. Ring closure and local conformational deformations of chain molecules. Macromolecules. 1970;3 (2):178–187. [Google Scholar]
- 15.Golub GH, Van Loan CF. Matrix computations. Vol. 3. JHU Press; 2012. [Google Scholar]
- 16.Graver JE. Counting on frameworks: mathematics to aid the design of rigid structures. 25. Cambridge University Press; 2001. [Google Scholar]
- 17.Hein J, Reid F, Smith L, Bush I, Guest M, Sherwood P. On the performance of molecular dynamics applications on current high-end systems. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2005;363 (1833):1987–1998. doi: 10.1098/rsta.2005.1624. [DOI] [PubMed] [Google Scholar]
- 18.Hendrickson B. Conditions for unique graph realizations. SIAM Journal on Computing. 1992;21 (1):65–84. [Google Scholar]
- 19.Jackson B, Jordán T. Connected rigidity matroids and unique realizations of graphs. Journal of Combinatorial Theory, Series B. 2005;94 (1):1–29. [Google Scholar]
- 20.Jackson B, Jordán T. The generic rank of body–bar-and-hinge frameworks. European Journal of Combinatorics. 2010;31 (2):574–588. [Google Scholar]
- 21.Jacobs DJ, Hendrickson B. An algorithm for two-dimensional rigidity percolation: the pebble game. Journal of Computational Physics. 1997;137 (2):346–365. [Google Scholar]
- 22.Jacobs DJ, Thorpe MF. Generic rigidity percolation: the pebble game. Physical review letters. 1995;75 (22):4051. doi: 10.1103/PhysRevLett.75.4051. [DOI] [PubMed] [Google Scholar]
- 23.Jagodzinski F, Clark P, Liu T, Grant J, Monastra S, Streinu I. Rigidity analysis of periodic crystal structures and protein biological assemblies. BMC Bioinformatics; selected articles from the Second IEEE International Conference on Computational Advances in Bio and Medical Sciences (ICCABS 2012), Bioinformatics; 2013. p. S2. http://www.biomedcentral.com/1471-2105/14/S18/S2. [Google Scholar]
- 24.Kasinath V, Sharp KA, Wand AJ. Microscopic insights into the NMR relaxation based protein conformational entropy meter. J Am Chem Soc. 2013;40:15092–15100. doi: 10.1021/ja405200u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Klepeis JL, Lindorff-Larsen K, Dror RO, Shaw DE. Long-timescale molecular dynamics simulations of protein structure and function. Current opinion in structural biology. 2009;19 (2):120–127. doi: 10.1016/j.sbi.2009.03.004. [DOI] [PubMed] [Google Scholar]
- 26.McDonald IK, Thornton JM. Satisfying hydrogen bonding potential in proteins. Journal of molecular biology. 1994;238 (5):777–793. doi: 10.1006/jmbi.1994.1334. [DOI] [PubMed] [Google Scholar]
- 27.Müller A, Rico J. Advances in Robot Kinematics: Analysis and Design. Springer; 2008. Mobility and higher order local analysis of the configuration space of single-loop mechanisms; pp. 215–224. [Google Scholar]
- 28.Nokleby SB, Podhorodeski RP. Identifying multi-dof-loss velocity degeneracies in kinematically-redundant manipulators. Mechanism and machine theory. 2004;39 (2):201–213. [Google Scholar]
- 29.Pachov D, van den Bedem H. Nullspace sampling with holonomic constraints reveals molecular mechanisms of protein Gαs. PLOS Comput Biol. 2015 doi: 10.1371/journal.pcbi.1004361. (in review) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schulze B, Sljoka A, Whiteley W. How does symmetry impact the flexibility of proteins? Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2014;372 (2008):20120041. doi: 10.1098/rsta.2012.0041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shai O, Müller A. A novel combinatorial algorithm for determining the generic/topological mobility of planar and spherical mechanisms. ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers; 2013. pp. V06BT07A073–V06BT07A073. [Google Scholar]
- 32.Tay TS. Rigidity of multi-graphs. i. linking rigid bodies in n-space. Journal of Combinatorial Theory, Series B. 1984;36 (1):95–112. [Google Scholar]
- 33.Tay T-S, Whiteley W. Recent advances in the generic ridigity of structures. Structural Topology. 1984;1984 núm. 9. [Google Scholar]
- 34.Thorpe M, Lei M, Rader A, Jacobs DJ, Kuhn LA. Protein flexibility and dynamics using constraint theory. Journal of Molecular Graphics and Modelling. 2001;19 (1):60–69. doi: 10.1016/s1093-3263(00)00122-4. [DOI] [PubMed] [Google Scholar]
- 35.van den Bedem H, Fraser JS. Integrative, dynamic structural biology at atomic resolution-It’s about time. Nat Meth. 2015;12:307–318. doi: 10.1038/nmeth.3324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.van den Bedem H, Lotan I, Latombe JC, Deacon AM. Real-space protein-model completion: an inverse-kinematics approach. Acta Cryst. 2005;D61:2–13. doi: 10.1107/S0907444904025697. [DOI] [PubMed] [Google Scholar]
- 37.Vorov OK, Livesay DR, Jacobs DJ. Nonadditivity in conformational entropy upon molecular rigidification reveals a universal mechanism affecting folding cooperativity. Biophys J. 2011;100(4):1129–38. doi: 10.1016/j.bpj.2011.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wenger P, Chablat D. Advances in Robot kinematics: Analysis and control. Springer; 1998. Workspace and assembly modes in fully-parallel manipulators: A descriptive study; pp. 117–126. [Google Scholar]
- 39.Whiteley W. Some matroids from discrete applied geometry. Contemporary Mathematics. 1996;197:171–312. [Google Scholar]
- 40.Whiteley W. Counting out to the flexibility of molecules. Physical Biology. 2005;2 (4):S116. doi: 10.1088/1478-3975/2/4/S06. [DOI] [PubMed] [Google Scholar]
- 41.Yao P, Zhang L, Latombe JC. Sampling-based exploration of folded state of a protein under kinematic and geometric constraints. Proteins. 2012;80:25–43. doi: 10.1002/prot.23134. [DOI] [PubMed] [Google Scholar]
- 42.Zlatanov D, Fenton RG, Benhabib B. Singularity analysis of mechanisms and robots via a motion-space model of the instantaneous kinematics. Robotics and Automation, 1994. Proceedings., 1994 IEEE International Conference on; IEEE; 1994. pp. 980–985. [Google Scholar]