Abstract
Objective
The P300 speller is a common brain–computer interface (BCI) application designed to communicate language by detecting event related potentials in a subject’s electroencephalogram (EEG) signal. Information about the structure of natural language can be valuable for BCI communication, but attempts to use this information have thus far been limited to rudimentary n-gram models. While more sophisticated language models are prevalent in natural language processing literature, current BCI analysis methods based on dynamic programming cannot handle their complexity.
Approach
Sampling methods can overcome this complexity by estimating the posterior distribution without searching the entire state space of the model. In this study, we implement sequential importance resampling, a commonly used particle filtering (PF) algorithm, to integrate a probabilistic automaton language model.
Main Result
This method was first evaluated offline on a dataset of 15 healthy subjects, which showed significant increases in speed and accuracy when compared to standard classification methods as well as a recently published approach using a hidden Markov model (HMM). An online pilot study verified these results as the average speed and accuracy achieved using the PF method was significantly higher than that using the HMM method.
Significance
These findings strongly support the integration of domain-specific knowledge into BCI classification to improve system performance.
Keywords: Brain-Computer Interfaces, Language Models, P300 Speller, Electroencephalography, Particle Filters
1 Introduction
The P300 Speller is a common brain-computer interface (BCI) system that uses electroencephalogram (EEG) signals to simulate keyboard input, providing a means of communication [1]. The P300 speller works by presenting a grid of characters on a graphical interface and instructing the user to focus on a target letter. Groups of relatively few characters (most commonly and in this report in rows and columns) are illuminated (i.e., “flashed”) in a pseudo-random manner and the neural responses are recorded in the user’s electroencephalogram (EEG). Because stimuli containing any given character are relatively uncommon, evoked responses known as P300 signals are elicited when a group containing the target character is flashed. A classifier detects these signals and then determines the corresponding target character. Because the signal to noise ratio is low, several trials must be combined in order to correctly classify responses. The resulting typing speed can therefore be slow, prompting many studies focused on system optimization. Approaches include varying the grid size [2–4], optimizing system parameters [5–6], and adopting different signal processing methods [7–10].
While the P300 speller is designed to provide a means for communication, signal classification methods traditionally have not taken advantage of existing knowledge about the language domain, treating character selections as independent elements chosen from a set with no prior information. While knowledge about the domain of natural language has been used for years to improve classification in other domains such as speech recognition [11], the usage of this information in the BCI field is a recent movement. BCI studies using n-gram language models have demonstrated improvements in system speed and accuracy [12–17]. However, these models provide a poor representation of natural language, as they ignore context and can give high probability to character strings that do not formulate words (Table 1). More sophisticated language models could improve accuracy by giving stronger prior probabilities to target characters, but are generally too computationally complex for classification algorithms currently in use.
Table 1.
String counts in the Brown corpus. Component trigrams for the string “_ing_” are common in the corpus, which results in a high probability in the trigram model, despite the exact string rarely occurring.
| String | Count | Probability |
|---|---|---|
| __i | 68440 | 0.07 |
| _in | 33783 | 0.49 |
| ing | 30454 | 0.34 |
| ng_ | 30035 | 0.78 |
| _ing_ | 1 | ~0 |
Stochastic methods such as particle filters (PF) can overcome this challenge by estimating probability distributions using sampling [18]. These methods can approximate distributions by projecting many samples through a model based on the observed output and then summing over the resulting states. PF methods can be adapted to any state-space model and are particularly useful for processing of on-line data [19]. In the context of BCI communication, PF methods can be applied by projecting samples through a state-space language model based on the observed EEG signals. The system can then determine the most likely output by finding the state that attracts the highest number of samples.
In this work, English words are modeled using a probabilistic automaton [20] and probability distributions are estimated using sequential importance resampling (SIR), a common PF algorithm [18]. These probability distributions are used as priors to classify EEG signals in the P300 speller system using Bayesian inference. The algorithm chooses the string that it determines is most probable and automatically makes the correction. This method was compared offline with a standard stepwise linear discriminant analysis (SWLDA) method with dynamic stopping as well as a previously presented hidden Markov model (HMM) classifier on a previously published data set consisting of 15 healthy subjects [16]. Prospective evaluation was then performed online using the HMM and PF algorithms on an additional 15 subjects.
2 Materials and methods
2.1 Data Collection
All data was acquired using g.tec amplifiers, active EEG electrodes, and electrode cap (Guger Technologies, Graz, Austria); sampled at 256 Hz, referenced to the left ear; grounded to AFZ; and filtered using a band-pass of 0.1 – 60 Hz. Data for offline analyses were obtained from 15 healthy graduate students and faculty with normal or corrected to normal vision between the ages of 20 and 35. The electrode set consisted of 32 channels placed according to a previously published configuration [6]. Only one subject (subject F) had previous experience using a BCI for typing. The system used a 6 × 6 character grid, row and column flashes, and a stimulus duration of 100 ms and an interstimulus interval of 25 ms for a stimulus onset asynchrony of 125 ms. Each subject underwent between 8 and 10 trials consisting of spelling a five letter word with 15 sets of 12 flashes (six rows and six columns) for each letter. The choice of target words for this experiment was independent of the trigram language model used in the NB and HMM methods.
The subjects for the online study consisted of 15 healthy volunteers with normal or corrected to normal vision between the ages of 20 and 30. The electrode set consisted of a reduced set of four channels (PO8, PO7, POz, and CPz) [21]. The training sessions for these subjects consisted of three sessions of copy spelling 10 character phrases. Each subject then chose a target phrase to spell in online sessions. In each session, the subject had five minutes to spell as much of the phrase as they could using one of the three analysis methods: SWLDA (with dynamic stopping), HMM, or PF. Subjects were instructed not to correct errors and to repeat the phrase if they completed it in under five minutes.
BCI2000 was used for data acquisition and online analysis [22]. Offline analysis was performed using MATLAB (version 7.10.0, MathWorks, Inc, Natick, MA).
2.2 Traditional Classifier
2.2.1 SWLDA
SWLDA is a classification algorithm that selects a set of signal features to include in a discriminant function [23]. Signals are assigned labels based on two classes: those corresponding to flashes containing the attended character and those without the attended character. The algorithm uses ordinary least-squares regression to predict class labels for the training set. It then adds the most significant features in the forward stepwise analysis and removes the least significant features in the backward analysis step. These steps are repeated until either the target number of features was met or it reached a state where no features were added or removed [10].
The score for each flash in the test set can then be computed as the dot product of the feature weight vector, w, with the features from that trial’s signal, . Traditionally, the score for each possible next character, xt, is computed as the sum of the individual scores for flashes that contain that character:
| (1) |
where is the set of characters illuminated for the ith flash for character t in the sequence. After a predetermined set of stimuli, the character with the highest score is selected.
2.2.2 Dynamic Stopping
It has been shown that scores can be approximated as independent samples from a Gaussian distribution given the target character [12]:
| (2) |
and
| (3) |
where μa, , μn and are the means and variances of the distributions for the attended and non-attended flashes, respectively. The conditional probability of a target given the EEG signal and typing history can then be found:
| (4) |
where p(xi|xi−1, …, x1) is the prior probability of character xi determined from a language model. In the simplest case, a uniform prior probability is used, simplifying the posterior to
| (5) |
Dynamic classification was implemented by setting a threshold probability, pthresh, to determine when a decision should be made. The program flashed characters until either or the number of sets of flashes reached the maximum (15). The classifier then selected the character that satisfied . In offline analysis, the speeds, accuracies, and bit rates were found for values of pthresh between 0 and 1 in increments of 0.01 and the threshold probability that maximized the bit rate was chosen for each subject.
2.3 HMM Classifier
HMMs represent language using an n-gram model that can only be observed indirectly via the user’s EEG signal. The goal of such systems is to use dynamic programming to determine the most probable states in the Markov process that could have produced the observed output signal [16].
2.3.1 Trigram Language Model
N-gram models are simple representations of language that produce probability distributions based on relative character frequency in a training corpus. States in these models represent characters in the alphabet with transitions based on the probability of their co-occurrence in text. For example, a state with the character “Q” would have a high probability transition to a state with the character “U” because the string “QU” is relatively common in English text while other strings beginning with “Q” are much less common. In this study, the second order Markov assumption is used, so prior probabilities can determined from relative trigram counts in the Brown English language corpus [24]. The prior probability of character, xt, given the previous characters, x1:t−1, is
| (6) |
where c(‘a’, ‘b’, ‘c’) denotes the number of times the string “abc” occurs in the corpus.
2.3.2 Viterbi Algorithm
In the Viterbi algorithm, a typed word is simply a sequence of states of the Markov process, x = (x0, …, xn). The goal of the algorithm is to search all possible state sequences to determine the most probable output given the known language model and the observed EEG signal. At any given time t, the Viterbi algorithm finds the highest probability path to each possible value for the target character, xt. It then determines the highest probability of those paths and returns it to the user. The lower probability paths are retained for calculation of the probability distribution for the next time step.
The EEG response at time t is dependent only on the current target character and governed by the conditional probability, p(yt|xt). At each time step, the joint probability of being in state xt and previously being in state xt−1 can then be computed by
| (7) |
where p(yt|xt) is computed as in equation 2 and p(xt|xt−2, xt−1) is determined by the language model (equation 6). The total probability of the target character xt can then be computed by summing over all possible previous states xt−1.
| (8) |
A back pointer to a previous state 〈xt−1, xt−2〉 is saved representing the highest probability path to the state 〈xt, xt−1〉, determined using the Viterbi algorithm.
| (9) |
As in the previous method, characters are selected when a threshold probability is reached (i.e., and the character xt is selected that satisfies . The back pointers are then followed from the selected character to find the optimal string up to the current time step. This string is then presented as the output of the system up to the current time. If this string differs from the previous output, the previous characters are assumed to be errors and are replaced by those in the current string.
2.4 PF Classifier
The PF algorithm uses a Bayesian process model to classify P300 signals. Prior probabilities are determined from a probabilistic automaton and movement in the model is estimated using SIR.
2.4.1 Probabilistic Automaton
The probabilistic automaton models the English language by creating states for every substring that starts a word in the corpus. Thus, the word “the” would result in three states: “t,” “th,” and “the.” The start state is the root node, x0, which corresponds to a blank string. Each state then links to every state that has a string that is a superstring that is one character longer. Thus, the state “t” will link to the states “th” and “to” (Figure 1).
Figure 1.
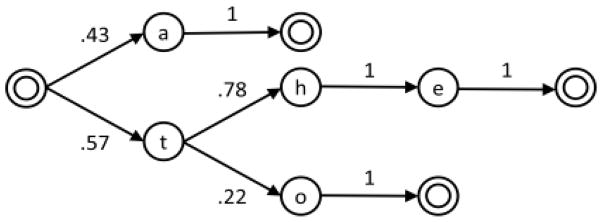
Example automaton for a reduced vocabulary consisting only of the words “a,” “the,” and “to.” Double circles represent possible termination states for a word. These states link back to the root node to represent the beginning of a subsequent word.
States that represent completed words contain links back to x0 to begin a new word. The state “the,” for instance, links to the terminal state “the_” which includes the valid English word “the” and a space indicating the intent to start a new word. The state “the” also contains links to nonterminal states such as “them” because it begins other English words in addition to being a complete word.
Similar to the trigram model, the transition probabilities are determined by the relative frequencies of words starting with the states’ substrings in the Brown English language corpus [24].
| (10) |
where c(‘a’, ‘b’) denotes the number of occurrences of a word that starts with the string “ab” in the corpus. When t =1, c( ) represents the total number of words in the corpus and p(x0:1|x0) is the fraction of words in the copus that begin with character ‘x1’. Similarly, the probability that a word ends and the model transitions back to the root, x0, is the ratio of the number of occurrences of complete words consisting of a string to the total number of occurrences of words beginning with that string.
| (11) |
where c(‘a’, ‘b’, ‘ ’) is the number of occurrences of the word “ab” in the corpus.
2.4.2 SIR
The SIR method estimates the probability distribution over possible outputs by sampling a batch of possible realizations of the model called particles. Each of these particles moves through the language model independently, based on the model transition probabilities. Low probability realizations are removed and replaced by more likely realizations by resampling the particles based on weights derived from the observed EEG response. The algorithm estimates the probability distribution of the possible output strings by computing a histogram of the particles after they have moved through the model.
Each particle j consists of a link to a state in the language model, x(j); a string consisting of the particle’s state history; and a weight, w(j). When the system begins, a set of P particles is generated and each is associated with the root node, x0, with an empty history and a weight equal to 1/P. At the start of a new character t, a sample xt(j) is drawn for each particle, j, from the proposal distribution defined by the language model’s transition probabilities from the particle’s history, x0:t−1(j).
| (12) |
where p(x0:t|x0:t−1(j)) is provided by the language model (equation 10). When a particle transitions between states, its pointer changes from the previous state in the model, x0:t−1(j), to the new state x0:t. The history for each particle, x0:t(j), is stored to represent the output character sequence associated with that particle. After each stimulus response, the probability weight is computed for each of the particles
| (13) |
where is computed as in equation 2. The weights are then normalized and the probability of the current character is found by summing the weights of all particles that end in that character.
| (14) |
where δ is the Kronecker delta. If the maximum probability is above a threshold, the particle with the maximum weight is selected and its history is used as the output text. As in the HMM algorithm, if characters in this output differ from the previous output text, the previous characters are assumed to be errors and are replaced by those in the current text. A new batch of particles, xt*, are then sampled from the current particles, xt, based on the weight distribution, wt. Each of the new particles are then assigned an equal weight wt*(j) = 1/P. The subject then moves on to the next character and the process then repeats with the new batch of particles.
The main concern with using this method is the number of particles to use. Using more particles increases the processing necessary for estimating the distributions. However, a low number of particles could result in undersampling the distributions and missing important possible sequences. Sensitivity analysis is performed on the number of particles by determining the offline performance using 10, 100, 1,000, 10,000 and 100,000 particles.
2.5 Evaluation
Evaluation of a BCI system must take into account two factors: the ability of the system to achieve the desired result and the amount of time required to reach that result. The efficacy of the system can be measured as the selection accuracy, which we defined as the percentage of characters in the final output that matched the target string. The speed of the system was measured using the selection rate (SR), the inverse of the average time required to make a selection.
As there is a tradeoff between speed and accuracy, we also use information transfer rate (ITR) (in bits/min) for evaluation, which takes both into account. The bits per symbol, B, is a measure of how much information is transmitted in a selection taking into account the accuracy and the number of possible selections [25]:
| (14) |
where N is the number of characters in the grid (36) and Acc is the selection accuracy. ITR can then be found by multiplying the selection rate by the bits per symbol. Significance was tested using Wilcoxon signed-rank tests. In offline analysis, the value of pthresh was determined independently for each algorithm for each subject. This optimization was impractical for online experiments, so a previously reported value of 0.95 was used for all trials [16].
3 Results
3.1 Sensitivity Analysis
Using 10 particles, the average ITR was 12.34 bits/min as no subject achieved an accuracy above 50% (Figure 2). Progressively changing the number of particles to 100, 1,000, and 10,000 resulted in significant improvements in average ITR value: 33.34 (p<0.001), 36.79 (p<0.001), and 38.07 (p=0.01), respectively. Increasing the number of particles to 100,000 did not result in a significant increase (ITR=38.21; p=0.35).
Figure 2.
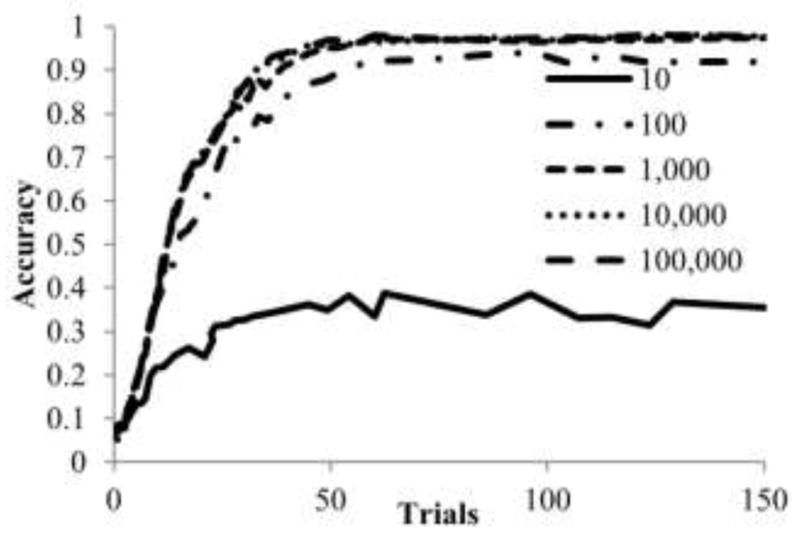
Analysis of the sensitivity of offline results to the number of particles used. Results were computed for each subject in the offline dataset using cross-validation with the particle filter classifier and the specified number of particles. Selection accuracies were then computed and averaged across all subjects. Optimal classifier performance was achieved when using at least 10,000 particles.
3.2 Offline Performance
When using SWLDA in offline analysis, all subjects were able to type with varying levels of performance. The best performer (subject D) was able to achieve 89% accuracy at a rate of 9.96 selections per minute, while the worst performer (subject C) achieved an accuracy of 80% at a rate of only 3.96 selections per minute (Table 2). The accuracy increased with the number of flashes for all subjects and 12 of the 15 were able to exceed 90% accuracy within 15 sets of flashes.
Table 2.
Optimal selection rates, accuracies, and information transfer rates for the 15 subjects in offline trials.
| SR (selections/min) | Acc (%) | ITR (bits/min) | |||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| Subject | SWLDA | HMM | PF | SWLDA | HMM | PF | SWLDA | HMM | PF |
| A | 8.07 | 9.80 | 10.74 | 93.33 | 95.56 | 97.78 | 36.13 | 45.87 | 51.33 |
| B | 5.33 | 7.42 | 7.33 | 88.89 | 88.89 | 88.89 | 21.82 | 30.38 | 30.05 |
| C | 3.96 | 8.45 | 6.71 | 80.00 | 67.50 | 85.00 | 13.54 | 21.91 | 25.43 |
| D | 9.96 | 10.83 | 11.75 | 88.89 | 97.78 | 95.56 | 40.82 | 53.08 | 54.99 |
| E | 3.98 | 5.20 | 6.54 | 95.56 | 97.78 | 91.11 | 18.64 | 25.47 | 27.98 |
| F | 7.21 | 8.99 | 10.63 | 95.56 | 95.56 | 95.56 | 33.76 | 42.09 | 49.74 |
| G | 5.33 | 6.56 | 9.33 | 94.00 | 92.00 | 92.00 | 24.18 | 28.60 | 40.64 |
| H | 8.66 | 10.17 | 9.77 | 88.00 | 90.00 | 96.00 | 34.86 | 42.59 | 46.13 |
| I | 5.08 | 9.38 | 10.68 | 78.00 | 78.00 | 80.00 | 16.68 | 30.77 | 36.55 |
| J | 4.78 | 5.86 | 6.55 | 90.00 | 94.00 | 98.00 | 20.03 | 26.57 | 32.28 |
| K | 3.98 | 6.68 | 7.81 | 84.00 | 80.00 | 84.00 | 14.80 | 22.85 | 29.01 |
| L | 5.62 | 7.36 | 7.71 | 92.00 | 90.00 | 98.00 | 24.47 | 30.80 | 37.98 |
| M | 4.13 | 6.19 | 6.16 | 82.00 | 84.00 | 90.00 | 14.72 | 22.98 | 25.82 |
| N | 7.60 | 8.98 | 9.58 | 94.00 | 90.00 | 100.00 | 34.48 | 37.62 | 49.55 |
| O | 4.40 | 6.28 | 9.43 | 88.00 | 84.00 | 82.00 | 17.71 | 23.33 | 33.62 |
|
| |||||||||
| Average | 5.87 | 7.88 | 8.70 | 88.82 | 88.34 | 91.59 | 24.44 | 32.33 | 38.07 |
Six of the subjects reached 100% accuracy within the 15 sets of flashes using the HMM method and subject D had all characters correct within two sets of flashes. The improvement in ITR from the static method to the HMM method ranged from 40% (subject N) to 100% (subject I). The average bit rate across subjects improved by 32% from 24.44 to 32.33 (p < 0.001). The selection rate rose from 5.87 to 7.88 (p < 0.001) and the accuracy increased stayed relatively constant (p = 0.39).
Using the PF classifier, 11 of the 15 subjects reached 100% accuracy within the 15 sets of flashes. Compared to HMM, the average bit rate rose significantly using this method from 32.33 to 38.07 (p < 0.001), with increases of at least five bits/min for nine of the 15 subjects. The average selection rate rose significantly over the HMM method from 7.88 to 8.70 (p = 0.01) and the accuracy showed significant improvement from 88.34% to 91.59% (p = 0.03).
3.3 Online Performance
In online experiments, all 15 subjects were able to type characters with at least 65% accuracy using each of the algorithms (Table 3). Using the HMM method, 11 of the 15 subjects achieved at least 80% accuracy and 6 characters per minute. All subjects selected characters with at least 74% accuracy using the PF method, with 13 of 15 subjects selecting over seven characters per minute on average. One subject (subject P) had substantially lower results than the rest of the data set, selecting fewer than three characters per minute on average with accuracy under 75% for both methods.
Table 3.
Online selection rates, accuracies, and information transfer rates for each subject using the hidden Markov model and particle filtering algorithms.
| SR (selections/min) | Acc (%) | ITR (bits/min) | ||||
|---|---|---|---|---|---|---|
|
| ||||||
| Subject | HMM | PF | HMM | PF | HMM | PF |
| P | 2.97 | 2.84 | 67.86 | 74.07 | 7.77 | 8.57 |
| Q | 10.39 | 10.64 | 87.38 | 98.11 | 41.30 | 52.55 |
| R | 7.80 | 8.62 | 90.91 | 94.19 | 33.25 | 39.22 |
| S | 9.65 | 9.98 | 69.47 | 82.11 | 26.22 | 35.66 |
| T | 11.21 | 11.23 | 91.89 | 90.09 | 48.73 | 47.13 |
| U | 8.36 | 9.14 | 90.36 | 96.67 | 35.27 | 43.79 |
| V | 7.30 | 8.18 | 86.11 | 100.00 | 28.29 | 42.31 |
| W | 8.45 | 9.77 | 90.48 | 98.97 | 35.74 | 49.19 |
| X | 6.21 | 6.51 | 95.08 | 86.15 | 28.80 | 25.25 |
| Y | 5.98 | 7.22 | 80.70 | 82.61 | 20.76 | 26.07 |
| Z | 7.77 | 7.51 | 88.00 | 76.06 | 31.28 | 23.63 |
| AA | 9.04 | 8.81 | 80.00 | 86.36 | 30.95 | 32.30 |
| AB | 6.93 | 8.56 | 65.15 | 87.01 | 16.99 | 33.80 |
| AC | 8.70 | 10.08 | 76.74 | 95.96 | 27.79 | 47.58 |
| AD | 10.00 | 10.49 | 95.96 | 97.12 | 47.18 | 50.70 |
|
| ||||||
| Average | 8.05 | 8.64 | 83.74 | 89.70 | 30.69 | 37.31 |
In this study, 12 of 15 subjects achieved a higher bit rate when using the PF classifier than when using the HMM method. On average, subjects selected 8.05 characters per minute with 83.74% accuracy, resulting in an average bit rate of 30.69 bits/minute using the HMM algorithm. When using the PF algorithm, subjects achieved significant improvements with an average selection rate of 8.64 characters/minute (p=0.002), an average accuracy of 89.70% (p=0.02), and an average bit rate of 37.31 bits/minute (p=0.005).
The PF algorithm successfully corrected 6.8 errors on average for each subject (Table 4). These corrections accounted for 49% of the classification errors in the initial classifications. All subjects had at least two errors corrected with correction rates varying between 20% (subject AA) and 100% (subject V). Automatic error correction was responsible for increasing classifier accuracy from 82.90% to 89.70% and the average bit rate from 31.55 bits/min to 37.31 bits/min.
Table 4.
Example online output for each of the tested methods. Each row is the result of subject Q attempting to spell “I want to be the very best like no one ever was to catch them is my real test” for five minutes. HMM* and PF* are the outputs of the two algorithms without error correction.
| Method | Output |
|---|---|
| TARGET | I WANT TO BE THE VERY BEST LIKE NO ONE EVER WAS TO CATCH THEM IS MY REAL TEST |
| HMM* | I WANT TE BERTHE VERY BEGN LIKE HELONE QVEREWAS TA C |
| HMM | I WANT TO BERTHE VERY BEGN LIKE HELONE EVEREWAS TO C |
| PF* | CFWANT TO BE THE WERE BESTSLIKE NO ONCHESER WAS TP CA |
| PF | I WANT TO BE THE WERE BEST LIKE NO ONE EVER WAS TO CA |
4 Discussion
PF algorithms are widely used for tracking the progress of a physical system using a state-space model [19]. In the PF classifier presented here, PF methods are applied to estimate target output strings by formulating typing as a series of transitions through a language model. The PF classifier required fewer samples and made more accurate selections than the standard classification and HMM methods. This improvement is due to the improved language model that biases selections towards English words rather than simply common character patterns. Because n-gram models only use a limited character history, they give high probability to strings that resemble correct patterns locally, which do not necessarily make sense in context (Table 1). Limitations in the language model result in incorrect prior distributions, which can mislead the classifier or cause the threshold probability to be met before sufficient observations were made.
Online performance was consistent with the results from offline analysis, with only a small decrease in average performance. This decrease is largely due to a single subject (subject P) as the average bit rates of the remaining subjects (32.32 bits/min for HMM and 39.37 bits/min for PF) are almost identical to the offline results (32.33 bits/min and 38.07 bits/min, respectively). A decrease was expected as online studies did not optimize the probability threshold, but this may have been offset by added user motivation resulting from feedback and free spelling [26].
Several subjects saw modest or no improvement over the HMM method. In general, the errors that these subjects saw were consistent with the language model. For instance, a typo that changes “UNITS” into “UNITY” cannot be solved by a single word language model as both are valid words. In this case, context would need to be incorporated into the system to truly determine the target character. For instance, previous words can help to determine the most likely part of speech of the current target word. This information could be used to change the probabilities on the automata, so that the model reflects the appropriate subset of the corpus.
Variance between subjects increased in online trials because allowing subjects to select the target sentence allowed for target strings that were not well represented by the training corpus for the language model. When implementing this system with “locked-in” patients, a targeted corpus could be developed that models likely words or phrases for a patient rather than a generic model of the English language. Such a model could also adapt based on context such as time of day or the subject’s environment. The model would then provide a stronger prior probability to the PF algorithm, resulting in faster selections and more accurate automatic error correction.
The performance of the PF algorithm was shown to be reliant on a sufficient number of particles as the algorithm failed to accurately classify characters for any subject when using only 10 particles. This is not surprising as undersampling the posterior distribution will not accurately reflect the true distribution, which can have highly volatile results. However, the algorithm proved fairly robust, as it was able to achieve good classification accuracy with as few as 100 particles and its results stabilized after increasing the number to 10,000. While the complexity of the algorithm is linear in the number of particles, it is important to limit the number used because of the short duration of a time step (125 ms) in the online system. In this instance, 10,000 is a reasonable number for online computation, but more particles will be needed as the complexity of the language model increases. Future implementations should be wary of the number of particles needed for a sufficient representation of the posterior distribution and the effect that will have on the performance of the classifier in a real-time setting.
4.1 Limitations and future directions
Final output strings from the PF algorithm could contain errors as it is not able to make all corrections automatically. Some errors are obvious to a reader and are unlikely to affect the ability of the user to convey intent. However, in some cases a small error can change the meaning of a sentence or make output incomprehensible. To handle these cases, the user can be given the option to make manual corrections in scenarios where the system is unlikely to be able to make a correction automatically. The system could alternatively present the user with a set of the candidate outputs rather than simply selecting the most probable. In such a system, a row in the matrix could be replaced with a set of word options as in systems with an autocomplete method [27–28]. Studying the relationship between error rate in BCI output and reader understanding could provide insight into the impact of misclassifications and optimal strategies for correcting errors.
This study was conducted using healthy volunteers who did not have the same constraints as “locked-in” patients, such as restrictions to eye gaze. As a result, studies implemented in the target patient population are likely to yield lower bit rates and are also likely to be more variable as patients will have differences in severity of disease. The PF algorithm is expected to have a similar improvement for these subjects as it does not change the front end of the system that is presented to the user. Therefore, the signal quality is not affected and the classification improves by incorporating external language domain knowledge. Performance using the P300 speller system with language domain knowledge needs to be tested in the target patient population in order to measure the true effect on performance.
5 Conclusion
Typing with a P300 system can be modeled as a Bayesian process that can be indirectly observed through EEG response signals. Stochastic importance sampling effectively incorporates domain information into signal classification, which greatly improves a user’s ability to create language. This study shows that incorporating this natural language information significantly improves the performance of a BCI communication system.
Acknowledgments
This work was supported by the NIH/NIBIB Training Grant T32-EB016640 (WS), the National Institute of Biomedical Imaging and Bioengineering Award Number K23EB014326 (NP), and the UCLA Scholars in Translational Medicine Program (NP).
Contributor Information
W Speier, Email: speier@ucla.edu.
CW Arnold, Email: cwarnold@ucla.edu.
A Deshpande, Email: aniket@ucla.edu.
J Knall, Email: jennyknall@ucla.edu.
N Pouratian, Email: npouratian@mednet.ucla.edu.
References
- 1.Farwell L, Donchin E. Talking off the top of your head: toward a mental prosthesis utilizing event-related brain potentials. Electroencephalogr Clin Neurophysiol. 1988;70:510–2. doi: 10.1016/0013-4694(88)90149-6. [DOI] [PubMed] [Google Scholar]
- 2.Sellers E, Krusienski D, McFarland D, Vaughan T, Wolpaw J. A P300 event-related potential brain-computer interface (BCI): the effects of matrix size and inter stimulus interval on performance. Biol Psychol. 2006;73:242–52. doi: 10.1016/j.biopsycho.2006.04.007. [DOI] [PubMed] [Google Scholar]
- 3.Townsend G, LaPallo BK, Boulay CB, Krusienski DJ, Frye GE, Hauser CK, Schwartz NE, Vaughan TM, Wolpaw JR, Sellers EW. A novel P300-based brain-computer interface stimulus presentation paradigm: moving beyond rows and columns. Clin Neurophysiol. 2010;121:1109–20. doi: 10.1016/j.clinph.2010.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jin J, Horki P, Brunner C, Wang X, Neuper C, Pfurtscheller G. A new P300 stimulus presentation pattern for EEG-based spelling systems. Biomed Tech. 2010;55:203–10. doi: 10.1515/BMT.2010.029. [DOI] [PubMed] [Google Scholar]
- 5.McFarland D, Sarnacki W, Townsend G, Vaughan T, Wolpaw J. The P300-based brain-omputer interface (BCI): effects of stimulus rate. Clin Neurophysiol. 2011;122:731–7. doi: 10.1016/j.clinph.2010.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lu J, Speier W, Hu X, Pouratian N. The effects of stimulus timing features on P300 speller performance. Clin Neurophysiol. 2012;124:306–14. doi: 10.1016/j.clinph.2012.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kaper M, Meinicke P, Grossekathoefer U, Lingner T, Ritter H. BCI competition 2003 - data set IIb: support vector machines for the P300 speller paradigm. IEEE Trans Biomed Eng. 2004;50:1073–6. doi: 10.1109/TBME.2004.826698. [DOI] [PubMed] [Google Scholar]
- 8.Xu N, Gao X, Hong B, Miao X, Gao S, Yang F. BCI competition 2003 - data set IIb: enhancing P300 wave detection using ICA-based subspace projections for BCI Applications. IEEE Trans Biomed Eng. 2004;51:1067–72. doi: 10.1109/TBME.2004.826699. [DOI] [PubMed] [Google Scholar]
- 9.Serby H, Yom-Tov E, Inbar G. An improved P300-based brain-computer interface. IEEE Trans Neural Syst Rehabil Eng. 2005;13:89–98. doi: 10.1109/TNSRE.2004.841878. [DOI] [PubMed] [Google Scholar]
- 10.Krusienski D, Sellers E, Cabestaing F, Bayoudh S, McFarland D, Vaughan T, Wolpaw J. A comparison of classification techniques for the P300 Speller. J Neural Eng. 2006;3:299–305. doi: 10.1088/1741-2560/3/4/007. [DOI] [PubMed] [Google Scholar]
- 11.Jelinek F. Statistical Methods for Speech Recognition. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- 12.Speier W, Arnold C, Lu J, Taira RK, Pouratian N. Natural language processing with dynamic classification improve P300 speller accuracy and bit rate. J Neural Eng. 2012;9:016004. doi: 10.1088/1741-2560/9/1/016004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Park J, Kim K. A POMDP Approach to Optimizing P300 Speller BCI Paradigm. IEEE Trans Neural Syst Rehabil Eng. 2012;20:584–94. doi: 10.1109/TNSRE.2012.2191979. [DOI] [PubMed] [Google Scholar]
- 14.Kindermans P, Verschore H, Verstraeten D, Schrauwen B. A P300 BCI for the Masses: Prior Information Enables Instant Unsupervised Spelling. NIPS. 2012;25:719–27. [Google Scholar]
- 15.Speier W, Knall J, Pouratian N. Unsupervised training of brain-computer interface systems using expectation maximization. IEEE EMBS Conf Neural Eng. 2013:707–10. [Google Scholar]
- 16.Speier W, Arnold C, Lu J, Deshpande A, Pouratian N. Integrating language information with a hidden Markov model to improve communication rate in the P300 speller. IEEE Trans Neural Syst Rehabil Eng. 2014;22:678–84. doi: 10.1109/TNSRE.2014.2300091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Oken BS, Orhan U, Roark B, Erdoqmus D, Fowler A, Mooney A, Peters B, Miller M, Fried-Oken MB. Brain-computer interface with language model-electroencephalography fusion for locked-in syndrome. Neurorehabil Neural Repair. 2014;28:387–94. doi: 10.1177/1545968313516867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gordon N, Salmond D, Smith A. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEEE Proc-F. 1993;140:107–13. [Google Scholar]
- 19.Arulampalam M, Maskell S, Gordon N, Clapp T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans Neural Syst Rehabil Eng. 2002;50:174–187. [Google Scholar]
- 20.Mohri M. On some applications of finite-state automata theory to natural language processing. Natural Language Engineering. 1996;2:61–80. [Google Scholar]
- 21.Speier W, Deshpande A, Pouratian N. A Method for Optimizing EEG Electrode Number and Configuration for Signal Acquisition in P300 Speller Systems. Clin Neurophsiol. 2014 doi: 10.1016/j.clinph.2014.09.021. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schalk G, McFarland D, Hinterberger T, Birbaumer N, Wolpaw J. BCI2000: A General-Purpose Brain-Computer Interface (BCI) System. IEEE Trans Biomed Eng. 2004;51:1034–43. doi: 10.1109/TBME.2004.827072. [DOI] [PubMed] [Google Scholar]
- 23.Draper N, Smith H. Applied Regression Analysis. 2. New York, NY: Wiley; 1981. [Google Scholar]
- 24.Francis W, Kucera H. Brown Corpus Manual. 1979. [Google Scholar]
- 25.Pierce J. An Introduction to Information Theory. New York, NY: Dover; 1980. [Google Scholar]
- 26.Yin E, Zhou Z, Jiang J, Chen F, Liu Y, Hu D. A speedy hybrid BCI spelling approach combining P300 and SSVEP. IEEE Trans Biomed Eng. 2014;61:473–483. doi: 10.1109/TBME.2013.2281976. [DOI] [PubMed] [Google Scholar]
- 27.Ryan DB, Frye GE, Townsend G, Berry DR, Mesa GS, Gates NA, Sellers EW. Predictive spelling with a P300-based brain-computer interface: increasing the rate of communication. Int J Hum-Comput Interact. 2011;27:69–84. doi: 10.1080/10447318.2011.535754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kaufmann T, Völker S, Gunesch L, Kübler A. Spelling is just a click away – a user-centered brain-computer interface including auto-calibration and predictive text entry. Front Neurosci. 2012;6:72. doi: 10.3389/fnins.2012.00072. [DOI] [PMC free article] [PubMed] [Google Scholar]


