Alternatives to hazard ratios for comparing efficacy or safety of therapies in noninferiority studies

Abstract

A noninferiority study is often used to investigate whether a treatment’s efficacy or safety profile is acceptable compared to an alternative therapy regarding the time to a clinical event. The empirical quantification of the treatment difference for such a study is routinely based on the hazard ratio estimate. The hazard ratio, which is not a relative risk, may be difficult to interpret clinically, especially when the underlying proportional hazards assumption is violated. The precision of the hazard ratio estimate depends primarily on the number of observed events, but not directly on either exposure times or sample size of the study population. If the event rate is low, the study may require an impractically large number of events to ensure that the prespecified noninferiority criterion for the hazard ratio is attainable. This article discusses deficiencies of the current approach for design and analysis of a noninferiority study. We then provide alternative procedures, which do not depend on any model assumption, to compare two treatments. For a noninferiority safety study, the patients’ exposure times are more clinically important than the observed number of events. If the study patients’ exposure times are long enough to evaluate safety reliably, these alternative procedures can effectively provide clinically interpretable evidence on safety, even with relatively few observed events. We illustrate these procedures with data from two studies. One explores the cardiovascular safety of a pain medicine; the second examines the cardiovascular safety of a new treatment for diabetes. These alternative strategies to evaluate safety or efficacy of an intervention lead to more meaningful interpretations of the analysis results than the conventional one via the hazard ratio estimate.

INTRODUCTION

Several statistical and clinical publications highlight concerns about the use of the hazard ratio as a summary measure for assessing the efficacy of a new therapy in superiority studies (1 – 3), but few if any address the use of the measure in noninferiority studies. The hazard ratio is a model-based measure of differences between two groups, and as such, assumes a specific relationship between the two distributions of the outcome variable. The interpretability of such a summary measure depends heavily on the validity of the model assumptions. Noninferiority studies have been often utilized for comparative evaluations of the efficacy or safety of therapies (4 – 6). This article uses two examples to illustrate the limitations of using the hazard ratio when designing and interpreting such studies, and discusses the pros and cons of using alternative measures such as the risk difference and the difference between two restricted mean survival times (See Appendix 1 for glossary of terms).

EXAMPLE 1: Celecoxib Study

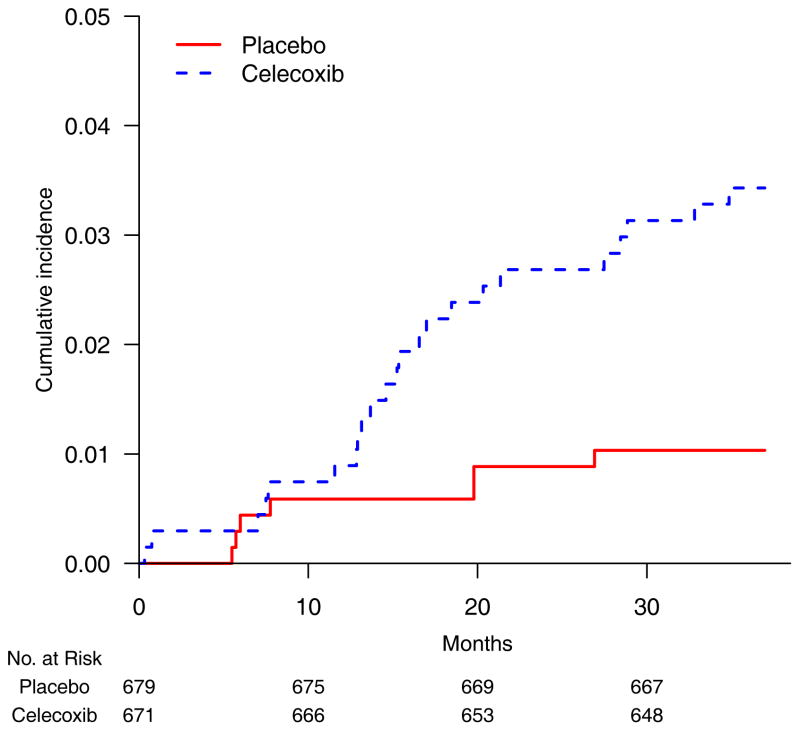
The Adenoma Prevention with Celecoxib trial tested whether 400 mg celecoxib BID would reduce the recurrence of colorectal adenoma after polypectomy (7). The study randomized 671 and 679 patients to celecoxib and placebo, respectively. The endpoint for cardiovascular (CV) safety was the time to a composite outcome of death from CV causes, myocardial infarction, stroke, and heart failure. At the advice of the Data Monitoring Committee, the trial ended early with 23 and 7 events in the celecoxib and placebo arms, respectively. Although the observed event rates were low, the cumulative incidence curves, which indicate the event rates over time (Figure 1), appear markedly different.

Figure 1.

Empirical cumulative incidence curves for patients randomized to celecoxib 400 mg BID (blue, dashed line) and placebo (red solid line) in the celecoxib study (7).

A conventional way to quantify the between-group difference is to calculate the hazard ratio under the assumption of proportional hazards (PH). The PH assumption requires the ratio of the two hazard functions to be approximately constant over time (8). For this example, the estimated hazard ratio was 3.35 (95% CI 1.44 to 7.81; p=0.005) (7). Clinically, even if the hazards were truly proportional, it is difficult to interpret a 3.4-fold increase in hazard for celecoxib compared with placebo because the hazard is not a probability measure, nor is the hazard ratio a relative risk. Rather, the hazard ratio is a ratio of hazard rates. Like other ratio-based measures, the estimated hazard ratio may convey a dramatic contrast between two groups when the observed event rates are low. For the celecoxib trial, the estimated event rates at 36 months for the treated and placebo groups were 3.0% and 1.0%. Thus, the tripling of the hazard ratio corresponded to only a 2.0% absolute increase (95% CI 0.8% to 3.2%) in rates (Table 1).

Table 1.

Treatment Contrast Measure Estimates (95% confidence intervals) for the Example Studies: Hazard ratio (active/placebo), Risk Difference (active - placebo), Restricted Mean Survival Time (placebo - active).

Contrast Measure	Study Celecoxib	Saxagliptin
Hazard ratio	3.35(1.44, 7.81)	1.00 (0.89, 1.12)
Risk difference at time t	2.0% (0.8%, 3.2%)	−0.2% (−1.2%, 0.9%)
	at month 36	on day 900
Restricted mean survival time difference*	0.43 (0.08, 0.78) months	0 (−5, 4) days

Estimates presented as point estimates (95% CI) and contrasts relative to a placebo group. For the difference metrics, a positive value indicates an increased risk of active treatment.

^*Restricted mean survival times calculated to 36 months (celecoxib) and to 900 days (saxagliptin).

The precision of the estimated hazard ratio depends mainly on the number of observed events, not on the number of patients or their exposure times. If we artificially added 1,000 exposure times censored at the end of the study without events to each arm of the celecoxib trial, the estimated hazard ratio would change little (HR 3.29; 95% CI 1.41 to 7.67). On the other hand, with those additional observations, the rate difference at 36 months would be 0.9% and the 95% confidence interval of 0.3% to 1.6% would be a much more precise estimate. Furthermore, when the proportional hazards assumption is violated (the hazard ratio is not actually constant over time), the clinical meaning of the hazard ratio is unclear. The two empirical cumulative incidence curves for the celecoxib trial (Figure 1) separate after ten months, but not during the initial study period. This indicates a possible violation of the PH assumption. Checking the plausibility of the PH assumption is problematic because there were few CV events in the celecoxib study, such that no goodness-of-fit test would have sufficient power to detect inadequacy of the PH model.

EXAMPLE 2: Saxagliptin Study

A randomized, placebo-controlled clinical trial was conducted to assess the potential CV risk of saxagliptin, a dipeptidyl peptidase 4 inhibitor for patients with type 2 diabetes (9). The primary endpoint was the time to the first occurrence of CV death, nonfatal myocardial infarction, or nonfatal ischemic stroke. In order to claim that saxagliptin is noninferior to placebo, the study investigators, following guidelines of the U.S. Food and Drug Administration (10), prespecified a noninferiority margin for the hazard ratio (saxagliptin vs. placebo) of less than 1.30 under the PH model (10–12). If the upper bound of the observed 95% confidence interval was less than 1.30, saxagliptin would be concluded to be safe. If noninferiority was established, the investigators planned to assess whether the CV safety of saxagliptin was superior to placebo.

Since the confidence interval for the hazard ratio depends mainly on the observed number of events, 1040 events were needed by the end of the study to satisfy noninferiority and superiority objectives, regardless of the number of participants or duration of follow-up. To obtain 1040 events, the investigators randomized 16,492 patients to saxagliptin or placebo in a 1:1 ratio; they were followed up to 2.9 years (median, 2.1 years). At the end of the study, 613 and 609 events had occurred in the saxagliptin and placebo arms, respectively. The estimated hazard ratio (saxagliptin vs. placebo) was 1.00 (95% CI 0.89 to 1.12). Because the upper bound of this interval was less than 1.30, the trial satisfied the prespecified criterion for noninferiority; however, the drug failed to meet the claim that the CV safety of saxagliptin was superior to placebo.

Designing and analyzing a safety trial to establish noninferiority using the hazard ratio is not ideal. Firstly, the threshold of 1.30 for the hazard ratio (10 - 12) fails to account for any background “absolute hazard” value for the placebo arm. If the event rate for the placebo arm is very low, a potential 30% (or higher) additional “hazard” may not represent a clinically meaningful increase in risk. If the event rate is high, a 30% increase may be unacceptably high.

Secondly, the width of the confidence interval for the hazard ratio depends mainly on the observed number of events but not on the exposure times. Had the few events been distributed evenly over a reasonably long follow-up time, the new therapy would have shown sufficient evidence of safety; however, with few events, the resulting confidence interval for the hazard ratio would be unacceptably wide. Conventionally, but in some cases inappropriately, a wide confidence interval suggests that evidence is insufficient to make conclusions about safety. Thirdly, if the PH assumption (8) is violated (especially when the hazard functions cross during the study period), the standard inferential procedure based on the hazard ratio may fail to detect a potential excess risk because the study would have inadequate power to detect a difference between two groups.

ALTERNATIVES TO THE HAZARD RATIO

The event rates are low in most safety studies (9, 11, 13, 14). The conventional design for a noninferiority study, such as the saxagliptin study, requires a large number of study patients or long study duration, or both, to demonstrate noninferiority. Using data from the saxagliptin study, here we discuss several well-known model-free alternatives to the hazard ratio and demonstrate that, had this trial been performed with a much smaller size, it would still have led to a statistically valid conclusion based on a clinically interpretable measure of the safety. Table 2 summarizes advantages and disadvantages of the alternative measures. Note that a model-free alternative to the hazard ratio does not require the assumption of a specific relationship between two groups with respect to the outcome distribution.

Table 2.

Pros and cons of between group difference measures for time to event analyses of noninferiority safety studies

Measures	Pros	Cons
Hazard ratio (model-based)	A valid summary for the difference of two cumulative incidence distributions (when the PH assumption is correct) with statistically efficient inference procedures.	Lacks a clinically meaningful reference value for the hazard from the control arm to assess the difference between groups. Difficult to interpret when the PH model is far from correct because it estimates a population quantity that depends in part on the censoring distributions. May not have adequate power to detect a safety signal especially when the two hazard functions cross during study follow up. May require an impractically large study because the precision of the estimated hazard ratio depends on the number of observed events and not directly on the number of patients and their exposure times. May selectively study a higher-risk population than the indicated patient population for the new treatment because many observed events are needed.
Relative time (model-based)	Provides a clinically meaningful summary of the differences between the groups if the model is correctly specified. For example, if the estimated ratio (treated vs. control) of two event times is 1.3, one can claim that on average a control patient if treated by the new therapy would gain an extra 30% “survival time.” This, coupled with the survival distribution of the control arm, provides a clinically meaningful interpretation of the treatment benefit.	Difficult to interpret when the model is not correct because the empirical relative time estimates a population quantity that depends on the censoring distributions.
Difference of percentiles (model-free)	Provides a clinically meaningful summary of the differences between groups and does not depend on a model assumption. Has a well-developed inference procedure for the difference (ratio).	May not be estimable if follow-up time is short or the event rate is low because in such studies not all the percentile can be observed. May be an unstable estimate because the median (i.e., the 50th percentile) is heavily dependent on the local shape of the cumulative incidence curve.
The t-year event rate difference (model-free)	Provides an easy to interpret and clinically meaningful summary of the differences between groups. Has a well-established and robust inference procedure. Probably the most relevant quantity for decision-making when one is interested in long-term survival.	Only reflects cumulative information at time t and does not reflect any differences in the profile of the cumulative incidence curves up to t
Restricted mean survival time (RMST) difference (model-free)	Provides a clinically meaningful summary of the differences between groups. Provides a more stable estimate than the median in survival time studies. Utilizes more information than its t-year event rate counterpart. May not need an impractically large study to assess noninferiority if the patient’s exposure time is sufficiently large for safety evaluation.	Needs prespecification of the time point of interest. May selectively study a relatively healthy population with low event rates rather than the indicated patient population in order to obtain a noninferiority claim.

Risk Difference

An obvious choice for a model-free measure is the difference in event rates at a specific time point. For example, in the saxagliptin study, we might choose 900 days (approximately 2.5 years) after randomization, which is the last time point shown in the cumulative incidence curves reported in Scirica et al. (9). The estimated risk difference (saxagliptin minus placebo) is −0.2% with an 8.9% event rate for the placebo group, indicating a small absolute reduction from saxagliptin. This between-group difference at a specific time provides a clinically interpretable comparison; however, it may not capture the overall profile of the difference between the two cumulative incidence curves. The methodology for event-rate differences at a specific time has been extensively discussed (15).

Percentile Difference

Another common measure, the difference of two median event times, can be easily obtained using the cumulative incidence curves (16); however, when the event rate is low or the follow-up time is short, the median event time may not be observable. Instead, one may use a difference of percentiles between two groups (17). For the above anti-diabetes drug study, the difference of the 5th percentiles (saxagliptin vs. placebo) is zero. While percentiles other than the median have a simple mathematical interpretation, their meanings may not be intuitively obvious to investigators or patients.

Restricted Mean Survival Time Difference

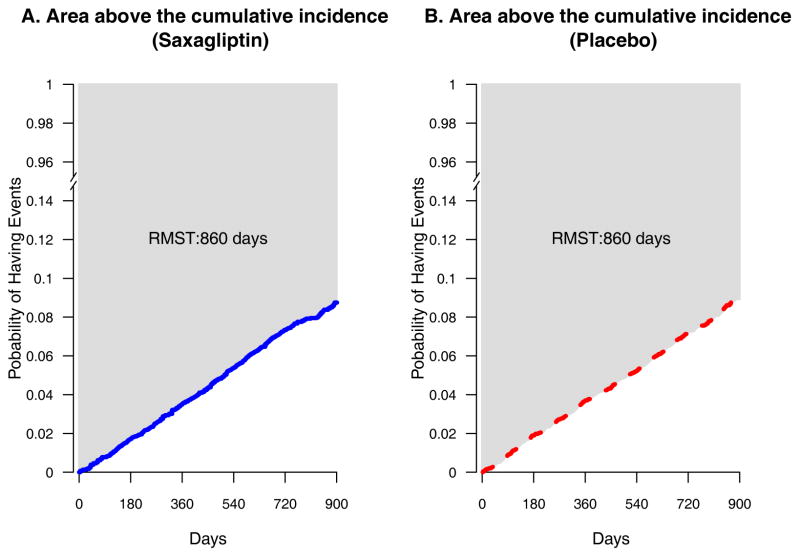
An attractive, but seldom used, alternative is the restricted mean survival (event-free) time (RMST) (18 – 21) up to a specific time point. The RMST is the expected time spent event-free for a future patient followed for a specified time. It is estimated by the area above the empirical cumulative incidence curve. Figure 2 presents the observed cumulative incidence curves to 900 days reported by Scirica et al. (9). The areas above the curves for saxagliptin (solid) and placebo (dotted), shown in light gray, are both approximately 860 days. That is, if we treat future patients from the study population and follow them for 900 days, the average time spent event-free would be approximately 860 days for both groups with an observed difference of 0 days between the two groups. These RMST estimates incorporate both the number of events and the exposure times. With the observed RMST for the placebo arm, the corresponding confidence interval estimate for the difference of RMSTs can be interpreted statistically and clinically for assessing a claim of noninferiority. Also, as with models for hazard ratios that can adjust for baseline covariates, models for event rate difference or RMST difference can adjust for baseline imbalances (22–24).

Figure 2.

Empirical cumulative incidence curves with reconstructed event time data for the saxagliptin study (9); (A) Saxagliptin arm (solid line) and (B) Placebo arm (dotted line). The shaded area (the area above the cumulative incidence curve) in each panel is the restricted mean survival time up to 900 days

To illustrate our proposals, we applied an algorithm developed by Guyot (25) to the observed incidence rate curves in the publication of the saxagliptin study to reconstruct individual patient-level data for making inferences about the risk and RMST differences (saxagliptin minus placebo) at 900 days. The 95% confidence interval for the risk difference is (−1.2%, 0.9%). For the difference in RMSTs (placebo minus saxagliptin), the 95% confidence interval is (−5, 4) days (Table 1). That is, at the confidence level of 95%, on average future patients treated with saxagliptin for 900 days would be expected to be free of CV events for as many as 5 days more to as many as 4 days fewer than their placebo counterparts. Coupled with the summary measure for the control group (the RMST of 860 days), these absolute group differences with time units provide clinically interpretable information regarding the group contrast than a hazard ratio (95% CI 0.89 to 1.12). Appendix 2 provides computer programs for implementing RMST analyses.

How Group Difference Measures Affect Study Size and Precision of Estimates

To explore the connection between the study size and the observed noninferiority bound for group difference measures with the reconstructed data from the saxagliptin study, we randomly selected a subset of patients using a fixed proportion of the original study size and constructed 95% confidence intervals for the hazard ratio and the difference of RMSTs at Day 900. We repeated the process 1000 times and obtained the average of the resulting 1000 confidence interval estimates for each measure. See Table 3 for the results with several sub-sample sizes --- 15%, 20%, and 25% of the saxagliptin study. For instance, had the saxagliptin trial enrolled only 2474 study subjects, that is, 15% of those actually enrolled, the resulting average 95% confidence interval for the hazard ratio would have been (0.76, 1.36), with the upper bound exceeding 1.3. On the other hand, for the difference of RMSTs, the average 95% confidence interval estimate would have been (−12 days, 12 days). This estimate provides a high degree of confidence that, on average, saxagliptin-treated patients would be free of events no more than 12 days less than the placebo patients through 900 days of follow-up. If a difference of 12 days out of 900 is a clinically acceptable noninferiority margin, the saxagliptin trial could have been conducted with many fewer patients.

Table 3.

Treatment Contrast Measures by Sample Size: the Saxagliptin Study

	Entire study population (n=16,492)	Sub-samples of the total study population** 25% (n=4123)	20% (n=3298)	15% (n=2474)
Hazard Ratio	(0.89, 1.12)	(0.80, 1.26)	(0.78, 1.29)	(0.76, 1.36)
RMST Difference*	(−5, 4) days	(−9, 9) days	(−11,10) days	(−12, 12) days
Risk Difference on Day 900	(−1.2%, 0.9%)	(−2.3%, 2.0%)	(−2.6%, 2.2%)	(−2.9%, 2.6%)

Abbreviation: RMST = restricted mean survival time

The numbers are presented as point estimates (95% CI) and contrasts relative to the placebo group. For the difference metrics, a positive value indicates an increased risk of saxagliptin treatment.

Data are reconstructed from the original report. See Appendix 3 for details.

^*Restricted mean survival times are calculated to day 900.

^**Estimates are based upon 1,000 repeated random samples of size 25%, 20% and 15% of the total study population.

Note that event-free observations at the end of the study may contribute information to the difference in RMST but not to the HR. Under the above simulation setting, for each generated sample of 2747 patients, if we were to add 6873 artificial observations of 900 days to each arm to match the original saxagliptin study sample size of 16492, the resulting average confidence interval for the difference of RMSTs would be (−2 days, 2 days). On the other hand, the corresponding confidence interval for the hazard ratio, which depends primarily on the observed number of events, is (0.75, 1.35), practically identical to the previously mentioned (0.76, 1.36). That is, censored observations (patients without events at 900 days) contribute essentially nothing to the precision of the hazard ratio.

USING ALTERNATIVE MEASURES TO DESIGN A NONINFERIORITY STUDY

To design a noninferiority study, we usually assume that two groups being compared are identical to each other with respect to the distribution of the endpoint (the time to a specific event). We also specify the following elements: the metric or parameter that will be used to compare groups; the noninferiority margin; the statistical inference procedure (e.g., the two-sided 95% confidence interval estimate for the group contrast measure) for assessing the noninferiority of the new therapy; the parametric distribution for the outcome variable; the patient’s potential exposure time for safety assessment; the number of patients expected to enroll; and the accrual profile over time. For a conventional design that uses the hazard ratio as the group contrast measure, the choice of the noninferiority margin for anti-diabetes drugs, is generally 1.30 for safety studies (10–12). The rationale for this choice of a specific hazard ratio has never been clear to us. In designing such a trial, survival times are often assumed to be exponential (i.e., constant hazard rates throughout the study), and the timing of the end of the study is determined by the total number of events such that the upper bound of the 95% confidence interval for the hazard ratio is likely (for example, a chance of 80%) to be less than the noninferiority margin.

If we design a study using the difference of the RMSTs, we need to specify a time point at which the RMST will be evaluated, which should be long enough to assess the treatment’s clinical safety profile. Under the conventional setting with the hazard ratio, the saxagliptin study would need 456 CV events to ensure enough evidence for assessing the drug’s safety no matter what the underlying event rates are. To show how to design a study similar to the saxagliptin study using the difference of two RMSTs, we assume that the time point for evaluating the RMST is 900 days with a noninferiority margin of 18 days, which is 2% of 900 days. The Appendix 4 presents a simple numerical procedure to calculate the study sample size under various patients’ accrual profiles over time. For instance, if 30 patients per day enter the study with at least 10% having 900 days of follow-up at the end, the study needs about 2100 participants and a total of 2.5 years to finish so that the above noninferiority margin of 18 days is attainable with high probability. Note that the corresponding upper bound of 95% confidence interval for the hazard ratio would be 1.52.

IMPACT OF MEASURE CHOICE ON STUDY POPULATION SELECTION

When designing a safety trial, the study subjects should be chosen appropriately from a target population that clinicians would treat in the real-life setting. Otherwise, the study investigators might “game” the system by selecting patients improperly in order to reaching their study goal faster. For instance, using the RMST as the primary parameter of interest, one may choose patients with low CV risk in a CV outcome trial. On the other hand, using the hazard ratio approach, the investigators might choose patients with high CV risk to collect a large number of events in a short time period. Note that a potential problem of using a relatively short term study for assessing safety is that such a trial might be too short to identify unexpected rare events from patients treated by a new therapy, For instance, in a recent large and long term clinical trial (TREAT) for evaluating safety of darbepoetin alfa, a small excess number of strokes was unexpectedly detected in the group assigned to darbepoetin alfa (26). However, how to utilize a controlled, comparative clinical study setting with limited resources to explore this potential problem in practice is unclear.

EVALUATING GROUP DIFFERENCES OVER A SET OF TIME POINTS SIMULTANEOUSLY

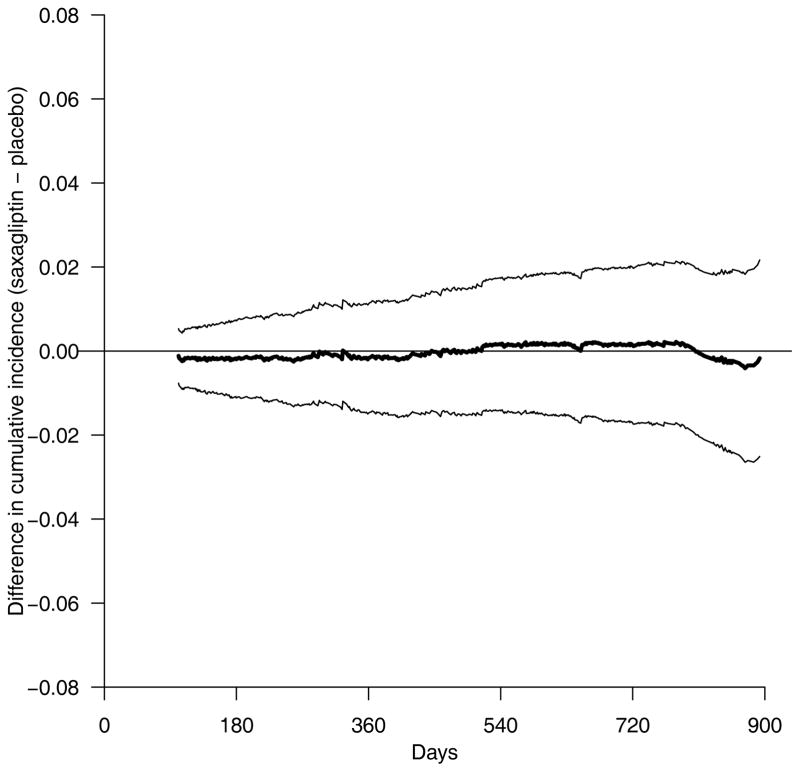
In some situations, it is important to compare two treatment groups across a set of time points simultaneously, rather than at a specific time point. The cumulative incidence curves (Figure 2) provide temporal profiles of the event rates. Although the two empirical curves for the saxagliptin study visually overlap, whether we can claim that their population counterparts are “equivalent” statistically and clinically collectively over time might be of interest. To this end, one may construct simultaneous confidence intervals for the curve of the difference between two cumulative incidence functions over time. Specifically, in the saxagliptin study, a 95% simultaneous confidence band between 100 and 900 days is given in Figure 3 (27). This band suggests that with a high probability, the true difference of two cumulative incidence curves would be contained entirely within the two dotted lines between 100 and 900 days. For example, at 300, 600, and 900 days, the true differences of the cumulative incidence curves are likely to fall in the intervals: (−1.1%, 1.0%), (−1.4%, 1.6%) and (−2.3%, 1.9%) simultaneously. This information, coupled with the empirical cumulative incidence curve for the placebo arm, provides additional useful information for decision-making concerning the CV safety of saxagliptin beyond that obtained from a single summary measure evaluated at 900 days.

Figure 3.

Saxagliptin versus placebo. Point estimate (solid) and 0.95 simultaneous confidence band (dotted) for the difference of the cumulative incidence

IMPLICATIONS FOR CLINICAL INTERPRETATION

Table 2, which presents advantages and disadvantages of various measures, shows that measures other than the hazard ratio facilitate clinically meaningful interpretation of findings. We further illustrate this point with data from the celecoxib trial (7) in which the estimated event rates at 36 months for the treated and placebo groups were 3.0% and 1.0%, respectively. The 95% confidence interval for the difference of the event rates was (0.8% to 3.2%). The estimated RMSTs through 36 months of follow-up for the treated and placebo groups were 35.33 and 35.76 months, respectively, a difference of 0.43 months (95% CI = 0.08 to 0.78, p= 0.015). That is, with 95% confidence, the celecoxib-treated patients would be event-free about, at most, 24 days (31*0.78) shorter than their placebo counterparts. Note that this statistically significant difference based on the cumulative incidence rate or RMST is more clinically interpretable than the corresponding hazard ratio estimate of 3.4.

CONCLUSIONS

Design and analysis of superiority and noninferiority studies differ fundamentally. Although the patients’ exposure times are important for both, the number of observed events is essential for evaluating a superiority claim for a new therapy over the control, but not for assessing safety through noninferiority. That is, “no news is bad news” for efficacy, but “no news could be good news” for safety.

Note that it is not clear how to compare the statistical efficiency of a robust estimation procedure discussed in this article with a model-based counterpart because the underlying hazard ratio and the RMST difference parameters are not directly comparable. For some special cases, the advantage of using the event rate or RMST difference to quantify the group difference is obvious, for instance, if no event occurs in one treatment group of the study, the confidence interval based on the hazard ratio is infinitely wide, but its counterpart for the absolute difference measure can be very narrow and provides sufficient evidence for assessing a noninferiority claim.

In summary, to explore toxicity, conventional study designs based on the hazard ratio have both statistical and clinical limitations. We encourage investigators at the design stage of the study to consider using the difference of two RMSTs, or some other robust and clinically interpretable model-free metrics rather than the hazard ratio. No matter which measure is used, the RMST or the event rate for the control arm is needed to provide context for clinical decision-making. Using RMST or the cumulative incidence rate at a particular time point as a summary of the distribution of the event-time observations, the investigator must prespecify an expected patient follow-up time that is sufficient for evaluating toxicity.

Appendix 1: Glossary (alphabetical order)

Cumulative incidence rate

The probability that an event has occurred before a specific time point.

Event-driven study

A study with time to an event as the endpoint whose total information or study size/time is based solely on the number of observed events, not directly on the patients’ exposure times or the number of patients involved.

Hazard rate

An instantaneous “force of mortality” (mortality is a generic term for event in survival analysis) at a specific time point approximating the probability that an event-free patient would experience the event in the next small time period divided by the length of such a time period (e.g., a day or week); this rate may not be estimated well empirically.

Hazard ratio

Ratio of the hazard rates

Model-based between-group summary measure

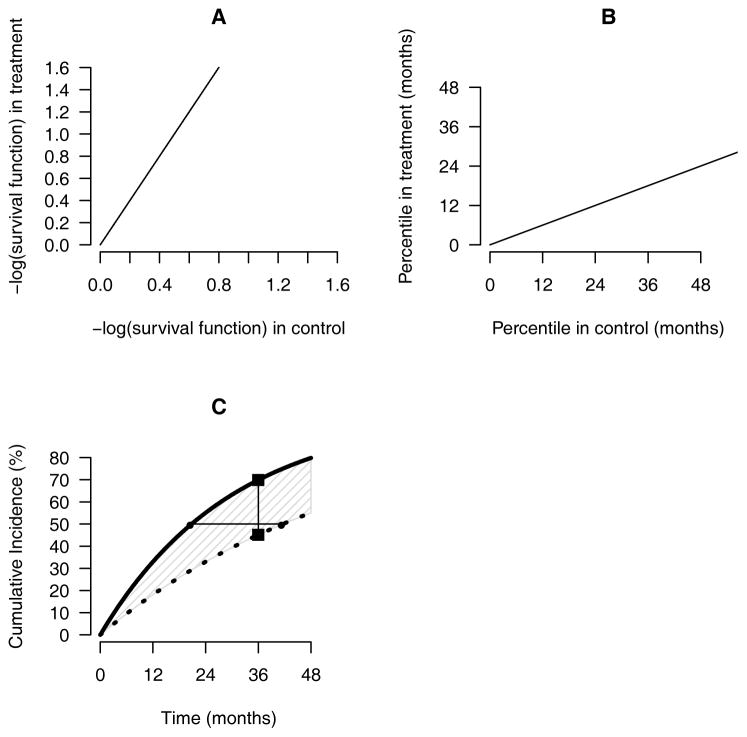
A population parameter for quantifying the difference between groups by imposing a specific relationship between two cumulative incidence functions; examples include the hazard ratio (assuming the hazard ratios are constant over the entire study time period) and the relative time (assuming that the ratio of percentiles of the two event time outcomes are constant); the slopes in Appendix Figure 1A and Appendix Figure 1B indicate the hazard ratio and the relative time, respectively.

• Proportional hazards (PH) model: the ratio of two hazard curves is assumed to be constant over the study duration.
• Model-based relative time model (accelerated failure time): the ratio of percentiles between two survival distributions is assumed to be constant over the study duration.

Model-free between-group summary measure

A population parameter for quantifying the between-group difference. This measure does not need to impose any relationship between two cumulative incidence curves; examples include the difference or ratio of RMSTs, the difference or ratio of t-year event rates, and the difference or ratio of median event times.

• Difference or ratio of t-year event rates: Difference or ratio of the event rates at a specific time point t; for example, the vertical distance between the two squares in Appendix Figure 1C is the difference of 36-month event rates.
• Difference or ratio of percentiles between two event times: Difference or ratio of percentiles between two event-time distributions; the horizontal distance between the two closed circles in Appendix Figure 1C is the difference of two median times.
• Difference or ratio of RMSTs: Difference or ratio of RMSTs; for example, the shaded area in Figure 4C is the difference in RMSTs at 48 months.

95% (ninety-five percent) simultaneous confidence band for a curve

A collection of confidence intervals over a time interval of interest such that the true curve (for example, the difference of two cumulative incidence functions) is entirely contained in the upper and lower boundaries of the band with a confidence level of 95%.

Noninferiority margin

A value for a group contrast measure (e.g., hazard ratio, the difference of RMSTs) under which a new treatment can be claimed to be noninferior to the control with respect to safety or efficacy.

Percentile of the event time

The time at which a given percentage of patients have experienced the clinical event.

Restricted mean survival (event-free) time at a specific time point (RMST)

The average “survival” (event-free) time of the patient followed up to a specific time point, measured by the area above the cumulative incidence curve from 0 to this time point; or equivalently, the area under the survival curve.

Appendix 2: Computer programs for restricted mean survival time

Computer programs to compare RMST between groups are available in three popular platforms (R, SAS, and Stata). This Appendix presents a brief illustration of the implementation with R (survRM2 packages). The R package is available from the CRAN website (http://cran.r-project.org/web/packages/survRM2/index.html). Similar program code is available for both SAS and Stata (http://bcb.dfci.harvard.edu/~huno).

For illustration, we use data from a randomized study (the primary biliary cirrhosis study) conducted by the Mayo Clinic. The details of the study and the data elements are seen in the help file in the survival package. The sample dataset used here can be loaded by the function rmst2.sample.data() in the surv2RM2 package. A listing of part of the sample dataset follows:

time	status	arm	age	edema	bili	albumin	protime
1.095140	1	1	58.76523	1.0	14.5	2.60	12.2
12.320329	0	1	56.44627	0.0	1.1	4.14	10.6
2.770705	1	1	70.07255	0.5	1.4	3.48	12.0
5.270363	1	1	54.74059	0.5	1.8	2.54	10.3
4.117728	0	0	38.10541	0.0	3.4	3.53	10.9
6.852841	1	0	66.25873	0.0	0.8	3.98	11.0

Here, time is time from randomization to either death or censoring; status indicates the survival status (1 means dead and 0 means alive); arm is the variable that indicates treatment assignment. In this sample, 0 denotes the placebo group and 1 represents the active treatment. The other 4 variables are covariates.

The following command implements the test of between-group differences based on RMST.

rmst2(time, status, arm, tau=10)

Here, tau is the truncation time used in the RMST calculation. Below is the output generated from this command.

The truncation time: tau = 10 was specified.

Restricted Mean Survival Time (RMST) by arm

	Est.	se	lower .95	upper .95
RMST (arm=1)	7.146	0.283	6.592	7.701
RMST (arm=0)	7.283	0.295	6.704	7.863

Restricted Mean Time Lost (RMTL) by arm

	Est.	se	lower .95	upper .95
RMTL (arm=1)	2.854	0.283	2.299	3.408
RMLT (arm=0)	2.717	0.295	2.137	3.296

Between-group contrast

	Est.	lower .95	upper .95	p
RMST (arm=1)-(arm=0)	−0.137	−0.939	0.665	0.738
RMST (arm=1)/(arm=0)	0.981	0.878	1.096	0.738
RMTL (arm=1)/(arm=0)	1.050	0.787	1.402	0.738

In this example, the difference in RMST (the first row of the “Between group contrast” block in the output) was −0.137 years. The point estimate indicated that patients on the placebo treatment survive 0.137 years longer than those on the active treatment group on average, when following up the patients for 10 years. While no statistical significance was observed (p=0.74), the 0.95 confidence interval (−0.939 to 0.665 years) was relatively tight around 0, suggesting that the difference in RMST would be at most +/− one year. For more detailed illustrations, please see the package vignette accompanied with survRM2 package.

Appendix 3. Reconstructing data from the saxagliptin study

Making inferences about the difference of two RMSTs requires individual patient’s event-time observations. The patient-level data from the saxagliptin study, however, are not publicly available. To illustrate the above procedures, we utilized an algorithm proposed by Guyot et al. (A1) to reconstruct an individual-level time-to-event dataset from the saxagliptin study using the information presented in Scirica et al. (A2). Specifically, we used the software DigitizeIt to scan the cumulative incidence curves with the reported numbers of patients at risk at various times to recreate the time-to-event observations. The reconstructed data led to cumulative incidence curves that are nearly identical to the originally published counterparts (not shown). Moreover, our reconstructed data yield a 95% confidence interval for the hazard ratio of (0.89, 1.12), which is identical to the interval reported in Scirica et al. (A2)

Appendix 4. Designing a noninferiority study with RMST difference (details)

We assume a Weibull distribution for the time to the composite CV events in the saxagliptin study (A2). The entire observed data give shape and scale parameters for this Weibull distribution of 1.05 and 8573, respectively. The observed accrual rate for this study was about 30 patients per day. Moreover, at the end of this study, about 10% of patients had follow-up times beyond 900 days. Assume that this Weibull distribution is the true model for the event times for both treatment groups. The resulting RMSTs are about 860 days. Under the above setting, for a range of potential numbers of study patients and 1:1 treatment allocation, we generate 2000 sets of realizations with each sample size. This results in 2000 interval estimates for the difference of two RMSTs. We then calculate the chance that the upper bounds of these 2000 intervals fall below 18 days. If the chance is lower than 80%, we increase the current sample size and repeat the above process. Then the final study sample size is chosen such that there is 80% chance for the upper bound of the 95% confidence intervals for the difference of two RMSTs to be below 18 days. An alternative way to design the study is to fix the study sample size but to choose the timing of the end of study (for example, with fewer patients, we need more than 10% of patients whose follow-up time would be beyond 900 days). In Appendix Table 1, we report cases with various accrual rates. For example, when we enroll 2094 patients with an accrual rate of 30 patients per day, we will need a total of 908 days to confirm the noninferiority with RMST difference. At the time of the analysis (i.e., 908 days after the study activation), the expected total number of observed event is 182. The corresponding upper bound of the interval estimates for the hazard ratio is be 1.52, which is much larger than 1.30.

Appendix Figure 1. Graphical presentation of between-group difference metrics.

(A) the hazard ratio, (B) the relative time, and (C) various model-free, between-group difference measures for a new treatment (solid curve) and a control (dotted curve); the slopes of the lines in A and B are the hazard ratio and the relative time, respectively, the distance between the two closed circles (horizontal line) in C is the difference for two medians; and the distance between the two closed squares in C (vertical line) is the difference of two event rates at 36-months; the shaded area in C is the difference in the restricted mean survival time up to 48 months

Appendix Table 1.

Upper 95% confidence bounds for HR and RD measures from a noninferiority study designed using RMST

Total study size	Accrual rate (per day)	The entire study time (days)	Total number of events observed	Estimated upper bound of 95% confidence interval for hazard ratio	Estimated upper bound of 95% confidence interval for risk difference at 900 days
2216	5	949	160	1.56	4.4%
2172	10	924	176	1.53	4.0%
2094	30	908	182	1.52	3.6%

Abbreviation: HR = hazard ratio; RD = risk difference; RMST = restricted mean survival time

Estimates of upper 95% confidence bounds for the HR and RD were calculated, assuming the following fixed inputs: total sample size, accrual rate, and total study time. All these configurations were figured out, so that the estimated upper bound of 95% confidence interval for difference in RMST at 900 days can meet a noninferiority margin of 18 days (2% of the 900 days).