Abstract
Poroelastic magnetic resonance elastography is an imaging technique that could recover mechanical and hydrodynamical material properties of in vivo tissue. To date, mechanical properties have been estimated while hydrodynamical parameters have been assumed homogeneous with literature-based values. Estimating spatially-varying hydraulic conductivity would likely improve model accuracy and provide new image information related to a tissue’s interstitial fluid compartment. A poroelastic model was reformulated to recover hydraulic conductivity with more appropriate fluid-flow boundary conditions. Simulated and physical experiments were conducted to evaluate the accuracy and stability of the inversion algorithm. Simulations were accurate (property errors were < 2%) even in the presence of Gaussian measurement noise up to 3%. The reformulated model significantly decreased variation in the shear modulus estimate (p≪0.001) and eliminated the homogeneity assumption and the need to assign hydraulic conductivity values from literature. Material property contrast was recovered experimentally in three different tofu phantoms and the accuracy was improved through soft-prior regularization. A frequency-dependence in hydraulic conductivity contrast was observed suggesting that fluid-solid interactions may be more prominent at low frequency. In vivo recovery of both structural and hydrodynamical characteristics of tissue could improve detection and diagnosis of neurological disorders such as hydrocephalus and brain tumors.
Index Terms: Hydraulic conductivity, magnetic resonance (MR) elastography, poroelasticity, soft prior
I. Introduction
MANUAL palpation is a well-established clinical standard for detecting changes in tissue health associated with pathological processes such as tumor growth, liver cirrhosis, and inflammation. In effect, the technique exploits the relationship between an applied force and the resulting displacement of tissue to characterize its local elastic modulus, and is a common diagnostic tool for breast cancers and hepatic fibrosis. Elastography is the quantitative imaging equivalent that produces mechanical property maps of tissue [1]. Magnetic resonance elastography (MRE) captures the internal tissue displacements resulting from an applied low frequency vibration [2], [3]. The resulting displacement field can be interpreted through a mechanical model to estimate the local mechanical properties of tissue like its shear modulus or damping ratio, which may inform differential diagnosis of disease. These elastograms can yield image information at high contrast that may not be evident from standard imaging techniques [4], [5].
MRE has been applied to a variety of organs and tissues including breast, heart, liver, brain, and muscle with varying levels of success [6]–[10]. The material models used to date in these cases have been linear elasticity or viscoelasticity, even though tissues exhibit a wide range of responses to applied stresses. For example, a viscoelastic model describes a single solid phase with both elastic and viscous behaviors, but does not otherwise represent the fluid phase in tissue and may be less appropriate for high water content tissues like brain (which is upwards of 75% fluid by volume). Poroelastic constitutive relations have enjoyed positive results when applied to these types of biological materials [11]–[13]. One form of poroelasticity is based on Biot’s consolidation theory [14], where a biphasic environment is assumed to consist of a porous elastic solid impregnated with a viscous fluid. The quasi-static equivalent of this poroelastic model has been used to describe hydrocephalus [15], [16] and intraoperative brain shift [17], [18]. More recently, the time-harmonic version has been developed for MRE and has been found to characterize porous materials more accurately than the corresponding linear elastic approach [19].
The poroelastic constitutive relation involves a set of structural and hydrodynamical material properties that are commonly assumed based on literature reports or empirical results. These properties include hydraulic conductivity, porosity, apparent mass density, fluid density, and solid density. While the relevant tissue densities are fairly well characterized, hydraulic conductivity and porosity are poorly understood and have been estimated through Darcy’s Law [20], [21] or by morphological staining techniques [22]. Moreover, neglecting the frequency dependence of hydrodynamic properties by using values derived from quasistatic experiments for MRE actuation frequencies will also lead to inaccurate modeling. Additionally, tissues such as brain have spatially-varying structural and fluid property parameters, in which case homogeneous assumptions are insufficient.
Hydraulic conductivity (κ) and porosity (ϕ) are interrelated properties where the former is a measure of the ease with which fluid travels through the pores of a material and the latter is a measure of the available void space, defined as a ratio of the void to total volumes. The influence of these properties on material response to an applied stress was examined by Perrinez et al. [19]. Displacement fields were calculated with varying values of κ, ϕ, and C (a function of the apparent mass density), and κ was found to cause the largest changes in displacement for a given material property change.
Hydraulic conductivity is a potentially important tissue property to consider because of the array of applications in which it could reveal clinically-significant information. For example, normal and malignant tissue have very different vasculatures [23], where perfusion properties can change dramatically based on tumor type [24]. Benign processes usually lack the vasculature of a malignancy, which is commonly described as being irregular, tortuous, and heterogeneous [25]. Fluid flow can be high or low as well, depending on the cellular mass that is present [26]. Furthermore, previous work [27] has related fluid-flow changes to disorders characterized by increased intracranial pressure (ICP). Specifically, hydrocephalus is caused by a blockage in cerebrospinal fluid transport, resulting in increased ventricular size and, in some cases, increased ICP. Currently, diagnosis occurs through standard imaging techniques that only depict a change in ventricular size, which can be confused with ex vacuo disease like cerebral atrophy. Alterations in structural and fluid-flow properties detected by MRE could increase the diagnostic accuracy of imaging and potentially eliminate the need for more invasive techniques such as lumbar puncture in the case of hydrocephalus.
This work reformulates the appropriate poroelastic finite element model (FEM) for spatially-varying hydraulic conductivity (previous studies assumed homogeneous values [19], [28]) and appropriate fluid flow boundary conditions. Simulated porous environments were evaluated to explore the accuracy and consistency of estimating κ in the presence of measurement noise. Inversion of shear modulus was robust in all cases, whereas κ was more sensitive to the added noise, yet its recovery was still spatially accurate with the correct contrast. Tofu phantoms were created with different contrasts and actuated at MRE frequencies to validate the new inversion algorithm with experimental data. Results show that the new model significantly improved the estimation of shear modulus while also producing κ contrast when spatial priors were encoded into the inversion technique. Also, a frequency dependence was found in κ, suggesting that poroelasticity may be a more accurate model, at least of tofu mechanical behavior, at low frequencies. These findings indicate the resulting poroelastic model can be applied to in vivo brain disease to characterize both the structural and hydrodynamical material properties through simultaneous recovery of images of spatially-resolved shear modulus and hydraulic conductivity.
II. Model Formulation For Spatially-Varying Hydraulic Conductivity
The constitutive relations describing a biphasic material experiencing a time-dependent applied load were first developed in the form of Biot’s theory of consolidation [14]. The model was extended to the time-harmonic case by Cheng et al. [29] and later by Perrinez et al. [28] to the frequency-domain equivalent set of equations for tissue elastography applications (known as poroelastic magnetic resonance elastography, or pMRE). The original coupled set of equations in the frequency domain for a fully-saturated porous medium undergoing time-harmonic forcing were given as
| (1a) |
| (1b) |
with β as
| (2) |
The vector ū is the complex-valued 3-D displacement, scalar p̄ is similarly for the pore-pressure, μ is the shear modulus, λ is Lamé’s first parameter, ω is the actuation frequency, ρ is the solid density, and ρf is the fluid density. The β term is a compilation of material properties including hydraulic conductivity (κ), porosity (ϕ), and apparent mass density (ρa). The overbar (—) symbolizes the frequency-dependent time-invariant amplitude of the variable of interest.
A. Spatially-Varying Hydraulic Conductivity
The original coupled set of (1) locates β outside of the divergence operator in (1b) because the properties within β were assumed to be constant. Spatially-varying κ (and therefore β) results in a form of the equations with β repositioned inside the divergence operator, resulting in
| (3) |
B. Finite Element Implementation
Fluid flow boundary conditions (BCs) are directly related to κ through Darcy’s Law, which in the quasistatic case is given by
| (4) |
where q̄ is the fluid flow and ∇p̄ is the pressure gradient. In a poroelastic material, q̄ · n̂ is the fluid flux, which represents the discharge through a boundary surface per unit area (given in (m/s)), and is related to the velocity of the fluid and the material porosity. Thus, based on the frequency domain poroelastic equations developed in Cheng et al. [29], the following four governing equations hold:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
where q̄ is a generalized form of Darcy’s Law, ζ is the water content, R is a measure of the change in water content, v̄ is the relative fluid-solid displacement vector that represents the fluid velocity, α is the Biot effective stress coefficient, and F describes the outside forces acting on the body. Under steady-state time-harmonic motion mediated by displacement BCs as in pMRE, no external forces are present (F = 0) and if we assume incompressible constituents, α and R reduce to 1 and ∞, respectively. Under these conditions, simplification of (5b) and (5d) produces
| (6) |
| (7) |
which is the new version of the pressure equation shown in (1b) and is a more compact form of (3) that is illustrative for FEM formulation and concomitant application of the appropriate fluid-related boundary conditions. The associated weighted residual weak form of (7) becomes
| (8) |
after application of the divergence theorem to the ∇ · q̄ term where n̂ is the outward pointing vector normal to the boundary surface and ϕi is the typical FEM weighting function for node i chosen here to be the same as the FEM basis function at this location—a piecewise continuous linear Lagrange interpolating polynomial with local support on an individual tetrahedral-shaped finite element. The symbol 〈 〉 indicates integration over the computational volume and ∮ denotes integration over its boundary surface.
The resulting system of equations (for N weighting and basis functions associated with N nodes in the FEM mesh) can be solved as
| (9) |
where matrix [A] is comprised of integrals of the basis functions, their derivatives, and the continuum’s physical properties, {x̂}is the unknown solution vector, and {b} is the known forcing vector. For the linear tetrahedral elements used in this work, the contribution to the stiffness matrix terms for weighting function i and node j, corresponding to the reformulated pressure equation with spatially-varying κ (and thus β), is expressed as
| (10a) |
| (10b) |
| (10c) |
| (10d) |
and {b} becomes
| (11) |
which allows fluid flow boundary conditions to be applied. The ′ in (10) and (11) represent additive contributions to the global system in (9).
C. Nonlinear Inversion
With the reformulated poroelastic model serving as the governing equations, an overlapping subzone, iterative parameter estimation algorithm analogous to the methods we have used in the past [28], [30] was implemented to recover spatial maps (images) of shear modulus and hydraulic conductivity. The inversion minimizes the difference between the computed (by the reformulated poroelastic model) and measured (via MRE) 3-D vector displacement field throughout the image acquisition volume by dividing the domain into a set of overlapping sub-zones and seeking minimization on the individual subzones by applying the measured displacements as boundary data on the subzone surface. The individual subzone minimization problem is solved with a Gauss-Newton (GN) method [31], which iteratively finds the solution of the nonlinear system of equations generated by setting the first derivatives of the sum-of-squared-differences between data and model (internal to the subzone surface) with respect to each material property parameter to be estimated (here shear modulus, μ, and hydraulic conductivity, κ) to zero. Regularization is added to stabilize the subzone inversion at each iteration [32]. The subzones are created randomly and change at each global iteration to reduce property bias. Based on previous experience, subzone size of approximately 25 mm in diameter has been empirically determined to balance computation time with minimizing any influence of the subzone boundaries on the property distribution (i.e., final image), while attaining spatial resolution commensurate with the displacement data sampling.
We also incorporated the option to include soft-prior regularization following the methods outlined in detail elsewhere [33] in which individual property parameters (i.e., nodes in the FEM mesh) are assigned a predefined and consistent property region index (for example, by segmenting another MR image acquisition into regions based on its contrast), and a region-based regularization matrix is constructed to favor similar property updates for nodes within a subzone identified as belonging to the same region (i.e., property variation within a predefined region is penalized). In this scheme, inter-subzone property variation is not penalized; hence, property variation at the subzone scale (25 mm) can occur.
III. Simulations and Experiments
A. Simulated Phantom Studies
Simulated phantoms were created to evaluate the accuracy and stability of the parameter estimation (inversion) algorithm. Specifically, a block phantom of size 50 mm ×50 mm × 100 mm incorporated two conical inclusions with a base diameter of 25 mm. The background property values were assigned to be μ = 3 kPa and κ = 1 × 10−9(m3s/kg), whereas the left cone had a positive μ contrast (μ = 3.2 kPa) and negative κ contrast (9 × 10−10(m3s/kg)) while the right cone had the opposite contrasts (μ = 2.8 kPa and κ = 2 × 10−9(m3s/kg)). The FEM mesh consisted of 34 081 nodes and 192 000 elements with an average nodal separation of 2.5 mm.
A second simulated phantom had three inclusions and was used to evaluate parameter coupling between estimates in the inclusions and background. This phantom was 50 mm × 50 mm × 120 mm with three 16-mm-diameter spherical inclusions. Here, the background property distribution was the same as the first simulated phantom (μ = 3 kPa and κ = 1 × 10−9(m3s/kg)), but the left inclusion had only shear modulus contrast (μ = 3.2 kPa), the center inclusion had shear modulus (μ = 3.2 kPa) and hydraulic conductivity (κ = 2 × 10−9(m3s/kg))contrast, and the right inclusion had only hydraulic conductivity contrast (κ = 2 × 10−9(m3s/kg)).
Gaussian noise was added to the displacement fields in all simulations to resemble data acquired during an MRE experiment. The level of displacement noise necessary to mimic MRE data was estimated from the error accrued in the phase and the number of measurements (phase offsets) acquired in typical MRE experiments (1.5% and 3% Gaussian noise was applied).
B. Experimental Phantom Studies
Tofu is commonly used to model porous materials [19], [34] and contrast phantoms were constructed from silken Mori-Nu tofu which can be purchased in three different stiffness grades. Here, a cylindrical coring tool (d = 28.5 mm) extracted columns of different tofu stiffnesses from tofu blocks creating voids that were replaced with the columns from a different tofu stiffness block to form contrast inclusions. The phantoms were placed on a plate and vibrated at 50 Hz with a piezoelectric actuator driven by an amplified signal generator. The displacement field was acquired on a Philips 3T Achieva MRI (Philips Medical Systems, Best, The Netherlands) with a standard segmented spin echo phase-contrast pulse sequence with motion sensitizing gradients. Imaging parameters included a 800/80 ms full slice block repetition/echo time, 150 mm field-of-view, and 2.0 mm × 2.0 mm × 1.8 mm voxel size (with 0.2 mm slice separation), and 10–16 slices were captured based on phantom size. Motion sensitization was repeated along three orthogonal directions with eight phase offsets acquired during one sinusoidal motion period. For one phantom, MRE data was recorded during 25, 50, 75, and 100 Hz vibrations. A shear strain signal-to-noise metric was applied to the measured data to ensure sufficient shear strain was introduced [35].
The original (assuming uniform hydraulic conductivity) and augmented (with spatially-varying hydraulic conductivity) poroelastic models were used to evaluate the influence of this property on the estimated shear modulus. Shear modulus images were generated with the original model having a homogeneous κ inserted over a range of values (1 × 10−6(m3s/kg) −1 × 10−11(m3s/kg)) that covers those reported in the literature [20]–[22]. Analogous results were generated with the augmented model having initial κ estimates over the same range that were subsequently updated by the inversion algorithm to produce the final κ image. F-test comparisons of variances were performed under the null hypothesis that the standard deviations of the shear modulus estimates over the hydraulic conductivity range were the same in the two models.
C. Dynamic Mechanical Analysis
To quantify whether the pMRE material contrast was recovered correctly in the phantom experiments for shear modulus and hydraulic conductivity, properties were measured with an independent dynamic mechanical analysis (DMA) approach developed specifically for porous materials [36]. Dynamic mechanical analysis is a material property measurement technique where a sinusoidal force is applied to the material of interest, and the corresponding displacement is acquired. The measured force-displacement information is supplied to an algorithm or expression which approximates the equations of motion for a viscoelastic material given the geometry and excitation under test, and reports the resulting complex-valued shear modulus. Implicit in the technique is the assumption that the material under test is best represented by a viscoelastic model. In [36], we substituted the viscoelastic assumption with the poroelastic equivalent [(1a) and (1b)] and used finite element modeling of equations to infer shear modulus and hydraulic conductivity from the DMA measurement data. For the phantom materials used here, shear modulus and hydraulic conductivity values were calculated from 1–14 Hz for the samples of the three types of tofu, and the property estimates derived from the DMA data are shown in Table I. While the same type and brand of tofu was measured in the subsequent MRE imaging experiments, the blocks were not identical because of the specimen preparation requirements involved in creating samples for use in the DMA.
TABLE I.
Material Property Results Acquired From the Poroelasticity-Based DMA at 14 Hz [36]. Columns Represent the Three Tofu Types Denoted “Soft,” “Firm,” and “Extra Firm.” κ Is Hydraulic Conductivity
| Type | Shear Modulus (kPa) |
|
|
|---|---|---|---|
| Soft | 3.0 ± 0.40 | −5.5 ± 0.39 | |
| Firm | 8.1 ± 1.2 | −6.6 ± 0.15 | |
| Extra Firm | 15 ± 2.4 | −7.0 ± 0.17 |
IV. Results
A. Simulated Phantom Studies
The results for both shear modulus and hydraulic conductivity in simulated phantoms are shown in Figs. 1 and 2. For the two-inclusion case, degradation increases in both parameters at the higher noise levels as expected. The shear modulus recovery is more robust and resolution of the tips of the cones remains intact with only a slight rounding effect caused by the spatial filtering applied during the inversion.
Fig. 1.

Shear modulus (left) and hydraulic conductivity (right) elastograms of a simulated phantom with two conical inclusions. Rows correspond to no displacement noise (Row 1), 1.5% noise (Row 2), and 3% noise (Row 3). True property values: background-μ = 3 kPa and κ = 1 × 10−9(m3s/kg), left cone-μ = 3.2 kPa and 9 × 10−10(m3s/kg), right cone-μ = 2.8 kPa and κ = 2 × 10−9(m3s/kg). Shear modulus is given in kPa and hydraulic conductivity in log10(m3s/kg).
Fig. 2.

Shear modulus (left) and hydraulic conductivity (right) elastograms of a simulated phantom with three spherical inclusions. Rows correspond to no displacement noise (Row 1), 1.5% noise (Row 2), and 3% noise (Row 3). True property values: background—μ = 3 kPa and κ = 1 × 10−9(m3s/kg), left inclusion-μ = 3.2 kPa, center inclusion - μ = 3.2 kPa and κ = 2 × 10−9(m3s/kg), right inclusion - κ = 2 × 10−9(m3s/kg). Shear modulus is given in kPa and hydraulic conductivity in log10(m3s/kg).
In Fig. 2, the three spherical inclusions were similarly depicted, even with some inclusions only having contrast in one of the two properties of interest. Little coupling between parameters is evident and little change occurs in the expected property contrast from a change in the other property. The averaged properties in the background and the three inclusions are close to their expected values (see Table II)—relative errors between the estimated and exact values are less than 2% of the background in all cases. Errors in the inclusions are higher (given average values), likely because blurring caused by spatial filtering influences a larger percentage of the total voxels in the inclusion that appear on the interface between the two regions relative to the background. The standard deviation in both properties increased with higher displacement noise, especially in hydraulic conductivity at the highest noise level where spatial degradation is apparent, but the absolute values remain close to the truth. As expected, shear modulus is less susceptible to displacement noise relative to hydraulic conductivity.
TABLE II.
Recovered Mean and Standard Deviation of the Background and Inclusion Shear Modulus and Hydraulic Conductivity Estimates for the Simulated Three-Inclusion Phantom Shown in Fig. 2
| Background | No Noise | 1.5% Noise | 3.0% Noise | |
|---|---|---|---|---|
| μ (kPa) | 3.0 ± 0.011 | 3.0 ± 0.012 | 3.0 ± 0.017 | |
| Error (%) | 0.13 | 0.15 | 0.22 | |
|
|
−9.0 ± 0.014 | −9.0 ± 0.031 | −8.9 ± 0.062 | |
| Error (%) | 0.10 | 0.47 | 1.3 |
| Left Inclusion | No Noise | 1.5% Noise | 3.0% Noise | |
|---|---|---|---|---|
| μ (kPa) | 3.2 ± 0.031 | 3.2 ± 0.033 | 3.2 ± 0.029 | |
| Error (%) | 1.34 | 1.32 | 1.48 | |
|
|
−9.0 ± 0.0058 | −9.0 ± 0.023 | −8.9 ± 0.040 | |
| Error (%) | −0.095 | 0.48 | 1.2 |
| Center Inclusion | No Noise | 1.5% Noise | 3.0% Noise | |
|---|---|---|---|---|
| μ (kPa) | 3.2 ± 0.026 | 3.2 ± 0.034 | 3.2 ± 0.033 | |
| Error (%) | 1.5 | 1.5 | 1.7 | |
|
|
−8.8 ± 0.027 | −8.8 ± 0.030 | −8.7 ± 0.050 | |
| Error (%) | 1.1 | 0.91 | 0.092 |
| Right Inclusion | No Noise | 1.5% Noise | 3.0% Noise | |
|---|---|---|---|---|
| μ (kPa) | 3.0 ± 8.1 × 10−4 | 3.0 ± 0.0055 | 3.0 ± 0.011 | |
| Error (%) | 5.7 × 10−4 | 0.027 | 0.069 | |
|
|
−8.8 ± 0.047 | −8.8 ± 0.043 | −8.7 ± 0.067 | |
| Error (%) | 1.5 | 1.3 | 0.057 |
B. Experimental Phantom Studies
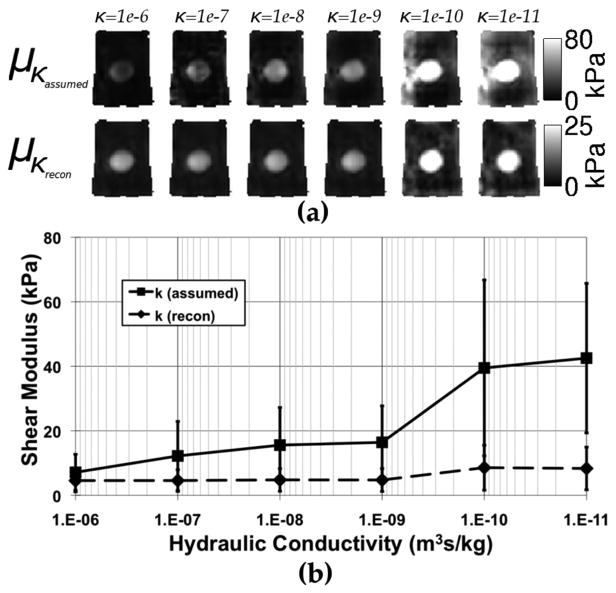
Fig. 3 demonstrates improvement in the shear modulus estimate when hydraulic conductivity varies spatially. Fig. 3(a) shows shear modulus elastograms from the same tofu image slices (background = soft tofu, inclusion = extra firm tofu), based on the original poroelastic model (top row) with assumed homogeneous κ-values and the new poroelastic model (bottom row) with spatially-varying and estimated κ-values. Clearly, assuming a known homogeneous value of κ causes significant bias in shear modulus values in cases where κ is not known accurately. Shear modulus estimates vary widely with different assumed κ-values (σ = 14 kPa), but become less variable when hydraulic conductivity is allowed to vary spatially (σ = 2.0 kPa). The differences in these standard deviations are statistically significant (p ≪ 0.001). With hydraulic conductivity less than 1 × 10−10(m3s/kg), the algorithm suffers in both cases, but reaches a more reasonable shear modulus estimate when κ varies spatially, although at very low κ-values the equations are approaching the incompressible linear elastic equivalent, which poorly estimates the shear modulus of porous media where fluid flow occurs [28].
Fig. 3.
Shear modulus elastograms for the homogeneous (a, top row—κ-value indicated above elastogram) and spatially-varying (a, bottom row) models of hydraulic conductivity. The average shear modulus estimated for the entire phantom is shown for each case in (b). Error bars represent the standard deviation over the whole phantom.
While the estimated shear modulus was more consistent when κ was allowed to vary spatially, the hydraulic conductivity image exhibited lower than expected contrast and localization of an inclusion. Some examples are presented in Fig. 4, where shear modulus images effectively localize the inclusion and correctly recover its contrast, however, hydraulic conductivity images are not as clear. To improve the κ images, soft-prior regularization was incorporated and these results appear in Fig. 5. The average shear modulus and hydraulic conductivity values in the background and inclusions of these phantoms are reported in Table III and indicate the recovered contrasts are consistent with values in Table I which were obtained through independent mechanical testing specifically designed to evaluate the material properties of porous media [36].
Fig. 4.
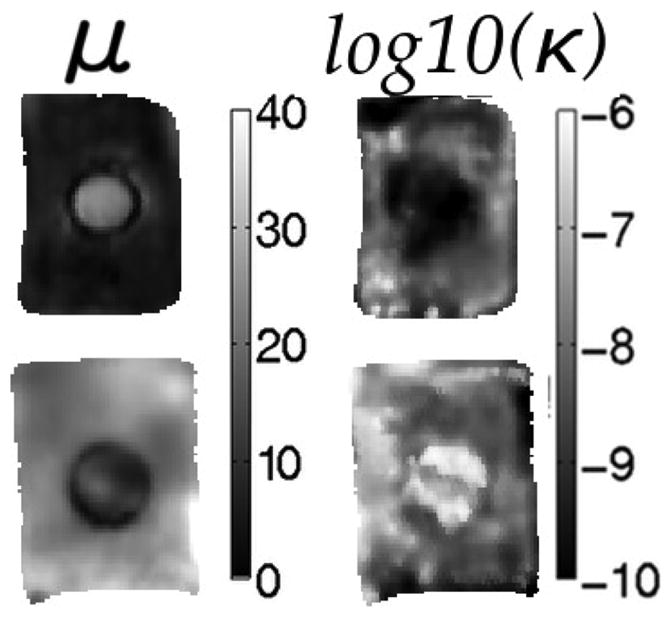
Sample elastograms of nodally-reconstructed shear modulus (left column) and hydraulic conductivity (right column) for tofu phantoms. Rows represent different combinations of soft and extra firm tofu (top = soft tofu background with extra firm tofu inclusion; bottom = extra firm tofu background with soft tofu inclusion). Shear modulus is given in kPa and hydraulic conductivity in log10(m3s/kg).
Fig. 5.

Elastograms showing the expected contrast in tofu-tofu phantoms when spatial priors were encoded in the hydraulic conductivity estimation. The left column indicates phantom geometry and composition (EF = extra firm tofu, F = firm tofu, S = soft tofu), the middle column contains the corresponding shear modulus images and the right column shows the recovered hydraulic conductivity images when spatial priors are included. Shear modulus is given in kPa and hydraulic conductivity is displayed as log10(m3s/kg).
TABLE III.
Mean and Standard Deviation of the Shear Modulus and Hydraulic Conductivity Values for the Three Types of tofu Estimated in the Phantoms Shown in Fig. 5
| Type | Shear Modulus (kPa) |
|
|
|---|---|---|---|
| Soft | 4.1 ± 1.9 | −6.4 ± 0.56 | |
| Firm | 11 ± 1.4 | −6.9 ± 0.087 | |
| Extra Firm | 15 ± 1.0 | −9.5 ± 0.68 |
Finally, one phantom (soft tofu background, extra firm tofu inclusion) was scanned at four different frequencies spanning 25–100 Hz, and shear modulus and hydraulic conductivity images are shown in Fig. 6. These results indicate that the contrast in shear modulus is consistent across the four frequencies, whereas the hydraulic conductivity contrast increases at lower frequencies. Specifically, background-to-inclusion κ contrast at 100 Hz is small (1.4:1), while at 25 Hz it increases substantially (to 7.5:1).
Fig. 6.

Elastograms representing the shear modulus (top row) and hydraulic conductivity (bottom row) estimates for a phantom with a soft tofu background and extra firm inclusion vibrated at the four different frequencies indicated. Shear modulus is presented in kPa and hydraulic conductivity is displayed as the log10(m3s/kg)..
V. Discussion
Accurate estimates of shear modulus and hydraulic conductivity are recovered from both simulated and experimental phantom data. Results from these two environments (simulations and experiments) suggest that shear modulus images are spatially accurate and consistent and hydraulic conductivity images are consistent but more susceptible to measurement noise. Images recovered from simulated two- and three-inclusion data demonstrate high property accuracy but with better spatial resolution for the dominant shear modulus property whereas variations increase more rapidly for hydraulic conductivity with increasing noise.
In experimental tofu phantoms, improvement in the recovered shear modulus was found for poroelastic MRE when hydraulic conductivity was allowed to vary spatially. A statistically significant decrease in shear modulus variation was observed in this case. Poor shear modulus images (values grew increasingly large) were recovered at very low hydraulic conductivity values in both models [Fig. 3(b)], which resulted from the material being incorrectly represented as a nearly linear elastic solid. Low hydraulic conductivity indicates that the deformation is dominated by the elastic solid matrix because of the increased resistance to fluid flow. Linear elastic solids have been shown previously to suffer from numerical instabilities and resonances that are better characterized by time-dependent behavior represented by viscoelasticity or poroelasticity [28]. Further, when hydraulic conductivity is assumed to be known and homogeneous (Fig. 3(a), top row), shear modulus variation is higher in the inclusion, likely because of the incorrect assumption of equal hydraulic conductivities in the two different types of tofu.
Hydraulic conductivity estimates recovered in the tofu phantoms produced excellent results when spatial priors were encoded. Noise introduced from the MRI/MRE acquisition and data processing had a larger influence on hydraulic conductivity as expected from the simulation results. Soft-prior regularization stabilized these effects by enforcing property values to be similar in preselected regions, but still allows the boundaries between material types to be described with high resolution. Further, for the subzone-based minimization technique used here, the effect of the spatial encoding of prior information is limited to the subzone level. In MRE, high resolution spatial information is already acquired with companion MRI sequences that can be readily used to inform the hydraulic conductivity estimation; hence, incorporation of spatial priors on this property parameter should be possible in practice. However, recovery of hydraulic conductivity without the use of spatial information is still possible and could be enhanced further with other stabilization techniques or other inversion methods that may be less susceptible to measurement noise.
Biological materials commonly exhibit frequency-dependent behavior, suggesting the need for viscoelastic or poroelastic characterization of tissue. However, the damping characteristics of these models vary—in a viscoelastic material, energy is lost in regions where shear strain is occurring whereas a poroelastic material has energy loss where differential displacement of the fluid and solid phases occurs (i.e., volumetric strain of the solid matrix). While viscoelastic damping forces increase at higher frequencies, the relative poroelastic fluid-solid differential displacement is more prominent at lower frequencies because there is more time for fluid redistribution. Hydraulic conductivity is not indicative of a damping term per se, but is directly related to the interaction between the fluid and solid phases, which is responsible for the energy losses in a porous material. Specifically, a low hydraulic conductivity represents high resistance to fluid flow, and concomitantly greater mechanical energy losses in the material, whereas high hydraulic conductivity represents low resistance and less energy loss within the system. The level of fluid flow in a material also strongly depends on hydraulic conductivity, therefore, maximum damping effect occurs at some intermediate value. The results in Fig. 6 indicate more contrast is recovered at lower frequencies, suggesting a poroelastic model may prove to be superior for low-frequency vibrations. Comparisons of images generated with a viscoelastic model using the same data may illustrate the frequency ranges for which one model is superior to the other. Further, poroviscoelasticity is another option for representing the full range of damping responses in tissues over the frequencies of interest.
Small variations in the recovered mechanical properties occurred for the three types of tofu (see Table III), but could have resulted from a number of experimental factors. For example, variation in the composition and consistency of store-purchased tofu is unknown and could be substantial between batches. Also, creating the contrast tofu phantoms is technically challenging because one material must be inserted into another material. Here, the cylindrical inclusions that were inserted do not necessarily adhere uniformly to the inside boundary surface of the background portion of the phantom, potentially causing slip boundary conditions to occur over portions of these interfaces. Hydrogels are common poroelastic materials that could alleviate these challenges. Another option is to create tofu through combinations of coagulant and soybean curd, or inject a cross-linker into the interior of the material to locally alter its property distribution eliminating the need for inclusion insertion.
The recovered values reported here vary modestly from those acquired by independent mechanical testing. A main difference between the two methods (pMRE and mechanical testing) is the assumption of Poisson’s ratio during mechanical testing, which is estimated from the MRE data in the experiments described in this paper. Changes in Poisson’s ratio influence the recovered property values; hence, some differences in their absolute values are expected. Additionally, the property estimates reported here were obtained at 50 Hz, a frequency significantly higher than the range attained in mechanical testing (limited to 14 Hz due to machine resonance). An independent measurement technique more suited to high frequency of very soft materials is necessary to compare poroelastic mechanical property estimates with poroelastic MRE in the same frequency range.
VI. CONCLUSION
In this paper, we successfully developed and evaluated a new pMRE algorithm which generates spatially-varying hydraulic conductivity images rather than assuming homogeneous values of this hydrodynamical property as in the past. Estimation of hydraulic conductivity also increased the accuracy of the recovered shear modulus in both simulation and physical phantom experiments. The lower sensitivity of this parameter (relative to shear modulus) was mitigated by encoding spatial information derived from another MR sequence and improved the contrast recovered in single-inclusion tofu experiments. Frequency dependence of the pMRE image contrast was observed and suggests that the technique functions better with lower frequency data, likely because the driving fluid-solid phase interactions are enhanced (and hence the sensitivity to hydraulic conductivity variation is increased). Understanding the fluid flow characteristics of a porous tissue (e.g., brain tissue) could lead to new contrast mechanisms with improved diagnostic potential when evaluating neurological disorders such as hydrocephalus, Alzheimer’s and Parkinson’s diseases, and brain tumors. Each of these pathologies has distinct influences on the tissue macro- and micro-environment that may be amenable to pMRE characterization but otherwise occult to conventional MRI sequences. On a macroscopic scale, tissue mechanical and hydrodynamical properties change in conditions such as hydrocephalus. From a microscopic point-of-view, the interstitial environment is disrupted, for example, with the loss of myelin sheath in Alzheimer’s disease. Estimating both structural and hydrodynamical property distributions with pMRE could enable greater understanding of any number of neurological disease processes.
Acknowledgments
The development of the algorithm was supported by a grant from the National Institutes of Health (R01EB018230).
Contributor Information
Adam J. Pattison, Email: adam.j.pattison.th@dartmouth.edu, Thayer School of Engineering, Dartmouth College, Hanover, NH 03755 USA
Matthew McGarry, Thayer School of Engineering, Dartmouth College, Hanover, NH 03755 USA.
John B. Weaver, Thayer School of Engineering, Dartmouth College, Hanover, NH 03755 USA and also with the Dartmouth-Hitchcock Medical Center, Lebanon, NH 03756 USA
Keith D. Paulsen, Thayer School of Engineering, Dartmouth College, Hanover, NH 03755 USA and also with the Dartmouth-Hitchcock Medical Center, Lebanon, NH 03756 USA
References
- 1.Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li XG. Elastography: A quantitative method for imaging the elasticity of biological tissues. Ultrason Imag. 1991;13:111–134. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- 2.Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science. 1995;269:1854–1857. doi: 10.1126/science.7569924. [DOI] [PubMed] [Google Scholar]
- 3.Manduca A, Oliphant TE, Dresner MA, Kruse SA, Mahowald JL, Amromin E, Felmlee JP, Greenleaf JF, Ehman RL. Magnetic resonance elastography: Non-invasive mapping of tissue elasticity. Med Image Anal. 2001;5:237–254. doi: 10.1016/s1361-8415(00)00039-6. [DOI] [PubMed] [Google Scholar]
- 4.Plewes DB, Bishop J, Samani A, Sciarretta J. Visualization and quantification of breast cancer biomechanical properties with magnetic resonance elastography. Phys Med Biol. 2000;45:1591–1610. doi: 10.1088/0031-9155/45/6/314. [DOI] [PubMed] [Google Scholar]
- 5.Mariappan YK, Glaser KJ, Ehman RL. Magnetic resonance elastography: A review. Clin Anat. 2010;23:497–511. doi: 10.1002/ca.21006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sinkus R, Lorenzen J, Schrader D, Lorenzen M, Dargatz M, Holz D. High-resolution tensor MR elastography for breast tumour detection. Phys Med Biol. 2000;45:1649–1664. doi: 10.1088/0031-9155/45/6/317. [DOI] [PubMed] [Google Scholar]
- 7.Elgeti T, Laule M, Kaufels N, Schnorr J, Hamm B, Samani A, Braun J, Sack I. Cardiac MR elastography: Comparison with left ventricular pressure measurement. J Cardiovasc Magn Reson. 2009 Jan;11:44. doi: 10.1186/1532-429X-11-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Talwalkar JA, Yin M, Fidler JL, Sanderson SO, Kamath PS, Ehman RL. Magnetic resonance imaging of hepatic fibrosis: Emerging clinical applications. Hepatology. 2008 Jan;47(1):332–342. doi: 10.1002/hep.21972. [DOI] [PubMed] [Google Scholar]
- 9.Pattison AJ, Lollis SS, Perriñez PR, Perreard IM, McGarry MDJ, Weaver JB, Paulsen KD. Time-harmonic magnetic resonance elastography of the normal feline brain. J Biomechan. 2010;43:2747–2752. doi: 10.1016/j.jbiomech.2010.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Heers G, Jenkyn TR, Dresner MA, Basford JR, Klein MO, Kaufman KR, Ehman RL, An KN. Measurement of muscle activity with magnetic resonance elastography. Clin Biomechan. 2003 Jul;18:537–542. doi: 10.1016/s0268-0033(03)00070-6. [DOI] [PubMed] [Google Scholar]
- 11.Franceschini G. PhD dissertation. Univ. Trento; Trento, Italy: 2006. The mechanics of human brain tissue. [Google Scholar]
- 12.Mow V, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. J Biomechan Eng. 1980 Feb;102(1):73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 13.Nia HT, Han L, Li Y, Ortiz C, Grodzinsky A. Poroelasticity of cartilage at the nanoscale. Biophys J. 2011 Nov;101(9):2304–2313. doi: 10.1016/j.bpj.2011.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Biot MA. General theory of three-dimensional consolidation. J Appl Phys. 1941;12(2):155–164. [Google Scholar]
- 15.Hakim S, Venegas J, Burton J. The physics of the cranial cavity, hydrocephalus and normal pressure hydrocephalus: Mechanical interpretation and mathematical model. Surg Neurol. 1976;5(3):187–210. [PubMed] [Google Scholar]
- 16.Taylorm Z, Miller K. Reassessment of brain elasticity for analysis of biomechanisms of hydrocephalus. J Biomechan. 2004 Aug;37:1263–1269. doi: 10.1016/j.jbiomech.2003.11.027. [DOI] [PubMed] [Google Scholar]
- 17.Paulsen KD, Miga MI, Kennedy FE, Hoopes PJ, Hartov A, Roberts DW. A computational model for tracking subsurface tissue deformation during stereotactic neurosurgery. IEEE Trans Biomed Eng. 1999 Feb;46(2):213–225. doi: 10.1109/10.740884. [DOI] [PubMed] [Google Scholar]
- 18.Miga MI, Paulsen KD, Hoopes PJ, Kennedy FE, Hartov A, Roberts DW. In vivo modeling of interstitial pressure in the brain under surgical load using finite elements. J Biomechan Eng. 2000 Aug;122(4):354–363. doi: 10.1115/1.1288207. [DOI] [PubMed] [Google Scholar]
- 19.Perriñez PR, Pattison AJ, Kennedy FE, Weaver JB, Paulsen KD. Contrast detection in fluid-saturated media with magnetic resonance poroelastography. J Med Phys. 2010;37(7):3518–3526. doi: 10.1118/1.3443563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zakaria ER, Lofthouse J, Flessner MF. In vivo hydraulic conductivity of muscle: Effects of hydrostatic pressure. Am J Physiol Heart Circ Physiol. 1997;273:2774–2782. doi: 10.1152/ajpheart.1997.273.6.H2774. [DOI] [PubMed] [Google Scholar]
- 21.Ivanchenko O, Sindhwani N, Linninger AA. Experimental techniques for studying poroelasticity in brain phantom gels under high flow microinfusion. J Biomechan Eng. 2010 May;132(5):051008. doi: 10.1115/1.4001164. [DOI] [PubMed] [Google Scholar]
- 22.Perriñez PR. PhD dissertation. Dartmouth College; Hanover, NH: 2008. Magnetic resonance poroelastography. [Google Scholar]
- 23.Jain RK, Gutierrez J, Narang J, Scarpace L, Schultz LR, Lemke N, Patel SC, Mikkelsen T, Rock JP. In vivo correlation of tumor blood volume and permeability with histologic and molecular angiogenic markers in gliomas. Am J Neuroradiol. 2011 Feb;32(2):388–394. doi: 10.3174/ajnr.A2280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jain RK. Determinants of tumor blood flow: A review. Cancer Res. 1988;48:2641–2658. [PubMed] [Google Scholar]
- 25.Yu H, Mouw JK, Weaver VM. Forcing form and function: Biomechanical regulation of tumor evolution. Trends Cell Biol. 2010 Sep;:1–10. doi: 10.1016/j.tcb.2010.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vaupel P, Kallinowski F, Okunieff P. Blood flow, oxygen and nutrient supply, and metabolic microenvironment of human tumors: A review. Cancer Res. 1989 Dec;49(23):6449–6465. [PubMed] [Google Scholar]
- 27.Pattison AJ, Perriñez PR, McGarry MDJ, Weaver JB, Paulsen KD. Feasibility study to measure changes in intracranial pressure using magnetic resonance poroelastography. Proc ISMRM. 2010;608:3406. [Google Scholar]
- 28.Perriñez PR, Kennedy FE, Van Houten EEW, Weaver JB, Paulsen KD. Magnetic resonance poroelastography: An algorithm for estimating the mechanical properties of fluid-saturated soft tissues. IEEE Trans Med Imag. 2010 Mar;29(3):746–755. doi: 10.1109/TMI.2009.2035309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cheng AH-D, Badmus T, Beskos DE. Integral equation for dynamic poroelasticity in frequency domain with BEM solution. J Eng Mechan. 1991;117(5):1136–1157. [Google Scholar]
- 30.Van Houten EEW, Paulsen KD, Miga MI, Weaver JB, Kennedy FE. An overlapping subzone technique for MR-based elastic property reconstruction. Magn Reson Med. 1999;42:779–786. doi: 10.1002/(sici)1522-2594(199910)42:4<779::aid-mrm21>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 31.Fletcher R. Practical Methods of Optimization. 2. New York: Wiley-Interscience; 2000. [Google Scholar]
- 32.Van Houten EEW, Miga MI, Weaver JB, Kennedy FE, Paulsen KD. Three-dimensional subzone-based reconstruction algorithm for MR elastography. Magn Reson Med. 2001 May;45(5):827–837. doi: 10.1002/mrm.1111. [DOI] [PubMed] [Google Scholar]
- 33.McGarry MDJ, Johnson CL, Sutton BP, Van Houten EEW, Georgiadis JG, Weaver JB, Paulsen KD. Including spatial information in nonlinear inversion MR elastography using soft prior regularization. IEEE Trans Med Imag. 2013 Oct;32(10):1901–1909. doi: 10.1109/TMI.2013.2268978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Righetti R, Garra BS, Mobbs LM, Kraemer-Chant CM, Ophir J, Krouskop TA. The feasibility of using poroelastographic techniques for distinguishing between normal and lymphedematous tissues in vivo. Phys Med Biol. 2007 Nov;52(21):6525–6541. doi: 10.1088/0031-9155/52/21/013. [DOI] [PubMed] [Google Scholar]
- 35.McGarry MDJ, Van Houten EEW, Perriñez PR, Pattison AJ, Weaver JB, Paulsen KD. An octahedral shear strain-based measure of SNR for 3-D MR elastography. Phys Med Biol. 2011 Jun;56(13):N153–N164. doi: 10.1088/0031-9155/56/13/N02. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Pattison AJ, McGarry MDJ, Weaver JB, Paulsen KD. Development of a poroelastic dynamic mechanical analysis technique for biphasic media. Proc SPIE Med Imag. 2013:86721P. [Google Scholar]