VISUALIZING THE STRESS DISTRIBUTION WITHIN VASCULAR TISSUES USING INTRAVASCULAR ULTRASOUND ELASTOGRAPHY: A PRELIMINARY INVESTIGATION

Abstract

A methodology for computing the stress distribution of vascular tissue using finite element-based, intravascular ultrasound (IVUS) reconstruction elastography is described. This information could help cardiologists detect life-threatening atherosclerotic plaques and predict their propensity to rupture. The calculation of vessel stresses requires the measurement of strain from the ultrasound images, a calibrating pressure measurement and additional model assumptions. In this work, we conducted simulation studies to investigate the effect of varying the model assumptions, specifically Poisson’s ratio and the outer boundary conditions, on the resulting stress fields. In both simulation and phantom studies, we created vessel geometries with two fibrous cap thicknesses to determine if we could detect a difference in peak stress (spatially) between the two. The results revealed that (i) Poisson’s ratios had negligible impact on the accuracy of stress elastograms, (ii) the outer boundary condition assumption had the greatest effect on the resulting modulus and stress distributions and (iii) in simulation and in phantom experiments, our stress imaging technique was able to detect an increased peak stress for the vessel geometry with the smaller cap thickness. This work is a first step toward understanding and creating a robust stress measurement technique for evaluating atherosclerotic plaques using IVUS elastography.

INTRODUCTION

Knowledge of the stress distribution within the fibrous cap could help cardiologists predict the propensity of plaque rupture—a known cause of cardiovascular-related deaths (Hoyert and Jiaquan 2012). Life-threatening plaques have large lipid cores, thin fibrous caps, inflammation and endothelial denudation (Alsheikh-Ali et al. 2010). Plaques rupture when the peak stress within their fibrous cap exceeds 300 kPa (Loree et al. 1992; Richardson et al. 1989). Consequently, there have been concerted efforts to develop accurate finite-element methods predicting the stresses within vessels. Current finite-element models now include anisotropy (Cheng et al. 1993; Finet et al. 2004; Loree et al. 1992), nonlinearity (Huang et al. 2001; Williamson et al. 2003), 3-D geometries (Chandran et al. 2003; Tang et al. 2005), elastic–fluid interactions (Glagov et al. 1988; Taylor et al. 1998) and residual stresses (Williamson et al. 2003). Despite these improvements, finite element-based stress analyses are limited because they require knowledge of the mechanical properties of the different vessel components, which are unknown in most in vivo applications.

Conventional imaging techniques (ultrasound, magnetic resonance imaging and computed tomography) provide accurate information about plaque morphology (Ohayon et al. 2001; Tang et al. 2005), but none can measure the mechanical properties directly. Acoustic shear wave imaging can visualize the mechanical properties of carotid atherosclerosis (Couade et al. 2010; Garrard and Ramnarine 2014; Garrard et al. 2013a, 2013b; Ramnarine et al. 2014), but it cannot image coronary arteries. Intravascular ultrasound elastography (IVUSe) can visualize the radial strain distribution within coronary arteries (de Korte et al. 1998; Maurice et al. 2008; Schaar et al. 2004), information that cardiologists could use to identify rupture-prone regions within the fibrous cap (Schaar et al. 2004). However, to predict the propensity that an atherosclerotic plaque will rupture requires knowledge of the internal stress distribution (Ferguson et al. 1988; Wierzbicki et al. 2005). Several groups, including our own, are developing IVUSe within the framework of solving an inverse problem (Baldewsing et al. 2004b; Le Floc’h et al. 2009; Richards and Doyley 2011). This approach to elastography uses the measured strains or displacements, knowledge of the geometry and the boundary conditions to compute the mechanical properties of different vessel components (Doyley 2012; Parker et al. 2011). In the work described here, we investigated the feasibility of using this approach to IVUSe to estimate the stress distribution within the fibrous cap.

The performance of the reconstructed mechanical parameters and the measured strain will determine the usefulness of stress elastograms. Computing modulus elastograms within the framework of solving an inverse problem produces useful modulus elastograms; however, the ill-posed nature of this problem makes it challenging (Barbone and Bamber 2002). To address this problem, a priori information (i.e., geometric) is now standard in most modulus reconstruction processes (Baldewsing et al. 2004a; Doyley et al. 2005; Le Floc’h et al. 2009; Richards and Doyley 2013). Intravascular ultrasound elastography typically reconstructs the modulus from the radial component of displacement because IVUS cannot measure the circumferential component of displacement precisely—a practice that trades accuracy for greater stability. We have reported that non-rigid registration methods provide more accurate estimates of the circumferential components of displacement than traditional displacement estimators (Richards and Doyley 2013)—information that when included in the image reconstruction process improved the accuracy of the recovered properties (Hansen et al. 2013). In this article, we hypothesize that besides a priori information and accurate radial and circumferential displacement estimates, the choice of boundary conditions and value of Poisson’s ratio assumed during image reconstruction are also important.

In vascular elastography, stresses on the outer boundary of the vessels are unknown. Consequently, image reconstruction is performed by (i) assuming the stresses on the outer boundary are traction free (i.e., zero) or (ii) using the measured displacements to impose Dirichlet boundary conditions on the outer boundary. The first case will decrease the accuracy of the reconstructed images when the stresses on the outer boundary are not traction free. The second approach could produce unique issues because different combinations of shear modulus and pressure (implicit) may yield the same displacement field. Poisson’s ratio could have a profound effect on performance because for “pseudo”-incompressible materials, the divergence term in the forward model (∇ • u) is dominated by the second Lamé constant (lambda modulus), and as Poisson’s ratio approaches 0.5 (incompressibility), the inverse reconstruction problem becomes more ill posed. The goal of this work was to corroborate these predictions by indicating how choices of boundary conditions and Poisson’s ratio used in the reconstruction process affect the accuracy and quality of the recovered modulus and stress distribution.

METHODS

In this section, we describe general methods used in both the simulation and experimental studies. More specifically, we describe the general approach used to create simulated and physical representations of coronary arteries. We also describe the protocol used to estimate (i) both components of displacements from radiofrequency (RF) echo frames obtained at different intraluminal pressures; (ii) the Young’s modulus from the measured displacement (radial and circumferential); (iii) stresses from the measured strain, estimated modulus and assumed value of Poisson’s ratio.

Displacement estimation protocol

All radial and circumferential displacement elastograms were estimated by applying a non-rigid image registration-based displacement estimator (Richards and Doyley 2013) to pre- and post-deformed RF echo frames. Identical processing parameters were used in both simulated and phantom studies.

All displacement elastograms were computed using a four-step process. First, a uniform mesh was constructed from manually segmented sonograms. This mesh was used in both the image registration and the modulus recovery process. Second, the echo tracking method described in Doyley et al. (2001) was used to obtained initial estimates of the radial component of the displacement field—a pre-requisite of the non-rigid image registration method. All echo tracking was performed with 0.385 mm (radial) × 14.1° (angular) kernels that overlapped by 80% and 50% in the radial and angular directions, respectively. Sub-pixel displacements were estimated by fitting a parabola to the hood of the cross-correlation function. Third, the measured radial displacements were interpolated to the nodal coordinates of the finite-element mesh. Fourth, the non-rigid displacement estimator was applied to the pre- and post-deformed RF echo frames to produced radial and circumferential displacements. Circumferential displacements were assumed to be zero at the start of the registration process. All analysis was performed in MATLAB (The Math-Works, Natick, MA, USA) computing environment.

Modulus recovery

All modulus elastograms were computed by applying the soft prior reconstruction method described in Richards and Doyley (2011) to both the radial and circumferential components of displacements obtained from the reconstruction field of view highlighted in Figure 1(a). The soft prior reconstruction method uses geometric information (i.e., plaque size and location) to impose additional constraints on the reconstruction process. Unlike the hard prior reconstruction method (Baldewsing et al. 2006; Le Floc’h et al. 2009), the soft prior reconstruction method is less susceptible to segmentation errors. Vascular tissue displays non-linear anisotropic mechanical behavior (Huang et al. 2001; Williamson et al. 2003); however, to simplify the modulus reconstruction process, in this work, vascular tissue was modeled as an isotropic, nearly incompressible linear elastic material whose deformation was described by the governing partial differential equation

Fig. 1.

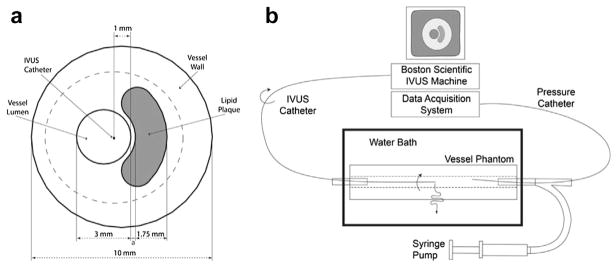
(a) Schematic of simulated vessel used to mimic an atherosclerotic plaque. The thickness of the fibrous cap, a, was varied from 0.25 to 0.45 mm. (b) Schematic of the experimental vessel phantom imaging setup. IVUS = intravascular ultrasound.

$$-\mathbf{\nabla }p+\mathbf{\nabla }·(\mu (\mathbf{\nabla }\mathbf{u}+\mathbf{\nabla }{\mathbf{u}}^{\mathrm{T}}))=0$$ (1)

where p = −λ ∇ · u, u represents the tissue displacement vector field, μ and λ are the Lamé constants, p represents the internal hydrostatic pressure and T represents the transpose. Equation (1) was solved using a nodal-based finite-element (FE) method as discussed in Richards and Doyley (2011). Shear modulus (μ) was reconstructed from the measured radial and circumferential components of displacements using the FE method and a quasi-Newton iterative method (Oberai et al. 2003, 2004; Richards et al. 2009); therefore, only a brief summary of the technique is provided in this section. The reconstruction process consists of minimizing the cost function

$${\pi }_{\mathbf{u}}[\mu ]=\frac{1}{2}\underset{\mathit{\Omega }}{\int }{(\mathrm{u}(\mu )-{\mathrm{u}}_{\mathit{mes}})}^2+{\pi }_R[\mu ,{\mu }_0]$$ (2)

where u_mes is the measured displacement (radial and circumferential), u is the displacements computed from the shear modulus distribution μ using a FE representation of eqn (1), μ₀ is a constant modulus for each region that was computed as part of the reconstruction process and π_R is a regularization function that is given by

$${\pi }_{\mathrm{R}}\left[\mu ,{\mu }_0^m\right]=\frac{\alpha }{2}\underset{\mathit{\Omega }}{\int }ln{\left(\mu /{\mu }_0^m\right)}^{2}d\mathit{\Omega }$$ (3)

where m = 1, M, and M is the number of segmented regions. Young’s modulus elastograms (E_rec) were calculated from the reconstructed shear modulus and the assumed Poisson’s ratio ν as

$$E_{\text{rec}}=2\mu (1+\nu )$$ (4)

All reconstructions were performed on a 16-core Intel Xeon Server that was operating at 2.93 GHz under the Centos 5.6 (64-bit) operating system. In the studies reported in this article, the reconstruction process typically converged within 200–300 iterations (i.e., within 5 min).

Stress recovery

We computed stress distributions from the recovered shear modulus (μ), the assumed Poisson’s ratio (ν) and the measured strains at the centroid of each element as

$${\sigma }_{ij}=2\mu \left(\frac{\nu }{1-2\nu }{\delta }_{ij}{\epsilon }_{kk}+{\epsilon }_{ij}\right)\text{and}{\sigma }_{zz}=\frac{2\nu \mu }{1-2\mu }{\epsilon }_{kk}$$ (5)

where ε_ij is the computed strain tensor, ε_kk is the trace of the strain tensor, σ_ij is the calculated 2-D stress tensor, σ_zz is the out-of-plane (z) component of the stress tensor and σ_ij is the Kroneker delta. The shape functions employed in the FE problem (bilinear quadrilaterals) were used to compute the modulus and strain at the centroid of each element. Principal stresses were calculated as (Holzapfel 2000)

$${\sigma }^{\mathrm{I}}=max({\gamma }_1,{\gamma }_2),{\sigma }^{\text{III}}=min({\gamma }_1,{\gamma }_2),\text{and}{\sigma }^{\text{II}}={\sigma }_{zz}$$ (6)

where γ₁ and γ₂ are the calculated eigenvalues of the 2-D stress tensor σ, and σ^I, σ^II, and σ^III are the maximum, middle and minimum principal stresses, respectively.

SIMULATION STUDY

Experiments were performed on simulated vessel phantoms to study how Poisson’s ratio and boundary conditions affect the performance of modulus and stress elastograms. More specifically, reconstructions were performed with Poisson ratios of 0.4, 0.495, 0.49995 and 0.499995. For each value of Poisson’s ratio, we performed reconstructions with four different outer boundary conditions: type 1, traction-free outer boundary conditions; type 2, use of the radial component of the measured displacements to impose Dirichlet boundary conditions and assume the circumferential component was traction free; type 3, use of the angular displacements to impose Dirichlet boundary conditions and assume the radial component was traction free; and type 4, use of both components of the measured displacements to impose Dirichlet boundary conditions.

Synthesizing RF echo frames

A commercially available FE software package (Abaqus, Dassault Systèmes, Vèlizy-Villacoublay, France) was used to simulate vessels (n = 2) with geometries similar to those described in Loree et al. (1992) and Richardson et al. (1989). Both models contained healthy vessel walls (Young’s modulus = 50 kPa) and a softer lipid plaque (Young’s modulus = 10 kPa). The traction-free boundary condition was applied on the outer boundary of the simulated vessel. Figure 1a is a schematic representation of the simulated vessels. The thickness of the fibrous caps in the simulated vessels was 0.25 and 0.45 mm. In both simulated vessels, a uniformly distributed pressure (0.5 kPa) was applied to the inner lumen. This pressure produced an average interframe strain of approximately 0.8% (2.1% average strain at the inner lumen), which is the optimum interframe strain used in the clinic (de Korte et al. 2002).

The Field II ultrasound simulation program (Jensen 1991) was used to synthesize pre- and post-deformed RF echo frames as described in Richards and Doyley (2011). Specifically, we used Field II to simulate the point response of a 40-MHz rotating-element IVUS catheter that had 30% fractional bandwidth. For each simulated vessel phantom, we computed the acoustic response of the pre-deformed state by randomly distributing point scatters (10 million) within a 78.54-mm² area to generate fully developed speckles (Wagner et al. 1983). To compute the acoustic response of the post-deformed tissue, we redistributed point scatterers of the pre-deformed tissues using displacement computed by solving the forward elasticity problem. To simulate non-uniform rotational distortion (NURD)—a problem synonymous with rotation-element IVUS—we displaced each scatterer in the pre- and post-deformed tissues by ±4° using circumferential displacements generated with an analytical model. More specifically, based on experimental observation, we model the circumferential displacements associated with NURD as

$$u_c^n=4cos{(3\theta A)}^2·2sin(3\theta B)$$ (7)

where A and B are random variables that are uniformly distributed between 0 and 1. Gaussian noise was added to the echo frames to generate images with a sonographic signal-to-noise ratio of approximately 12 dB.

Displacement, modulus and stress recovery

We used a non-rigid displacement estimator to estimate radial and circumferential displacement elastograms as described under Methods. Modulus elastograms were computed by applying the soft prior reconstruction method described in Richards and Doyley (2011) to both components of displacements. All reconstructions were performed using an initial guess of 1 kPa. The optimum value of the regularization parameter (4e⁻¹⁶) was determined empirically, using the L-curve method as described in Richards and Doyley (2011). Stress elastograms were computed by using eqn (5) to combine the measured strain and estimated modulus. Principal stresses were computed by applying eqn (6) to the 2-D stress tensor.

Performance evaluation

Two metrics are used to evaluate the accuracy of the recovered Young’s modulus. The recovered modulus contrast was computed from the average value of the Young’s modulus within the background of the vessel (Ē_bkg, where the overbar denotes a spatial average) and the plaque (Ē_plq) as Ē_bkg/Ē_plq. The modulus root-mean-squared (RMS) error was evaluated as

$${\text{RMS}}_E=\sqrt{\frac{\overline{{(E_{\text{rec}}-E_{\text{true}})}^2}}{E_{\text{true}}^2}}$$ (8)

where E_rec and E_true represent the recovered and reference Young’s moduli, respectively. The stress RMS errors were calculated as

$${\text{RMS}}_i^{\sigma }=\sqrt{\frac{\overline{{\left({\sigma }_{\text{rec}}^i-{\sigma }_{\text{true}}^i\right)}^2}}{{\left({\sigma }_{\text{true}}^i\right)}^2}}$$ (9)

where i indexes the principal stresses.

EXPERIMENTAL STUDY

To corroborate the findings of the simulation results under realistic physiologic conditions, we performed an experimental study with two vessel phantoms. Like the simulation study, we performed reconstructions with four different types of outer boundary conditions (types 1–4) with Poisson ratios of 0.4, 0.495, 0.49995 and 0.499995.

Phantom fabrication and independent mechanical testing

A two-step process was used to create vessel phantoms (both 21 mm outer diameter × 15 cm long) from polyvinyl alcohol (PVA). First, the vessel wall was fabricated by pouring 10% by weight PVA into a cylindrical mold (21 mm diameter × 15 cm long) that contained a 3-mm central rod as described (Fromageau et al. 2003; Richards and Doyley 2011). A crescent-shaped metal rod was placed adjacent to the first rod. The mold was sealed and subjected to three freeze–thaw cycles from +20° C to −20° C, over a 72-h (24-h per cycle) period. Next, the crescent-shaped rod was removed, and the vacant cavity was filled with 10% by volume PVA. The entire phantom was then subjected to two additional freeze–thaw cycles. In one phantom, the distance between the crescent-shaped plaque and the inner lumen was approximately 0.7 mm (thick cap); in the other, it was approximately 0.3 mm (thin cap). After thermal cycling, the phantoms were carefully removed from their molds and stored at room temperature in water.

A Landmark Servohydraulic Test System (MTS, Eden Prairie, MN, USA) and a 5-lb load cell were used to measure the mechanical properties of the vessel wall and plaque. All measurements were performed on cylindrical disks (19.0 mm diameter × 20.0 mm height) that were manufactured from the same batch of PVA used for the vessel phantoms (10% PVA) that were subjected to a similar number of thermal cycles. For each tissue type, five different disks were created and tested to quantify the variability in the phantom fabrication process.

Elastographic data acquisition

Figure 1(b) is a schematic diagram of the equipment used in the experimental study. The vessel phantom was placed in a water bath and connected to a proximal and distal sheath. The proximal sheath was closed, whereas the other sheath was connected to a syringe pump. Echo imaging was performed with a commercially available intravascular ultrasound scanner (ILab Boston Scientific/Scimed, Marlborough, MA, USA), which was equipped with a 40-MHz Atlantis Pro imaging scanner (Boston Scientific). A PCI bus data acquisition card (Compuscope 14200–1 GB 14-bit 400 MS/s, Gage Applied, Lockport, IL, USA) was used to stream RF echo frames from the IVUS scanner at full frame rate (30 fps) to a high-performance computer workstation. Each frame contained 256 echo lines and 1024 samples per echo line. All RF echo frames were digitized to 14 bits at 200 MHz. A pressure catheter (Millar Instruments, Houston, TX, USA) was used to measure the pressure within the vessel, simultaneous with the RF acquisition.

Displacement, modulus and stress recovery

The elastography estimation protocol used in the simulation study was applied to pairs of experimentally acquired RF echo frames that represented approximately 1% strain to generate displacement, modulus and stress elastograms. Finite element representations of the vessel phantoms used in the protocol were constructed from manually segmented IVUS sonograms. All reconstructions were performed using an initial guess of 1 kPa with a regularization parameter of 4e⁻¹⁶.

RESULTS

Simulation study

Figures 2i(a) and 3i(a) illustrat the true Young’s modulus distributions within the small- and large-cap simulated vessels, respectively. Figures 2ii(a) and 3ii(a) illustrate the true maximum principal stress distributions (σ^I) within the small- and large-cap simulated vessels, respectively. The peak stress values of the true maximum principal stress distributions were σ_max=1.43 kPa and σ_max=1.13 kPa, respectively, for the small- and large-cap vessels. Figures 2ii(c) and 3ii(c) illustrate the true middle principal stress distributions (σ^II) within the small- and large-cap vessels, respectively. Figures 2ii(e) and 3ii(e) illustrate the true minimum principal stress distributions (σ^III) within the small- and large-cap vessels, respectively.

Fig. 2.

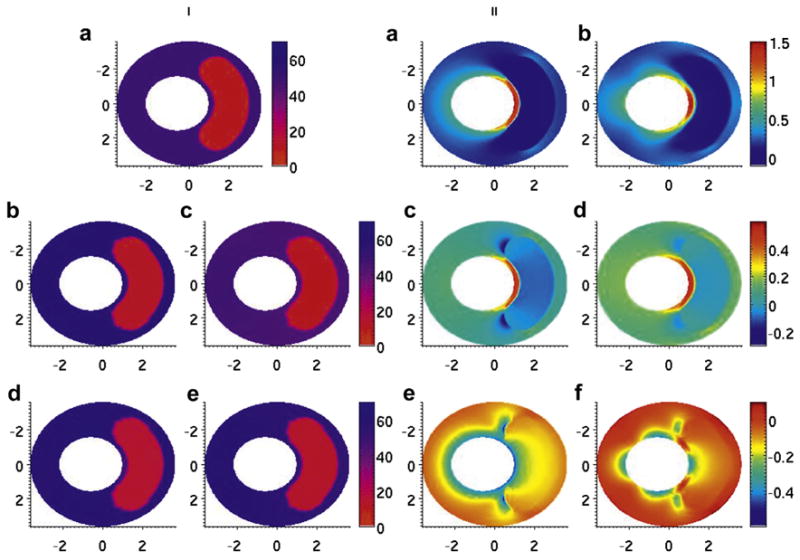
Modulus and stress elastograms of thin-capped simulated vessel phantom in kilopascals. (i, a) Modulus distribution used in the forward simulation. (i, b–e) Modulus elastogram reconstructed under type 1–4 boundary conditions. (ii, a, c, e) minimum, middle and maximum principal stress elastograms computed with the finite-element method. (ii, b, d, f) Minimum, middle and maximum principal stress elastograms computed with reconstruction.

Fig. 3.

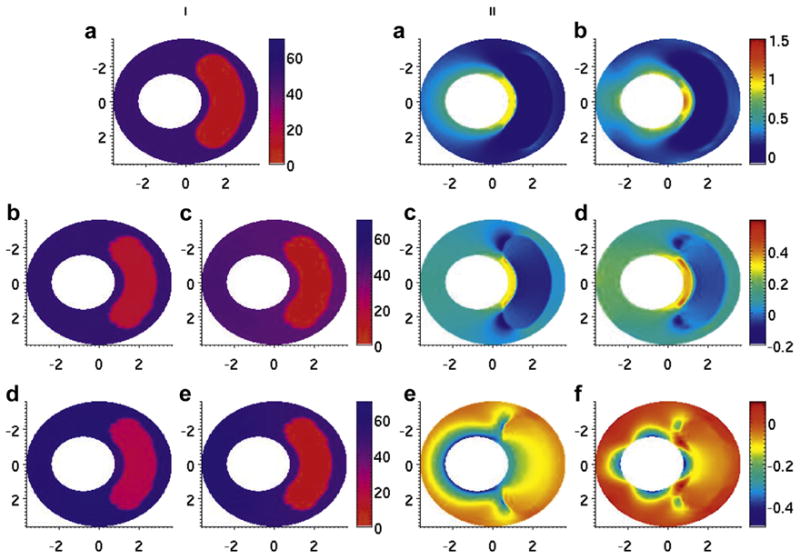
Modulus and stress elastograms of thick-capped vessel phantom in kilopascals. (i, a) Modulus distribution used in the forward simulation. (i, b–e) Modulus elastogram reconstructed under type 1–4 boundary conditions. (ii, a, c, e) Minimum, middle and maximum principal stress elastograms computed with the finite-element method. (ii, b, d, f) Minimum, middle and maximum principal stress elastograms computed with reconstruction.

The modulus elastograms reconstructed with all Poisson ratios used in this study had similar accuracy and image quality. Figures 2i(b–e) and 3i(b–e) are representative examples of modulus elastograms recovered from the thin- and thick-cap fibroatheromas, respectively. For both vessel geometries, the modulus in the vessel wall was higher in elastograms computed under type 2 boundary conditions than in those computed under type 1 or 3 boundary conditions. Tables 1 and 2 summarize the performance (i.e., accuracy and contrast recovery) of the modulus recovery process when image reconstructions were done under different boundary conditions and values of Poisson’s ratio. These tables reveal several observations. The recovered contrast accuracy was independent of the choice of Poisson’s ratio used in the reconstruction process. Boundary conditions marginally affected recovered modulus contrast; however, the mixed boundary conditions with fixed circumferential displacements (type 3) provided slightly more accurate results than type 2 or 4 boundary conditions. The largest errors were incurred when reconstruction was performed under type 4 boundary conditions with Poisson ratios >0.495.

Table 1.

Accuracy of RMS error (%) of modulus elastograms, when image reconstruction was performed at different values of Poisson’s ratio and under different boundary conditions

	Boundary conditions	Poisson’s ratio
		ν = 0.45	ν = 0.495	ν = 0.4995	ν = 0.49995	ν = 0.499995
Vessel 1	Type 1: Zero traction	54.12 ± 1.60	57.02 ± 1.57	54.86 ± 1.16	55.35 ± 1.80	52.52 ± 1.77
	Type 2: Mixed ur fixed	47.07 ± 5.33	49.12 ± 4.52	47.90 ± 5.78	45.01 ± 1.11	48.48 ± 4.57
	Type 3: Mixed uθ fixed	55.65 ± 1.23	57.89 ± 1.27	56.39 ± 1.36	54.97 ± 4.49	57.08 ± 1.13
	Type 4: Fixed	45.76 ± 4.90	49.45 ± 6.12	60.30 ± 9.26	68.00 ± 6.84	68.46 ± 5.02
Vessel 2	Type 1: Zero traction	54.57 ± 1.33	55.31 ± 2.72	59.49 ± 3.06	56.66 ± 1.03	56.23 ± 2.53
	Type 2: Mixed ur fixed	43.21 ± 3.38	45.40 ± 7.85	50.08 ±11.30	46.59 ± 7.56	47.52 ± 7.42
	Type 3: Mixed uθ fixed	55.60 ± 1.35	55.82 ± 1.24	63.13 ± 1.12	58.79 ± 1.13	58.37 ± 1.31
	Type 4: uθ and ur fixed	42.19 ± 4.83	45.42 ± 8.35	65.40 ± 6.78	65.52 ± 5.81	65.52 ± 5.03

Table 2.

Contrast recovered from elastograms when image reconstruction was performed at different values of Poisson’s ratio and under different boundary conditions.

	Boundary conditions	Poisson’s ratio
		ν = 0.45	ν = 0.495	ν = 0.4995	ν = 0.49995	ν = 0.499995
Vessel 1	Type 1: Zero traction	4.01 ± 0.27	4.15 ± 0.52	3.58 ± 0.44	3.59 ± 0.15	2.92 ± 0.70
	Type 2: Mixed ur fixed	4.34 ± 0.57	4.60 ± 0.14	4.03 ± 0.30	3.87 ± 0.44	3.97 ± 0.26
	Type 3: Mixed uθ fixed	4.44 ± 0.07	4.50 ± 0.09	4.14 ± 0.06	3.59 ± 0.98	4.19 ± 0.11
	Type 4: Fixed	3.21 ± 0.86	3.82 ± 0.18	3.552 ± 0.14	3.41 ± 0.44	3.40 ± 0.13
Vessel 2	Type 1: Zero traction	5.09 ± 0.35	4.53 ± 0.58	6.83 ± 1.17	5.47 ± 0.46	4.82 ± 0.75
	Type 2: Mixed ur fixed	4.75 ± 0.44	4.83 ± 0.29	7.29 ± 0.75	5.14 ± 0.23	5.63 ± 0.49
	Type 3: Mixed uθ fixed	5.36 ± 0.12	5.25 ± 0.16	6.96 ± 0.54	6.62 ± 0.62	6.39 ± 0.38
	Type 4: uθ and ur fixed	2.72 ± 0.23	2.63 ± 0.27	3.02 ± 0.75	2.96 ± 0.13	3.03 ± 0.11

Figures 2ii(b) and 3ii(b) are examples of maximum principal stress distributions (σ^I) recovered from the simulated vessels using type 3 boundary conditions. The peak values, spatially, of the maximum principal stress were σ_max = 1.55 kPa and σ_max = 1.12 kPa for the thin- and thick-capped fibroatheromas, respectively. Figures 2ii(d) and 3ii(d) are the corresponding middle principal stress elastograms (σ^II), and Figures 2ii(f) and 3ii(f) are the corresponding minimum principal stress elastograms (σ^III).

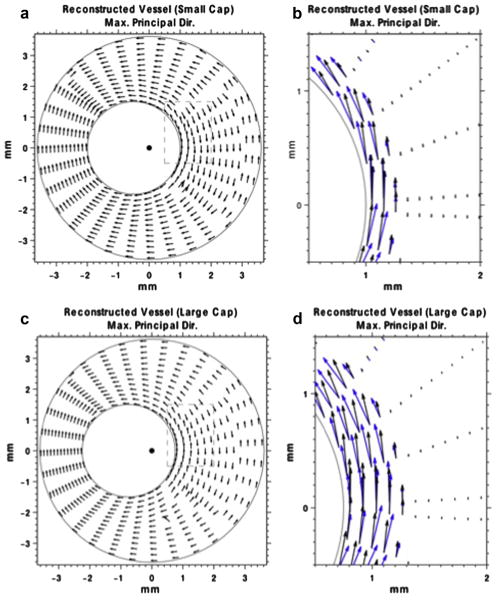
In Figure 4(a, c) are vector plots of maximum principal stress recovered from the thin- and thick-capped simulated vessels, respectively. These plots indicate that (i) the primary stress component was in the circumferential direction of the vessel, and (ii) the circumferential stress was concentrated within the vessel cap, which is consistent with previously reported results (Lee et al. 1996). Figure 4(b, d) are close-up views of the areas within the dashed boxes in Figure 4(a, c), respectively. These views indicate that stress is concentrated within the fibrous cap.

Fig. 4.

(a) Directional plot of the maximum principal stress vector, corresponding to the smaller capped vessel. The lengths of the arrows have been normalized to unity. (b) Zoomed in portion of the maximum principal stress vector (dashed box in [a]). The lengths of the arrows are proportional to the magnitude of the maximum principal stress. (c) Directional plot of the maximum principal stress vector, corresponding to the large-cap vessel. The lengths of the arrows are normalized to unity. (d) Zoomed in portion of the maximum principal stress vector (dashed box in [c]). The lengths of the arrows are proportional to the magnitude of the maximum principal stress. The blue arrows represent the true maximum principal stress vector, corresponding to the stress image in Figure 6(iii,b).

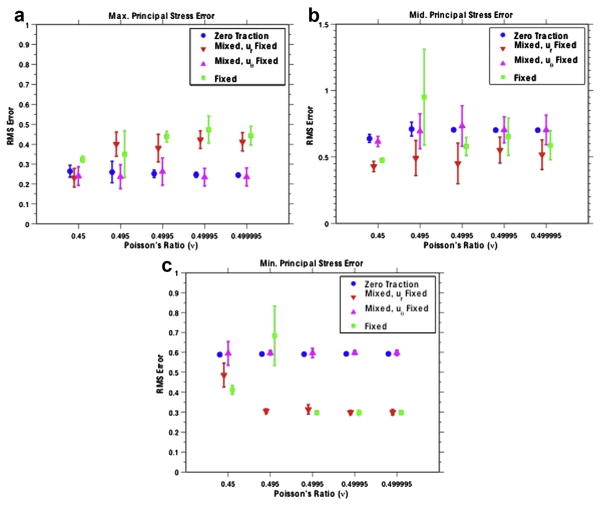
Figure 5(a–c) illustrates the RMS error of the recovered maximum, middle and minimum principal stress values, respectively, for the thin-cap fibroatheroma. The means and standard deviations were computed from 10 statistically independent reconstructions. For the reconstructions with a traction-free radial component (boundary condition types 1 and 3), the error in the maximum principal stress was ~25% relative to the reconstructions with fixed radial displacements, whose error was ~40%. For the minimum principal stress values, this was reversed. The error in the maximum principal stress was higher when traction-free radial components were used (~60%) than when fixed radial components were used (~30%). The middle principal stress exhibited a similar trend. Specifically, the error was higher when traction-free components were used (~60%) than when fixed radial components were used (~50%).

Fig. 5.

Root-mean-squared error of the maximum (a), middle (b) and minimum (c) principal stress values reported for the small-cap vessel reconstructions. The means and standard deviations are reported over 10 reconstructions with independent scatter locations and image noise.

Phantom study

Figures 6i(a) and 7i(a) are representative of sonograms obtained from the vessel phantoms. Figures 6ii(a–d) and 7ii(a–d) are representative modulus elastograms recovered from the thick- and thin-capped vessel phantoms, respectively. All image reconstructions were performed using a Poisson ratio of 0.495 with four outer boundary conditions (i.e., types 1–4). Table 3 summarizes the accuracy of reconstructed modulus elastograms recovered from the thin- and thick-capped vessel phantoms when reconstructions were performed using different boundary conditions (types 1–4) and values of Poisson’s ratio. As in the simulation study, the recovered modulus contrast was independent of the choice of Poisson’s ratio, but larger errors were incurred when reconstructions were performed with type 4 boundary conditions and Poisson ratios exceeding 0.495. In general, the reconstructed values were higher than those measured with the Landmark Servohydraulic Test system, which is consistent with the simulation results (i.e., Fig. 6b). The Young’s moduli measured by independent mechanical testing for the thin-capped phantom were 48.8 ± 4.8 kPa (vessel all) and 16.6 ± 1.4 kPa (plaque); and those for the thick-capped phantom were 43.0 ± 1.9 kPa(vessel wall) and 17.4 ± 2.0 kPa (plaque). The differences in the Young’s moduli of the phantoms were due to variability in our manufacturing process and also because the phantoms were manufactured on different days.

Fig. 6.

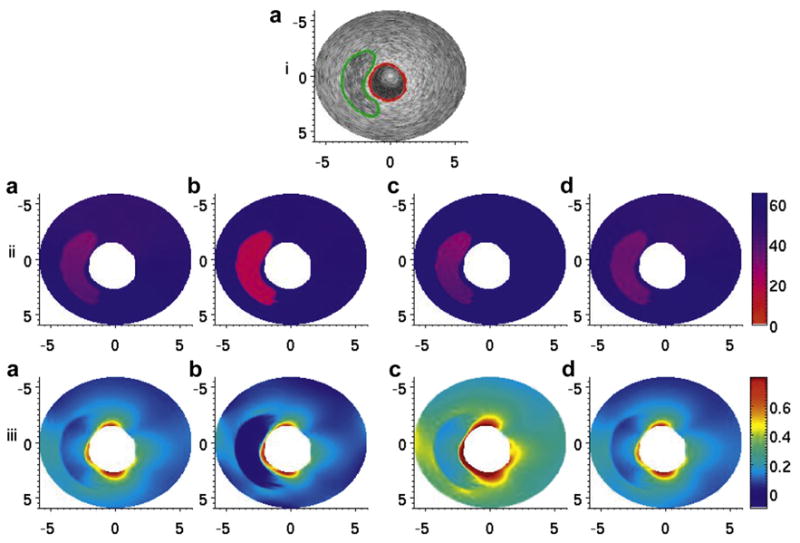
(i, a) B-Mode image of the thick-capped vessel phantom. The red line denotes the manual segmentation of the inner lumen, and the green line denotes the manual segmentation of the soft plaque region. (ii, a–d) Modulus elastograms reconstructed under type 1–4 boundary conditions. (iii, a–d) Maximum principal stress distribution, calculated via eqns (2) and (3) from the modulus elastograms in (ii, a–d). The stress values in each image were normalized to an applied pressure of 500 Pa for comparison.

Fig. 7.

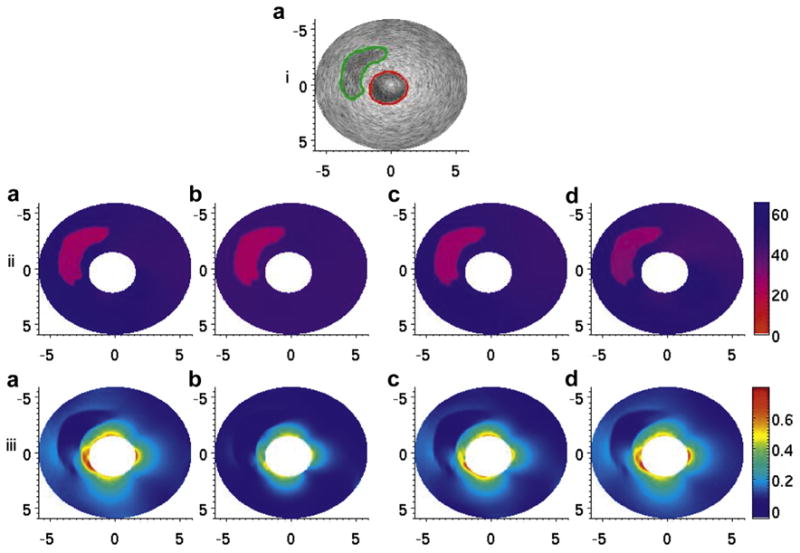
(i, a) B-Mode image of the thin-capped vessel phantom. The red line denotes the manual segmentation of the inner lumen, and the green line denotes the manual segmentation of the soft plaque region. (ii, a–d) Modulus elastograms reconstructed under type 1–4 boundary conditions. (iii, a–d) Maximum principal stress distribution, calculated via eqns (2) and (3) from the modulus elastograms in (ii, a–d). The stress values in each image were normalized to an applied pressure of 500 Pa for comparison.

Table 3.

Young’s modulus (E) and modulus contrast recovered from thin (phantom 1) and thick capped (phantom 2) vessels

Boundary conditions	Poisson’s ratio
	ν = 0.45	ν = 0.495	ν = 0.4995	ν = 0.49995	ν = 0.499995
Phantom 1 background
Type 1: Zero traction	51.30 ± 4.92	50.92 ± 4.78	50.89 ± 4.77	50.87 ± 4.77	50.80 ± 4.76
Type 2: Mixed ur fixed	47.02 ± 2.88	50.65 ± 2.67	11.29 ± 0.61	11.11 ± 0.58	11.10 ± 0.58
Type 3: Mixed uθ fixed	52.56 ± 5.40	52.77 ± 4.35	52.09 ± 5.13	52.12 ± 5.13	52.09 ± 5.13
Type 4: uθ and ur fixed	46.72 ± 0.77	46.81 ± 0.78	11.14 ± 0.18	11.03 ± 0.17	11.07 ± 0.17
Phantom 1 contrast
Type 1: Zero traction	1.77	1.72	1.72	1.72	1.72
Type 2: Mixed ur fixed	1.85	1.94	1.85	1.92	1.93
Type 3: Mixed uθ fixed	2.07	2.09	1.99	1.99	2.00
Type 4: uθ and ur fixed	1.87	1.93	1.89	1.96	2.00
Phantom 2 Background
Type 1: Zero traction	55.99 ± 5.26	55.27 ± 5.07	55.24 ± 5.04	55.18 ± 5.04	55.25 ± 5.06
Type 2: Mixed ur fixed	55.59 ± 7.85	73.13 ± 9.65	6.00 ± 0.83	5.82 ± 0.77	5.83 ± 0.77
Type 3: Mixed uθ fixed	55.80 ± 7.20	55.15 ± 6.78	55.19 ± 6.77	55.06 ± 6.72	55.20 ± 6.77
Type 4: uθ and ur fixed	53.57 ± 2.08	56.12 ± 2.38	6.06 ± 0.25	55.84 ± 0.25	5.78 ± 0.33
Phantom 2 contrast
Type 1: Zero traction	1.66	1.61	1.61	1.59	1.61
Type 2: Mixed ur fixed	2.13	2.14	1.90	2.05	2.07
Type 3: Mixed uθ fixed	1.61	1.56	1.57	1.55	1.57
Type 4: uθ and ur fixed	2.44	2.88	2.42	2.92	2.58

Figures 6iii(a–d) and 7iii(a–d) are the corresponding principal stress elastograms recovered when image reconstructions were performed under four different sets of boundary conditions. In both phantoms, the maximum peak stress occurred at the interface between the cap and the vessel wall, the most rupture-prone region of the vessel. In the phantoms with the thinner cap, the maximum peak stress was approximately 1.18 kPa when a pressure of 500 Pa was applied to the inner lumen. In the phantom with the thicker cap, the maximum peak stress value was approximately 0.84 kPa when a similar pressure was applied to the inner lumen.

In Figure 8(a, c) are directional plots of the maximum principal stress vector within the thin- and thick-capped vessel phantoms, respectively. Figure 8(b, d) are enlarged views of the areas within the dashed boxes in Figure 8(a, c), respectively. These figures corroborated the simulation results, more specifically, that the principal direction of the maximum principal stress is in the circumferential direction within the cap, which is also consistent with the simulation results.

Fig. 8.

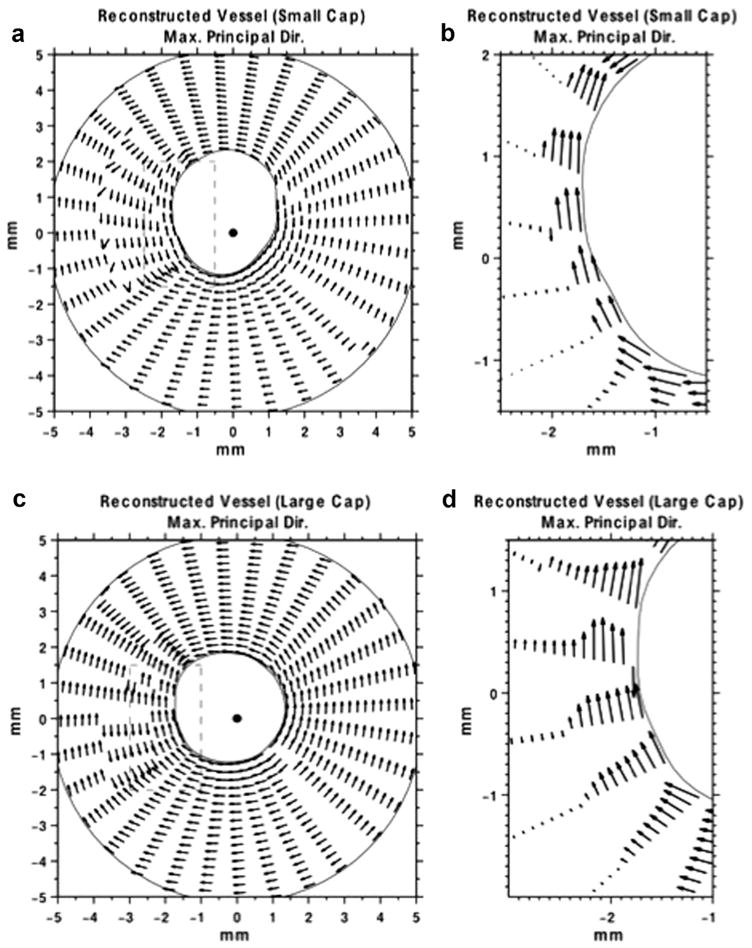
(a) Directional plot of the maximum principal stress vector, corresponding to the image in (ii, a) of the small-cap vessel phantom. The lengths of the arrows have been normalized to unity (b) Zoomed in portion of the maximum principal stress vector (dashed box in [a]). The lengths of the arrows are proportional to the magnitude of the maximum principal stress. (c) Directional plot of the maximum principal stress vector, corresponding to the image shown in Figure 7(iii,b) of the large-cap vessel phantom. The lengths of the arrows are normalized to unity. (d) Zoomed in portion of the maximum principal stress vector (dashed box in [c]). The lengths of the arrows are proportional to the magnitude of the maximum principal stress.

DISCUSSION

Knowledge of the stress distribution within the fibrous cap could allow clinicians to predict the propensity of an atherosclerotic plaque to rupture; however, none of the conventional imaging modalities can visualize stress in vivo. In this study, we investigated whether IVUS elastography can visualize the stress distribution within vascular tissues. More specifically, we investigated how assumptions made during the modulus reconstruction process (i.e., Poisson’s ratio and boundary conditions) affect the performance of stress elastograms. The key findings of this study were as follows. First, the reconstruction process recovered modulus contrast with an accuracy of approximately 20%–30% (Tables 2 and 3), which was consistent with our previously reported results (Richards and Doyley 2011). Second, stress and shear modulus elastograms generally performed the same irrespective of the value of Poisson’s ratio used in the reconstruction process, except when reconstruction was performed under type 4 boundary conditions (Tables 1 and 3, Fig. 5). The analytical model reported in the Appendix predicted this behavior. More specifically, for the “pseudo”-incompressibility case, both the shear modulus and the pressure on the outer boundary will influence displacements computed during the image recovery process (see eqn 16) when type 2–4 boundary conditions are employed. This occurs because different combinations of modulus and pressure could yield the same displacement field, which becomes more significant as Poisson’s ratio approaches 0.5 (see Fig. 9). Second, the magnitude of shear and the second Lamé coefficient (kPa for shear and GPa for lambda modulus) are noticeably different. Therefore, the displacement divergence (∇•u) term is dominated by lambda modulus, and displacements with very high signal-to-noise ratio will be needed to observe the changes in the divergence term when Poisson’s ratio is varied from 0.45 to 0.495. Modulus and stress elastograms computed using type 1 boundary conditions were independent of Poisson’s ratio because the displacement divergence term in the forward elasticity model was dominated by lambda modulus rather than shear modulus. Third, type 3 and 4 boundary conditions produced the most and least accurate elastograms (modulus and maximum principal stress), respectively (Fig. 5). Fourth, maximum principal stress was more prevalent in the circumferential than other coordinate directions (Figs. 4 and 8), which was consistent with theoretical predictions (Lee et al. 1993; Loree et al. 1992).

Fig. 9.

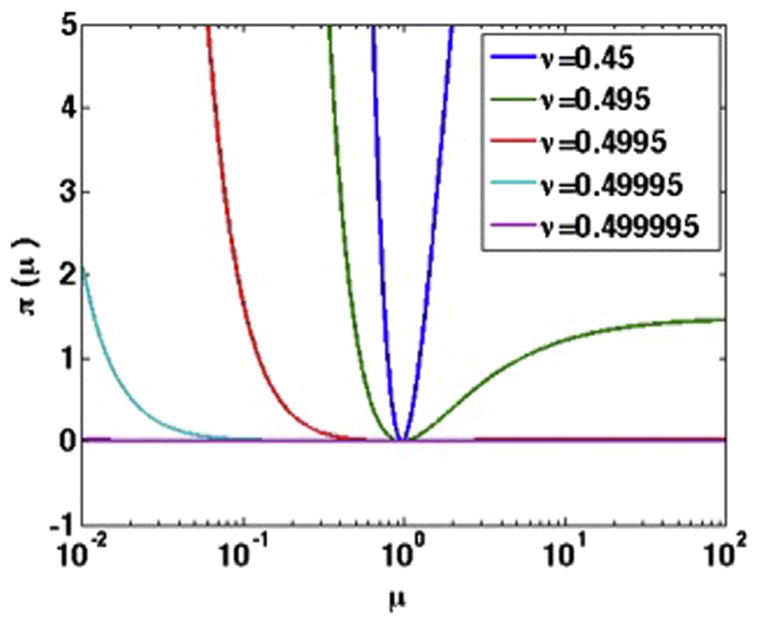
How the objective function used to solve the inverse problem varies with increasing shear modulus and Poisson’s ratio.

Stress imaging demands absolute values of shear modulus, which depends on the mechanical excitation (harmonic or quasi-static) and the boundary conditions (Dirichlet or Neumann) assumed during image reconstruction (Doyley et al. 2001). In general, most quasi-static inversion schemes provide relative estimates of shear modulus because Dirichlet boundary conditions are assumed during image reconstructions (Doyley 2012). However, a reference tissue or material of known modulus could be used to convert relative estimates of shear modulus to absolute values. In breast elastography, this is achieved by imaging through a standoff pad (Ophir et al. 1991); however, this approach is not feasible in intravascular applications. A better approach is to employ Neumann boundary conditions (stress or pressure) during image reconstruction, because clinicians routinely measure the pressure within the lumen during interventional procedures. Neumann boundary conditions allow the reconstruction process to provide absolute estimates of shear modulus without the need for calibration (Baldewsing et al. 2004b; Le Floc’h et al. 2009; Richards and Doyley 2011) and provide more accurate estimates of shear modulus (Barbone and Bamber 2002). However, because the pressure on the outer boundary is unknown, one could ask the question, What would be the consequence of reconstructing shear modulus with an imprecise estimate of the traction on the outer boundary, that is, assuming traction is zero at the boundary?

The traction on the outer boundary may be specified implicitly by imposing Dirichlet boundary conditions (see Appendix, eqn 18) or explicitly by assigning a known traction (in our case, zero) to the boundary nodes. Table 1 indicates that the reconstruction process overestimated shear modulus when Dirichlet boundary conditions were imposed using the radial component of displacements (type 4). This bias was introduced by errors in the radial component of displacement (over regularized) that force the forward model used in the reconstruction process to overemphasize the tractions (normal component). The pressure on the outer boundary is governed primarily by the radial component of displacements. Reconstructing modulus under type 3 boundary conditions produced better results (more accurate) than that under type 4 boundary conditions because the circumferential component of displacement had less impact on the outer pressure. Because radial stress decreases rapidly from the inner lumen to the outer vessel, it may be assumed that the radial component of pressure on the outer boundary is zero (traction free) when solving the forward elasticity problem; however, this may not necessarily be the case. Equation (21) (see Appendix) predicts that the error incurred in modulus when traction-free boundary conditions are employed is inversely proportional to inverse square distance from the outer boundary, assuming that the pressure on the outer boundary is zero. Table 1 indicates that the reconstruction process overestimated shear modulus when the outer boundary was incorrectly assumed to be traction free. Because the forward IVUS elastography problem is sensitive to boundary conditions, we are developing a hybrid finite-element formation (combination of the finite-element and boundary-element methods) to solve the forward elasticity problem with infinite boundary conditions where both components of traction (radial and angular) are zero, but reconstruct shear modulus with a smaller mesh. We plan to report the results of this reconstruction technique in a future communication.

To reduce cardiac-related deaths, we need an objective criterion to predict the propensity of plaque rupture. Loree et al. (1992) recommend that the peak stress normalized by the applied pressures (σ_max/p_in) be used to assess plaque vulnerability. We obtained vulnerability indices of 3.1 and 2.3, for the thin- and thick-capped simulated vessels, respectively, when the criterion of Loree et al. (1992) was applied to the stress elastograms in Figure 7. Similarly, vulnerability indices of 2.2 and 1.6 were obtained when the vulnerability criterion was applied to stress elastograms obtained from the thin-and thick-capped phantoms, respectively (Figs. 6 and 7). This criterion suggests that the vessels with the thinner cap are more likely to rupture (36% and 27% for the simulated and physical vessel phantoms, respectively) than the vessels with the thicker cap, which is consistent with histologic observations that the propensity of plaque rupture increases with decreasing thickness of the cap (Finet et al. 2004; Hatsukami et al. 2000).

In this work, strain was simulated in the linear elastic range (near diastole) where the probability of plaque rupture is negligible. Several clinical studies have reported that acute coronary events typically occur in the morning when blood pressure is high (Kario et al. 2003). Therefore, if stress elastography is to become a viable technique, methods will have to be developed to visualize the stresses induced by high blood pressures. Consequently, we plan to develop more sophisticated finite-element models that include non-linearity (geometric and material) and the pre-stresses induced within the vessel during the diastolic phase of the cardiac cycle. The disadvantage of using large pressures in elastography is that larger strains will be induced within the vessels that will increase decorrelation noise, which, in turn, will decrease the accuracy of the strain estimates (Varghese and Ophir 1997). The incremental tracking strategy employed in breast elastography could solve this problem (Varghese and Ophir 1996), but in addition to this global motion, compensation techniques such as that described in Doyley et al. (2001) will also have to be implemented.

This study had three main limitations. First, the boundary conditions for the vessels and the samples used for mechanical testing were different, which could create discrepancy. A better approach would be to use the sonometry method described by Bernal et al. (2011) to measure the shear modulus of the vessel along the cross section from which RF echo data were acquired. Second, the errors incurred in this study were high, which was due partly to the high displacement errors. These problems can be minimized by performing either multi-compression elastography or improving the performance of the displacement estimation strategy. Third, unwanted catheter motion and the anisotropic nature of vessels will degrade performance. We plan to mitigate these problems by employing electrocardiographic gating and using an anisotropic finite-element model in the image reconstruction process.

CONCLUSIONS

Assumptions made regarding the outer boundary conditions had the greatest impact on our ability to recover modulus and internal tissue stress. Reconstructions performed under type 3 boundary conditions produce the most accurate estimates of modulus and stress when the traction on the outer boundary is unknown.

APPENDIX

To understand the impact of boundary conditions and Poisson’s ratio on the modulus reconstruction process, we have to examine the forward elasticity problem. For simplicity, let us consider the analytic solution of the thick-walled homogeneous vessels (de Korte et al. 1997; Timoshenko and Goodier 1970). The radial displacements in the vessel can be computed analytically as

$$u_r(r)=\frac{r}{2\mu (b^2-a^2)}\left((p_{\mathrm{i}}{a}^2-p_{\mathrm{o}}{b}^2)(1-2\upsilon )-a^2{b}^2(p_{\mathrm{o}}-p_{\mathrm{i}})\frac{1}{r^2}\right);u_{\theta }=0.$$ (10)

where a and b represent the inner and outer radii, respectively; p_i and p_o represent the pressure on the inner outer lumens, respectively; μ represents the modulus, ν represents Poisson’s ratio; r is the radial position; and θ is the circumferential position. If the vessel is incompressible (i.e., ν = 0.5), then the radial displacement becomes

$$u_r(r)=\frac{-a^2{b}^2(p_{\mathrm{o}}-p_i)}{2\mu (b^2-a^2)}\frac{1}{r}$$ (11)

If the hypothetical vessel has the following geometric and mechanical properties: a = 1, b = 5, p_i = 1, p_o = 0 and μ = 1. Then the radial displacement is given by

$$u_r^m(r)=\frac{25}{48}\frac{1}{r}$$ (12)

For the inverse problem, the known parameter are a = 1, b = 5 and p_i = 1, and the unknown parameters are p_o and μ. Assuming incompressibility, then the required displacements is given by (i.e., dependent on both pressure and modulus):

$$u_r(r;\mu ,p_{\mathrm{o}})=\frac{-25(p_{\mathrm{o}}-1)}{48\mu }\frac{1}{r}$$ (13)

Assuming the displacement on the outer boundary is fixed (i.e., u_r(b) = 5/48), solving for p_o yields

$$\begin{array}{ll}\hfill u_r(b;\mu ,p_{\mathrm{o}})& =\frac{-5(p_{\mathrm{o}}-1)}{48\mu }=\frac{5}{48}=u_r^m(b)\text{or}\hfill \\ \hfill p_{\mathrm{o}}& =1-\mu ,\text{giving}{u}_r(r)=\frac{25}{48}\frac{1}{r}\hfill \end{array}$$ (14)

Equation (14) reveals the consequences of fixing the displacements on the outer boundary. More specifically, the desired displacements are independent of modulus and the pressure on the outer boundary. An important question is what happens for the “nearly” incompressible case (i.e., ν < 0.5). Solving the inverse problem for eqn (10) gives

$$u_r(r;\mu ,p_o,\nu )=\frac{r}{48\mu }\left((1-25p_{\mathrm{o}})(1-2\nu )-25(p_{\mathrm{o}}-1)\frac{1}{r^2}\right)$$ (15)

Let us assume fixed displacements on the outer boundary c (i.e., u_r(b) = 5/48), simplifying the resulting expression gives:

$$u_r(b;\mu ,p_o,\nu )=\frac{5}{48\mu }((1-25p_o)(1-2\nu )-(p_o-1))=\frac{5}{48}=u_r^m(b),$$ (16)

and thus

$$p_{\mathrm{o}}=\frac{\mu -2+2\nu }{50\nu -26}.$$ (17)

The desired displacement as a function of Poisson’s ratio and shear modulus is given by

$$u_r(r;\mu ,\nu )=\frac{r}{48\mu }\left(\left(1-25\left(\frac{\mu -2+2\nu }{50\nu -26}\right)\right)(1-2\nu )-25\left(\left(\frac{\mu -2+2\nu }{50\nu -26}\right)-1\right)\frac{1}{r^2}\right)$$ (18)

Figure 9 illustrates how the objective function $\pi (\mu )=\underset{r}{\int }{(u_r(r;\mu )-u_r^m(r))}^{2}dr$ varies with μ and Poisson’s ratio. The figure predicts that as ν approaches 0.5, the value of μ that minimizes π becomes less obvious.

Let us consider the alternative inverse problem, where the outer boundary is traction free, in this example, p_o = 0, and eqn (11) reduces to

$$u_r(r)=\frac{28}{48\mu }\frac{1}{r}$$ (19)

If we used eqn (12) to synthesize ideal displacements, then the value μ that minimizes π is μ =1. Consider an inverse problem in which we can measure the displacement field only up to r = c = 4, at which point the unknowns would be p_c (the pressure at c) and μ. If we assume that p_c =0 then the assumed displacements would be

$$u_r(r;\mu )=\frac{16}{30\mu }\frac{1}{r},$$ (20)

and thus the value μ that minimizes π (i.e., μ_c) is given by

$${\mu }_c=\mu \frac{\left(1-\frac{a^2}{b^2}\right)}{\left(1-\frac{a^2}{c^2}\right)}$$ (21)

This equation predicts that the error in the estimated modulus, μ_c = 128/125 =1.024, is inversely proportional to the square distance of the true outer radius, b, relative to the inner radius, a, and the outer measurement radius c, also relative to a. Furthermore, this equation also predicts that, if the tube were infinitely thick (i.e., b–> ∞) then the approximation of μ_c would be more accurate for c ≫ a.