Extension of TOPAS for the simulation of proton radiation effects considering molecular and cellular endpoints

Abstract

The aim of this work is to extend a widely used proton Monte Carlo tool, TOPAS, towards the modeling of relative biological effect (RBE) distributions in experimental arrangements as well as patients.

TOPAS provides a software core which users configure by writing parameter files to, for instance, define application specific geometries and scoring conditions. Expert users may further extend TOPAS scoring capabilities by plugging in their own additional C++ code. This structure was utilized for the implementation of eight biophysical models suited to calculate proton RBE. As far as physics parameters are concerned, four of these models are based on the proton linear energy transfer (LET), while the others are based on DNA Double Strand Break (DSB) induction and the frequency-mean specific energy, lineal energy, or delta electron generated track structure. The biological input parameters for all models are typically inferred from fits of the models to radiobiological experiments.

The model structures have been implemented in a coherent way within the TOPAS architecture. Their performance was validated against measured experimental data on proton RBE in a spread-out Bragg peak using V79 Chinese Hamster cells.

This work is an important step in bringing biologically optimized treatment planning for proton therapy closer to the clinical practice as it will allow researchers to refine and compare pre-defined as well as user-defined models.

1. Introduction

1.1. The TOPAS Monte Carlo system

Monte Carlo simulations are becoming increasingly valuable in radiation therapy. Not only are they useful for dose calculations but they also allow for a better understanding of beam characteristics as well as aid in the design of detector systems. Proton therapy can particularly benefit from Monte Carlo techniques because highly conformal dose distributions are especially sensitive to uncertainties in analytical dose calculation methods (Schuemann et al 2014). However, Monte Carlo techniques often require advanced programming skills as well as a deep understanding of the underlying physics since most codes have been developed by the nuclear and particle physics communities. One multi-particle and multi-purpose code is the Geant4 toolkit (Agostinelli et al 2003), which is frequently used for proton therapy applications (e.g. (Paganetti et al 2004)). In 2009 the Massachusetts General Hospital (MGH), the SLAC National Accelerator Laboratory (SLAC), and the University of California San Francisco (UCSF) launched a project to make Monte Carlo simulations more widely available to the proton therapy community. The goal of the TOPAS (Tool for Particle Simulation) project was to develop a Monte Carlo tool that would be easy to use without requiring programming knowledge (Perl et al 2012). In addition, it would be well validated against experimental data (Testa et al 2013), allow four-dimensional simulations (Testa et al 2014, Shin et al 2012), and use proton specific variance reduction techniques (Ramos-Mendez et al 2013). Furthermore, the goal was to create a modular structure in order to facilitate inter-institutional collaborations and the ability for users to add their own components, tailored to their individual research interests.

TOPAS has subsequently been developed and has now been widely accepted in the proton therapy field with more than 250 registered users at over 80 institutions worldwide. The success is due to a series of software innovations and close collaborations between medical physicists and software experts.

A key to the reliability of TOPAS is that each simulation is built with the same compiled code. What is different from one application to the next is the set of “parameter files” specifying geometry, particle source, fields, motion, scoring, and physics settings. Parameter files are very simple text files that users can configure without needing to know any programming languages. Each simulation is controlled by a hierarchy of parameter files which allows decoupling of computational tasks facilitating collaboration amongst research or clinical groups while delivering robustness against user errors. One aspect of this hierarchy is that several parameter files can depend on each other so that an application can be designed in which a user only has to deal with the parameters of interest to him while relying on default settings for others. TOPAS provides a large library of ready-made software modules for geometry, scoring, filtering, etc. TOPAS’ ease of use does not come at the expense of flexibility. Advanced users can write new geometry components, new scoring classes, etc., utilizing the full power of C++ and the underlying Geant4 simulation toolkit.

In addition to allowing treatment head and detector simulations, TOPAS can calculate dose based on proton therapy treatment plans of individual patients (Schuemann et al 2014). This feature is being used at MGH for passive scattering as well as beam scanning.

1.2. TOPAS for biology

Medical physics is reaching a boundary where further improvements require an interdisciplinary effort of connecting the physics to the underlying biology. Proton therapy has controversies related to biological effects that need to be studied further, both experimentally and theoretically (Paganetti 2014, Paganetti and van Luijk 2013). To achieve this goal, close collaborations between physicists, biologists and clinicians is required. It has been demonstrated that Monte Carlo simulations can play a major role in understanding biological phenomena in radiation oncology (El Naqa et al 2012). Consequently, it was decided to expand TOPAS with not only physicists but also biologists as users in mind. Our aim is to connect the TOPAS physics simulation results to basic biophysical models to aid biologists in the design of experiments or to analyze experiments based on the simulated underlying energy deposition characteristics.

Furthermore, the goal is to provide a tool that connects physical dose to RBE (relative biological effectiveness) weighted dose for clinical studies in proton therapy (Sethi et al 2014). Prescription doses to the target, dose constraints to critical structures and fractionation schemes are largely based on clinical experience with low LET photons. Proton therapy planning generally applies a constant RBE of 1.1 (Paganetti et al 2002). The RBE is known to vary as a function of dose, tissue penetration (as proton energy decreases) and as a function of the molecular, cellular or clinical endpoint of interest. The use of a constant RBE in proton therapy is controversial and research on proton RBE modeling has increased (Giantsoudi et al 2013, Sethi et al 2014, Wedenberg and Toma-Dasu 2014). Models developed in the past span a wide area, from predominantly mechanistic to predominantly phenomenological. The input of physics parameters varies, e.g. delta-electron track structure of the particle path, microdosimetric energy deposition characteristics, or linear energy transfer (LET). Some radiobiological models predict absolute radiation effects while others focus on prediction of relative effects (i.e. an RBE).

The goal is to expand TOPAS to provide a platform for these models, with users able to select and adjust models from parameter files. Monte Carlo simulations that model the underlying physics could then be used to compare model results. Monte Carlo simulations can correlate detailed track structure information within detailed geometries in a flexible framework so that established biophysical models can be tested and novel models can be developed. Furthermore, simulations can model experimental conditions accurately so that the uncertainty of model parameters gained from experiments can be reduced.

We envision that TOPAS can do for the radiation biology community what it has already done for the proton therapy physics community, making advanced Monte Carlo simulations more accessible to non-experts.

2. Methods

2.1. Biophysical models for the prediction of the RBE

The RBE for proton beams is defined as the ratio of the isoeffect doses of a reference low-LET radiation D_x and the dose of the proton radiation D. We consider eight different models for the implementation in TOPAS. Seven of those rely on the linear-quadratic (LQ) model (based on the parameters α and β), which expresses the RBE as:

$$\mathrm{RBE}=\frac{D_{\mathrm{x}}}{D}=-\frac{1}{2D}{\left(\frac{\alpha }{\beta }\right)}_{\mathrm{x}}+\frac{1}{D}\sqrt{\frac{1}{4}{\left(\frac{\alpha }{\beta }\right)}_{\mathrm{x}}^2+\frac{\alpha }{a_{\mathrm{x}}}{\left(\frac{\alpha }{\beta }\right)}_{\mathrm{x}}D+\frac{\beta }{{\beta }_{\mathrm{x}}}{D}^2},$$ (1)

where x indicates the reference radiation. One of the models (the track structure model) is based on the multi-target equation / single-hit equation.

As for considering the underlying physics, most of the implemented models relate the LET to the RBE and assume a linear relationship of RBE as a function of LET. It is clear that LET cannot describe the proton track structure with its delta electrons of up to 500 keV energy in detail (Liamsuwan et al 2011). However, other than in heavy ion therapy, dose-averaged LET is a reasonably good approximation of the physical properties of the radiation field for protons up to the depth at which the Bragg peak occurs. This is because at typical therapeutic doses there are hundreds or thousands of proton tracks passing through cell-sized targets (Paganetti 2005). Only far downstream of the Bragg peak may the dose-averaged LET (LET_d) be less useful for predicting trends in proton RBE. The LET_d is a physical quantity that can be easily extracted from Monte Carlo simulations.

A model would typically calculate an RBE relative to a given reference radiation parameterized, for example, with α_x and β_x. If the RBE relative to a different reference radiation is requested, it can be accomplished by using a relative LET_d value (LET_d for protons relative to the reference photons) if a linear relationship between LET_d and RBE is assumed (Paganetti 2014).

2.1.1. The model by Wedenberg et al

Wedenberg et al (Wedenberg et al 2013) assume the quadratic parameter β to be constant, while the ratio α/α_x is assumed to depend on LET_d and (α/β)_x:

$$\alpha ={\alpha }_{\mathrm{x}}\left(1+\frac{c_1}{{(\alpha ∕\beta )}_{\mathrm{x}}}{\mathrm{LET}}_{\mathrm{d}}\right),\beta ={\beta }_{\mathrm{x}}.$$ (2)

The constant c₁ was fitted to a total of 10 different cell lines resulting in a value of 0.434 Gy μm/keV (Wedenberg et al 2013).

2.1.2. The model by Carabe et al

Carabe et al (Carabe et al 2012, Carabe-Fernandez et al 2007) used the concept of maximum RBE, corresponding to α/α_x, and minimum RBE, corresponding to $\sqrt{\beta ∕{\beta }_{\mathrm{x}}}$. The behavior of each as a function of LET_d and (α/β)_x was then fitted to experimental data. The model does explicitly assume a dependency of β on LET_d:

$${\mathrm{RBE}}_{\max }=c_2+c_3\frac{2.686\mathrm{Gy}}{{(\alpha ∕\beta )}_{\mathrm{x}}}{\mathrm{LET}}_{\mathrm{d}},{\mathrm{RBE}}_{\min }=c_4+c_5\frac{2.686\mathrm{Gy}}{{(\alpha ∕\beta )}_{\mathrm{x}}}{\mathrm{LET}}_{\mathrm{d}}.$$ (3)

In equation (3), 2.686 Gy is the mean value of (α/β)_x of the cell line that was used for fitting the constants c₂ to c₅ to published data for V79 Chinese hamster cells. The constants were obtained as c₂ = 0.843, c₃ = 0.154 μm/keV, c₄ = 1.09 and c₅ = 0.006 μm/keV.

2.1.3. The model by Chen and Ahmad

Chen and Ahmad (Chen and Ahmad 2012) assumed a constant value of β and a more complex dependency of α on LET_d:

$$\alpha =c_6+\frac{1-e^{-c_7{\mathrm{LET}}_{\mathrm{d}}^2}}{c_8{\mathrm{LET}}_{\mathrm{d}}},\beta ={\beta }_{\mathrm{x}}.$$ (4)

Fits to experimental V79 data resulted in c₆ = 0.1 Gy⁻¹, c₇ = 0.0013 (μm/keV)² and c₈ = 0.045 μm/keV.

2.1.4. The model by Wilkens and Oelfke

Wilkens and Oelfke (Wilkens and Oelfke 2004) applied a simple relationship between α and LET_d while β is constant:

$$\alpha =c_9+c_{10}{\mathrm{LET}}_{\mathrm{d}},\beta ={\beta }_{\mathrm{x}},$$ (5)

with c₉ = 0.1 Gy⁻¹ and c₁₀ = 0.02 μm/keV Gy⁻¹ from fits to V79 survival data.

2.1.5. The repair-misrepair-fixation (RMF) model

In the RMF model (Carlson et al 2008, Frese et al 2012), the effects of particle type and kinetic energy (and hence LET) on α and β are explicitly linked to the initial formation of DNA double strand breaks (DSBs), i.e., in the limit when the dose is small compared to α/β, $\alpha =\theta \Sigma +\kappa {\stackrel{‒}{z}}_F{\Sigma }^2,\beta =\kappa {\Sigma }^2∕2,\alpha ∕\beta =2(\theta ∕\kappa )∕\Sigma +2{\stackrel{‒}{z}}_F$. Here, Σ is the number of DSB Gy⁻¹ Gbp⁻¹ (or per cell), ${\stackrel{‒}{z}}_F$ is the frequency-mean specific energy in a cell nucleus, and θ and κ are two cell-specific adjustable parameters that relate to the biological processing of DSBs into more lethal forms of damage, such as chromosome aberrations. As a first approximation: ${\stackrel{‒}{z}}_F\cong 0.204{\mathrm{LET}}_{\mathrm{d}}∕d^2$. An attractive aspect of the RMF model is that θ and κ are independent of proton LET up to at least 75 to 100 keV/μm, i.e., the entire energy range relevant to clinical proton beams. In the RMF model, the RBE for reproductive cell death varies with particle type and energy because DSB induction (Σ) and ${\stackrel{‒}{z}}_F$ vary with particle type and energy. For MV x-rays and other low LET reference radiations, the RMF model predicts that the minimum and maximum RBE for the endpoint of reproductive cell death is

$${\mathrm{RBE}}_{\max }\equiv \frac{\alpha }{{\alpha }_{\mathrm{x}}}\cong {\mathrm{RBE}}_{\mathrm{DSB}}\left(1+\frac{2{\stackrel{‒}{z}}_F{\mathrm{RBE}}_{\mathrm{DSB}}}{{(\alpha ∕\beta )}_{\mathrm{x}}}\right),{\mathrm{RBE}}_{\min }\equiv \sqrt{\frac{\beta }{{\beta }_{\mathrm{x}}}}={\mathrm{RBE}}_{\mathrm{DSB}},$$ (6)

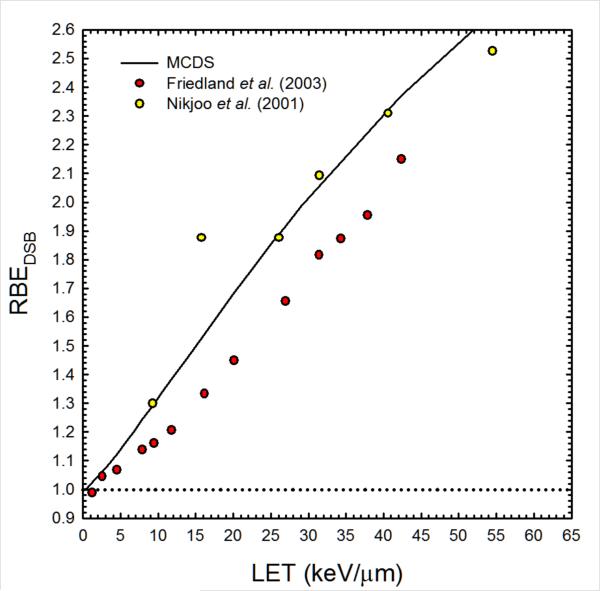
where RBE_DSB is the ratio of Σ for the proton to Σ for the ⁶⁰Co reference radiation. Estimates of RBE_DSB for protons with energies from 1 keV to 1 GeV relative to γ-rays from ⁶⁰Co (LET = 0.24 keV/μm) were obtained from the Monte Carlo Damage Simulation (MCDS) developed by Stewart and colleagues (Stewart et al 2011). As illustrated in figure 1, the MCDS produces estimates of RBE_DSB comparable to event-by-event Monte Carlo track structure simulations. In TOPAS, α and β are estimated using

$$\alpha ={\mathrm{RBE}}_{\mathrm{DSB}}\left[{\alpha }_{\mathrm{x}}+2{\beta }_{\mathrm{x}}{\mathrm{RBE}}_{\mathrm{DSB}}\left(0.204\frac{{\mathrm{LET}}_{\mathrm{d}}}{d^2}\right)\right],\beta ={\beta }_x\cdot {{\mathrm{RBE}}^2}_{\mathrm{DSB}}.$$ (7)

Figure 1.

Estimates of the proton RBE for DSB induction from the MCDS (Stewart et al 2011) and track structure simulations (Friedland et al 2003, Nikjoo et al 2001).

For situations in which the reference radiation is something other than ⁶⁰Co γ-rays, estimates of RBE_DSB in equations (6) and (7) need to be divided by the RBE_DSB of the desired reference radiation (e.g. kV x-rays) relative to ⁶⁰Co γ-rays.

2.1.6. The microdosimetric-kinetic model (MKM)

A more accurate representation of a radiation field can be done without the use of LET and instead using the framework of microdosimetry. Here, a radiation field is characterized by the energy deposited in a small subcellular volume called domain. The quantity of interest is the lineal energy $y=\epsilon ∕\stackrel{‒}{l}$, where ε is the energy deposited in the sensitive volume and $\stackrel{‒}{l}$ is the mean chord length of the volume. Due to large fluctuations of energy deposition in sub-micrometer volumes, the ionizing radiation is characterized by the probability distribution of lineal energy events, f(y), and its expectation values frequency-mean lineal energy, ${\stackrel{‒}{y}}_D$, and dose-mean lineal energy, ${\stackrel{‒}{y}}_D$ . The MKM (Hawkins 1994, 1998, 1996) combines assumptions from microdosimetry with kinetic relations for lesion repair and transformation. The radiosensitivity parameter β is assumed to be constant while α is calculated from ${\stackrel{‒}{y}}_D$:

$$\alpha ={\alpha }_0+\frac{1}{\rho \pi r_{\mathrm{d}}^2}{\stackrel{‒}{y}}_D\beta ,\beta ={\beta }_{\mathrm{x}},$$ (8)

where ρ and r_d are the density and radius of a spherical domain. The cell-line dependent parameters α₀ and β are independent of radiation quality and are equal to the LQ parameters in the limit of zero LET. Values for the cell-dependent parameters r_d and α₀ are published (Hawkins 1998, 2006, Kase et al 2008, Sato el al 2011).

2.1.7. The amorphous track based MKM

In this MKM implementation, an amorphous track structure model for the evaluation of the energy deposition at the subcellular level is used, following the approach described in Kase et al (Kase et al 2008). The parameters of the model θ_MKM = (α₀, β, r_n, r_d) are cell-dependent and have the same meaning as those introduced in equation (8), with the addition of r_n, the radius of the cell nucleus. These parameters were considered as free parameters of the MKM to be adjusted phenomenologically to describe experimentally measured RBE values from published experiments. For this purpose, the experimental in-vitro data collected in the Particle Irradiation Data Ensemble (PIDE) (Friedrich et al 2013) were used. The experimental RBE_α and RBE₁₀, the RBE values corresponding to cell survivals S → 1 and S = 0.1 were obtained from PIDE for V79 cells (asynchronous phase) irradiated with monoenergetic ions with atomic number Z ≤ 8. The data for RBE_α, RBE₁₀ and different ions were fitted simultaneously by evaluating the following minimization:

$${\theta }_{\mathrm{MKM}}=\underset{{\theta }_{\mathrm{MKM}}}{\mathrm{argmin}}\left({\omega }_{\alpha }\sum _{{\{Z,\mathrm{LET}\}}_{\exp }}{({\mathrm{RBE}}_{\alpha }-{{\mathrm{RBE}}_{\alpha }}^{\mathrm{MKM}})}^2+{\omega }_{10}\sum _{{\{Z,\mathrm{LET}\}}_{\exp }}{({\mathrm{RBE}}_{10}-{{\mathrm{RBE}}_{10}}^{\mathrm{MKM}})}^2\right),$$ (9)

where the sum is carried out over all available LET experimental data with ions with Z ≤ 8, and ω_α = ω₁₀ = 1 are the relative weights. For example, the results of the fitting procedure are α₀ = 0.1295 Gy⁻¹, β = 0.01095 Gy⁻², r_d = 0.19 μm and r_n = 3 μm for clonogenic cell survival of V79 cells. Similar fits would have to be done if the PIDE database is to be used for other endpoints or cell lines. In this specific implementation of the MKM, the obtained parameters α₀ and β were considered as representative of the reference radiation LQ parameters for this endpoint. Following this assumption we approximated RBE → 1 in the limit of LET → 0. This approximation is the same used in Kase et al (Kase et al 2008) and was knowingly made in this context to avoid the use of further ad hoc parameters in the model, since the experimental reference radiation α_x and β_x show a huge variability in the PIDE database.

The implemented model evaluates the LQ parameter $\alpha ={\mathrm{RBE}}_{\alpha }^{\mathrm{MKM}}\cdot {\alpha }_0$ as a function of the LET (or kinetic energy) and ion type, while β is assumed to be constant. The RBE(D) is obtained by setting α_x = α₀ and β_x = β in equation (1).

2.1.8. The track structure model

The track structure model considers the halo around a proton track that is generated by emitted delta electrons. The model considers the sensitive site of a cell to consist of subtargets (Butts and Katz 1967). The biological effect depends on the overlap of the delta-electron extended track with the target (Butts and Katz 1967, Katz et al 1971, Katz and Sharma 1973, 1974). The biological endpoint is characterized by four radiosensitivity parameters m, E₀, σ₀ and κ (Katz and Sharma 1973, Katz et al 1972, Roth et al 1976, Waligorski 1994) and two modes of cell killing. The saturation value of the action cross-section of the cell nucleus, σ₀, describes the cell nucleus response. The γ-ray dose-response curve is parameterized by the multi-target equation with the parameter E₀ and m to account for the sub-target concept. The sensitive target radius is characterized by a dimensionless variable κ. For a disc-shaped target κ is proportional to the intrinsic radiosensitivity, E₀, times the square of the sub-target radius. The biological response (e.g. the survival fraction S) is calculated from the radiosensitivity parameters, the effective charge Z*, the relative velocity β and the fluence F (Katz et al 1971, Katz et al 1976, Katz and Sharma 1973):

$$\sigma ={\sigma }_0{\left[1-\exp \left(-\frac{Z^{\ast 2}}{\kappa {\beta }^2}\right)\right]}^m,D_{\gamma }=\left(1-{\left[1-\exp \left(-\frac{Z^{\ast 2}}{\kappa {\beta }^2}\right)\right]}^m\right)D,$$ (10)

$$S=\left(1-{\left[1-\exp \left(-\frac{D_{\gamma }}{E_0}\right)\right]}^m\right)\exp (-\sigma F),D_x=-E_0\ln {[1-(1-S)]}^{1∕m}.$$ (11)

2.2. TOPAS

The TOPAS architecture has been described previously in detail (Perl et al 2012). We used TOPAS version beta12, which is layered on top of Geant4.9.6p02.

While text based parameter files can control all features that are provided by TOPAS, a mechanism for advanced users to expand the functionality of TOPAS has been developed. The extension manager (TsExtensionManager) in TOPAS includes options for advanced users to add their own code. The extension manager provides full access to most base classes and can be used to create specialized scorers, geometries, filters, organ effect models and “physics lists” (Geant4 code classes that define what set of physics processes and models should be used for a given simulation).

A scorer is a function called by the user to record a specific simulation property, e.g. a histogram showing the dose in a certain area. The default physics lists and settings as described in detail elsewhere (Perl et al 2012, Testa et al 2013) were used for all simulations.

2.3. Example calculations and comparison to experimental data

Predicted RBE values for clonogenic cell survival of V79 Hamster cells using the models described above and implemented in TOPAS were compared to experimental data taken from Wouters et al (Wouters et al 2014). The strength of this particular data set is that it has not been used for extracting the fit parameters for this cell line. The experiments were carried out at MGH using a cell sorter assay similar to the ones used previously by the same group of investigators (Wouters et al 1996). To simulate the experimental conditions, a spread-out Bragg peak (SOBP) with a beam energy of 160 MeV, a modulation width of 10 cm and a range of 16.1 cm was simulated using TOPAS. The physics input parameters (e.g. LET_d) were simulated and used as input for the models. The scoring of all quantities (e.g. LET, dose) was performed in 200 bins of 0.1 cm in a cylindrical volume of 2 cm radius and 10 cm length placed in a water phantom with size 10 cm × 10 cm × 10 cm. The biological input parameters were defined in a parameter file as described above.

2.4. Example calculations using a patient specific treatment plan

A pediatric head and neck patient was randomly selected from the MGH clinical patient database to demonstrate the Monte Carlo RBE calculation. The patient is a pediatric medulloblastoma patient treated with a posterior fossa boost. The MGH double scattering treatment head has been implemented in TOPAS previously (Paganetti et al 2004, Testa et al 2013). At the MGH a script is used that links the treatment planning system to TOPAS. It creates TOPAS input parameter files based on the patient CT, isocenter position, prescribed fields and doses from the planning system. Subsequently, separate scripts process the submission of simulations on a computing cluster, add the resulting dose, LET and RBE files and produce a complete patient dose distribution in CERR (Deasy et al 2003) or alternatively, in DICOM format.

The simulations are performed in three automated steps. First, an SOBP dose distribution in a water phantom is simulated to determine the dose delivered per proton at the treatment head entrance. Second, protons are transported through the treatment head geometry to generate a phase space file downstream of the patient-specific hardware. Third, protons from the phase space are transported through the patient geometry.

For this work, all simulations were performed on the ‘Partners Research Computing’ cluster with 30 parallel simulations per patient field, each with 250,000 protons starting at the entrance of the treatment head. Variance reduction techniques were employed increasing the statistical accuracy by a factor of 64 (Ramos-Mendez et al 2013).

2.5. Combining calculations of dose-averaged LET and biophysical parameters

Values of RBE or biological dose cannot simply be added when more than one simulation is performed independently, e.g. when considering patient treatments with multiple fields. The reason lies in the dose dependency of the RBE. There are two methods to add multiple simulations.

First, for those models that are based on LET_d, LET_d values can be added in a dose-weighted fashion for each region of interest (e.g. a voxel in a patient) and the RBE can be calculated subsequently.

Second, a more general approach, which works independent of the model, is to score α and β values during the simulations instead of RBE directly. Subsequently, a dose-weighted sum to obtain the total α and β values can be applied which considers each α_k and β_k per region of interest (voxel) k and potentially separate Monte Carlo runs i according to equations (12) and (13):

$${\alpha }_{\mathrm{k}}=\frac{\sum _{\mathrm{i}}^{\mathrm{runs}}{\alpha }_{\mathrm{i},\mathrm{k}}{D}_{\mathrm{i},\mathrm{k}}}{\sum _{\mathrm{i}}^{\mathrm{runs}}{D}_{\mathrm{i},\mathrm{k}}},$$ (12)

$${\beta }_{\mathrm{k}}={\left(\frac{\sum _{\mathrm{i}}^{\mathrm{runs}}\sqrt{{\beta }_{\mathrm{i},\mathrm{k}}}{D}_{\mathrm{i},\mathrm{k}}}{\sum _{\mathrm{i}}^{\mathrm{runs}}{D}_{\mathrm{i},\mathrm{k}}}\right)}^2.$$ (13)

Multiple fields were used in the patient simulation and α and β were calculated for all fields using equations (12) and (13). In the current preliminary implementation, this summation has to be performed outside of the TOPAS environment.

3. Results

3.1. Implementation of biological scorers in TOPAS

The RBE scorers were at first implemented relying entirely on the extension manager from an earlier TOPAS version, which presented an interesting test case to assess how much flexibility users have in designing their own scorers. Several features were then added to the TOPAS base scoring class to make the extension to RBE calculations easier. Scorers are now allowed to initialize so-called sub-scorers. These sub-scorers are identical to individual scorer instances with the exception that the primary scorer instantiates the sub-scorers and can read and manipulate their scoring map. This facilitates, for example, calculation of RBE values from the α and β sub-scorers. In this case, the α sub-scorers (depending on the model) can initiate an LET_d sub-scorer, which in turn needs to initiate a sub-scorer for the energy deposition. Sub-scorers are evaluated recursively thereby enforcing consistent handling of multiple-layers of sub-scorers.

In order to further incorporate RBE modeling directly into TOPAS, we migrated the RBE scorers into the general TOPAS framework. A virtual RBE scorer has been developed. The virtual RBE scorer inherits the virtual scorer class of TOPAS, thereby guaranteeing full compatibility with the TOPAS framework. The virtual RBE scorer includes basic functionality common to all RBE scorers.

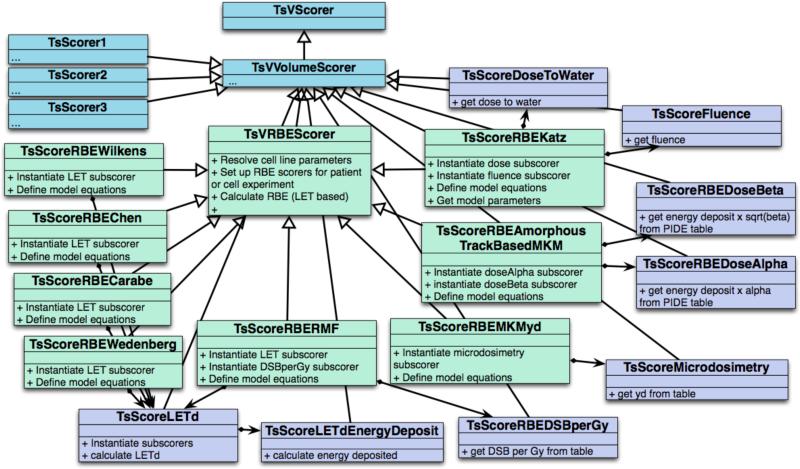
Figure 2 shows the class diagram for the biology related scoring part of TOPAS indicating some of the functions available in the virtual class. The biological scorers implemented in TOPAS allow scoring of RBE, biological dose, survival fraction and the radiosensitivity parameters α and β for the models based on the LQ equation. All biological scorers include a sub-scorer of the physical dose (to water) as this is required to determine the biological dose. When calculating RBE values for radiobiological experiments, the RBE values are calculated for a user-defined dose prescribed to the cell culture. For patient calculations the user has two options. A user can define a prescribed dose and the corresponding structure, for example the tumor volume, to normalize the dose distribution and calculate RBE considering doses relative to the dose in the target volume for each voxel. Structures, such as the target volume, in TOPAS can be defined via DICOMRT structure sets or via a user defined structure map. Alternatively, if no structures are defined, the maximum dose can be used for normalization to the prescribed dose.

Figure 2.

Scoring scheme to include biological modeling in TOPAS.

3.2. Model dependent scorers

3.2.1. Models based on LET

The scorer for the LET_d is obtained as the energy loss dE of a particle multiplied by the energy loss per particle step dx divided by the density ρ summed over all events relative to the total energy deposited as shown in equation (14) (Grassberger and Paganetti 2011):

$${\mathrm{LET}}_{\mathrm{d}}=\frac{{\sum }_{events}dE(dE∕dx)1∕\rho }{{\sum }_{events}dE}.$$ (14)

All primary and secondary protons and secondary electrons are taken into account. Here, the energy of secondary electrons is deposited at the position of their creation. The LET_d scorer is called as a sub-scorer by the biological scorer. A loop over the resulting LET_d map is performed in the CombineSubScorers function at the end of the simulation and the biological parameters are determined for each entry in the event map. The functions listed in section 2.1 are applied to convert the dose and LET_d maps into RBE.

3.2.2. The RMF model

For this model TOPAS uses a look-up table and linear interpolation to estimate number of DSB Gy⁻¹ Gbp⁻¹ (Σ in the RMF model) for monoenergetic protons and then computes the ratio of the yield of DSB for a proton of kinetic energy E_kin divided by the yield of DSB for the reference radiation, i.e., the RBE_DSB parameter in equations (6) and (7). After all particle histories are executed, the LET_d and the dose-averaged RBE_DSB are inserted into equation (7) to compute α and β for use in equation (1). This approximation assumes a linear relationship between RBE_DSB and LET_d, which is valid for clinically relevant proton energies.

TOPAS also has the ability to output spatial maps of the RBE for reproductive cell death (equation (1)) and the RBE for DSB induction (RBE_DSB). Note that, although the current implementation of the RMF suffices for lower LET protons (LET < 10-15 keV/μm), the approach used by Frese et al (Frese et al 2012) provides a more accurate accounting on the non-linear relationship between proton LET and changes in α.

3.2.3. The MKM

Microdosimetric quantities for protons are computed in TOPAS by means of a mathematical function to model the probability distribution of lineal energy events as described elsewhere (Sato et al 2006). The distribution depends on the kinetic energy of the proton at a given step and the size of the virtually traversed volume. In this way, microdosimetric quantities can be computed without making use of the track structure, which is computationally inefficient. The scorer for the MKM implementation calls the microdosimetric sub-scorer to get the map of the ${\stackrel{‒}{y}}_D$ distribution for protons with kinetic energy down to 1 MeV. A loop over all entries in the map is performed in the CombineSubScorer function and the biological parameters are calculated.

3.2.4. The amorphous track based MKM

The output of the fitting procedure is used to extrapolate the α values, which are tabulated in a TOPAS parameter file in terms of particle type and energy per nucleon. Whenever energy is deposited by a certain radiation type in the scoring region, a characterization of the charged particle traversal (charge, mass, and energy per nucleon) is performed which allows TOPAS to interpolate the correct α value from the table.

The amorphous track based MKM scorer initiates an α sub-scorer and the is calculated in the CombineSubScorer routine.

3.2.5. The track structure model

The kinetic energy E_kin of the protons is scored in each step of the Monte Carlo simulation. The relative velocity of a proton is calculated by

$$\beta =\sqrt{1-{\left(\frac{E_0}{E_0+E_{\mathrm{kin}}}\right)}^2}.$$ (15)

The rest energy E₀ of protons is 938.272 MeV. The effective charge Z* is obtained from the atomic number Z of the particle via

$$Z^{\ast }=Z\left(1-\exp \left(-125\beta Z^{-2∕3}\right)\right).$$ (16)

The activation cross-section σ is calculated through equation (9) and scaled from subcellular to cellular response by an empirical factor ${\sigma }_0∕\left(1.4\pi a_0^2\right)$ using the following relation between κ and a₀ (Katz and Sharma 1973):

$$\kappa =\frac{E_0{a}_0^2}{2\cdot {10}^{-11}\mathrm{Gy}{\mathrm{cm}}^2}.$$ (17)

The γ-kill dose D_γ is calculated from the scored dose for each event in the map. The TOPAS fluence scorer is instantiated as a sub-scorer. The survival fraction is then determined in the CombineSubScorers function using equation (10). The isoeffective x-ray dose D_x can be determined from the survival fraction. Relating D_x to the proton dose in CombineSubScorers gives the RBE.

3.3. Parameter files for biological scoring

We designed the biological modeling in TOPAS to use the same parameter file for multiple models and if applicable the same parameter definition. All cell line (or end point) dependent parameters of the biophysical models are defined in a parameter text file we call “cell line file”. It is not required to specify parameters for all models in this file. In this work, as an example, a file for V79 Hamster lung fibroblasts was defined. The radiosensitivity parameters α_x and β_x were obtained from the experimental cell survival curve of V79 cells after ⁶⁰Co irradiation using non-linear least squares regression (Wouters et al 2014), giving α_x = 0.072 Gy⁻¹ and β_x = 0.050 Gy⁻². The parameters for the models that are based on the LET are given in the literature (Carabe et al 2012, Chen and Ahmad 2012, Wedenberg et al 2013, Wilkens and Oelfke 2004). The yield in energy dependent DSBs per Gray and cell that is required in the RMF model has been determined in Monte Carlo Damage Simulations for a nuclear diameter of 5 μm. A look-up table of the DSBs depending on the kinetic energy of the protons is included in the cell line file. The values of the radiosensitivity parameters for the track structure model were defined according to Cucinotta et al (Cucinotta et al 1995): m = 3, E₀ = 1.82 Gy, σ₀ = 4.28 × 10⁻⁷ cm² and κ = 612. The parameters r_d and α₀ of the MKM are taken from Hawkins (Hawkins 1996). A value of zero for α₀ and a domain diameter of 0.69 μm were used. For the amorphous track based MKM, the PIDE database was applied to generate look-up tables containing α and β values depending on the kinetic energy.

The concept of a cell line file allows a user to write cell line rather than model dependent input. TOPAS parameter files for different cell lines can be shared amongst users. The general user input file includes the cell line file and defines the parameters for the scoring, such as the model that is used, the scoring volume, the binning and the cell line, each definition typically taking one simple line in the input file. As output parameters, the RBE, the biological dose, the survival fraction or the radiosensitivity parameters α and β can be chosen.

3.4. Comparison to experimental data

To illustrate the TOPAS framework for RBE calculations, the predictions of the LET based models are shown in figure 3. Accordingly, figure 4 shows the predictions of the RMF model, the MKM, the amorphous track based MKM and the track structure model. For comparison, figures 3 and 4 also show experimental data from Wouters et al (Wouters et al 2014).

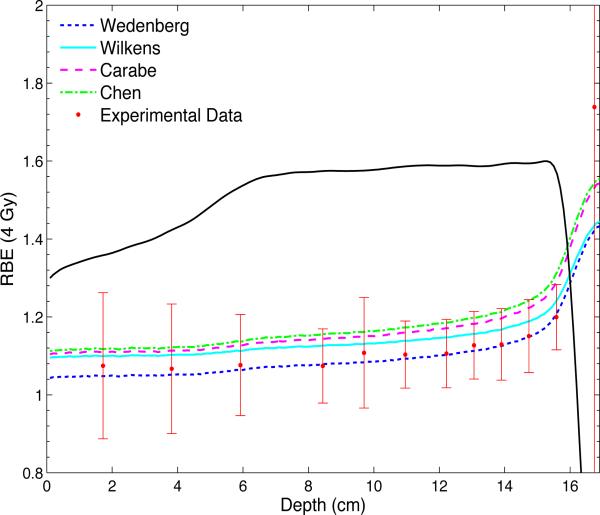
Figure 3.

The predicted RBE values for a dose of 4 Gy according to the models by Wedenberg et al, Wilkens and Oelfke, Carabe et al, and Chen and Ahmad are shown together with the experimental data for clonogenic cell survival of V79 cells. The SOBP is generated with a beam energy of 160 MeV and has a modulation width of 10 cm and a range of 16.1 cm. The dose profile is plotted in arbitrary units.

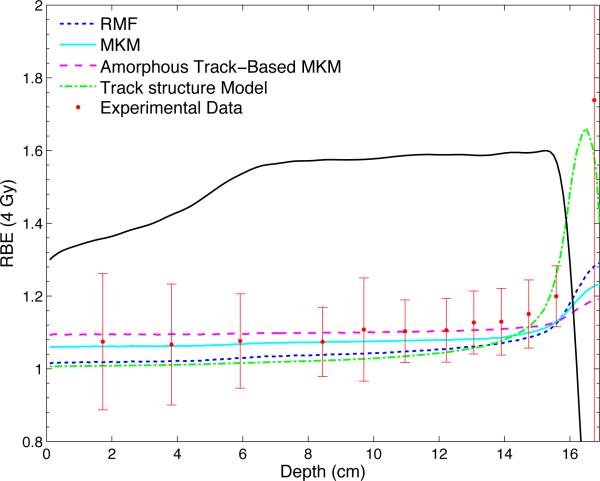
Figure 4.

The predicted RBE values for a dose of 4 Gy according to the RMF model, the MKM, the amorphous track based MKM and the track structure model are shown together with the experimental data from Wouters et al. The SOBP is generated with a beam energy of 160 MeV and has a modulation width of 10 cm and a range of 16.1 cm. The dose profile is plotted in arbitrary units.

All models predict a relatively stable value for the RBE proximal to the SOBP and a steep increase beginning in the distal part of the SOBP. Except for the amorphous track based MKM, there is a modest increase in RBE throughout the proximal and central plateau of the SOBP. With the parameters implemented in the current V79 cell line file, the model by Wedenberg et al reproduces the experimental data best. A reasonable agreement is also achieved by the MKM. The models by Wilkens and Oelfke, Carabe et al and Chen and Ahmad estimate RBE values that are higher than the experimental mean but give predictions within one standard deviation for the majority of the measurement points. The RMF predicts lower RBE values than the models by Wedenberg et al, Wilkens and Oelfke, Carabe et al, Chen and Ahmad and the MKM. However, the estimated values for the RBE are well within error bars for all data points. The track structure model gives RBE estimations even lower than the RMF model upstream of the SOBP as well as throughout the proximal and central part of the SOBP. The predicted slope of the curve in the distal part of the SOBP and at the distal edge is significantly steeper than predicted by all other models. The amorphous track based MKM produces the smallest rise in RBE throughout the SOBP.

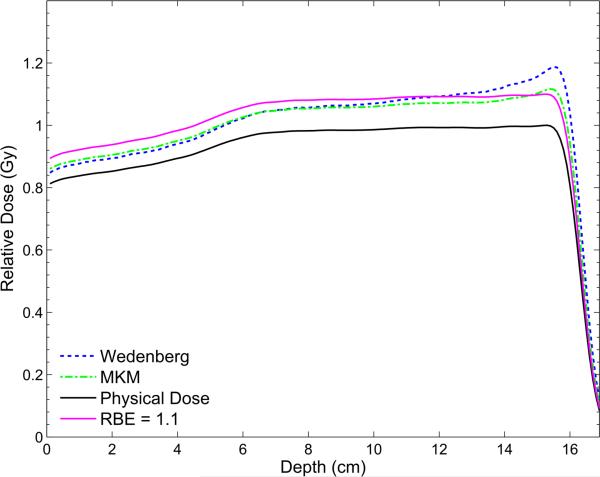
Proton therapy treatment planning assumes a generic constant RBE of 1.1 (Paganetti 2014). To demonstrate the potential behavior of the RBE as a function of depth in an SOBP, figure 5 shows the prediction of two of the models, i.e. the simulated biological dose according to the model by Wedenberg et al and the MKM are shown in figure 5. Resembling the typically used fractionation of 2 Gy, the biological dose calculated as the RBE_{2 Gy} weighted physical dose is shown together with the physical dose and the biological dose for a constant RBE of 1.1, as used as current clinical practice. The scored biological dose is lower than the biological dose with the constant RBE at the beam entrance and the proximal part of the SOBP, approximately equal in the center of the SOBP and exhibits a peak close to the distal fall-off of the SOBP. However, the results are for V79 cells a low α/β and are not necessarily applicable to clinically relevant tissues. It has been shown though that averaged over all cell lines that have been experimentally studied in vitro, the proton RBE for clonogenic cell survival increases with increasing LET_d and thus with depth in an SOBP from ~1.1 in the entrance region, to ~1.15 in the center, ~1.3 at the distal edge and ~1.65 in the distal fall-off (Paganetti 2014).

Figure 5.

The biological doses calculated with the model by Wedenberg et al and the MKM implemented into TOPAS for a dose of 2 Gy are shown together with the biological dose for a constant RBE of 1.1 and the physical dose. The SOBP is generated with a beam energy of 160 MeV and has a modulation width of 10 cm and a range of 16.1 cm. The doses are plotted relative to the maximum physical dose.

The results are meant to demonstrate the use of biological models in TOPAS rather than provide a detailed comparison of the models and its interpretation.

3.5. Patient case simulation

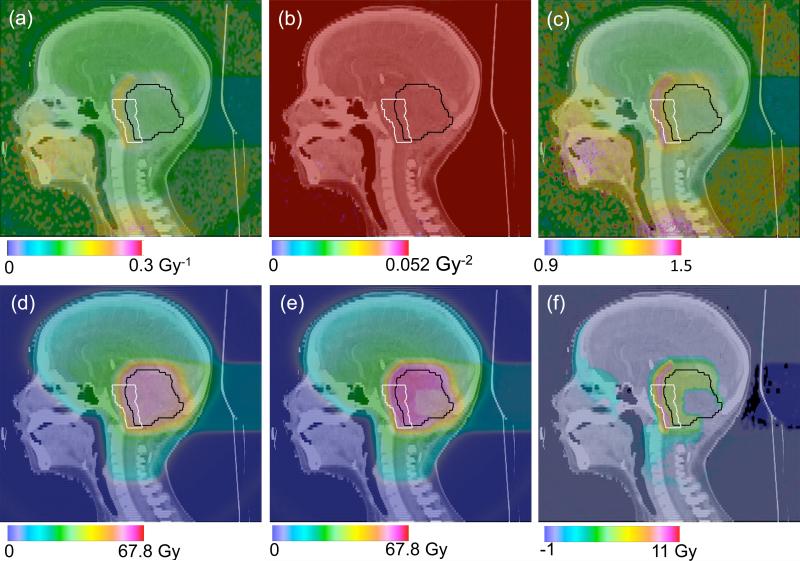
The biological scorers were implemented and tested on a pediatric head and neck proton treatment plan. For the patient study, the model by Wedenberg et al was used as example. The total RBE for each voxel k is calculated from equations (11) and (12) using α_k and β_k with α_x = 0.0722 Gy, β_x = 0.0502 Gy and (α/β)_x = 1.412 Gy. These values are not representative for clinically relevant tissues but are applied to demonstrate the use of identical parameter files for either simulating experimental data (section 3.4) or RBE distributions in patients. The top panel of figure 6 shows the simulated values for both α (a) and β (b) as well as the corresponding calculated RBE value (c) in the patient combining all treatment fields for the total prescribed dose of 1.8 Gy per fraction. The bottom panel of figure 6 shows the simulated biological dose assuming a constant RBE of 1.1 as used clinically (d), the biological dose when using a variable RBE (e) and the dose difference between simulations using the generic and the variable RBE (f). The α values are relatively constant throughout the targeted tumor region (pink contour) with a value of ~0.12 Gy⁻¹. However, in the region just outside the target volume, the brain stem (green contour), the α values increase to ~0.18 Gy⁻¹. In the model by Wedenberg et al β is constant. The RBE map thus shows higher values in the sensitive brain stem region (~1.4) compared with the targeted region (~1.2). Note that figure 6 is shown to demonstrate the potential of TOPAS for biological treatment planning and that the biological input parameters used here are not necessarily representative for the relevant tissues.

Figure 6.

Patient case simulation study of a pediatric head and neck proton treatment. The model by Wedenberg et al was used to score the values for α (a) and β (b) as well as the corresponding RBE value (c). The resulting biological dose with a constant RBE = 1.1 (d) is shown together with the biological dose when using the model (e). (f) shows the dose difference between (d) and (e).

4. Discussion

TOPAS, a Monte Carlo simulation framework for proton therapy was extended towards the simulation of relative biological effects. Eight biophysical models for the prediction of the RBE were implemented. This was achieved by developing scorers tailored to the input parameters of these models. Furthermore, a parameter file structure was developed that allows the specification of input parameters for various models in a single cell line (or endpoint) specific file. TOPAS provides a unique tool to compare Monte Carlo based model predictions and investigate the dependence of a variety of models on biological parameters. New models can be added to TOPAS via the extension manager. We anticipate that the biological scoring in TOPAS will help researchers to improve and validate the predictive power of RBE models.

To demonstrate the functionality of the framework, two examples were presented, i.e. a comparison of model results with experimental data and the simulation of biological quantities, e.g. RBE distributions, in a patient. The simulations show an increase in RBE throughout an SOBP and the differences between the various models when predicting the magnitude of the RBE increase in the distal region of the SOBP.

Our example uses a cell line file for V79 cells. We anticipate that experts for each model may contribute their data to further cell line parameter files that can be shared by all TOPAS users, eventually providing a large database of cell line specific parameter files.

The TOPAS framework for biophysical modeling still has weaknesses that will be addressed in future releases of the code. For instance, TOPAS simulates biological parameters in a single Monte Carlo run, i.e. dose, LET_d or α and β distributions. Some of these parameters cannot be simply added. For example, LET_d values for each voxel need to be added in a dose-averaged manner. Consequently, when running multiple TOPAS simulations in parallel on a computing cluster or when combining multiple treatment fields for patient, post-processing of the results is currently required.