Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jul 22.
Published in final edited form as: Phys Med Biol. 2012 Nov 29;57(24):8217–8229. doi: 10.1088/0031-9155/57/24/8217

Dual-Dictionary Learning-Based Iterative Image Reconstruction for Spectral Computed Tomography Application

Bo Zhao 1, Huanjun Ding 1, Yang Lu 2, Ge Wang 3, Jun Zhao 2, Sabee Molloi 1
PMCID: PMC4511115  NIHMSID: NIHMS426171  PMID: 23192234

Abstract

In this study, we investigated the effectiveness of a novel Iterative Reconstruction (IR) method coupled with Dual-Dictionary Learning (DDL) for image reconstruction in a dedicated breast Computed Tomography (CT) system based on a Cadmium-Zinc-Telluride (CZT) photon-counting detector and compared it to the Filtered-Back-Projection (FBP) method with the ultimate goal of reducing the number of projections necessary for reconstruction without sacrificing image quality. Postmortem breast samples were scanned in a fan-beam CT system and were reconstructed from 100–600 projections with both IR and FBP methods. The Contrast-to-Noise Ratio (CNR) between the glandular and adipose tissues of the postmortem breast samples was calculated to compare the quality of images reconstructed from IR and FBP. The spatial resolution of the two reconstruction techniques was evaluated using Aluminum (Al) wires with diameters of 643, 813, 1020, 1290 and 1630 µm in a plastic epoxy resin phantom with diameter of 13 cm. Both the spatial resolution and the CNR were improved with IR compared to FBP for the images reconstructed from the same number of projections. In comparison with FBP reconstruction, the CNR was improved from 3.4 to 7.5 by using the IR method with 6-fold fewer projections while maintaining the same spatial resolution. The study demonstrated that the IR method coupled with DDL could significantly reduce the required number of projections for a CT reconstruction compared to FBP method while achieving a much better CNR and maintaining the same spatial resolution. From this, the radiation dose and scanning time can potentially be reduced by a factor of approximately 6 by using this IR method for image reconstruction in a CZT-based breast CT system.

Keywords: Iterative reconstruction, Dual-dictionary learning, Contrast-to-noise ratio, Spatial resolution, Spectral breast computed tomography

1. Introduction

The recent interest in the applications of energy discriminating photon-counting detectors, such as CZT, in spectral CT systems (Bert et al., 2003; Chmeissani et al., 2004; Bisogni et al., 2007; Shikhaliev, 2008; Wang et al., 2010; Taguchi et al., 2009; Barber et al., 2009; Shikhaliev and Fritz, 2011; Le et al., 2010) has provided a new means to produce higher quality images compared to current breast CT systems based on charge-integrating CsI scintillation flat panel detectors. CZT has several advantages over traditional detectors, such as high quantum detection efficiency as a result of its large effective atomic number (49.6), high mass density (5.8 g/cm3) and excellent energy resolution. It has been investigated and implemented as an x-ray detector due to recent advances in the manufacturing of Application Specific Integrated Circuits (ASIC). However, CZT detectors suffer from issues such as pulse pileup from high-count rate x-ray sources. Limited by the current counting capability of a CZT detector, a CT scan usually takes a long time to produce high quality images (Schlomka et al., 2008). For current CT reconstruction, FBP method is widely used because it is computationally fast, accurate and easily implemented (Herman, 1980; Kak and Slaney, 1988). However, a large number of projections, typically 500 or more, are needed for the FBP method to reconstruct CT images because projections must be discretized at a high sampling rate for the image quality to be satisfactory. To shorten scanning time, and also reduce the radiation dose, the number of projections can be reduced. The downside to this, however, is degradation in image quality of the reconstruction using the FBP method, leading to high noise and streak artifacts (Xu et al., 2011). Therefore, new image reconstruction algorithms are desirable to reduce the number of required projections while retaining image quality. For this purpose, several algorithms have been developed, such as Algebraic Reconstruction Techniques (ART) in 1970 (Gordon et al., 1970) and Simultaneous Algebraic Reconstruction Techniques (SART) in 1984 (Anderson and Kak, 1984), which assume that a set of projections through the object are modeled by a linear system of equations based on the discretization of the Radon transform which is then solved iteratively. Although these techniques have long been developed, they are computationally demanding and have been overlooked due to their performance requirements. With the dramatic development of high-performance computing techniques over past decades, these prior unfeasible methods have been rediscovered (Elbakri and Fessler, 2002; Bian et al., 2012; Casteele et al., 2012; Hernandez et al., 2012; Makeeva et al., 2012; Pachon et al., 2012) and applied to the image reconstruction of low-dose CT. In these techniques, one of the mechanisms is the total variation (TV) minimization, which minimizes the TV of the estimated images with the assumption that the image gradient is sparse. It can be used for low-dose, few-view, limited-angle, and truncated data CT (Donoho, 2006; Sidky et al., 2006; Yu and Wang, 2009). However, it may lead to undesirable biases and artifacts as well as loss of fine features, which may reduce the diagnostic values of reconstructed images. In contrast to TV, another algorithm is the use of the redundant dictionaries tailored specifically to a particular application and more effective in terms of a sparse representation (Xu et al., 2011). Dictionary learning (DL) and Sparse Representation (SR) techniques have been successfully applied to image processing and recognition areas, such as image denoising, image restoration, face recognition, and texture classification (Elad and Aharon, 2006; Mairal et al., 2006). Unlike conventional techniques, which process the image in pixel by pixel, the dictionary-based methods process the image patch by patch. Thus, strong structural constraints are naturally and adaptively imposed.

DL and SR techniques were further developed on few-view image reconstruction in recent studies (Xu et al., 2011; Yu and Wang, 2010, 2012), where a global or adaptive dictionary derived from the K-Singular Value Decomposition (K-SVD) algorithm (Elad and Aharon, 2006) was employed in the whole processing and the DL step was incorporated in the iterative reconstruction procedure to update an intermediate image. Motivated by the success of a single-dictionary method, two dictionaries are applied to improve the image quality further. One dictionary is extracted from a set of low-quality sample images reconstructed from few-view projections, while another dictionary is extracted from a set of high-quality sample images reconstructed from full-view projections. The dictionaries are connected by a transform operator. If the coefficients of a low-quality image patch are found under the transitional dictionary and multiplied by the global dictionary to recover the high-quality image patch, the image quality is improved when all the low-quality patches in a few-view reconstructed image are replaced by the high-quality patches (Lu et al., 2012).

We study the effectiveness of a novel IR method based on the DDL technique for the image reconstruction of a spectral breast CT using a CZT photon-counting detector and the feasibility of reducing the scanning time and the radiation dose for future Multi-Slit Multi-Slice (MSMS) breast CT systems by reducing the number of required projections. In section II, we introduce the DDL technique and briefly describe the experiment using the dedicated breast CT system based on a CZT photon-counting detector in our lab. In section III, we report our results by comparing the spatial resolution and the CNR of the images reconstructed from FBP method and this novel IR method. In section IV, we discuss relevant issues and the possible application of the IR method in future MSMS breast CT systems.

2. Methods and experiments

2.1. IR method based on DDL technique

In this study, a novel iterative algorithm consisting of ART and DDL was applied to improve the image quality (Xu et al., 2011; Lu et al., 2012). In this algorithm, a whole image is disintegrated into many small patches. These patches are partially overlapped. The distance between two adjacent patches describes the degree of overlapping. The pixel values in a patch, as well as its first and second gradients, are written as a single vector and stored in a large matrix as one column called a dictionary. The dictionary can be built from high-quality or low-quality sample images, called high-quality dictionary Dh or low-quality dictionary Dl, respectively. DDL makes full use of the information of both Dh and Dl so that the targeted low-quality image could be well approximated by Dl at first and then updated by Dh.

With the use of DDL, our problem is mathematically expressed as

minx,aj{‖Mx−y‖22+∑j‖Dnaj−Rjx‖22},n=l,hsubject to‖aj‖0≤ρ∀j,x≥0 (1)

Where M is the system matrix, Dn is Dl or Dh, Rj is an operator extracting the jth patch from image x, and ρ is the maximum number of non-zero elements in vector aj. The first term in the cost function aims at minimizing the difference between the forward projections Mx and the true projections y. A variety of iterative algorithms such as ART, SART and Expectation Maximization Maximum Likelihood (EMML) can be used to solve this problem. The second term in the cost function represents DDL. It contains two sub-problems for Dl and Dh, respectively:

minaj∑j‖Dlaj−Rjx‖22subject to‖aj‖0≤ρ∀j (2)
minx∑j‖Dhaj−Rjx‖22 (3)

In equation (2), image x is fixed, and we want to find a sparse representation aj with respect to the lowquality dictionary Dl. ρ = 1 means finding an atom in Dl, which has the shortest Euclidean distance to the patch Rjx. In equation (3), sparse representation aj is fixed and each patch Rjx corresponds to its new version Dhaj. Then the whole image is updated as x=(∑jRjTRj)−1∑jRjTDhaj.

In order to construct the dual dictionaries, we need two sets of sample images. Sample images in the high-quality set are reconstructed from adequate projections. Ideally, they are noise-free and artifacts-free. In the other set, i.e. low-quality set, the sample images are reconstructed from down-sampled projections. Usually they are noisy and contain a lot of artifacts. The degree of down-sampling depends on the targeted image. For example, if the targeted image is reconstructed from only 200 projections, the sample images in low-quality set should be also reconstructed from around 200 projections. However, this rule is flexible. As an empirical experience, low-quality set reconstructed from 300 projections works for most cases. Images in these two sets are in one-to-one correspondence. When building the dual dictionaries, we do the same operations on a pair of images. That is, patches are extracted from the same positions of one high-quality sample image and its corresponding low-quality sample image, and then recorded at the same columns of dual dictionaries.

2.2. Breast CT with CZT photon-counting detector

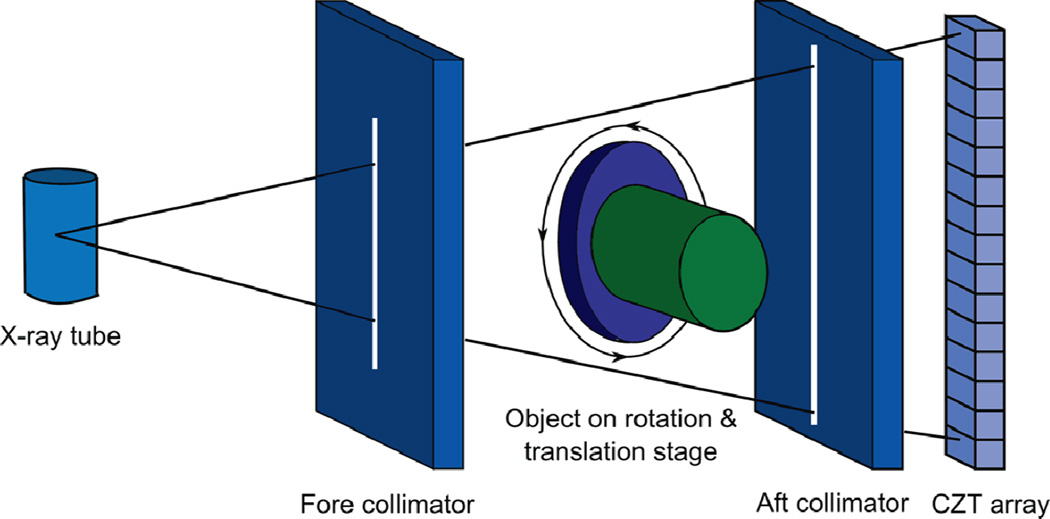
The breast CT system used in this study is shown in figure 1, composed of an x-ray tube, fore and aft collimators, rotation and translation stage platforms and CZT detector (Ding and Molloi, 2012). A tungsten target x-ray tube (Dynamax 78E) is coupled to a constant potential x-ray generator (Phillips Optimus M200) with the pre-filter of 2 mm Al and 0.15 mm Cu. The fore and aft collimators made of 3 mm thick lead sheets are used to minimize x-ray scatter, and the slit widths are 0.3 and 0.8 mm, respectively. A high precision Direct Drive Rotary (DDR) motor (Kollmorgen Goldline DDR D062M, Danaher Motion, Wood Dale, IL) served as the rotation platform for the sample. It was mounted on a translation stage, which provides both vertical and horizontal translations to extend the field of view beyond the size limitation of the detector. The distance between the source and isocenter is approximately 0.93 m.

Figure 1.

Figure 1

Open in a new tab

Schematic drawing of the spectral CT system based on CZT photon-counting detector.

The CZT photon-counting detector (eV2500, eV Microelectronics Inc., Saxonburg, PA) is placed 1.35 m from the x-ray tube and consists of a linear row of four CZT crystals with 12.8 mm length, 3 mm width and 3 mm thick. Each crystal consists of 16 pixels, yielding a total of 64 pixels with an effective pitch of 0.8 mm in each pixel. The entrance beam to the detector is shaped by a brass collimator and collimated at the height of each pixel to 0.8 mm (Ding and Molloi, 2012). The peaking time of the detector is set at 160 ns. A Field Programmable Gate Array chip (FPGA) is used to count the trigger pulses generated by five comparators from each pixel over a user defined collection period, selectable from 1 ms to 50 ms, which sends each frame to the workstation over a USB interface for data processing, storage and visualization (Szeles et al., 2008; Prokesch et al., 2010). The acquired photons are sorted into five user-definable energy bins with the energy resolving capability of the detector. The energy resolution is calibrated up to 140 keV by the manufacturer of the detector (Endicott Interconnect Detection & Imaging Systems). The maximum count rate of the detector is calibrated to be approximately 2.3 × 106 cps/mm2, but the linear count rate range derived from a thickness dependent study is less than 1.2 × 106 cps/mm2. The detector itself does not have any pulse pileup and charge sharing correction mechanisms (Ding and Molloi, 2012). The CZT data was acquired in fluoroscopic mode because of the low tube output required by the photon-counting detector.

A bias voltage of 1000 V is placed across the CZT crystal and the detector is operated in Ohmic mode. As a photon interacts with the CZT crystal and transfers energy above 4.64 eV to the crystal, an electron hole pair is created. Electrons generated from interaction of x-ray photons within the crystal are collected at the back electrode, which then form a pulse whose height is proportional to the energy of the incoming photon by the ASIC. A count is registered if the pulse height was higher than the given threshold value. The lower boundaries of the energy bins are defined by five user-definable thresholds, therefore the count within an energy bin can be easily obtained by subtracting the count from its two adjacent thresholds. The detector can also be used in the spectrum collection mode where two thresholds can be simultaneously scanned over the whole energy range. The count difference between the two thresholds provides the number of recorded counts as a function of energy (Ding and Molloi, 2012).

2.3. Phantom and postmortem breast samples preparation

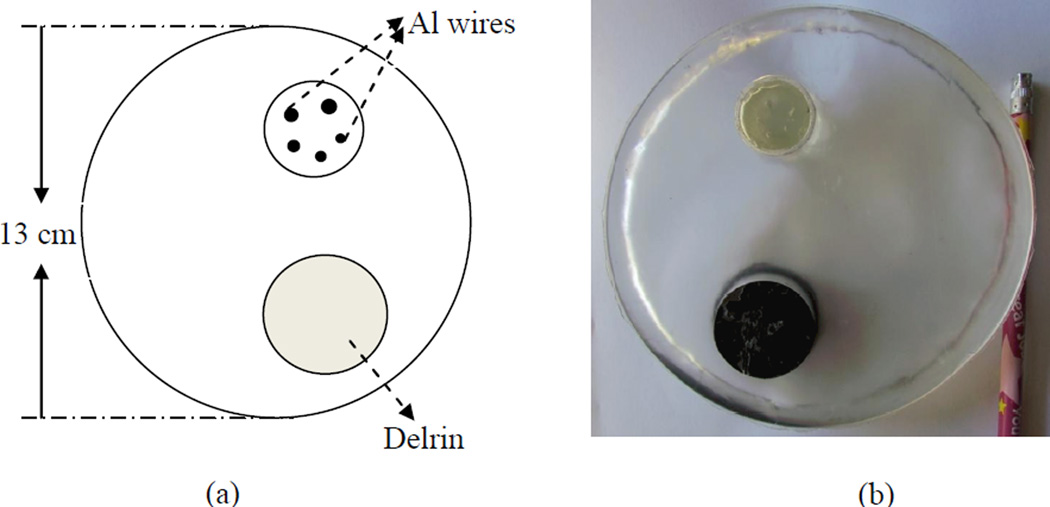
Figure 2(a) illustrates the construction of the high resolution phantom used in this study, which is motivated by a previous study (Shen et al., 2010). A cylinder with 13 cm in diameter and 2 cm in length is constructed of resin as the phantom base and an insert with 5 fine Al wires of various diameters (643, 813, 1020, 1290 and 1630 µm in diameter) is placed in this base. The resin is chosen not only for its similar x-ray attenuation to breast tissue (0.2076 cm2/g for resin and 0.2186 cm2/g for breast tissue at 50 keV) (Hubbell and Seltzer, 1995), but also for its low cost and convenience in fabricating the phantom base and inserting Al wires. The Al wires in this insert are orientated vertically, and the profiles extracted from reconstructed CT images are proposed to study spatial resolution. These wires are arranged with enough space between each of them to minimize interacted artifacts in the image reconstruction. Figure 2(b) shows a photo of this high-resolution phantom and Al wires inside. Postmortem breast samples were obtained from Willed Body Program in School of Medicine at University of California Irvine, sealed in plastic bags. 6 samples were selected for this study with the mass varying from 114 to 924 gram and the breast density varying from 21% to 72%. These samples were placed in a cylindrical container approximately 10 cm in diameter made of high-density polyethylene plastic during the image acquisition.

Figure 2.

Figure 2

Open in a new tab

(a) Layout and (b) picture of high resolution phantom with Al wire insert. The wire diameters are 643, 813, 1020, 1290 and 1630 µm.

2.4. Image acquisition and reconstruction

During the CT scanning, the object was placed on translation stage platform shown in figure 1 and was rotated at 1.0 rpm. With the frame rate of 20 fps, a full CT scan that covered 360° of rotation yielded a total of 1229 frames. This meant that each frame covered about 0.3° and the data was acquired approximately in a mode of step-and-shoot. A 100 kVp beam and a tube current of 1.00 mA were used for the CT scan. The total entrance skin air kerma (ESAK) without back scattering under the current setting was estimated to be 2.4 mGy. All x-ray photons interacting with the CZT detector were sorted into five user-definable energy bins. The lowest energy threshold to optimally eliminate electronic noise was set at 22 KeV, which is used as lower threshold of the first energy bin. The other thresholds were selected so that the recorded counts were evenly distributed among all energy bins. These settings were used to acquire all the images. All data acquired with the CZT detector were corrected for non-uniformity across pixels, using a previously reported flat field correction technique (Le et al., 2010). The flat field correction was made using an open source image processing software package (Sheffield, 2007).

In order to reconstruct images, the dictionaries need to be built first. For the images of high resolution phantom, the high-quality and low-quality dictionaries were built from the images reconstructed by FBP at 1229 and 307 projections, respectively. The subsequent Al wire images were reconstructed using these 2 dictionaries. For the images of postmortem breast samples, 5 samples were scanned with 1229 projections using the breast CT system based on a CZT photon-counting detector, and then the high-quality dictionaries were built from images reconstructed by the FBP algorithm with 1229 projections and their counterparts reconstructed with 307 projections. Each dictionary contained 60000 atoms and the patch size was 6×6. With the built dictionaries, the CT images of an additional postmortem breast sample were reconstructed with a voxel size of 0.53 × 0.53 × 0.53 mm3 from FBP and IR with DDL for a range of projections (102, 204, 307, 409 and 614) which were down-sampled from the original dataset of 1229 projections. The reason to reconstruct CT images with different number of projections was to compare the image quality using FBP and IR reconstructions.

2.5. Quantitative image analysis

To evaluate the performance of this IR method, we compared the spatial resolution and CNR of this IR reconstructed images to those produced by FBP with data from the first energy bin 22.1 – 42 KeV. For the spatial resolution comparison, we compared the line profiles of each Al wire from the high-resolution phantom images reconstructed by the FBP method with 614 projections with images reconstructed by the IR method with 102 projections. The line profiles were then fitted with Gaussian functions to evaluate the Full Width at Half Maximum (FWHM) (Wang et al., 2009; Casteele et al., 2012). For the CNR comparison, two ROIs were selected from glandular and adipose tissue of the postmortem breast sample images to calculate the CNR. The size of the ROI was determined by selecting a region in the glandular tissue or adipose tissue. The region was made as large as possible to calculate the average mean gray value and the standard deviation, including the pure glandular tissue or adipose tissue only. The CNR was calculated by:

CNR=MG−MAσG2+σA2 (4)

Where Mi and σi are the average mean gray value and the standard deviation of the glandular (G) tissue and adipose (A) tissue from the selected ROIs, respectively.

3. Results

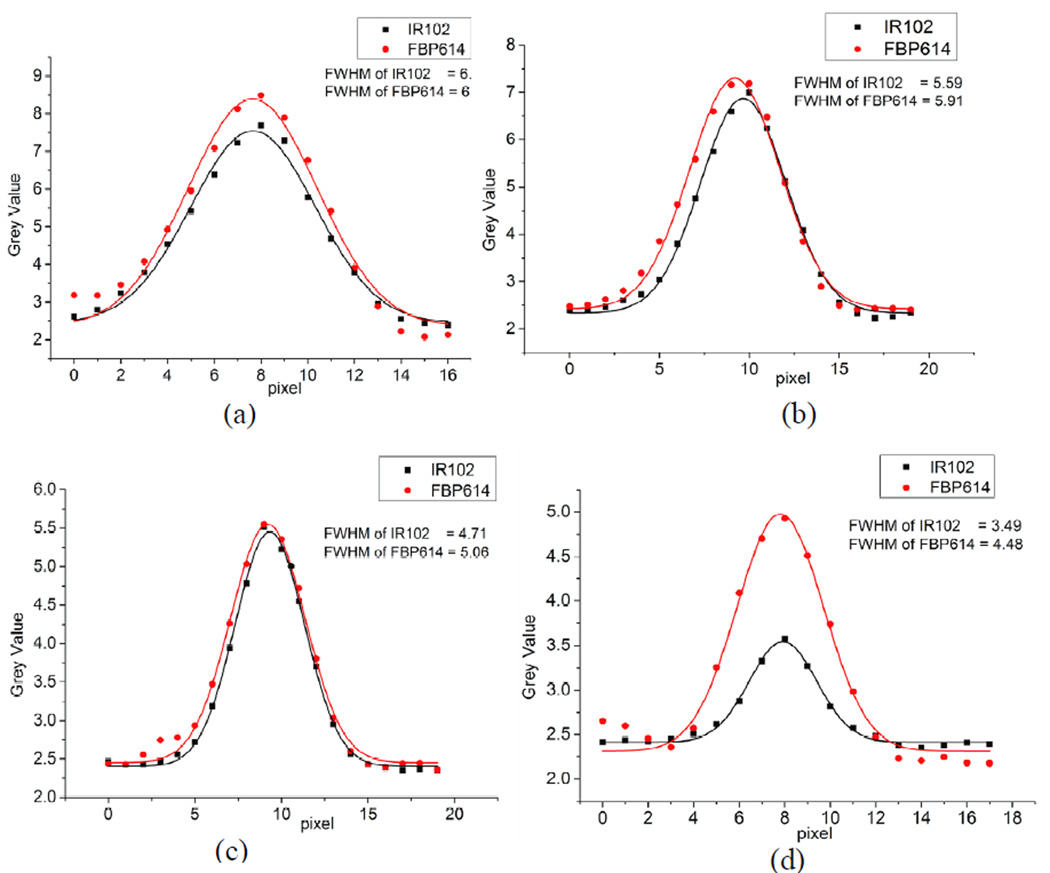
The reconstructed images of the high-resolution phantom (with Al wire insert) from IR and FBP with various numbers of projections are shown in figure 3. The top row shows the images reconstructed from IR while the bottom row shows the images reconstructed from FBP at 102, 204, 307, 409, 512 and 614 projections, corresponding to the 6 columns, respectively. To evaluate the spatial resolution of the images, two line ROIs are drawn across the center of an Al wire (see red lines in bottom right plot in figure 3). The average line profile was then calculated. A similar procedure was applied to the other three Al wires for the images reconstructed by IR at 102 projections (IR102) and by FBP at 614 projections (FBP614), as shown in figure 4. Each line profile was fitted with a Gaussian function to estimate the FWHM. It can be seen that the FWHM of IR102 is smaller than that of FBP614 for all 4 comparisons. This shows that compared to FBP method, the IR method can reconstruct the image with 6-fold fewer projections, but without a loss in spatial resolution. The diameter of the smallest Al wire is smaller than our detector pixel size and the reconstructed image is blurred. This is due to the fact that when the downsampled image is updated with the dictionaries, some patches are not correctly matched because DDL is executed for each image patch with fixed sliding distance and the final image is the average value of the overlapped image patches. This can be improved by a hybrid technique of DDL and FBP in the future.

Figure 3.

Figure 3

Open in a new tab

Images of high-resolution phantom (Al wires insert) reconstructed from IR and FBP at various projections. Red lines in bottom right plot indicate the line ROIs to extract the profiles.

Figure 4.

Figure 4

Open in a new tab

Line profiles comparison between the images reconstructed from IR at 102 projections (IR102) and from FBP at 614 projections (FBP614) for the various-diameter Al wires: 1630 µm (a), 1290 µm (b), 1020 µm (c) and 813 µm (d).

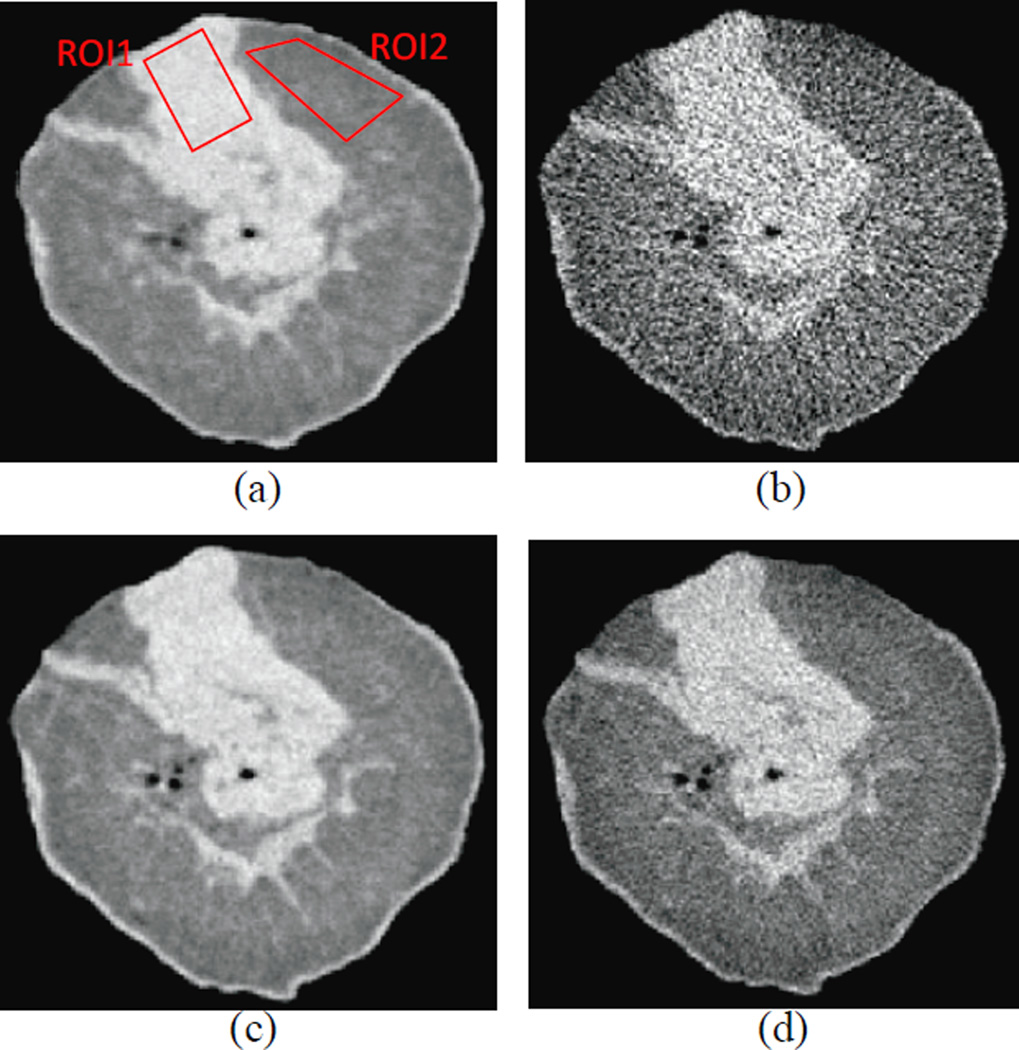
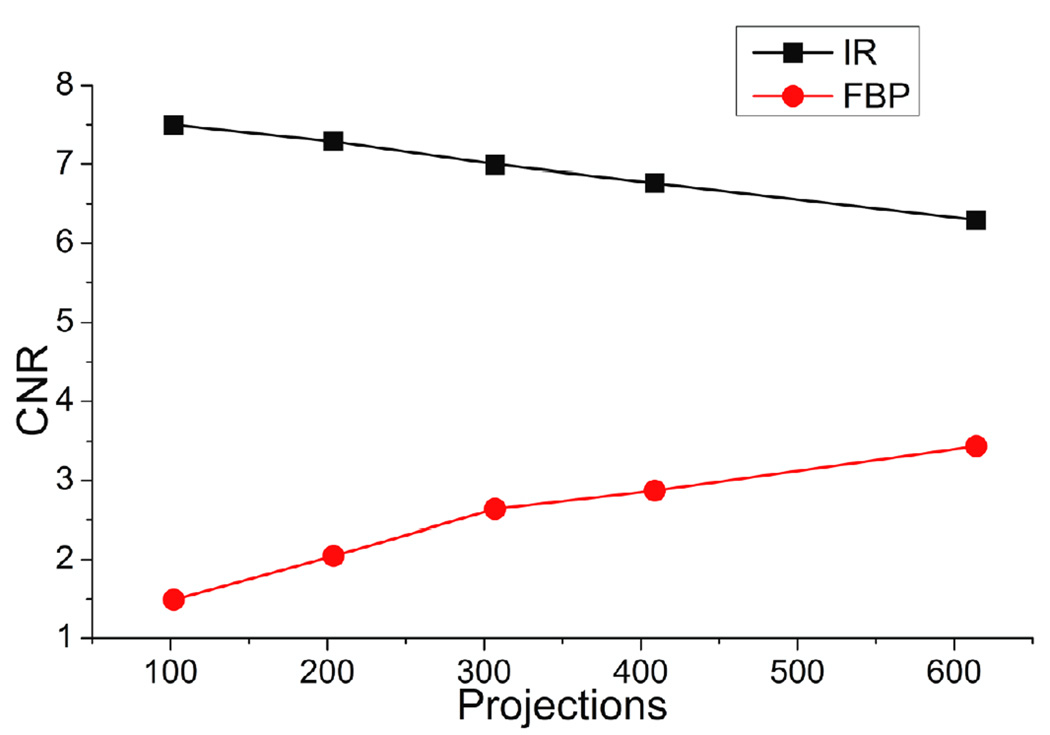
The IR method was then applied to the image reconstruction of a postmortem breast sample. Figure 5 shows an image reconstructed from IR (the first column) and from FBP (the second column) at 102 projections (top row) and 614 projections (bottom row). A qualitative comparison of postmortem breast images using IR with 102 projections and FBP with 614 projections indicates that they have comparable spatial resolutions. The CNR calculated for the postmortem sample images reconstructed from IR and FBP at 102, 204, 307, 409 and 614 projections is shown in figure 6. From figure 6, it is apparent that the CNR from the IR method is significantly better than that from the FBP method. For example, the CNR of the image from IR with 102 projections is 7.5, 5 times higher than that from FBP with 102 projections (1.5) and it is also 2 times higher than that from FBP with 614 projections (3.5). CNR was also measured for the thickest Al wire using IR with 102 projections and FBP with 614 projections and the CNR values were 5.56 and 4.71, respectively. This is consistent with the results from the postmortem breast images.

Figure 5.

Figure 5

Open in a new tab

A slice image of a postmortem breast sample reconstructed from, (a) IR with 102 projections, (b) FBP with102 projections, (c) IR with 614 projections and (d) FBP with 614 projections. Two rectangles indicate the ROIs selected from Glandular tissue (ROI1) and from Adipose tissue (ROI2) to calculate the CNR.

Figure 6.

Figure 6

Open in a new tab

CNR of a slice image of a postmortem breast sample reconstructed from IR and FBP at various projections.

4. Discussions

In this study, we evaluated the spatial resolution and CNR for FBP and IR reconstruction coupled with DDL. For the spatial resolution comparison, line profiles from different diameter Al wires were used. The spatial resolution comparison was made in a phantom with uniform background. Further improvement is expected in the case of actual tissue background because our IR method can reconstruct better images with dictionaries built from more samples.

During the image reconstruction of breast samples from IR coupled with DDL, the high-quality and low-quality dictionaries were built from full-projection images of 5 postmortem breast samples. The accuracy of these dictionaries is dependent on the number of images they contain. More images will lead to improved quality of the reconstructed images. Furthermore, once the dictionaries are built for a given system, a new full-projection scan is no longer required and only 102 projections are acquired for image reconstruction. We expect good image quality with even less than 100 projections if the dictionaries are built with more images. However, there is a lower limit to the number of projections that can be used for reconstruction, as IR requires a minimum number of projections to run. For application of this method in future breast CT systems, the number of full-projection breast images to build the dictionaries should be investigated due to the complicated structure and variance between breasts from different patients, but this is beyond the scope of this study. It is also worth noting that for an unknown object, IR coupled with DDL may not yield a high-quality reconstructed image before good dictionaries are built.

CNR is another quantity used in this study to evaluate the image quality. In figure 6, for the images reconstructed from the FBP method, CNR increases as the number of projections increases, which is expected because the noise is reduced with more projections. However, for the images reconstructed by the IR method, CNR decreases as the number of projections increases. This is due to the algorithm of this IR method itself. The algorithm is divided into two parts: ART and DDL. The ART part is responsible for the image spatial resolution, while the DDL part is involved in noise level control. As the number of projections increase ART is enhanced to increase the image consistency for spatial resolution, but since DDL requires more effort to control the noise level with more projections, high-frequency noise is introduced more prominently. With the IR method, 102 projections provided the best balance between the spatial resolution and CNR, both of which were better than those of FBP.

The IR algorithm coupled with DDL introduced in this study has shown that the number of needed projections can be reduced by a factor of 6 from approximately 600 to 100, while image quality is maintained. It should be noted that the image processing time of IR is still longer as compared to FBP. With a 2.5 GHz Intel Xeon CPU and 16 G of RAM running CPU based processing in MATLAB, IR requires approximately 2 hours to reconstruct 100 projection-quality images (including loading image information and building dictionaries) as opposed to 5 minutes with FBP. However, with the fast development of computer technology and GPU (Graphics Processing Unit) assisted processing techniques; computational time can be reduced in the future.

In a MSMS spiral CT system, the scanning time is determined by the detector frame time and the number of projections required for reconstruction. The frame time, which is limited by the counting capability of the detector, is typically in the range of 1 to 50 ms (Prokesch et al., 2010; Barber et al., 2010; Chmeissani et al., 2004). Further reduction of the frame time may result in incomplete collection of the charges generated by a single photon, leading to a poor energy resolution. However, it is more efficient to reduce the number of projections needed to reconstruct a high quality image. As was shown in this study, a reduction by a factor of 6 in the number of projections can be expected with the proposed IR algorithm as compared to the conventional FBP method. Therefore, the scanning time may be greatly reduced with implementation of the proposed IR algorithm for image reconstruction. It is thus possible to design a MSMS breast CT system with a scanning time of approximately 10s (Molloi and Ding, 2011). Compared to the current breast CT based on the flat-panel detectors, the proposed scanning time is comparable, but the radiation dose can be reduced by a factor of approximately 2 using photon counting detectors.

In this study, the images were reconstructed with 102, 204, 307, 409 and 614 projections by IR and FBP and here the numbers of projections were down-sampled from the original dataset of 1229 projections. It assumed that the projection was acquired in a mode of step-and-shoot. For example, every 12th projection was extracted from the whole set of 1229 projections to reconstruct the 102-projection image. Equivalently, for a full 360° scan, the object is rotated by 3.53° in a step, and then the projection is recorded. The same assumption was used in the previous study (Lu et al., 2012). The current study mainly focuses on the comparison between the proposed IR method with respect to the standard FBP reconstruction. The large number of projections used in the CT scan lead to a small rotating angle within the time of each frame, which avoids the problem of smearing the object located away from the center of rotation. However, in practical applications, where a small number of projections, 100 or even less, are used in favor of dose reduction, the CT systems have to be specifically designed to avoid smearing the object located away from the center of rotation during image acquisition. This can be accomplished using a high-power pulsed x-ray tube to acquire the projections at particular rotation angles, where the x-ray tube emits a high flux beam in a short time compared to continuous x-ray sources, and the detector is synchronized with the emission timing of the x-ray source to acquire an image. A similar technique has previously been implemented (Do, 2012).

5. Conclusion

This study demonstrated that the IR coupled with DDL method could significantly reduce the required number of projections for a CT reconstruction compared to FBP method while achieving an improved CNR and maintaining the same spatial resolution. The results indicate that the required number of projections can be reduced by a factor of approximately 6. The application of the IR method coupled with DDL can potentially reduce the radiation dose by a factor of approximately 2 in a MSMS spiral CT system.

Acknowledgements

This work was supported in part by NIH/NCI grant R01CA13687.The authors would like to thank David Rundle from Endicott Interconnect Detection & Imaging Systems for his technical support and fruitful discussions.

Reference

  1. Anderson A, Kak A. Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm. Ultrasonic Imaging. 1984;6:81–94. doi: 10.1177/016173468400600107. [DOI] [PubMed] [Google Scholar]
  2. Barber WC, Nygard E, Wessel JC, Malakhov N, Wawrzyniak G, Hartsough NE, Gandhi T, Beck TJ, Taguchi K, Iwanczyk JS. Large area photon counting X-ray imaging arrays for clinical dual-energy applications; 2009 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC 2009); 2009. pp. 3029–3031. [Google Scholar]
  3. Barber WC, Nygard E, Wessel JC, Malakhov N, Wawrzyniak G, Hartsough NE, Gandhi T, Iwanczyk JS. Fast photon counting CdTe detectors for diagnostic clinical CT: dynamic range, stability, and temporal response. Proceedings of the SPIE - The International Society for Optical Engineering. 2010;76221E:8. [Google Scholar]
  4. Bert C, Niederlohner D, Giersch J, Pfeiffer KF, Anton G. Computed tomography using the Medipix1 chip. Nuclear Instruments & Methods in Physics Research Section a-Accelerators Spectrometers Detectors and Associated Equipment. 2003;509:240–250. [Google Scholar]
  5. Bian J, Han X, Yang K, Sidky E, Boone J, Pan X. A Preliminary Investigation of Reduced-view Image Reconstruction from Low-dose Breast CT Data. Proceedings of the SPIE - Physics of Medical Imaging. 2012;8313:831325. [Google Scholar]
  6. Bisogni MG, Del Guerra A, Lanconelli N, Lauria A, Mettivier G, Montesi MC, Panetta D, Pani R, Quattrocchi MG, Randaccio P, Rosso V, Russo P. Experimental study of beam hardening artifacts in photon counting breast computed tomography. Nuclear Instruments & Methods in Physics Research Section a-Accelerators Spectrometers Detectors and Associated Equipment. 2007;581:94–98. [Google Scholar]
  7. Casteele E, Parizel P, Sijbers J. Quantitative evaluation of ASiR image quality: An adaptive statistical iterative reconstruction technique. Proceedings of the SPIE - Physics of Medical Imaging. 2012;8313:83133F. [Google Scholar]
  8. Chmeissani M, Frojdh C, Gal O, Llopart X, Ludwig J, Maiorino M, Manach E, Mettivier G, Montesi MC, Ponchut C, Russo P, Tlustos L, Zwerger A. First experimental tests with a CdTe photon counting pixel detector hybridized with a Medipix2 readout chip. IEEE Transactions on Nuclear Sciences. 2004;51:2379–2385. [Google Scholar]
  9. Ding H, Molloi S. Image-based spectral distortion correction for photon-counting x-ray detectors. Med. Phys. 2012;39:1864–1876. doi: 10.1118/1.3693056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Do S. Ultra-short pulsed X-ray imaging. 8238514. US Patent. 2012
  11. Donoho DL. Compressed sensing. IEEE Transactions on Information Theory. 2006;52:1289–1306. [Google Scholar]
  12. Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries. Ieee T Image Process. 2006;15:3736–3745. doi: 10.1109/tip.2006.881969. [DOI] [PubMed] [Google Scholar]
  13. Elbakri IA, Fessler JA. Statistical image reconstruction for polyenergetic X-ray computed tomography. IEEE Trans Med Imaging. 2002;21:89–99. doi: 10.1109/42.993128. [DOI] [PubMed] [Google Scholar]
  14. Gordon R, Bender R, Herman G. Algebraic Reconstruction Techniques (ART) for Three-dimensional Electron Microscopy and X-ray Photography. Journal of Theoretical Biology. 1970;29:471–476. doi: 10.1016/0022-5193(70)90109-8. [DOI] [PubMed] [Google Scholar]
  15. Herman GT. Image Reconstruction from Projections: Fundamentals of Computerized Tomography. New York: Academic Press; 1980. [Google Scholar]
  16. Hernandez D, Michel E, Kim HS, Kim JG, Han BH, Cho MH, Lee SY. Iterative image reconstruction in spectral-CT. Proceedings of the SPIE - Physics of Medical Imaging. 2012;8313:831330. [Google Scholar]
  17. Hubbell JH, Seltzer SM. Tables of x-ray mass attenuation coeeficient and mass energy absorption coefficients 1 keV to 20 MeV for elements Z=1 to 92 and 48 additional substances of dosimetric interest. NIST Report No. NISTIR 5632. 1995 [Google Scholar]
  18. Kak AC, Slaney M. Principles of Computerized Tomographic Imaging. New York: IEEE Press; 1988. [Google Scholar]
  19. Le HQ, Ducote JL, Molloi S. Radiation dose reduction using a CdZnTe-based computed tomography system: Comparison to flat-panel detectors. Med. Phys. 2010;37:1225–1236. doi: 10.1118/1.3312435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lu Y, Zhao J, Wang G. Few-view image reconstruction with dual dictionaries. Physics in Medicine and Biology. 2012;56:173–189. doi: 10.1088/0031-9155/57/1/173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Mairal J, Elad M, Sapiro G. Sparse representation for color image restoration. Ieee T Image Process. 2006;17:53–69. doi: 10.1109/tip.2007.911828. [DOI] [PubMed] [Google Scholar]
  22. Makeeva A, Dasb M, Glicka SJ. Investigation of statistical iterative reconstruction for dedicated breast CT. Proceedings of the SPIE - Physics of Medical Imaging. 2012;8313:83131W. doi: 10.1118/1.4811328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Molloi S, Ding H. Low-dose spectral computed tomography for measuring breast tissue composition. Proposal to NIH. 2011 [Google Scholar]
  24. Pachon J, Yadava G, Pal D, Hsieh J. Image Quality Evaluation of Iterative CT Reconstruction Algorithms: A Perspective from Spatial Domain Noise Texture Measures. Proceedings of the SPIE - Physics of Medical Imaging. 2012;8313:83132K. [Google Scholar]
  25. Prokesch M, Bale DS, Szeles C. Fast High-Flux Response of CdZnTe X-Ray Detectors by Optical Manipulation of Deep Level Defect Occupations. IEEE Transactions on Nuclear Science. 2010;57:2397–2399. [Google Scholar]
  26. Schlomka JP, Roessl E, Dorscheid R, Dill S, Martens G, Istel T, Baumer C, Herrmann C, Steadman R, Zeitler G, Livne A, Proksa R. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography. Physics in Medicine and Biology. 2008;53:4031–4047. doi: 10.1088/0031-9155/53/15/002. [DOI] [PubMed] [Google Scholar]
  27. Sheffield JB. ImageJ, a useful tool for biological image processing and analysis. Microscopy and Microanalysis. 2007;13:200–201. [Google Scholar]
  28. Shen Y, Yi Y, Zhong Y, Lai C, Liu X, You Z, Ge S, Wang T, Shaw C. High resolution dual detector volume-of-interest cone beam breast CT–Demonstration with a bench top system. Med. Phys. 2010;38 doi: 10.1118/1.3656040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Shikhaliev PM. Computed tomography with energy-resolved detection: a feasibility study. Physics in Medicine and Biology. 2008;53:1475–1495. doi: 10.1088/0031-9155/53/5/020. [DOI] [PubMed] [Google Scholar]
  30. Shikhaliev PM, Fritz SG. Photon counting spectral CT versus conventional CT: comparative evaluation for breast imaging application. Physics in Medicine and Biology. 2011;56:1905–1930. doi: 10.1088/0031-9155/56/7/001. [DOI] [PubMed] [Google Scholar]
  31. Sidky E, Kao C, Pan X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. Journal of XRay Science and Technology. 2006;14:119–139. [Google Scholar]
  32. Szeles C, Soldner SA, Vydrin S, Graves J, Bale DS. CdZnTe semiconductor detectors for spectroscopic x-ray imaging. IEEE Transactions on Nuclear Science. 2008;55:572–582. [Google Scholar]
  33. Taguchi K, Srivastava S, Kudo H, Barber WC. Enabling photon counting clinical X-ray CT; 2009 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC 2009); 2009. [Google Scholar]
  34. Wang G, Yu H, Ye Y. A scheme for multisource interior tomography. Med. Phys. 2009;36:3575–3581. doi: 10.1118/1.3157103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wang X, Meier D, Oya P, Maehlum GE, Wagenaar DJ, Tsui BMW, Patt BE, Frey EC. Microcomputed Tomography with A Second Generation Photon-counting X-ray Detector - Contrast Analysis and Material Separation. Proceedings of the SPIE - The International Society for Optical Engineering. 2010;76221B:8. [Google Scholar]
  36. Xu Q, Yu H, Mou X, Wang G. Dictionary learning based low-dose x-ray CT reconstruction; 2011 11th Int. Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine; Potsdam, Germany. 2011. pp. 258–261. [Google Scholar]
  37. Yu H, Wang G. SART-type image reconstruction from a limited number of projections with the sparsity constraint. International Journal of Biomedical Imaging. 2010;2010:934847. doi: 10.1155/2010/934847. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yu H, Wang G. A soft-threshold filtering approach for reconstruction from a limited number of projections. Physics in Medicine and Biology. 2012;55:3905–3916. doi: 10.1088/0031-9155/55/13/022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Yu HY, Wang G. Compressed sensing based interior tomography. Physics in Medicine and Biology. 2009;54:2791–2805. doi: 10.1088/0031-9155/54/9/014. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES