Abstract
Many drug candidates fail in clinical trials due to an incomplete understanding of how small-molecule perturbations affect cell phenotype. Cellular responses can be non-intuitive due to systems-level properties such as redundant pathways caused by co-activation of multiple receptor tyrosine kinases. We therefore created a scalable algorithm, DIONESUS, based on partial least squares regression with variable selection to reconstruct a cellular signaling network in a human carcinoma cell line driven by EGFR overexpression. We perturbed the cells with 26 diverse growth factors and/or small molecules chosen to activate or inhibit specific subsets of receptor tyrosine kinases. We then quantified the abundance of 60 phosphosites at four time points using a modified microwestern array, a high-confidence assay of protein abundance and modification. DIONESUS, after being validated using three in silico networks, was applied to connect perturbations, phosphorylation, and cell phenotype from the high-confidence, microwestern dataset. We identified enhancement of STAT1 activity as a potential strategy to treat EGFR-hyperactive cancers and PTEN as a target of the antioxidant, n-acetylcysteine. Quantification of the relationship between drug dosage and cell viability in a panel of triple-negative breast cancer cell lines validated proposed therapeutic strategies.
Graphical abstract

Introduction
Candidate drugs have an alarmingly low success rate in clinical trials. The FDA approved only 13.4% of agents introduced between 1993-2004 for cancer treatment.1 An inability to accurately predict cellular responses induced by network perturbations prohibits efficient drug discovery.2 Systems pharmacology, defined as the study of a drug perturbation on a biological system, can improve predictions of the efficacy and side effects of potential cancer therapies by incorporating emergent (or non-intuitive, systems-level) properties into computational models. In this study, we combine efficient chemical perturbations, systems-level biological assays, and predictive computational modeling to improve drug discovery by incorporating the emergent behavior of signal transduction networks.
Deriving correlations between biomolecules, such as RNA expression or protein abundance, and cell phenotype by sampling the cell under diverse perturbations can elucidate factors that actively drive carcinogenesis, known as drivers. However, correlations can uncover neutral or compensatory mutations, known as passengers, complicating the search for effective molecular targets in disease.3 Deriving the underlying network structure may provide additional predictive information by elucidating control structures such as feedback loops and redundant pathways. Signaling networks can be modeled using nodes, representing phosphorylation abundance, and directed edges which represent information flow between phosphorylation sites. Network visualization can reveal the chronological order of phosphorylation events elucidating nodes downstream of known molecular drivers, thereby suggesting new drug targets in defined cancer subtypes.
In this study, we derived the network architecture of a model epidermoid carcinoma driven by overexpression of the Epidermal Growth Factor Receptor (EGFR). EGFR is a receptor tyrosine kinase that is often mutated, overexpressed, or misregulated in many cancer types, including breast, lung, gastric, prostate, and cervical cancers.4 We sampled protein phosphorylations and cell viability after 32 perturbations with media, small-molecules, and/or growth factors, designed to activate or inhibit subsets of receptor tyrosine kinases such as EGFR. The phosphorylation levels combined with a high-throughput measure of cell viability were used to discover potential vulnerabilities within the network. To gain the statistical power necessary to infer specific and effective drug targets, we employed a modified version of the high-confidence assay of protein abundance and modification, the MicroWestern Array (MWA).
New technologies continually strengthen our understanding of the mechanisms that proteins use to relay information. Assays that allow for direct quantification of protein abundance and phosphorylation states provide a particularly useful source of data with predictive value because proteins are often the functional entities of cellular decision-making processes.5 Higher resolution time-course studies6 and greater numbers of assayed phosphosites greatly expand our ability to understand the emergent properties of biological systems. ‘Mesoscale’ protein assays, defined as those that can observe the tens to hundreds of predefined proteins over many perturbations and time points, provide an efficient means to obtain mechanistic insight into defined network behavior.7–10 Because the MWA methodology incorporates the separation of proteins using electrophoresis, the sizes of proteins can be cross-referenced against molecular standards, eliminating much of the uncertainty that convolutes the quantification of proteins due to non-specific antibody-antigen binding. The ability to increase the number of time points and conditions allows for accurate network reconstruction with fewer false positives. Here, we utilize a modified version of the microwestern array and a high-throughput cell viability assay to create a large-scale cue-signal-response matrix11–13 on which to reconstruct the cellular network architecture.
While many algorithms have been successfully used to reverse engineer biological networks from measurements of the concentration of biomolecules after chemical perturbation,14 we created a new algorithm that is scalable to the large number of time-resolved phosphosite abundances that can be reliably assayed with the microwestern array from a minute biological sample. This computationally-efficient algorithm, termed Dynamic Inference Of NEtwork Structure Using Singular values (DIONESUS), employs partial least squares regression with variable reduction using the Variance of Importance in Projection (VIP) score. DIONESUS derives network architecture with minimal computational time by removing latent sources of variance with little predictive value. In this study, we applied the DIONESUS algorithm to derive the architecture of a prototypical carcinoma cell that overexpresses EGFR, from the microwestern dataset. This predictive model suggested several strategies, specifically enhancement of the signal transducer, STAT1, for combating cancers driven by EGFR hyperactivation.
Results
Informed perturbation yields high statistical power for computational models
We quantified the systems-level properties of the A431 epidermoid cervical carcinoma cell line and the resultant cell phenotype (viability) after perturbations to the EGFR signaling network. A431 cells grossly overexpress EGFR and therefore are not a direct representation of cancer cell behavior in vivo. A431 cells, however, display several attractive features for understanding how information flows within protein networks, making them an ideal model to reverse engineer cell signaling architecture. A431 cell viability is increased by low levels of Epidermal Growth Factor (EGF) stimulation but is reduced by high levels of EGF stimulation (Supplementary Fig. 1). This unique, biphasic response allows for both positive and negative protein influences on cell viability to be observed from stimulation with a single ligand.15 Additionally, in A431 cells, EGFR and many other receptor tyrosine kinases and downstream signaling proteins undergo rapid and robust phosphorylation in response to growth factors, enabling us to quantify many protein modifications and relate them to cell viability with high confidence. The high statistical confidence of our conclusions is largely due to the wide covariance among observed phosphorylation profiles made possible by the unique properties of cell signaling in A431 cells. For this reason, results from this cell line may not apply to those reflecting more physiological levels of EGFR abundance.
We perturbed A431 cells with growth factors and/or cell-permeable small molecules, referred to as cues. These cues were chosen to activate or inhibit distinct cell signaling pathways by modulating potential mechanisms of Receptor Tyrosine Kinase (RTK) crosstalk, defined as phosphorylation of multiple receptors, such as c-MET, after activation with a single ligand, such as EGF. Following each perturbation, phosphorylation abundance, defined as signals, were quantified at four time points in 60 unique signal transduction protein residues using the microwestern array (Fig. 1A). Growth factors were applied at the 0-min time point. Small molecules were applied 30 mins before growth factor stimulation. We assayed the phosphorylation state at -30, 0, 5, and 15 mins, and quantified cell viability, defined as the response, 24 hrs post-perturbation. The conditions consisted of combinations of cell growth medium, 4 growth factors, and 13 diverse small molecules. Supplementary Table 1 summarizes the panel of cues.
Fig. 1. Network inference reveals targets for cancer therapy from microwestern array data.

(A) Following perturbation of the A431 cell line with a panel of growth factors and/or small molecules (cues), protein phosphorylation kinetics (signals) were quantified by microwestern arrays in tandem with cell viability (response). Small molecules with fresh media were added 30 mins prior to growth factor stimulation. Growth factors were applied at 0 mins and cells were lysed at -30, 0, 5, and 15 mins. (B) Representative microwestern arrays demonstrate common and unique phosphorylation kinetics after perturbation. (C) The fold changes (mean ± s.e.) in phosphorylation were quantified following each perturbation along with a measure of cell viability. (D) To define the architecture, each signal was iteratively set as the response vector to identify relevant predictors for each phosphosite. The significant connections from each regression problem was folded into a single network.
We perturbed A431 cells on six separate days due to the number of samples that could feasibly be cultured per day. Experiments 1-6 refer to each set of experimental perturbations. For each experiment, we perturbed cells with 200 ng ml−1 EGF and media-alone in order to quantify the amount of inter-experimental biological variance in the experimental method. In addition, we perturbed the cells with 2-7 unique growth-factor and/or small-molecule perturbations in each experiment. As RTK coactivation is a means by which cancer cells can evade precise targeted therapy,16 we chemically interfered with RTK cross-phosphorylation, thereby decreasing the covariance between phosphosite abundances. This rational selection of perturbants increased the statistical power to reconstruct an accurate network model.
In Experiment 1, we treated A431 cells with a panel of four growth factors, either alone or in combination. EGF, Insulin, Hepatocyte Growth Factor (HGF), and Insulin-like Growth Factor (IGF) were expected to induce both specific and overlapping signaling pathways.
In Experiment 2, we treated cells with EGF in the presence of a SRC kinase, PLCγ, or PI3K inhibitor. Proteins that contain the phosphotyrosine-binding SH2-domains, such as SRC kinase, PLCγ, and PI3K, are often directly downstream of receptor tyrosine kinases17 and therefore potential mediators of the transactivation of other receptor tyrosine kinases following EGFR activation.18
In Experiment 3, we treated cells with EGF in the presence of a series of protease inhibitors expected to inhibit cleavage of extracellular growth factors and other matrix proteins. Previous studies suggest autocrine and paracrine signaling due to cleavage of growth factors as a potential extracellular mechanism of receptor tyrosine kinase transactivation in response to EGFR activation.19
In Experiment 4, we treated cells with antioxidant agents. Antioxidants were expected to induce activation of tyrosine phosphatases, resulting in reduced amplitude of specific tyrosine phosphorylations following EGF stimulation.20 Tyrosine phosphatases can become inactivated by reactive oxygen species through oxidation of active site catalytic cysteines.20
In Experiments 5 and 6, we treated cells with small molecules intended to modulate the endogenous release of reactive oxygen species in the cell produced by the NOX complex and its regulatory subunit RAC1.21 In addition, we used a lower concentration of the SRC kinase inhibitor, PP2, and a SHP2-phosphatase inhibitor, PHPS1, to further increase the variance of the phosphosignaling dynamics.
In summary, we chose experimental perturbations that were expected to modulate unique and overlapping subsets of protein signaling networks by modulating receptor-tyrosine-kinase crosstalk. These perturbations powered a predictive computational model describing the systems-level mechanisms that determine cell fate.
The microwestern array quantifies high-confidence, dynamic phosphoproteomic data
Figure 1B summarizes the microwestern array data following treatment with the panel of cues (consisting of EGF, HGF, insulin, and combinations thereof). In this study, we modified the microwestern array platform to print 16 samples per antibody partition. This modification allowed us to quantify more samples with each antibody in comparison to the previous configuration of 6 samples per partition.10 Each fluorescent band can be cross-referenced with a molecular weight standard to validate that the signal corresponds with the protein of interest. This novel characteristic of the MWA differentiates it from many other antibody-based assays that do not separate antigens by molecular weight. Separation improves data precision as well as the diversity of useful antibodies. The MWA is therefore amenable to the analysis of up to 10 times more proteins in comparison to antibody-based technologies that do not employ separation.10 The MWA has very high specificity and sensitivity across a wide range of antibodies and sample conditions as it shares the fundamental mechanism of the tried-and-true western blot. Accordingly, MWAs were employed to derive the mechanisms of drug synergy in Squamous Cell Carcinoma of the Head and Neck (SCCHN);22 the immune-sensing signaling components of dendritic cells;23 and the anti-cancer activity of bioactive natural products24. The ability to assay larger numbers of variables with the MWA versus standard western blots allows for inference of larger phosphonetworks and enables a deeper understanding of complexity and emergent mechanisms inherent in cell signaling architecture.
The quantifications of the fold change in phosphorylation along with the cell viability after each perturbation are shown in Figure 1C. The fold change of each phosphorylation was assayed in technical triplicate and the errorbars, representing standard error, are displayed to reiterate the low experimental variance of the MWA method.10 The response of the system is defined as cell viability at 24 hrs after the addition of growth factor.
To infer the network architecture, we iteratively defined each phosphosite, as well as the phenotypic response across all conditions, as the new response vector. We evaluated the relevant predictors systematically to identify significant connections to the response variable. The resulting networks were folded (i.e. the resulting adjacency vectors were concatenated into a single square adjacency matrix) to form an overall network model of the signal transduction network (Figure 1D).
Phosphoprotein signaling is modular and highly collinear
Figure 2A shows the phosphorylation dynamics of the 60 assayed phosphosites and the quantification of cell viability. Hierarchical clustering of the data demonstrated several distinct, collinear modules of phosphosites, suggesting common pathways or regulatory modules (for the full dataset, see Supplementary Figs. 2-13, Supplementary Table 2, and Supplementary Note 1). Volcano plots further illustrate the significance and effect size of individual perturbations on phosphorylation kinetics (Supplementary Fig. 14).
Fig. 2. Clustering of phosphoproteomic data from the microwestern array reveals a broad-range and highly collinear dataset on which to inform a predictive model.
(A) Cell viability is displayed above the phosphorylation heatmap in a grayscale heatmap. The log10 fold change in phosphorylation from the time of application of small molecules or media (-30 mins) was quantified and displayed by MWA at 0, 5, and 15 mins after growth factor stimulation. (B) The log10 fold change of four phosphoprotein signaling metrics with high correlation to cell viability are marked with a red circle on the heatmap and graphed against the phenotype. The Pearson correlation coefficient is given between the explanatory variables and the normalized viability (mean ± s.e.). (C) A histogram of the correlation coefficients among the log fold changes of all phosphoprotein signaling metrics suggests a highly collinear set of explanatory variables.
To explore the architecture controlling cell phenotype, we began by identifying phosphosites that are accurate predictors of cell viability. To find the quantitative relationship between phosphorylation and phenotype, we plotted cell viability against the log10 fold change of four predictors (Fig. 2B). These predictors consisted of the two phosphorylation states with the highest absolute Pearson correlation coefficient (p-EGFR(Y1086)[5m] and p-STAT1(Y701)[5m]) and the two with the highest positive Pearson correlation coefficient (p-GAB2(S159)[5m] and p-PDK1(S241)[15m]) in relation to cell viability. Figure 2C and Supplementary Table 4 display the pairwise Pearson correlation coefficients between all explanatory variables. There are 180 predictor variables in this dataset (60 assayed phosphosites × 3 informative time points). The number of pairwise correlations is therefore 32,220 (180×179 = 32,220). The number of correlation coefficients with an absolute value above 0.5, specifically 6096 of the 32,220 pairwise comparisons, suggests a highly collinear set of predictors. As a result, we employed regularized linear regression to identify relevant pathways from the large number of collinear associations in order to resolve the specific phosphosites most predictive of cell phenotype.
Regularized regression improves the predictive capacity of computational models
Linear regression, optimized using cross-validation, can identify variables with high predictive value.25 In addition, regression provides a scalable means to quantify and select significant explanatory variables inherent in directed network inference. We inquired which regression method is most useful in identifying predictors given the cue-signal-response matrix.
The general form for linear regression can be written as y = Xβ, where X is a matrix of predictors, y is a response vector, and β is a vector of weights. We compared results from several variations of linear regression to develop predictive models of biological systems. The accuracy of each computational model was quantified using the goodness of prediction metric calculated through leave-one-out validation, . Q2 quantifies the error associated with predicting a given condition that is excluded from, or left out of, the training data.12,26
We began the regression analysis by inquiring whether a single phosphoprotein signaling metric would be sufficient to explain cell viability by using simple linear regression. We calculated the βi-coefficients upon defining y as the unit-normalized and mean centered (z-score) of cell viability measurements, and x as the z-score of the given vector of values for the given phosphoprotein signaling metric, i, across all conditions. Resulting model predictions are shown in comparison to experimental measurements in Supplementary Figure 15. Predictions using data from all observations are shown in green full circles, whereas predictions in which the predicted perturbation is left out of the training set are shown in empty blue circles. A model with high fitness corresponds to an observed-experimental plot with solid green data points close to the line of unity (depicted as a dotted gray line) and a high correlation coefficient, R2. A model with a high predictive capacity will have empty blue data points close to the diagonal and a high leave-one-out validation coefficient, Q2. As p-STAT1(Y701)[5m], p-EGFR(Y1086)[5m], p-PDK1(S241)[15m], and p-GAB2[5m] were found to be highly correlated with cell viability, we used these phosphoprotein signaling metrics as single variable predictors in the creation of a computational model for cell viability. The Q2 metric was 0.717, 0.687, and 0.610 for the simple linear regression model using predictors p-EGFR(Y1086)[5m], p-STAT1(Y701)[5m], and p-GAB2(S159)[5m] respectively, suggesting that these variables have high predictive capacity. While p-PDK1 is highly correlated with cell viability, it is not predictive in context of a simple linear regression model (Q2 = -0.018). This fact demonstrates that strong correlation does not also imply accurate prediction, underscoring the importance of regression in separating correlates from predictors in computational models. Additionally, while p-STAT1 is negatively correlated with viability, p-GAB2 is positively correlated with cell viability, suggesting that in this system, both significant positive and negative pathways influence cell viability. Therefore, we employed multiple linear regression (MLR), which uses multiple variables to explain the response.
As the MWA data exhibited many collinear variables, we employed a panel of MLR methods that limit overfitting by employing a penalty proportional to the magnitude of β (Supplementary Table 5). As a baseline comparison and negative control, we used Ordinary Least Squares (OLS), which solves for the linear regression coefficients by minimizing the squared deviation of the model predictions from the data. While OLS regression is a straightforward approach that relates input to output variables, overfitting is a common problem that leads to poor predictive capacity in cases where input variables are numerous or collinear.27 As the MWA data exhibited many collinear variables, we compared OLS with a panel of regularized methods that limit overfitting by assigning a penalty to the magnitude of β-coefficients.
We used three related methods: LASSO,28 ridge regression, and elastic-net regression.29 The LASSO method adds an L1-norm penalty to the regression problem forcing many regression coefficients towards zero, yielding a sparse β-vector. Only variables with a non-zero regression coefficient are assumed to be relevant for prediction, providing a suitable algorithm for variable selection. Similarly, ridge assigns an L2-penalty, while elastic net combines both L1 and L2 penalties.29 These methods have been used successfully to identify associations in several large and collinear datasets.29
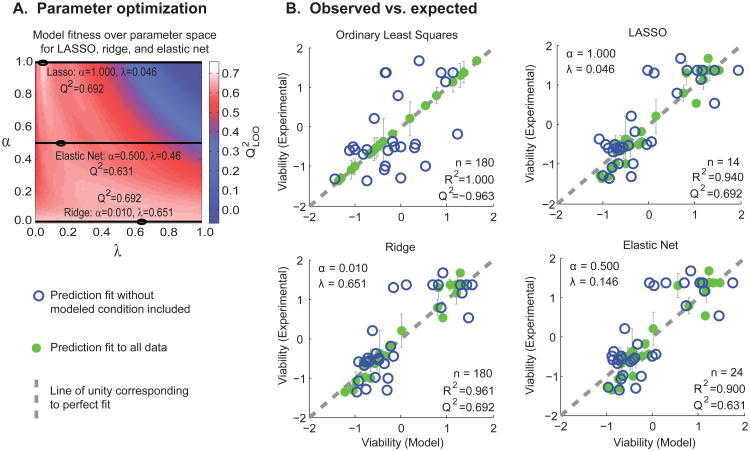
Aside from λ, the parameter defining the weight through which β is penalized, LASSO, ridge, and elastic-net regression employ an addition model parameter, α, the ratio of the L1 to L2 penalties. These tuning parameters were empirically optimized by identifying the maximal over the solution space. In order to compare different constraints, regression was performed with α = 1.0 for LASSO, α = 0.01 for ridge, and α = 0.5 for a representative elastic-net solution. A map of the fitness landscape over the defined parameter space is shown in Figure 3A. LASSO, ridge, and elastic-net regression had optimal λ values of 0.692, 0.651, and 0.631 respectively.
Fig. 3. Comparison of multiple linear regression algorithms shows improved predictive capacity over ordinary least squares.
(A) A comparison of linear regression methods reveals significant predictors for explaining cell viability. The optimal tuning parameters, α and λ, were identified empirically and selected to maximize the fit given α = 1.000 for LASSO, α = 0.010 for ridge, and α = 0.500 for elastic-net regression. (B) The observed cell viability versus the model predictions are shown for each optimized algorithm. The R2 and metrics are given for each optimized regression method to quantify its fitness and predictive capacity, respectively. The number of predictors used in each algorithm is defined by n. Solid green circles show predicted response for conditions that are trained on the complete data set. Open blue circles show predictions that were trained on data omitting the predicted condition.
Fig. 3B shows plots summarizing the cross-validation scores for each optimized regression method. With the exception of OLS, all methods had relatively high Q2 values, suggesting that they offer predictive insight for this model system. As LASSO and elastic-net regression utilize the L1 penalty leading to a sparse set of predictors, the number of non-zero predictors is indicated as n. The optimized LASSO model had 14 significant predictors (n = 14) whereas the elastic net had 24 (n = 24). In general, sparser solutions yield simpler models that are less likely to overfit the data; this sparsity is often preferable when trying to recover and resolve biological mechanism by reducing the search space for effective drug targets.
A disadvantage of these restrained least squares regression methods such as LASSO is the fact that selected predictors may not reflect the actual underlying causal variables.30,31 This problem can be more pronounced in biological contexts where the data is inherently noisy.30,31 For this reason, we utilized a method to identify separate sources of variances in the response variable by projecting the data onto a lower dimensional space. Noise can be reduced by eliminating non-predictive sources of variance from the computational model.
PLS-VIP identifies seven significant predictors of cell viability
We implemented Partial Least Squares Regression (PLSR) using the Variance of Importance in Projection (VIP)32 variable selection criteria to identify predictors that explained significant sources of variance in the response variable, cell viability. A benefit of PLSR is the minimal computational expense required to assign importance to each of the explanatory variables using the VIP metric, as no resampling is necessary. Metrics can be ordered by VIP score and eliminated in reverse order of VIP magnitude, in a method known as PLS-VIP.32 The PLSR approach is desirable for a number of reasons; the approach has been shown to perform well with input matrices containing highly collinear data, missing data, or many input variables.27 The PLSR method has been used previously to determine novel signal-response relationships from protein signaling and cell response data.8,33–35
We predicted cell viability as a function of phosphorylation metrics using the Non-Iterative PArtial Least Squares (NIPALS) algorithm.36 Explanatory variables were rank ordered by VIP score and eliminated from the model in a stepwise progression starting with the variable having the lowest VIP score. The Q2 values corresponding to the range of explanatory variables included in the model are shown in Figure 4A. Three principal components and seven significant phosphoprotein signaling metrics show maximal predictive capacity without overfitting. We utilized these parameters for the final PLS-VIP-based computational model. The resulting observed vs. expected plot is shown for PLS-VIP (Fig. 4B), demonstrating a model with high predictive capacity. The seven significant phosphoprotein signaling metrics (p-EGFR(Y1086)[5m and 15m], p-AKT(S473)[5m and 15m], p-CDK2[15m], p-S6RIBPROT[15m], and p-STAT1(Y701)[5m]), as well as the corresponding β-coefficients and VIP score for each phosphosite in the computational model, are shown in Figure 4C. While these seven phosphosites have been shown to be involved in EGFR signaling, this sparse set of predictors refines and constrains the search space to include only those molecular targets, or effective combinations of targets, that reflect the most confident specificity to EGFR-hyperactive cancer models.
Fig. 4. PLSR with variable reduction by VIP score is an accurate and scalable means of calculating edge confidence for network reconstruction.
(A) Inclusion of three principal components and seven explanatory variables yield a local maximum of model predictive capacity without overfitting. (B) The optimized observed vs. expected responses (mean ± s.e.) are shown using the optimized parameters. Green filled circles show the responses for conditions that are trained on the complete data set. Open blue circles show the responses that were not trained on the given condition. The number of predictors used in each algorithm is given by n. The coefficient of determination (R2) and the coefficient of prediction using leave-one-out cross-validation are given for the optimized computational model. (C) The seven significant predictors determined using PLS-VIP are listed with blue arrows for positive β-values and red tees for negative β-values. The VIP scores are listed as a measure of confidence for a predictor being useful in explaining cell viability. (D) The receiving-operating characteristic (ROC) curves for DIONESUS and top-performing inference algorithms for the reconstruction of a 100-node in silico network from synthetic time-course data. Higher accuracy of inference corresponds to a higher Area Under the ROC curve (AUROC). (E) The Precision-Recall (PR) curves corresponding to the same analyses displayed in part D are shown. A higher Area Under the PR curve (AUPR) corresponds to a more accurate algorithm. (F) The computational time for each network inference algorithm to reverse engineer an in silico network is displayed as a function of the number of assayed nodes. All algorithms show a roughly linear relationship for networks greater than 150 nodes. The change in computational time over the change in the number of assayed nodes over 150 is given by the slope, m. A lower value of m corresponds to a algorithm that can be more easily scaled to infer larger signaling networks.
We found PLSR to have a slightly higher predictive capacity than LASSO, elastic-net, and ridge regression based on the Q2 metric. PLS-VIP also had the sparsest solution with n = 7, narrowing the search space for therapeutic targets. Inclusion of only three principal components eliminated many extraneous sources of variance in the model, securing greater confidence that the selected predictors offer causal insight on the cell phenotype. Therefore, these data suggest that each of the seven nodes could be effective targets for general modulation of cell viability in this cell line. Interestingly, all variable selection methods (PLS-VIP, LASSO, and elastic net) selected p-STAT1[5m] as a significant predictor, securing its relevance and centrality in controlling cell viability in A431 cells (Supplementary Tables 5-6).
DIONESUS accurately infers in silico networks from kinetic data
To identify strategies for cancer treatment, we reconstructed the cell signaling network of 60 phosphosites in the A431 model system. We considered several network inference algorithms, many of which were developed in context of gene regulatory networks,14 but with unknown utility and application to phosphorylation networks. Regression based network-inference methods have proven increasingly useful in predicting large-scale networks.37 As PLS-VIP outperforms other regression methods for predicting cell viability, we hypothesized it would also be useful in inferring edges between phosphosites. An additional advantage of PLSR is that edge confidence can be quantified explicitly using the VIP score rather than using more computationally expensive methods such as bootstrapping, a common approach in regression-based network inference methods. This advantage greatly reduces the computational time, a limiting factor in resolving large networks.
Therefore, we propose a novel method of inferring signaling networks using PLS-VIP. We named this algorithm DIONESUS (for Dynamic Inference Of NEtwork Structure Using Singular values). DIONESUS iterates through the cue-signal matrix, defining each of the signals as a response and calculates whether the other signals and cues are significant predictors. The edge confidences are defined as the VIP score corresponding to each regression problem. The edges confidences are combined and confidences are rank ordered. The list of edge confidences are then thresholded to create a representative computational model of the cell signaling network. To our knowledge, this study is the first to utilize PLS-VIP for the inference of phosphonetworks.
We compared DIONESUS with three top performing network inference algorithms (GENIE3,38 the Inferelator,39 and TIGRESS40) as defined by the Dialogue for Reverse Engineering Assessments and Methods (DREAM5) In Silico Multifactorial challenge for the identification of genetic regulatory network architecture.37 In order to create an unbiased assessment of DIONESUS, kinetic models were created from three separate one-hundred node in silico benchmarks that were extracted from a yeast interactome using GeneNetWeaver as previously described.41,42 The algorithms were implemented to reverse engineer the network structure using the default parameters implemented on the GenePattern server, GP-DREAM.43 The performance of the algorithms were assessed using the area under the receiver operating characteristic (AUROC) curve (Fig. 4C).44 DIONESUS had the highest AUROC at 0.637, compared with 0.620 for GENIE3, 0.609 for TIGRESS, 0.566 for the Inferelator, and 0.573 for pairwise Spearman correlations. These values are in comparison to a theoretical AUROC of 0.500 for a random network. A comparison of AUROCs is given in Supplementary Figure 16 for two other randomly generated in silico networks. For the second in silico network, DIONESUS had the second highest AUROC, slightly lower than GENIE3 (AUROC of 0.585 and 0.595, respectively). For the third in silico network, DIONESUS had the highest performance as rated by the AUROC.
To further compare the performance of DIONESUS in comparison to top performing algorithms, the precision and recall were quantified using the area under the precision-recall curve (AUPR).44 For the first in silico network, DIONESUS had the highest AUPR at 0.219, compared with 0.215 for GENIE3, 0.216 for TIGRESS, 0.176 for the Inferelator, and 0.180 for pairwise Spearman correlations (Fig. 4D). These values are in comparison to a random network having a theoretical AUPR of 0.117. DIONESUS had the highest AUPR scores among all algorithms tested for the subsequent in silico networks (Supplementary Figure 16).
In order to further obtain an unbiased test of the accuracy of our algorithm versus other network inference techniques, DIONESUS was submitted to the DREAM8 Breast Cancer Network Inference Challenge. The submission scored in the top ten for the in silico challenge, supporting its use as an accurate method for network reconstruction (in publication). In summary, DIONESUS accurately reconstructs networks at comparable or superior performance to other top-performing network inference algorithms as assessed by the AUROC and AUPR metrics under the model conditions.
DIONESUS is a scalable algorithm for reconstruction of large networks
We next inquired how the computational expense of DIONESUS scaled with the number of assayed nodes within a network. A major strength of DIONESUS is its fast speed, as no resampling is necessary to derive a quantitative assessment of edge confidence. To quantitively assess the scalability of DIONESUS, we calculated the computational time for the implementation of the network inference algorithms as a function of the number of assayed nodes. Kinetic data was generated from in silico benchmarks using 100, 150, 200, 250, and 300 node networks produced with GeneNetWeaver.42 The computational expense was timed for DIONESUS and compared with GENIE3, the Inferelator, TIGRESS, and pairwise Spearman correlations (Fig. 4E) All of these inference algorithms showed a roughly linear relationship between these variables for networks greater than 150 nodes. The slope, m, was calculated for each algorithm from 150-300 nodes and represents the change in computational time over a change in the number of assayed nodes. The basic correlation method had the smallest value of m at 0.019 suggesting that this method was highly scalable. DIONESUS had a slope comparable to Spearman correlations at an m equal to 0.082. These values were far lower than those calculated for GENIE3 (m = 1.248), TIGRESS (m = 4.240), and the Inferelator (m = 1.483). These data suggest that DIONESUS can easily scale to very large networks and could be efficiently utilized for full genomic, proteomic, or phosphoproteomic studies, common in systems biology.
To assess the propensity of DIONESUS to infer the proper directionality of edges, we developed three separate 3-node in silico toy models using GeneNetWeaver42 to demonstrate the strengths and limitations of inference in resolving the activating or inhibitory nature of each edge. The models characterized linear cascade motifs of the structure: P1→P2→P3. While none of these networks were inferred with 100% accuracy, in each case, the algorithm correctly inferred whether each true edge was activating or inhibitory. In addition, the true edges (e.g. P1→P2) always reflected higher confidence (indicated by the VIP score) than the reverse, false positive edge (e.g. P2→P1). Furthermore, the indirect edge from P1→P3 reflected the least confidence and was consistently below the edge threshold in all three examples. Taken together, the DIONESUS algorithm was able to uncover the most salient features of the in silico models. A summary of these findings is shown in Supplementary Figure 17.
DIONESUS elucidates the A431 signaling network
After assessing the accuracy and scalability of DIONESUS, we applied the algorithm to form a network connecting the cues, signals, and responses of the A431 signaling network. DIONESUS inferred the entire 60-node network in less than one second on a standard desktop computer without parallel processing (Intel Core i7-3770 CPU, 20 GB RAM), demonstrating its ultrafast speed.
An additional advantage of regression-based network inference algorithms, including DIONESUS, is the straightforward incorporation of cues as relevant predictors of phosphosite response. In this way, the mechanism of small molecules, including synthetic chemicals (e.g. n-acetylcysteine) and natural products (e.g. wortmannin), can be elucidated by inferring edges between cue-nodes and signal-nodes. Probable protein targets of a given small molecule are comprised of nodes immediately downstream of the cue within the inferred network.
The architecture of the A431 cell signaling network, as defined by DIONESUS, is shown in Fig. 5. DIONESUS identified many well-characterized edges, such as c-MET→GAB1 (Supplementary Tables 11-12). EGF was identified as the main predictor of p-EGFR(Y1173) and p-EGFR(Y1068). Similarly, IGF was the strongest predictor of p-IGF1R(Y1135/1136), as expected, adding confidence to our methodology.
Fig. 5. The DIONESUS algorithm reveals the network architecture of the cell signaling network in A431 cells.
The DIONESUS algorithm was used to find small molecules and growth factors (cues, as blue rhombi) and phosphosites (signals, as gray or red ovals) that predict each additional phosphosite and cell viability (the response, as a green rectangle). The confidence in each connection is assessed by the VIP score and represented by the thickness of the edge. The sign and magnitude of the β-value associated with each connection is represented by the color of the edge. As cell viability was only quantified at a single time point (24 hrs), the edges pointing to cell viability were quantified separately for each time point. All edges shown in the figure have a corresponding normalized VIP score greater than 3.65; the inset graph shows the distribution of edge weights in comparison to the threshold (assigned using the elbow rule). Nodes corresponding to phosphosites for FGFR, PDGFR, and c-Kit are not shown in this figure for ease of visualization. Signals downstream of the EGF receptor are shown as red ovals to highlight potential therapeutic targets for EGFR-hyperactive cancers.
Further results highlighted the strong antioxidant, n-acetylcysteine, as a significant activator of p-PTEN(S380). This edge might be due to the suppression of the reversible inactivation of phosphatases by the oxidation of the cysteine in the functional group by reactive oxygen species.45 The inferred edge further supports the hypothesis that PTEN is a major sensor of reactive oxygen species in the cellular environment. Surprisingly, the canonical PI3K inhibitor, wortmannin, was shown to inhibit phosphorylation of ribosomal regulator 4EBP1. This suggests that wortmannin may have alternate or additional targets to PI3K including the regulation of p-4EBP1(T37/46), perhaps through inhibition of MTOR.46 These findings highlight the utility of combining the microwestern array with the DIONESUS algorithm to infer the complex behaviors of newly synthesized compounds or natural products with ill-characterized mechanisms of action, revealing primary and off-target effects of drug candidates.
A DIONESUS-inferred network has a high overlap with alternate methods for modeling cell signaling
A prior knowledge list was compiled from ten online databases (BIND, DIP, IntAct, MINT, pdzbase, SAVI, Stelzi, vidal, ncbi _hprd, and kegg _mammalian) using the Genes2Networks tool.47 Although connections between phosphosites are heavily cell line and context dependent, several previously reported edges were confirmed by employing DIONESUS to dynamic phosphoproteomic data in A431 cells, reinforcing DIONESUS as a powerful algorithm to infer pathways in the phosphorylation network (Supplementary Table 13). Prior knowledge was not incorporated in the inferred network in the study, but was used to confirm the accuracy of the algorithm and to determine connections that were not previously reported.
To compare DIONESUS to established network inference algorithms, we applied GENIE3, TIGRESS, and the Inferelator to the identical phosphoproteomic dataset. Results are summarized in Supplementary Note 2 and Supplementary Tables 7-10. Supplementary Figure 18a illustrates a significant overlap of edge detection among DIONESUS and these established methods, specifically with TIGRESS, which employs regularized regression to infer network structure. To quantify the overlap of the inferred edges between algorithms, we calculated the Jaccard similarity coefficient, which is defined by the union divided by the intersection of two adjacency matrices.48 A Jaccard index of 1 corresponds to two perfectly overlapping matrices, whereas an index of 0 corresponds to two completely discordant matrices. Thresholding the inferred edge list at a value of 500, we found the overlap between DIONESUS and GENIE3 to be significant with a Jaccard index of 0.515 (p-value < 10−3). DIONESUS and the Inferelator had a Jaccard index of .362 (p-value < 10−3), while DIONESUS and TIGRESS had an index of .544 (p-value < 10−3). Note that the Jaccard index between the DIONESUS-inferred adjacency matrix and 100 randomly generated 500-edge adjacency matrices is 0.075 ± 0.009 (st. dev.). A full table containing the Jaccard distances between methods is shown in Supplementary Figure 18b.
STAT1 is a significant mediator of EGF-induced cell death
The DIONESUS network identified several key phosphosites downstream of EGFR: p-STAT5(Y694), p-STAT1(Y701), p-CDC2(Y15), p-MET(Y1349), p-SRC(Y416), p-PYK2(Y402), p-SHP2(Y542), p-GAB1(Y627), and p-4EBP1(T37/46). As p-STAT1(Y701) was also inferred to be a significant predictor for cell viability, we hypothesized that enhancing STAT1 signaling in cells overexpressing EGFR is a specific vulnerability that can be exploited to decrease cancer phenotype. The network architecture derived using DIONESUS supports the centrality of STAT1, placing it downstream of EGFR. The model suggests STAT1 is a modulator of cell viability and also an effective target for therapy in EGFR-hyperactive cancers. To validate this finding, we used small molecules to validate inferred edges in a larger panel of cancer model systems.
Small-molecule perturbations validate newly inferred predictors of cell viability
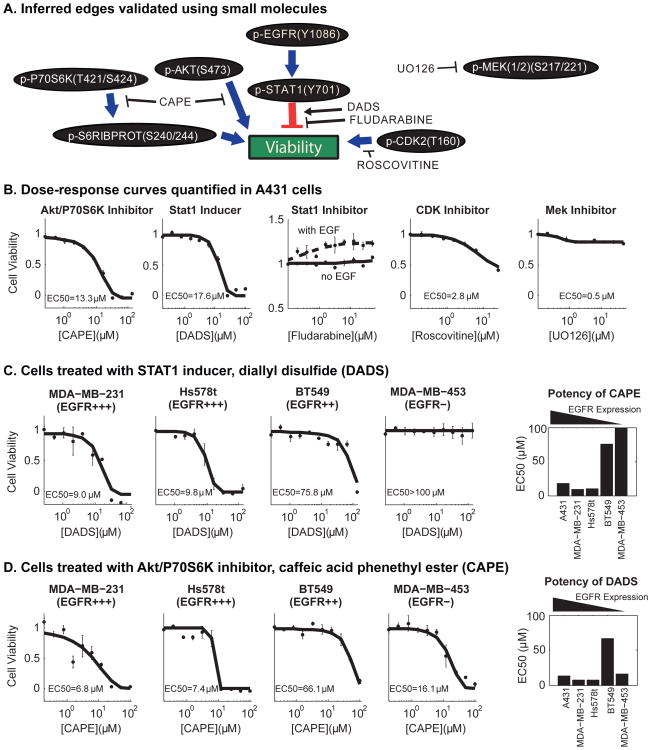
To validate phosphosite interactions, we employed a panel of inhibitors and activators in A431 cells to modulate the following network edges: p-AKT→Viability, p-S6RIBPROT→Viability, p-CDK2→Viability, and p-STAT1→Viability. We employed small-molecule inhibition instead of RNA interference to measure the confidence of an edge, as small molecules have a shorter time scale for action. The shorter time scale of action helps prevent rewiring of the network after removal of the specific signaling node, which can occur after RNA interference.
We tested the validity of these edges by employing a p-AKT/p-P70S6K-inhibitor (Caffeic Acid Phenylethyl Ester, CAPE)24 a CDK2-inhibitor (roscovitine)49, STAT1-inducer (Diallyl Disulfide, DADS)50, and the STAT1-inhibitor (fludarabine)51. As a negative control we used the MEK-inhibitor, UO12652, as MEK and its downstream partner, ERK, were not predicted to have significant effect on cell viability.
In order to obtain a quantitative metric for the effect of each small molecule on cancer cell lines, viability of A431 cells after 24 hrs was quantified after addition of a serial dilution of each small molecule(Figure 6A). The dose-response curves are shown in Figure 6B. As predicted by the network model, inhibition of AKT/P70S6K and CDK2 significantly lowered cell viability, with CAPE having an EC50 (potency) of 13.3 M and roscovitine having an EC50 of 2.5 M. The STAT1-inducer also lowered cell viability at 100% efficacy (EC∞). We found it compelling that the STAT1-inhibitor increased cell viability with no exogenous EGF stimulation. The relative increase in cell number was more pronounced when culturing the cells with 200 ng ml−1 of EGF, further supporting the centrality of this node in controlling EGF-induced cell death. Conversely, the MEK-inhibitor had minimal effect on cell viability, confirming this node as a negative control. These results offer strong evidence for the strength of the MWA in quantifying critical network connections and for the DIONESUS algorithm in identifying interactions between cues, signals, and responses.
Fig. 6. Validation with dose-response curves supports inferred edges from DIONESUS algorithm.
(A) Select nodes and edges from the inferred network model show STAT1 as an intermediary between phosphorylated EGFR and cell viability in addition to other significant contributors to cell phenotype. Small-molecules were chosen from previous reports24,49–52 to enhance or attenuate inferred edges in order to validate connections in the network model. (B) A431 cells were treated with serial dilutions of each small molecule to calculate the potency (EC50) and efficacy (Emax). Points on the dose-response curves show the relative viability (mean ± s.e.) at each concentration. (C) In order to show the relevance of the STAT1-inducer, DADS, in cell lines of varying EGFR expression, dose-response curves were quantified for four triple negative breast cancer cell lines. DADS had lower efficacy in cells with lower EGFR expression and had no effect at the highest soluble dosage in the cell line lacking EGFR expression (MDA-MB-453). (D) As a negative control, a serial dilution of the p-AKT inhibitor, CAPE, was applied to the same panel of cells lines and was shown to be effective in reducing cell viability in all cell lines, but not specific to cells expressing EGFR.
STAT1 stimulation decreases viability specifically in EGFR-overexpressing cancer cells
We assessed the broader applicability of this therapeutic strategy by inquiring whether enhanced STAT1 activity would drive other cancer cell models toward cell death. We used the STAT1-inducer, DADS, on a panel of breast cancer cell lines with varying amounts of EGFR expression: MDA-MB-231 (EGFR+++), Hs578t (EGFR+++), BT549 (EGFR++), and MDA-MB-453 (EGFR-).53 To minimize the effect of molecular drivers of carcinogenesis outside of the scope of this study, we chose breast cancer cell lines lacking the common prognostic biomarkers: ER, PR, and HER2. We found that increasing expression of STAT1 using DADS was effective in lowering the viability of cell lines with higher levels of EGFR but had undetectable potency in a cell line that did not express detectable amounts of EGFR (MDA-MB-453), suggesting that this treatment is cancer subtype specific (Fig. 6C). As a negative control we treated the same panel of cell lines with the AKT/P70S6K inhibitor, CAPE. We found CAPE to be effective in lowering the viability in all cell lines, suggesting that CAPE efficacy was not specific to EGFR overexpressing cells (Fig. 6D). As AKT and P70S6K are downstream of PI3K and significant predictors of cell viability, this particular small molecule might be specific to tumors that have carcinogenic mutations in PTEN or PI3K.24
Discussion
The scalable DIONESUS algorithm allows for quick iteration between experimental design and computational modeling to accelerate systems-level drug discovery. DIONESUS can be easily implemented to infer directed, cyclic networks of whole genomes, proteomes, or phosphoproteomes with negligible computation time and minimal computational complexity. This scalability allows DIONESUS to be highly applicable to infer large network structures using data from such technologies as RNA sequencing or quantitative mass spectrometry.
As DIONESUS uses PLSR to infer network edges, less significant sources of variance may be eliminated to allow more accurate inference from noisy biological datasets. The computational strengths of DIONESUS promotes expansion of the algorithm to detect non-additive relationships between multiple parents of a node allowing rational prediction of synergistic relationships between small molecules affecting a response. The algorithm can be further refined by imposing temporal constraints where information, or directionality, flows from earlier to later time points. Detection of such non-additive relationships and time-dependent signaling would deepen our understanding of regulatory mechanisms within the network. Inference of the cell signaling network across a panel of cell lines with varying amounts of EGFR expression could further elucidate how phosphonetwork architecture changes in cancer and inform new therapeutic strategies. In addition, this method would be useful for identifying phosphoproteomic biomarkers in clinical samples to inform diagnosis and personalized treatment for disease.
Dysregulation of EGFR signaling is common in many cancer subtypes. Our studies identify p-STAT1(Y701) as a significant predictor, or regulator, of cell viability downstream of EGFR. STAT1 expression54,55 and phosphorylation56 have been reported to be necessary for EGF-induced cell death in A431 cells. Our analysis confirmed these reported results, and suggested other possible upstream modulators of STAT1, such as STAT6. In addition, we identified a subset of significant predictors of cell viability suggesting candidate therapies that may have synergistic effect in decreasing cell viability in this cell line; for instance, a combination of Akt-inhibition and STAT1-activation. A compelling further direction of this study would be to create a dynamic model from DIONESUS-derived network architecture to predict synergy between drug combinations. As DIONESUS was able to explicitly calculate the confidence of each edge, it can be valuable in informing experimental design by rank ordering hypothetical new targets to for treating diseases caused by signaling dysregulation.
We demonstrated that enhancing STAT1 expression through treatment with the small molecule, DADS, decreased cell viability specifically in cell lines overexpressing EGFR. This finding suggests that enhancement of STAT1 activity is a potential primary or adjuvant therapeutic option for EGFR-hyperactive cancers. Diallyl disulfide has several favorable properties as a cancer therapy. As DADS is a bioactive natural product derived from aged garlic, it is available without costly approval from the US Food and Drug Administration (FDA).57 Natural products have historically provided all medicinal preparations and continue to inform compounds that have successfully passed clinical trials for the treatment of cancer.57 The DADS molecule may be used as a backbone to synthesize other effective anticancer therapies or be used in combination with other proven anti-cancer drugs. As DADS has been reported to have multiple targets in the cell,58–60 identification of other compounds that specifically enhance STAT1 would be a compelling direction to further improve cancer treatment. We additionally identified PTEN as a target of the antioxidant, n-acetylcysteine, suggesting PTEN may be a sensor for reactive oxygen in the cellular environment.
The difficulty in identifying effective therapeutic agents that are bioavailable and that preferentially inhibit the proliferation and progression of cancer cells represents a major obstacle in the development of effective anti-cancer strategies. For these reasons, we developed a novel pipeline of integrating scalable network inference with the unprecedented protein data acquisition capabilities of the microwestern array. This method represents an attractive means for the development of strategies in molecular systems biology to preferentially treat numerous pathological cellular states. Furthermore, our study suggests a general pipeline for inferring the main targets of small molecules in the cell through direct assay of phosphorylation kinetics with efficient network reconstruction. This study tackles a major challenge in integrative biology: targets of small-molecule modulators such as natural products and synthetic compounds can be inferred in order to understand the complex mechanisms of action for ill-characterized drugs. In addition, off-target effects of approved therapies can be quantified in order to understand, and control for, possible adverse effects. Knowledge of newly discovered targets can also be used to mitigate common adverse effects of current pharmaceutical treatment and to repurpose FDA-approved drug therapies.
Materials and methods
Cell perturbation with growth factors and small molecules
A431 cells were cultured in DMEM with 8% FBS, 0.5% penicillin/streptomycin, and 20 g/mL ciprofloxacin. Cells were then synchronized by incubation in serum-free media for 24 hrs prior to stimulation. Media was replaced with fresh, serum-free DMEM with 0.5% pen/strep, and 20 g/mL ciprofloxacin 30 minutes prior to stimulation (defined as the -30 min time point). For perturbations including small molecules, the chemical perturbants were added with the media at the -30 min time point. Cells were stimulated with minimal growth media, EGF, HGF, IGF, insulin, or a combination thereof, at the 0 time point and collected at -30, 0, 5, and 15 mins post-stimulation. Cell lysates were processed and subjected to microwestern array analysis with a panel of antibodies directed at 60 phosphosites, GAPDH, β-actin, and α-tubulin, as previously described.10 Antibodies were selected from a pool of 91 candidates that generated a relatively high signal to background ratio from the previous study.10 Protein load was normalized per lane by dividing by the average intensity of the following control antibodies: GAPDH, β-actin, and α-tubulin. Fold change was calculated by dividing the 0, 5, and 15 min measurements by the mean signal intensity at the -30 min time point. In order to accommodate 18 samples, microwestern arrays were fabricated with antibody-dividing gaskets containing a width of 18 mm rather than the 9 mm width described previously.10 In cases where there were multiple fluorescent bands in close proximity in the microwestern lane, ImageJ image visualization software was used to graph the pixel intensities from the top to the bottom of the lane. The width of the band was calculated as the distance between the inflection points of the pixel intensity graph over the band length. An example plot showing the determination of band location is shown in Supplementary Figure 19.
Cell viability as the response variable for high-throughput assays
Cell viability was quantified in parallel with the microwestern array assay of short-term phosphorylation kinetics in 24-well dishes following 24 hrs of treatment by fixing, permeabilizing, and staining cells with Syto-60 fluorescent DNA-binding dye (Invitrogen).61 Cell viability was assayed in biological triplicate (3 wells of a 24-well dish) and quantified as the relative percentage of viable cells treated with growth factors and/or small molecules divided by the control cells treated with media alone. Following each perturbation, cells were cultured for 24 hrs in serum-free media in the presence or absence of a perturbing agent. Fluorescence intensities were quantified using the LI-COR Odyssey Image Analysis software (version 1.2). This assay was previously validated against direct cell counts and showed a strong positive correlation with cell number (R2 = 0.995).61
A cue-signal-response matrix derived from the microwestern array assay
The signal matrix in this study was compiled from the quantification of 60 phosphosites following 31 directed cell perturbations over four time points. The perturbation with the small molecule, EGCG, was removed from the matrix as it yielded zero viable cells, barring its use in a useful quantitative regression model. Each phosphorylation was assayed in technical triplicate, and the mean of the three log fold changes was used to inform the model. Although missing data was rare, imperfections in the microwestern array image leading to missing datapoints were replaced with a fold change of 1 (corresponding to a log fold change of 0). Missing datapoints are highlighted in bold in Supplementary Table 3. Since, by definition, the log fold change is zero for the -30 min timepoint, the remaining 30 perturbations over 3 non-zero time points with 60 phosphoantibodies yielded 5400 informative signals. Cues were encoded with dummy variables; the matrix element was set at 1 for conditions where the cue was present and 0 where the cue was absent.
Clustering
All clustering was performed using the clustergram() function in Matlab 2013a using the ‘average’ linkage.
OLS, LASSO, ridge, and elastic-net regression
The general OLS equation is given by the following:
| (1) |
where argmin() is a function that provides the set of parameters, βfit,that minimizes the value of the contained function, here the squared difference between the response and the prediction. Values in the calculated β fit vector represent the predicted weight of variables in X on explaining y. OLS was performed using the polyfit() function in Matlab 2013a. LASSO, ridge, and elastic-net regression were performed using the lasso() function in Matlab 2013a, with λ and α parameters of (0.046,1.000), (0.651,0.010), and (0.4600,0.500), respectively. Data was z-scored by column (condition) to normalize for inter-experimental variance prior to regression. The general equation for these constrained methods is given by the following:
| (2) |
Supplementary Table 9 was used as the input for all methods.
Assessment of model fitness and predictive capacity
Leave-one-out cross-validation was used in this study for all Q2 calculations. R2 and Q2 are defined as the following.
| (3) |
| (4) |
where y is the experimental response variable, and ȳ is the expected value of the experimental response data for each perturbation. ŷ is the predicted response trained on all of the data, and y̌(i) is the predicted response variable from a computational model that is not trained on the condition, i.12,26,62
Partial least squares regression
The following equations were used for PLSR:
| (5) |
| (6) |
| (7) |
where T and U are latent variables that are optimized iteratively to have the maximal covariance. P and C are matrices of the X loadings and y loadings respectively. W is the matrix of X weights.32,62 From these values, the Variance of Importance in Project (VIP) score, which is a metric of the contribution of an explanatory variable to a response, can be calculated. The VIP score for a given predictor is calculated from the following:
| (8) |
where pcs is the number of principal components, Varpc is the variance in the response explained by the principal component, and Wpc is the weight of a given predictor.27,32,62 PLSR was performed using the Non-linear Iterative Partial Least Squares (NIPALS) algorithm36 in Matlab 2013a using the pls_nipals.m code from the library: “libPLS: An Integrated Library for Partial Least Squares Regression and Discriminant Analysis”. The VIP score was calculated using vipp.m, also from libPLS library. Variables were eliminated stepwise in order of reverse magnitude of the VIP metric to find the optimal model fit using leave-one-out cross-validation. Data was z-scored by column (condition) to normalize for inter-experimental variance. Supplementary Table 3 was used as an input for all methods.
Generation of benchmark dynamical models from in silico networks
Three separate one-hundred node realistic in silico networks were extracted from a known in vivo genetic regulatory network of S.cerevisiae using GeneNetWeaver. Kinetic models were simulated from the network to produce time-series protein expression data as previously described.42 Dynamic in silico data was sampled from GeneNetWeaver to have similar characteristics to the phosphopro-teomic, microwestern dataset assayed in this study. The dataset consisted of 50 times series and 6 timepoints. Inference algorithms were applied to the datasets with the same form as those generated in the international DREAM4 competition (Dialogue for Reverse Engineering Assessments and Methods). Three-node in silico models were extracted from the yeast interactome using the same parameters in GeneNetWeaver.
DIONESUS
The input matrix for the DIONESUS algorithm is provided in Supplementary Table 7 and the list of edge confidences is provided in Supplementary Tables 11 and 12. In order to infer the structure of signaling networks, we performed n + o independent regression problems with n being the number of signals and o being the number of responses. For each regression problem, one signal or response was defined as the y vector. We iteratively solved for the relevant cue and signals that predicted each defined response in the regression problems. We compiled the vectors of cues across conditions (assigning 1 for presence of a cue and 0 for its absence in each condition) and the vectors for the phosphorylation state under each condition to create the input matrix, X. Here, all of the time points were treated as separate conditions to give higher statistical power to the network inference. The response vector, y, was excluded as a predictor to avoid self-edges. The rows (explanatory variables) were mean-centered and unit normalized (z-scored). The VIP metric was calculated for all potential edges. Explanatory variables with a VIP<1 were eliminated and the VIP scores were recalculated. The final VIP scores were compiled and sorted in descending order of magnitude. The only two tuning parameters of the DIONESUS algorithm are the number of principal components and the number of edges to include in the network analysis. The former parameter was set to three as inclusion of 3 PCs had the highest average value of . The threshold for edge confidence was set to 3.65 by using the elbow rule.64 Edges with scores above this threshold were included in the network diagram. As cell viability and phosphorylations were assayed at separate time points, the inferred edges between phosphosites and cell viability were calculated separately using PLS-VIP as described above. The edges from each regression problem were combined to form the complete network diagram in Figure 4.
Assessment of TIGRESS, GENIE3, the Inferelator, Spearman correlation, and DIONESUS
TIGRESS, GENIE3, the Inferelator, and Spearman correlation inference algorithms were implemented on the GP-DREAM server43 (http://dream.broadinstitute.org/) using the default parameters. DIONESUS was performed using Matlab 2013a. The tic/toc function was used to calculate computational time. While all methods including DIONESUS are able to run with parallel processing due to the iterative nature of these algorithms, it was not implemented in this study.
Quantification of small-molecule induced viability
Serial dilutions (1:2) of both small molecules and combinations thereof were dissolved in DMSO, and the dilutions were applied to each cell line after being synchronized by 12 hr incubation in serum-free DMEM with high glutamine, sodium pyruvate, 0.5% penicillin/streptomycin, and 20 g/mL ciprofloxacin. The final concentration of DMEM in media was 0.5% for all wells. The impact of small-molecule treatment on cell viability was quantified 24 hrs after treatment by staining with Syto-60 in biological triplicate as described above.61 The data was fit to the following equation using least squares optimization:
| (9) |
where D is the concentration of the small molecule, E is the effect (cell viability), EC50 is the dose causing half-maximal cell viability in comparison to media alone, H is the Hill coefficient, and EC∞ is the limit of the effect as the concentration approaches infinity.65 A431 cells were cultured as described above. All other cell lines were cultured as recommended by ATCC. The cells were synchronized by incubating in serum-free media for 12 hrs prior to drug application.
Statistical analysis
Fold changes in phosphorylation were calculated by dividing by the phosphorylation abundance at the -30 min time point. For the visual illustration in Figure 1, fold changes below 1 were replaced by its negative inverse and centered to 0 by subtracting 1. For all graphs, error bars represent the standard error over three technical replicates.
Supplementary Material
Reconstruction of a signaling network from a phosphoproteomic dataset suggests that enhancement of STAT1 activity is an effective strategy to specifically target EGFR-hyperactive cancer cells. We measured 60 phosphosites at 4 time points after 30 diverse perturbations, designed to interrupt receptor-tyrosine-kinase co-activation, with a modified microwestern array. Microwestern arrays can utilize a broad range of antibodies as electrophoretic separation allows epitopes to be cross-referenced to a size standard. We developed a highly scalable, iterative network inference algorithm, termed DIONESUS, which employs partial least squares regression to remove uninformative sources of variance from the dataset. Integration of DIONESUS with systems-level phosphoprotein measurements efficiently identified new drug targets and inferred the mechanism of action for ill-characterized drug candidates in validation studies.
Acknowledgments
A431 cells were provided by S. Liao (The University of Chicago). MDA-MB-231, MDA-MB-453, BT549, and Hs578t cells were provided by M. Coyle and O. Olapade (The University of Chicago). We thank J.J. Wu, J.J. Muldoon, A.D. Oppenheimer, J.S. Yu, A.Y. Xue, J.D. Finkle, and M.K. Fassia (Northwestern); H.D. Kim, J.L. Barkinge, E. Leypunskiy, G. Yu, and R.J. Hause for their thoughtful feedback on the experiments and manuscript. We thank K.P. White, S.J. Kron, W.J. Tang, and G.L. Greene (University of Chicago) for their respective expertise. We thank J. Barkinge and C. Archer for operating support with microarraying (University of Chicago Microwestern Array Core Facility).
This work was supported, in part, by awards from the Training Grant for Oxygen Biology for pre-doctoral trainees (M.F.C.), Hartwell Postdoctoral Fellowship (M.F.C.), NIH Chicago Center for Systems Biology (R.B.J.), American Cancer Society - Illinois Division (R.B.J.), NIH Chicago Breast Cancer S.P.O.R.E. (R.B.J), National Cancer Institute of the National Institutes of Health under Award Number U54CA143869 (N.B.), and Northwestern University (N.B.). The content is solely the responsibility of the authors and does not represent the official views of the National Institutes of Health or any other funding agency.
Footnotes
Electronic Supplementary Information (ESI) available: [details of any supplementary information available should be included here]. See DOI: 10.1039/b000000x/
Author Contributions: M.F.C., V.C.C., and R.B.J. designed the experiments; M.F.C. and N.B. designed the computational analysis and model. M.F.C. and V.C.C. performed the cell culture. M.F.C. and R.B.J. designed the MWA method. M.F.C. and V.C.C. carried out cell stimulations and cell viability analysis. M.F.C. carried out microwestern array experiments. M.F.C. and N.B. designed the DIONESUS algorithm. M.F.C and N.B. performed computational analysis. M.F.C., R.B.J., and N.B. wrote the manuscript. All authors read and revised the manuscript.
References
- 1.DiMasi JA, Reichert JM, Feldman L, Malins A. Clinical Pharmacology & Therapeutics. 2013;94:329–335. doi: 10.1038/clpt.2013.117. [DOI] [PubMed] [Google Scholar]
- 2.Hopkins AL. Nature Chemical Biology. 2008;4:682–690. doi: 10.1038/nchembio.118. [DOI] [PubMed] [Google Scholar]
- 3.Marcotte R, Brown KR, Suarez F, Sayad A, Karamboulas K, Krzyzanowski PM, Sircoulomb F, Medrano M, Fedyshyn Y, Koh JLY, Dyk Dv, Fedyshyn B, Luhova M, Brito GC, Vizeacoumar FJ, Vizeacoumar FS, Datti A, Kasimer D, Buzina A, Mero P, Misquitta C, Normand J, Haider M, Ketela T, Wrana JL, Rottapel R, Neel BG, Moffat J. Cancer Discovery. 2012;2:172–189. doi: 10.1158/2159-8290.CD-11-0224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sebastian S, Settleman J, Reshkin SJ, Azzariti A, Bellizzi A, Paradiso A. Biochimica et Biophysica Acta (BBA) - Reviews on Cancer. 2006;1766:120–139. doi: 10.1016/j.bbcan.2006.06.001. [DOI] [PubMed] [Google Scholar]
- 5.Srinivas PR, Srivastava S, Hanash S, Wright GL. Clinical Chemistry. 2001;47:1901–1911. [PubMed] [Google Scholar]
- 6.Bagheri N, Taylor SR, Meeker K, Petzold LR, Doyle FJ. Journal of The Royal Society Interface. 2008;5:S17–S28. doi: 10.1098/rsif.2008.0045.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Amit I, Regev A, Hacohen N. Nature Reviews Immunology. 2011;11:873–880. doi: 10.1038/nri3109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Janes KA, Albeck JG, Gaudet S, Sorger PK, Lauffenburger DA, Yaffe MB. Science (New York, NY) 2005;310:1646–1653. doi: 10.1126/science.1116598. [DOI] [PubMed] [Google Scholar]
- 9.Hause RJ, Kim HD, Leung KK, Jones RB. Expert Review of Proteomics. 2011;8:565–575. doi: 10.1586/epr.11.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ciaccio MF, Wagner JP, Chuu C, Lauffenburger DA, Jones RB. Nature Methods. 2010;7:148–155. doi: 10.1038/nmeth.1418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cosgrove BD, Alexopoulos LG, Hang Tc, Hendriks BS, Sorger PK, Griffith LG, Lauffenburger DA. Molecular bioSystems. 2010;6:1195–1206. doi: 10.1039/b926287c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ciaccio MF, Finkle JD, Xue AY, Bagheri N. Integrative and Comparative Biology. 2014:icu037. doi: 10.1093/icb/icu037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Janes KA, Kelly JR, Gaudet S, Albeck JG, Sorger PK, Lauffenburger DA. Journal of Computational Biology. 2004;11:544–561. doi: 10.1089/cmb.2004.11.544. [DOI] [PubMed] [Google Scholar]
- 14.Bonneau R. Nature Chemical Biology. 2008;4:658–664. doi: 10.1038/nchembio.122. [DOI] [PubMed] [Google Scholar]
- 15.Bravo R, Burckhardt J, Curran T, Mller R. The EMBO Journal. 1985;4:1193–1197. doi: 10.1002/j.1460-2075.1985.tb03759.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xu AM, Huang PH. Cancer Research. 2010;70:3857–3860. doi: 10.1158/0008-5472.CAN-10-0163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Leung KK, Hause RJ, Barkinge JL, Ciaccio MF, Chuu CP, Jones RB. Molecular & Cellular Proteomics. 2014 doi: 10.1074/mcp.M113.034876. mcp.M113.034876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stommel JM, Kimmelman AC, Ying H, Nabioullin R, Ponugoti AH, Wiedemeyer R, Stegh AH, Bradner JE, Ligon KL, Brennan C, Chin L, DePinho RA. Science. 2007;318:287–290. doi: 10.1126/science.1142946. [DOI] [PubMed] [Google Scholar]
- 19.Singh AB, Harris RC. Cellular Signalling. 2005;17:1183–1193. doi: 10.1016/j.cellsig.2005.03.026. [DOI] [PubMed] [Google Scholar]
- 20.Lou Y, Chen Y, Hsu S, Chen R, Lee C, Khoo K, Tonks NK, Meng T. The FEBS Journal. 2008;275:69–88. doi: 10.1111/j.1742-4658.2007.06173.x. [DOI] [PubMed] [Google Scholar]
- 21.Cattaneo F, Iaccio A, Guerra G, Montagnani S, Ammendola R. Free Radical Biology and Medicine. 2011;51:1126–1136. doi: 10.1016/j.freeradbiomed.2011.05.040. [DOI] [PubMed] [Google Scholar]
- 22.Liu J, Kuo W, Seiwert TY, Lingen M, Ciaccio MF, Jones RB, Rosner MR, Cohen EEW. Head & Neck. 2011 doi: 10.1002/hed.21701. [DOI] [PubMed] [Google Scholar]
- 23.Chevrier N, Mertins P, Artyomov MN, Shalek AK, Iannacone M, Ciaccio MF, Gat-Viks I, Tonti E, Degrace MM, Clauser KR, Garber M, Eisenhaure TM, Yosef N, Robinson J, Sutton A, Andersen MS, Root DE, von Andrian U, Jones RB, Park H, Carr SA, Regev A, Amit I, Hacohen N. Cell. 2011;147:853–867. doi: 10.1016/j.cell.2011.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chuu C, Lin H, Ciaccio MF, Kokontis JM, Hause J, Ronald J, Hiipakka RA, Liao S, Jones RB. Cancer Prevention Research (Philadelphia, Pa) 2012;5:788–797. doi: 10.1158/1940-6207.CAPR-12-0004-T. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Picard RR, Cook RD. Journal of the American Statistical Association. 1984;79:575–583. [Google Scholar]
- 26.Hawkins DM, Basak SC, Mills D. Journal of chemical information and computer sciences. 2003;43:579–586. doi: 10.1021/ci025626i. [DOI] [PubMed] [Google Scholar]
- 27.Wold S, Sjöström M, Eriksson L. Chemometrics and Intelligent Laboratory Systems. 2001;58:109–130. [Google Scholar]
- 28.Tibshirani R. Statistics in Medicine. 1997;16:385–395. doi: 10.1002/(sici)1097-0258(19970228)16:4<385::aid-sim380>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 29.Zou H, Hastie T. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2005;67:301–320. [Google Scholar]
- 30.Efron B, Hastie T, Johnstone I, Tibshirani R. The Annals of Statistics. 2004;32:407–499. [Google Scholar]
- 31.Tjarnberg A, Nordling T, Studham M, Nelander S, Sonnhammer E. Mol BioSyst. 2014 doi: 10.1039/c4mb00419a. [DOI] [PubMed] [Google Scholar]
- 32.Höskuldsson A. Journal of Chemometrics. 1988;2:211–228. [Google Scholar]
- 33.Janes KA, Yaffe MB. Nature Reviews Molecular Cell Biology. 2006;7:820–828. doi: 10.1038/nrm2041. [DOI] [PubMed] [Google Scholar]
- 34.Miller-Jensen K, Janes KA, Brugge JS, Lauffenburger DA. Nature. 2007;448:604–608. doi: 10.1038/nature06001. [DOI] [PubMed] [Google Scholar]
- 35.Gaudet S, Janes KA, Albeck JG, Pace EA, Lauffenburger DA, Sorger PK. Molecular & Cellular Proteomics. 2005;4:1569–1590. doi: 10.1074/mcp.M500158-MCP200. [DOI] [PubMed] [Google Scholar]
- 36.Miyashita Y, Itozawa T, Katsumi H, Sasaki S. Journal of Chemometrics. 1990;4:97–100. [Google Scholar]
- 37.Marbach D, Costello JC, Kuffner R, Vega NM, Prill RJ, Camacho DM, Allison KR, Kellis M, Collins JJ, Stolovitzky G The DREAM5 Consortium. Nature Methods. 2012;9:796–804. doi: 10.1038/nmeth.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Huynh-Thu VA, Irrthum A, Wehenkel L, Geurts P. PLoS ONE. 2010;5:e12776. doi: 10.1371/journal.pone.0012776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bonneau R, Reiss DJ, Shannon P, Facciotti M, Hood L, Baliga NS, Thorsson V. Genome Biology. 2006;7:R36. doi: 10.1186/gb-2006-7-5-r36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Haury AC, Mordelet F, Vera-Licona P, Vert JP. BMC systems biology. 2012;6:145. doi: 10.1186/1752-0509-6-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Marbach D, Schaffter T, Mattiussi C, Floreano D. Journal of Computational Biology: A Journal of Computational Molecular Cell Biology. 2009;16:229–239. doi: 10.1089/cmb.2008.09TT. [DOI] [PubMed] [Google Scholar]
- 42.Schaffter T, Marbach D, Floreano D. Bioinformatics (Oxford, England) 2011;27:2263–2270. doi: 10.1093/bioinformatics/btr373. [DOI] [PubMed] [Google Scholar]
- 43.Reich M, Liefeld T, Gould J, Lerner J, Tamayo P, Mesirov JP. Nature Genetics. 2006;38:500–501. doi: 10.1038/ng0506-500. [DOI] [PubMed] [Google Scholar]
- 44.Prill RJ, Marbach D, Saez-Rodriguez J, Sorger PK, Alexopoulos LG, Xue X, Clarke ND, Altan-Bonnet G, Stolovitzky G. PloS One. 2010;5:e9202. doi: 10.1371/journal.pone.0009202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lee SR, Yang KS, Kwon J, Lee C, Jeong W, Rhee SG. Journal of Biological Chemistry. 2002;277:20336–20342. doi: 10.1074/jbc.M111899200. [DOI] [PubMed] [Google Scholar]
- 46.Brunn GJ, Williams J, Sabers C, Wiederrecht G, Lawrence JC, Abraham RT. The EMBO Journal. 1996;15:5256–5267. [PMC free article] [PubMed] [Google Scholar]
- 47.Berger SI, Posner JM, Ma'ayan A. BMC Bioinformatics. 2007;8:372. doi: 10.1186/1471-2105-8-372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Levandowsky M, Winter D. Nature. 1971;234:34–35. [Google Scholar]
- 49.Meijer L, Borgne A, Mulner O, Chong JPJ, Blow JJ, Inagaki N, Inagaki M, Delcros JG, Moulinoux JP. European Journal of Biochemistry. 1997;243:527–536. doi: 10.1111/j.1432-1033.1997.t01-2-00527.x. [DOI] [PubMed] [Google Scholar]
- 50.Lu H, Yang J, Lin Y, Tan T, Ip S, Li Y, Tsou M, Chung J. Cancer Genomics - Proteomics. 2007;4:93–97. [PubMed] [Google Scholar]
- 51.Frank DA, Mahajan S, Ritz J. Nature Medicine. 1999;5:444–447. doi: 10.1038/7445. [DOI] [PubMed] [Google Scholar]
- 52.Duncia JV, Santella JB, III, Higley CA, Pitts WJ, Wityak J, Frietze WE, Rankin FW, Sun JH, Earl RA, Tabaka AC, Teleha CA, Blom KF, Favata MF, Manos EJ, Daulerio AJ, Stradley DA, Horiuchi K, Copeland RA, Scherle PA, Trzaskos JM, Magolda RL, Trainor GL, Wexler RR, Hobbs FW, Olson RE. Bioorganic & Medicinal Chemistry Letters. 1998;8:2839–2844. doi: 10.1016/s0960-894x(98)00522-8. [DOI] [PubMed] [Google Scholar]
- 53.Subik K, Lee JF, Baxter L, Strzepek T, Costello D, Crowley P, Xing L, Hung MC, Bonfiglio T, Hicks DG, Tang P. Breast Cancer : Basic and Clinical Research. 2010;4:35–41. [PMC free article] [PubMed] [Google Scholar]
- 54.Jf B, Z F, C B, J M, J D., Jr Cell growth & differentiation : the molecular biology journal of the American Association for Cancer Research. 1998;9:505–512. [PubMed] [Google Scholar]
- 55.Grudinkin PS, Zenin VV, Kropotov AV, Dorosh VN, Nikolsky NN. European Journal of Cell Biology. 2007;86:591–603. doi: 10.1016/j.ejcb.2007.05.009. [DOI] [PubMed] [Google Scholar]
- 56.Kozyulina PY, Okorokova LS, Nikolsky NN, Grudinkin PS. Biochemical and Biophysical Research Communications. 2013;430:331–335. doi: 10.1016/j.bbrc.2012.11.041. [DOI] [PubMed] [Google Scholar]
- 57.Harvey AL, Edrada-Ebel R, Quinn RJ. Nature Reviews Drug Discovery. 2015;14:111–129. doi: 10.1038/nrd4510. [DOI] [PubMed] [Google Scholar]
- 58.Nakagawa H, Tsuta K, Kiuchi K, Senzaki H, Tanaka K, Hioki K, Tsubura A. Carcinogenesis. 2001;22:891–897. doi: 10.1093/carcin/22.6.891. [DOI] [PubMed] [Google Scholar]
- 59.Lei X, Yao S, Zu X, Huang Z, Liu L, Zhong M, Zhu B, Tang S, Liao D. Acta Pharmacologica Sinica. 2008;29:1233–1239. doi: 10.1111/j.1745-7254.2008.00851.x. [DOI] [PubMed] [Google Scholar]
- 60.Sundaram SG, Milner JA. Carcinogenesis. 1996;17:669–673. doi: 10.1093/carcin/17.4.669. [DOI] [PubMed] [Google Scholar]
- 61.Widberg CH, Newell FS, Bachmann AW, Ramnoruth SN, Spelta MC, Whitehead JP, Hutley LJ, Prins JB. American Journal of Physiology Endocrinology and Metabolism. 2009;296:E121–131. doi: 10.1152/ajpendo.90602.2008. [DOI] [PubMed] [Google Scholar]
- 62.Miraldi ER, Sharfi H, Friedline RH, Johnson H, Zhang T, Lau KS, Ko HJ, Curran TG, Haigis KM, Yaffe MB, Bonneau R, Lauffenburger DA, Kahn BB, Kim JK, Neel BG, Saghatelian A, White FM. Integrative Biology. 2013;5:940–963. doi: 10.1039/c3ib40013a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Li H, Xu Q, Liang Y. 2014;1 year. [Google Scholar]
- 64.Thorndike RL. Psychometrika. 1953;18:267–276. [Google Scholar]
- 65.Fallahi-Sichani M, Honarnejad S, Heiser LM, Gray JW, Sorger PK. Nature chemical biology. 2013;9:708–714. doi: 10.1038/nchembio.1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.