A Method for Automated Cortical Surface Registration and Labeling

Abstract

Registration and delineation of anatomical features in MRI of the human brain play an important role in the investigation of brain development and disease. Accurate, automatic and computationally efficient cortical surface registration and delineation of surface-based landmarks, including regions of interest (ROIs) and sulcal curves (sulci), remain challenging problems due to substantial variation in the shapes of these features across populations. We present a method that performs a fast and accurate registration, labeling and sulcal delineation of brain images. The new method presented in this paper uses a multiresolution, curvature based approach to perform a registration of a subject brain surface model to a delineated atlas surface model; the atlas ROIs and sulcal curves are then mapped to the subject brain surface. A geodesic curvature flow on the cortical surface is then used to refine the locations of the sulcal curves sulci and label boundaries further, such that they follow the true sulcal fundi more closely. The flow is formulated using a level set based method on the cortical surface, which represents the curves as zero level sets. We also incorporate a curvature based weighting that drives the curves to the bottoms of the sulcal valleys in the cortical folds. Finally, we validate our new approach by comparing sets of automatically delineated sulcal curves it produced to corresponding sets of manually delineated sulcal curves. Our results indicate that the proposed method is able to find these landmarks accurately.

1 Introduction

Human cerebral cortex is often modeled as a highly convoluted sheet of gray matter. Inter- and intra-subject comparison involving anatomical changes over time or differences between populations requires the spatial alignment of the cortical surfaces, such that they have a common coordinate system that is anatomically meaningful. Sulcal curves are fissures in the cortical surface and are commonly used as surrogates for the cytoarchitectural boundaries in the brain. Therefore, there is also great interest in direct analysis of the geometry of these curves for studies of disease propagation, symmetry, development and group differences (e.g. [10,8]). Labels of cortical regions of interest (ROIs) or sulcal curves that are often required for these studies and can be produced using manual [13] or automatic delineation [15,17]. Manual delineation is often performed using an interactive software tools [13]. This, however, can be a tedious and subjective task that also requires substantial knowledge of neuroanatomy and is therefore confounded by intra- and inter-rater variability. This variability is reduced to some extent using rigorous definitions of a sulcal tracing protocol and extensive training as described in [9,13].

An alternative approach to this problem is to use automatic surface registration to align surface curvature or sulcal depth [2]. Sulcal curves can be delineated on a reference atlas brain surface, which is then aligned with the subject brain surface using automated registration. The sulci from the atlas are then transferred to the subject using the point correspondence defined by the surface mapping. While this approach can find the sulcal location approximately, there is often substantial residual error [9]. This is because automatic methods align the whole surface using curvature and do not focus specifically on the sulcal locations and label boundaries, which are sometimes biased by the reference atlas chosen. Also, the variability of the atlas and subject folds can be reflected in the misalignment of sulcal curves, thus the transferred sulcal curves may not lie at the valleys of the subject surfaces. A local refinement of the curves representing sulci and label boundaries can alleviate this problem. This paper describes a fast and accurate surface registration and curve refinement method based on 2D flat mapping and geodesic curvature flow on surfaces where the sulcal curves are represented as curvature weighted geodesics. The surface registration method presented here extends the surface registration method presented in [4] that required manually traced sulcal inputs. The cortical labels from the atlas cortex surface model are then transferred to the subject cortex surface model using the point correspondence. The local refinement of this registration is performed by using geodesic curvature flow of the label boundaries as described for parametric surfaces in [14]. Here, we use a level set based formulation similar to [19,6] and apply it to the label boundary refinement and sulcal detection problem. The curve evolution is defined in terms of evolution of a zero level set. The flow is discretized in the surface geometry using a finite element method.

2 Materials and Methods

We assume as input, an atlas brain surface mesh with manually delineated surface labels as well as sulcal landmarks and a subject brain surface mesh. The goal is to perform atlas to subject cortical surface registration and transfer cortical labels and delineated sulci from atlas surface to the subject surface. First, we briefly describe an automated curvature based registration approach that performs alignment of the atlas surface and the subject surface. The cortical labels and sulci from the atlas surface are then transferred to the subject surface.

2.1 Cortical surface registration

We developed a single subject anatomical atlas brain based on a T1-weighted MRI from which we generated inner cortical and pial surfaces using our BrainSuite software [12]. These surfaces were labeled with anatomical structures (35×2 ROIs) and sulcal curves (26×2) that were delineated manually by an expert neuroanatomist (Fig 1). We apply a surface-based registration method that establishes one-to-one correspondence between the atlas surface $\mathcal{A}$ and the subject surface $\mathcal{S}$. The method for surface registration has three stages: (i) for subject and atlas, we generate a smoothed representation of the subject and atlas surfaces and then perform a L₂ energy based 3D matching, (ii) for each subject, we parameterize the surface of each cortical hemisphere to a unit square (iii) find a vector field with respect to this parameterization which aligns curvature of the surfaces and the 3D aligned coordinates from step (i).

Fig. 1.

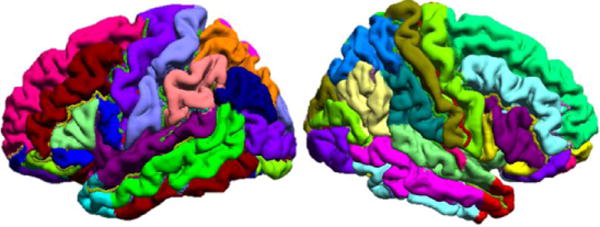
Rendering of the brain atlas cortical surface used in this work. The gyri have been labeled manually and are coded with different colors on the surface. Manually traced sulcal curves are also shown.

First, the multiresolution representation of curvature, as shown in Fig. 2, is generated using an iterative smoothing of the cortical surface and computation of the mean curvature at each iteration. The smoothing is performed by mean curvature flow [16]. Additionally, we also use the computed mean curvature as a feature for surface matching in the subsequent steps. The reason for using the mean curvature is that it represents the sulcal fundi with negative values and gyral crowns with positive values, therefore its alignment leads to accurate alignment of the cortex.

Fig. 2.

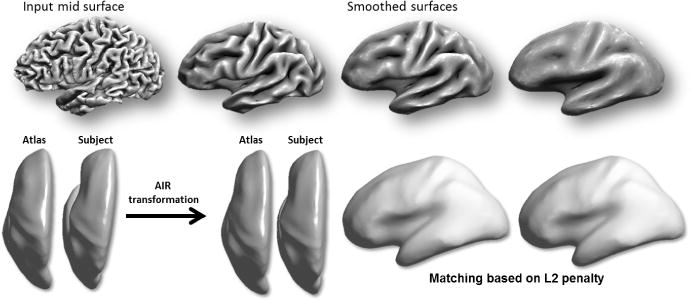
(Top) Mid-cortical surface iteratively inflated by mean curvature flow to generate a multiresolution representation of the cortical surface. (Bottom) Initial 3D alignment of the cortex, first by using deformation field of AIR and later by L₂ energy minimization.

Next, we perform a coarse alignment of these smooth surfaces in 3D. For this purpose, we first apply a 5th order polynomial warping field to the subject and atlas surfaces; this field is computed using AIR [18] as part of BrainSuite’s extraction sequence. This is followed by an L₂ surface registration procedure described in [5] as shown in Fig. 2. We chose initial alignment of the cortex based on the 5th degree polynomial initialization which is followed by L² surface registration. This rough alignment is fast because it is surface based and is performed in 3D rather than in the flat space. Additionally at this point our goal is compute an alignment of the major lobes and these are better defined by their 3D locations rather than local features such as curvature. Curvature registration in flat space then refines this alignment.

The subject and atlas surfaces are mapped to the unit square using p-harmonic mappings as described in [4]. The p-harmonic maps generate a one-to-one correspondence between a unit square and the cortical surfaces such that the inter-hemispherical fissure dividing the left and right hemisphere maps to the boundary of the unit square as a uniform speed curve. The cumulative curvature maps generated in the previous step are then transferred to the unit squares using the point correspondence established by the p-harmonic maps. To perform the curvature based alignment, we model the brain surface as an elastic sheet and solve the associated linear elastic equilibrium equation using the Finite Element Method (FEM) as described in [4]. The alignment of the curvature maps is then performed by minimizing a cost function with elastic energy as a regularizing penalty. This reparameterizes the cortical hemisphere surfaces and establishes a one-to-one point correspondence between subject and atlas surfaces. For every point s in the unit square space, let $C_{\mathcal{A}}(s)$ and $C_{\mathcal{S}}(s)$ denote the cumulative mean curvature values at s for atlas and subject, respectively. Also, X(s) = [x(s),y(s),z(s)]^T denotes the 3D vertex coordinates of the surface at the mapped point s; $X_{\mathcal{A}}$ and $X_{\mathcal{S}}$ denotes aligned atlas and subject surfaces 3D coordinates described in the previous paragraph. Let E denotes elastic energy regularizer computed on the surface mesh. Then we find a deformation field ϕ that minimizes the cost function:

$$C(\varphi )=E(\varphi (s))+{\sigma }_1{\Vert C_{\mathcal{A}}(\varphi (s))-C_{\mathcal{S}}(s)\Vert }^2+{\sigma }_2{\Vert X_{\mathcal{A}}(\varphi (s))-X_{\mathcal{S}}(s)\Vert }^2.$$ (1)

The parameters σ₁ = .5, σ₂ = .1 were chosen empirically. The cost function minimizes the weighted sum of a curvature matching penalty and a 3D coordinate matching penalty, regularized by an elastic energy [4]. The optimization of the cost is performed by applying the L-BFGS optimization scheme [7]. The flat maps corresponding to the subject, atlas and warped subject are shown in Fig. 4.

Fig. 4.

Flat maps produced by the automatic surface registration sequence. Shown are the atlas, subject, and warped subject flatmaps, shaded according to curvature (bright=positive; dark=negative); and the atlas-color flatmap colored according to anatomical ROI labels.

After performing the atlas to subject registration, the sulcal curves and cortical labels from the atlas are transferred to the cortical surface (Fig. 5).

Fig. 5.

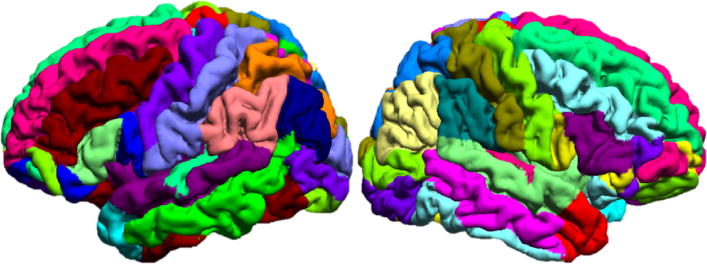
Lateral views of the left and right hemispheres of an automatically labeled subject cortical surface. The labels from the atlas surface were transferred to the subject’s surface by using the correspondence established by registration.

2.2 Geodesic curvature flow on surfaces

The second major step in our method performs local refinement of the transferred sulcal curves and label boundaries using a geodesic curvature flow [6,19] so that these boundaries conform to sulcal fundi as represented by the curvature minima. In this section, we discuss the refinement of these sulcal curves, but note that the label boundaries are refined in a similar manner. The numerical implementation and FEM formulation of this method is described in detail in [3]; we describe it here briefly but omit the details. By using the point correspondence established by the registration, the sulcal curves on the atlas are transferred to the subject surface; we refer to these as the RT curves. The RT curves are typically in the correct sulcal valley, but are not precisely at their desired locations at the bottoms of these valleys. It has been noted that the sulci propagated by automatic registration generally lie withing 3cm of the true sulcal valleys [9]. Therefore, to reduce the computational burden, we calculate a surface patch around the sulcus of interest using front propagation for 3cm (Fig. 6).

Fig. 6.

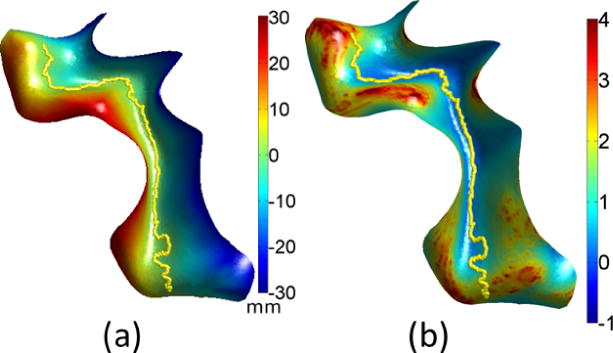
(a) Initial sulcal curve and signed distance function; (b) curvature weighting function f shown as color-coded overlay on the surface patch around that sulcus.

The geodesic curvature flow is performed over this surface patch around the sulcus of interest using a level set formulation. The approach presented here is based on [6], but in our case we add curvature weighting when computing minimizing geodesics. Assume $\mathcal{M}$ is a general 2D manifold representing the surface patch embedded in ℝ³ and let Γ be the sulcal curve on the surface. Let the curve Γ be represented by the zero level set of a function $\varphi :\mathcal{M}\to \text{ℝ}$, i.e., Γ = {s: ϕ (s) = 0}. Suppose that $c:\mathcal{M}\to \text{ℝ}$ is the curvature of the surface $\mathcal{M}$. It has been noted that for sulcal tracing, a sigmoid function of the curvature works well as a weighting function on the paths for sulcal tracing [13]. Therefore, we define $f(s)=\frac{1}{1+e^{-2c(s)}}$ as the curvature based weights on the surfaces and seek to minimize the weighted length of Γ given by

$$E(\Gamma )={\displaystyle {\int }_{\Gamma :\varphi =0}\mathit{fds}}$$ (2)

where integration is computed over the surface at the curve points. Following [6,14,19], the Euler-Lagrange equations for the energy functional minimization of E(Γ) yield

$$\{\begin{array}{ll}-\mathrm{div}\left(f\frac{\nabla \varphi }{|\nabla \varphi |}\right)\hfill & =0\hfill \\ \frac{\partial \varphi }{\partial \overrightarrow{n}}|\partial \mathcal{M}\hfill & =0,\hfill \end{array}$$ (3)

where $\partial \mathcal{M}$ is the boundary of $\mathcal{M}$ and $\overrightarrow{n}$ is the intrinsic outward normal of $\partial \mathcal{M}$. A gradient descent flow of the equation [1] is given by:

$$\{\begin{array}{l}\frac{\partial \varphi }{\partial t}=|\nabla \varphi |\mathrm{div}\left(f\frac{\nabla \varphi }{|\nabla \varphi |}\right)\hfill \\ \frac{\partial \varphi }{\partial \overrightarrow{n}}|\partial \mathcal{M}=0\hfill \\ \varphi (0)={\varphi }_0\hfill \end{array}$$ (4)

where we choose ϕ₀ to be a signed distance function from the initial sulcal curve. The boundary condition is discretized using standard finite element approaches (see [11] and [3] for details). This system of equations is solved using a preconditioned conjugate gradient method with a Jacobi preconditioner.

We implemented the algorithm in Matlab. We choose Δt = .5 and the number of iterations N_iter = 20. The algorithm takes approximately 1.5 hours per subject hemisphere for the refinement of all sulci and boundary labels on a 4 core Intel i7 computer. The final refined curves and label boundaries were extracted by finding the zero level set of the function ϕ after 20 iterations.

To refine the label boundaries between two adjacent ROIs, we first extract the surface patch corresponding to the two label surfaces. The level set function is then initialized using the signed distance function such that the zero level set corresponds to the ROI boundary. The geodesic curvature flow procedure described above is then applied to refine this boundary.

3 Results

To evaluate the performance of our method, we performed a validation study on a set of 6 subject brains. We used the ICBM Single Subject Template as our atlas (http://www.loni.ucla.edu/Atlases/Atlas_Detail.jsp?atlas_id=5). The BrainSuite software [12] was applied to extract cortical surface meshes from the subject and atlas MRI data. BrainSuite includes a multistage cortical modeling sequence. First, the brain is extracted from the surrounding skull and scalp tissues using a combination of edge detection and mathematical morphology. Next, the intensities of the MRI are corrected for shading artifacts. Each voxel in the corrected image is then labeled according to tissue type using a statistical classifier. A standard atlas with associated structure labels is aligned to the subject volume, providing a label for cerebellum, cerebrum, brainstem, and subcortical regions. These labels are combined with the tissue classification to identify the cerebral white matter automatically, to fill the ventricular spaces, and to remove the brainstem and cerebellum. This produces a volume whose boundary surface represents the outer white-matter surface of the cerebral cortex. Prior to tessellation, topological defects are identified and removed automatically from the binary volume using a graph based approach. An isosurface algorithm is then applied to the topologically corrected white matter volume, yielding a genus zero surface. This surface is then expanded to identify the pial surface, i.e., the boundary between grey matter and CSF. The inner cortical and pial surfaces are then split into left and right hemispheres based on the registered atlas labels.

We delineated sulcal curves using BrainSuite’s interactive delineation tools [13] following a sulcal protocol with 26 sulcal curves [9]. These sulci are consistently seen in normal brains and are distributed throughout the entire cortical surface. A thorough description of the sulcal curves with instructions on how to trace them is available on the web site (http://neuroimage.usc.edu/CurveProtocol.html). The protocol specifies methods for identifying the 26 sulci by making consistent decisions in delineation in case of ambiguity in the brain anatomy. We traced the curves on the midcortical surface because it provides better access to the depth of the sulci than the pial surface, and the valleys of the sulci are more convex than they are on the white matter surface, thus allowing more stable tracing of the curves. The same procedure was repeated on the single subject atlas. Next, we performed the subject to atlas registration as described in Sec. 2.1 and transferred the curves of the atlas to the subject brains. The transferred curves were refined using the geodesic curvature flow as discussed in Sec 2.2. The evolution of one sulcal curve in shown in Fig. 7 (online link:http://sipi.usc.edu/~ajoshi/GCF_Sulci.html).

Fig. 7.

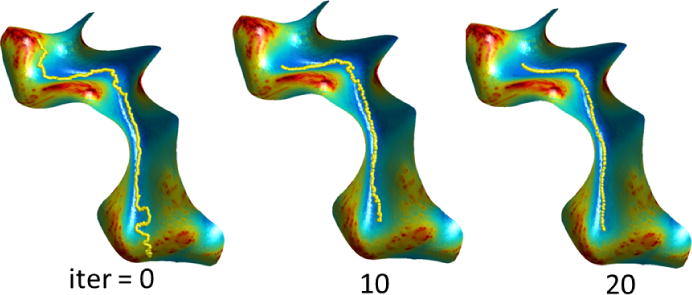
Evolution of the sulcal curve by geodesic curvature flow for different iterations. The curvature weighting function f is shown as color-coded overlay

To compare the alignment of transferred curves, as well as the refined curves, we mapped the 26 protocol curves from all subjects to the target surface. We then quantified their accuracy using their variance on the subject surface, which is estimated as follows. We use a distance measure based on the Hausdorff distance metric:

$$d(D_i,D_j)=0.5\frac{1}{N}{\displaystyle \sum _{p\in D_i}\underset{p\in D_i}{min}{\left|p-q\right|}^2+0.5\frac{1}{N}}{\displaystyle \sum _{p\in D_j}\underset{p\in D_j}{min}{\left|p-q\right|}^2}$$

where d(D_i,D_j) is the distance between the curves D_i and D_j. This distance is computed between subject’s manual curve and RT curve, as well as manual curve and GCF curve.

The results for some of the prominent sulci are presented in Table 1. It can be seen that the sulcal error is reduced substantially after geodesic curvature flow. This improvement is most pronounced in the sulci that are clearly defined by curvature extrema and shortest length paths on the cortex such as central sulcus and superior frontal sulcus.

Table 1.

Sulcal errors measured by Hausdorff distance metric. The table shows mean error for N=6

	manual vs transferred curves (mm)	manual vs refined curves (mm)
Cent. sulcus	1.9	1.4
Sup. Front. sulcus	2.9	1.9
Calc. sulcus	2.6	2.0
Sup. Temp. sulcus	3.9	3.4
Avg over all 26 sulci	3.6	2.9

4 Conclusion

This paper presents a method for accurate and automatic cortical registration and delineation of sulcal curves on human brain cortex. The 2D mapping, level set approach and FEM formulations enabled us to perform surface registration and geodesic curvature flow on the surface in a computationally efficient manner. A more extensive evaluation is planned. The software with source code will be made available online in the near future.

Fig. 3.

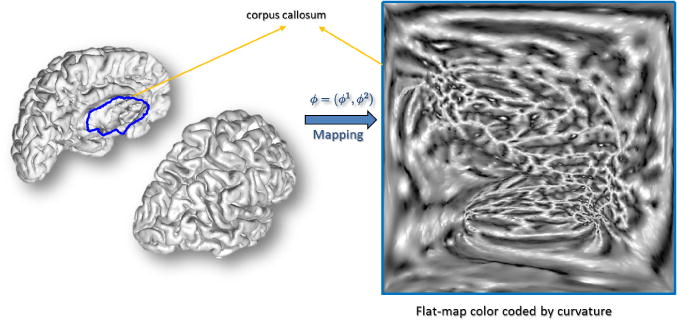
p-harmonic mapping of the cortex generated by p-harmonic energy minimization. The corpus callosum denoted by the blue boundary is mapped to the boundary of the square. After the energy minimization the cortical hemisphere maps to the inside of the square.