Spatially Weighted Principal Component Regression for High-dimensional Prediction

Abstract

We consider the problem of using high dimensional data residing on graphs to predict a low-dimensional outcome variable, such as disease status. Examples of data include time series and genetic data measured on linear graphs and imaging data measured on triangulated graphs (or lattices), among many others. Many of these data have two key features including spatial smoothness and intrinsically low dimensional structure. We propose a simple solution based on a general statistical framework, called spatially weighted principal component regression (SWPCR). In SWPCR, we introduce two sets of weights including importance score weights for the selection of individual features at each node and spatial weights for the incorporation of the neighboring pattern on the graph. We integrate the importance score weights with the spatial weights in order to recover the low dimensional structure of high dimensional data. We demonstrate the utility of our methods through extensive simulations and a real data analysis based on Alzheimer’s disease neuroimaging initiative data.

1 Introduction

Our problem of interest is to predict a set of response variables Y by using high-dimensional data x = {x_g : g ∈ } measured on a graph ζ = ( , ), where is the edge set of ζ and = {g₁, …, g_m} is a set of vertexes, in which m is the total number of vertexes in . The response Y may include cognitive outcome, disease status, and the early onset of disease, among others. Standard graphs including both directed and undirected graphs have been widely used to build complex patterns [10]. Examples of graphs are linear graphs, tree graphs, triangulated graphs, and 2-dimensional (2D) (or 3-dimensional (3D)) lattices, among many others (Figure 1). Examples of x on the graph ζ = ( , ) include time series and genetic data measured on linear graphs and imaging data measured on triangulated graphs (or lattices). Particularly, various structural and functional neuroimaging data are frequently measured in a 3D lattice for the understanding of brain structure and function and their association with neuropsychiatric and neurodegenerative disorders [9].

Fig. 1.

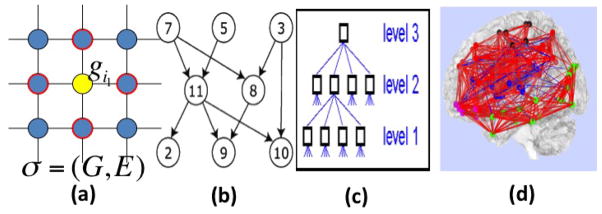
Illustration of graph data structure ζ = ( , 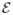): (a) two-dimensional lattice; (b) acyclic directed graph; (c) tree; (d) undirected graph.

The aim of this paper is to develop a new framework of spatially weighted principal component regression (SWPCR) to use x on graph ζ = { , 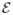} to predict Y. Four major challenges arising from such development include ultra-high dimensionality, low sample size, spatially correlation, and spatial smoothness. SWPCR is developed to address these four challenges when high-dimensional data on graphs ζ share two important features including spatial smoothness and intrinsically low dimensional structure. Compared with the existing literature, we make several major contributions as follows:

• (i) SWPCR is designed to efficiently capture the two important features by using some recent advances in smoothing methods, dimensional reduction methods, and sparse methods.

• (ii) SWPCR provides a powerful dimension reduction framework for integrating feature selection, smoothing, and feature extraction.

• (iii) SWPCR significantly outperforms the competing methods by simulation studies and the real data analysis.

2 Spatially Weighted Principal Component Regression

In this section, we first describe the graph data that are considered in this paper. We formally describe the general framework of SWPCR.

2.1 Graph Data

Consider data from n independent subjects. For each subject, we observe a q × 1 vector of discrete or continuous responses, denoted by y_i = (y_i,1, …, y_i,q)^T, and a m × 1 vector of high dimensional data x_i = {x_i,g : g ∈ } for i = 1, …, n. In many cases, q is relatively small compared with n, whereas m is much larger than n. For instance, in many neuroimaging studies, it is common to use ultra-high dimensional imaging data to classify a binary class variable. In this case, q = 1, whereas m can be several million number of features. In many applications, = {g₁, …, g_m} is a set of prefixed vertexes, such as voxels in 2D or 3D lattices, whereas the edge set 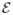may be either prefixed or determined by x_i (or other data).

2.2 SWPCR

We introduce a three-stage algorithm for SWPCR to use high-dimensional data x to predict a set of response variables Y. The key stages of SWPCR can be described as follows.

• Stage 1. Build an importance score vector (or function) W_I: → R⁺ and the spatial weight matrix (or function) W_E: × → R.

• Stage 2. Build a sequence of scale vectors {s₀ = (s_E,0, s_I,0), ···, s_L = (s_E,L, s_I,L)} ranging from the smallest scale vector s₀ to the largest scale vector s_L. At each scale vector s_ℓ, use generalized principal component analysis (GPCA) to compute the first few principal components of an n × m matrix X = (x₁ ··· x_n)^T, denoted by A(s_ℓ), based on W_E(·, ·) and W_I(·) for ℓ = 0, …, L.

• Stage 3. Select the optimal 0 ≤ ℓ^* ≤ L and build a prediction model (e.g., high-dimensional linear model) based on the extracted principal components A(s_ℓ^*) and the responses Y.

We slightly elaborate on these stages. In Stage 1, the important scores w_I,g play an important feature screening role in SWPCR. Examples of w_I,g = W_I(g) in the literature can be generated based on some statistics (e.g., Pearson correlation or distance correlation) between x_g and Y at each vertex g. For instance, let p(g) be the Pearson correlation at each vertex g and then define

$$w_{I,g}=-mlog(p(g))/\left[-\sum _{g\in \mathcal{G}}log(p(g))\right].$$ (1)

In Stage 1, without loss of generality, we focus on the symmetric matrix W_E = (w_E,gg′) ∈ R^p×p throughout the paper. The element w_E,gg′ is usually calculated by using various similarity criteria, such as Gaussian similarity from Euclidean distance, local neighborhood relationship, correlation, and prior information obtained from other data [21]. In Section 2.3, we will discuss how to determine W_E and W_I while explicitly accounting for the complex spatial structure among different vertexes.

In Stage 2, at each scale vector s_ℓ = (s_E,ℓ, s_I,ℓ), we construct two matrices, denoted by Q_E,ℓ and Q_I,ℓ based on W_E and W_I as follows:

$$Q_{E,\ell }=F_1(W_E,{\mathbf{s}}_{E,\ell })\text{and}{Q}_{I,\ell }=\text{diag}(F_2(W_I,s_{I,\ell })),$$ (2)

where F₁ : R^p×p × R⁺ → R^p×p and F₂ : R^p × R⁺ → R^p are two known functions. For instance, let 1(·) be an indicator function, we may set

$$F_2(W_I,s_{I,\ell })={(\mathbf{1}(w_{I,g_1}\ge s_{I,\ell }),\cdots ,\mathbf{1}(w_{I,g_m}\ge s_{I,\ell }))}^T,$$ (3)

to extract ‘significant’ vertexes. There are various ways of constructing Q_E,ℓ. For instance, one may set Q_E,ℓ as

$$Q_{E,\ell }=(\mid w_{E,g{g}^{\prime }}\mid \mathbf{1}(\mid w_{E,g{g}^{\prime }}\mid \ge s_{E,\ell ;1},D(g,g^{\prime })\le s_{E,\ell ;2})),$$

where s_E,ℓ = (s_E,ℓ;1, s_E,ℓ;2)^T and D(g, g′) is a graph-based distance between vertexes g and g′. The value of s_E,ℓ;2 controls the number of vertexes in {g′ ∈ : D(g, g′) ≤ s_E,ℓ;2}, which is a patch set at vertex g [18], whereas s_E,ℓ;1 is used to shrink small |w_E,gg′|s into zero.

After determining Q_E,ℓ and Q_I,ℓ, we set ${\mathrm{\sum }}_c=Q_{E,\ell }{Q}_{I,\ell }{Q}_{I,\ell }^T{Q}_{E,\ell }^T$ and Σ_r = I_n for independent subjects. Let X̃ be the centered matrix of X. Then we can extract K principal components through minimize the following objective function given by

$${\Vert \stackrel{\sim }{\mathbf{X}}-U{DV}^T\Vert }^2\text{subject}\text{to}{U}^T{\mathrm{\sum }}_{r}U=V^T{\mathrm{\sum }}_{c}V=I_K\text{and}\text{diag}(D)\ge 0.$$ (4)

If we consider correlated observations from multiple subjects, we may use Σ_r to explicitly model their correlation structure. The solution (U_ℓ, D_ℓ, V_ℓ) of the objective function (4) at s_ℓ is the SVD of X̃_R,ℓ = X̃Q_E,ℓQ_I,ℓ. The we can use a GPCA algorithm to simultaneously calculate all components of (U_ℓ, D_ℓ, V_ℓ) for a fixed K as follows. In practice, a simple criterion for determining K is to include all components up to some arbitrary proportion of the total variance, say 85%.

For ultra-high dimensional data, we consider a regularized GPCA to generate (U_ℓ, D_ℓ, V_ℓ) by minimizing the following objective function

$${\Vert {\stackrel{\sim }{\mathbf{X}}}_{R,\ell }-\sum _{k=1}^K{d}_{k,\ell }{\mathbf{u}}_{k,\ell }{\mathbf{v}}_{k,\ell }^T\Vert }^2+{\lambda }_{\mathbf{u}}\sum _{k=1}^K{P}_1(d_{k,\ell }{\mathbf{u}}_{k,\ell })+{\lambda }_{\mathbf{v}}\sum _{k=1}^K{P}_2(d_{k,\ell }{\mathbf{v}}_{k,\ell })$$ (5)

subject to ${\mathbf{u}}_{k,\ell }^T{\mathbf{u}}_{k,\ell }\le 1$ and ${\mathbf{v}}_{k,\ell }^T{\mathbf{v}}_{k,\ell }\le 1$ for all k, where u_k,ℓ and v_k,ℓ are respectively the k-th column of U_ℓ and V_ℓ. We use adaptive Lasso penalties for P₁(·) and P₂(·) and then iteratively solve (5) [1]. For each k₀, we define ${\mathbf{E}}_{\ell ,k_0}={\stackrel{\sim }{\mathbf{X}}}_{R,\ell }-{\sum }_{k\ne k_0}{d}_{k,\ell }{\mathbf{u}}_{k,\ell }{\mathbf{v}}_{k,\ell }^T$ and minimize

$${\Vert {\mathbf{E}}_{\ell ,k_0}-d_{k_0,\ell }{\mathbf{u}}_{k_0,\ell }{\mathbf{v}}_{k_0,\ell }^T\Vert }^2+{\lambda }_{\mathbf{u}}{P}_1(d_{k_0,\ell }{\mathbf{u}}_{k_0,\ell })+{\lambda }_{\mathbf{v}}{P}_2(d_{k_0,\ell }{\mathbf{v}}_{k_0,\ell })$$ (6)

subject to ${\mathbf{u}}_{k_0,\ell }^T{\mathbf{u}}_{k_0,\ell }\le 1$ and ${\mathbf{v}}_{k_0,\ell }^T{\mathbf{v}}_{k_0,\ell }\le 1$. By using the sparse method in [12], we can calculate the solution of (6), denoted by (d̂_k0,ℓ, û_k0,ℓ, v̂_k0,ℓ). In this way, we can sequentially compute (d̂_k,ℓ, û_k,ℓ, v̂_k,ℓ) for k = 1, …;, K.

In Stage 3, select ℓ^* as the minimum point of the objective function (5) or (6). let $Q_{F,{\ell }^{\ast }}=Q_{E,{\ell }^{\ast }}{Q}_{I,{\ell }^{\ast }}{V}_{{\ell }^{\ast }}{D}_{{\ell }^{\ast }}^{-1}$ and then K principal components A(s_ℓ^*) = XQ_F,ℓ^*. Moreover, K is usually much smaller than min(n, m). Then, we build a regression model with y_i as responses and A_i (the i-th row of A(s_ℓ^*)) as covariates, denoted by R(y_i, A_i; θ), where θ is a vector of unknown (finite-dimensional or nonparametric) parameters. Specifically, based on {(y_i, A_i)}_i≥1, we use an estimation method to estimate θ as follows:

$$\widehat{\mathit{\theta }}={\text{argmin}}_{\mathit{\theta }}\{\rho (R,\mathit{\theta },{\{({\mathbf{y}}_i,A_i)\}}_{i\ge 1})+\lambda P_3(\mathit{\theta })\},$$

where ρ(·, ·, ·) is a loss function, which depends on both the regression model and the data, and P₃(·) is a penalty function, such as Lasso. This leads to a prediction model R(y_i, A_i; θ). For instance, for binary response y_i = 1 or 0, we may consider a sparse logistic model given by $\text{logit}(P({\mathbf{y}}_i=1\mid A_i))=A_i^T\mathit{\theta }$ for R(y_i, A_i; θ).

Given a test feature vector x^*, we can do predictions from our prediction model as follows:

• Center each component of x^* by calculating x̃^* = x^* − μ̂_x, in which μ̂_x is the mean and learnt from the training data;

• Optimize an objective function based on R(y, x̃^*TQ_F,ℓ^*; θ̂) to calculate an estimate of y, denoted by ŷ^*.

Our prediction model is applicable to various regression settings for continuous and discrete responses and multivariate and univariate responses, such as survival data and classification problems.

2.3 Importance Score Weights and Spatial Weights

There are two sets of weights in SWPCR including (i) importance score weights enabling a selective treatment for individual features, and (ii) spatial weights accommodating the underlying spatial dependence among features across neighboring vertexes on graph. Below, we propose the strategy of determining both importance score weights and spatial weights.

Importance Score Weights

As discussed in Section 2.3, at each vertex g, w_I,g, such as the Pearson correlation in (1), is calculated based on a statistical model between x_g and Y in order to perform feature selection according to each feature’s discriminative importance. Statistically, most existing methods use a marginal (or vertex-wise) model by assuming

$$p({\mathbf{x}}_i,{\mathbf{y}}_i)=\prod _{g\in \mathcal{G}}p({\mathbf{x}}_{i,g},{\mathbf{y}}_i;\mathit{\beta }(g)),$$

where β = (β(g): g ∈ ) and β(g) is introduced to quantify the association between y_i and x_i,g at each vertex g ∈ . At the g–th vertex, w_I,g is a statistic based on the marginal model ${\prod }_{i=1}^{n}p({\mathbf{x}}_{i,g},{\mathbf{y}}_i;\mathit{\beta }(g))$. However, those w_I,gs largely ignore complex spatial structure, such as homogenous patches defined below, across all vertexes on graph.

For a graph ζ = ( , 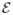), it is common to assume that β(g) across all vertexes are naturally clustered into P homogeneous patches, denoted by { 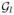: l = 1, …, P}, such that P ≪ m, $\mathcal{G}={\cup }_{l=1}^P{\mathcal{G}}_l$, and β(g) varies smoothly in each 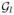. Note that a patch 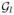consists of a set of vertexes that are completely connected through edges in 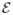. That is, if g, g′ ∈ 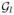, then there is a sequence of vertexes g₀ = g, ···, g_M = g′ in 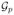such that (g_j−1, g_j) ∈ 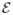for all j = 1, …, M. It has been shown that for graph data, algorithms based on patch information have led to state-of-the art techniques for classification and denoising. See for example, [18] for overviews of imaging patches.

We propose the strategy to jointly model x_i and y_i and simultaneously calculate w_I,g across all vertexes, while learning the homogenous patches 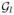. The strategy is to model the conditional distribution of x_i given y_i, denoted by p(x_i|y_i, β). Then we can learn the patches 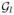in from the estimated β.

Here we consider a set of vertexes with unknown edge information 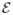. It is important to learn the homogeneous patches 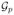and then form the edge s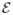et . Let 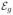(h) be an edge set at scale h at each vertex g. We consider a sequence of nested edge sets across multiscales h_s such that h₀ = 0 ≤ h₁ ≤ ··· ≤ h_S and 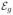(h₀) = {g} ⊂ ··· ⊂ 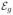(h_S). To learn the homogeneous patches, a general framework of Multiscale Adaptive Regression Model (MARM) developed in [13] is to maximize a sequence of weighted functions as follows:

$$\widehat{\mathit{\beta }}(g;h_s)={\text{argmax}}_{\mathit{\beta }(g)}\sum _{i=1}^n\sum _{g^{\prime }\in {\mathcal{E}}_g(h_s)}\omega (g,g^{\prime };h_s)logp({\mathbf{x}}_{i,g^{\prime }}\mid {\mathbf{y}}_i,\mathit{\beta }(g))\text{for}s=1,\dots ,S,$$ (7)

where ω(g, g′; h) characterizes the similarity between the data in vertexes g′ and g with ω(g, g; h) = 1. If ω(g, g′; h) ≈ 0, then the observations in vertex g′ do not provide information on β(g). Therefore, ω(g, g′; h) can prevent incorporation of vertexes whose data do not contain information on β(g) and preserve the edges of homogeneous regions. Let D₁(g, g′) and D₂(β̂(g; h_s−1), β̂(g′; h_s−1)) be, respectively, the spatial distance between vertexes g and g′ and a similarity measure between β̂(g; h_s−1) and β̂(g′; h_s−1). The ω(g, g′; h_s) can be defined as

$$\omega (g,g^{\prime };h_s)={\mathbb{K}}_1(D_1(g,g^{\prime })/h_s)·{\mathbb{K}}_2(D_2(\widehat{\mathit{\beta }}(g;h_{s-1}),\widehat{\mathit{\beta }}(g^{\prime };h_{s-1}))/{\gamma }_n),$$ (8)

where 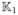(·) and 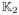(·) are two nonnegative kernel functions and γ_n is a bandwidth parameter that may depend on n. See the detailed algorithm of MARM in [13]. After the iteration h_s, we can obtain β̂(g; h_S) and its covariance matrix, denoted by Cov(β̂(g; h_s)), across all g ∈ and ω(g, g′; h_s) for all g′ ∈ 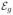(h_s) and g ∈ . Finally, we calculate statistics w_I,g based on β̂(g; h_s) and Cov(β̂(g; h_s)), such as the Wald test, and then we use a clustering algorithm, such as the K-mean algorithm, to group {β̂(g; h_s): g ∈ } into several homogeneous clusters, in which β̂(g; h_s) varies very smoothly in each cluster. Moreover, each homogenous cluster can be a union of several homogeneous patches.

Spatial Weights

As discussed in Section 2.3, w_E,gg′ often characterizes the degree of certain ‘similarity’ between vertexes g and g′. The locally spatial weighting matrix consists of non-negative weights assigned to the spatial neighboring vertexes of each vertex. It is assumed that

$$w_{E,g{g}^{\prime }}=\frac{\omega (g,g^{\prime };h_s)\mathbf{1}(g^{\prime }\in {\mathcal{E}}_g(h_s))}{{\sum }_{g^{\prime }\in {\mathcal{E}}_g(h_s)}\omega (g,g^{\prime };h_s)\mathbf{1}(g^{\prime }\in {\mathcal{E}}_g(h_s))},$$ (9)

in which ω(g, g′; h_s) is defined in (8). Therefore, w_E,gg′= 0 for all g′ ∉ 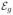(h_s) and 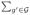w_E,gg′ = 1. The weights 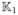(D₁(g, g′)/h_s) give less weight to vertex g′ ∈ 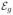(h_s), whose location is far from the vertex g. The weights 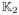(u) down-weight the vertex g′ with large D₂(β̂(g; h_s), β̂(g′; h_s)), which indicates a large difference between β̂(g′; h_s) and β̂(g; h_s). Moreover, by following [4, 13, 15, 16], we set 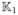(x) = (1−x)₊ and 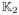(x) = exp(−x). Although m is often much larger than n, the computational burden associated with the local spatial weights is very minor when h_s is relatively small.

3 Simulation Study

In this section, we conducted one set of simulation study corresponding to binary responses, in order to examine the finite-sample performance of SWPCR in the high-dimensional classification analysis. We demonstrate that SWPCR outperforms many state-of-the-art methods for at least in the simulated dataset.

We simulated 20 × 20 × 10 (x × y × z) 3D-images from a linear model given by

$${\mathbf{x}}_{i,g}=B_0(g)+B_1(g){\mathbf{y}}_i+{\epsilon }_i(g)\text{for}i=1,\cdots ,n,$$ (10)

where y_i is the class label coded as either 0 or 1 and ε_i(g) are random variables with zero mean. The true mean images of class y_i = 0 and class y_i = 1 are shown in Figure 2. Voxels in the red cuboid region have the maximum difference 1 between classes 0 and 1. The dimension of red cuboid is 3 × 3 × 4 and contains 36 voxels. In this case, m = 4, 000 and we set n = 100 with 60 images from Class 0 and the rest from Class 1. We consider three types of noise ε_i(g) in (10). First, ${\epsilon }_i^{(1)}(g)$ were independently generated from a N(0, 2²) generator across all voxels g. Second, ${\epsilon }_i^{(2)}(g)={\sum }_{\Vert g^{\prime }-g\Vert \le 1}{\epsilon }_i^1(g^{\prime })/m_g$ were generated from ${\epsilon }_i^{(1)}(g)$ in order to introduce the short range spatial correlation, where m_g is the number of voxels in the set {||g′ − g|| ≤ 1}. Third, to introduce long range spatial correlation, ${\epsilon }_i^{(3)}(g)$ were generated according to ${\epsilon }_i^{(3)}(g)=2sin(\pi g_1/10){\xi }_{i,1}+2cos(\pi g_2/10){\xi }_{i,2}+2sin(\pi g_3/5){\xi }_{i,3}+{\epsilon }_i^{(1)}(g)$, where ξ_i,k for k = 1, 2, 3 were independenly generated from a N(0, 1) generator. Moreover, the noise variances in all voxels of the red cuboid region equal 4, 4/6, and 4{sin(πg₁/10)² +cos(πg₂/10)² +sin(πg₃/5)²} +4 for Type I, II, and III noises, respectively. Therefore, among the three types of noise, Type III noise has the smallest signal-to-noise ratio and Type II noise has the largest one.

Fig. 2.

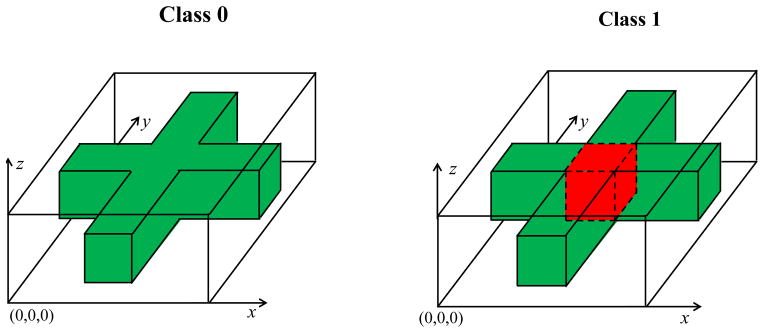
True mean images for the simulation study: Class 0 in the left panel and Class 1 in the right panel. The white, green, and red colors, respectively, correspond to 0, 1, and 2.

We ran the three stages of SWPCR as follows. In Stage 1, let {h_ℓ = 1.2^ℓ, ℓ = 0, 1, …, S = 5}, and for each g ∈ , w_I,g = −m log(p(g))/[− 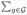log(p(g)), where p(g) is the p-value of Wald test B₁(g) = 0 in (7) (β(g) = (B₀(g), B₁(g))^T) for each voxel g. The spatial weight W_E is given by (9). Here we haven’t used the simple Pearson correlation (1) for computing weights because it neglects the spatial correlation of the data set. In Stage 2, for each h_ℓ, we define Q_E,ℓ = W_E and generate Q_I,ℓ through (2) and (3), where s_I,ℓ thresholds out the w_I,g with p(g) < 0.01. Then we extract different K principal components of GPCA to reconstruct the low dimensional representations of simulated images and then do classification analysis. The results are very stable for different number of principal components and here we let K = 5. In Stage 3, we tried different classification methods, including linear regression, k-Nearest Neighbor (k-NN) [11] and support vector machine (SVM) [14], on these low dimensional spaces. Based on the misclassification error for the leave-one-out cross validation, the linear regression is slight better than others. The linear regression uses class label y_i as dependent variable and principal components as explanatory variables. If the prediction value is less than 0, the image is classified as 0. Otherwise, the image is classified as 1.

We compared SWPCR with other state-of-the-art classification methods. The leave-one-out cross validation is used here to calculate the misclassification rates of the different methods. Other classification methods considered here include sparse linear discriminant analysis (sLDA) [6], sparse partial least squares (SPLS) analysis [5], sparse logistic regression (SLR) [20], SVM, and regularized optimal affine discriminant (ROAD) [8]. These methods are well known for their excellent performance in various simulated and real data sets. Inspecting Table 1 reveal that except SWPCR, all classification methods perform pretty poor, when the signal-to-noise ratio is low in those simulated datasets with Type I and II noises. Except SPLS, PCA, and SWPCR, all other methods are seem to be sensitive to the presence of the long-range correlation structure in Type III noise.

Table 1.

Classification results for the first set of simulations: comparison between SWPCR and other Classification Methods. sLDA denotes sparse linear discriminant analysis; SPLS denotes sparse partial least squares; SLR denotes sparse logistic regression; SVM denotes support vector machine; ROAD denotes regularized optimal affine discriminant; and PCA denotes principal component analysis.

Noise	sLDA	SPLS	SLR	SVM	ROAD	PCA	SWPCR
Type I	0.28	0.43	0.45	0.38	0.36	0.36	0.10
Type II	0.27	0.08	0.18	0.26	0.08	0.45	0.03
Type III	0.52	0.30	0.61	0.60	0.50	0.35	0.09

4 Real Data Analysis

4.1 ADNI PET Data

The real data set is the baseline fluorodeoxyglucose positron emission tomography (FDG-PET) data downloaded from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) web site (www.loni.ucla.edu/ADNI). The ADNI1 PET data set consists of 196 subjects (102 Normal Controls (NC) and 94 AD subjects). There are three subjects, missing the gender and age information. Among the rest of the subjects, there are 117 males whose mean age is 76.20 years with standard deviation 6.06 years and 76 females whose mean age is 75.29 years with standard deviation 6.29 years.

The dimension of the processed PET images is 79 × 95 × 69. Left panel in Figure 3 shows some selected slices of the processed PET images from 2 randomly selected AD subjects and 2 randomly selected NC subjects.

Fig. 3.

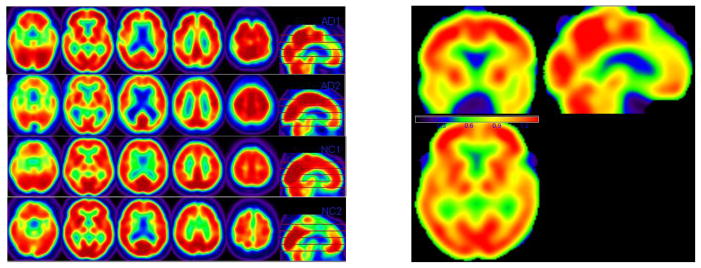
ADNI1 pet data and the important score weight matrix Q_I,ℓ in SWPCR. In the left panel, one row sequence of 2-D images belongs to one subject. The first two rows respectively belongs to AD subjects and the rest belongs to NC subjects. In the right panel, the three plots (left -right-bottom) are three view slices of the weight matrix Q_I,ℓ at the coordinate (40, 57, 26). The red region corresponds to large weight score and contains the most classification information.

4.2 Binary Classification

Our first goal is to apply SWPCR in classifying subjects from ADNI1 to AD or CN group based on their FDG-PET images. Such goal is associated with the second primary objective of ADNI aiming at developing new diagnostic methods for AD intervention, prevention, and treatment. Similar as in Section 3, SWPCR contains the three detailed stages that will not be repeated again. The right panel in Figure 3 is the three view slices of the weight matrix Q_I,ℓ at the coordinate (40, 57, 26) in the stage 2 of SWPCR. The red region in three slices corresponds to the large important score weight and contains the most classification information.

We compared SWPCR with six other classification methods including sLDA, SPLS, SLR, SVM, ROAD, and PCA. We used their leave-one-out cross validation rates. Table 2 shows the classification results of all the seven methods. sLDA performs much worse than all other six methods. ROAD performs slightly better than PCA. SPLS and SVM are comparable with each other, but they outperform SLR and ROAD. SWPCR outperforms all six classification methods. It suggests that the classification performance can be significantly improved by incorporating spatial smoothness and simple dimension reductions methods, such as PCA.

Table 2.

Misclassification Rates of Different Methods for ADNI 1 Pet Data

sLDA	SPLS	SLR	SVM	ROAD	PCA	SWPCR
0.255	0.163	0.179	0.168	0.189	0.194	0.117

4.3 Age Prediction

Our second goal is to apply SWPCR in predicting subjects’ age based on their FDG-PET images. The response variable y is the age of the subjects and the explanatory variables are the latent scores, extracted from image data. It is very interesting to use memory test scores as the response variable y. However, the data set here contains no such information. The three subjects without the age information are deleted and then we have 193 images left. y_i in model (10) becomes age of the subjects. Here we will not repeat the detailed stages of SWPCR again, which is similar as in Section 3. The slight difference is stage 3. Here we run regression rather than classification methods between age and the SWPCR latent scores.

First, we compared SWPCR with three other dimensional reduction methods including PCA, weighted PCA (WPCA) [17], and supervised PCA (SPCA) [2]. We used the leave-one-out cross validation to compute the prediction errors of all the four methods. Let ŷ_i be the fitted response value based on the regression model, and the prediction error is defined as |ŷ_i − y_i|/|y_i|. Subsequently, we calculated the error difference between SWPCR and all three other methods across different numbers (K = 5, 7, 10) of principal components. Panels (a)–(c) in Figure 4 show the boxplots of the error difference between SWPCR and PCA, WPCA, and SPCA, respectively. The error differences are almost always less than 0 (under the dashed line) and these results show the better performance of SWPCR in dimension reduction.

Fig. 4.

Performance of SWPCR Regression for ADNI 1 Pet Data. Panels (a)–(c) shows the boxplots of error difference between SWPCR and PCA (WPCA and SPCA). Panel (d) compares SWPCR regression with several other regression methods, including PR, SIS, SVR and SPLS.

Second, we compared SWPCR with several other high-dimensional regression methods including penalized regression (PR) [19], sure independence screening (SIS) regression [7], support vector regression (SVR) [3], and SPLS [5]. Panel (d) in Figure 4 shows the boxplots of the prediction error difference between SWPCR and all the other regression methods. The analysis results further confirm the better performance of SWPCR in regression.

5 Discussion

SWPCR enables a selective treatment of individual features, accommodates the complex dependence among features of graph data, and has the ability of utilizing the underlying spatial pattern possessed by image data. SWPCR integrates feature selection, smoothing, and feature extraction in a single framework. In the simulation studies and real data analysis, SWPCR shows substantial improvement over many state-of-the-art methods for high-dimensional problems.