Detection of Low Back Pain Using pH Level-Dependent Imaging of the Intervertebral Disc Using the Ratio of R_1ρ Dispersion and –OH Chemical Exchange Saturation Transfer (RROC)

Abstract

Purpose

Low pH is associated with intervertebral disc (IVD)-generated low back pain (LBP). The purpose of this work was to develop an in vivo pH level-dependent magnetic resonance imaging (MRI) method for detecting discogenic LBP, without using exogenous contrast agents.

Methods

The ratio of R_1ρ dispersion and chemical exchange saturation transfer (CEST) (RROC) was used for pH-level dependent imaging of the IVD while eliminating the effect of labile proton concentration. The technique was validated by numerical simulations and studies on phantoms and ex vivo porcine spines. Four male (ages 42.8 ± 18.3) and two female patients (ages 55.5 ± 2.1) with LBP and scheduled for discography were examined with the method on a 3.0 Tesla MR scanner. RROC measurements were compared with discography outcomes using paired t-test.

Results

Simulation and phantom results indicated RROC is a concentration independent and pH level-dependent technique. Porcine spine study results found higher RROC value was related to lower pH level. Painful discs based on discography had significant higher RROC values than those with negative diagnosis (P < 0.05).

Conclusion

RROC imaging is a promising pH level dependent MRI technique that has the potential to be a noninvasive imaging tool to detect painful IVDs in vivo.

INTRODUCTION

Low back pain (LBP) is a musculoskeletal disorder that leads to suffering and disability (1). It is a major medical condition estimated to affect up to 85% of the US population (2). Intervertebral disc (IVD) degeneration is often associated with back pain (3). Standard LBP diagnosis includes provocative discography, during which the suspected discs are pressurized to provoke pain. However, this is an invasive procedure associated with pain and known to further accelerate disc degeneration, disc herniation, and loss of disc height and affect the adjacent endplates (4). In addition, the diagnostic accuracy is subjective to variations of the needle placement, injection pressure, ability of patient to report pain and subjectivity of the tester.

The IVD is composed of the nucleus pulposus (NP), the annulus fibrosus (AF), and the cartilaginous endplate (EP) (5). NP is rich in proteoglycan (PG), which has numerous glycosaminoglycan (GAG) chains of chondroitin sulfate and keratan sulfate attached (6). GAGs play a critical role in supporting IVD functions including generating hydrostatic pressure to bear load from body weight. Metabolism of disc cells is mainly through anaerobic glycolysis, leading to significant lactate production. Diffusion is the primary pathway for supply of nutrients such as glucose and oxygen to disc cells, as well as the depletion of metabolic wastes such as lactate. The lactate concentration in the center of the disc can be up to 8–10 times higher than in the plasma. As a consequence, disc pH is acidic (7,8). Though pathogenesis of LBP remains elusive (9,10), previous researches emphasized on the important role of pH. An in vitro study found decreased cell viability under low pH and glucose deprivation (11). PG synthesis rate was shown to be sensitive to pH (12). A study in 1969 noted significant correlation between preoperative impression of pain and low pH measured by a pH-electrode during lumbar rhizopathy operations (13). A recent review article proposed that “low back pain may be caused by low pH” (3). Another review article emphasized the inflammatory response and PG depletion following lowered pH, and hypothesized low pH as the possible cause of development and progression of LBP (14).

Magnetic resonance spectroscopy (MRS) has been exploited to noninvasively assess lactate in IVD. Zuo et al (15) demonstrated the feasibility of acquiring localized ¹H spectra on a 3.0 Tesla (T) scanner on intact bovine and human cadaveric discs to quantify lactate, the source of low pH. A later study (16) characterized IVD in vivo. Although a significantly elevated water/PG area ratio was found in painful discs based on discography, no lactate peak was reliably detected. In vivo MRS suffers from several limitations that prohibit lactate detection: limited signal-to-noise ratio (SNR), physiological motion, bone susceptibility induced line broadening, difficulty in differentiating lactate from lipid peaks as their resonance frequencies are close, collapsed disc space in certain patients, etc.

Recently MRI has been exploited to noninvasively assess pH in IVD. Melkus et al adopted both endogenous and exogenous approaches to investigate the pH dependence of chemical exchange saturation transfer (CEST) in porcine IVDs (17). Endogenous CEST of hydroxyl (–OH) protons on GAGs (gagCEST) demonstrated pH sensitivity on phantoms and ex vivo porcine IVD specimens at 7.0T. CEST of exogenous computed tomography (CT) contrast agent Iopromide that was injected into the discs also demonstrated pH imaging potential. Iopromide, together with similar types of contrast agents such as Iopamidol and Iohexol, has been investigated as pH probes in several applications such as mice kidney, mice tumor, and human bladder (18–20). While both the endogenous and exogenous IVD pH imaging approaches are promising, limitations remain. First, the existing gagCEST pH measurement approach is confounded by GAG concentration. Because both pH and GAG concentration will affect gagCEST signal, further correction is needed. Second, despite the feasibility demonstrated at 7.0T, no efforts were made to translate the techniques onto 1.5 or 3.0T. Third, the CT contrast agent approach may be unsuitable for in vivo imaging. Diffusion is the primary pathway for exogenous contrast agent to enter the IVD, the largest avascular structure in human body. In a normal disc, it may take several hours for exogenous contrast agent to diffuse into central NP (21). Such a long waiting time may hamper the technique’s applicability in clinic. Moreover, to quantify the amide CEST signal at 4.2 ppm and 5.6 ppm, high-enough Iopromide concentration in the IVD is required. If Iopromide is to be administrated intravenously, a prohibitively high dose may be needed so that enough contrast enters the IVD, which could elicit safety concerns. Direct injection of Iopromide into the disc could also work on humans, yet as an invasive technique it will potentially cause side effects including pain and infection. These contrast delivery issues may challenge the application of exogenous CT contrast agents for pH imaging on humans.

In this work, we aim to develop a MRI technique for in vivo IVD pH level-dependent imaging on a 3.0T clinical scanner, without using exogenous contrast agents. The proposed technique uses the ratio of R_1ρ dispersion and –OH CEST (RROC). It was verified by numerical simulations and studies on chondroitin sulphate phantoms and ex vivo porcine spines. The technique’s potential in diagnosing painful discs is then explored in a study involving LBP patients.

THEORY

CEST

Pulsed-CEST effect can be approximated by the analytical solution of continuous-wave CEST signal (22). Considering a two-pool (labile and water pool) exchange model with no back exchange of saturated protons or direct saturation (DS) on water protons, the analytical solution for continuous-wave CEST is shown to be (23):

$$\mathit{CEST}=\mathrm{f}·\mathrm{\alpha }·{\mathrm{k}}_{\text{sw}}·{\mathrm{T}}_{1\mathrm{w}}(1-{\mathrm{e}}^{-{\mathrm{t}}_{\text{sat}}/{\mathrm{T}}_{1\mathrm{w}}})$$ [1]

where f is the relative concentration of labile protons, α is the saturation coefficient and is a function of exchange rate k_sw, T_1w is the longitudinal relaxation time of water pool, and t_sat is saturation time. According to Eq. [1] the measured CEST effect is proportional to concentration f, and is a function of exchange rate k_sw, which in turn is a function of pH. It is worth mentioning that the above assumptions are not completely valid for –OH CEST at 3.0T, as back exchange and DS cannot be neglected. Nevertheless when the concentration is small enough, as an approximation the above equation provides valuable insights on CEST signal’s relationship with pH and concentration. In fact, a roughly linear relationship between –OH CEST and GAG concentration was discovered on phantoms (24,25). The pH dependence of –OH CEST has also been shown at 7.0T by Melkus et al (17), yet no effort has been made to characterize such relationship at 3.0T.

R_1ρ Dispersion

R_1ρ (the longitudinal relaxation rate in the rotating frame) dispersion, the dependence of R_1ρ on spin-lock amplitude (SLA), is sensitive to chemical exchanges with intermediate exchange rate (26,27). Considering a two-pool exchange model (labile and water pool) with highly unequal population (labile proton concentration p_l ≪ water pool concentration p_w), R_1ρ can be obtained as (26):

$${\mathrm{R}}_{1\mathrm{\rho }}={\mathrm{R}}_1·{\text{cos}}^2\mathrm{\theta }+\left({\mathrm{R}}_2+\frac{{\mathrm{p}}_1·{\mathrm{\delta }}^2·{\mathrm{k}}_{\text{ex}}}{{(\mathrm{\delta }-\mathrm{\Omega })}^2+{{\mathrm{\omega }}_1}^2+{{\mathrm{k}}_{\text{ex}}}^2}\right)·{sin}^2\mathrm{\theta }$$ [2]

where R₁ is the longitudinal relaxation rate of water, R₂ is the intrinsic water transverse relaxation rate in absence of chemical exchange, δ is the chemical shift of labile pool relative to water pool, k_ex is the exchange rate between the two pools. θ = arctan (ω₁/Ω) is the angle between the effective B₁ in the rotating frame and Z-axis, where ω₁ is the SLA and Ω is the frequency off-set of locking pulses. In addition, the exchange rate from water to labile pool (k_w) and labile to water pool (k_l) satisfy p_w · k_w = p_l · k_l, and k_ex = k_w) k_l. When spin-lock pulses are applied on-resonance, θ = 90° and Ω = 0

In an on-resonance spin-lock study when R_1ρ values are respectively measured at a low achievable SLA ω_1L (eg. 100 Hz), and at a high achievable SLA ω_1H (eg. 400 Hz), the difference R_1ρ value can be obtained as:

$${\mathrm{R}}_{1\mathrm{\rho }-\text{Disp}}={\mathrm{R}}_{1\mathrm{\rho }}({\mathrm{\omega }}_{1\mathrm{L}})-{\mathrm{R}}_{1\mathrm{\rho }}({\mathrm{\omega }}_{1\mathrm{H}})=\frac{{\mathrm{p}}_1·{\mathrm{k}}_{\text{ex}}·[{({\mathrm{\omega }}_{1\mathrm{H}}/\mathrm{\delta })}^2-{({\mathrm{\omega }}_{1\mathrm{L}}/\mathrm{\delta })}^2]}{[1+{({\mathrm{\omega }}_{1\mathrm{H}}/\mathrm{\delta })}^2+{({\mathrm{k}}_{\text{ex}}/\mathrm{\delta })}^2]·[1+{({\mathrm{\omega }}_{1\mathrm{L}}/\mathrm{\delta })}^2+{({\mathrm{k}}_{\text{ex}}/\mathrm{\delta })}^2]}$$ [3]

Obviously R_1ρ–Disp is proportional to p_l, the concentration. Because ω_1L and ω_1H can be predetermined and δ value is fixed, R_1ρ–Disp then also depends on k_ex, which in turn is a function of pH level.

RROC

The above discussion revealed that both CEST and R_1ρ dispersion are roughly proportional to GAG concentration, and are pH level-dependent. Theoretically, CEST = C · f₁(pH) and R_1ρ–Disp = C · f₂(pH), where C is concentration, and f₁ and f₂ are functions describing the pH dependence of CEST and R_1ρ dispersion, respectively. RROC is defined as the ratio of R_1ρ dispersion to CEST:

$$\mathit{RROC}=\frac{f_1(pH)}{f_2(pH)}=f(pH)$$ [4]

where f is a new function describing RROC’s pH dependence. When f₁ and f₂ have different pH responses, RROC is independent of C and yet still dependent of pH as described by f (pH). Therefore, it could be used for pH level-dependent imaging.

R_1ρ measurement at low SLA

On-resonance R_1ρ measurement is susceptible to B₀ and B₁ inhomogeneities. Various sequence improvements attempted to address these problems (28–32). Among these is an interesting spin-lock preparation called “phase-cycled composite spin-lock,” which combines phase-cycling and a composite pulse scheme for inhomogeneities compensation (30). This technique was proven analytically to eliminate B₁ inhomogeneity effect. In addition, B₀ inhomogeneity effect was also claimed to be corrected, although no analytical proof was provided. Here the analytical description of this technique’s dependence on B₀ off-resonance (assuming perfect B₁) is sought, following the approach used by Li et al (29). The magnetization after spin-lock preparation, for odd and even number of acquisitions respectively, can be obtained as:

$$M_{\mathit{odd}}=R_x(\mathrm{\beta })·R_y(\mathrm{\alpha })·(R_x(\mathrm{\theta })·R_z(\partial )E_{\mathrm{\rho }}·R_{-x}(\mathrm{\theta }))·R_y(\mathrm{\alpha })·R_x(\mathrm{\beta })·M(t_0)$$ [5]

$$M_{\mathit{even}}=R_{-x}(\mathrm{\beta })·R_y(\mathrm{\alpha })·(R_x(\mathrm{\theta })·R_z(\partial )E_{\mathrm{\rho }}·R_{-x}(\mathrm{\theta }))·R_y(\mathrm{\alpha })·R_x(\mathrm{\beta })·M(t_0)$$ [6]

where M(t₀) is the initial magnetization, R_ϕ(Φ) represents a rotation matrix with flip angle Φ and orientation ϕ, β = 90° is the flip angle of tip-down/tip-up pulse, α = 135°, θ is the angle between effective spin-lock field and z-axis, $\mathrm{\theta }={tan}^{-1}\left(\frac{{\mathrm{\omega }}_1}{\mathrm{\Omega }}\right)$ with ω₁ and Ω being SLA and frequency offset respectively, E_ρ is a matrix to describe T_1ρ and T_2ρ (=1/R_2ρ, the transverse relaxation time in the rotating frame) relaxation, and ∂ is the flip angle of spin-lock pulse. The longitudinal magnetization M_z after phase-cycling is equal to (M_even –M_odd)/2, and can be obtained as:

$$M_z=M_0·(E_{1\mathrm{\rho }}·{\mathit{sin}}^2\mathrm{\theta }+E_{2\mathrm{\rho }}·{\mathit{cos}}^2\mathrm{\theta }·\mathit{cos}\mathrm{\xi })$$ [7]

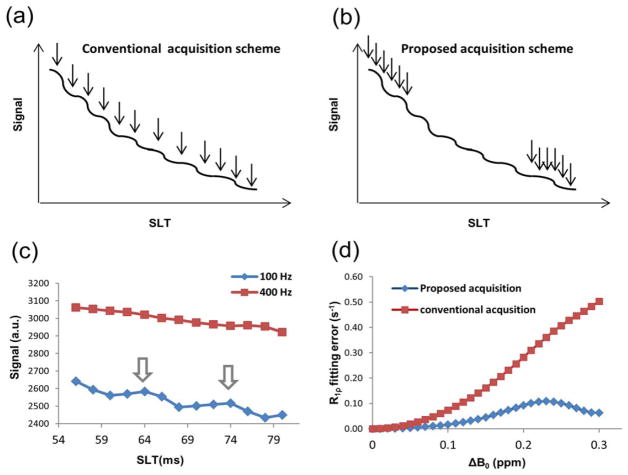
where M₀ is longitudinal magnetization, E_1ρ = e^{−SLT·R_1ρ}, E_2ρ = e^{−SLT·R_2ρ}, $\mathrm{\xi }=2\mathrm{\pi }·\mathit{SLT}·\sqrt{{({\mathrm{\omega }}_1)}^2+{(\mathrm{\Omega })}^2}$, and SLT is spin-lock time. When there is B₀ off-resonance, the second term in Eq. [7] becomes non-zero, causing “R_2ρ contamination”. This contamination is dependent on SLA: for a given Ω, a lower ω₁ causes heavier R_2ρ contamination. Although it is generally not a problem when imaging with 400 Hz SLA, R_1ρ measurement at a low SLA of 100 Hz is complicated by this contamination (Fig. 1c), and correction is needed. The second term in Eq. [7] is oscillating at a frequency determined by $\sqrt{{({\mathrm{\omega }}_1)}^2+{(\mathrm{\Omega })}^2}$. For ω₁ = 100 Hz, this value is much higher than either R_1ρ or R_2ρ that are on the order of tens of Hz. Thus it is possible to “filter” the oscillation effects using various data-processing, and obtain only R_1ρ related signal.

FIG. 1.

Spin-lock acquisition scheme under low spin-lock amplitude. a: Conventional acquisition scheme. b: Proposed acquisition scheme. c: Spin-lock data of a typical pixel acquired with 100 Hz and 400 Hz amplitude, respectively. Obvious oscillation can be observed in 100 Hz data, whereas 400 Hz data has less oscillation. Arrows points to “peaks” within the oscillation cycle. d: Simulated fitting error of R_1ρ under B₀ inhomogeneity, for the two acquisitions schemes. The propose scheme has better immunity to inhomogeneity, and when ΔB₀ < 0.10 ppm the fitting error is small, indicating the proposed method can compensate B₀ inhomogeneity. Simulation is performed with: R_1ρ = 10 s⁻¹, R_2ρ = 20 s⁻¹, and spin-lock amplitude of 100Hz.

Here a simple strategy that can easily be applied in a clinical setting is used. Whereas conventional R_1ρ measurement includes several SLTs that are usually evenly distributed, in the proposed scheme SLTs are divided into two groups with short and long SLTs respectively, and within each group several SLTs are used to fully sample at least one cycle of the oscillation. As an example these two types of schemes were compared by numerical simulation: the conventional scheme included 12 SLTs evenly distributed between 10 ms and 150 ms, while the SLTs in the proposed scheme had SLTs of from 10 ms to 20 ms in step of 2 ms, and from 140 ms to 150 ms in step of 2 ms (Fig. 1a,b). R_1ρ value was obtained by fitting signal to a mono-exponential decay function using least-squares fitting. The absolute errors between fitted R_1ρ and the “true” R_1ρ value used in simulation, under different B₀ off-resonance, were plotted in Figure 1d. The proposed scheme performed better under B₀ off-resonance, especially when |ΔB₀| < 0:10 ppm R_1ρ quantification can be achieved with high accuracy as the absolute error is close to zero.

METHODS

Numerical Simulations

Simulations require knowledge on exchange rate between –OH protons and water protons. An on-resonance spin-lock dispersion study (discussed below) was performed on 9.4T, and R_1ρ values were fitted to Eq. [2] to obtain exchange rate under different pH levels. δ was assumed to be 1.0 ppm. Results (Table 1) were subsequently used for simulations. CEST effect on 3.0T was numerically simulated using Bloch-McConnel two-pool exchange model in Matlab (The Mathworks, Natick, MA), as described in Sun (33). The relaxation and chemical exchange parameters used were chosen to represent typical human IVD: T_1w = 1000 ms, T_2w = 100 ms, T_1s = 500 ms, T_2s = 50 ms. –OH proton offset was 1.0 ppm. GAG concentration was 150 mM assuming three –OH protons on each GAG unit. Simulation parameters matched our in vivo imaging protocol: it included a train of eight Gaussian pulses of 1440° and a 50% duty cycle, with each pulse lasting 90 ms. The RF pulse profile was extracted from programming platform (IDEA, Siemens AG Healthcare, Erlangen, Germany). It has a normalized average amplitude (p1) of 0.50, and a normalized average power (p2) of 0.38, measured using the metrics previously introduced by Zu et al (22). –OH CEST was calculated as the integral of MTR_asym between 0.5 ppm and 1.5 ppm. R_1ρ dispersion between SLAs of 100 Hz and 400 Hz was simulated based on Eq. [3]. RROC was calculated subsequently.

Table 1.

Fitted Results under Different pH Levels

pH	6.00	6.40	6.68	7.04
Exchange rate kex (s−1)	504	646	749	834
Concentration pl	0.011	0.012	0.016	0.015
Transverse relaxation rate R2 (s−1)	1.71	1.76	1.65	1.72

B₁ inhomogeneity is known to be a problem on 3.0T human system. In addition, IVD degeneration is associated with reductions in T₁ and T₂ times that may confound the use of RROC for pH-level dependent imaging. To understand RROC’s dependence on these factors, numerical simulations were performed by using a variety of B₁ errors, T₁ times, and T₂ times, respectively.

Phantoms

Phantom I

To quantify the exchange rate of GAG phantoms under different pH levels at 9.4T, GAG samples with concentration of 150 mM were prepared from chondroitin sulphate A (Aldrich-Sigma, St. Louis, MO) in a standard solution of phosphate-buffered saline (PBS), and their pH levels were subsequently titrated to 7.04, 6.68, 6.40, and 6.00, respectively. The concentration refers to the number of disaccharide units in GAGs.

Phantom II

To verify the dependence of CEST and R_1ρ dispersion on GAG concentration and pH at 3.0T, in a different study 4 samples of GAGs with concentrations of 50, 100, 150, and 200 mM, respectively, were prepared from chondroitin sulphate A in a standard solution of PBS. Then each sample was divided evenly into five smaller tubes, and their pH levels were titrated to values around 7.2, 7.0, 6.7, 6.3, and 6.0, respectively. At time of imaging the samples were placed in gadolinium-doped water bath. Phantoms were imaged at room temperature. Chondroitin sulphate was soluble in PBS at the concentrations and pH levels in this study.

Porcine Spine

Porcine spine thoracolumbar was harvested from a freshly killed Yucatan minipig. Sample was immediately taken to a −20° C freezer for storage and taken to room temperature at least 24 h before MRI to defrost. After removal of the surrounding muscles and posterior elements, a small cut (~3 mm) was made at the middle of each intervertebral disc parallel to the endplates using a scalpel. 0.05mL Na-Lactate (Sodium L-Lactate, Sigma Aldrich, St. Louis, MO) with different concentrations was injected into nucleus pulposus to induce a variety of pH levels within the discs, similar to Melkus et al (17). pH was measured using a custom-made tissue pH probe (Warner Instruments, LLC, Hamden, CT) by inserting the electrode into the center of the disc.

Human Subjects

Four male (ages 42.8 ± 18.3) and two female (ages 55.5 ± 2.1) subjects with chronic low back pain (> 6 months) due to moderate degenerative disc disease at any lumbar level and scheduled for provocative discography were recruited. Inclusion criteria were: failure of conservative therapy for at least 3 months (including physical therapy), low back pain of at least 40 mm on a 100 mm Visual Analog Scale with either leg pain less than back pain or nonradicular of origin, lumbar disc pathology having a modified Pfirrmann score of 3, 4, 5, or 6, with a herniation of no greater than 6 mm and no neurological compression, and pain/pathology not originated from facet joints or stenosis. Outcomes of discography were classified as either positive or negative: positive discography replicated patient’s symptoms, while negative ones did not. A total of 23 disc levels were studied. MRIs were performed 1–4 (average = 1.9) weeks before scheduled discography to avoid compounding effects of potential disc damage caused by the procedure. The study was approved by our Institutional Review Board and informed consent was obtained from all volunteers.

MRI Acquisitions

Phantom I was scanned on a 9.4T Bruker Biospec Imager (Bruker Biospin, Billerica, MA), using a volume transmit and receive RF coil. Image readout was single-slice rapid acquisition with refocused echoes (RARE) sequence with spin-lock preparation. SLAs were from 298 Hz to 1746 Hz in step of 85 Hz. SLTs were 50, 100, 150, and 200 ms. Phantom II and porcine spine were performed on a 3.0T clinical scanner (Magnetom Verio, Siemens AG Healthcare, Erlangen, Germany). RF was transmitted using body coil. CEST and water saturation shift referencing (WASSR) preparation were similar to our previous study (34). Shimming was done manually. Spin-lock preparation was achieved by using phase-cycling preparation and the new acquisition scheme. SLAs were 100 and 400 Hz. SLTs were from 22 ms to 40 ms in step of 2 ms, and from 122 ms to 140 ms in step of 2 ms. Imaging of Phantom II in the axial plane was conducted using CEST and spin-lock turbo-spin-echo (TSE), with a 24-elements spine coil and a body matrix coil. Three IVDs of the porcine spine were individually scanned with a 2D axial slice, using CEST and spin-lock TSE.

A two-dimension (2D) reduced field-of-view (rFOV) TSE CEST sequence was previously introduced (34). rFOV can effectively suppress motion artifacts caused by bowel movement, and improve measurement reproducibility. This is important for quantitative IVD imaging which is susceptible to artifacts. The same rFOV TSE pulse sequence design was applied to spin-lock preparation, forming an rFOV TSE spin-lock sequence for human imaging at 3.0T. Following localizer and standard T₁/T₂-weighted TSE acquisitions, on each patient a 2D sagittal slice cutting through the center of IVDs was used for CEST and spin-lock imaging. Only the spine coil was used for signal receiving. The WASSR offset frequency range was sufficient to cover maximum frequency shift after careful shimming with the shim box selected to only cover interested spine region. The WASSR saturation power was enough to achieve water resonance frequency quantification. Imaging parameters are shown in Table 2. CEST and WASSR preparation parameters are shown in Table 3. For spin-lock preparation, SLAs were 100 and 400 Hz. SLTs were from 22 ms to 40 ms in step of 2 ms, and from 102 ms to 120 ms in step of 2 ms.

Table 2.

3.0T Human Imaging Parameters

Sequence	TE (ms)	TR (ms)	TH (mm)	FOV (mm2)	ETL	Matrix	No. of averages	TA (min)
rFOV CEST	9	3000	8	73×220	42	32×192 (interpolated to 64×384)	4	5.4
rFOV Spin-lock	9	3000/5830–8050a	8	73×220	42	32×192 (interpolated to 64×384)	4	11.8–18.5

^aTR was fixed at 3000 ms for 100 Hz scan. The minimum allowable TR was used for 400 Hz scan.

TE = echo time; TR = repetition time; TH = slice thickness; rFOV = reduced field-of-view; ETL = echo train length; TA = imaging time.

Table 3.

3.0T Human CEST Parameters

Sequence	FA (°)	RF duration (ms)	No. of RFs	No. of offsets	Offset range (ppm)	Irradiation time (ms)	Irradiation power (μT)
CEST	1440	90	8	15	−2.1 to 2.1	1350	0.9
WASSR	60	30	2	11	−1.0 to 1.0	90	0.09

Data Analysis

Post processing was performed with custom-written programs in Matlab (The Mathworks, Natick, MA). CEST images were processed as previously described (34). Spin-lock images at different SLTs were fitted into a mono-exponential decay model to obtain R_1ρ values using least-squares fitting, pixel by pixel. On phantom images user-defined region-of-interest (ROI) containing at least 100 pixels inside GAG regions was drawn manually. For porcine and human IVD data, ROI was chosen to only include central NP region that has high signal on MRI, due to concerns of insufficient SNR in outer NP and AF regions. When drawing ROI on porcine IVDs, regions with NP leakage as a result of opened disc were carefully avoided. CEST and R_1ρ dispersion values were averaged within ROI before RROC calculation. In addition, normalized RROC for each human IVD was calculated by dividing the corresponding RROC value by the lowest value in each subject. This normalization could help to reduce variations among subjects. Two discs from patient #2 were excluded from subsequent analysis because of negative R_1ρ dispersion values, which were possibly caused by small R_1ρ dispersion, noises due to limited SNR, and poor shimming. A total of 21 human discs were analyzed.

Statistics

Statistical analysis was performed using SPSS v. 16.0 (SPSS, Chicago, IL). Paired-t test was used to test RROC value differences between IVDs with positive and negative discography outcomes with the significant level defined at α = 0.05. Receiver-operating characteristic (ROC) curves were generated for RROC as disc pain biomarker and areas under the curve (AUC) were calculated.

RESULTS

Fitted exchange rate k_ex of the –OH protons under different pH levels are shown in Table 1. These rates are in the intermediate exchange regime and lower pH leads to reduction in exchange rate, meaning –OH exchange is mainly base-catalyzed, similar to measurements of amine protons (27).

Simulation results are shown in Figure 2. Both CEST and R_1ρ dispersion were proportional to concentration as shown in Figure 2a and 2b. Compared with CEST, R_1ρ dispersion was more sensitive to pH changes as reflected by a larger slope in Figure 2e compared with in Figure 2d. RROC was almost independent of concentration and dependent on pH as shown in Figure 2c and 2f. Simulation indicates that RROC can serve as a concentration independent, pH level-dependent imaging biomarker. Simulations also suggested that, even though RROC can be affected by B₁ inhomogeneity and changes in T₂ and T₁ (g–i), its dependence on pH exceeded that on these confounding factors, indicating RROC is largely dominated by pH effect. Nevertheless compensation techniques taking into consideration of these factors may further enhance the accuracy of pH imaging by RROC.

FIG. 2.

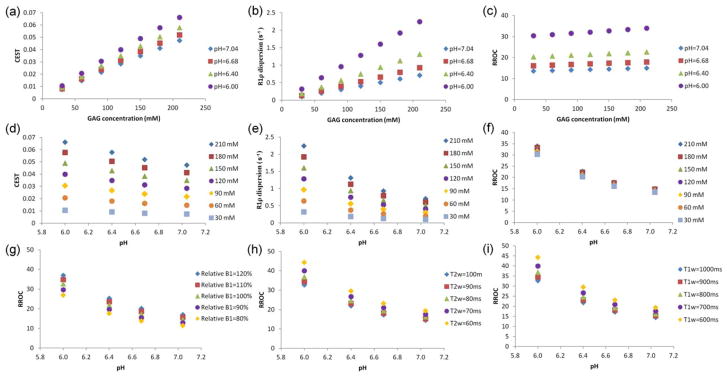
Simulated GAG CEST, R_1ρ dispersion, and RROC with respect to GAG concentration (a–c) and to pH (d–f), and dependence of RROC on B₁ error (g), T_2w (h), and T_1w (i). RROC is almost insensitive to changes in concentration, because the division of R_1ρ dispersion and CEST has cancelled the concentration effect but maintains its dependence on pH. RROC is moderately affected by changes in relative B₁, T_2w, and T_1w.

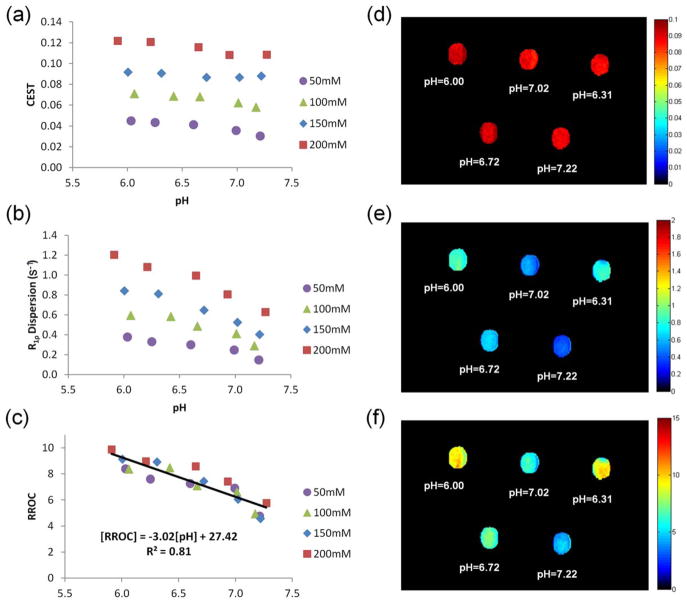
Phantom II results are shown in Figure 3. While both CEST and R_1ρ dispersion were dependent on pH, R_1ρ dispersion was more sensitive to changes in pH level, as seen by the larger slope in Figure 3b compared with in Figure 3a. Results shown in Figure 3c confirmed the concentration independence and pH level dependence of RROC. CEST, R_1ρ dispersion, and RROC images (Fig. 3d–f) of the 150 mM phantoms demonstrated the pH level-dependent imaging capability of the proposed technique, as GAGs with different pH levels were well discriminated in Figure 3f. It is worth mentioning that Phantom II and simulation RROC results differ in values, because simulations were performed with parameters that of typical in vivo IVD rather than GAGs. Nevertheless similar pH dependence trends were observed in both studies, supporting that RROC is suitable for pH level-dependent imaging.

FIG. 3.

GAG phantoms results on 3.0T. a–c: Show the pH dependence of CEST, R_1ρ dispersion, and RROC of phantoms with various concentrations, respectively. d–f: Show CEST, R_1ρ dispersion, and RROC images for the 150 mM GAGs.

The ability of pH level-dependent imaging was tested on porcine spine IVDs, with results shown in Figure 4. Of the three discs studied, a reduced pH was correlated with higher RROC. These RROC values differ from that of GAG phantoms because they had different MR parameters such as T₁ and T₂. Nevertheless a similar pH dependence trend was observed.

FIG. 4.

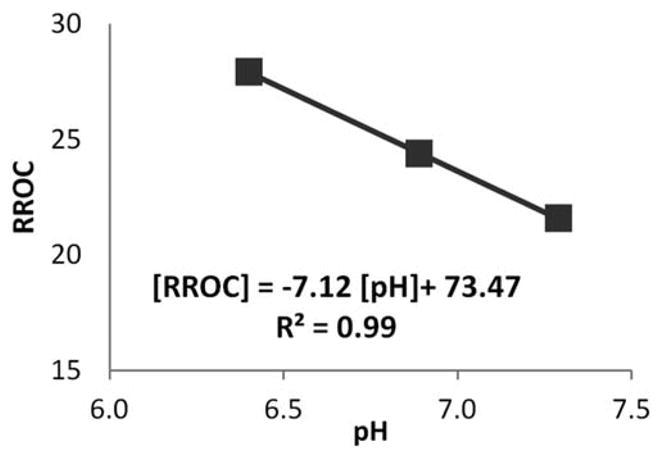
Results of three porcine IVDs following Na-Lactate injection to manipulate pH level. A negative correlation was observed between RROC and pH.

Patient results are shown in Figure 5. The average –OH CEST values of painful and nonpainful discs based on discography were 1.7% ± 0.9% and 2.3% ± 0.9%, respectively (mean ± SE), and the difference was non-significant by paired t-test (P = 0.143). The average R_1ρ dispersion values of painful and nonpainful discs were 1.7 ± 0.3 and 1.5 ± 0.5, respectively (mean ± SE), and the difference was nonsignificant by paired t-test (P = 0.212). The average RROC values of painful and nonpainful discs were 135 ± 75 and 73 ± 36, respectively (mean ± SE), and significant difference was identified between them by paired t-test (P = 0.024). The higher RROC values in painful discs suggested a lower pH level. This finding was in line with predictions from LBP pathogenesis theories and studies (3,13,14). ROC analysis had an AUC of 0.76, indicating it is a fair predictor for painful discs. To correct for variations between human subjects, RROC values were then normalized by the smallest value in each subject. The average normalized RROC values of painful and nonpainful discs based on discography were 3.3 ± 2.6 and 1.1 ± 0.2, respectively (mean ± SE), and significant difference was identified between them by paired t-test (P = 0.013). ROC analysis revealed that this approach has high prediction power with an AUC of 1.00. Normalization improved the technique’s predictability.

FIG. 5.

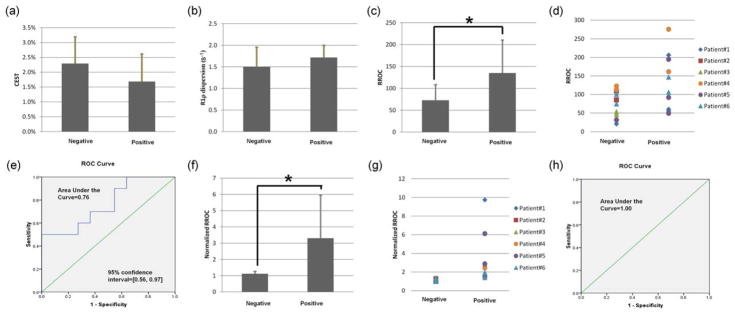
Patient results. a,b: –OH CEST and R_1ρ dispersion values for positive and negative discs, respectively. c,f: the difference in RROC and normalized RROC between positive and negative discs, respectively. d,g: RROC and normalized RROC of individual discs, respectively. e,h: ROC curves for RROC and normalized RROC, respectively. Stars indicate significant difference by paired t-test (P < 0.05).

Imaging results of a typical patient are shown in Figure 6. In this subject, two positive and two negative discs were identified by discography (Fig. 6a). Thresholds can be drawn between painful and nonpainful discs, both in RROC and normalized RROC results (Fig. 6b,c).

FIG. 6.

Typical patient result (62Y/M). T_2w TSE image with discography outcome (“+” and “−” for positive and negative, respectively) (a), RROC (b), and normalized RROC (c) values, respectively, for the four discs labeled.

DISCUSSION

In this study, a novel pH level-dependent imaging technique was developed. This technique does not depend on exogenous contrast agents, and can be applied on a 3.0T scanner. A concentration independent and pH level-dependent new index, RROC, was proposed as a suitable biomarker for pH imaging in the IVDs. A negative correlation between RROC and pH levels was discovered by numerical simulations, phantoms and porcine spine studies, in a physiological pH range. Patient study showed significantly higher RROC values in painful IVDs, and normalized RROC demonstrated great power in predicting painful discs. These results suggest that (i) painful discs are associated with lower pH levels, and (ii) the proposed technique is a promising, noninvasive method for detecting discogenic low back pain.

The GAG phantoms scan in our study is different from that reported by Melkus et al (17). First, their study was performed at 7.0T, which has a larger resonance frequency separation between –OH and water protons than 3.0T. An exchange rate of 600 Hz may be considered to fall within intermediate exchange regime at 3.0T, at 7.0T it may be closer to slow exchange regime. Second, direct saturation of water pool as a result of nonnegligible saturation pulse bandwidth is more prominent at 3.0T. This is especially relevant for –OH imaging as their resonance frequencies are close to water (~125 Hz on 3.0T and ~292 Hz on 7.0T). At higher magnetic field because –OH protons are more separated from water peak therefore generally less direct saturation effect is expected. Third, saturation pulse profile could be different. It has been previously shown that pulse shape has influences on gagCEST (35). Zu et al has proposed the use of normalized average amplitude (p1) and normalized average power (p2) as metrics to describe pulsed-CEST (22). Even though both studies used Gaussian pulses, pulse profile differences (e.g., p1 and p2) could lead to different CEST signal. Fourth, different trends between –OH CEST and pH were found in the two studies. When focusing on the physiological pH range of ~7.2 to 6.0, –OH CEST in our study increased with decreased pH level, whereas the opposite trend was observed in their study. The sources of discrepancies are unknown, but could be attributed to differences in irradiation power.

The two-pool R_1ρ dispersion model as shown in Eq. [2] only involves –OH and water protons, and neglects –NH protons. Jin et al. concluded that on-resonance spin-lock is most sensitive to intermediate exchange regime (27). GAG –OH has exchange rate between ~500 s⁻¹ and ~830 s⁻¹ as measured in our experiment. The exact GAG –NH exchange rate is unknown. In the brain –NH exchange rate has been measured to be ~ 10–30 s⁻¹ (36). Previous ex vivo results revealed that GAG –NH CEST signal is roughly one order smaller than –OH (37), indicating GAG –NH is likely to exchange with a slow rate as well. Therefore in this case the two-pool R_1ρ chemical exchange model should be sufficient. In cases where there are multiple exchanging protons each having substantial contribution, a multi-pool model should be considered. In these cases contribution to R_1ρ from chemical exchange is the sum of contributions of each of the proton pools (38).

Some confounding factors remain that could complicate pH-level dependent imaging with the proposed RROC technique. The first type of confounders includes MR parameters such as T₁, T₂, and B₁ inhomogeneity. Although no mathematical description is available for pulsed-CEST imaging, for continuous-pulse imaging T₁ and T₂ do contribute to CEST signal as revealed by analytical solutions discussed previously (23). B₁ inhomogeneity can affect both CEST and R_1ρ dispersion. As revealed by simulations, these MR parameters could confound pH level-dependent imaging by affecting CEST signal, and may require further correction. In fact when RROC values were normalized by subject in our patient study, the AUC value in ROC test increased from 0.76 to 1.00, indicating the normalization process brought more prediction power in identifying painful discs, possibly by reducing variations in B₁ inhomogeneity, T₁ and T₂ between subjects but not within subject. Another potential approach is to first examine the relationship between RROC and T₁ and T₂ using numerical simulations and phantom studies, then perform T₁ and T₂ quantification during MRI acquisition, and finally correct the measured RROC value using T₁ and T₂ values. However, this approach comes at a cost of prolonged imaging time, and needs further investigation. The second type of confounders includes alternative saturation transfer mechanisms including conventional MT and nuclear Overhauser effect (NOE). Underlying MT effects stem from semi-solid components such as macromolecules, and always accompany CEST in tissues (39). MT is asymmetric and cannot be corrected by MTR_asym analysis. NOEs on GAG were identified at −2.6 ppm and −1.0 ppm (37). These negative NOEs lowers measured CEST signal. Although in healthy IVDs the high –OH CEST as a result of high GAG concentration may over-ride the NOE at −1.0 ppm, in severely degenerated IVDs this may not be true. Therefore further investigation should focus on correcting these effects.

There are limitations in this study. First, the number of patients is relatively small. Even though statistical results were significant, clinical study involving a larger patient pool is desired to test RROC’s power in diagnosing painful discs. Second, certain parameters were not experimentally optimized. For example, the amplitudes of 100 Hz and 400 Hz used for R_1ρ dispersion measurement were chosen empirically. The 400 Hz was chosen because it permits pulse sequence execution on all subjects without encountering any problem with specific absorption rate (SAR) or RF amplifier. A higher ω_1H should be used whenever possible, because a larger dispersion allows more accurate measurement. The 100 Hz was chosen because sometimes artifacts were found at a SLA lower than 100 Hz in our experiment. Alternatively instead of 100 Hz spin-lock one would think of using T₂ quantification, which provides a larger dispersion. T₂ quantification may require a separate preparation as compared to spin-lock, as recently demonstrated by Li et al (40). Care has to be taken interpreting dispersion data measured using two different preparation schemes. Nevertheless, optimization involving numerical simulations, phantom study and in vivo study is recommended.

CONCLUSIONS

In this study, we developed a pH level-dependent, concentration independent index RROC for pH imaging in the IVDs, by combining R_1ρ dispersion and CEST imaging. To facilitate measuring this new index on a 3.0T scanner, rFOV technique and a novel spin-lock acquisition scheme under low spin-lock amplitude were used. Studies demonstrated a negative correlation between RROC values and pH levels. Normalized RROC successfully detected all painful discs in the preliminary patient study. As a noninvasive, pH level-dependent imaging tool, we believe this technique has the potential to (i) diagnose painful discs, (ii) contribute to the understanding of LBP pathogenesis, and (iii) provide insights on development of novel therapeutic approaches.