Leaf movements and their relationship with the lunisolar gravitational force

Abstract

Background Observation of the diurnal ascent and descent of leaves of beans and other species, as well as experimental interventions into these movements, such as exposures to light at different times during the movement cycle, led to the concept of an endogenous ‘clock’ as a regulator of these oscillations. The physiological basis of leaf movement can be traced to processes that modulate cell volume in target tissues of the pulvinus and petiole. However, these elements of the leaf-movement process do not completely account for the rhythms that are generated following germination in constant light or dark conditions, or when plants are transferred to similar free-running conditions.

Scope To develop a new perspective on the regulation of leaf-movement rhythms, many of the published time courses of leaf movements that provided evidence for the concept of the endogenous clock were analysed in conjunction with the contemporaneous time courses of the lunisolar tidal acceleration at the relevant experimental locations. This was made possible by application of the Etide program, which estimates, with high temporal resolution, local gravitational changes as a consequence of the diurnal variations of the lunisolar gravitational force due to the orbits and relative positions of Earth, Moon and Sun. In all cases, it was evident that a synchronism exists between the times of the turning points of both the lunisolar tide and of the leaftide when the direction of leaf movement changes. This finding of synchrony leads to the hypothesis that the lunisolar tide is a regulator of the leaftide, and that the rhythm of leaf movement is not necessarily of endogenous origin but is an expression of an exogenous lunisolar ‘clock’ impressed upon the leaf-movement apparatus.

Conclusions Correlation between leaftide and Etide time courses holds for leaf movement rhythms in natural conditions of the greenhouse, in conditions of constant light or dark, under microgravity conditions of the International Space Station, and also holds for rhythms that are atypical, such as pendulum and relaxation rhythms whose periods are longer or shorter than usual. Even the apparently spontaneous short-period, small-amplitude rhythms recorded from leaves under unusual growth conditions are consistent with the hypothesis of a lunisolar zeitgeber. Two hypotheses that could account for the synchronism between leaftide and Etide, and which are based on either quantum considerations or on classical Newtonian physics, are presented and discussed.

INTRODUCTION AND HISTORICAL OVERVIEW

The periodic movements of plants and animals have long held a fascination for naturalists. For example, the observation that leaves of certain plants adopt different positions during night and day is recorded in the writings of Pliny the Elder (AD 23–79) (Sweeney, 1969); and centuries later, Carl von Linné (Linnaeus) proposed that such movements were associated with a type of plant ‘sleep’ and its converse, ‘wakefulness’, strengthening his idea for the construction of a floral clock ‘by which one could tell the time, even in cloudy weather, as accurately as by a watch’ (Blunt, 1971, p. 198). However, some years earlier, as recorded by Marchant (1729), the astronomer, J.-J. de Mairan, in the course of making observations on leaves of Mimosa pudica, realized that the transitions between their sleep and wakefulness movements were not associated with the passage from night to day (and vice versa) because he found that the rhythm of movement continued even when the dark period was artificially prolonged.

The development of the kymograph for use with plants enabled the automatic recording of these ‘sleep’ movements of leaves (Pfeffer, 1875). This apparatus inscribes the leaf’s own movements on the surface of a rotating cylinder. A timescale can easily be fitted to the leaf trace so recorded. Hence, accurate estimates can be made of not only the times of day when leaves performed their various movements but also the amplitudes of even the smallest movement. Primary leaves of bean seedlings (mainly species of Phaseolus, as well as the more robust common jack bean, Canavalia ensiformis) were favoured material for investigation.

de Mairan’s early work with Mimosa suggested that the rhythm of its leaf movements originated within the plant, perhaps by retention of a memory of previous night and day times, a conclusion also drawn by Pfeffer (1915) from observations on Acacia (=Albizzia) lophantha plants which had been kept in continuous light. The memory hypothesis was also favoured by Semon (1905) who, by exposing leaves of A. lophantha to a light/dark (LD) rhythm of 6 : 6 h, found that they maintained their usual 24-h rhythm of movement throughout this unnatural LD period. The rhythm also persisted when the plants were transferred to continuous light (the free-running condition) (Semon, 1905). Evidently, none of these situations provided the plants with an environmental cue (zeitgeber), which would account for the 24-h rhythm of movement. Memory was shown later to be an untenable hypothesis when it was found that the 24-h leaf rhythm could become established in plants raised from seed in continuous light, and so this idea was then replaced by the proposal that heredity was the basis of diurnal rhythmicity [see Daan (2010) for a history of this aspect of chronobiology].

Further early work on leaf movements, notably by Stoppel (1912, 1916), was equally unsuccessful in finding any significant environmental cue that could act as a zeitgeber. Diurnal variations of temperature and barometric pressure, as well as gravitational effects due to the mass and position of the leaf itself, were all ruled out as possibilities. More local effects were then sought, the most frequently considered being the daily variation of atmospheric electrical conductivity (‘Luftfähigkeit’) (Stoppel, 1916, 1926). In Stoppel’s experimental chambers maximum conductivity was consistently recorded just after midnight, a minimum at around midday, and a small peak sometimes appeared in the late afternoon (Stoppel, 1916). Over the course of a day, the time course of conductivity appeared to coincide with the rise and fall of the leaves of her experimental plant, Phaseolus coccineus. In this era, there was widespread interest in the potential applications of electricity to plant growth (see Lemström, 1902; Blackman, 1924; Blackman et al., 1923), so Stoppel’s inclination towards air ions as an explanation of leaf movements is understandable in this context.

Not everyone was convinced by the putative relationship between leaf movement and air ions, however. Accordingly, experiments were performed which involved the transportation of experimental plants to and from underground sites (Cremer, 1923; Fehse, 1926) where constant atmospheric conditions were considered to prevail. Use was even made of the properties of the newly discovered element ‘mesothorium’ (the radioactive isotope, ²²⁸Ra) to discover whether artificially induced bursts of ionizing radiation would affect leaf movements of dark-grown plants (Schweidler and Sperling, 1922). Eventually, Bünning et al. (1930), after reviewing all the available evidence as well as performing new experiments, concluded that the cause of the leaf sleep movement did not lie with the changing electrical properties of the surrounding air and experimental work of this type came to a halt. Nevertheless, some researchers (Brouwer, 1926; Stoppel, 1932, 1938) continued to be interested in the inexplicable nature of such movements and suggested that an all-pervading environmental ‘Factor X’ – what Stoppel (1932) called ‘Erdströme’ – was responsible. There were also suggestions that Factor X was linked to variations in the geomagnetic field (Fehse, 1926), a possibility which has continued to be discussed (see Tibbits et al., 1973). Recently, periodic changes in atmospheric radiation in the form of radon (²²²Rn) gas (Crockett et al., 2006) has been proposed as a synchronizing agent in biological processes (Zakhvataev, 2015), although these processes are more likely to be expressed over periods of weeks and months, rather than days.

It is conceivable that all of these phenomena – variations of air ions, geomagnetic fluxes and barometric pressure – could be traced back to a common regulator such as the gravitational ‘pull’ of the Moon, (for references see Barlow et al., 2013). The idea of a ‘kosmische Einflüße’ can be found in the work of the physical chemist, Svante Arrhenius, in Sweden, who proposed the Moon to be a regulator of some of the more long-term rhythms which he had meticulously chronicled in relation to human physiology (Arrhenius, 1898). Properties of these two cosmic bodies, Moon and Sun, join to create a third force, the lunisolar tidal acceleration. This force is experienced by the Earth, its oceans and its atmosphere, and also by its biological inhabitants: and, moreover, the Moon can modulate the impact of the cosmic radiation which impinges upon the Earth’s atmosphere, thereby affecting features such as air conductivity (Mehra, 1989) and the geomagnetic flux (Bigg, 1963). This complex interrelationship of cosmological and meteorological factors may account for the remarkable coherence between fluctuating geophysical variables such as the ap (the daily average level of geomagnetic activity) and Disturbance Storm time (Dst) indices, the gravimetric variable δg, and biological variables, such as tree-trunk diameter variation and root elongation rate (Barlow et al., 2010, 2013; Barlow and Fisahn, 2012).

The question therefore is whether the lunisolar tidal force is the elusive Factor X, which, if translated into a time series of quantifiable units, would hold the key to some of the fundamental features of chronobiological phenomena, including the clock-like regularity of bean-leaf movements. This was the view taken by Gunter Klein (2007), who proposed that the movements of bean leaves were responses to a lunar zeitgeber. As the title of Klein’s book suggests, Klein was contradicting the prevailing notion that leaf movements were expressions of a physiological, or endogenous, clock, as proposed by Bünning (1973) and which, when first mooted (Bünning, 1932, 1935a), was just as speculative as the case for air-ions, and with even less evidence to support it. The clock’s putative endogenous nature arose out of the finding that its periodicity could be inherited and was therefore genetically determined. And this meant, ipso facto, that it was endogenous. Such a clock would naturally ‘explain’ the rhythm of leaf movements, even though nothing could be said about any of its constituents.

Examination of Klein’s original time courses of leaf movements of Phaseolus spp. provided cautious support for Klein’s view of a lunar zeitgeber (Barlow et al., 2008; Barlow and Fisahn, 2012). The lunisolar tidal acceleration varies from day to day with a regular pattern throughout a lunar month, which means that, if there is correlation between the time courses of the tidal acceleration and the leaf movements, the two time courses should show a measure of coherence. Moreover, the prediction (Barlow, 2007) that correspondence of both biological and lunar rhythms should be found in experiments conducted simultaneously in two or more different locations has now been realized: in each location, the biological rhythm – in this case the rhythm of biophoton production by germinating wheat seedlings – correlates with the local rhythm of the lunisolar tidal variation (Gallep et al., 2012, 2014). Moreover, correlations have been shown between the rhythms of the lunisolar tidal force and those of leaf movements of Arabidopsis plants within the International Space Station (Fisahn et al., 2015). Thus, in these cases, at least, the rhythm is not an innate feature of the biological material, genetically imprinted or otherwise memorized, but has developed, or been entrained, in synchrony with the exogenous lunisolar rhythm experienced either on Earth or in Space (Fig. 1).

Fig. 1.

Interplay of exogenous and endogenous timing mechanisms upon an organism. Rhythmic physico-chemical features of the external environment that are components of the biotic complex (light, temperature, food) can be intercepted by plants by means of specific receptors which transduce and integrate the biophysical properties into the network of metabolism. The rhythmic nature of these features then becomes translated into physiological rhythms (outer ring of the diagram) that can be adjusted in accordance with the capture and summation of the relevant inflow of physico-chemical units. The inner ring of the diagram represents a second class of external environmental variables that are components of the Earth’s geophysical fields. These fields cannot be altered and may not show predictable long-term rhythms and therefore there may be no specific receptor designated for their transduction. The response to them is direct, according to physical principles, even if these are presently not fully understood. The adjustable physiological rhythms and the more rigorous geophysically dependent rhythms both feed into (arrows) and participate in the living processes and behaviour of the organism, represented by the circular ‘core’ of the diagram. It is possible, however, that should a geophysical rhythm extend from one day to the next, its consequences, which may be mediated by the organism itself, might then be briefly integrated as an adjustable physiological rhythm (J-shaped arrows). However, given the variable, or arrhythmic nature of geophysical in-flows, integration is short-lived and supplanted by the in-flow of novel information. The figure is based on fig. 2 in Brown (1964), but with much modification.

The early observers of bean leaf movements – Brouwer, Kleinhoonte, and Bünning and his associates – have provided a rich source of data for a retrospective analysis of the relationship of these movements with the progress of the lunisolar tide. The various kymographic records are dated, and the locations of the observations are known. These details permit estimation of the lunisolar tidal variation δg for the dates and locations in question, making use of the Etide program, which is based on the computations of Longman (1959), and which has been used in similar analyses (Barlow et al., 2010; Barlow and Fisahn, 2012). The Etide estimates can then be superimposed upon the biological time courses and the inflections, or ‘turning’ points, in the lunar tide and ‘leaf-tide’ time courses can be examined for their degree of synchrony. The synchronous state would be expected if a critical event in the time course of one variable (the lunisolar tide) were the predictor, or even the cause, of an analogous critical event in the other (biological) variable.

The lunisolar tidal variation δg is a gravimetric variable which stands proxy for the gravitational force exerted by the Sun and Moon upon the Earth and upon living organisms and their cells. By examining the original biological data in the context of the above-mentioned relationship with this cosmo-geophysical variable it is possible not only to scrutinize the foundations upon which the physiological, or endogenous, clock was proposed, but also to view this concept from an alternative point of view – that is, in the light of knowledge of the exogenous lunisolar tidal force exactly as it was when operating upon the experimental material. In fact, just as much data need to be appraised in this way as were required to develop the concept of the endogenous clock in the first instance. A partial survey would be neither sufficient nor sufficiently convincing.

The intention of the present review is not to overturn the concept of the endogenous physiological clock but, rather, to unpick its elements, and thence to propose that the diurnal rhythm of leaf movements, as exemplified by the bean leaf system, actually represents the ‘hands’ of an exogenous lunar clock. Only the leaf-movement clock is explored, and only the conventional interpretation that this clock is endogenous is challenged. No doubt other physiological ‘clocks’ exist which are genuinely endogenous; but these, it is contended, belong to another category of rhythms, such as that proposed for the photo-control of flowering (Bünning, 1936).

MATERIALS AND METHODS

Published leaf traces obtained by kymography were analysed only if they were accompanied by times and dates (hh/dd/mm/yy) of their collection, and where the location was unambiguous. Time axes referred to the local time at the location in question. Traces from reference leaves were enlarged and leaf height, L, in arbitrary units was recorded with respect to the time axis. The error was approx. ±0·25 h with respect to the time of the inflections along a trace, when a leaf starts to change its direction of movement.

The convention in the older scientific literature was for the leaf movements to be published exactly as inscribed by the kymograph apparatus. Thus, leaves appear to move in a direction opposite to their actual direction. To display the leaf movement more realistically, the published traces have been inverted, so that when a leaf has actually moved from ‘up’ to ‘down’, say, this direction is represented in the corresponding figure. Also, in the early recordings of leaf movement (e.g. Stoppel, 1916), mid-day (1200 h) on the time axis coincides with the placement of the date. This date/noon-time correspondence provides the reference for the re-drawn timescales. The absence of a date and precise local time (real solar and lunar time) on many modern time courses, after about 1949 — see Flügel (1949), dealing with biological rhythms is regrettable because it is impossible, now, to interpret the data in any way other than the context of a subjective timescale provided by the author (cf. Burns, 2000).

Contemporary recordings of leaf movement use photographic techniques or electronic recording devices to trace leaf movements (e.g. Hoshizaki and Hamner, 1964). Here, the directions of movement are as they would appear to an observer.

Time courses of variations of the lunisolar tidal acceleration (±δg) were estimated by the Etide program. Required inputs are: (1) latitude and longitude – degrees: minutes N, and degrees: minutes E, and altitude (m) of the location where the leaf movements were recorded, all these being obtainable from GoogleEarth (version 7.1.1.1888, Microsoft Windows 7); and (2) the dates on which observations took place. Estimates of δg are computed at 15-min intervals on a timescale corresponding to UTC (≡ GMT) and, hence, were adjusted to the local time at which the observations were made. Relevant for this are: (a) the time difference with respect to UTC and whether daylight saving was in operation [e.g. CET (UTC + 1 h) or CEST (UTC + 2 h)] and, if so, (b) the dates on which such shifts occur. Information for (a) is available at http://www.timeanddate.com/worldclock/converter.html, and for (b) at http://en.wikipedia.org/wiki/Daylight_saving_time_by_country.

The phase of the Moon on any given date was ascertained at http://www.moonconnection.com/moon_phases_calendar.phtml for dates after 1930, and for earlier dates at http://eclipse.gsfc.nasa.gov/phase/phasecat.html. The latter site also facilitates the construction of a time axis that includes the lunar ‘days’ of a given lunar month, which can then be interpolated within a time axis constructed according to a 24-h solar day. Lunar ‘days’ run only approximately in concurrence with solar days because (a) the duration of the lunar day is 0·8 h longer than the solar day, and (b) the hour at which the lunar month commences on lunar day no. 1 (New Moon) may occur at any time during the solar day upon which it falls.

Times of sunrise and sunset, and of moonrise and moonset, for a given location were obtained at http://aa.usno.navy.mil/data/docs/RS_OneYear.php, using the appropriate local time. The corresponding altitude (degrees above or below the horizon) of Sun and Moon, as well as the azimuth (measured as degrees E from N) of each body, was obtained at http://aa.usno.navy.mil/data/docs/AltAz.php

Relationships between daily or monthly variations of the Etide values and the variation of the marine tide, in terms of height and timing of high and low tides, were examined using the location of Brest, France, which was considered typical with respect to marine tides. The desired data were found at http://tides.mobilegeographics.com/locations/719.html?y=1976&m=6&d=21.

In previous publications statistical methods, such as cross-correlation and local Pearson correlation, were used to evaluate the degree of synchrony between the time courses of Etide and biological variables (e.g. Barlow et al., 2013). For the present purpose it was sufficient simply to plot the rates of change of the values in each timeseries [i.e. δ(δg) and δL] on an hourly basis, and reading the time-displacement, if any, between pairs of zero rate values. Time offsets of approx. ±0·5 h could be resolved. This procedure of comparing plots of δ(δg) and δL provides a reasonable representation of the correspondence between the Etide and the leaf-movement time courses.

RESULTS

Lunar phases, marine tide and Earthtide

To appreciate the relationship between leaf movements and the lunisolar tidal variation estimated by the Etide program, it is instructive to examine the complementary relationship between the Etide output and the time courses of both the marine tide and the Earthtide. The presentation of these topics is given in Supplementary Data S1. Additional details concerning the relationship between Sun and Moon and Etide values are presented in Supplementary Data S2.

Movements of entire leaves

Movements of articulated leaves in relation to the solar day

The first observations on leaf movements by Brouwer (1926) and by Kleinhoonte (1929) (Figs 1 and 2 in Supplementary Data S3) were made using bean plants (Canavalia ensiformis) raised in a greenhouse and subject to natural daylight and darkness. Brouwer’s observations took place in mid-December 1924, whereas Kleinhoonte made her observations in mid-June 1926. Brouwer’s recordings were usually from one leaf of the first pair of leaves on the stem. Each test was performed several times, using two, or sometimes four, plants. For publication, he reproduced one of the replicated kymograph traces, ‘selecting [that] which shows the results obtained in the finest way’. The results from leaf P16 (Brouwer, 1926) are shown in Fig. 2, together with details from leaf P15 from a different plant. The movements of leaf P36 recorded by Kleinhoonte (1929) are shown in Fig. 3. The recordings were made using the same apparatus as had been employed by Brouwer.

Fig. 2.

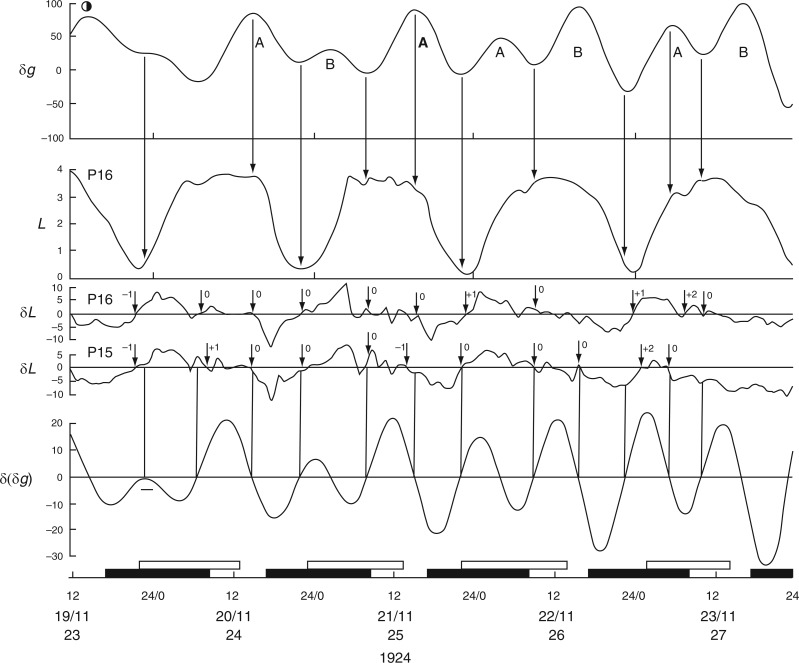
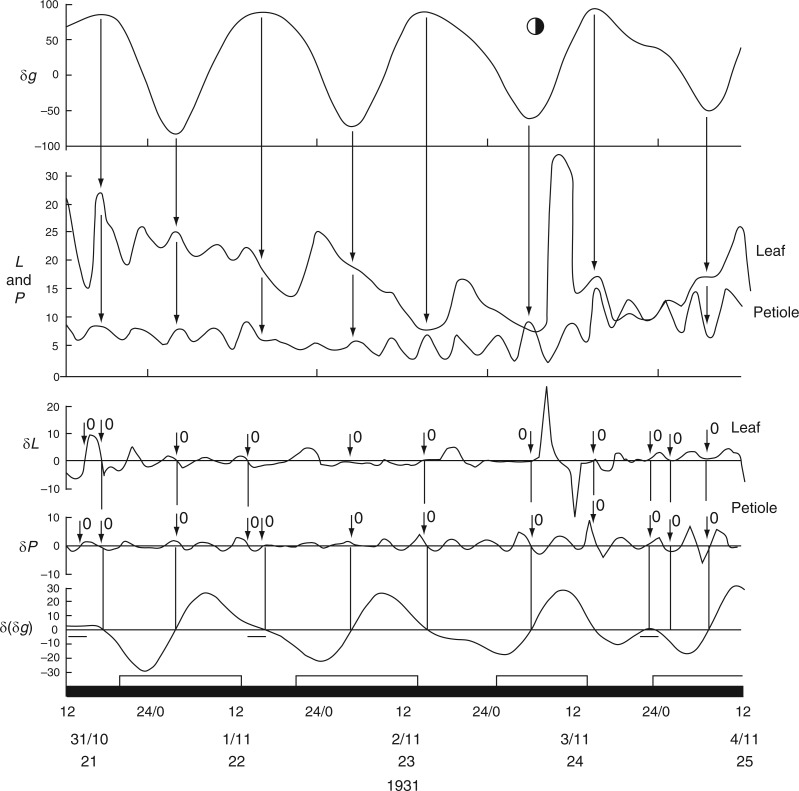
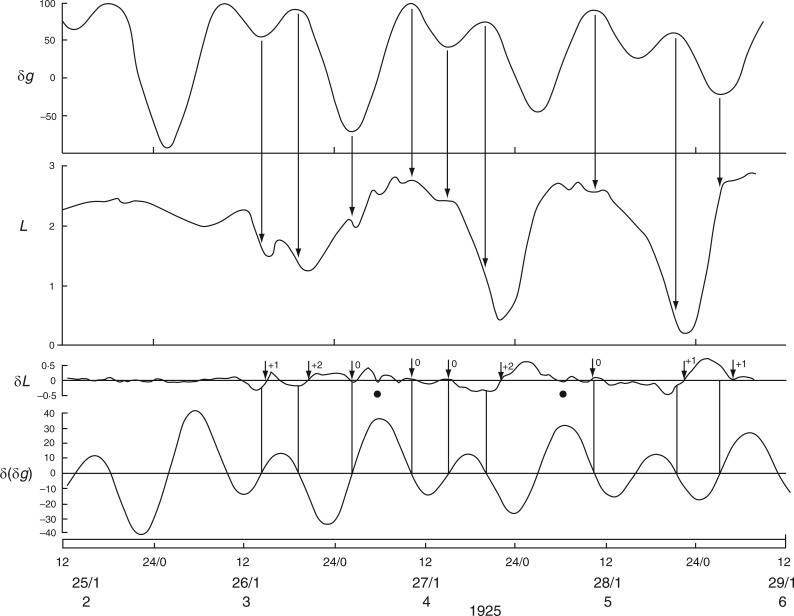
Kymographic record of the height (L) of leaf P16 of young plants of Canavalia ensiformis over a 4-d period, during November 1924, commencing at Last Quarter (LQ) Moon (lunar day 23). Units of L are arbitrary. The corresponding Etide trace (±δg) is shown in the top panel, together with an indication of the tidal structure of double [A,B] and single [A] peaks, the latter being the singular peak which occurs on a day close to LQ Moon. Vertical arrows indicate the correspondences between the time course of the Etide δg and features of the leaftide L, notably the times of their respective turning points. The two middle panels δL show the hourly rates of leaf movement, up or down, for leaf P16, and for leaf P15 of a replicate plant. Short vertical arrows associated with the two δL traces indicate turning points in the respective leaftides. The numeral beside each arrow indicates the degree of displacement between a leaftide turning point and an Etide turning point. A zero (0) indicates the two turning points are synchronous, and values of −1, +1, etc. (h) indicate displacements of the leaftide turning points with respect to those of the Etide. The houly rate of change of the Etide values [δ(δg)] is shown in the lower panel. The correspondence of the Etide turning points [when δ(δg) = 0] with the leaftide traces (δL) is emphasized by vertical lines linking the traces in the respective δ(δg) and δL panels. The short horizontal bar on the trace for δ(δg) at 19–20/11 indicates a small range of values around zero which might serve as an effective threshold at the Etide turning point in relation to a leaftide turning point. The lower horizontal time-scale supports open bars, which represent the times between moonrise and moonset, and filled bars, which represent the times between sunset and sunrise (i.e. filled bars span the night period). Time of day, date, lunar day number and year constitute the horizontal time axis. The leaf trace data have been redrawn from figs 4 and 5 in Brouwer (1926). In the original figures, leaf heights are presented in an inverted fashion; but here the orientation is as indicated, with the descended ‘down’ position and the ascended ‘up’ position of the leaf conforming to the vertical orientation of the Figure. Plants were raised in a greenhouse.

Fig. 3.

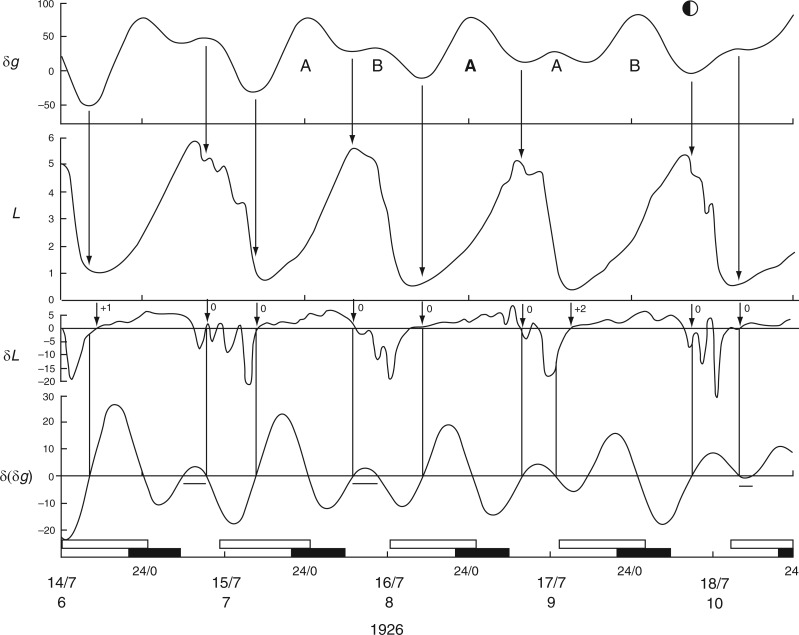
Leaf movements of C. ensiformis recorded by Kleinhoonte (1929) during July 1926, over a 4-d period immediately before FQ Moon. The conventions which apply to the various panels of this figure are the same as for Fig. 2. The horizontal bars under portions of the trace for δ(δg) indicate a small range of values above and below zero which might serve as an effective threshold of an Etide turning point in relation to a leaftide turning point. Leaf trace redrawn from fig. 1 in Kleinhoonte (1929).

The mean periods (τ) of leaf movements, as observed by Brouwer, were estimated from Fig. 2 as τ = 24·6 ± 0·2 h (n = 5) and τ = 24·5 ± 0·3 h (n = 6), using the successive ‘up’ and ‘down’ positions, respectively, as referents. Similarly, in the case of Kleinhoonte’s observations (Fig. 3), the mean periods were τ = 24·6 ± 0·4 h (n = 5) and τ = 23·8 ± 0·5 h (n = 5). Variation between plants (e.g. leaves P15 and P16, and also P19 and P20, of Brouwer, 1926; see his figs 4, 5 and 19) in the times of attainment of the first ‘up’ and ‘down’ position of each cycle was approx. 1 h; similar 1-h variations are evident in observations of replicate plants made by Kleinhoonte (1929, 1932).

Fig. 4.

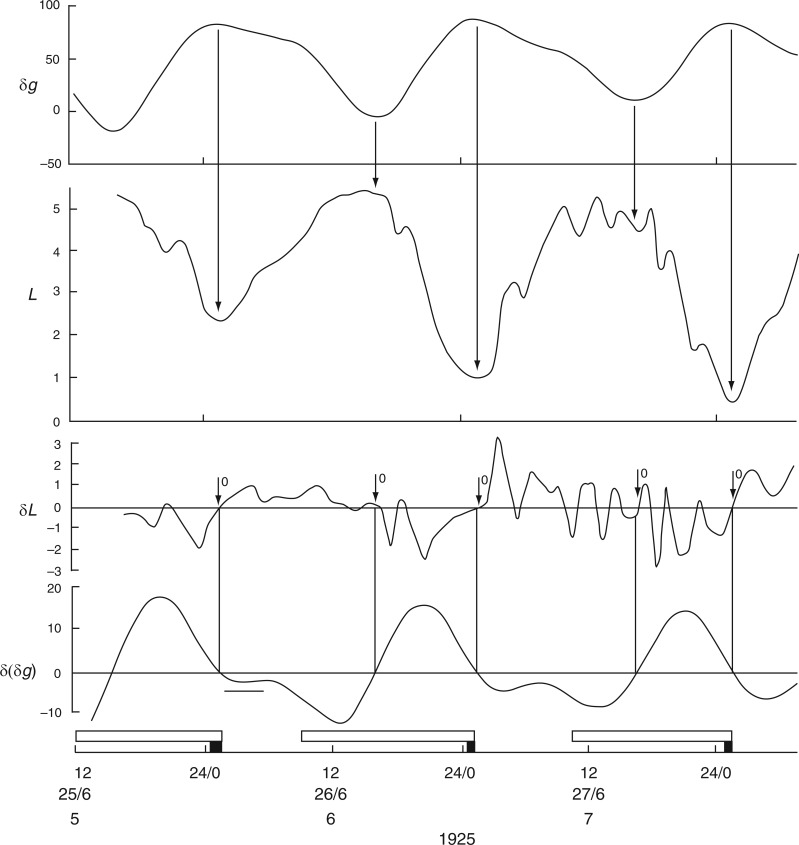
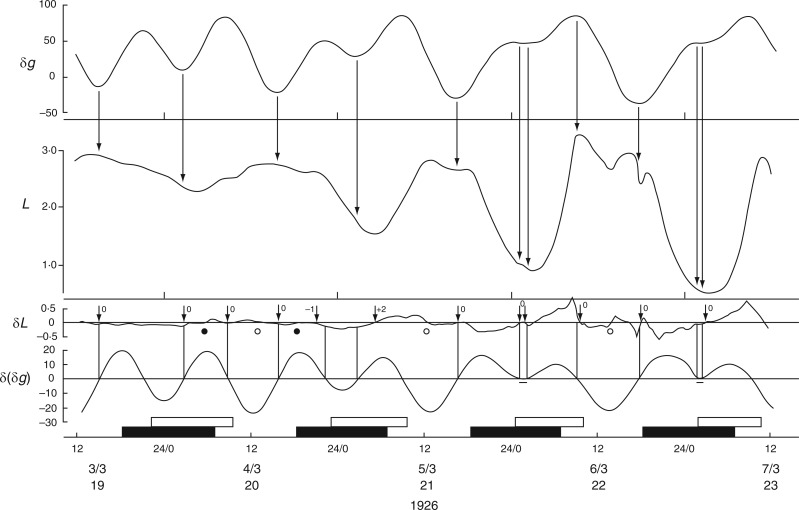
Leaf movements of Phaseolus coccineus recorded by Stoppel in Iceland during June 1926, when the night periods were approx. 90 min. The conventions which apply to the various panels of this figure are the same as for Figs 2 and 3. The plant was grown in natural conditions. Leaf trace redrawn from fig. 1 in Stoppel (1926).

Fig. 5.

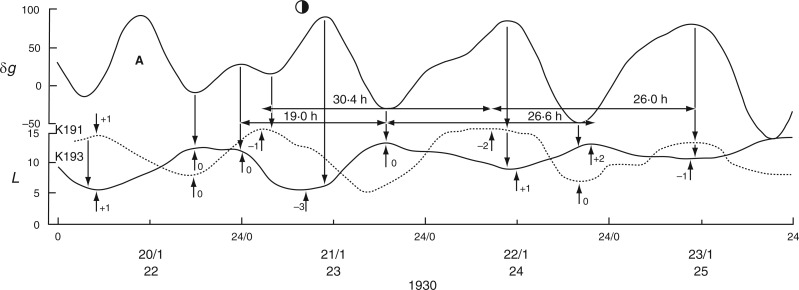
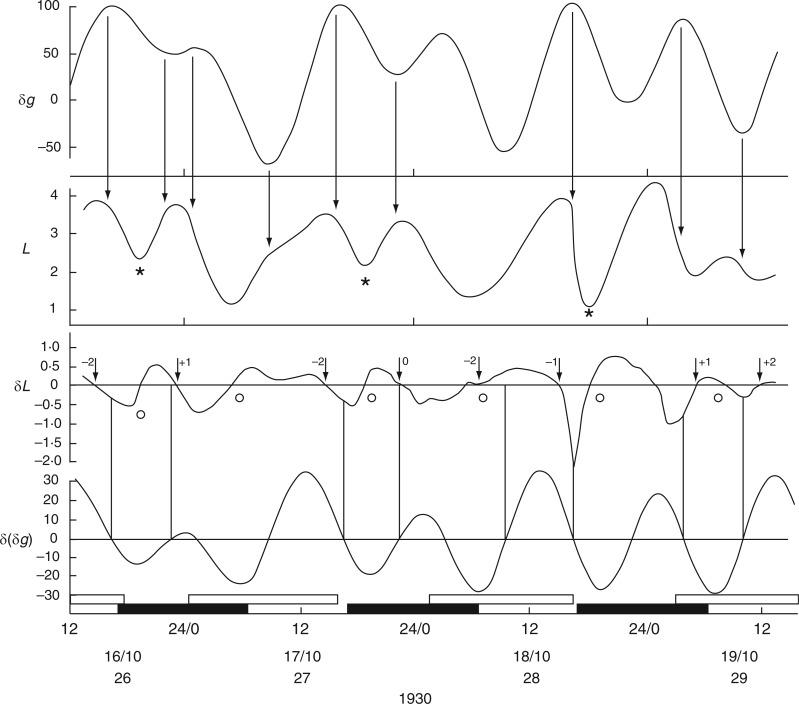
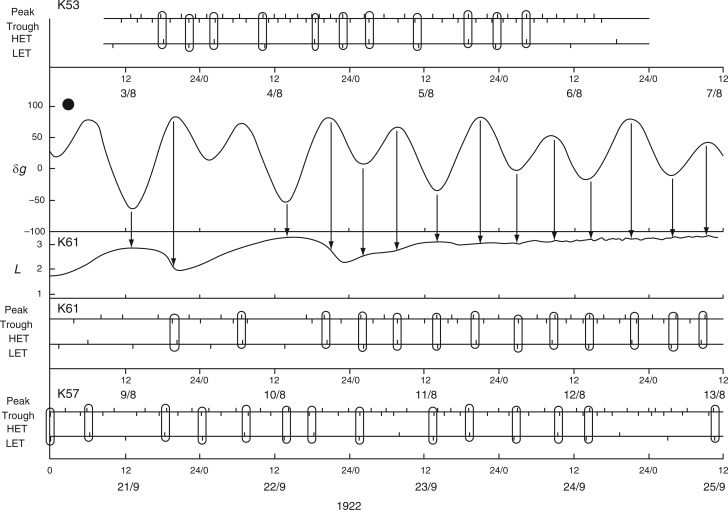
Alternative relationships between the rhythms of the Etide (upper panel) and of the movements of two different leaves, K191 and K193, recorded simultaneously (lower panel) from Ph. coccineus. K191 is mainly ‘in phase’ with the Etide, K193 is mainly ‘in antiphase’ with the Etide. The phase relationships become inverted on the first day shown (20/1/1930) when a singular A peak is present in the Etide profile, on the day before LQ Moon. Also noted are the displacements (h) between turning points of leaftide and Etide (short vertical arrows and numerals – upper arrows and τ values apply to K191, lower arrows and τ values to K193, using leaf maxima as the reference), whatever their phase relationship. Note also the range of leaftide periods, τ (horizontal arrows and values in h). Variations of τ are possible because of the changing structure of the Etide and its continuing influence upon leaf movement. Conventions which apply to the figure are the same as those for Figs 2 and 3. Leaf movements have been redrawn from fig. 5 in Bünning and Stern (1930).

Fig. 19.

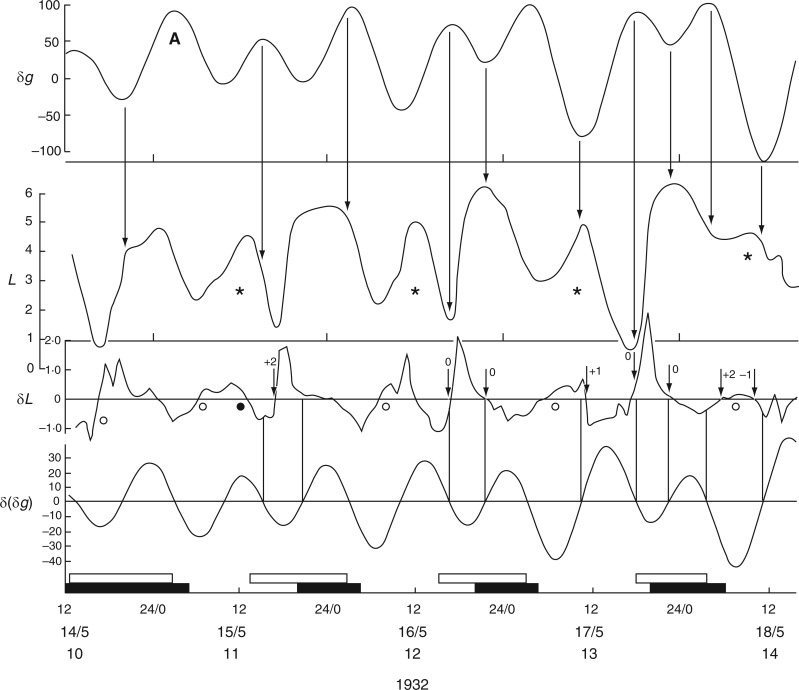
Leaf trace of Ph. coccineus showing part of a pendulum movement within which a downward movement has been interpolated (*). This unexpected descent coincides with an Etide turning point at 1200 h. The pendulum ascent continues at 2000 h. Leaf movements redrawn from fig. 9b in Bünning (1932).

Evident from Figs 2 and 3 is that leaves achieved their two semi-stable, diurnal positions, ‘up’ and ‘down’, during, respectively, the periods of natural light and dark, and did so regardless of the season, winter or summer. However, during the 16-h nights which pertained to Brouwer’s observations, each successive ascent of the reference leaf to the ‘up’ position commenced during the second (morning) part of the night (Fig. 2). The subsequent descent of the leaf began either in the last hour of each 8-h daytime period, or in the first hour of the night period. During the 16-h days, which pertained to Kleinhoonte’s observations (Fig. 3), each ascent was initiated during the second half of each daytime period, continued during the following 8-h night period, and maximal height was achieved at the beginning of the next daytime period. Descent of the leaf commenced about halfway through each daytime period, and was followed immediately by a new ascent. The rate of ascent of the leaf was less than that of its previous descent. Furthermore, the ascent occurred in two phases: a slow phase during daytime and a faster phase commencing about 2 h after the start of the dark period. Variations in the rate of transpiration throughout the days of summer (June 1926) may have accounted for some of these different rates of leaf movement. No such differences between the rates of leaf movement during the ascent or descent phases are evident in Brouwer’s results from wintertime (Fig. 2).

It therefore seems that the light–dark transitions of the natural day neither determine when the leaves would move from one semi-stable position to another (i.e. from ‘up’ to ‘down’ positions, and vice versa), nor their direction of movement. However, the relationship between leaf movement and the 24-h solar day becomes clearer when the times of moonrise and moonset are taken into account. Of interest is that the mean periods of the leaf movements, as estimated from Figs 2 and 3, are similar to the mean duration of the lunar day, 24·8 h.

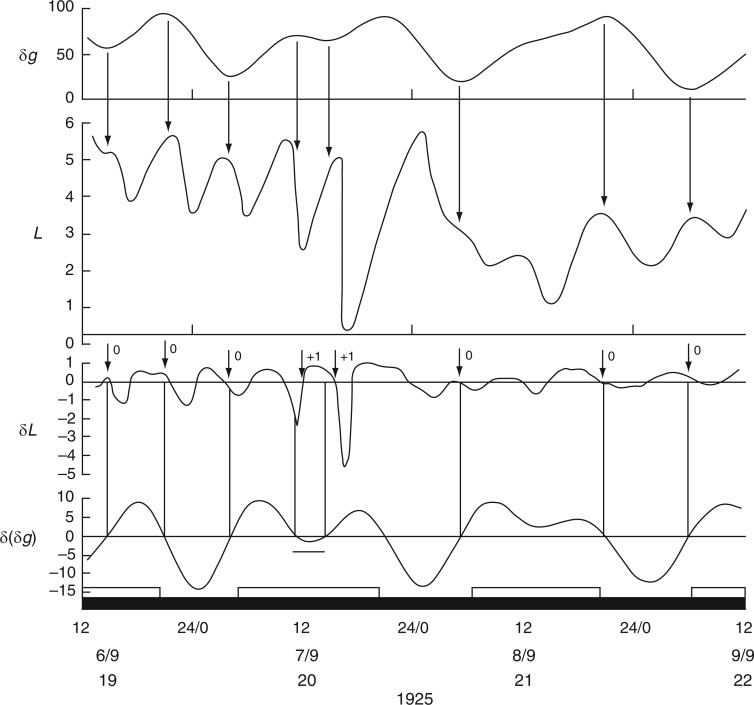
Further indications that the bean-leaf movements are not closely tied to the natural day/night cycle comes from observations made by Stoppel (1926; Fig. 3 in Supplementary Data S3) during the summer months at Akureyri, Iceland. Using plants of Phaseolus multiflorus (= Ph. coccineus), leaf movements were recorded 4 d after the Northern Solstice on 21 June 1925, on which date the night period lasted only 92 min. Leaf movements during the 4-d period 25–28 June 1925 are shown in Fig. 4. The reference leaf started to ascend at noon and descended shortly after midnight on each day, events approximately coinciding with the times of moonrise and moonset. The leaf was fully ascended during the brief night. When the respective turning points – i.e. when the rates of change of leaf movement δL and of the Etide δ(δg) are both zero – are inspected, they are coincident (Fig. 4). [For further remarks on the possibility of alternative timings of leaf movements on a given day such as 25 June, at Akureyri, see Supplementary Data S4.]

Leaf movements in relation to Etide

The relationships between the diurnal changes of direction of leaf movement and the times of the rising and setting of Sun and Moon become clearer when the contemporaneous time courses of the Etide variation are considered.

In Figs 2–4, the time courses of L and δg are complemented by their respective rates of change, δL and δ(δg). The superimposed plots of δL or δ(δg) reveal times when the two turning points are in synchrony. Synchronism is associated not only with major transitions of leaf position but also with some of the minor leaf movements.

Leaf movements in relation to Etide: thresholds

It is possible that a turning point in Etide facilitates a turning point in the leaftide. This leads to the question of the threshold Etide for this facilitation (Rensing et al., 2001): does an Etide turning point act upon leaf movement only when δ(δg) = 0, or is there a range of values either side of δ(δg) = 0 which are equally effective? A hint of an answer to this question is shown in Fig. 4. Although the ascent of the reference leaf on lunar day 6 coincides with δ(δg) = 0, there is also a 5-h period when a steady value of δ(δg) < –3 µGal h^–1 is maintained (Fig. 4). Temporary stasis of δ(δg) occurs because of the peculiar lunisolar characteristics which apply at Akureyri. On the day in question (26 June 1925) the value of δg declines slowly from a maximum over an interval of approx. 8 h (Fig. 4). The leaf turning point occurs during the period when δ(δg) = 0 to −3 µGal h^–1. Leaf movement accelerates later, when the threshold range is exceeded. On the next two days the δ(δg) thresholds are quickly passed and leaf ascents proceed more swiftly.

Although there is often coincidence between the leaftide and Etide turning points, the turning points of δL are sometimes displaced by ±1 h (see Figs 2 and 3 and elsewhere). However, the replicate experiments of both Brouwer and Kleinhoonte show that 1-h displacements of leaf movements between pairs of plants are possible. Thus, the ± 1-h leaf-turning displacements with respect to δ(δg) may be accounted for by biological variability.

Leaf movements in relation to Etide: phase relationships

Alternative couplings between the two time courses – the geophysical and the biological – are noticeable in Figs 2–4. On some calendar dates, minimum extremas of δg are associated with minimal leaf positions (leaves in the ‘down’ position). The two time courses are thus ‘in phase’. On other dates, δg minimum extremas coincide with ‘up’ leaf positions: the time courses are thus ‘in antiphase’. The ‘in phase’ and ‘in antiphase’ relationships alternate during the course of a lunar month. In Fig. 2, for example, the leaftide and Etide δg time courses are ‘in phase’ early in the month: on lunar days 5–8, leaf ascents coincide with ascending values of δg (Fig. 2). On lunar day 10, however, the relationship switches to being ‘in antiphase’. This is the day of first quarter (FQ) Moon, the significance of which will be discussed later. In the example shown in Fig. 3, the time courses span a later portion of the month. On lunar days 21–25 the two time courses are ‘in antiphase’, but on lunar days 26–28 the alternative, ‘in phase’, relationship is found (Fig. 3).

Continuous leaftide time courses spanning an entire lunar month are unavailable from the published literature. Nevertheless, sufficient time courses, from different segments of a number of lunar months, have been analysed to suggest that this switching of the leaftide/Etide phase relationship within the lunar month is the rule. To generalize, over the period of New Moon (NM), when the lunar month commences, the leaftide time course and the Etides are either ‘in phase’ or ‘in antiphase’ until around the day of FQ Moon; later, across the period of Full Moon (FM), the same phase relationship persists until the time of Last Quarter (LQ) Moon. The relationship then reverses: an ‘in phase’ relationship switches to ‘in antiphase’, or vice versa. The new relationship persists across the next NM, remaining so until the following FQ Moon. Further details relevant to this topic are presented more fully in Supplementary Data S5 and S6.

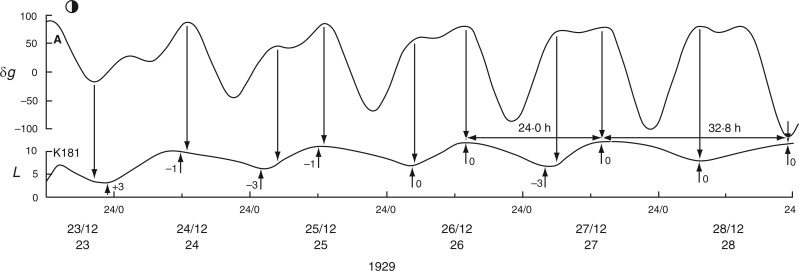
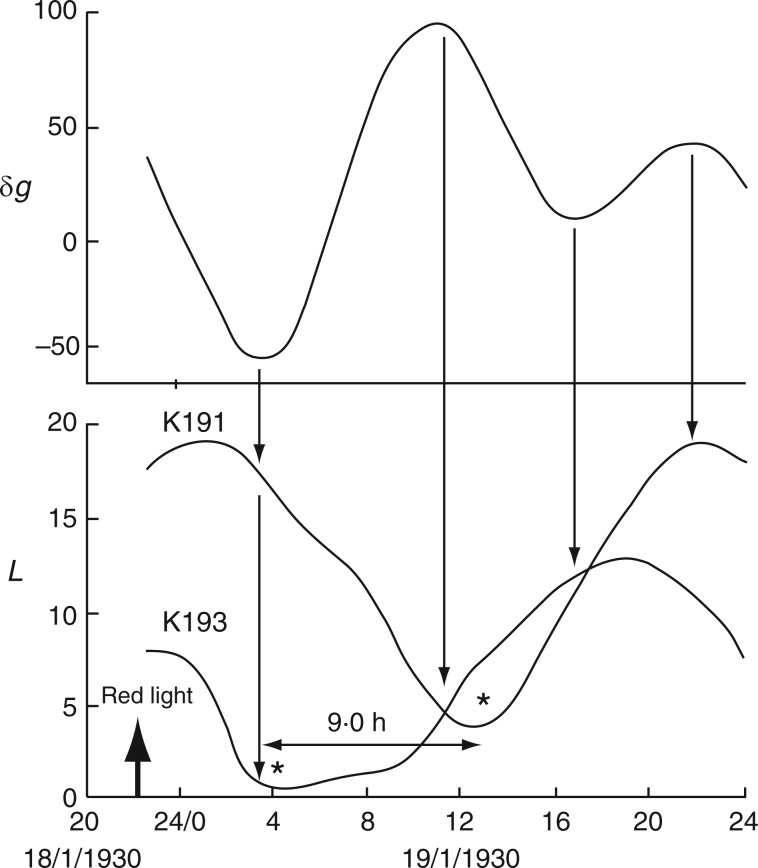
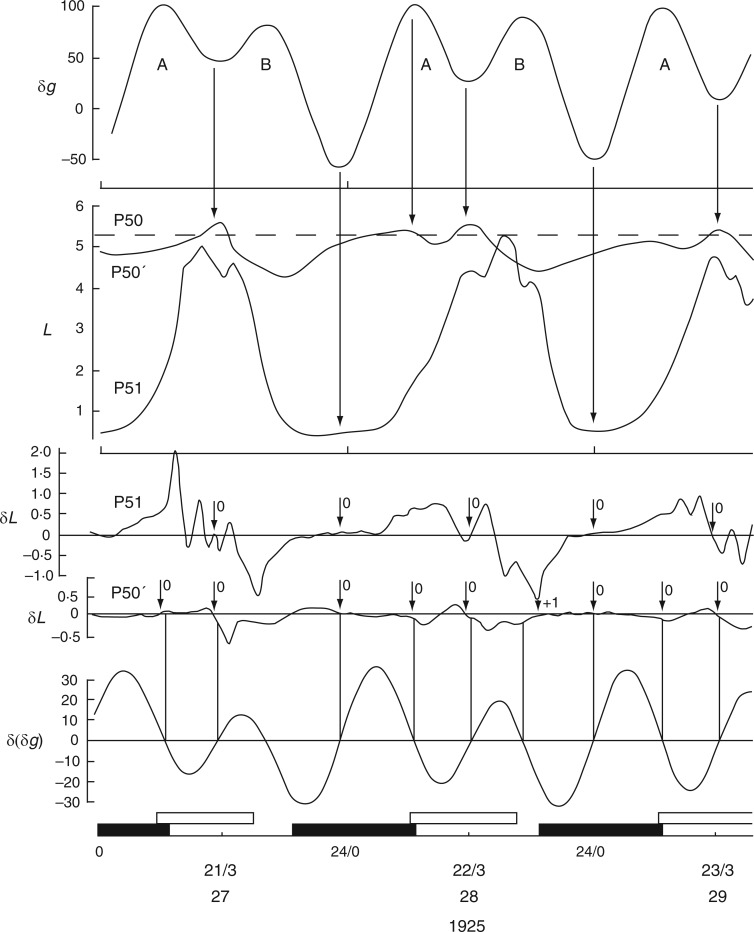
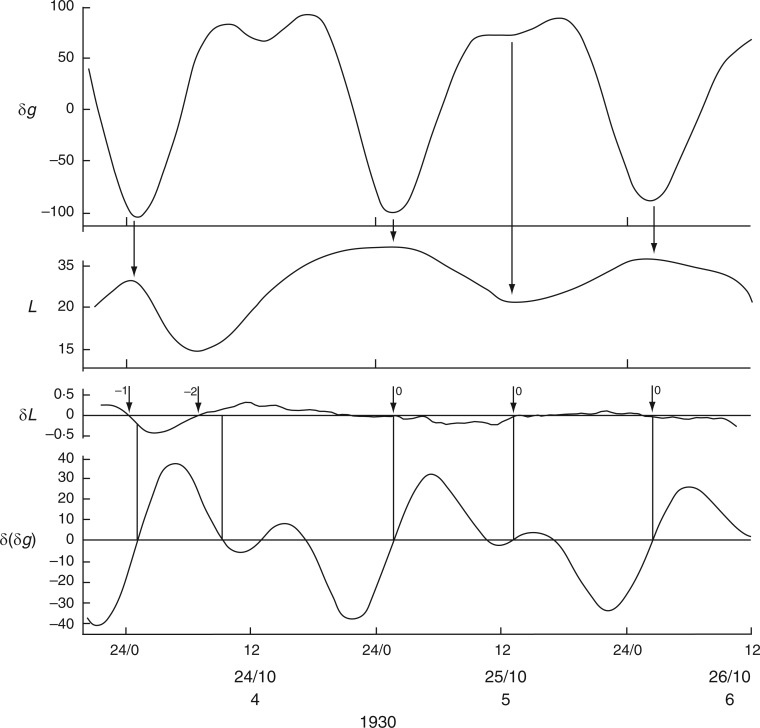
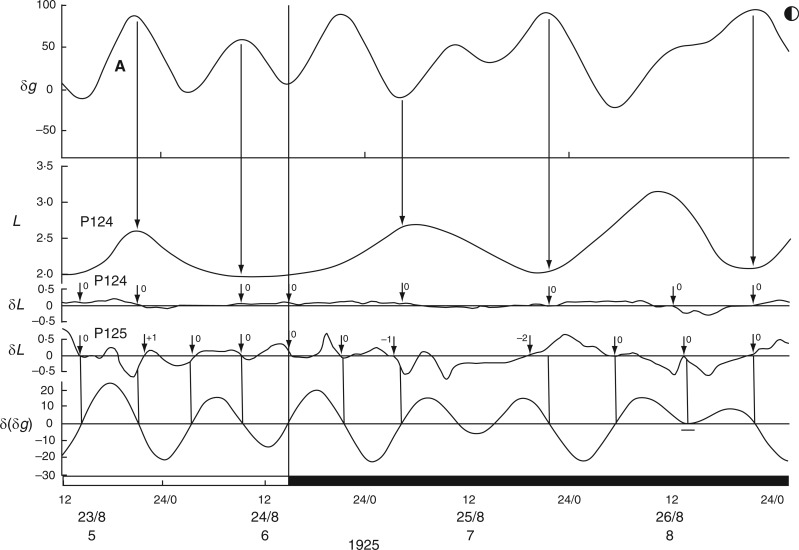
Relatively long (31 d), but discontinuous and partially complete time courses of leaf movements of Ph. coccineus were published by Bünning and Stern (1930, their fig. 5a,c,d). Unbroken recordings were made from (a) 23 Dec. 1929 up to 4 Jan. 1930 (K181 – fig. 5a), (b) 7–12 Jan. 1930 (K184 – fig. 5c) and (c) 19–24 Jan. 1930 (K191 and K193 – fig. 5d). The start dates of each of these three time courses were within 2 d of either LQ or FQ Moon. Switches in the leaftide/Etide relationship were evident. Between 20 and 22 Jan., in time course (c) for K193, the relationship changed from ‘in phase’ to ‘antiphase’, the last ‘in phase’ day on 20 Jan. coinciding with the singular Etide peak A (Fig. 5). Leaf K191 recorded at the same time (broken line in Fig. 5) shows movements in the opposite direction to those of leaf K193. Again, its phase relationship switches to the alternative mode on the day of the singular tide A.

A similar switch (‘in phase’ to ‘antiphase’) occurs in the time course K181, recorded one month earlier, between 23 and 28 Dec. 1929 (with LQ on 23 Dec.) (Fig. 6), and also at the start of the following month in time course K184, recorded on 7–9 Jan. 1930, when the last ‘in phase’ day coincides with FQ on 8 Jan., before switching to antiphase (data not shown).

Fig. 6.

Changing phase relationship between Etide (upper panel) and the leaftide K181 (Ph. coccineus). It is ‘in phase’ soon after LQ Moon together with the presence of the singular A Etide peak on 23/12/1929, but alters to ‘in antiphase’ on the last date shown (28/12/1929). Note the contrasting leaftide periods τ on the last two dates. Conventions are the same as for Figs 2 and 3. Leaf movements redrawn from fig. 5 in Bünning and Stern (1930).

Periodicity of articulated leaf movements

The time courses mentioned above were used by Bünning and Stern (1930) to examine day-to-day variation of the period of leaf movements (see their tables 12–14). Over a span of 4–5 d, the periods varied from τ = 22·0 to 27·7 h; on some days periods of τ ≥ 30 h were found. Estimates of the Etide for these days help to answer the question of whether these disparate estimates represent variations around a stable mean period – which Bünning and Stern favoured, the means being estimated from the three groups (a–c above) as 25·4 ± 0·7, 24·1 ± 0·9 and 25·6 ± 0·5 h, respectively – or whether there is another reason for this variability, which might have a basis in the Etide. The observations made by Bünning and Stern (1930) are important because they produced the first ideas for an ‘endogenous’ clock.

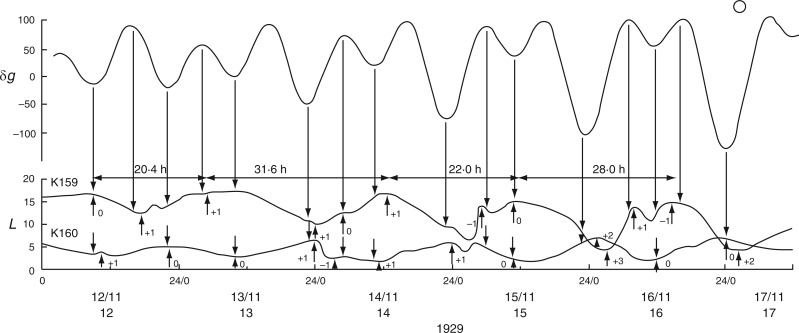
Bünning and Stern used the minimal leaf position as the indicator of the start and end of each oscillation cycle. Figure 5 shows data relevant to the oscillations of leaves K191 and K193, but data from leaves of another pair of plants (K159 and K160) can also be examined (Fig. 7) for variation of τ, as can the leaf trace K181 in Fig. 6.

Fig. 7.

Alternative relationships between the rhythms of the Etide (upper panel) and of the movements of two different leaves, K159 and K160 (Ph. coccineus), recorded simultaneously. The Etide structure is strongly bimodal on days immediately before FM, on 17/11/1929. K159 is mainly ‘in phase’ with the Etide, whereas K160 is mainly ‘in antiphase’ with the Etide. Leaftide periods τ vary according to the relationship between leaftide and Etide turning points (only the τ values for K159 are shown). Conventions are the same as for Figs 2 and 3. Leaf movements redrawn from fig. 6 in Bünning and Stern (1930).

Time course K193 (Fig. 5) reveals three leaftide periods, 1aa, 2aa and 3aa. Using the published material in Bünning and Stern (1930), these periods can be expressed in two ways: (1) according to my estimate (τ = x,…) read from the published leaf traces, also using the ‘down’ position as reference, and (2) according to Bünning and Stern’s estimate (τ = …, xB). Values of τ are in hours. The respective pairs of estimates τ = (x, xB) from K193 are: 1aa – (26, 26B), 2aa – (27·5, 26·3B), 3aa – (25, 27·7B) Then, using the times at which the closest Etide maximum occurs in relation to the leaftide minimum, Etide periods 1ab, 2ab and 3ab are obtained: 1ab – (31), 2ab – (24), 3ab – (24·5). The values of leaftide and Etide periods used for comparison (1aa vs. 1ab, and so on) are underlined. It is evident that the correspondence between the leaftide and Etide periods is not close (the mean difference is 3 h). However, the time of attainment of a leaftide maximum in K193 can be used as another referent for period determination. The three leaftide periods τ are now: 1ba – (25), 2ba – (27), 3ba – (26). There is only a single value, τ = x, in this 1–3ba series because Bünning and Stern did not estimate the periods using the leaf maxima. The Etide periods of the corresponding nearest Etide minima, in hours, are: 1bb – (25), 2bb – (25), 3bb (25). In these cases, and taking into account the inherent variation in the time of occurrence of leaf extrema, the underlined leaftide and Etide periods (1ba vs. 1bb etc.) are similar (mean difference of 1 h). Here, and in a further analysis (see below), the periods obtained from leaftide maxima are closer to the corresponding Etide periods than are the periods obtained from the leaftide minima used by Bünning and Stern (1930).

Similar conclusions can be drawn from leaftide time course K191 (Fig. 5), which is here ‘in phase’ with the Etide. The graphical representations of the data show close coincidence between turning points in all three time course, the two leaftides (K191 and K193) and the contemporaneous Etide. Figure 5 also shows the way in which the leaftide periods may vary from one cycle of movement to the next (e.g. τ = 30·4 h and then τ = 26·0 h in trace K191); and in trace K193 there are successive leaftide periods of τ = 19·0 h and τ = 26·6 h. The variation of τ is evidently due to the Etide: the leaf is responding to the Etide peaks and troughs (Fig. 5). The same is true for time course K181 where there are two successive leaf cycles of τ = 24·0 h and τ = 32·8 h (Fig. 6). The lengthening of the cycle is due to the interaction of the leaf with Etide. In one cycle, the leaf interacts with the [B] peaks of the [A,B] pair to give the τ = 24·0 h period, and with a [B] peak and the trough of the next Etide cycle, thus extending the leaftide period to τ = 32·8 h (Fig. 6).

Data from pair K159 and K160 can be analysed in the same way as for K191 and K193 (see Fig. 7). As before, using the leaftide maxima yields periods that conform with those of the Etide turning points. The periods of K160 for leaftide minima and maxima also correspond with the periods of the ‘antiphase’ Etide.

Time courses K159 and K160 (Fig. 7) reveal various irregularities in these leaftide traces. They can be accounted for as temporary responses to a close succession of Etide turning points. They also illustrate how easy it might be for leaftide periods to become altered according to which Etide turning points affect the leaf movement pattern.

In summary, the results in Figs 5–7 show that the periods of successive leaftides and of the contemporaneous Etide periods can vary to the same extent, and that various possible relationships between the two time courses might account for the variation in leaftide periods. This conclusion was already arrived at in another way, by examining the coincidences between δL and δ(δg) (Figs 2–4). In many cases, displacement between the respective zero points is 0 h, indicating synchrony of turning points, or amounts to only +1 h (i.e. the leaf changes direction 1 h after a turn of the Etide). Sometimes displacement is negative (e.g. −1 h), the leaf turning apparently in anticipation of a turn of the Etide. These small displacement times are also within the ranges of error introduced (a) when digitizing the original graphical data, (b) by a certain range of thresholds of δ(δg) at which a leaf turning event is initiated and (c) by variability inherent to the mechanics of the leaf system that affect synchrony of leaf movements between paired plants.

Light and temperature effects upon periodicity

The period of leaf movements can be modified by light intensity. The articulated leaves of Glycine max, for example, showed lengthened periods in constant light (LL) as compared with those found in constant dark (DD) conditions (Ninomiya, 1984). Mean cycle time varied by about 4 h, depending on the light environment. However, in LL the periods of successive cycles were also rather variable: when one cycle lengthened, the next was shortened. Moreover, when placed in LL of 11 klx, leaf movement was arrested in the ‘up’ position (Ninomiya, 1984).

Bünning (1931) encountered what is perhaps an analogous situation regarding period prolongation when he investigated the effect of temperature on leaf movement. Different temperatures caused longer or shorter temporal displacements of the first cycle of movements, but not of later cycles. This had the effect of increasing or decreasing the mean period of all movement cycles measured, depending on whether the temperature was decreased or increased. Later, Bünning (1973) accepted the conclusion of Leinweber (1956) that the duration of the leaf movement cycle was unaffected by temperature, a situation that would be expected if the period was regulated by an external regulator, such as the lunar tidal force. The conventional ‘explanation’ for temperature invariance, however, is one of temperature compensation (Bünning, 1973, 1974), whereby the period of leaf movement is regulated by a series of temperature-sensitive metabolic processes which, in some extraordinary way, are able to adapt to temperature changes at the same time as maintaining a constant periodic output.

Interestingly, insensitivity to varied light intensity was noted in relation to the oscillations of floral stem elongation of A. thaliana (Jouve et al., 1998). Although absolute rates of extension (the amplitude of the elongation rate cycle) could be varied by a factor of 50 % according to the LD regime, the period of the growth rhythm was unaffected. Again, an external zeitgeber, such as the lunisolar tidal force, could be responsible for the invariant rhythm.

Asynchrony of leaf movements between plants

Simultaneous time courses (Bünning and Stern, 1930) for pairs of leaves, (K159, K160) and (K191, K193), have shown that their vertical movements can be out of phase with respect to each member of the pair (Figs 5 and 7). Phase differences between the movements of leaves are not often mentioned in the early literature. Klein (2007), however, referred to this phenomenon as ‘partial group behaviour’. He believed that each leaftide turning point coincided with an Etide turning point, but if a leaf ‘missed’ an Etide turning point it had to wait for the next one. Leaves could therefore be 6·2, 12·4 or 18·6 h out of phase with each other, these times being the harmonics of the 24·8-h Etide period.

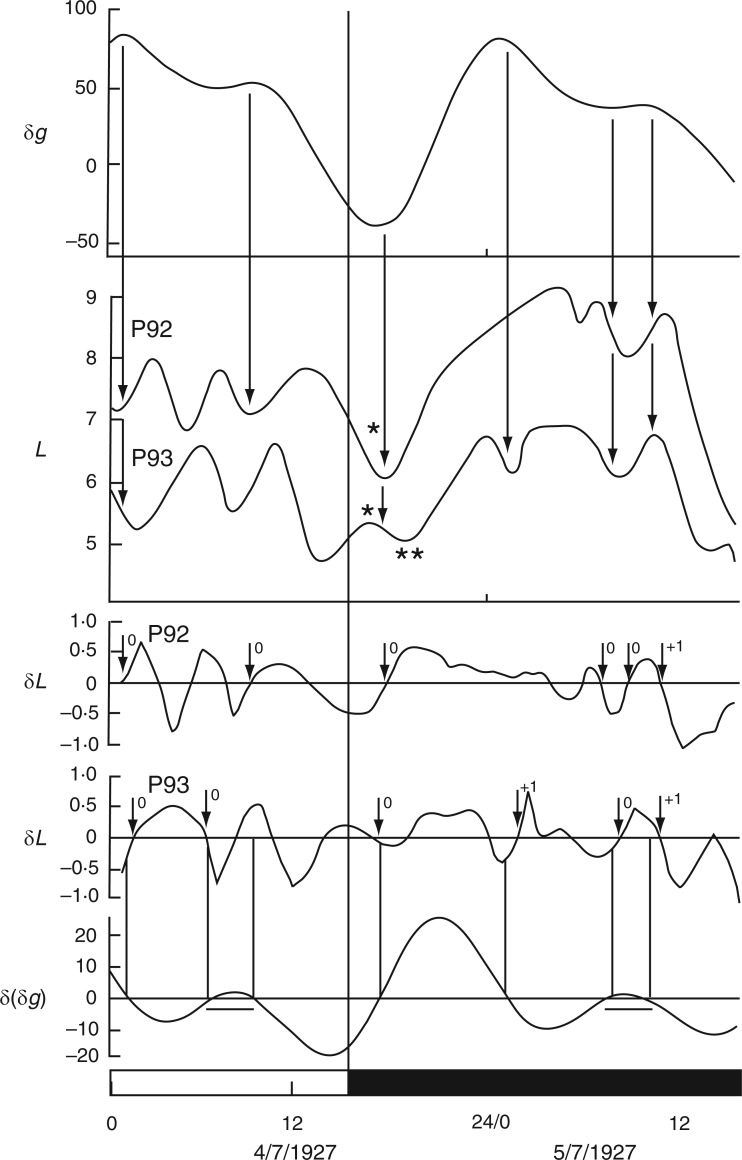
In the aforementioned cases, the plants were part of an investigation into the effect of light on leaf movement (Bünning and Stern, 1930). The results obtained may have been influenced by the leaftide/Etide phase relationships. After a preparatory period, the two plants whose leaves were recorded (K191 and K193) were exposed to red light at 2230 h on the evening of 18 Jan. 1930; leaf movements occurred soon afterwards (Fig. 8), leaf K193 reaching a minimum position after 7·5 h, at 0400 h on 19 Jan. 1930, and leaf K191 reaching a minimum at 1300 h, 9 h after its companion. The different times at which these positions were attained probably explains the subsequent out-of-phase relationship of the same two leaves illustrated in Fig. 5. The 9-h difference in the time between the changes of direction of the two leaves (marked by * in Fig. 8) is close to the 8-h difference between the Etide minimum and the next maximum.

Fig. 8.

Movements of two leaves, K191 and K193 (Ph. coccineus), in relation to the Etide following exposure to red light at the time indicated by the arrow. The leaves respond differently. The respective turning movements at the ‘down’ positions (*) occur 9 h apart. Leaf movements redrawn from fig. 4 in Bünning and Stern (1930).

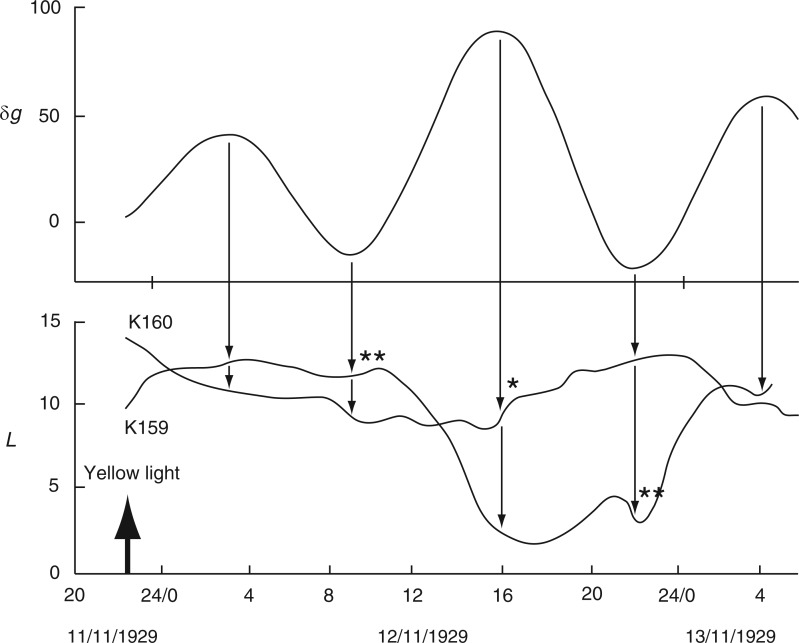
Leaf traces K159 and K160 in Fig. 9 are from two plants exposed to yellow light, at 2230 h on 11 Nov. 1929. On the following day, K159 shows a downward movement at 1000 h, and then an upward movement commencing at 1800 h, whereas K160 was identified by Bünning and Stern (1930) to commence an upward movement 5 h earlier, at 1300 h. The redrawn trace (Fig. 9) shows, however, that both of the upward movements commenced at approximately the same time (single * in Fig. 9). In view of the contemporaneous Etide time course, the two patterns of leaf movements can be interpreted differently: the upward movement of K160 at 1600 h on 12 Nov. 1929 coincides with an Etide maximum (marked by * in Fig. 9). The initial downward movement of K159 at 1000 h and the subsequent upward movement at 2200 h both coincide with Etide turning points (marked by ** in Fig. 9).

Fig. 9.

Movements of two leaves, K159 and K160 (Ph. coccineus), in relation to the Etide following exposure to yellow light at the time indicated by the arrow. The leaves respond differently. K159 initiates a descent (**) at about mid-day and then ascends (**) 12 h later, whereas K160 descends slowly at first, but then ascends (*) at approx. 1600 h. Leaf movements redrawn from Fig. 2 in Bünning and Stern (1930).

Bünning and Stern (1930) suggested that red light advanced the commencement of the leaf movement cycle. The present interpretation would be that the red-light stimulus sensitized leaves K191 and K193 to the subsequent Etide turning point (Fig. 8). In the case of leaves K159 and K160 in yellow light, there was no advancement of leaf turning and one Etide turning point passed before either leaf responded (Fig. 9).

Alford and Tibbitts (1970) found that leaf movements of neighbouring plants of Ph. angularis placed in constant light were not necessarily synchronized, their cycles having different ‘start’ times owing to unsynchronized leaf development following germination. Moreover, the periods of successive cycles of any given plant were found to differ by as much as 4·5 h, even though the mean period estimated from all plants was τ = 27·3 ± 0·7 h. The proximate regulator of leaf movement could, as argued above, be associated with Etide turning points.

Asynchrony of leaf movements within plants

Hoshizaki and Hamner (1964) examined pairs of sister primary leaves of young Ph. vulgaris plantlets growing in constant light and found cases where sister leaves changed their direction of movement at different times. When one leaf reached the minimal ‘down’ position at midnight, say, the other, sister leaf reached its ‘down’ position on average 8·8 h later (see fig. 1 of Hoshizaki and Hamner, 1964). The authors do not state the frequency of plants showing asynchrony of paired leaf movement, but they do indicate that this was a typical finding. It may be significant that the time difference between the asynchronous movements of the leaf pairs was of the order of 8–9 h, one of the harmonic periods of Etide. Unfortunately, no dates are attached to their published record of leaf movements, but if the experiments took place at either FM or NM, with two equally expressed tides, [A,B], then, in the asynchronous case, it could be that one leaf was responding to Etide peak A, whereas the sister leaf was responding to peak B. In the synchronous case, both leaves could be responding to the same A or B peak.

In an intriguing experiment, Kübler (1969) entrained movements of a single leaf on a stem of Glycine max to conform with an LD period of 12 : 12 h. He found that information of this rhythm was passed to the leaf positioned above the entrained leaf but was passed less efficiently to the leaf below. Given that leaf movements evoke electrical impulses (Freudling et al., 1980), it may be that information moving between leaves was of this form.

Movements of excised articulated leaves of greenhouse-grown plants

Both Brouwer and Kleinhoonte recorded the movements of leaves cut from the stem of Canavalia bean seedlings. The node at the base of the petiole was first removed because its retention impaired movements, probably because it formed a suberized abscission layer. As Brouwer remarked, it was practically impossible to distinguish movements of an excised leaf from those of an intact leaf upon the whole plant.

Rhythms of excised-leaf movements have been compared with the contemporaneous Etide using superimposed plots of δL and δ(δg) as a guide to leaftide/Etide synchrony. Taking two time courses each, from Brouwer (1926, his figs 10 and 12) and from Kleinhoonte (1929, her figs 3 and 4), it was found that, of a total of 24 pairs of major turning points, 15 were synchronous with an Etide turning point, seven were displaced by +1 h, one was displaced by + 2 h and one was displaced by −1 h. [Some of the early work using excised leaves for experimental purposes is mentioned in the online Supplementary Data S7.]

Fig. 10.

Leaf movements after surgical intervention at the pulvinus of a leaf of C. ensiformis. The leaf trace P51 is from an intact plant grown in a greenhouse. P50 is from a leaf where the extensor has been removed: the leaf lamina remains motionless in the ‘up’ position (broken line). P50′ is the trace from the opposite sibling leaf of P50, but here the flexor has been cut away: the lamina is mainly in the ‘up’ position but is still capable of movement. Correspondences between rates of leaf movement δL and rates of change of the Etide time course δ(δg) are shown in the lower panels. Other conventions are as for Figs 1 and 2. Leaf movements redrawn from figs 17 and 18 in Brouwer (1926).

Fig. 12.

Leaf movements of C. Penzigii and their relationship with the Etide variations. The derivatives of these variables and the degree of synchrony of their respective turning points are shown in the panels δL and δ(δg). Some maxima of δL appear to coincide with maxima of δ(δg), marked by a filled circle (•). The rise in height of the leaf over the 3-d period recorded in panel L is due to the growth of the main stem. Other conventions are as for Figs 2 and 3. Leaf movements redrawn from fig. 2 in Schmitz (1934).

Sites responsible for leaf movement

Diurnal movements of intact bean leaves are expressions of growth events at the upper and lower sites of two nodes, the petiolar node, at the junction with the stem, and the leaf node, or pulvinus, at the junction of petiole and leaf lamina. The pulvinus consists of cells which undergo both expansion and contraction (Mayer et al., 1985). The differential growth at the upper and lower sides causes the pulvinus to act as a hinge for the vertical movements of the leaf blade. The pulvinar node drives the greater part of the movements shown by the leaf as a whole, although the petiolar node is responsible for movements of the petiole. Movements associated with each of these two nodes could be recorded simultaneously using the kymograph (Brouwer, 1926).

Petiolar and pulvinar nodal movements

Records from a petiolar node (Brouwer, 1926, his fig. 20, petiole P29′) placed in a greenhouse during January 1925 revealed that, each day, this structure made a sequence of four types of movements in the vertical plane: a descent at 0400 h, a small upward movement at 0800–1000 h, a rapid descent between 1000 and 1400 h, and a prolonged upward movement commencing at 1400 h and continuing into the following morning. The turning points initiating the three last-mentioned movements coincided with Etide turning points (data not shown). The second descent phase coincided with the hours of daylight and may also have been associated with leaf transpiration.

Fig. 20.

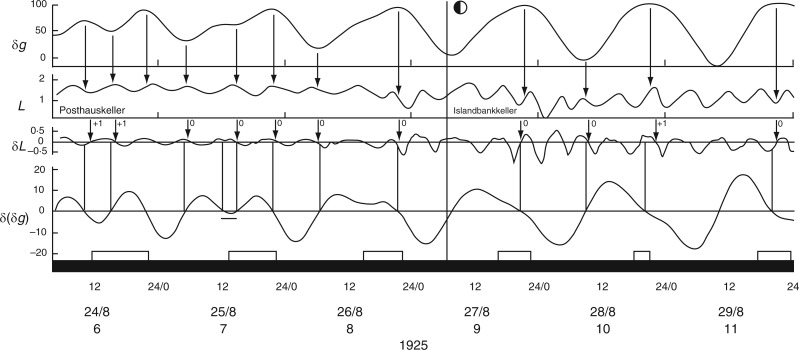
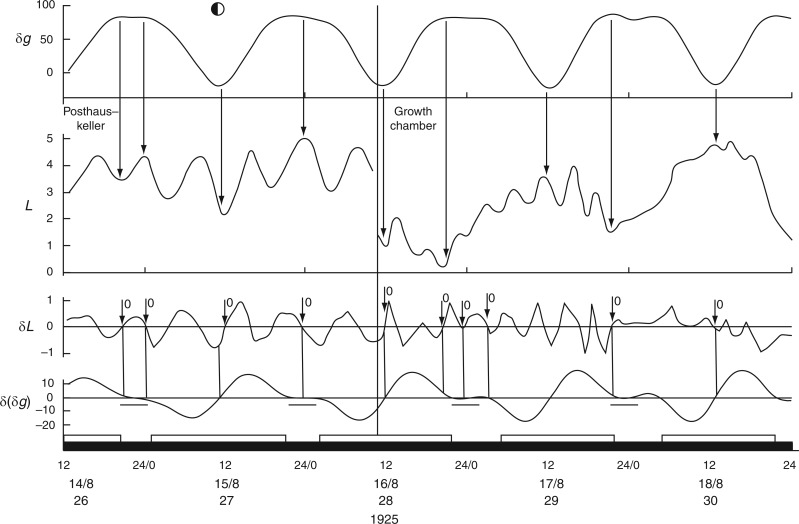
Short-period leaf movements (τ approx. 6–8 h) of Ph. coccineus in continual darkness, first in the Posthauskeller, Akureyri, Iceland, and then after transfer to the Islandbankkeller at the time and date indicated by the vertical line. Conventions which apply to the panels of this figure are as for Figs 2 and 3. Leaf trace redrawn from fig. 3 in Stoppel (1926).

These movements at the petiolar node contributed about 6–8 % of the total movement displayed by the leaf itself. It may be significant that the timing and directions of petiolar movement, which are out-of-phase with respect to those of the pulvinar node, are in accord with movements of non-articulated leaves, discussed in the next section.

To clarify the contribution of each node to the leaf movement as a whole, Brouwer (1926) immobilized the petiole of leaf P29, the sibling of P29′, mentioned above. Movements recorded from P29 could be due to the pulvinar node only. In this case, turning points of leaf movement due solely to the pulvinar node coincided with Etide turning points. A small descending movement, shown by both P29 and P29′, at about 1400 h on each of the three days of observation, coincided with an Etide turning point on each day. This suggests that both nodes are sensitive to the Etide, even though the two nodes move in opposite directions.

Observations by Mayer and Sadleder (1972) using Ph. coccineus showed that the two nodes have different responses to light. In darkness, both structures produced movements which were in phase and had similar mean periods of approx. τ = 26·8 h (s.d. ± 1·0–1·3 h). At high light intensity (30 000 lx) the mean period of each increased to approx. τ = 29·8 h (s.d. ±1·0 – 1·2 h), but now the movements were 180° out of phase. As already indicated, experiments with high-intensity or continuous light seem generally to provoke anomalous movements, as though the physiology of movements is disturbed.

Dissecting pulvinar movements

The anatomical structures, and physiological and electrochemical characteristics that regulate rhythmic leaf movements are quite well known, in particular those of Phaseolus and Samanea (Moran, 2007a, b). The pulvinus of Canavalia leaves is almost certainly similar. Nevertheless, in view of what has been said above about the relationship of pulvinar movements to the progression of the Etide, it is worth recalling the pioneering experiments of Brouwer (1926) which characterized the movement properties of the pulvinus to the ultimate point possible in his day.

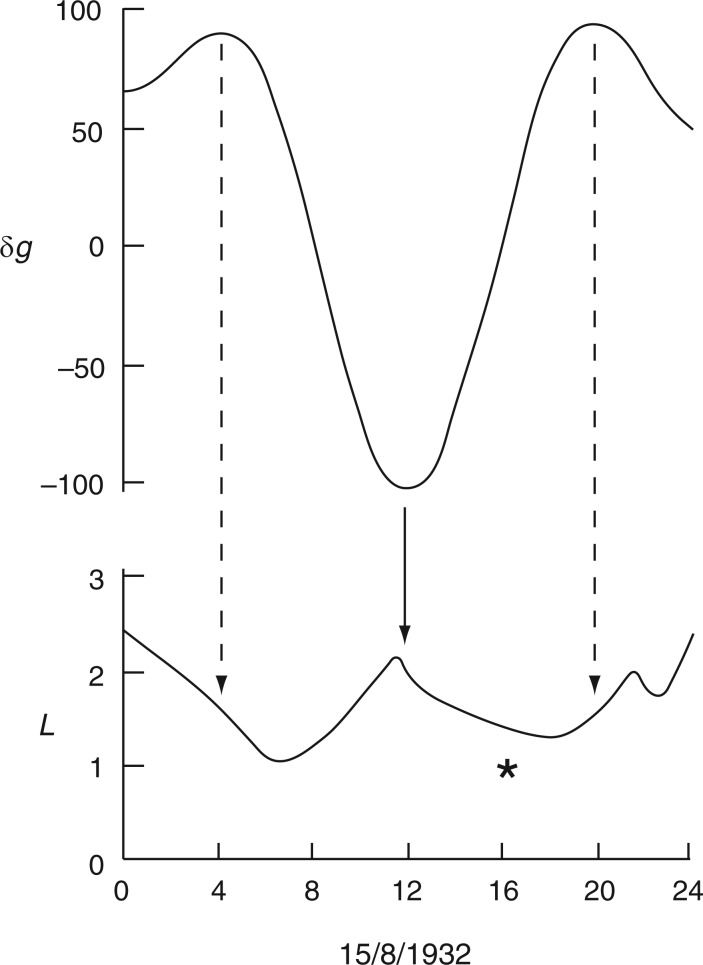
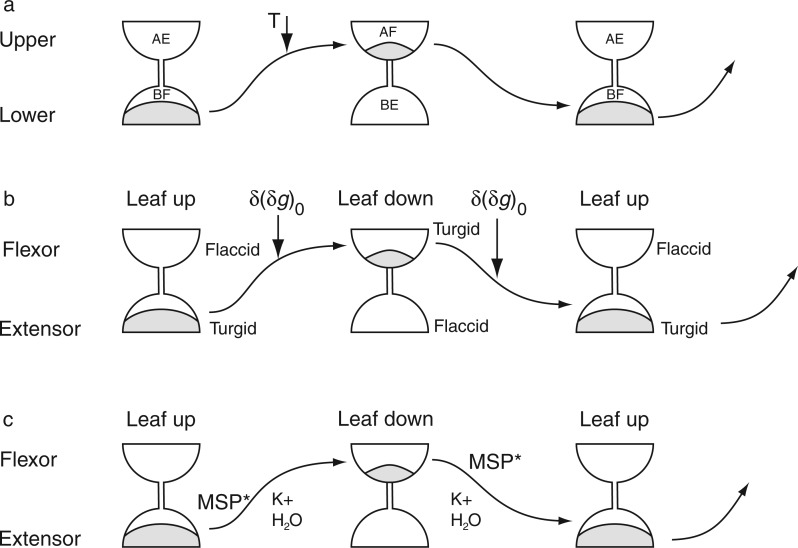
Brouwer (1926) performed microsurgery at the pulvinus of Canavalia leaves and found that when the abaxial (underside) portion of this node (the extensor) (Brouwer, 1926, his figs 17 and 18) was cut away, the reference leaf (P50) remained motionless in the ‘up’ position (Fig. 10). However, when the adaxial side of the pulvinus (the flexor) was removed, leaf movements continued, but in a disturbed manner (record P50′ in Fig. 10): the leaf mainly remained ‘up’, but shallow descents commenced at noon each day. Large movements were shown by the intact leaf (P51) of the control plant (Fig. 10). The ‘down’ position of leaf P50′, lacking its flexor, could not be maintained and, after a minimal position had been reached at about 1800 h, the leaf began to ascend. On the dates of recording, leaf descents, of both the operated P50′ and the intact P51, commenced exactly when the Etide on each day reached a minimum between two [A,B] peaks, at 1200 h (Fig. 10). This result suggests that the flexor exerts a biomechanical force which maintains the ‘down’ position of the leaf until such times as the extensor develops a counteractive force and, hence, permits the ascent of the leaf. It seems that the ‘up’ position is the default position of the leaf.

Fig. 17.

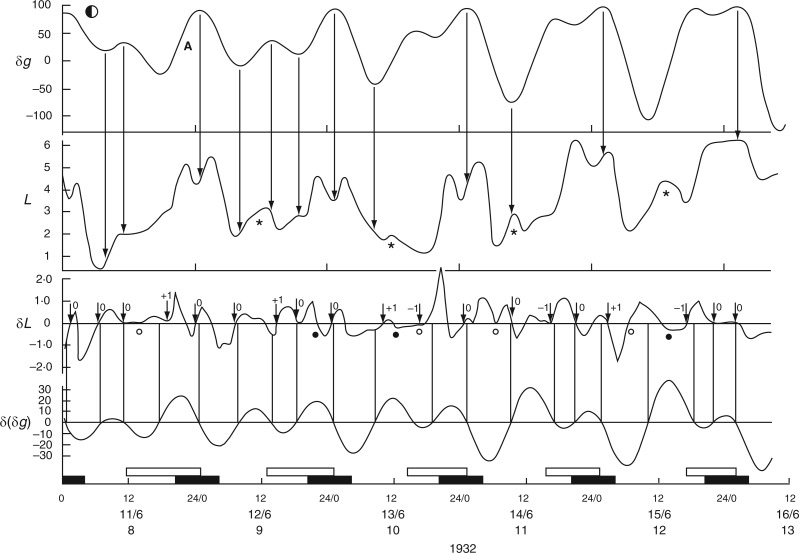
More complex leaf movement oscillations in Coleus Penzigii. ‘Relaxation’, night-time-like ascents occur during the day; they are marked with asterisks (*). At this stage of the lunar month, just after FQ Moon, there are many Etide turning points which appear to evoke leaftide responses, but there are also times at which leaftide turning points coincide with maximal rates of change of the Etide (○, •). Other conventions are the same as those for Figs 2, 3 and 12. Leaf movements redrawn from fig. 11 in Schmitz (1934).

Fig. 18.

Pendulum oscillations of a leaf of Ph. coccineus. Each leaftide turning point coincides with an Etide turning point. Conventions which apply to this figure are the same as those for Figs 2 and 3. Leaf movements redrawn from fig. 17 in Bünning (1931).

As mentioned, diurnal movements of the articulated type of leaf depend upon alternating expansion and contraction of the cells constituting the flexor and extensor portions of the pulvinus. An approach to the cellular aspect of the organ movement is through observations on protoplasts obtained from cells of the two pulvinar zones. In one set of observations (Mayer and Fischer, 1994), protoplasts were prepared from the flexor, extensor and flank regions of pulvini from 3- to 4-week-old plants of Ph. coccineus and then kept in continuous light. Measurements of protoplast diameter, using samples from the three sites, commenced at 2000 h on an unspecified date. The oscillations of diameter within both the flexor and the extensor samples were found to be ‘in phase’ with respect to each other, but the flank samples were out of phase by about 145° (40 % or 11 h behind the cycle of the other two zones).

The average period of the first expansion/contraction cycle for all three zones (Mayer and Fischer, 1994) was approx. τ = 26–28 h. In a long time course (216 h) from another experiment using flexor protoplasts, Mayer and Fischer (1994) found notable variation of periods. Four near-successive periods, which can be determined from their fig. 3, are: τ = 29, 32, 29 and 23 h. Even if the ‘clock’ that determines the period is endogenous, it does not run smoothly. Disturbance of cell physiology due to the continuous light conditions is one possibility, though responsiveness to the harmonics of the Etide rhythm could bring about such variation of periodicity, as mentioned earlier. Clearly, the diameter variations of flexor and extensor protoplasts were ‘in phase’ with each other, whereas in planta they would have been ‘in antiphase’. Even so, the ‘in phase’ rise and fall of diameter in both extensor and flexor protoplasts may be a direct response to the prevailing Etide.

In a study in which the importing activity of K⁺ channels in the plasma membrane was the marker of activity and, indirectly, of protoplast swelling and shrinkage (but with only a limited time course of approx. 21 h), a 180° phase shift was found by Kim et al. (1993) with respect to the flexor and extensor protoplasts obtained from pulvini of the tropical tree Samanea saman (Fabaceae). It seems that the authors’ technique of protoplast preparation retained intact the K⁺ import/export relationship between extensor and flexor zones that existed at the time of pulvinus selection.

Movements of non-articulated leaves

The two pulvinate nodes of bean leaves – those attached to the stem axis and to the leaf lamina – are organelles into which is concentrated the differential and reversible growth which gives expression to the leaftide. The non-articulated leaf of Coleus Penzigii (= Plectranthus barbatus) represents a contrasting system (Schmitz, 1934) for the study of diurnal leaf movements. Leaves of another species of Coleus, a hybrid of C. blumei, have been used to study circadian rhythm (Halaban, 1968); and leaves of Arabidopsis thaliana (Engelmann et al., 1992) and certain weed species (Andersen and Koukkari, 1979) have provided additional examples of non-articulated diurnal movements. Furthermore, arabidopsis leaf movements are of interest in the context of waterlogging stress, a condition to which the plant responds by raising its leaves (Polko et al., 2013; Rauf et al., 2013). In both cases – articulate and non-articulate – the leaf movements have been postulated to confer advantage to those plants and species which possess them (Enright, 1982).

The differential growth which raises and lowers the non-articulated leaf of Arabidopsis is located in the proximal portion of the petiole. Data from ascended leaves show an approx. 80 % increase in cell elongation in the first millimetre of the abaxial petiole (Rauf et al., 2013). In some types of non-articulated leaves, although there may be no external indication of a distinct articulation at the proximal zone of the petiole, nevertheless they may have a zone with a particular vascular anatomy which facilitates movement of the lamina, such as was described for the photonastic leaves of Malva neglecta (Yin, 1938) and of Abutilon theophrasti (Fuhrman and Koukkari, 1981).

An additional possibility (which may apply also to A. thaliana) is that this complex type of leaf movement is part of the general rhythm of shoot growth, as suggested for the movements of tobacco (Nicotiana tabacum) leaves by both Schirmacher (1935) and Spurný (1972). Leaf movements may therefore be regulated by differential auxin contents between upper and lower sides of the lamina, as proposed by Yin (1941) to explain the diurnal leaf movements of Carica papaya. In addition, the movements of non-articulated leaves (e.g. Nicotiana sp., Linum usitatissimum) are sensitive to meteorological conditions, especially humidity (Schirmacher, 1935). Nevertheless, when care was taken to avoid external variations of light intensity, humidity and temperature, which might have disturbed leaf-movement rhythms, it was concluded that some as yet undiscovered factor (electrical or magnetic influences were proposed) affected these rhythms (Schirmacher, 1935). As will be described, many of these non-articulated leaf movements appear to coincide with turning points in the lunisolar tide.

Schmitz (1934), using a kymograph, prepared leaf-movement traces from C. Penzigii grown in a greenhouse during a 250-week period. The centre of the lamina and the distal end of the petiole were the two recording locations. The lamina tended to move upwards at night and downwards during the day – the reverse pattern of the movements of articulated leaves. But, as noted, this pattern is a feature of the petiolar node of beans.

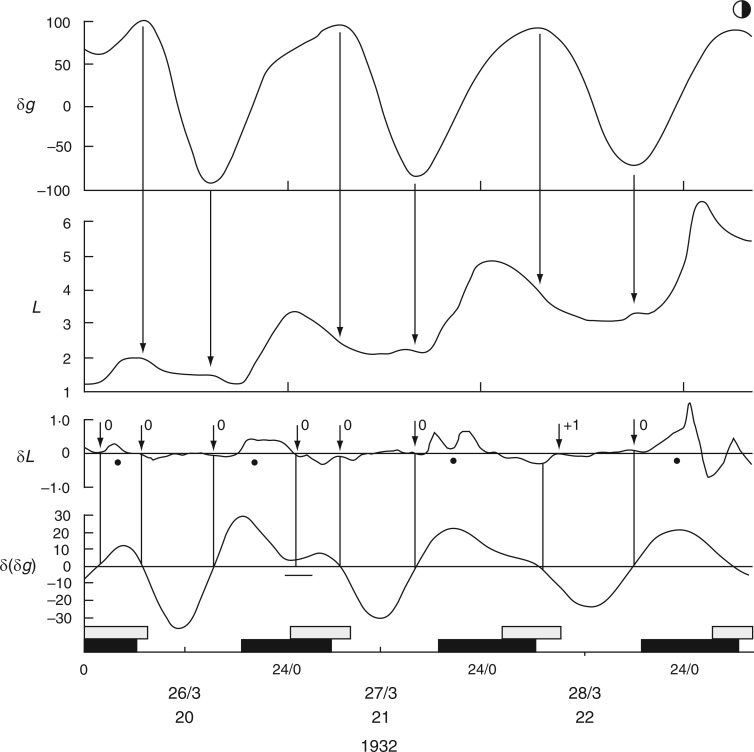
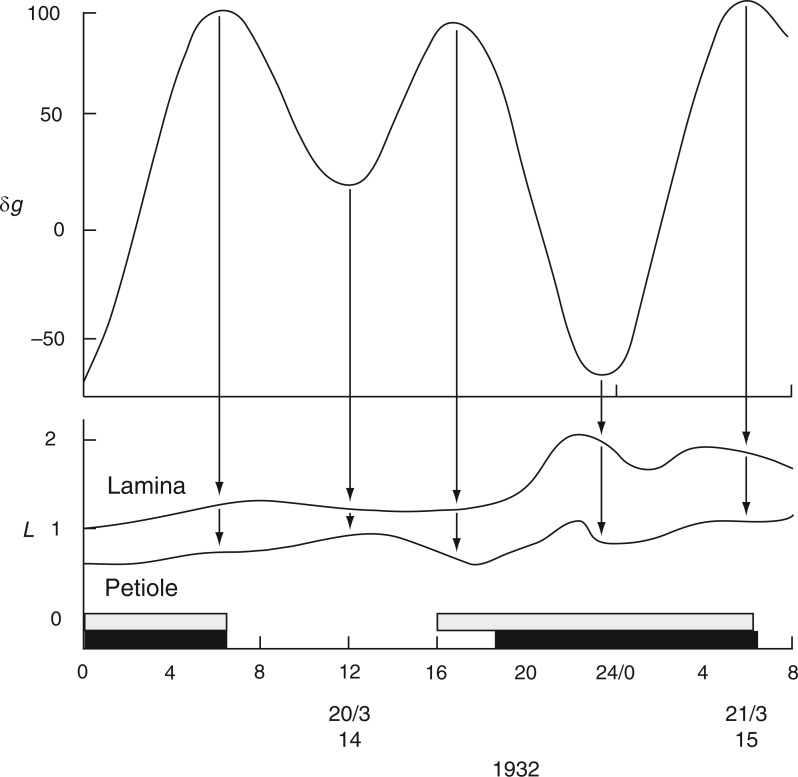
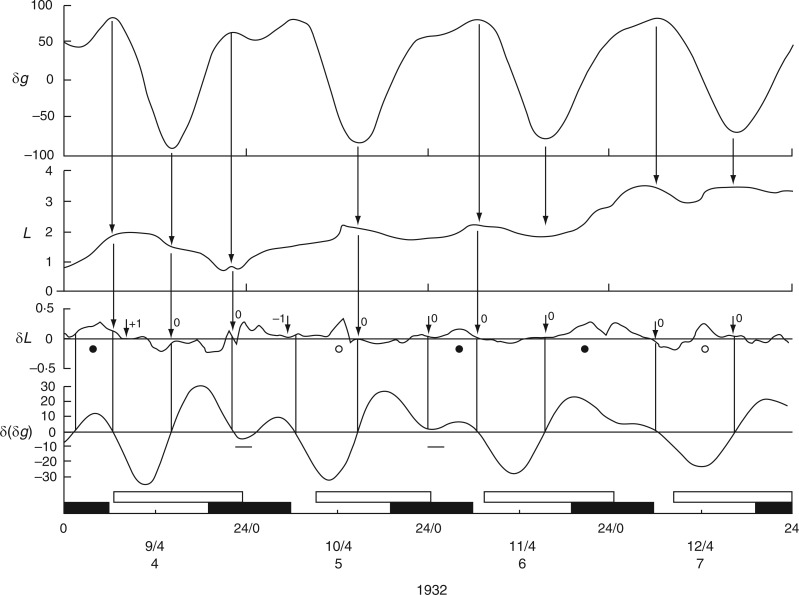
The first time course from C. Penzigii commenced with an upward movement of the petiole at 1700 h on 20 Mar. 1932 (Schmitz, 1934, his fig. 1), and was followed 1–2 h later by an upward movement of the leaf (Fig. 11). Then, at 2300 h on this day, both petiole and leaf made a descent. Each of these movements commenced at the estimated time of an Etide turning point and the leaftide–Etide relationship was in ‘antiphase’ on these days. Six days later, on 26 Mar. 1932, the relationship changed to ‘in phase’ (Fig. 11). This relationship persisted until early in the next lunar month, when the relationship switched to ‘in antiphase’ at the time of the singular Etide A peak. During this recording period (Fig. 12) there is always synchronization of turning points of Etide and leaftide, irrespective of whether their interrelationship is ‘in phase’ or ‘in antiphase’; the synchrony of the two turning points even applies to small elevations of the leaf just prior to the major night-time ascent (Fig. 12).

Fig. 11.

Commencement of movements of the non-articulated leaf of a greenhouse-grown plant of Coleus Penzigii in relation to the Etide. Recordings were made simultaneously from the mid-lamina and the petiole. Other conventions are as for Figs 2 and 3. Leaf movements redrawn from fig. 1 in Schmitz (1934).

The question of the δ(δg) threshold arises in connection with the night-time leaf-turning on 26–27 March. Times when δ(δg) are close to zero are marked in Fig. 12, and similarly in Fig. 13, which shows the exactness of these leaftide/Etide turning-point relationships. On lunar days 4–7 there were seven leaftide turning points, all of them coinciding with turning points of the Etide.

Fig. 13.

Coincidences between turning points exhibited by the leaftide of C. Penzigii and the Etide at a different portion of the lunar month from that shown in Fig 12. Some maxima of δL appear to coincide with maxima of δ(δg) (•), whereas other maxima of δL appear to coincide with minima of δ(δg) (○). Other conventions are as for Figs 2 and 3. Leaf movements redrawn from fig. 4 in Schmitz (1934).

Another noticeable feature is that the rates of Coleus leaf movement appear to be adjusted to the rates of change of the Etide. In the time courses shown in Figs 12 and 13, where the leaftide/Etide relationship is ‘in phase’, on some occasions maximal rates of δL coincide with maximal rates of δ(δg), as indicated by filled circles (•). However, there are other occasions, indicated by open circles (○), when this does not hold. It is possible that the daytime ascents (with positive rates δL) were either anomalous movements in response to unexpected circumstances in the growth environment, or were a type of ‘relaxation’ movement, as described later.

The oscillations of non-articulated leaf movements of the weed species studied by Andersen and Koukkari (1979) were recorded in two types of experiments. However, the findings cannot be directly related to variations of the Etide because the leaf movement recordings are not dated. In the first experiment, plants were maintained under a 15 : 9-h LD period, where the leaf movements were entrained to a period of τ = 24·0 h. Plants were then transferred to free-running conditions of continuous light, LL. In the second experiment plants were grown continuously in LL. In the two experiments, LD→LL and LL→LL, the leaf periods τ in the respective free-running LL period departed from the entrained 24·0-h periodicity. In the free-running period of the first and second experiment, periods were, respectively: τ = 23·5 and <22·0 h for Sinapis arvensis (wild mustard); τ = 27·0 and 25·5 h for Amaranthus retroflexus (redroot pigweed); τ = 18·0 and approx. 22·0 h for Datura stramonium (jimsonweed); and τ = 23·0–25·0 and 23·0–25·3 h for Xanthium strumarium (common cocklebur). In most cases, the times at which leaftide turning points occurred did not coincide with the times anticipated from the entrained τ = 24·0-h rhythm of the control plants maintained in LD 15 : 9 h and grown alongside the free-running plants. Thus, the periods of the free-running leaf movements were no longer constrained by the entraining LD conditions but were now regulated in some other manner, perhaps by some factor exogenous to the plant, such as the lunisolar rhythm.

Other weed species examined by Andersen and Koukkari (1979) possessed articulated leaves with a pulvinus: e.g. Senna obtusifolia (sicklepod) and Senna occidentalis (coffee senna). When these plants were handled in the same way as mentioned above, their leaf movement rhythms under free-running LL conditions no longer adhered to the entrained period of τ = 24·0 h. In these cases, the statistical estimates of their periods were more reliable. In the two mentioned species, leaf-movement periods during the free-running state were τ = 25·8–27·8 and τ = 24·8–26·0 h, respectively, while those of a third species, Chenopodium album (common lambsquarters), were τ = 24·8–26·0 h. These were clear departures from the τ = 24·0-h rhythm found during the preceding LD regime. Adoption of an Etide rhythm by these free-running leaves is a possibility, although a disturbed physiology due to the LL condition cannot be ruled out.

Other types of rhythmic leaf movement

Leaf movements of bean (especially Phaseolus spp.) and Coleus plants do not always display typical rhythms of one major ascent and one major descent per day. Five other types of rhythm can occasionally be discerned; they, too, can be considered in relation to the lunar day and its estimated Etide values, keeping in mind that atypical rhythms, which presumably have physiological bases, may also be moulded by the Etide rhythm.

Supernumerary, or ‘relaxation’, oscillations: articulated leaves

The first type of atypical rhythm includes diurnal, double leaf movements: the ‘Nebenschwingen’ described by Bünning (1931, 1932) for leaves of Ph. coccineus. Bünning (1973) proposed them to be ‘relaxation’ movements inserted into the primary oscillatory cycles of the leaf (see also Bünning, 1960; Klotter, 1960). They seem to be of occasional occurrence, although moderate temperatures (15 °C) were experienced by the plants from which these movements were first recorded. Bünning (1931, his fig. 18) found that these ‘relaxation’ movements were preceded by unscheduled ascents of the leaf during the night. These were in addition to the usual single, major ascents, which raised the leaf during the day. The two successive ‘up’ positions were separated by approx. 8 h.

Secondary leaf movements were also found when metabolic inhibitors, such as dinitrophenol or KCN, were supplied to excised leaves via the transpiration stream (Bünning, 1956; Keller, 1960; Mayer, 1981). Small upward leaf movements developed immediately after the treatment had been administered, at the time of leaf descent. However, after some hours the treated leaves continued to descend from their interpolated supernumerary ‘up’ positions (Keller, 1960, her figs 9–11).

If, as mentioned earlier, the ‘up’ position of the leaf is considered as a ‘default’ position, then a secondary upward movement induced by an inhibitory treatment does appear to be a ‘relaxation’ movement. It follows that a descending leaf movement requires some active input (energy), as Mayer (1981) concluded, to move the leaf downwards, away from its default position. The treatment may interrupt this energy input and, hence, the leaf ‘relaxes’ and moves to its default position. It is suggested that the lunisolar (Etide) turning point supplies at least part of this active input, to bring about leaf descent. Unfortunately, neither Keller (1960) nor Mayer (1981) place dates on the time axes in their figures, so possible relationships between leaf movement and Etide cannot be explored. However, the earlier examples of these movements due to Bünning (1931, 1932) and Kleinhoonte (1929), using Ph. coccineus and C. ensiformis, respectively, can be revisited from this point of view.

In the first example (Bünning, 1931), leaf ascents were found to occur every 12 h (Fig. 14). The first ascent of the double cycle, which occurred during daytime, is typical of the usual diurnal leaf-movement cycle. However, the ‘up’ position was not maintained and a brief ‘relaxation’ descent followed; then, a new, second ascent occurred during the night-time (marked by * in Fig. 14). This sequence was repeated during four successive days. Although the secondary ascents do not coincide with Etide turning points, they do, perhaps fortuitously, coincide with maximum rates [δ(δg)] of descent from an Etide maximum (marked by ○ in panel δL in Fig. 14).

Fig. 14.

Leaf ‘relaxation’ movements in Ph. coccineus. Apparently normal ascents were initiated at the start of the daytime period but could not be maintained, and the leaf descended. The descent was temporary and was reversed by a ‘relaxation’ ascent (*). Timings of secondary ascents were close to maximum rates of descent of the Etide values δ(δg) (○). Other conventions are as for Figs 2 and 3. Leaf movements redrawn from fig. 18 in Bünning (1931).

Analogous results were obtained by Cremer (1923; see his Kurve 9) from Phaseolus plants placed in continuous darkness. During a 5-d period, two or three relaxation events occurred each day. The major ascents of the leaf commenced at 2400–0400 h, coinciding with an Etide turning point. The unscheduled descents and subsequent ‘relaxation’ ascents consistently followed 4 and 6 h later, respectively, and were not associated with Etide turning points. Each final descent, however, was coincident with an Etide turning point (data not shown). In this case and in the one described above from Bünning (1931), the ‘relaxation’ movements represent temporary but self-correcting failures to maintain the leaf in its ‘up’ position. Self-correction of leaf position is not dependent on an Etide turning point.

Kleinhoonte (1929, her fig. 5) also recorded what appear to be secondary leaf movements. Here, primary ascents coincided with minimal-value Etide turning points during the night-time, whereas secondary, ‘relaxation’ ascents (marked by * in Fig. 15) commenced during the daytime, but were coincident with minimal Etide turning points. These latter turning points seem to ‘rescue’ the leaf from its premature descent, thus enabling it to achieve the ‘up’ position for the remainder of the day. According to the tension/relaxation/energy hypothesis (Bünning, 1973; Mayer, 1981), the first of the two descents of the leaf in each movement cycle would be due to a depletion of the energy which helps maintain the leaf in the ‘up’ position.

Fig. 15.

‘Relaxation’ movements of an excised leaf of C. ensiformis. The start of each secondary, ‘relaxation’ ascent is marked with an asterisk (*). It occurs close to an Etide minimal extrema. The primary ascent, which occurs at the commencement of the dark period, is associated with an Etide maximum turning point. Other conventions are as for Figs 2 and 3. Leaf movements redrawn from fig. 5 in Kleinhoonte (1929).

In two other cases illustrated by Bünning (1931, his figs 19 and 20), the commencement of secondary leaf ascents are coincident with Etide maxima (data not shown). In one case, over a 3-d period, the Etide maxima are those of a single, broad [A] peak, occurring on lunar days 21–23. Secondary ascents occurred at 1600 h, coincident with the daily Etide maximum. In the second case, also over a 3-d period, commencement of two secondary ascents at 1800 h are associated with the Etide B peak of an [A,B] pair of peaks. Each of the subsequent descents of these two supernumerary movements, at 0100 h, appears to be driven by a minimum Etide extrema. In the other case (Bünning, 1931, his fig. 21), prolonged secondary ascents were completed at midnight on two successive days. A 1-h exposure to red light at 1800 h on the second day appeared to curtail the secondary ascent. Nevertheless, both the primary and the secondary ascents commenced at the time of Etide turning points.

Fig. 21.

Short-period leaf movements (τ approx. 8 h) of Ph. coccineus in continual darkness. Conventions which apply are the same as for Figs 2 and 3. Leaf trace data redrawn from fig. 6 in Stoppel (1926).

A further, more complex example from Bünning (1932, his fig. 7a) shows the occurrence, over a 3-d period (09–11 Dec. 1932), of eight leaf oscillations, five of which are additional to the three mid-day movements which would naturally occur during this time-span. On the first and second days, secondary, ‘relaxation’ ascents were completed at approx. 2400 h. These ascents followed earlier unsustained daytime ascents. Descents from both the feeble primary ascents and the subsequent ‘relaxation’ ascents coincided with minimum Etide turning points.

Whereas the results of Kleinhoonte (1929) clearly show relationships between Etide turning points and primary and secondary leaf movements (Fig. 15), some of the results of Bünning (1931, 1932) are quite confusing and suggest that there are several types of ‘relaxation’ movements, which display different responses to the lunisolar turning points. Thus, some relaxation events associate with Etide turning points, whereas others do not. Nevertheless, in general, a secondary, ‘relaxation’ ascent occurs after a failure to maintain a primary ascent. The intervening descent is partial and can be reversed by an Etide turning point. The secondary ascent then occurs, often at an unusual time (e.g. during the night).

Supernumerary, or ‘relaxation’, oscillations: non-articulated leaves

The diurnal, double leaf movements recorded from Coleus plants by Schmitz (1934) are also evidence of the interpolation of ‘relaxation’ oscillations within the usual movement cycles of a non-articulated type of leaf (Fig. 16). The secondary movements are upwards and occur during the day, when the leaves are customarily moving downwards (cf. Fig. 12). The ‘up’ position in this case appears to be the default position, as it is in the bean leaves, although the physiological consequences may be different from those that apply to the ‘up’ position of articulated leaves. Moreover, the presence of relaxation movements in Coleus indicates that this type of movement is not some peculiarity of the articulated type of leaf.

Fig. 16.

‘Relaxation’ movements of a leaf of C. Penzigii take the form of secondary, upward movements during the daytime (marked with *). While there are coincidences between Etide and leaftide turning points, there are also coincidences between the turning points of the ‘relaxation’ movements and maximal rates of change in the Etide (○, •). FQ Moon occurs on 13/5/1932, and singular A Etide peak is present on the following day. Other conventions are the same as those for Figs 2, 3 and 12. Leaf movements redrawn from fig. 9 in Schmitz (1934).

A time course of Coleus leaf movements, extending over the 5-d interval 14–18 May 1932 (see Schmitz, 1934, his fig. 9) in which ‘relaxation’ oscillations appear, is presented in Fig. 16 along with the contemporaneous Etide time course. A singular Etide peak [A] occurred on 14 May and the Etide double-peak structure [A,B] became established on the days that followed. Over this time span, the diurnal leaf-tide pattern changed from a double to a single oscillation due to a progressive suppression of premature day-time descents and subsequent ‘relaxation’ ascents (marked by * in Fig. 16). During the last 3 d of this period, coincidences between leaf and Etide turning points are evident. As in the case of the secondary leaf movements of Phaseolus (Fig. 14), the relaxation movements of Coleus seem to commence at times of maximal rates of change of the Etide (marked by ○ in the δL panel of Fig. 16).

A second time course of leaf movement in Coleus was prepared 1 month later (June 1932), and a series of double (or even triple) diurnal oscillations was found (Fig. 17, based on Schmitz, 1934, his fig. 11). These oscillations occurred within a 5-d period when double [A,B] Etide peaks were developing from a singular Etide [A] peak. Double diurnal, secondary, relaxation oscillations occurred on all days (marked by * in Fig. 17). Interestingly, in both May and June 1932, double oscillations occurred not only in the leaf blade but also in the petiole (data not shown). The petiolar oscillations were always in phase with those of the leaf, the amplitudes of each increasing considerably during the May–June period. The daily primary maximum ‘up’ position of the Coleus leaf during 11–15 June 1932 (Fig. 17) is divided into two parts, with the cleft in the night-time peak coinciding with an Etide turning point (cf. similar results shown in Fig. 15). As remarked above, some of the leaf turning points, both primary and secondary, seem to be associated with maximal rates of change of the Etide (marked by ○ and • in Fig. 17).

The double leaf movement of Coleus may be regulated by the day length. On the dates in May–June 1932 when the diurnal, double oscillations were recorded, the natural LD cycle was approx. 16 : 8 h, whereas in March and April, when double oscillations were infrequent or absent, LD was 12 : 12 and 14 : 10 h, respectively. It is suggested that, during the longer daylight period during May–June, the leaf and petiole became increasingly sensitive to the Etide turning points, perhaps due to increasing transpiration. For example, two, or even three, Etide turning points occurred per day during the 16-h light period of May–June (Figs 16 and 17), and each one could potentially have initiated a change in the direction of the leaf movements, thereby accounting for the diurnal, double oscillation of both leaf and petiole. By contrast, the shorter and less intense light periods of earlier months (Figs 12 and 13) contained fewer Etide turning points and fewer relaxation movements.

Disintegrated movements

A more extreme form of relaxation movements in Ph. coccineus was described by Bünning (1935b, his fig. 1a, b). He named them ‘Teilschwingungen’ – divided or disintegrated movements, believing that separate parts (cells or cell groups) of the movement apparatus were no longer coordinated and so brought about their own individual and independent contributions to movement of the leaf lamina (Bünning, 1973). This may well be so; but it is worth noting that the sub-periods into which the diurnal leaf movement cycle is divided have mean values of approx. τ = 6·6 h and τ = 8·2 h (in the two published leaf traces), values close to the 6·2-h harmonic of the Etide.

Pendulum oscillations

The third type of atypical rhythms comprises the so-called ‘pendulum oscillations’ (Bünning, 1931, 1973). These are of relatively small amplitude but of long period. Consequently, articulated leaves may be in the ‘up’ position mostly during the night, and (briefly) in the ‘down’ position during the day (Bünning, 1931, 1932). All the recordings of these leaf movements were from plants of Ph. coccineus grown in darkness and controlled temperature.

The first example of pendulum movements is illustrated in Fig. 18, and was recorded, in darkness, during October 1930 (Bünning, 1931, his fig. 17). The leaf turned from an ‘up’ position at 0000 h on 24 Oct. 1930 to a minimal ‘down’ position, reached at 0400 h, and which lasted for about 4 h. An unusually slow ascent followed, and a new ‘up’ position was attained at 0000 h. The period of movement, estimated between successive minimal ‘down’ positions, is τ ≈ 30 h. Significantly, descent from the first ‘up’ position commenced at a time coincident with a minimum Etide extrema, and subsequent ascents and descents also commenced in synchrony with further Etide turning points (Fig. 18).

Asymmetry of leaf movement is evident in Fig. 18. Ascents proceed more quickly than descents. Asymmetry of leaf movement was also noticed by Bünning (1973, his fig. 85) in a plant grown in continuous light. He thought the asymmetry indicated the superpositioning of two or more processes within the period of leaf movement. A second example (from Bünning, 1932, his fig. 7b) is similar (not shown), except that the leaf movement period is longer – τ ≈ 36 h. Turning points in this leaf movement cycle are again close to, if not coincident with, the times of Etide turning points.

Figure 19 is a portion of a record from a Phaseolus leaf of a pendulum movement within which a ‘relaxation’ movement is inserted. The period of the complete cycle was τ ≈ 36 h, but on 15 Aug. 1932 an ascent commenced 2 h after an Etide turning point at 0400 h. This ascent was annulled soon afterwards in coincidence with the next Etide turning point (a minimum extrema) at 1200 h, and the leaf relaxed to its ‘down’ position. A second ascent commenced at 1800 h (* in Fig. 19), assisted by a further Etide turning point, at 2000 h. However, interpretation of this observation is complicated because of the amputation of this leaf from the plant at 1100 h. Whether the cutting had an effect is not certain; possibly it does so temporarily because a similar amputation (Bünning, 1932, his fig. 9a), when the leaf was ascending, resulted in a downward movement which reverted to an ascent at a time coincident with an Etide turning point. The pendulum oscillation continued for two more days (16–18 Aug. 1932) with a period of τ = 37 h (approx.). Kleinhoonte (1929, her fig. 5) also excised a Canavalia leaf when it was engaged in a descent but found no effect on its movement.

Short-period oscillations

A fourth type of leaf movement includes those exhibiting short periods of τ = 6–8 h (Stoppel, 1926; Bünning, 1934). Although they have been suggested as evidence of disintegration of some process within a major oscillation (Bünning, 1934), some of them may be comparable to the ‘relaxation’ movements already mentioned. These short-period movements relate to the Etide.

Another characteristic is their relatively small amplitude – about 50 % of that associated with a cycle of diurnal leaf movements. However, this is probably because the leaf does not move far, either up or down, before its movement is reversed. Short-period oscillations are found in both articulated and non-articulated types of leaves.

Articulated leaves

Leaf movements were recorded by Stoppel during 24–29 Aug. 1925 (Stoppel, 1926, her fig. 3) from a plant of Ph. coccineus placed in continuous darkness, first in the Posthauskeller at Akureyri, Iceland, and then, after relocation on 27 Aug., in the Islandbankkeller. The period of the movements before relocation was τ = 8 h, but afterwards the periods shortened to τ = 4–6 h (Fig. 20). The 8-h rhythm appeared to be regulated by the Etide, each cycle of movement being renewed at the time of an Etide turning point. On dates after relocation, however, the turning points of the Etide had become separated by longer intervals and the new leaftide rhythm might be typical of days when there was only one maximum and one minimum Etide per day. Thus, two Etide turning points during 24 h might support four short-period cycles of leaf movement, two of which could be relaxation movements, possibly assisted by a maximal rate δ(δg).

Over a 4-d period in September 1925, Stoppel (1926, her fig. 6) recorded other types of disturbance to the periods of leaf movements (Fig. 21), similar to those described 1 month earlier. As in that case (Fig. 20), they commenced at a time when the Etide was evolving from two maxima per day, on 6–7 Sept. 1925, to one maximum per day, on 7–8 Sept. 1925. In this latter period, the leaftide pattern followed suit, its periods switching from τ = 6 h to τ = 10 h, apparently in conformity with the altered pattern of the Etide.

Stoppel’s bean plants were grown in darkness and, although the leaves were still able to make small, short-period movements, they generally remained in the ‘up’ position and did not establish major diurnal movement cycles; however, there were occasions when they did so. One such (Stoppel, 1926, her fig. 7) was from a plant placed in the Posthauskeller, Akureyri. Here, the period of small movements of the leaf, nearly frozen in its ‘up’ position, was τ = 8 h. After relocation to a growth chamber on 16 Aug. 1925, the leaf immediately entered a diurnal movement cycle for the next 2 d, with τ = 24·0 h (Fig. 22). Superimposed upon this longer cycle were secondary oscillations, with τ = 4 h. These 4-h oscillations were absent on the second day, and the trace of the leaf movement was relatively smooth, except for a few wavering movements at the time when the leaf had reached the ‘up’ position. On all three days (i.e. before and after relocation) many turning points in each type of leaf movement cycle were coincident with Etide turning points (Fig. 22).

Fig. 22.

Short-period leaf movements of Ph. coccineus in continual darkness, first in the Posthauskeller, Akureyri, Iceland, and then after transfer to a growth chamber at the time and date indicated by the vertical line, whereupon the relatively short-period rhythm of movement becomes incorporated into a longer rhythm. Conventions which apply are the same as for Figs 2 and 3. Leaf trace redrawn from fig. 7 in Stoppel (1926).

Leaf movements recorded by Bünning (1932, his figs 7b and 9b) also revealed short-period movements at the same time as the leaf was engaged in pendulum-like movements of longer period. These small wavering movements had periods of τ ≈ 1–3 h, with amplitudes one-tenth those of the pendulum movements upon which these minor movements were superimposed.

It is evident from the work of Lörcher (1958) that short-period rhythms are influenced by the quality of the light to which the leaves are exposed. For example, Phaseolus leaves exposed to 12 h of either blue or red light, and then placed in darkness, exhibited short-period oscillations of τ ≈ 2–3 h, these being superimposed upon a major 24-h leaf movement cycle. When the leaves were exposed continuously to red and dark-red light given together, the major movements were abolished, yet the τ = 2-h oscillations persisted. The latter movements may thus belong to a fifth movement type, of aitionomic movements, mentioned below.

Non-articulated leaves

Movements with short τ ≈ 6-h periods were recorded from both the lamina and the petiole of Coleus leaves by Schmitz (1934, his fig. 14). The plant had been placed in continuous darkness. During the 4 d when leaf movements were recorded, the Etide pattern consisted of monotidal [A] peaks only. The broad A peaks provide extended times when non-zero thresholds of δ(δg) may be present and perhaps relate to some of the short-period leaf and petiole oscillations (Fig. 23).

Fig. 23.

Short-period movements of the leaf and petiole of C. Penzigii in continual darkness. Conventions which apply are the same as for Figs 2 and 3. Leaf movements redrawn from fig. 14 in Schmitz (1934).

Aitionomic movements

The fifth type of atypical leaf movements comprises aitionomic movements, or self-correcting deviations, often with periods τ ≈ 1–2 h. Although of extremely shallow amplitude, they can nevertheless be resolved by kymography: what appears to be a ‘flat’ kymographic trace from a leaf actually contains minute fluctuations occurring at 1- to 2-h intervals. These movements persist in circumstances where all other movements – the major diurnal oscillations and the more shallow movements of τ = 4–6 h (see above) – are absent. An example is found in the leaf movements recorded by Cremer (1923, his traces K53 and K57) from a plant of Ph. coccineus grown in darkness within a chamber of the 600-m-deep König Wilhelm II rock-salt mine at Kochendorf, near Würzburg, Germany.

In connection with these barely visible leaf movements, Palmer (2002, p. 113) recalls that when a student (unnamed) repeated the experiment of Cremer (1923) with bean plants in the same Kochendorf salt mine 33 years later, the leaves again failed to show any movement. Probably the aitionomic movements were present, but these were not mentioned. Following this later experiment, the supposition was formed (Palmer, 2002) that the atmosphere of the mine was so laden with salt ions that the internal fluxes of K⁺ and Cl^–, which normally drive the leaf movement, were overwhelmed, causing the usual mechanism of osmotically driven cell expansion in the pulvinus to be suspended. However, this should not be taken for granted because it is clear that certain biochemical reactions proceed differently in deep mine shafts (Takata, 1951) where they might be subjected to very low-frequency radiation (3–30 kHz), which continues to travel within the Earth’s crust.

A close examination of the leaf traces recorded by Cremer (1923, his K53, K57, K61, K62), some of which extended over a span of 6 d, reveals that many of them can be resolved into ‘flat’ portions broken periodically by minute peaks and troughs. About one in six of these vertical movements coincides with Etide maximum and minimum turning points (Fig. 24).

Fig. 24.

Leaf movements of Ph. coccineus grown in continual darkness within the Kochendorf saltmine (Würzburg, Germany) on the dates indicated. The record K61 (middle panel, L) shows two apparently spontaneous cycles of movement on the first two days (9–10/8/1922). The δg panel (above) relates to this record K61. When the leaf reaches the ‘up’ position, on 11/8/1922, the former relatively long cycles, which also include small aitionomic movements (not shown), give way to aitionomic movements only. These occur at approx. 4-h intervals. The timings of the aitionomic movements from K61 are summarized in the panel Peak/Trough immediately below, and are related to the high and low Etide turning points (HET and LET) below. Similar summaries of the aitionomic movements and the corresponding Etide turning points are shown in the separate traces K53 and K57 prepared on other dates. Synchronisms between Peak/Trough and HET/LET are enclosed in rectangles. Leaf traces redrawn from Kurves 53, 57 and 61 in Cremer (1923).

Occasionally a major leaf movement occurred in the darkness of the salt mine (K61 in Fig. 24). Two smooth ascents and descents of the leaf, on 9–10 Aug. 1922, were preceded by a movement cycle upon which small, short-period oscillations were superimposed (this detail is not shown in Fig. 24), similar to the movements recorded by Stoppel (cf. Fig. 22). K61 attained its maximum ‘up’ position on 10 Aug. 1922, but then only aitionomic movements were seen on the following 2 d.

One cannot be sure where the aitionomic movements originate; they may be due to the leaf pulvinus, to the petiolar node or to the lamina itself. Although the minute movements and the major movements coexist, it does not necessarily mean that they trace to a single source.

It seems that aitionomic movements are a basic property of bean leaves. For example, when Spurný and Konečná (1978) filmed the germination of Ph. vulgaris they found that the first movements shown by the emerging leaves had periods of τ = 1·6–2·3 h and amplitudes of 2·6–5·1 mm. These small movements preceded (but may have continued to coexist with) the movements with periods of τ = 23·3–25·8 h and amplitudes of 12–16 mm, which manifested as the leaves grew older.

Aitionomic movements may also be responses to Earthly gravitational acceleration acting upon the leaf, given that it was found that when plants of Ph. vulgaris were inverted, the leaves made a small movement lasting about 1·5–2 h before reversing direction (Hosokawa and Kiyosawa, 1983a). Intriguingly, the direction (up or down) of these gravi-aitionomic leaf movements depended upon the time of day: when the plants were inverted at 1100 h the movements were upwards, whereas when the inversion was at 2300 h the movements were downwards. Although the authors proposed a relationship with the respective prevailing light or dark periods, the presumed graviresponse may have been determined in accordance with turning points of the lunisolar tide.

The frequency of aitionomic movements, as illustrated in Fig 24, suggests that they are like the micronutations of certain roots (Fisher, 1964): they are ‘hunting’ movements, anticipating a stimulus which, when perceived – perhaps in the form of an Etide turning point – will cause a descent from the semi-stable ‘up’ position and, hence, initiate a new cycle of leaf movement.

Restoration of leaf movement rhythms after a period of stasis

Experiments have tested whether rhythmic leaf movements can resume after an enforced period of stasis. Intact or excised leaves were transferred from a light/dark environment to one of continuous light, thereby abolishing the former rhythm of leaf movement. Later, when the plant or leaf was placed in darkness, the restoration of leaf movements could be detected by kymography. Movements did indeed return, and the recovered rhythm was much the same as it had been previously, before their abolition in continuous illumination. A second approach was to germinate seeds in continuous light and observe whether rhythmic leaf movements would develop under this environment.

Brouwer performed the first type of experiment using C. ensiformis plants (Brouwer, 1926, his figs 35 and 36). He recorded simultaneously the time courses of movements of primary leaves of intact plants and of excised leaves. After transfer to continuous light for 4 d, excised reference leaf P124 became static in the ‘up’ position, and showed only short-period oscillations. On the following days, and still in continuous light, leaf P124 commenced a movement similar to the ‘pendulum’ type, all ascents and descents commencing at times of Etide maxima. The leaves were then placed in continuous darkness where this pattern of movement and coordination with Etide turning points persisted during the remainder of the experiment (Fig. 25). Intact leaf P125 followed the same pattern. Its more numerous changes of direction (it did not share the pendulum-like movement of leaf P124) and their adherence to the Etide turning points are indicated in the panel δL, P125, in Fig. 25.

Fig. 25.

Movements of excised leaf P124 of C. ensiformis exposed first to constant light and then to continuous darkness. The period of leaf oscillations becomes shorter upon transfer from light to dark. At the same time, a whole plant was treated similarly and its leaf movement recorded (P125) – see panel δL. The more frequent movements of P125 become synchronized with those of P124, when placed in darkness. Conventions which apply are the same as for Figs 2 and 3. Leaf traces redrawn from figs 35 and 36 in Brouwer (1926).

A similar experiment was performed by Kleinhoonte (1929, her fig. 37), but in this case the Canavalia plants were kept in continuous light for 13 d. This was a longer timespan than used by Brouwer; it was also more effective in abolishing the previous movement rhythm. During the last 3 d, the movements of two leaves, P92 and P93, from two plants, showed only short-period (τ = 4 h) oscillations, only the last few of which are shown in Fig. 26. Upon exposure to darkness, leaf movements of greater amplitude commenced immediately, and diurnal rhythms, synchronous between the two plants, were established on the second day of darkness. At the time of entry into the dark period, however, the reference leaves of each plant were behaving differently with respect to their movements: P92 was descending, whereas P93 was ascending. Four hours into the dark period, both leaves changed their direction of movement, P93 doing so twice (see * and ** in Fig. 26). Both leaves now ascended in synchrony. The initial change in direction coincided with an Etide turning point (Fig. 26). The subsequent leaftide movements proceeded in conformity with the Etide.

Fig. 26.

Two leaves, P92 and P93, of a whole plant of C. ensiformis were exposed to constant light, where they showed movements of short period. The leaves were then placed in continuous darkness at the time indicated (vertical line), whereupon both leaves adopted longer periods of movement. At the time of transfer, leaf P92 was descending, while leaf P93 was ascending (marked by single asterisks *). P93, after a temporary descent, adjusted its movement to an ascent (double asterisk **), and thus its movements became in phase with that of P92. Conventions are as for Figs 2 and 3. Leaf traces redrawn from fig. 37 in Kleinhoonte (1929).

Another way of determining the relationship between the onset of leaf movements and variations in the Etide is by examining the leaves of seedlings germinated in constant light. The movements of leaves under such conditions could not have been entrained by any obvious cues in the immediate environment. Using this approach during January 1925, Brouwer (1926) noted that, ‘To my amazement, I saw that the leaves were by no means motionless, but that they had a clearly expressed daily period.’ And, later, with respect to his observations on replicate plants, ‘Nowhere do the movements of leaves act against each other.’ In other words, all leaves moved in phase and changed direction simultaneously. At first, the movements were evidently irregular, but when rhythmic movement became evident, leaf descent commenced at mid-day and the maximum ‘down’ position was attained shortly before midnight, in the manner usual for bean leaves. Figure 27 shows how, after a preceding 3–4 d (23–25 Jan. 1925) with irregular movements, strong leaf oscillations were developed subsequently. Again, turning points in the contemporaneous Etide not only coincide with changes in the direction of the major leaf movements but also seem to associate with some of the smaller movements of the leaf whilst in the ‘up’ position. This association is illustrated by the correspondence between the time courses of δL and δ(δg) (Fig. 27).

Fig. 27.

Leaf movements of a plantlet of C. ensiformis germinated in continuous light. After about 24 h during which time the leaves were held in the ‘up’ position, rhythmic leaf movements commenced, as though in response to the succession of Etide turning points. Two minor leaftide turning movements coincide with the maximal rates of increase of δ(δg), marked with filled circles (•). Conventions are the same as for Figs 2 and 3. Leaf trace redrawn from fig. 21 in Brouwer (1926).

One month later, Brouwer (1926) made a new set of observations on the leaf movements of Canavalia seedlings raised in constant light. Leaf movements were rather erratic but, nevertheless, some abrupt descents were recorded (Brouwer, 1926, his figs 22 and 23). These descents coincide exactly with turning points in the Etide, or were within 2 h of a turning point (data not shown). Surprisingly, the clearly defined ascents of the leaf were not associated with Etide turning points, suggesting that, under these constant light conditions, an ascended, ‘up’ phase, as well as its commencement, was a default process that would occur without assistance from an Etide turning point, as soon as a preceding descent had been accomplished. Bünning (1973) was apparently unaware of these experiments of Brouwer. He believed that seedling leaves in constant light would express their ‘endogenous’ rhythm only after experiencing a short period of darkness, the relevant experiments with Ph. coccineus having been performed by Wassermann (1959) who showed that a dark period of about 9 h was necessary for rhythm establishment. However, it may be that Canavalia and Phaseolus differ in their light requirement for rhythm establishment.

Observations partially complementing those of Brouwer were provided by Kleinhoonte (1929, her fig. 8). She used leaves from Canavalia plantlets germinated and raised in continuous darkness. For a long while (duration not specified) the test leaf (P16) was motionless in the ‘down’ position, but over a period of 4 d, after returning the plant to the greenhouse with natural light, it ascended and showed oscillations of progressively increasing amplitude with a mean period of τ = 23·8 h, using the minimal ‘down’ leaf position as reference (Fig. 28). The movements of this leaf in relation to the time course of the Etide show that the commencement of each descent is nearly coincident with minimum Etide extremas, whereas the ascents are clearly synchronized with the other minimal Etide turning points. Later, when the usual amplitude of movement had been achieved, a near-perfect coincidence of each of the respective turning points is evident [see the panels for δL and δ(δg) in Fig. 28]. The pattern of leaf movements appears to be more consistently related to the pattern of the Etide than to the events of sunrise and sunset.

Fig. 28.

Onset of leaf movement of a plantlet of C. ensiformis germinated in continuous darkness. Initially the leaf was frozen in the ‘up’ position but began to oscillate when returned to the greenhouse on 3/3/1926, as though in response to the succession of Etide turning points. Some leaftide turning points coincide with the maximal and minimal rates of change of δ(δg), marked with filled and open circles (•, ○), respectively. Conventions are the same as for Figs 2 and 3. Leaf trace redrawn from fig. 8 in Kleinhoonte (1929).

Rescheduling of leaf movement rhythms

Although leaf movement rhythms under constant conditions may become entrained to a lunisolar tidal rhythm, as the preceding section indicated, the former rhythms are also susceptible to alternating light and darkness. Some of Brouwer’s experiments are instructive in this respect. By prolonging either the light or the dark period during the course of a single cycle of leaf movement, it was possible to displace the leaftide rhythms with respect to the solar day; the ‘up’ position, for example, could be achieved in the late evening during a period of darkness (Brouwer, 1926, see his figs 29 and 35), or the ‘down’ position could be achieved at mid-morning during a period of light (Brouwer, 1926, see his fig. 30). This feature of displacement is also evident in Fig. 25. Once a new rhythm had become established, it could be maintained in free-running conditions of either constant light or constant darkness, and ‘up’ and ‘down’ positions could be attained at uncharacteristic times of day (cf. Fig. 26).

Fig. 29.

Scheme for rhythmic expansion and contraction of the pulvinar nodal tissue responsible for diurnal movements of articulated leaves. (a) A simple sand-glass model in which, when the lower compartment (B) is full (F), the sand-glass inverts (T and arrow). The former B compartment becomes uppermost (A) and, being now full, the sand flows from it into the lower, empty compartment (BE). When that compartment becomes filled, the compartmental emptying/filling cycle begins again. (b) Analogizing the bi-compartmental sand-glass to the nodes of the pulvinus, the upper nodal portion (flexor), when turgid, is emptied of water, which then flows into the lower, flaccid nodal portion (extensor). However, there is no inversion of compartments, as in (a), only a reversal of the direction of water flow. Flow is always from the turgid compartment to the flaccid compartment. The flow commences coincident with a lunisolar turning point, δ(δg)₀. In accordance with the water-flow and turgid/flaccid cycles of the pulvinar zones, the leaf moves either up or down, the direction of movement being reversed when another turning point δ(δg)₀ is experienced. (c) The model in (b) suggests that the turgid state of cells of either flexor or extensor activates (*) mechano-sensitive proteins (MSP), and this, in turn, regulates the outflow of water and ions, K⁺, in particular, from either flexor or extensor. Thus, in co-operation with MSP*, the alternating turgid and flaccid states of flexor and extensor are regulated by fluxes of H₂O and K⁺, the periodicity of the whole being governed by the succession of Etide minima and maxima, when δ(δg) = 0.

These new, but displaced rhythms, although taken as evidence of a re-setting of an endogenous clock (Bünning, 1973), can also be interpreted as examples of a re-setting of the relationship between the leaf movement process and the lunisolar tidal rhythm. Delays within the leaf movement cycle, brought about by altered light and dark periods, allow the leaftide to interact with an unanticipated set of lunisolar tidal turning points. This is not difficult because on most days of the lunar month such turning points occur approximately every 6 h. Thus, it is the harmonic property of the lunisolar gravitational rhythm which enables the leaftide to maintain unusual patterns of behaviour with respect to the time of the solar day.

The ability of leaves to adopt new rhythms of movement with respect to the solar day after being exposed to altered light and dark periods, and then exposed to continuous light or dark, proved an important step in uncovering the nature of the rhythm itself. With respect to those leaf movements which continued under free-running conditions, Brouwer remarked, ‘The great problem is still whether the autonomy of movements is the cause of the unweakened continuations [i.e. the leaf movement rhythms were implicitly being recognized as inherent to the plant], or if it is the often-mentioned Factor X, which by its periodic changes brings about sleep movements when “all” external conditions are apparently kept constant’ (Brouwer, 1926, p. 85 of the original article, and with his ironic emphasis on ‘all’). Here the mention of ‘periodic changes’ of Factor X is significant, for his experiments seem to indicate that Factor X was not some property of the solar day which modulated the level of ion conductivity of the surrounding atmosphere, as had been thought previously (Stoppel, 1916) to regulate leaf movements. This hypothesis was excluded by the fact that new rhythms of leaf movement could be made to occur out of phase with the solar day, and to persist either in total darkness or in continuous light, even though they would (according to the air-ion hypothesis) still have been experiencing rhythmic modulation due to an air-borne Factor X.

Brouwer was right to emphasize the constancy of ‘external conditions’, at least those that were immediately perceptible or quantifiable. Nevertheless, although he could eliminate direct perception of the onset of daylight and of darkness, he could not eliminate the risings or settings of the Sun; nor could the risings and settings of the Moon be abolished. These were ever-present cosmic events during his experiments, as were the consequent rhythm of the lunisolar tide, which may now be hypothesized to be the embodiment of the putative Factor X whose nature so puzzled these early investigators of leaf movements.

DISCUSSION

Time courses of rhythmic leaf movements extending for 2–3 d or more have been presented together with the contemporaneous time courses of the gravimetric tidal variation δg estimated by the Etide program, a variation which, in turn, relates to the Earthly gravitational acceleration. This latter parameter P1 has a standardized value of 1 g = 9·80665 m s^–2 (or 1 g = 9·81 × 10^–8 µGals). The rhythmical variation of the Etide δg values at any given location on Earth are governed by two further composite parameters: P2, the positions of the Sun and Moon relative to that location; and P3, the attractive gravitational forces exerted upon the Earth by the Sun and Moon. The interaction of the respective variables results in an increase or decrease (±δg) of the standardized Earthly gravitational acceleration P1. All variables associated with parameters P1–P3 are experienced by all animate and inanimate material upon or within the Earth. In addition, the relative positions of Sun and Moon (P2) determine the amount, duration and quality of sunlight and moonlight received at a given location. It is proposed that these variations as well as those due to one or both of the gravitational forces underlie the leaftide rhythms.

The variation ±δg by which the Earthly local gravitational attraction (P1) is altered is often considered too weak to have a perceptible effect upon sensitive and rapid graviresponses of plants. The gravitional threshold of root gravitropism, for example, has been estimated to be approx. 25 s of applied 1 g acceleration (Perbal and Driss-Ecole, 1994; Volkmann and Tewinkel, 1996); or, in a continuous gravity field, the response threshold is approx. 0·01 g (Laurinavičius et al., 2001). However, such relatively high estimates in comparison with the ±δg variation may be a feature of (a) the resolution of growth events and (b) an inherent low sensitivity of roots to gravitational displacement. Leaftide rhythms may be more sensitive to gravity and kymography provides high resolution of movements. Nevertheless, the gravity thresholds which apply in the case of these rhythms is not known (see Kleinhoonte, 1932).

Graphical representation of the numerical values of the Etide time courses show the combined Earthly and lunisolar gravitational forces (P1, P3) to oscillate like a series of high and low tides in accordance with the passage of the Moon and Sun relative to the location in question. This lunisolar gravitational rhythm manifests not only as an Earthtide (Fig. 1 in Supplementary Data S2) but also as a marine tide (Fig. 1a,b in Supplementary Data S1). In the present study, the Etide rhythms of particular interest are those at locations where time courses of leaf movement were recorded.

A large number of examples of leaf movements are presented in Figs 2–28. In the era during which they were recorded, all of them contributed in some measure to the development of the concept of an endogenous ‘clock’ (Bünning, 1973), especially as it related to the rhythmic movement of bean leaves (Pfeffer, 1915; Bünning, 1958, 1973). Superimposition of the Etide time courses upon the leaf movement time courses provides an alternative perspective from which to appraise the leaftide rhythm. The coincidence, or synchronization, of the respective turning points in the two time courses suggests strongly that the leaftide is guided, if not directly regulated, by the lunisolar tidal force, as expressed through the Etide estimates. It follows that as many experimental examples as were needed to consolidate the original hypothesis of an endogenous clock are required to establish a convincing alternative hypothesis: namely, that there is a causal relationship between the lunisolar tidal force and the leaftide. The rhythm of leaf movement is thus the outward expression of an exogenous zeitgeber (cf. Brown, 1962, 1970, 1972) in the form of a lunar clock (Fig. 1).

Except for some of the leaf ‘relaxation’ movements, turning points in the leaftide time courses generally associate with turning points in the Etide. The converse is not true, however: some turning points in the leaftide time courses are not coincident with Etide turning points. It is as though some Etide turning points are ignored by the leaf, suggesting that a leaf – or, more precisely, the petiolar pulvinus, this being the major executor of leaf movement – following an earlier leaftide turning point, enters a refractory state that renders it unresponsive to an ensuing Etide turning point(s). An unresponsive phase may occur, for example, when the leaf is maintained in an ‘up’ position during a period of illumination. Here, leaf transpiration may affect the ability to respond with a movement. Moreover, conditions of continuous light may result in some derangement of the pulvinar system due to excessive accumulation of photosynthetic assimilates (Simon et al., 1976).

To understand leaf movements in relation to the lunisolar tide, it is useful to consider a model of the process. The model is prepared as simply as possible, but modified when necessary in order to conform to ongoing observations of the movements. The basic components of the model are cells, cell groups or tissues, a conduit for solute flow (via apoplasm and/or symplasm) between tissues, osmolytes and suitable membrane-based transporter molecules. A further requirement is that cellular water should exist as a complex of macromolecular water aggregates. This latter is within the scope of present-day findings on water structure where, under certain conditions, such as contact with hydrophilic surfaces (Zheng et al., 2006; Elia et al., 2013), water assumes a macromolecular composition (Chaplin, 1999; Del Giudice and Tedeschi, 2009; Lo et al., 2009; Del Giudice et al., 2010). Cellular water may also exist in two forms, bound and free (Wiggins, 2008). Under the influence of the lunisolar tidal force, the water aggregates are moved in and out of cells in synchrony with the lunisolar tidal rhythm.

There are two competing notions about how the movement of water in and out of cells might be regulated by the lunisolar tide. The first is based on the hypothesis of Dorda (2010) in which gravity, mass and time are each treated in quantized form. Each quantal timestep of the quantized gravity force (analogous to quantized units of δg) attracts the movement of a quantum aggregate of water, estimated as approx. 10⁸ water molecules, towards or away from the total cellular water mass, estimated as approx. 10¹³ water molecules (Dorda, 2010, pp. 102–105). This hypothesis provides one theoretical framework for the observed plant movements in relation to lunisolar gravitation, and a worked example, in relation to a time course of δg and its synchronization with tree-stem diameter variation, was presented by Dorda (2010). The postulate of lunisolar-driven water-aggregate movement into and out of cells would run in parallel with effects resulting from the differences between the osmotic potentials π_i and π_o of the intra- and extra-cellular environments, respectively.

In the second possibility, where water is not treated in quantized form, the movement of water into and out of cells is viewed in terms of ‘classical’ Newtonian physics. Here, Jurin’s Law of capillarity can be applied, where the height h of a water meniscus within a capillary of radius r is governed according to the expression:

$$h=(\text{2 γ cosθ})/(r\text{ρ}g)$$

where γ is the liquid surface tension, θ is the contact angle of the liquid with the capillary wall, ρ is the liquid density and g is the gravitational acceleration. The equation holds providing that r is less than the length of the capillary. The last-mentioned term g governs the value of h, the distance to which water meniscus will rise in the capillary. It follows that variations of g due to the lunisolar (Etide) gravity variable δg can be inserted into the equation because at each timestep δg is added to or subtracted from the constant g. Thus, δg will influence the degree to which water is either held within or allowed to pass through a molecular capillary, such as an aquaporin molecule (Gonen and Walz, 2006) with aperture radius of 0·5 nm and length of 5 nm. Hence, the lunisolar variation δg could define a cellular ‘water tide’ fluctuating in height at the aquaporin boundary between the apoplasm and symplasm. Moreover, should a change in the structure of water apply at such boundaries (see Elia et al., 2013), then this may modify the capillarity effect, perhaps by affecting γ. Likewise, alternative forms of water, by their contact with the molecular structure of the aquaporin capillary, may modify θ, the contact angle, or even behave in completely novel ways (see Yu et al., 2014). It is in the frame of this classical model that the relationship between the osmotic potentials π_i and π_o and cellular turgor pressure, P, the motive force for leaf movement, usually apply, and which, under favourable conditions, notably of infinitely elastic walls and membranes, may be written as P = π_o – π_i.

The model for the regulation, by water flux, of leaf movement is introduced in its simplest form through an analogy. A vertical sand clock is taken to be the analogue of the mechanism generating rhythmic leaf movement (the leaftide) with its succession of turning points, from one or other of its two semi-stable positions, ‘up’ and ‘down’ (Fig. 29a). The sand clock has two compartments, A and B, connected by a narrow conduit. At first, the lower compartment B is full of sand (BF); the upper compartment A is empty (AE). When the clock is inverted, or tipped (T), by an external agency (or zeitgeber), sand flows via the conduit from the full compartment, which has now become uppermost, into the empty compartment below. Only when the previously empty compartment is filled and the sand clock tipped again by the zeitgeber, either immediately or after some delay, does sand commence to flow from the full compartment into the empty one below.

The sand glass analogy could logically be taken a step further in the realization that the sand flows under the influence of gravity and, consequently, the rate of this fall would be subject to the gravimetric (lunisolar) tidal increment or decrement δg, in addition to the Earthly gravitational acceleration of 1 g.

Transposing this analogy to the anatomy and physiology of the leaf pulvinus and its movements, we see that compartment A represents the upper (adaxial) flexor portion of the pulvinus, and compartment B represents the lower (abaxial) extensor portion. The compartmental states, full and empty, F and E, correspond, respectively, to turgid and flaccid cells or tissues. Moreover, in contrast to the sand glass analogue, there is no inversion of pulvinus position, of upper to lower and vice versa; the sand glass/pulvinus remains stationary, but the two compartments regularly fill, empty and re-fill. The way in which the pulvinus manages this exchange necessitates the first modification of the model.

The step whereby non-turgid, flaccid cells fill with water results in a longitudinal expansion of the tissue. The converse, where water leaves turgid cells, results in tissue shrinkage and the reversal of any previous expansion. This occurs in the flexor and extensor compartments of the pulvinus: the reciprocal emptying and filling of the two compartments thereby either opens or closes the hinge-like pulvinus, and leads, respectively, either to the raising or the lowering of the leaf lamina (Mayer et al., 1985; Gorton, 1987). It is proposed, therefore, that when cells of the upper flexor become sufficiently turgid, they are ready to expel water from the upper flexor, which thence is guided, via a conduit, towards the lower, flaccid extensor. Later, when the tissue of the extensor has become turgid, the same system is now ready for a reversal of the water flow; the expelled water flows from the lower extensor towards the upper flexor, where it is accepted. The system could operate automatically and, hence rhythmically, like a self-tipping sand clock; to do so would depend upon a sensing of ‘fullness’ (the capacity, or maximum turgor) by the cells, leading them to initiate an emptying of their water. This situation of self-tipping would be independent of any external zeitgeber. It could be what happens in the extensor, so accounting for the short time spent in the ‘down’ phase and for the ‘U’-shape of the minimum position on the kymograph trace.

However, ‘fullness’ alone may not be a sufficient tipping condition for the emptying of a pulvinar compartment, as in the sand clock analogy, but requires a zeitgeber. Therefore, the model is joined by a feature which links lunar gravity (quantized or otherwise) with water and its movement (as quantized aggregates or otherwise): thus, a lunisolar tidal turning point is hypothesized to be the zeitgeber, or tipping signal, which initiates the outflow of water aggregates from fully turgid cells (Fig. 29b). The water released in response to this signal passes via an apoplasmic, and perhaps also a symplasmic, conduit (Campbell et al., 1981) whence it is taken up by the flaccid cells on the opposite side of the pulvinus. Accordingly, the leaf moves from one metastable position to the other, alternative position.

In the sequence shown in Fig. 29(b), lunisolar turning points would initiate only the descent of leaves from their ‘up’ position due to the extensor’s loss of water and its entry into the flexor. The ascent of the leaf, due to water movement out of the flexor and into the extensor, could, however, proceed independently of δ(δg)₀. The leaf would appear to reach the ‘up’ position by default. However, at present, the simplest solution is that there is no differential sensitivity of either extensor or flexor to the δ(δg)₀ threshold.

A further feature of the upper and lower pulvinar compartments is that they are composed of many hundreds of differently sized cells, which accordingly construct flexor and extensor tissues, each containing zones of slightly different K⁺ concentrations (Ruge and Hampp, 1994). Thus, it is unlikely that cells in these zones would commence filling or emptying their water at the same instant or, once started, that these processes would proceed at exactly similar rates. There would therefore be scope for variability in the means of regulating not only the rates of ascent or descent of the leaf but also the amplitude of these movements.

Even so, an additional modification to the biological aspect of the model is needed to account for the prolonged periods during which leaves remain at the ‘up’ position, in spite of the passage of one or more lunisolar turning points. So, recalling that, when the leaf is ‘up’ the flexor is ‘empty’ and the lower extensor is ‘full’ (Fig. 29b), some means of maintaining this state is required, even though the passage of a lunisolar tidal turning point might potentially reverse this state. Leaves usually attain the ‘up’ position during a period of illumination. In this state, water is transpired from the leaves, with water moving through the vascular strands within petiole and pulvinus. Transpiration might thus maintain the leaf in the ‘up’ position by stabilizing the water status of the already full extensor compartment and, hence, engender a refractory period with respect to the leaf’s response towards the lunisolar tidal turning points. Of course, this requirement for transpiration to maintain leaf position has to be questioned because this process is probably relatively weak in darkness, yet cycles of leaf movement can continue under such a condition, indicating that this rhythmic process does not require light and can be driven entirely by the lunisolar cycle and its turning points.

Although a transpirational influence on leaf movement can occur under alternating light/dark conditions, it is of interest that Gorton et al. (1989) demonstrated that, under free-running conditions of constant light, there is still a rhythmic variation of stomatal aperture. The period of this rhythm was estimated as τ = 22–25 h, using the maximal aperture of Vicia faba leaves as reference. Moreover, the period was unaffected by a change of temperature, a feature expected of a rhythm governed by an exogenous zeitgeber. Likewise, a period of τ = 24·2–24.8 h for stomatal closure/opening was found in leaves of Phaseolus vulgaris shortly after being placed in free-running conditions of continuous darkness (Holmes and Klein, 1986). A diurnal periodicity of stomatal conductance was also in synchrony with the rhythmic movement of leaves of Abutilon theophrasti (Fuhrman and Koukkari, 1982).

Time courses of stomatal aperture closure and opening in Tradescantia virginiana grown under the free-running condition of constant light (1500 lx) were published by Martin and Meidner (1971) and, because the dates of the observations were recorded, the corresponding Etide time courses could be estimated. From a comparison of the two time courses it is evident that the significant changes of stomatal aperture – i.e. when maximal aperture was first achieved, when apertures commenced closure and when they started to open again – coincided with turning points of the lunisolar tide (data not shown). Therefore, the commencement of the descent of a leaf from its ‘up’ position in a leaf-movement cycle during a period of illumination may be brought about by a lunisolar-directed closure of stomata and a consequent reduced flow of transpired water which can no longer maintain turgidity of the extensor zone of the pulvinus.

Much effort has been expended on uncovering the detailed physiology of leaf movements, the leaves of Samanea saman having been intensively studied in this respect (Satter et al., 1988; Moran, 2007a, b). In the pulvinus of this species, K⁺ and Cl⁻ ions are the main osmolytes. The movements of these ions within the water fluxes between the flexor and extensor compartments create differentials of osmotic potentials, π_i and π_o, which lead to the generation of turgor. Particular attention has been paid to the role of K⁺ in leaf movements, not only because of the great diversity of molecular species which can act as K⁺ transporters but also because of their location at the plasmalemma and tonoplast (Szczerba et al., 2009; Voelker et al., 2010; Dreyer and Uozumi, 2011). Molecular diversity extends to the Samanea pulvinus where different K⁺ transporters characterize the flexor and extensor (Moshelion and Moran, 2000).

The first clue that K⁺ was involved in the leaf movements of Phaseolus came from the finding that valinomycin, which selectively interferes with K⁺ transport, altered the movement rhythm (Bünning and Moser, 1972). Later, elemental microassays of tissue samples taken during the leaf movement cycle confirmed the predicted movement of K⁺ across the pulvinus (Kiyosawa and Tanaka, 1976; Mayer, 1977; Kiyosawa, 1979; Hosokawa and Kiyosawa, 1983b). Schrempf and Mayer (1980) characterized the time course of the movement of K⁺ and Cl⁻ in relation to the internal structure of the pulvinus of Ph. coccineus. Using X-ray microanalysis and scanning electron microscopy, the distribution of K⁺ and Cl^– was determined in cross-sections of an entire pulvinus. By preparing density maps of ion distributions, and sampling pulvini at different stages of the leaf movement cycle, information about the dynamics of ion movement was obtained. As expected, both K⁺ and Cl⁻ were abundant in the extensor when the leaf was ‘up’. During leaf descent, K⁺ first, and Cl⁻ later, became abundant in the flexor. However, K⁺, and to a lesser extent Cl⁻, were also abundant in the flank regions when the leaf was ‘up’. It seems that the flank zone contributed K⁺ and Cl⁻ to the flexor during leaf descent. Moreover, as Freudling et al. (1988) showed, cell walls act as reservoirs of K⁺, so that when the K⁺ content is low in the cellular apoplasm, it is high in the surrounding cell walls, and vice versa. Because it is the flexor rather than the extensor which shows the greatest change in ion distribution – the extensor always remaining with an overall high level of K⁺ and Cl⁻ − it may be that the flexor, where changes in ion concentration are more pronounced, is the major site for the regulation of the leaf movement process.

Accompanying the movements of ions within the pulvinus are rhythms of altered electrical membrane properties which are the result of alternating light and dark (L : D) conditions. An active electrogenic pump, for example, coincides with low turgor pressure in the extensor cells (Freudling et al., 1980). During the L period of an L : D regime, the component wavelengths of blue, red and far-red light interact with their respective photoreceptors and thereby either initiate or inhibit K⁺ transporter activity (Nishizaki, 1987; Lowen and Satter, 1989; Moran et al., 1996; Moran, 2007a, b). Through these interactions, light and darkness help to regulate leaf movement, doing so in a way that is superimposed upon the putative lunisolar regulation of movement. Nevertheless, the fact that leaf movement rhythms persist in constant conditions of light or darkness indicates that the lunisolar regulation is the primary phenomenon, sufficient in itself, and that photoregulation of leaf movement is a secondary phenomenon. The movement of ions within the pulvinus during cycles of leaf movement in DD or LL conditions have not been studied.

If, as proposed, the lunisolar turning point δ(δg)₀ acts upon turgid cells (Fig. 29b), then the question is how this is achieved. It may be by fortunate coincidence: maximum turgor is reached exactly at the time when δ(δg)₀ is achieved during the Etide time course, due to the selection and then calibration of rates of water and ion flux against the value of δ(δg). One way in which cells are able to sense their turgid state is by means of mechanosensitive proteins (MSPs) (Kung, 2005; Vogel and Sheetz, 2006) located at the plasma membrane. When MSPs of pulvinar cells are activated by turgor (Fig. 29c), as was postulated by Moran et al. (1996), and achieved in coincidence with δ(δg)₀, they then enable an action. This action is the forcing of water from the cells either via hydrophilic aquaporin channels in the plasma membrane (Moshelion et al., 2002; Uehlein and Kaldenhoff, 2006, 2008), or via exocytotic vesicles. Furthermore, activation of MSPs might also have an impact upon membrane-based K⁺ transporters, perhaps due to some physical link between the two macromolecules. These transporters have a bidirectional mode of action, switching from either inward (import) to outward (export), or vice versa, when activated. In their ‘outward’ transportation mode, initated by MSPs in response to turgor at the time when δ(δg)₀ is reached, both K⁺ ions and water are proposed to exit the cell (Fig. 29c), across the plasma membrane, as a cascade; consequently, ions and water flow between the upper and lower zones of the pulvinus via the flank zone. This cascade ceases when the cells are empty and MSP activity is relaxed, whereupon the K⁺ transporters may switch their polarity in readiness for an influx of ions and water. The aquaporins may have no polarity and permit water to move in whatever direction the osmotic potentials due to Cl⁻ and K⁺ ion concentrations determine. Whether the amount of water movement is related to lunisolar gravity variation in accordance with Jurin’s law, or whether it moves as quantized aggregates, remain open questions.

This model could apply to any plant growth zone where maximum turgor is achieved, where there is cellular asymmetry and wherever it is possible for K⁺ to shuttle between apoplasm and symplasm (cell walls). The model could be extended to root (Fisahn et al., 2012) and shoot (Moraes et al., 2012; Yamamoto, 2012) growth, and the rhythmic and reversible dilatation growth of tree stems (Barlow et al., 2010) and, hence, account for the action of the lunisolar force and its tidal turning points, on these processes. The model might also extend to simple life forms, such as cyanobacteria in which a significant fraction of the genome shows rhythms of transcription that accord with the lunisolar period (Kondo et al., 1994). Interestingly, in the cyanobacterium Synechococcus elongatus, the rhythm of growth during the free-running condition of continuous light is approx. 25 h (i.e. within the range of period of the major lunisolar rhythm) and where the natural asynchrony of rhythms in simultaneously replicated cultures can be out of phase by approx. 7–8 h (i.e. the period of a lunisolar harmonic) (Mihalcescu et al., 2004).

Testing the model in higher plants might involve mutants in which mechanosensing is compromised (Haswell et al., 2008) or, alternatively, employ experimental manipulation of osmoregulation of turgor and growth. For example, the positions and movements of the non-articulated leaves of Arabidopsis can be altered by waterlogging the roots (Polko et al., 2013; Rauf et al., 2013) and, in species with articulated leaves, mutations exist which disturb the development of the pulvinus (Zhou et al., 2012). Adjustments to internal and external potassium levels, for example, may also give leads to other details of leaf-movement control in response to environmental conditions (Tavlos et al., 2008).

A lunisolar clock, in which the zeitgeber is exogenous and independent of metabolism, has been suggested as lying within a category of ‘primal’ phenomena (Barlow, 2012). By contrast, many other clocks are derived clocks; they are endogenous and adhere to, and are re-set by, metabolic zeitgebers (Moore-Ede et al., 1982). And with respect to what is primary or derived amongst clock phenomena, it was proposed by Lewis and Lobban (1957), on the basis of a study of physiological rhythms in humans, that there could be a range of clocks which vary in the degree to which they can be entrained by the external environment. Heart rate, for example, was found to manifest an extremely plastic rhythm, easily affected by the environment. By contrast, rhythms of excretion of K⁺, and to a lesser extent water and Cl⁻, were invariant, and held to an exact 24-h rhythm, despite attempts at entrainment. It is interesting to note that these materials, K⁺, Cl⁻ and water, are also those whose movements in and out of cells are modulated during the leaf movement cycles of plants. Further evidence for the primary nature of the lunar clock comes from the finding, based on data from 2 years of continual observation, that a deep-seated lunisolar rhythmic component relates to the amplitude of daily activity patterns of hamsters (Brown and Park, 1967). Several other observations point in the same direction (Barlow, 2012), including the observation that a 24- to 26-h rhythm of eclosion of Drosophila larvae was able to persist, without variation, for 600 generations in a population of flies kept in complete darkness (Sheeba et al., 1999). Other observations suggest that many circadian rhythms tend to desynchronization in the absence of a zeitgeber (Bünning, 1973; Moore-Ede et al., 1982). The continual tracking of a lunisolar tidal rhythm with its 24- to 26-h period seems a possible explanation for long-lived biological rhythm, such as the Drosophila and hamster examples. Similarly, recent work with the marine isopod Eurydice pulchra, whose circadian and circatidal rhythms have been extensively studied, indicates that these two rhythms are distinguishable through environmental, genetic and pharmacological manipulations (Zhang et al., 2013). The circatidal rhythm, analogous to the proposed leaftide rhythm, was found to be autonomous, independent of temperature, and also functionally independent of the circadian rhythm. The recognition of an autonomous circatidal zeitgeber, putatively identified as the lunisolar tidal force, could lead a new class of chronobiological experimentation.

The primal nature of the lunisolar clock allows both animal and plant organisms to continue to express rhythmic patterns of behaviour under conditions where light is absent, such as during long-term cloud cover, whereby the organism would be denied necessary vital cues for survival. It might be presumed that a lunar clock should be of ancient origin, manifesting as a ‘tidal’ movement of water in and out of the cells and tissues of early living forms. Then, by an ‘efficacious coincidence’ (Alexander, 2005), the primary phenomenon of the lunisolar-driven tidal period became internalized within a structure such as the petiole, hence conferring the possibility for leaf movement to be regulated by the periodic movement of water within its tissues. It is by such apparently chance events that innovations develop in living forms.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Data S1: details of Etide, Marine tide and Earthtide. Data S2: relationships between Sun, Moon and Etide. Data S3: pictures of Gerrit Brouwer, Anthonia Kleinhoonte and Rose Stoppel. Data S4: alternative timings of leaf movement at Akureyri, Iceland. Data S5: Etide during the lunar month. Data S6: lunar timekeeping and leaf movements. Data S7: details of experimental work with excised leaves.