Time-Dependent Predictive Accuracy in the Presence of Competing Risks

Summary

Competing risks arise naturally in time-to-event studies. In this article, we propose time-dependent accuracy measures for a marker when we have censored survival times and competing risks. Time-dependent versions of sensitivity or true positive (TP) fraction naturally correspond to consideration of either cumulative (or prevalent) cases that accrue over a fixed time period, or alternatively to incident cases that are observed among event-free subjects at any select time. Time-dependent (dynamic) specificity (1–false positive (FP)) can be based on the marker distribution among event-free subjects. We extend these definitions to incorporate cause of failure for competing risks outcomes. The proposed estimation for cause-specific cumulative TP/dynamic FP is based on the nearest neighbor estimation of bivariate distribution function of the marker and the event time. On the other hand, incident TP/dynamic FP can be estimated using a possibly nonproportional hazards Cox model for the cause-specific hazards and riskset reweighting of the marker distribution. The proposed methods extend the time-dependent predictive accuracy measures of Heagerty, Lumley, and Pepe.

1. Introduction

The general objective of a prognostic survival model is “to relate the descriptive characteristics of the patients at a given time—e.g., time of diagnosis or inclusion into a randomized clinical trial—with the occurrence of a well-defined endpoint, e.g., death in the subsequent follow-up period” (Christensen, 2004). For example, in breast cancer research a 70-gene signature has been identified that can distinguish among patients with different 10-year survival outcomes (Buyse et al., 2006). In studies of ovarian cancer, biomarkers have been identified to predict 5-year progression-free survival (Zheng et al. 2007). Predicting the time until an event like death or cancer diagnosis based on a set of covariates or markers is important in medicine because the predicted risk can help guide the choice of therapeutic decisions that are targeted at those subjects with the greatest risk of progression. Furthermore, time-to-event prediction also has a significant role in disease screening programs because it is hoped that early diagnosis can help reduce mortality and morbidity. Thus, in numerous medical applications, the development of an accurate model for the prediction of a future clinical event is a primary goal that can ultimately be used to guide medical management or the choice and timing of interventions.

In studies with time-to-event outcomes, we are usually interested in a single primary type of “failure” time such as death or disease progression, and for each individual we observe a possibly censored univariate outcome. However, frequently the event time for a subject can be classified as one of several distinct types or causes and substantive interest may focus on events of a specific type. For example, in cardiovascular studies subjects may experience one or more of the following outcomes: coronary heart disease, myocardial infarction, stroke or congestive heart failure, and death (Arnold et al., 2005). In breast cancer studies such as Buyse et al. (2006), distant metastases are important events; however, many other clinical event times may preclude the researcher from observing distant metastases for a particular patient. In such a competing risks setting, a major biomedical goal may be to accurately predict those subjects who progress to a specific clinically significant event, and in this case the competing events must be considered in the choice of inferential target.

Development of predictive survival models naturally leads to questions such as: how well can the model predict the event time, or, how well can the model distinguish between those subjects who experience the event in the next 5 years (cases) from those subjects who are event free for 5 years (controls)? Statistical methods that can summarize the accuracy of a predictive survival model have been developed and largely have progressed in two parallel directions. Because censored survival data share features of both continuous and binary data, the extension of predictive accuracy methods from either of these approaches is possible. Extension of the methods for continuous data has been proposed that includes a generalized proportion of variation summary (Schemper and Henderson, 2000), and a Brier score approach that measures the distance between the observed time-dependent survival status, and predicted probability of the status (Gerds and Schumacher, 2006; Schoop, Graf, and Schumacher, 2008). A second approach stems from looking at the time-to-event process from a binary data perspective (e.g., vital status at time t) and extending the standard binary classification accuracy measures like sensitivity, specificity, and receiver operating characteristics (ROC) curves (Heagerty, Lumley, and Pepe, 2000; Heagerty and Zheng, 2005). Time-dependent ROC methods classify the subjects as cases or controls depending on their time-dependent survival status and compare their observed vital status with a predicted risk at some or all times. Because these methods are based on classifying subjects into different time-dependent outcome groups, the presence of competing risks can easily be accommodated using a finer partition of the “case” subjects based on their specific cause and time of failure. On the other hand, methods motivated by measuring the proportion of explained variation (R²) are typically built upon consideration of the event time, T_i, or its counting process representation, $N_i(t)=1(T_i^{*}\le t,{\delta }_i=1)$, where $T_i^{*}$ is the follow-up time, and δ_i is a censoring indicator. In the presence of competing risks the outcome of interest cannot be represented by an underlying single cause-specific event time without invoking latent outcome concepts, and potentially shifting focus to scenarios where competing events are considered not to operate (Kalbfleisch and Prentice, 2002). In addition, statistical methods that depend on the principle of redistributing the information from the censored observations “to the right” (Gooley et al., 1999) may not be easily extended when there is more than one cause of failure.

Current methods for the estimation of time-dependent sensitivity and specificity do not consider competing risk events and have only been developed for standard univariate event-time settings. In this article, we propose new cause-specific accuracy summaries and outline appropriate estimation methods that naturally extend existing approaches, and which can meaningfully accommodate competing causes of failure. In the next section, we introduce the notation and set the background for competing risk analysis. The existing time-dependent accuracy methodology is reviewed in Section 3. In Section 4, we discuss the extension of these methods for events with competing risks. In Section 5, we analyze the Multicenter AIDS Cohort Study (MACS) dataset. Finally we conclude with a brief discussion.

2. Background: Competing Risks

2.1 Notation

In this section, we establish notation and provide general background on competing risks. Let T_i denote the event time for subject i, i = 1, 2, …, n. We assume that a single event time T_i can be classified into J mutually exclusive types or causes of failure, j = 1, 2, …, J and we may be interested in one or more specific cause. When T_i is the time of death we may be interested in specific causes of death such as death due to a specific disease. In other settings we consider T_i to be the first event type that is observed, where a common interest is in using T_i to denote either disease progression or death (whichever is observed first). Let δ_i = j denote that subject i experienced a competing event of type j. Let C_i denote the censoring time for subject i.We assume independence of T_i and C_i, and we assume that we observe the follow-up time, Z_i = min{T_i, C_i}. A censored observation has Z_i = C_i and this is recorded by using δ_i = 0. Thus the observed outcome data consist of (Z_i, δ_i) and this codes what cause-specific event was observed at time Z_i or indicates that a subject was censored at time Z_i. For example, we will illustrate methods using the MACS data where subjects are followed from the time they are observed to seroconvert until the time of progression to AIDS or death. In this example the outcome (Z_i = 36, δ_i = 1) will denote a subject observed to progress to AIDS (e.g., δ_i = 1) at 36 months, while (Z_i = 36, δ_i = 2) will denote a subject observed to die at 36 months prior to progressing to AIDS. To summarize the cause-specific incidence of an event of type j we will adopt standard summaries used in the analysis of competing risks. We denote n_j(t) to be the number of subjects who had an event from cause j at time t. Next, λ_j(t) will denote the cause-specific hazard of event type j. Let R_i(t) = 1 if subject i is still at risk at time t and 0 otherwise and let ℝ_t denote the number of subjects who are at risk at t or the size of the riskset at t. We will use M_i to denote the (baseline) marker for subject i while for a time-dependent marker we use M_i(t). Higher marker values are assumed to be more indicative of disease. We seek to quantify the predictive accuracy of the marker M to distinguish between the subjects who would experience an event of interest versus those who would not.

2.2 Cumulative Incidence

For standard survival data the Kaplan–Meier (KM) product limit estimator is used to estimate the underlying population distribution of event times. In this situation there is a single event type such as death, and KM methods account for the censored observations in a nonparametric fashion. In competing risks situations the event time T_i may be a mixture of cause-specific event times of more than one type, or may be the composite endpoint which is the first time that one of several clinical endpoints are observed. In either situation it is less clear that a single one-sample summary of event times is a meaningful concept.

One mathematical representation of competing risks data uses underlying latent variables $T_i^{(1)},T_i^{(2)},\dots ,T_i^{(J)}$ to denote the J specific cause-specific event times. In this representation $T_i^{(1)}$ may be the time of death due to breast cancer for subject i, while $T_i^{(2)}$ represents the time of death due to all other causes (e.g., J = 2). In this formulation only one death time is observed and T_i is assumed to be the minimum of cause-specific times $T_i^{(j)}$. One generalization of the survival curve, S(t) = P(T_i > t) uses the marginal survivor function of latent failure times $S^{(j)}(t)=P(T_i^{(j)}>t)$ but these summaries implicitly remove all other causes. We refer the reader to Kalbfleisch and Prentice (2002), Section 8.2.4 for a full discussion of issues associated with the use of marginal survivor functions. Naive use of KM methods to estimate cause-specific survival curves illustrate some of the issues. Under the assumption of noninformative censoring it is assumed that the subjects censored at time t, had they been continued to be observed, would experience the same conditional risk of failure after t as those subjects who are still at risk at time t. Thus in KM methods the probability mass for censored subjects is “distributed to the right” to the subjects who are present in the riskset at time t (Gooley et al., 1999). When there is more than one cause of failure and a subject dies at t due to a competing cause, he is no longer at risk of death due to any other cause and his share of risk should not be distributed to the other subjects who are present in the riskset beyond t. If, however, these subjects are treated as censored, the censoring mechanism no longer remains uninformative and thus KM estimator of survival probability is not appropriate and estimates a hypothetical distribution of cause-specific event times after removing other competing risks.

An alternative summary that is used for competing risks data is the cumulative incidence function (CIF) and this simply characterizes the fraction of the population that experiences cause-specific events of type j by time t:

$$C_j(t)=P(T\le t,\delta =j);j=1,2,\dots ,J.$$

For each j these functions are increasing functions of t but they do not necessarily approach 1.0 in the limit. In general we may assume that each subject ultimately experiences an event implying

$$\underset{t\to \infty }{\text{lim}}\sum _{j=1}^J{C}_j(t)=1.0.$$

There are standard methods for handling censored observations in the estimation of cause-specific CIFs. The censored subjects and those experiencing competing risk events are treated differently; the subjects censored before t are assumed to have the same risk of failure after t had they been observed as the ones who are still at risk beyond t and under observation, but deaths from other causes (δ_i ≠ j) are not treated as censored—rather these are cases that are known to not contribute to cause-specific cumulative incidence of type j. However, we note that cause-specific hazard can be estimated by treating events due to other causes of failure as censored.

3. Background: Time-Dependent ROC Curves

In this section, we give an overview of key extensions of classification error concepts that have been proposed for survival endpoints. In particular, we discuss time-dependent versions of sensitivity and specificity that naturally correspond to consideration of cumulative (or prevalent) cases that accrue over a fixed time period, and alternatively to incident cases that are observed for any select time.

3.1 Cumulative Cases/Dynamic Controls

Cumulative cases (ℂ) and dynamic control (𝔻) definitions are appropriate when we want to evaluate the prediction accuracy of a marker measured at baseline to distinguish between the subjects who have an event before time t from those who do not. Thus, cases are defined as subjects with T_i ≤ t and controls are those with T_i > t. Such definitions are particularly relevant in biomedical scenarios where available measurements are used to identify those subjects who are at “high risk” and for whom intervention is warranted. In this situation classification error concepts would correspond to sensitivity defined as the probability of a high marker value (positive test) among those subjects who experience the event in T ∈ (0, t] (cases), and specificity defined as the probability of a low marker value (negative test) among subjects who are event free through time t (controls). We adopt the following definition of true positive (TP or sensitivity), false positive (FP or 1–specificity), and ROC curve:

$$\mathrm{T}{\mathrm{P}}_t^{ℂ}(c)=P(M_i>c|T_i\le t)\mathrm{F}{\mathrm{P}}_t^{𝔻}(c)=P(M_i>c|T_i>t)\mathrm{R}\mathrm{O}{\mathrm{C}}_t^{ℂ/𝔻}(p)=\mathrm{T}{\mathrm{P}}_t^{ℂ}\{{\left[\mathrm{F}{\mathrm{P}}_t^{𝔻}\right]}^{-1}(p)\}.$$

In the absence of censoring, the case status, T_i < t, can be determined for all subjects at any time t, but when follow-up is incomplete the censoring of T_i can be accommodated through nonparametric estimation methods based on the nearest neighbor estimator (NNE) for the bivariate distribution function of (M, T). For details about the method, see Heagerty et al. (2000). Estimation of $\mathrm{R}\mathrm{O}{\mathrm{C}}_t^{ℂ/𝔻}(p)$ is implemented in the R package survivalROC, which is publicly available from The Comprehensive R Archive Network (CRAN).

3.2 Incident Cases/Dynamic Controls

An alternative classification scenario arises when scientific interest focuses on correct classification of subjects at time t among those who are still at risk. For example, baseline or time-dependent data may be available through time t and a therapeutic decision focuses on identifying and treating those subjects who are still alive, but likely to fail in the near future. Here we focus on the incident events (𝕀) at time t and can characterize the sequence of predictions or classifications that occur over time among members of the risksets at times t₁, t₂, …, t_K, or continually for any time t. Thus, cases at time t are those with T_i = t (incident or 𝕀) and controls are those with T_i > t (dynamic or 𝔻). We adopt the following definition of TP, FP, and ROC curve:

$$\mathrm{T}{\mathrm{P}}_t^{𝕀}(c)=P(M_i>c|T_i=t)\mathrm{F}{\mathrm{P}}_t^{𝔻}(c)=P(M_i>c|T_i>t)\mathrm{R}\mathrm{O}{\mathrm{C}}_t^{𝕀/𝔻}(p)=\mathrm{T}{\mathrm{P}}_t^{𝕀}\{{\left[\mathrm{F}{\mathrm{P}}_t^{𝔻}\right]}^{-1}(p)\}.$$

Estimation with censored observations can be based on Cox model methods using associated riskset reweighting based on the estimated hazard in order to estimate $\mathrm{T}{\mathrm{P}}_t^{𝕀}(c)$. For details, see, Heagerty and Zheng (2005). Estimation of $\mathrm{R}\mathrm{O}{\mathrm{C}}_t^{𝕀/𝔻}(p)$ and the associated area under the curve function, AUC(t), is implemented in the R package risksetROC.

4. Time-Dependent ROC Curves with Competing Risks

Prospective accuracy methods discussed above do not account for more than one cause of failure. However, natural modifications to both approaches are possible that permit incorporation of competing risk outcomes. In this section, we will consider extensions of the ℂ/𝔻 and 𝕀/𝔻 ROC curve methods—introducing both a conceptual framework for the classification of interest, and then providing details on estimation methods that can accommodate censored observations.

4.1 C/D ROC and Competing Risks

For simplicity we consider an event time, T_i, and two distinct causes of failure: δ_i = 1, 2. To generalize the ℂ/𝔻 ideas, we will consider a single (common) dynamic control group, because controls are free of any event. On the other hand, cases may accrue due to either of the two event types, and we stratify the cases according to the event type they experience through time t:

$$\text{Case}1:T\le t,\delta =1\text{Case}2:T\le t,\delta =2\text{Control}:T>t.$$

These are the three mutually exclusive groups that we could form on the basis of cumulative events through time t. For a given marker M, we then consider the following TP and FP classification rates:

$$\mathrm{T}{\mathrm{P}}_1^{ℂ}(c,t)=P(M>c|T\le t,\delta =1)\mathrm{T}{\mathrm{P}}_2^{ℂ}(c,t)=P(M>c|T\le t,\delta =2)\mathrm{F}{\mathrm{P}}^{𝔻}(c,t)=P(M>c|T>t,\delta =[1,2]).$$

We modify the notations of TP and FP to introduce the time of interest t as the second argument and use subscript to denote the cause of failure. In general, when J competing causes of failure exist, we define cause-specific TP and common FP as:

$$\mathrm{T}{\mathrm{P}}_j^{ℂ}(c,t)=P(M>c|T\le t,\delta =j),j=1,2,\dots ,J\mathrm{F}{\mathrm{P}}^{𝔻}(c,t)=P(M>c|T>t,\delta =[1,2,\dots ,J]).$$

An ROC curve for each event type can be obtained by plotting the cause-specific TP versus the common FP. These ROC curves measure the predictive accuracy of the marker M to distinguish among subjects who experience the particular type of competing risk events by time t and those who do not experience any type of event by time t. A marker that is selected to seek the subjects who are likely to die due to breast cancer is expected to have a high sensitivity to detect these cases, while it may be less sensitive at identifying those subjects who die from other causes. Such a cause-specific prognostic marker would be reflected by a higher ROC curve for breast cancer deaths as compared to the ROC curve for deaths due to other causes.

4.2 I/D ROC and Competing Risks

Again, consider an event time, T_i, and two distinct causes of failure, δ_i = 1, 2. To generalize the 𝕀/𝔻 ideas we will also consider a single (common) control group, but consider the two types of incident cases associated with each cause of failure for a choice of classification time, t:

$$\text{Case}1:T=t,\delta =1\text{Case}2:T=t,\delta =2\text{Control}:T>t.$$

These are the three mutually exclusive groups that we could form on the basis of events at time t among those subjects still at risk for an event at time t. For a given marker M, we then consider the following TP and FP classification rates:

$$\mathrm{T}{\mathrm{P}}_1^{𝕀}(c,t)=P(M>c|T=t,\delta =1)\mathrm{T}{\mathrm{P}}_2^{𝕀}(c,t)=P(M>c|T=t,\delta =2)\mathrm{F}{\mathrm{P}}^{𝔻}(c,t)=P(M>c|T>t,\delta =[1,2]).$$

ROC curves for each type of event can be obtained by plotting the pair of TP rates versus the common FP rate. These curves address the issue of the predictive accuracy of the marker M to distinguish between those subjects who experience event of type 1 (type 2) at time t and those subjects who do not experience any event by time t. Again, a marker selected to indicate the subjects who are likely to die due to breast cancer at t would ideally have high sensitivity to detect these cases, while the marker may not separate the controls and subjects who die from other causes.

Because 𝕀/𝔻 methods are naturally related to the classification of riskset members into incident cases and current controls, we can easily extend the TP and FP definitions to allow evaluation of a time-dependent marker. For all-cause mortality, we define

$$T{P}^{𝕀}(c,t)=P[M_i(t)>c|T_i=t]F{P}^{𝔻}(c,t)=P[M_i(t)>c|T_i>t]$$

and then use $T{P}_j^{𝕀}(c,t)=P[M_i(t)>c|T_i=t,{\delta }_i=j]$ for cause-specific analysis.

Note that for application with a time-dependent marker we only focus on the ability of M_i(t) to discriminate in an “instantaneous” fashion through separation of the current riskset into incident cases and controls. As such we do not attempt to characterize the marker’s ability to forecast future survival. Issues associated with use of time-dependent markers for such residual lifetime estimation are discussed by Jewell and Nielsen (1993), and extension of time-dependent ROC curve estimation to this setting has been considered by Zheng and Heagerty (2007).

4.3 Estimation

Existing methods proposed for estimation of prospective predictive accuracy (Heagerty et al., 2000; Heagerty and Zheng, 2005) do not address the issue of more than one cause of failure. However, natural modifications to these methods allow estimation of accuracy in the presence of more than one event type. In this section, we outline methods for estimation of cause-specific time-dependent ROC curves in the presence of censoring. Note that, for the ℂ/𝔻 ROC curves, we consider a time-independent covariate, whereas for the 𝕀/𝔻 ROC curves, we also consider the case of time-dependent covariates.

4.3.1 C/D ROC curves

With censored event times, the NNE for the bivariate distribution function of the marker M and the event time T was used to estimate the TP and FP (Heagerty et al., 2000). This estimation method can be modified to accommodate competing risk events. Instead of the bivariate distribution function of marker and time, we use the cumulative incidence associated with each cause of failure. We use weighted conditional CIF to estimate the TP

$$T{P}_1^{ℂ}(c,t)=\frac{P(M>c,T\le t,\delta =1)}{P(T\le t,\delta =1)}=\frac{{\int }_c^{\infty }{C}_1(t|M=u)g_M(u)du}{{\int }_{-\infty }^{\infty }{C}_1(t|M=u)g_M(u)du}$$

where g_M (.) denotes the probability density function of the marker. The CIF is estimated as

$${\widehat{C}}_j(t|M=M_i)=\sum _{s<t}{\widehat{S}}_{{\epsilon }_n}(s|M=M_i){\widehat{\lambda }}_j(s|M=M_i)$$ (1)

based on the locally weighted KM estimator

$${\widehat{S}}_{{\epsilon }_n}(t|M=M_i)=\prod _{s\in {𝒯}_n,s\le t}\{1-\frac{\sum _k{K}_{{\epsilon }_n}(M_k,M_i)\mathrm{𝟙}(Z_k=s){\delta }_k}{\sum _k{K}_{{\epsilon }_n}(M_k,M_i)\mathrm{𝟙}(Z_k\ge s)}\}$$

and the observed hazard for event type j at time t,

$${\widehat{\lambda }}_j(s|M=M_i)=\frac{\sum _k\mathrm{𝟙}\{T_k=s,{\delta }_k=j,M_k\in (M_i-{\epsilon }_n,M_i+{\epsilon }_n)\}}{\sum _k\mathrm{𝟙}\{T_k\ge s,M_k\in (M_i-{\epsilon }_n,M_i+{\epsilon }_n)\}}.$$

Here, K_εn (M_j, M_i) = 𝟙{−ε_n ≤ Ĝ_M (M_i) − Ĝ_M (M_j) ≤ ε_n} is a nearest neighbor kernel with 2ε_n ∈ (0, 1) representing the proportion of observations that are included in each neighborhood (except for the boundaries) of the marker distribution, and 𝒯_n represents the unique observed event times for the event type of interest. Finally, Ĝ_M is the empirical marker distribution function and 𝟙(.) denotes the indicator function.

To estimate the FP fraction among the controls, we note that

$$F{P}^{𝔻}(c,t)=\frac{P(M>c,T>t)}{P(T>t)}=\frac{{\int }_c^{\infty }P(T>t,M=u)du}{{\int }_{-\infty }^{\infty }P(T>t,M=u)du}=\frac{{\int }_c^{\infty }P(T>t|M=u)g_M(u)du}{{\int }_{-\infty }^{\infty }P(T>t|M=u)g_M(u)du}$$

and exploit the following relationship:

$$P(T>t|M=m)=1-\sum _{j}P(T\le t,\delta =j|M=m)=1-\sum _j{C}_j(t|M=m).$$ (2)

Although we could directly use the FP estimator from Heagerty et al. (2000) to estimate the marker distribution among controls (FP function) we keep the control estimate coupled to the subcase estimates and use CIF conditional on marker for estimation of both TP and FP. Akritas (1994) showed that the NNE is a semiparametric efficient estimator. The local CIF given in equation (1) along with the empirical distribution of the marker provide consistent estimators of cause-specific TP and common FP. Additional details can be found in the Appendix.

For the NNE approach for estimation of the cause-specific ℂ/𝔻 ROC, we note that Akritas (1994) presents bounds on the sequence of smoothing parameters ε_n that are sufficient to yield weak consistency of the bivariate distribution function estimator. Using ε_n = O(n^−1/3) satisfies these conditions and can be used to guide the choice of ε_n in practice. The resulting estimators are consistent. The estimation only requires conditional independence between T and C given the marker, and hence the censoring process is allowed to depend on the marker.

4.3.2 I/D ROC curves

When only one cause of failure exists, the incident cause-specific TP can be estimated using a possibly nonproportional hazards Cox model for the cause-specific hazards. Heagerty and Zheng (2005) show that P(M_i > c | T_i = t) can be estimated using a reweighting of the marker distribution observed among the riskset at time t. Such riskset reweighting can also be used with competing risks data.

To illustrate estimation, we first assume a proportional hazard model for the event of type 1: λ₁(t | M_i) = λ_0,1(t) exp(M_iγ₁) with λ_0,1(t) as baseline hazard. Here γ₁ is the cause-specific hazard for event of type 1 associated with the marker and can be estimated using the Maximum Partial Likelihood Estimation (MPLE) by censoring all other causes of failure. The TP can be estimated as:

$${\widehat{TP}}_1^{𝕀}(c,t)=\widehat{P}(M>c|T=t,\delta =1)=\sum _k\mathrm{𝟙}(M_k>c)\times {\pi }_k^1({\widehat{\gamma }}_1,t)$$ (3)

where ${\pi }_k^1({\gamma }_1,t)=R_k(t)\text{exp}(M_k{\gamma }_1)/W(t),\text{with}W(t)={\sum }_k{R}_k(t)\text{exp}(M_k{\gamma }_1)$. Under a nonproportional hazard model λ₁(t | M_i) = λ_0,1(t)exp[M_iγ₁(t)], we simply use an estimate of the time-varying hazard γ₁(t).

The estimation of FP is straightforward using the empirical distribution function of the marker among the subjects who remain event free at time t:

$$P(M>c|T>t)\stackrel{\wedge}{=}\frac{\sum _i\mathrm{𝟙}\{M_i>c,T_i>t\}}{\sum _i\mathrm{𝟙}\{T_i>t\}}.$$ (4)

Details are presented in the Appendix.

For a time-dependent marker, M_i(t), once an estimate of the cause-specific hazard is available from the time-dependent hazard model λ₁[t | M(t)] = λ_0,1(t)exp[M(t)γ₁(t)], the estimation of the ROC curve would proceed by using equation (3) and simply replacing M_i with M_i(t). Standard use of partial likelihood is valid with time-dependent markers (see Sections 6.3 and 6.4 of Kalbfleisch and Prentice, 2002). Therefore, a key feature of 𝕀/𝔻 ROC estimation is that adoption of the instantaneous definition of sensitivity given in Section 4.2 allows characterization of the accuracy of time-dependent markers without attempting to estimate future survival beyond time t. Jewell and Nielsen (1993) discuss the challenges associated with use of a time-dependent marker and estimation of conditional survival curves or “residual lifetime”.

Note that, for the TP, the conditional distribution of M given T = t, δ = j is consistently estimated by equation (3) provided the hazard model obtains for the event of interest (Xu and O’Quigley, 2000). The FP is an empirical distribution function resulting in a consistent estimator for the ROC curve.

For a varying coefficient hazard model the incident sensitivity needs to be estimated either via simple methods such as direct smoothing of Schoenfeld residuals or via more formal local linear Cox regression. Cai and Sun (2003) showed that the theoretical optimal bandwidth (in terms of integrated mean squared error) for estimation of γ₁(t), is proportional to n^−1/5.

The bandwidth h_opt is of the form:

$$h_{\text{opt}}={\left\{\frac{{\upsilon }_0\int \sigma (t)w(t)dt}{{\mu }_2^2\int {[{\gamma }_1^{″}(t)]}^{2}w(t)dt}\right\}}^{-1/5}{n}^{-1/5}$$

where v₀ = ∫ K²(u) du, μ² = ∫ u²K (u) du, $\sigma (t)=Q_2(t)-Q_1^2(t)/Q_0(t)$ with Q_k(t) = E[P[t | M(t)]λ(t | M(t))M^k(t)], k = 0, 1, 2 P[t | m] = P[T ≥ t | M(t) = m]. Finally, w(.) denotes a nonnegative and integrable weight function, K(.) denotes the kernel that is used for smoothing the hazard coefficient γ₁(t), with ${\gamma }_1^{″}(t)$ denoting the second derivative of the hazard coefficient γ₁(t). If we express the optimal bandwidth as h_opt= C · n^−1/5, then the proportionality constant depends on unknown quantities like σ(t) and ${\gamma }_1^{″}(t)$, and hence we propose the following approach to approximate the optimal bandwidth. First, we choose an initial bandwidth and use this to estimate the second derivative ${\gamma }_1^{″}(t)$. Second, as suggested by Scheike and Martinussen (2004), we estimate the variance σ(t) using a robust variance estimator. Finally with the estimates of the needed quantities we can approximate the optimal bandwidth, h_opt. Although this procedure is a common practical solution for bandwidth selection, care is needed in selecting the initial bandwidth (Scheike and Martinussen, 2004). Therefore, sensitivity of final estimates should be evaluated using different initial bandwidth values that are used to determine the optimal bandwidth.

The bias associated with this optimal bandwidth at an interior point t is given simply by $h_{\text{opt}}^2/2{\mu }_2{\gamma }_1^{″}(t)$ with μ₂ = 0.2 for an Epanechnikov kernel as was used for this presentation. Note that the bias involves the second derivative of the hazard coefficient function and can be large where the curvature of this function is large. Hence, the coverage of empirical confidence interval may be less than the nominal coverage. However, in a nonparametric setting, Dikta (1990) showed that up to this bias term, a type of pointwise bootstrap confidence interval is asymptotically correct. We suggest the following two ways to adjust for this bias. The first approach undersmooths such that the variance dominates the bias and this can be accomplished by use of a smaller bandwidth, for example, one that is proportional to n^−1/4 instead of n^−1/5 as in the optimal bandwidth. Alternatively, we can estimate the bias associated with the use of the optimal bandwidth and then adjust the confidence intervals to account for the bias and therefore obtain proper coverage. Nevertheless, Cai and Sun (2003) show that local-linear estimation leads to a consistent and asymptotically normal estimator of the parameter γ₁(t). Because the cause-specific TP rate is based on use of exp[M_iγ̂₁(t)] to reweight the marker distribution among subjects who are at risk at time t, the consistency of γ̂₁(t) combined with a consistent estimate of the marker distribution leads to a consistent estimate of cause-specific TP.

4.4 Simulation Study

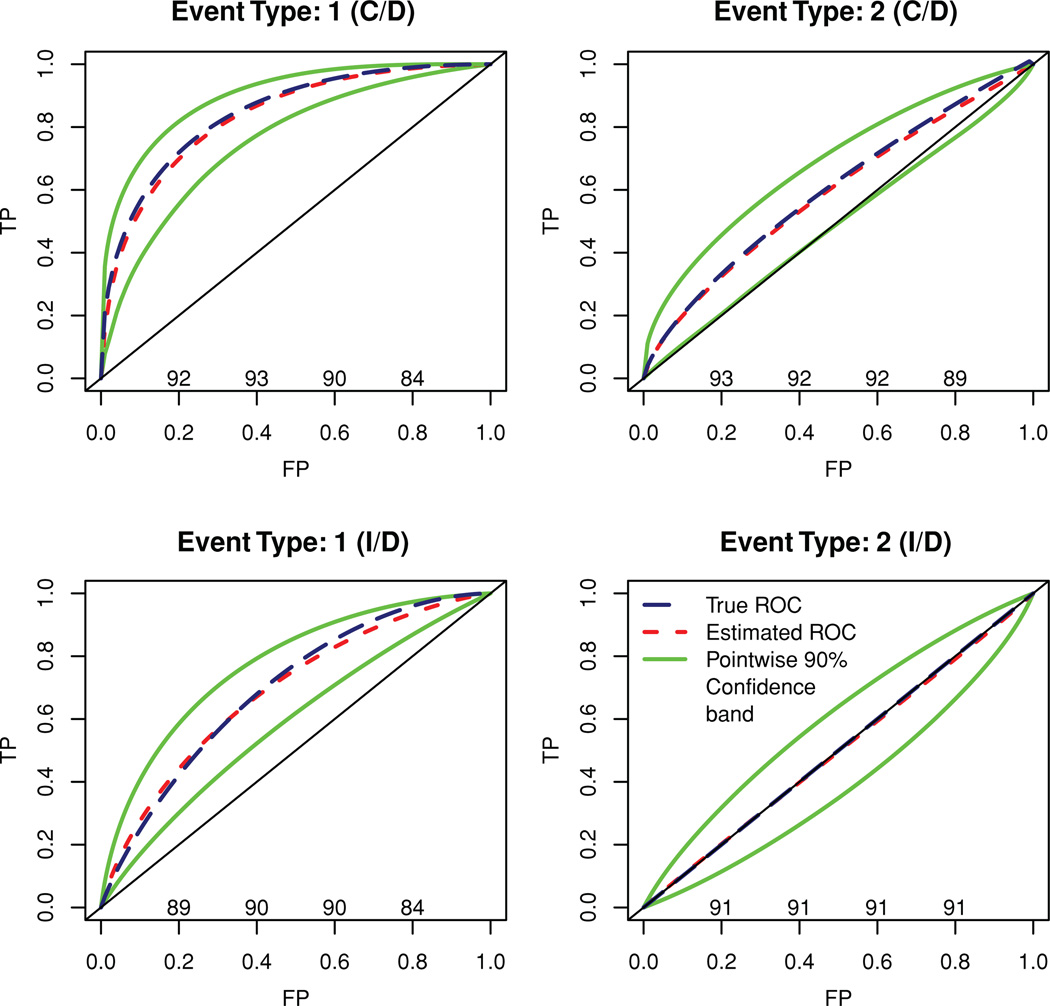
To demonstrate the validity of the competing risks ROC methods introduced here and the applicability of bootstrap for confidence band estimation for the ROC curve (ℂ/𝔻 and 𝕀/𝔻) and AUC curve (𝕀/𝔻), we conducted a set of simulation studies. We assumed two causes of failure and a single marker that was correlated with one of the causes but not with the other. Suppose T₁ denotes the (log) time until failure due to the cause of interest and T₂ denotes the (log) time until failure due to a competing cause while M denotes the marker. We assumed a bivariate normal distribution for (T₁, M) with correlation ρ = −0.7 and an independent standard normal distribution for T₂. Further, an independent normal (log) censoring time was assumed, such that 20% subjects were censored. Note that, because M and T₂ were independent, $T{P}_2^{𝕀}(c,t)=F{P}^{𝔻}(c,t)$, and hence the 𝕀/𝔻 ROC curve for the competing cause of failure lies diagonally on the null ROC curve. However, the same is not true for the induced ℂ/𝔻 ROC curve for the competing cause of failure (see Figure 1 for illustration).

Figure 1.

Bootstrapped ROC curves, confidence bands, and coverage (nominal level—90%). This figure appears in color in the electronic version of this article.

For each of m = 500 simulated datasets, a sample of n = 300 outcomes was generated. For each simulated dataset, we performed 200 bootstrap simulations and estimated the ℂ/𝔻 ROC curve at log(T) = 0. The sampling variability of the ROC curve was assessed by the variability of TP at fixed FP = 0.01, 0.02, …, 0.99. The average ROC curve and average 90% confidence limits for each failure type is plotted in Figure 1 along with the coverage probability (×100) at FP values 0.2, 0.4, 0.6, and 0.8. The average of bootstrap mean, SD, and coverage (percentile based: 5th–95th) for the ℂ/𝔻 AUC for both causes of failure can be found in Table 1. The estimates of ℂ/𝔻 AUC for either of the causes had a relative absolute bias of less than 2% and the coverage was also close to the nominal level of 90%.

Table 1.

Average of bootstrap mean, SD, and coverage (percentile-based, nominal level—90%) of AUC

		Cause 1				Cause 2
log(Time)	ΣRi(t)	AUC	Mean	SD	Coverage	AUC	Mean	SD	Coverage
Cumulative/dynamic
0.0	52.8	0.844	0.831	0.0344	89.2	0.601	0.590	0.0476	90.2
Incident/dynamic
−1.5	426.0	0.833	0.815	0.0460	90.0	0.5	0.504	0.0827	90.8
−1.2	374.8	0.802	0.783	0.0504	89.6	0.5	0.503	0.0781	91.2
−0.9	306.7	0.771	0.753	0.0531	89.6	0.5	0.499	0.0756	90.0
−0.6	228.7	0.743	0.727	0.0551	93.4	0.5	0.501	0.0709	86.8
−0.3	151.6	0.716	0.707	0.0569	90.0	0.5	0.494	0.0690	90.2
0.0	87.4	0.693	0.684	0.0580	90.2	0.5	0.496	0.0652	91.4
0.3	43.0	0.672	0.670	0.0598	89.0	0.5	0.505	0.0628	90.4
0.6	17.8	0.654	0.653	0.0599	92.6	0.5	0.496	0.0623	89.2
0.9	6.1	0.639	0.578	0.1195	82.1	0.5	0.471	0.1037	92.0

For the 𝕀/𝔻 method, we simulated m = 500 datasets with a sample of n = 500 and for each simulated dataset 200 bootstrap simulations were performed. The sample size was increased to ensure that the size of the riskset remains moderate at larger follow-up times. For each simulation, we estimated the 𝕀/𝔻 ROC curve and the AUC at log(T) = −1.5,−1.2, …, 0.9 using a time-varying hazard model. In Figure 1 we present the average 𝕀/𝔻 ROC curve for each failure type at log(T) = 0, average 90% confidence bands and coverage probability (×100) at FP values 0.2, 0.4, 0.6, and 0.8. The pointwise confidence band for the AUC curve at log(T) = −1.5,−1.2, …, 0.9 along with average of bootstrapped mean and SD for the estimated AUC curve can be found in Table 1. Note that except for the edges (log(T) > 0.6) where the size of the riskset is small (Σ R_i(t) < 10), the relative absolute bias of the 𝕀/𝔻 AUC estimates is less than 2.5% for cause 1 and less than 1.2% for cause 2. The coverage is also close to the nominal coverage of 90% in most of the cases.

As mentioned earlier, for 𝕀/𝔻 ROC curves, the use of an optimal bandwidth proportional to n^−1/5 for estimation of time-varying hazard γ₁(t) may lead to bias and pose challenges in the construction of bootstrap confidence bands. For 𝕀/𝔻 ROC curves, this bias can be estimated and then a corrected ROC curve can be obtained for each bootstrap sample when computing confidence intervals. For this simulation, we analytically approximated the bias, which ranged from −0.809 · n^−1/5 to 0.053 · n^−1/5 across values of t, and was less than 0.1 in absolute value for n = 500 for the range of time considered. Details can be found in the Appendix. Additionally, we estimated 𝕀/𝔻 ROC curves using the bias-corrected hazard estimate and obtained nearly identical estimates of the ROC curves and of nominal confidence interval coverage.

5. Example

5.1 MACS Data: Description and Scientific Objectives

In this section, we apply methods for cause-specific predictive accuracy to data from the MACS (Kaslow et al., 1987). The study enrolled 5622 homosexual and bisexual men, among them 3426 were sero-negative at baseline and 479 of them became sero-positive between 1984 and 1996. We analyzed a subset of the subjects (N = 438) who became sero-positive and for whom the dates of sero-conversion were known to within ± 4.5 months. These subjects had an average of 13 measurements per person (3807 total observations). We evaluate the ability of percent CD4 lymphocyte (henceforth, CD4) measures as predictors of progression to an AIDS diagnosis, and use the 1987 CDC definition of AIDS, which relies on the symptoms rather than CD4 lymphocyte counts to define AIDS. Under this definition 176 sero-converters developed AIDS during the study period. However, 34 subjects died before the AIDS diagnosis leading to a competing risk situation.

The objective of the present analysis is twofold—first we use reduction in CD4 around sero-conversion as the marker of choice and evaluate its performance to discriminate between subjects who progressed to AIDS by 5 years versus those who were alive by 5 years and did not progress to AIDS. We also look at the predictive ability of this marker to distinguish subjects who would die within 5 years before progressing to AIDS versus those who were alive and AIDS free by 5 years. The cumulative/dynamic approach is used for this analysis based on “baseline” or time-independent marker values of this marker. We also evaluate the performance of a time-dependent marker as a classifier of the riskset subjects into three groups—subjects progressing to AIDS, subjects dying before AIDS, and subjects who were alive and AIDS free—over a period of time using the incident/dynamic approach. Time-dependent CD4 measurements were used for this approach.

5.2 ℂ/𝔻 ROC Analysis Using a Baseline Marker

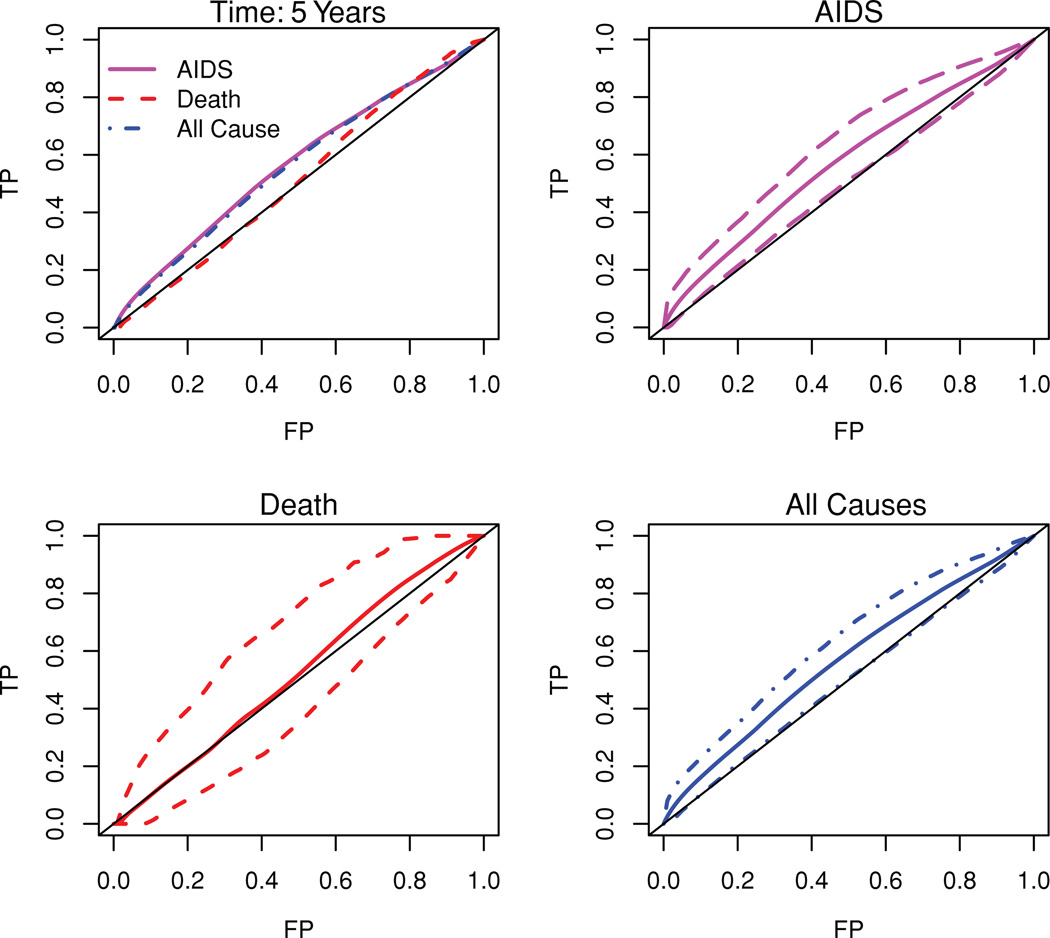
We use the reduction in CD4 associated with sero-conversion as the marker of choice for the ℂ/𝔻 analysis and define the marker as M = first CD4 measurement after sero-conversion minus the last CD4 measurement prior to sero-conversion. A large reduction in CD4 around the time of sero-conversion is expected to be more indicative of a poor prognosis. Note that 65 subjects acquired AIDS and 8 died before AIDS within 5 years of sero-conversion. Figure 2 plots the observed ROC curves for AIDS only (with competing risk adjustment due to deaths), death (with competing risk adjustment due to AIDS), and all causes (considering both AIDS and death as events of interest). The associated observed AUCs are estimated by numerically integrating the ROC curve and are 0.575 (AIDS), 0.552 (death), and 0.573 (all causes). We also plot the average of 500 bootstrapped ROC curves and 95% confidence bounds for AIDS, death, and all-cause failure. The 95% confidence interval for AUC corresponding to AIDS is (0.503, 0.633), for death is (0.411, 0.673), and for all-cause failure the 95% confidence interval for AUC is (0.502, 0.624).

Figure 2.

C/D ROC curves at 5 years after sero-conversion using reduction in CD4 as a time-independent marker. The first figure displays the observed ROCs. The second through last figures display the average of bootstrapped ROC curves and pointwise 95% confidence bounds for AIDS only, death only and all-cause failure. This figure appears in color in the electronic version of this article.

Note that we expect a baseline marker to be less predictive of a death due to other causes, but to be more predictive of AIDS and the ROC curves emphasize the view that the reduction in CD4 around sero-conversion is indeed better, though marginally so, at discriminating between the subjects who would have AIDS by 5 years of sero-conversion and those who would be alive and AIDS free, than distinguishing those who would die before AIDS by 5 years of sero-conversion and those who would not and also remain AIDS free.

5.3 𝕀/𝔻 ROC Analysis Using a Time-Dependent Marker

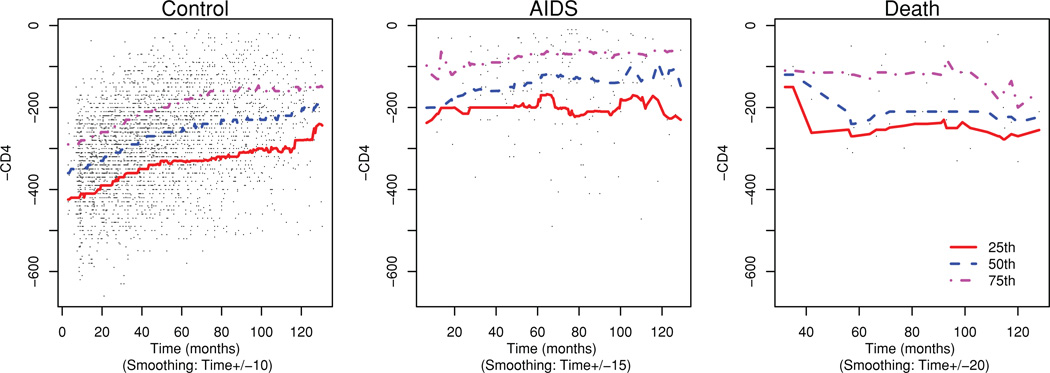
For the 𝕀/𝔻 analysis, we use time-varying CD4 measurement times (−1) as the marker: M(t) = −CD4(t). This is in keeping with the convention that higher marker values are more indicative of a poor prognosis. We display this longitudinal marker and the 25th, 50th, and 75th percentiles for the subjects stratified by their disease status in Figure 3. Note that the median of this marker for the AIDS cases is higher than the controls throughout the time period considered here. Here we try to answer the question of the predictive ability of the marker to distinguish between the controls (alive and AIDS free) and two case groups (subjects progressing to AIDS and subjects dying before AIDS).

Figure 3.

Biannual (−1)·CD4 measurements and the quartiles for sero-converter subjects. This figure appears in color in the electronic version of this article.

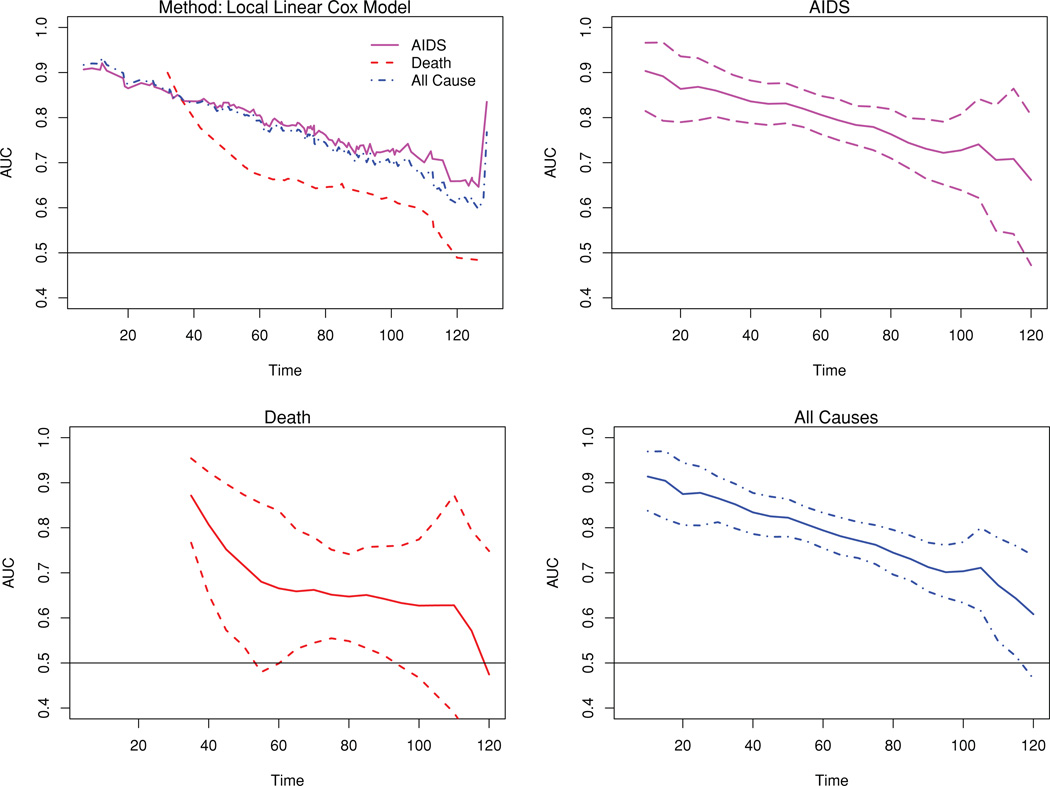
The observed AUC curves for AIDS accounting for competing risk, death accounting for competing risk, and all causes (AIDS or death before AIDS) are plotted in Figure 4. The C-index corresponding to each of these are 0.795, 0.656, and 0.778, respectively, indicating a better discrimination for AIDS than death. The pointwise bootstrap confidence bounds are also plotted separately for each event type of interest and for all-cause failure. The 95% bootstrapped confidence interval for the C-index are (0.759, 0.831) for AIDS, (0.562, 0.762) for death, and (0.744, 0.812) for all-cause failure. We also estimated the ROC curves with bias-corrected hazard estimate and obtained nearly identical results.

Figure 4.

I/D AUC curves using biannual (−1)·CD4 measurements for sero-converter subjects. The first figure displays the observed AUCs. The second through last figures display the average of bootstrapped AUC curves and pointwise 95% confidence bands for AIDS only, death only, and all-cause failure. This figure appears in color in the electronic version of this article.

6. Discussion

In this article, we introduce two methods for analyzing the prospective accuracy of a marker when several causes of failure coexist. In a time-to-event study, at a time t, we can define cumulative cases (ℂ) as those subjects who failed on or before t, or incident cases (𝕀) as those subjects who failed at time t. Controls are the subjects who are event free at t (dynamic or 𝔻). When there is only a single cause of failure, ℂ/𝔻 definitions stratify all the subjects as cases or controls while the 𝕀/𝔻 definition stratifies only the subjects in the riskset. In the presence of competing causes of failures, both cumulative and incident definitions further stratify the cases depending on the cause of failure. We show that two existing statistical methods (Heagerty et al., 2000; Heagerty and Zheng, 2005) can be adapted to account for the competing risk events. We present a nonparametric estimator of ℂ/𝔻 ROC based on local cumulative incidence estimator, which in turn uses an NNE of both the survival function and the local cause-specific hazard function. The 𝕀/𝔻 ROC method that we outline is semiparametric and uses a Cox model for cause-specific hazards to estimate cause-specific TP and uses the empirical proportion for FP. In this case, the estimated cause-specific TP is a weighted average of the empirical distribution function for the marker among the riskset subjects. This way, we incorporate the information from all the riskset subjects rather than using the information from possibly a single incident case. The common FP is the empirical distribution function for marker values among the controls. In this article, we use a marker that may be a single marker or a linear predictor from a model like a proportional hazard model and may be generated from several covariates. We allow the marker generation process to be separate from the ROC curve estimation methodology so that a more flexible model for the marker generation can be used without any modification in the evaluation of accuracy. In general, external validation of a marker is recommended using separate test data. For both accuracy summaries (ℂ/𝔻, 𝕀/𝔻), a single control group is used to estimate the FP rate, resulting in the same comparison group being used for each cause-specific case group. Hence, a comparison of cause-specific ROC curves results in a calibrated comparison of cause-specific sensitivity. The higher this TP rate is for a particular cause of failure, the better the marker is able to distinguish those cases from controls. In our example, the derived marker correctly identifies more AIDS cases than subjects who died prior to development of AIDS, which is what we would expect for such an immune marker. The 𝕀/𝔻 method requires that the event time and censoring time are independent, while this assumption can be relaxed for the ℂ/𝔻 method to allow conditional dependence between the marker and the censoring time.

At any fixed time t, the ℂ/𝔻 approach stratifies the subjects into controls and different groups of cases depending on the cause of failure. Each individual plays the role of control before his/her failure time (t < T_i), but contributes to different case subgroups for later times (t ≥ T_i). This approach is appropriate when we are interested in a small set of times and we want to discriminate between the subjects who would die due to a particular cause versus those who would not. We propose modification of existing methods of marker accuracy to account for the competing risk events that arise frequently in practice. In the presence of competing causes of failure, a meaningful summary is cumulative incidence rather than the survival probability. The proposed nonparametric estimators of cause-specific TP and a common FP are based on a local cumulative incidence estimator that uses an NNE of bivariate distribution of the marker and the event time (Akritas, 1994) and a local empirical cause-specific hazard. Though it is possible to use asymptotic distributions theory for inference, bootstrap techniques can be used alternatively for confidence interval estimation and hypothesis testing. Here, the estimation of ℂ/𝔻 ROC is based on conditional CIF. There are other statistical methods to estimate conditional CIF directly (Scheike, Zhang, and Gerds, 2008) or indirectly via estimation of survival function and cause-specific hazard function (Watson and Leadbetter, 1964; Tanner and Wong, 1983). A comparison of these methods in terms of efficiency and robustness is warranted.

The 𝕀/𝔻 approach stratifies the subjects who are still at risk at time t into a single control group and different case groups. A subject is considered a control at t if t < T_i and is a case at t = T_i. This approach allows inclusion of a time-varying marker M(t) instead of M and is suitable when no particular time is of more interest than the other. Here, we assume that the censoring time and the survival time are marginally independent. Nearest neighbor estimation that allows conditional independence between censoring and event time can be employed to estimate the ROC curve. However, this warrants further investigation. We recommend using the bootstrap for confidence interval estimation and for hypothesis testing. Development of analytical approximations to the large sample distribution for approximate inference also warrants attention.

We also show that the time-dependent markers can be incorporated using an 𝕀/𝔻 ROC curve. If a time-dependent covariate is an internal variable, the estimation of hazard via a Cox model would proceed in the usual way. The estimated hazard is in turn used to reweight the at-risk subjects for estimating TP while the FP is estimated empirically. We emphasize that the ROC methods introduced here can be applied on any scalar predictor and the generation of the predictive score can be separate from the use of the proposed methods for estimation of ROC or AUC curves.

In many applications interest will focus on the accuracy of a model score, or some scalar function of multiple predictor variables. The ROC methods can be adapted for this purpose first by estimating the model score based on the covariates of interest and then evaluating the performance of this score by treating this as the marker of interest M = β̂^TX. Time-dependent covariate or time-dependent effect of a covariate can be accommodated in a similar fashion using M(t) = β̂^TX(t) for time-dependent covariates or $M(t)={\widehat{\beta (t)}}^T$ X(t) for time-dependent effect of a covariate. However, estimation of a composite marker, and subsequent evaluation of the discrimination potential using the same training sample, may lead to overestimation of accuracy associated with such a derived marker and invalid confidence interval coverage. Copas and Corbett (2002) discuss this issue in the context of logistic regression and corresponding ROC curves, and they note that the degree of bias is O(n⁻¹), where n is the sample size. In addition, Copas and Corbett (2002) discuss a number of methods to correct for this bias including use of relatively simple computational approaches such as the jackknife (repeated case deletion and crossvalidation) or a bootstrap procedure. However, any composite or derived marker should ultimately be validated on a test sample that is separate from the initial training sample.

There are other approaches to measure prediction accuracy for a survival model. As mentioned earlier, extensions of approaches suitable for continuous data have been proposed (Schemper and Henderson, 2000; Gerds and Schumacher, 2006; Schoop et al., 2008). These methods essentially measure the distance between the observed survival status and the prediction from a model. Censored subjects are accommodated by using the same principle as the KM survival estimates. The implicit assumption here is that the censored subjects have the same risk of failure as the subjects who are still in the riskset. In the presence of competing risks, this assumption may not hold for subjects who died of a competing cause and hence risk redistribution is not appropriate. The prediction accuracy measures proposed here are based on binary classification accuracy schemes like sensitivity and specificity, and stratifies the subjects as cases or controls depending on their time-dependent survival status. Competing risks can be incorporated by making finer partition of the subjects based on their event status as well as the cause of failure. Censoring and multiple causes of failure are handled by formulating the key quantities in terms of cause-specific incidence and cause-specific hazard and are easily interpreted. Extension for the multistate model is possible and needs further investigation.

Lastly, we have proposed methods that partition subjects into J + 1 groups using j = 1, 2, …, J cause-specific case groups and a single comparison event-free control group. However, in some applications it may be of interest to characterize the ability of a marker to separate subjects into only two groups defined as cases of type j, and all other subjects. To estimate ROC curves for this scientific objective the FP rate is alternatively defined as a weighted combination of the cause-specific TP rates for causes k ≠ j and the common control FP rate.

Appendix

C/D ROC Curves

The TP fraction associated with event type j can be expressed as:

$$P(M>c|T\le t,\delta =j)=\frac{P(M>c,T\le t,\delta =j)}{P(T>t)}.$$

The numerator is

$$P(M>c,T\le t,\delta =j)=P(T\le t,\delta =j|M>c)·P(M>c)={\int }_c^{\infty }P(T\le t,\delta =j|M=m).P(M=m)dm={\int }_c^{\infty }{C}_j(t|M=m).P(M=m)dm.$$

The weighted conditional CI estimator in equation (1) can be used to estimate TP associated with a particular cause of failure.

The FP fraction among the controls is:

$$P(M>c|T>t)=\frac{P(M>c,T>t)}{P(T>t)}=\frac{{\int }_c^{\infty }P(M=m,T>t)dm}{{\int }_{-\infty }^{\infty }P(M=m,T>t)dm}.$$

Note that the numerator can be expressed as:

$$P(M>c,T>t)={\int }_c^{\infty }P(T>t|M=m)·P(M=m)dm.$$

We then use equation (2) and equation (1) to obtain an estimate of FP among controls.

I/D ROC Curves

Consider the cause-specific TP for cause j:

$$P(M>c|T=t,\delta =j)={\int }_c^{\infty }P(M=m|T=t,\delta =j)dm$$

$$P(M=m|T=t,\delta =j)=\frac{P(T=t,\delta =j,M=m)}{P(T=t,\delta =j)}=\frac{P(T=t,\delta =j,M=m,T\ge t)}{P(T=t,\delta =j)}.$$

Now, note that the TP is proportional to

$$P(T=t,\delta =j|M=m,T\ge t)·P(M=m|T\ge t)={\lambda }_j(t|M=m)·P(M=m|T\ge t).$$

This relationship is the key to estimation proposed in Heagerty and Zheng (2005) (with J = 1) and can be simply generalized to cause-specific hazard when J > 1.

Estimation of Bias Associated with Optimal Bandwidth

In this subsection, we evaluate the bias associated with the use of optimal bandwidth when (log) T and M is distributed as bivariate normal with correlation ρ as in the simulation. Note that for an interior point, Cai and Sun (2003) give an expression of this asymptotic bias as

$$\text{bias}(t)=\frac{h^2}{2}{\mu }_2\gamma ″(t),$$

where h is the bandwidth and ${\mu }_2={\int }_{-1}^1{u}^{2}K(u)du$. Here we use an Epanechnikov kernel, hence μ₂= 0.2. The bandwidth used in the simulation is h = 0.1 · n^−1/5. To estimate the second derivative of the hazard, we proceed as follows. First note that, (T,M) ~ N₂(0, 0, 1, 1, ρ), and

$$\lambda (t|m)=\frac{1}{\surd (1-{\rho }^2)}\frac{\varphi (\frac{\rho m-t}{\surd (1-{\rho }^2)})}{\mathrm{\Phi }(\frac{\rho m-t}{\surd (1-{\rho }^2)})}\approx \text{exp}[\gamma (t)\cdot m+\delta (t)],$$

where $\varphi (x)=\frac{1}{\surd (2\pi )}{e}^{-\frac{x^2}{2}}$.

Because the coefficient of m in the log of the above expression is implicit, we will assume that the expression associated with the linear term m is the hazard expression of interest. To estimate this hazard, we note that if the log hazard is linear in the marker, then $\gamma (t)\approx \frac{\partial }{\partial m}\text{log}\lambda (t){|}_{m=0}$.

Now,

$$\text{log}\lambda (t|m)=C+\text{log}\varphi (\frac{\rho m-t}{\surd (1-{\rho }^2)})-\text{log}\mathrm{\Phi }(\frac{\rho m-t}{\surd (1-{\rho }^2)}=C-\frac{1}{2}\text{log}[2\pi (1-{\rho }^2)]-\frac{{(\rho m-t)}^2}{2(1-{\rho }^2)}-\text{log}\mathrm{\Phi }(\frac{\rho m-t}{\surd (1-{\rho }^2)})$$

$$\frac{\partial }{\partial m}\text{log}\lambda (t|m)=-\frac{1}{2(1-{\rho }^2)}(2{\rho }^{2}m-2\rho t)-\frac{\partial }{\partial m}\text{log}\mathrm{\Phi }(\frac{\rho m-t}{\surd (1-{\rho }^2)})$$

$$\frac{\partial }{\partial m}\text{log}\mathrm{\Phi }(\frac{\rho m-t}{\surd (1-{\rho }^2)})=\frac{\rho }{\surd (1-{\rho }^2)}\frac{\varphi (\frac{\rho m-t}{\surd (1-{\rho }^2)})}{\mathrm{\Phi }(\frac{\rho m-t}{\surd (1-{\rho }^2)})}$$

$$\frac{\partial }{\partial m}\text{log}\lambda (t|m){|}_{m=0}=\frac{\rho t}{1-{\rho }^2}-\frac{\rho }{\surd (1-{\rho }^2)}\frac{\varphi (-\frac{t}{\surd (1-{\rho }^2)})}{\mathrm{\Phi }(-\frac{t}{\surd (1-{\rho }^2)})}\Rightarrow \gamma (t)\approx \frac{\partial }{\partial m}\text{log}\lambda (t|m){|}_{m=0}.$$

Note that, if we approximate the Φ(.) using a Taylor series approximation around $-\frac{t}{\surd (1-{\rho }^2)}$ up to a linear term in m and then expanded the log(1 + x) ≈ x, then also we would get the same expression for γ(t).

Hence, the second derivative in the expression of bias can be approximated by the second derivative of $\frac{\partial }{\partial m}\text{log}\lambda (t|m)$ with respect to t:

$$\gamma \prime (t)\approx \frac{\rho }{1-{\rho }^2}-\frac{\rho }{\surd (1-{\rho }^2)}\times [\frac{\varphi \prime (-\frac{t}{\surd (1-{\rho }^2)})}{\mathrm{\Phi }(-\frac{t}{\surd (1-{\rho }^2)})}+\frac{1}{\surd (1-{\rho }^2)}\frac{{\varphi }^2(-\frac{t}{\surd (1-{\rho }^2)})}{{\mathrm{\Phi }}^2(-\frac{t}{\surd (1-{\rho }^2)})}]$$

$$\gamma ″(t)\approx \frac{\rho }{\surd (1-{\rho }^2)}\times \left\{\right[\frac{\varphi ″(-\frac{t}{\surd (1-{\rho }^2)})}{\mathrm{\Phi }(-\frac{t}{\surd (1-{\rho }^2)})}+\frac{\varphi \prime (-\frac{t}{\surd (1-{\rho }^2)})\varphi (-\frac{t}{\surd (1-{\rho }^2)})\frac{1}{\surd (1-{\rho }^2)}}{{\mathrm{\Phi }}^2(-\frac{t}{\surd (1-{\rho }^2)})}]+\frac{1}{\surd (1-{\rho }^2)}[\frac{2\varphi \prime (-\frac{t}{\surd (1-{\rho }^2)})\varphi (-\frac{t}{\surd (1-{\rho }^2)})}{{\mathrm{\Phi }}^2(-\frac{t}{\surd (1-{\rho }^2)})}+\frac{{\varphi }^3(-\frac{t}{\surd (1-{\rho }^2)})\frac{t}{\surd (1-{\rho }^2)}}{{\mathrm{\Phi }}^3(-\frac{t}{\surd (1-{\rho }^2)})}\left]\right\}.$$

For n = 500, we estimate this bias to be less than 0.1 in absolute value for the range considered in the simulation.