Converging Nuclear Magnetic Shielding Calculations with Respect to Basis and System Size in Protein Systems

Abstract

Ab initio chemical shielding calculations greatly facilitate the interpretation of nuclear magnetic resonance (NMR) chemical shifts in biological systems, but the large sizes of these systems requires approximations in the chemical models used to represent them. Achieving good convergence in the predicted chemical shieldings is necessary before one can unravel how other complex structural and dynamical factors affect the NMR measurements. Here, we investigate how to balance trade-offs between using a better basis set or a larger cluster model for predicting the chemical shieldings of the substrates in two representative examples of protein-substrate systems involving different domains in tryptophan synthase: the N-(4′-trifluoromethoxybenzoyl)-2-aminoethyl phosphate (F9) ligand which binds in the α active site, and the 2-aminophenol (2AP) quinonoid intermediate formed in the β active site. We first demonstrate that a chemically intuitive three-layer, locally dense basis model that uses a large basis on the substrate, a medium triple-zeta basis to describe its hydrogen-bonding partners and/or surrounding van derWaals cavity, and a crude basis set for more distant atoms provides chemical shieldings in good agreement with much more expensive large basis calculations. Second, long-range quantum mechanical interactions are important, and one can accurately estimate them as a small-basis correction to larger-basis calculations on a smaller cluster. The combination of these approaches enables one to perform density functional theory NMR chemical shift calculations in protein systems that are well-converged with respect to both basis set and cluster size.

1 Introduction

The ab initio calculation of chemical shifts has added to the arsenal of techniques available to characterize chemical state and identify unknown molecular compounds. In favorable cases, the ability to screen and rank competing chemical/ structural models for consistency with experimental shifts from nuclear magnetic resonance (NMR) spectroscopy can allow single structural models to be determined. This general approach is broadly applicable to molecular systems, but it is essential in the development of nuclear magnetic resonance-assisted crystallography, which seeks to define the atomic-resolution, three-dimensional structure of crystalline solids using a synergistic combination of X-ray diffraction, computational chemistry, and solid-state NMR spectroscopy (Facelli and Grant (1993); Rajeswaran et al. (2002); Olsen et al. (2003); Lai et al. (2011); Brouwer et al. (2005); Harris et al. (2006); Harper et al. (2006); Salager et al. (2010); Webber et al. (2010); Luchinat et al. (2012); Pooransign-Margolis et al. (2006); Gupta et al. (2015)).

Indeed, interpreting the experimental NMR chemical shifts in a complex biological system is challenging, since they depend not only on the state of the probe atom but also the three-dimensional chemical environment surrounding that atom. X-ray diffraction can provide this structural context, but also has limitations as it does not directly identify protonation states, even at high resolution. Computational chemistry therefore plays a crucial role in NMR crystallography by linking the detailed local NMR spectroscopic information with the coarse x-ray structures. In particular, it allows one to predict chemical shifts and other NMR observables for putative structural models to determine which correlate best with the experimental observables.

Reliably discriminating among different structural models requires high accuracy chemical shift predictions. Structural details, such as the optimization/ refinement procedure, choice of local conformations, and dynamical averaging can all have major impacts on the predicted chemical shifts. Before one can meaningfully address questions about the details of local structure and dynamics, it is critical to obtain ab initio chemical shieldings that are well-converged with respect to both the chemical model and the quantum chemistry techniques. In small molecules, achieving such convergence is relatively straightforward—one simply combines density functional theory, second-order Møller-Plesset perturbation theory, or even coupled cluster chemical shielding calculations with large basis sets.

One the other hand, achieving such theoretical convergence for a substrate inside a biological enzyme containing hundreds of amino acids is much more challenging. One generally cannot perform a brute-force electronic structure calculation on the entire protein system. Rather, one often performs calculations on a protein sub-cluster surrounding the substrate or region of interest using either a purely quantum mechanical (QM) or a hybrid quantum/ classical molecular mechanics (QM/MM) cluster model. Sometimes multiple such QM/MM calculations are performed using a fragment approach (Zhu et al. (2012); Frank et al. (2011); Tan and Bettens (2013); Gao et al. (2014)).

In such models, one seeks to balance the cluster size (number of atoms treated quantum mechanically) with the quality of the quantum mechanical treatment, including the basis set. Linear-scaling and other efficient algorithms (Ochsenfeld et al. (2004); Beer et al. (2011); Kussmann et al. (2013)) enable QM/MM calculations with large quantum regions, but the chemical shieldings in the quantum region of a QM/MM calculation converge slowly with respect to cluster size (Flaig et al. (2012); Steinmann et al. (2014)). At the same time, large basis sets are typically required to obtain theoretically converged chemical shieldings, even with gauge-invariant atomic orbitals (Moon and Case (2006); Kupka et al. (2010); Flaig et al. (2014); Reid et al. (2014)). The linear regression procedures (Lodewyk et al. (2012)) often used to map from predicted chemical shielding to observed chemical shift typically cancel a sizable fraction of the finite basis set error for small molecules in solution (e.g. Jain et al. (2009); Konstantinov and Broadbelt (2011)). However, in complex, inhomogeneous environments such as substrates bound inside proteins, the finite basis set effects can be more apparent and the degree of error cancellation is significantly reduced (Frank et al. (2012)).

Consequently, given finite computational resources, one must often choose: should one use a larger cluster model or should one use a smaller model cluster and utilize a better basis set? Multilayer ONIOM strategies (Svensson et al. (1996); Zheng et al. (2004)) and the use of locally dense basis sets can help address these issues. The local nature of the chemical shielding makes locally dense basis set models, in which large basis sets are used only near the atoms of interest, particularly effective (Chesnut and Moore (1989); Chesnut et al. (1993); Moon and Case (2006); Zhu et al. (2013); Reid et al. (2014); Samultsev et al. (2014); Holmes et al. (2014)). Fragment-based approaches also demand similar choices, because the fragment size is not uniquely defined in covalently bonded systems, and one must include sufficient buffer region in individual fragment calculations to obtain reliable chemical shifts (Zhu et al. (2012)).

In other words, the researcher modeling biological systems is faced with a wide variety of potential modeling choices that will affect the resulting chemical shielding predictions. How do we combine the salient features of the various modeling strategies found in the literature to obtain converged chemical shielding predictions in protein-substrate systems? How well do the appropriate modeling decisions about system size and basis sets correlate with chemical intuition?

In this paper, we assess the performance of a variety of existing approximations and develop a set of physically-motivated recommendations for modeling chemical shieldings in a complex system. Specifically, we address the question of how to handle the issues of basis set and cluster size simultaneously in the NMR chemical shielding calculations. We assume that one has obtained a plausible chemical structure through other means (e.g. QM/MM refinement of x-ray crystal structures), though of course that step also involves its own subtleties which have been addressed elsewhere (Senn and Thiel (2009); Sumner et al. (2013)).

To investigate these questions, we consider two examples from different domains of tryptophan synthase with recently reported x-ray crystal structures (Niks et al. (2013)). First, we examine the quinonoid intermediate formed by the reaction of 2-aminophenol (2AP) and serine with the pyridoxal-5′-phosphate (PLP) coenzyme in the β-subunit of tryptophan synthase. 2AP is a nucleophile and analogue of the natural substrate indole, which forms a stable quinonoid complex with tryptophan synthase and is the subject of ongoing investigations (Lai et al. (2011); Caulkins et al. (2014)). Second, we investigate the N-(4′-trifluoromethoxybenzoyl)-2-aminoethyl phosphate (F9) ligand bound at the α-subunit active site for the resting internal aldimine form of tryptophan synthase. F9 is a tight-binding analogue of the natural substrate, 3-indole-D-glycerol 3′-phosphate. Though both systems involve tryptophan synthase, the two substrates are chemically distinct and they occupy different binding sites separated by more than 25 Å: the β active site is centered within the β-subunit, while the α site lies near the interface between the two domains.(Dunn et al. (2008))

In the end, we demonstrate that a combination of locally dense basis sets and ONIOM-type approaches provide a cost-effective means of capturing well-converged chemical shifts on the substrate atoms. Furthermore, the basis set and cluster size requirements mesh nicely with chemical intuition about the physical interactions between the substrate and various portions of the surrounding protein. Very similar behaviors are observed for the models in both systems here, which suggests that the insights obtained here can likely be generalized to other to protein-bound substrates and/or other systems where one is interested in the chemical shifts for a particular region of the biomolecule. Finally, we demonstrate that techniques such as the ones considered here lead to improved agreement between the predicted and experimentally measured chemical shifts of the 2AP quinonoid intermediate.

2 Computational Methods

The active site enzyme-substrate complexes and surrounding protein cavity were generated from our (Mueller, Neubauer) recent (1) 1.45 Å resolution crystal structure of tryptophan synthase in complex with the quinonoid formed by reaction of serine and 2-aminophenol (2AP) in the β site (the 2AP quinonoid intermediate; PDB ID: 4HPJ) and (2) 1.30 Å resolution crystal structure of the resting internal aldimine form of the enzyme with F9 bound at the alpha-subunit active site (PDB ID: 4HT3) (Niks et al. (2013)). In both cases, the surrounding protein cavity was generated by including residues that had more than 2 heavy atoms within 7 Å (2AP) or 8 Å (F9) of any heavy atom of the substrate. The larger 8 Å F9 cluster reflects a slightly more conservative pruning of the protein structure.

Wherever possible, peptide backbone segments were preserved; where necessary, broken peptide bonds were terminated by replacing N-terminal nitrogens with hydrogen atoms and C-terminal carbonyls with carboxamides. Two exceptions in the 2AP structure were the isolated residues His313 and Phe280, which were fairly distant from the coenzyme/substrates and with side chains pointed toward the active site; for these two residues, only the side chains (C^β on) were retained, with C^α replaced by a hydrogen atom. In the end, the 7 Å 2AP and 8 Å F9 substrate/protein complexes contain 615 and 857 atoms, respectively. The structures of the clusters were geometry optimized as described below.

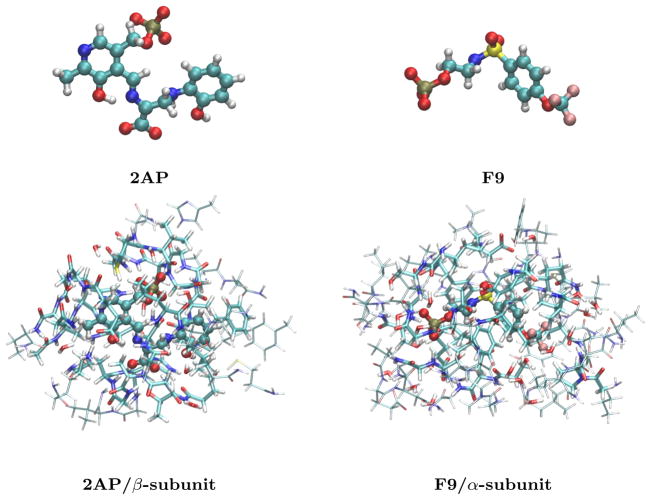
The smaller 5 Å cuts were generated from the larger geometry-optimized 7–8 Å structures by selecting only those residues with 2 or more heavy atoms that fell within 5 Å of the coenzyme/substrate. In the 2AP case, side chains of Phe 306, Leu166, and Lys382 were also truncated at C^β. No such exceptions were needed for the F9 case. The 5 Å cuts were not further geometry optimized. These smaller systems contain 461 (2AP) and 422 (F9) atoms, respectively. See Figures 1 and 2. Cartesian coordinates for the final structures are provided as Electronic Supplementary Information.

Fig. 1.

The bare 2AP quinonoid substrate-coenzyme complex and F9 ligand (top) and their structures bound in the β and α subunits of tryptophan synthase, respectively. The bottom structures indicate the 5 Å clusters (cylinders) and the larger 7–8 Å clusters (wireframe) extracted from tryptophan synthase.

Fig. 2.

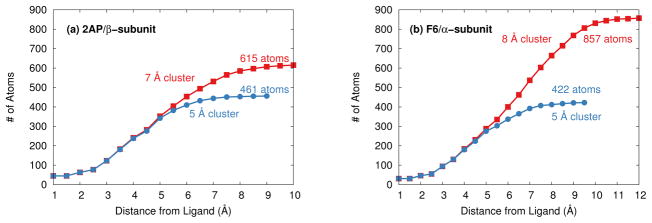
Distribution of atoms relative to the (a) 2AP and (b) F9 substrates in the tryptophan synthase cluster models.

All electronic structure calculations were performed using Gaussian 09 (Frisch et al. (2009)). The protein/substrate clusters were relaxed using a mixed B3LYP/6-31G** (substrates) and PM3 semi-empirical (protein) ONIOM model (Stephens et al. (1994); Hehre et al. (1972); Hariharan and Pople (1973)). Non-hydrogen protein atoms were held fixed at their crystallographically determined positions, while added protons and all atoms of the substrate-coenzyme were geometry optimized. Additional details have been provided previously (Lai et al. (2011)).

The ab initio chemical shielding calculations were performed using the B3LYP functional and Pople 6-311++G**, 6-311G**, 6-31G*, and 6-31G basis sets (Hehre et al. (1972); Hariharan and Pople (1973); Krishnan et al. (1980); McLean and Chandler (1980); Frisch et al. (1984); Clark et al. (1983)). The choice of density functional is obviously important in the quality of the results obtained. Many benchmark chemical shielding/shift studies exist (e.g. Lodewyk et al. (2012); Teale et al. (2013); Flaig et al. (2014); Zhang et al. (2006); Keal and Tozer (2004); Jain et al. (2009); Konstantinov and Broadbelt (2011)), with sometimes conflicting density functional recommendations. B3LYP performs reasonably well in many of these studies (especially when linear regressions are employed to map from absolute shielding to chemical shift). Of course, hybrid functionals are more computationally demanding than GGAs. In any case, this paper focuses primarily on the convergence of the chemical shieldings, rather than the observed chemical shifts. This convergence behavior should be fairly insensitive to the specific functional used.

A numerically tight exchange-correlation grid containing 99 radial points and 590 Lebedev angular points was used. In certain cases described below, point charge embedding or polarizable continuum models (PCM) were employed for the chemical shielding calculations. Mulliken point charges for the larger 7–8 Å cluster model atoms were calculated at the B3LYP/6-31G* level and used to embed the 5 Å cluster models. For the PCM model, dielectric constants of either ε = 2, 4, or 8 were employed.

3 Results and Discussion

In this section, we examine strategies for treating both basis set and cluster size effects for the quantum mechanical chemical shift predictions for the two different tryptophan synthase examples. As motivated by recent solid-state NMR experiments (Lai et al. (2011); Caulkins et al. (2014)), we focus on the chemical shieldings of the active-site substrates/coenzyme rather than those of the protein. The substrate shifts often provide key information regarding the enzyme mechanism.

For the discussion below, bear in mind the typical errors in the isotropic chemical shifts obtained with density functional theory. Based on many benchmark studies, errors of at least ~0.2 ppm for hydrogen (Lodewyk et al. (2012)), ~2–3 ppm for carbon (Lodewyk et al. (2012)), ~3–4 ppm or more for nitrogen (Samultsev et al. (2014); Blanco et al. (2007)), and several ppm for oxygen (Auer (2009); Teale et al. (2013)) are common with DFT, depending on the density functional used. These errors arise from a mixture of factors: the limitations of the density functionals, basis sets, choice of geometry, solvation/ environment effects, etc. In employing various approximations below, we seek to identify approximations that ensure the errors associated with the cluster size and basis set are small compared to those arising from other sources. That is, we seek errors of no more than a couple tenths of a ppm for carbon and hydrogen, half a ppm for nitrogen, and one ppm for oxygen.

The convergence of chemical shielding tensors with respect to basis set size can be slow (Kupka et al. (2010); Moon and Case (2006); Flaig et al. (2014)) However, empirical evidence suggests that the combination of DFT and triple-zeta basis sets often provides chemical shifts in fortuitously good agreement with experiment (Moon and Case (2006)), especially when the standard linear regression scaling factors are employed (Lodewyk et al. (2012)). Because they combine useful accuracy with reasonable computational demands, triple-zeta basis sets are widely used in ab initio chemical shielding calculations, and they are used here as well.

3.1 Basis set effects

To examine basis set effects, we first consider the 5 Å cluster model (461 atoms) for the 2AP quinonoid intermediate of tryptophan synthase. This model is small enough to allow relatively large basis calculations on the entire cluster. Figure 3(a) plots the root-mean-square (rms) difference between a full B3LYP/6-311G** chemical shift calculation on this system and calculations employing a locally dense approximation in which the smaller 6-31G* basis is used for the atoms beyond a given cutoff distance from any atom of the coenzyme-substrate covalent complex.

Fig. 3.

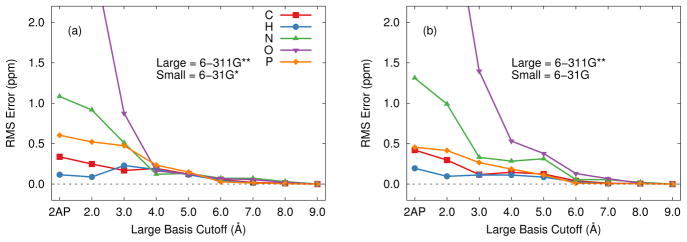
Root-mean-square errors in the isotropic chemical shieldings for the 2AP 5 Å cluster using the locally dense basis approximation relative to a full calculation in the 6-311G** basis. (a) 6-311G** and 6-31G* basis sets. (b) 6-311G** and 6-31G basis sets.

In the simplest case, the larger basis is used only on the coenzyme-substrate complex, while the smaller basis is used for the surrounding protein, thereby reducing the number of basis functions by a third, from 5703 to 3828. Nevertheless, this extreme model simplification already reproduces the conventional 6-311G** basis shieldings for the 2AP substrate fairly well, with root mean errors of only a few tenths of a ppm for ¹H and ¹³C shieldings. Nitrogen and oxygen nuclei are more sensitive to the electronic environment, and they exhibit errors of 1.1 ppm and 4.8 ppm respectively.

These errors are already comparable to or better than the “typical” DFT chemical shift prediction errors discussed above. On the other hand, when attempting to distinguish among different but related models of charge and protonation states based on the agreement between experimental and predicted chemical shifts (a key component of NMR crystallography), the chemical shifts will often vary over a small range, making more precise evaluation of the chemical shifts important.

Expanding the radius of the atoms which use the large basis leads to significant improvement in the nitrogen and oxygen chemical shieldings. Including all protein atoms within 3 Å of 2AP in the large-basis region reduces the errors further by a factor of 2–4. The value of a 3 Å cutoff has been noted previously, especially for carbon atoms (Frank et al. (2012)). However, expanding the large-basis region to include all atoms within a 4 Å radius of 2AP improves the situation further, reducing the rms errors for all atom types below 0.5 ppm. Subsequent expansion of the large-basis region beyond 4 Å has a relatively small impact on the results.

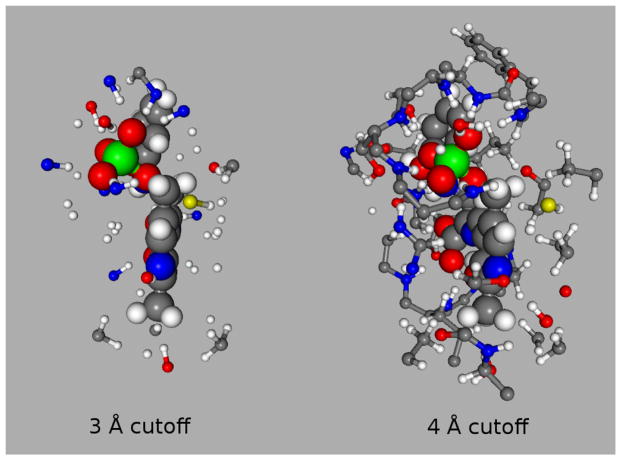
The sensitivity of chemical shielding to the non-covalent interactions with the surrounding chemical environment is well known. Participation in a hydrogen bond often has a strong impact on the chemical shielding, for instance, which explains the sharp decrease in errors for the 3 Å large-basis cutoff. This distance is just enough to include all donor and acceptor atoms (both hydrogen and the associated heavy atom) directly involved in hydrogen bonding to the coenzyme-substrate complex in the large-basis region (see Figure 4). Non-specific interactions with the atoms forming the van der Waals cavity around the complex also play an important role in the substrate chemical shieldings, and extending the large-basis cutoff to 4 Å to improve the treatment of these interactions (Figure 4) improves the chemical shielding predictions significantly.

Fig. 4.

Side view of 2AP (45 atoms) bound in the β-subunit of tryptophan synthase with 3 Å and 4 Å cutoff models. The 3 Å cutoff primarily includes hydrogen bond partners (2AP + 78 atoms), while the 4 Å cutoff captures most of the van der Waals cavity (2AP + 196 atoms).

Atoms lying more than 4 Å from 2AP interact less directly with the substrate. The smaller 6-31G* basis provides a reasonable description of the electron densities for these distant atoms, thereby providing an adequate electrostatic embedding environment. The largely electrostatic role of these distant atoms raises the possibility that one might be able to use the even smaller 6-31G basis which lacks polarization functions. Indeed, as shown in Figure 3(b), using the 6-31G basis instead of 6-31G* for the small basis region slightly slows the convergence toward the full 6-311G** results with respect to the large-basis cutoff, but the rms errors at the 3 Å and 4 Å cutoffs still lie within ~0.5 ppm or less for all nuclei types. Eliminating the polarization functions in the small basis region reduces the number of basis functions from 4144 to 3274 (3 Å cutoff) or from 4604 to 4079 (4 Å cutoff), resulting in computational savings of roughly 1/3 and 1/6, respectively, on 12 Intel Xeon 2.26 GHz cores and 40 GB of RAM.

Very similar behavior is observed for F9 in the 5 Å cut of the α subunit of tryptophan synthase (Table 1). Including atoms out to 3–4 Å from the substrate in the large basis region captures the most important interactions and significantly improves the quality of the predicted NMR chemical shieldings. This behavior is particularly notable for nitrogen, oxygen, and fluorine. Once again, these distances correspond to placing large basis functions on the substrate-protein hydrogen bonding partners and the atoms forming the van der Waals cavity around the substrate.

Table 1.

Root-mean-square errors in the computed chemical shieldings (ppm) for the 5 Å cluster models of both systems using a locally dense basis approximation relative to a calculation using only the large basis.

System	Basis Sets	Size of Large Basis Region (Distance from Substrate)
		Substrate	2 Å	3 Å	4 Å	5 Å	6 Å	7 Å	8 Å
Hydrogen
2AP	6-311++G** / 6-31G a	0.13	0.12	0.10	-	-	-	-	-
	6-311G** / 6-31G*	0.12	0.09	0.23	0.18	0.12	0.05	0.01	0.01
	6-311G** / 6-31G	0.20	0.10	0.11	0.11	0.09	0.03	0.00	0.01
F9	6-311++G** / 6-31G a	0.20	0.10	0.05	-	-	-	-	-
	6-311G** / 6-31G*	0.08	0.11	0.20	0.25	0.13	0.05	0.03	0.01
	6-311G** / 6-31G	0.19	0.09	0.16	0.22	0.09	0.02	0.01	0.00
Carbon
2AP	6-311++G** / 6-31G a	0.29	0.21	0.15	-	-	-	-	-
	6-311G** / 6-31G*	0.34	0.25	0.17	0.19	0.12	0.05	0.02	0.01
	6-311G** / 6-31G	0.42	0.30	0.12	0.15	0.12	0.04	0.01	0.01
F9	6-311++G** / 6-31G a	0.23	0.14	0.06	-	-	-	-	-
	6-311G** / 6-31G*	0.25	0.19	0.16	0.25	0.13	0.05	0.03	0.01
	6-311G** / 6-31G	0.34	0.23	0.13	0.22	0.09	0.02	0.01	0.01
Nitrogen
2AP	6-311++G** / 6-31G a	1.06	0.71	0.16	-	-	-	-	-
	6-311G** / 6-31G*	1.08	0.92	0.51	0.12	0.13	0.07	0.07	0.03
	6-311G** / 6-31G	1.31	0.99	0.33	0.28	0.31	0.06	0.05	0.02
F9	6-311++G** / 6-31G a	−0.14	−0.07	0.09	-	-	-	-	-
	6-311G** / 6-31G*	0.43	0.44	0.25	0.45	0.08	-0.05	0.03	0.02
	6-311G** / 6-31G	0.76	0.47	−0.09	0.34	0.09	0.03	0.00	0.01
Oxygen
2AP	6-311++G** / 6-31G a	1.66	0.82	0.28	-	-	-	-	-
	6-311G** / 6-31G*	4.85	2.89	0.88	0.16	0.12	0.07	0.06	0.02
	6-311G** / 6-31G	5.72	3.77	1.40	0.53	0.38	0.13	0.07	0.01
F9	6-311++G** / 6-31G a	2.17	0.81	0.29	-	-	-	-	-
	6-311G** / 6-31G*	4.12	2.44	1.05	0.31	0.24	0.08	0.03	0.01
	6-311G** / 6-31G	4.72	2.96	1.29	0.37	0.17	0.09	0.03	0.01
Fluorine
F9	6-311++G** / 6-31G a	0.48	0.27	0.22	-	-	-	-	-
	6-311G** / 6-31G*	2.88	2.95	0.83	0.11	0.17	0.05	0.04	0.02
	6-311G** / 6-31G	2.96	3.07	0.71	0.21	0.17	0.04	0.05	0.01
Phosphorous
2AP	6-311++G** / 6-31G a	0.35	0.58	0.13	-	-	-	-	-
	6-311G** / 6-31G*	0.60	0.52	0.47	0.23	0.15	0.03	0.01	0.00
	6-311G** / 6-31G	0.46	0.41	0.27	0.19	0.11	0.01	0.01	0.00
F9	6-311++G** / 6-31G a	0.86	0.98	0.34	-	-	-	-	-
	6-311G** / 6-31G*	0.48	0.28	0.23	0.24	0.11	0.03	0.04	0.01
	6-311G** / 6-31G	0.66	0.44	0.27	0.20	0.11	0.04	0.02	0.00
Sulfur
F9	6-311++G** / 6-31G a	0.05	0.36	0.12	-	-	-	-	-
	6-311G** / 6-31G*	0.10	0.18	0.15	0.11	0.01	0.01	0.05	0.01
	6-311G** / 6-31G	0.13	0.08	0.08	0.15	0.03	0.02	0.01	0.01

^aRelative to 6-311++G** / 6-31G calculation with 4 Å large-basis cutoff.

Unsurprisingly, the largest improvements in chemical shielding for both 2AP and F9 occur on atoms directly involved in hydrogen bonding and those which experience strong electrostatic interactions with the protein. The negatively charged phosphate group and carboxylate oxygens are particularly sensitive to their environment. In both systems considered here, adding large basis functions to nearby protein atoms reduces the errors on the oxygens in the phosphate group by an order of magnitude, from 5–8 ppm to 0.1–0.4 ppm. Comparable improvements are also observed for the electronegative fluorine atoms in the F9 ligand, reducing the errors from several ppm to a few tenths of a ppm.

Nitrogen atoms on the substrate also often interact strongly with the protein and benefit significantly from large basis functions on nearby protein atoms. As might be expected, substrate oxygen and nitrogen atoms which accept hydrogen bonds from the protein benefit more than those which act as hydrogen bond donors to the protein, those which hydrogen bond internally within the substrate, or those that are not involved in hydrogen bonds at all.

The improvements seen for the carbon and hydrogen atom shieldings upon adding basis functions to the protein atoms are less dramatic. Nevertheless, aromatic carbons in the substrate, which interact more strongly with their environment than aliphatic carbons, benefit the most from the inclusion of the protein environment. For hydrogen, the atoms near the phosphate group and bonded to the nitrogen prove most sensitive, probably because of their proximity to strong electrostatic environments and/or their direct participation in hydrogen bonding.

Diffuse basis functions are often used when computing chemical shieldings, and they play an important role in describing non-covalent interactions. Once again, a locally dense basis approach proves effective. While full reference 6-311++G** calculations proved computationally impractical, Table 1 shows good convergence of the chemical shieldings with increasing size of the large basis region for 6-311++G**/6-31G relative to the 4 Å large-basis region calculation. As expected from the earlier 6-311G** results, the root-mean-square differences between using 6-31G and 6-31G* for the small basis in the 2AP system are only a 0.1–0.3 ppm for carbon, hydrogen, nitrogen, and phosphorus, and 0.6 ppm for oxygen.

Unfortunately, the inclusion of spatially diffuse basis functions decreases integral sparsity and therefore significantly increases the computational costs. Large numbers of diffuse functions also introduce linear dependencies to the basis set which can hinder the numerical convergence of the underlying DFT self-consistent field equations. Therefore, we also explore a three-tier locally dense basis model in which a large 6-311++G** basis is used to model the 2AP substrate (the chemical shifts of interest), a medium 6-311G** basis is used to model the adjacent region of the protein, and a small 6-31G basis is used on the remaining outlying atoms.

The performance of the three-tier model is measured in two ways. First, one can examine the performance of using 6-311G** for the protein atoms near the coenzyme complex instead of 6-311++G**. For example, employing the 6-311++G** basis on 2AP, 6-311G** out to 4 Å, and 6-31G for the rest of the protein introduces rms errors of 0.15 ppm for hydrogen, 0.16 ppm for carbon, 0.27 ppm for nitrogen, 0.53 ppm for oxygen, and 0.41 ppm for phosphorous compared to the much more expensive two layer model with 6-311++G** to 4 Å and 6-31G for the rest. Similarly, doing the same for the F9 system produces errors of only 0.1–0.2 ppm for hydrogen, carbon, nitrogen, and sulfur, 0.33 ppm for fluorine, 0.41 ppm for oxygen, and 0.58 ppm for phosphorous.

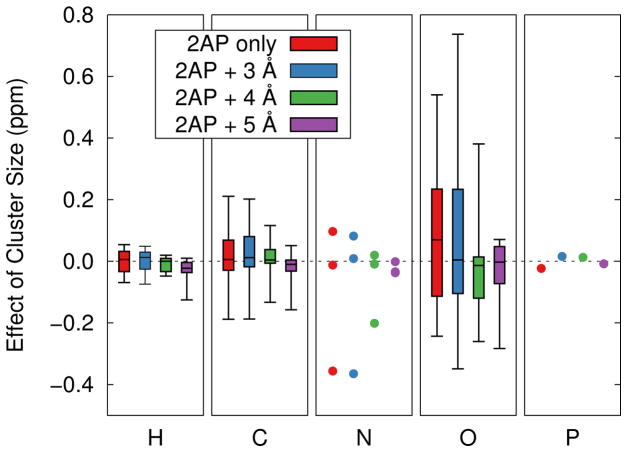
Second, one can examine the impact of replacing the 6-311G** basis on the more distant atoms with 6-31G functions. Indeed, this approximation works very well—switching from the medium 6-311G** basis to the smaller 6-31G basis after 3–4 Å from either 2AP or F9 introduces errors of only 0.5 ppm or less (Figure 5). Note that using at least a triple-zeta quality appears critical for the medium basis region. Test calculations with double-zeta basis sets like 6-31G* or 6-31G** in the medium range (not shown) provide only marginal improvements over the corresponding 6-311++G** substrate plus 6-31G protein model.

Fig. 5.

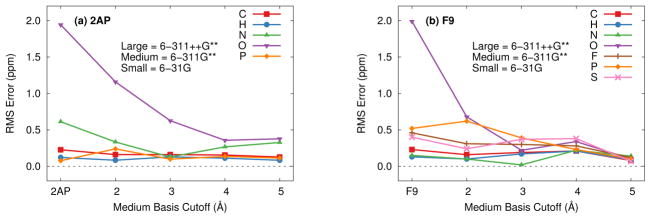
Root-mean-square errors in the isotropic chemical shieldings for the 5 Å cluster of each system using the three-tier locally dense basis approximation relative to a calculation with 6-311++G** on the substrate and 6-311G** on the protein. The 6-311++G** basis is used on the substrate, 6-311G** on protein atoms out to the medium basis cutoff, and 6-31G* is used for all remaining atoms in the protein. A medium basis cutoff of “2AP” or “F9” corresponds to no medium basis (i.e. small basis on the entire protein).

Taken together, these results provide a chemical intuitive picture: one should employ the largest basis for the atoms of interest (e.g. the substrate). One can then use a relatively compact triple zeta basis set for protein atoms that define the van derWaals cavity of the substrate, while even a poor-quality 6-31G basis can be used to model the more distant atoms beyond ~4 Å.

3.2 Effect of cluster size and estimation strategies

The size of the finite cluster used to approximate the protein system is equally important. Increasing from the 5 Å to 7 Å increases the number of atoms in the 2AP cluster by a third to 615, while increasing the F9 cluster to 8 Å more than doubles the number of atoms to 857 (Figure 1).

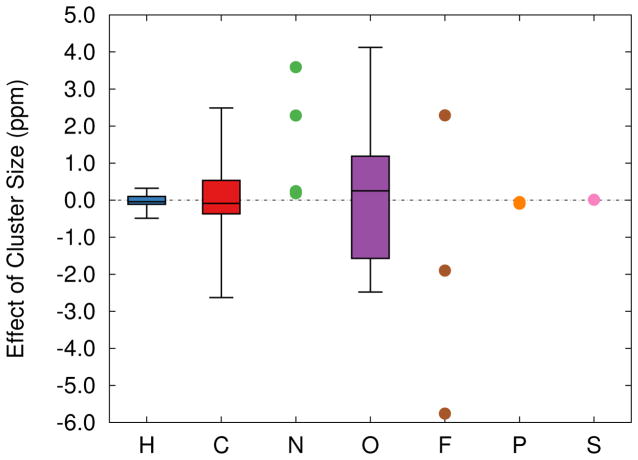
Including these additional atoms significantly alters the predicted chemical shieldings. Figure 6 plots the distributions of how the chemical shieldings on individual atoms change as the protein cluster size is increased. The cluster size effect for both 2AP and F9 behave similarly, so they are plotted together in Figure 6 to improve the statistical sample sizes. Atoms like carbon, nitrogen, oxygen, and fluorine are most sensitive to the cluster size effects here, with changes in the chemical shieldings of up to several ppm.

Fig. 6.

Box plots showing how increasing from the 5 Å to 7–8 Å cluster models affects the 6-311G** isotropic chemical shieldings in the two systems. Boxes indicate the median (central line), middle 50% (colored box), and range (whiskers) of the data. Ordinary points are used to represent the data for the smaller numbers of nitrogen, fluorine, phosphorous, and sulfur atoms.

Unlike the basis set effects described in Section 3.1, however, no obvious trends emerge regarding the local functional groups for a given atom type in either 2AP or F9. Rather, the more distant protein atoms define the inhomogeneous electrostatic potential which polarizes the atoms in and around the substrate. It is worth noting, though, that strong electrostatic perturbations from the protein environment are especially important. For example, some of the largest changes in the 2AP chemical shieldings introduced by the larger cluster occur on atoms closest to the sodium cation, which is found in the 7 Å cluster but not in the 5 Å one.

These cluster size effects are consistent with earlier studies that found that ¹³C chemical shieldings often do not converge within ~0.5 ppm rms error until the QM clusters reach 6–8 Å (Flaig et al. (2012); Johnson and DiLabio (2009)). Earlier studies also demonstrate that using hybrid QM/MM methods can help accelerate the convergence somewhat (Flaig et al. (2012)), particularly when polarizable force fields are used (Steinmann et al. (2014)). Indeed, the magnitude of the cluster size effect is often larger than the basis set effects discussed earlier, reinforcing the importance of using as large of a cluster model as possible.

In other words, one should perform the chemical shift calculations using the largest QM cluster feasible, ideally with a radius of at least 6–8 Å. If one cannot afford to compute such a cluster, how should one best approximate the cluster size effects? Several possibilities exist, including the use of a polarizable continuum model, MM electrostatic embedding, or ONIOM-type approaches.

MM point-charge embedding provides a simple means of incorporating long-range electrostatic effects into the chemical shielding calculations. QM/MM modeling has a long history with many techniques for treating the interactions between the QM and MM regions (Gao (1995); Lin and Truhlar (2006); Senn and Thiel (2009)). Here, however, we use the simplest approximation by placing B3LYP/6-31G* Mulliken point charges corresponding to the distant atoms in the larger 7–8 Å cluster models around the 5 Å cluster model atoms. To avoid double counting, charges were omitted for any atoms in the larger cluster that lie directly on top of or within 1 Å of the atoms in the 5 Å cluster (i.e. Z1 scheme for capping atoms in Lin and Truhlar (2006)).

As shown in Table 2, fixed point-charge embedding the 5 Å cluster model for 2AP modestly reduces the differences in the chemical shieldings relative to the 7 Å cluster models for most atom types other than nitrogen. On the other hand, doing the same for the F9 system provides little or no improvement in the chemical shifts. Once again, the nitrogen shifts become notably worse, as do the fluorine ones. The results also prove very sensitive to the minimum distance between the point charges and the atoms. Excluding all charges within 1.5 Å of the F9 5 Å cluster model dramatically reduces the errors: to 0.10 ppm for hydrogen, 0.65 ppm for carbon, 1.06 ppm for nitrogen, and 1.62 ppm for fluorine. On the other hand, similarly excluding more short-range charges in the 2AP system has the opposite effect, with errors on the oxygen and nitrogen in particular rapidly increasing by several ppm.

Table 2.

Root-mean-square errors in the B3LYP/6-311G** substrate chemical shieldings (ppm) in the 5 Å clusters relative to the larger clusters ones with various size-effect estimation strategies.

Size Effect Correction
	None	MM Point Chargesa	PCM (ε= 2)b	PCM (ε= 4)b	PCM (ε= 8)b	ONIOMc
2AP system
H	0.17	0.14	0.15	0.14	0.12	0.11
C	1.04	0.73	0.93	0.79	0.64	0.04
N	1.33	2.45	1.12	0.94	0.80	0.21
O	1.88	0.92	1.58	1.30	1.13	0.26
P	0.09	0.01	0.05	0.01	0.03	0.02
F9 system
H	0.21	0.25	-	0.12	-	0.19
C	1.43	1.41	-	0.66	-	0.19
N	3.59	5.05	-	1.75	-	0.42
O	1.71	1.87	-	1.16	-	0.59
F	3.74	5.02	-	1.83	-	0.24
P	0.05	0.02	-	0.03	-	0.06
S	0.01	1.17	-	0.47	-	0.17

^aB3LYP/6-31G* Mulliken charges.

^bThe PCM was applied to both the 5 Å and the larger clusters.

^cThe cluster size effect in Eq 1 is approximated using 6-311G** on 2AP and 6-31G on all protein atoms.

Better results might be obtained with a more elaborate polarizable MM embedding approach (Steinmann et al. (2014)). Still, using charge embedding to estimate cluster size effects on protein/substrate clusters of this size introduces errors that are considerably larger than those introduced by the basis set approximations discussed earlier. One likely needs to use a larger explicit cluster before the point charge embedding proves more reliable (Flaig et al. (2012)).

An alternative approach to capture long-range effects involves surrounding the protein cluster in a polarizable continuum model to approximate the influence of longer-range interactions on the nuclei of interest. To test this, the PCM model was employed around both the 5 Å and larger 7–8 Å clusters to capture bulk contributions equivalently. Much discussion surrounds the appropriate dielectric constant to use (Schutz and Warshel (2001); Li et al. (2013); Kukic et al. (2013); An et al. (2014)), but values around 4 are common. Here, we consider three different dielectric constants: ε = 2, 4, or 8. Table 2 shows that, for both the 2AP and F9 systems, employing a PCM reduces the errors of the smaller cluster relative to the larger one by ~30–50%. Larger dielectric constants appear to capture the cluster size effects better, though the differences are fairly modest. Overall, the improvement provided by the PCM model is somewhat better than what was obtained with the point-charge embedding scheme. Others have obtained similar results when using PCM models (Frank et al. (2012)).

A third approach, which proves much more effective than either the simple point-charge embedding or the PCM model, is to adopt a QM/QM ONIOM style model. Specifically, if one cannot perform the calculation on a sufficiently large cluster with the desired basis set(s), one can perform the large basis (Basis1) calculation on a smaller cluster (e.g. the 5 Å cluster model here) and then use smaller-basis (Basis2) calculations to estimate the effects of increasing the cluster size from 5 Å to 7 Å on the chemical shieldings σ:

$${\sigma }_{7A}^{\mathit{Basis}1}\approx {\sigma }_{5A}^{\mathit{Basis}1}+\left({\sigma }_{7A}^{\mathit{Basis}2}-{\sigma }_{5A}^{\mathit{Basis}2}\right)$$ (1)

It turns out that the cluster size effect correction in parentheses in Eq 1 can be estimated even with fairly crude basis set calculations. Figure 7 shows the errors introduced by computing the cluster size effect in the 2AP system using a locally dense 6-311G**/6-31G approach instead of a full 6-311G** calculation. While the quality of the cluster size estimate does improve as more atoms are treated with the large basis set, very good results are already obtained even if most of the atoms are treated in the small 6-31G basis. For instance, using a 6-311G** basis on the substrate and 6-31G for the protein reproduces the 5 Å to 7–8 Å cluster size effect in both the 2AP and F9 systems to within 0.1 ppm for hydrogen, 0.2 ppm for carbon, 0.4 ppm for nitrogen, and 0.6 ppm for oxygen. Such errors are appreciably smaller than the errors observed from either the point charge embedding or PCM models, and they are much smaller than the errors which arise if the more distant atoms are neglected entirely. They also fall well within the typical errors one expects from DFT for the various nuclei.

Fig. 7.

Errors introduced in the 2AP system by approximating the 5 Å to 7 Å cluster size effect on the isotropic chemical shieldings with a 6-311G**/6-31G locally dense basis approach instead of a full 6-311G** calculation. The cluster size effect can be well-estimated using modest basis set calculations.

The notable success of the ONIOM approach with locally dense basis sets for capturing cluster size effect is unsurprising: these long-range effects largely arise from long-range electrostatics, and even the 6-31G basis does a reasonable job of describing a the electron density at a distance. Compact basis sets like 6- 31G are particularly amenable to linear-scaling chemical shielding approaches (Ochsenfeld et al. (2004); Kussmann and Ochsenfeld (2007); Beer et al. (2011); Kussmann et al. (2013)), which means one can treat quite large systems in this manner.

The efficiency of such ONIOM-style estimates for the cluster size effect will of course depend on the differences in the small and large systems and the basis sets involved. In the example here, the savings is only 5–10%. Larger savings could be obtained if the differences between Basis1 and Basis2 were greater and if a bigger “large” cluster were used.

3.3 Impact on chemical shift prediction

Finally, we examine the impact of techniques like these on the prediction of experimental chemical shifts for the 2AP quinonoid intermediate. Isotopically labeled substrate-coenzyme complex has been synthesized, and several key isotropic ¹³C and ¹⁵N chemical shifts have been measured, as described in Supporting Information. The detailed chemistry of this system is still under experimental investigation, but the structure used here represents one putative model.

To make a preliminary comparison between the calculations and experiments, we rescale the computed chemical shieldings σ_i into chemical shifts δ_i according to:

$${\delta }_i=A{\sigma }_i+B$$ (2)

The parameters A and B were obtained via least-squares fitting the predicted shieldings against the experimental shifts for each model and nucleus type. Given the small number of experimental data points, over-fitting is a significant concern here, and it potentially leads to an overly-optimistic agreement between the calculations and experiment. Still, this straightforward referencing approach provides insight into the potential benefits that can be obtained from these sorts of models without worrying about the details of what the most appropriate referencing schemes are for these protein/substrate systems. Details of the fits are provided in Supporting Information.

The approaches discussed in Sections 3.1 and 3.2 allow one to perform large-basis calculations on large cluster models. As shown in Table 3, the 7 Å model with the 6-311++G** basis on the substrate-coenzyme complex, the 6- 311G** basis out to 3 Å, and the 6-31G basis for the remaining atoms reduces the root-mean-square errors relative to the 5 Å model with the same basis sets by roughly 1 ppm for both carbon (from 3.4 ppm to 2.6 ppm) and nitrogen (5.2 ppm to 4.2 ppm). Using the larger cluster provides a clear benefit here.

Table 3.

Isotropic B3LYP chemical shifts (in ppm) for the isotopically label ¹³C and ¹⁵N atoms in the 2AP quinonoid intermediate.

	5 Å Cluster	7 Å Cluster	5 Å ONIOM	Experiment
Cα (Ser)	108.5	107.8	107.9	105.1
Cβ (Ser)	47.1	46.9	46.9	47.0
C′ (Ser)	176.7	176.1	176.1	173.1
C2 (PLP)	139.2	140.9	140.7	144.6
C3 (PLP)	151.5	151.2	151.2	153.1
C rms	3.4	2.6	2.7
N (Ser)	304.2	303.2	303.2	298.6
N (2AP)	57.2	56.9	56.9	55.9
N1 (PLP)	258.1	259.4	259.4	265.0
N rms	5.2	4.2	4.3

^a6-311++G** on 2AP, 6-311G** out to 3 Å, and 6-31G on the rest.

^bONIOM results correct the 5 Å model using the 6-311++G**/6-311G**/6-31G triple basis model with the difference between the 5 Å and 7 Å model results in the 6-31G basis.

Second, as discussed previously, an ONIOM-style approach provides an effective means for estimating the cluster size effect. For example, taking the same 5 Å triple basis results considered above and correcting for the difference between the 5 Å and 7 Å clusters using inexpensive calculations in which all atoms are modeled using the crude 6-31G basis, we obtain nearly identical chemical shieldings as in the 7 Å model (rms errors of 2.7 and 4.3 ppm for ¹³C and ¹⁵N, respectively; see Table 3).

Further investigation regarding the detailed structure of the 2AP quinonoid intermediate/protein complex and a more careful treatment of the referencing for the predicted chemical shifts are needed to obtain a better understanding of the chemistry in this system. Nevertheless, these encouraging preliminary results suggests that using models such as those discussed here do improve our ability to predict substrate chemical shifts in enzymes.

4 Final Recommendations

When performing NMR crystallography studies on complex protein systems, it is important to converge the ab initio chemical shielding predictions with respect to the theoretical model in order to unravel the interplay among theoretical methods, structural features like protonation states, conformational sampling and dynamics, etc. For typical studies on biological systems using DFT, convergence in this context means using both an adequate basis sets and sufficiently large cluster models.

The calculations presented here demonstrate that it is most critical to saturate the basis on the atoms of interest. Triple-zeta basis sets were employed here, but it might be worthwhile to use even larger ones on the key substrate atoms (Reid et al. (2014)). However, nearest-neighbor atoms, which physically correspond to the hydrogen-bonding partners and the van der Waals cavity of the protein binding pocket are also important and need to be treated accurately. More distant atoms primarily provide an electrostatic environment which is reasonably described even with crude basis sets. Nevertheless, the atoms of interest should be surrounded by a large QM region whenever possible. Based on these insights, we recommend the following modeling strategies for performing QM chemical shielding calculations in protein systems:

1. Use a cluster model extending at least ~7 Å from the key nuclei of interest. One may include longer-range MM interactions, if desired.

2. Employ multi-tier locally dense basis approximations. The requisite size of the basis set meshes well with chemical intuition for the importance of the atoms. For a substrate/protein system, one should employ a large (triple-zeta or better) basis set with diffuse functions for the key substrate atoms, a compact triple-zeta basis without diffuse functions for the adjacent hydrogen bonding partners/van der Waals cavity, and a small, inexpensive basis (e.g. 6-31G) for the more distant atoms. Unsurprisingly, substrate atoms which interact strongly with the protein (e.g. hydrogen bond donors/acceptors, charged functional groups, etc) benefit the most from using a reasonable basis set in the middle tier.

3. If one cannot computationally afford to use a large enough cluster model for the full calculations, the effects of increasing cluster size can be well-estimated using ONIOM-type calculations which combine larger locally dense basis calculations on a smaller cluster with a cluster size correction computed using smaller locally dense basis sets on both the smaller and a larger cluster. This ONIOM approach is much more effective than embedding the smaller cluster in either a polarizable continuum model or simple fixed point charges. Because the long-ranged contributions to the substrate chemical shieldings are typically non-specific, no obvious trends indicate which substrate atoms will be most sensitive to including contributions from a large protein cluster.

Given efficient modern algorithms for DFT chemical shielding calculations and inexpensive computer hardware, these strategies allow one to obtain well- converged quantum mechanical predictions of the chemical shifts in biological systems. The errors introduced by the modeling approximations discussed here will typically fall below those inherent in DFT itself and any errors introduced by inadequacies in the protein geometry and/or dynamical averaging. With such well-converged chemical shieldings in hand, one can begin to tackle the chemically and biologically interesting questions driving the research in the first place.