Cuff-Free Blood Pressure Estimation Using Pulse Transit Time and Heart Rate

Abstract

It has been reported that the pulse transit time (PTT), the interval between the peak of the R-wave in electrocardiogram (ECG) and the fingertip photoplethysmogram (PPG), is related to arterial stiffness, and can be used to estimate the systolic blood pressure (SBP) and diastolic blood pressure (DBP). This phenomenon has been used as the basis to design portable systems for continuously cuff-less blood pressure measurement, benefiting numerous people with heart conditions. However, the PTT-based blood pressure estimation may not be sufficiently accurate because the regulation of blood pressure within the human body is a complex, multivariate physiological process. Considering the negative feedback mechanism in the blood pressure control, we introduce the heart rate (HR) and the blood pressure estimate in the previous step to obtain the current estimate. We validate this method using a clinical database. Our results show that the PTT, HR and previous estimate reduce the estimated error significantly when compared to the conventional PTT estimation approach (p<0.05).

I. Introduction

Blood pressure (BP) is one of the most important vital signs of the cardiovascular system and the general health. It is recommended that BP be measured regularly for health maintenance, and this is especially important for people of advanced age and who have, or are at a high risk of develop, heart disease [1]. BP varies continuously due to physical activity, medication, emotion and stress. Different oscillometric methods, such as stethoscopes and phonocardiograms are conventional non-invasive techniques to measure blood pressure [2]. However, these cuff-based methods have some disadvantages, which limit their use in certain clinical or home settings, especially during certain a certain physical activity in which the cardiac output increases. A continuous BP cannot be measured using cuff-based methods because a pause of at least 1–2 minutes between two BP measurements is necessary to reduce errors in the measurement. Further, the patient may be disturbed by the inflation of the cuff and this disturbance may cause a sudden elevation of the BP. A continuous measurement of blood pressure is desirable in a multitude of clinical and home settings. For example, in perioperative care, the American Society of Anesthesiologists requires continuous perioperative BP monitoring for patients with severe systemic disease [3]. For other patients, conventional intermittent BP monitoring (NBP) may miss important clinical information because BP is not monitored at all times. An intra-arterial catheter has been used to continuously measure BP, but this costly and invasive method increases risks of arterial injury and skin infection [4]. Noninvasive, continuous and cuff-less BP measurement methods are thus highly desirable. Currently, the relationship between the BP and pulse transit time (PTT) has been studied extensively [5,6,] and the PTT has been demonstrated to be a valid and well accepted measure of BP [7,8]. Since PTT can be estimated from the measured ECG and photoplethysmogram (PPG), this method has been used to develop wearable devices to measure BP continuously and conveniently [9]. However, BP measurement using the PTT is not highly accurate due in part to the unaccounted physiological factors in the blood regulation mechanism. The heart rate (HR), for example, has been demonstrated to be correlated with the BP[10]. Whenever a person’s BP decreases, the HR increases in order to pump more blood and the arterial walls contract to increase the BP. As a result, besides the PTT and HR, the previous BP estimate may also play an important role in the current BP estimation. In this paper, we validate a new estimation model using simultaneously recorded arterial blood pressure (ABP), ECG and PPG signals documented in the standard Multi-parameter Intelligent Monitoring in Intensive Care (MIMIC) database [11]. We have found that the PTT, HR and previous BP estimate improve measurement result significantly..

II. Cuffless Blood Pressure Estimation

As the blood flows through arteries, pressure waves propagate at a certain velocity called pulse wave velocity (PWV). The PWV depends on the elastic properties of both arteries and blood. The Moens–Korteweg equation defines PWV as a function of vessel and fluid characteristics [12]:

$$PWV=\frac{L}{PTT}=\sqrt{\frac{E.h}{2r\rho }}$$ (1)

where L is the vessel length, PTT is the time that a pressure pulse spends in transmitting through that length, ρ is the blood density, r is the inner radius of the vessel, h is the vessel wall thickness, and E is the elastic modulus of vascular wall. In this equation, the elasticity parameter E is closely related to BP according to the following equation [13]:

$$E=E_0{e}^{\alpha p}$$ (2)

where α is a constant, E₀ is the zero-pressure modulus of the vessel wall, and P is the BP within the vessel.

Based on these two equations, the BP can be computed from PTT assuming all other parameters are held constant. From (1) and (2), we can obtain a logarithmic dependency between BP and PTT:

$$BP=-\frac{2}{\mathrm{\alpha }}·\mathit{\text{ln}}PTT+\frac{\text{ln}\frac{2\mathrm{r}\mathrm{\rho }{\mathrm{L}}^2}{\mathrm{h}{\mathrm{E}}_0}}{\mathrm{\alpha }}$$ (3)

There are many physical factors that influence cardiac output and BP, such as the blood volume, resistance of the blood vessels, and blood thickness. BP is the product of cardiac output and peripheral resistance. In practice, each individual's autonomic nervous system responds to and regulates all these interacting factors. When BP decreases, the nervous system is stimulated. In response, HR increases in an effort to increase cardiac output and the arterial walls contract to increase BP. In other words, BP is related to both HR and the previous BP [14]. Therefore, we formulate the BP estimation function as:

$$B{P}_n=a·\mathit{\text{ln}}PTT+b·HR+c·B{P}_{n-1}+d$$ (4)

where PTT can be obtained from the time difference between ECG and PPG signals, HR can be easily measured from the ECG, and BP_n−1 is the previous BP estimate. The four coefficients (a,b,c and d) can be calculated by applying the least square method.

III. Data Processing

The MIMIC database, maintained by the Massachusetts Institute of Technology (MIT), is a collection of physiological data recorded from patients in the Intensive Care Unit (ICU). We chose continuous, synchronized ABP, ECG and finger PPG signals for our study. The signals were recorded at 125 Hz with a 12-bit resolution. The following procedure was utilized to extract HR, PTT, and SBP/DBP from the original data.

1) Baseline removal

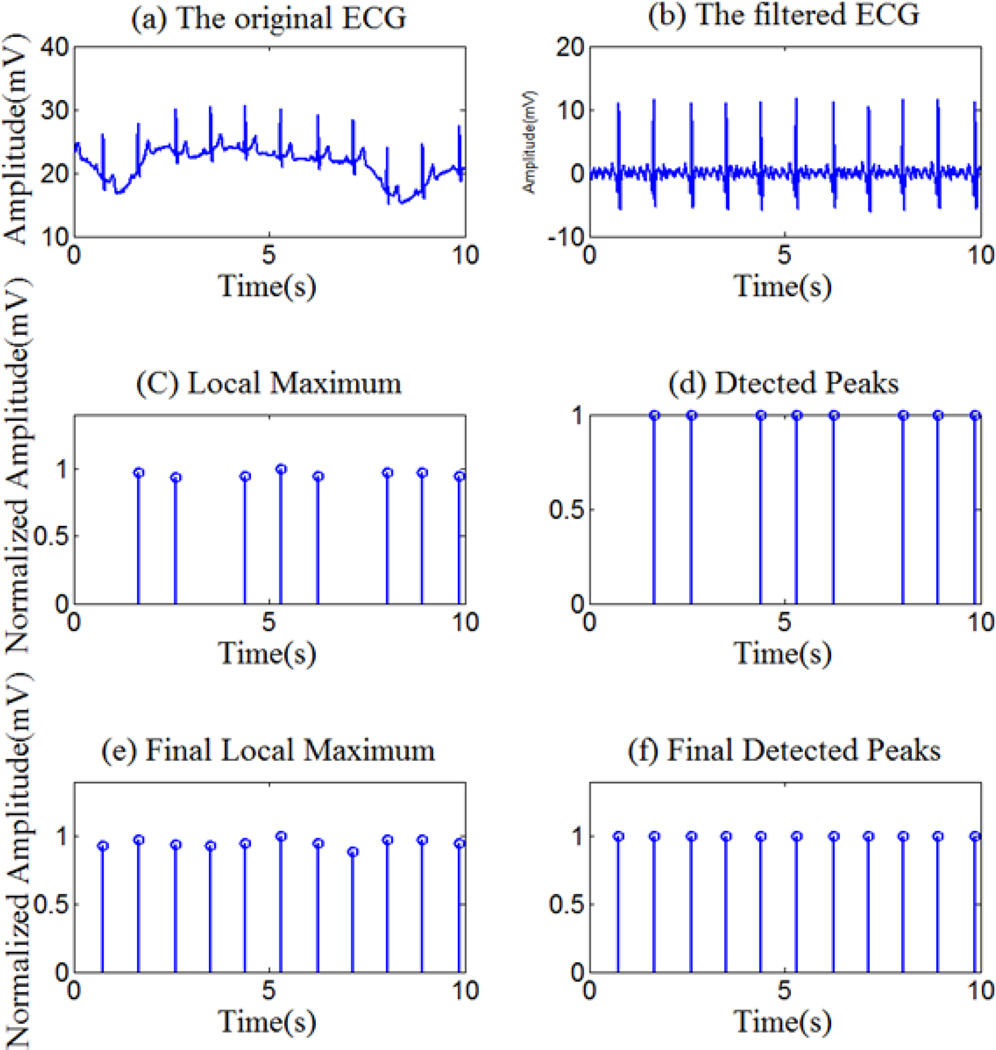
Slow drift component in each signal (ECG, PPG and ABP) is removed using a modified denoising algorithm in the wavelet domain. The input signal is first decomposed into approximation and detail coefficients in different scales. Because the frequency of the drift component is usually low, the approximtion coefficients at the coarsest scale level (correspondng to a frequency around 0.5Hz) were set to zero, before the signal is reconstructed by the inverse wavelet transform. The Daubechies-wavelet was used in this modified denoising procedure. An example of a signal before and after the baseline removal is shown in Fig. 1(a) and (b).

Figure.1.

The original, the filtered ECG and R wave peak detection results

2) Calculation of HR and PTT

After waveket processing, the peaks in the ECG and PPG signals are mostly well-defined. Therefore, we utilize a thresholding method for peak detection. In order to correct variations in signal amplitude and reduce peak detection error, the ECG and PPG signals are normalized with respect to their respective value ranges prior to peak detection. Taking the ECG as an example, first, we use a two-second window within which the maximum signal value is found. This value normally corresponds to an R-peak, but sometimes it does not. In order to aviod false detection, we used a threshold, which is 60% of the maximum value of the peak value computed from all windows to suppress misdetections. However, due to the use of a fixed-size window (two seconds), in some cases, two or more peaks may be present within the same window, thus some peaks may be missed as shown in Fig.1(c) and (d). Thus, in the next step, we estimate the average R-R interval from the detection result. For locations where peaks are missing indicated by a sudden increase in R-R intervals, the input signal is re-examined using the same algorithm but with an adjusted window size according to the average R-R interval. As the result, the missing R-peaks are recovered (Fig.1 (e) and (f)). The HR is determined by calculating the time interval between the nearest R peaks. Similarly, the delay between each R-peak and the corresponding PPG-peak is calculated as the PTT.

The HR and the logorithm of the PTT, denoted by ln(PTT), are normalized using the following equation so that the HR and ln(PTT) are in approximately the same scale:

$$\mathrm{y}=\frac{\mathrm{x}-\text{mean}(\mathrm{x})}{\mathrm{s}\mathrm{t}\mathrm{d}(\mathrm{x})}$$ (5)

where mean(x) and std(x) are the mean and the standard deviation of HR or ln(PTT), respectively, and y is the normalized HR and ln(PTT). The distributions of ln(PTT). and HR are considered normal, so the data points, at which y is greater than 2 or less than −2, are regarded as outliers and thus removed.

3) Detection of SBP and DBP

The peak detection algorithm described previouysly is also used to detect the extrema in the ABP signal. Two types of extrema are identified, local maxima and local minima which correspond to the SBP and DBP, respectively. They are located with a slide window detector sliding from the right to the left. The local maxima, which correspond to the SBP, are detected. Then, near each local maximum, the local minimum, corresponding to a DBP point, is detected within the window. If the minimum is at the edge of the window, the minimum is generally not a DBP point and the window slides one point to the left util a local minimum is found. We repeat this process to obtain all SBP and DBP points.

4)Linear regression model for BP estimation

The regression model (Equation (4)) is built with the least square method for BP estimation. The ten-fold cross-validation method is used to evaluate the model. The input dataset is first randomly divided into ten equal sized subsets. Nine of them are used for training the regression model, while the remaining one is left as the testing data. This validation procedure is then repeated ten times (ten folds) with each subset used once as the testing data. The estimation error for this segment is calculated by averaging the errors in all ten testing subsets.

In each model training, an error bar, which is defined as the 95% confidence interval (CI) of the differences between the ground truth and the estimates using the regression model[15], is obtained. If the boundary values of the CI have the same sign, the estimate is considered biased and the corresponding data points are determined to be outliers. They are then removed from the trainng data and the model is retrained with the updated training data. This process is repeated until the final model is obtained in which no outliers are found or the R-square statistic is above 0.85.

III. RESULTS

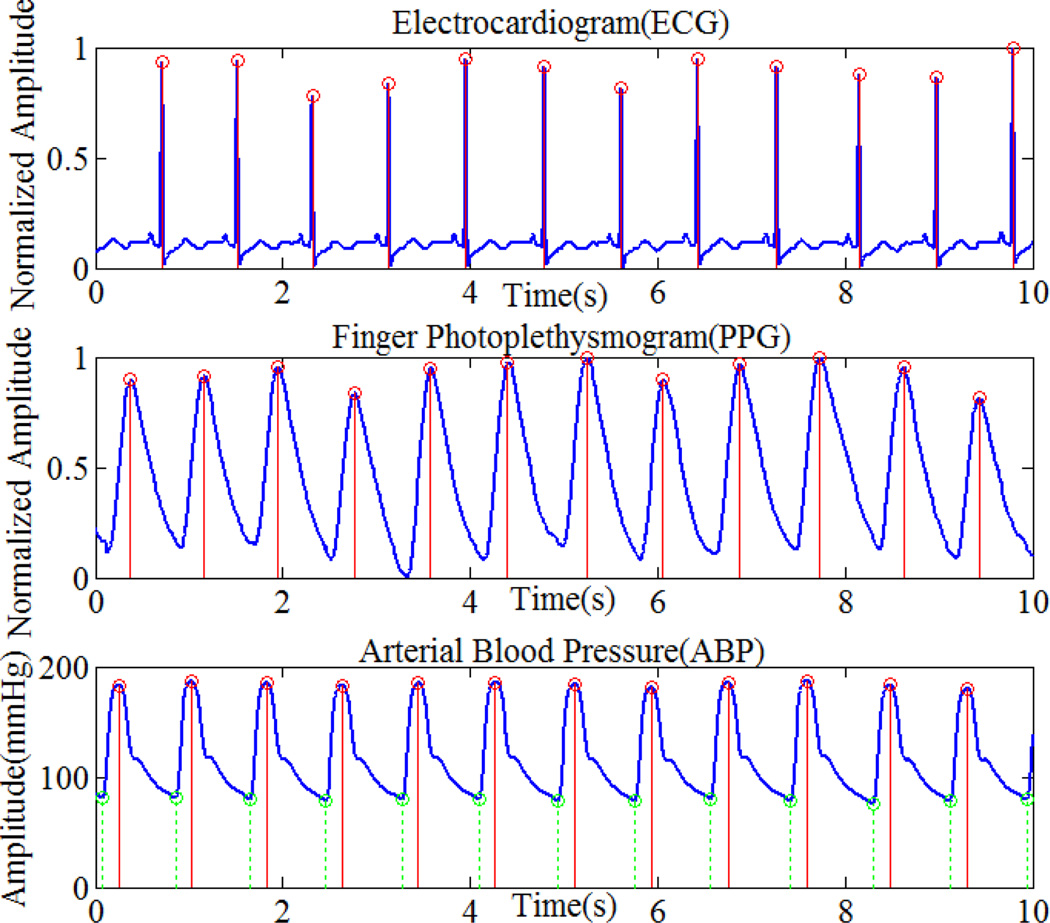
Data recorded from six patients with complete ECG, PPG, and ABP signals were extracted from the MIMIC database. Each data record contains twenty five-minute segments. The PhysioBank Automated Teller Machine (ATM) software was used to extract the signals from the database [11]. Fig. 2 shows part of the ABP data with detected maxima (top panel), R-peaks in the ECG signal (middle panel), and peaks in the PPG signal (bottom panel).

Figure.2.

Maxima of ABP, R-peak of ECG, and peaks of PPG

Table 1 shows the average correlation of BP-PTT and that of BP-HR over the twenty input segments for each patient. The correlation coefficients for both the SBP and DBP cases are more than 0.6, indicating that both the PTT and HR are important for the estimation of BP. However, traditionally, BP has been commonly estimated using PTT only. In order to compare BP estimation performances, we implemented the PTT model (Equation (3)) and our proposed PTT-HR-BP_n−1 model (Equation (4)). For each patient record, twenty pairs of averaged estimation errors were obtained for both models. The mean and the standard derivation of the estimation error of each record are shown in Table 2. A one-sided paired t-test with an alpha value of 0.05 was used to compare whether the average estimation errors obtained from the second models is smaller. Our results show that the average estimation error of the second model was significantly smaller than that of the first model (p<0.05).

Table 1.

Correlation for PTT versus SBP and DBP

Correlation		Arterial Blood Pressure
		SBP(mmHg)	DBP(mmHg)
S1	PTT	−0.7528±0.1222	−0.7789±0.1168
	HR	0.7452±0.1187	0.7878±0.1798
S2	PTT	−0.6753±0.1328	−0.6812±0.0.1272
	HR	0.6673±0.1388	0.6634±0.1872
S3	PTT	−0.7498±0.1565	−0.6878±0.1718
	HR	0.7021±0.1689	0.7234±0.1412
S4	PTT	−0.7982±0.1761	−0.7567±0.1273
	HR	0.7312±0.1547	0.7121±0.1668
S5	PTT	−0.7045±0.1086	−0.6891 ±0.1154
	HR	0.6882±0.1067	0.6432±0.1123
S6	PTT	−0.7789±0.1344	−0.7979±0.1502
	HR	0.7523±0.1225	0.7655±0.1126

Table 2.

Error Mean, Error Standard Deviation (s.d.) and Mean-Square Error(MSE)

SUB	BP (mmHg)	Estimation model
		Model 1			Model 2
		mean	s.d.	Mse	mean	s.d.	Mse
S1	SBP	−0.22	7.54	69.87	0.14	3.45	25.76
	DBP	0.32	6.48	60.11	0.16	4.55	32.29
S2	SBP	0.33	4.67	35.89	−0.14	4.85	4204
	DBP	0.18	5.22	46.57	0.13	4.92	42.14
S3	SBP	0.28	8.79	90.11	−0.12	3.47	24.89
	DBP	0.28	6.02	42.43	−0.21	4.21	30.08
S4	SBP	−0.33	5.72	47.10	0.22	3.42	29.32
	DBP	−0.28	5.44	43.34	0.03	3.87	22.56
S5	SBP	−0.33	7.66	89.97	0.22	4.02	19.97
	DBP	−0.34	7.42	78.77	−0.25	5.48	51.02
S6	SBP	0.15	3.18	25.85	−0.07	3.22	21.95
	DBP	−0.11	3.34	23.42	0.09	2.99	23.09

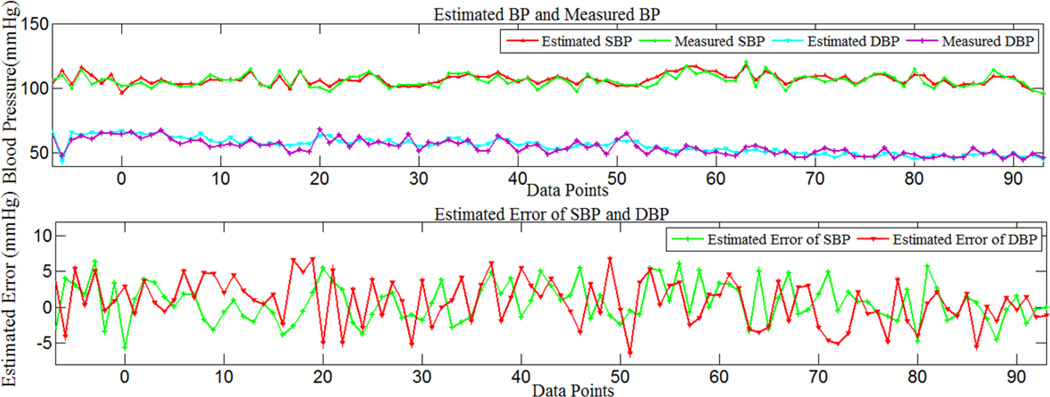
As a typical example, Fig.3 shows the estimated error, measured BP and the estimated BP using the second model for a segment of Record 221. It can be seen that the measured and estimated signals are in close agreement, and the estimated waveform follows the trend of the measured BP waveform. The mean estimated error was less than 1 mmHg.

Figure 3.

Measured and estimated SBP and DBP, estimated errors of SBP and DBP using model 2, for part of record 221.

V. DISCUSSION AND CONCLUSIONS

This paper proposes, justifies, and validates the use of a combination of the PTT, HR and BP_n−1 to estimate the current BP value. Our study on the signals extracted from the MIMIC database showed that there were considerable correlations among these physiological variables, and that taking advantage of these correlations can improve BP estimation significantly.

Since the continuous BP data are not attainable from healthy people, we had to utilize data from patients. The data provided by the MIMIC database were recorded from patients with cardiovascular or pulmonary diseases. Some patients might have taken medications or been treated in certain ways which were not fully documented. Therefore, their BP values may have been affected by these unknown factors. In our future work, we plan to test the model on healthy people using a different measurement as the ground truth. In addition, the ultimate goal of this project is to carry out real-time, continuous measurement of BP unobtrusively using a mobile (e.g., a smartphone) or a wearable device. The new model presented in this paper is suitable for this extremely important application because the required variables, i.e., PTT, HR and BP_n−1, can be obtained easily in practice. We will continue this work which may greatly benefit numerous people who have, or have a high risk to develop, heart disease and certain other life-threatening conditions.