A Framework for Brain Registration via Simultaneous Surface and Volume Flow

Abstract

Volumetric registration of brain MR images presents a challenging problem due to the wide variety of sulcal folding patterns. We present a novel volumetric registration method based on an intermediate parameter space in which the shape differences are normalized. First, we generate a 3D harmonic map of each brain volume to unit ball which is used as an intermediate space. Cortical surface features and volumetric intensity are then used to find a simultaneous surface and volume registration. We present a finite element method for the registration by using a tetrahedral volumetric mesh for registering the interior volumetric information and the corresponding triangulated mesh at the surface points. This framework aligns the convoluted sulcal folding patterns as well as the subcortical structures by allowing simultaneous flow of surface and volumes for registration. We describe the methodology and FEM implementation and then evaluate the method in terms of the overlap between segmented structures in coregistered brains.

1 Introduction

Inter-subject studies for detecting systematic patterns of brain structure and function in human populations require that the data first be transformed to a common coordinate system in which anatomical structures are aligned [1, 2]. Similarly, inter-subject longitudinal studies or group analyses of functional data also require that the images first be anatomically aligned. Such an alignment is commonly performed either with respect to the entire volumetric space or is restricted to the cortical surface [3–7]. While volumetric approaches [8–10] perform well at aligning the interior of the brain e.g. subcortical structures, they often fail to align the folding patterns of the sulcal anatomy [11]. On the other hand, surface based registration techniques align the sulcal folds, but they do not define a volumetric correspondence between points in the interior. In order to overcome the shortcomings of these two types of methods, approaches have been developed recently to combine surface and volume registration [12, 13]. In these methods surface registration is performed first and then used to constrain the full volumetric registration. In contrast to these methods, we present a novel framework in which both surface and volume registrations are performed simultaneously. This is achieved by using an intermediate unit ball parameter space in which the shape differences in the two brain volumes are normalized.

The motivation for using an intermediate parameter space for volumetric registration is derived from surface registration approaches in which the challenging problem of normalizing large folding pattern differences is solved by mapping the surface to a flat space such as a sphere [14, 5, 15] or a square [3]. We extend this idea to volume registration where we first generate a harmonic map of the two volumes to a unit ball and thus generate an initial diffeomorphism between between two volumes exhibiting very different folding patterns on their surfaces. The point correspondence defined by this initial mapping is further refined by using additional information in the form of intensity values and surface curvature information. This approach presents a unified framework in which surface and volume data can be combined together for their joint registration.

2 Methods

2.1 Problem Statement and Formulation

Given two 3D manifolds Ω₁ and Ω₂ representing subject and target brain volumes, with boundaries ∂Ω₁ and ∂Ω₂ representing corresponding cortical surfaces, we want to find a map from Ω₁ to Ω₂ such that ∂Ω₁, the surface of Ω₁, maps to Ω₂, the surface of Ω₂, and the intensities of the images in the interior of Ω₁ and Ω₂ are matched. The boundaries, ∂Ω₁ and ∂Ω₂, representing the cortical surfaces of the two brain volumes are assumed to have a spherical topology. We perform this registration in the following steps:

• – The two surfaces ∂Ω₁ and ∂Ω₂ are flattened and are mapped to spheres.

• – The interior volumes of the two brains Ω₁ and Ω₂ are mapped to the interior of unit balls by 3D harmonic maps.

• – The induced mapping from subject brain Ω₁ to Ω₂ is refined by minimizing a cost function with intensity matching and surface curvatures matching terms.

Parameterization-based methods are commonly used for surface registrations especially for registration of the cortical sheet because the intermediate flat space, either a square or a sphere, provides a convenient common space in which structural and functional surface data can be used for performing the alignment. The large-scale differences are normalized in this representation and so the registration problem is simplified to some extent. The disadvantage of this approach is that the metric distortion that takes place during the flat mapping can affect the registration results in locations where the Jacobian of the map is not close to unity. However this can be accounted for by weighting the cost function by the determinant of the Jacobian for the transformation from subject brain to the target brain.

2.2 Surface-Volume Parameter space

In this section we describe the unit ball parameter space [16–18] used for simultaneous surface and volume registration. As a first step, the cortical surfaces of subject and target denoted by ∂Ω₁ and ∂Ω₂ are mapped to unit balls [19]. We choose the unit ball as a parameter space because the harmonic maps from brain to the ball are known to be diffeomorphic [18]. To compute mappings of the brain manifolds to the unit ball, we first compute a mapping of the brain surface to the unit sphere. To map the interior of the manifold to the interior of the unit ball B(0, 1), the mapping energy

$$E(v)={\int }_{{\Omega }_i}{\Vert \nabla v\Vert }^{2}dV,i=1,2$$ (1)

is minimized to get v with the constraint that the surface ∂N maps to the unit sphere, the boundary of B(0, 1). Here ∇ is the usual gradient operator in 3D Euclidean space and dV denotes the volume integral. This mapping is performed for both the brains Ω₁ and Ω₂. The minimization is performed by using numerical integration over the voxel lattice and finite differences to approximate the gradients. The resulting discretized cost function is minimized by conjugate gradient. The result of this minimization is a harmonic map to the unit ball. This map is known to be diffeomorphic [18]. The one-to-one point correspondence between the brain volume and the unit ball is then used to map the intensity data to the interior of the unit ball and the curvature data to the spherical boundary of the ball (see Fig. 2). In this manner we generate harmonic maps v₁ and v₂ from subject and target brains to the unit ball.

Fig 2.

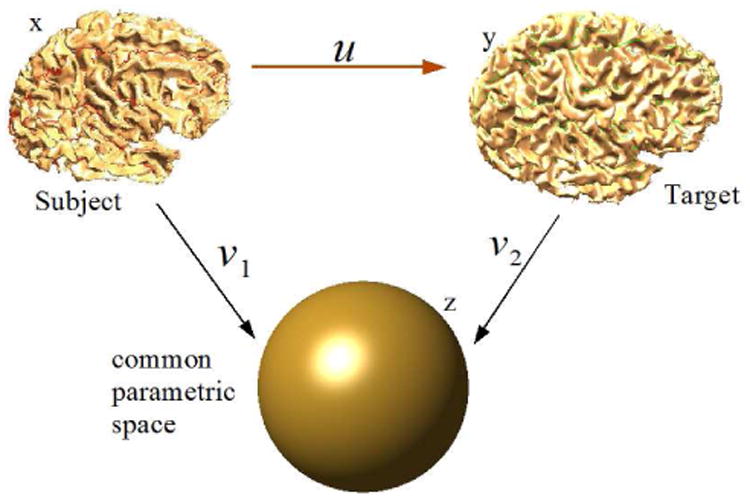
Schematic of our method. The intermediate unit ball is used as a common space for volumetric registration.

2.3 Generation of the Tetrahedral Mesh

We applied TetGen [20] to create a standard unit ball using using 2, 663, 731 tetrahedrons and 81, 920 triangles (see Fig. 1) on its surface. The mapped intensity volumes and curvature maps for the two brains were resampled to the nodes of the tetrahedral mesh, representing the common parameter space, by using linear interpolation. The resampled image intensities and curvatures as shown in figure 2 are used in the subsequent sections for the registration. We denote the resampled intensities are denoted by I₁ and I₂ and curvatures by $I_1^c$ and $I_2^c$.

Fig 1.

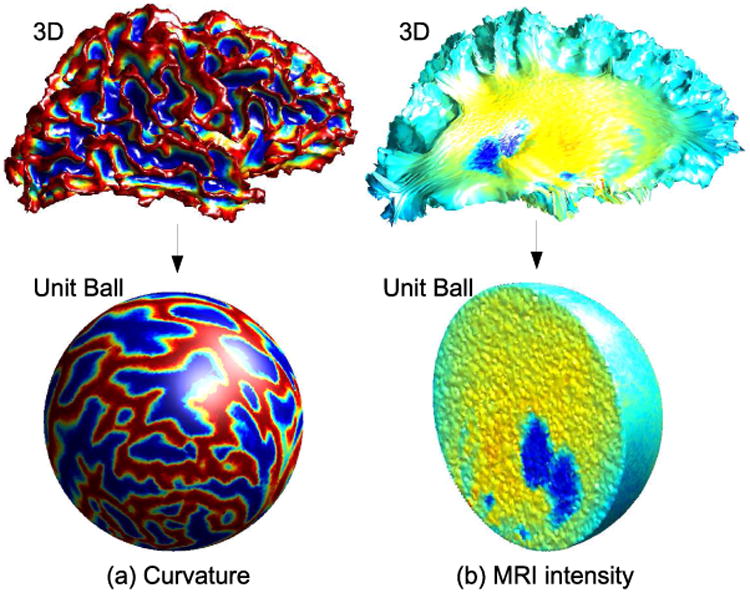
Mapping of (a) the surface curvature to the unit sphere and (b) MRI intensities to the interior of the unit ball.

2.4 Cost Function

In order to register the surface and volume data of the brain, a dissimilarity cost function is minimized. We develop a cost function for registration with four terms designed to control different requirements of the registration warp:

• – We want the intensity across the two brain volumes to match

• – We want the curvature on the surface of the brains to match

• – The deformation from one brain to the other should be smooth

• – The Jacobian of the transformation should be non-negative

Let x = (x₁, x₂, x₃) denote 3D coordinates of the subject, y = (y₁, y₂, y₃) denote 3D coordinates of the target and z = (z₁, z₂, z₃) denotes the 3D coordinates of the unit ball.

Intensity and Curvature Mismatch

The intensity mismatch term is computed with respect to the target coordinates. Let U denotes the unit ball. Therefore we define a intensity mismatch cost:

$$C_1(u)={\int }_U{(I_1(x+d(x))-I_2(x))}^{2}dV$$ (2)

where the integration is over the whole brain volume V. The mapping from subject to target u is u(x) = x + d(x). Similarly for curvature,

$$C_2(u)={\int }_{\partial U}{(I_1^c(x+d(x))-I_2^c(x))}^{2}dS$$ (3)

where the integration is over the whole brain surface ∂Ω₁.

Smoothness of the Deformation

We want the displacement vector field from the subject brain to the target be smooth. This is done by penalizing the displacement by an elastic energy, i.e., C₃(d) corresponding to deformation d [13, 21]:

$$C_3(d)=f=-\mathit{\text{div}}[(I+\nabla d)\widehat{S}]\widehat{S}:\Omega \to {\mathbb{R}}^3,$$ (4)

where Ŝ denotes the second Piola-Kirchoff stress tensor defined by Ŝ = λTr (Ĝ)I + 2μĜ with $\widehat{G}=\frac{1}{2}(\nabla d^T+\nabla d+\nabla d^T\nabla d)$ representing the Green-St. Venant strain tensor. The coefficients λ and μ are Lamés elastic constants. Commonly, these coefficients are used in formulae for computing the Young's modulus $Y=\mu \frac{3\lambda +2\mu }{\lambda +\mu }$ and the Poisson ratio $\nu =\frac{\lambda }{2(\lambda +\mu )}$. Linearization of (4) using Fréchet derivatives leads to

$$C_3(d)=-\mathit{\text{div}}(S),$$ (5)

where, S = λTr(G) + 2μG is the linearized stress tensor and $G=\frac{1}{2}(\nabla d+\nabla d^T)$ is the linearized strain tensor [13]. The elasticity operator C₃ is discretized by using a finite element method as described in the Appendix. In brief, the equilibrium equation in (5) is formulated by applying a variational principle for energy minimization, that leads to a quadratic form d^TKd, where d = [d₁, d₂…, d_N]^T is the vector of displacements at N nodes in the tetrahedral mesh. The matrix K discretizes the elastic energy operator and is defined in the Appendix. The discretized elastic energy becomes:

$$C_3(d)=d^{T}Kd.$$ (6)

Non-positive Jacobian

We want the transformation to be non-singular and hence we would like to have a large penalty on negative and small Jacobian. We use the chain rule to compute the Jacobian

$$D(u){|}_x=D(v^{-1}\circ \stackrel{\sim }{u}){|}_x=D(v_2^{-1}){|}_{v_1(x)}\circ D({\stackrel{\sim }{v}}_1){|}_x$$ (7)

where D denotes the derivative operator. Therefore, its determinant is calculated as

$$|D(u){|}_x|=|D(v_2^{-1}){|}_{v_1(x)}||D(v_2){|}_x|$$ (8)

$$={|D(v_2){|}_{v_1(x)}|}^{-1}|D(v_2){|}_x|$$ (9)

the associated cost function can be calculated

$$C_4(u)=\int {(1-\mathrm{\text{sgm}}(|D(u){|}_x|))}^{2}dV$$ (10)

where $\mathrm{\text{sgm}}(x)=\frac{1}{1+e^{-t}}$. This cost function penalizes small and negative Jacobians and thus reduces the probability of folding in the registration maps.

3 Volume Image Displacement Vector Field

The key to the function minimization is computing derivatives of the intensity difference cost function (eq. 2) on the tetrahedral mesh inside of the unit ball, and curvature difference cost function (eq. 3) on the triangulated mesh of the sphere. Here we show the discretization of the intensity image for the tetrahedral mesh using finite elements. Discretization of the curvature image on the triangulated mesh is performed similarly, except that in case of surface, the vector field on the sphere is constrained to be tangential to the sphere.

3.1 Tetrahedral mesh image similarity cost function

The intensity dissimilarity cost function (eq. 2) for a tetrahedral mesh is given by:

$$C(d_1,d_2,d_3)=\iiint {[I_1(z_1+d_1(z),z_2+d_2(z),z_3+d_3(z))-I_2(z_1,z_2,z_3)]}^{2}d{z}_{1}d{z}_{2}d{z}_3$$

Let $I_1(z_1+d_1(z),z_2+d_2(z),z_3+z_3(z))={\sum }_{j\in V}{\widehat{I}}_1^j{\varphi }_j(z_1,z_2,z_3)$ where V is the set of vertices and ϕ_j(z₁, z₂, z₃) denotes piecewise linear interpolating basis functions [22], ${\widehat{I}}_1^j$ is the warped subject image I₁(z₁ + d₁, z₂ + d₂, z₃ + d₃) interpolated at the set of vertices and $I_2(z_1,z_2,z_3)={\sum }_{j\in V}{I}_2^j{\psi }_j(z_1,z_2,z_3)$ where $I_2^j$ is I₂(z₁, z₂, z₃) interpolated at the vertex points. Also let $d_1(z_1,z_2,z_3)={\sum }_{j\in V}{z}_1^j{\psi }_j(z_1,z_2,z_3)$, $d_2(z_1,z_2,z_3)={\sum }_{j\in V}{d}_2^j{\psi }_j(z_1,z_2,z_3)$ and $d_3(z_1,z_2,z_3)={\sum }_{j\in V}{d}_3^j{\psi }_j(z_1,z_2,z_3)$.

Therefore the intensity dissimilarity cost function becomes

$$C({\mathit{d}}_{\mathbf{1}},{\mathit{d}}_{\mathbf{2}},{\mathit{d}}_{\mathbf{3}})=\iiint {(\sum _{j\in V}({\widehat{I}}_1^j-I_2^j){\psi }_j(z_1,z_2,z_3))}^{2}d{z}_{1}d{z}_{2}d{z}_3$$

We minimize the intensity difference cost function by using gradient descent. Therefore the gradient of the cost function needs to be calculated. The derivative with respect to one coordinate is given by:

$$\frac{\partial C}{\partial d_1^k}=\iiint \sum _{j\in V}2({\widehat{I}}_1^j-I_2^j){\psi }_j(z_1,z_2,z_3)\frac{\partial I_1(z_1+d_1(z),z_2+z_2(z),z_3+d_3(z))}{\partial (z_1+d_1^k)}\frac{\partial (z_1+d_1(z))}{\partial (d_1^k)}d{z}_{1}d{z}_{2}d{z}_3=\iiint \sum _{j\in V}2({\widehat{I}}_1^j-I_2^j){\psi }_j(z)\frac{\partial I_1(z_1+d_1(z),z_2+d_2(z),z_3+d_3(z))}{\partial (z_1+d_1^k)}{\psi }_k(z)d{z}_{1}d{z}_{2}d{z}_3=2\sum _{j\in V}({\int }_z{\psi }_j(z){\psi }_k(z)d{z}_{1}d{z}_{2}d{z}_3)W^j,$$

where W^j indicate the rest of terms. Derivatives with respect to coordinates $u_2^j$ are found similarly. The terms in the integral have a closed form for the tetrahedral mesh and are given by:

$${\int }_{z_1,z_2,z_3}{\psi }_j(z_1,z_2,z_3){\psi }_k(z_1,z_2,z_3)\mathit{\text{dxdydz}}=\{\begin{array}{cc}20{\sum }_{t\in T_{jk}}{V}_t& j=k\\ 10{\sum }_{t\in T_{jk}}{V}_t& j\ne k\end{array}$$

where T_jk denotes a set tetrahedrons with vertices j and k [22]. The cost function C(d) = C₁(d) + C₂(d) + C₃(d) + C₄(d) is minimized by using steepest descent. The point correspondence between the two brains induced in their unit-ball representations is then applied to the 3D volumes to find a displacement field in 3D using linear interpolation.

4 Implementation and Results

Assuming T1 weighted MR images of the subject and the target brains, the method assumes extracted cortical surface and pial surface, as well as, the brain masks corresponding to the subject and target brains. Here we used a combination of BrainSuite [23] and FreeSurfer [5] for surface extraction, spherical mapping and computation of the curvature. This spherical representation was then used as described in Sec. 2.3 for generating a volumetric harmonic map. This sequence of operations is performed for both target and subject brains to generate a unit ball representation of the two brains. The registration of the two unit ball representations of the brains is then performed and the mapping induced by this intermediate unit ball space is applied to the 3D volumes. The registration results are shown in Fig. 4. For validating our method we used manually labeled brain data from IBSR database at the Center for Morphometric Analysis at Massachusetts General Hospital. These data include volumetric MR data and hand segmented and labeled structures. We then applied the HAMMER software and our method. HAMMER is an automated method for volume registration which is able to achieve improved alignment of geometric features by basing the alignment on an attribute vector that includes a set of geometric moment invariants rather than simply the voxel intensities. To evaluate accuracy, we computed the Dice coefficients [24] for each subcortical structure, where the structure names and boundaries were taken from the IBSR database. The method was implemented in Matlab and in a current non-optimized implementation takes 8 hours to perform a total of 100 iterations of gradient descent on a Pentium IV 3.2GHz desktop workstation. We performed 100 iterations of gradient descent. Reduction of the cost function with iteration number is shown in Fig. 3(c). Dice coefficients averaged over all structures show a small improvement compared to HAMMER. More importantly, the resulting registration has one to one correspondence between all points on the cortical surface and should have improved sulcal alignment due to the curvature matching term in our cost function. A more detailed validation will quantify performance in terms of volumetric and surface alignment.

Fig 4.

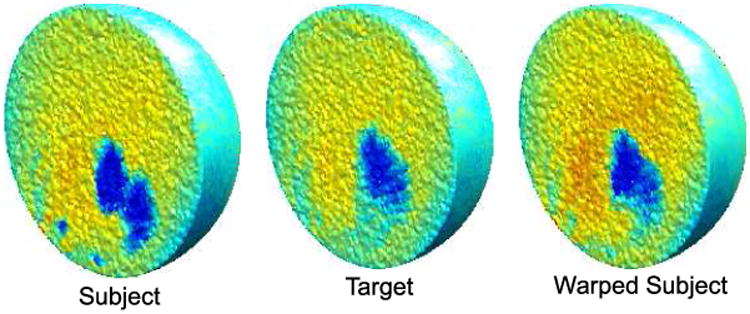
MR intensity images in the tetrahedral mesh of the unit ball space for subject, target and warped subject.

Fig 3.

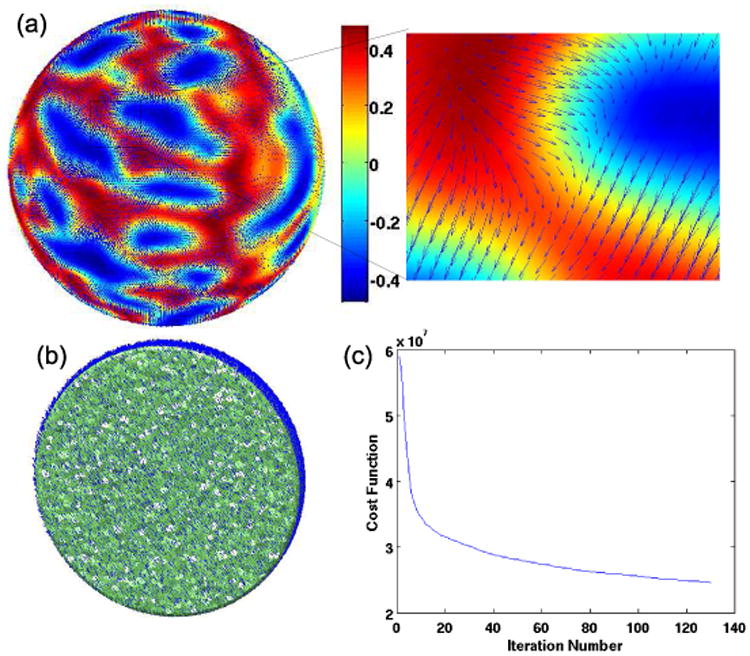
(a) Displacement field on the surface overlaid on the curvature map, (b) volumetric displacement field (c) cost function as a function of iteration number.

5 Discussion and Conclusion

We presented a parameterization-based framework for registration in which surface-based and volumetric features can be combined together for registration. We used MR intensity as a volumetric features and curvature as surface-based feature. For multimodality images, additional volumetric features can be used if available. By mapping the two brains to the unit ball and performed the registration in the parameter space, instead of the 3D space, the sulcal folding pattern differences between the two brains are normalized. This framework also allows for the surfaces to flow while internal MR intensity values register. Note that our method is limited to brain representations with a genus zero surface which might not be the case for abnormal anatomy, e.g. when legions are present. In such cases, a mask could be used for the brains with abormalities, with cost function modified appropriately to exclude the differences in the masked region. The method presented aligns cortical surface as well as subcortical structures accurately in the volumetric space by performing their simultaneous alignment.

Fig 5.

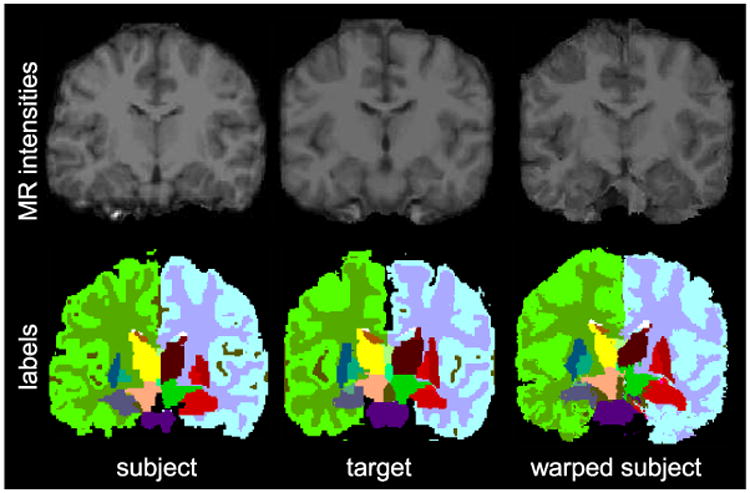
MR intensity images as well as subcortical labels for subject, target MR and warped subject.

Table 1. Comparison of Dice coefficients.

Subcortical Structure	HAMMER	Our Method
Left Thalamus	0.7365	0.8463
Left Caudate	0.5820	0.6912
Left Putamen	0.5186	0.7700
Left Hippocampus	0.6837	0.8918
Right Thalamus	0.8719	0.8291
Right Caudate	0.8107	0.6474
Right Putamen	0.6759	0.7862
Right Hippocampus	0.5974	0.8188
Average dice coeffs	0.7658	0.7920

Appendix

The solution to the elastic energy minimization problem in section 2.4 is obtained by finite element method. We use tetrahedral elements in order to perform the volumetric discretization of the elastic energy. The objective is to get the displacement field at every point in the unit ball. The 3D unit ball is divided into tetrahedral elements such that every point in the space lies inside exactly one tetrahedron. We denote the 3 spatial coordinates by x, y, z for simplicity. We assume that the displacement field d(x, y, z) is piecewise linear. i.e., if the point is inside tetrahedron, then

$$d(x,y,z)=a_0^i+a_1^{i}x+a_2^{i}y+a_3^{i}z,$$ (11)

for some coefficients $a_0^i$, $a_1^i$, $a_2^i$, $a_3^i$. Therefore, for the tetrahedron i with nodes ( $x_1^i$, $y_1^i$, $z_1^i$), ( $x_2^i$, $y_2^i$, $z_2^i$), ( $x_3^i$, $y_3^i$, $z_3^i$), and ( $x_4^i$, $y_4^i$, $z_4^i$), we can write expressions for u in matrix form as:

$$\left[\begin{array}{c}d(x_1^i,y_1^i,z_1^i)\\ d(x_2^i,y_2^i,z_2^i)\\ d(x_3^i,y_3^i,z_3^i)\\ d(x_4^i,y_4^i,z_4^i)\end{array}\right]=\underset{M}{\underbrace{\left[\begin{array}{cccc}1& x_1^i& y_1^i& z_1^i\\ 1& x_2^i& y_2^i& z_2^i\\ 1& x_3^i& y_3^i& z_3^i\\ 1& x_4^i& y_4^i& z_4^i\end{array}\right]}}\left[\begin{array}{c}{a}_0^i\\ a_1^i\\ a_2^i\\ a_3^i\end{array}\right].$$ (12)

Therefore, the derivative operators for a tetrahedral element el are given by

$$D_x^{\mathit{\text{el}}}=\frac{1}{|M|}{\left[\begin{array}{c}{z}_3{y}_4-y_3{z}_4+y_2{z}_4-y_4{z}_2-y_2{z}_3+y_3{z}_2\\ y_3{z}_4-z_3{y}_4-y_1{z}_4+y_4{z}_1+y_1{z}_3-y_3{z}_1\\ z_2{y}_4-y_2{z}_4+y_1{z}_4-y_4{z}_1-y_1{z}_2+y_2{z}_1\\ y_2{z}_3-z_2{y}_3-z_3{y}_1+z_1{y}_3+y_1{z}_2-z_1{y}_2\end{array}\right]}^T,$$ (13)

$$D_y^{\mathit{\text{el}}}=\frac{1}{|M|}{\left[\begin{array}{c}{z}_3{x}_4-x_3{z}_4+x_2{z}_4-x_4{z}_2-x_2{z}_3+x_3{z}_2\\ x_3{z}_4-z_3{x}_4-x_1{z}_4+x_4{z}_1+x_1{z}_3-x_3{z}_1\\ z_2{x}_4-x_2{z}_4+x_1{z}_4-x_4{z}_1-x_1{z}_2+x_2{z}_1\\ x_2{z}_3-z_2{x}_3-z_3{x}_1+z_1{x}_3+x_1{z}_2-z_1{x}_2\end{array}\right]}^T,$$ (14)

$$D_z^{\mathit{\text{el}}}=\frac{1}{|M|}{\left[\begin{array}{c}{y}_3{x}_4-x_3{y}_4+x_2{y}_4-x_2{y}_4-x_2{y}_3+x_3{y}_2\\ x_3{y}_4-y_3{x}_4-x_1{y}_4+x_4{y}_1+x_1{y}_3-x_3{y}_1\\ y_2{x}_4-x_2{y}_4+x_1{y}_4-x_4{y}_1-x_1{y}_2+x_2{y}_1\\ x_2{y}_3-y_2{x}_3-y_3{x}_1+y_1{x}_3+x_1{y}_2-y_1{x}_2\end{array}\right]}^T,$$ (15)

and,

$$D_x=\sum _{\mathit{\text{el}}}r(D_x^{\mathit{\text{el}}}),D_y=\sum _{\mathit{\text{el}}}r(D_y^{\mathit{\text{el}}}),D_z=\sum _{\mathit{\text{el}}}r(D_z^{\mathit{\text{el}}}),$$ (16)

where r is a resizing function that keeps track of indices of the individual nodes in the whole mesh. This kind of re-indexing is commonly done in FEM techniques [22]. Let the matrices L, L^W and K be defined as

$$L=\left[\begin{array}{ccc}{D}_x& 0& 0\\ 0& D_y& 0\\ 0& 0& D_z\\ D_y& D_x& 0\\ 0& D_z& D_y\\ D_z& 0& D_x\end{array}\right],$$ (17)

$$L^W=\left[\begin{array}{ccc}(1-\nu )D_x& \nu D_y& \nu D_z\\ \nu D_x& (1-\nu )D_y& \nu D_z\\ \nu D_x& \nu D_y& (1-\nu )D_z\\ \frac{1-2\nu }{2}{D}_y& \frac{1-2\nu }{2}{D}_x& 0\\ 0& \frac{1-2\nu }{2}{D}_z& \frac{1-2\nu }{2}{D}_y\\ \frac{1-2\nu }{2}{D}_z& 0& \frac{1-2\nu }{2}{D}_x\end{array}\right],$$ (18)

$$K=\frac{Y}{(1+\nu )(1-2\nu )}{L}^T{L}^W.$$ (19)

Let the x, y, z components of the displacement (U_x, U_y, U_z) at nodal points is arranged in a column U = [U_x, U_y, U_z]^T. Then the elastic energy, without any external forces, is given by

$$E_{\mathit{\text{elastic}}}(U)=U^{T}KU.$$ (20)