Abstract
Semilocal and hybrid density functional theory was used to study the charge transfer and the energy-level alignment at a representative interface between an extended metal substrate and an organic adsorbate layer. Upon suppressing electronic coupling between the adsorbate and the substrate by inserting thin, insulating layers of NaCl, the hybrid functional localizes charge. The laterally inhomogeneous charge distribution resulting from this spontaneous breaking of translational symmetry is reflected in observables such as the molecular geometry, the valence and core density of states, and the evolution of the work function with molecular coverage, which we discuss for different growth modes. We found that the amount of charge transfer is determined, to a significant extent, by the ratio of the lateral spacing of the molecules and their distance to the metal. Therefore, charge transfer does not only depend on the electronic structure of the individual components but, just as importantly, on the interface geometry.
Keywords: integer charge transfer, density functional theory, alkali halides, copper, TCNE, charge localization, growth, work function, coverage dependence
Inorganic/organic hybrid interfaces present a versatile avenue for improving inorganic electronic devices. Intriguing functionalities, such as molecular switches,1,2 thermoelectrics,3,4 cargo-lifters,5 memories,6 transistors,7−9 or spintronics10 have already been demonstrated. Moreover, cheap, easy-to-process, and mechanically flexible light-emitting or light-harvesting devices11−15 are within reach.
The key to optimizing the interface functionality lies in a systematic, fundamental understanding of its electronic structure. Of particular interest is the energy-level alignment at the interface between weakly coupled inorganic and organic components since it determines important properties such as the Seebeck coefficient16 or the electrical conductance.17,18 In organic (opto-)electronic devices in particular, charge transfer between a metallic electrode and layers of semiconducting molecules governs the injection of electrons or holes into the active organic device component or the collection of electrons or holes from the active organic device region.19−23 Optimizing this charge injection or extraction can significantly improve the performance of, e.g., organic light-emitting diodes (OLEDs) for display and lighting applications or organic photovoltaic cells (OPVCs).8 Decades of intense research have revealed that, for optimal performance, the Fermi level should be brought into resonance with the occupied manifold of molecular states for a hole injecting or extracting metallic electrode and into the unoccupied manifold for an electron-injecting or -extracting electrode. For such Fermi-level positions, interfacial charge transfer is promoted already in the absence of an applied bias voltage.8
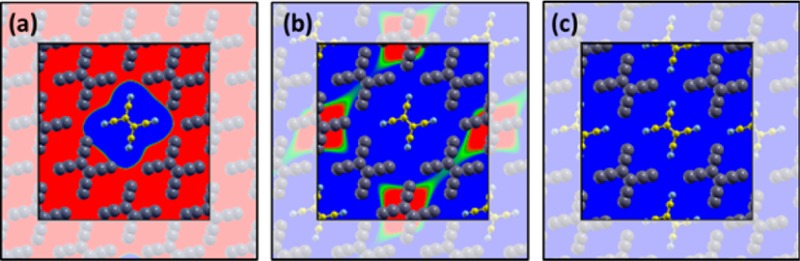
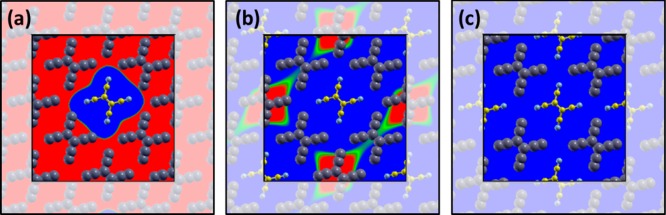
However, the mechanisms and the microscopic details of interfacial charge transfer are still under debate.24,25 When the surface of an inorganic substrate is completely covered by an organic material, experimental and theoretical studies typically report concordantly that the charge transfer per molecule is less than one.26−33 However, it is often unclear whether the excess charge is distributed homogeneously among all molecules, leading to (formally) fractionally charged moieties (Figure 1b), or whether some molecules are integer charged, while others remain neutral (Figure 1c). Fractional-charge transfer (FCT), characterized by a partial filling of the frontier orbitals of all adsorbates, has been repeatedly reported for a variety of molecules on atomically clean metal surfaces.29,28,34−36 A number of density-functional theory (DFT) based atomistic calculations support the FCT scenario in such systems,37−42 revealing a complex interplay between electron-donation from the substrate to the molecule and back-donation from the molecule to the substrate, which is often accompanied by an interaction-induced distortion of the molecular geometry.43,34,32,44
Figure 1.

(a) Level alignment of a metal and a molecular electron acceptor prior to interaction. (b) Weak chemisorption: hybrid metal–molecule states form, leading to a laterally homogeneous layer of partially filled adsorbates. (c) Physisorption: charge tunnels from the substrate to individual adsorbate molecules. Other adsorbate molecules remain electrically neutral.
The alternative scenario of integer charge transfer (ICT) has been invoked for an equally broad range of systems,45−47 in particular for weakly interacting interfaces,48 when the frontier molecular orbitals cannot hybridize with the metal substrate due to spacer groups,49 when the substrate is chemically inert,30,50−52 or when molecules and metal are electronically decoupled by an ultrathin buffer layer. Such buffer layers can easily arise from unintentional surface contamination or oxidation during sample handling, but alkali halide interlayers, in particular, are sometimes also deliberately introduced because they have been found to dramatically increase the performances of OLEDs and OPVCs.53−55
While the phenomenological features of ICT and FCT can be qualitatively understood within the framework of the (extended) Hubbard and the Newns–Anderson56,57 model, respectively, the technological relevance of charge transfer across metal/(insulator/)organic interfaces and the continuous drive to optimize materials and device geometries necessitates a deeper, microscopic understanding. However, insights from atomistic, first-principles electronic-structure calculations, abundant for the FCT case, are suspiciously absent for ICT. Note that while some DFT-based studies do find molecules with (almost) integer charge (e.g., refs (49) and (58)), they do not reproduce the coexistence of charged and uncharged molecules, i.e., the lateral inhomogeneity within monolayers, which are an integral part of the ICT model. We attribute this, at least in part, to the way such calculations are commonly done. On the one hand, ICT systems inherently exhibit lateral inhomogeneity and capturing it requires supercells that are sufficiently large to contain both charged and uncharged molecules, which is associated with substantial computational costs. On the other hand, the method of choice is usually density functional theory with (semi)local functionals. These functionals tend to artificially overdelocalize electrons, thereby unphysically favoring fractional over integer charge.59 While this delocalization problem can, in principle, be mitigated by using hybrid functionals, the further increase in computational cost associated with their use has only recently made their application to interfacial charge-transfer systems tractable.
Here, we report on an extensive DFT study of a prototypical metal/(insulator/)organic charge-transfer system using both semilocal and hybrid functionals. We start by studying the small organic acceptor tetracyanoethene (TCNE) adsorbed directly onto a Cu(100) surface, as shown in Figure 2a. We demonstrate that, in this case, both types of density functionals produce FCT and yield qualitatively the same electronic structure. This is reflected in consistent predictions for observables like the core and valence density of states, intramolecular bond lengths, or the adsorption-induced work-function modification, ΔΦ, which is an indicator for the amount of interfacial charge transfer. However, when we electronically decouple the TCNE layer from the copper substrate with a double layer of NaCl, we find that semilocal and hybrid functionals now yield diverging results for the charge-transfer mechanism, which is clearly reflected in the aforementioned observables. Last, we discuss how the geometry of the interface, in particular the ratio of the spacing between the molecules and the distance between the molecular layer and the metal, determines the amount of charge transfer in the ICT case. Using a simplified model, we then analyze how this affects the coverage-dependence of ΔΦ for different growth modes of the organic adsorbate.
Figure 2.

Systems investigated in this work: side view of the unit cell of TCNE on (a) Cu and (b) one double-layer NaCl on Cu. The inset in (a) shows the chemical structure of TCNE. (c) Top view of the Cu/NaCl/TCNE system, with the unit cell employed in the calculations highlighted. Color legend: brown, Cu; blue, N; gray, C; yellow, Na; green, Cl.
Results and Discussion
TCNE on Cu(100)
The organic molecule TCNE is a strong electron acceptor with its gas-phase electron affinity experimentally determined to lie between 2.360 and 3.2 eV.61 It readily forms charge-transfer complexes with copper,62,63 and in addition, CN-bearing molecules are known to (weakly) chemisorb on Cu surfaces,29,64 which, according to the classification by Braun et al.,48 is expected to lead to FCT. The choice of TCNE/Cu(100) is furthermore motivated by practical considerations. Scanning tunneling microscopy (STM) has revealed that TCNE forms extended, well-ordered, rectangular monolayers on this substrate.65 We note that here, in order to use a Cu supercell that is commensurate with an NaCl layer (see below), we had to deviate to a rhombohedral packing in order to maintain a distance of approximately 7.2 Å between the individual TCNE molecules, which is observed experimentally.66 This allows us to consider up to eight molecules per unit cell (see Figure 2 and discussion in the Methods) without affecting the conclusions presented in this work. Supercells of this size, or larger, are critical if ICT is to be allowed to occur in the calculations in principle, especially if predictions about the ratio of charged and uncharged molecules are of interest.
We start to characterize this system using DFT with the semilocal functional by Perdew, Burke, and Ernzerhof (PBE),67 augmented by the vdWsurf scheme68,69 to account for the missing long-range van der Waals forces (see the Methods). The same (or similar) functional(s) have been used in the past to study metal/organic interfaces, and40,70,34 despite the fact that the polarization-induced band gap renormalization at metal surfaces is absent in PBE,71,72 the obtained ΔΦs and densities of states (DOS) have often been found to be in good agreement with experimental results.37−42
Here, after geometry optimization of our Cu/TCNE interface, we find that all eight molecules in the unit cell buckle slightly and adsorb with the nitrogen atoms closer to the surface than with the C=C backbone (Figure 2a). This geometry, which is corroborated by STM,65 is a typical indication for weak chemisorption. Despite the fact that both Pauli pushback73 and the bending-induced molecular dipole64 act to reduce the work function, we find a positive ΔΦ of ca. 0.4 eV, which can be explained only with electrons transferring from Cu to TCNE.74 To study their spatial distribution within the molecular layer, we calculated the adsorption-induced electron-density rearrangement, Δn, as
| 1 |
where nsys is the electron density of the combined system and nslab and nmonolayer are the electron densities of the isolated Cu slab and the isolated TCNE monolayer, respectively, both in their geometry after adsorption. The result, depicted in Figure 3a, clearly shows that the additional electrons are completely delocalized across the entire monolayer. All molecules are equivalent, and moreover, the shape of the electron density on each molecule closely resembles the TCNE LUMO, shown in Figure 3b. The persistence of free-molecule orbitals is another sign of weak chemisorption,75 which allows us to study the bonding mechanism in more detail.
Figure 3.

(a) Electron-density difference Δn, in PBE, upon adsorption of TCNE on Cu. For the sake of clarity, the Cu atoms are omitted. The unit cell is highlighted, and part of the surrounding layer is shown for orientation. (b) LUMO of a TCNE molecule in the gas phase. (c) CN orbitals responsible for bonding to the surface.
The density of states in the adsorbate layer is shown separately for each molecule in Figure 4a. It corroborates that all molecules are essentially equal. Furthermore, it illustrates that the TCNE LUMO-derived peak (now called LUMO′) is noticeably broadened, reflecting its hybridization with the surface. Zooming into the region around the Fermi energy, EF, Figure 4b reveals that the LUMO′ level is mostly, but not completely, below the Fermi energy (EF). Formal occupations for each molecular orbital can be derived by projecting the density of states of the entire system onto the molecular orbitals of TCNE76 and by integrating the resulting “MO–DOS” up to EF. This procedure reveals a filling of each LUMO by ca. 1.8 electrons. At the same time, the occupation of several lower lying CN-orbitals (depicted in Figure 3c) is reduced, indicating electron back-donation29,64 from TCNE to the metal. As a result, all eight molecules exhibit a (Mulliken) charge of only ca. 0.25 electrons each. This result is in excellent agreement with the values obtained previously by Bedwani et al.,66 who calculated the same system using the local-density approximation to the exchange-correlation functional.
Figure 4.

TCNE adsorbed on Cu. (a, d) Density of states near the Fermi edge, projected onto each molecule individually and vertically offset for clarity. Occupied levels are shaded. (b, e) Kohn–Sham N 1s levels, convoluted by a Gaussian function with σ = 0.5 eV. (c, f) Bond lengths of the central C=C bond after adsorption. For comparison, the optimized values for the neutral, the singly negatively, and the doubly negatively charged molecule in the gas phase are shown. Panels a–c show results for the PBE functional and d–f for the PBEh* functional.
Another indicator for charge transfer is the length of the central C=C bond in TCNE. For each molecule in the adsorbed layer, this quantity is shown in Figure 4c. Although all molecules carry a charge of significantly less than 1 electron (see above), they assume a C=C bond length comparable to that of the TCNE dianion in the gas phase. The reason for this lies in the aforementioned peculiarities of electron transfer. By definition, the TCNE dianion in the gas-phase is obtained by filling two electrons into the LUMO of the neutral molecule and also for TCNE/Cu(100) the occupation of this orbital is found to be close to two. Furthermore, the filling of the LUMO weakens the C=C bond because it is antibonding with respect to the central molecular axis (Figure 3b). This causes the observed elongation of the C=C bond. In contrast, the CN orbitals responsible for electron back-donation to Cu (depicted in Figure 3c) are nonbonding with respect to the C=C bond, and therefore, their occupation does do not affect its length.
In summary, all quantities we discussed fit the FCT picture. However, semilocal functionals are known to artificially overdelocalize electrons,59 yielding fractional electron transfer even in systems where this is clearly unphysical, such as dimers at large interatomic distance,77 during the dissociation of charged homonuclear dimers,78 or of heteronuclear dimers like HF.78−80 The problem originates from the so-called many-electron self-interaction error.81 This term describes the fact that semilocal functionals consistently underestimate the total energy of a given system for any fractional electron number, which for exact DFT would be piecewise linear between integer fillings.81 The many-electron self-interaction error, which is sometimes also referred to as a delocalization error, can be mitigated by using hybrid functionals,82 which mix a fraction α of Hartree–Fock exchange with semilocal exchange (cf. discussion in the Supporting Information). It is well documented that a sufficiently large α will cause the localization of charge in molecules or bulk materials when the number of electrons is kept constant.83−87 Whether this also occurs when the material is coupled to a charge reservoir (the metal in our case) and whether our calculations predict integer charging of all molecules or a coexistence of charged and uncharged moieties is a central question of our work. A significantly improved description of electron transfer is obtained when α is tuned such that the orbital energies of HOMO and LUMO correspond to the electron removal and addition energies calculated by the total-energy difference between the respectively charge states and the neutral moiety.88,89 For TCNE in the gas phase, this criterion is satisfied at α ≈ 0.8, and we will apply the corresponding functional, which we refer to as PBEh* in the following, also for the combined system of adsorbed TCNE and substrate. Note, however, that such a large α often results in a worsening of the description of the metal90 and of some molecular properties, such as atomization energies.91 We discuss the choice of the functional and in particular the impact of other choices of α on the charge localization in detail in the Supporting Information.
Even after accounting (to some extent) for the “delocalization error” by using the PBEh* functional, the results for the TCNE/Cu(100) interface remain qualitatively the same: Geometry optimization (again including van der Waals forces within the vdWsurf scheme) still yields buckled molecules. The electron-density difference, Δn, is virtually indistinguishable from the PBE result in Figure 3a. The molecular density of states and the C=C bond length after adsorption are shown in the bottom row of Figure 4. In agreement with previously reported results for metal/organic interfaces,92 the LUMO′ (Figure 4d) is moved to lower energies and is now found at ca. 3.5 eV below EF. The zoom into the region around EF, depicted in Figure 4e, shows that it is now almost completely filled and that there is no noticeable density of states directly at EF. Analyzing the bonding in more detail using the MO–DOS reveals that the back-donation from the CN orbitals to the copper surface is approximately the same as for PBE. The C=C bond length after adsorption is slightly shorter than it was for PBE, which, however, is only related to the fact that the C=C bond length in PBEh* is generally shorter than in PBE, again owing to the many-electron self-interaction error.93 In accordance with the PBE result, the C=C bond length after adsorption is the same as in the TCNE dianion in the gas phase when both are calculated with PBEh*. Despite the absence of a state at the Fermi energy, all molecules are still fractionally charged and there is no lateral inhomogeneity in the distribution of that charge. Therefore, PBEh* still predicts FCT as the electron-transfer mechanism for TCNE directly adsorbed on atomically clean Cu(100) surfaces, although in the limit of a completely filled LUMO. This is in line with our recent observation that hybrid functionals yield only minor quantitative improvements and sometimes even worsen the theoretical description of FCT systems.92
TCNE on Cu/NaCl
A qualitatively different result for the electron-transfer mechanism may occur when electronic interaction between the metal and the molecular orbitals is prevented, e.g., by introducing an ultrathin film of NaCl. In fact, this is a common procedure in STM94−96 investigations. Metal/NaCl/organic interfaces can be reliably grown and characterized,97−99 while a bilayer of NaCl is still sufficiently thin to allow for the tunneling of electrons between the metal and the adsorbate.100 Furthermore, TCNE readily adsorbs on metal-supported NaCl.101 Consequently, one would expect this to be a textbook example for the occurrence of ICT.
Let us again start with the discussion of the results obtained with the semilocal functional. After geometry relaxation with PBE+vdW, the buckling of the molecules is significantly smaller than for the direct adsorption on Cu(100). Still, the molecules are not perfectly flat, presumably because they follow the corrugation of the NaCl surface that originates from the different “sizes” of Na and Cl atoms. Interestingly, the Δn in Figure 5a shows that the electrons transferred to the TCNE layer are still delocalized over all molecules. Compared to the adsorption on the pristine Cu surface, the net electron transfer per molecule is reduced to roughly 0.2 electrons. The charging of each TCNE molecule can now be exclusively attributed to the partial filling of its former LUMO. A MO-DOS analysis no longer shows any noticeable back-donation from deeper lying σ-orbitals.
Figure 5.
Electron-density difference upon adsorption of TCNE on Cu/NaCl in PBE (left) and PBEh* (right). For the sake of clarity, only positive values are shown and the substrate atoms are omitted. The unit cell is highlighted, and part of the surrounding layer is shown for orientation.
Experimentally, the simultaneous presence of charged and uncharged molecules can be revealed by core-level spectroscopy.102 Here, we calculated the core levels in the initial-state approximation,103,104 which often yields binding-energy shifts that are in reasonable agreement with experiment, even though the absolute values of the binding energies are inaccurate.103,104 Like the valence density of states, also the N 1s core levels (Figure 6b), convoluted with a Gaussian of σ = 0.5 eV for more convenient comparison with experiment, are essentially equal for all molecules. Furthermore, the C=C bond length assumes a value that is roughly halfway between the bond length of the neutral and the singly charged TCNE molecule in the gas phase. Thus, with the PBE functional, TCNE on NaCl-passivated copper does not only exhibit FCT, it even does so more clearly than for direct adsorption on Cu.
Figure 6.
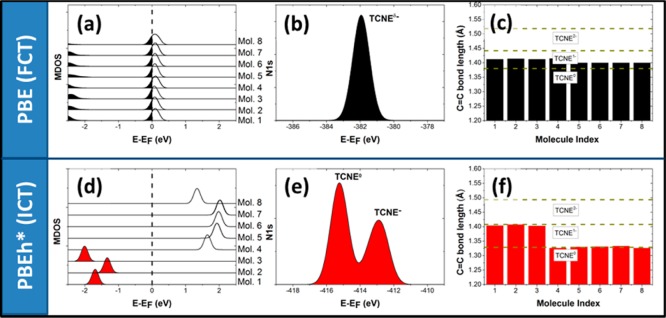
For TCNE adsorbed on Cu/NaCl. (a, d) Density of states near the Fermi edge, projected onto each molecule individually and vertically offset for clarity. Occupied levels are shaded. (b, e) Kohn–Sham N 1s levels, convoluted by a Gaussian function with σ = 0.5 eV. (c, f) Bond lengths of the central C=C bond after adsorption. For comparison, the values for the neutral, the singly negatively, and the doubly negatively charged molecule in the gas phase are shown. Panels a–c show results for the PBE functional and d–f for the PBEh* functional.
In contrast to direct adsorption on Cu, however, the situation now changes fundamentally when we repeat the calculations with PBEh*+vdW. As shown in Figure 5, Δn now localizes on only three out of the eight molecules in the unit cell. The other molecules remain charge neutral and only show a slight polarization in response to the charged molecules in their vicinity. The density of states in Figure 6d nicely reflects the broken-symmetry electron distribution. Molecules 1–3 exhibit a singly occupied molecular orbital (SOMO) ca. 1–2 eV below EF. Interestingly, these three molecules are not exactly equal but exhibit small offsets in their density of states, which we attribute to slightly different adsorption sites and, therefore, slightly different local environments (the system contains a 2 × 2 supercell of the TCNE layer on top of a 3 × 3 NaCl supercell). For all three of the charged molecules, the counterpart of the SOMO, the singly unoccupied molecular orbital (SUMO) can be found 6.4 eV above the respective SOMO. The other five molecules in the unit cell remain spin-unpolarized and have their (of course, completely empty) LUMO between the charged molecules’ SOMO and SUMO, at 1–2 eV above EF. The total Mulliken charge on all eight molecules together amounts to 3.0 electrons. Thus, surprisingly, the average charge per molecule is comparable to the case of direct adsorption on Cu, although its lateral distribution is clearly different. This should also be reflected in STM experiments, where both positive and negative tip bias could be used to sample SOMO and LUMO, respectively, which would both exhibit the same shape, but be localized on different molecules. Whether such an experiment would be successful or not, however, depends on the time scale of charge-fluctuations in the system. For example, for the buckled Si-dimers at the Si(100) surface, XPS clearly shows two differently charged Si-moieties, while STM images show only equally charged, parallel Si-dimers.105
The results for the core levels are depicted in Figure 6e. Like the valence density of states, the core levels are now distributed into two sets, corresponding to charged and neutral molecules. The additional electrons on the charged species screen their N 1s levels and move them to 3 eV lower binding energy compared to the core levels of the neutral molecules.
After full geometry optimization with PBEh*+vdW, the ICT mechanism of electron-transfer is also reflected in the length of the central C=C bond. The three charged molecules all display a bond length that agrees almost perfectly with the bond length of the TCNE anion in the gas phase, while for the five remaining molecules the bond length is virtually indistinguishable from that in the neutral molecule. We stress that the electron localization characteristic of ICT also occurs if the molecular layer is kept fixed at the PBE + vdW geometry, i.e., if all molecules are geometrically identical. (However, this requires a break in the spin-symmetry of the electronic wave function in the initialization of the SCF cycle; see the Methods). The observed geometry relaxation is, therefore, a consequence of the broken symmetry in the electron density, rather than vice versa. Likewise, a PBE calculation on top of the relaxed PBEh* + vdW geometry still results in FCT with an essentially delocalized electron distribution that is only minutely geared toward electron accumulation on the distorted molecules.
Summarizing this section, we have seen that the metal/organic interface between Cu(100) and TCNE clearly exhibits a homogeneous distribution of electrons within the organic layer and, therefore, FCT. This finding is independent of the employed functional. Moreover, because TCNE is an extraordinarily strong acceptor, the interface is characterized by either a very small or the complete absence of molecular density of states at the Fermi energy and an internal C=C bond length that corresponds to the bond length of the gas-phase dianion. Finally, the FCT mechanism in this case should be reflected by only a single nitrogen species appearing in core-level spectroscopy.
For the Cu/NaCl/TCNE interface, traditional (semi)local functionals also predict a homogeneous distribution of charge in the organic layer and, thus, FCT. This is accompanied by a partially occupied peak in the molecular density of states at the Fermi energy and an intermolecular C=C bond length that is halfway between that of the neutral molecule and its anion. In contrast, our hybrid functional spontaneously breaks the symmetry, leading to only a fraction of integer charged molecules, that is, to ICT. This is again reflected by the absence of density of states at EF but, in addition, the system now exhibits two clearly separated sets of nitrogen core levels and also two sets of different C=C bond lengths are found. Thus, our computational approach(es) allow us to describe either charge-transfer scenario and extract observable quantities that can be verified, or refuted, by experiment.
What Governs the Amount of Transferred Electrons in ICT?
Our work produces two open questions. The first, more technical, question is why PBE and PBEh* yield qualitatively different results for the same system and what the “default” fraction of exact exchange (α = 0.25) would yield? Obviously, this is related to the many-electron self-interaction error of semilocal functionals, and it is explained in the Supporting Information. The second, maybe more obvious, question is what determines the amount of electron-transfer in the ICT case? Specifically, for TCNE on Cu/NaCl, why are three electrons per unit cell transferred, rather than two or four? To answer this question, we investigate hypothetical, dilute TCNE layers at “low coverage” and study changes in the electronic structure as the complete monolayer is gradually built up. To do so, we repeat the PBEh* calculations with the same Cu/NaCl supercell as depicted in Figure 1c, but with fewer TCNE molecules in it. While this is a convenient and previously employed106,107 procedure to study coverage-dependent effects, it implies that, due to the periodic boundary conditions imposed in the calculations, a regular and well-ordered film is actually considered even at submonolayer coverage. This might not necessarily be a realistic assumption, and we will discuss the impact of this approximation in a subsequent section of this paper.
First, however, we note that, with PBEh*, we find that the SOMO of an individual TCNE anion in the gas phase is 1.8 eV below the Fermi energy of the Cu/NaCl substrate. Since hybrid functionals do not capture band gap renormalization effects due to substrate polarization,71 the TCNE SOMO is not expected to change upon adsorption, and indeed, its energy in the interacting monolayer is almost exactly the same. In other words, upon adsorption on copper-supported NaCl, a TCNE molecule will become charged unless its SOMO is somehow lifted up in energy by at least 1.8 eV.
To elucidate the mechanism by which that happens, it is instructive to study how the adsorption of individual molecules at submonolayer coverage affects the level alignment of subsequently deposited molecules. To that end, we calculate the adsorption-induced change of the electron potential energy in analogy to eq 1
| 2 |
where Esys is the electron potential energy of the combined system, while Eslab and ETCNE are the potential energies of the isolated slab and the adsorbed TCNE, respectively, as obtained from our PBEh* calculations. In Figure 7, the results for different numbers of molecules in the unit cell are depicted. The molecules that are actually present are shown in yellow, while the hypothetical positions of the other molecules, those that are “not yet” deposited, are shown in gray. ΔE is represented by a color code: blue regions indicate ΔE > 1.8 eV, while red regions correspond to ΔE < 1.8 eV. Were an additional molecule to adsorb in a red region, its SOMO would end up below EF, and hence, it would get charged. Conversely, molecules adsorbing in blue regions would have their SOMO lifted to above EF due to the presence of nearby charged ones already on the surface and would, therefore, remain electrically neutral. For brevity, we call the blue region the charge exclusion region, or CER for short. We note here that the SOMO energy, like the energy of the HOMO, depends on the choice of the functional and is higher the larger the chosen value for α is. Generally speaking, the larger the α, the smaller the CER will be, resulting in a larger electron transfer per cell. Although the origin is conceptually different, the trend is identical with the trend observed for the FCT case of direct adsorption on metal substrates.92
Figure 7.
Adsorption-induced change in the electron potential energy, ΔE for (a) one, (b) two, and (c) three molecules in the unit cell. Red indicates regions where the potential energy is so low that the SOMO is below EF, while blue indicates regions where the SOMO would be pushed above EF. The gray molecules indicate where, at full coverage, the other molecules would be located.
Figure 7a shows the situation for a single TCNE molecule in the unit cell, which corresponds to a nominal coverage of Θ = 12.5%. The extra electron on this molecule causes a significant increase of the electron potential energy throughout the entire unit cell, which is, naturally, largest in its immediate vicinity. Most importantly, on the molecule itself, it causes a split of the two spin-channels of the LUMO (into SOMO and SUMO) by the charging energy U. The CER has a shape similar to that of the TCNE molecule and extends up to ca. 3 Å beyond the terminal N atom. Nonetheless, any additional molecule that adsorbs on one of the sites occupied in the full monolayer (shown in gray) is completely outside this CER. Therefore, it inevitably gets charged as well, independently of where it is introduced to the system, a claim which we, of course, explicitly verified using PBEh* calculations.
In Figure 7b, we exemplarily show ΔE for the situation where a second molecule in the unit cell is adsorbed as far as possible away from the first one (both now highlighted in yellow). With two charged moieties on the surface, the CER now covers most of the adsorption sites occupied in a full monolayer (again shown in gray) with only two remaining outside. As expected, PBEh* calculations show that when a third molecule is adsorbed within the CER, it remains neutral. Conversely, when the third molecule occupies one of the sites outside the CER, it becomes charged. Finally, Figure 7c illustrates that with three charged molecules in the unit cell the CER now covers all remaining adsorption sites. Consequently, any additional molecule stays neutral irrespective of its position.
Coverage Dependence of ΔΦ for ICT and FCT
To illustrate the impact of the charge-transfer mechanism on ΔΦ, we show its dependence on the molecular coverage Θ in Figure 8. Starting with the Cu/TCNE system, where both PBE and PBEh* unanimously yield FCT, we find an approximately linear dependence of ΔΦ on the coverage with both functionals (Figure 8a). A similar trend, albeit with a more pronounced curvature reminiscent of Topping-like depolarization,108 is seen in the PBE results for the Cu/NaCl/TCNE system, where this functional yields FCT as well. This corroborates that, within the FCT mechanism, each molecule arriving on the surface gets charged and, therefore, contributes to ΔΦ.
Figure 8.

(a) Coverage dependence of ΔΦ for Cu/TCNE, where both PBE (black) and PBEh* (red) yield FCT. (b) Same for TCNE on one bilayer of NaCl on Cu, where PBE yields FCT (black) and PBEh* yields ICT (red). (c) Same for TCNE on two bilayers of NaCl on Cu. ΔΦ is normalized to 100% at full coverage (Θ = 1). The insets depict side views of the respective systems.
In contrast, whether an additional molecule becomes charged in the ICT case depends on whether it adsorbs outside or inside the CER. This anticipates a pronounced impact of the growth mode on the coverage dependence of ΔΦ, which we will return to momentarily. First, however, we consider the case where molecules exclusively adsorb outside the CER until it completely covers all remaining adsorption sites. The corresponding results obtained with PBEh* for the Cu/NaCl/TCNE system are shown in Figure 8b: ΔΦ increases linearly up to a coverage of 3/8 (i.e., the first three molecules arriving at the surface get charged) and then stays essentially constant (i.e., all further molecules remain neutral). This finding is equivalent to the experimental observations for the deposition of PTCDA on ZnO, where integer-charged PTCDA anions form up to approximately half-monolayer coverage.58 Concomitantly, after deposition of half a monolayer of PTCDA, the work function remains constant.
In our calculations, the slight decrease of ΔΦ after Θ = 3/8 can be understood in terms of a “surface dipole” of the organic layer.109 Such a maximum of ΔΦ at submonolayer coverage has indeed been observed for other systems.24 More importantly, however, if we increase the thickness of the NaCl layer (Figure 8c), the linear increase of ΔΦ saturates already at a coverage of only 2/8. This experimentally well-documented result,102,110i.e., a decreasing fraction of charged molecules with increasing thickness of the insulating layer, can be rationalized by considering that the extent of the CER is determined by two factors: First, the difference between the molecular SOMO and the substrate EF and, second, the lateral decay of the electrostatic potential originating from both the charged molecules within the layer and the corresponding countercharges in the substrate. As such, the CER is to a significant part determined by the geometry of the combined system and, for any given molecule, by the distance between organic layer and metallic substrate.
Impact of the Growth Mode
Returning to the impact of the growth mode on ΔΦ in the ICT scenario, we recall that the periodic boundary conditions exploited in the DFT calculations impose an ordered superstructure on the molecular layer at submonolayer coverage. This clearly limits the range of growth scenarios that can be described. To expand the accessible phenomenological range, we therefore expand an electrostatic model recently proposed by Amsalem et al.(102)
Going beyond the original work, we treat the metal substrate as a finite, planar, and regular grid of n × m pointlike adsorption sites at an intersite distance d. The equally pointlike adsorbate is characterized solely by its adsorption distance z from the substrate and its “pinning level”, ε, which is given relative to the Fermi level of the hypothetical substrate. If an adsorbate gets charged, then the corresponding (pointlike) image charge in the metal is taken to lie at –z below the metal surface. The model then iteratively performs the following steps:
-
(1)
It selects an unoccupied adsorption site according to a predefined algorithm corresponding to a certain “growth mode” (see below).
-
(2)It calculates the electron potential energy E at this site due to all other charged molecules already adsorbed on the surface (as well as their countercharges) according to
where e is the charge of an electron, ri is the distance between the selected site and charged molecule number i (carrying a charge qi = e) or its countercharge qi = −e. If the pinning level is still below the Fermi energy, that is, if
the molecule on the selected site becomes charged by a single electron, we re-evaluate the potential for each site anew until self-consistency in the number and distribution of charge is obtained.
-
(3)It evaluates ΔΦ at the present coverage Θ, that is, the number of adsorbed molecules (charged and uncharged combined) divided by the total number of available sites, following
where N is the number of charged molecules and A the area of the entire substrate.
-
(4)
It returns to (1) and repeats until all sites of the substrate are occupied.
For the sake of simplicity, we chose an orthogonal grid with n = m = 300 sites. This size yields ΔΦs converged to within 0.1 eV. To test the effect of the regular adsorption pattern inevitably introduced by the periodic boundary conditions in the DFT calculations, any reasonable combination of the three model parameters d, z, and ε should suffice in principle. In practice, however, the results are most instructive if these parameters are chosen so as to reproduce the DFT results. Using a site-occupation algorithm that selects successive adsorption sites in the same way as in our DFT calculations (denoted as “regular growth” in Figure 9), we find this to be the case for d = 6.5 Å, z = 8.5 Å, and ε = −1.5 eV. As shown in Figure 9a, the ΔΦ values obtained with this parameter set increase linearly up to a coverage of 37.5% and then remain constant. The mild decline after 37.5%, which was observed in DFT, is not reproduced because its origin (see above) is not included in the electrostatic model.
Figure 9.

ΔΦ as a function of coverage. (a) Results obtained with PBEh* for the Cu/NaCl/TCNE system (red) and with the electrostatic model described in the text (dark yellow) . (b) Results obtained with the electrostatic model for different growth mechanims.
Using the same set of parameters, we could consider other growth modes. The respective coverage dependences of ΔΦ are shown in Figure 9b. In the “cluster growth” mode, we started by adsorbing a single molecule in the middle of the substrate area and then added subsequent adsorbates in concentric squares. Because this essentially corresponds to a superposition of a region with Θ = 1 (the central island) and a surrounding region with Θ = 0, ΔΦ increases linearly with coverage.
As a second alternative growth mode, we chose “hit-and-stick”. Successive adsorption sites are selected randomly, which reflects a scenario where molecules do not diffuse after adsorption to form 2D-islands or to dewet into multilayer structures. To adequately sample configuration space, we averaged over 10 different runs. The results show that the sharp kink observed for the “regular” growth mode is smeared out and that ΔΦ now increases smoothly and sublinearly with coverage. Despite the fact that our electrostatical model is based on ICT, this evolution is virtually indistinguishable from that calculated with PBE, where FCT is found. Therefore, if a smooth coverage dependence of ΔΦ is observed experimentally, we cannot immediately distinguish between FCT and ICT. Rather, it is the change of the coverage dependence with the growth mode that reveals ICT. We note in passing, however, that the results for the “hit-and-stick” mode become more and more similar to those obtained with the “regular” growth mode the larger the ratio of z/d is. This provides another possibility to experimentally determine the mechanism of interfacial charge transfer and, to some extent, vindicates the use of periodic boundary conditions to study dilute monolayers.
Conclusions
We have contrasted the mechanism of electron transfer across the prototypical metal/organic interface Cu(100)/TCNE with that in the metal/insulator/organic heterostructure Cu/NaCl/TCNE. In our DFT-based study, we found that hybrid-exchange–correlation functionals with a sufficiently high fraction of Hartree–Fock exchange are able to capture both the FCT mechanism for the Cu/TCNE and the ICT mechanism for Cu/NaCl/TCNE, while (semi)local functionals fail in the latter scenario. The breaking of translational symmetry in the case of ICT is reflected in several observables, in particular, the intermolecular C=C bond length, the core and valence density of states, as well as the change in sample work function with increasing molecular coverage and the growth-mode dependence of that evolution. The amount of charge transfer and the fraction of charged molecules are determined by the difference between the singly occupied frontier molecular orbitals of the adsorbate and the Fermi energy of the substrate, as well as by the ratio of intermolecular and metal–molecule distance. Complementing prior work on FCT systems, we extended the phenomenological range accessible by DFT also to ICT, which allowed us to highlight experimentally testable differences between the two charge-transfer mechanisms. Now that we have ascertained that density-functional theory can be used to study integer charge transfer (ICT) in organic/inorganic systems, our work forms a basis for future functional development and experimental studies into ICT. We expect our results to help focus the ongoing discussion regarding such interfacial phenomena, and we envisage that the insights we provided will be conducive for the design of future applications based on functional organic/inorganic interfaces.
Methods
The lateral dimensions of the surface unit-cell we employed are governed by the commensurability between Cu and NaCl. We use a square base-area of 20.48 Å edge length, corresponding to 64 Cu atoms per layer. The NaCl lattice constant was reduced accordingly to form a commensurate supercell. All calculations were performed with the Fritz-Haber Institute ab initio molecules simulations package (FHI-aims).111 Periodic boundary conditions were employed in all three spatial directions. Perpendicular to the interface, the unit-cell replicas are decoupled by a vacuum layer of at least 28.3 Å (for bilayer NaCl, accordingly more for direct adsorption), including a dipole correction to prevent spurious electrostatic interactions. A 2 × 2 × 1 k-point grid was employed, which yields ΔΦs converged to within 0.1 eV. A Gaussian occupation scheme with a smearing of 0.1 eV was used throughout. FHI-aims expands the (generalized) Kohn–Sham orbitals into numerically tabulated atomic orbitals, which are hierarchically ordered into tiers. For the present calculations, we employed tier-1 for all inorganic and tier-2 basis functions for all organic constituents.
Semilocal calculations were performed using the functional of Perdew, Burke, and Ernzerhof67 (PBE). Hybrid-functional calculations were performed using PBEh,112 which mixes a variable fraction α of Hartree–Fock exchange with PBE exchange. Unless otherwise noted, we set α to 0.8 (see main text for discussion), which we refer to as PBEh*. Geometry optimizations were performed separately for both PBE and PBEh*. To account for the missing long-range tail of van der Waals forces, these functionals were augmented by the van der Waals scheme of Tkatchenko and Scheffler,68 using the appropriate parametrization for surface (Cu)69 and ionic semiconductors (NaCl),113 respectively.
All calculations were performed in a spin-unrestricted manner. The spin symmetry of the initial guess for the wave function was broken by assigning each TCNE nitrogen atom an initial spin moment of 0.1. The (semi)local calculations collapsed back into the spin-unrestricted solution, while the PBEh* calculations of TCNE on NaCl did not. Note, however, that a nonuniform initialization of the TCNE molecules was not generally needed to obtain an ICT solution. The different unit-cell sizes of organic and NaCl layers sufficed to the break the lateral symmetry.
Acknowledgments
We thank Viktor Atalla for fruitful discussions. Funding by the Deutsche Forschungsgemeinschaft (DFG) through SFB 951 “HIOS” and by the Austrian Science Fund (FWF) through Erwin-Schrödinger Grant No. J 3258-N20 is gratefully acknowledged.
Supporting Information Available
Discussion of the self-interaction error, choice of the functional, impact of the parameter α on the localization in a free-standing monolayer for PBEh and HSE. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.5b01164.
The authors declare no competing financial interest.
Supplementary Material
References
- Katsonis N.; Lubomska M.; Pollard M.; Feringa B.; Rudolf P. Synthetic Light-Activated Molecular Switches and Motors on Surfaces. Prog. Surf. Sci. 2007, 82, 407–434. [Google Scholar]
- McNellis E.; Meyer J.; Baghi A.; Reuter K. Stabilizing a Molecular Switch at Solid Surfaces: A Density Functional Theory Study of Azobenzene on Cu(111), Ag(111), and Au(111). Phys. Rev. B 2009, 80, 035414. [Google Scholar]
- Paulsson M.; Datta S. Thermoelectric Effect in Molecular Electronics. Phys. Rev. B 2003, 70, 241403(R). [Google Scholar]
- Reddy P.; Jang S.-Y.; Segalman R. A.; Majumdar A. Thermoelectricity in Molecular Junctions. Science 2007, 315, 1568–1571. [DOI] [PubMed] [Google Scholar]
- Ferri V.; Elbing M.; Pace G.; Dickey M. D.; Zharnikov M.; Samorì P.; Mayor M.; Rampi M. A. Light-Powered Electrical Switch Based on Cargo-Lifting Azobenzene Monolayers. Angew. Chem., Int. Ed. 2008, 47, 3407–3409. [DOI] [PubMed] [Google Scholar]
- Cho B.; Song S.; Ji Y.; Kim T.-W.; Lee T. Organic Resistive Memory Devices: Performance Enhancement, Integration, and Advanced Architectures. Adv. Funct. Mater. 2011, 21, 2806–2829. [Google Scholar]
- Veres J.; Ogier S.; Lloyd G.; de Leeuw D. Gate Insulators in Organic Field-Effect Transistors. Chem. Mater. 2004, 16, 4543–4555. [Google Scholar]
- Koch N. Organic Electronic Devices and Their Functional Interfaces. ChemPhysChem 2007, 8, 1438–1455. [DOI] [PubMed] [Google Scholar]
- Virkar A. A.; Mannsfeld S.; Bao Z.; Stingelin N. Organic Semiconductor Growth and Morphology Considerations for Organic Thin-Film Transistors. Adv. Mater. 2010, 22, 3857–3875. [DOI] [PubMed] [Google Scholar]
- Sanvito S. Molecular Spintronics. Chem. Soc. Rev. 2011, 40, 3336–3355. [DOI] [PubMed] [Google Scholar]
- Hung L. S.; Chen C. H. Recent Progress of Molecular Organic Electroluminescent Materials and Devices. Mater. Sci. Eng. R Rep. 2002, 39, 143–222. [Google Scholar]
- Riede M.; Mueller T.; Tress W.; Schueppel R.; Leo K. Small-Molecule Solar Cells—Status and Perspectives. Nanotechnology 2008, 19, 424001. [DOI] [PubMed] [Google Scholar]
- Meredith P.; Bettinger C. J.; Irimia-Vladu M.; Mostert A. B.; Schwenn P. E. Electronic and Optoelectronic Materials and Devices Inspired by Nature. Rep. Prog. Phys. 2013, 76, 034501. [DOI] [PubMed] [Google Scholar]
- Cao H.; He W.; Mao Y.; Lin X.; Ishikawa K.; Dickerson J. H.; Hess W. P. Recent Progress in Degradation and Stabilization of Organic Solar Cells. J. Power Sources 2014, 264, 168–183. [Google Scholar]
- Lee C. W.; Kim O. Y.; Lee J. Y. Organic Materials for Organic Electronic Devices. J. Ind. Eng. Chem. 2014, 20, 1198–1208. [Google Scholar]
- Malen J. A.; Yee S. K.; Majumdar A.; Segalman R. A. Fundamentals of Energy Transport, Energy Conversion, and Thermal Properties in Organic–inorganic Heterojunctions. Chem. Phys. Lett. 2010, 491, 109–122. [Google Scholar]
- Evers F.; Weigend F.; Koentopp M. Conductance of Molecular Wires and Transport Calculations Based on Density-Functional Theory. Phys. Rev. B 2004, 69, 235411. [Google Scholar]
- Nitzan A. Electron Transport in Molecular Wire Junctions. Science 2003, 300, 1384–1389. [DOI] [PubMed] [Google Scholar]
- Campbell I. H.; Rubin S.; Zawodzinski T. A.; Kress J. D.; Martin R. L.; Smith D. L.; Barashkov N. N.; Ferraris J. P. Controlling Schottky Energy Barriers in Organic Electronic Devices Using Self-Assembled Monolayers. Phys. Rev. B 1996, 54, 14321–14324. [DOI] [PubMed] [Google Scholar]
- Koch N.; Duhm S.; Rabe J. P.; Rentenberger S.; Johnson R. L.; Klankermayer J.; Schreiber F. Tuning the Hole Injection Barrier Height at Organic/metal Interfaces with (sub-) Monolayers of Electron Acceptor Molecules. Appl. Phys. Lett. 2005, 87, 101905. [Google Scholar]
- Richard J.; Salaneck W. R. Charge Injection Barrier Heights Across Multilayer Organic Thin Films. Jpn. J. Appl. Phys. 2005, 44, 3751–3756. [Google Scholar]
- Grobosch M.; Knupfer M. Charge-Injection Barriers at Realistic Metal/Organic Interfaces: Metals Become Faceless. Adv. Mater. 2007, 19, 754–756. [Google Scholar]
- Jaeckel B.; Sambur J. B.; Parkinson B. A. The Influence of Metal Work Function on the Barrier Heights of Metal/Pentacene Junctions. J. Appl. Phys. 2008, 103, 063719. [Google Scholar]
- Soos Z. G.; Topham B. J. Surface Dipole of F4TCNQ Films: Collective Charge Transfer and Dipole–Dipole Repulsion in Submonolayers. Org. Electron. 2011, 12, 39–44. [Google Scholar]
- Monti O. L. A. Understanding Interfacial Electronic Structure and Charge Transfer: An Electrostatic Perspective. J. Phys. Chem. Lett. 2013, 2342–2351. [DOI] [PubMed] [Google Scholar]
- Vázquez H.; Oszwaldowski R.; Pou P.; Ortega J.; Pérez R.; Flores F.; Kahn A. Dipole Formation at metal/PTCDA Interfaces: Role of the Charge Neutrality Level. Europhys. Lett. EPL 2004, 65, 802–808. [Google Scholar]
- Lindell L.; de Jong M. P.; Osikowicz W.; Lazzaroni R.; Berggren M.; Salaneck W. R.; Crispin X. Characterization of the Interface Dipole at the Paraphenylenediamine-Nickel Interface: A Joint Theoretical and Experimental Study. J. Chem. Phys. 2005, 122, 084712. [DOI] [PubMed] [Google Scholar]
- Duhm S.; Glowatzki H.; Cimpeanu V.; Klankermayer J.; Rabe J. P.; Johnson R. L.; Koch N. Weak Charge Transfer between an Acceptor Molecule and Metal Surfaces Enabling Organic/Metal Energy Level Tuning. J. Phys. Chem. B 2006, 110, 21069–21072. [DOI] [PubMed] [Google Scholar]
- Romaner L.; Heimel G.; Brédas J.-L.; Gerlach A.; Schreiber F.; Johnson R.; Zegenhagen J.; Duhm S.; Koch N.; Zojer E. Impact of Bidirectional Charge Transfer and Molecular Distortions on the Electronic Structure of a Metal-Organic Interface. Phys. Rev. Lett. 2007, 99, 256801. [DOI] [PubMed] [Google Scholar]
- Braun S.; Salaneck W. R. Fermi Level Pinning at Interfaces with Tetrafluorotetracyanoquinodimethane (F4-TCNQ): The Role of Integer Charge Transfer States. Chem. Phys. Lett. 2007, 438, 259–262. [Google Scholar]
- Fernandez-Torrente I.; Monturet S.; Franke K.; Fraxedas J.; Lorente N.; Pascual J. Long-Range Repulsive Interaction between Molecules on a Metal Surface Induced by Charge Transfer. Phys. Rev. Lett. 2007, 99, 176103. [DOI] [PubMed] [Google Scholar]
- Tseng T.-C.; Urban C.; Wang Y.; Otero R.; Tait S. L.; Alcamí M.; Écija D.; Trelka M.; Gallego J. M.; Lin N.; et al. Charge-Transfer-Induced Structural Rearrangements at Both Sides of Organic/metal Interfaces. Nat. Chem. 2010, 2, 374–379. [DOI] [PubMed] [Google Scholar]
- Bokdam M.; Çakır D.; Brocks G. Fermi Level Pinning by Integer Charge Transfer at Electrode-Organic Semiconductor Interfaces. Appl. Phys. Lett. 2011, 98, 113303. [Google Scholar]
- Glowatzki H.; Bröker B.; Blum R.-P.; Hofmann O. T.; Vollmer A.; Rieger R.; Müllen K.; Zojer E.; Rabe J. P.; Koch N. Soft” Metallic Contact to Isolated C 60. Nano Lett. 2008, 8, 3825–3829. [DOI] [PubMed] [Google Scholar]
- Hofmann O. T.; Rangger G. M.; Zojer E. Reducing the Metal Work Function beyond Pauli Pushback: A Computational Investigation of Tetrathiafulvalene and Viologen on Coinage Metal Surfaces. J. Phys. Chem. C 2008, 112, 20357–20365. [Google Scholar]
- Rissner F.; Rangger G. M.; Hofmann O. T.; Track A. M.; Heimel G.; Zojer E. Understanding the Electronic Structure of Metal/SAM/Organic-Semiconductor Heterojunctions. ACS Nano 2009, 3, 3513–3520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crispin X.; Geskin V.; Crispin A.; Cornil J.; Lazzaroni R.; Salaneck W. R.; Brédas J.-L. Characterization of the Interface Dipole at Organic/ Metal Interfaces. J. Am. Chem. Soc. 2002, 124, 8131–8141. [DOI] [PubMed] [Google Scholar]
- Vazquez H.; Flores F.; Kahn A. Induced Density of States Model for Weakly-Interacting Organic Semiconductor Interfaces. Org. Electron. 2007, 8, 241–248. [Google Scholar]
- Flores F.; Ortega J.; Vázquez H. Modelling Energy Level Alignment at Organic Interfaces and Density Functional Theory. Phys. Chem. Chem. Phys. 2009, 11, 8658–8675. [DOI] [PubMed] [Google Scholar]
- Romaner L.; Nabok D.; Puschnig P.; Zojer E.; Ambrosch-Draxl C. Theoretical Study of PTCDA Adsorbed on the Coinage Metal Surfaces, Ag (111), Au (111) and Cu (111). New J. Phys. 2009, 11, 053010. [Google Scholar]
- Bröker B.; Blum R.-P.; Frisch J.; Vollmer A.; Hofmann O. T.; Rieger R.; Müllen K.; Rabe J. P.; Zojer E.; Koch N. Gold Work Function Reduction by 2.2 eV with an Air-Stable Molecular Donor Layer. Appl. Phys. Lett. 2008, 93, 243303. [Google Scholar]
- Dell’Angela M.; Kladnik G.; Cossaro A.; Verdini A.; Kamenetska M.; Tamblyn I.; Quek S. Y.; Neaton J. B.; Cvetko D.; Morgante A.; et al. Relating Energy Level Alignment and Amine-Linked Single Molecule Junction Conductance. Nano Lett. 2010, 10, 2470–2474. [DOI] [PubMed] [Google Scholar]
- Hauschild A.; Karki K.; Cowie B.; Rohlfing M.; Tautz F.; Sokolowski M. Molecular Distortions and Chemical Bonding of a Large Π-Conjugated Molecule on a Metal Surface. Phys. Rev. Lett. 2005, 94, 036106. [DOI] [PubMed] [Google Scholar]
- Heimel G.; Duhm S.; Salzmann I.; Gerlach A.; Strozecka A.; Niederhausen J.; Bürker C.; Hosokai T.; Fernandez-Torrente I.; Schulze G.; et al. Charged and Metallic Molecular Monolayers through Surface-Induced Aromatic Stabilization. Nat. Chem. 2013, 5, 187–194. [DOI] [PubMed] [Google Scholar]
- Osikowicz W.; Crispin X.; Tengstedt C.; Lindell L.; Kugler T.; Salaneck W. R. Transparent Low-Work-Function Indium Tin Oxide Electrode Obtained by Molecular Scale Interface Engineering. Appl. Phys. Lett. 2004, 85, 1616. [Google Scholar]
- Tengstedt C.; Unge M.; de Jong M.; Stafström S.; Salaneck W.; Fahlman M. Coulomb Interactions in Rubidium-Doped Tetracyanoethylene: A Model System for Organometallic Magnets. Phys. Rev. B 2004, 69, 165208. [Google Scholar]
- Johansson N.; Osada T.; Stafström S.; Salaneck W. R.; Parente V.; dos Santos D. A.; Crispin X.; Brédas J. L. Electronic Structure of tris(8-Hydroxyquinoline) Aluminum Thin Films in the Pristine and Reduced States. J. Chem. Phys. 1999, 111, 2157–2163. [Google Scholar]
- Braun S.; Salaneck W. R.; Fahlman M. Energy-Level Alignment at Organic/Metal and Organic/Organic Interfaces. Adv. Mater. 2009, 21, 1450–1472. [Google Scholar]
- Lindell L.; Unge M.; Osikowicz W.; Stafström S.; Salaneck W. R.; Crispin X.; de Jong M. P. Integer Charge Transfer at the tetrakis(dimethylamino)ethylene/Au Interface. Appl. Phys. Lett. 2008, 92, 163302. [Google Scholar]
- Osikowicz W.; de Jong M. P.; Salaneck W. R. Formation of the Interfacial Dipole at Organic-Organic Interfaces: C60/Polymer Interfaces. Adv. Mater. 2007, 19, 4213–4217. [Google Scholar]
- Murdey R. J.; Salaneck W. R. Charge Injection Barrier Heights Across Multilayer Organic Thin Films. Jpn. J. Appl. Phys. 2005, 44, 3751–3756. [Google Scholar]
- Gao W.; Kahn A. Electronic Structure and Current Injection in Zinc Phthalocyanine Doped with Tetrafluorotetracyanoquinodimethane: Interface versus Bulk Effects. Org. Electron. 2002, 3, 53–63. [Google Scholar]
- Hung L. S.; Tang C. W.; Mason M. G. Enhanced Electron Injection in Organic Electroluminescence Devices Using an Al/LiF Electrode. Appl. Phys. Lett. 1997, 70, 152. [Google Scholar]
- Wakimoto T.; Fukuda Y.; Nagayama K.; Yokoi A.; Nakada H.; Tsuchida M. Organic EL Cells Using Alkaline Metal Compounds as Electron Injection Materials. IEEE Trans. Electron Devices 1997, 44, 1245–1248. [Google Scholar]
- Wang X. J. Enhancement of Electron Injection in Organic Light-Emitting Devices Using an Ag/LiF Cathode. J. Appl. Phys. 2004, 95, 3828. [Google Scholar]
- Newns D. Self-Consistent Model of Hydrogen Chemisorption. Phys. Rev. 1969, 178, 1123–1135. [Google Scholar]
- Anderson P. Localized Magnetic States in Metals. Phys. Rev. 1961, 124, 41–53. [Google Scholar]
- Gruenewald M.; Schirra L. K.; Winget P.; Kozlik M.; Ndione P. F.; Sigdel A. K.; Berry J. J.; Forker R.; Bredas J.-L.; Fritz T.; et al. Integer Charge Transfer and Hybridization at an Organic Semiconductor/Conductive Oxide Interface. J. Phys. Chem. C 2015, 119, 4865–4873. [Google Scholar]
- Perdew J. P.; Ruzsinszky A.; Constantin L. A.; Sun J.; Csonka G. I. Some Fundamental Issues in Ground-State Density Functional Theory: A Guide for the Perplexed. J. Chem. Theory Comput. 2009, 5, 902–908. [DOI] [PubMed] [Google Scholar]
- Lyons L.; Palmer L. The Electron Affinity of Tetracyanoethylene and Other Organic Electron Acceptors. Aust. J. Chem. 1976, 29, 1919–1929. [Google Scholar]
- Chowdhury S.; Kebarle P. Electron Affinities of Di- and Tetracyanoethylene and Cyanobenzenes Based on Measurements of Gas-Phase Electron-Transfer Equilibria. J. Am. Chem. Soc. 1986, 108, 5453–5459. [Google Scholar]
- Webster O. W.; Mahler W.; Benson R. E. Chemistry of Tetracyanoethylene Anion Radical. J. Am. Chem. Soc. 1962, 84, 3678–3684. [Google Scholar]
- Shabaka A. A.; El-Behery K. M.; Fadly M. Infrared Spectroscopic Study of the Molecular Structure of Some Transition Metal TCNE Complexes. J. Mater. Sci. Lett. 1988, 7, 685–687. [Google Scholar]
- Rangger G.; Hofmann O.; Romaner L.; Heimel G.; Bröker B.; Blum R.-P.; Johnson R.; Koch N.; Zojer E. F4TCNQ on Cu, Ag, and Au as Prototypical Example for a Strong Organic Acceptor on Coinage Metals. Phys. Rev. B 2009, 79, 165306. [Google Scholar]
- Wegner D.; Yamachika R.; Wang Y.; Brar V. W.; Bartlett B. M.; Long J. R.; Crommie M. F. Single-Molecule Charge Transfer and Bonding at an Organic/Inorganic Interface: Tetracyanoethylene on Noble Metals. Nano Lett. 2008, 8, 131–135. [DOI] [PubMed] [Google Scholar]
- Bedwani S.; Wegner D.; Crommie M.; Rochefort A. Strongly Reshaped Organic-Metal Interfaces: Tetracyanoethylene on Cu(100). Phys. Rev. Lett. 2008, 101, 216105. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
- Tkatchenko A.; Scheffler M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [DOI] [PubMed] [Google Scholar]
- Ruiz V.; Liu W.; Zojer E.; Scheffler M.; Tkatchenko A. Density-Functional Theory with Screened van Der Waals Interactions for the Modeling of Hybrid Inorganic-Organic Systems. Phys. Rev. Lett. 2012, 108, 146103. [DOI] [PubMed] [Google Scholar]
- Sini G.; Sears J. S.; Brédas J.-L. Evaluating the Performance of DFT Functionals in Assessing the Interaction Energy and Ground-State Charge Transfer of Donor/Acceptor Complexes: Tetrathiafulvalene–Tetracyanoquinodimethane (TTF–TCNQ) as a Model Case. J. Chem. Theory Comput. 2011, 7, 602–609. [DOI] [PubMed] [Google Scholar]
- Biller A.; Tamblyn I.; Neaton J. B.; Kronik L. Electronic Level Alignment at a Metal-Molecule Interface from a Short-Range Hybrid Functional. J. Chem. Phys. 2011, 135, 164706. [DOI] [PubMed] [Google Scholar]
- Freysoldt C.; Rinke P.; Scheffler M. Controlling Polarization at Insulating Surfaces: Quasiparticle Calculations for Molecules Adsorbed on Insulator Films. Phys. Rev. Lett. 2009, 103, 056803. [DOI] [PubMed] [Google Scholar]
- Bagus P.; Staemmler V.; Wöll C. Exchangelike Effects for Closed-Shell Adsorbates: Interface Dipole and Work Function. Phys. Rev. Lett. 2002, 89, 096104. [DOI] [PubMed] [Google Scholar]
- Hofmann O. T.; Egger D. A.; Zojer E. Work-Function Modification beyond Pinning: When Do Molecular Dipoles Count?. Nano Lett. 2010, 10, 4369–4374. [DOI] [PubMed] [Google Scholar]
- Norsko J. K. Chemisorption on Metal Surfaces. Rep. Prog. Phys. 1990, 53, 1253–1295. [Google Scholar]
- Nelin C. J.; Bagus P. S.; Philpott M. R. The Nature of the Bonding of CN to Metals and Organic Molecules. J. Chem. Phys. 1987, 87, 2170–2176. [Google Scholar]
- Avilov I.; Geskin V.; Cornil J. Quantum-Chemical Characterization of the Origin of Dipole Formation at Molecular Organic/Organic Interfaces. Adv. Funct. Mater. 2009, 19, 624–633. [Google Scholar]
- Ruzsinszky A.; Perdew J. P.; Csonka G. I.; Vydrov O. A.; Scuseria G. E. Density Functionals That Are One- and Two- Are Not Always Many-Electron Self-Interaction-Free, as Shown for H2+, He2+, LiH+, and Ne2+. J. Chem. Phys. 2007, 126, 104102. [DOI] [PubMed] [Google Scholar]
- Ruzsinszky A.; Perdew J. P.; Csonka G. I.; Vydrov O. A.; Scuseria G. E. Spurious Fractional Charge on Dissociated Atoms: Pervasive and Resilient Self-Interaction Error of Common Density Functionals. J. Chem. Phys. 2006, 125, 194112. [DOI] [PubMed] [Google Scholar]
- Perdew J.; Ruzsinszky A.; Csonka G.; Vydrov O.; Scuseria G.; Staroverov V.; Tao J. Exchange and Correlation in Open Systems of Fluctuating Electron Number. Phys. Rev. A 2007, 76, 040501(R). [Google Scholar]
- Perdew J. P. Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar]
- Adamo C.; Barone V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0Model. J. Chem. Phys. 1999, 110, 6158. [Google Scholar]
- Gavartin J. L.; Sushko P. V.; Shluger A. L. Modeling Charge Self-Trapping in Wide-Gap Dielectrics: Localization Problem in Local Density Functionals. Phys. Rev. B 2003, 67, 035108. [Google Scholar]
- Mori-Sánchez P.; Cohen A.; Yang W. Localization and Delocalization Errors in Density Functional Theory and Implications for Band-Gap Prediction. Phys. Rev. Lett. 2008, 100, 146401. [DOI] [PubMed] [Google Scholar]
- Clark S. J.; Robertson J.; Lany S.; Zunger A. Intrinsic Defects in ZnO Calculated by Screened Exchange and Hybrid Density Functionals. Phys. Rev. B 2010, 81, 115311. [Google Scholar]
- Sai N.; Barbara P. F.; Leung K. Hole Localization in Molecular Crystals from Hybrid Density Functional Theory. Phys. Rev. Lett. 2011, 106, 226403. [DOI] [PubMed] [Google Scholar]
- Körzdörfer T.; Brédas J.-L. Organic Electronic Materials: Recent Advances in the DFT Description of the Ground and Excited States Using Tuned Range-Separated Hybrid Functionals. Acc. Chem. Res. 2014, 47, 3284–3291. [DOI] [PubMed] [Google Scholar]
- Kronik L.; Stein T.; Refaely-Abramson S.; Baer R. Excitation Gaps of Finite-Sized Systems from Optimally-Tuned Range-Separated Hybrid Functionals. J. Chem. Theory Comput. 2012, 8, 1515–1531. [DOI] [PubMed] [Google Scholar]
- Karolewski A.; Kronik L.; Kümmel S. Using Optimally Tuned Range Separated Hybrid Functionals in Ground-State Calculations: Consequences and Caveats. J. Chem. Phys. 2013, 138, 204115. [DOI] [PubMed] [Google Scholar]
- Paier J.; Marsman M.; Kresse G. Why Does the B3LYP Hybrid Functional Fail for Metals?. J. Chem. Phys. 2007, 127, 024103. [DOI] [PubMed] [Google Scholar]
- Zhang W.; Truhlar D. G.; Tang M. Tests of Exchange-Correlation Functional Approximations Against Reliable Experimental Data for Average Bond Energies of 3d Transition Metal Compounds. J. Chem. Theory Comput. 2013, 9, 3965–3977. [DOI] [PubMed] [Google Scholar]
- Hofmann O. T.; Atalla V.; Moll N.; Rinke P.; Scheffler M. Interface Dipoles of Organic Molecules on Ag(111) in Hybrid Density-Functional Theory. New J. Phys. 2013, 15, 123028. [Google Scholar]
- Körzdörfer T.; Parrish R. M.; Sears J. S.; Sherrill C. D.; Brédas J.-L. On the Relationship between Bond-Length Alternation and Many-Electron Self-Interaction Error. J. Chem. Phys. 2012, 137, 124305. [DOI] [PubMed] [Google Scholar]
- Bennewitz R.; Foster A.; Kantorovich L.; Bammerlin M.; Loppacher C.; Schär S.; Guggisberg M.; Meyer E.; Shluger A. Atomically Resolved Edges and Kinks of NaCl Islands on Cu(111): Experiment and Theory. Phys. Rev. B 2000, 62, 2074–2084. [Google Scholar]
- Repp J.; Meyer G.; Stojković S. M.; Gourdon A.; Joachim C. Molecules on Insulating Films: Scanning-Tunneling Microscopy Imaging of Individual Molecular Orbitals. Phys. Rev. Lett. 2005, 94, 26803. [DOI] [PubMed] [Google Scholar]
- Repp J. Imaging Bond Formation Between a Gold Atom and Pentacene on an Insulating Surface. Science 2006, 312, 1196–1199. [DOI] [PubMed] [Google Scholar]
- Villagomez C. J.; Zambelli T.; Gauthier S.; Gourdon A.; Stojkovic S.; Joachim C. STM Images of a Large Organic Molecule Adsorbed on a Bare Metal Substrate or on a Thin Insulating Layer: Visualization of HOMO and LUMO. Surf. Sci. 2009, 603, 1526–1532. [Google Scholar]
- Mohn F.; Gross L.; Moll N.; Meyer G. Imaging the Charge Distribution within a Single Molecule. Nat. Nanotechnol. 2012, 7, 227–231. [DOI] [PubMed] [Google Scholar]
- Karacuban H.; Koch S.; Fendrich M.; Wagner T.; Möller R. PTCDA on Cu(111) Partially Covered with NaCl. Nanotechnology 2011, 22, 295305. [DOI] [PubMed] [Google Scholar]
- Oehzelt M.; Koch N.; Heimel G. Organic Semiconductor Density of States Controls the Energy Level Alignment at Electrode Interfaces. Nat. Commun. 2014, 5, 4174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wegner D. Private communication.
- Amsalem P.; Niederhausen J.; Wilke A.; Heimel G.; Schlesinger R.; Winkler S.; Vollmer A.; Rabe J. P.; Koch N. Role of Charge Transfer, Dipole-Dipole Interactions, and Electrostatics in Fermi-Level Pinning at a Molecular Heterojunction on a Metal Surface. Phys. Rev. B 2013, 87, 035440. [Google Scholar]
- García-Gil S.; García A.; Ordejón P. Calculation of Core Level Shifts within DFT Using Pseudopotentials and Localized Basis Sets. Eur. Phys. J. B 2012, 85, 239. [Google Scholar]
- Methfessel M.; Hennig D.; Scheffler M. Ab-Initio Calculations of the Initial- and Final-State Effects on the Surface Core-Level Shift of Transition Metals. Surf. Sci. 1993, 287–288, 785–788. [Google Scholar]
- Dąbrowski J.; Scheffler M. Self-Consistent Study of the Electronic and Structural Properties of the Clean Si(001)(2 × 1) Surface. Appl. Surf. Sci. 1992, 56–58, 15–19. [Google Scholar]
- Romaner L.; Heimel G.; Zojer E. Electronic Structure of Thiol-Bonded Self-Assembled Monolayers: Impact of Coverage. Phys. Rev. B 2008, 77, 045113. [Google Scholar]
- Obersteiner V.; Egger D. A.; Heimel G.; Zojer E. Impact of Collective Electrostatic Effects on Charge Transport through Molecular Monolayers. J. Phys. Chem. C 2014, 118, 22395–22401. [Google Scholar]
- Topping J. On the Mutual Potential Energy of a Plane Network of Doublets. Proc. R. Soc. Math. Phys. Eng. Sci. 1927, 114, 67–72. [Google Scholar]
- Duhm S.; Heimel G.; Salzmann I.; Glowatzki H.; Johnson R. L.; Vollmer A.; Rabe J. P.; Koch N. Orientation-Dependent Ionization Energies and Interface Dipoles in Ordered Molecular Assemblies. Nat. Mater. 2008, 7, 326–332. [DOI] [PubMed] [Google Scholar]
- Wang H.; Amsalem P.; Heimel G.; Salzmann I.; Koch N.; Oehzelt M. Band-Bending in Organic Semiconductors: The Role of Alkali-Halide Interlayers. Adv. Mater. 2014, 26, 925–930. [DOI] [PubMed] [Google Scholar]
- Blum V.; Gehrke R.; Hanke F.; Havu P.; Havu V.; Ren X.; Reuter K.; Scheffler M. Ab Initio Molecular Simulations with Numeric Atom-Centered Orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar]
- Perdew J. P.; Ernzerhof M.; Burke K. Rationale for Mixing Exact Exchange with Density Functional Approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar]
- Zhang G.-X.; Tkatchenko A.; Paier J.; Appel H.; Scheffler M. Van Der Waals Interactions in Ionic and Semiconductor Solids. Phys. Rev. Lett. 2011, 107, 245501. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



