MRI reconstruction of multi-image acquisitions using a rank regularizer with data reordering

Abstract

Purpose:

To improve rank constrained reconstructions for undersampled multi-image MRI acquisitions.

Methods:

Motivated by the recent developments in low-rank matrix completion theory and its applicability to rapid dynamic MRI, a new reordering-based rank constrained reconstruction of undersampled multi-image data that uses prior image information is proposed. Instead of directly minimizing the nuclear norm of a matrix of estimated images, the nuclear norm of reordered matrix values is minimized. The reordering is based on the prior image estimates. The method is tested on brain diffusion imaging data and dynamic contrast enhanced myocardial perfusion data.

Results:

Good quality images from data undersampled by a factor of three for diffusion imaging and by a factor of 3.5 for dynamic cardiac perfusion imaging with respiratory motion were obtained. Reordering gave visually improved image quality over standard nuclear norm minimization reconstructions. Root mean squared errors with respect to ground truth images were improved by ∼18% and ∼16% with reordering for diffusion and perfusion applications, respectively.

Conclusions:

The reordered low-rank constraint is a way to inject prior image information that offers improvements over a standard low-rank constraint for undersampled multi-image MRI reconstructions.

1. INTRODUCTION

Multi-image MRI encompasses a wide variety of imaging scenarios such as dynamic imaging, diffusion imaging, real time imaging, and T1 mapping. Accelerating multi-image MRI acquisitions is a developing area that can have a high practical impact. Many groups have applied acceleration methods for dynamic (multiple time frame) MRI,^1–7 although the concepts typically also apply to other multi-image acquisitions. These methods undersample k-space data and then use algorithms beyond the inverse Fourier transform (IFT) to exploit redundancies between images and obtain high quality diagnostic images. These methods can be used to reduce the total scan time or they can lead toward obtaining new or additional clinical information. For example, higher temporal resolution and increased slice coverage can be obtained for dynamic contrast enhanced imaging of the heart.⁴

Recent developments in matrix completion theory^8,9 have translated to exciting results from low-rank reconstruction methods applied to MRI.^6,10–14 Rank constrained reconstructions have been applied in the context of static imaging¹⁵ as well as in dynamic MRI. Promising results have been shown for myocardial perfusion MRI (Ref. ⁶) and breast imaging,¹⁰ among other applications.^11,13 The dynamic image reconstruction methods are based on the assumption that the matrix containing all of the images from a dynamic sequence has a rank that is much lower than the number of images. The idea of using the rank penalty is related to the partially separable functions approach for dynamic imaging,¹⁶ which exploits the fact that dynamic images can be represented using relatively few underlying basis functions. Constraining the temporal basis functions to be K-th order partially separable translates to constraining the image matrix to be rank K.¹⁶ However, as shown in Refs. ⁶ and ¹⁷, the rank constraint term by itself cannot preserve the quality of images at high acceleration factors or when there is significant respiratory motion in the data. In Ref. 6, the rank constraint was used in conjunction with a total variation (TV) penalty term¹⁸ in a joint spectral-spatial framework. The method produced improved image quality over standard rank constrained reconstruction. In Ref. 17, the standard rank constraint applied to perfusion data with breathing motion resulted in blurring of the images. In that work, a large dictionary of temporal bases was used with a sparsity constraint on the dictionary coefficients in a blind compressed sensing (CS) framework to improve the standard rank constrained reconstruction.

Here, we present a new reordering-based rank constrained reconstruction method for undersampled multi-image MR data that can improve the standard low-rank method especially when the dynamic images do not have a very low rank before reordering (for example, inter-frame motion can increase the rank, requiring a larger number of basis functions¹⁹). The new constraint implements a modification of the standard rank constraint that incorporates prior multi-image information. The reordering method can be thought of as a data-specific transformation that enhances the low-rank property of the images making the rank penalty a more powerful regularization constraint. Similar intensity reordering approaches have recently been proposed in the context of compressed sensing reconstruction for improving image sparsity by incorporating prior knowledge about the image into the reconstruction.^20–22 Here, we extend the reordering method to low-rank reconstructions of multi-image MRI data.

2. METHODS

2.A. Theory

Consider data acquired in k–t space, d(k, t), which is the complex k-space data acquired at instance “t” in a multi-image acquisition. We use this notation to also include diffusion imaging acquisitions, where in that case, t indexes images with different diffusion weightings. More generally, t is an index that can include all multi-image k-space data acquisitions. Putting all of the acquired data together in a data matrix D of size M × N, we have

$${\displaystyle D=\left[\begin{array}{ccccc}\hfill d({\mathit{k}}_1,t_1)\hfill & \hfill d({\mathit{k}}_1,t_2)\hfill & \hfill d({\mathit{k}}_1,t_3)\hfill & \hfill \cdots \hfill & \hfill d({\mathit{k}}_1,t_N)\hfill \\ \hfill d({\mathit{k}}_2,t_1)\hfill & \hfill d({\mathit{k}}_2,t_2)\hfill & \hfill d({\mathit{k}}_2,t_3)\hfill & \hfill \cdots \hfill & \hfill d({\mathit{k}}_2,t_N)\hfill \\ \hfill d({\mathit{k}}_3,t_1)\hfill & \hfill d({\mathit{k}}_3,t_2)\hfill & \hfill d({\mathit{k}}_3,t_3)\hfill & \hfill \cdots \hfill & \hfill d({\mathit{k}}_3,t_N)\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill d({\mathit{k}}_M,t_1)\hfill & \hfill d({\mathit{k}}_M,t_2)\hfill & \hfill d({\mathit{k}}_M,t_3)\hfill & \hfill \cdots \hfill & \hfill d({\mathit{k}}_M,t_N)\hfill \end{array}\right],}$$

where M is the total number of k-space data points in a given “time” frame and N is the total number of time frames. Each column in D represents a vectorized version of a k-space frame. The corresponding complex image matrix “I” obtained by inverse Fourier transforming each k-space frame of fully acquired data can be represented as the Casorati matrix,

$${\displaystyle \mathit{I}=\left[\begin{array}{ccccc}\hfill i({\mathit{x}}_1,t_1)\hfill & \hfill i({\mathit{x}}_1,t_2)\hfill & \hfill i({\mathit{x}}_1,t_3)\hfill & \hfill \cdots \hfill & \hfill i({\mathit{x}}_1,t_N)\hfill \\ \hfill i({\mathit{x}}_2,t_1)\hfill & \hfill i({\mathit{x}}_2,t_2)\hfill & \hfill i({\mathit{x}}_2,t_3)\hfill & \hfill \cdots \hfill & \hfill i({\mathit{x}}_2,t_N)\hfill \\ \hfill i({\mathit{x}}_3,t_1)\hfill & \hfill i({\mathit{x}}_3,t_2)\hfill & \hfill i({\mathit{x}}_3,t_3)\hfill & \hfill \cdots \hfill & \hfill i({\mathit{x}}_3,t_N)\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill i({\mathit{x}}_M,t_1)\hfill & \hfill i({\mathit{x}}_M,t_2)\hfill & \hfill i({\mathit{x}}_M,t_3)\hfill & \hfill \cdots \hfill & \hfill i({\mathit{x}}_M,t_N)\hfill \end{array}\right].}$$

Each column in I represents a vectorized version of an image frame. When k-space data are undersampled, the missing entries in matrix D are not recovered here by directly minimizing the rank of the matrix D, instead a rank penalty on the image matrix I is used as a regularizer with fidelity to the sampled entries in D. This approach works because images in a multi-image acquisition are generally correlated resulting in a significantly lower rank than the number of columns in I. Low-rank constrained reconstruction from undersampled data can be mathematically represented as

$${\displaystyle \tilde{\mathit{I}}=\underset{\tilde{\mathit{I}}}{min}\left({∥E\left(\tilde{\mathit{I}}\right)-\tilde{\mathit{D}}∥}_2^2\text{ + }\alpha \left(\text{rank}\left(\tilde{\mathit{I}}\right)\right)\right)\text{.}}$$ (1)

The first data fidelity term in Eq. (1) ensures that the final reconstructed image has its k-space match the acquired data. In this term, $\tilde{\mathit{D}}$ is the undersampled k-space data matrix, $\tilde{\mathit{I}}$ is the reconstructed image estimate, and E is the encoding operator that computes Fourier transform of the image estimate at the sampled k-space locations. The regularization constraint ensures that the image matrix $\tilde{\mathit{I}}$ has a low rank. Directly minimizing Eq. (1) is theoretically not feasible due to the nonconvexity of the rank penalty term (L⁰ norm of the singular values of $\tilde{\mathit{I}}$), but in practice, methods have been proposed to minimize the nonconvex functions.^6,15

Also, the nonconvex constraint can be relaxed to a convex version without a significant loss in practical performance^8,9 by minimizing ${\tilde{I}}^{\prime }\text{s}$ nuclear norm (NN) denoted as ${∥\tilde{\mathit{I}}∥}_{*}$ which is the L¹ norm of its singular values. A number of fast and efficient algorithms^23,24 have been proposed to minimize the nuclear norm of a matrix in the context of matrix completion to recover missing entries exactly. These algorithms can be applied for reconstructing multi-image MRI data using a relaxed rank constraint in Eq. (1).

2.A.1. Reordering for lowering the nuclear norm

Reordering image matrix values can lower the nuclear norm of a matrix. That is, shuffling the elements in a matrix based on a certain predetermined order for the indices can lower the nuclear norm. For example, when each column’s real and imaginary parts in a large rectangular matrix with complex entries are reordered independently so that each component is monotonic, its nuclear norm is significantly lowered.

2.A.2. Row vs column reordering

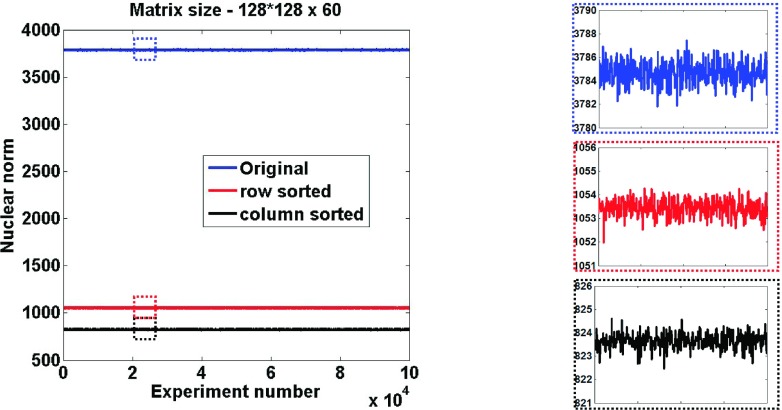
Figure 1 shows the result of a Monte Carlo simulation with several different randomly generated rectangular matrices of a fixed size 16 384 × 60 (128*128 = 16 384). This size is on the order of the sizes typically encountered in diffusion and cardiac perfusion imaging. In these random matrices with complex entries, real and imaginary parts were independently picked from a uniformly random distribution and the nuclear norms were computed before and after reordering. The random distribution makes this initial example full rank and thus a worst case for the nuclear norm. Reordering either along columns or along rows was performed to make the values monotonically ascending. Reordering along columns significantly reduced the nuclear norm (by ∼80%) for all of the 100 000 experiments. While reordering along rows also lowered the original nuclear norm, higher reductions were obtained when reordering was done along columns. This was expected since the number of values in a row (N) was far fewer than the number of values in a column (M). This figure serves only to introduce the method, since such perfect reordering is not attainable without the true image.

FIG. 1.

Illustration of nuclear norm reduction with reordering. Plots of nuclear norms for randomly generated complex matrices without and with reordering. Corresponding zoomed regions of the plots are also shown.

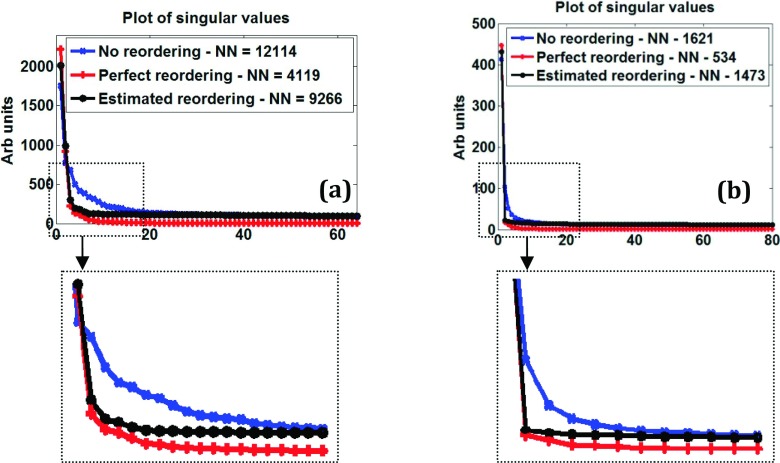
In actual scanner data as well, the nuclear norm can be significantly reduced by reordering. Figure 2(a) shows singular values and nuclear norms from a brain diffusion imaging dataset matrix (size 4096 × 64). Values without reordering, with perfect reordering, and with estimated reordering based on an initial compressed sensing reconstruction are plotted in Fig. 2(a). “Perfect reordering” means the sorting order that gives monotonic ascending values when applied on the true underlying images (separately for real and imaginary parts). The nuclear norm of the perfectly reordered matrix is ∼66% lower than that for the original matrix. The estimated reordering reduces the nuclear norm by ∼24% and can be realized in practice.

FIG. 2.

Nuclear norm reduction in actual scanner data. Plot of singular values of image matrix obtained from (a) a fully sampled diffusion imaging dataset with 64 directions and (b) a fully sampled perfusion dataset with 80 time frames. Nuclear norms (NNs) without and with reordering are also shown. Corresponding zoomed versions are also shown.

Figure 2(b) shows an example for a dynamic myocardial perfusion imaging matrix (size 18 432 × 80) that has significant inter-frame respiratory motion. Perfect reordering reduces the nuclear norm to approximately one-third of the original value. Although not shown here, a similar trend was observed for different slices and for different coils in these datasets. And as in the Monte Carlo experiments in Fig. 1, reordering along the columns lowered the nuclear norm more than reordering along rows.

2.A.3. Mixing ascending and descending reorderings

While there are many options on how to reorder the data, we tested two scenarios using the cardiac perfusion dataset (i) if monotonic ordering of all of the columns gave a low rank and (ii) if ordering the real and imaginary parts differently within each column lowered the nuclear norm.

2.A.3.a. Across columns.

Figure 3(a) shows the nuclear norms of myocardial perfusion Casorati matrix in which randomly selected columns are reordered to be ascending and the remaining columns to be descending. For all of the 100 000 different sets of random selections, the nuclear norm was lower when all of the columns were ascendingly or when all of the columns were descendingly reordered.

FIG. 3.

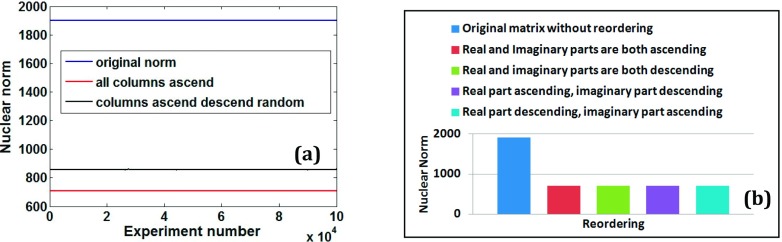
Determining optimal reordering of columns using Casorati matrix from a cardiac perfusion dataset. (a) Comparison of nuclear norms (i) without any reordering (labeled original norm) with (ii) reordering all columns in an ascending fashion (labeled all columns ascend) and with (iii) reordering only a random subset of columns in ascending fashion while the remaining columns reordered in descending fashion for 100 000 experiments. (b) Comparison of nuclear norms with different ascending/descending reordering combinations for real and imaginary parts to determine optimal reordering within each column.

2.A.3.b. Within a column.

No significant differences in nuclear norms were observed with different ascending/descending combinations for real and imaginary parts within a column. Figure 3(b) compares the nuclear norms for four possible scenarios in which reordering both real and imaginary parts of each column independently to be ascending (or descending) gave the lowest nuclear norm.

2.B. Reconstruction using a low-rank regularizer with reordering

We now introduce a new and modified regularizer that better satisfies the low-rank assumption given as $min{∥O\left(\tilde{\mathit{I}}\right)∥}_{*}$, where O is an operator that reorders each column in multi-image set $\tilde{\mathit{I}}$ independently, based on a predetermined ordering from a prior. Within each column, ordering is independent for its real and imaginary components. O can be thought of as a data-specific transformation operator that injects prior image information to better suit the low-rank constraint. Reconstruction is now performed as

$${\displaystyle \tilde{\mathit{I}}=\underset{\tilde{\mathit{I}}}{min}\left({∥E\left(\tilde{\mathit{I}}\right)-\tilde{\mathit{D}}∥}_2^2\text{ + }\alpha {∥O\left(\tilde{\mathit{I}}\right)∥}_{*}\right)\text{.}}$$ (2)

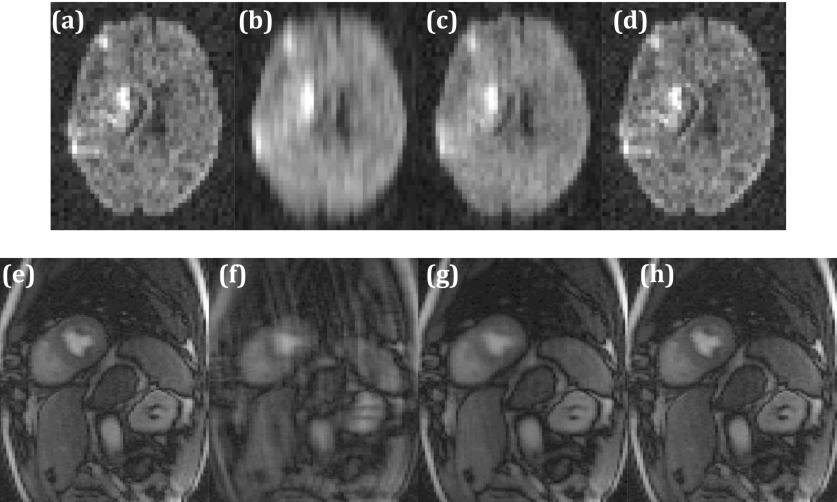
Figure 4 shows an example of reconstruction from R = 4 data with perfect reordering for diffusion and perfusion datasets. Injecting the correct prior information into the reconstruction significantly improves the image quality as compared to standard rank constrained reconstruction with no prior information.

FIG. 4.

Illustration of rank constrained reconstruction with perfect reordering. (a) Fully sampled data with IFT reconstruction. One diffusion encoding direction is shown. (b) Corresponding R = 4 IFT reconstruction. (c) Corresponding R = 4 standard low-rank reconstruction. (d) Corresponding R = 4 low-rank reconstruction with reordering. [(e)–(h)] Same as [(a)–(d)] but for a time frame in a perfusion dataset.

2.B.1. Obtaining prior image information

In practice, it is not possible to obtain the exact ordering to drastically reduce the nuclear norm. However, a number of schemes can be used that can provide an “approximately perfect” ordering. Here, we use a compressed sensing reconstruction as a prior to obtain the ordering for the low-rank reconstructions. Undersampled data are first reconstructed using a spatiotemporal constrained reconstruction (STCR)²⁰ with temporal and spatial total variation constraints by minimizing the cost function C shown as follows:

$${\displaystyle C={∥E\left(\tilde{\mathit{I}}\right)-\tilde{\mathit{D}}∥}_2^2+{\alpha }_1{\text{TV}}_t\left(P\left(\tilde{\mathit{I}}\right)\right)+{\alpha }_2{\text{TV}}_s\left(\tilde{\mathit{I}}\right).}$$ (3)

TV_t and TV_s are the temporal and spatial TV constraints⁴ and P is a temporal reordering operator that uses the central low resolution images obtained from variable density undersampling for reordering each pixel’s “time curve.”²⁰ Minimization of C is performed using an iterative gradient descent method.²⁰ Having the preliminary reordering in the temporal TV term in Eq. (3) improves the image quality for the prior generation step. α₁ and α₂ are the weighting factors for “temporal” and spatial constraint terms, respectively, and are chosen empirically. Figure 2 shows an example of the effect of the reorderings based on reconstructions from Eq. (3). The singular values labeled as “estimated reordering” are from using Eq. (3) and those singular values decay more rapidly compared to the original singular values, though not as rapidly as with perfect reordering. This effect holds for both the diffusion and perfusion imaging cases.

2.B.2. Low-rank reconstruction with reordering

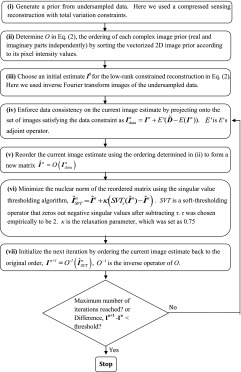
After the compressed sensing reconstruction, the real and imaginary parts of these complex prior images are sorted according to their pixel intensity values and the sorting order is used subsequently for a reordered rank constrained reconstruction. A projection onto convex sets (POCSs) based alternating minimization scheme is used to minimize Eq. (2). The current image estimate is projected on the data fidelity term [step (iv) in the flowchart below] and then a singular value thresholding (SVT) algorithm²⁴ is used to enforce the regularization. We note that the reordering step in the algorithm injects prior information into the nuclear norm constraint and does not change the convexity of the cost function. The convergence of SVT for nuclear norm minimization is established in Ref. 24. The reconstruction steps are summarized in the flowchart below.

2.C. Application to multi-image data

The reordered rank constrained reconstruction method was tested on two different multi-image MR acquisitions that could benefit from an accelerated acquisition: (i) diffusion imaging of the brain and (ii) dynamic cardiac perfusion imaging. All of the data were acquired in accordance with Institutional Review Board regulations at The University of Utah.

2.C.1. Diffusion imaging

Fully sampled diffusion imaging data of the brain of a patient with a recent stroke were obtained using a simultaneous image refocusing (SIR) sequence²⁵ on a Siemens 1.5 T scanner. The SIR sequence allows acquisition of multiple slices simultaneously, which is faster than a conventional slice by slice EPI acquisition when the diffusion preparation period is sizable, and is complemented by undersampling. A SIR factor of two was used to image two slices in one EPI readout. The scan parameters were TR = 5.7 s, TE = 138 ms, slice thickness = 2.5 mm, matrix size = 128 × 64 (for two slices), and in-plane pixel size was 1.8 mm². One image with b-value = 0 and 64 encoding directions with a b-value of 800 were acquired for 36 slices. The k-space data for the two SIR slices acquired in a single readout were undersampled offline in a variable density random fashion by a factor of three with 13 lines fully sampled in the center and higher frequency lines randomly sampled for different diffusion encoding directions. A compressed sensing reconstruction prior from Eq. (3) with total variation constraints was generated for each coil data with α₁ and α₂ chosen as 0.02 and 0.005, respectively. The low-rank reconstruction with reordering was then performed using the sorting orders from the prior images and the individual coil images were combined in a sum-of-squares fashion.

2.C.2. Dynamic cardiac perfusion imaging

Fully sampled dynamic cardiac perfusion data were acquired on a Siemens 3 T scanner using a saturation recovery sequence. The scan parameters were TR = 1.8 ms, TE = 1.36 ms, slice thickness = 8 mm, in-plane resolution = 2.2 × 3 mm², matrix size = 192 × 96, and gadolinium DTPA-BMA dose = 0.05 mmol/kg. Fully sampled k-space data for each coil were undersampled in a variable density random fashion by a factor of 3.5 with 14 fully sampled phase encodes in the center. The phase encodes toward the outer regions of k-space were sampled in a random fashion for different time frames. The data had significant inter-frame motion due to breathing. Compressed sensing reconstruction by Eq. (3) with α₁ and α₂ chosen as 0.025 and 0.008, respectively, was used to create the prior for rank reconstruction with reordering.

For both of the applications, the α₁ and α₂ parameters for generating the prior were chosen to minimize the reconstruction error compared to the true reconstructions using fully sampled data. For the low-rank reconstruction stage, the reconstruction parameter τ was also chosen to optimize the reconstruction error compared to the true reconstructions using fully sampled data. We have found in previous works that typically these same reconstruction parameters work for prospectively undersampled datasets of the same data type and size, without the need to tune parameters for individual datasets.^4,20

2.D. Evaluation of the reconstructions

Undersampled data reconstructions were compared to fully sampled inverse Fourier reconstructions that were considered as ground truth. General as well as application specific evaluation metrics described below were used.

2.D.1. Diffusion imaging

Reconstructions from undersampled data were compared to ground truth in terms of difference images for different encoding directions to visualize any loss of structure or resolution. Root mean squared errors were also computed as a first-order error metric to compare the two rank constrained reconstructions—without and with reordering—relative to ground truth.

2.D.2. Dynamic cardiac perfusion imaging

The spatial and temporal characteristics of the undersampled reconstructions were compared to those from ground truth images from fully sampled IFT reconstructions. Reconstruction errors were quantified in terms of root mean squared differences between estimated and true pixel intensities over all time frames. Mean signal intensity time curves for regions of interest in the left ventricular blood and the myocardium were computed and compared.

3. RESULTS

3.A. Diffusion imaging

Figure 5 shows the results and evaluation of the proposed reconstruction method for diffusion imaging. Figure 5(c) shows that R = 3 reconstruction with reordered rank constraint is sharper than the standard low-rank reconstructions shown in Fig. 5(b), respectively. Absolute difference images corresponding to low-rank reconstruction without reordering have more structures than those corresponding to reordered rank constraint. Root mean squared error was 18% lower for the proposed method than the low-rank method without reordering.

FIG. 5.

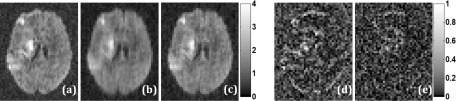
Comparison of diffusion imaging reconstructions. (a) Ground truth image for a diffusion direction reconstructed using inverse Fourier transform from fully sampled k-space data. [(b) and (c)] Corresponding R = 3 rank constrained reconstructions without and with reordering, respectively. [(d) and (e)] Absolute difference images between (a) and (b) and between (a) and (c), respectively.

3.B. Dynamic cardiac perfusion imaging

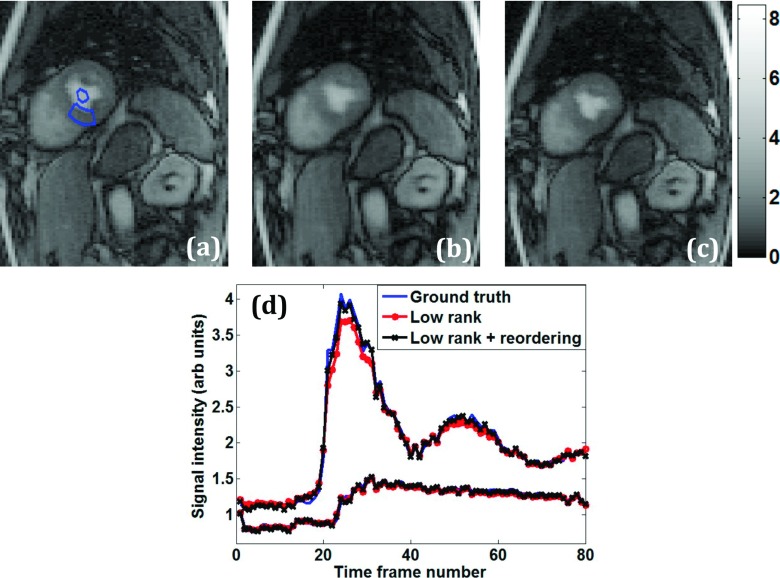
Figure 6 compares and evaluates the results obtained from the undersampled rank constrained reconstructions with reordering. Figure 6(b) from the standard low-rank reconstruction is more blurred in the heart region compared to the reordered rank reconstruction in Fig. 6(c). The RMS error for reordering was lower than that without reordering by 16%. In Fig. 6(d), the left ventricular blood pool time curve for the reordered rank constraint, labeled “low rank + reordering,” matches the true time curve better at the peak intensity. Lower peak intensity in the left ventricular blood pool curve would cause inaccurate perfusion estimates when performing quantitative analysis.²⁶

FIG. 6.

Comparison of perfusion imaging reconstructions—spatial and temporal characteristics. (a) Ground truth postcontrast image reconstructed using inverse Fourier transform from fully sampled k-space data. ROIs are shown in the myocardium and left ventricular blood pool. Corresponding R = 3.5 reconstruction with standard rank constraint (b) and with reordered rank constraint (c). (d) Mean intensity time curves from the blood pool and myocardium ROIs.

4. DISCUSSION

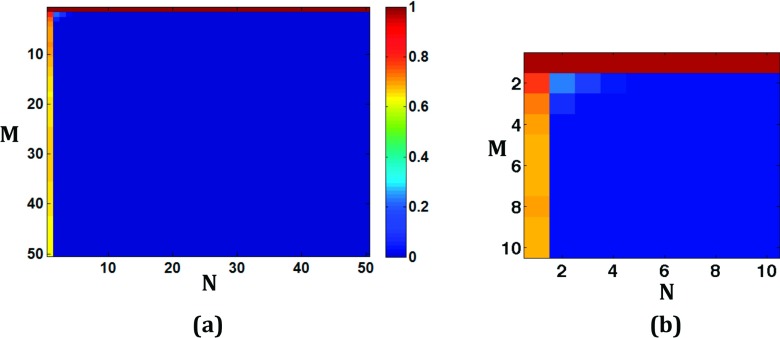
We presented a novel framework to improve rank constrained reconstructions of multi-image MRI data by injecting prior information via intensity reordering. That is, a data reordering derived from an initial image reconstruction was used so that image estimates similar to the prior would have a reduced nuclear norm. The method of reordering employed here made the prior be monotonically increasing along the columns of its Casorati matrix. However, reordering a matrix along columns to make them monotonic may not always lower the nuclear norm. For example, consider $\left[\begin{array}{cc}\hfill 1+i\hfill & \hfill -1-i\hfill \\ \hfill 1-i\hfill & \hfill -1+i\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$. In this case, the matrix rank increases from 1 to 2 after reordering the real and imaginary components independently along columns. Since similar examples can be found in cases of relatively small matrices and rank = 1 matrices where reordering increases the original nuclear norm, we performed simulations to estimate how often an increase in rank could occur. Figure 7 shows results of Monte Carlo simulations in the form of error maps.

FIG. 7.

Monte Carlo simulations using random matrices of smaller sizes to determine if reordering increases the nuclear norm. (a) Map in which color represents the fraction of the number of times (out of 100 000 randomly generated complex matrices of a fixed size) reordering resulted in a nuclear norm that was equal to or greater than the nuclear norm of the original matrix. The size of the matrix is given by the x and y coordinates of the location. (b) Detail of the top left corner of the map for low values of N and M.

Each intensity in the error map indicates the number of times (out of 100 000 randomly generated complex matrices of a fixed size) that the reordered nuclear norm was equal to or greater than the original norm. For example, a value of 1 means that in all of the 100 000 cases reordering increased or did not change the nuclear norm. Any nonzero value in the image reflects that reordering increased or did not change the matrix’s original nuclear norm in at least 1 out of 100 000 matrices. The location in the error map represents the matrix size. Reordering can increase or keep the original nuclear norm for small sized matrices or for matrices with rank-1 or when the matrices already have extremely low rank and are not compressible further. But as the matrix size increases and becomes more rectangular, the fraction is zero. This is consistent with the results in Fig. 1 that showed Monte Carlo simulations for large rectangular matrices and for multi-image data of interest, where reordering columns with a good prior always resulted in lowering the nuclear norm. Making the columns monotonic is the only one way to reorder and lower the nuclear norm of a complex Casorati matrix and other even more data-specific ways to reorder entries of the Casorati matrix could lead to lower nuclear norms.

Reordering all of the time frames with the same pixel ordering in each would not change the nuclear norm, so it is the differences in reordering relative to other image frames (vectors) that is important. Promising results were shown from R = 3 diffusion imaging data and from R = 3.5 perfusion imaging data that had significant inter-frame respiratory motion during contrast uptake. Note that undersampling k-space data by a factor of three for diffusion imaging does not directly translate to threefold scan time reduction because of the predominant diffusion preparation time in echo planar acquisitions. But the undersampling and reconstruction scheme proposed here can be used in conjunction with SIR or multiband acquisitions^27,28 to give a true threefold scan time reduction. Higher accelerations with reordering may be possible with improved priors.

As well, higher acceleration factors (beyond 3.5) for perfusion imaging may be possible when there is no motion in the data. Acceleration factors up to 8 (that correspond to a net factor of ∼5–6 due to training data) have been reported for breath-hold cardiac perfusion acquisitions.^29–31 However, good breath-hold acquisitions are not always possible especially at stress imaging. We also note that the “R” factor for a reconstruction method depends on the size of the fully sampled acquisition matrix and the acquired spatial and temporal resolution. Higher R may be possible if the fully sampled matrix has a large number of phase encodes.

4.A. Relation to previous reordering and motion-compensation methods

Reordering-based approaches have been proposed previously in the context of CS reconstructions in order to inject prior information and enhance signal sparsity.^20–22 In Ref. 20, low resolution images were used to obtain the multi-image ordering of each pixel. Monotonic reordering was used with the TV constraint in the multi-image direction. We found that using low resolution images for rank reconstructions with reordering along columns was detrimental, reordering along rows may be more appropriate in that case. This could be due to the fact that low resolution images are better at preserving overall temporal information as compared to preserving spatial features of the images. Wu et al.²¹ used SENSE (Ref. ³²) reconstructions as a prior to determine reorderings in order to improve static brain imaging CS reconstructions. In Ref. 22, reordering of blocks of pixels led to improvements in cardiac cine imaging reconstructions over keyhole, sliding window and k–t BLAST methods. In contrast to these previous methods, here, we (i) used reordering based on CS priors and (ii) used reordering to reduce the nuclear norm of the dataset for improved reconstructions. As well, here, we do a vectorized spatial reordering for each multi-image or time frame. This is because reordering along columns outperformed reordering rows since the image matrices are very rectangular. Depending on the application, a “hybrid prior” can be generated by combining different types of initial reconstructions that could then be used for final reconstruction with reordering for improved quality. Reconstruction for prior generation as well as the final reconstruction could also conceivably benefit from nonconvex formulations.^6,33,34

Motion compensation methods that help improve standard rank constrained reconstructions have also been proposed recently.^33,35,36 The methods require motion estimation and compensation steps every iteration to reduce between-frame motion and increase temporal correlations. Reordering can be thought of as a different way to improve rank constrained reconstructions, without the need to estimate and compensate for motion. In this light, reordering may be more applicable for multi-image datasets like diffusion imaging where the signals can change significantly across diffusion directions even without any inter-image motion.

4.B. Sensitivity to prior

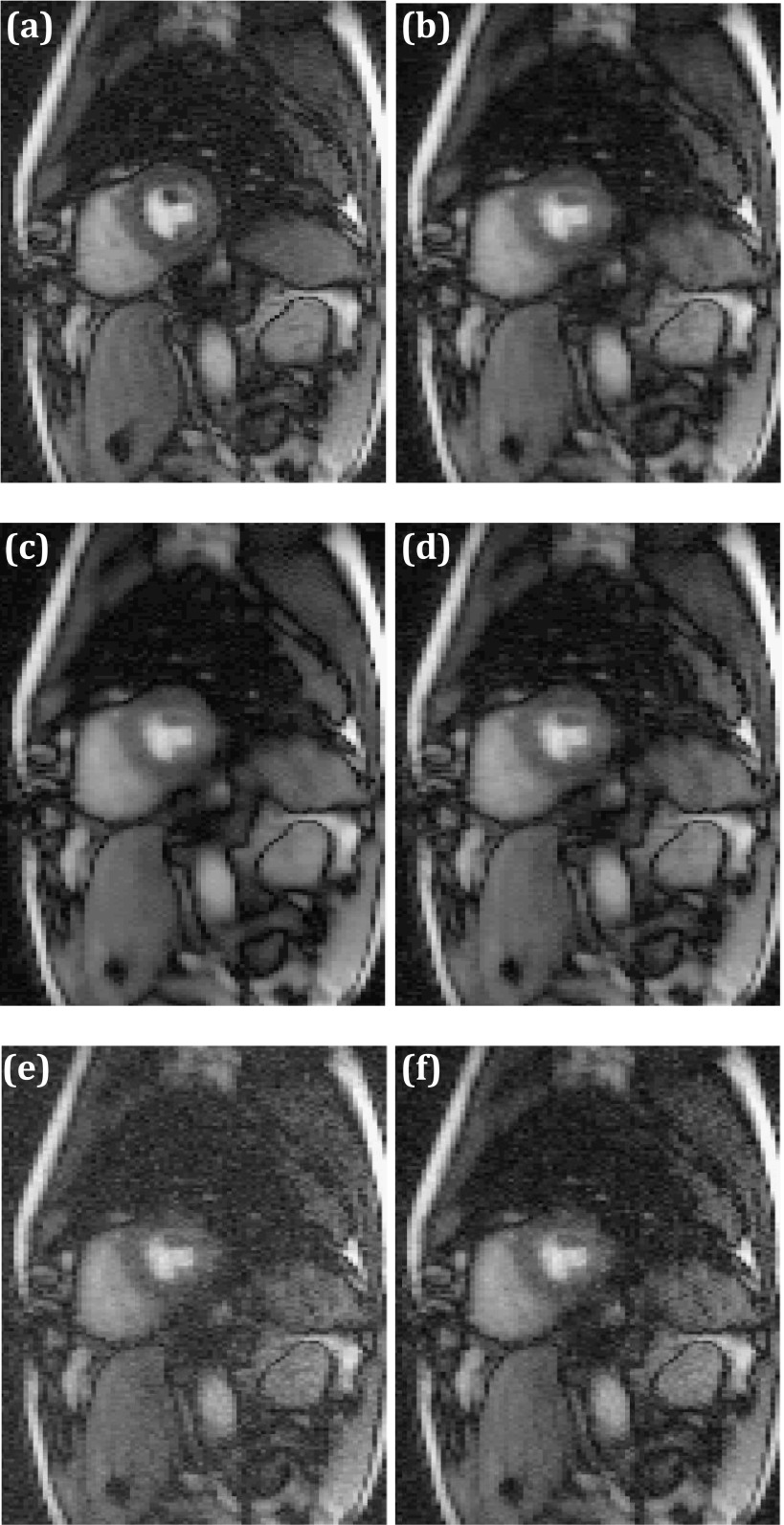
Having a good quality prior is important to obtain improvements with reordering for low-rank reconstructions. While use of a high quality prior may not offer significant improvements over the prior (for example, if the prior is very close to the true image), injecting a poor image prior can be detrimental to final reconstructions. Figure 8 shows the effect of using different quality priors for low-rank reconstructions with reordering.

FIG. 8.

Reconstruction sensitivity to prior image quality. (a) Ground truth fully sampled time frame reconstructed using IFT. (b) Reordered rank constrained reconstruction with prior estimated using spatiotemporal TV reconstruction [Eq. (3)]. (c) Overly smoothed version of the STCR prior obtained with a spatial total variation filter. (d) Reordered rank constrained reconstruction using the smoothed STCR prior in (c). (e) Noisy version of STCR prior obtained by adding complex random Gaussian noise. (f) Reordered rank constrained reconstructions using noisy STCR prior in (e).

When ordering from the optimal STCR prior [Eq. (3)] is used, we obtained reconstruction shown in Fig. 8(b), RMS error for this reconstruction was ∼10-fold higher than the RMS error for the reconstruction when using ground-truth/perfect prior. Using a blurred prior shown in Fig. 8(c) (obtained by smoothing of the optimal STCR prior) results in Fig. 8(d) which although sharper (9% lower blur metric³⁷) and with 12% lower RMS error than the prior, the result is blurred compared to Figs. 8(a) and 8(b). A similar detrimental effect is observed when a noisy prior is used. Figure 8(e) is obtained by adding random Gaussian noise to the real and imaginary parts of the complex valued optimal STCR prior. While Fig. 8(f) has 31% lower RMS error and 31% lower standard deviation of pixels in a background ROI when compared to its corresponding prior, the quality is degraded compared to Fig. 8(b). In practice, for a given application, a rigorous analysis can be performed using different priors to assess the improvements before choosing a method for clinical use.

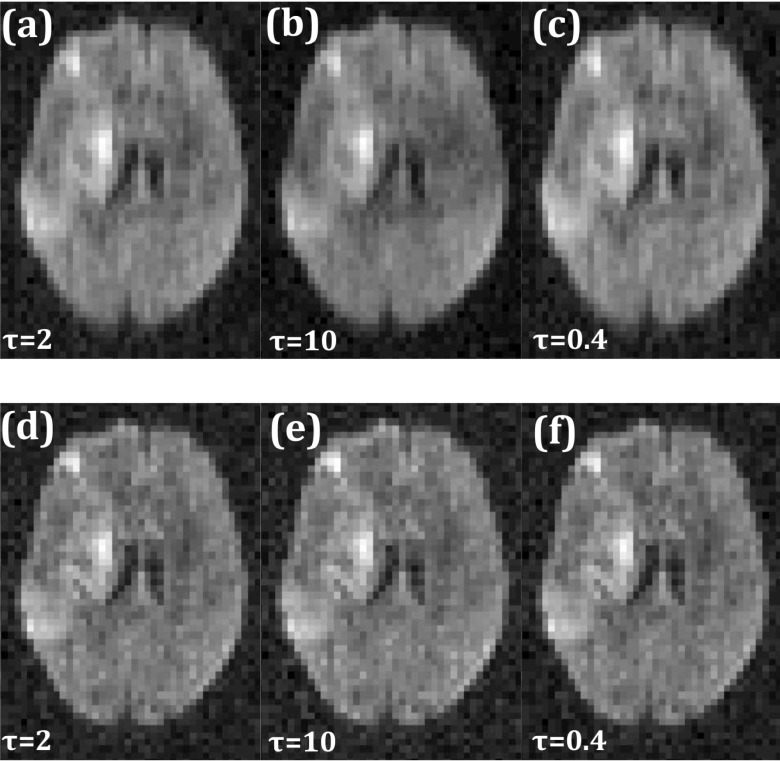
4.C. Sensitivity to threshold parameter, τ

The threshold parameter τ in the singular value thresholding algorithm [step (vi) in the flowchart] is an important parameter that affects the reconstructed image quality. A significantly lower value than optimal does not remove undersampling artifacts while a large value results in a loss of temporal dynamics in multi-image acquisitions. Figure 9(b) shows increased blurring with artifacts as compared to Fig. 9(a) when the optimal τ value was scaled up by a factor of five. Scaling down τ by a factor of five, to 0.2, increased noise although imperceptibly. However, compared to standard low-rank reconstruction, reordered rank reconstruction is less sensitive to variations in optimal τ. As an example, the second row of Fig. 9 shows reconstructions using orderings obtained from fully sampled data. Figures 9(e) and 9(f) show images corresponding to the same changes in τ values as in the top row, but the image quality is not significantly different from that obtained with the optimal τ, shown in Fig. 9(d).

FIG. 9.

Reconstruction sensitivity to reconstruction parameter τ. (a) Low-rank reconstruction with optimal τ value. Corresponding image with τ scaled up by a factor of five (b) and scaled down by a factor of five (c). [(d)–(f)] Same as [(a)–(c)] but with reordered rank constraint.

4.D. Increasing undersampling

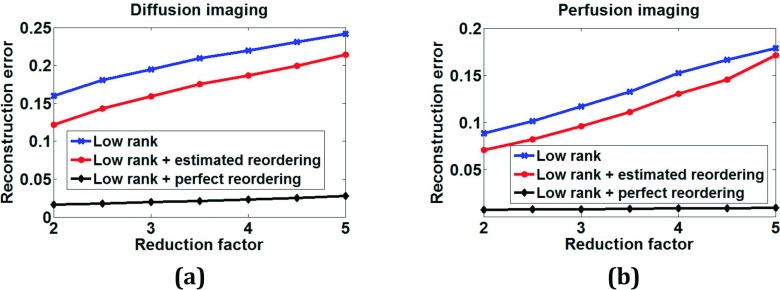
For diffusion imaging of brain and perfusion imaging of the heart with respiratory motion, the method achieved acceleration factors of R = 3 and R = 3.5, respectively, without a significant loss in image quality. Increasing the amount of undersampling causes increased reconstruction error that is almost linear with the undersampling factor. Figure 10 shows plots of normalized total reconstruction error with respect to ground truth for different undersampling factors. Ground truth images and images reconstructed using STCR with TV constraints, Eq. (3), were used as priors for all of the undersampling factors. While the errors increase for both cases with increases in undersampling, the plots with reordering estimated using STCR prior [Eq. (3)] have lower errors than the corresponding plots without reordering. The error increases are much lower and increase at a slower rate for the perfect reordering case that uses ground truth images. While dependent on the quality of the prior used for reordering, the image quality degradation at large undersampling factors could be comparable to the standard rank constrained approach.

FIG. 10.

Normalized reconstruction error plot for different undersampling factors without any reordering (labeled “low rank”) and with estimated and perfect reordering for (a) diffusion imaging and (b) perfusion imaging data.

4.E. Computation time

Reordered rank constrained reconstruction was faster than the standard low-rank reconstruction except for the additional time required for generating the prior (which approximately doubles the time). The main computational load for the rank reconstruction is from the SVT step in each iteration. This step took ∼0.3 s/iteration in matlab on a computer with 96 GB RAM and an eight core processor for the perfusion dataset with matrix size 18 432 × 80 (192^∗96 × 80). Ordering and its inverse operations took an additional ∼0.1 s/iteration. However, the reordering algorithm converged within 80 iterations while the standard low-rank reconstruction took approximately 150 iterations to converge. We note that the number of iterations for convergence can change depending on the underlying data resolution, quality, and also the amount of undersampling.

5. CONCLUSION

Use of a low-rank constraint with signal intensity reordering offers a flexible and relatively simple way to improve low-rank constrained reconstructions of undersampled multi-image acquisitions by injecting prior information in the form of signal intensity ordering. While it is impossible to ascertain a perfect reordering in practice, approximate orderings gleaned from existing reconstruction schemes can offer improvements. While similar to published methods applying reordering with CS methods, low rank with reordering has different trade-offs and different ordering options for reducing the nuclear norm. Reordering done column-wise on each image vector in the Casorati matrix with separate real and imaginary orderings gave improved results for low-rank reconstructions.