Dosimetric verification of lung cancer treatment using the CBCTs estimated from limited-angle on-board projections

Abstract

Purpose:

Lung cancer treatment is susceptible to treatment errors caused by interfractional anatomical and respirational variations of the patient. On-board treatment dose verification is especially critical for the lung stereotactic body radiation therapy due to its high fractional dose. This study investigates the feasibility of using cone-beam (CB)CT images estimated by a motion modeling and free-form deformation (MM-FD) technique for on-board dose verification.

Methods:

Both digital and physical phantom studies were performed. Various interfractional variations featuring patient motion pattern change, tumor size change, and tumor average position change were simulated from planning CT to on-board images. The doses calculated on the planning CT (planned doses), the on-board CBCT estimated by MM-FD (MM-FD doses), and the on-board CBCT reconstructed by the conventional Feldkamp-Davis-Kress (FDK) algorithm (FDK doses) were compared to the on-board dose calculated on the “gold-standard” on-board images (gold-standard doses). The absolute deviations of minimum dose (ΔD_min), maximum dose (ΔD_max), and mean dose (ΔD_mean), and the absolute deviations of prescription dose coverage (ΔV_100%) were evaluated for the planning target volume (PTV). In addition, 4D on-board treatment dose accumulations were performed using 4D-CBCT images estimated by MM-FD in the physical phantom study. The accumulated doses were compared to those measured using optically stimulated luminescence (OSL) detectors and radiochromic films.

Results:

Compared with the planned doses and the FDK doses, the MM-FD doses matched much better with the gold-standard doses. For the digital phantom study, the average (± standard deviation) ΔD_min, ΔD_max, ΔD_mean, and ΔV_100% (values normalized by the prescription dose or the total PTV) between the planned and the gold-standard PTV doses were 32.9% (±28.6%), 3.0% (±2.9%), 3.8% (±4.0%), and 15.4% (±12.4%), respectively. The corresponding values of FDK PTV doses were 1.6% (±1.9%), 1.2% (±0.6%), 2.2% (±0.8%), and 17.4% (±15.3%), respectively. In contrast, the corresponding values of MM-FD PTV doses were 0.3% (±0.2%), 0.9% (±0.6%), 0.6% (±0.4%), and 1.0% (±0.8%), respectively. Similarly, for the physical phantom study, the average ΔD_min, ΔD_max, ΔD_mean, and ΔV_100% of planned PTV doses were 38.1% (±30.8%), 3.5% (±5.1%), 3.0% (±2.6%), and 8.8% (±8.0%), respectively. The corresponding values of FDK PTV doses were 5.8% (±4.5%), 1.6% (±1.6%), 2.0% (±0.9%), and 9.3% (±10.5%), respectively. In contrast, the corresponding values of MM-FD PTV doses were 0.4% (±0.8%), 0.8% (±1.0%), 0.5% (±0.4%), and 0.8% (±0.8%), respectively. For the 4D dose accumulation study, the average (± standard deviation) absolute dose deviation (normalized by local doses) between the accumulated doses and the OSL measured doses was 3.3% (±2.7%). The average gamma index (3%/3 mm) between the accumulated doses and the radiochromic film measured doses was 94.5% (±2.5%).

Conclusions:

MM-FD estimated 4D-CBCT enables accurate on-board dose calculation and accumulation for lung radiation therapy. It can potentially be valuable for treatment quality assessment and adaptive radiation therapy.

1. INTRODUCTION

The respiratory motion makes radiotherapy of lung cancer challenging. Recent developments of imaging techniques such as 4D-CT (Ref. 1) enable us to capture the anatomical and respirational information of lung tumors and normal structures. Based on the anatomical and respirational information, dedicated motion management² techniques are developed for radiotherapy, including³ the free-breathing (FB) treatment and the breath-hold (BH) treatment. In the free-breathing treatment, patients breathe freely during treatment. The radiation beams are designed to treat the whole region encompassing the tumor motion. In the breath-hold treatment, patients are asked to hold their breath. The radiation beams are designed to only treat the tumor when the patients successfully hold their breath above a predefined threshold to minimize the motion of the tumor.

However, treatment plans are designed based on the anatomical and respirational information from the planning 4D-CT. The radiotherapy treatment usually contains a course of multiple fractions. Between planning 4D-CT acquisition and different treatment fractions, substantial patient anatomical and respirational variations⁴ may occur, leading to deviations from the planned dose to the actual on-board treatment dose. This dose deviation can be clinically significant especially for stereotactic body radiation therapy (SBRT),⁵ which is less tolerant of interfractional variations due to its high fractional dose and few treatment fractions. Therefore, dosimetric verification is important for lung cancer treatments as it allows us to assess the treatment quality throughout the treatment course and adapt the plan to account for the dose deviation if needed.

To track the interfractional variations, multiple on-board imaging techniques⁶ have recently been developed. By acquiring the most up-to-date patient information, on-board imaging potentially enables patient setup correction, on-board treatment dose verification/tracking,^7–11 and treatment plan adaptation.¹² For lung cancer patients, on-board cone-beam (CB)CT images have been used^13,14 for setup correction, dose verification, and adaptive planning. However, conventional lung CBCT has two limitations: 1. it can potentially underestimate the internal target volume (ITV),¹⁵ which can cause errors in target delineation and localization; 2. the limited image quality and inaccurate Hounsfield unit (HU) in the CBCT images cause dose calculation errors, especially in heterogeneous regions of the lung.^16–18 The erroneous dose calculation makes on-board dose verification and treatment plan adaptation inaccurate.

Compared with conventional CBCT, 4D-CBCT overcomes the first limitation by providing respiratory-phase-resolved volumetric images similar to 4D-CT, enabling more accurate target delineation and localization. However, the current clinical gold-standard Feldkamp-Davis-Kress (FDK) reconstruction algorithm¹⁹ needs more on-board projections for 4D-CBCT reconstruction than conventional CBCT. The resulting long scan time and high imaging dose prevent the wide application of 4D-CBCT in clinics. In addition, the FDK-based 4D-CBCT is still limited by the low image quality, which leads to inaccurate dose verifications.

Recently, we developed a motion modeling and free-form deformation (MM-FD)^20,21 method to estimate lung 4D-CBCT images using prior knowledge and limited-angle projections. With the guidance of limited-angle projections, the 4D-CBCTs are obtained by deforming the planning 4D-CT images. By using limited-angle projections, the scan time and dose of 4D-CBCT are substantially reduced. As the 4D-CBCT is estimated by MM-FD through deforming the planning 4D-CT images, it has similar image quality as planning 4D-CT and therefore can potentially improve the dose verification accuracy. In this work, we performed a comprehensive study to investigate the feasibility of using MM-FD estimated 4D-CBCT images for on-board dose verification in lung SBRT treatments. The dose verification accuracy of the conventional CBCT images reconstructed by FDK was also investigated for comparison. In addition, the 4D-CBCT estimated by MM-FD was used for dose accumulation²² to track the actual tumor dose. The accumulated doses were compared to point dose measurements using optically stimulated luminescence (OSL) detectors²³ and 2D dose measurements using radiochromic EBT2 films.²⁴

2. MATERIALS AND METHODS

2.A. General scheme of the MM-FD technique

In contrast to other 4D-CBCT reconstruction techniques,^19,25–28 the MM-FD method estimates new 4D-CBCT images through deforming prior high quality 4D-CT images. The deformation is driven by the data fidelity constraint, which requires the digitally reconstructed radiographs (DRRs) of the deformed 4D images to match with the 4D on-board projections. To solve the deformation fields, MM-FD uses two additional deformation models: motion modeling and free-form deformation.

First of all, MM-FD uses motion modeling to extract a principal component analysis (PCA) based motion model from the prior 4D-CT. The weightings of the extracted motion model components are optimized to construct coarse deformation fields to deform the prior 4D-CT to on-board 4D-CBCT. These coarse deformation fields are then further fine-tuned by a free-form deformation step combining data fidelity constraint enforcement and deformation energy minimization. For more details, please refer to our previous publications.^20,21,29,30

To comprehensively evaluate the MM-FD estimated images for on-board dose verification, studies were performed using a digital human phantom [extended-cardiac-torso (XCAT)^31–33] and an anthropomorphic physical phantom (cirs 008A, Computerized Imaging Reference Systems, Norfolk, VA). Details are shown in the following.

2.B. XCAT study

The XCAT phantom is a digital human phantom with customizable respiratory motion capabilities. Spherical tumors can be simulated inside the phantom body volume with variable sizes and locations. The respiratory motions of the body volume and the tumor are controlled by four curves: the SI curve-body, the AP curve-body, the SI curve-tumor, and the AP curve-tumor. The SI curves mainly control the respiratory motion along the superior–inferior direction. In contrast, the AP curves mainly control the motion along the anterior–posterior direction. Respiratory motions can be simulated independently for the body volume and the tumor through defining their corresponding SI curves and AP curves.

2.B.1. Planning 4D-CT simulation

We simulated two patient scenarios using the XCAT phantom: one with a tumor in the middle of the lung (MOL) and the other with a tumor near the chest wall (CHW). For each of the two patient scenarios, a corresponding planning 4D-CT of ten respiratory phases was simulated. In both planning 4D-CT sets, the tumor and the body volume moved synchronously, sharing the same SI curve (sinusoidal, 5 s cycle, 3 cm amplitude) and AP curve (sinusoidal, 5 s cycle, 2 cm amplitude).

2.B.2. Treatment planning

For both the MOL and the CHW patient scenarios, the tumors in the planning 4D-CT sets were automatically contoured using HU thresholding in eclipse (Varian Medical Systems, Palo Alto, CA). Both breath-hold and free-breathing SBRT plans were designed, with details in the following.

2.B.2.a. BH plan.

The BH plan was designed on the end-inspiration phase of the planning 4D-CT. Planning target volume (PTV) was generated by adding a 5 mm margin to the end-inspiration phase’s tumor contour. For both the MOL and CHW patient scenarios, the SBRT dose was prescribed to 18 Gy/fraction× 3 fractions. The plan was normalized to have 95% of the PTV covered by the prescription dose. For the MOL patient scenario, the tumor was in the middle of the lung without adjacent critical structures. A simple dynamic conformal arc³⁴ rotating from −20° to −130° (by IEC 1217 Varian scale convention) was designed to treat the PTV. In contrast, for the CHW patient scenario, the tumor was close to the chest wall and the spinal cord. An IMRT (Ref. 35) plan using seven beams from 160° to 280° with 20° interval was designed to treat the PTV and avoid critical structures. All dose calculations throughout this study used the analytical anisotropic algorithm³⁶ in eclipse with heterogeneity corrections.

2.B.2.b. FB plan.

In contrast to the BH plan, the FB plan was designed on the average intensity projection (AIP) of the planning 4D-CT. The ITV was generated by combining the tumor volumes contoured in all ten phases. PTV was then generated from ITV with a 5 mm margin and mapped to the AIP images for planning. Other parameters of the FB plan were the same as the BH plan.

2.B.3. Interfractional variation simulation and imaging

Eight on-board scenarios featuring different interfractional variations from planning 4D-CT to on-board images were simulated for both the MOL and CHW patient scenarios. The simulated interfractional variations include motion trajectory change, tumor size change, and tumor average position change. The details of all on-board scenarios are shown below.

• 1.The body volume and the tumor still moved synchronously, according to the same SI and AP curves. However, compared with the planning 4D-CT, the amplitude of the SI curve was reduced to 2 cm and that of the AP curve was reduced to 1.2 cm.
• 2.Scenario 1+ tumor shrank 5 mm in diameter.
• 3.Scenario 1+ tumor expanded 10 mm in diameter.
• 4.Scenario 1+ tumor average position shifted 8 mm along superior–inferior direction.
• 5.Scenario 1+ tumor average position shifted 8 mm along anterior–posterior direction.
• 6.Scenario 1+ tumor average position shifted 5 mm along each of the superior–inferior, anterior–posterior, and medial–lateral directions.
• 7.Scenario 1+ tumor had 20% phase shift relative to the body volume’s respiratory cycle.
• 8.The body volume and the tumor moved nonsynchronously, according to different SI and AP curves. For the tumor, the amplitude of the SI curve-tumor was 4 cm and that of the AP curve-tumor was 3 cm. For the body volume, the amplitude of the SI curve-body was 2 cm and that of the AP curve-body was 1.2 cm.

For each on-board scenario mentioned above, we generated a corresponding on-board ten-phase 4D-CT in XCAT to calculate the gold-standard on-board dose for reference. The accuracy of doses calculated on reconstructed on-board CBCT images can be evaluated through comparisons with the gold-standard on-board dose. Both 4D-CBCTs estimated by MM-FD and CBCTs reconstructed by FDK were evaluated for their dose verification accuracy.

To perform dose verifications using MM-FD estimated 4D-CBCT images, we simulated limited-angle on-board projections. These projections were then used to guide the estimation of 4D-CBCT images through deforming the planning 4D-CT. In detail, for each respiratory phase, orthogonal-view 30° projections were simulated from both anterior–posterior (from −15° to 15°) and left-lateral (from 75° to 105°) directions with an angular sampling of 1.2° per projection. In total, 520 projections were simulated for all ten phases. The phase-binned on-board projections were then fed into the MM-FD algorithm to estimate 4D-CBCT images. The end-inspiration phase of the estimated 4D-CBCT images was used for the dose verification of the BH plan. The AIP of the estimated 4D-CBCT images was used for the dose verification of the FB plan.

For comparison, conventional CBCT volumes were also reconstructed by FDK for dose verification. For the BH plan, we simulated projections of the BH phase (end-inspiration) to reconstruct a BH CBCT. For the FB plan, we simulated projections of evenly mixed ten phases to reconstruct a FB CBCT. In detail, 520 projections covering a full 360° scan angle were simulated for both BH and FB CBCT reconstructions. We used 520 projections for FDK reconstruction to achieve a similar dose level to 4D-CBCT imaging by MM-FD.

2.B.4. On-board dose verification

Similar to the planning 4D-CT, the tumors were automatically contoured in the gold-standard on-board 4D-CT sets. As mentioned in the Introduction, the FDK-based conventional CBCT suffers from potential target underestimation.¹⁵ In light of this issue, the PTV contours from the gold-standard on-board images were mapped to the corresponding FDK CBCT images to eliminate the contouring biases. For fair comparison, the gold-standard PTV contours were also mapped to the corresponding MM-FD estimated CBCT images.

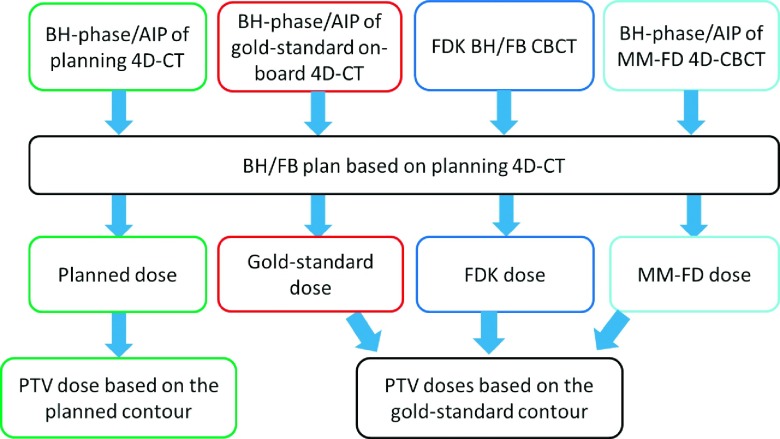
The original treatment plans were mapped to the CBCT images generated by the MM-FD method or the FDK method to calculate the actual on-board dose delivered. The detailed on-board dose comparison schemes are shown in Fig. 1.

FIG. 1.

The detailed schemes of on-board dose comparisons between the planned dose, the gold-standard dose, the FDK dose, and the MM-FD dose.

For quantitative evaluation, the planned, FDK, and MM-FD dose distributions were compared to the gold-standard dose distributions by the following metrics: (1) isodose curves, (2) PTV dose volume histogram (DVH) curves, (3) the absolute deviations of minimum dose (ΔD_min), maximum dose (ΔD_max), and mean dose (ΔD_mean) of PTV (all normalized by the prescription dose), and (4) the absolute deviations of PTV coverage (ΔV_100%, V_100% measures the percentage PTV covered by the prescription dose).

2.C. Physical phantom study

The cirs 008A anthropomorphic physical phantom was used to further evaluate the dose verification accuracy of different images. The cirs phantom uses a soft-tissue equivalent spherical insert to simulate the tumor and a mechanical rod to drive the insert to mimic the tumor motion.

2.C.1. Planning 4D-CT acquisition and treatment planning

A 3 cm diameter sphere was inserted in the phantom to simulate the tumor and programmed to move along a cos⁴(x) curve with 2 cm peak-to-peak amplitude and 4 s cycle. The planning 4D-CT of the phantom was acquired on a PET-CT scanner (Siemens Biograph mCT, Siemens Medical Solutions, Malvern, PA), using 120 kVp and 40 mAs/rotation. Same as the XCAT study, the tumors in the planning 4D-CT were automatically contoured using HU thresholding. Both BH and FB SBRT treatment plans were designed, using 3D static beam (7 beams, 0°–150° with 25° interval), dynamic conformal arc (−20° to 130°), and IMRT (7 beams, −20° to 130° with 25° interval) with the same dose prescription and PTV coverage as in the XCAT study.

2.C.2. Interfractional variation simulation and imaging

Three on-board scenarios of different interfractional variations from planning 4D-CT to on-board images were simulated, with details shown below.

• 1.The motion amplitude of the spherical insert was increased to 3 cm.
• 2.The size of the spherical insert was shrunk to 2 cm (achieved through using another 2 cm insert with the same material).
• 3.The motion amplitude of the spherical insert was increased to 3 cm and the size of the spherical insert was shrunk to 2 cm.

For each on-board scenario, a 4D-CT was acquired using the same PET-CT scanner to calculate the gold-standard on-board dose for reference. Similar to the XCAT study, both 4D-CBCTs estimated by MM-FD and CBCT reconstructed by FDK were evaluated for their dose verification accuracy.

For each on-board scenario, limited-angle cone-beam projections were acquired on a Linac (TrueBeam, Varian Medical Systems, Palo Alto, CA). The projections were acquired using an in-house developed slow-gantry rotation protocol in the TrueBeam developer mode. Each projection was acquired in full-fan mode, using 120 kVp, 20 mA, and 16 ms. In total, ∼840 projections covering the orthogonal-view 30° scan angle were acquired at a gantry rotation speed of 0.5°/s and an acquisition frame rate of 7 frames/s. These 4D projections were manually sorted into ten phase bins to estimated 4D-CBCT images through deforming the planning 4D-CT.

For comparison, FDK-based BH and FB CBCT images were also acquired in the TrueBeam clinical mode, using the same dose level as the 4D-CBCT (∼270 mAs).

2.C.3. PTV based on-board dose verification

Similar to the planning 4D-CT, the tumors were automatically contoured in the gold-standard on-board 4D-CT sets. The gold-standard PTV contours were also mapped to the FDK-based BH and FB CBCT sets and MM-FD estimated CBCT images. The same dose comparison scheme as the XCAT study (Fig. 1) was employed.

2.C.4. Gross tumor volume (GTV) based on-board dose measurement

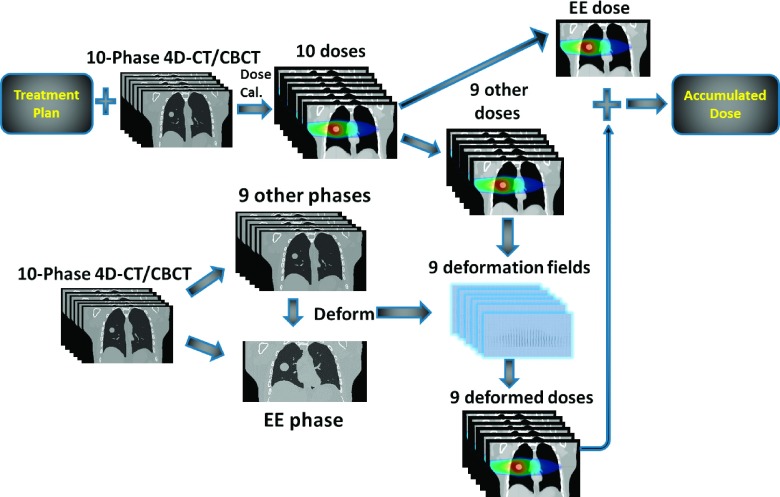
PTV is a virtual volume accounting for the motion/setup error/subclinical region of the tumor. Its dose does not directly correlate with the actual GTV dose. 4D-CBCT enables actual GTV dose verification through accumulating the doses from each respiration-resolved phase image.²² In this study, we performed GTV dose accumulations (Fig. 2) for the physical phantom using MM-FD estimated 4D-CBCT images. As shown in Fig. 2, phase-specific doses were first calculated on each phase image of 4D-CT/CBCT. The dose at the end-expiration (EE) phase was selected as the reference dose. Doses at all the other phases were then deformed and accumulated to the reference dose, using deformation fields derived from image registration. After accumulation, the GTV dose can be extracted and analyzed.

FIG. 2.

Dose accumulation scheme using 4D-CT/4D-CBCT.

To evaluate the accuracy of accumulated doses based on MM-FD estimated 4D-CBCT images, we compared the accumulated doses to point dose measurements by OSL detectors and 2D dose measurements by radiochromic EBT2 films. Figure 3 shows the OSL insert [3(a)] and the film insert [3(b)], both of which can be placed in the movable rod [3(c)] of the physical phantom for actual tumor dose measurement.

FIG. 3.

The (a) OSL and (b) film inserts for dose measurements; (c) both inserts can be placed in the movable rod of the physical phantom for dose measurement.

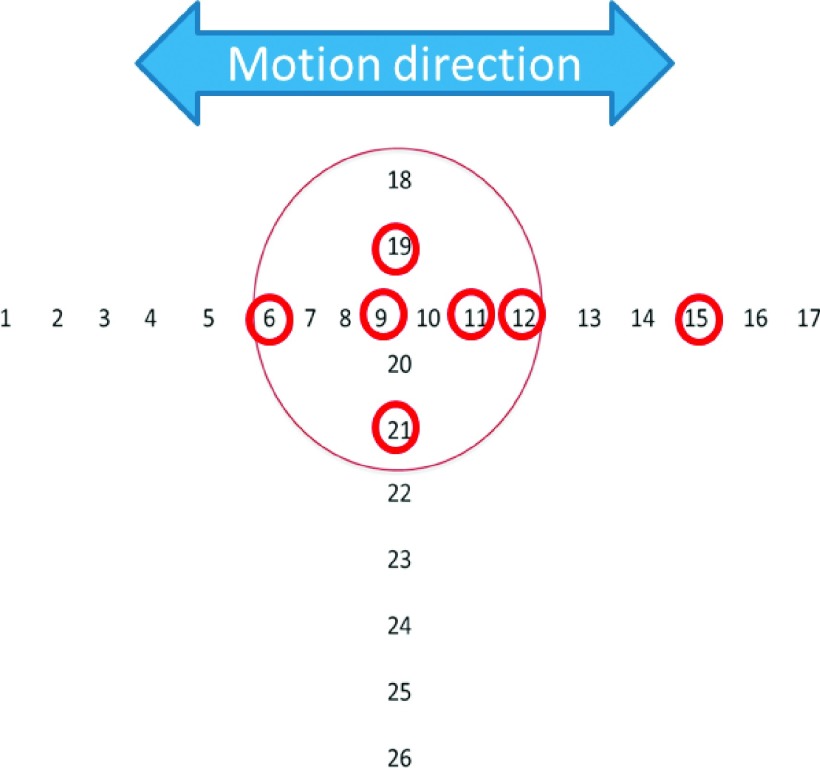
Figure 4 shows the point dose locations selected for OSL measurements. Locations including tumor center, tumor peripheral region, and off-tumor region were all measured. For the radiochromic film based measurements, the film was placed in between the two halves of the tumor [Fig. 3(b)]. The measured film dose distribution was compared to the central dose distribution extracted from the accumulated tumor doses. Both the dose profile and the gamma index (3 mm/3%)³⁷ were evaluated.

FIG. 4.

Point dose measurements using the OSL detectors. The circled number indicates the location where the point dose was measured.

All three FB treatment plans in Sec. 2.C.1 were delivered for the GTV dose measurement study. Only the scenario about tumor motion amplitude change (Sec. 2.C.2: scenario 1) was selected for the measurement study, due to the lack of OSL and film inserts with a shrunk tumor. In addition to the selected scenario (simulating on-board tumor motion amplitude increase from 2 to 3 cm), we simulated another scenario featuring tumor amplitude increase from 2 to 4 cm. For both the 3 cm and the 4 cm tumor motion scenarios, we acquired 4D cone-beam projections according to the protocol described in Sec. 2.C.2 and estimated 4D-CBCT images through deforming the planning 4D-CT using the MM-FD technique. The accumulated doses using the estimated 4D-CBCTs were compared to the corresponding OSL and radiochromic film measurements as described above.

Based on the scheme shown in Fig. 2, we also accumulated the tumor doses using the planning 4D-CT which features 2 cm tumor motion. The 4D-CT accumulated doses were also compared with the measured doses as well as the 4D-CBCT accumulated doses.

3. RESULTS

3.A. XCAT study results

3.A.1. Comparison between HU values

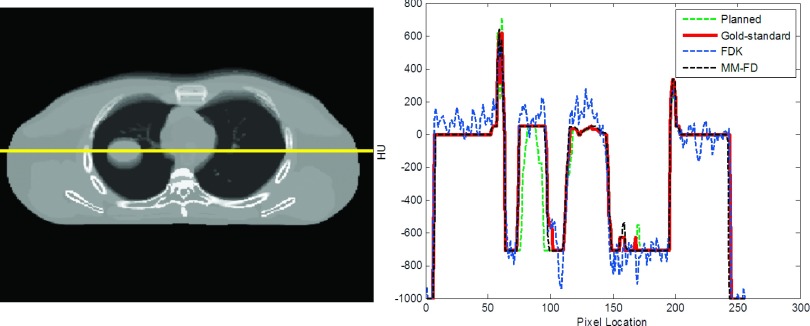
Figure 5 shows the comparison of HU profiles between the planned AIP, the gold-standard AIP, the FDK FB CBCT, and the MM-FD AIP for the XCAT scenario simulating on-board tumor size expansion (Sec. 2.B.3: XCAT on-board scenario No. 3). Compared to the planned AIP and the FDK FB CBCT, the HU profile of the MM-FD AIP matched much better with that of the gold-standard AIP, which enables more accurate dose verification.

FIG. 5.

The line profile comparison between the AIP of the planning 4D-CT (“planned”), the AIP of the gold-standard on-board 4D-CT (gold-standard), the FB CBCT reconstructed by FDK (“FDK”), and the AIP of the MM-FD estimated 4D-CBCT (“MM-FD”), for the XCAT scenario simulating on-board tumor size expansion (Sec. 2.B.3: XCAT on-board scenario No. 3).

3.A.2. Comparison between isodose distributions

Figure 6 compares the isodose distributions between the planned, the gold-standard, the FDK, and the MM-FD doses for the XCAT study. The first row shows the dose distributions calculated on the MOL patient scenario using the FB dynamic conformal arc plan. Correspondingly, the second row shows the dose distributions calculated on the CHW patient scenario using the FB IMRT plan. In both cases, the planned dose distributions deviated substantially from the gold-standard distributions due to the simulated on-board tumor size expansion (Sec. 2.B.3: XCAT on-board scenario No. 3). As shown, the MM-FD isodose distributions matched better with the gold-standard than the planned and the FDK isodose distributions for the higher isodose lines (pointed to by arrows in Fig. 6).

FIG. 6.

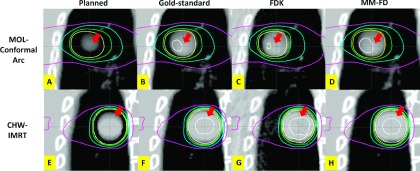
Comparison of isodose distributions between the planned [(A) and (E)], the gold-standard [(B) and (F)], the FDK [(C) and (G)], and the MM-FD [(D) and (H)] doses for the XCAT scenario simulating on-board tumor size expansion (Sec. 2.B.3: XCAT on-board scenario No. 3). (A)–(D) are the dose distributions calculated on the MOL patient scenario. The isodose curves, from outermost to innermost, indicate 110%, 100%, 95%, 80% and 50% of prescription dose, respectively. (E)–(H) are the dose distributions calculated on the CHW patient scenario. The isodose curves, from outermost to innermost, indicate 105%, 100%, 95%, 80% and 50% of prescription dose, respectively.

3.A.3. Comparison between PTV DVH curves

Figure 7 shows the comparison between the planned, the gold-standard, the FDK, and the MM-FD PTV DVH curves. The planned PTV DVH curve deviated substantially from the gold-standard curve due to the simulated on-board tumor size expansion (Sec. 2.B.3: XCAT on-board scenario No. 3). The PTV DVH curve calculated on the FDK CBCT also deviated from the gold-standard curve. In comparison, the MM-FD DVH curve matched well with the gold-standard curve.

FIG. 7.

Comparison of PTV DVH curves between the planned, the gold-standard, the FDK, and the MM-FD doses for the XCAT scenario simulating on-board tumor size expansion (Sec. 2.B.3: XCAT on-board scenario No. 3) for the CHW patient with the FB IMRT plan.

3.A.4. Quantitative evaluation using PTV dose deviation metrics

Table I shows the average (± standard deviation) dose deviation metric values of PTV for the eight on-board scenarios of the XCAT simulation study. Considering all different scenarios, the average (± standard deviation) ΔD_min, ΔD_max, ΔD_mean, and ΔV_100% of planned PTV doses as compared to the gold-standard PTV doses were 32.9% (±28.6%), 3.0% (±2.9%), 3.8% (±4.0%), and 15.4% (±12.4%), respectively. The corresponding values of FDK PTV doses were 1.6% (±1.9%), 1.2% (±0.6%), 2.2% (±0.8%), and 17.4% (±15.3%), respectively. In comparison, the corresponding values of MM-FD PTV doses were 0.3% (±0.2%), 0.9% (±0.6%), 0.6% (±0.4%), and 1.0% (±0.8%), respectively.

TABLE I.

Dose deviation metric values of PTV for the XCAT simulation study. The values are the averaged results (± standard deviation) of the simulated eight on-board scenarios (Sec. 2.B.3). All values are normalized by the prescription dose.

Dose deviation metrics			ΔDmin (%)	ΔDmax (%)	ΔDmean (%)	ΔV100% (%)
MOL (dynamic conformal arc plan)	BH	Planned	41.9 ± 29.9	2.1 ± 1.2	6.9 ± 5.5	20.3 ± 13.4
		FDK	0.9 ± 0.9	1.3 ± 0.1	1.4 ± 0.1	4.0 ± 1.0
		MM-FD	0.5 ± 0.4	1.5 ± 0.1	1.1 ± 0.1	2.0 ± 0.4
	FB	Planned	22.1 ± 22.5	1.5 ± 1.1	2.6 ± 2.6	9.6 ± 8.7
		FDK	1.6 ± 1.0	1.3 ± 0.2	1.6 ± 0.1	5.1 ± 0.7
		MM-FD	0.4 ± 0.2	1.4 ± 0.1	0.9 ± 0.1	1.3 ± 0.5
CHW (IMRT plan)	BH	Planned	37.4 ± 30.9	5.6 ± 3.7	3.3 ± 3.5	17.6 ± 13.7
		FDK	1.6 ± 2.1	1.2 ± 1.1	2.7 ± 0.6	28.7 ± 12.7
		MM-FD	0.2 ± 0.1	0.4 ± 0.1	0.3 ± 0.1	0.4 ± 0.2
	FB	Planned	30.3 ± 31.7	2.9 ± 3.1	2.4 ± 2.5	14.2 ± 13.0
		FDK	2.5 ± 2.9	1.1 ± 0.4	3.0 ± 0.5	31.8 ± 10.6
		MM-FD	0.3 ± 0.2	0.2 ± 0.0	0.1 ± 0.1	0.2 ± 0.1

3.B. Physical phantom study results

3.B.1. Comparison between HU values

Figure 8 shows the comparison of HU profiles between the planned AIP, the gold-standard AIP, the FDK FB CBCT, and the MM-FD AIP for the cirs phantom scenario simulating concurrent tumor shrinkage and motion amplitude change (Sec. 2.C.2: cirs on-board scenario No. 3). Similar to the XCAT study, the HU profile of MM-FD AIP matched best with the gold-standard.

FIG. 8.

The line profile comparison between the planned AIP, the gold-standard AIP, the FDK FB CBCT, and the MM-FD AIP for the cirs phantom scenario simulating concurrent tumor shrinkage and motion amplitude change (Sec. 2.C.2: cirs on-board scenario No. 3).

3.B.2. Comparison between isodose distributions

Figure 9 compares the isodose distributions between the planned, the gold-standard, the FDK, and the MM-FD doses for the cirs phantom study. Similar to the XCAT study, the MM-FD isodose distributions matched better with the gold-standard than the planned and the FDK isodose distributions for the higher isodose lines (pointed to by arrows in Fig. 9).

FIG. 9.

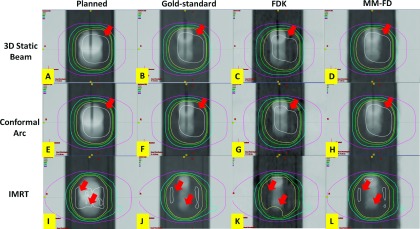
Comparison of isodose distributions between the planned [(A), (E), and (I)], the gold-standard [(B), (F), and (J)], the FDK [(C), (G), and (K)], and the MM-FD [(D), (H), and (L)] doses for the cirs phantom scenario simulating concurrent tumor shrinkage and motion amplitude change (Sec. 2.C.2: cirs on-board scenario No. 3). (A)–(D) are the dose distributions calculated using the FB 3D static beam plan. (E)–(H) are the dose distributions calculated using the FB dynamic conformal arc plan. For (A)–(H), the isodose curves, from outermost to innermost, indicate 110%, 100%, 95%, 80% and 50% of prescription dose, respectively. (I)–(L) are the dose distributions calculated using the FB IMRT plan. For (I)–(L), the isodose curves, from outermost to innermost, indicate 105%, 100%, 95%, 80% and 50% of prescription dose, respectively.

3.B.3. Comparison between PTV DVH curves

Figure 10 shows the comparison between the planned, the gold-standard, the FDK, and the MM-FD PTV DVH curves for the cirs phantom study. As shown, MM-FD DVH curve matched well with the gold-standard curve, better than the planned and FDK curves.

FIG. 10.

Comparison of PTV DVH curves between the planned, the gold-standard, the FDK, and the MM-FD doses for the cirs phantom scenario simulating concurrent tumor shrinkage and motion amplitude change (Sec. 2.C.2: cirs on-board scenario No. 3) for the FB IMRT plan.

3.B.4. Quantitative evaluation using PTV dose deviation metrics

Table II shows the dose deviation metric values of PTV for the cirs phantom study using 3D static beam planning, dynamic conformal arc planning, and IMRT planning. Considering all the scenarios, the average ΔD_min, ΔD_max, ΔD_mean, and ΔV_100% of planned PTV doses were 38.1% (±30.8%), 3.5% (±5.1%), 3.0% (±2.6%), and 8.8% (±8.0%), respectively. The corresponding values of FDK PTV doses were 5.8% (±4.5%), 1.6% (±1.6%), 2.0% (±0.9%), and 9.3% (±10.5%), respectively. In comparison, the corresponding values of MM-FD PTV doses were 0.4% (±0.8%), 0.8% (±1.0%), 0.5% (±0.4%), and 0.8% (±0.8%), respectively.

TABLE II.

Dose deviation metric values of PTV for the cirs phantom study using different treatment techniques. The values are the averaged results (± standard deviation) of the simulated three on-board scenarios (Sec. 2.C.2). All values are normalized by the prescription dose.

Dose deviation metrics			ΔDmin (%)	ΔDmax (%)	ΔDmean (%)	ΔV100% (%)
3D static beam plan	BH	Planned	38.5 ± 37.0	0.9 ± 0.4	3.4 ± 3.6	10.5 ± 10.0
		FDK	7.1 ± 5.0	0.5 ± 0.4	1.7 ± 0.9	3.7 ± 1.2
		MM-FD	0.4 ± 0.3	0.3 ± 0.1	0.4 ± 0.1	0.4 ± 0.3
	FB	Planned	38.6 ± 37.9	1.5 ± 1.7	2.5 ± 2.0	5.9 ± 5.2
		FDK	5.9 ± 3.4	1.3 ± 1.4	2.5 ± 1.1	4.5 ± 0.8
		MM-FD	0.1 ± 0.1	0.8 ± 0.6	0.6 ± 0.6	0.6 ± 0.2
Dynamic conformal arc plan	BH	Planned	31.3 ± 34.7	1.2 ± 1.1	2.9 ± 3.1	10.3 ± 9.8
		FDK	3.7 ± 1.3	0.5 ± 0.5	1.8 ± 0.9	4.0 ± 1.2
		MM-FD	0.2 ± 0.2	0.3 ± 0.1	0.4 ± 0.3	0.5 ± 0.5
	FB	Planned	39.7 ± 36.4	1.6 ± 1.7	2.4 ± 2.0	5.8 ± 5.2
		FDK	6.8 ± 8.1	1.5 ± 1.3	2.4 ± 1.0	3.9 ± 1.3
		MM-FD	1.2 ± 1.9	0.8 ± 0.7	0.6 ± 0.6	0.4 ± 0.2
IMRT plan	BH	Planned	42.6 ± 39.0	9.4 ± 9.1	3.6 ± 3.7	13.6 ± 13.3
		FDK	7.0 ± 6.8	1.3 ± 1.0	1.5 ± 1.0	26.7 ± 15.8
		MM-FD	0.2 ± 0.1	0.4 ± 0.3	0.4 ± 0.3	2.2 ± 0.8
	FB	Planned	37.8 ± 33.4	6.3 ± 6.5	3.5 ± 3.4	6.9 ± 6.8
		FDK	4.4 ± 2.5	4.3 ± 1.7	2.4 ± 1.1	13.0 ± 6.3
		MM-FD	0.3 ± 0.3	2.3 ± 1.8	0.6 ± 0.7	0.4 ± 0.1

3.B.5. GTV dose measurement results

For the GTV dose measurement study (Sec. 2.C.4), the point dose measurement results were shown in Table III.

TABLE III.

Absolute dose discrepancies between accumulated and measured doses (values normalized by the local measured doses). Both planning 4D-CT dose accumulations (shown as column “planning 4D-CT”) and on-board 4D-CBCT dose accumulations (shown as column “on-board 4D-CBCT”) were performed and compared to the OSL measurements. The “OSL No.” indicates individual OSL measurements at locations numbered in Fig. 4. Please note that the end-inspiration phase location was fixed for different motion amplitudes. When motion amplitude increased, doses at different OSL measurement locations were affected differently.

Absolute dose discrepancy [absolute (accumulated-measured)/measured*100]
		3D static beam		Dynamic conformal arc		IMRT
	OSL No.	Planning 4D-CT (%)	On-board 4D-CBCT (%)	Planning 4D-CT (%)	On-board 4D-CBCT (%)	Planning 4D-CT (%)	On-board 4D-CBCT (%)
3 cm on-board motion	6	6.2	5.5	2.3	1.4	2.2	2.9
	9	4.1	3.7	1.4	0.2	0.3	2.5
	11	3.3	0.6	3.1	1.2	9.2	5.5
	12	5.1	1.6	3.8	0.2	13.8	11.2
	15	63.6	2.2	50.6	6.5	43.4	2.4
	19	3.7	2.3	0.0	0.6	5.1	4.8
	21	3.5	2.0	0.5	0.9	4.5	5.1
	Mean	12.8	2.5	8.8	1.6	11.2	4.9
	SD	22.4	1.6	18.5	2.2	14.9	3.0
4 cm on-board motion	6	4.0	1.0	3.2	2.2	1.5	1.8
	9	7.2	4.5	3.3	1.1	1.7	6.9
	11	48.5	1.5	36.3	5.8	68.6	9.6
	12	76.2	9.1	66.8	3.8	96.9	1.2
	15	105.1	4.8	90.5	4.0	87.9	7.0
	19	4.6	0.4	2.9	0.4	2.8	4.7
	21	6.8	2.7	3.0	2.0	2.1	3.1
	Mean	36.1	3.4	29.4	2.8	37.3	4.9
	SD	41.3	3.0	36.4	1.9	44.8	3.1

When the tumor motion increased from 2 cm (planning 4D-CT) to 3 cm (on-board) and 4 cm (on-board), the average discrepancies between the planning 4D-CT accumulated doses and measured doses were 12.8% (±22.4%) and 36.1% (±41.3%) for the 3D static beam plan, 8.8% (±18.5%) and 29.4% (±36.4%) for the dynamic conformal arc plan, and 11.2% (±14.9%) and 37.3% (±44.8%) for the IMRT plan. Using the MM-FD estimated on-board 4D-CBCTs for dose accumulation, the average dose discrepancies decreased to 2.5% (±1.6%) and 3.4% (±3.0%) for the 3D static beam plan, 1.6% (±2.2%) and 2.8% (±1.9%) for the dynamic conformal arc plan, and 4.9% (±3.0%) and 4.9% (±3.1%) for the IMRT plan.

As shown in Fig. 11, the increment of on-board tumor motion amplitude (from 2 to 3 cm) rendered substantial deviations from the planning 4D-CT accumulated doses to the measured doses. In contrast, the accumulated doses on 4D-CBCT substantially reduced the deviations, as shown in dose profile comparison (Fig. 11) and gamma index computation (Table IV). The high quality on-board 4D-CBCTs successfully captured the on-board motion changes and enabled accurate dose accumulation to track the GTV dose.

FIG. 11.

Comparison between dose distributions of different treatment plans for the 3 cm on-board motion scenario. The planning 4D-CT accumulated dose distributions (row 1), the MM-FD on-board 4D-CBCT accumulated dose distributions (row 2), and the measured doses using radiochromic EBT2 film (row 3) were shown. The line dose profiles of these dose distributions were compared (row 4).

TABLE IV.

Gamma indices (3 mm/3%) computed between planning 4D-CT accumulated doses and measured doses (shown as row planning 4D-CT) and gamma indices between on-board 4D-CBCT accumulated doses and measured doses (shown as row on-board 4D-CBCT).

		3D static beam	Dynamic conformal arc	IMRT
3 cm on-board motion	Planning 4D-CT (%)	68.6	64.3	56.4
	On-board 4D-CBCT (%)	96.3	97.2	94.3
4 cm on-board motion	Planning 4D-CT (%)	43.0	38.3	33.7
	On-board 4D-CBCT (%)	95.8	93.1	90.4

4. DISCUSSION

4.A. PTV dose verification accuracy of the MM-FD estimated images

In radiation therapy, the quality of a treatment is largely determined by the successful coverage of the tumor volume. Different interfractional tumor variations were simulated in this study, including the tumor motion pattern change, tumor size change, and tumor average position change (Secs. 2.B.3 and 2.C.2). Consequently, large variations in PTV dose coverage were observed from planned doses to gold-standard on-board doses (Figs. 6, 7, 9, and 10; Tables I and II). The calculated PTV doses on conventional FDK-based BH and FB CBCTs failed to fully capture these variations, due to the noise in images and less accurate HU distributions (Figs. 5 and 8). In contrast, the MM-FD estimated 4D-CBCTs not only captured the interfractional variations of the tumors but also preserved the correct CT HU value of 4D-CTs as the images were obtained from deforming the planning 4D-CTs. Using accurately estimated 4D-CBCTs with correct HU distributions (Figs. 5 and 8), the calculated MM-FD PTV doses successfully captured the dosimetric impacts of different interfractional variations (Figs. 6, 7, 9, and 10; Tables I and II).

In this study, 3D static beam plans, dynamic conformal arc plans, and IMRT plans were designed to evaluate the dose verification accuracy. As IMRT plans had more complex fluence modulation within the target, inaccurate image intensities led to more severe dose verification errors, as observed in the FDK doses (Figs. 6 and 9; Tables I and II). In contrast, the MM-FD doses were more robust for IMRT plans, although some small variations from gold-standard doses can be observed [Figs. 9(J) and 9(L)].

4.B. Dose accumulation using MM-FD estimated images

MM-FD estimated 4D-CBCTs enabled dose accumulations to track the actual GTV doses, which is another benefit of 4D-CBCT imaging. Using highly accurate geometric and HU information from MM-FD estimated 4D-CBCTs, the accumulated doses matched very well with the actual measurements (Fig. 11; Tables III and IV). The 4D-CBCT accumulated doses show slightly larger errors for the IMRT deliveries (Tables III and IV), which are potentially caused by the interplay effects³⁸ between the collimator motion and the target motion. Besides, the cirs phantom we used is a simplified digital anthropomorphic phantom. The image registration-based dose accumulation may introduce larger errors in real patient scenarios, which needs to be further investigated in future studies.

4.C. Additional benefits of MM-FD based image estimation

MM-FD allows limited-angle projection acquisition to substantially reduce scan time and dose and to reduce the risk of secondary cancers.³⁹ The MM-FD estimation only used a dose level equivalent to the conventional CBCT scan (Secs. 2.B.3 and 2.C.2), in both digital phantom and physical phantom studies. Another benefit of the limited-angle scanning is the improved mechanical clearance⁴⁰ when imaging peripheral tumors in large patients or patients with life-supporting devices.

On-board dose verification not only enables treatment dose tracking and treatment quality assessment but also facilitates image-guided adaptive radiation therapy.^41–43 The MM-FD solves the scan time/dose limitations of the 4D-CBCT imaging and provides high quality images for accurate target delineation and dose verification, making lung adaptive radiotherapy more promising.

4.D. Comparison with other methods

To improve on-board dose verification accuracy, multiple other methods have been developed, including HU-electron density calibration of CBCT (Refs. 16, 17, and 44) and deformable electron density mapping between CT and CBCT.⁹ The HU-electron density calibration of CBCT tries to establish a modified electron density map based on CBCT HU values, which requires additional hardware based calibration efforts. The calibration curve can also be machine-specific, scan mode-specific, treatment site-specific, and even patient-specific, leading to uncertainties in the calibration results.⁴⁴ Residual errors ranging from 2% to 4% can still be observed after the correction. On the other hand, the deformable electron density mapping method tries to map the correct electron densities of CT to CBCT through deformable image registration, whose efficacy is highly dependent on the registration accuracy. Accurate deformable registration can be very challenging in the presence of lung motion blurriness and imaging artifacts, leading to potential dose verification errors. Moreover, full-angle projections are needed to reconstruct a high quality CBCT image for registration, which cannot be achieved through limited-angle projections used by MM-FD.

Besides the MM-FD method in this study, recently several other methods using similar deformation-based image estimation approaches have been developed,^45–47 which all have the potential to improve the dosimetric verification accuracy. Compared with these methods, the MM-FD method is proved more robust to the motion pattern/anatomical structure variations between 4D-CT and 4D-CBCT (Ref. 20) and can utilize only limited-angle projections for image estimation.

4.E. Limitations of the current study

Currently, the study is focused on the dose verification using digital and physical phantom studies. No patient studies were performed. The current issue with the patient study is the lack of on-board 4D-CT images to provide gold-standard on-board dose. Such gold-standard can be obtained by a CT on-rail system, which is however currently not available in our clinic. Future patient studies are warranted when the data become available.

The MM-FD 4D-CBCT estimation uses a deformation-based approach, of which the efficacy may be limited in some scenarios. The “content change” is one scenario needs to be further studied in the future. For instance, the radiation may cause inflammations in lung and lead to content/intensity changes in 4D-CBCT, which cannot be estimated from deformations of prior 4D-CT. The traditional direct reconstruction methods like FDK will not be limited by this content change issue. Further studies are warranted to investigate the effects and solution of the content change issue, potentially through developing new methods to combine the benefits of MM-FD and the traditional direct reconstruction methods. The MM-FD 4D-CBCT estimation accuracy can also be potentially affected in scenarios where the on-board projections are very noisy or the tumors are of very low visibility in the projections. Future studies investigating more clinical scenarios are needed to further evaluate the robustness of the dosimetric verification accuracy of MM-FD estimated images.

The simulations and measurements performed in this study did not consider the breathing irregularities in patient breathing traces. The dosimetric impacts from the breathing irregularities depend on the types of irregularities (respiratory cycle variations, amplitude variations, baseline shifts, etc.), the magnitudes of breathing irregularities, and the start/end time of the treatments along the patient breathing curves. In addition, the breathing irregularities will potentially introduce motion artifacts in 4D-CT and 4D-CBCT and thus affect the dosimetric verification accuracy of MM-FD. However, introducing breathing irregularities into the dose verification process of this study requires the quantification of its dosimetric effects to determine the gold-standard dose, which is very challenging considering the continuous variations of the irregular breathing curves. The gold-standard images used in this study are difficult to define considering the on-board imaging time (within several minutes) is usually much shorter than the treatment time (usually >10 min), thus failing to fully reflect the tumor motion pattern during the treatment. Future studies on the dosimetric effects of breathing irregularity are warranted when these variables can be better controlled and quantified. In clinical practice, studies have also been performed to investigate methods to reduce the patient breathing irregularity. Patient breathing audio–visual coaching has been studied and found effective in improving breathing pattern reproducibility.^48,49

Another limitation of the study is that the MM-FD uses kV projections acquired prior to treatment for dose verification. It can only track the interfractional respirational and anatomical variations. The intrafractional variations cannot be tracked, which may also have an impact on the on-board treatment doses. We are currently developing a 4D-CBCT estimation technique⁵⁰ using aggregated kV and MV projections acquired concurrently during the treatment, which can be used for real-time on-board dose verification during treatment delivery. Its feasibility is warranted to be investigated in future studies.⁵¹

5. CONCLUSIONS

The study has validated the feasibility of using MM-FD estimated 4D-CBCT images for on-board dose calculation and accumulation, through both digital phantom and physical phantom studies. The estimated dose by the MM-FD technique can potentially be valuable for both treatment assessment and adaptive radiotherapy. Future patient studies are warranted to further investigate its clinical feasibility.