Assessing allele-specific expression across multiple tissues from RNA-seq read data

Abstract

Motivation: RNA sequencing enables allele-specific expression (ASE) studies that complement standard genotype expression studies for common variants and, importantly, also allow measuring the regulatory impact of rare variants. The Genotype-Tissue Expression (GTEx) project is collecting RNA-seq data on multiple tissues of a same set of individuals and novel methods are required for the analysis of these data.

Results: We present a statistical method to compare different patterns of ASE across tissues and to classify genetic variants according to their impact on the tissue-wide expression profile. We focus on strong ASE effects that we are expecting to see for protein-truncating variants, but our method can also be adjusted for other types of ASE effects. We illustrate the method with a real data example on a tissue-wide expression profile of a variant causal for lipoid proteinosis, and with a simulation study to assess our method more generally.

Availability and implementation: http://www.well.ox.ac.uk/~rivas/mamba/. R-sources and data examples http://www.iki.fi/mpirinen/

Contact: matti.pirinen@helsinki.fi or rivas@well.ox.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Advancements in sequencing technologies are enabling unprecedented possibilities to study the transcriptome (Montgomery et al., 2010; Pickrell et al., 2010). In RNA-sequencing studies, it is possible to distinguish between transcripts from the two haplotypes of an individual using heterozygous sites. This approach, called allele-specific expression (ASE) analysis, allows an alternative way to quantify cis-regulatory variation, complementary to eQTL analysis. In addition, ASE has been utilized to analyze transcriptome effects of nonsense-mediated decay (NMD) triggered by predicted loss-of-function variants (Lappalainen et al., 2013; MacArthur et al., 2012; Montgomery et al., 2011).

The Genotype-Tissue Expression (GTEx) project is establishing a resource database and tissue bank for the scientific community to study the relationship between genetic variation and gene expression in human tissues (GTEx-Consortium, 2013), with an aim to interpret GWAS findings for translational research. The project is analyzing gene expression from various perspectives, including transcript structure, expression quantity and diversity, eQTLs, and ASE differences. Furthermore, as medical genetics pursues exploration of rare variants, insights gained from the study of DNA and RNA sequencing data in the GTEx project will become important for functional interpretation of rare variants (Rivas et al., 2011, 2013; Zuk et al., 2014).

To date, some methods have been proposed for the analysis of ASE data, but these methods largely focus on a single tissue (Degner et al., 2009; Ronald et al., 2005; Sun, 2012; Zhang et al., 2009) although some could be applied also to multiple tissues (Skelly et al., 2011). The multi-tissue aspect is important for interpreting disease association findings (Grundberg et al., 2012; McCarroll et al., 2008) since eQTL and early ASE studies suggest widespread tissue-specific effects of cis-regulatory variants (Dimas et al., 2009; Gutierrez-Arcelus et al., 2013). Currently, more sophisticated methods for cross-tissue eQTL analysis are emerging (Flutre et al., 2013). However, eQTL analysis requires large sample sizes, while ASE analyses can be conducted with significantly smaller datasets.

In this article, we present novel statistical methods for analyzing ASE patterns from RNA-seq data across multiple tissues. Our main motivation is phenomena such as NMD that can lead to a substantial imbalance of transcripts from the two alleles (Fig. S37 in Lappalainen et al., 2013) and can vary considerably between cell types (Linde et al., 2007). From a statistical point of view, an advantage of prominent ASE is that it can be detected even with a single individual and with as small a read count as 10. (See Middle panel of Fig. 4 for an example dataset.)

Fig 4.

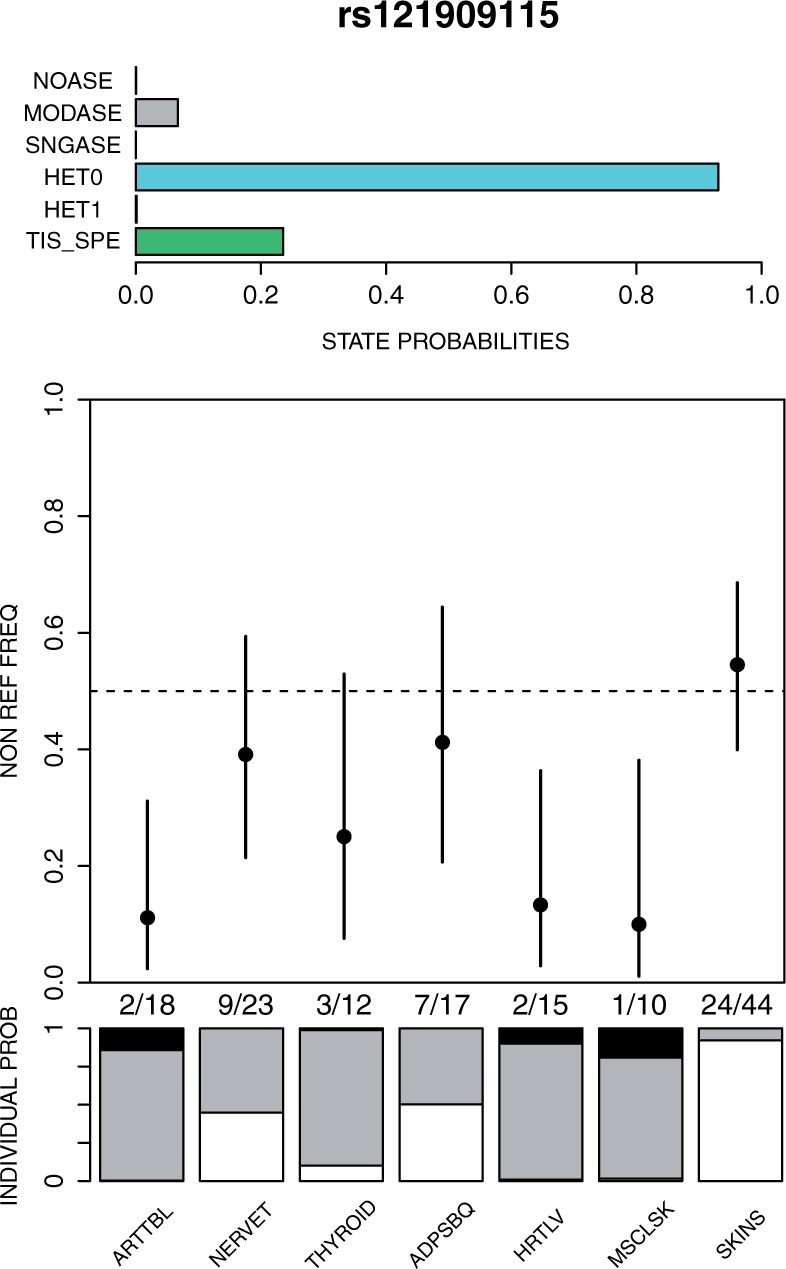
Data on rs121909115. Top panel shows the posterior probabilities for six states as defined in Methods. The tissue specific state (TIS_SPE) is a subset of the heterogeneity states (HET0 and HET1) and the probabilities of the other five states sum to one. Middle panel shows the point estimates of the non-reference allele frequency among RNA-seq reads across seven tissue types (named at the bottom) together with their 95% credible intervals. Non-reference read counts/total read counts are given below middle panel. Bottom panel shows the posterior probability distribution of the group indicator (γ_s) for each tissue type, where white, gray and black denote groups $\mathcal{N},\mathcal{M}$ and $\mathcal{S}$, respectively. Tissue types: ARTTBL, Artery tibial; NERVET, Nerve tibial; ADPSBQ, Adipose subcutaneous; HRTLV, Heart ventricle; MSCSKL, Muscle skeletal; SKINS, Skin sun exposed

We address three main questions:

• In which tissues does a heterozygous site show ASE?

• Which tissues show similar ASE effects at the site studied?

• What proportion of a certain class of variants, such as protein truncating variants (PTV), show ASE in all tissues, only in some tissues, or in no tissues?

For the first question, a standard frequentist version of the binomial test is commonly used. However, an interpretation of such a test depends on factors like the read count and simultaneous analysis of multiple tissues is very challenging. Hence, we require that our statistical framework allow a simultaneous comparison between several cross-tissue models for observed data. For example, we want to weigh relative support of the model where all tissues show ASE to the models where only a single tissue shows ASE and to the null model where none of the tissues show ASE. For this purpose, we adopt a Bayesian model comparison framework. Among its favorable properties are natural ways to compare models with differing number of parameters and to fully account for the amount of available data when evaluating relative support of the models.

2 Methods

2.1 Grouped tissue model

We consider RNA-seq read counts overlapping a particular genomic position from multiple tissues of one individual who is heterozygous at that position. (See Section 4 and Supplementary Information for extensions to multiple sites and individuals.) For tissue $s=1,\dots ,T$, let $y_{s1}$ and $y_{s2}$ be the number of reads supporting the reference and non-reference allele, respectively, and let $n_s=y_{s1}+y_{s2}$. We classify the tissues into three groups: no ASE ($\mathcal{N}$), moderate ASE ($\mathcal{M}$) and strong ASE ($\mathcal{S}$) and denote the group of tissue s by ${\gamma }_s\in \{\mathcal{N},\mathcal{M},\mathcal{S}\}$. Motivation for introducing a separate group for strong ASE is to identify the variants with the most extreme ASE effects. Such effects require careful checking for possible biases in the data (Degner et al., 2009; Panousis et al., 2014) and have been seen, for example, among PTVs that exhibit a whole spectrum from none to complete ASE (Fig. S37 in Lappalainen et al., 2013; Kukurba et al., 2014). For each group $G\in \{\mathcal{N},\mathcal{M},\mathcal{S}\}$, we denote the proportion of the transcripts with the reference allele by $\theta (G)$. We use a binomial sampling model for the data conditional on the group indicators:

$$y_{s1}|{\gamma }_s\sim \text{Bin}(n_s,\theta ({\gamma }_s))$$ (1)

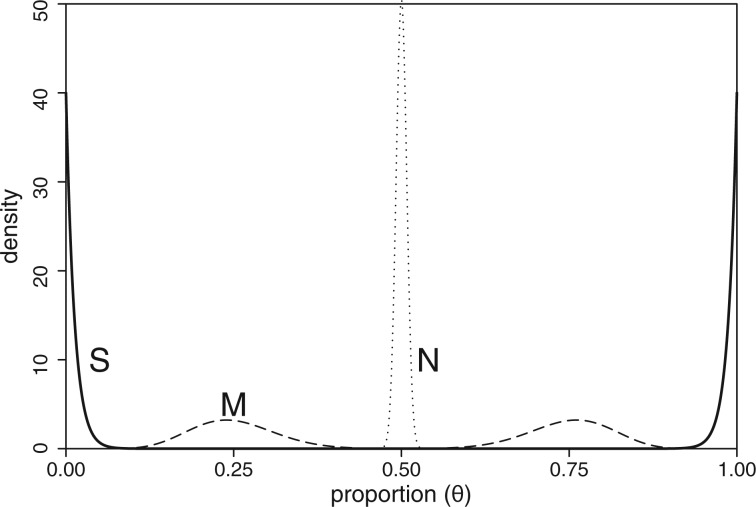
Possible expression states of the tissues differ in the prior assumptions about parameters $\theta (·)$. We use the following priors (Fig. 1) to describe different groups:

$$\begin{array}{l}\theta (\mathcal{N})\sim \text{Beta}(2000,2000)\\ \theta (\mathcal{M})\sim \frac{1}{2}\text{Beta}(36,12)+\frac{1}{2}\text{Beta}(12,36)\\ \theta (\mathcal{S})\sim \frac{1}{2}\text{Beta}(80,1)+\frac{1}{2}\text{Beta}(1,80)\end{array}$$

Under no ASE model $\mathcal{N}$ both alleles are expressed (almost) equally and hence $\theta (\mathcal{N})\approx 0.5$. As in Skelly et al. (2011), our $\mathcal{N}$ model allows small deviations from the exact point value of 0.5 to be robust against some technical measurement bias (Fig. S28 in Lappalainen et al., 2013) as well as very small ASE effects that are not a main focus in this study. The parameters for Beta distributions have been chosen in a way that clearly separates the three groups from each other (Fig. 1) and thus gives an informative framework to classify the tissues into three groups In supplementary information, we further discuss the prior specification, extensions to truncated priors and independence across tissues and a restriction to only one ASE group. Our implementation allows user to easily modify the prior parameters as well as use one-sided versions of the prior distributions instead of the two-sided versions used in our simulation experiments. For example, when studying NMD, we may require that the reference allele is expressed more strongly, and hence consider only the one-sided ASE states. Conversely, the two-sided ASE states are tailored for the situations where we do not want to make an assumption about which allele might be dominating. This is useful, for example, when studying imprinting.

Fig 1.

Densities of the prior distributions for the proportion of reference allele for the three groups: $\mathcal{N},\mathcal{M}$ and $\mathcal{S}$

Configurations

For fixed prior distributions, the model space consists of $3^{\text{T}}$ configurations represented by $\overline{\gamma }=({\gamma }_1,\dots ,{\gamma }_{\text{T}})$ vector where each tissue-specific indicator ${\gamma }_s\in \{\mathcal{N},\mathcal{M},\mathcal{S}\}.$

We partition the space of configurations into five ASE states:

$$\begin{array}{l}\text{NOASE}=\{\overline{\gamma }|\text{\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}s:{\gamma }_s=\mathcal{N}\}\\ \text{MODASE}=\{\overline{\gamma }|\text{\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}s:{\gamma }_s=\mathcal{M}\}\\ \text{SNGASE}=\{\overline{\gamma }|\text{\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}s:{\gamma }_s=\mathcal{S}\}\\ \text{HET0}=\{\overline{\gamma }|\text{\hspace{0.17em}\hspace{0.17em}exist\hspace{0.17em}}s,t:{\gamma }_s=\mathcal{N}\text{\hspace{0.17em}and\hspace{0.17em}}{\gamma }_t\ne \mathcal{N}\}\\ \text{HET1}=\{\overline{\gamma }|\text{\hspace{0.17em}\hspace{0.17em}exist\hspace{0.17em}}s,t:{\gamma }_s\ne {\gamma }_t\text{\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}u:{\gamma }_u\ne \mathcal{N}\},\end{array}$$

where the states represent configurations for no ASE (NOASE), moderate ASE (MODASE), strong ASE (SNGASE), heterogeneity with at least one tissue showing no ASE (HET0) and heterogeneity with all tissues showing some ASE (HET1). We also consider a tissue-specific sub state of the heterogeneity states:

$$\text{TIS\_SPE}=\{\overline{\gamma }|\text{\hspace{0.17em}\hspace{0.17em}exist\hspace{0.17em}}s,t:{\gamma }_s\ne {\gamma }_t\text{\hspace{0.17em}and\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}u\ne t:{\gamma }_u={\gamma }_s\}.$$

To do probabilistic comparison between the states we need to define prior probabilities for each state. We do this by defining prior for each configuration in a way which depends on its distance from homogeneity. We define a distance $d(\overline{\gamma })$ for each configuration $\overline{\gamma }$ as the smallest number of tissues whose group indicators need to be changed in order to turn $\overline{\gamma }$ into a homogeneous configuration (either NOASE, MODASE or SNGASE). Formally, $d(\overline{\gamma })=T-\max \{{\ell }_N,{\ell }_M,{\ell }_S\}$, where ${\ell }_N,{\ell }_M$ and ${\ell }_S$ are the number of tissues that $\overline{\gamma }$ assigns to $\mathcal{N},\mathcal{M}$ and $\mathcal{S}$, respectively. In particular, the configurations with d = 0 are the three homogeneous configurations and the configurations with d = 1 form the set TIS_SPE.

We specify the total prior probability for each possible value of $d=0,\dots ,T-\lceil T/3\rceil$ and then distribute it equally among the configurations with the same distance. This prior allows us to easily implement the idea that among the vast space of configurations we favor a priori the parsimonious ones, i.e. those where many tissues are similar. Our prior distribution extends the one recently used for multi-tissue eQTL setting (Flutre et al., 2013) to the case of more than two expression states. In the results reported in this work, we have set a prior mass of 0.75 to d = 0 (i.e. 0.25 for each of NOASE, MODASE and SNGASE) and the remaining 0.25 has been divided equally among all possible values of $d=1,\dots ,T-\lceil T/3\rceil$. This choice was made because it gives an equal prior weight for the four main patterns of ASE: three homogeneous states and general heterogeneity. If a previous estimate of configuration probabilities were available, it could be utilized instead.

2.2 Multi-locus grouped tissue model

For settings where many variants are available for a joint analysis, we extend grouped tissue model (GTM) to a hierarchical multi-locus grouped tissue model (GTM*) that learns from the data the proportion of variants belonging to each of the five states, $\mathit{\pi }=({\pi }_N,{\pi }_M,{\pi }_S,{\pi }_{H0},{\pi }_{H1})$, and thus avoids the need to fix prior probabilities of the states. Our default prior for the proportions is

$$\mathit{\pi }\sim \text{Dirichlet}(1,1,1,1,1).$$

We describe the technical details of GTM* and compare it to GTM in Supplementary Information.

2.3 Computation

We use a standard Gibbs sampler to explore the posterior distribution of the configuration indicators $\overline{\gamma }$ under GTM (see Supplementary Information for details).

The basic building block for model comparison is the Bayes factor between configuration $\overline{\gamma }$ and the NOASE state

$$\text{BF}(\overline{\gamma })=\frac{p(y|\overline{\gamma })}{p(y|\text{NOASE})},$$ (2)

where $y=(y_{1·},\dots ,y_{\text{T·}})$. Evaluation of $\text{BF}(\overline{\gamma })$ can be done analytically by using Beta-binomial likelihood separately for the numerator and the denominator. Thus we can quickly evaluate the Bayes factor for any particular configuration and compare even hundreds of configurations. However, when the number of tissues is large (say T > 10), the number of possible configurations grows too large to be exhaustively evaluated (analogous to a problem with eQTLs in Flutre et al., 2013). This becomes problematic in particular when assessing heterogeneity (either HET0 or HET1), which in principle would require a consideration of all those groupings that assume differences between some tissues. Therefore, we introduce an approximation that avoids enumerating all groupings when assessing heterogeneity, by focusing on only configurations that are strongly supported by the data. Thus we assume that the configurations with d > 1 that have not been visited by the Gibbs sampler and are not among a few dozen top heterogeneity models defined by tissue-specific group membership probabilities, have negligible marginal likelihood and can be ignored. This leads to a lower bound for the marginal likelihoods of the heterogeneity states. In practice, a comparison to the exact values for cases where exact values can be calculated ($T\le 10$) shows that the lower bound is actually a good estimate in most cases (see Section 3).

By combining the Bayes factors with the prior probabilities of the states we have the posterior probabilities of the states.

2.4 Q-statistic for heterogeneity

We compare GTM to a standard heterogeneity measure (Cochran, 1950)

$$Q={\displaystyle \sum _{s=1}^T\frac{n_s{(\widehat{{\theta }_s}-\overline{\theta })}^2}{\widehat{{\theta }_s}(1-\widehat{{\theta }_s})}},$$

where $\widehat{{\theta }_s}=y_{s1}/n_s$ and $\overline{\theta }$ are the empirical proportion of the reference allele at tissue s and across all tissues, respectively. (If $y_{s1}=0$, we set $y_{s1}=0.5$ and $y_{s2}=n_s-0.5$ to avoid numerical problems.) The idea is that this measure increases with the heterogeneity of the tissue-specific θ_s parameters, and can thus be used as a measure of heterogeneity. The Q-statistic is typically used for statistical testing for heterogeneity rather than for quantifying the amount of heterogeneity, and is known to have low power when sample size is small (Higgins et al., 2003). An empirical P-value of the Q-statistic is estimated by simulating datasets where the number of tissues and reads match with the observed data and where all tissues have the same value for ${\theta }_s=\overline{\theta }$.

3 Results

We first assess performance of GTM on simulated data and compare it with a standard heterogeneity measure. Second, we illustrate GTM on a real data example taken from the GTEx project. Results of GTM* are presented in Supplementary Information.

Data simulation

For three values for the number of tissues (T = 5, 10, 30) and four values for the number of reads per each tissue ($n_s=10,30,50,200$, for all s), we simulated 1000 datasets for nine scenarios given in Table 1. The reference allele read count for each tissue s was sampled from $\text{Bin}(n_s,{\theta }_s)$, where θ_s is 0.5 for group $\mathcal{N}$, 0.75 for group $\mathcal{M}$ and 0.99 for group $\mathcal{S}$.

Table 1.

Scenarios for simulations

	$\mathcal{N}$	$\mathcal{M}$	$\mathcal{S}$	STATE
1	T	0	0	NOASE
2	0	T	0	MODASE
3	0	0	T	SNGASE
4	T – 1	0	1	HET0
5	1	0	T – 1	HET0
6	0	T – 1	1	HET1
7	0	1	T – 1	HET1
8	$\lceil T/2\rceil$	$\lfloor T/2\rfloor$	0	HET0
9	0	$\lceil T/2\rceil$	$\lfloor T/2\rfloor$	HET1

For each of the nine scenarios, the table shows how many tissues (out of total T) belong to each of the three possible groups, $\mathcal{N},\mathcal{M}$ and $\mathcal{S}$, whose θ parameters are 0.5, 0.75 and 0.99, respectively. The STATE column shows to which of the five combined states each scenario belongs

GTM results

We applied GTM on the simulated datasets with 2000 Gibbs sampler iterations. The results for read counts 10 and 50 are shown in Figure 2 and for the remaining read counts in Supplementary Figure S4. The run time was 8, 16 and 53 s per dataset, for T = 5, 10 and 30, respectively (Intel i7/3.40 GHz).

Fig 2.

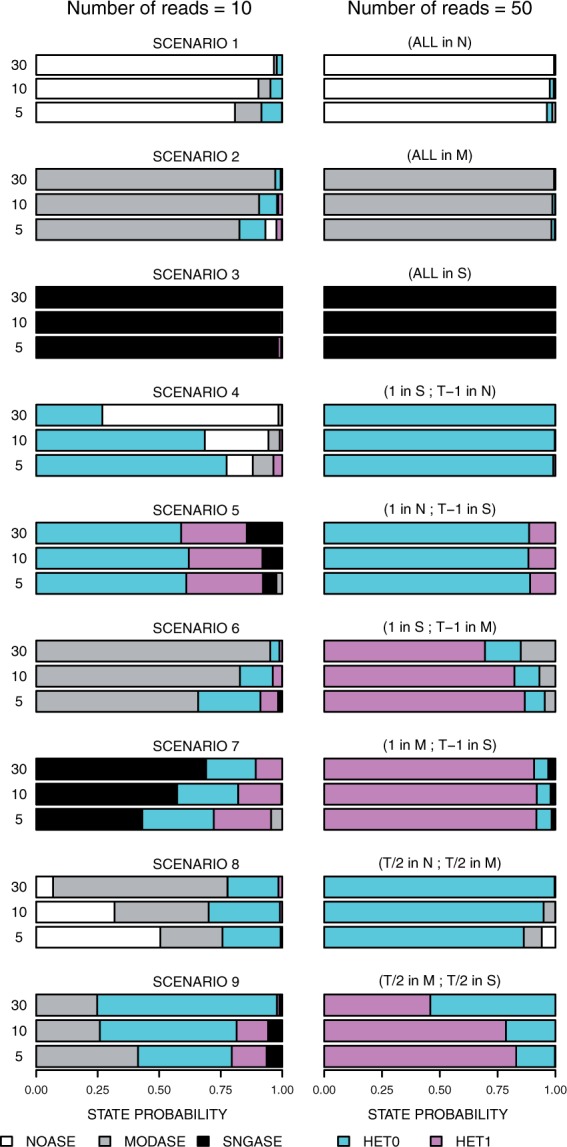
Each of the nine simulation scenarios (Table 1) is represented by three numbers of tissues (5, 10, 30) and two values for number of reads (10, left column and 50, right column). Each bar is divided into five colors (map given at the bottom) according to the (average) posterior probability of the five states when GTM was applied to the simulated datasets

For the homogeneous scenarios 1, 2 and 3, the detectability of the true state increases with the number of tissues, and in general is already high with only 5 tissues and 10 reads per each tissue. In particular, when the true state is SNGASE (scenario 3), there is no noticeable uncertainty about the correct state in any of the datasets, while for NOASE (scenario 1) and MODASE (scenario 2) the data are not equally decisive. This is related to the fact that the variance in the read counts is larger for $\theta =0.5$ (NOASE) and $\theta =0.75$ (MODASE) than it is for the extreme value of $\theta =0.99$ (SNGASE).

Our scenarios 4, 5, 6 and 7 consider the smallest possible amount of heterogeneity: a single tissue is different from the others. In these scenarios, we see an opposite trend from the homogeneous ones: the true heterogeneous state becomes harder to distinguish from the closest homogeneous one as the number of tissues increases. This is because, according to our prior, a configuration where a single tissue differs from the others becomes less probable as the number of other tissues increases. Information about the true state increases with the number of reads per tissue, and the overall heterogeneity probability (HET0 + HET1) is high for all heterogeneous scenarios for read count 50.

The scenarios 8 and 9 represent stronger heterogeneity where about half of the tissues belong to one group and the remaining half to another. When the true underlying groups are $\mathcal{N}$ and $\mathcal{M}$ (scenario 8), then 10 reads is not yet enough to clearly separate the true pattern from the homogeneous states (NOASE and MODASE), while 50 reads is enough for this purpose. In the scenario 9, where tissues are divided between $\mathcal{M}$ and $\mathcal{S}$, the overall heterogeneity probability is always fairly large, but it is difficult to exclude the possibility that at least one tissue belongs to $\mathcal{N}$, especially when many tissues are available. As a consequence, the HET0 state gets a considerable probability even though the true underlying state is HET1. To distinguish between the two heterogeneity states in this scenario requires read counts larger than 50 (Supplementary Fig. S4).

Taken together, the results in Figure 2 and Supplementary Figure S4 show that the model is correctly able to distinguish between all five combined states but an amount of information required for accurate classification varies between scenarios.

Comparisons with Q-statistic

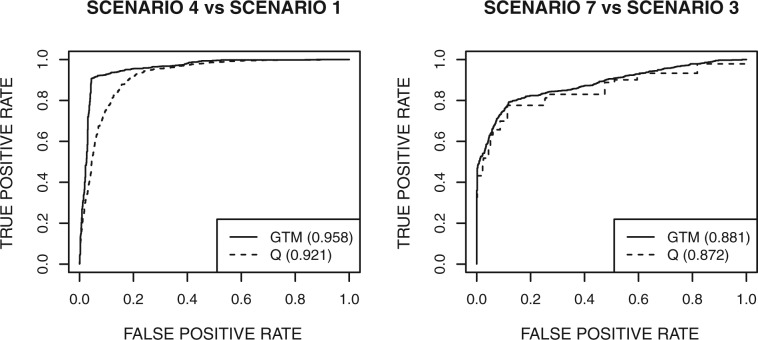
To show differences between our GTM heterogeneity probability and Q-statistic in detecting heterogeneity we show ROC curves for two settings (Fig. 3). In the first one, we use the 1000 datasets from simulation scenario 1 to represent a homogeneous state and the 1000 datasets from scenario 4 to represent a heterogeneous state, with T = 30 tissues and n = 10 reads per tissue. The ROC curve on the left panel of Figure 3 shows how those 2000 datasets are ranked by the posterior probability of HET0 + HET1 state from GTM and by the empirical P-value of Q. The right panel in Figure 3 shows similar results when comparing the homogeneous scenario 3 to the heterogeneous scenario 7. In both settings GTM is slightly better in detecting heterogeneity than the Q-statistic: ROC curve of GTM is consistently above that of Q. We discuss the difference between the two approaches in Section 4.

Fig 3.

ROC curves for detecting heterogeneity using GTM and Q-statistic on simulated datasets. Left: scenario 1 (homogeneity) versus scenario 4 (heterogeneity). Right: scenario 3 (homogeneity) versus scenario 7 (heterogeneity). Parameters are T = 30 tissues and n = 10 reads per tissue. Heterogeneity statistics are the posterior probability of HET0+HET1 from GTM and the empirical P-value from the Q-statistic. The legends show percent concordance measures for the ROC curves

Accuracy of approximation

To assess how accurate our approximation for marginal likelihoods of the heterogeneity states is, we compared the posterior probabilities of the five states from GTM with the exact values on all 9000 datasets simulated with T = 10 tissues and n = 10 reads per tissue. As a measure of accuracy we use the total variation (TV) distance, which for discrete distributions $(p_i)$ and $(q_i)$ is defined as $\frac{1}{2}{\displaystyle {\sum }_i|}{p}_i-q_i|$. TV describes how much of the probability mass needs to be relocated in order to turn the first distribution into the other, and also gives an upper bound for the maximal difference in probability that the two distributions assign to any one state.

We observed (Table 2) that 95% of the datasets had $\text{TV}<0.05$, and 0.5% had $\text{TV}>0.10$, with maximal TV being 0.168. As TV less than 0.10 is unlikely to change our inference on the underlying state, our approximation works well for a great majority of the datasets tested. However, there are large differences in the accuracy between the scenarios with scenario 8 (5 tissues in $\mathcal{N}$ and other 5 in $\mathcal{M}$) showing the strongest discrepancy. An explanation for this is that with only 10 reads per tissue the scenario 8 assigns non-negligible posterior probability to so many of the configurations showing heterogeneity between $\mathcal{N}$ and $\mathcal{M}$ groups that some of them are missed during our default number of 2000 Gibbs sampler iterations.

Table 2.

Accuracy of GTM

SCENAR	TV <0.01	TV <0.05	TV <0.10	$\max$
1	0.462	0.972	1	0.092
2	0.452	0.959	0.995	0.129
3	1	1	1	0.006
4	0.160	0.986	0.999	0.105
5	0.997	1	1	0.011
6	0.327	0.973	1	0.070
7	0.994	1	1	0.012
8	0.081	0.663	0.962	0.168
9	0.565	1	1	0.025

For each of the nine scenarios, Table shows the proportion of simulated datasets (out of total 1000 with T = 10 tissues and n = 10 reads per tissue) for which TV distance between GTM estimates and the exact posterior distribution of the five states is less than 0.01, 0.05 or 0.10. The $\max$ column shows the maximum TV distance observed

In Section 4, we propose an additional heterogeneity measure to complement our approximation for the posterior probability of heterogeneity states, especially for datasets with large number of tissues.

3.1 A PTV in ECM1

We consider read count data on SNV rs121909115 in chromosome 1, whose non-reference allele (T) introduces a stop codon in some transcripts of the gene ECM1. This is an example of a protein-truncating mutation that we expect to experience NMD leading to a reduction in the transcripts from the non-reference allele. However, the strength of NMD and its consistency across different tissue types is unknown. In the currently available GTEx data, we have one individual who is heterozygous at this SNV and Figure 4 shows the data and GTM results across seven tissues.

The results show that, as expected, most tissue types show ASE where the non-reference allele has lower read counts than the reference allele. In addition, there is evidence of heterogeneity between the tissue ($p(\text{HET0}|y)=0.93$) and that heterogeneity could result from a tissue-specific effect where the skin tissue escapes ASE ($p(\text{TIS}\_\text{SPE}|y)=0.24$). None of the tissues shows strong evidence for complete ASE (group $\mathcal{S}$), but rather the other six tissue types (apart from skin) are likely to belong to either the moderate ASE group $\mathcal{M}$, or to no ASE group. In particular, the nerve and adipose samples cannot be assigned to any one of our groups with high confidence, which can be seen from their membership probabilities being evenly split between the groups $\mathcal{N}$ and $\mathcal{M}$.

The non-reference allele (T) at the SNV rs121909115 is one of the known protein truncating mutations in ECM1 that in homozygous carriers lead to lipoid proteinosis, also known as Urbach-Wiethe disease (OMIM 247100; Hamada et al., 2003). The symptoms of this disease include scarring and infiltration of skin and mucosae (Hamada, 2002). Therefore, it is an interesting observation that in our data the observed allelic ratio of the nonsense mutation is higher in the skin tissue than in several other tissue types.

The isoform view of the GTEx portal (2014-01-17, dbGaP phs000424.v4.p1) shows four isoforms for ECM1 of which only one (ENST00000470432) does not annotate rs121909115 as stop-gain variant. However, the relative abundance of this transcript does not seem particularly high in skin tissue compared with the other tissues. Another observation is that one of the remaining three transcripts (ENST00000346569) is expressed in only a few tissues. These tissues include mucous membrane and skin tissue where symptoms of lipoid proteinosis are seen.

4 Discussion

We have introduced a statistical framework to assess similarities and differences in ASE between tissue types. A motivation for our work comes from ongoing RNA-sequencing projects such as the GTEx project (GTEx-Consortium, 2013) that generates data on up to 30 tissue types per individual with read counts per tissue and per site starting from around 10.

We have chosen a Bayesian approach because it leads to a consistent probabilistic quantification of the support that the data provide for each of the competing models. We see this as an advantage over a series of separate analyses, such as, for example, would be needed by an approach that first assessed heterogeneity using the Q-statistic and if no (statistically significant) heterogeneity was observed, would further classify the dataset into one of the homogeneous states. Previously, two excellent studies on Bayesian models for expression data have been published by Skelly et al. (2011) and Flutre et al. (2013).

Skelly et al. (2011) consider a three-stage hierarchical model for allele read counts from genome-wide RNA-seq data of one individual. They observe allele counts at each heterozygous SNV (1st level) which are assigned to genes (2nd level) whose common properties are controlled by genome-wide parameters (3rd level). Their model would be directly applicable also to multi-tissue RNA-seq data where tissue-specific allele counts replace SNV-specific allele counts and sites replace genes at the second level of the model. Suppose, for example, that we had multi-tissue RNA-seq data on a set of individuals who are heterozygous for at least one PTV. The model of Skelly et al. (2011) would produce posterior distribution on the global proportion of the PTVs that show ASE in at least one tissue type, as well as variant-specific posterior probability of ASE. However, it would not give as refined characterization of ASE at each PTV as our hierarchical model GTM* (Supplementary Information) and it would not do inference on tissue-specific group indicator parameters (γ_s) that allow probabilistic model comparison between different patterns of ASE.

Flutre et al. (2013) developed a method for a joint eQTL analysis across multiple tissues. They work with micro-array expression data using a linear model that is not directly applicable to the datasets we have in mind: read count data from several tissues of a single individual. They use tissue-specific binary indicator parameters that tell whether a variant is an eQTL in each tissue and introduce three ways to assign prior probabilities to different configurations of the indicators. Their ‘lite’ model gives positive prior on only those configurations whose distance from homogeneity is at most 1. Their ‘BMA’ model is similar to what we have used in that the prior of a configuration depends only on its distance from homogeneity and that the total prior probability corresponding to each value of distance is the same. Finally, their most complex ‘BMA-HM’ model treats the weights of the configurations as random variables and estimates them across genes using a hierarchical model. Similar hierarchical model, that would learn joint ASE patterns between tissues by a simultaneous analysis of a set of genetic variants (e.g. PTVs) is also an important topic for further development of our hierarchical model GTM*.

Even though hierarchical models, such as our GTM* and those of Skelly et al. (2011) and Flutre et al. (2013), are conceptually attractive, we believe that GTM’s ability to analyze one PTV at a time has its merits from a practical point of view: it is quick to run, easy to understand and requires read count data on only one variant.

Heterogeneity measures. Our model assumes that all tissues in a same group have the same reference allele read frequency θ. In practice, we expect that our model is robust to some heterogeneity within each group, since the priors for different groups are so clearly separable from each other (Fig. 1 and Supplementary Fig. S1). Our main interest is to assign tissue types into (three) broad categories of ASE, and consequently we call a dataset heterogeneous only if some pair of tissues show fairly strong difference in the non-reference allele frequency. Standard heterogeneity measures, such as Q, ask a slightly different question of whether parameters θ_s have exactly the same value across the tissues. A frequentist answer to this latter question is given by an empirical P-value of heterogeneity measures Q or $p(\text{HET}|y)$ estimated under the null hypothesis that all tissues have the same value for θ parameter which is estimated from the data. By this approach, heterogeneity P-values in the ECM1 example of Figure 4 are 0.011 and 0.006 by using Q and $p(\text{HET0}|y)$, respectively, as a test statistic. While these P-values point to general heterogeneity between the tissue types, our GTM analysis leads to more detailed information considering the type of heterogeneity: we see heterogeneity where at least one tissue type escapes ASE (our HET0 state).

Our heterogeneity probabilities are based on a lower bound of the true marginal likelihoods of the heterogeneity states. We showed that in a large majority of our datasets (with 10 tissues) the approximation is accurate, but the approximation may not always work as well with larger number of tissues. Therefore, in addition to the heterogeneity probabilities, we also compute, for each pair of tissues, a posterior expectation of the distance between them. Here we define the distance between two tissues to be 0 if they belong to a same group and 1 otherwise. Maximum of all pairwise distances gives an indication whether there is heterogeneity between tissues. By further defining the distance between the ASE groups $\mathcal{M}$ and $\mathcal{S}$ to be 0, we have a measure for particular kind of heterogeneity (HET0) where at least one tissue belongs to the no ASE group $\mathcal{N}$.

4.1 Application of the method

Nonsense-mediated decay

We envisage that a primary application of our method will be in analyzing NMD. PTVs are usually subject to NMD, a cellular mechanism that detects premature termination codons and prevents expression of truncated proteins. Integrated genome and transcriptome sequencing studies in lymphoblastoid cell lines have demonstrated that ASE can be used for testing variants predicted to trigger NMD (Lappalainen et al., 2013; MacArthur et al., 2012; Montgomery et al., 2010, 2011). To test whether the predicted NMD truly happens, we can use the one-sided ASE models rather than the two-sided ones to explicitly require that an ASE signal is present only if the minor allele, and not the major allele, is silenced. We applied the one-sided approach in our example analysis of a PTV in ECM1.

Imprinting

Genomic imprinting is a phenomenon where only an allele inherited from the parent of a particular sex is expressed (Babak et al., 2008). To assess imprinting for one tissue type one could consider a common coding variant of the gene of interest in that tissue across multiple heterozygous individuals. If the gene is imprinted, then in about half of the individuals the allele 1 should be silenced, because we expect that in about half of the individuals the allele 1 at this locus is inherited from the mother and in the other half it originates from the father. We could extend our framework to such a case by allowing each ASE group to be divided into two subgroups representing parental origin of the allele 1. If one of the subgroups had proportion θ of the reads from allele 1 then the corresponding proportion for the other subgroup should be $1-\theta$. We could model θ with a Beta-prior as in our GTM model.

Modest ASE effects

An interesting application of ASE is in the study of cis-regulatory variants in LD with coding variants. When regulatory variants have only modest effects (Dimas et al., 2009), we could modify our prior on ASE states to reflect this (see Supplementary Information section S8 and Fig. S6). With this approach we envision that researchers are able to study the effect of cis-regulatory variants on transcription across a broad range of tissues where the number of samples per tissue may be limited. However, compared to strong ASE effects, more modest effects require much larger read counts per tissue and decrease the ratio between biological signal and possible technical noise (Degner et al., 2009).

Multiple individuals

Suppose we have RNA-seq data on same tissue types from several individuals who are heterozygous at a particular variant. We could first assess, for each tissue type, whether the individuals are heterogeneous in their ASE status. If there is no evident heterogeneity, a simple approach is to combine the reads from the same tissue type across the individuals before analyzing the data across the tissues. A more refined model that accounts for possible individual-specific effects that are shared across the tissues requires further work.

5 Conclusion

We have presented GTM and its multi-site extension (GTM*), to (i) classify tissues into three groups at each site according to their ASE patterns and (ii) classify the sites into five combined ASE states according to their tissue-wide ASE profiles. We see major applications of our approach in assessing homogeneity, heterogeneity and tissue specificity across a group of genetic variants such as variants predicted to trigger NMD, variants in genes with evidence of imprinting, or variants in LD with GWAS loci for a particular disease.

As an example, we presented an application of the method to read count data from the GTEx project for one heterozygote carrier of a premature truncating mutation (p.R53X, rs121909115) in the ECM1 gene. For this variant, which in homozygous form is known to cause lipoid proteinosis, we identified heterogeneous gene expression effects across tissues and evidence for a complete escape from NMD in skin tissue.

The identification and characterization of ASE, in particular for PTVs with a putative complete loss of function effect, will provide a better understanding of the biological mechanisms that are involved in transcriptional regulation and will improve our computational models for annotating variants identified in case–control or clinical genome sequencing studies.

Funding

This work was supported by the Academy of Finland [257654 to M.P.]; Wellcome Trust [095552/Z/11/Z to P.D., 098381 and 090532 to M.I.M.]; National Institutes of Health [R01-MH101814 and MH-090941 to M.I.M.]; Royal Society Wolfson Merit Award to P.D.; and a Clarendon Scholarship, NDM Studentship, and Green Templeton College Award from the University of Oxford to M.R.

Conflict of interest: none declared.