DISSCO: direct imputation of summary statistics allowing covariates

Abstract

Background: Imputation of individual level genotypes at untyped markers using an external reference panel of genotyped or sequenced individuals has become standard practice in genetic association studies. Direct imputation of summary statistics can also be valuable, for example in meta-analyses where individual level genotype data are not available. Two methods (DIST and ImpG-Summary/LD), that assume a multivariate Gaussian distribution for the association summary statistics, have been proposed for imputing association summary statistics. However, both methods assume that the correlations between association summary statistics are the same as the correlations between the corresponding genotypes. This assumption can be violated in the presence of confounding covariates.

Methods: We analytically show that in the absence of covariates, correlation among association summary statistics is indeed the same as that among the corresponding genotypes, thus serving as a theoretical justification for the recently proposed methods. We continue to prove that in the presence of covariates, correlation among association summary statistics becomes the partial correlation of the corresponding genotypes controlling for covariates. We therefore develop direct imputation of summary statistics allowing covariates (DISSCO).

Results: We consider two real-life scenarios where the correlation and partial correlation likely make practical difference: (i) association studies in admixed populations; (ii) association studies in presence of other confounding covariate(s). Application of DISSCO to real datasets under both scenarios shows at least comparable, if not better, performance compared with existing correlation-based methods, particularly for lower frequency variants. For example, DISSCO can reduce the absolute deviation from the truth by 3.9–15.2% for variants with minor allele frequency <5%.

Availability and implementation: http://www.unc.edu/∼yunmli/DISSCO.

Contact: yunli@med.unc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Recent large international efforts, including the International HapMap Project (The International HapMap Consortium, 2007, 2010) and the 1000 Genomes Project (Abecasis et al., 2012; The 1000 Genomes Project Consortium, 2010), have provided comprehensive catalogs of genetic variants and linkage disequilibrium (LD) patterns in various populations around the world. Using these publicly available data as reference panels, imputation of individual genotypes at untyped variants has facilitated recent genome-wide association studies (GWAS) and meta-analysis (Berndt et al., 2013; Chambers et al., 2011; Dastani et al., 2012; Huang et al., 2012). Therefore, when individual level genotype data are available in study samples, it has become a standard practice to perform genotype imputation (Auer et al., 2012; de Bakker et al., 2010; Duan et al., 2013; Li et al., 2009; Pasaniuc et al., 2012).

Unfortunately, individual level genotype data are not always available, particularly in multisite meta-analysis GWASs that can include many individual study GWASs. The process of gathering proper institutional human subjects research approval, including formal data-sharing agreements, can be very time consuming. Association summary statistics, on the other hand, are routinely available and are not subject to the same human subjects research bottlenecks. Two methods have been proposed recently to directly impute association summary statistics at untyped markers in the absence of individual level genotypes (Lee et al., 2013; Pasaniuc et al., 2014). Both methods assume the summary statistics across typed and untyped markers follow a multivariate Gaussian distribution. Gaussian models have been routinely used in other related genetic applications (Conneely and Boehnke, 2007; Wen and Stephens, 2010). For both imputation methods using association summary statistics, the correlation structure between the summary statistics is estimated based on the LD structure between the corresponding markers in an external reference panel(s). Both methods assume that the correlations between the association summary statistics are the same as the correlations between the genotypes at the corresponding markers.

In this study, we provide a general analytical proof that in the absence of confounding covariates, estimating the covariance structure between summary statistics using marker LD information between the corresponding markers is reasonable. However, in practice, confounding covariates are often present. In particular, we consider two scenarios: association studies including genetically admixed individuals (Scenario I) and association studies in the presence of general confounders (Scenario II). In Scenario I, the underlying LD between markers among participants in the usually cosmopolitan reference panel, obtained from the public domain likely differs from the corresponding LD among subjects in the study sample. In Scenario II, we consider the presence of general confounder covariates or mediators, such as socialeconomic factors, environmental factors, etc., which are inevitable in real association studies; for example, the adjustment of body mass index (BMI) for association with risk with diabetes (Narayan et al., 2007), smoking with lung cancer (Wynder and Hoffmann, 1994), Duffy dose for white blood cell count (WBC) (Reiner et al., 2011), just to name a few. For Scenario I, we propose to use the top principal components (PCs) to adjust the correlation estimates. For Scenario II, we develop a unified framework for DISSCO to deal with general confounders and mediators.

2 Methods

2.1 Existing methods for the imputation of association summary statistics

Two methods for direct imputation of association summary statistics (Lee et al., 2013; Pasaniuc et al., 2014) have been proposed recently. Both of these methods assume a multivariate Gaussian distribution on the association summary statistics across typed and untyped markers. The correlation structure between the summary statistics is estimated based on the LD structure between the corresponding markers using an external reference panel(s). Denote the vectors containing summary, or Z, statistics at typed and imputed/untyped markers as Z_t and Z_i, respectively. Denote the correlation matrices containing the correlations between the typed markers estimated from the study sample and reference panel as ${\widehat{\sum }}_{\text{t},\text{t}}^{\text{corr,study}}$ and ${\widehat{\sum }}_{\text{t},\text{t}}^{\text{corr,refer}}$, respectively, and the correlation matrices containing the correlation estimates between typed and untyped markers in the study sample and reference panel as ${\widehat{\sum }}_{\text{i},\text{t}}^{\text{corr,study}}$ and ${\widehat{\sum }}_{\text{i},\text{t}}^{\text{corr,refer}}$, respectively.

DIST (Lee et al., 2013) uses the following formula to impute the summary statistics for the untyped variants contained in Z_i:

$$Z_{\text{i}}^{\text{DIST}}={\widehat{\sum }}_{\text{i,t}}^{\text{corr,refer}}{\left({\widehat{\sum }}_{\text{t,t}}^{\text{corr,refer}}\right)}^{-1}{Z}_{\text{t}}$$

ImpG-Summary and ImpG-SummaryLD are normalized versions of DIST (Pasaniuc et al., 2014), designed to improve the performance in finite samples. Specifically,

$$Z_{\text{i}}^{\text{ImpSummary}}=\frac{Z_{\text{i}}^{\text{DIST}}}{\sqrt{{\widehat{\sum }}_{\text{i,t}}^{\text{corr,refer}}{\left({\widehat{\sum }}_{\text{t,t}}^{\text{corr,refer}}\right)}^{-1}({\widehat{\sum }}_{\text{i,t}}^{\text{corr,refer}}{)}^{\prime }}}$$

$$\begin{array}{c}{Z}_{\text{i}}^{\text{ImpSummaryLD}}\\ =\frac{Z_{\text{i}}^{\text{DIST}}}{\sqrt{{\widehat{\sum }}_{\text{i,t}}^{\text{corr,refer}}{\left({\widehat{\sum }}_{\text{t,t}}^{\text{corr,refer}}\right)}^{-1}{\widehat{\sum }}_{\text{t,t}}^{\text{corr,study}}{\left({\widehat{\sum }}_{\text{t,t}}^{\text{corr,refer}}\right)}^{-1}({\widehat{\sum }}_{\text{i,t}}^{\text{corr,refer}}{)}^{\prime }}}\end{array}$$

In addition, ImpG-Summary and ImpG-SummaryLD adopt a regularization procedure similar to ridge regression to adjust for statistical noise in the estimation of the covariance matrix. Specifically, ${\widehat{\sum }}^{\text{adj}}={\widehat{\sum }}^{\text{unadj}}+\lambda I$ where ${\widehat{\sum }}^{\text{unadj}}$ is the unadjusted correlation matrix with its elements equal to Pearson correlation, and by default, $\lambda =0.001$ is used for adjustment in the study sample and $\lambda =0.1$ is used for adjustment in the reference panel.

2.2 Theoretical motivation

We and others (Han et al., 2011, 2009; Kostem et al., 2011; Pasaniuc et al., 2014) theoretically justify existing methods in the absence of confounders (Supplementary Material S1). However, the justification fails when confounders exist. In this study, we show that in the presence of confounders, the correlation between the association summary statistics is the partial correlation, conditional on the confounders, instead of the marginal correlation between the corresponding marker genotypes (Supplementary Material S2). The result implies that when partial and marginal correlations differ confounders need to be properly incorporated for more accurate imputation of association statistics. Herein, we describe our method, direct imputation of summary statistics allowing covariates (DISSCO), which addresses this issue.

2.3 Motivating simulations

We first conducted proof-of-principle simulations to confirm the theoretical findings that (i) Z statistics estimated in two simple linear regression models without confounding covariates have correlations close to the correlation between two predictor variables and (ii) Z statistics estimated in two multiple regression models with the same set of confounding covariates have correlation close to the partial correlation instead of the marginal correlation between two predictor variables.

2.4 Our DISSCO imputation method

Both DIST and ImpG-Summary/LD assume that the correlations between the association summary statistics are the same as those between the corresponding marker genotypes. In the presence of confounding covariates, we have shown both analytically and through proof-of-principle simulations (results in Sections 3.1 and 3.2) that the correlations between the summary statistics are the partial correlations instead of the marginal correlations between the genetic markers. Thus, we propose our method DISSCO based on partial correlations as below:

$$Z_{\text{i}}^{\text{DISSCO}}={\widehat{\sum }}_{\text{i,t}}^{\text{adj-parcorr,refer}}{\left({\widehat{\sum }}_{\text{t,t}}^{\text{adj-parcorr,refer}}\right)}^{-1}{Z}_{\text{t}},$$

where ${\widehat{\sum }}_{\text{t,t}}^{\text{adj-parcorr,refer}}={\widehat{\sum }}_{\text{t,t}}^{\text{unadj-parcorr,refer}}+\lambda I$, and the elements in ${\widehat{\sum }}_{\text{t,t}}^{\text{unadj-parcorr,refer}}$ are equal to partial correlations. We follow the ImpG-Summary/LD method and also adopt the ridge-like regularization procedure. To achieve a desirable balance between performance and computational efficiency, we only include markers within a pre-specified window size of each untyped maker of interest. The impact of including only closely linked markers is negligible, as markers further away have little effect on the estimation of the summary statistic for the untyped marker given the low LD between these markers and the untyped marker of interest. Similar strategies were adopted by DIST and impG-Summary/LD. We provide more details in the Section 5.

We describe two real-life scenarios where the correlation and partial correlation likely make practical difference.

2.4.1 Scenario I: admixed samples

Genotype imputation in admixed populations is particularly challenging due to increased genetic heterogeneity across study participants and a deficit of well-matched reference panels. Considerable efforts have been devoted to the selection of ancestry appropriate reference panels for imputation (Egyud et al., 2009; Huang et al., 2009; Pemberton et al., 2008). However, even after the selection of an appropriate ancestry-matched reference panel, between-study heterogeneity makes the naïve uniform utilization of the same phased reference panel for different study samples suboptimal. Commonly used Markov model-based methods for the imputation of individual level genotypes, including IMPUTE (Marchini et al., 2007), IMPUTE2 (Howie et al., 2009), MaCH (Li et al., 2010), minimac (Howie et al., 2012), MaCH-Admix (Liu et al., 2012) and Beagle (Browning and Yu, 2009), alleviates this issue by modeling, separately for each study, the genetic data from the study sample together with genetic data from the reference panel when phasing the individual reference haplotypes. Unfortunately, this approach is only possible when there is individual level genotype data available from the study participants.

Motivated by the common analytic practice used for controlling for population stratification, DISSCO employs the following PC-analysis-based procedure for the imputation of summary statistics in admixed participants: (i) perform LD-based SNP pruning using PLINK (Purcell et al., 2007), (ii) construct PCs using EigenSoft (Patterson et al., 2006) on the study samples and reference samples together using the pruned set of markers, (iii) perform single marker association analyses controlling for the top PCs to obtain a Z statistic for every typed marker and, finally, (iv) perform imputation of the Z statistics at untyped markers by DISSCO. A unique aspect of this scenario is that the PCs in the reference and study samples are obtained in a unified manner from a single PCA analysis (Step 2). In contrast, general confounding covariates that are directly measured in study participants are typically not available among reference individuals.

2.4.2 Scenario II: in the presence of general confounding covariates

Similar to any association analysis, in GWAS, it is often necessary to control for other confounders, or possibly mediators, such as demographic information, environmental exposures and lifestyle factors. In GWAS, a single-marker analysis using a multiple regression framework is typically adopted to simultaneously model each single marker of interest together with covariates, including those that could confound the association. As aforementioned, unlike PCs, which can be directly obtained in a unified manner for both the reference and study individuals by applying PCA, general covariates available in study samples are often not available in the reference population.

We project the relevant covariates into the reference participants based on the covariate values in the study participants and the observed genotypes at the typed markers within a window (window defined the same manner as in Pasaniuc et al., 2014), surrounding the subset of markers currently being imputed, in both the study and reference samples. We use these imputed covariates, which we call ‘pseudo-covariates’, to calculate partial correlations in the reference sample. To obtain these pseudo covariates, we first regress the covariates C on genotypes at typed markers in the study sample, ($G_{\text{t}}^{\text{study}}$), and estimate the regression coefficients by $\hat{\beta }={([1 G_t^{\text{study}}]\text{'}[1 G_t^{\text{study}}])}^{-1}[1 G_t^{\text{study}}]\text{'}C$ and sample residuals $\hat{\epsilon }=C-\left[1 G_t^{\text{study}}\right].$ We then project the pseudo-covariates into the reference samples using the estimated regression coefficients from the study samples and the genotypes in the reference samples, by ${\hat{C}}^{\text{refer}}=[1 G_t^{\text{refer}}]\hat{\beta }+{\epsilon }^{*}$, where ${\epsilon }^{*}$ is a bootstrap sample of $\hat{\epsilon }$.

Based on these ‘pseudo-covariates’, we then calculate ${\widehat{\sum }}_{\text{i,t}}^{\text{parcorr,refer}}$ and ${\widehat{\sum }}_{\text{t,t}}^{\text{parcorr,refer}}$. Finally, we apply the DISSCO formula to impute the Z statistics at untyped markers. The entire process is repeated across all possible windows of genotyped markers spanning the genome to obtain imputed summary statistics for all markers.

2.4.3 Covariate projection accuracy and impact on partial correlation estimation

In our DISSCO framework, covariate projection accuracy, particularly its impact on the estimation of partial correlations, is the key factor that determines the gains over existing methods. We therefore performed simulations to evaluate both the accuracy of the projected covariates and the impact of the projected covariates on the partial correlation estimates the association summary statistics calculations.

2.5 Post-imputation quality filtering

Following the imputation quality index

$$\widehat{r^2}\text{pred}={\widehat{\sum }}_{i,t}^{\text{corr,refer}}{\left({\widehat{\sum }}_{t,t}^{\text{corr,refer}}\right)}^{-1}({\widehat{\sum }}_{i,t}^{\text{corr,refer}}{)}^{\prime }$$

proposed for ImpG-Summary/LD (Pasaniuc et al., 2014), we use

$$\widehat{r^2}\text{predCO}={\widehat{\sum }}_{\text{i,t}}^{\text{parcorr,refer}}{\left({\widehat{\sum }}_{\text{t,t}}^{\text{parcorr,refer}}\right)}^{-1}({\widehat{\sum }}_{\text{i,t}}^{\text{parcorr,refer}}{)}^{\prime }$$

as a post-imputation quality measure.

3 Simulation Results

3.1 Gaussian predictors and covariate

We first consider the case where the predictors of interest (X₁ and X₂) as well as the confounder (C) follow a Gaussian distribution. We simulated a random vector $(C X_1 X_2)$ following a standard trivariate Gaussian distribution with correlations ${\rho }_{C{X}_1},{\rho }_{C{X}_2}$ and ${\rho }_{X_1{X}_2}$. We then generated the response variable $\gamma ={\beta }_0+{\beta }_{C}C+\epsilon$, where $\epsilon$ is an independent Gaussian random variable with mean zero and variance V. We fit the following two models, mimicking GWAS single marker analysis, to obtain Z statistics testing the association between $X_1 (X_2)$ and Y controlling for C: $Y\sim$ $X_1+C$ and $Y\sim X_2+C.$

We considered eight different model settings, reflecting different combinations of $({\rho }_{C{X}_1},{\rho }_{C{X}_2},{\rho }_{X_1{X}_2})$, and conducted 10 000 simulations for each model based on 300 observations (Table 1). We observed that in all settings, the point estimate of the correlation between Z statistics, ${\widehat{\rho }}_{Z_1{Z}_2}$, was considerably closer to the true partial correlation ${\rho }_{X_1{X}_2|C}$ than to the marginal correlation ${\rho }_{X_1{X}_2}$. The 95% confidence interval for ${\widehat{\rho }}_{Z_1{Z}_2}$ always included the partial correlation but not the marginal correlation (except under Setting 6 where the two correlations were simulated to be identical). For example, in Setting 7, where the marginal correlation was positive (0.3) but partial correlation was negative (−0.38), the point estimate of the correlation between the Z statistics was −0.37 and the 95% confidence interval was [−0.38,−0.35].

Table 1.

Gaussian predictors and confounder

Setting	${\rho }_{C{X}_1}$	${\rho }_{C{X}_2}$	${\rho }_{X_1{X}_2}$	${\rho }_{X_1{X}_2|C}$	${\widehat{\rho }}_{Z_1{Z}_2}$
1	0.5	0.9	0.8	0.93	0.93 [0.92,0.93]
2	0.5	0.9	0.5	0.13	0.14 [0.12,0.16]
3	0.4	0.5	0	−0.25	−0.24 [−0.26,−0.22]
4	0	0.8	0.3	0.50	0.50 [0.49,0.52]
5	0.6	0	0.5	0.63	0.63 [0.62,0.64]
6	0	0	0.5	0.50	0.51 [0.49,0.52]
7	0.6	0.8	0.3	−0.38	−0.37 [−0.38,−0.35]
8	0.9	0.8	0.5	−0.84	−0.84 [−0.84,−0.83]

${\widehat{\rho }}_{Z_1{Z}_2}$ includes the point estimate and 95% confidence interval for the correlation between the two Z statistics. Neither ${\beta }_0$, ${\beta }_C$ nor V affects the values of the partial or marginal correlations. Therefore, without loss of generality, we set ${\beta }_0$ = 1, ${\beta }_C$ = 1 and V = 1.

3.2 Multinomial predictors $\left({\mathit{G}}_1 {\mathit{G}}_2\right)$ and Gaussian covariate

To mimic the discrete nature of observed genotypes, we simulated a categorical vector $(G_1 G_2)$ containing genotypes at two typed markers. Here too, we found that the correlations of the Z statistics are consistent with the partial correlations and not marginal correlations, for all settings examined (Supplementary Material S3). For example, in Setting 2, where the marginal correlation is positive (0.223) but the partial correlation is negative (−0.6), the point estimate of the correlation between the Z statistics was −0.6 with a corresponding 95% confidence interval [−0.612,−0.587].

3.3 Covariate projection accuracy and its impact on partial correlation estimation and association summary statistics imputation

Although the ultimate goal of DISSCO is to impute association summary statistics, one key factor influencing its capability to achieve this goal is the accuracy of partial correlation estimates based on any projected covariates. We therefore first evaluated the accuracy of DISSCO’s covariate projection and then its impact on the estimation of partial correlations via simulations. We observed that the accuracy of the covariate projection depends on the extent of the correlation between the typed markers and the covariate(s) to be projected. However, regardless of the absolute level of projection accuracy, the partial correlations among typed markers can be better estimated: the partial correlation estimator based on projected covariates, i.e. ${\widehat{\rho }}_{X_1{X}_2|\hat{C}}$ better approaches ${\rho }_{X_1{X}_2|C}$ than ${\widehat{\rho }}_{X_1{X}_2}$ across all settings. The difference can be dramatic: for example, for Setting 2 when true partial correlation ${\rho }_{X_1{X}_2|C}=0.133$, ${\widehat{\rho }}_{X_1{X}_2|\hat{C}}=0.132$ but ${\widehat{\rho }}_{X_1{X}_2}=0.5$ (Supplementary Table S3A). Partial correlation estimates between typed and untyped show mixed results, but in general, through covariate projection and subsequent partial correlation estimation based on the projected covariates, DISSCO tends to generate more accurate imputed Z statistics than approaches that ignore the confounding. Details are documented in Supplementary Material S4.

4 Real data analysis

We applied DISSCO, DIST*, ImpG-Summary*/LD* (where * indicates our own implementation of existing methods) to two real datasets: (i) the Women’s Health Initiative (WHI) study; and (ii) the Cebu Longitudinal Health and Nutrition Survey (CLHNS) study.

4.1 Real data set 1: WHI African Americans

WHI was established by the National Institutes of Health in 1991 to address major health issues causing morbidity and mortality in postmenopausal women (Anderson et al., 1998). The SNP Health Association Resource (SHARe) consortium genotyped 8421 African Americans in WHI using the Affymetrix 6.0 genotyping platform. Standard quality controls were applied previously (Reiner et al., 2011), including removing markers with call rate <90%, Hardy Weinberg equilibrium exact test P-value < 10⁻⁶, or sample minor allele frequency (MAF) < 1%.

4.1.1 WHI Scenario I: accommodating admixture via PCs

We randomly masked 20% of the markers as untyped markers. Because of the instability in the estimated correlations for markers with MAF < 1%, we imputed and compared the performance of DISSCO, DIST* and ImpG-Summary*/LD* for markers with MAF > 1%. Our final dataset contained 653 877 typed markers and 162 443 untyped markers with MAF > 1%.

We first used PLINK to prune the typed markers (−pairwise 0.1). We then applied EigenSoft on the pruned markers to obtain PCs for the study and reference (from 1000 Genomes Phase I v3) samples, using default parameters. The phenotype we examined was BMI. We first regressed BMI on age and the proportion of African ancestry estimated using FRAPPE (Tang et al., 2005) to remove their effects. We then used the residuals to perform single marker association analyses for all markers, adjusting for PCs only, to evaluate DISSCO’s PCA-based procedure for imputation in admixed populations.

For the masked experimental genotypes, we obtained the true Z statistics, denoted by $Z_{\text{i}}^0$. The Z statistics at typed markers $Z_{\text{t}}^0$ were used to impute Z statistics at the untyped markers by DISSCO, DIST* and Imp-Summary*/LD*, which are denoted by $Z_{\text{i}}^{\text{DISSCO}}$, $Z_{\text{i}}^{\text{DIST}}$, $Z_{\text{i}}^{\text{ImpSummary}}$ and $Z_{\text{i}}^{\text{ImpSummaryLD}}\text{.}$ We evaluated the performance of these methods using three measures (i) D: the absolute deviation between true and imputed Z statistics, (ii) %D: the absolute relative percentage deviation between the difference of the true and imputed Z statistics and the true Z statistics, $\left|\frac{Z_{\text{i}}^{\text{Method}}-Z_{\text{i}}^{\text{true}}}{Z_{\text{i}}^{\text{true}}}\right|\times 100$, where the subscript Method = DISSCO/DIST*/ImpG-Summary*/ImpG-SumaryLD*; and (iii) R²: the squared Pearson correlation between the imputed and true Z statistics.

We evaluated the average performance of all four methods across all 162 443 untyped markers without any post imputation filtering and across the subset of 150 534 markers where $\widehat{r^2}\text{pred}$ > 0.6 for ImpG-Summary*/LD* and DIST*, and $\widehat{r^2}\text{predCO}$ > 0.6 for DISSCO. In addition, for each marker and competing approach, we tabulated whether the Z statistic estimated by DISSCO was closer than the Z statistic estimated by the competitor to the true Z statistic and we conducted a one-sided Wilcoxon signed rank test to test the null hypothesis that there was no difference in accuracy between the different approaches. We found that DISSCO provided imputed summary Z statistics at the untyped markers that were, on average, consistently more accurate than the other approaches across all quality metrics and marker sets (Table 2). Based on the individual marker results, DISSCO significantly outperformed all three competitors (P < 0.001 for all three comparisons).

Table 2.

Estimation accuracy of association summary statistics in WHI data set: accommodating admixture via PCs

Measure	Post-imputation filtering	#SNPs	DIST*	ImpG-Summary*	ImpG-Summary LD*	DISSCO
D	None	162 443	0.417 (4.1%)	0.410 (2.4%)	0.408 (2.0%)	0.400
%D	None	162 443	56.1 (8.0%)	54.7 (5.7%)	55.1 (6.4%)	51.6
R2	None	162 443	0.697 (2.2%)	0.701 (1.6%)	0.708 (0.6%)	0.712
D	>0.6	150 534	0.386 (3.1%)	0.378 (1.1%)	0.377 (0.8%)	0.374
%D	>0.6	150 534	52.3 (6.9%)	50.6 (3.8%)	51.2 (4.9%)	48.7
R2	>0.6	150 534	0.743 (1.6%)	0.750 (0.7%)	0.755 (0.0%)	0.755

Best performing methods are highlighted as bold. The estimated accuracy of the association summary statistics is compared across different methods using three metrics: D, %D and R². Smaller D, smaller %D and larger R² reflect more accurate estimation of the true Z statistic. The values in parentheses are the relative improvement of DISSCO over DIST*/ImpG-Summary*/ImpG-SummaryLD*.

4.1.2 WHI Scenario II: accommodating general covariates

We performed a second comparison between DISSCO and the existing methods using a GWAS of WBC, for which the Duffy blood group null variant is known to account for 15–20% of the variation among African Americans and is, therefore, routinely controlled for in association studies (Auer et al., 2012; Reiner et al., 2011). Besides the Duffy variant, we additionally performed covariate adjustment for age, BMI and African ancestry. We again randomly masked 20% of markers as untyped markers and imputed those with MAF > 1%. In this analysis, our final set contained 150 934 imputed variants.

We conducted single-marker association analyses with natural-logarithm transformed WBC, adjusting for the aforementioned covariates. We again evaluated the performance of all four methods by comparing the imputed with true summary statistics, which were established using masked experimental genotypes.

Results summarized in Table 3 indicate superior performance of DISSCO over existing methods in the presence of general confounding covariates, with or without post-imputation quality filtering. Similar to the results for BMI, based on the individual marker results, DISSCO significantly outperformed all three competitors (P < 0.001 for all three comparisons).

Table 3.

Estimation accuracy of association summary statistics in WHI data set: accommodating general covariates

Measure	Post-imputation filtering	#SNPs	DIST*	ImpG-Summary*	ImpG-SummaryLD*	DISSCO
D	None	150 934	0.422 (5.7%)	0.412 (3.4%)	0.416 (4.3%)	0.398
%D	None	150 934	56.8 (9.2%)	55.1 (6.4%)	56.8 (9.2%)	51.6
R2	None	150 934	0.694 (3.0%)	0.699 (2.3%)	0.703 (1.7%)	0.715
D	>0.6	140 128	0.392 (5.1%)	0.380 (2.1%)	0.384 (3.1%)	0.372
%D	>0.6	140 128	53.4 (8.6%)	51.2 (4.7%)	52.9 (7.8%)	48.8
R2	>0.6	140 128	0.738 (2.6%)	0.749 (1.1%)	0.752 (0.7%)	0.757

Best performing methods are highlighted as bold. The estimated accuracy of the association summary statistics is compared across different methods using three metrics: D, %D and R². Smaller D, smaller %D and larger R² are better. The values in parentheses are the relative improvement of DISSCO over DIST*/ImpG-Summary*/ImpG-SummaryLD*.

4.2 Real data set 2: CLHNS study

To evaluate the performance in a relatively homogeneous study sample, we applied all methods to another dataset, the Cebu Longitudinal Health and Nutrition Survey (CLHNS) study (Adair et al., 2011). The study genotyped 1800 Filipino women using the Affymetrix Genomewide Human SNP Array 5.0 GWAS chip (Lange et al., 2010). The 1800 subjects were previously found to be relatively genetically homogeneous and match closely to the East Asians (specifically, CHB [Han Chinese from Beijing] and JPT [Japanese from Tokyo]) in the International HapMap Project (Marvelle et al., 2007).

Our outcome measure was adiponectin levels, an adipocyte-secreted protein involved in a variety of metabolic processes, including glucose regulation and fatty acid catabolism. Several recent studies have examined the genetic association with adiponectin (Croteau-Chonka et al., 2012; Dastani et al., 2012; Wu et al., 2010). We performed association analyses adjusting for age, household assets, natural logarithm transformed income and waist circumference. We again masked 20% of the directly typed markers and excluded markers with MAF < 1%. Our final set contained 265 340 typed markers, which were used for imputation, and 65 992 untyped markers that were imputed using Phase I v3 ASN haplotypes (http://csg.sph.umich.edu/abecasis/MACH/download/1000G.2012-03-14.html) from the 1000 Genomes Project.

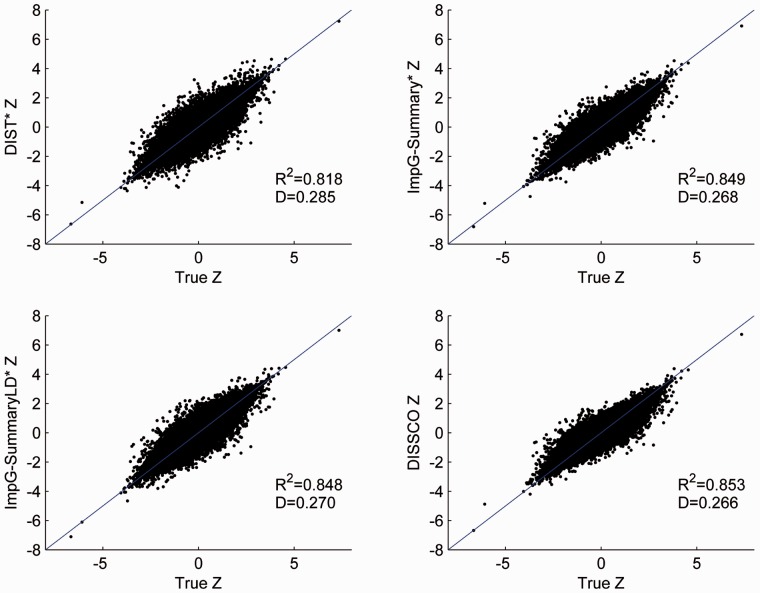
Results summarized in Figure 1 and Table 4 again show advantages of DISSCO over existing methods in the presence of general confounding covariates, both before and after post-imputation quality filtering of markers. Similar to the results for WHI, based on the Wilcoxon sign rank test across the individual marker results, DISSCO significantly outperformed all three competitors (P < 0.001 for all three comparisons).

Fig. 1.

CLHNS dataset: accommodating general covariates. Scatter plots comparing true Z statistics to the corresponding imputed Z statistics from DISSCO and three competing methods for markers passing post imputation quality filtering

Table 4.

Estimation accuracy of association summary statistics in CLHNS dataset: accommodating general covariates

Measure	Post-imputation filtering	#SNPs	DIST*	ImpG-Summary*	ImpG-Summary LD*	DISSCO
D	None	65 992	0.352 (9.4%)	0.333 (4.2%)	0.336 (5.1%)	0.319
%D	None	65 992	47.0 (13.6%)	44.3 (8.4%)	45.5 (10.8%)	40.6
R2	None	65 992	0.716 (8.1%)	0.747 (3.6%)	0.747 (3.6%)	0.774
D	>0.6	58 448	0.284 (6.3%)	0.267 (0.4%)	0.270 (1.5%)	0.266
%D	>0.6	58 448	38.7 (10.1%)	36.1 (3.6%)	37.1 (6.2%)	34.8
R2	>0.6	58 448	0.819 (4.3%)	0.849 (0.6%)	0.848 (0.7%)	0.854

Best performing methods are highlighted as bold. The estimated accuracy of association summary statistics is compared across different methods using three metrics: D, %D and R². Smaller D, smaller %D and larger R² reflect better estimation. The values in parentheses are the relative improvements of DISSCO over DIST*/ImpG-Summary*/ImpG-SummaryLD*.

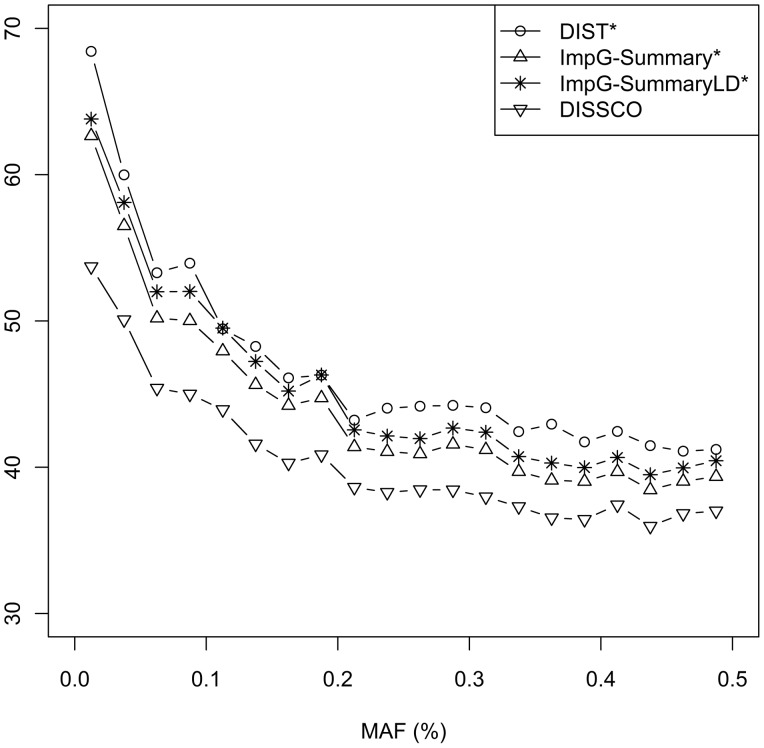
4.3 More pronounced improvement for lower frequency variants

Interestingly, we found that DISSCO had more pronounced summary statistic improvements for lower frequency variants. Figure 2, for example, shows the performance of all methods across the entire MAF spectrum in the CLHNS dataset. Compared with existing methods, DISSCO had an average of 7.5–12.3% lower absolute relative deviation from the true value for markers with MAF < 10% while the improvement reduced to 3.2–8.4% for markers with MAF > 10%. Similar results were obtained for the WHI dataset and presented in Supplementary Materials S6.

Fig. 2.

Performance (measured by absolute relative percentage deviation from truth [Y-axis]) by MAF in CLHNS dataset

5 Discussion

Two recent studies have proposed methods for direct imputation of summary statistics that approach the quality of gold standard genotype-based imputation, at reduced computational costs. These methods are valuable particularly for meta-analysis studies when individual level genotypes are not readily available. Both methods assume summary association statistics follow multivariate Gaussian distributions, with the correlations between the summary statistics being the same as the correlations between the corresponding marker genotypes that are estimated from publicly available reference panels.

In this study, we show analytically that, in the presence of confounders, the correlation matrix among the summary statistics is the partial correlation matrix among the corresponding markers, conditional on the confounders. With this theoretical underpinning, we propose DISSCO for direct imputation of summary statistics accommodating confounding covariates.

We consider two scenarios where covariate adjustment can be helpful, if not necessary: in the study of admixed samples and in the presence of other known risk factors and mediators. The first scenario presents the challenge of estimating the correlation matrix appropriate for admixed samples using cosmopolitan reference panels commonly available in the public domain rather than a single well-matched reference dataset. Our solution of using PCs can be interpreted as sample-adjusted weighting of the reference individuals for the estimation of the correlation structure. Our PC-based solution in this scenario of admixed samples also effectively transforms the issue into the need of controlling for the special covariates: PCs, thus enabling the unified DISSCO framework under both scenarios.

For practical usage, Scenario I entails the estimation of PCs for the reference individuals, which can be achieved either by performing PC analysis on the study and reference samples together, which is commonly conducted in studies involving admixed samples; or when PCA is performed on study samples only, one could choose to project the top PCs in the same manner as general covariates (results presented in Supplementary Material S7).

DISSCO leads to more noticeable gains for lower frequency variants. We believe this is largely due to the smaller number of LD tags (variants in high LD) for lower frequency variants compared with that for more common variants. For example, based on the 1000 Genomes Phase 1 datasets, we found on average 9.8 (7.6, 5.9) LD tags (at LD r2 threshold of 0.8) for low frequency variants (MAF < 5%) and 23.2 (24.4, 8.9) LD tags on average for common variants (MAF > 5%) among individuals with European (Asian, African) ancestry. Since not every marker is affected by confounding covariates when estimating partial correlations, with more LD tags, a common variant is less susceptible to the inaccurate estimation of partial correlation for a subset of its LD tags than is a low frequency variant. In Supplementary Material S8, we use simulations to illustrate that the performance of methods based on either the partial or marginal correlation increases with the number of LD tags and, more importantly, that additional information from covariates leads to relatively more gains when the number of LD tags is smaller.

Computationally, following ImpG-Summary/LD, DISSCO also divides each chromosome into non-overlapping blocks with predetermined length (1 MB by default). Assume there are $p=p_{\text{t}}+p_{\text{ut}}$ markers, including $p_{\text{t}}$ typed and $p_{\text{ut}}$ untyped markers, $N_{\text{study}}$ individuals in the study sample, $N_{\text{refer}}$ individuals in reference sample, and S covariates. After obtaining $Z_{\text{t}}$, Z statistics at typed markers, imputation of summary statistics involves some of the following steps (i) calculation of the reference correlation matrix ${\widehat{\text{Σ}}}^{\mathit{unadj}}$, (ii) calculation of the sample correlation matrix between typed markers, (iii) generation of reference sample pseudo-covariates, (iv) calculation of reference sample partial correlations and (v) actual imputation via the following formula:

$$Z_{\text{i}}^{.}={\widehat{\Sigma }}_{\mathit{\text{i,t}}}^{\mathit{\text{.,refer}}}{\left({\widehat{\Sigma }}_{\mathit{\text{t,t}}}^{\mathit{\text{.,refer}}}\right)}^{-1}{Z}_{\text{t}},$$

where the subscript “.” differs across methods as detailed in Section 2, and (vi) the normalization of imputed values. All methods need step (v). DIST also needs (i); ImpG-Summary also needs (i) and (vi); ImpG-SummaryLD also needs (i), (ii) and (iv); and DISSCO also needs (i), (iii) and (iv). Computational complexity of (i)–(vi) is O($N_{\text{refer}}{p}^2$), O($N_{\text{study}}{p}_t^2$), O($p_t^3+N_{\text{study}}{p}_t^2$), O($N_{\text{refer}}Sp$), O($p_{\text{ut}}{p}_t^3$) and O($p_{\text{ut}}{p}_t^2$), respectively (detailed in Supplementary Material S9). We report in Table 5 the computing time for each of the steps in the real data sets on a 2.53 GHz Intel(R) Xeon(R) processor. Real-time using actual software implementation is also reported. The DIST software takes the longest mainly for two reasons: (i) it re-calculates the reference correlation matrix within a window of ±50 markers for every untyped marker; and (ii) it uses numerical integration to calculate P-values from Z-scores. In contrast, ImpGSummary has an efficient implementation, at the cost heavy I/O burden: thousands of small intermediate files written to and read from hard disk. Memory consumption was comparable across the different software, with 1–2 GB maximum RAM for all the real data experiments.

Table 5.

Computing time in each step for different imputation methods in three real data analysis (time in seconds)

Scenario	Step	DIST*	ImpG-Summary*	ImpG-SummaryLD*	DISSCO
WHI PCs	1	668	668	668	668
	2	—	—	437	—
	3	—	—	—	922
	4	—	—	—	507
	5	4078	4078	4078	4078
	6	—	4244	6048	—
	1–6	4746	8990	11231	6175
	Software	11477	3531	NA	6175
WHI GCs	1	660	660	660	660
	2	—	—	408	—
	3	—	—	—	1043
	4	—	—	—	593
	5	4056	4056	4056	4056
	6	—	4172	5806	—
	1–6	4716	8888	10930	6352
	Software	10797	3536	NA	6352
CLHNS	1	125	125	125	125
	2	—	—	86	—
	3	—	—	—	90
	4	—	—	—	125
	5	497	497	497	497
	6	—	502	605	—
	1–6	622	1124	1313	837
	Software	2443	473	NA	837

“—”: step not required for the corresponding method. “Software” row reports the actual time by directly using DIST (v0.1.4), ImpG-Summary (v1.0) and DISSCO (v1.0) software implementation. “NA” in the ImpG-SummaryLD column is because it does not allow missing values in the sample genotypes.

There are multiple other factors that affect performance. Among them, the important ones are (i) window size, (ii) regularization and (iii) normalization. Specifically, a larger window size tends to improve performance by providing more information. However, a larger window size also means increased computational cost. Including a larger number of typed markers does not guarantee better results because the larger number of markers is more likely to make the correlation matrix singular. As noted by the ImpG-Summary/LD development team, regularization alleviates this issue by adjusting for statistical noise in the estimation of the covariance matrix in the reference sample. Following their work, DISSCO also uses 1 MB as default window size with regularization. The normalization procedure in ImpG-Summary/LD improves performance in small samples. Since our focus in this article is on the improvement of using partial-correlations instead of marginal correlations, we compare our method to existing methods using the default parameter values.

We have primarily focused our performance comparisons between DISSCO and existing methods by comparing accuracies of summary Z statistics to their true values. Since DISSCO directly imputes association statistics, it is also critical to establish its validity. Following Pasaniuc et al. (2014), we generated real-data-based null datasets and found that DISSCO maintains the desired type-I error rate across a range of nominal values (10-1–10-5) with our default level of regularization (λ = 0.03) (Supplementary Materials S10 and Tables S5A–D).

Unlike imputation for individual genotypes, the selection of a reference panel matching the study sample is much more crucial for the accurate imputation of association summary statistics because the correlation structure from the reference sample as a whole instead of individual haplotypes are used in the calculations. Although, when the reference and study samples are similar, these methods for direct imputation of association statistics tend to work well (Han et al., 2011), prudency is warranted as discussed in Pasaniuc et al. (2014). As an illustration, our simulation studies using a mismatched reference panel (the EUR haplotypes from the 1000 Genomes Project for the CLHNS dataset) resulted in inflated type-I error rates when using our default level of regularization (Supplementary Table S5E).

Finally, a key step in DISSCO is the projection of covariates into the reference based on genotypes of typed markers. As top PCs capture a large amount the variation in these genotypes, it is conceptually natural to anticipate that projection based on the top PCs (thus completely bypassing the need of individual level genotypes) might achieve similar performance gains. We indeed have observed comparable performance gains using the top PCs (Table 2) as compared with using general covariates (Table 3) in the admixed dataset. Additional analysis in the CLHNS dataset using only the top five PCs also showed near identical results as in Table 4 (identical up to the third digit after the decimal point using all three measures, i.e. D, %D and R²). Although a certain degree of information loss is possible due to discarding information not captured by the top PCs, we recommend using the top PCs as a convenient substitute for actual covariate projection when individual level genotypes are not available.

In summary, we provide analytical justifications for two methods recently proposed for the imputation of association summary statistics in the absence of confounding covariates. We further extend the analytical work in the presence of confounders and propose a method accordingly to accommodate confounding covariates. Our proof-of-concept simulations and applications to two real datasets demonstrate the value of our method, DISSCO, particularly for low-frequency variants. Our method is implemented in JAVA and freely available online http://www.unc.edu/∼yunmli/DISSCO/.

Funding

This work was supported by the National Institutes of Health [grant numbers R01-HG006292, R01-HG006703 and R01-DA030976 to Y.L., R01-HG004517 and R01-HG005854 to M.L. and R01-HG007458 to W.C.

Conflict of Interest: none declared.