Power and sample-size estimation for microbiome studies using pairwise distances and PERMANOVA

Abstract

Motivation: The variation in community composition between microbiome samples, termed beta diversity, can be measured by pairwise distance based on either presence–absence or quantitative species abundance data. PERMANOVA, a permutation-based extension of multivariate analysis of variance to a matrix of pairwise distances, partitions within-group and between-group distances to permit assessment of the effect of an exposure or intervention (grouping factor) upon the sampled microbiome. Within-group distance and exposure/intervention effect size must be accurately modeled to estimate statistical power for a microbiome study that will be analyzed with pairwise distances and PERMANOVA.

Results: We present a framework for PERMANOVA power estimation tailored to marker-gene microbiome studies that will be analyzed by pairwise distances, which includes: (i) a novel method for distance matrix simulation that permits modeling of within-group pairwise distances according to pre-specified population parameters; (ii) a method to incorporate effects of different sizes within the simulated distance matrix; (iii) a simulation-based method for estimating PERMANOVA power from simulated distance matrices; and (iv) an R statistical software package that implements the above. Matrices of pairwise distances can be efficiently simulated to satisfy the triangle inequality and incorporate group-level effects, which are quantified by the adjusted coefficient of determination, omega-squared (${\omega }^2$). From simulated distance matrices, available PERMANOVA power or necessary sample size can be estimated for a planned microbiome study.

Availability and implementation: http://github.com/brendankelly/micropower.

Contact: brendank@mail.med.upenn.edu or hongzhe@upenn.edu

1 Introduction

Microbiome studies often compare groups of microbial communities with different environmental exposures, or to which different interventions have been applied. For example, a study may evaluate the difference between the respiratory tract microbial communities of human subjects with exposure to different antibiotic treatments. The fundamental measure in such a study is the count of community members (species or operational taxonomic units—OTUs), typically accomplished via sequencing a marker gene such as the 16S ribosomal RNA gene for bacteria. Pairwise distance metrics facilitate standardized comparison of community membership between individual study subjects by addressing the problems of differential membership and mutual absence. To assess differences between groups of subjects (i.e. the explanatory power of a grouping factor, such as antibiotic exposure), pairwise subject-to-subject distances must be arrayed in a square distance matrix. Group-level differences can then be analyzed by ordination methods such as principal coordinates analysis or by a significance test such as PERMANOVA (Anderson, 2001; Legendre and Legendre, 2013; McArdle and Anderson, 2001).

The design of microbiome studies demands consideration of statistical power—an adequate number of subjects must be recruited to ensure that the effect expected from the exposure or intervention of interest can be detected. Here, we focus on the power of 16S tag sequencing studies that are analyzed using pairwise distances (specifically, UniFrac and Jaccard distances) and PERMANOVA. UniFrac is a distance metric based upon the unique fraction of branch length in a phylogenetic tree built from two sets of taxa. Comparison of microbiome samples can be performed via unweighted UniFrac, which considers strictly the presence or absence of taxa, or weighted UniFrac, which also considers relative abundance (Lozupone and Knight, 2005; Lozupone et al., 2007, 2010). Jaccard distance, a non-phylogenetic measure of difference between two sample sets, is calculated as one minus the ratio of the intersection to the union; it can also be calculated in unweighted (‘binary’) or abundance-weighted fashion (Chao et al., 2005; Levandowsky and Winter, 1971).

The power of PERMANOVA, like the power of traditional analysis of variance, depends on the number of exposure or intervention groups (degrees of freedom), the number of subjects per group (residual degrees of freedom), the within-group distances (within-group sum of squares) and the size of the effect (the difference between the between-group sum of squares and within-group sum of squares). Type II error increases and statistical power decreases with more groups, fewer subjects, greater within-group distance and lesser effects (Zar, 1999). However, the pseudo-F ratio is not distributed like Fisher’s F-ratio under the null hypothesis, so standard methods of power estimation for parametric ANOVA do not apply to the studies analyzed by PERMANOVA (Anderson, 2001). Furthermore, the relationship between microbiome community structure and within-group distances is often obscure, and the effect size to be expected from anticipated exposures or planned interventions upon the microbiome is often uncertain.

Here, we present a framework for PERMANOVA power and sample size estimation tailored to marker-gene microbiome studies that will be analyzed with pairwise distances. We first describe a novel method for distance matrix simulation that permits modeling within-group pairwise distances according to pre-specified population parameters. We then demonstrate how to incorporate effects of different sizes within the simulated distance matrix. Building on the capacity to accurately model within- and between-group distances, we present a simulation-based method for estimating PERMANOVA power. Finally, we outline an R statistical software package (The R Foundation for Statistical Computing, www.r-project.org—R Core Team, 2014) that implements the above, and provide examples of its use.

2 Methods

2.1 PERMANOVA and effect size

In many microbiome studies, one is interested in testing the null hypothesis that there is no difference in overall microbiome compositions of p bacterial taxa among the a exposure groups. Consider the simple case that we have a exposure or intervention groups and n observations in each group with a total of N = na observations. The microbiome composition between two subjects i and j determines their distance d_ij. We focus on UniFrac and Jaccard distances because they are widely used and conveniently implemented in bioinformatic analysis packages (Caporaso et al., 2010; Schloss et al., 2009). Distance-based multivariate analysis of variance therefore provides a non-parametric test of the null hypothesis of no differences in overall bacterial compositions among the a exposure groups.

PERMANOVA is a non-parametric method of multivariate analysis of variance based on pairwise distances (Anderson, 2001). It extends traditional analysis of variance to a square matrix of pairwise distances with significance testing performed by permutation. Let d_ij be the distance of microbiome between observation i and j, and ϵ_ij takes the value 1 if observation i and j are in the same group and 0 otherwise. For pairwise distances, the within-group sum of squares (SS_W) is defined as the sum of the squares of distances within groups divided by the number of subjects per group,

$${\text{SS}}_{\text{W}}=\frac{1}{n}{\displaystyle \sum _{i=1}^{N-1}{\displaystyle \sum _{j=i+1}^N{d}_{ij}^2}}{ϵ}_{ij},$$

and the total sum of squares SS_T is defined as

$${\text{SS}}_{\text{T}}=\frac{1}{N}{\displaystyle \sum _{i=1}^{N-1}{\displaystyle \sum _{j=i+1}^N{d}_{ij}^2}}.$$

The between-group sum of squares (SS_A) is defined as the difference between the total sum of squares SS_T and SS_W, ${\text{SS}}_{\text{A}}{\text{\hspace{0.17em}=\hspace{0.17em}SS}}_{\text{T}}-{\text{SS}}_{\text{W}}$. The PERMANOVA test statistic, termed the pseudo F-ratio, is analogous to Fisher’s F-ratio; it is based upon the ratio of the sum of the squared between-group distances to the sum of the squared within-group distances

$$F=\frac{{\text{SS}}_{\text{A}}/(a-1)}{{\text{SS}}_{\text{W}}/(N-a)},$$

where $a-1$ are the degrees of freedom defined by the grouping factor and N − a are the residual degrees of freedom. The significance of the pseudo F-ratio can be assessed by permutations.

As with the conventional ANOVA, the effect size of the pseudo F-ratio can be quantified as the coefficient of determination (R²), which is one minus the ratio of the within-group sum of squares to the total sum of squares. This is equivalent to the ratio of the between-group sum of squares to the total sum of squares,

$$R^2=1-\frac{{\text{SS}}_{\text{W}}}{{\text{SS}}_{\text{W}}+{\text{SS}}_{\text{A}}}=\frac{{\text{SS}}_{\text{A}}}{{\text{SS}}_{\text{T}}}.$$

However, the R², which is the proportion of distance accounted for by the grouping factor, is biased because it depends solely on the sums of squares of the sample, without adjustment to estimate the effect size in the general population. Omega-squared (${\omega }^2$) provides a less biased measure of effect size for ANOVA-type analyses by accounting for the mean-squared error (Olejnik and Algina, 2004; Ziegler and Bühner, 2009) of the observed samples,

$${\omega }^2=\frac{{\text{SS}}_{\text{A}}-(a-1)\frac{{\text{SS}}_{\text{W}}}{N-a}}{{\text{SS}}_{\text{T}}+\frac{{\text{SS}}_{\text{W}}}{N-a}}.$$

The power of PERMANOVA depends on the sample sizes, the alternative hypothesis that can be specified by different population-level microbial compositions among a groups, and their variances. These parameters determine the pairwise distances and their variances, the between-group sum of squares SS_A and the total sum of squares SS_T. In planning microbiome studies, the key to sample size/power calculation is to specify these key quantities. We present in the following sections a novel way of generating the pairwise distances that can be used to calculate the within- and between-group sums of squares and the effect size ${\omega }^2$. This provides a valid method for simulation-based sample-size/power calculations.

2.2 Simulating within-group pairwise distances by random subsampling from OTU counts

Many different distributions of community members may yield the same distance between two microbiome samples. PERMANOVA testing operates on distances, not species or OTU counts. Therefore, multiple different species distributions may serve to model microbiome community structure for the purposes of PERMANOVA testing so long as the species distributions accurately recapitulate the distribution of distances. We developed a technique to simulate a pre-specified distribution of pairwise distances based upon random subsampling from a simple, uniform OTU vector.

We began with a uniform vector of species or OTU counts, representing the microbial community of a single subject. For example, we generated a vector of 1000 OTUs with a single sequence count in each OTU bin. We then sampled the OTU vector, randomly selecting a proportion of the sequences to retain (Hughes and Hellmann, 2005). We found that random subsampling from two subject vectors at the same level (i.e. with the same proportion of sequence counts retained) generated a predictable pairwise distance. Though the subsampling procedure operates randomly and independently on each subject vector, its effect upon pair-wise distance is consistent: the fewer sequences retained, the greater the distance between subjects.

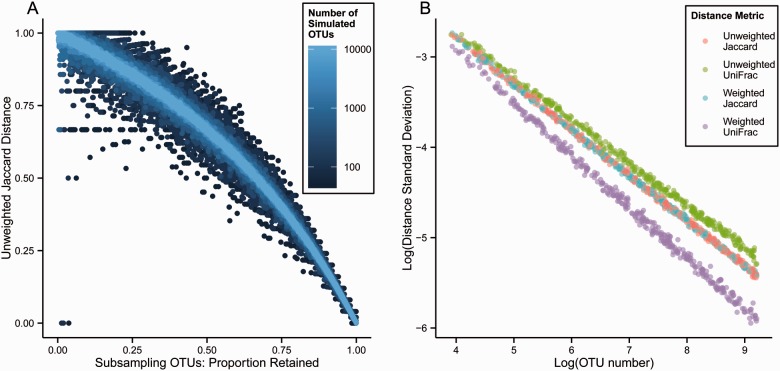
Figure 1 depicts the relationship between subsampling and pairwise distance for four distance metrics. Each point represents a subject pair, and each panel depicts 10 000 pairs. Pairs are identical subject vectors that were subsampled to randomly generated levels; each subject in a pair was assigned the same proportion of sequences to be retained, but the retained sequences were randomly chosen for individual subjects and differed between subjects in a pair. We observed that, for unweighted and weighted Jaccard and UniFrac metrics, the distances between subjects varied according to the proportion of sequences retained. Where all sequences were retained the distance was 0, and as fewer sequences were retained, the distance approached 1. (Weighted UniFrac is presented in normalized form for this and all subsequent analyses.) The pattern of this increase varied among distance metrics. For weighted metrics, it also varied according to the number of sequences included in each OTU bin prior to subsampling (data not shown). Nevertheless, random subsampling applied to uniform OTU vectors served to generate a set of pairwise distances matching any pre-specified mean distance; this was accomplished by choosing the proportion of retained OTUs from a distance–metric-specific hash table with the form of Figure 1. Because all distances were calculated from OTU count data, the simulated pairwise distances satisfied the triangle inequality. Thus, we were able to simulate a distance matrix with pre-specified mean distance and any number of subjects for use in the estimation of PERMANOVA power. For unweighted Jaccard, expected distance can be calculated directly from the proportion of OTUs retained; as shown in Figure 1, the calculated distances confirm our simulation-based method.

Fig. 1.

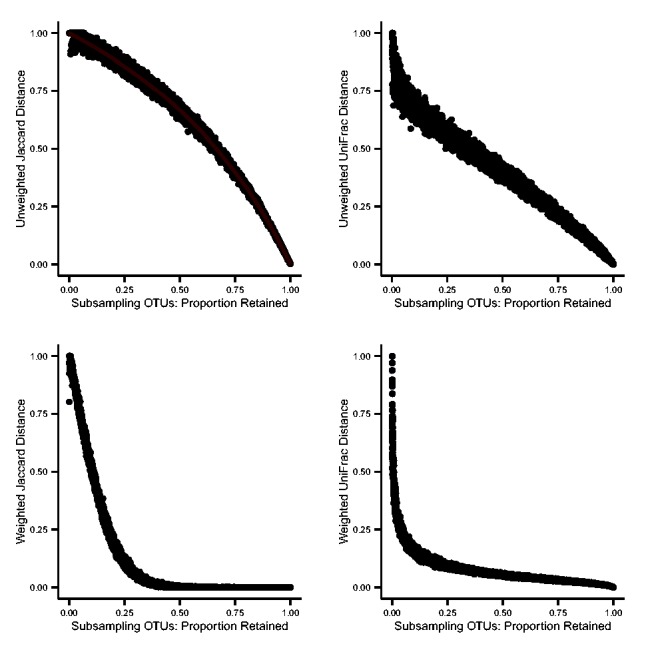
Random subsampling from OTUs permits simulation of specified pairwise distances. Each point represents a pair of uniform OTU vectors randomly subsampled without replacement to the same proportion of retained OTUs. The relationship between the proportion of OTUs retained in subsampling and the distance between the members of the pair is shown for four different distance metrics: as the proportion retained increases, the distance decreases from 1 to 0. For unweighted distances, subsampling was applied to uniform OTU vectors with a single sequence read per OTU bin; for weighted distances, subsampling was applied to uniform OTU vectors with 10 sequence reads per OTU bin. For unweighted Jaccard distances, a line is also shown to indicate direct computation of expected distance from the proportion of OTUs retained

2.3 Simulating within-group distance variance by specifying the number of OTUs in the simulated vector

Just as the mean pairwise distance of a group of simulated subjects can be specified by random subsampling from the sequence counts in OTU bins, we found that the variance of the pairwise distances can be specified by the number of simulated OTU bins. Repeated random subsamples from a uniform OTU vector with 5000 OTUs produced a distribution of distances with less variance than repeated random subsamples from a uniform OTU vector with 500 OTUs, which in turn produced a distribution of distances with less variance than subsampling a uniform vector of 50 OTUs. Figure 2A depicts the same analysis of unweighted Jaccard distance generated between subject pairs subsampled to a proportion of retained OTUs as was depicted in Figure 1, but with subject pairs generated to include different numbers of OTUs per subject. As the number of OTUs per sample increased, the variance of unweighted Jaccard distances decreased. The same relationship was observed for weighted Jaccard distances, unweighted and weighted UniFrac distances.

Fig. 2.

The number of OTUs subsampled determines the variance of simulated distances. The variance of simulated distances depends upon the number of simulated OTUs in the vector to which the random subsampling procedure is applied. (A) depicts the relationship between the proportion of OTUs retained and the resulting unweighted Jaccard distance. As in Figure 1, each point represents a pair of OTU vectors randomly sampled without replacement to the same level. The color of points indicates the number of OTUs in the vector. (B) quantifies the relationship between number of OTUs in the subsampled vector and the standard deviation of the resulting distances. The relationship between OTU number and distance standard deviation is linear on a log–log plot, though the relationship differs for the four distance metrics depicted. All data shown are from subsampling at 50%

We found that the relationship between the number of OTUs in the subsampled OTU vector and the standard deviation of the pairwise distances that result from subsampling is linear on a log–log plot. Figure 2B depicts this relationship for unweighted and weighted Jaccard and UniFrac distances. The pairwise distances depicted were simulated by subsampling to retain 50% of the simulated OTUs. The relationship between the number of OTUs and standard deviation of pairwise distances was found to also depend upon the extent of subsampling (Fig. 2A). Therefore, accurate modeling of a pre-specified distance standard deviation can be accomplished by choosing the number of OTUs after the proportion of OTUs to be retained in subsampling was decided (based upon the pre-specified mean distance parameter). This strategy allows specification of pairwise distance variance as well as mean in a simulated square distance matrix.

2.4 Group differences incorporated into simulated distance matrices by segregating OTU membership

We next sought to incorporate group differences into simulated distance matrices, a necessary step to allow specification of effect size in power analysis. Having modeled within-group distances by subsampling OTUs and the variance of within-group distances by specifying the number of OTUs to be subsampled, we found that groups of simulated subjects could be distinguished by segregating community membership between groups. For example, for a simulated study of three exposure groups, with 10 subjects per group, we specified the within-group distance distribution across all groups by specifying the number of OTUs in the simulated community and the proportion of OTUs to be retained per sample in subsampling. We then selected at random a single group of subjects as the affected group. For this group of subjects alone, we renamed a proportion of OTUs. By renaming the OTUs only in a single group we preserved the modeled distribution of within-group distances across all groups, but with greater between-group distances (i.e. with an effect of the exposure). The effect size was determined by the proportion of unique OTUs in the affected group, relative to the unaffected groups.

In this way, a range of effect sizes could be generated: where the affected group included no unique OTUs, the between-group distances matched the within-group distances, and the effect was near 0; where the affected group included entirely unique OTUs (i.e. community membership was completely segregated between affected and unaffected groups), the effect size was large. As we proceeded to quantify these effect sizes, we found that the definition of small and large effects is contingent upon the chosen distance metric and sampling site—i.e. upon the distribution of within-group distances (see Section 2.8).

2.5 Estimation of PERMANOVA power using simulated distance matrices

In order to estimate statistical power for PERMANOVA testing, we first simulated a set of distance matrices. The within-group pairwise–distance distributions were specified to be the same across the entire set of distance matrices, but each simulated distance matrix differed in its simulated effect size (i.e. in the proportion of unique OTUs that distinguish subjects in a randomly selected affected group from subjects in the unaffected groups). The set of simulated distance matrices thus encoded a range of effects, extending from very small effects (no specified difference in group membership, only the stochastic differences in group membership that may result from the subsampling procedure) to very large effects (no common membership between affected and unaffected groups).

We then selected bootstrap samples of subjects from each of the simulated distance matrices. For example, to analyze the PERMANOVA power for a study that includes 10 subjects per exposure group, we randomly selected with replacement 10 subjects from each exposure group in each simulated distance matrix, and we repeated the selection procedure 100 times. The result of each bootstrap selection was a small matrix of pairwise distances—a subset of the larger simulated distance matrix. The 100 bootstrap selections taken from each simulated distance matrix thus served as 100 estimates of the true effects encoded in the larger distance matrices.

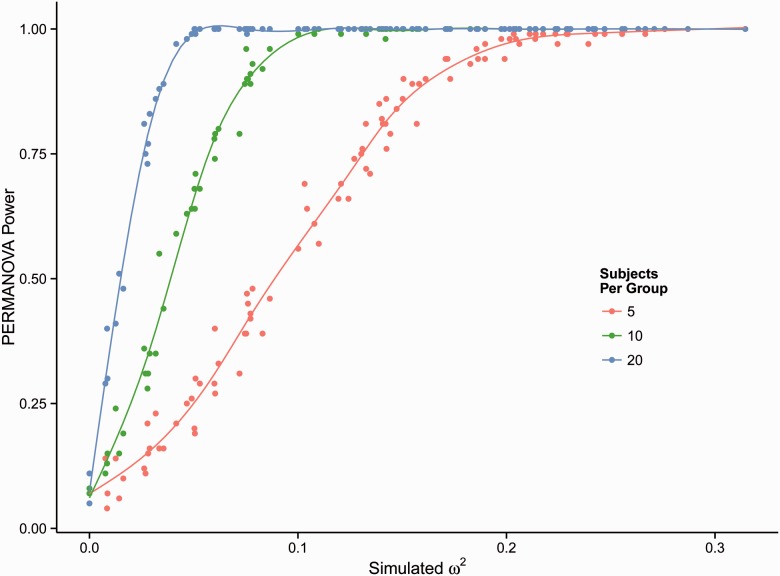
We next performed PERMANOVA testing on each bootstrap distance matrix and compared the PERMANOVA P-value with the pre-specified threshold for type I error (typically, 0.05). For bootstrap distance matrices drawn from distance matrices that incorporate true effects, the proportion of PERMANOVA P-values that exceed the type I error threshold (i.e. which would be deemed not statistically significant despite the true group-level effect) is the type II error. For each simulated effect, PERMANOVA power can be calculated as the proportion of bootstrap distance matrices for which PERMANOVA P-values are less than the pre-specified threshold for type I error. Figure 3 depicts the result of this procedure: along the horizontal axis the ${\omega }^2$ values associated with the simulated distance matrices (true effects) are shown; the vertical axis shows the PERMANOVA power that corresponds with each simulated effect, based upon PERMANOVA testing of bootstrap distance matrices. We performed the bootstrap procedure with five, 10 and 20 subjects per group. As expected, PERMANOVA power increased with the number of subjects per group.

Fig. 3.

Bootstrap sampling of simulated distance matrices allows PERMANOVA power estimation. An example of PERMANOVA power estimation by bootstrap sampling from simulated distance matrices is shown. The horizontal axis depicts the effect sizes simulated by segregating OTU group membership, and the vertical axis represents the power to detect the effect, as determined by the proportion of bootstrap distance matrices drawn from the simulated distance matrix for which PERMANOVA P-values were below the specified type I error threshold. The simulated study includes three exposure groups; the power to detect effects with five, 10 and 20 subjects per group is depicted in red, green and blue, respectively. Power estimated for a null effect (i.e. differences between subjects but not between groups) was equal to PERMANOVA type I error

To confirm the accuracy of our estimation method, the PERMANOVA power observed under the null hypothesis was calculated from a null distance matrix, which was generated by calculating pairwise distances from a set of simulated samples in which all groups of subjects were identical (i.e. without any difference between groups, only differences between subjects within groups). The described bootstrap procedure applied to the null distance matrix produced an estimate of PERMANOVA power equal to the pre-specified threshold for type I error, as should be the case. We thus validated our method of power estimation.

2.6 The micropower package permits convenient estimation of statistical power for microbiome studies

We implemented the strategy described above in a package for R statistical software in order to facilitate planning of microbiome studies that are to be analyzed by pairwise distances and PERMANOVA. The package is freely available under a GPLv2 license and is available online via Github (http://github.com/brendankelly/micropower). The package can be installed with the R commands:

library(devtools)

install_github(repo=“micropower”,username=“brendankelly”)

2.7 Human Microbiome Project datasets provide parameters for within-group distances

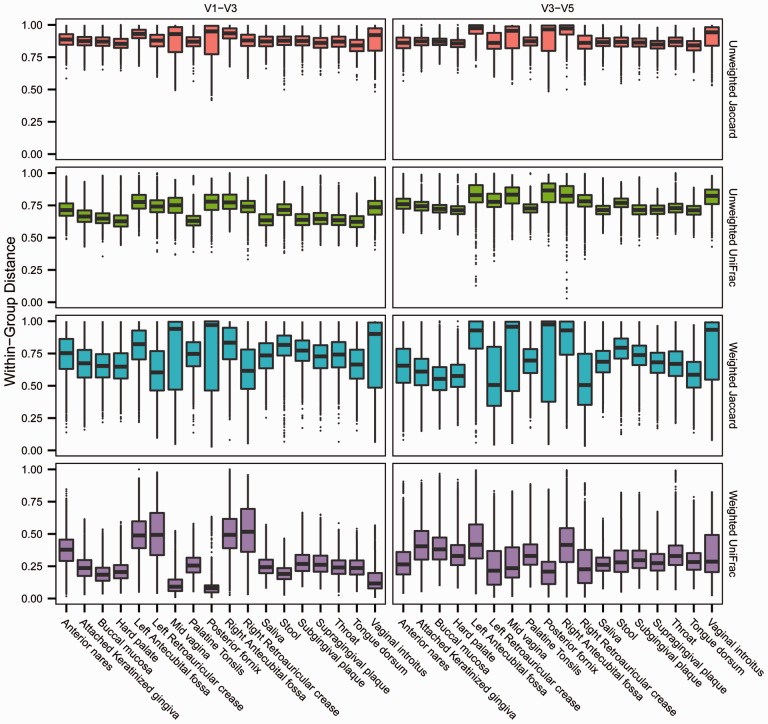
Having established techniques to simulate pairwise–distance matrices with pre-specified distance mean and standard deviation, we sought to define the range of these parameters observed in biological data. The Human Microbiome Project (HMP) dataset provides extensive 16S rRNA marker gene data from the human microbiome sampled at multiple body sites. As such, it is a resource from which population parameters (i.e. mean pairwise distance and distance standard deviation) can be drawn to specify simulated distance matrices. We analyzed the distributions of unweighted and weighted Jaccard and UniFrac distances calculated from 16S rRNA marker gene samples from 18 human body sites, which provide parameters for modeling the expected within-group distance distribution (HMP Consortium, 2012a, b). The within sampling-site distance distributions observed in the HMP datasets (July 2010 16S data freeze; NCBI SRA projects SRP002395 and SRP002012; http://hmpdacc.org/HMQCP/), which comprise 2910 samples from which V1–V3 16S rRNA amplicon sequencing was performed and 4788 samples from which V3–V5 amplicon sequencing was performed, are depicted in Figure 4.

Fig. 4.

HMP data provide parameters for modeling the distribution of within-group distances. The distribution of within-sampling-site distances is shown for 18 different human microbiome sampling sites. Four different distance metrics are depicted as applied to data from two different 16S rRNA amplicons (V1–V3 and V3–V5). The colored boxes delineate the interquartile range (IQR), and the whiskers extend to 1.5 × IQR. Outliers are depicted as points. The HMP data provide parameters according to which the within-group distance distribution can be modeled to estimate power for planned microbiome studies

2.8 Effect sizes based on published microbiome datasets

We cataloged the effect size in several published microbiome studies, representing a variety of sampling sites, exposures and interventions (Charlson et al., 2010, 2012; Peterfreund et al., 2012; Wu et al., 2011). Table 1 depicts the results of this analysis, with observed ${\omega }^2$ values calculated from unweighted and weighted Jaccard and UniFrac distances. We restricted our analysis to comparisons within distance metrics because the choice of distance metric is a decision to be determined by a priori hypotheses regarding the most important features of community membership.

Table 1.

Effect sizes observed from various exposures/interventions in studies of various microbiome sampling sites are shown as measured by omega-squared (${\omega }^2$) statistics, together with the P-values from PERMANOVA test

Site	Comparison groups		${\omega }^2$/P-value
	Control	Exposure	Weighted	Unweighted	Weighted	Unweighted	Reference
			UniFrac	UniFrac	Jaccard	Jaccard
Nares	Non-smoker (33)	Smoker (29)	0.042/0.001	0.009/0.001	0.023/0.001	0.007/0.001	Charlson et al. (2010)
Oral	Non-smoker (33)	Smoker (29)	0.032/0.001	0.008/0.001	0.024/0.001	0.007/0.001	Charlson et al. (2010)
Gut	Before feeding (10)	After feeding (10)	0.056/0.138	0.013/0.986	0/0.989	0.014/0.985	Wu et al. (2011)
Oral	No azithromycin (42)	Azithromycin (6)	0.063/0.01	0.039/0.001	0.099/0.004	0.032/0.001	Charlson et al. (2012)
Lung	No azithromycin (34)	Azithromycin (6)	0.065/0.005	0.038/0.001	0.019/0.089	0.033/0.001	Charlson et al. (2012)
Skin	Left retroauricular (186)	Right retroauricular (187)	0.000/0.828	0.0001/0.327	0.000/0.986	0.000/1.000	HMP Consortium (2012b)
Human	Anterior nares (161)	Stool (187)	0.567/0.001	0.201/0.001	0.230/0.001	0.117/0.001	HMP Consortium (2012b)

The range of observed effect sizes differs according to the metric of pairwise distance chosen for analysis. HMP data are shown to demonstrate a large effect (the degree of difference between two different human microbiome sampling sites) and a negligible effect (the degree of difference between skin sampling in the left versus right retroauricular crease)

Comparison of ${\omega }^2$ values across different studies demonstrated the range of effect sizes observed. For weighted UniFrac, ${\omega }^2$ values ranged from 0 to 0.646; for unweighted UniFrac, from 0.0001 to 0.201. For weighted Jaccard, ${\omega }^2$ values ranged from 0 to 0.230; for unweighted Jaccard, from 0 to 0.117. (By convention, negative ${\omega }^2$ values are treated as 0.) The scale of effects was different for the different distance metrics, but the rank order of effect sizes observed for different interventions was largely consistent.

The HMP data described above provided a helpful comparator, by which we judged large and small effects. The large effect observed with clindamycin treatment exceeded even the effect of human anatomy—i.e. the difference observed between two distinct sampling sites (grouping samples from anterior nares versus stool yields ${\omega }^2$ of 0.567 using weighted UniFrac distance). And, though the observed effects of smoking upon the microbial communities of the human nares and oral cavity were small (${\omega }^2$ from 0.007 to 0.042), they did exceed the presumably stochastic effect observed between left and right retroauricular crease skin microbiome samples (${\omega }^2$ from 0 to 0.0001).

3 Application and results

Here, we provide two examples of applications of the micropower package in order to demonstrate its use.

3.1 Example 1: power calculation based on unweighted Jaccard distances

For the first example, we estimated statistical power for a study of the impact of antibiotic exposure upon the human stool microbiome. The study includes three antibiotic exposure groups, with a primary outcome of community structure difference between groups to be analyzed by unweighted Jaccard distances and PERMANOVA. Given the study plan, we began by simulating a set of matrices of pairwise distances for which within-group distances match the distribution of distances observed in the HMP stool sample set analyzed by unweighted Jaccard distance (see Fig. 4). In order to determine the level of subsampling and number of OTUs necessary to model the expected within-group distances, we applied the hashMean and hashSD commands: simulating 100 OTUs and subsampling to retain 23% of OTUs generated the desired mean within-group distance of 0.87 and within-group distance standard deviation of 0.05. A set of OTU tables, incorporating a range of between-group effects in addition the desired within-group-distance distribution, was then generated using the simPower command. For unweighted Jaccard distances, the calcUJstudy function was applied to simPower output to compute pairwise distances from simulated OTU tables within R. Having calculated pairwise distances for each simulated OTU table, we proceeded with power analysis using the bootPower command, which produced a data frame that relates power to simulated ${\omega }^2$. We applied the bootPower command three times, to assess PERMANOVA power with either five, 10 or 20 subjects per group. We found that five subjects per group allows 90% power to detect a ${\omega }^2$ of 0.05; 10 subjects per group allows 90% power to detect an ${\omega }^2$ of 0.02; and 20 subjects per group allows 90% power to detect an ${\omega }^2$ of 0.008. The effect detectable with the targeted statistical power, typically 90%, was estimated by LOESS regression of the power and simulated ${\omega }^2$ variables from the bootPower dataframe. From Table 1, an ${\omega }^2$ of 0.02 is smaller than the effects observed in studies of antibiotic exposure that were analyzed by unweighted Jaccard distances; therefore, a sample size of 10 subjects per group (30 total subjects) likely affords adequate statistical power for the primary outcome measure.

3.2 Example 2: power calculation based on weighted UniFrac distances

As a second example, we analyzed the same study—but with the primary outcome to be measured by weighted UniFrac distances rather than unweighted Jaccard distances. To do so we used the same commands to perform our power analysis, but we specified a sequence depth >1. Because the micropower package only includes tools to compute Jaccard distances, we then exported the simulated OTU tables for pairwise distance computation by applying the writeOTUlist function directly to the output of simPower. This produced tab-delimited OTU table files that are compatible with bioinformatics analysis pipelines capable of computing many pairwise distance metrics (Caporaso et al., 2010; McMurdie and Holmes, 2013; Schloss et al., 2009). To compute UniFrac distances also requires a phylogeny. We used the simTreeList command to produce a phylogeny to match the OTU tables produced by simPower; the ape package, which loads with micropower, includes a write.tree command to export this simulated phylogeny in Newick tree format (Paradis, 2012). The matrices of pairwise distances produced from the OTU tables and phylogenetic tree can be read with the readDMdir command, and bootPower can be applied to the resulting list. In the case of analysis by weighted UniFrac distances, the mean within-group distance was simulated as 0.2, and the standard deviation of within-group distances as 0.07 (see Fig. 4). We found that five subjects per group afford 90% power to detect an ${\omega }^2$ of 0.17, 10 subjects per group an ${\omega }^2$ of 0.08, and 20 subjects per group an ${\omega }^2$ of 0.04. From Table 1, an ${\omega }^2$ of 0.04 is smaller than the effect observed in a studies of antibiotic exposure that were analyzed by weighted UniFrac distances; therefore, a sample size of 20 subjects per group (60 total subjects) likely affords adequate statistical power for the primary outcome measure if weighted UniFrac distances are used.

4 Discussion

The accurate estimation of statistical power for planned microbiome studies demands a detailed accounting of the steps involved in data analysis. We focused on the 16S rRNA gene sequencing studies that are analyzed using pairwise distances (specifically, UniFrac and Jaccard distances) and PERMANOVA. To ensure adequate statistical power for such studies, one must quantify the expected within-group variance and the effect to be expected from the planned exposure or intervention. We built a framework for PERMANOVA power estimation that depends upon prior knowledge of these two essential parameters. The planned sampling site and chosen pairwise distance metric influence both within-group variance and range of possible effect sizes (as quantified with ${\omega }^2$). We analyzed datasets from the HMP and other published studies to provide references from which the within-group distance distribution and expected effect can be estimated. These tools, combined with the micropower R package described above, permit power estimation for planned microbiome studies.

Since the UniFrac distances depend on the phylogenetic tree of the OTUs, we reviewed the phylogenetic trees generated from the HMP project’s V1–V3 and V3–V5 16S rRNA gene sequencing data, and we observed that the distribution of phylogenetic tree branch lengths was approximately log-normal. To simulate a phylogenetic tree for a set of simulated OTU tables (the simTreeList function in the ‘micropower’ package), we first extract all OTU names from the simulated OTU tables, set each OTU name as a tip of the tree and finally generate random branch lengths to connect the tips, with the branch lengths specified according a log-normal distribution. The final step of random tree generation makes use of the ape package’s rtree command (Paradis, 2012). We explored other distributions of branch lengths. The distribution of the branch lengths in the simulated phylogenetic tree does impact the distribution of phylogenetic (e.g. UniFrac) distances calculated from the simulated OTU table. For example, simulating branch lengths according to a normal distribution inflates the distance variance. But we found that all distributions of phylogenetic tree branch lengths preserve the observed relationship between level of OTU subsampling and mean distance, as well as the observed relationship between number of OTUs subsampled and distance standard deviation.

La Rosa et al. (2012) recently proposed another method for the detection of significant between-group differences in microbiome data based on parametric testing of overdispersed taxonomic data against the Dirichlet-multinomial (DM) distribution and implemented their method as an R package, HMP. HMP allows the estimation of power or necessary sample size for studies with microbiome outcome measures, based on the framework of hypothesis testing at the level of the OTU vectors themselves. However, the DM distribution must be specified, via parameters representing the degree of overdispersion, the number of taxa and the expected composition of taxonomic frequencies in both groups, in order to detect a significant difference. Under the DM model, the effect size is defined by how far apart the vector of taxa frequencies are from each other. Specifying the taxonomic frequencies is often difficult, especially when many such taxa are considered. In addition, one has to specify the number of reads, which can also be quite variable from sample to sample. The micropower package, in contrast, uses the distribution of pairwise distances to be expected from the chosen distance metric and planned sampling site, and provides data on empirical distributions for comparison (e.g. Fig. 4 and Table 1). By using PERMANOVA, our method is non-parametric; by allowing for the use of different distance metrics, our method allows incorporation of phylogenetic relationships among the taxa in power calculation. We have demonstrated that the choice of distance metric may significantly influence the observed effect, and that the within-group variance depends upon both the chosen distance metric and planned sampling site.

By focusing on 16S rRNA sequencing studies analyzed by pairwise distances and PERMANOVA significance testing, we have limited the application to power estimation for global measures of community structure. In some cases, there are advantages to modeling OTU vectors themselves, rather than analyzing community structure via beta diversity—particularly in cases where categorical community types and transitions between community types may match observed biological phenomena (Ding and Schloss, 2014). Nevertheless, we believe that the presented method will prove useful given the utility of pairwise distances to the analysis of microbiome data and the intuitive appeal of an ANOVA-type test in studies with categorical exposures/interventions and microbiome outcome measures. One limitation of our method and that of La Rosa et al. (2012) is that these methods can only perform power calculation for categorical covariates. For a continuous covariate such as age or body mass index, one can test its association with microbiome composition using kernel-based regression (Chen and Li, 2013), where the kernel matrix can be defined based on the pairwise distances. We can then perform power analysis using simulations or analytical calculation based on score test. Alternatively, for the purpose of power calculation, one can discretize the data into categories and apply our proposed method, which should provide a conservative estimate of power.

Funding

B.J.K. was supported by two National Institutes of Health T32 training grants (T32 AI055435 and T32 HL758627). R.G., R.G.C. and F.D.B. were supported by the Penn Center for AIDS Research (5P30AI045008-15). R.G.C. and F.D.B. were supported by National Institutes of Health (U01 HL098957). J.D.L. was supported by National Institutes of Health (K24-DK078228 and UH3-DK083981). H.L. was supported by National Institutes of Health (GM097505 and CA127334). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.

Conflict of Interest: none declared.