Towards Ubiquitous Blood Pressure Monitoring via Pulse Transit Time: Theory and Practice

Abstract

Ubiquitous blood pressure (BP) monitoring is needed to improve hypertension detection and control and is becoming feasible due to recent technological advances such as in wearable sensing. Pulse transit time (PTT) represents a well-known, potential approach for ubiquitous BP monitoring. The goal of this review is to facilitate the achievement of reliable, ubiquitous BP monitoring via PTT. We explain the conventional BP measurement methods and their limitations; present models to summarize the theory of the PTT-BP relationship; outline the approach while pinpointing the key challenges; overview the previous work towards putting the theory to practice; make suggestions for best practice and future research; and discuss realistic expectations for the approach.

I. Introduction

Ubiquitous blood pressure (BP) monitoring is on the horizon for two reasons. One reason is a profound need. Hypertension is a major cardiovascular risk factor that is treatable, yet high BP detection and control rates are abysmally low, especially in low resource settings [1, 2]. Ubiquitous BP monitoring is expected to improve hypertension detection by providing serial, out-of-clinic measurements [3] in the mass population and could even enhance hypertension control by providing continual feedback to the patient [4]. The second reason is feasibility. There have been many relevant technological advances in the recent past such as in wearable sensing, miniaturization, pervasive computing, and smartphones [5]. Further, there is mounting evidence that pulse transit time (PTT, i.e., the time delay for the pressure wave to travel between two arterial sites) can provide the basis for convenient, cuff-less BP measurement. While major progress on PTT-based BP monitoring has been made, research is still needed to best realize this approach. The objective of this review is to facilitate the achievement of reliable, ubiquitous BP monitoring via PTT. We begin by describing the existing BP measurement methods and their limitations. We then summarize foundational work to explain the theory of the PTT-BP relationship. After discussing the PTT-based approach for BP monitoring and its challenges, we review previous work towards putting the theory to practice while making recommendations for best practice. We conclude by suggesting future research directions.

II. Existing BP Measurement Methods and Their Limitations

Several BP measurement methods are now available. The main methods include catheterization, auscultation, oscillometry, volume clamping, and tonometry.

Catheterization is the gold standard method [6]. This method measures instantaneous BP by placing a strain gauge in fluid contact with blood at any arterial site (e.g., radial artery, aorta). However, the method is invasive.

Auscultation, oscillometry, and volume clamping are noninvasive methods. These methods employ an inflatable cuff.

Auscultation is the standard clinical method [7]. This method measures systolic and diastolic BP by occluding an artery with a cuff and detecting the Korotkoff sounds using a stethoscope and manometer during cuff deflation. The first sound indicates the initiation of turbulent flow and thus systolic BP, while the fifth sound is silent and indicates the renewal of laminar flow and thus diastolic BP.

Oscillometry is the most popular non-invasive, automatic method [8, 9]. This method measures mean, diastolic, and systolic BP by also using a cuff but with a pressure sensor inside it. The measured cuff pressure not only rises and falls with cuff inflation and deflation but also shows tiny oscillations indicating the pulsatile blood volume in the artery. The amplitude of these oscillations varies with the applied cuff pressure, as the arterial elasticity is nonlinear. The BP values are estimated from the varying oscillation amplitudes using the empirical fixed-ratios principle. When evaluated against auscultation using an Association for the Advancement of Medical Instrumentation (AAMI) protocol, some oscillometric devices achieve BP errors within the AAMI limits of 5 mmHg bias and 8 mmHg precision [10]. However, oscillometry is unreliable in subjects with certain conditions such as atrial fibrillation, stiff arteries, and pre-eclampsia [11].

Volume clamping is a non-invasive, automatic method used in research [12, 13]. This method measures instantaneous (finger) BP by using a cuff and a photoplethysmography (PPG) sensor to measure the blood volume (see Section V.A). The blood volume at zero transmural pressure is estimated via oscillometry. The cuff pressure is then continually varied to maintain this blood volume throughout the cardiac cycle via a fast servo-control system. The applied cuff pressure may thus equal BP. Volume clamping devices also achieve BP errors within AAMI limits when evaluated against auscultation and near AAMI limits when evaluated against radial artery catheterization [14].

However, cuff use has several drawbacks. In particular, cuffs are cumbersome and time consuming to use, disruptive during ambulatory monitoring, especially while sleeping, and do not readily extend to low resources settings.

Tonometry is another non-invasive method used in research that, in theory, does not require an inflatable cuff [15, 16]. This method measures instantaneous BP by pressing a manometer-tipped probe on an artery. The probe must flatten or applanate the artery so that its wall tension is perpendicular to the probe. However, manual and automatic applanation have proven difficult. As a result, in practice, the measured waveform has been routinely calibrated with cuff BP whenever a BP change is anticipated [17].

In sum, the existing BP measurement methods are invasive, manual, or require a cuff. So, none are suitable for ubiquitous (i.e., ultra-convenient, unobtrusive, and low cost) monitoring.

III. Theory of the PTT-BP Relationship

PTT is the time delay for the pressure wave to travel between two arterial sites. As shown in Fig. 1a, the pressure wave can be visualized as acute dilation of the arterial wall and typically moves much faster than blood [18]. As shown in Figs. 1a–b, PTT is often inversely related to BP and can be estimated simply from the relative timing between proximal and distal waveforms indicative of the arterial pulse. Hence, PTT could permit non-invasive, automatic, and cuff-less BP monitoring.

Figure 1.

Pulse transit time (PTT) provides a basis for ubiquitous blood pressure (BP) monitoring. (a) PTT is the time delay for the pressure wave to travel between two arterial sites and can be estimated simply from the relative timing between proximal and distal arterial waveforms. (b) PTT is often inversely related to BP.

The PTT-BP relationship has been studied by many investigators over many decades (see, e.g., references within this section). We use models in an attempt to summarize – in a mechanistic way – the large body of experimental work on this relationship. We present both models of arterial wall mechanics and wave propagation in the arteries. The arterial wall models establish the relationship between BP and arterial elasticity. The arterial wave propagation models establish the relationship between arterial elasticity and PTT. Note that these models account for the crucial facets of the physiology rather than all known behaviors. Based on the models, we then draw conclusions on the optimal arterial sites to measure PTT for cuff-less BP monitoring, the fundamental limitation of the approach, and exactly how to measure PTT from the waveforms. Readers who are knowledgeable or uninterested in the detailed physiology may move directly to Section III.C.

A. Arterial Wall Models

The composition of the arterial wall and the function of its components are well understood [19–23]. We briefly outline the most salient information here. The arterial wall is composed of four major components: endothelium, elastin, collagen, and smooth muscle. Endothelium is a single cell layer that provides a smooth wall for blood flow and helps regulate smooth muscle contraction. However, it contributes little to arterial wall mechanics. Elastin is highly extensible (about a magnitude more than rubber) and produces tension as soon as the arterial wall expands. Collagen is much (about 400 times) stiffer than elastin and does not exert tension until the arterial wall is stretched. So, elastin determines arterial elasticity at low BP, whereas collagen significantly contributes to the elasticity at high BP. Smooth muscle produces tension when contracted via physiologic control or medication and can thereby modulate arterial elasticity. It also makes the arterial wall viscous in addition to elastic. Note that inertial effects of the wall may be negligible. The relative contributions of these components differ throughout the arterial tree. Elastin is more abundant in the central arteries (hence the name “elastic” arteries), while smooth muscle is most prevalent in the peripheral arteries (hence the name “muscular” arteries). Further, it is well known that aging alters the composition in the central arteries but not the peripheral arteries [24–26]. A hallmark change with aging is the replacement of elastin with collagen. This change contributes to arteriosclerosis – the process of wall thickening and stiffening as well as lumen dilation. Note that arteriosclerosis can occur independently of atherosclerosis, which is a more well-known disease wherein plaque builds up inside the arteries. We will first discuss elastic properties alone and then consider viscoelastic properties. We will thereafter describe the mechanical properties with aging and disease.

1) Elastic Properties

We employ a Maxwell-type model from the literature [27] to illustrate the elastic properties of the central and peripheral arterial walls. As will be seen, the models for the two walls differ. We hypothesized the differences by assimilating experimental data from a review [19], in vitro animal studies [20, 28, 29], and an in vivo human study [27].

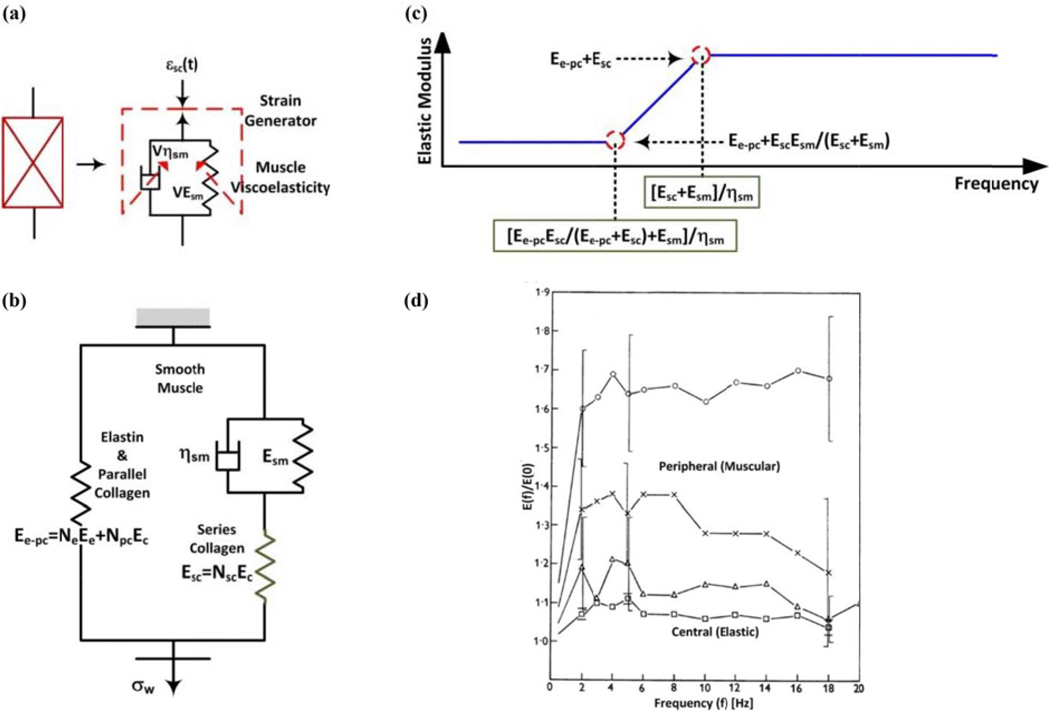
Figs. 2a–d show the central arterial wall model. Here, elastin is modeled as N_e·400 springs, each with elastic modulus E_e. Collagen is represented with a disconnecting hook model in which springs with higher elastic modulus E_c (= 400·E_e) are recruited as the wall extends (parallel collagen) or as smooth muscle contracts (series collagen). (So, in Fig. 2, one elastin spring has the same elastic modulus as one collagen spring.) The elastic modulus of the parallel and series collagen is E_c times the number of recruited fibers N_pc and N_sc, respectively. As indicated, series collagen is recruited more easily than parallel collagen. Smooth muscle is assumed to (a) bear no stress and freely extend when relaxed and (b) elongate the series collagen, while bearing the same stress, when contracted. A model of the smooth muscle is a strain generator in series with a spring with variable elastic modulus VE_sm, which increases with strain generation (i.e., Fig. 4a without the dashpot). When relaxed, no strain is generated on the series collagen and VE_sm is small such that the smooth muscle freely extends. When contracted, strain is generated on the series collagen and VE_sm is large such that series collagen determines the elasticity. In general, both VE_sm and strain generation increase with smooth muscle contraction.

Figure 2.

Arterial wall models predict that central arterial elasticity is dependent on BP, but peripheral arterial elasticity is dependent on BP and smooth muscle contraction. (a)–(d) Model of the central arterial wall in low and high extension states during smooth muscle relaxation (a, b) and contraction (c, d). (e) Model of the peripheral arterial wall in low extension state during smooth muscle relaxation.

Figure 4.

Models and experimental data indicate that the central arterial wall is mainly elastic, while the peripheral arterial wall is viscoelastic. (a) Viscoelastic model of smooth muscle. (b) Complete viscoelastic model of central and peripheral arterial walls for a fixed smooth muscle contraction and small changes in ε_w. (c) Model predicted elastic modulus (magnitude) as a function of frequency. (d) Experimental elastic moduli (magnitudes) as a function of frequency for central and peripheral arteries [31].

Figs. 2a–b show the model during smooth muscle relaxation. Here, the strain generated on the series collagen ε_sc is zero, so none of these fibers are recruited. Fig. 2a shows that in the low extension state, the wall stress σ_w and strain ε_w increase but not enough to recruit any parallel collagen. So, elastin determines the incremental elastic modulus E_inc of the arterial wall in this “hypotensive” state. Fig. 2b shows that in the high extension state, the wall stress σ_w and strain ε_w increase considerably so as to recruit all of the parallel collagen. Hence, E_inc increases, and parallel collagen in addition to elastin contribute in this “hypertensive” state.

Figs. 2c–d show the model in the same two states but during smooth muscle contraction. Here, ε_sc increases so as to recruit all of the series collagen. Also, due to the isotonic conditions, ε_w decreases (but not as much as ε_sc increases) to maintain σ_w. Fig. 2c shows that in the low extension state, there is again no parallel collagen recruitment, so elastin and series collagen determines E_inc. Fig. 2d shows that in the high extension state, there is some parallel collagen recruitment, E_inc increases, and all three components contribute. Importantly, E_inc and ε_w do not change much compared to the corresponding states during smooth muscle relaxation. The reason is that N_sc is not large, as central arteries are relatively sparse in smooth muscle. In addition, in the high extension state, the reduction in ε_w causes a decrease in N_pc, which fully offsets the increase in N_sc.

In conclusion, central arterial elasticity is determined by BP but not smooth muscle contraction. Fig. 3a shows exemplary experimental data indicating that pressure-diameter relationships of a central artery (thoracic aorta) are indeed similar in the relaxed and contracted states [28].

Figure 3.

Experimental data show that central arterial elasticity is dependent on BP and age, while peripheral arterial elasticity is dependent on BP and smooth muscle contraction. (a)–(b) Pressure-diameter relationship of a central artery and peripheral artery during smooth muscle (SM) changes [28]. (c) Volume-pressure relationship of a central artery as a function of age [36].

Fig. 2e shows the peripheral arterial wall model. Compared to the central arterial wall model, N_e is smaller, whereas N_sc is much larger, due to the different wall compositions. (Note that the number of hooks and springs in these models represent relative amounts and the number of hooks indicates recruitable rather than total fibers.) Hence, during smooth muscle relaxation, E_inc is smaller compared to the central arterial wall model in the hypotensive state but similar in the hypertensive state. During smooth muscle contraction, unlike the central arterial wall model, E_inc and ε_w respectively increase and decrease to a significant extent. The reason is that N_sc is larger. In addition, N_pc is smaller than N_sc such that the decrease in N_pc cannot fully offset the increase in N_sc in the high extension state.

In conclusion, peripheral arterial elasticity is determined by BP and smooth muscle contraction. Fig. 3b shows exemplary experimental data indicating that pressure-diameter relationships of a peripheral artery (renal artery) are indeed different in the relaxed and contracted states [28]. That is, the pressure-diameter relationship in the contracted state is shifted far to the left (i.e., reduced ε_w) and the slope of this relationship is often higher (i.e., higher E_inc). Note that the gap between the pressure-diameter relationships in the two states decreases with increasing diameter. One reason is that the slope indicates arterial compliance rather than E_inc (see Section III.B). Another reason is that smooth muscle contraction may actually decrease over high diameters [30].

2) Viscous Properties

We include viscosity in the arterial wall models to arrive at unified, viscoelastic models. We likewise hypothesized these models based on a review [19], in vitro animal studies [29, 31, 32], in vivo animal studies [22], and an in vitro human study [33].

Fig. 4a shows that viscosity is specifically introduced in the smooth muscle model by including a dashpot with variable viscosity Vη_sm in parallel with the spring. When relaxed, Vη_sm is small such that the wall is purely elastic. When contracted, Vη_sm is large such that the wall is viscoelastic (i.e., has frequency dependent elastic modulus). In general, Vη_sm increases with smooth muscle contraction.

Fig. 4b shows the complete viscoelastic model of either arterial wall for a fixed smooth muscle contraction and small changes in ε_w such that the number of recruited fibers remains constant. In response to a step increase in ε_w, the stress is immediately borne by elastin and all recruited collagen. The dashpot then gradually extends until the stress is equally shared by the smooth muscle and series collagen. Hence, the stress decreases to a non-zero value with a time constant governed by these two components. The elastic modulus (magnitude) as a function of frequency may thus be obtained and is shown in Fig. 4c. The low frequency elastic modulus is E_e-pc+E_sc·E_sm/(E_sc+E_sm), while the high frequency elastic modulus is E_e-pc+E_sc, which is larger than its low frequency counterpart. The lowest frequency for which the higher elastic modulus is reached (“corner frequency”) is (E_sc+E_sm)/η_sm. E_sm and η_sm are assumed to be larger for peripheral arteries than central arteries due to the differences in smooth muscle composition. Since E_sc is small in the central arterial wall model, the elastic modulus does not change much with frequency. By contrast, E_sc is large in the peripheral arterial wall model, so the elastic modulus has greater frequency dependence. Further, since all three terms in the corner frequency change concomitantly with either arterial site or smooth muscle contraction, this frequency is nearly invariant.

In conclusion, central but not peripheral arterial viscosity is small. Fig. 4d shows exemplary experimental data indicating that experimental elastic modulus magnitudes indeed have little frequency dependence for central arteries but not peripheral arteries [31]. The corresponding phases were small in both arteries (not shown). Other exemplary studies indicate that the corner frequency is around 1 Hz and indeed insensitive to smooth muscle contraction [29, 33]. But, in contrast to the model prediction, one of these studies suggests that the elastic modulus of peripheral arteries may actually increase above the corner frequency [33].

3) Impact of Aging and Disease on Mechanical Properties

We again employ the Maxwell-type model to illustrate the mechanical properties of the central arterial wall during age-induced arteriosclerosis or disease-induced arteriosclerosis (i.e., atherosclerosis). We similarly hypothesized the model from reviews [24, 25], in vitro animal studies [32, 34], an in vivo animal study [35], an in vitro human study [36], and an in vivo human study [33].

Fig. 2a shows the basic model. As arteriosclerosis progresses, N_e decreases and N_pc increases but N_sc does not change. So, E_inc becomes smaller in the hypotensive state but larger in the hypertensive state. Also, regardless of the degree of arteriosclerosis, E_inc and ε_w change little during smooth muscle contraction, and viscous effects are small.

In conclusion, central arterial wall elasticity is also determined by age and disease. Fig. 3c shows exemplary experimental data indicating that volume-pressure relationships of a central artery (thoracic aorta) indeed markedly differ based on age [36]. Other exemplary studies suggest that aging (a) may cause smooth muscle contraction to contribute even less to central arterial elasticity [32, 34, 35] and (b) does not alter central arterial viscoelasticity (e.g., the corner frequency of around 1 Hz is maintained) [33].

B. Arterial Wave Propagation Models

Pressure waves propagate along arterial vessels with the aforesaid wall properties. We employ basic models of arterial wave propagation to relate wall elasticity to PTT.

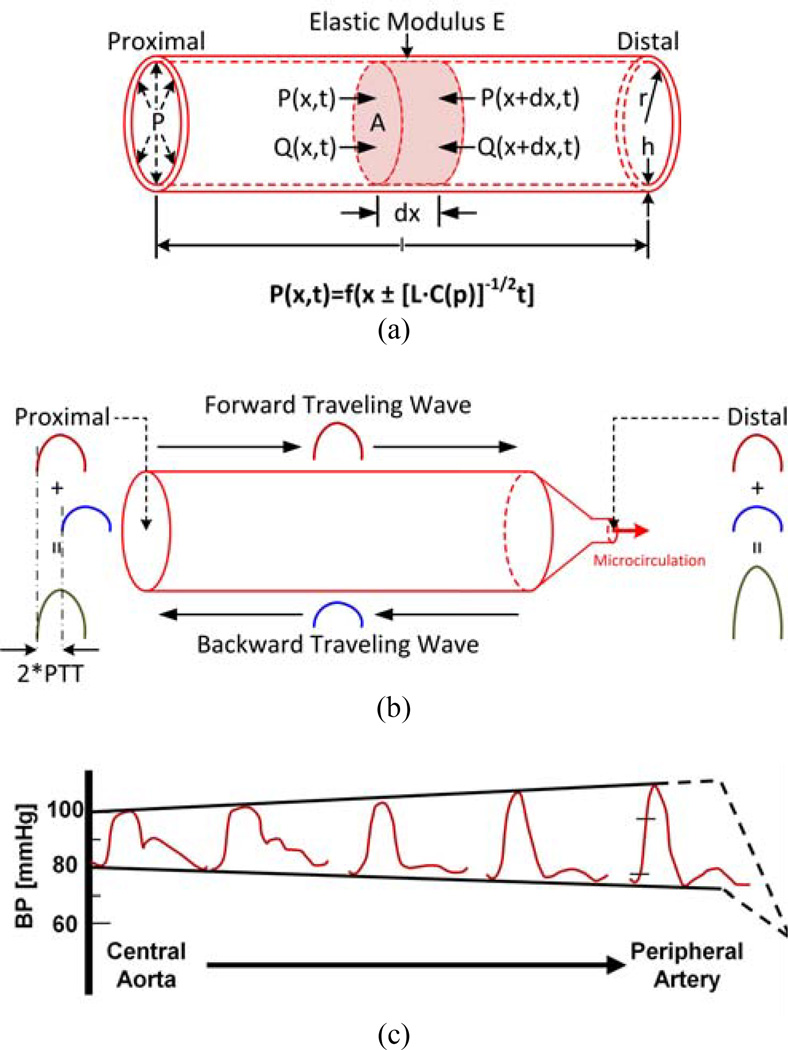
Fig. 5a shows the arterial vessel model as an elastic, cylindrical tube. Here, viscous effects are neglected. The ignored effects include both wall viscosity and resistance to blood flow, which goes with the inverse fourth power of the lumen radius r and is thus small in central and peripheral arteries [37]. The elasticity of the tube is characterized in terms of compliance C, which is defined as the change in tube cross-sectional area A divided by the change in pressure in the tube P (i.e., dA/dP). Compliance is determined by the geometry of the tube in addition to the elastic modulus of the tube wall E. For example, by invoking Laplace’s law for a cylindrical tube and assuming constant E, C = 2πr³/(E·h), where h is the wall thickness [37]. Of course, E is not constant but rather increases with P. For example, E has been shown to be related to P for central arteries as follows:

$$\mathrm{E}(\mathrm{P})={\mathrm{E}}_0{\mathrm{e}}^{\mathrm{\alpha }\mathrm{P}}$$ (1)

where E₀ and α > 0 are subject-specific parameters [38]. E is also dependent on smooth muscle contraction and aging. However, E is assumed to only depend on P here. Note that this assumption, with the exception of aging, and the omission of wall viscosity are tenable for central arteries but not for peripheral arteries.

Figure 5.

PTT through central arteries as estimated via the foot-to-foot time delay between proximal and distal waveforms is a good marker of diastolic BP for time periods shorter than aging and disease processes. (a) Model of wave propagation in a central artery. (b) Same model with a terminal wave reflection site predicting that BP waveforms are amplified with increasing distance from the heart. (c) Experimental BP waveforms confirming this prediction and showing that diastolic BP (i.e., the waveform feet) is less impacted by wave reflection (reproduced after [18]).

By applying conservation of mass and momentum, while assuming that variations in A are minor (i.e., no tapering and small changes with P), the following model equations result:

$$\mathrm{Q}(\mathrm{x})-\mathrm{Q}(\mathrm{x}+\text{dx})+\frac{\mathrm{d}(\text{Adx})}{\text{dt}}=0\to \frac{\partial \mathrm{Q}}{\partial \mathrm{x}}+\mathrm{C}(\mathrm{P})\frac{\partial \mathrm{P}}{\partial \mathrm{t}}=0$$ (2a)

$$\mathrm{A}[\mathrm{P}(\mathrm{x})-\mathrm{P}(\mathrm{x}+\text{dx})]=\mathrm{\rho }\text{dx}\frac{\text{dQ}}{\text{dt}}\to \frac{\partial \mathrm{P}}{\partial \mathrm{x}}+\mathrm{L}\frac{\partial \mathrm{Q}}{\partial \mathrm{t}}=0$$ (2b)

Here, x and t refer to space and time, Q is volume flow rate, ρ is blood density, L=ρ/A is a constant that represents the arterial inertance per unit length (i.e., the pressure required to accelerate blood [37]), while C is a function of P. C generally decreases as P increases. For example, C has been shown to be related to P for central arteries as follows:

$$\mathrm{C}(\mathrm{P})=\frac{{\mathrm{A}}_{\mathrm{m}}}{\mathrm{\pi }{\mathrm{P}}_1[1+{\left(\frac{\mathrm{P}-{\mathrm{P}}_0}{{\mathrm{P}}_1}\right)}^2]}$$ (3)

where A_m, P₀, and P₁ are subject-specific parameters [39] .

The equations of continuity and motion (Eq. (2)) are identical to the equations governing an ideal, lossless transmission line but with voltage-dependent capacitors (see Chapter 3 of [40]). Pressure waves propagating on this line take on the following form:

$$\mathrm{P}(\mathrm{x},\mathrm{t})=\mathrm{f}(\mathrm{x}\pm \mathrm{t}/\sqrt{\text{LC}(\mathrm{P})})$$ (4)

(see Chapter 3 of [40] for derivation). Hence, the velocity of propagation (i.e., pulse wave velocity (PWV)) is [L·C(P)]^−1/2, where C and P are again inversely related. So, the peak of the pressure wave moves faster than its trough (which could lead to pressure discontinuities or “shock waves”; see Chapter 3 of [40]). The time for the wave to travel along the tube length l (i.e., PTT) is thus:

$$\text{PTT}=1\sqrt{\text{LC}(\mathrm{P})}$$ (5)

In conclusion, under the above assumptions, PTT and BP are precisely related in an inverse fashion. Experimental data indicate that PWV, in fact, continuously varies with BP throughout the cardiac cycle [41, 42]. However, for a fixed l, experimentally measured PTT generally decreases with increasing BP, smooth muscle contraction, distance from the heart, heart rate (due to wall viscosity), and age.

Note that if C is assumed to be constant, the PWV formula reduces to:

$$\text{PWV}=\frac{1}{\sqrt{\mathrm{L}\cdot \mathrm{C}}}=\sqrt{\frac{\text{AdP}}{\mathrm{\rho }\text{dA}}}=\sqrt{\frac{\text{Eh}}{2\mathrm{r}\mathrm{\rho }}}$$ (6)

These formulas are the well-known Bramwell-Hill and Moens-Korteweg equations, which relate wall elasticity in terms of C and E to PWV, respectively [18].

The actual arterial system is obviously not a simple tube but rather branches, tapers (elastically and geometrically), and terminates with the microcirculation. Wave reflection occurs at all of these sites of impedance mismatch but is most pronounced at the arterial terminations [24, 35, 43]. One reason is that these sites are where the lumen radius changes most abruptly. Another reason is that tapering tends to be offset by branching in the forward direction so as to achieve relative impedance matching.

Fig. 5b shows the same tube model but with a terminal load representing the microcirculation. Here, C is assumed to be constant for the sake of simplicity. When the heart ejects blood, a pressure wave is initiated that travels along the tube. When this wave reaches the tube end, part of the wave is reflected back towards the heart. As a result, the BP waveform at a given tube site arises as the sum of the forward and backward traveling waves at that site. (Note that the backward wave is related to the forward wave via the reflection coefficient: Γ(f) = (Z_l(f)-Z_c)/(Z_l(f)+Z_c), where f is frequency, Z_l(f) is the load impedance, and Z_c = [L/C]^1/2 is the tube characteristic impedance [18].) Since wave reflection occurs at the tube end, there is no time delay between the forward and backward waves at this point. So, adding the backward wave to the forward wave increases peripheral pulse pressure (i.e., systolic minus diastolic BP). On the other hand, the forward and backward waves at the tube entrance are shifted by the time it takes for the wave to travel to the tube end and back (i.e., 2·PTT). So, summing the backward wave with the forward wave has much less effect on central pulse pressure. For this reason, pulse pressure should become amplified with increasing distance from the heart.

In conclusion, wave reflection profoundly impacts the shape of BP waveforms. Fig. 5c shows exemplary experimental data indicating that waveforms indeed become progressively amplified with increasing distance from the heart [18]. Note that the increasing distortion in shape may also be due to other mechanisms including BP-dependent compliance. Hence, proximal and distal waveforms generally do not differ simply by a single time delay. Any time delay determined from the waveforms is contaminated by wave reflection and thus does not truly reflect PTT. However, as indicated in Fig. 5c, diastolic BP changes little with arterial site. So, wave reflection interference is small at the minima or feet of the BP waveform [18].

C. Conclusions Drawn from the Models

Based on these models, PTT can be used to effectively monitor BP (i.e., Eq. (5) is valid) if the following conditions are met: (a) smooth muscle contraction and viscous effects are negligible; (b) aging and disease do not alter arterial elasticity; and (c) wave reflection interference is absent. These conditions are best satisfied by measuring PTT through central arteries and via the foot-to-foot time delay between the proximal and distal waveforms and limiting the monitoring duration to a period shorter than aging and disease processes (e.g., perhaps up to a few years). Since the level of the waveform feet is diastolic BP, such PTT measurements may best correspond to diastolic BP [44, 45]. Note that condition (b) sets the fundamental limitation of the approach, namely that PTT cannot be used for chronic BP monitoring without periodic recalibration (see Section IV).

These conclusions are supported by experimental data from several studies in which PTT through central arteries was measured as the foot-to-foot time delay between invasive proximal (e.g., aortic, carotid artery) and distal (e.g., iliac, femoral artery) BP waveforms during large, acute BP changes and then correlated with diastolic BP [46–49]. Table I shows high correlation (see Fig. 1b for a visual example).

Table I.

The correlation between pulse transit time – through central arteries and estimated via the foot-to-foot time delay between invasive proximal and distal blood pressure (BP) waveforms – and diastolic BP is high.

Ref #	Subjects	Underlying BP Range [mmHg]	Correlation with BP
[47]	10 Dogs	15–250	r=0.76–0.86
[49]	3 Dogs	53±12	r=0.96–0.99
[48]	10 Dogs	Control 115±13 / Intervention 106±45	r=0.91–0.98
[46]	12 Dogs	67±14	r=0.94

IV. Overview and Challenges of the PTT-Based Approach for BP Monitoring

The PTT-based approach for cuff-less BP monitoring thus involves the following three steps: (a) measurement of proximal and distal arterial waveforms; (b) estimation of PTT from the waveforms: and (c) calibration of PTT (in units of ms) to BP (in units of mmHg). There are several challenges in successfully implementing these steps. The greatest challenge is calibration. According to Eq. (5), the calibration curve relating PTT to BP is dependent on the distance between the waveform measurement sites (l), blood density (ρ, which is close to that of water), the average cross-sectional area of the arteries between the measurement sites (A), and the precise function relating BP to compliance (C(P)). Except for blood density, these parameters are all subject-specific. Experimental data indeed confirm the dependency of the calibration curve on the subject [50]. Hence, a calibration curve that is tailored to each subject would be optimal. However, constructing such a curve would appear to require cuff BP measurements from the subject, and the calibration curve would have to be updated at a rate faster than the arteriosclerotic process (e.g., up to a few years at a time). Another major challenge is convenient waveform measurement. If the waveforms are not significantly easier to measure than cuff BP, then the PTT-based approach is obviously not worthwhile. But, in general, the more convenient the waveform measurement is, the more noise contamination can be expected [51–62]. Hence, an ancillary challenge is artifact-robust estimation of PTT. A final major challenge is independent determination of both systolic BP and diastolic BP. This challenge is important, as isolated systolic hypertension often occurs in the elderly [63]. However, as we have explained, conventionally estimated PTT may only be a marker of diastolic BP.

V. Putting the Theory to Practice

The PTT-based approach for cuff-less BP monitoring has captured the interest of many investigators. Much of the previous research represents a balance between theory and practice. We summarize this work, explain the underlying principles, make suggestions for best practice, and include efforts that could potentially be employed as part of the approach. Our review is categorized in terms of the three aforementioned steps and concludes with a summary of the results obtained to date.

A. Waveform Measurement

We first review waveform measurement methods that have been commonly employed for cuff-less BP monitoring and automated and non-invasive cardiovascular monitoring in general. We then briefly introduce potential methods for more convenient, contact or even noncontact measurement. Note that we have restricted this review to those methods that are described in peer-reviewed publications and are automated and non-invasive. So, for example, ultrasound which generally requires a skilled operator, is not discussed. Importantly, while the theory of the PTT-BP relationship outlined above is based on BP waveform measurement, most of the described methods do not measure such waveforms. Rather, as explained below, they measure related waveforms.

1) Classical Waveform Measurement Methods

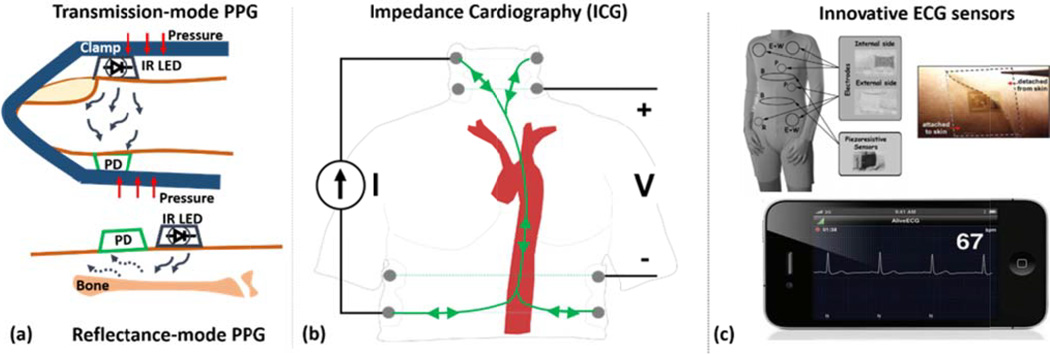
PPG, electrical bioimpedance (EBI) / impedance cardiography (ICG), and electrocardiography (ECG) have been the most popular methods. These methods are based on either optical or electrical principles, as shown in Fig. 6.

Figure 6.

A few waveform measurement methods have been commonly used for cuff-less BP monitoring and non-invasive and automated cardiovascular monitoring. (a) Photoplethysmography (PPG), in transmission- and reflectance-mode, for measuring proximal and distal waveforms from various body sites; (b) Impedance cardiography (ICG) for measuring a proximal waveform that may permit estimation of PTT through central arteries; (c) Innovative ECG systems for conveniently measuring a surrogate of the proximal waveform [5, 215].

PPG

This method is the basis of pulse oximeters, which are widely used in clinical practice to measure arterial oxygen saturation. (Note that commercial pulse oximeters may not be suitable for PTT estimation, as they heavily process the PPG waveform [64].) It employs optical transmittance or reflectance to measure waveforms indicative of proximal and distal blood volumes [65]. Several reviews have been written on PPG in the past decade [64, 66–68]. We summarize the relevant points.

As shown in Fig. 6a, a light-emitting diode (LED) is paired with a photodetector (PD); a small volume of tissue is illuminated by the LED; and the light transmitted through, or reflected back from, the tissue is measured by the PD. The measured light intensity is reduced and includes both DC and AC components. The DC component mainly indicates light absorption by non-pulsatile blood, skin, bone, and other tissue. The AC component represents light absorption by mostly pulsatile arterial blood but also venous blood. (PPG systems usually output only the AC component.) According to the Beer-Lambert-Bouguer law, as light of a given intensity (I₀) is incident on a volume, the transmitted light (I(t)) – assuming a non-scattering, homogeneous medium – is given as follows:

$$\text{ln}\left(\frac{\mathrm{I}(\mathrm{t})}{{\mathrm{I}}_0}\right)=-\mathrm{\epsilon }\text{CV}$$ (7)

where ε is the absorption coefficient, C is the concentration of the chromophore, and V is the volume of the medium. Hence, the AC component of I(t) is inversely related to the instantaneous arterial blood volume. Blood volume is, in turn, related to BP via the viscoelastic properties of the arterial wall (see above). In this way, PPG is useful for PTT estimation. Note that the main light absorber in blood at wavelengths typically used in PPG is hemoglobin [65].

Transmission-mode and reflectance-mode PPG offer different advantages. The advantage of reflectance-mode PPG is that it is less restrictive in terms of measurement locations [66, 67, 69]. Transmission-mode PPG measurements are mainly limited to the earlobe, fingertip, and toe. By contrast, reflectance-mode PPG is applicable to additional locations including the forehead, forearm, supraorbital artery, under the legs, and the wrist. We refer to a tutorial on how to place PPG sensors on the finger, toe, or ear [70]. The finger, palm, face, and ear represent the best locations for maximizing the signal-to-noise ratio (SNR) [71]. However, the disadvantage of reflectance-mode PPG is that the SNR is typically lower for any common location, since tissue is highly forward-scattering such that the reflected energy back to the photodetector is low [72]. Furthermore, reflectance-mode PPG is more prone to motion artifact and varies more with sensor positioning and distance between the light source and the sensor [69, 73]. If the sensor location is not a factor, we suggest using transmission-mode PPG. Transmission-mode PPG at the fingertip has been the most widely used method for obtaining the distal waveform (see Section V.D).

Infrared (IR) and red optical wavelengths should be used for transmission-mode PPG due to the “optical water window” [66] and higher tissue penetration depth [66, 67, 74]. IR wavelengths may be preferred, as they are less sensitive to the oxygen content of hemoglobin and thus yield waveforms that are more stable over time [64]. For reflectance-mode PPG, the green wavelength produces greater signal amplitude and lower motion artifact than IR and red [69, 75–77]. However, the shorter green wavelength is only able to penetrate the skin rather than deeper in the tissue wherein larger arteries reside. Since the green wavelength waveform reflects skin blood flow, it does not exhibit features that are as well-defined as IR and red waveforms [76] and is more influenced by ambient temperature than these waveforms [78]. To the best of our knowledge, the various wavelengths have not been compared in the context of PTT estimation. If a reduced SNR can be tolerated, we suggest using an IR wavelength for reflectance-mode PPG applications to obtain the timing of pulses in the larger arteries rather than from the skin wherein cutaneous vasodilation/vasoconstriction and ambient temperature changes are of concern. The IR wavelength has often been used for PTT estimation (see, e.g., references in Table II).

Table II.

Summary of methods and results of studies that have employed ECG and finger PPG (RMSE is root-mean-squared error; LOA is limits-of-agreement).

REF #	Waveform Detection	Calibration (Model/BP Perturbation/Period)	Evaluation (# of Subjects/Interventions)	Results
				Correlation (r Value or RMSE [mmHg])			Calibration Error (Various Metrics) Mean (SD)
				SP	MP	DP	SP	MP	DP
[169]	R→Minimum	Linear in PTT Change Surgery/5-min	20/Surgery	-	-	-	RMSE 3.7 (1.9)	-	-
[94]	R→Threshold	Log & Quadratic in PTT−1 Population Parameter/One-Time	85/Natural Variability (Weeks)	-	-	-	0.6 (9.8)	-	0.9 (5.6)
[142]	R→Minimum	-	10 Normal/LBNP - Hand Grip	0.73–0.92	-	-	-	-	-
[98]	R→Minimum	-	12/Hemodynamic Drugs	0.62	0.28	0.14	-	-	-
[179]	R→Max Tangent	-	18/Exercise	RMSE 3.6	-	-	-	-	-
[170]	R→Maximum	Linear in PTT Cuff Deflation/One-Time	11/Exercise	-	-	-	-	4.5 (6.6)	-
[148]	Max Deriv→Max Deriv	Linear in PTT Exercise/One-Time	14/Exercise	0.90	-	0.34	First: 0.0 (5.3) Repeat: 1.4 (10.2)	-	First: 0.0 (2.9) Repeat: 2.1 (7.3)
[92]	R→Minimum	-	22/ICU	0.43	0.42	0.37	-	-	-
[172]	R→Max Deriv	Linear in PTT & HR ICU/60-min	25/ICU	-	-	-	−0.4 (7.8)	-	−0.1 (5.0)
[180]	SP: R→Max Deriv DP: Diastole Duration	Linear in PTT Step Climbing/One-Time	5/Step Climbing	0.74–0.89	-	0.44–0.74	Absolute % 9–14	-	Absolute % 4–11
[208]	R→Max 2nd Deriv	-	18/Exercise	RMSE 4.1	-	RMSE 2.3	-	-	-
[174]	R→Minimum	Linear in PTT−1 Exercise/One-Time	33/Exercise	0.79	-	0.77	LOA −13/+13 (ST) −17/+13 (MT)	-	LOA -11/+11 (ST) -12/+11 (MT)
[149]	R→Minimum	-	10/ICU	-	0.45	-	-	-	-
	R→10% Height			-	0.39	-	-	-	-
	R→Max Deriv			-	0.27	-	-	-	-
	R→90% Height			-	0.33	-	-	-	-
	R→Maximum			-	0.32	-	-	-	-
[145]	R→Max Deriv	Nonlinear in PTT−1 Population Parameters/One-Time	63/Exercise	0.75–0.99	-	-	LOA −20/+20	-	-
[143]	R→Minimum	Linear in PTT ICU/60-min	25/ICU	0.09	-	−0.02	3.1 (6.3)	-	1.9 (3.9)
	R→50% Height			0.32	-	0.22
	R→Maximum			0.71	-	0.69
[185]	R→Maximum	Linear in PTT Change Population Parameter/6-min	15/Natural Variability (Minutes)	-	-	-	1.0 (2.4)	-	-
	R→Maximum	Log & Quadratic in PTT−1 Population Parameter/8-min		-	-	-	1.1 (9.7)	-	-
[150]	R→Maximum	Linear in PTT Exercise/One-Time	5/Exercise	-	-	-	0.0 (12.0)	-	-
	R→Max 2nd Deriv						1.8 (14.0)
	R→Minimum						5.2 (40.4)
[182]	R→50% Height	Linear in PTT & HR Natural Variability (Hours)/~110 min	10/Natural Variability (Hours)	-	-	-	RMSE 1.7	-	RMSE 1.0
[183]	R→Maximum	Linear in PTT−1 & PTT Variations Posture Change/One-Time	30/Posture Holding (Sitting)	-	-	-	−0.2 (2.4)	-	−0.5 (3.9)
[184]	R→Max Deriv	Linear or Nonlinear in PTT−1 Valsalva/One-Time	4/Valsalva	-	-	-	RMSE 12.6–15.4	-	-
[209]	R→Maximum	-	25/Step Climbing	0.90 (.03)	-	0.82 (.04)	-	-	-
[187]	R→Max Deriv	-	20/Exercise	0.93–0.99	-	0.10–0.89

The contact pressure between the PPG sensor and the skin is often overlooked but greatly influences the amplitude and shape of the waveforms [67, 68, 76, 79, 80]. The contact pressure required to maximize the amplitude is near the mean BP (i.e., a transmural pressure of zero). However, a much lower pressure should be applied to avoid tissue/vessel damage and discomfort to the user, especially for long-term application [67, 73]. A disadvantage of most reflectance-mode PPG systems is that the contact pressure is essentially zero, which both reduces the measured amplitude and preserves venous pulsation [68, 79]. At the same time, the fact that these systems are not perturbing the physiology may also be considered an advantage [68]. Note that the impact of contact pressure on amplitude and shape is more pronounced for shorter wavelengths (e.g., green) compared to longer wavelengths (e.g. red or IR), since the tissue volume being probed includes only the superficial region for the former and the deeper arteries for the latter [76]. The contact pressure may also influence the PTT estimate. Indeed, PTT was shown to increase with contact pressure, reaching a maximum at zero transmural pressure and remaining at a constant level at negative transmural pressures [81]. However, the optimal contact pressure for cuff-less BP monitoring via PTT has not been examined. We suggest adhering the PPG sensor to the body with a contact pressure that exceeds the venous pressure (to obtain a pure arterial waveform) but not tight enough to be uncomfortable for the user. Placing the sensor so that it does not fall off should meet this requirement. We also suggest using a clip sensor so that the contact pressure can be better maintained, if it does fall off or is temporarily removed.

In general, PPG waveforms can be well measured from a variety of healthy subjects and patients with cardiovascular disease. However, the waveform becomes unreliable during peripheral hypo-perfusion (e.g., due to cold temperature).

EBI/ICG

EBI exploits the electrical conductivity of blood to measure waveforms indicative of proximal and distal blood volumes. ICG is a type of EBI that measures electrical blood conductivity in the thorax and thus a proximal waveform. ICG is often used to estimate cardiac output, and many reviews have been written on this method [82–84]. We likewise summarize the relevant information.

As shown in Fig. 6b, in EBI/ICG, surface electrodes are placed on a volume of tissue; a tiny, high frequency electrical current is injected typically into the outer electrodes; and the resultant differential voltage is measured usually across the inner electrodes and then demodulated synchronously with the excitation frequency. Since blood is an excellent electrical conductor, the current tends to travel through paths filled with blood. So, the AC component of the measured impedance (voltage divided by current) represents the pulsatile blood volume within the tissue. The parallel-column model relates quantitatively the EBI measurement to blood volume based on the assumption that the tissue volume consists of two parallel conducting paths. One path is cylindrical and represents the pulsatile blood (AC impedance component), while the other path represents all other tissues including bone, fat, muscle and non-pulsatile fluids (DC impedance component) [85, 86]. Under this and other assumptions, blood volume changes (ΔV) are related to the AC component of EBI (ΔZ) as follows:

$$\mathrm{\Delta }\mathrm{V}=-\mathrm{\rho }\frac{{\mathrm{L}}^2}{{{\mathrm{Z}}_0}^2}\mathrm{\Delta }\mathrm{Z}$$ (8)

where ρ is the resistivity of blood, L is the length of the cylinder, and Z₀ is the DC component of EBI. Hence, ΔZ is inversely related to ΔV. Since blood volume is again related to BP via the viscoelastic properties of the arterial wall, EBI/ICG is useful for PTT estimation.

ICG is the most popular EBI measurement. The main reason, as mentioned above, is that it permits estimation of cardiac output specifically from the derivative of the impedance with respect to time (dZ/dt) [82–84]. Another reason is that it offers systolic time intervals [82–84]. For cuff-less BP monitoring, ICG has been used to measure a proximal waveform for estimation of PTT through central arteries (see references in Section V.D-3).

In theory, the injected electrical current travels through the blood-filled aorta, as shown in Fig. 6b, so ICG indicates the pulsatile aortic blood volume. However, ICG pioneers showed that changes in blood volume in intra-thoracic cardiovascular structures other than the aorta (e.g., atria) are likely to play a major role in the genesis of the ICG waveform [87]. They even showed that aortic blood volume changes can contribute < 30% of the measured waveform. Further, the measured impedance via ICG rises with inspiration and falls with expiration, as air is a poor electrical conductor. In fact, the respiratory component of the ICG waveform is 10–100 times greater in magnitude than the cardiac component. (EBI is therefore often used to measure respiration in clinical practice; this approach is referred to as impedance pneumography.) However, respiratory activity is usually slower than cardiac activity, so the respiratory component of the ICG waveform can be mitigated via high-pass filtering.

In ICG, the applied electrical current is typically in the 10–100kHz and 1–5 mA range [82–84, 88, 89]. The cardiac component relative to the respiratory component increases with decreasing excitation frequency [62]. The overall ICG amplitude increases with the excitation amplitude. We thus recommend around 10 kHz and 5 mA for the applied current. Traditionally, “band” electrodes were used to inject the current and measure the impedance. These electrodes wrap around the tissue volume, enabling both low skin-electrode interface impedance and uniform excitation of the tissue volume. However, due to their inconvenience, modern systems typically use silver/silver-chloride (Ag/AgCl) gel electrodes, which are commonly used for ECG measurements [84]. As shown in Fig. 6b, the standard configuration is two electrode pairs at the neck and two electrode pairs at the upper-abdomen. Other configurations such as forehead to lower torso, limb-to-limb, or upper arm to upper calf have also been demonstrated [83, 90]. The positioning of these electrodes may be critical for estimating cardiac output but is likely less important for PTT estimation. To our knowledge, the optimal number and position of the electrodes for cuff-less BP monitoring has not been determined.

EBI can also be used for measuring a distal waveform by appropriate positioning of the electrodes [86]. This approach is also referred to as impedance plethysmography. A tetrapolar configuration is commonly used, with all four electrodes positioned locally on a limb such as the lower leg or forearm. Similar to ICG, the electrodes must be positioned along the length of the limb such that blood is flowing from one set of electrodes to the other. The frequency ranges and currents used in these configurations are similar to ICG [88, 89, 91]. Note that the respiratory component is minimal however. EBI has been applied to measure the distal waveform [92].

Unlike PPG, EBI can yield low quality waveforms in many subjects. Examples include obese individuals, critically ill patients, heart failure patients, patients with aortic/mitral valve problems, or other patients with generally weak circulations [82–84]. Electrical bioreactance (the phase of the impedance rather than its magnitude) may improve the SNR [93].

ECG

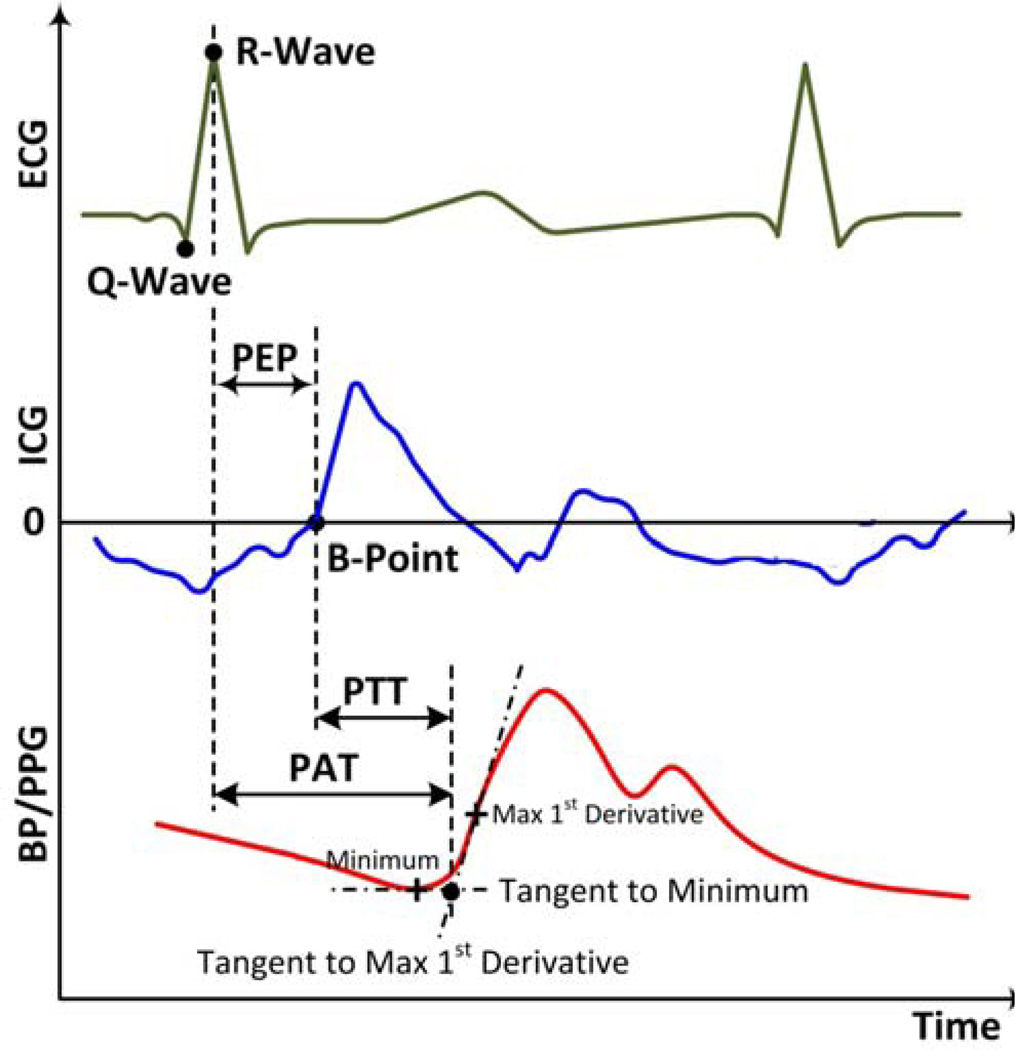
This method provides the timing of cardiac electrical activity, which precedes the arterial pulse. The time delay between the ECG waveform and a distal arterial waveform has been called the pulse arrival time (PAT) [47], m-pulse wave transit time [48], or simply PTT [94]. For convenience, we adopt the PAT nomenclature. PAT is equal to the sum of PTT and the pre-ejection period (PEP) [44]. PEP is determined by the ventricular electro-mechanical delay (VEMD) and isovolumic contraction period [95], which is, in turn, determined by ventricular and arterial pressures [96]. More specifically, PEP may be expressed as follows:

$$\text{PEP}=\text{VEMD}+(\text{CP}-\text{VEDP})/\text{dVICP}$$ (9)

where VEDP and dVICP are respectively the ventricular end-diastolic pressure and average slope of ventricular isovolumic contraction pressure, and DP is diastolic BP. Note that the maximum slope of ventricular pressure, which may be nearly equal to dVICP, is a well-known index of ventricular contractility [97]. Also note that ventricular contractility and VEDP may be modulated by short-term physiologic control and medication [96]. PEP is a significant fraction of PAT, as indicated in Section V.B, and indeed varies considerably (e.g., 10 to 35% of PTT) [98]. Hence, PAT does not have a precise relationship to BP a la Eq. (5). Even so, the ECG waveform has been widely used as a surrogate proximal waveform due to the ease of measurement and robustness to artifact (see, e.g., references in Table II). In addition, as discussed in Section V.D, this waveform happens to allow for better tracking of systolic BP. Lead I or II is a reasonable choice for electrode placement, as the QRS axis normally aligns with these leads [96].

There has been a tremendous evolution in sensing technologies, which has driven ECG instrumentation from bulky, bench-top systems into miniature devices based on smart-patches or integrated into smartphones and clothing, as shown in Fig. 6c. We refer to a recent review for more on advances in ECG and other sensing technologies [5].

2) Potential Waveform Measurement Methods

A number of other waveform measurement methods are available. Some have been studied for decades. However, for the most part, they have yet to be demonstrated in the context of cuff-less BP monitoring. We describe a few such methods here including both contact and noncontact methods.

Contact Methods

Ballistocardiography (BCG) measures the reactionary forces of the body in response to cardiac ejection of blood into the aorta [99–101]. This method has been recently implemented using inexpensive and convenient instrumentation such as chairs [102], beds [103], weighing scales [104], and on-body accelerometers [105]. Although BCG provides a proximal waveform [106, 107], it can be applied at a distal location (e.g., from the feet with a weighing scale [104] or the wrist with an accelerometer [108]). Flexible strain or pressure sensors placed over a superficial artery can measure waveforms indicative of BP via the tonometric principle [109–112]. While such “electronic-skin” is convenient, applanation will likely be challenging. Note that while phonocardiography can measure a proximal waveform via the first heart sound, it neither eliminates PEP nor is more convenient than ECG.

Noncontact Methods

Videoplethysmography (VPG) employs a regular camera to measure arterial waveforms from the skin. The principle is the same as reflectance-mode PPG but with ambient/external light serving as the excitation source. The instantaneous blood volume is registered as a subtle color change in each pixel of the camera [113–119]. Both proximal and distal waveforms can be obtained from, for example, the face and hand [120, 121]. Infrared thermal imaging employs a highly sensitive camera to likewise measure arterial waveforms from the skin [122, 123]. However, the principle is that the measured skin temperature changes with pulsatile blood flow due to heat exchange between vessels and surrounding tissue. Both proximal and distal waveforms have been obtained from the neck and wrist. Radar based detection of chest movement due to the heartbeat, which provides a proximal waveform, has also been demonstrated [124, 125]. Recent developments of an ultra-wide band (UWB) class of radars are portable and inexpensive. Higher frequency ranges are more suitable for measuring cardiac activity. Measuring relative displacements of arterial walls at different locations with UWB could potentially be used for measuring both proximal and distal waveforms.

B. PTT Estimation

We first review classical PTT estimation methods that employ feature detection and have been applied for cuff-less BP monitoring. We then briefly mention potential methods that are based on arterial tree models.

1) Classical Feature Detection Methods

These methods estimate PTT using the following steps: (a) sampling and filtering the proximal and distal waveforms; (b) detecting the beats in the waveforms; (c) detecting the feet or other features within the beats; and (d) calculating PTT as the time delay between the features. Handling artifact in the waveforms (e.g., due to motion) is also crucial in practice, yet often not mentioned. The detection of beats and artifact are significant enterprises by themselves. Full discussion of these steps is thus worthy of its own review. We simply provide references for these steps while discussing the remaining steps in detail for the commonly measured waveforms.

Aortic PTT (in the form of PWV = l/PTT) is often determined from proximal and distal BP waveforms for large artery stiffness quantification and improved cardiovascular risk stratification [126]. Hence, much of our knowledge of PTT estimation stems from these waveforms.

BP Waveforms

For cuff-less BP monitoring (e.g., via un-calibrated BP waveforms obtained with electronic-skin), we suggest a sampling rate of 1 kHz, which would yield a BP measurement resolution of about 1.5 mmHg or less for calibration curves reported in the literature (see Section V.C). (Note that this BP measurement resolution was derived by dividing the slopes of the calibration curves reported therein by the sampling rate.) The 1 kHz sampling rate is actually suitable for all waveforms discussed below. We also suggest subsequent application of a low-pass filter with cutoff frequency of 15–20 Hz (or lower for artifact suppression), as BP energy almost entirely resides within this frequency even for heart rates up to 180 bpm. Alternatively, a lower sampling rate may be used to acquire the waveform (e.g., 40 Hz), and the BP measurement resolution may then be improved by digitally upsampling the waveform to 1 kHz or averaging the PTT estimates over many beats. We also make reference to a few methods for BP beat and artifact detection [127–131].

As discussed above, the BP waveform foot represents the preferred feature for detection, since it is minimally impacted by wave reflection. The foot location may be strictly defined as the diastolic minimum time [43, 47, 132, 133]. However, other definitions of the foot location have also been used, including the time of (a) the maximum (or a fraction of the maximum) first derivative with respect to time between the diastolic minimum and systolic maximum [48, 133], (b) the maximum second derivative with respect to time between the diastolic minimum and maximum first derivative with respect to time [134], (c) a fraction of the pulse pressure [49, 135], and (d) the intersection of the horizontal line through the minimum and the tangent line fitted through points near the maximum first derivative with respect to time (i.e., intersecting tangent method) [43, 45, 134].

As with any type of waveforms, PTT is then estimated by subtracting the distal foot time from the proximal foot time of the same beat. Averaging or taking the median of the PTT estimates over a number of beats is often employed to mitigate the effects of measurement and physiologic (e.g., respiratory) artifact as well as erroneous beat detections [136, 137].

The various foot definitions have been compared in terms of the consistency of the PTT estimates [134] and correlation between PTT and BP [46]. Overall, the intersecting tangent method, as shown in Fig. 7, revealed the best PTT-BP correlation and robustness to artifact. Note that PTT determined from carotid and femoral artery BP waveforms ranges from about 30 ms (old and hypertensive) to 90 ms (young and optimal BP) at rest [138, 139].

Figure 7.

Feature detection methods are classically applied to proximal and distal waveforms to estimate PTT and pulse arrival time (PAT). PEP is the pre-ejection period.

PPG Waveforms

These waveforms are morphologically similar to BP waveforms, so many of the methods used for the latter have been applied to the former. But, as is typical of non-invasive measurements, PPG waveforms are highly susceptible to measurement (e.g., motion) and physiologic (e.g., respiratory) artifact [51–56, 140]. We thus suggest heavy band-pass filtering (low and high cutoff frequencies of about 0.5 and 10 (or even lower) Hz) prior to beat detection and make reference to several PPG beat detection and artifact handling methods [51–56, 140, 141]. Similar foot location definitions have been applied to PPG waveforms, including the (a) diastolic minimum time [142–144], (b) intersecting tangent method [98], (c) times of maximum derivatives with respect to time [145–148], and (d) time to reach a fraction of the pulse height [143, 147]. Some studies have compared the efficacy of such definitions, but the overall results are inconclusive [143, 149, 150]. The definitions were also studied for blood volume waveforms measured via ultrasound rather than PPG, and the intersecting tangent method (see Fig. 7) and the time to reach 20% of the pulse height performed best in terms of consistency of the PTT estimates [151]. The most popular definitions for PPG foot detection, however, appear to be the diastolic minimum time and the times of maximum derivatives with respect to time (see Table II). Interestingly, the systolic maximum time has also been successfully used as a feature [143]. By contrast, the peak-to-peak time delay between BP waveforms is often a poor marker of BP and can even be negative due to wave reflection (see, e.g., Fig. 4.23 in [18]). The timing of the PPG foot referenced to the ECG R-wave (PAT in Fig. 7) at rest typically ranges from 180 to 260 ms (finger) [98, 147, 148, 152, 153], 125 to 155 ms (ear) [152, 153], and 180 to 330 ms (toe) [144, 152, 153].

ICG Waveforms

As alluded to above, the ICG waveform is usually given as the derivative of the thoracic impedance with respect to time (dZ/dt). The “B-point” of the dZ/dt waveform represents the onset of cardiac ejection. The most popular definition of the B-point time is the location of zero-crossing prior to the maximum dZ/dt as shown in Fig. 7 [83]. Since the B-point can occur after this zero-crossing, another definition is the time where dZ/dt reaches 15% of its maximal value [154]. However, both of these definitions do not consider respiration, which can cause baseline shifts in dZ/dt [83]. In general, ICG waveforms are heavily corrupted by artifact similar to PPG waveforms [57–62]. As indicated above, respiration is particularly problematic. We thus suggest heavy band-pass filtering prior to beat detection [57–62]. Since differentiation amplifies high-frequency noise, another possibly more effective approach is to first integrate dZ/dt and then process the waveform along the lines of PPG waveforms. Note that the timing of the B-point referenced to the ECG R-wave (PEP in Fig. 7) typically ranges from 80 to 140 ms at rest [62].

Noisy Waveforms

Straightforward application of the above feature definitions to noisy waveforms has been shown to result in unreliable PTT estimates [134]. One possible method to improve noise robustness is to represent the upstroke of each beat with a parametric model, estimate the model parameters by fitting the model to the waveform, and then detect the foot time using a model parameter [155]. Another potential method, which is applicable to proximal and distal waveforms of the same type, is to extract the upstroke of the distal waveform, shift this upstroke leftward in time until the squared error between it and the normalized proximal waveform is minimized (or until the cross correlation between it and the normalized proximal waveform is maximized), and then select this “least squares” time shift as the foot-to-foot time delay [43]. Other possible methods are described below.

ECG Waveforms

These waveforms are different in shape from arterial waveforms. An advantage of using ECG waveforms is that they facilitate detection. That is, R-waves are easier to detect than waveform feet due to their unique, high frequency nature. A number of effective R-wave detection methods have been described, with the most popular being the Pan and Tompkins method [156]. Note that R-wave detection eliminates the need to locate the beats of the distal waveform. We also make reference to a few ECG artifact handling methods [157–159]. While the R-wave location has been most widely used to define ECG timing [47, 155], other features such as the Q-wave time [160] and the time of the maximum derivative of ECG with respect to time [146, 148] have also been employed. As shown in Fig. 7, the R-wave is the peak of the QRS complex, while the Q-wave is defined as the minimum in the complex before the occurrence of the R-wave [161]. Since the Q-wave indicates the start of the ventricular electro-mechanical delay and this delay may be relatively constant [162], detection of this feature may reduce PEP variability. Further, the Q-wave is less sensitive to electrode positioning [146]. But, R-wave detection is easier.

2) Potential Arterial Model-Based Methods

Recently, and as indicated in the next paragraph, methods based on arterial tree models have been proposed in an attempt to improve PTT estimation. The crux of these methods is to estimate PTT from the entire waveforms rather than just a single feature by mathematically eliminating the reflected wave. These methods may thus provide an artifact-robust estimate of the true PTT (i.e., PTT in the absence of wave reflection) without requiring the need for beat detection. However, the methods have been tested mostly on invasive BP waveforms only. Further, they carry great complexity, which may increase the PTT error variance.

These methods model the arterial tree using a transfer function. The transfer function is either defined by 1) a black-box model [163, 164] or 2) a physics-based model of wave propagation and reflection (such as the one shown in Fig. 5b) wherein the model parameters include the true PTT [46, 165, 166]. The transfer function is identified for each individual by optimally coupling one waveform to the other waveform. For the black-box models, PTT is then derived as the slope of the phase response [163], the average of the phase response [167], or the time delay of the impulse response (time domain version of the transfer function) [163, 164]. For the physics-based models, PTT is given as the corresponding subject-specific parameter. One of the methods is able to track PTT from just two distal waveforms [168]. This method defines the transfer functions relating the proximal waveform to each distal waveform by the model of Fig. 5b and then estimates the model parameters per individual using multi-channel blind system identification.

C. Calibration of PTT to BP

We first review the standard method for calibrating PTT estimates to BP values. We then describe less investigated methods that could improve upon the standard method.

1) Standard Calibration Method

The standard method for constructing a calibration curve from PTT to BP is shown in Fig. 8a and is employed as follows: (1) define a mathematical model to relate PTT to BP in terms of (typically) two unknown parameters; (2) measure PTT and cuff BP from a subject during interventions that perturb BP and thereby obtain multiple pairs of PTT and BP values; and (3) estimate the parameters for that subject by fitting the model to the PTT-BP measurements [38, 94, 135, 143, 145, 150, 155, 169–186]. While the model may be fitted to arrive at separate parameter estimates for calibrating PTT to diastolic, mean, and systolic BP, calibration of a single PTT estimate to multiple BP values cannot be effective when these values are not varying in the same direction. BP values may then be monitored from the subject without a cuff by obtaining PTT estimates and invoking the calibration curve. This curve is periodically updated to account for changes due to aging and disease or errors in the curve. We elaborate on these steps.

Figure 8.

Calibration of PTT estimates to BP values typically involves one-time (or periodic) cuff BP measurements and interventions to perturb BP. (a) Standard calibration method. (b) Well-known interventions for perturbing BP. SP and DP are systolic and diastolic BP.

Step 1

The mathematical relationship from PTT to BP has been defined using physical models and empirical regression models. Most of the physical models are based on the Moens-Kortweg and Bramwell-Hill equations (Eq. (6)) with an assumed function to relate the elastic modulus or compliance to BP [94, 169, 171, 173, 175–177, 187, 188]. A popular physical model, which may be derived by substituting Eq. (1) into Eq. (6), is given as follows:

$$\text{BP}={\mathrm{K}}_1\text{ln}(\text{PTT})+{\mathrm{K}}_2$$ (10)

where K_i are unknown, subject-specific parameters. Another popular physical model, which may be derived by substituting Eq. (3) into Eq. (5) and assuming (P-P₀) > P₁ (i.e., collagen recruitment has initiated), is given as follows:

$$\text{BP}=\frac{{\mathrm{K}}_1}{\text{PTT}}+{\mathrm{K}}_2$$ (11)

Experimental studies have indeed shown that 1/PTT, rather than PTT, is linearly related to BP over a wide BP range (see Fig. 1b) [44, 45, 179]. Further, one study did indicate that this model fitted BP-PTT data better than Eq. (10) [179]. Note that other physical models have also been derived from Eqs. (5) and Eqs. (6) by invoking a sigmoidal compliance-BP relationship [188], assuming the elastic modulus to be a function of pulse pressure [94], or accounting for the changes in arterial vessel radius [175]. However, the physical models of Eqs. (10) and Eqs. (11) are not satisfying asymptotically (i.e., as PTT approaches 0 or ∞). A more recent physical model based on Eq. (6) is able to predict reasonable asymptotic behavior and is given as follows:

$$\text{BP}=\frac{{\mathrm{K}}_1}{{(\text{PTT}-{\mathrm{K}}_2)}^2}+{\mathrm{K}}_3$$ (12)

[187]. Regression models based on experimental PTT-BP data from the literature have been more popular [143, 145, 150, 155, 170, 172, 174, 178–180, 182–184, 187]. Many of these studies assume PTT is related to BP via a line with a slope and intercept. However, some studies have used quadratic and other nonlinear functions [145, 179, 184]. Nonlinear models including Eq. (12) may afford reasonable asymptotic behavior and greater accuracy overall. However, they are generally characterized by more than two unknown parameters, which carry the burden of requiring more PTT-BP pairs for their estimation (see Step 3 below). Further, since practical interventions may not markedly change BP (see Fig. 8b), the parameters of a linear model may be all that is possible to estimate. Taking all factors into consideration, we recommend Eq. (11) for the mathematical model, with some care to preclude non-physiologic BP values.

Step 2

To estimate the parameters in the calibration curve accurately, PTT and BP should be simultaneously obtained over a wide range of BP values. A commonly employed intervention to acutely increase BP has been exercise (e.g., climbing steps, cycling on an ergometer) [145, 150, 174, 175, 180]. Some other interventions for perturbing BP that have been performed include postural changes (i.e., seated, supine, standing) to increase and decrease BP [183, 184], sustained handgrip to increase BP [155], and the Valsalva maneuver to transiently decrease BP [184]. Fig. 8b shows the extent to which these and other well-known interventions perturb BP as well as their limitations, with references providing further information on the interventions [189–200]. As can be seen, inducing appreciable, steady-state BP changes, especially reductions in BP, is challenging. We can at least recommend cold pressor and mental arithmetic to increase BP. Note that other interventions for perturbing BP that have been employed include anesthesia induction [178], surgery [169], and ICU therapies [143, 172]. While these methods produce major BP changes [171], they are limited to hospitalized subjects and are therefore not very germane to hypertension management. Further note that these interventions induce BP changes via different physiologic mechanisms. Hence, a calibration curve constructed via one intervention may not be effective when tested during another intervention.

Step 3

To estimate the model parameters, the number of measured PTT-BP pairs must obviously exceed the number of parameters. Further, the accuracy of the parameter estimates generally improves with the ratio of the number of data pairs to the number of parameters. Straightforward least squares regression has been the most commonly employed method for parameter estimation [143, 145, 155, 172–175, 181, 183]. More sophisticated methods, such as maximum likelihood estimation, could also be employed. However, we doubt that the improved parameter estimation accuracy would make a difference overall, as there are far greater sources of error in the PTT-based approach for cuff-less BP monitoring. Some calibration curves reported in the literature are as follows: diastolic BP = m·PTT+b, where m = −1.4, −0.5, −1.6 mmHg/ms and b = 197, 164, 125 mmHg for an animal (Fig. 1), healthy human [98], and inpatient [134], respectively.

Calibration Frequency

The calibration curve has been constructed both one-time at the beginning of a study [94, 145, 155, 170, 173–176, 179, 180] and periodically throughout a study [143, 169, 172, 177, 178, 182]. However, in most of the one-time calibration studies, it was mentioned that periodic calibration should be considered to improve the BP measurement accuracy. Amongst the periodic calibration studies, the period between calibrations was always within two hours. The very short periods (i.e., far less than the time constants governing aging and disease) may possibly be due to the fact that PTT values have most commonly been obtained as PAT through peripheral arteries, which is affected by PEP and smooth muscle contraction changes (see Section V.D).

2) Potential Calibration Methods

A few methods for improving the accuracy of calibration have been proposed. These methods all involve including covariates in addition to PTT in the mathematical model so as to better predict BP. The additional covariates that have been employed include heart rate [172, 182] and short-term PTT variability as a marker of neural control [183]. These and other covariates may be particularly useful for calibrating PAT through peripheral arteries to BP by mitigating the effects of PEP and smooth muscle contraction. Note, however, that heart rate and PEP may not correlate well [95].

Several methods for improving the convenience of calibration have been proposed. These methods attempt to eliminate the need for interventions to perturb BP and/or cuff BP measurements.

One relatively popular method uses a population average value for one model parameter while estimating the other parameter from one cuff BP measurement [94, 145, 185]. In this way, a BP perturbation is avoided. However, using population averages can yield less accurate BP values.

Another method exploits the cuff deflation to both perturb and measure BP [170]. In particular, average BP is lowered along the length of the arm by the cuff deflation; the amount of the BP decrease is estimated using a finger-cuff PPG sensor; and PTT is estimated before cuff deflation and during the BP decrease. A calibration curve may then be defined from the two resulting PTT-BP pairs. However, the requirement of a finger-cuff PPG is a disadvantage.

A third method capitalizes on the natural pulsatile variation in BP (i.e., BP nominally varies from 80 to 120 mmHg with each heartbeat [181]). That is, the parameters of a nonlinear arterial model are estimated by optimal coupling of a proximal BP waveform to a distal BP waveform. The parameter estimates then define the calibration curve. However, the BP waveform requirement is a drawback.

A fourth method exploits the hydrostatic effect on BP [173]. More specifically, PTT is obtained while the subject’s hand is lowered and then raised by a known amount. In this way, the corresponding BP change may be determined without a cuff as ρgh, where ρ is blood density, g is gravity, and h is the vertical displacement of the hand raise. However, this method is only applicable to PTT estimates from the hand.

A final method employs subject anthropomorphic data to determine the model parameters [171]. More specifically, multiple calibration curves are constructed using the standard method for groups of subjects of similar age and gender, and the appropriate calibration curve is subsequently determined for a new subject from just this information. However, a vast amount of data is required for this “universal calibration” method to be effective.

D. Summary of Results

We summarize the results of studies performed to date that have applied the PTT-based approach for measuring BP values and/or tracking BP changes (i.e., excluding the calibration step). Our summary includes only those studies that have employed continuous and non-invasive waveform measurement methods (see Section V.A) and reported quantitative results on experimental data. About four-fifths of these studies employed ECG to obtain a surrogate of the proximal waveform; about three-fifths of the studies employed PPG at the finger to measure the distal waveform; and about half the studies used both ECG and finger PPG to measure the proximal and distal waveforms.

1) Studies Employing ECG and Finger PPG

Table II provides a summary of the methods and results of each study. While these studies are common in terms of the waveform measurement methods, they are methodologically different otherwise. Hence, this table should be interpreted with caution. Firstly, the reported results via correlation and Bland-Altman analyses are dependent on the investigated BP range. In particular, the correlation coefficient is often higher for wider BP ranges, whereas the root-mean-squared-error (RMSE) is typically lower for narrower BP ranges [201, 202]. Note that, in many of the studies, the diastolic BP range was narrower than the systolic BP range. Secondly, the degree of difficulty of the evaluation varied considerably from easy (e.g., calibration curve constructed and tested on the same subjects using the same intervention or frequent recalibrations) to hard (e.g., ICU subjects with wide BP changes). So, while we do not advise direct comparisons of the results of different studies in the table, we do attempt to make some useful observations regarding the results in the table on the whole below.

Several of the studies in Table II report correlation coefficients between finger PAT (or some transformation thereof) and BP values. Hence, we aggregated their results by computing a simple average of the mean correlation coefficient of each study. For the study in which multiple PAT estimates were reported [143], we used the highest correlation coefficient. The resulting correlation coefficients were 0.58±0.09 (mean±SE) for diastolic BP and 0.79±0.05 for systolic BP. So, finger PAT correlated well with systolic BP while showing some relationship to diastolic BP.

Finger PAT is affected by smooth muscle contraction, as it includes PTT through peripheral arteries, and by PEP. Yet, the correlation between finger PAT and systolic BP in particular was fairly good. Although systolic BP generally varied more than diastolic BP in these studies, we believe there are other reasons for this result. One such reason could be that the ventricle and arteries are common determinants of PAT and systolic BP (which equals pulse pressure plus diastolic BP). Another reason is that, for ethical considerations, the testing was often conducted only over limited physiologic conditions in each subject. For example, several of the studies employed exercise wherein both PEP and PTT may decline while systolic BP rises. Invasive animal studies conducted over a wide BP range have indeed shown that PAT correlates much less with both systolic BP [44, 45] and diastolic BP [44, 45] than PTT. However, ECG can be easily and robustly measured, which is a great advantage in practice.

For the studies employing periodic calibration, the calibration periods ranged from 5-min to ~110-min. Not surprisingly, one-time calibration studies generally showed higher errors than these studies. The average BP RMSE of the one-time calibration studies was about 8 mmHg. Further, in contrast to the correlation results, diastolic BP appears to have been consistently measured with greater accuracy than systolic BP on the whole. However, this finding could again be due to the fact that diastolic BP often changed less than systolic BP.

We also point out two unique studies [94, 185] in the table. One of these studies [185] provided an independent assessment of two PTT-based BP monitoring methods in terms of the required period for calibration. It was concluded that one of the methods [169] could provide very accurate BP measurements for calibration periods up to 6-min, while the other method [94] better reflected BP changes. The other study [94] was the only one in the table to employ an AAMI protocol and reported BP errors near AAMI limits.

2) Studies Employing ECG and Other Distal Waveform Measurement Methods

We classify these studies into two groups based on the distal waveform measurement site. In the first group, the site was an arm location other than the finger [92, 133, 176, 203–206]. In the second group, the site was the head or lower body [175, 204, 207].

In the first and larger group of studies, the distal waveform was measured by placing a non-flexible pressure sensor over the radial artery [133, 203, 204, 206], reflectance-mode PPG sensor on the brachial artery [176, 205], or EBI electrodes around the brachial artery [92]. Various PAT estimation methods were used similar to Table 2. Since these studies all estimated PAT through the arm, we likewise computed aggregate correlation coefficients between the arm PAT estimates and BP values. The resulting correlation coefficients were 0.72±0.07 for systolic BP and 0.43±0.09 for diastolic BP. Not surprisingly, these values are similar to those obtained from finger PPG (see above). Despite their methodological differences, the studies largely yielded similar results. The one exception was the study employing EBI, which reported a correlation coefficient of only up to 0.28.

In the second group of studies, the distal waveform was measured by placing a non-flexible pressure sensor over the temporal artery (forehead) [204], a transmission-mode PPG sensor on the earlobe [175], or a reflectance-mode PPG sensor on the buttocks (via a toilet seat) [207]. PAT was likewise estimated. The first and third studies reported correlation coefficients of about 0.80 for systolic BP, while the second study showed a systolic BP RMSE of 8.6 mmHg via a onetime calibration and exercise. While these results are comparable to those obtained from arm distal waveforms, the number of studies is so small that it is difficult to draw any conclusions on the best distal waveform measurement site when ECG is used for proximal waveform measurement.

3) Studies Employing Actual Proximal Arterial Waveform Measurement Methods

We also classify these studies into two groups based on where PTT was estimated. In the first group, PTT was estimated through peripheral arteries and the arm in particular [92, 98, 178, 206, 210]. In the second group, PTT was estimated through central arteries [155, 171].

The first group comprised most of the studies. One of these studies offered a unique assessment of PTT estimates by employing hemodynamic drugs in healthy subjects so as to vary BP over a wide range [98]. ICG and finger PPG were employed to obtain the proximal and distal waveforms, and PTT was estimated as the time delay between the standard B-point definition of the ICG waveform and the minimum of the PPG waveform. PAT to the finger was also estimated. Compared to these estimates, the PTT estimates showed higher correlation with diastolic and mean BP (0.66 versus 0.21) but comparable correlation with systolic BP (0.60). By contrast, two of the studies reported that PAT estimates provided better correlation to BP values than PTT estimates [92, 206]. One of the studies employed ICG and ECG to obtain proximal waveforms and finger PPG and brachial EBI to obtain distal waveforms from ICU patients [92]. Standard foot definitions were employed to estimate various time delays. All resulting PTT and PAT estimates showed relatively low correlation with BP values. The best correlation was between finger PAT estimates and systolic BP values (0.43). The other study used non-flexible pressure sensors on the brachial, radial, and dorsal pedal arteries as well as ECG and standard foot definitions to estimate various time delays during a sustained handgrip and exercise. In contrast to any of the PTT estimates (e.g., from brachial to radial arteries), the radial PAT estimates showed good correlation to systolic BP (0.73) during both interventions. The final pair of studies in the first group did not perform any comparisons with PAT estimates [178, 210]. One of these studies applied BCG (with a cushion seat form factor) and finger PPG to measure proximal and distal waveforms [210]. PTT was estimated as the time delay between the J-point of the BCG waveform and the peak of the PPG waveform. A subject-specific calibration curve was constructed via a linear model in PTT and exercise. The diastolic BP RMSE was small but only determined from five data points. The other study employed ear and finger PPG to obtain the waveforms and estimate PTT in patients undergoing anesthesia induction [178]. A calibration curve was constructed and updated every 5-min using a reference BP measurement. Diastolic BP was estimated best, with limits-of-agreement of −14.7 to 14.7 mmHg. Given the variability in the studies, it is difficult to conclude whether proximal arterial waveforms offer value over ECG waveforms when the distal waveform is measured from the arm.

There were two studies in the second group. One study employed ear and toe PPG and standard foot definitions to estimate PTT during surgery [171]. First, multiple calibration curves for different age (young/old) and gender groups were formed via an exponential model and training data from patients. The calibration curves for the different age and gender groups were noticeably different. Then, using an AAMI protocol, BP was measured from a new set of young and old patients by obtaining PTT estimates from these subjects and invoking the appropriate calibration curve. The diastolic BP error was 1.4±7.5 mmHg, which is within AAMI limits. The second study employed ICG and applied four reflectance-mode PPG sensors on the chest to obtain the proximal and distal waveforms [155]. PTT was estimated as the time delay between the standard B-point definition of the ICG waveform and a robust feature of the PPG waveform derived via parametric modeling (see Section V.B). A onetime calibration curve was constructed using a linear model in PTT and a sustained handgrip. The mean BP error was −0.8±5.1 mmHg for measurements made during the same intervention but two weeks after construction of the calibration curve. However, neither of these studies reported systolic BP errors.

VI. Conclusions

A. Summary

In summary, there is a mismatch between the theory and current practice of PTT-based monitoring of BP. The theory indicates that diastolic BP may be tracked for periods on the order of months to a few years by estimating PTT through central arteries via the foot-to-foot time delay between proximal and distal waveforms (see Section III). However, for convenience, common practice has been to employ ECG to measure a surrogate of the proximal waveform, obtain the distal waveform from the arm via mainly finger PPG, and detect the R-wave-to-foot (or sometimes even the R-wave-to-peak) time delay between these waveforms (see Section IV.D). The resulting PAT estimates through peripheral arteries correlate well with systolic BP, rather than diastolic BP, and can require re-calibration with a cuff on the order of just minutes to hours for accurate BP readings (see Table II). In fact, we found only two out of about 40 studies aiming to achieve non-invasive, automated, and cuff-less BP monitoring that estimated PTT through central arteries [155, 171]. Both of these studies happened to report promising accuracy in measuring diastolic and mean BP, which often correlate tightly. However, due to the paucity of studies, there is no proof that strict following of the theory affords greater accuracy than taking practical deviations from the theory.

B. Suggested Future Research

There are a number of directions for future research on the PTT-based approach for cuff-less BP monitoring. We suggest a few that we feel would be particularly fruitful.

Research is needed to establish more convenient methods for measuring the proximal arterial waveforms. The ECG waveform as a surrogate of the proximal waveform has at least three important advantages. In particular, it is easy to measure, robust against artifact, and uniquely affords tracking of systolic BP. However, this waveform introduces PEP, which may be a major confounding factor (see Eq. (9)) that necessitates frequent recalibration. By contrast, ICG can measure an actual proximal waveform but not with enough convenience. Some possible methods for investigation include BCG, electronic-skin, and imaging modalities such as VPG and UWB radar. However, use of such ultra-convenient methods may bring up more problems. Likely problems include waveform artifact and measurement of systolic BP. These problems could be at least partially solved using improved PTT estimation methods based on arterial modeling or advanced signal processing.

Basic scientific studies are needed to understand the limitations of PPG. This method appears to be quite effective in measuring the requisite waveforms. In particular, it can provide distal waveforms from the finger or toe, the latter of which would permit PTT estimates through central arteries, and a proximal waveform from the ear. Further, PPG may have unknown potential. However, one concern is as follows. PPG and BP waveforms obtained from the same arterial site are not time aligned. Rather, the PPG waveform often lags behind the BP waveform. This viscoelastic delay could vary with BP and smooth muscle contraction. One study showed that, for the same BP level, PAT estimates via finger PPG were larger during exercise than recovery [211]. This finding could be due to a variable viscoelastic delay (though other causes are also possible). Hence, this phenomenon should be carefully investigated. The impact of PPG contact pressure on PTT estimates also deserves more attention.

Studies are needed to determine if arrhythmias adversely impact PTT estimates. We specifically suggest a systematic comparison of PTT estimates during normal sinus rhythm and atrial fibrillation, which is a common arrhythmia.

Research is surely needed to improve the calibration of PTT to BP in terms of accuracy and convenience. Methods involving a BP perturbing intervention or frequent re-calibrations with a cuff may not be adopted. One potential method is universal calibration wherein the parameters of the model relating PTT to BP are determined simply from the subject’s age, gender, and other such information including cardiovascular risk factors. To enhance the accuracy without significantly compromising convenience, a single cuff BP measurement could be obtained from the subject every so often. However, to implement this method, the following steps would first have to be performed: (a) collection of training data comprising pairs of PTT estimates and BP values during a set of BP varying interventions per subject from a vast number of diverse subjects; (b) estimation of the parameters of a calibration model for each subject; and (c) regression of these parameters on simple subject information. Collecting the necessary training data is a serious endeavor but may be the best way to popularize the PTT-based BP monitoring approach.

Research is needed to enable independent determination of systolic and diastolic BP. As mentioned above, a single PTT estimate cannot indicate these two BP values when they are not varying in the same direction (e.g., isolated systolic hypertension). This problem could be addressed by including additional simple covariates, such as heart rate, in the calibration model [172, 182] or by estimating multiple PTT values per beat via arterial modeling [46]. Note that PTT estimates should correlate better with BP values than these covariates do to offer any real value.

Finally, research is needed to find the right compromise between accuracy and convenience. We hypothesize that accuracy will increase, but convenience will decline, with greater adherence to the theory. Studies should be performed to compare the accuracy of methods of increasing compliance to the theory. A plot of accuracy versus adherence to theory may show a monotonic relationship. However, the “knee of the curve” would indicate the optimal balance between theory and practice. Ideally, these and other studies would obtain reference BP measurements via expert-operated auscultation rather than oscillometry, which can be inaccurate in subjects with certain conditions (see Section II) [11].

C. Expectations for PTT-Based BP Monitors

Our expectations for a useful PTT-based BP monitor for hypertension management are as follows. In terms of usability, the monitor must be non-invasive and automated. Further, the form factor should be easier-to-use than a cuff, else it will not be adopted. A single sensor unit form factor such as a smartphone or wearable would be ideal. Note that the monitor must also account for hydrostatic effects, which can greatly impact BP [212]. In terms of accuracy, our expectations for initial monitors are tempered by the reality that there are a number of significant sources of error in the approach. We would hope that first-generation monitors could do at least one of the following: (a) reliably estimate aortic PWV in order to assess cardiovascular risk independent of BP more conveniently than traditionally employed tonometry [126]; (b) track BP changes (rather than BP levels) to help control BP in patients with known hypertension; and (c) indicate whether BP levels are not of concern or should be measured with a cuff to better detect hypertension. If serious innovations can be made, it may then be reasonable to expect that second-generation monitors and beyond would be able to reliably measure both absolute BP levels and BP changes in subjects with a broad array of conditions. In addition, we hope that all monitors would comply with the AAMI standard [10], the British Society of Hypertension standard [213], and/or the new IEEE Standard for Wearable Cuff-less Blood Pressure Monitoring Devices (IEEE Standard 1708) [214].

In conclusion, while much progress has been made on ubiquitous BP monitoring via PTT, significant work is still needed to best realize this approach in practice. We hope that this review facilitates future advances in this area.