Perceptual decision related activity in the lateral geniculate nucleus

Abstract

Fundamental to neuroscience is the understanding of how the language of neurons relates to behavior. In the lateral geniculate nucleus (LGN), cells show distinct properties such as selectivity for particular wavelengths, increments or decrements in contrast, or preference for fine detail versus rapid motion. No studies, however, have measured how LGN cells respond when an animal is challenged to make a perceptual decision using information within the receptive fields of those LGN cells. In this study we measured neural activity in the macaque LGN during a two-alternative, forced-choice (2AFC) contrast detection task or during a passive fixation task and found that a small proportion (13.5%) of single LGN parvocellular (P) and magnocellular (M) neurons matched the psychophysical performance of the monkey. The majority of LGN neurons measured in both tasks were not as sensitive as the monkey. The covariation between neural response and behavior (quantified as choice probability) was significantly above chance during active detection, even when there was no external stimulus. Interneuronal correlations and task-related gain modulations were negligible under the same condition. A bottom-up pooling model that used sensory neural responses to compute perceptual choices in the absence of interneuronal correlations could fully explain these results at the level of the LGN, supporting the hypothesis that the perceptual decision pool consists of multiple sensory neurons and that response fluctuations in these neurons can influence perception.

we have known for decades that in mammals the retina sends input directly to the lateral geniculate nucleus (LGN) of the thalamus, which, in turn, relays this information to the primary visual cortex. In primates this pathway is critical for conscious visual perception (Casagrande and Ichida 2011; Jones 2007; Logothetis 1998; Saalmann and Kastner 2011; Schmid et al. 2010; Sherman and Guillery 2001). What has remained a huge puzzle is what the LGN contributes to this process. Neurons in the LGN have been found to behave physiologically very much like their retinal inputs (reviewed in Kaplan 2013; Shapley 1990; Sherman and Guillery 2001), even though the LGN receives most of its synapses from nonretinal sources (reviewed in Casagrande and Norton 1991; Nassi and Callaway 2009). The argument has been made that these nonretinal inputs gate, or modulate, the main driving input from the retina depending on the behavioral context of the animal (reviewed in Casagrande et al. 2005). No studies to date, however, have examined LGN neural responses when an animal is actively making a perceptual decision. Specifically, the few studies that have measured LGN neural responses in awake behaving animals all reported that the basic receptive field characteristics are similar between awake and anesthetized preparations but that these responses are often modulated by eye movements, attention, and the arousal/alertness states of the awake animal (Alitto et al. 2011; Martinez-Conde et al. 2002; McAlonan et al. 2008; Ramcharan et al. 2001; Reppas et al. 2002; Royal et al. 2006; Ruiz et al. 2006). None of these studies, however, directly measured neural responses in the LGN when the animal was required to make a perceptual decision using the information available within the receptive fields of those LGN cells.

To explore the functional involvement of LGN during perceptual decision making, we aimed to address three main questions in this study. First, how sensitive are LGN parvocellular (P) cells and magnocellular (M) cells in detecting small changes in contrast compared to a monkey performing the same task? Second, do LGN cells show neural signatures differentiating a task that requires active detection from one that only requires passive fixation? Finally, can the activity of single LGN cells actually reflect a perceptual decision?

These questions are particularly interesting and relevant to study at the level of the LGN for several reasons. First, early physiological recordings revealed that single sensory neurons in the retina and LGN were exquisitely sensitive in detecting contrast (Barlow et al. 1971; Derrington and Lennie 1984; Enroth-Cugell and Robson 1966; Hubel and Wiesel 1961; Kaplan and Shapley 1986; Shapley et al. 1981), but rarely was the sensitivity of these single neurons directly compared with the simultaneously obtained psychophysical performance of the animal (but see Kang and Malpeli 2009). Second, early studies in anesthetized preparations also established that different LGN cell classes show distinct response profiles. Specifically, M cells, on average, are more sensitive to contrast compared with P cells (Kaplan 2013; Shapley 1990), implying that these M cells are largely responsible for sustaining our perception of contrast. In reality, however, behavioral measurements in monkeys with localized LGN lesions revealed the opposite effect, with P layer lesions producing a pronounced deficit in contrast sensitivity, whereas M layer lesions mostly only affected motion sensitivity (for example see Merigan et al. 1991; Merigan and Maunsell 1990; Schiller et al. 1990). Finally, it is known that stimulus-independent, random fluctuations of sensory neural responses can covary with the perceptual decisions of the animal. The strength of this covariation, quantified as “choice probability” (Britten et al. 1996), may carry information about the causal contribution of a sensory neuron to an emergent perceptual decision (Parker and Newsome 1998). Many studies have confirmed the presence of a weak but significantly above-chance choice probability in a number of visual cortical areas (Britten et al. 1996; Cook and Maunsell 2002; Dodd et al. 2001; Grunewald et al. 2002; Liu and Newsome 2005; Nienborg and Cumming 2006; Palmer et al. 2007; Purushothaman and Bradley 2005; Uka and DeAngelis 2004; Uka et al. 2005), but similar measurements are seldom made in subcortical structures (however, see Liu et al. 2013) and never in the LGN.

Therefore, in this study we measured the sensitivity and choice probability of LGN neurons during contrast detection, taking advantage of identified cell types in the LGN and the relative simplicity of its neural circuitry (Briggs and Usrey 2011; Casagrande and Norton 1991; Nassi and Callaway 2009). In addition, we also examined whether LGN P and M cells differ in their sensitivity, choice probability, and response dynamics. Finally we compared, in detail, LGN neural responses during active detection and passive fixation tasks. Aspects of the data presented in this article were previously published in abstract form (Jiang et al. 2012, 2013).

MATERIALS AND METHODS

Subjects

Two macaque monkeys (monkey 1: Macaca radiata, male, 7 kg, 10 yr old; monkey 2: Macaca mulatta, male, 8 kg, 12 yr old) served as subjects. These monkeys were treated and cared for under an approved protocol in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and the guidelines of the Vanderbilt University Animal Care and Use Committee.

LGN localization and Surgeries

The surgical procedures were described in detail in our previous publications (Royal et al. 2006; Ruiz et al. 2006). Briefly, these procedures were as follows. The LGNs first were localized via anatomic images created with a GE Signa 1.5-Tesla MRI scanner. Under general anesthesia (15 mg/kg ketamine), each monkey was secured in a titanium stereotaxic apparatus fitted with water-filled ear bars, which were used to define the anterior-posterior (AP) zero and the horizontal plane. A series of 1-mm-thick coronal images were taken anterior to the ear bars in overlapping 0.5-mm increments. LGN coordinates were calculated from images produced by GE 3.9 software and compared with the coordinates in a standard macaque stereotaxic atlas (Paxinos et al. 1999).

After the LGNs were located, the monkeys underwent surgeries for the implantation of head posts and recording chambers. Under general anesthesia (1–2% isoflurane in O₂) and using sterile procedures, a stainless steel head post (custom-made at Vanderbilt or courtesy of Dr. Andrew Rossi, National Institute of Mental Health) was secured to the front of each monkey's skull with titanium screws (2–4 mm; Synthes, West Chester, PA) and methyl methacrylate cement (Biomet, Warsaw, IN). A recording chamber (stainless steel, ∼20-mm diameter, custom-made at Vanderbilt or purchased from Crist, Hagerstown, MD) was centered over the right (monkey 1) or left (monkey 2) LGN using coordinates calculated from the MRI images (monkey 1: AP = 7, ML = 12.5; monkey 2: AP = 7, ML = 12) and was secured to the skull using titanium screws and methyl methacrylate cement. The bone enclosed within the recording chamber was removed in a subsequent sterile surgery.

Visual Stimulus Presentations and Behavioral Tasks

A computer-based real-time experimental operating system (Visual TEMPO; Reflective Computing, St. Louis, MO) controlled stimulus presentation time, monitored eye movements, and delivered reward or punishment in every trial. Eye position data were collected via an infrared camera (1 kHz, spatial resolution 0.1° × 0.1°, EyeLink 1000; SR Research, Kanata, ON, Canada) and fed to both the operating system (TEMPO) and the recording system (Plexon, Dallas, TX) via analog channels. Visual stimuli were generated in MATLAB Psychtoolbox (The MathWorks, Natick, MA) running on a Macintosh computer (G5) and displayed on a SONY Multiscan G420 monitor (refresh rate 90 Hz, resolution 1,280 × 1,024 pixels, visible area 36° × 29°; SONY, San Jose, CA). The RGB-to-luminance table for the monitor was calibrated periodically, and the nonlinearity was corrected accordingly.

Fixation task.

After recovering from the surgeries, the monkeys were initially trained to enter and exit primate chairs on command and to tolerate head fixation for extended periods. They were then placed in a dark recording room (∼2 cd/m²) and conditioned to fixate on a central fixation spot (0.1° × 0.1°, Michelson contrast 80%, on a uniform gray background with average luminance of ∼15 cd/m²) on the computer monitor positioned 57 cm in front of the monkeys. The monkeys were required to maintain fixation within a 1° × 1° (range: 0.5° × 0.5° to 1.5° × 1.5°) invisible window centered on the fixation spot. Continuous fixation for an extended period of time (200 to 800 ms) was rewarded with a drop of juice (0.1 to 1 ml).

Contrast detection task.

After learning to maintain stable fixation, the monkeys were trained to perform a two-alternative, forced-choice (2-AFC) contrast detection task (see Fig. 1A). The detection task was distinguished from the simple fixation task by changing the central fixation spot from a filled to a hollow square. This fixation square appeared at the beginning of each detection trial, and the monkey initiated the trial by bringing its gaze into the fixation window within 1,000 ms. After an initial fixation period of 200–500 ms (fixed at 350 ms during recordings), a monochromatic circular contrast patch (2° in diameter) or a Gaussian contrast profile (larger in size but containing the same overall energy as the circular patch) appeared on either the left or the right of the fixation spot. The contrast stimuli were 5.5° away (horizontally) from the central fixation spot during initial training and were subsequently moved around to establish threshold performance at different locations. During recordings, the diameter and position of the stimulus were adjusted daily so that in 50% of the trials the stimulus completely covered the classical receptive field (center and surround) of the cell despite small fixational eye movements, and in the other 50% of the trials the same stimulus appeared at a symmetrical location in the opposite visual hemifield. Both the contrast stimulus and the fixation point remained on for 200 ms (pulse function), after which two target dots (50–80% contrast) appeared, one in each hemifield. During initial training, the target dots were 8° away (horizontally) from the central fixation spot. During recordings, target dot positions were sometimes adjusted, but always nonoverlapping with the stimulus locations. Upon target onset, the monkey was allowed to make a saccade to one of the two target locations to indicate the side on which it had detected the contrast stimulus. If the monkey made a saccade to the correct target location within 2,000 ms after target onset and maintained its gaze within the invisible target window (1° × 1° to 10° × 10°, centered on the target dot) for 200 ms, it would receive a drop of juice reward (0.1 to 1 ml) at the end of the trial.

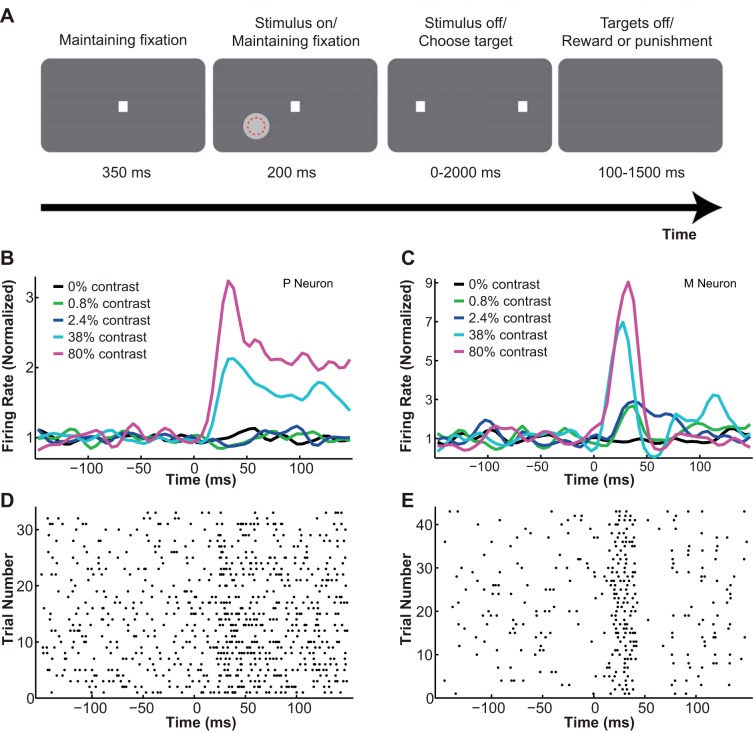
Fig. 1.

Contrast detection task. A: the two-alternative, forced-choice (2-AFC) contrast detection task. A contrast patch profile was briefly presented either in the receptive field of the cell (red dotted circle) or at a symmetric location in the other hemifield. The monkey made a saccade to 1 of 2 target locations to indicate its choice. B and C: peristimulus time histograms (PSTHs) of example lateral geniculate nucleus (LGN) P (B) and M neurons (C) at different contrasts. Stimulus onset, 0 ms. D and E: raster plots of the same LGN P (D) and M neurons (E) at high contrast (80%). Stimulus onset, 0 ms.

Circular patches and Gaussian contrast profiles.

To ensure that our threshold measurements were not biased by the type of contrast stimulus we chose, we compared the psychometric and neurometric performance using circular contrast patches as well as Gaussian contrast profiles in both the fixation and the detection tasks. For the patch, the stimulus diameter equaled the classical receptive field (center and surround) plus the fixation window diameter, ensuring that the same contrast would always fall onto the cell's receptive field despite the small fixational eye movements that continuously occur. To enable comparisons between the patch and the Gaussian profile, the Gaussian stimuli always had the same contrast levels (defined by the peak of the Gaussian curve) and the same energy levels (defined by the area under the Gaussian curve) as the corresponding patch stimuli. This meant the matching Gaussian profiles were larger in diameter compared with their circular patch counterparts. Fourier analysis on individual stimuli determined that during recordings, most (>90%) of the contrast stimuli used (both patch and Gaussian) had a significant amount (>50%) of energy distributed in the low to medium spatial frequency range (<10 cycles/deg), which can effectively drive most LGN P and M neurons under dim light conditions such as ours (Derrington and Lennie 1984). We did not, however, tailor our stimuli to optimally drive the receptive field center of each LGN cell, as is commonly done in anesthetized and paralyzed preparations. Because of a combination of factors such as the constant fixational eye movements in awake monkeys, the small receptive field sizes of LGN neurons, and the large number of trials required to establish stable psychometric and neurometric functions, we determined that it would not be feasible to optimize the stimulus for every neuron on every trial. We consider our choice of the visual stimulus to be appropriate for the purpose of this study because 1) our main goal was to study the link between LGN activity and perceptual choices, not to measure the absolute sensitivity of LGN neurons; and 2) our contrast patch stimulus was able to elicit brisk responses from both P and M LGN neurons (see Fig. 1, B–E). Compared with the contrast patches, the Gaussian profiles with the same overall energy yielded slightly poorer neurometric performance, presumably due to the fact that only a limited proportion of their total energy fell in the receptive field center of the cell.

Measuring psychophysical thresholds.

During each recording session, visual stimuli of 5 or 9 different contrast levels (ranging from −99% to 80% in contrast and encompassing the psychophysical threshold) were displayed in each hemifield. Contrast in this case was defined as the luminance difference between the stimulus and its background, divided by their sum. The polarity of the stimulus matched the sign of the cell being recorded (>0% contrasts for ON-center cells and <0% contrasts for OFF-center cells). Different contrast levels and stimulus locations were randomly mixed, with equal probabilities of left or right appearance and higher proportions of low- to medium-contrast trials to ensure accurate estimations of the threshold. When no stimulus was presented (i.e., 0% contrast, catch trials), the monkey was randomly rewarded in 50% of the trials for choosing either side. These trials were used to monitor the behavioral bias of the animal as well as to establish the link between LGN neural responses and the monkeys' choices in the absence of any physical stimulus.

Correction of behavioral biases in the detection task.

Precautions were taken to ensure unbiased estimations of the true threshold (Purushothaman and Bradley 2005). For example, during initial training, only high-contrast stimuli were used to teach the monkeys the procedures and rules of the detection task. After the monkeys' performance reached >95% correct, contrasts were gradually dropped until a stable psychophysical threshold was reached and an overall performance of 70%–85% correct was maintained around that threshold for >3 days. After threshold performance was established for the initial set of stimulus parameters, the monkey was taught to generalize the task over a number of dimensions including variations in stimulus size, stimulus eccentricity, and stimulus location (upper or lower visual field). The psychophysical threshold often increased when one or a few of these parameters were initially changed, in which case additional training was necessary to reestablish stable threshold performance under the new configuration. During training, behavioral biases (i.e., preferring to choose one side over the other) were monitored online via catch trials (i.e., 0% contrast, no stimulus present), and if found to be significant, biases were corrected by adjusting the relative frequencies of stimulus presentation on each side. It is noteworthy, however, that the 50:50 presentation ratio was always maintained during LGN recordings. Random guesses were strongly discouraged by introducing a between-trial “time-out” period for wrong choices (discounting trials in which no stimulus was present). Correct choices were encouraged by progressively increasing the reward size for consecutive correct trials. Additionally, before measuring the threshold each day, the monkeys spent at least 45 min in the recording room to fully adapt to the dim light condition.

Single-Unit Recordings

Extracellular activities from single and pairs of LGN neurons were recorded with Parylene-coated tungsten microelectrodes (1–3 MΩ; FHC, Bowdoinham, ME). The electrode was placed within a stainless steel guide tube (both sterilized), and then the electrode and the guide tube were both mounted on the recording chamber of the monkey via an adapter (FHC). The guide tube was manually pushed down to penetrate the dura, after which the electrode was slowly advanced into the brain via a motorized microdrive (FHC). Neural responses were amplified, band-pass filtered, and recorded (30 kHz; Plexon). Single-unit activities were sorted offline using a combination of principle component analysis (PCA), the Template Matching algorithm, and the Valley Seeking algorithm in three-dimensional feature space (Offline Sorter; Plexon).

Cell mapping and classification.

LGN cells were hand mapped first with a flashlight and then with an elongated bar (drawn in Psychtoolbox, MATLAB) sweeping across the visual field while the monkey was rewarded for maintaining fixation (0.1–1 ml of juice/500 ms). The bar's height, width, luminance, orientation, and direction of motion were adjusted by the experimenter to best define the receptive field borders. According to its location and response properties, each LGN cell was categorized as either ON- or OFF-center and either P or M type. Specifically, cells that showed increases in firing rates to contrast increments in their receptive field centers were classified as ON-center cells, whereas those that showed increases in firing rates to contrast decrements in their receptive field centers were classified as OFF-center cells. P or M LGN cells were classified offline on the basis of their physiological properties. According to our previous experience (Norton et al. 1988; Royal et al. 2006; Ruiz et al. 2006; Xu et al. 2001), two of the most reliable classification criteria were visual response latency and visual response transiency: 1) visual response latency: compared with P cells, M cells demonstrated shorter onset and peak latencies. To determine each neuron's latency, we plotted its peristimulus time histogram (PSTH) at high contrast (80% contrast for ON-cells and −99% contrast for OFF-cells) in 5-ms bins. We defined the onset latency as the time from stimulus onset to the first bin on the rising edge of the PSTH surpassing 3 SDs above base firing rate, and the peak latency as the time from stimulus onset to the bin with the highest amplitude in the PSTH. In our data set, compared with P neurons, M neurons had, on average, shorter onset latencies (P neurons: 25.2 ± 2.0 ms; M neurons: 19.6 ± 2.2 ms; P = 0.041, t-test) and shorter peak latencies (P neurons: 72.9 ± 5.3 ms; M neurons: 43.5 ± 3.3 ms; P = 0.000, t-test) (see Fig. 1, B–D, for example PSTHs and raster plots for typical P and M neurons). 2) Visual response transiency: compared with P cells, M cells exhibited greater transient bursts to the onset of visual stimuli. Using the same PSTH at high contrast, we computed for each neuron a transiency index, which was similar to the phasic/tonic index used in our previous studies (Irvin et al. 1986; Norton et al. 1988; Norton and Casagrande 1982). In this study the transiency index = 100 − (100–200 ms response − spontaneous response)/(0–100 ms response − spontaneous response) × 100. A larger transiency index indicated a greater level of transiency in the neural response. In our data set, M neurons responded more transiently than P neurons (P index: 22.95 ± 5.97; M index: 39.53 ± 7.5; P = 0.044, t-test) (see Fig. 1, B–D, for example PSTHs and raster plots for typical P and M neurons).

Some or all of the following classification criteria also were used in this study depending on the cell: 1) relative depth of the electrode and shifts in ocular dominance within the same penetration: the macaque LGN has 6 layers in the central 0°–17° of visual field representation, with the M neurons (layers 1–2) lying below the P neurons (layers 3–6). The ipsilateral eye projects to layers 2, 3 and 5, whereas the contralateral eye terminates in layers 1, 4 and 6. Shifts in ocular dominance therefore were useful for cell classification if all the receptive fields encountered in the same penetration remained at or below the horizontal meridian representation, in which case the electrode passed from the P layers at the top to the M layers at the bottom without reentering P layers (Erwin et al. 1999). 2) Receptive field size: at the same eccentricity, M neurons had larger receptive fields than P neurons.

Finally, because previous literature suggests significant overlap for the two populations in most response features (for example, see Norton et al. 1988; Irvin et al. 1993; Xu et al. 2001; White et al. 2001), we did not establish strict cutoff points for any of these classification criteria. Instead, we took into consideration all of these features together to achieve a more holistic, albeit not completely quantitative, method of cell classification.

Single-unit data set.

All the cells that could be clearly mapped and maintained long enough to characterize both psychophysical and neural responses (≥150 trials) in the detection task were included in our data set (overall: n = 89; monkey 1: n = 61; monkey 2: n = 28). We identified in this data set 41 ON-center P neurons, 27 OFF-center P neurons, 19 ON-center M neurons, and 2 OFF-center M neurons. Among these 89 neurons, 49 were also recorded in the fixation task. An additional 20 pairs of neurons were recorded only in the fixation task and incorporated only in our analysis of interneuronal correlation (see below).

Data Analysis

Behavioral, physiological, and eye movement data were recorded in Plexon; data analyses were performed using self-developed scripts in NeuroExplorer (Nex Technologies, Madison, AL) and MATLAB.

Psychometric functions.

Only recording sessions in which the monkey completed ≥150 trials and achieved an overall performance of >65% correct were included in this analysis. To generate a psychometric function, the proportion of correct responses at each contrast was plotted, and a Weibull function was fitted to the data:

$$P\left(c\right)=1-\left[0.5\cdot e^{-\left(c/\alpha \right)\beta }\right]$$ 1)

where P(c) is the probability of correct responses at a certain contrast level c, α is the contrast that supports threshold performance (82% correct), and β is the slope of the function.

Neurometric functions.

Basic procedures in computing neurometric functions were similar to those described in previous studies (Barlow et al. 1971; Britten et al. 1992; Purushothaman and Bradley 2005). To generate neurometric functions, we used spike counts in fixed time windows (0–150 ms after stimulus onset). For each neuron at each contrast level, an ROC (receiver operating characteristic) curve was computed, plotting for all possible signal detection criteria (spikes/s) the proportion of stimulus-inside-receptive-field (test) trials against the proportion of stimulus-outside-receptive-field (reference) trials in which the spike count exceeded the criteria. The area under the ROC curve indicated the predicted detection performance of an ideal observer using only the information available in this neuron's responses (Green and Swets 1966). To generate a neurometric function, each value for area under the ROC curve was plotted against its corresponding contrast, a Weibull function (Eq. 1, as described above) was fitted, and the neurometric threshold and slope were obtained from the fitted curve.

Eye movement analysis.

We analyzed fixational eye movements by computing 1) the average eye position deviation from central fixation, and 2) the average eye speed (i.e., moment-to-moment change in eye position) during fixation. An eye movement was characterized as a saccade if it met the following criteria: at least 8 ms of monotonic change in eye position and a peak velocity of at least 30°/s. The onset of the saccade was defined as the moment it reached a speed of 10°/s. The reaction time of the monkey was defined as the time from stimulus onset to saccade onset.

Choice probability.

Basic procedures in computing choice probability were similar to those described in previous studies (Britten et al. 1996). To compute choice probabilities, we used spike counts in fixed time windows (0–150 ms after stimulus onset). The choice probability at each contrast was measured by plotting as an ROC curve the proportion of choice-inside-receptive-inside trials (i.e., trials in which the monkey chose to saccade toward the receptive field location) against the proportion of choice-outside-receptive-field trials that exceeded each spike count criterion, and then computing the area under the ROC curve. A one-way ANOVA was used to test whether the stimulus contrast level had a significant effect on choice probability values. For all the contrast levels at which choice probability distributions did not differ (<4% contrast), neural responses were z-score normalized (with reference to the mean and SD of the neural response at each contrast level) and pooled together to generate a single choice probability value for each neuron. A grand choice probability was derived for the entire population by z-score normalizing each neuron's response, pooling together all the choice-inside and choice-outside-receptive-field trials, and then performing an ROC analysis on the population response distributions. Recent literature suggests that such grand choice probabilities derived from z-score normalized responses can sometimes underestimate the population choice probability (Kang and Maunsell 2012), so we also reported the mean choice probability alongside the grand choice probability. The significance of these choice probabilities was assessed using a permutation (i.e., bootstrapping) test (see below). To accurately estimate choice probability, only neural recordings that met the following criteria were included in this analysis: 1) behavioral bias ratio (choice-inside/choice-outside-receptive-field trials) >0.25 and <4, and 2) at least 10 choice-inside and 10 choice-outside-receptive-field trials were recorded. Of the 89 neurons recorded in the detection task, 75 (P neurons: 54, M neurons: 21) were included in the choice probability analysis according to these criteria.

Permutation test.

The significance of a choice probability value was assessed using a permutation (i.e., bootstrapping) test. Specifically, for all the z-score normalized trials used to compute choice probability, each trial was randomly reassigned as either a choice-inside or choice-outside-receptive-field trial, with the same probability that the monkey chose that location during the detection task. A choice probability value was then recomputed for the new spike count distributions using an ROC analysis. For each neuron this process was repeated 1,000 times to construct a “random” choice probability distribution. A measured choice probability was considered to be significant if it fell outside the 95% confidence interval of the mean of this “random” choice probability distribution.

Temporal dynamics of neurometric threshold, choice probability, and Fano factor.

The initial assessment of neurometric threshold and choice probability was done in a fixed time period (0–150 ms after stimulus onset). To characterize the temporal changes of these variables on a finer scale, we used two types of moving time windows: 1) a “growing” window started at 0 ms and grew in its width (i.e., duration) in steps of 12.5 ms. For example, the neurometric threshold at 100 ms was computed from the neural response during the 0–100 ms period, and the threshold at 200 ms was computed from the neural response during the 0–200 ms period. 2) A “sliding” window had a fixed width (i.e., duration) of 50 ms and advanced in steps of 12.5 ms. In this case, the neurometric threshold at 100 ms was computed by counting spikes in the 50–100 ms period, and the threshold at 200 ms was derived by counting spikes in the 150–200 ms period. To accurately describe the fine temporal changes in threshold and choice probability, only the most sensitive M and P neurons were included in this analysis. The criteria for choosing such neurons were as follows: 1) neurometric threshold <100% in at least 4 consecutive sliding time windows, 2) behavioral bias ratio (choice-inside/choice-outside-receptive-field trials) >0.25 and <4, and 3) at least 10 choice-inside and 10 choice-outside-receptive-field trials were recorded. According to these criteria, 57 neurons (P neurons: 37; M neurons: 20) from the detection task were included in the temporal dynamics analysis. Mean ± SE values are reported for the population dynamics of threshold and choice probability. Additionally, for the same data set, we also analyzed the temporal dynamics of the Fano factor using fixed 50-ms sliding windows that advanced in steps of 12.5 ms. For each neuron at each contrast level (stimulus-inside-receptive-field trials only), we computed the mean and variance of its firing rate. For each time window, individual variances were plotted against their corresponding means, with each data point representing one neuron at one contrast condition. The Fano factor for that time window was defined as the slope of the regression relating the variance to the mean. The estimated slope and its 95% confidence interval values are reported for the population dynamics of the Fano factor.

Interneuronal noise correlation.

Interneuronal correlations between pairs of LGN neurons (recorded on the same electrode) were computed by first z-score normalizing each neuron's response in each trial, according to its response mean and SD at each contrast, and then estimating the (nonparametric) correlation coefficient between the two z-scored firing rates. Because the Pearson correlation coefficient (r) is a biased estimator of the true correlation, especially for small sample sizes (n), an adjusted, unbiased estimator r′ (Lehmann 1957; Olkin and Pratt 1958) was reported alongside the Pearson r:

$$r\mathrm{\prime }=r\left[1+\left(1-r^2\right)/2\left(n-3\right)\right]\mathrm{.}$$ 2)

Additionally, fixed 50-ms sliding windows were used to characterize the temporal changes in interneuronal correlations during the detection and the fixation tasks.

Pooling Model

To simulate a perceptual decision pool of n units, n single neurons were randomly chosen, with replacement, from our entire data set. To construct a single trial at a given contrast, each chosen neuron's response was simulated by randomly drawing a number from a Gaussian distribution. The mean and variance of this Gaussian distribution were determined by that neuron's measured response at that contrast. Because the spontaneous response rates of LGN neurons were quite high (16.15 ± 1.73 spikes/s in our sample), we considered it appropriate to approximate the Poisson distributions of neural responses with Gaussian distributions. In each trial, a decision was made by comparing the summed activity of the neural pool at the test contrast to the summed activity of the same neurons at the reference (i.e., 0%) contrast. Fifty such trials were simulated for each of the five contrast levels. The “psychophysical” performance was calculated as the percentage of correct choices at each contrast and was then fitted with the cumulative Weibull function (Eq. 1). The “psychophysical” threshold was extracted from the fitted function as described above. The choice probability for each neuron was quantified as the covariation between the simulated neural response and the simulated choice at 0% contrast. At each parameter combination (see below), the same set of simulations (50 trials × 5 contrasts) was repeated 200 times, each time with a new random sample of n neurons, thus giving reliable estimations of model performance. The fitness of the model was evaluated by computing a goodness-of-fit (GoF) index:

$$\text{GoF}=1/3\times (\left|\text{simulated threshold}-\text{measured threshold}\right|/\text{measured threshold}+\left|\text{simulated P choice probability}-\text{measured P choice probability}\right|/\text{measured P choice probability}+|\text{simulated M choice probability}-\text{measured M choice probability}|/\text{measured M choice probability})\times 100\%$$ 3)

Model parameters.

The following parameters were varied in the pooling model: the number of P and M neurons in the pool (n = 1–512), the integration time window (t = 25–200 ms), the Fano factor (f = 0.5–2.0), interneuronal noise correlation (r = 0–0.3), and downstream pooling noise (p = 0–4.0). For most simulations, the Fano factor, interneural correlation, and pooling noise were fixed at their experimentally measured values. Specifically, an average Fano factor was derived for each integration time window, ranging from 0.8 to 1.4. The interneuronal correlation for LGN P-P and M-M neuron pairs was measured as 0.028. The interneuronal correlation between M and P neurons could not be estimated from our data, because it was nearly impossible to record from an M-P neuron pair on the same electrode at the same eccentricity. Several M-P correlation values were tested in our model, ranging from 0 to 0.05. The simulation results did not change significantly within this range of M-P correlations (data not shown). For the simulations reported in this article, a fixed value of 0.01 was used. The pooling noise was assumed to be 2.0. The choice of these values was considered neurobiologically realistic and meaningful for the following reasons: 1) Fano factor: recordings in anesthetized as well as alert animals have reported significant variability in the responses of single cortical neurons (Fano factor = 1–3) (McAdams and Maunsell 1999; Oram et al. 1999; Tolhurst et al. 1983). The Fano factor of subcortical visual neurons, however, was relatively low (∼1.0). This is true for retinal ganglion cells (RGCs) (Berry et al. 1997; Levine et al. 1992; Reich et al. 1997) as well as LGN cells (Kara et al. 2000). The Fano factors measured in our detection task and adopted by the model were thus in agreement with those previously reported measurements. 2) Interneuronal correlation: in sensory cortex, interneuronal correlations between pairs of nearby neurons are typically weak but positive (∼0.1–0.2) (Averbeck et al. 2006). In the LGN, convergent feedforward, divergent feedforward, and lateral connections are sparser than those in the cortex (Casagrande and Xu 2004; Nassi and Callaway 2009). It is therefore within expectation that the average interneuronal correlation for LGN P-P and M-M neuron pairs would be close to 0 (0.028). The interneuronal correlation between M and P neurons is likely to be even smaller, because the M and P pathways remain segregated in different layers of the LGN, have different RGC inputs, and retain separate feedback loops with V1 (Briggs and Usrey 2011; Ichida and Casagrande 2002; Ichida et al. 2014; Nassi and Callaway 2009). In addition, our simulations could always approach >99% GoF at some parameter combinations, given any interneuronal correlation value between 0–0.05 for P-P, M-M, and P-M pairs. 3) Pooling noise: the downstream pooling noise in our model can be considered the average Fano factor of cortical neurons onto which LGN neurons converge (Shadlen et al. 1996). In most simulations this number was fixed at 2.0, which is the average estimation of the Fano factor in cortex (see above). The success of our simulations (i.e., approaching >99% GoF at some parameter combinations), however, did not depend on this assumption about the pooling noise. Similar model results could be obtained by simply assuming a true Poisson distribution for all downstream neurons (i.e., pooling noise = 1.0). It is noteworthy that we only simulated independent downstream pooling noise values that were not associated with the local interneuronal correlations within the LGN, and that these noise values were fixed and did not change with the duration of the integration window. Finally, the pooling scheme for the model was assumed to be uniform (i.e., responses of all neurons were equally weighted).

RESULTS

We describe our main findings in several subsections below. First, we present data comparing the contrast sensitivity of the monkeys to the sensitivity of single LGN P and M neurons measured during active detection. We then present neural sensitivity data for LGN neurons measured during passive fixation. The next section compares the pairwise interneuronal correlations measured during the detection and fixation tasks. We follow with a section on choice probability and then another on the temporal dynamics of neural sensitivity as well as choice probability. Finally, we model these measured relationships using different numbers of LGN P and M neurons.

LGN Single Neurons Were Less Sensitive Than the Monkeys During Active Detection

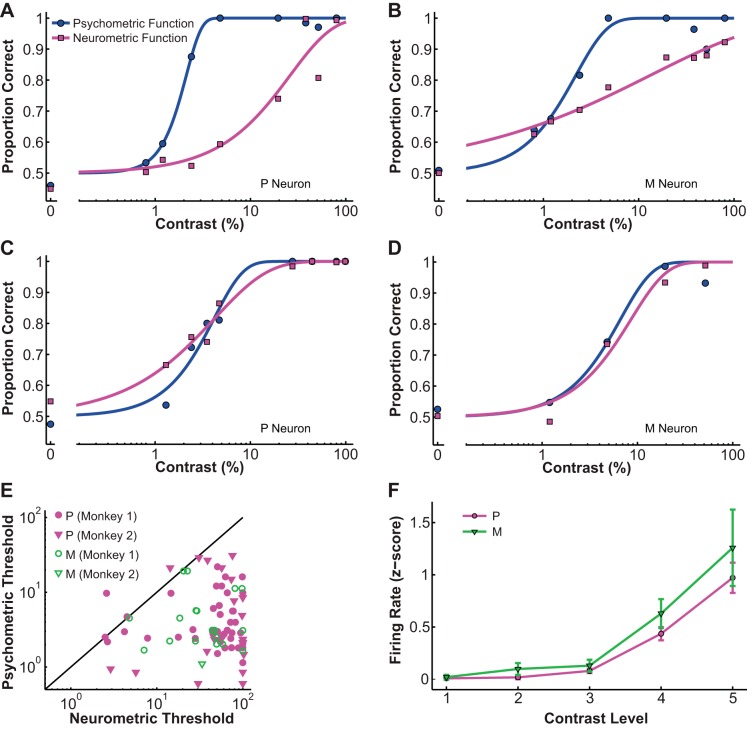
Compared with the simultaneously obtained psychometric functions, typical neurometric functions had higher contrast thresholds and shallower slopes, as demonstrated by an example P cell in Fig. 2A and an example M cell in Fig. 2B. A small percentage of the cells in both classes, however, were as sensitive as the monkeys, as shown by an example P cell in Fig. 2C and an example M cell in Fig. 2D. For the entire data set (n = 89), the average neurometric threshold (54.4 ± 4.78% contrast) was significantly different from the simultaneously measured psychometric threshold (5.76 ± 0.72% contrast; P = 0.000, Wilcoxon signed rank test; Fig. 2E). The average ratio of neurometric to psychometric threshold was 40.74 ± 10.75, indicating that the average LGN neuron was much less sensitive than the monkey during active contrast detection. Nonetheless, a subpopulation of LGN neurons (n = 12/89, 13.5%) demonstrated contrast sensitivities comparable to the monkey (permutation test, P > 0.05). Additionally, in our sample, M neurons had slightly lower thresholds than P neurons (P threshold = 58.85 ± 3.84%, M threshold = 49.22 ± 7.37%; P = 0.047, Kolmogorov-Smirnov test for small sample size). To relate this result to previously reported LGN contrast responses in anesthetized monkeys (Derrington and Lennie 1984; Purpura et al. 1988; Shapley et al. 1981), we also plotted z-score normalized contrast response functions (CRFs) for each cell group (Fig. 2F). Two-way ANOVA on the population CRFs of M and P neurons showed that M neurons were indeed more sensitive than P neurons (F = 3.87, P = 0.049), but there was considerable overlap between the two populations.

Fig. 2.

Psychometric and neurometric functions. A–D: example neurometric functions (magenta) and simultaneously recorded psychometric functions (blue) in P neurons (A and C) and M neurons (B and D). Filled circles indicate psychometric performance, filled squares indicate neurometric performance, and the solid line is the fitted Weibull function. E: the neurometric thresholds of most LGN neurons were higher than the simultaneously recorded psychometric thresholds. Filled magenta symbols represent P neurons, and open green symbols represent M neurons: circles, monkey 1; inverted triangles, monkey 2; solid line, unity line; neurometric threshold = psychometric threshold. F: z-score normalized contrast response functions (CRFs) for LGN P and M populations, showing higher contrast sensitivity for M neurons. The magenta line with circles represents P neurons, and the green line with inverted triangles represents M neurons. Values are means ± SE (error bars); contrast levels: 1, 0%; 2, 0.8–1.3%; 3, 2.4–4.8%; 4, 19.5–38%; 5, 80–99%.

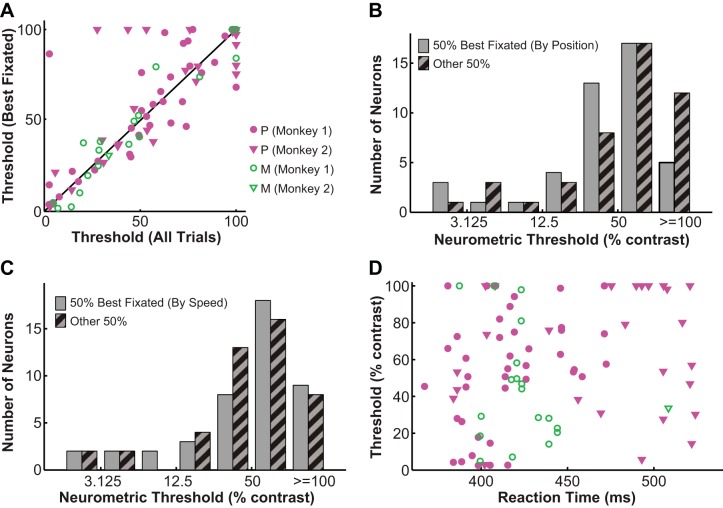
The relatively high neurometric threshold observed in the LGN led us to run a series of necessary controls. First, finer sampling of contrasts (measuring 9 contrast levels instead of 5) did not significantly alter the measured psychometric and neurometric threshold (psychometric: n = 12, P = 0.88, Wilcoxon signed-rank test; neurometric: n = 5, P = 0.56, Wilcoxon signed-rank test). Using Gaussian contrast profiles instead of circular patches resulted in slightly higher psychometric (n = 6, P = 0.037, Wilcoxon signed-rank test) and neurometric thresholds (n = 6, P = 0.009, Wilcoxon signed-rank test) but did not alter the ratio of neurometric to psychometric threshold (neurometric/psychometric ratio = 46.48 ± 12.32; P = 0.93, Wilcoxon signed-rank test). Additionally, within the range of receptive field eccentricities in our data set (average = 4.72 ± 0.32°), neurometric threshold was not significantly influenced by eccentricity (r = −0.14, P = 0.191). Similarly, the spontaneous firing rates of the neurons (average = 16.15 ± 1.73 spikes/s) did not significantly influence their thresholds either (r = −0.15, P = 0.161). To rule out the possibility that the poor sensitivity of LGN neurons was due to unstable fixation (including fixational eye movements and premature saccades), we performed several eye movement analyses. First, we computed the threshold for each neuron using only the 50% best-fixated trials and found that the neurometric threshold derived from these best-fixated trials (58.84 ± 3.61%) was not significantly different from the threshold derived from all trials (54.4 ± 4.78%; P = 0.374, Wilcoxon signed-rank test for dependent variables; Fig. 3A). Second, to control for fixational tremors and drifts, we calculated the average deviation of the eye (from central fixation point) for each neuron and ordered neurons by increasing value of eye position deviation. By this criterion, the top 50% of neurons (average eye position deviation = 0.18 ± 0.01°, n = 44) had slightly smaller neurometric thresholds (49.74 ± 4.65%) than the rest of the neurons (eye position deviation = 0.4 ± 0.02°, n = 45, neurometric threshold = 59.28 ± 4.9%; P = 0.044, Wilcoxon rank sum test; Fig. 3B). Thresholds for these top 50% of neurons, however, were still significantly higher than the simultaneously measured psychometric thresholds (psychometric threshold = 5.22 ± 0.87%; P = 0.000, Wilcoxon signed-rank test). Third, to control for microsaccades, we calculated the average eye speed during fixation (i.e., first derivative of eye position) for each neuron and ordered neurons by increasing value of eye speed. By this criterion, the top 50% of neurons (average eye speed = 1.12 ± 0.03°/s, n = 44) had neurometric thresholds (54.69 ± 5.01%) that were not significantly different from the rest of the neurons (eye speed = 1.84 ± 0.05°/s, n = 45, threshold = 54.47 ± 4.72%; P = 0.928, Wilcoxon rank sum test; Fig. 3C). Finally, to rule out the possibility of premature saccades, we characterized the relationship between reaction time (average = 0.43 ± 0.04 s) and neurometric threshold and found no significant overall correlation between the two (r = 0.17, P = 0.111; Fig. 3D).

Fig. 3.

Controls for eye movements during contrast detection. A: the neurometric threshold derived from the 50% best-fixated trials was similar to the threshold derived from all trials. Filled magenta symbols represent P neurons, and open green symbols represent M neurons: circles, monkey 1; inverted triangles, monkey 2; solid line, unity line; 50% best-fixated threshold = all-trial threshold. B: the top 50% of neurons with smaller average eye position deviations had neurometric thresholds that were slightly smaller than those for the rest of the neurons. C: the top 50% of neurons with smaller average eye speeds had neurometric thresholds that were similar to those for the rest of the neurons. D: the neurometric threshold was not significantly correlated with reaction time. Symbols are defined as in A.

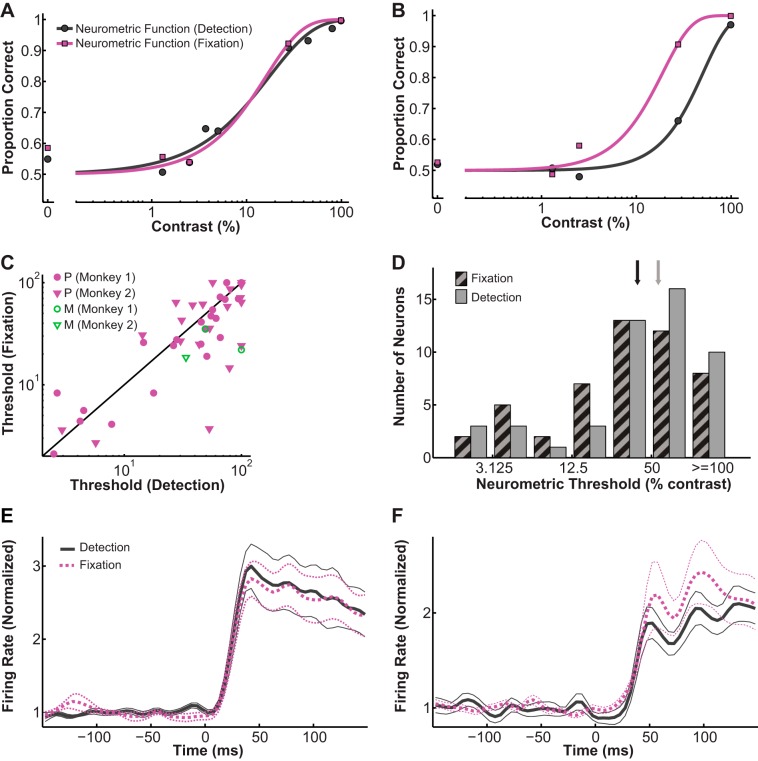
Neural Performance Improved During Simple Fixation

Because of the well-documented effects of attention and other types of modulations on the responses of single LGN neurons (for review see Casagrande et al. 2005; Saalmann and Kastner 2009), we had predicted that contrast thresholds for single neurons would be elevated when the monkey was required to passively fixate rather than to actively engage in making perceptual decisions. Instead, we found the opposite. Specifically, for a few LGN neurons, the neurometric functions measured in fixation and detection were quite similar (see Fig. 4A for an example). For most others, however, thresholds measured during fixation were lower than those during detection (see Fig. 4B for an example). For the 49 neurons (P: n = 46; M: n = 3) that were tested in both tasks, their neurometric thresholds were significantly correlated across tasks (r = 0.74, P = 0.000; Fig. 4C), and their thresholds during passive fixation were consistently lower compared with those obtained in active detection (fixation = 46.17 ± 4.76%; detection = 54.38 ± 4.78%; P = 0.001, Wilcoxon signed-rank test; Fig. 4D).

Fig. 4.

Comparison of neurometric thresholds during detection and fixation. A and B: example neurometric functions of the same neurons during fixation (magenta line with squares) and detection (gray line with circles). C: neurometric thresholds during fixation and detection were significantly correlated with each other. Filled magenta symbols represent P neurons, and open green symbols represent M neurons: circles, monkey 1; inverted triangles, monkey 2; solid line, unity line; fixation threshold = detection threshold. D: neurometric thresholds during fixation (hatched bars) were on average lower than those during detection (solid bars). Black arrow indicates mean fixation threshold; gray arrow indicates mean detection threshold. E and F: population PSTHs for monkey 1 (E) and monkey 2 (F) measured at the same contrast (high contrast, 80–99%), showing that LGN neurons maintained their firing rate patterns across tasks. Solid gray line indicates detection and dashed magenta line indicates fixation; thick lines are mean response and thin lines are mean ± SE.

To determine if the higher neural thresholds measured in the active detection task could be explained by behavioral or physiological changes across the two tasks, we made several additional comparisons. First, eye movement analyses revealed significant differences between the two tasks, in terms of both average eye position deviation (detection = 0.26 ± 0.02°, fixation = 0.33 ± 0.02°; P = 0.000, pairwise t-test) and average eye speed (detection = 1.54 ± 0.08°/s, fixation = 1.65 ± 0.07°/s; P = 0.000, pairwise t-test). Specifically, both eye position deviation and eye speed were smaller during active detection (detection/fixation ratio, eye position = 0.83 ± 0.05, eye speed = 0.93 ± 0.02), indicating that the decrease in neural sensitivity observed in the detection task could not be attributed to unstable fixations of the monkeys. Furthermore, population PSTHs measured at the same contrast for both monkeys (Fig. 4E, monkey 1; Fig. 4F, monkey 2) confirmed that recordings from the same neurons were stably maintained across the two tasks, and all neurons were sufficiently stimulated in both tasks.

Interneuronal Correlations Differed Between Detection and Fixation

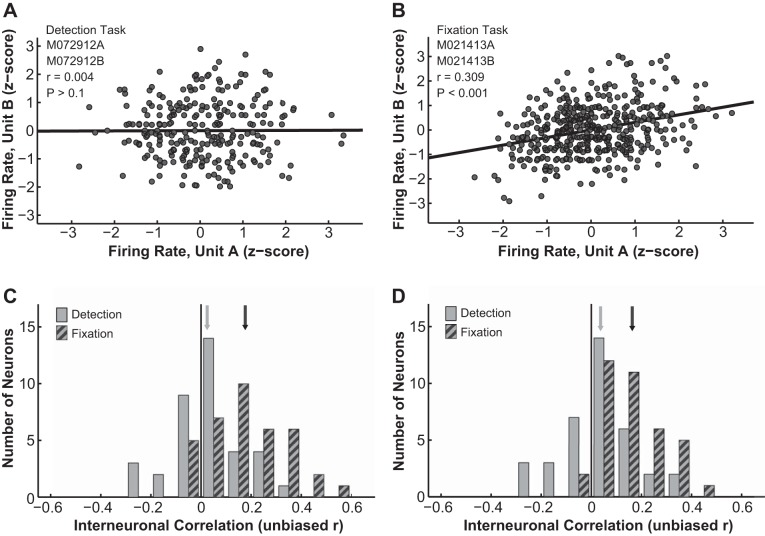
The next variable that we examined was the interneuronal correlation between pairs of simultaneously recorded LGN neurons during either active detection or passive fixation. To determine interneuronal noise correlation, each neuron's response in each trial was first z-normalized to remove the “signal” (i.e., contrast response) and leave only the trial-to-trial “noise” fluctuations. Such scaled firing rates of one neuron were then plotted against the correspondingly scaled firing rates of the other neuron, and the correlation coefficient between the two responses was taken as their interneuronal correlation. An unbiased estimator of the correlation coefficient (r′) (Lehmann 1957; Olkin and Pratt 1958; see Eq. 2) was reported for each neuron pair. In the detection task, noise correlations between pairs of LGN neurons were typically close to 0 (see Fig. 5A for an example pair). During fixation, however, LGN neuron pairs often were significantly and positively correlated (see Fig. 5B for an example pair). In our data set the overall noise correlation during detection was not significantly different from 0 (average = 0.028 ± 0.023, n = 37 pairs, P = 0.423, t-test), whereas the noise correlation during fixation was significantly different from 0 (average = 0.175 ± 0.025, n = 37 pairs, P = 0.001, t-test; Fig. 5C). Using the Pearson r instead of the unbiased estimator r′ yielded similar results (data not shown). Furthermore, the noise correlations in blank trials (i.e., 0% contrast, no stimulus present) still differed significantly between the detection (0.031 ± 0.024) and the fixation (0.16 ± 0.02) tasks (P = 0.000, t-test), indicating that the decrease in noise correlation observed in the active perceptual detection task was most likely due to global modulations such as changes in the motivation or the alertness state of the animal (Fig. 5D). Finally, as shown above, the stability of fixation differed slightly between detection and fixation. To rule out the possibility that the noise correlation during fixation was inflated by excessive fixational eye movements, we obtained eye position matched samples of interneuronal correlations from the two tasks (detection: n = 36 of 37, average eye position deviation = 0.27 ± 0.02°; fixation: n = 26 of 37, average eye position deviation = 0.30 ± 0.02°; P = 0.37, t-test). Within these samples, the interneuronal correlation distributions still differed significantly between the detection (0.028 ± 0.024) and the fixation (0.159 ± 0.025) tasks (P = 0.000, t-test).

Fig. 5.

Interneuronal correlation. A and B: interneuronal correlations between example pairs of LGN neurons during detection (A) and fixation (B). Filled circles indicate z-score normalized responses; solid line indicates linear regression fit. C: interneuronal correlation distributions during detection (solid bars) and fixation (hatched bars) significantly differed from each other. Solid line indicates correlation = 0; gray arrow indicates mean detection correlation; and black arrow indicates mean fixation correlation. D: the noise correlations computed using only blank trials (i.e., 0% contrast) still differed significantly between the detection (solid bars) and the fixation tasks (hatched bars). Line and arrows as in C.

LGN Responses Were Correlated with the Monkeys' Choices During Detection

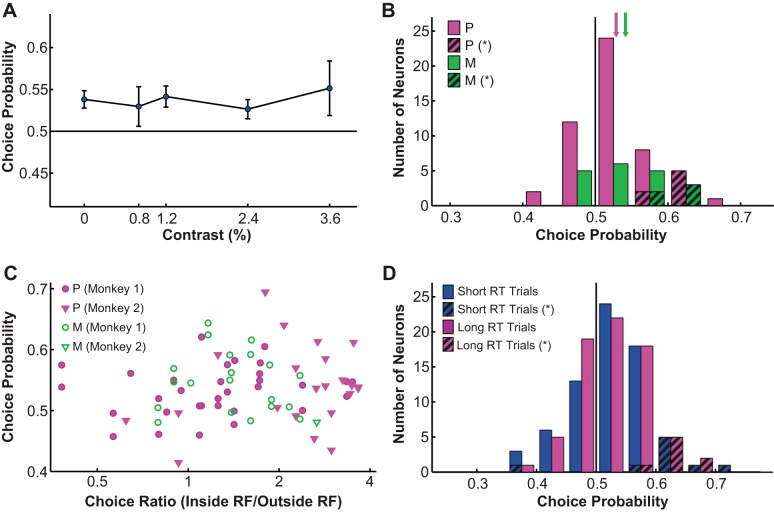
We quantified the covariation between LGN responses and behavioral choices as choice probability (Britten et al. 1996). When no stimulus was presented (i.e., 0% contrast trials only), overall choice probability was 0.54 for P neurons and 0.54 for M neurons, both above chance according to permutation (i.e., bootstrapping) tests (P neurons: P = 0.015; M neurons: P = 0.033). Next, we combined all low (<4%)-contrast trials within which choice probabilities did not significantly differ from each other (F = 0.05, P = 0.995, 1-way ANOVA; Fig. 6A) and derived a combined choice probability for each cell as well as a grand choice probability for all cells. We found that the neural activities of LGN P and M neurons were both significantly correlated with choice (P neurons: 0.53 ± 0.01; M neurons: 0.54 ± 0.01; grand choice probability: 0.54; P < 0.05, permutation tests; Fig. 6B). Choice probability showed a small negative correlation with neurometric threshold that was not statistically significant (r = −0.12, P = 0.305).

Fig. 6.

Choice probability. A: choice probability was not significantly influenced by contrast (<4% contrast). Solid line indicates choice probability = 0.5. Values are means ± SE (error bars). B: LGN neurons had significantly above-chance choice probabilities. Magenta bars represent P neurons, and green bars represent M neurons; hatched bars represent P (magenta) and M neurons (green) with significant choice probabilities. Solid line indicates choice probability = 0.5; arrows indicate mean choice probability. C: choice probability was not significantly correlated with the monkey's behavioral bias in choosing the receptive field location over its mirror image location. Filled magenta symbols represent P neurons, and open green symbols represent M neurons: circles, monkey 1; inverted triangles, monkey 2. D: recomputing choice probability using the 50% of trials with the fastest reaction time (short RT) or the slowest reaction time (long RT) did not yield significantly different choice probability distributions. Blue bars represent choice probability computed with short RT trials, magenta bars represent choice probability computed with long RT trials; hatched bars represent choice probabilities computed with short RT (blue) and long RT trials (magenta) that were significantly different from 0.5. Solid line indicates choice probability = 0.5.

The observed above-chance choice probabilities in the LGN were not dependent on the monkeys' behavioral bias in choosing the receptive field location over its mirror image location (r = 0.08, P = 0.495; Fig. 6C). Additionally, choice probability was not correlated with the spontaneous response rate of the cell (r = −0.08, P = 0.495). We also characterized the relationship between eye movements and choice probability and found no significant correlation between the two (data not shown). Furthermore, choice probability was not correlated with reaction time (r = 0.03, P = 0.798), and using only the 50% of trials with the fastest reaction times or the slowest reaction times did not yield significantly different choice probability distributions (P = 0.854, permutation test; Fig. 6D). Finally, previous literature suggests that choice probability can be significantly influenced by top-down, task-related gain modulations (Nienborg and Cumming 2009). For our data we characterized task-related gain modulations of LGN neurons in several different ways by comparing the neural responses during the detection and fixation tasks, and we found such modulations could not explain the observed choice probability values either (data not shown). Similarly, choice probability was not correlated with other factors that could have influenced the monkeys' motivation, including day-to-day changes in reward rate, overall reward value, or the monkeys' psychophysical performance (data not shown).

Neural Sensitivity, Choice Probability, and the Fano factor, But Not Interneuronal Correlation, Were Modulated By Time

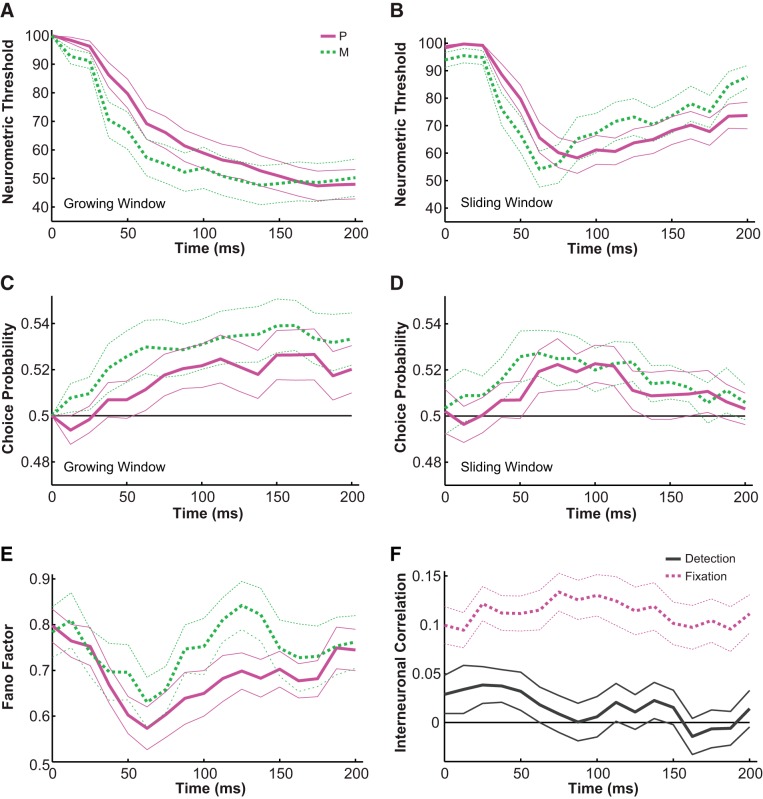
We next asked how the above-characterized physiological properties, including neural sensitivity, choice probability, and interneuronal correlation, changed with time. We first characterized the changes in neurometric threshold using time intervals that started at stimulus onset (0 ms) and increased in duration in steps of 12.5 ms (i.e., growing windows) and found that P (n = 37) and M (n = 20) neurons had significantly different temporal dynamics (Fig. 7A). Specifically, compared with P neurons, M neurons exhibited more sensitive profiles (F = 7.51, P = 0.006, 2-way ANOVA, main effect for cell group) that developed faster [P: 62.5–200 ms thresholds deviated from 0 ms threshold; M: 50–200 ms thresholds deviated from 0 ms threshold; P < 0.05, Tukey's honestly significant difference test (HSD)]. Next, computing neurometric thresholds in sliding time windows that were 50 ms wide and advanced in steps of 12.5 ms, we confirmed that P and M neurons had significantly different temporal dynamics (Fig. 7B), with M neurons showing more transient developments in sensitivity that degraded faster in the later half of the stimulus presentation (P: 62.5–200 ms thresholds deviated from 0 ms threshold; M: 62.5–75 ms thresholds deviated from 0 ms threshold; P < 0.05, Tukey's HSD).

Fig. 7.

Temporal dynamics. A and B: the temporal dynamics of neurometric threshold computed using growing time windows (A) and sliding time windows (B). Solid magenta lines represent P neurons, dashed green lines represent M neurons; thick lines are mean threshold, and thin lines indicate mean ± SE. X-axis indicates when the time window ends (after stimulus onset). C and D: the temporal dynamics of choice probability computed using growing time windows (C) and sliding time windows (D). Solid magenta lines represent P neurons, dashed green lines represent M neurons; thick lines are mean choice probability, and thin lines indicate mean ± SE. Solid black line indicates choice probability = 0.5. X-axis indicates when the time window ends (after stimulus onset). E: the temporal dynamics of Fano factor computed using sliding time windows. Solid magenta lines represent P neurons, dashed green lines represent M neurons; thick lines represent Fano factor estimation, and thin lines indicate the 95% confidence interval. F: the temporal dynamics of interneuronal correlation computed using sliding time windows. Solid gray lines represent detection, and dashed magenta lines represent fixation; thick lines are mean correlation, and thin lines indicate mean ± SE. Solid black line indicates correlation = 0.

Using growing windows on choice probability, we determined that compared with P neurons, M neurons also showed stronger covariations with choice (F = 11.09, P = 0.001, 2-way ANOVA, main effect for cell group) that developed faster in time (P: 100–200 ms choice probabilities deviated from chance; M: 62.5–200 ms choice probabilities deviated from chance; P < 0.05, permutation tests) (Fig. 7C). Similarly, in sliding windows, choice probabilities in the 75–112.5 ms range for P neurons and in the 62.5–125 ms range for M neurons were significantly different from chance (P < 0.05, permutation tests; Fig. 7D). Z-normalized temporal changes in neurometric threshold were negatively correlated with the temporal changes in choice probability (in sliding windows, P neurons: r = −0.84, P = 0.000; M neurons: r = −0.85, P = 0.000), indicating that when the neuron was the most sensitive, it also correlated the most with the monkey's choice. Since neural sensitivity developed earlier in time for M neurons, choice probability also evolved significantly earlier for M neurons, capturing a subtle, very early difference in the transient onset responses of the two cell types. Additionally, the Fano factor (i.e., variance/mean firing rate) of LGN P and M neurons also changed significantly with time in a similar fashion (sliding window, Fig. 7E), as previously reported in a number of cortical areas (Churchland et al. 2010) as well as the thalamus (Victor et al. 2007). Specifically, for both M and P cells, the Fano factor showed a sharp dip following stimulus onset (F = 14.10, P = 0.000, 2-way ANOVA, main effect for time), and the temporal course of the Fano factor was also significantly correlated with that of the neurometric threshold (P: r = 0.62, P = 0.008; M: r = 0.5, P = 0.041).

Finally, we characterized the temporal dynamics of interneuronal correlations in both the detection and the fixation tasks (sliding window, Fig. 7F). As described above, the average interneuronal correlation was found to be significantly different between the detection and the fixation tasks (F = 205.1, P = 0.000, 2-way ANOVA, main effect for task), and this difference was persistent throughout time (F = 0.51, P = 0.943, 2-way ANOVA, main effect for time).

Psychophysical Threshold and Choice Probability Could Be Modeled with a Simple Pooling Scheme with No Significant Interneuronal Correlations

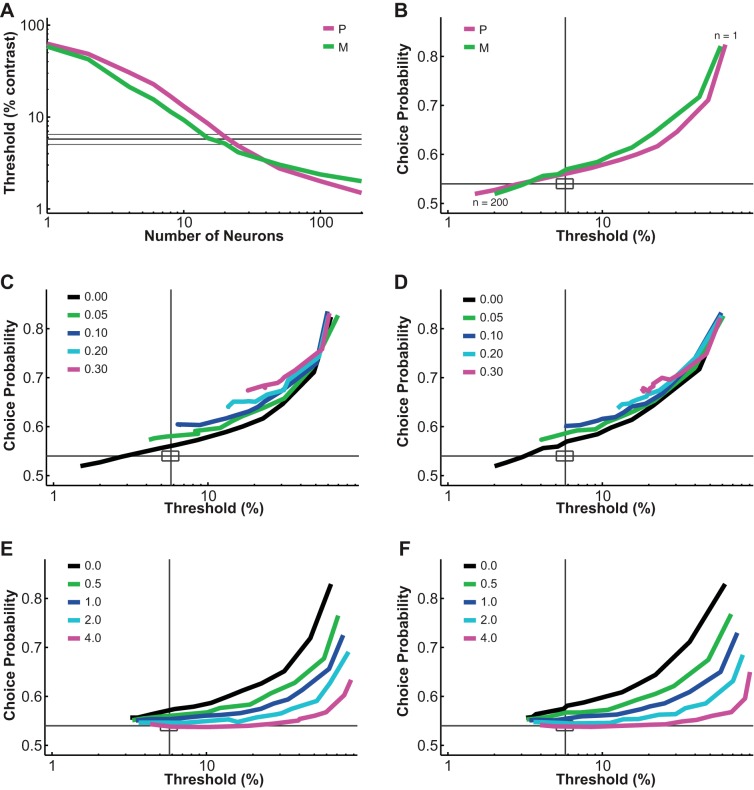
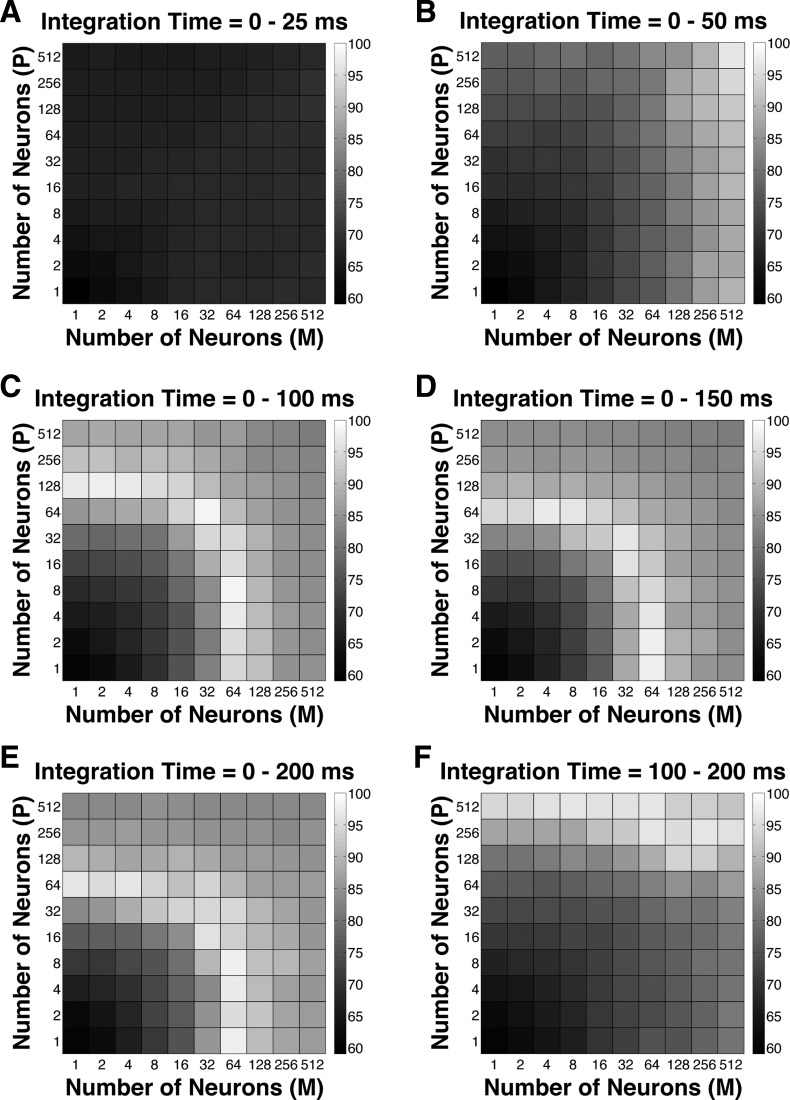
The pooling model used in this study was similar to those previously proposed to account for psychophysical performance and choice probability based on sensory neural responses (Cohen and Newsome 2009; Haefner et al. 2013; Liu et al. 2013; Purushothaman and Bradley 2005; Shadlen et al. 1996). Inputs to the model were single LGN P and M neural responses at different contrasts. Outputs were the simulated psychophysical threshold of the model and choice probabilities for individual “neurons.” Variable parameters in the model included 1) the number of P and M neurons (n), 2) the duration of the integration time window (t), 3) the Fano factor (f), 4) the interneuronal noise correlation (r), 5) the downstream pooling noise (p), and 6) the pooling strategy. In agreement with Shadlen et al. (1996), our model behaved in a predictable way when one of these parameters was changed. For example, increasing the number of neurons in the pool decreased the psychophysical threshold and choice probability (Fig. 8, A and B). Increasing interneuronal correlation increased threshold as well as choice probability (Fig. 8, C and D). Increasing pooling noise increased threshold and decreased choice probability (Fig. 8, E and F). For the simulation results reported in this article, the Fano factor, interneuronal correlation, downstream pooling noise, and the pooling strategy were fixed according to either measurements in our data set or previous literature (see materials and methods for a detailed description of the choice of these parameters). Only the number of P and M neurons in the pool (n) and the time window (t) were manipulated here to answer a critical question: at different integration durations, how many P neurons and how many M neurons were likely to contribute to the monkey's perceptual decision?

Fig. 8.

Parametric analysis of the pooling model. A and B: increasing the number of neurons in the pool decreased the simulated threshold and choice probability. Interneuronal correlation and pooling noise were assumed to be 0; integration time was 0–150 ms. Magenta lines represent simulated values for P neurons, and green lines represent simulated values for M neurons; thick gray lines indicate measured mean psychophysical threshold/choice probability, and thin gray line/rectangles indicate mean ± SE. C and D: increasing interneuronal correlation increased simulated threshold and choice probability for both P neurons (C) and M neurons (D). Pooling noise was assumed to be 0; integration time was 0–150 ms. As in B, each simulation line moved from the upper right corner to the lower left corner as more neurons were added to the pool. Gray lines indicate measured mean psychophysical threshold/choice probability, and rectangles indicate mean ± SE. E and F: increasing pooling noise increased simulated threshold and decreased choice probability for both P neurons (E) and M neurons (F). Interneuronal correlation was assumed to be 0.028 (measured value); integration time was 0–150 ms. As in B, each simulation line moved from the upper right corner to the lower left corner as more neurons were added to the pool. Lines are defined as in C and D.

To evaluate the fitness of the model, a GoF index (see Eq. 3) was reported for each parameter combination. The GoF index (ranging from 0 to 100%, with 100% indicating perfect fitting) reflected three factors equally: 1) how close the model threshold approached the measured psychophysical threshold, 2) how close P choice probability in the model approached the measured choice probability for P neurons, and 3) how close M choice probability in the model approached the measured choice probability for M neurons. Simulation results indicated that 1) at extremely short integration intervals (25 ms), incorporating many neurons from both classes still failed to reproduce the observed threshold and choice probabilities (Fig. 9A); 2) at relatively brief intervals (50 ms), incorporating more M neurons rather than P neurons in the pool could explain the observed threshold as well as choice probabilities (Fig. 9B); and 3) at medium to long intervals (100–200 ms), a wider range of M/P neuron combinations (1–128 neurons) yielded good model performance (Fig. 9, C–E). Finally, when information from only the second 100 ms of the stimulus presentation was integrated, it was beneficial to incorporate a large number of P neurons, presumably because M neural responses were significantly degraded in the second half of the stimulus presentation (Fig. 9F).

Fig. 9.

Goodness-of-fit (GoF) index for different pool sizes (n) and integration time windows (t). A GoF of 100% (white) indicates that the model perfectly matches the observed psychometric threshold as well as choice probabilities for both P and M neurons. A: t = 0–25 ms. B: t = 0–50 ms. C: t = 0–100 ms. D: t = 0–150 ms. E: t = 0–200 ms. F: t = 100–200 ms.

DISCUSSION

Our study is the first to examine the link between neural activity and perceptual decisions in the LGN of awake monkeys. Using a 2AFC contrast detection task, we found that a small percentage (13.5%) of LGN P and M cells were as sensitive as the monkey, whereas the majority of LGN P and M neurons were far less sensitive in detecting contrast (Fig. 2E). Second, having the monkeys perform a simple fixation task instead of active detection slightly improved the neural sensitivity (Fig. 4, C and D). Third, the average interneuronal correlation between LGN neuron pairs was not different from 0 during active detection but was significantly above 0 during simple fixation (Fig. 5, C and D). Importantly, the covariation between neural responses and perceptual decisions, measured as choice probability, was significant for both P and M neurons (Fig. 6B). The temporal dynamics of choice probability closely tracked those of neural sensitivity, reflecting subtle temporal differences between P and M neural responses (Fig. 7, A–D). Finally, modeling work suggested that both psychophysical threshold and LGN choice probability could be fully explained with a simple pooling model without assuming significant interneuronal correlations or top-down gain modulations (Fig. 9). Together, these results support the hypothesis that the perceptual decision pool for contrast detection consists of multiple LGN P and M neurons, and that response fluctuations in these neurons can influence perception. In the discussion below we consider the implications of these results in light of previously published findings.

The Neural Sensitivities of LGN P and M Cells

In our detection task, the psychophysical threshold of the monkey (5.76 ± 0.72% contrast) was similar to previous measurements made under similar conditions (De Valois et al. 1974; Merigan 1980). Single-unit recordings in anesthetized, paralyzed animals, in which visual stimuli are presented only to the receptive field centers of single visual neurons (for example see Derrington and Lennie 1984; Purpura et al. 1988; Shapley et al. 1981), showed that the contrast sensitivity of the most sensitive LGN neurons was comparable to the psychophysical sensitivity of the animal. Intuitively, one might expect LGN neurons to be more sensitive in an active detection task compared with the anesthetized condition. In reality, we found that only a small percentage (13.5%) of LGN neurons had neurometric thresholds comparable to that of the monkey, whereas the majority (86.5%) of LGN neurons were much less sensitive (Fig. 2E).

There are several explanations for this observed difference in sensitivity between our study in awake, behaving monkeys and previous studies in anesthetized animals. First, to study the link between LGN activity and perceptual choices, we constructed visual stimuli (circular patches and Gaussian profiles) that were large enough to ensure stable, consistent stimulation of LGN neurons despite the constant fixational eye movements of awake animals. Because of surround inhibition (Enroth-Cugell and Robson 1966; Rodieck 1965) and extraclassical surround inhibition (Alitto and Usrey 2008; Solomon et al. 2006), large stimuli such as ours are not optimal for estimating the absolute sensitivity of LGN neurons (see also Kang and Malpeli 2009 for similar results in using low spatial frequency stimuli and measuring LGN sensitivity in passively fixating cats). Second, it is important to note that the majority of the commonly used anesthetics alter the normal LGN inhibitory circuitry as well as other modulatory inputs to the LGN (Franks 2008; Rudolph and Antkowiak 2004). These circuitries are, of course, critical to understanding the function of the LGN (Casagrande et al. 2005; Saalmann and Kastner 2011; Sherman 2007). For example, anesthetics such are propofol, isoflurane, halothane, or barbiturates interact strongly with GABA_A receptors (Franks 2006; Garcia et al. 2010; Krasowski and Harrison 1999), which may play an important role in regulating the transfer ratio of retinal input to LGN output (Casagrande and Ichida 2011; Norton and Godwin 1992). Therefore, it is unclear to what extent the properties of LGN cells measured under anesthesia reflect the normal functional state of the LGN in awake, behaving animals.

Despite this difference in absolute sensitivity, our study agreed with previous work in terms of the relative differences in sensitivity and temporal dynamics (see below) between the LGN P and M populations (Derrington and Lennie 1984; Kaplan and Shapley 1982; Purpura et al. 1988; Sclar et al. 1990; Shapley et al. 1981). Specifically, we found that M neurons had, on average, slightly higher contrast sensitivity and contrast gain than P neurons (Fig. 2F), but the population responses of M and P neurons overlapped extensively (Kaplan 2008, 2013; Norton et al. 1988; Xu et al. 2001).

Comparing Active Detection with Passive Fixation

We observed the nonintuitive result that LGN neurons were more sensitive during the passive fixation task than the active detection task (Fig. 4, C and D). Given the fact that detecting contrast (especially at or near the psychophysical threshold) can be attentionally demanding compared with simple fixation, and that attention is known to boost the visually driven responses of LGN neurons (Casagrande et al. 2005; McAlonan et al. 2008), this result seems counterintuitive. Eye movement and other control analyses revealed that this difference in sensitivity could not be simply explained by the instability of the monkeys' fixation or our physiological recordings. We think one possible explanation is that pronounced, long-lasting presaccadic suppressions (Reppas et al. 2002; Royal et al. 2006) occurred only during the detection task but not during the passive fixation task, as the monkeys were only required to make saccades in the former case.

Another significant difference we observed between the detection and the fixation tasks was in terms of interneuronal correlations between LGN neuron pairs (Fig. 5). Specifically, during passive fixation, LGN interneuronal correlations were significantly above 0, much like what has been reported in the retina (DeVries 1999; Mastronarde 1983, 1989; Meister et al. 1995) as well as in a number of cortical areas (see below). During active detection, however, we observed that LGN interneuronal correlations were not significantly different from 0, in agreement with recent data obtained from anesthetized marmoset LGN (Cheong et al. 2011) as well as from large populations of V1 neurons in awake monkeys (Ecker et al. 2010, 2014). It remains controversial why the average interneuronal correlation values vary greatly from study to study (Cohen and Kohn 2011), and the small sample sizes limit the types of conclusions that we can draw based on our data. We believe, however, that the relative decrease in interneuronal correlation we observed when the monkeys were engaged in active detection could be attributed to the fact that both attention and perceptual learning de-correlate pairs of single neurons (Cohen and Maunsell 2010; Gu et al. 2011; Mitchell et al. 2009). Another possibility is that during the fixation task, it might be more difficult for the monkeys to maintain long fixations or suppress the impulse to saccade to a very salient target. Therefore, the frequency of microsaccades might increase slightly during the fixation task, which in turn could enhance neural sensitivities and raise interneuronal correlations at the same time (Collewijn and Kowler 2008; Martinez-Conde et al. 2002, 2004, 2013; Rolfs 2009).

Parallel Pathways in Fast Detection

We reported in our temporal analyses that the average LGN neuron achieved its peak sensitivity and choice probability within 100 ms after stimulus onset, with M neurons being slightly faster than P neurons in almost all cases (Fig. 7, A–D). These results are well within expectation given the nature of our task and the known differences in response dynamics between LGN P and M neurons. In many visual tasks, the psychophysical performance of human and monkey subjects plateaus within 100–300 ms after stimulus onset (Angelaki and Cullen 2008; Nachmias 1967; Purushothaman and Bradley 2005; Snowden and Braddick 1991; Tulunay-Keesey and Jones 1976). Physiological recordings also have revealed great single-neuron sensitivities based solely on the early, transient components of visually driven responses (Buracas et al. 1998; Ghose and Harrison 2009; Müller et al. 2001; Oram and Perrett 1992; Price and Born 2010; Tovee et al. 1993). This transient response has been reported to have higher contrast gain, higher response gain, and lower variability (Müller et al. 2001) and to contain ∼80% of all the information available throughout the stimulus presentation (Osborne et al. 2004; Tovee et al. 1993). Under natural viewing conditions, humans and monkeys saccade once every ∼300 ms (Wilson and Goldman-Rakic 1994). Thus, for a simple detection task such as ours, it may be more beneficial for the visual system to take in all the information available “at a glance” and then quickly move on (Ghose and Harrison 2009; Osborne et al. 2004; Uchida et al. 2006). In this scenario, the distinctive temporal dynamics of LGN P and M neurons (Schiller and Malpeli 1978; Schmolesky et al. 1998) determine how they are differentially pooled together to perform the task (Merigan and Maunsell 1993; Stone 1983).

Choice Probability in the LGN and Its Implications

Moderately above-chance choice probability values (0.5–0.6) have been found in numerous cortical areas during a variety of behavioral tasks, regardless of the sensitivity of single neurons (Bosking and Maunsell 2011; Britten et al. 1996; Cook and Maunsell 2002; Dodd et al. 2001; Grunewald et al. 2002; Liu and Newsome 2005; Nienborg and Cumming 2006; Palmer et al. 2007; Parker et al. 2002; Price and Born 2010; Purushothaman and Bradley 2005; Uka and DeAngelis 2004; Uka et al. 2005). Similarly, we found choice probability in the LGN (0.54) to be comparable in its magnitude to choice probabilities in the cortex, despite the relative insensitivity of most single LGN neurons (Fig. 6B).

Compared with the cortex, the LGN is closer to the sensory surface and is thus expected to more faithfully reflect the physical reality of the outside world. It is therefore surprising that in the absence of a physical stimulus, fluctuations in the spontaneous responses of LGN neurons were still significantly correlated with the monkey's choices. The theoretical implication of this above-chance choice probability is twofold. First, previous modeling work indicated that choice probability values are heavily influenced by interneuronal correlations (Nienborg et al. 2012; Nienborg and Cumming 2010; Shadlen et al. 1996). Thus far, almost all cortical areas where choice probabilities have been measured also exhibit ubiquitous interneuronal correlations (Averbeck et al. 2006; Cohen and Kohn 2011). In contrast, we found that LGN P and M neurons exhibited above-chance choice probabilities during contrast detection, even though the average interneuronal correlation was not significantly different from 0. In agreement with our results, recordings in the subcortical vestibular nucleus (VTN) during a heading direction discrimination task (Liu et al. 2013) also observed above-chance choice probabilities in the absence of positive noise correlations. Importantly, recent modeling results reveal that it is not the average interneuronal correlation level but the structure of a specific type of differential correlation that determines choice probability values in neural pools of different sizes (Haefner et al. 2013; Moreno-Bote et al. 2014). Our experimental and modeling results are consistent with this hypothesis. Additionally, it is known that above-chance choice probabilities can arise from both feedforward connections (i.e., response fluctuations in sensory neurons) and feedback connections, such as top-down attentional modulation (Cohen and Maunsell 2010; Nienborg and Cumming 2009). Our results support a bottom-up rather than top-down origin of choice probability because 1) we found no significant gain modulations in the attentionally demanding detection task, and 2) in our models we were able to successfully simulate threshold and choice probability results using a very short integration window (i.e., 50 ms). Taken together, our data and the success of our model demonstrate that, at least for peripheral sensory structures such as the LGN, random response fluctuations in single neurons can be linked to changes in the perceptual behavior of the subject.

GRANTS

This work was supported by National Institutes of Health (NIH) Grants EY001778 and R21 EY019132 (to V. A. Casagrande), NIH Core Grants EY008126 and HD15052, and funds from the Department of Cell and Developmental Biology at Vanderbilt University.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Y.J., G.P., and V.A.C. conception and design of research; Y.J. performed experiments; Y.J., D.Y., and G.P. analyzed data; Y.J., G.P., and V.A.C. interpreted results of experiments; Y.J. prepared figures; Y.J. drafted manuscript; Y.J., D.Y., G.P., and V.A.C. edited and revised manuscript; Y.J., D.Y., G.P., and V.A.C. approved final version of manuscript.