Abstract
In order to compare anatomical and functional brain imaging data across subjects, the images must first be registered to a common coordinate system in which anatomical features are aligned. Intensity-based volume registration methods can align subcortical structures well, but the variability in sulcal folding patterns typically results in misalignment of the cortical surface. Conversely, surface-based registration using sulcal features can produce excellent cortical alignment but the mapping between brains is restricted to the cortical surface. Here we describe a method for volumetric registration that also produces an accurate one-to-one point correspondence between cortical surfaces. This is achieved by first parameterizing and aligning the cortical surfaces using sulcal landmarks. We then use a constrained harmonic mapping to extend this surface correspondence to the entire cortical volume. Finally, this mapping is refined using an intensity-based warp. We demonstrate the utility of the method by applying it to T1-weighted magnetic resonance images (MRI). We evaluate the performance of our proposed method relative to existing methods that use only intensity information; for this comparison we compute the inter-subject alignment of expert-labeled sub-cortical structures after registration.
Index Terms: Image Registration, deformable registration, brain mapping, harmonic mapping
I. Introduction
Morphometric studies of anatomical changes over time or of differences between populations require that the data first be transformed to a common coordinate system in which anatomical structures are aligned. Similarly, inter-subject longitudinal studies or group analyses of functional data also require that the images first be anatomically aligned. Alignment is commonly performed either with respect to the entire volumetric space [1] or is restricted to the cortical surface [2]. Here we describe an approach to brain image registration based on harmonic maps that combines these two approaches producing a volumetric alignment in which there is also a one-to-one correspondence between points on the two cortical surfaces.
Talairach normalization based on a piecewise affine transformation [3] was the first commonly used volumetric alignment technique. Because it uses a restricted set of anatomical landmarks and is piecewise affine, it results in relatively poor alignment and has been largely replaced by automated intensity-based alignment methods that also allow non-rigid deformations [4], [5]. There are a vast array of such methods, differing in how they measure the fit between the two images (e.g., squared error, correlation, mutual information), the parameterization of the transformation (e.g., polynomial, splines, discrete cosine transform or other eigenfunction bases), and the procedure used to regularize the transformation (e.g., elastic, biharmonic, or viscous fluid models) [6]. Polynomial warps and linear elastic deformations implicitly assume that deformations are small and do not guarantee preservation of topology for larger deformations [7]. The viscous fluid approach [8] and more recent approaches using large-deformation diffeomorphic metric mapping [9], [10] were developed to address the problem of ensuring diffeomorphic maps and are better able to register objects whose alignment requires large deformations while conserving their topology.
Since these intensity-based methods do not explicitly model the cortical surface, alignment can be rather poor. An illustration of this is shown in Fig. 1, where we have used the Automated Image Registration (AIR) software [5], [11] to align two brain volumes using a 5th order polynomial (168 parameters). While the regions of cortical grey matter exhibit reasonably good correspondence between the two images, the cortical surfaces themselves do not align well. Since cytoarchitectural and functional parcellation of the cortex is intimately related to the folding of the cortex, it is important when comparing cortical anatomy and function in two or more subjects that the surfaces are aligned. For this reason, there has been an increasing interest in analyzing the cerebral cortex based on alignment of surfaces rather than volumes.
Fig. 1.
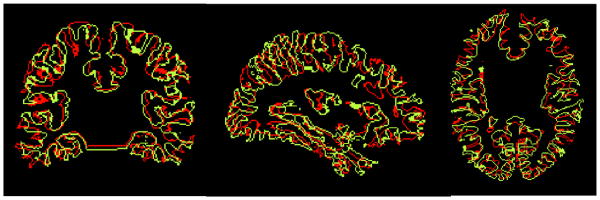
Cortical surface alignment after using air software for intensity based volumetric alignment with a 168 parameter 5th order polynomial. Note that although the overall morphology is similar between the brains, the two cortical surfaces do not align well.
Various surface-based techniques have been developed for inter-subject registration of two cortical models. One class of techniques involves flattening the two cortical surfaces to a plane [12] or to a sphere [13] using mechanical models or variational methods and then analyzing the data in the common flattened space [14]. Other surface based techniques work in the surface geometry itself rather than a plane or a sphere and choose to account for the surface metric in the inter-subject registration [15], [16]. The advantage of such techniques is that they produce registration results that are independent of the intermediate flat space (or, equivalently, the specific parameterization of the cortex) resulting in a more consistently accurate registration throughout the cortex. These approaches involve manually delineated sulcal landmark matching [16] in the intrinsic surface geometry. While some progress has been made recently towards automating the matching process using mutual information [17] or optical flows of mean-curvature images in the surface parameter space [18], [19], fully automatic alignment of high resolution cortical surfaces remains a challenging problem.
While the volume registration methods described above do not provide suitable cortical alignment, the cortical registration methods do not define any volumetric correspondence. One approach to this problem is to combine landmark points, curves and surfaces as additional constraints in an intensity-based warping method [20], [2], [21], [22], [23], [24], [25]. For example, landmarks, curves [25] and image matching [24] can be applied in a hierarchical manner in a large deformations framework ensuring generation of diffeomorphisms [26], [27]. Registration methods such as the Hierarchical Attribute Matching Mechanism for Image Registration (HAMMER) algorithm [28] incorporate surface as well as volume information for the alignment using geometric attributes of the images. Alignment of brain images often involves relatively large displacements which need to be obtained incrementally using large deformation or fluid models [29], [30] and hence are computationally expensive. Accurate alignment of the cortical surface as part of a volumetric registration procedure remains a challenging task mainly due to the complex folding pattern variability of the cortex.
In this paper, we (i) propose a novel landmark based surface matching technique based on elastic energy minimization in the intrinsic geometry of the cortex, (ii) propose a new method based on harmonic mappings for extending the surface matching to the entire cortical volume, and (iii) present a modified intensity alignment based on [31] to compute the final map. The resulting method, comprising the three steps outlined above, gives an inverse consistent map which is capable of aligning both subcortical and sulcal features.
II. Problem Statement and Formulation
Here we address the following problem: produce a one-to-one mapping between two brain volumes such that subcortical structures and sulcal landmarks are aligned and that there is also a one-to-one correspondence between the cortical surfaces of the two volumes. Equivalently, given 3D manifolds M and N representing the two brain volumes, with boundaries ∂M and ∂N representing their respective cortical surfaces, we want to find a map from M to N such that ∂M, the surface of M, maps to ∂N, the surface of N, and the intensities of the images in the interior of M and N are matched. In addition the map must satisfy a sulcal matching constraint so that labelled sulci on the surface ∂M map onto homologous sulci on ∂N. The boundaries, ∂M and ∂N, are assumed to have a spherical topology.
We solve the mapping problem in three steps:
Surface matching, which computes a map between ∂M and ∂N, the cortical surfaces of the two brains. The mapping is based on minimization of an elastic strain energy subject to the constraint that a set of interactively labelled sulci are aligned, as described in Section III.
Extrapolation of the surface map to the entire cortical volume such that the cortical surfaces remain aligned. This is done by computing a harmonic map between M and N subject to a surface matching constraint. As we describe in Section IV, an intermediate spherical representation is used to facilitate enforcement of this constraint. We note also that while the sulci are constrained to remain in correspondence, the cortical surfaces can flow with respect to each other when computing the volume harmonic map provided we retain the one-to-one mapping between ∂M and ∂N.
Refinement of the harmonic map on the interiors of M and N to improve intensity alignment of subcortical structures. For this step we use an inverse consistent linear elastic registration method as described in Section V.
The mapping in Step 2 requires large scale deformation to ensure that ∂M and ∂N are aligned. Linear elastic or thin-plate spline registration based on landmarks cannot be used for this purpose [32]. Harmonic maps on the other hand are suitable since they are bijective provided that the boundary (the cortical surface in this case) is mapped bijectively. Conversely, the final step requires a more local refinement of the mapping to align subcortical structures so that use of linear elastic methods is appropriate.
III. Surface Registration
We describe a method that sets up one-to-one correspondence between the surface ∂M of brain M and the surface ∂N of the brain N, using labeled sulcal curves as constraints. Our earlier methods for surface registration were computed in two stages: (i) for each subject, parameterize the surface of each cortical hemisphere to either a unit square or disk, and (ii) find a vector field with respect to this parameterization that aligns sulcal landmarks between subjects. Registration can use linear elastic [33] or thin-plate bending energy [16] for regularizing the displacement field and covariant derivatives to make the alignment independent of parameterization. However, in order to solve the resulting variational minimization problem, numerical derivatives must be computed by resampling the brain on a uniform grid with respect to the parameterization. In addition to the computational cost of resampling and interpolation, this step results in a loss of resolution since the regular or semi-regular grid in flat space is not necessarily optimal for representing the brain in 3D space. In our new surface registration approach, we incorporate sulcal landmark alignment directly in our parameterization method and thus avoid the resampling and reparameterization step completely. This approach also has the advantage that the computation cost is relatively small and that the resulting alignment is inverse consistent [30] as will become clear from the symmetry of the cost function defined below.
In order to generate such a parameterization with prealigned landmarks, we model the cortical surface as an elastic sheet and solve the associated linear elastic equilibrium equation using the Finite Element Method (FEM). We choose the more general elastic model over a surface based harmonic mapping method [34], [35], [36] because we found that the surface based harmonic mappings do not remain bijective when multiple sulcal landmark constraints are imposed on the interior of the flat parameter space. However, for the elastic model, we have found improved bijective behavior with appropriate choices of model parameters λ and μ. The reason for this situation, intuitively, is that relative to the power of the Laplacian alone, the Cauchy-Navier elasticity operator provides additional control over the gradient of the divergence of the surface vector field, and this indirectly controls the Jacobian of the mapping, constraining it from taking on extreme values and thereby violating the smoothness assumption. If the smoothness were a problem, the flow could be discretized in time and integrated to prevent singularities, as described by Christensen et al. [8].
A. Mathematical Formulation
We map the surfaces of each cortical hemisphere of a pair of brains M and N to the unit square such that in the flat map the manually delineated sulcal landmarks align in the square parameter space. The resulting parameterization then defines a correspondence between the two cortices. We describe the process for identifying the surfaces and delineating the sulci in Section IIIC. For now it is sufficient to assume two surfaces with spherical topology on which are traced two homologous sets of continuous, non-intersecting sulcal curves. The corpus callosum maps to the boundary of the square with the boundary condition assuring continuity between the two hemispheres of each brain when subsequently mapping these flat maps to the surface of a sphere.
Let ϕ = [ϕ1, ϕ2]T be the two coordinates assigned to every point on a given cortical surface such that the coordinates ϕ satisfy the linear elastic equilibrium equation with Dirichlet boundary conditions on the boundary of each cortical hemisphere, represented by the corpus callosum. We constrain the corpus callosum to lie on the boundary of the unit square mapped as a uniform speed curve.
We solve the linear elastic equilibrium equation in the geometry of the cortical surface using the form:
| (1) |
where μ and λ are Lamé's constants which model the elastic material response to linear strain and shear respectively [37]. The operators Δ and ∇ represent the Laplace-Beltrami and covariant gradient operators, respectively, with respect to the surface geometry. The solution of this equation can be obtained variationally by minimizing the integral on the cortical surface [38]:
| (2) |
where Dϕ is the covariant derivative of the coordinate vector field ϕ. The integral E(ϕ) is the total strain energy. Though the elastic equilibrium equation models only small deformations, we have found that in routine practice, our method is able to produce a flat map of the cortex by using the parameters μ = 100 and λ = 1. Intuitively, they control the ‘stretching’ and ‘bending’ properties of the desired map.
Let ϕM and ϕN denote the 2D coordinates to be assigned to corresponding hemispheres of M and N respectively. Then we define the cost function C(ϕM, ϕN) as
| (3) |
where ϕM(xk) and ϕN(yk) denote the coordinates assigned to the set of K sulcal landmarks xk ∈ M, yk ∈ N and ρ is a penalty parameter. Here sulcal matching is represented by a set of point constraints obtained by sampling each curve at a fixed number of points taken along its length. Note that we do not constrain the locations of the sulci in the flat map but simply constrain homologous landmarks in the two maps to lie at the same coordinates. The method is easily modified for subject to template matching by fixing the parameters of the sulcal constraints in the template.
B. Finite Element Formulation
To minimize (3) on a tessellated surface we use an FEM to discretize the strain energy E(ϕ). Since the strain energy at a point is independent of coordinate system, it is justifiable to compute it locally at each vertex point by assigning a local coordinate system (x, y) to its neighborhood.
For each triangle the covariant derivative Dϕ in the local coordinates x, y becomes the Jacobian matrix:
| (4) |
We compute the strain energy Ei(ϕ) for the ith triangle Δi using (2) as:
| (5) |
We now describe the FEM discretization of the partial derivatives with respect to the local coordinates. Let α be any piecewise linear real-valued scalar function defined over the surface, and let x, y denote local coordinates for triangle i. Also denote the local coordinates of the three vertices as (x1, y1), (x2, y2) and (x3, y3) respectively. Since α is linear on the ith triangle, we can write,
| (6) |
Writing this expression at three vertices of the triangle i in matrix form,
| (7) |
The coefficients , and can be obtained by inverting the matrix Ei. From (6) and by inverting the matrix in (7), we obtain
| (8) |
| (9) |
Denote the discretization of and at triangle i by and respectively. Also note that |Ei| = 2Ai where Ai is area of the ith triangle. Then we have:
| (10) |
| (11) |
Substituting these in (5) and (3), we have
| (12) |
| (13) |
where M is given by
| (14) |
This method is used to discretize both E(ϕM) and E(ϕN). The resulting cost function (3) is then minimized using a conjugate gradient method as described in the next section. We note from (13) and (3) that the cost function is quadratic. We minimize (3) with respect to both ϕM and ϕN, with the corpus callosum fixed at the boundary of the unit square, to compute the sulcally coregistered flat maps for both brains simultaneously.
C. Implementation
We assume as input two T1-weighted MR volumes Cortical surfaces were extracted from volume images using the BrainSuite software [39]. BrainSuite includes a six stage cortical modeling sequence First the brain is extracted from the surrounding skull and scalp tissues using a combination of edge detection and mathematical morphology Next the intensities of the MRI are corrected for shading artifacts Each voxel in the corrected image is labeled according to tissue type using a statistical classifier A standard atlas with associated structure labels is aligned to the subject volume, providing a label for cerebellum cerebrum brainstem and subcortical regions These labels are combined with the tissue classification to automatically identify the cerebral white matter to fill the ventricular spaces and to remove the brainstem and cerebellum This produces a volume whose boundary surface represents the outer white-matter surface of the cerebral cortex It is likely that the tessellation of this volume will produce surfaces with topological handles Prior to tessellation these handles are identified and removed from the binary volume automatically using a graph based approach [40]. A tessellated isosurface of the resulting mask is then extracted to produce a genus zero surface based on the registered atlas labels that is subsequently split into two cortical hemispheres.
We then use BrainSuite to interactively label 23 major sulci on each cortical hemisphere according to a sulcal labeling protocol with established intra- and inter-rater reliability [41]. This protocol specifies that sulci do not intersect and that individual sulci are continuous curves that are not interrupted If interruptions are present the human raters specify the path across any interrupting gyri In cases where a full set of sulci cannot be defined a subset can be used without requiring any changes in the algorithm described here.
We note that the procedure implemented in BrainSuite to find the cortical surface uses the inner grey/white boundary of cortex as the surface Consequently the images shown here do not include cortical grey matter but are restricted to white matter ventricles and subcortical grey matter However, the method can be used with any of the approaches for cortical segmentation that produce a genus-zero representation of the cortical surface, e.g, [42], [13]. Automated extraction of a topologically spherical surface from MRI using BrainSuite takes 4-5 min. and interactive sulcal labeling takes approximately 1-2 hours per brain.
As described above, E(ϕM) and E(ϕN) are discretized using (14) and (13). The resulting quadratic cost function (3) is minimized using a preconditioned conjugate gradient method with Jacobi preconditioner. In practice the minimization algorithm converges in approximately 500 iterations, requiring 2-3 mins on a desktop computer for tessellations with on the order of 105 vertices.
We show an example of this flattening and alignment procedure in Fig. 2. Shown in (a) and (b) are the sulci traced on the white matter surface for two brains. In (c) and (d) we show the flat maps of one hemisphere in each brain computed with the penalty parameter ρ = 0 in (3), which corresponds to the case where the two hemispheres are flattened independently. Similarly, (e) and (f) show the flat maps for the case ρ = 3, which forces approximate alignment of the sulci in the flat maps. Note that we only enforce the matching approximately via the penalty term in (3). Maps with and without sulcal alignment appear quite similar, so we show in (g) the two sets of curves in the flat space when they are not constrained to align (ρ = 0), and in (h) when they are constrained (ρ = 3). These figures illustrate the procedure and demonstrate alignment of the curves in the flat space. In Fig. 3 we show the results of applying the mapping procedure separately from five subjects to a single template brain. Each pair of flattenings produces a different parameterization of each subject and of the template. In each case, there is a one-to-one map between the surfaces so that the sulcal curves of each subject can be mapped back onto the template surface. Shown in the figure are the set of sulcal curves mapped onto the template for cases where the alignment constraint is (ρ = 0) and is not (ρ = 3) applied.
Fig. 2.
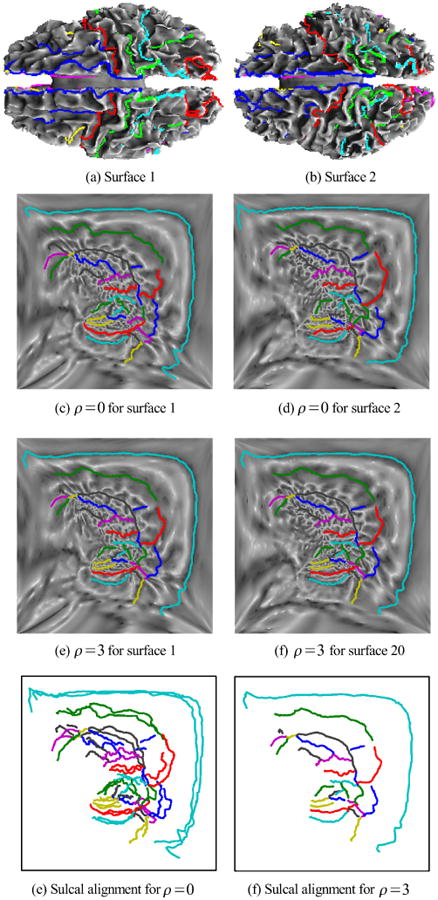
(a),(b) Two cortical surfaces with labeled sulci as colored curves; (c),(d) flat maps of a single hemisphere for each brains without the sulcal alignment constraint; (e),(f) flat maps with sulcal alignment; (g),(h) overlay of sulcal curves on the flat maps, without and with sulcal alignment.
Fig. 3.
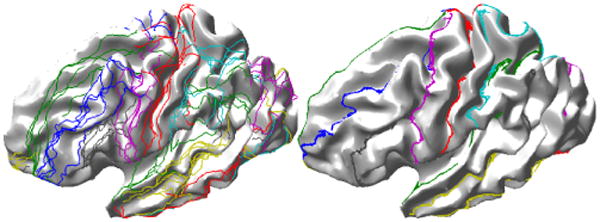
Result of mapping of sulcal landmarks from 5 subjects to a single brain using the linear elastic mapping described here (left) without and (right) with the sulcal alignment constraint.
IV. Harmonic mapping
The surface registration procedure described in Section III sets up a point to point correspondence between the two cortical surfaces, which represent the boundary of the two cerebral volumes. Extrapolating this correspondence from the boundary surface to the entire cerebral volume in a one-to-one manner is challenging due to the convoluted nature of the cortex. In fact, most of the linear models such as linear elastic or thin-plate splines become non-bijective under relatively mild landmark matching constraints [32]. 3D harmonic maps are attractive for this purpose due to their tendency to be bijective if the boundary (cortical surface) is mapped bijectively, which is the case here. In this section we describe a framework for computing a harmonic mapping between two 3D volumes as well as the computational approach used for implementation. Details of harmonic maps and their properties can be found in [43].
Let u : M → N be a C∞ map from a 3 dimensional Riemannian manifold (M, g) to a 3 dimensional Riemannian manifold (N, h) where g and h are Riemannian metrics for M and N respectively. A Riemannian metric defines an inner product at every point in the manifold and thus helps in defining the notion of distance on the manifold [43]. Let {gij; i, j ∈ {1, 2, 3}} denote components of the Riemannian metric tensor g and {hαβ; α, β ∈ {1, 2, 3}} denote the components of the Riemannian metric tensor h. The inverse of the metric g = {gij} is denoted by {gij}. Let (x1, x2, x3) and (u1, u2, u3) be local coordinates for x and u(x) respectively. Let Du denote the derivative (generalized Jacobian) of the map. The energy density function e(u) of map u is defined to be the norm of Du [44] and is given by
| (15) |
| (16) |
which can be thought of as the rate of expansion of the map u in orthogonal directions, at point x ∈ M [44],. The mapping energy is defined as
| (17) |
The mapping energy in coordinate form [44], is given by
| (18) |
where the integration is over the manifold M with respect to the intrinsic measure dμg induced by its Riemannian metric g.
A harmonic map from (M, g) to (N, h) is defined to be a critical point of the mapping energy E(u). In this sense harmonic maps are the least expanding maps in C∞(M, N), the space of all smooth maps from M to N. Therefore, among all possible smooth maps between two manifolds, the harmonic maps have the tendency to avoid overlaps and folds in the map, resulting in a bijective map.
A number of existence, uniqueness, and regularity results have been proven for harmonic maps [45]. Eells and Sampson [46] proved the existence of a harmonic map from any compact Riemannian manifold to a compact Riemannian manifold of non-positive sectional curvature. Hamilton [47] generalized this result to manifolds with boundaries. In medical imaging, harmonic mappings and p-harmonic mappings, their generalized counterparts [48], have been used for various applications such as surface parameterization and registration [34], [49], [35] and image smoothing [36]. Wang et al. [50] describe a method for volumetric mapping of the brain to the unit ball B(0, 1). Here we use harmonic maps to align two brain volumes so that both the brain volumes and cortical surfaces are aligned.
When computing the harmonic maps we could fix the correspondence between the two surfaces using the method from Section III and map only the interior of the two volumes. This would result in a suboptimal mapping with respect to the 3D mapping energy. To overcome this limitation, we instead allow the surface M to flow within the surface of N when computing the map. The only constraints placed on the surfaces are that the maps are aligned at the set of user defined sulcal landmarks and that the boundary ∂M maps onto ∂N. This less restrictive surface mapping constraint cannot be formulated directly in the ambient Euclidean 3D space since there is no analytical expression for the surfaces. It could be accomplished without parameterizing the surface using a level set approach [36], [51]. Here we use an intermediate representation for the manifolds which allows us to enforce the boundary matching constraint while allowing one boundary to flow within the other. We achieve this by first mapping to the unit ball as described below. This mapping to the unit ball results in a non-Euclidean representation of N thus requiring the use of the Riemannian metric in computing the harmonic map.
A. Mathematical Formulation
We find the map v of the 3D brain manifold N to the 3D unit ball B(0, 1) [50] using the method described in Sec. IV-C. Let v = (v1, v2, v3) denote the three coordinates of the map v. This map is bijective and therefore we can treat the unit ball B(0, 1) as an alternative representation (N, h) of the manifold N, with associated metric h, that has the advantage over the Euclidean space (N, I) that the cortical surface lies on the surface of the sphere (here I represents the identity metric for the Euclidean space); h is the metric induced by the map v. With this alternative representation of N, the components of its metric hαβ at point x = (x1, x2, x3) are given by
| (19) |
Now instead of needing to directly compute the harmonic map u : (M, I) → (N, I), we instead find the harmonic map ũ : (M, I) → (N, h) ≈ B(0, 1) subject to the constraint that the cortical surface ∂M maps to the spherical boundary of the unit ball, as illustrated in Fig. 4.
Fig. 4.
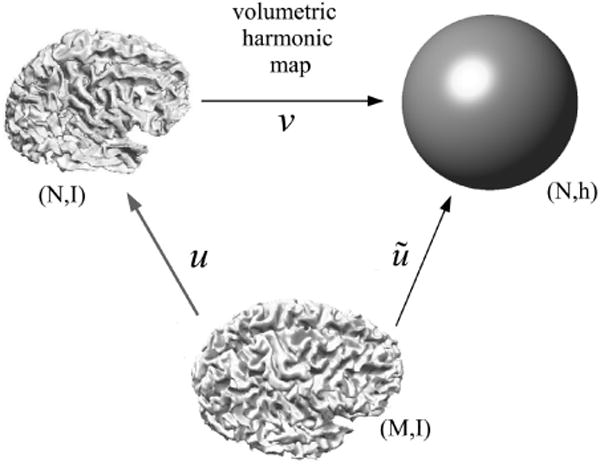
Illustration of our general framework for surface-constrained volume registration. We first compute the map v from brain manifold (N, I) to the unit ball to form manifold (N, h). We then compute a map ũ from brain (M, I) to (N, h). The final harmonic map from (M, I) to (N, I) is then given by u = v−1 ○ ũ.
Since M remains in the Euclidean space, its metric is I, so gij(x) is the identity operator and the harmonic mapping problem (18) becomes:
| (20) |
subject to ‖ũ(x)‖2 = 1 for x ∈ ∂M, the surface of M. Note that this constraint allows the surface map to flow within the spherical boundary. We also want to constrain the maps so that predefined sulcal landmarks are aligned. To achieve this we impose the additional constraints that ũ(c) = uc for c ∈ Mc where Mc are the set of sulcal landmark points in M and uc are the locations of the homologous landmarks in (N, h). Having obtained ũ by minimizing the integral in (20), the final harmonic mapping from u : (M, I) → (N, I) can then be computed as u = v−1 ○ ũ as illustrated in Fig. 4.
B. Initialization Procedure
Because the minimization problem (20) is nonquadratic, it is important to have a good initial estimate of the map ũ in order to achieve convergence in reasonable time. We therefore generate an initial estimate ũ0 of ũ by computing a map of the second manifold (M, I) to the unit ball, just as we do for the first manifold (N, I) (Fig. 4). Thus our initialization generates a bijective initial map, which is not necessarily harmonic. The procedure is illustrated in Fig. 5.
Fig. 5.
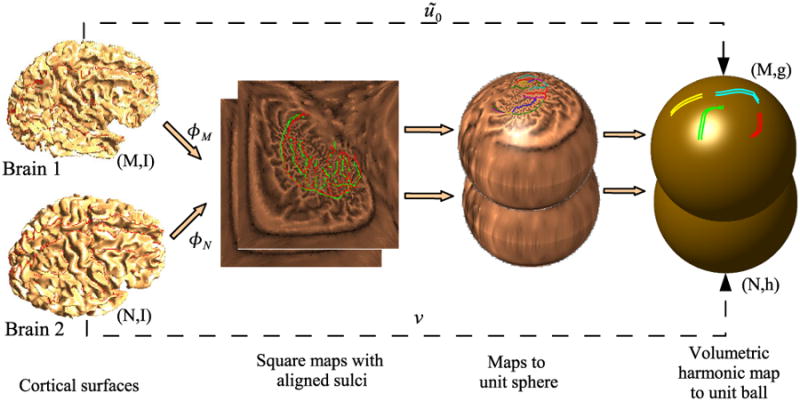
Initialization for harmonic mapping from M to N. First we generate flat square maps of the two brains, one for each hemisphere, with pre-aligned sulci. The squares corresponding to each hemispheres are mapped to a disk and the disks are projected onto the unit sphere. We then generate a volumetric maps from each of the brains to the unit ball. Since all these maps are bijective, the resulting map results in a bijective point correspondence between the two brains. However, this correspondence is not optimal with respect to the harmonic energy of maps from the first brain to the second, but is used as an initialization for minimization of (20).
The initialization consists of the following steps. We first compute flat maps to the unit square for each hemisphere of the two brains with aligned sulci as described in Section III. A stereographic projection then maps the two hemispheres of each brain to the unit sphere so that the corpus callosum that forms the boundary of the unit squares maps to the equator. Using these surface maps as constraints, we then map N and M to the unit ball to provide, respectively, the unit ball manifold (N, h) and an initial estimate ũ0 of the desired map ũ from (M, I) to (N, h). The initial map obtained in this manner is smooth and bijective. With this initialization, the 3D harmonic map is computed by minimizing (20) to obtain the final harmonic mapping from M to N.
C. Mapping to the Unit Ball B(0, 1)
In the special case when (M, g) and (N, h) are 3D Euclidean manifolds, then , , the Kronecker delta, or identity tensor, for α, β, i, j ∈ 1, 2, 3, and the mapping energy simplifies to
| (21) |
where ∇ is the usual gradient operator in 3D Euclidean space and dV is the volume integral [50]. In order to map the given cortical brain volume M to the unit ball, this energy is minimized subject to the constraint that the surface of M maps to the surface of the unit ball using the point-to-point correspondence defined by the flat mapping obtained as described in Section III. This is computed by numerical integration over the voxel lattice using finite differences to approximate the gradients in (21). The resulting function is minimized using a preconditioned conjugate gradient method. The process of mapping to the unit ball is illustrated in Fig. 6 where we show iso-surfaces in brain coordinates corresponding to different radii, r, within the unit ball. At r = 1 we are at the outer surface of the brain and see the full cortical surface. As r is reduced we see successively less distortion since the harmonic map is driven entirely by the surface constraint.
Fig. 6.
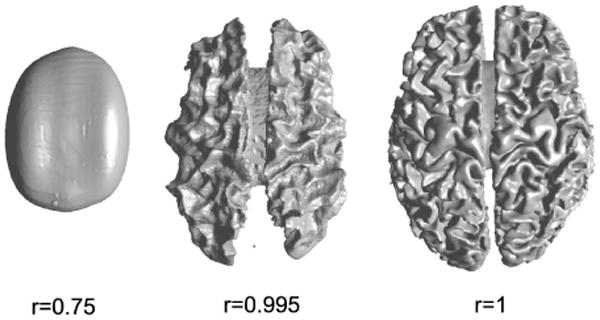
Illustration of the deformation induced with respect to the Euclidean coordinates by mapping to the unit ball. Shown are iso-surfaces corresponding to the Euclidean coordinates for different radii in the unit ball. Distortions become increasingly pronounced towards the outer edge of the sphere where the entire convoluted cortical surface is mapped to the surface of the ball.
D. Harmonic Mapping Between the Two Brains
The mapping to the unit ball is applied to both brain volumes M and N. The mapping of the Euclidean coordinates in M to the unit ball provides the initial estimate ũ0 of the harmonic map ũ. We then refine this map by minimizing the harmonic energy in (20) from (M, I) to (N, h), the unit ball representation of N. Again, the problem is solved using numerical integration and finite difference operators, in this case accounting for the metric h according to (20) when computing these derivatives. In this mapping, the locations of the sulci in M are constrained using their initial mappings ũ0 computed when flattening and matching the cortical surfaces. Other points on the surface are allowed to move freely to minimize the harmonic energy, subject to the constraint that all points on the surface map to ‖ũ‖2 = 1, which is achieved by adding a penalty function ϱ(‖ ũ‖2 = 1)2 to the discretized form of (20). The penalty parameter ϱ is set to 1000 for the purpose of numerical implementation.
E. Implementation
We first describe a numerical method for computation of the metric hij (x) and then outline the harmonic mapping method.
1) Computation of Metric
The metric hij (x), x ∈ N is associated with the unit ball coordinates B(0, 1) given to N by the map v = (v1, v2, v3) (Fig. 4). It is given by with α, β ∈ {1, 2, 3} at x = (x1, x2, x3). Note that although x ∈ N is in the regular grid, v(x) ∈ B(0, 1) is not necessarily so, and hence computation of partial derivatives with respect to v directly is difficult. In order to compute , first compute using finite differences and then use the chain rule identity
| (22) |
to solve for . The metric hij is computed by substituting these partial derivatives in the above equation.
2) Harmonic Mapping
The harmonic mapping procedure can now be summarized as follows:
Align the surfaces of both the brains M and N using the procedure described in Sec. III.
Map the unit squares to unit disks by the transformation and then project them onto two hemispheres using .
Using this mapping of the cortical surface to the unit sphere as the boundary condition, generate volumetric harmonic maps of M and N to the unit ball B(0, 1) as described in Sec. IV-C.
Compute the metric h associated with the unit ball B(0, 1) coordinates of N as described above.
Minimize (20) holding the matched sulci fixed, and letting the cortical surface ∂M slide along boundary of the unit ball. This is done by minimizing (20) with the constraint that ‖ũ(x)‖2 = 1 for x ∈ ∂M and ũ(c) = ũ0(c) for c ∈ Mc where Mc ⊂ M denotes the set of sulcal points on M. The partial derivatives in (20) are discretized by finite differences and the minimization is done by gradient descent.
Compute the displacement vector field u(x) – x where u = v−1 ○ ũ and apply this to map brain volume M to N. Trilinear interpolation is used for this deformation.
V. Volumetric Intensity Registration
The surface constrained harmonic mapping procedure described above produces a bijective mapping between the two brain volumes. However, it uses only surface shape and sulcal labels and does not use the MRI intensity values to compute the map. The result is a large scale deformation that aligns surface features but will benefit from an intensity-based refinement aimed at aligning subcortical features. In order to do this refinement and also make the final map inverse consistent, we use linear elastic inverse consistent registration based on Christensen's approach [31] with the modifications described below to ensure that the entire mapping process, rather than just this last step, is inverse consistent. Alternatively, inverse consistency can be achieved by symmetric intensity based registration method suggested by Tagare et al. [52]
A. Formulation
The surface constrained volumetric harmonic mapping procedure described above can be used to generate two maps uM : M → N and uN : N → M, each harmonic, but not necessarily inverses of each other. The corresponding displacement fields for these maps can be expressed as and . Note that both of these displacement fields accurately align the two surfaces and corresponding sulci, and are one-to-one. These deformations are used to initialize the volumetric inverse consistent intensity registration procedure that we now describe.
Let fM(x), x ∈ M denote intensity at point x ∈ M and fN(x), x ∈ N denote intensity at point x ∈ N. The situation can be summarized as follows and is illustrated in Fig. 7: We have harmonic maps uM : M → N uN : N → M that change the shapes of domains M and N to match their respective targets N and M. In order to align the intensities, we seek refinement maps wM : M → M and wN : N → N such that the mapped intensity value fM ○ wM ○ uN matches fN (or equivalently fM ○ wM matches fN ○ uN)−1), and fN ○ wN ○ uM matches fM (or fN ○ wN matches fM ○ (uM)−1). For inverse consistency, we need wN ≈ (uM ○ wM ○ uN)−1 and wM ≈ (uN ○ wN ○ uM)−1. Let , denote the displacement fields corresponding to wM, wN and let , denote the displacement fields for (uN ○ wN ○ uM)−1, (uM ○ wM ○ uN)−1.
Fig. 7.
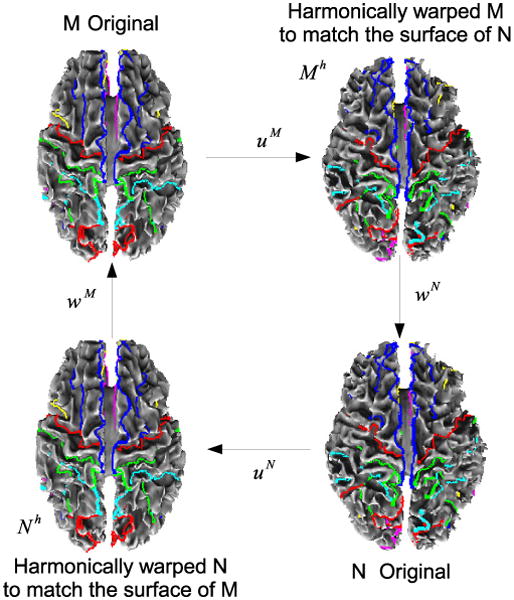
Schematic of the intensity alignment procedure. Once harmonic maps uM and uN are computed, we refine these with intensity driven warps wM and wN while imposing constraints so that the final deformations are inverse consistent.
The inverse consistency similarity cost function C( , ), can now be defined as the sum of three terms:
| (23) |
where the boundary constraints ensure that the cortices remain aligned after registration and the three constituent terms are defined as follows:
| (24) |
The first term is the regularizer where and denote the Cauchy Navier elasticity operators in M and N respectively. The parameter values of α = 10, β = 2 and γ = 0.1 are used for the purpose of numerical implementation. The second term measures the intensity match between the transformations in both directions and the third term is a measure of deviation from the inverse consistent condition. The similarity cost CSIM is linearized by using Tayor series so that the approximation is quadratic. Note that the inverse consistency cost CICC and regularizing cost CREG are quadratic. The resulting quadratic cost function C can be efficiently minimized by the conjugate gradient method. We use a preconditioned conjugate gradient method with Jacobi preconditioner for this purpose.
B. Implementation
First, the harmonic maps uM : M → N and uN : N → M are computed using the procedure described in Section IV-D.
The inverses of the map is computed. This is done by interpolating the correspondence from points to the regular voxel grid of N using Matlab's griddata3 function with linear interpolation. This function implements the method based on Delauney triangulation as described in [53] although it can also be computed using the method described in [31]. is computed similarly.
Set and .
Compute the maps , y ∈ N, w̃M = (uN ○ wN ○ uM)−1 and .
Compute the difference term fN(x) – fM(uN−1(x)).
Compute an updated estimate of the displacement field from (23) using a preconditioned conjugate gradient method.
Repeat steps 4-6 with M and N interchanged.
Test inverse consistency error CICC for convergence, otherwise go to Step 4.
This final refinement completes the surface-constrained registration procedure. While there are several steps required to complete the registration, each step can be reduced to either a surface or a volume mapping cast as an energy minimization problem, with constraints, and can be effectively computed using a preconditioned conjugate gradient method. The different effects of the harmonic mapping, producing large scale deformations, and the linear elastic intensity-driven refinement, producing small scale deformations, are illustrated in Fig. 8
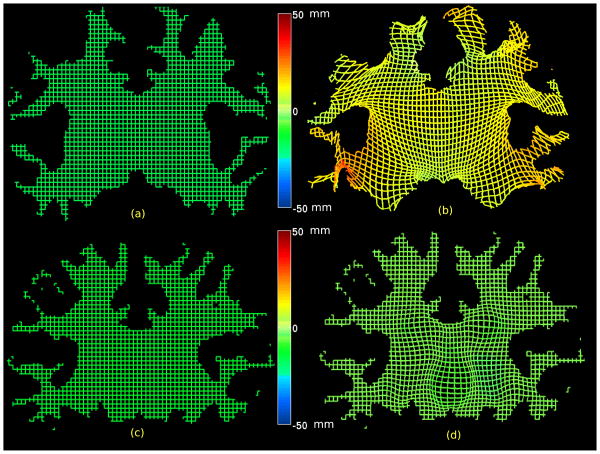
Fig. 8.
Illustration of the effects of the two stages of volumetric matching is shown by applying the deformations to a regular mesh representing one slice. Since the deformation is in 3d, the third in-paper value is represented by color. (a) Regular mesh representing one slice in the subject; (b) the regular mesh warped by the harmonic mapping which matches the subject cortical surface to the template cortical surface. Note that deformation is largest near the surface since the harmonic map is constrained only by the cortical surface; (c) Regular mesh representing one slice in the harmonically warped subject; (d) the intensity-based refinement now refines the deformation of the template to improve the match between subcortical structures. In this case the deformation is constrained to zero at the boundary and are confined to the interior of the volume.
VI. Results and Validation
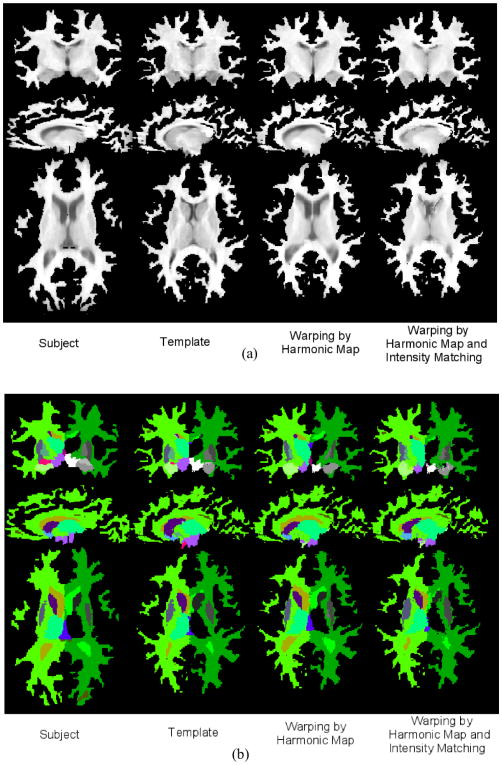
In order to illustrate the application of our surface constrained registration procedure to T1-weighted MR brain images and validate its performance, we obtained labeled brain data from the Internet Brain Segmentation Repository (IBSR) dataset at the Center for Morphometric Analysis at Massachusetts General Hospital. This consists of T1-weighted MR images with 1.5mm slice thickness as well as expert segmentations of 43 individual structures. The cortical masks were obtained and their topology corrected using the BrainSuite software as described in Sec. III-C. The cortical surfaces were then interactively labelled with 23 sulcal curves on each hemisphere using a standard labeling protocol [41]. Our registration algorithm was applied by performing surface matching, harmonic mapping and volumetric intensity registration as described above. Shown in Fig. 9 are three orthogonal views of a subject before and after alignment to the template image. Note that before alignment the surfaces of the subject and template are clearly different, while after the harmonic mapping the deformed subject surface almost exactly matches the morphology of that of the template. However, since at this point we do not take the image intensities into account, the interior structures do not align well. Following the final intensity-based alignment procedure the subcortical structures of the warped subject show improved agreement with those in the the template. Also shown in Fig. 9b are the labels provided by the IBSR data set before and after mapping.
Fig. 9.
Examples of surface constrained volumetric registration. (a) Original subject volume, original template, registration of subject to template using surface constrained harmonic mapping, intensity-based refinement of the harmonic map of subject to template is shown. Note that the surface of the warped subject matches to the surface of the template. (b) Anatomical labels of the subject and the template followed by labels of the subject warped by surface constrained harmonic mapping and intensity-based refinement of the harmonic map are shown.
Our method for evaluating the quality of our registration results is based on the following two desirable features:
Alignment of the cortical surface and sulcal landmarks. We expect the sulcal landmarks to be accurately aligned after registration and for the two surfaces to coincide.
Alignment of subcortical structures. We also expect the boundaries of subcortical structures (e.g., thalamus, lateral ventricles, corpus callosum) to be well aligned after registration.
To evaluate performance with respect to 1, we used a set of 6 MR volumes on which we labeled 23 sulci in each hemisphere. For comparison we use a 5th order polynomial intensity-driven warp computed using the AIR software [5], [11]. We also compare performance with the HAMMER [28], [54] algorithm. HAMMER is an automated method for volume registration which is able to achieve improved alignment of geometric features by basing the alignment on an attribute vector that includes a set of geometric moment invariants rather than simply the voxel intensities. We note that since our approach uses explicitly labelled sulci we can expect better performance than either AIR or HAMMER in terms of the alignment of these features. However, AIR and HAMMER provide a basis for comparison since they are among the most widely used and best performing algorithms for volumetric registration.
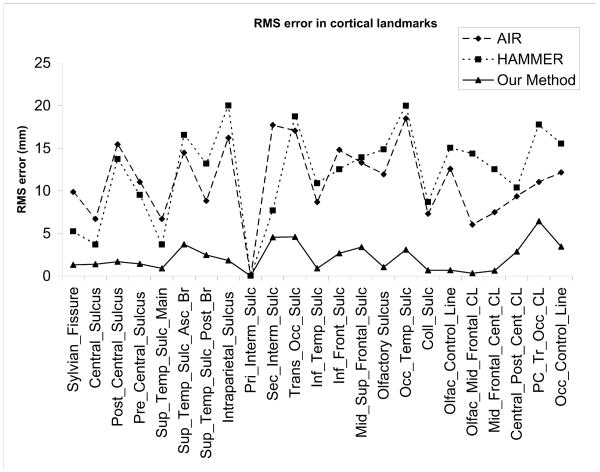
We measured the mean squared distance between pairs of homologous landmarks corresponding to uniform samples along each of the 23 labeled sulci. We repeated this procedure for each of the 30 possible pairwise registrations of two from six brains and computed the average mean squared distance over all registrations. We found that the mean squared misalignment between sulcal landmarks was 11.5mm for HAMMER, 11mm for AIR and 2.4mm for our cortically constrained method. Results for individual sulci are included in Fig. 10. The significantly lower error for our approach is unsurprising since matching of sulci is imposed as a constraint. The reason that the error is not zero is that the constraint is imposed using a penalty function rather than strictly using Lagrange multipliers.
Fig. 10.
RMS errors in alignment of different sulci using AIR (5th order), HAMMER and our surface constrained mapping.
To evaluate performance in terms of subcortical structures we used the manually labeled regions in the IBSR data set. To evaluate accuracy, we computed the Dice coefficients between the template and warped subject for each subcortical structure, where the structure names and boundaries were taken from the IBSR database. The Dice coefficient measures overlap between two sets representing regions S1 and S2, and is defined as where | · | denotes size of the set [55]. Values range from zero for disjoint sets to unity for identical sets. A comparison of the Dice coefficients for some major subcortical organs is shown in Table I, where we show Dice coefficients for our method before and after application of the intensity-based alignment step. This comparison shows similar results for all three methods, with each producing superior results in some subcortical structures. For example, HAMMER produced superior results in thalamus, while our proposed method produced superior results in hippocampus. Thus the geometric invariants in HAMMER seem to improve performance relative to our intensity based alignment of deeper subcortical structures, while our use of a cortical constraint leads to superior performance with respect to sulcal alignment and structures that are more superficial with respect to the cerebral cortex, such as the hippocampus. This is a preliminary validation and larger scale validation is needed on a larger population with a larger range of brain structures.
Table I. Comparison of Dice coefficients.
| Subcortical Structure | AIR | Harmonic | HAMMER | Harmonic with intensity |
|---|---|---|---|---|
|
| ||||
| Left Thalamus | 0.6588 | 0.5294 | 0.7303 | 0.5856 |
| Left Caudate | 0.4426 | 0.4336 | 0.5688 | 0.5716 |
| Left Putamen | 0.4079 | 0.3497 | 0.4905 | 0.5092 |
| Left Hippocampus | 0.4676 | 0.3069 | 0.3916 | 0.3930 |
| Right Thalamus | 0.6326 | 0.5018 | 0.7495 | 0.6230 |
| Right Caudate | 0.3671 | 0.3572 | 0.5098 | 0.5116 |
| Right Putamen | 0.3096 | 0.2358 | 0.4111 | 0.4679 |
| Right Hippocampus | 0.5391 | 0.3455 | 0.1989 | 0.4342 |
|
| ||||
| Avg. Dice coeff. for all structures | 0.3021 | 0.3821 | 0.3621 | 0.4019 |
|
| ||||
| Std. Dev. of Dice coeff. | 0.1937 | 0.2547 | 0.2390 | 0.2671 |
VII. Conclusion
We have presented a framework for coregistration of brain volume data using harmonic maps. Through the use of an intermediate spherical map, we are able to constrain the surfaces of the two brain volumes to align while enforcing point matching only at a set of hand labeled sulcal curves. Using harmonic maps we are able to compute large scale deformations between brain volumes.
We have also described, as an initialization procedure, a new method for cortical surface parameterization and sulcal alignment in which the two problems are solved in a single step using a finite element method. This method has the properties that it is inverse consistent between the two brains and can be computed directly from a tessellated representation of the surface, rather than requiring resampling using a regular grid with respect to the induced parameterization.
The examples shown here demonstrate the cortical matching properties and the ability to also align subcortical structures. One of the limitations of this evaluation was that cortical grey matter was not included in the registration since the cortical surfaces were generated by BrainSuite [56], which selects the inner grey/white boundary as the cortical surface. However, this is a limitation of the preprocessing step rather than the method itself, and the process can be applied to the full cerebral volume provided that a genus-zero brain volume and sulcal labels are supplied. A second limitation is that the cerebellum and brainstem are not included in the analysis since the volume of interest that is mapped is restricted to the cerebrum, bounded by the outer cortical sheet. We can address this issue in practice by modifying the final intensity-based matching step by first adding the brainstem and cerebellum back to the cerebrum. This would also require extrapolation of the displacement field from the harmonic map outwards to these structures as an initialization of the intensity based warp. Alternatively, the cerebellum could also be explicitly modelled using a surface based approach (see, e.g., Hurdal et al. [12]), and its surface and enclosed volume could be treated in a similar fashion to the cerebrum.
Acknowledgments
The authors would like to thank the Center for Morphometric Analysis at Massachusetts General Hospital for providing the MR brain data sets and their manual segmentations. The MR and segmentation data sets are available at http://www.cma.mgh.harvard.edu/ibsr/. The registration softwares AIR by Dr. Woods was downloaded from http://bishopw.loni.ucla.edu/AIR5 and HAMMER was made available for download by Dr. Shen. The authors would like to thank Dr. Woods and Dr. Shen for sharing their software. The BrainSuite software is available at http://brainsuite.usc.edu/.
This work is supported under grants r01 eb002010 and p41 rr013642. p.m.t. is also supported by ag016570, lm05639, eb01651, rr019771 and ns049194.
References
- 1.Christensen GE, Joshi SC, Miller MI. Volumetric transformation of brain anatomy. IEEE TMI. 1997 Dec;16(6) doi: 10.1109/42.650882. [DOI] [PubMed] [Google Scholar]
- 2.Thompson PM, Toga AW. A surface-based technique for warping 3-dimensional brain. IEEE Transactions on Medical Imaging. 1996;15(4):1–16. doi: 10.1109/42.511745. [DOI] [PubMed] [Google Scholar]
- 3.Talairach J, Tournoux P. Co-planar Stereotaxic Atlas of the Human Brain: 3-Dimensional Proportional System - an Approach to Cerebral Imaging. NY: Thieme Medical Publishers, New York; 1988. [Google Scholar]
- 4.Ashburner J, Friston K. Spatial normalization. In: Toga A, editor. Brain Warping. Academic Press; 1999. pp. 27–44. [Google Scholar]
- 5.Woods RP, Grafton ST, Holmes CJ, Cherry SR, Mazziotta JC. Automated image registration: I. General methods and intrasubject, intramodality validation. Journal of Computer Assisted Tomography. 1998;22:139–152. doi: 10.1097/00004728-199801000-00027. [DOI] [PubMed] [Google Scholar]
- 6.Hill DLG, Batchelor PG, Holden M, Hawkes DJ. Medical image registration. Phys Med Biol. 2001 Mar;46(4):r1–r45. doi: 10.1088/0031-9155/46/3/201. [DOI] [PubMed] [Google Scholar]
- 7.Christensen GE, Rabbitt RD, Miller MI, Joshi SC, Grenander U, Coogan TA, Essen DCV. Topological properties of smooth anatomic maps. In 14 Conference on Information Processing in Medical Imaging; France. Kluwer Academic Publishers; 1995. pp. 101–112. [Google Scholar]
- 8.Christensen GE, Rabbit RD, Miller MI. Deformable templates using large deformation kinematics. IEEE Transactions on Image Processing. 1996;5(10):1435–1447. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]
- 9.Glaunés J, Vaillant M, Miller MI. Landmark matching via large deformation diffeomorphisms on the sphere. J Math Imaging Vis. 2004;20(1-2):179–200. [Google Scholar]
- 10.Avants BB, Gee JC. Shape averaging with diffeomorphic flows for atlas creation. ISBI. 2004 [Google Scholar]
- 11.Woods RP, Grafton ST, Watson JDG, Sicotte NL, Mazziotta JC. Automated image registration: II. Intersubject validation of linear and nonlinear models. Journal of Computer Assisted Tomography. 1998;22:153–165. doi: 10.1097/00004728-199801000-00028. [DOI] [PubMed] [Google Scholar]
- 12.Hurdal MK, Stephenson K, Bowers PL, Sumners DWL, Rottenberg DA. Coordinate system for conformal cerebellar flat maps. NeuroImage. 2000;11:s467. [Google Scholar]
- 13.Fischl B, Sereno MI, Tootell RBH, Dale AM. High-resolution inter-subject averaging and a coordinate system for the cortical surface. Human Brain Mapping. 1998;8:272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bakircioglu M, Grenander U, Khaneja N, Miller MI. Curve matching on brain surfaces using frenet distances. Human Brain Mapping. 1998;6:329–333. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<329::AID-HBM1>3.0.CO;2-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Thompson PM, Wood RP, Mega MS, Toga AW. Mathematical/computational challenges in creating deformable and probabilistic atlases of the human brain (invited paper) Human Brain Mapping. 2000 Feb;9(2):81–92. doi: 10.1002/(SICI)1097-0193(200002)9:2<81::AID-HBM3>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Joshi AA, Shattuck DW, Thompson PM, Leahy RM. A framework for registration, statistical characterization and classification of cortically constrained functional imaging data. Lecture Notes in Computer Science. 2005 Jul;3565:186–196. doi: 10.1007/11505730_16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang Y, Chiang MC, Thompson PM. Automated surface matching using mutual information applied to Riemann surface structures. In: Duncan J, Gerig G, editors. MICCAI 2005, LNCS 3750. Springer-Verlag; Berlin Heidelberg: 2005. pp. 666–674. [DOI] [PubMed] [Google Scholar]
- 18.Tosun D, Prince JL. Cortical surface alignment using geometry driven multispectral optical flow. Information Processing in Medical Imaging, ser LNCS. 2005;3565:480–492. doi: 10.1007/11505730_40. [DOI] [PubMed] [Google Scholar]
- 19.Tosun D, Rettmann ME, Prince JL. Mapping techniques for aligning sulci across multiple brains. Medical Image Analysis. 2005;8(3):295–309. doi: 10.1016/j.media.2004.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pelizzari CA, Chen GTY, Spelbring DR, Weichselbaum RR, Chen CT. Accurate three-dimensional registration of CT, PET and/or MR images of the brain. J Comput Assist Tomogr. 1989;13(1):22–26. doi: 10.1097/00004728-198901000-00004. [DOI] [PubMed] [Google Scholar]
- 21.Krahnstover N, Lorenz C. Development of point-based shape representation of arbitrary three-dimensional medical objects suitable for statistical shape modeling. Proc SPIE-Medical Imaging 1999:Image Processing. 1999;3661:620–631. [Google Scholar]
- 22.Downs JH, Lancaster JL, Fox PT. Brain Warping. San Diego, CA: Academic; 1999. Surface based spatial normalization using convex hulls. [Google Scholar]
- 23.Hartkens T, Hill D, Castellano-Smith AD, Hawkes D, Maurer C, Martin A, Hall W, Liu CTH. Using points and surfaces to improve voxel-based non-rigid registration. MICCAI. 2002:565–572. [Online]. Available: citeseer.ist.psu.edu/571972.html.
- 24.Davatzikos C, Prince J, Bryan R. Image registration based on boundary mapping. IEEE Transactions on Medical Imaging. 1996 doi: 10.1109/42.481446. [DOI] [PubMed] [Google Scholar]
- 25.Davatzikos C, Prince J. Brain image registration based on curve mapping. IEEE Workshop Biomedical Image Anal. 1994:245–254. [Google Scholar]
- 26.Joshi SC, Miller MI. Landmark matching via large deformation diffeomorphisms. IEEE Transactions on Image Processing. 2000 Aug;9(8) doi: 10.1109/83.855431. [DOI] [PubMed] [Google Scholar]
- 27.Gerig G, Joshi S, Fletcher T, Gorczowski K, Xu S, Pizer SM, Styner M. Statistics of population of images and its embedded objects: Driving applications in neuroimaging. ISBI. 2006 Apr;:1120–1123. [Google Scholar]
- 28.Liu T, Shen D, Davatzikos C. Deformable registration of cortical structures via hybrid volumetric and surface warping. NeuroImage. 2004;22(4):1790–1801. doi: 10.1016/j.neuroimage.2004.04.020. [DOI] [PubMed] [Google Scholar]
- 29.Christensen GE, Yin P, Vannier MW, Chao KSC, Dempsey JL, Williamson JF. Large-deformation image registration using fluid landmarks. Image Analysis and Interpretation, 2000 Proceedings 4th IEEE Southwest Symposium. 2000:269–273. [Google Scholar]
- 30.Johnson HJ, Christensen GE. Consistent landmark and intensity-based image registration. IEEE Transactions on Medical Imaging. 2002;21(5):450–461. doi: 10.1109/TMI.2002.1009381. [DOI] [PubMed] [Google Scholar]
- 31.Christensen GE. Consistent linear-elastic transformations for image matching. Lecture Notes in Computer Science. 1999;1613:224–237. [Google Scholar]
- 32.Eriksson AP, Åström K. On the bijectivity of thin plate transforms. Swedeish Symposium on Image Analysis. 2005:53–56. [Google Scholar]
- 33.Thompson PM, MacDonald D, Mega MS, Holmes CJ, Evans AC, Toga AW. Detection and mapping of abnormal brain structure with a probabilistic atlas of cortical surfaces. Journal of Computer Assisted Tomography. 1997 Jul-Aug;21(4):567–581. doi: 10.1097/00004728-199707000-00008. [DOI] [PubMed] [Google Scholar]
- 34.Angenent S, Haker S, Tannenbaum A, Kikinis R. Laplace-Beltrami operator and brain surface flattening. IEEE Transactions on Medical Imaging. 1999;18:700–711. doi: 10.1109/42.796283. [DOI] [PubMed] [Google Scholar]
- 35.Joshi AA, Leahy RM, Thompson PM, Shattuck DW. Cortical surface parameterization by p-harmonic energy minimization. ISBI. 2004:428–431. doi: 10.1109/ISBI.2004.1398566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tang B, Sapiro G, Caselles V. Diffusion of general data on non-flat manifolds via harmonic maps theory: The direction diffusion case. International Journal of Computer Vision. 2000;36(2):149–161. [Google Scholar]
- 37.Segel LA. Mathematics Applied to Continuum Mechanics. Dover Publications; 1987. [Google Scholar]
- 38.Chefd'Hotel C, Hermosillo G, Faugeras O. A variational approach to multi-modal image matching. IEEE Workshop on Variational and Level Set Methods in Computer Vision. 2001:21–28. [Google Scholar]
- 39.Shattuck DW, Leahy RM. Brainsuite: An automated cortical surface identification tool. Medical Image Analysis. 2002;8(2):129–142. doi: 10.1016/s1361-8415(02)00054-3. [DOI] [PubMed] [Google Scholar]
- 40.Shattuck DW, Leahy RM. Graph based analysis and correction of cortical volume topology. IEEE Transactions on Medical Imaging. 2001;20(11):1167–1177. doi: 10.1109/42.963819. [DOI] [PubMed] [Google Scholar]
- 41.Thompson PM, Hayashi KM, de Zubicaray G, Janke AL, Rose SE, Semple J, Doddrell DM, Cannon TD, Toga AW. Detecting dynamic and genetic effects on brain structure using high dimensional cortical pattern matching. Proceedings of ISBI. 2002 doi: 10.1109/ISBI.2002.1029297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Han X, Xu C, Prince J. A topology preserving geometric deformable model and its application in brain cortical surface reconstruction. In: Osher S, Paragios N, editors. Geometric Level Set Methods in Imaging, Vision, and Graphics. Springer Verlag; 2003. [Google Scholar]
- 43.Jost J. Riemannian geometry and geometric analysis. Springer Verlag; 2002. [Google Scholar]
- 44.Nishikawa S. Variational Problems in Geometry, ser Translations of Mathematical Monographs. Vol. 205 AMS; 2001. [Google Scholar]
- 45.Xin Y. Geometry of harmonic maps. Birkhäuser; 1996. [Google Scholar]
- 46.Eells J, Sampson JH. Harmonic mappings of Riemannian manifolds. Ann J Math. 1964:109–160. [Google Scholar]
- 47.Hamilton R. Lecture Notes in Mathematics, ser. Vol. 471. Springer; 1975. Harmonic maps of manifolds with boundary. [Google Scholar]
- 48.Fardoun A, Regbaoui R. Heat flow for p-harmonic maps between compact Riemannian manifolds. Indiana Univ Math J. 2002;51:1305–1320. [Google Scholar]
- 49.Kanai T, Suzuki H, Kimura F. Three-dimensional geometric metamorphosis based on harmonic maps. The Visual Computer. 1998;14(4):166–176. [Google Scholar]
- 50.Wang Y, Gu X, Yau ST. Volumetric harmonic map. Communications in Information and Systems. 2004;3(3):191–202. [Google Scholar]
- 51.Mémoli F, Sapiro G, Osher S. Solving variational problems and partial differential equations mapping into general target manifolds. J Comput Phys. 2004;195(1):263–292. [Google Scholar]
- 52.Tagare HD, Groisser D, Skrinjar O. A geometric theory of symmetric registration. CVPRW. 2006;0:73. [Google Scholar]
- 53.Barber CB, Dobkin DP, Huhdanpaa H. The quickhull algorithm for convex hulls. ACM Transactions on Mathematical Software. 1996 [Google Scholar]
- 54.Shen D, Davatzikos C. Hammer: Hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging. 2002;21(11) doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- 55.Zijdenbos AP, Dawant BM, Margolin RA, Palmer A. Morphometric analysis of white matter lesions in mr images. IEEE Transactions on Medical Imaging. 1994 Dec;13:716–724. doi: 10.1109/42.363096. [DOI] [PubMed] [Google Scholar]
- 56.Shattuck DW, Leahy RM. BrainSuite: An automated cortical surface identification tool. In: Delp SL, DiGioia AM, Jaramaz B, editors. MICCAI, ser Lecture Notes in Computer Science. Vol. 1935. Springer; 2000. pp. 50–61. [Google Scholar]
- 57.Thompson PM, Hayashi KM, Sowell ER, Gogtay N, Giedd JN, Rapoport JL, de Zubicaray GI, Janke AL, Rose SE, Semple J, Doddrell DM, Wang YL, van Erp T, Cannon TD, Toga AW. Mapping cortical change in Alzheimer's disease, brain development and schizophrenia. NeuroImage. 2004 Sep;23(1):S2–S18. doi: 10.1016/j.neuroimage.2004.07.071. [DOI] [PubMed] [Google Scholar]
- 58.Leow A, Thompson PM, Protas H, Huang SC. Brain warping with implicit representations. ISBI IEEE. 2004:603–606. [Google Scholar]
- 59.Mémoli F, Sapiro G, Thompson P. Implicit brain imaging. NeuroImage. 2004;23(1):S179–S188. doi: 10.1016/j.neuroimage.2004.07.072. [DOI] [PubMed] [Google Scholar]
- 60.Wang Y, Gu X, Hayashi K, Chan T, Thompson P, Yau S. Brain surface parameterization using Riemann surface structure. MICCAI. 2005;2005:657–665. doi: 10.1007/11566489_81. [DOI] [PubMed] [Google Scholar]
- 61.Grenander U, Miller MI. Computational anatomy: an emerging discipline. Q Appl Math. 1998;LVI(4):617–694. [Google Scholar]
- 62.Christensen GE, Rabbitt R, Miller MI. 3D brain mapping using a deformable neuroanatomy. Physics in Medicine and Biology. 1994 Mar;39:609–618. doi: 10.1088/0031-9155/39/3/022. [DOI] [PubMed] [Google Scholar]
- 63.Camion V, Younes L. Geodesic interpolating splines. Lecture Notes in Computer Science. 2001:513–527. [Google Scholar]
- 64.Ge Y, Fitzpatrick JM, Kessler RM, Jeske-Janicka M, Margolin RA. Intersubject brain image registration using both cortical and subcortical landmarks. In: Loew Murray H., editor. Proc SPIE Vol 2434, p 81-95, Medical Imaging 1995: Image Processing. May, 1995. pp. 81–95. [Google Scholar]
- 65.Thompson PM, Vidal C, Giedd JN, Gochman P, Blumenthal J, Nicolson R, Toga AW, Rapoport JL. Mapping adolescent brain change reveals dynamic wave of accelerated gray matter loss in very early-onset schizophrenia. PNAS. 2001;98(20):11650–11655. doi: 10.1073/pnas.201243998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Sowell ER, Peterson BS, Thompson PM, Welcome SE, Henkenius AL, Toga AW. Mapping cortical change across the human life span. Nature Neuroscience. 2003;6:309–315. doi: 10.1038/nn1008. [DOI] [PubMed] [Google Scholar]
- 67.Thompson PM, Hayashi KM, de Zubicaray G, Janke AL, Rose SE, Semple J, Herman D, Hong MS, Dittmer SS, Doddrell DM, Toga AW. Dynamics of gray matter loss in Alzheimer's disease. The Journal of Neuroscience. 2003;23(3):994–1005. doi: 10.1523/JNEUROSCI.23-03-00994.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Shattuck DW, MacKenzie-Graham A, Toga AW. Duff: software tools for visualization and processing of neuroimaging data. IEEE International Symposium on Biomedical Imaging: Macro to Nano, 2004. 2004 Apr;1:644–647. [Google Scholar]
- 69.Ray N, Levy B. Hierarchical least squares conformal map. PG'03: Proceedings of the 11th Pacific Conference on Computer Graphics and Applications; Washington, DC, USA. IEEE Computer Society; 2003. p. 263. [Google Scholar]
- 70.George JS, Aine CJ, Mosher JC, Schmidt DM, Ranken DM, Schlitt HA, Wood CC, Lewine JD, Sanders JA, Belliveau JW. Mapping function in the human brain with magnetoen-cephalography, anatomical magnetic resonance imaging, and functional magnetic resonance imaging. J Clin Neurophysiol. 1995 Sep;12(5):406–431. doi: 10.1097/00004691-199509010-00002. [DOI] [PubMed] [Google Scholar]
- 71.Bookstein FL. Principal warps: Thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1989 Jun;11:567–585. [Google Scholar]
- 72.Kreyzig I. Differential Geometry. Dover; 1999. [Google Scholar]
- 73.Do Carmo M. Differential Geometry of Curves and Surfaces. Prentice-Hall; 1976. [Google Scholar]
- 74.Thompson PM, Mega MS, Vidal C, Rapoport J, Toga AW. Detecting disease-specific patterns of brain structure using cortical pattern matching and a population-based probabilistic brain atlas. Proc. 17th IPMI2001; Davis, CA, USA. 2001; pp. 488–501. [DOI] [PMC free article] [PubMed] [Google Scholar]