Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Jun 1.
Published in final edited form as: Psychol Sci. 2015 Apr 24;26(6):826–833. doi: 10.1177/0956797615572232

Money Earlier or Later? Simple Heuristics Explain Intertemporal Choices Better than Delay Discounting1

Keith M Marzilli Ericson 2, John Myles White 3, David Laibson 4, Jonathan D Cohen 5
PMCID: PMC4516222  NIHMSID: NIHMS658080  PMID: 25911124

Abstract

Heuristic models have been proposed for many domains of choice. We compare heuristic models of intertemporal choice, which can account for many of the known intertemporal choice anomalies, to discounting models. We conduct an out-of-sample, cross-validated comparison of intertemporal choice models. Heuristic models outperform traditional utility discounting models, including models of exponential and hyperbolic discounting. The best performing models predict choices by using a weighted average of absolute differences and relative (percentage) differences of the attributes of the goods in a choice set. We conclude that heuristic models explain time-money tradeoff choices in experiments better than utility discounting models.

Keywords: Delay of gratification, decision-making, heuristics, judgment

Introduction

People make many decisions with both short-term and long-term consequences. For example, smoking a cigarette has the immediate benefit of averting nicotine withdrawal and the long-term risk of lung cancer. Decisions involving consequences at different points in time are referred to as intertemporal choices (see Frederick, Loewenstein, & O'Donoghue, 2002, for a review).

The primary theoretical paradigm that has been used to explain intertemporal choice has been the theory of delay discounting (Ainslie, 1975; Frederick, Loewenstein, & O'Donoghue, 2002), which assumes that delayed rewards are discounted more as they are moved further into the future. The rate at which delayed consequences lose value is referred to as a discount rate. Discount rates are sometimes used as a measure of impatience.

There are several well-known models of delay discounting, including the classical economic model of exponential discounting, which assumes a constant discount rate (Samuelson, 1937); and the more recent hyperbolic discounting model, which assumes that discount rates decline as time to delivery increases (Ainslie, 1975). A large body of research has measured discount rates to characterize individual differences in impatience (e.g., Kirby, Petry & Bickel, 1999; Shamosh et al., 2008).

With delay discounted utility, intertemporal preferences are modeled with a discount function, D(t), and a utility (or value) function u(x). The utility function translates rewards (e.g. $1 or a serving of food) into units of value for the individual (20 servings of food may not be 20 times as valuable as a single serving to an individual). The discount function measures how that unit of utility decays if it is delivered at a time delay of t periods. The total value of a reward x at time t is the (multiplicative) product of the discount function and the utility function.

The canonical experimental task used to measure discount functions is an intertemporal choice task in which individuals choose between a smaller-earlier monetary reward and a larger-later monetary reward. We refer to such tasks as Money Earlier or Later (MEL) tasks. MEL tasks are typically assumed to measure a decision-maker's discount function directly (Frederick, Loewenstein, & O'Donoghue, 2002). However, the results of MEL tasks exhibit several empirical regularities that cannot be accounted for easily by theories of delay discounting. For example, an extensive body of research has found that individuals are more impatient (per unit time) for shorter time horizons than longer ones (Ainslie, 1975; Loewenstein & Prelec, 1992; Laibson, 1997; Prelec, 2004) — a finding that cannot be explained by simple exponential discounting. Several different (and complementary) extensions have been offered to account for this apparent anomaly. Some researchers have argued that decreasing impatience reflects nonlinear perceptions of time (Ebert & Prelec, 2007; Zauberman, Kim, Malkoc, & Bettman, 2009) or diminished sensitivity to delay (Scholten and Read 2010). Other researchers have explained it with hyperbolic discounting, which has become the leading model of intertemporal choice in psychology. But a large accumulation of additional findings, including studies of sub-additive discounting (Read, 2001), date/delay discrepancies (Read, Frederick, Orsel, & Rahman, 2005), similarity effects (Rubinstein, 1988; Rubinstein, 2003), delay/speedup asymmetries, and query-order effects (Loewenstein & Thaler, 1989; Weber et al., 2007) suggests that intertemporal choice is not well described by either exponential or hyperbolic discounted utility models.

Heuristics provide an alternative approach to understanding intertemporal choice behavior. Heuristics are shortcuts that afford simpler, if not optimal solutions to a problem. We describe a model of decision-making, which we call the intertemporal choice heuristic (ITCH) model, in which decisions are made by using simple arithmetic heuristics to compare earlier and later options. This approach is consistent with a general preference for earlier rewards, without making any assumptions about the existence of an underlying discount function. In this respect, it is closely related to two other heuristic models of decision making in intertemporal choice— the DRIFT model of Read et al. (Read, Frederick & Scholten, 2013), and the tradeoff model of Scholten and Read (2010). The ITCH model is motivated by a large literature concerning the use of heuristics in decision making, including attribute-based models of choice (Tversky, 1972; Payne, Bettman, & Johnson, 1988) and proportional thinking (Bordalo, Gennaioli, & Shleifer, 2012; Tversky & Kahneman, 1981). Here, we compare how heuristic models compare to models that assume systematic discounting.

First, we show that the functional form of the ITCH model can account for a number of the anomalies concerning human performance in MEL tasks reported in the literature. In the ITCH model, decisions depend on the sum of absolute and relative (percentage) differences of the attributes of reward – specifically, the absolute and relative differences in dollars and the absolute and relative differences in time. By considering both absolute and relative comparisons, the ITCH model is able to account for patterns of decision-making that have been a challenge to explain in terms of utility and discount functions.

Second, to make rigorous comparisons between different models used to interpret behavior in MEL experiments, we collect data on MEL choices in a variety of framing conditions and use these to conduct model comparisons. Unlike earlier studies, our use of out-of-sample evaluation methods to conduct model comparisons provides an unbiased estimate of the extent to which different models fit the empirical data collected in typical MEL tasks. To do so, we employ cross-validation techniques that are now widely used for model comparison in contemporary statistics and machine learning (Kohavi, 1997; Arlot & Celisse, 2010). By conducting a quantitative, out-of-sample comparison of the fit of heuristic and discounting models to empirical data, we show that the heuristic models do significantly better at accounting for people's intertemporal choice behavior than standard discounting models. We conclude by discussing the differences among the heuristic models. Critically, however, our results show that, when confronted with intertemporal choices involving money, people use heuristics rather than systematic discounting to make their decisions.

Intertemporal Choice Heuristics Model (ITCH Model)

As suggested above, the ITCH model is based on psychological principles rather than economic theory. In particular, the ITCH model is inspired by a large body of research in judgment and decision-making that provide support for attribute-based models of choice. In attribute-based models, a decision-maker weighs several distinct reasons for and against taking a decision. For example, Lichtenstein and Slovic's seminal study of risky choice found that the relevant weight placed on certain attributes reliably shifts when participants make binary choices versus situations in which people estimate the monetary value of a gamble (Lichtenstein & Slovic, 1971). Similarly, Shafir et al. describe decision-making in terms of reasons for and against a decision that can be used as retrospective justifications for a decision (Shafir, Simonson & Tversky, 1993).

Likewise, the ITCH model assumes that decision-makers compare the two options in a typical MEL task in terms of the reasons that would argue for or against each option. These heuristic comparisons generate a vector of arguments for and against selecting the earlier or later option. Using these comparisons, participants construct a weighted combination that determines the probability of choosing each of the two options in a MEL task.

The specific heuristics used in the ITCH model involve the simplest arithmetic comparisons that can be made between the two options (e.g., subtracting and/or dividing them) along each of the two relevant dimensions (i.e., dollar value and time of delivery). The application of each heuristic to a particular pair of options generates a vector of four features for that choice (i.e., the results of each simple arithmetic computation), each of which favors one option or the other. The model assumes that the final decision is made based on a weighted sum of these four features. The weights can be interpreted as reflecting the attentional focus and/or importance placed on each heuristic comparison. The model is consistent both with individuals using all four heuristics and attaching different weights to them and/or as an approximation to a model in which each individual relies only on a single (or subset of) heuristics, and the heuristics that are used are chosen probabilistically (across tasks or individuals).

Below, we show that the ITCH model provides a good fit to data from five different variants of a MEL task. The pattern of weights it assigns to the heuristics is broadly consistent across participants and task variants, suggesting that people use a stable combination of heuristics when evaluating MEL questions, irrespective of manipulations of content and context. In addition, the differences in relative weights assigned to different heuristics across task variants offer additional insights into the decision-making process, as these weights provide a mechanism for quantifying the differential importance assigned to different heuristics in different framing contexts.

The heuristics of the ITCH model implement four basic psychological principles: (a) participants compare each option relative to a reference point (Kahneman & Tversky, 1979); (b) comparisons are performed in both absolute terms (by subtraction) and relative terms (by division) (Thurstone, 1927); (c) comparisons are performed independently along the monetary and time dimensions (Lichtenstein & Slovic, 1971); and (d) the results of these comparisons are then aggregated linearly using a set of decision weights (Busemeyer & Townsend, 1993). We apply these principles to intertemporal choice, but these could also be applied to develop heuristic choice models in other domains; see the heuristic model of risky choice in Mellers et al. (1995).

Mathematical Specification of the ITCH Model

We formalize the ITCH model (for binary choices) as follows. The ITCH model treats the dimensions of time and money symmetrically. Each of the two options is written in the form (x, t), where x is the option's monetary value and t is the time the money would be received. The probability of choosing the larger later option, denoted P(LL), in a choice between a smaller, earlier amount of money, (x1, t1), and a larger, later amount of money, (x2, t2), is expressed as,

P(LL)=L(βI+βxA(x2−x1)+βxRx2−x1x∗+βtA(t2−t1)+βtRt2−t1t∗)

where (x*, t*) represents a reference point that is the arithmetic average of the two options along each dimension:

x∗=x1+x22,t∗=t1+t22.

In this equation, L is the cumulative distribution function (CDF) of a logistic distribution with mean 0 and variance 1. Thus, each term of the model represents either an absolute or proportional arithmetic operation that compares the options along a particular dimension (dollar value and time). Each term is multiplied by a parameter β that represents the weight given to each heuristic in making the decision between the two choices. The weighted sum of the outcomes predicted by each heuristics then determines the probability of choosing one option or the other. This model can be fit to data from different versions of a MEL task to estimate and compare the parameters across conditions. (See SOM-R).

The ITCH model can explain the two most robust and widely observed phenomena in MEL tasks— decreasing impatience and the absolute magnitude effect— in terms of a single, consistent set of heuristics: the simultaneous consideration of absolute and relative differences between the two options. For example, when the weight on relative time βtR is negative (as in our fitted estimates), the ITCH model predicts that the probability of choosing the larger, later amount will increase as both options are delayed by an additional identical amount of time—e.g. by adding a front-end delay to both options. Such decreasing impatience (Prelec, 2004) has often been interpreted as evidence of hyperbolic discounting (Ainslie, 1975). According to the ITCH model, this is a natural consequence of including both relative and absolute differences in time: the relative difference between the timing of the two goods decreases as the earliest available option moves into the future – even as the absolute difference is held fixed.

Consider the following concrete example. If the participant uses weights (0.0, 0.1, 0.1, -0.1, -0.1) and selects between $10 today and $20 tomorrow, then the probability of choosing the later option is

P(LL)=L(0+0.1(20−10)+0.120−10(20+10)/2−0.1(1−0)−0.11−0(1+0)/2)=0.68

In contrast, if the participant selects between $10 in 10 days and $20 in 11 days, only the relative time term changes. The probability of choosing the later option increases to

P(LL)=L(0+0.1(20−10)+0.120−10(20+10)/2−0.1(11−10)−0.111−10(11+10)/2)=0.72

ITCH also makes the prediction that, when the weight on the monetary difference term βxA is positive, multiplicatively scaling up the magnitude of the monetary amounts will make participants more likely to take the later option. This prediction has been confirmed in virtually all MEL tasks that have tested it and is often referred to as the Absolute Magnitude Effect (Loewenstein & Prelec, 1992). Using the same weights as before (0.0, 0.1, 0.1, -0.1, -0.1), consider what happens when the stakes are scaled up by a factor of ten. The probability of choosing the later option when choosing between $10 today and $20 tomorrow is still 0.68. However, when choosing between $100 today and $200 tomorrow, only the absolute monetary difference term changes. The probability of choosing the later option will be:

P(LL)=L(0+0.1(200−100)+0.1200−100(200+100)/2−0.1(1−0)−0.11−0(1+0)/2)=0.99

The magnitude effect can also be generated by a concave value function for rewards (e.g. as in the tradeoff model). In general, a model in which decisions are made based on a combination of absolute and relative comparisons mimics the effects otherwise attributed to psychophysical curvature or diminishing marginal utility.

Moreover, by letting the intercept term βI vary across different framing conditions, the ITCH model can also capture the large number of anomalies that can be conceptualized as presenting the same information in different frames (e.g. βI might be higher in a task that presents time-dated payments as dates rather than delays). Finally, ITCH is an example of a heuristic model that produces non-additive discounting behavior (i.e. total discounting over an interval depends on whether it is presented as one long interval or subdivided into separate intervals); see an extended discussion for a similar model in Scholten and Read (2010).

The ITCH model is similar to other heuristic models of MEL behavior, including both Scholten and Read (2010)'s tradeoff model and Read et al. (2013)'s DRIFT model. Unlike systematic discounting models, they do not produce a discounted utility value by multiplying a discount function and utility function. Instead, like ITCH, they explain choice in terms of the sum of different factors, including allowing the effects of money and time to be additively separable. However, these models differ in a few potentially important ways. ITCH includes absolute and percentage comparisons for time delay, whereas DRIFT only includes an absolute comparison. The model fits we present below suggest that the percentage comparison for time delay is statistically significant. DRIFT includes an interest rate term and a term that captures consumption versus investment framing. The tradeoff model assumes concave functional forms for perceived time delay and perceived reward magnitude, which are used to account for diminishing sensitivity. In contrast, ITCH relies exclusively on simple arithmetic comparisons, which are symmetrically applied to both money and time. Our results below indicate that ITCH provides a slightly better fit to the data than the alternative heuristic models. However, what is most significant — in both a statistical and conceptual sense — is that all three heuristic models provide a substantially better fit than the current standard economic models of intertemporal decision-making, suggesting that further work developing and refining heuristic models of intertemporal choice will be fruitful.

Model Comparisons across Five Experiments

We conducted five closely related experiments to compare the three heuristic models with three standard economic models — the exponential, hyperbolic, and quasi-hyperbolic models of discounting (Samuelson, 1937; Ainslie, 1975; Laibson, 1997). One thousand participants were recruited from the Mturk.com online labor market. These participants were randomly assigned to one of five task variants under which 25 hypothetical choices were presented in a random order. Each condition involved a MEL task that differed in the framing of the two time-dated options:

  1. Absolute $, Delay Framing: $5 today vs. $5 plus an additional $5 in 4 weeks

  2. Relative $, Delay Framing: $5 today vs. $5 plus an additional 100% in 4 weeks

  3. Standard MEL Format: $5 today vs. $10 in 4 weeks

  4. Absolute $, Speedup Framing: $10 in 4 weeks vs. $10 minus $5 today

  5. Relative $, Speedup Framing: $10 in 4 weeks vs. $10 minus 50% today

The use of conditions framing the choices as delay vs. speedup parallels the order manipulations used in the studies by Weber et al. (2007). Within a framing condition, each participant answered 25 randomly generated MEL questions designed to span a large range of dollar amounts and delays. (See SOM-R)

To compare models, we used a cross-validation approach in which each model was fit to one subset of our data and then tested on another subset of data. In order to generate many training and test datasets, we randomly subsampled 75% of the data as a training dataset and 25% as a test set; we repeated this subsampling procedure 100 times. Cross-validation provides an unbiased method for comparing the predictive power of models with different numbers of parameters, which is necessary in our case because the each of the heuristic models has more parameters than some of the discounting models with which they were compared (Kohavi, 1995). Cross-validation is a type of out-of-sample analysis. In contrast, standard measures of model fit applied in-sample (e.g. the calculation of R2 values) do not provide reliable indicators of the generalizability of fitted models.

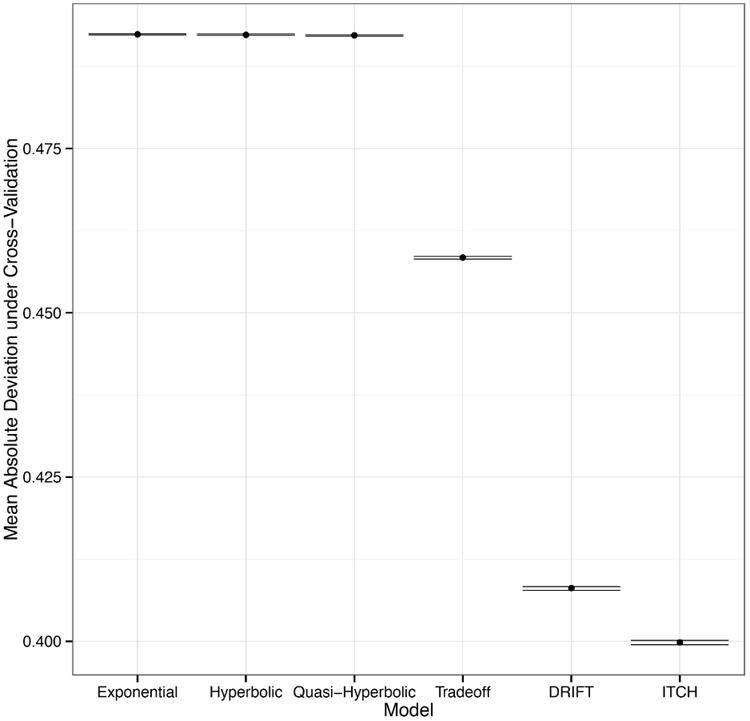
In all five experiments, the three heuristic models (ITCH, DRIFT, and tradeoff) outperformed all of the standard delay discounted utility models of intertemporal choice in predicting participants' choices. The specification of each model is listed in the SOM-R. Within the heuristic class, the ITCH model outperformed the tradeoff and DRIFT models. Table S1 shows the results when, separately for each experimental condition, we fit the model on the training data and tested it on the testing data for that condition. (Note that this method thus lets model parameters vary by condition, capturing generalizations of each model that would let parameters differ between delay v. speedup and absolute v. relative frames).

Since relative model performance results are similar across conditions, Figure 1 presents a pooled analysis of model performance across conditions. In this analysis, for each cross-validation subsample, we estimated one set of model parameters on the training data pooled from all five experimental conditions and then assessed the fit on the pooled testing data.

Figure 1. The predictive accuracy of the standard and heuristic models of intertemporal choice for pooled data from all five experiments. Errors are measured using mean absolute deviation. The error bars reflect the variability of the model comparison results under cross-validation.

Figure 1

Open in a new tab

For the ITCH model, we found that the β decision weights for the four component heuristics were relatively stable across experimental conditions. Figure 2 plots six sets of decisions weights: the weights when estimated separately on the five conditions, plus a set of weights estimated on the pooled data across all conditions (see also Table S3 for raw numbers). Absolute time and relative time were weighted similarly, but relative money received much higher weight than absolute money; we speculate that this was due to a much larger range in dollar reward amounts available than time delays available.

Figure 2.

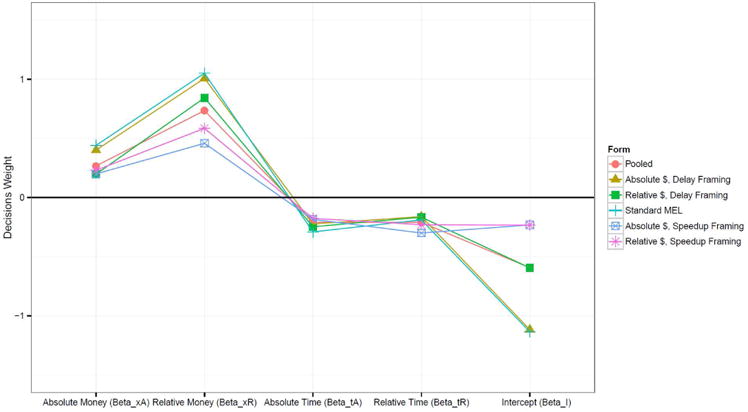
Figure 2

Open in a new tab

The pattern of decision weights is highly consistent across different forms of MEL tasks. Six sets of decision weights are shown: one for each of the five condition, plus a sixth set estimated on the pooled data. To make decision weights more readily comparable, we z-scored all inputs. We tested the consistency of decision weights by computing the pairwise correlations between decision weights across the six data sets and comparing this against the null hypothesis of no correlation (t = 125.977, df = 35, p < 10-14).

Although the magnitude of the parameters varied across fits, the pattern of decision weight β parameters were stable across framing conditions. The estimates imply that participants assigned a qualitatively similar pattern of relative weights to the heuristics represented by each term of the ITCH model, irrespective of manipulations of task content or context. Moreover, variations in parameter estimates across conditions capture variations between the comparisons made salient by each of the tasks. The ratios of the relative to absolute comparison coefficients are higher in the conditions that emphasize relative differences of money than in conditions that emphasize absolute differences in money. Because our frames always presented time delays in absolute, not relative, terms, we expected to see less variation in the coefficients on relative time. Finally, the variation in the intercept term βI also captures differences between conditions in generalized impatience.

Discussion

To understand the anomalous decision-making behavior observed in MEL experiments, we developed an alternative account of behavior in MEL tasks – the ITCH model – based on basic psychological principles, including reference points and simple arithmetic comparisons. The results of our model comparisons show that both this model and the other two heuristic models provide substantially better fits to choices in MEL tasks than standard economic models of intertemporal choice that rely on a discount function.

The fit of the ITCH model demonstrated that the relative weights assigned to each of the heuristics in the model were stable across individuals and a range of conditions. Moreover, the variations in the weights across framings were themselves interpretable in terms of the relative salience of different comparisons suggested by question framing. Thus, while participants' decision making behavior in MEL tasks may not be meaningfully described by a discount function, our findings suggest that decision-making in MEL tasks nevertheless exhibits a form of psychological stability that may generalize to other tasks.

In summary, our findings raise two important points. The ability of heuristic models to predict behavior in MEL tasks suggests that for these tasks, as for many other decision-making tasks, people may apply simple heuristics to generate a response that is sufficient for their purposes rather than employ a decision-process that mirrors conventional economic models. The ITCH model and related models show that a weighted combination of simple heuristics can model time-money tradeoffs in MEL tasks well. Future research should evaluate the usefulness of this approach for other types of intertemporal choices besides MEL, as decision-making tasks in other domains, such as risky choice.

Supplementary Material

sup file

Footnotes

1

We thank Gretchen Chapman, Sam Gershman, Marc Scholten, Chris Wiggins, and anonymous referees for valuable feedback on this work. JMW and JDC were funded by NIA R01AG030310, NIA P30AG024361 and NIDA T90 DA023419. JDC was also funded by the John Templeton Foundation. KMME and DL were funded by NIA R01AG030310. DL was funded by the Pershing Square Fund for Research on the Foundations of Human Behavior, NIA R01AG021650, and NIA P01AG005842. The content of this publication is solely the responsibility of the authors and does not necessarily represent the views of NIA, NIH, any agency of the Federal Government, the NBER, the Pershing Square Foundation, or the John Templeton Foundation.

References

  1. Ainslie G. Specious reward: a behavioral theory of impulsiveness and impulse control. Psychological Bulletin. 1975;82(4):463–496. doi: 10.1037/h0076860. [DOI] [PubMed] [Google Scholar]
  2. Arlot S, Celisse A. A survey of cross-validation procedures for model selection. Statistics Surveys. 2010;4:40–79. [Google Scholar]
  3. Bordalo P, Gennaioli N, Shleifer A. Salience theory of choice under risk. Quarterly Journal of Economics. 2012;127(3):1243–1285. [Google Scholar]
  4. Busemeyer JR, Townsend JT. Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychological Review. 1993;100(3):432–459. doi: 10.1037/0033-295x.100.3.432. [DOI] [PubMed] [Google Scholar]
  5. Ebert JE, Prelec D. The fragility of time: Time-insensitivity and valuation of the near and far future. Management Science. 2007;53(9):1423–1438. [Google Scholar]
  6. Frederick S, Loewenstein G, O'Donoghue T. Time discounting and time preference: a critical review. Journal of Economic Literature. 2002;40:350–401. [Google Scholar]
  7. Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk. Econometrica: Journal of the Econometric Society. 1979:263–291. [Google Scholar]
  8. Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection. International Joint Conference on Artificial Intelligence. 1995;14:1137–1145. [Google Scholar]
  9. Laibson D. Golden eggs and hyperbolic discounting. The Quarterly Journal of Economics. 1997;112(2):443–478. [Google Scholar]
  10. Lichtenstein S, Slovic P. Reversals of preference between bids and choices in gambling decisions. Journal of Experimental Psychology. 1971;89(1):46–55. [Google Scholar]
  11. Loewenstein G, Thaler RH. Anomalies: intertemporal choice. The Journal of Economic Perspectives. 1989;3(4):181–193. [Google Scholar]
  12. Loewenstein G, Prelec D. Anomalies in intertemporal choice: Evidence and an interpretation. The Quarterly Journal of Economics. 1992;107(2):573–597. [Google Scholar]
  13. Mellers BA, Weber EU, Ordónez LD, Cooke AD. Utility invariance despite labile preferences. In: Busemeyer JR, Hastie R, Medin DL, editors. Decision Making from a Cognitive Perspective The Psychology of Learning and Motivation. Vol. 32. San Diego: Academic Press; 1995. pp. 221–246. [Google Scholar]
  14. Payne JW, Bettman JR, Johnson EJ. Adaptive strategy selection in decision making. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1988;14(3):534–552. [Google Scholar]
  15. Prelec D. Decreasing impatience: A criterion for non-stationary time preference and “hyperbolic” discounting. The Scandinavian Journal of Economics. 2004;106(3):511–532. [Google Scholar]
  16. Read D. Is time-discounting hyperbolic or subadditive? Journal of Risk and Uncertainty. 2001;23(1):5–32. [Google Scholar]
  17. Read D, Frederick S, Orsel B, Rahman J. Four score and seven years from now: The date/delay effect in temporal discounting. Management Science. 2005;51(9):1326–1335. [Google Scholar]
  18. Read D, Frederick S, Scholten M. DRIFT: An Analysis of Outcome Framing in Intertemporal Choice. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2013;39(2):573–588. doi: 10.1037/a0029177. [DOI] [PubMed] [Google Scholar]
  19. Samuelson PA. A note on measurement of utility. The Review of Economic Studies. 1937;4(2):155–161. [Google Scholar]
  20. Scholten M, Read D. The Psychology of Intertemporal Tradeoffs. Psychological Review. 2010;117(3):925–944. doi: 10.1037/a0019619. [DOI] [PubMed] [Google Scholar]
  21. Shafir E, Simonson I, Tversky A. Reason-based choice. Cognition. 1993;49(1):11–36. doi: 10.1016/0010-0277(93)90034-s. [DOI] [PubMed] [Google Scholar]
  22. Shamosh NA, DeYoung CG, Green AE, Reis DL, Johnson MR, Conway AR, Engle RW, Braver TS, Gray JR. Individual differences in delay discounting relation to intelligence, working memory, and anterior prefrontal cortex. Psychological Science. 2008;19(9):904–911. doi: 10.1111/j.1467-9280.2008.02175.x. [DOI] [PubMed] [Google Scholar]
  23. Thurstone LL. A law of comparative judgment. Psychological Review. 1927;34(4):273–286. [Google Scholar]
  24. Tversky A. Choice by elimination. Journal of Mathematical Psychology. 1972;9(4):341–367. [Google Scholar]
  25. Tversky A, Kahneman D. The framing of decisions and the psychology of choice. Science. 1981;211(4481):453–458. doi: 10.1126/science.7455683. [DOI] [PubMed] [Google Scholar]
  26. Weber EU, Johnson EJ, Milch KF, Chang H, Brodscholl JC, Goldstein DG. Asymmetric discounting in intertemporal choice: A Query-Theory account. Psychological Science. 2007;18(6):516–523. doi: 10.1111/j.1467-9280.2007.01932.x. [DOI] [PubMed] [Google Scholar]
  27. Zauberman G, Kim BK, Malkoc SA, Bettman JR. Discounting time and time discounting: Subjective time perception and intertemporal preferences. Journal of Marketing Research. 2009;46(4):543–556. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

sup file
NIHMS658080-supplement-sup_file.doc (467KB, doc)

RESOURCES