Characterization of the Local Structure in Liquid Water by Various Order Parameters

Abstract

A wide range of geometric order parameters have been suggested to characterize the local structure of liquid water and its tetrahedral arrangement, but their respective merits have remained elusive. Here, we consider a series of popular order parameters and analyze molecular dynamics simulations of water, in the bulk and in the hydration shell of a hydrophobic solute, at 298 and 260 K. We show that these parameters are weakly correlated and probe different distortions, for example the angular versus radial disorders. We first combine these complementary descriptions to analyze the structural rearrangements leading to the density maximum in liquid water. Our results reveal no sign of a heterogeneous mixture and show that the density maximum arises from the depletion in interstitial water molecules upon cooling. In the hydration shell of the hydrophobic moiety of propanol, the order parameters suggest that the water local structure is similar to that in the bulk, with only a very weak depletion in ordered configurations, thus confirming the absence of any iceberg-type structure. Finally, we show that the main structural fluctuations that affect water reorientation dynamics in the bulk are angular distortions, which we explain by the jump hydrogen-bond exchange mechanism.

Introduction

Characterizing the local structure of liquid water is often ambiguous. A convenient and much employed description focuses on the distortion with respect to the structure of crystalline ice, where water molecules are regularly positioned on a well-defined lattice and where the nearest neighbors form a regular tetrahedron due to the hydrogen-bond interactions. In liquid water, this long-range order disappears and only a partial short-range order remains.¹⁻⁴ The first solvation shell of each water molecule forms an approximate tetrahedron, distorted by the frequent exchanges between the first and second shells and by the increased probability to find water molecules in an interstitial position between these two shells.⁵ How much the local structure of liquid water deviates from an ideal tetrahedron is influenced by a number of factors. For example, decreasing the temperature enhances the local order and the liquid structure becomes more tetrahedral, even though it remains far from the ideal icelike arrangement.^1,2,4,6 Solutes may enhance or reduce the local tetrahedral order of neighboring water molecules, and classifications of solutes in structure-makers and -breakers have been suggested but remain ambiguous.⁷ In particular, the influence of hydrophobic groups on the local water structure is still debated due to its potential importance in the measured entropy decrease upon hydration of hydrophobic groups.⁸⁻¹⁶

A large number of different geometric order parameters have been suggested to characterize the local structure in liquid water, and extensively employed to analyze numerical simulations (see, e.g., refs (15 and 17−20)). However, it is not clear that all of these parameters are equivalent and can be used equally.

Here, we consider a selection of five widely used order parameters, respectively the angular (q) and radial (S_k) tetrahedral order parameters, the local structure index (LSI), the local density (ρ), and the asphericity of the Voronoi cell (η). We further include in our study the water–water angular distribution function and the local electric field experienced by a water hydrogen atom. The latter is approximately measured in Raman experiments¹⁰ probing the local water structure. We use molecular dynamics simulations to assess the similarities and differences between these measures of the local order, and establish what type of structural changes they are sensitive to. We then successively study the structural changes induced by decreasing the temperature from ambient conditions down to 260 K and their connection with the density maximum in liquid water. We further analyze the structural perturbation induced by a (partly) hydrophobic propanol solute, and we finally determine the key structural fluctuations affecting the water hydrogen-bond and reorientation dynamics.

Methodology

Molecular Dynamics Simulations

Classical molecular dynamics simulations of dilute n-propanol in water are performed at two different temperatures, 298 and 260 K. We use the TIP4P/2005 water model,²¹ which provides one of the best available classical descriptions of the water phase diagram²² and dynamics,^6,23 and which was shown to properly reproduce structural and dynamical properties of hydrophobic hydration shells.¹⁶n-Propanol is described with the CHARMM general force field (CGenFF).²⁴ The simulation box contains a single propanol together with 550 water molecules, corresponding to a molality of approximately 0.1 mol kg^–1. The density of the box is set at the experimental density of neat water at each temperature, that is, respectively, 0.99704 and 0.99710 kg/L at 298 and 260 K.²⁵ The system is first equilibrated in the NVT ensemble for 1 ns at 298 K and 2 ns at 260 K with a time step of 2 fs, before a production run in the NVT ensemble using a Langevin thermostat with a damping frequency of 0.2 ps^–1. The length of the production runs is 8 ns with a time step of 1 fs, and coordinates are saved every 25 fs. The simulations are performed with NAMD,²⁶ with periodic boundary conditions and a Particle Mesh Ewald treatment of long-range electrostatic interactions.²⁷ A 11 Å cutoff is applied to nonbonded interactions with a switching function between 9 and 11 Å. Bonds between hydrogen and heavy atoms are constrained using the SHAKE²⁸ and SETTLE²⁹ algorithms.

Local Order Parameters

We selected a wide range of order parameters among the most frequently used ones to characterize the local structure of liquid water. For each of these parameters, we compute the probability distribution of the parameter in the bulk, and in the hydrophobic part of the hydration shell of the n-propanol solute. A water molecule is considered to be respectively bulklike if its oxygen atom lies further than 8 Å from any atom of the solute and within the hydrophobic part of the hydration shell if its oxygen atom lies less than 4.5 Å away from any carbon atom of the solute and more than 3 Å from the propanol oxygen atom (recent calculations showed that the local structure in the second hydration shell is already bulklike¹³). We now describe the seven selected order parameters.

Orientational Tetrahedral Order q

This is probably the most widely used tetrahedral order parameter (see, e.g., refs (13 and 30−37)). It was originally proposed by Chau and Hardwick,¹⁷ and subsequently rescaled by Errington and Debenedetti¹⁸ so that the average value of q varies from 0 for an ideal gas to 1 for a regular tetrahedron. It focuses on the four nearest water oxygen neighbors and is defined as

1

where ψ_jk is the angle formed by the lines joining the oxygen atom of the water molecule under consideration and its nearest neighbor oxygen atoms j and k. We note that by construction this parameter is only sensitive to the angular order, and not to the radial order. q has been used, for example, to study the structure of supercooled water^30,35,38,39 and to examine the changes in the local water structure next to a variety of solutes and surfaces.^{13,33,36,40−45}

Translational Tetrahedral Order S_k

It was introduced in ref (17) and measures the variance of the radial distances between a central water oxygen atom and the four nearest neighbor water oxygen atoms. Following the suggestion of ref (17), we adopt the following definition of S_k,

2

where r_k is the radial distance from the central oxygen atom to the kth peripheral oxygen atom and r̅ is the arithmetic mean of the four radial distances. S_k increases when the local tetrahedral order increases and reaches a maximum value of 1 for a perfect tetrahedron. While this translational tetrahedral order is much less used than the orientational order q, it was shown to be more sensitive than q to density fluctuations⁴⁶ and it is frequently combined with other order parameters.^47,48 We note that another translational order parameter has been introduced in ref (18), but the latter requires the calculation of average structures and cannot be used to characterize an instantaneous structure.

Local Structure Index LSI

The LSI aims at measuring the extent of the gap between the first and the second hydration shells surrounding a water molecule.¹⁹ Once the oxygen–oxygen distances between the central water molecule and its ith water neighbor are ordered so that r₁ < r₂ <...<r_i < r_i+1 <...<r_n < 3.7 Å < r_n+1, the LSI is defined as¹⁹

3

where Δ(i) = r_i+1 – r_i and Δ̅ is the arithmetic mean of Δ(i) . The LSI thus focuses on the translational order and probes the local structure beyond the first hydration shell. It has been especially used to study the structure of supercooled water,⁴⁹⁻⁵¹ of protein hydration shells,^52,53 and of water next to hydrophobic interfaces.⁴³

Local Density ρ

Two different approaches can be followed to calculate the local density in liquid water: either one determines the average number of water molecules in a fixed probe volume, or one determines the volume occupied by a single water molecule in the liquid. The fixed volume approach has for example been successfully used in ref (54) but it requires a probe volume that is sufficiently large to contain several water molecules. The density cannot thus be resolved at the molecular level, which is an important limitation for example for the study of solute hydration shells. Here we calculate the density as the inverse of the intrinsic volume occupied by a single water molecule,

4

The volume V is calculated using the Voronoi cell associated with the water molecule, i.e. it is the volume of the polyhedron including all points in space which are closer to the oxygen atom under consideration than to any other heavy atom in the system. With this approach, the density is determined with a spatial resolution finer than the intermolecular distance. Voronoi polyhedra have been extensively used to characterize the structure of liquids,⁵⁵⁻⁵⁷ of liquid and supercooled water,^6,20,50,58 of aqueous mixtures^16,59 and of protein hydration shells.^60,61

Asphericity of the Voronoi Cell η

The shape of the Voronoi polyhedron is conveniently characterized by the asphericity parameter, defined as²⁰

5

where V and A are, respectively, the volume and area of the polyhedron. η values range from 1 for a perfect sphere to 2.25 for ice I_h and 3.31 for a regular tetrahedron.^20,62 The asphericity specifically reports on the shape of the polyhedron and is independent of the size of the polyhedron, that is, of the local density. It has been widely employed to characterize the local structure of liquid^31,63 and especially supercooled^6,38,58 and supercritical⁴⁶ water, together with the hydration structure of small hydrophobic solutes.^16,64 (The same parameter, designated as the isoperimetric quotient, has also been used in a different context to predict the type of complex structures formed by building blocks with different shapes.⁶⁵)

Local Electric Field E and OH Vibrational Frequency ω_OH

Experimentally, the local structure of liquid water has been indirectly probed via infrared and Raman spectroscopies.^10,34,66 The vibrational frequency of the water OH stretch mode reflects the strength of the hydrogen bond (H-bond) in which it is engaged. Stronger H-bonds lead to a OH frequency red-shift, while weaker bonds lead to a blue-shift. With respect to the spectrum of ambient liquid water, that of ice is thus narrower and red-shifted,⁶⁷ and that of water at liquid/air⁶⁸ and water/organic solvent⁶⁹ interfaces exhibits blue-shifted peaks due to dangling OH bonds. For an isotopically substituted water molecule HOD, where the two stretching modes are decoupled, the OH (respectively OD) vibrational frequency was shown to be approximately proportional to the local electric field experienced by the water hydrogen (respectively deuterium) atom,⁷⁰⁻⁷² projected along the OH (respectively OD) bond direction. We therefore probe the local structure through this local electric field E. Since frequency maps relating E to the vibrational frequency have been determined for the SPC/E water model but not for the TIP4P/2005 model, we follow the approach successfully used in ref (73). We calculate the electric field in each configuration by transforming each TIP4P/2005 water molecule into a SPC/E molecule, keeping the oxygen atom fixed and moving the two hydrogen atoms while conserving the molecular plane and the dipole moment orientation. (As shown in the Supporting Information, this transformation does not affect our conclusions regarding the difference between the bulk and shell electric field distributions.) While other order parameters are defined for an entire water molecule, the local field is determined for an individual hydrogen atom. We therefore consider each water hydrogen atom and correlate E with the order parameters of its parent molecule.

Water–Water Angular Distribution Function P(θ)

The θ angle is defined as the smallest O···O–H angle formed by two neighboring water molecules. While θ is often called the hydrogen-bond angle, the pair of water molecules under consideration may not necessarily be hydrogen-bonded. The probability distribution of θ angles has been used to characterize the local structure of water, for example, in the bulk,^14,15 next to hydrophobic interfaces,^12,14,15 and in protein hydration shells,⁷⁵ and similar ideas have been applied to the water–anion hydrogen-bond strength.⁷⁶ Because what is usually analyzed is not the instantaneous θ value but the shape of the P(θ) distribution, we only include θ in our studies of the structural changes induced by a decrease in temperature and by a hydrophobic group. As detailed in the Supporting Information (Figure S6), several limitations of this parameter should be kept in mind when analyzing the results. The distribution usually exhibits two peaks, respectively, at low and high θ values. The peak at low θ values reports on the linearity, and therefore on the strength of the hydrogen-bonds, but does not probe the tetrahedral order of the entire shell. Regarding the peak at higher θ values, it does not correspond to a distorted hydrogen-bond but rather to second shell water molecules which do not form a hydrogen-bond with the central water molecule but are normally hydrogen-bonded to their nearest neighbors. Finally, the shape of this distribution and in particular the relative heights of these two peaks are extremely sensitive to the chosen cutoff distance between the water oxygen atoms. Values of, for example, 3.5 Ź⁵ and 4.0 Å⁷⁵ have been used in the literature and we adopt here a 4.0 Å cutoff.

Pearson Correlation

The correlation between a pair of order parameters x and y is measured by the Pearson correlation coefficient, defined as

6

where ⟨...⟩ designates the ensemble average. r = ± 1 if x and y are, respectively, perfectly correlated and anticorrelated, and r = 0 if x and y are independent variables.

Analysis of Water Reorientation Dynamics

From the probability distributions of each order parameter in the bulk, we determine the ranges of parameter values corresponding to the 25% least ordered water molecules (first quartile of the distribution) and to the 25% most ordered water molecules (fourth quartile of the distribution). We then follow the reorientation dynamics of water OH bonds depending on the initial value of the order parameter. The reorientation of each water OH bond vector u is followed through the second-order Legendre polynomial time-correlation function (TCF),⁷⁷

7

and the characteristic reorientation time τ_reor is obtained by numerical integration of the TCF,

8

Correlations between Order Parameters

We first aim at determining whether these order parameters with very different definitions actually probe the same structural features. We therefore focus on liquid water at ambient temperature and compute the normalized correlations between the respective fluctuations for each pair of order parameters. The resulting Pearson coefficients r listed in Table 1 range between −0.21 and 0.52 and thus reveal that the correlation between the order parameters is at best limited. These various order parameters thus report on different aspects of the local structure that we now elucidate.

Table 1. Pearson Correlation Coefficient r (eq 6) between Order Parameters for Water Molecules in Bulk Liquid Water at 298 K.

	asphericity η	density ρ	q	Sk	LSI	electric field E
asphericity η	1	–0.01	0.52	0.24	0.46	0.40
density ρ	–0.01	1	0.12	0.38	–0.21	0.27
q	0.52	0.12	1	0.26	0.20	0.30
Sk	0.24	0.38	0.26	1	0.09	0.17
LSI	0.46	–0.21	0.20	0.09	1	0.23
electric field E	0.40	0.27	0.30	0.17	0.23	1

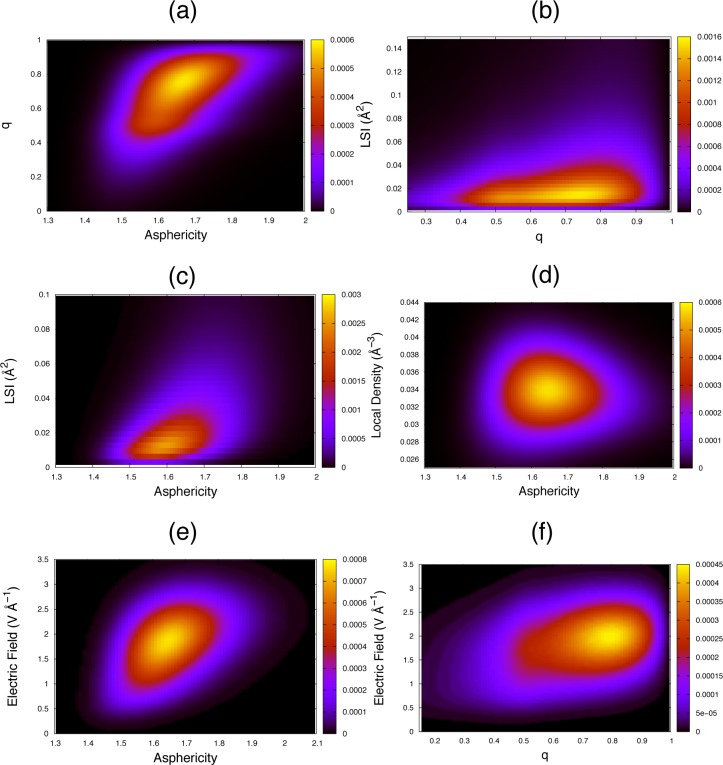
We start with the popular tetrahedral order parameter q whose definition focuses on the angular ordering of the first hydration shell. The two-dimensional probability density distributions in Figure 1a,b show that a low q value systematically implies low η and LSI values. The angular distortion reported by a low q value therefore always leads to a local disorder to which the η and LSI parameters are also sensitive. However, a high q value can be found for structures with a broad range of η and LSI values. This dispersion arises from the definition of q, which exclusively reports on the angular order of the first four neighbors, while η and LSI are also sensitive to the radial order and probe both the first shell and the inner side of the second shell (up to 3.7 Å for the LSI). Therefore, high-q structures include not only fully ordered, tetrahedral configurations but also structures where the hydration shell is angularly ordered but radially disordered (i.e., the first shell neighbors lie in the directions they would have in a regular tetrahedron but not at the right distance) or where the second shell is not as separated from the first shell as it is in fully ordered structures (see the detailed analysis of these configurations in the Supporting Information (Table S1)). This shows that all structures reported to be disordered according to q are indeed disordered but that all ordered structures according to q are not necessarily tetrahedral because q only considers the angular distortions.

Figure 1.

Two-dimensional probability density distributions of water local structures in the bulk at 298 K for selected pairs of order parameters (additional correlation plots are provided in the Supporting Information (Figure S1)).

We now turn to the LSI which is a radial factor probing the separation between first and second shells. Figure 1b,c shows that a high LSI value always implies an ordered structure for η and q, but that a low LSI value can be found for structures with a broad range of η and q values. As expected, configurations where the first shell is disordered and where there is no clear separation between first and second shells do lead to a low LSI value. However, configurations where the first shell is ordered but with a high density and where many second shell neighbors lie within the arbitrary 3.7 Å cutoff used in the LSI definition (eq 3) also lead to a misleadingly low LSI value (the anticorrelation between LSI and ρ is shown in Table 1 and spurious effects on the LSI due to fluctuations in the coordination number are further analyzed in the Supporting Information (Table S2)). High-LSI structures are therefore always ordered and the LSI is a sensitive probe of interstitial water molecules. However, some structures where the four closest neighbors are ordered in a regular tetrahedron do not lead to a high LSI value when the second shell is not clearly separated from the first shell.

Regarding the Voronoi asphericity η, Figure 1a,c,d shows that low η values systematically indicate structures which are also reported to be disordered by the LSI (but not by q for those which are radially distorted), and that high η values always identify structures which are also ordered according to q (but not by the LSI for those which have a high density). η therefore seems to be less ambiguous than q and the LSI in bulk water, because it simultaneously probes both the angular and radial orders, together with the presence of nearby interstitial water molecules that distort the shape of the Voronoi cell. η values can thus report with a greater confidence on locally ordered and disordered structures.

The translational order parameter S_k is a radial equivalent of q and our study shows that it is rather poorly correlated with the other order parameters (Table 1). The two-dimensional correlation diagrams are provided in the Supporting Information (Figure S1) and show that S_k does not seem to offer a useful complementary measure of the local structure in water.

The local density ρ is found to be poorly correlated with the other order parameters (see Table 1) and the two-dimensional probability density distribution in Figure 1d shows that the density fluctuations are almost completely independent of the η fluctuations. While in ice the local structure is both tetrahedral and of low density, in liquid water one can frequently find compact ordered structures and disordered expanded first shells. The local density is thus not an adequate probe of the local tetrahedral arrangement in liquid water.

The local electric field E that is probed in Raman spectroscopy experiments is found to be best correlated with the asphericity η (Table 1 and Figure 1e,f), that we showed to be a good probe of the local tetrahedral order. However, the electric field measures the hydrogen-bond strength for a given water OH bond, i.e. only for a single apex of the tetrahedron and the ordering of the rest of the first shell is not directly probed. This explains why low E values indicative of a weak hydrogen-bond always correspond to a low-η disordered structure, while high E values are found for a broader range of medium to high η values, since one strong hydrogen-bond does not necessarily imply that the entire first shell is ordered.

Structural Changes around the Temperature of Maximum Density

Now that we have established which specific molecular features are probed by the different order parameters, we combine these complementary descriptions to determine which structural rearrangements lead to the well-known density maximum in liquid water just above the melting point. We therefore compare the structures of liquid water at two temperatures on each side of the density maximum, respectively, 298 and 260 K, where the densities are similar (we note that the TIP4P/2005 water model correctly reproduces the maximum density temperature, even if its melting temperature is below 260 K²¹). Table 2 shows that upon cooling the average values of all considered parameters describe an increase in the local order (q, LSI, η, S_k) and in the hydrogen-bond strength (E). These changes are all consistent with the well-established shift toward a more icelike structure and corroborate prior studies performed with these order parameters (see, e.g., refs (49 and 51) for LSI; refs (6 and 20) for η; refs (30 and 39) for q; and ref (47) for S_k). However, the simultaneous comparison of the different parameters further reveals that the different distortions probed by these order parameters are not affected by cooling in the same proportions. Within the first shell, the angular order probed by q increases noticeably while the radial order measured by S_k is almost unchanged, and the largest structural change when the temperature decreases is the reduced probability to find water molecules in an interstitial position between the first and second shells, as reported by the LSI.

Table 2. Mean Values of the Order Parameters for Bulk Water Molecules at 298 and 260 K, Together with Their Relative Change between 298 and 260 K (the Half-Width of the Student 95% Confidence Interval Calculated on Three Blocks Is Given in Parentheses).

	bulk at 298 K	bulk at 260 K	relative change (%)
asphericity η	1.6624 (0.0014)	1.7048 (0.0009)	+2.55 (0.14)
density ρ (Å–3)	0.03372 (0.00001)	0.033639 (0.00004)	–0.26 (0.02)
q	0.6686 (0.0023)	0.7297 (0.088)	+9.14 (1.35)
Sk	0.99900 (0.00001)	0.999171 (0.000003)	+0.020 (0.001)
LSI (Å2)	0.0382 (0.0004)	0.0509 (0.0003)	+33.5 (12.6)
E (V Å–1)	1.8290 (0.0014)	1.9648 (0.0032)	+7.43 (0.86)

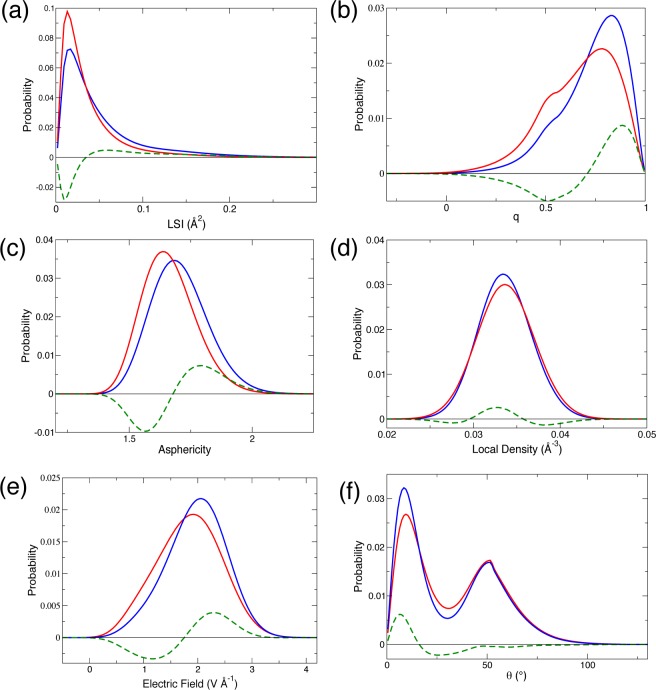
We extend our analysis beyond the average structural shifts and consider the full probability distributions of some selected order parameters in liquid water at 298 and 260 K (Figure 2). First, we find that while the average local densities are similar at these two temperatures, their distributions are different (Figure 2d). When the temperature decreases, the amplitude of the density fluctuations is reduced, the distribution is narrower and reveals a depletion both in very low and very high density structures. Regarding the η, q, and LSI distributions (Figure 2a–c), they all show a depletion in disordered structures and an enrichment in tetrahedral structures upon cooling. Similarly, the distribution of θ angles between pairs of water molecules displays an enhanced peak at small angles at 260 K, consistent with the greater hydrogen-bond strength also revealed by the electric field distribution (Figure 2e,f).

Figure 2.

Probability distributions in bulk water at 298 K (red) and at 260 K (blue) together with their difference (green) for the following series of order parameters: (a) LSI, (b) tetrahedral order q, (c) asphericity η, (d) density ρ, (e) electric field E, and (f) θ angle between pairs of water molecules.

None of the distributions shown in Figure 2 for a series of complementary structural order parameters display any sign of a heterogeneous mixture.⁷⁸ These results therefore provide further support to a description of liquid water as a homogeneous liquid exhibiting fast structural fluctuations,^37,54,79 and the density maximum observed in liquid water is thus not due to a mixture of two stable structures with different densities. Our study highlights the key role played by water molecules in interstitial positions between two hydration shells in the existence of this density maximum, in agreement with prior suggestion.⁴⁷ The reduced probability to find water molecules in such interstitial arrangements between the first and second shells upon cooling is manifest in the dramatic increase in the LSI value with decreasing temperature. Therefore, when the temperature is decreased below room temperature, liquid water exhibits not only the typical contraction of the nearest neighbor distance⁸⁰ observed in all liquids and which leads to a density increase, but also a depletion in interstitial water molecules, which leads to a density decrease. These two competing effects then give rise to the density maximum observed at 4 °C (the presence of these interstitial structures explains the angular distortions recently discussed in the context of the density maximum^79,80). The decrease in density at low temperature is therefore not due to an expansion of the first shell but to the reduced occurrence of interstitial geometries.

Structural Perturbations Induced by a Hydrophobic Solute

We now use the series of order parameters to characterize the influence of a hydrophobic solute on the local structure of water molecules in its vicinity. We focus on the hydration shell of the n-propanol methyl groups in a dilute aqueous solution, and we do not consider water molecules lying next to the hydroxyl end group. (While n-propanol is amphiphilic and not entirely hydrophobic, our choice is motivated by recent Raman studies¹⁰ of its hydration shell structure and by prior NMR⁸¹ and simulation⁸² results which have shown that for similar solutes the hydrophobic hydration shell properties vary little with the hydrophilic moiety.) A long-standing and much debated question is whether the hydration shell of hydrophobic groups is more or less structured than the bulk (see, e.g., refs (8−15)). Our study shows that while all the order parameters under consideration paint a consistent picture for the structural change induced by a decreasing temperature (see previous section), they yield contradictory answers regarding the influence of a small hydrophobic solute. As detailed in Table 3, some parameters (respectively ρ and LSI) report a moderate to strong enhancement of the local order in the shell relative to the bulk, while several others (e.g., η, S_k, E) find very little difference and another one (q) measures a decrease in the local order.

Table 3. Mean Values of Order Parameters for Water Molecules Respectively in the Bulk and in the Hydrophobic Part of the n-Propanol Hydration Shell at 298 K, Together with Their Relative Change from Bulk to Shell (the Half-Width of the Student 95% Confidence Interval Calculated on Three Blocks Is Given in Parentheses)^a.

	bulk	shell	relative change (%)
asphericity η	1.6624 (0.0014)	1.6639 (0.0021)	+0.09 (0.07)
density ρ (Å–3)	0.03372 (0.00001)	0.03300 (0.00001)	–2.2 (0.2)
q	0.6686 (0.0023)	0.6489 (0.0023)	–2.94 (0.46)
Sk	0.99900 (0.00001)	0.99872 (0.00001)	–0.003 (0.001)
LSI (Å2)	0.0382 (0.0004)	0.0537 (0.001)	+40.8 (1.0)
E (V Å–1)	1.8290 (0.0014)	1.8185 (0.0050)	–0.6 (0.1)

^aThe same comparison at 260 K is provided in the Supporting Information (Table S4).

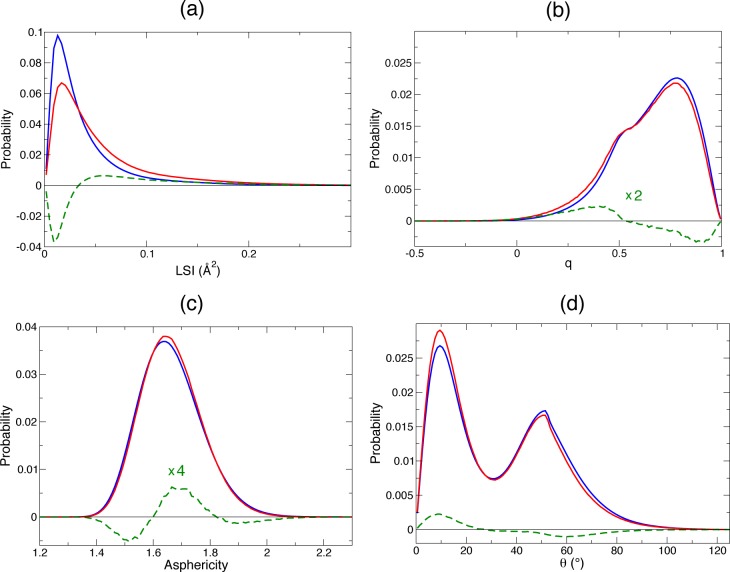
These contrasted results can be further analyzed by comparing the changes in the probability distributions of these different order parameters between the bulk and shell environments. Figure 3 shows that while the LSI and p(θ) water–water angle distributions exhibit a clear enrichment in more ordered structures in the shell relative to the bulk, the q distribution points to a depletion in ordered structures, and the asphericity suggests a depletion both in very ordered and very disordered structures. For each order parameter, similar results had been found in prior works on other hydrophobic solutes (see, e.g., ref (12) for θ, ref (13) for q, and ref (16) for η), but because each of these studies focused on a single order parameter, the dramatic dependence of the conclusions on the chosen order parameter had so far not been fully recognized.

Figure 3.

Probability distributions at 298 K of the following series of order parameters together with their difference (green) for water molecules in the bulk (blue) and in the shell of hydrophobic methyl groups (red): (a) LSI, (b) tetrahedral order q, (c) asphericity η, and (d) θ angle between a water molecule within the shell and any other water molecule.

These contradictory results could arise either from a structural perturbation that affects differently the types of local orders probed by these parameters (e.g., orientational vs radial order), or from the different ways to treat the solute in the order parameter definitions. We first consider the possible artifacts that can be induced by the solute. Next to a small hydrophobic solute, a water molecule retains an intact first hydration shell containing approximately four water neighbors. However, its second hydration shell is incomplete since it partly overlaps with the hydrophobic solute. Therefore, local order parameters focusing exclusively on the four nearest neighbors should not suffer from artifacts and can be directly used to compare the bulk and shell structures. In contrast, all the order parameters which partially probe the second shell may suffer from different degrees of distortion. We now examine each order parameter.

Since q and S_k focus on the four nearest water neighbors, they can be directly used in the shell of a small hydrophobic solute. However, we note that they may suffer from artifacts when used for water molecules next to other types of interfaces, especially when some of the four nearest water neighbors lie beyond the first solvation shell. These situations can be found, for example, next to an extended hydrophobic interface and next to solutes with hydrogen-bond donor and acceptor sites. It was recently shown that for both a small amphiphilic solute⁴⁵ and a protein interface⁸³ the definition of q should be extended to consider the four nearest hydrogen-bond donor and acceptor groups, whether they are water molecules or not.

Regarding the LSI (eq 3), it probes the arrangement of all water molecules within 3.7 Å. The depletion in the number of second-shell neighbors caused by the solute yields a drop in the coordination number within 3.7 Å from 6.0 in the bulk to 5.3 in the shell, and consequently leads to a dramatic but artifical increase in the LSI value (Table 3).

We now turn to the asphericity η. A small fraction of the Voronoi polyhedron can be in contact with second shell neighbors, which could induce artifacts next to a solute. For water molecules within the shell of propanol, the fraction of surface in contact with the solute is found to be small (below 10%), but it varies with η. The comparison between η distributions in the shell and in the bulk may thus suffer from a spurious distortion. The surface in contact with the solute increases in low-η disordered structures, where the second shell is less separated from the first shell (see the Supporting Information (Figure S5)). But because the solute interface is rigid, the asphericity cannot decrease as much as in the bulk, leading to possible artifacts. In our simulations, while both q and η report a depletion in ordered structures in the shell relative to the bulk, η suggests an additional depletion in very disordered structures that is not seen by q. The difference between the shell and bulk two-dimensional probability distributions along q and η presented in Figure 4 reveals the origin of this discrepancy. From our analysis of the bulk two-dimensional correlations (see the Supporting Information), the depletion observed for moderate q and low η structures correspond to situations where the first shell is ordered but where the low η value is caused by the proximity of the second shell. In the propanol hydration shell, these situations are less likely because of the rigid solute interface and this depletion is thus probably for the most part an artifact.

Figure 4.

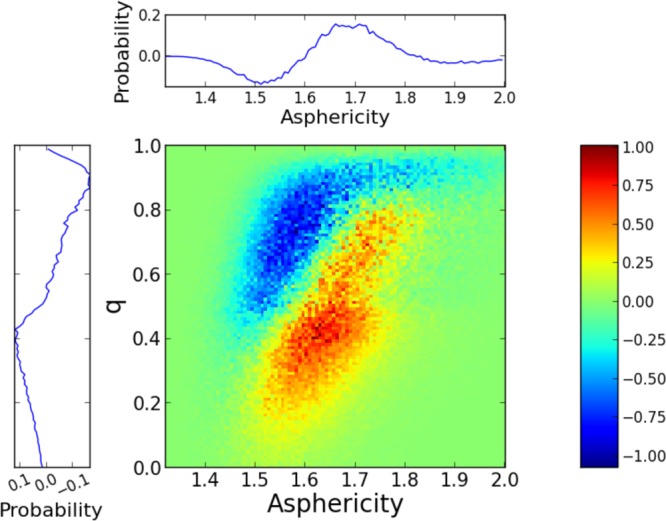
Difference between the two-dimensional probability distributions of water local structures in the hydrophobic shell and in the bulk at 298 K for the q and η order parameters, together with the projected one-dimensional distribution differences which repeat what is already shown in Figure 3. The color code shows an excess in the shell in red and a depletion in blue.

Regarding the local density, although some ambiguities exist due to the difference in the van der Waals radii of the solute sites and of the water oxygen atoms,⁵³ the density decrease in the shell relative to the bulk is consistent with neutron scattering studies (see, e.g., ref (84)) and can be explained by the large solute–water distance in absence of any hydrogen-bond interaction.

Concerning the local electric field E, while it includes long-range contributions and may be affected by the replacement of some second-shell polar water molecules by an apolar hydrophobic group, it is dominated by the nearest hydrogen-bond acceptor and by the first hydration shell. Its contamination by the hydrophobic solute should thus be limited.⁸⁵

A final comparison is required between our present data suggesting that the shell is very slightly less ordered than the bulk, and the results of a pioneering simulation⁸⁶ of a hydrophobic solute in aqueous solution, which had shown that the pair interaction energy with the nearest water neighbor is stronger when the pair lies in the shell than when it is in the bulk. While our simulations have been performed with a different force field, they do confirm this latter observation (Figure 5a). However, when all pairs with the first shell neighbors are considered (and not only the nearest neighbor pair), the shell and bulk distributions of pair interaction energies become almost identical (Figure 5b). These results are thus consistent with what we found for the E field which is another probe of the interaction energy and whose distribution is very similar in the shell and in the bulk (see the Supporting Information). (We note that while pair interactions between two water molecules in the shell are especially strong probably due to the geometric constraints imposed on the shell water molecules, the average interaction energy of a shell water molecule with its four nearest neighbors includes a dominant contribution from its neighbors lying beyond the solute first shell, with which the interaction is similar to that between two bulk molecules.)

Figure 5.

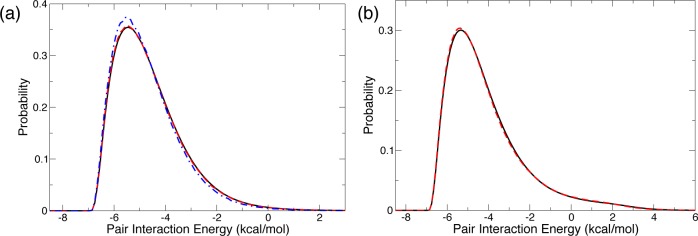
(a) Distribution of the pair interaction energy with the nearest water neighbor of a molecule lying in the bulk (black solid line) and in the hydration shell, respectively with its nearest neighbor in the bulk (red dashed line) or in the hydration shell (dot-dashed blue line ). (b) Distribution of pair interaction energies between a water molecule lying in the bulk (solid black line) or in the hydration shell (red dashed line) with each one of its four nearest water neighbors.

The combination of these diverse order parameters thus suggests that once potential artifacts are excluded, the structural perturbation induced by a small hydrophobic solute on its first hydration shell is very weak. This therefore shows that there is no iceberg-like structure in all or part of the hydration shell, in agreement with neutron scattering experiments¹¹ but in contrast with a recent simulation study.¹³ Only a small depletion in ordered structures is observed in our simulations. This result differs from the conclusions of a recent Raman study,¹⁰ suggesting that the hydration shell of alcohols is depleted in weakly hydrogen-bonded water molecules at room temperature. However, as already mentioned in the discussion of Figure 1, the connection between the local electric field essentially measured in the Raman spectra and the local structure can be ambiguous, and further work will thus be necessary to connect these subtle structural perturbations with the measured Raman spectra.

Structural Fluctuations Affecting the Water Reorientation Dynamics

We now determine to what extent the local structural fluctuations that we have described affect the dynamical properties of water. Our goal is to identify which local structural fluctuations have an effect on the reorientation dynamics of water molecules. We therefore calculate the reorientation time-correlation function (eq 7) of OH bonds belonging to water molecules whose local order parameter initially lies respectively in the first, second and third, and fourth quartiles of the order parameter distribution. This provides a comparison of the reorientation dynamics for water molecules which are initially in very ordered and disordered environments with the average dynamics.

We showed in prior works that, in the bulk and in a wide range of environments including hydrophobic hydration shells, water reorientation proceeds mostly via large-amplitude angular jumps due to an exchange of hydrogen-bond acceptors.^77,87−89 We further demonstrated that these jumps are retarded in ordered local environments because of the greater free energy costs induced by the rearrangements required by the breaking of the initial hydrogen-bond and by the arrival of a new hydrogen-bond partner from the second shell.^6,16

The reorientation times reported in Table 4 confirm that water reorientation slows down when the local order increases. This is verified for all order parameters except the local density ρ for which both an increase and a decrease with respect to the average density lead to a slight acceleration, due to its competing effects on the jump free energy barrier.⁹⁰

Table 4. Integrated OH reorientation times τ_reor (eq 8) in ps of Bulk Water Molecules at 298 K Whose Initial Order Parameter Value Respectively Lies in the First (Q1), Second and Third (Q2–Q3), and Fourth (Q4) Quartiles of the Order Parameter Distribution.

	Q1	Q2–Q3	Q4
asphericity η	1.67	2.20	2.67
density ρ (Å–3)	2.16	2.22	2.11
q	1.71	2.22	2.61
Sk	1.95	2.21	2.36
LSI (Å2)	1.86	2.17	2.56
field E (V Å–1)	1.69	2.26	2.51

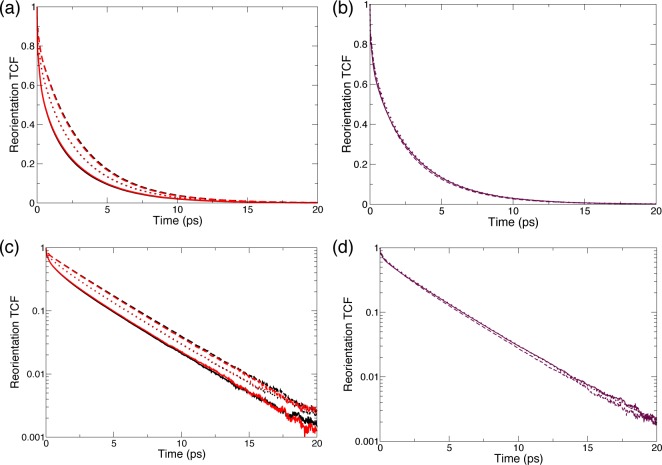
Among the order parameters under consideration, the most sensitive probes of the structural fluctuations affecting the reorientation dynamics are the asphericity η and the angular tetrahedral order q, for which the spread in reorientation times is the greatest (see Table 4 and Figure 6). This is explained by the excellent ability of these order parameters to probe the distortions induced by the presence of an interstitial water molecule. This latter molecule can be a potential new hydrogen-bond partner and thus facilitates jump hydrogen-bond exchanges which lead to a molecular reorientation.^77,87 We recently formalized this connection through a quantitative model relating the asphericity fluctuations and the water reorientation time, and applied it to explain the reorientation dynamics of water over a broad temperature range including the liquid and supercooled regimes, in the bulk and in the hydration shell of hydrophobic groups and of proteins.^6,16,83 However, we insist that while the correlation between η and the reorientation time is significant, it remains limited because η is also sensitive to structural rearrangements which do not affect the jump dynamics, for example due to the first shell neighbors not involved in the jump.

Figure 6.

Water OH bond reorientation time correlation functions (eq 7) for bulk water molecules at 298 K whose initial order parameter value lies in the first (Q1, solid lines), second and third (Q2–Q3, dots), and fourth (Q4, dashes) quartiles of the order parameter distribution. Water molecules are respectively selected based on their initial asphericity η (black) and q (red) values in panel (a), and on their initial density in panel (b). Panels (c) and (d) show the same time correlation functions with a semilog scale.

As shown in Table 4, the susceptibility of water reorientation dynamics vis-a-vis the local electric field E is also fairly large. Since E probes the strength of the hydrogen-bond donated by the OH group, E has been shown to monitor the breaking of the initial hydrogen-bond.⁹¹ However, since E does not probe the presence of a new hydrogen-bond acceptor which is required for a hydrogen-bond exchange leading to a large-amplitude reorientation,⁹¹ the correlation with the reorientation time remains very approximate. The approach of a potential new partner in an interstitial position is probed by the LSI. However, the latter is very little sensitive to the stretching of the initial bond and in addition the new interstitial neighbor could be anywhere around the water molecule and may not be available for a jump of the OH bond under consideration. Both factors explain the weak effect of the LSI on the reorientation time.

In addition, it is interesting to note the contrast between the large sensitivity of the reorientation dynamics on the first shell orientational order probed by q and η compared to the small effect caused by the radial disorder measured by S_k. This difference is probably caused by the high frequency of the hydrogen-bond stretching motions which can cause fast fluctuations of the radial order but whose effect is quickly averaged before the jump occurs, while the angular disorder can indirectly report on the presence of a fifth water molecule in the first hydration shell to which hydrogen-bond jumps can occur.

We finally repeated our study for water molecules initially in the hydration shell of hydrophobic groups (see the Supporting Information), in order to investigate recent suggestions^13,92 about a potential structural origin of the slowdown in water reorientation dynamics next to hydrophobic solutes. Our results exhibit the same trends as in the bulk and confirm that the most sensitive probes of the structural fluctuations relevant for the reorientation dynamics are η and q, which shows that the potential solute-induced artifacts on these parameters are very limited. But the major result is that, for similar local structures in the bulk and in the shell, the reorientation dynamics is slower next to the hydrophobic solute. This shows that, in agreement with our recent analysis,¹⁶ the main cause of the slowdown is not the (very limited) structural perturbation induced by the interface (e.g., a slight change in the local density as suggested in ref (92)). In contrast, the origin of the slowdown is essentially an entropic, excluded volume factor caused by the solute which hinders the approach of potential new hydrogen-bond partners, while local structure effects are very limited at room temperature (but can become dominant at very low temperature¹⁶).

Concluding Remarks

Our study of a broad range of local order parameters for liquid water demonstrates that different parameters probe different aspects of the local structure. For example, the widely used tetrahedral order q is most sensitive to the angular disorder, while the separation between first and second shells is sensitively probed by the LSI, and the asphericity of the Voronoi cell is sensitive to both. Using a unique order parameter can thus be ambiguous. We therefore employed a series of complementary order parameters to study the structural rearrangements occurring in liquid water around the temperature of maximum density. Our results show no sign indicative of a heterogeneous mixture, and our combination of several order parameters confirms prior suggestions⁴⁷ and establishes that when the temperature decreases the density maximum arises from the competing effects of a contraction of the first-shell oxygen–oxygen distances and of a depletion in interstitial water molecules located between the first and second shells. When applied to the structure of water in the hydration layer of a hydrophobic group, the order parameters have to be corrected for potential artifacts in their definitions, and show that the hydration shell of a small hydrophobic solute has a local structure which is very similar to that found in the bulk, with only a weak depletion in ordered configurations. We have finally characterized the key structural fluctuations that affect the reorientation dynamics of water. The presence of a potential new hydrogen-bond partner which is key for the jump reorientation dynamics induces angular distortions that are best probed by the asphericity η and by the tetrahedral order parameter q. However, structural fluctuations have a limited effect on water reorientation dynamics, and the slowdown induced by a hydrophobic interface remains essentially due to an excluded-volume effect at room temperature.

Supporting Information Available

Complementary plots and analyses of the local order parameter distributions in the bulk and in the propanol hydration shell. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.5b02936.

The authors declare no competing financial interest.