Role of Charge and Solvation in the Structure and Dynamics of Alanine-Rich Peptide AKA₂ in AOT Reverse Micelles

Abstract

The propensity of peptides to form α-helices has been intensely studied using theory, computation, and experiment. Important model peptides for the study of the coil-to-helix transition have been alanine–lysine (AKA) peptides in which the lysine residues are placed on opposite sides of the helix avoiding charge repulsion while enhancing solubility. In this study, the effects of capped versus zwitterionic peptide termini on the secondary structure of alanine-rich peptides in reverse micelles are explored. The reverse micelles are found to undergo substantial shape fluctuations, a property observed in previous studies of AOT reverse micelles in the absence of solvated peptide. The peptides are observed to interact with water, as well as the AOT surfactant, including interactions between the nonpolar residues and the aliphatic surfactant tails. Computation of IR spectra for the amide I band of the peptide allows for direct comparison with experimental spectra. The results demonstrate that capped AKA₂ peptides form more stable α helices than zwitterionic AKA₂ peptides in reverse micelles. The rotational anisotropy decay of water is found to be distinctly different in the presence or absence of peptide within the reverse micelle, suggesting that the introduction of peptide significantly alters the number of free waters within the reverse micelle nanopool. However, neither the nature of the peptide termini (capped or charged) nor the degree of peptide helicity is found to significantly alter the balance of interactions between the peptides and the environment. Observed changes in the degree of helicity in AKA₂ peptides in bulk solution and in reverse micelle environments result from changes in peptide confinement and hydration as well as direct nonpolar and polar interactions with the water–surfactant interface.

I. Introduction

Investigating factors that influence the stability of the secondary structure of peptides and proteins, such as confinement, competitive solvation in a heterogeneous environment, and peptide functional group modifications, is important to our understanding of why proteins misfold and aggregate. Reverse micelles (RMs) are a convenient environment in which to encapsulate and probe biological molecules.¹⁻³ The water cores of RMs are similar to cavities found in biological systems,⁴ such as water molecules near the water–membrane interface of a cell. Because the size of RMs is determined by the water to surfactant ratio (water loading, w₀ = [H₂O]/[surfactant]), RMs represent a “tunable” environment for the study of the effects of limited hydration and confinement on protein folding, aggregation, and function.⁵ A significant effort has been made to explore the properties of RMs using computer simulation, beginning with the influential work of Ladanyi and coworkers.⁶⁻⁸ That work provided the foundation for subsequent studies of RMs employing all-atom and coarse-grained models.⁹⁻¹⁴ Subsequent studies explored the nature of water dynamics in RM environments,¹⁵⁻¹⁹ where it has been shown that water rotational relaxation is dramatically slowed relative to water in the bulk.

The seminal experimental work of Mukherjee et al.¹ explored the structure of capped alanine-rich peptides AKA_n (Ace-YGAKAAAA-(KAAAA)_nG-NH₂) in AOT RMs (using nonpolar solvent isooctane = 2,2,4-methylpentane) and in bulk water. Sodium bis(2-ethylhexyl) sulfosuccinate (AOT) is a widely used anionic surfactant that forms monodisperse RMs in nonpolar solvents.^20,21 Using CD and IR spectroscopy, they observed that upon encapsulating the peptides in RMs of low w₀ the helical content increased significantly as compared with that measured in bulk water or a buffer.

Tian and Garcia²² performed molecular dynamics simulations of self-assembling RMs and encapsulated zwitterionic AKA₄ peptides. They observed nonspherical shape fluctuations of the RMs and also found that the peptides preferred to reside at the water–AOT interface. Abel and coworkers²³ obtained similar results for previous simulations of zwitterionic octa-alanine peptides in RMs.

Martinez and coworkers²⁴ performed simulations on capped AKA₂ peptide in bulk water and in RMs of w₀ = 6 that were both spherically restrained and unrestrained. For reference RMs of w₀ = 6, spherically restrained and unrestrained with no peptide were simulated. The results indicated that the peptides were more helical in RMs than in bulk water. Additionally, the shape of unrestrained RMs fluctuated significantly from an initial spherical geometry, facilitating interaction between the dehydrated peptide and the AOT aliphatic tails that appears to be important in stabilizing the peptide’s partial helical character.²⁴ These results are in agreement with experiments¹ as well as previous computational studies.^9,22,23

These prior studies leave a number of critical questions unanswered. It is known that the treatment of N- and C-termini with neutral caps can influence the peptide structure. However, while experimental studies of alanine-rich peptides in RMs were performed with capped peptides,¹ simulations studies by Abel and coworkers²³ and Tian and Garcia²² have employed zwitterionic termini, and those by Martinez and coworkers²⁴ have employed capped termini. The experimental observables in the original studies of Mukherjee et al.¹ were CD and IR spectra. However, no simulation studies have computed spectra to be directly compared with experiment.

This study explores the effects of capped versus zwitterionic N- and C-termini on the helix stability of these same peptides in RMs using two force fields. We performed simulations of the AKA₂ peptide in two forms, capped (Ace-YGAKAAAA-(KAAAA)₂G-NH₂) and zwitterionic (NH₃⁺-YGAKAAAA-(KAAAA)₂G-COO^–), in spherically restrained and unrestrained RMs of w₀ = 6. The results demonstrate that capped AKA₂ peptides form more stable helices than zwitterionic AKA₂ peptides. The IR spectra of the amide I bond of the peptides were computed and directly compared with experiment.¹ The computed peptide amide I IR spectra and water rotational anisotropy decay were found to be largely insensitive to the treatment of the peptide termini, while showing a distinct dependence on shape fluctuations in the RM environment. Overall, our results provide insight into the nature of peptide confinement and hydration in a RM environment and the importance of considering shape fluctuations in characterizing the RM ensemble.

II. Methods

The RMs each contained a peptide monomer, and the starting structure for the peptides was an α-helix. Table 1 contains a summary of the simulation details for all systems, including the number of all molecules (surfactant, ions, water, and solvent) used and simulation times. The composition of the RMs was determined from the SAXS experiments of Amararene et al.²⁵ This composition differs from that suggested by the experiments of Eicke and Rehak.²⁶ In a separate study, we have explored the structure and dynamics of alternative interpretations of the water loading for comparison.²⁷

Table 1. Simulation Details of the Composition of All Simulations, Including Water Loading (w₀), Number of AOT Molecules (n_AOT), Counterions (n_counterions), Water Molecules (n_H2O), Isooctane Molecules (n_iso), As Well As Production Run Time (t (ns)).

system	w0	nAOT	ncounterions	nH2O	niso	t (ns)
AKA2 + restrained RM	6	76	3 Cl–	456	∼2300	50
AKA2 + unrestrained RM	6	76	3 Cl–	456	∼2300	50

RM systems were generated using the CHARMM32 package²⁸ with the CHARMM27 all-atom force field for proteins and lipids and the TIP3P water model for CHARMM. CHARMM parameters for AOT and isooctane were taken from the work of Abel et al.⁹

To construct the RMs, we used the same method described in ref (27). The helical structure generated for the peptide was solvated with a sphere of water, and random water molecules were replaced with 76 sodium cations (one for each AOT molecule to be added) and three chlorine anions (one for each LYS) to create a neutral system. A spherical AOT shell was added to the RM and was centered in a truncated octahedron of isooctane. For the spherically restrained RMs, a massless dummy atom was fixed in the center of the RM, and a harmonic restraint was placed on the sulfur atom of each AOT molecule to keep it within 11.25 and 15.25 Å of the dummy atom. The distance restraints were chosen to agree with experimental measurements of the solution density.²⁵

NAMD²⁹ was used for the production runs. The cutoff for the short-range electrostatics calculations was set to be 12 Å, and particle-mesh Ewald was used to treat the long-range electrostatics. The temperature was held constant at 300 K, and the pressure was held constant at 1 atm using the Langevin piston.^30,31 SHAKE was used to keep bonds containing hydrogen atoms rigid. Each trajectory was run for 50 ns using a 1 fs time step and saving data every 0.1 ps.

The same systems were also run using GROMACS and the GROMOS96 53a6 united atom force field.³² The electrostatics were treated as in the CHARMM simulations. The temperature was held constant at 300 K, and the pressure was held constant at 1 atm using the Berendsen piston.³³ Each trajectory was run for 50 ns using a 2 fs time step and saving data every 0.1 ps. Analysis of all systems was performed using CHARMM, GROMACS, MDAnalysis,³⁴ and VMD.³⁵

III. Results and Discussion

Reverse Micelle Shape Is Not Spherical

Consistent with experimental observations by Halle³⁶ and theoretical considerations by Chandler,³⁷ recent results from simulation and experiment^11,12,24,27 suggest that unrestrained RMs showed significant shape fluctuation. Figure 1 shows representative structures taken from unrestrained CHARMM simulations after 50 ns of simulation time. The water and AOT molecules are found to pucker around the peptide, allowing for significant interaction of the AOT tail groups and at times the isooctane with the nonpolar surface of the peptide. These observations of nonspherical RM shape fluctuations and contacts between the peptide and the environment were also observed by Tian and Garcia in their simulations of similar systems.¹⁰ To characterize these structural fluctuations, we calculated the average elliptical radii and the radius of gyration for each RM system. The results (not shown) indicate an elliptical geometry for the unrestrained RMs that are consistent with the results of previous experimental and simulations studies.^{9−14,24,27,38}

Figure 1.

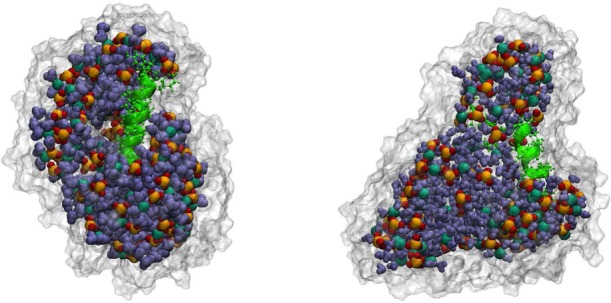
CHARMM unrestrained reverse micelles with capped (left) AKA₂ and zwitterionic (right) AKA₂ peptides. The components of the RM are colored as follows: AOT tail groups, white surface; sulfonate head groups, yellow and red; sodium ions, dark green; water molecules, blue; peptide, bright green.

α-Helices Are More Stable for Capped AKA₂ Peptides

Helical peptides form dipoles with a partial positive charge at the N-terminus and a partial negative charge at the C-terminus. Capping the termini eliminates the charge repulsion present when the terminal residues are charged and tends to stabilize the helix.³⁹ Figure 2 shows the secondary structure progression with respect to time for the residues of each of the AKA₂ peptides in RMs for the CHARMM trajectories. The structure of the capped AKA₂ peptides changes very little during the simulation with the peptides remaining almost entirely α-helical. The structure of the terminal residues of the zwitterionic AKA₂ peptides shows significant fluctuations, especially in the case of the unrestrained RMs, suggesting that the zwitterionic termini contribute to the destabilization of the helical secondary structure. Similar results were found for the GROMACS trajectories (data shown in Supporting Information). The secondary structure definitions used are those of Kabsch and Sander’s DSSP method.⁴⁰

Figure 2.

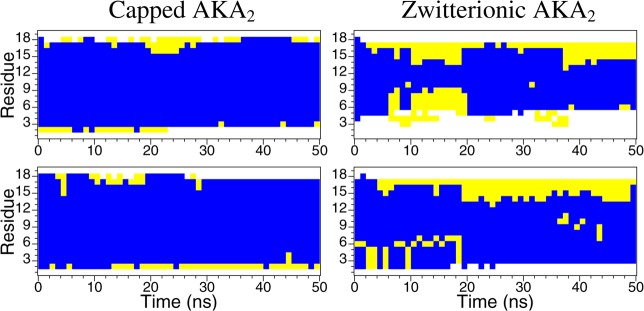
Secondary structure progression with respect to time of AKA₂ peptides in unrestrained (top) and spherically restrained (bottom) reverse micelles for the CHARMM systems: capped AKA₂ (left) and zwitterionic AKA₂ (right). The secondary structure is indicated as helix (blue), turn (yellow), and coil (white).

Another way to evaluate secondary structure stability is the root-mean-square deviation (RMSD) with respect to time. Figure 3 presents a histogram of the observed peptide RMSD, demonstrating that the two capped AKA₂ peptides have a more stable backbone structure and undergo smaller fluctuations compared with the zwitterionic peptides. Comparison of the DSSP and RMSD plots suggests that fluctuations in RMSD for the capped AKA₂ peptide, in the unrestrained RM, in particular, result from the changes in the secondary structure in the terminal residues.

Figure 3.

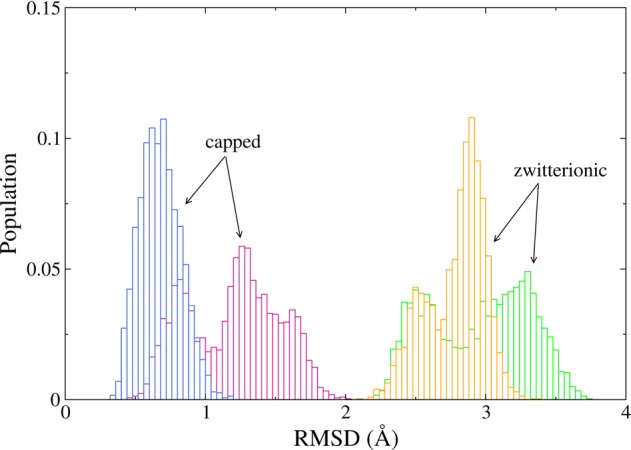
Distribution of the peptide backbone RMSD for the last 30 ns of simulation for the AKA₂ peptides in RMs for the CHARMM systems. Data are shown for capped/zwitterionic peptides in restrained (blue/yellow) and unrestrained (pink/green) RMs. Fluctuations of the capped peptides are substantially smaller than for the zwitterionic peptides.

Peptides Interact Strongly with the Water–Surfactant Interface

Significant interaction of the AKA₂ peptides with the surrounding environment of the RM is observed in all systems studied. In the unrestrained RMs, however, in addition to the interaction between the peptides and water molecules, there is significant contact between the peptides and the surfactant molecules, especially the aliphatic AOT tail groups.

Figure 4 shows the average number of AOT tail groups and water molecules within 4 Å of each residue of the AKA₂ peptides in RMs for the CHARMM systems. The core residues of the peptides in the restrained RMs are significantly more hydrated than the residues of the peptides in the unrestrained RMs, which are in contact with more AOT tail groups.

Figure 4.

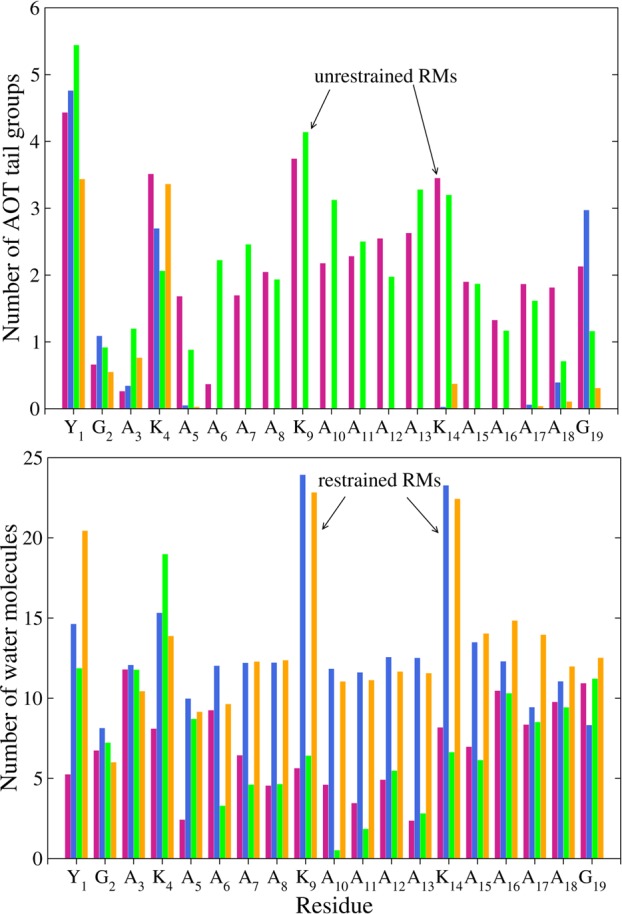
Average number of AOT tail groups (top) and water molecules (bottom) within 4 Å of each AKA₂ residue in the CHARMM RMs. Data are shown for capped/zwitterionic peptides in restrained (blue/yellow) and unrestrained (pink/green) RMs.

Figures 5 and 6 show the number of AOT tail groups and water molecules within 4 Å of each of the AKA₂ peptides. The distributions show good agreement between peptides in the same environment (restrained or unrestrained RM) regardless of nature of the N– and C–termini. The distribution of the hydration values of the two peptides in the restrained RMs is almost identical.

Figure 5.

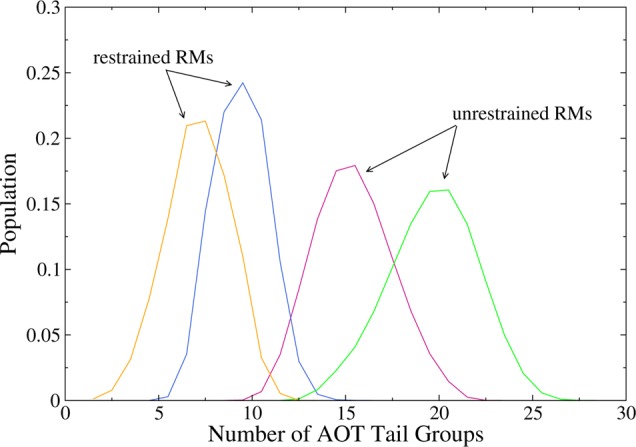
Number of AOT tail groups within 4 Å of AKA₂ peptides. Peptides in the unrestrained RMs have more contact with the tail groups than peptides in the restrained RMs. Data are shown for capped/zwitterionic peptides in restrained (blue/yellow) and unrestrained (pink/green) RMs.

Figure 6.

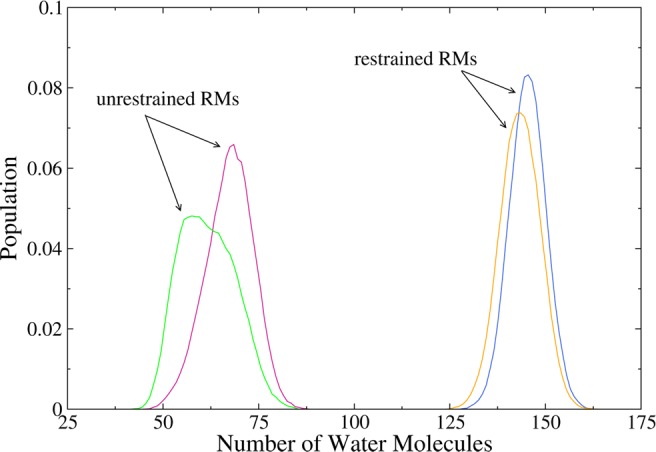
Number of water molecules within 4 Å of AKA₂ peptides. Data are shown for capped/zwitterionic peptides in restrained (blue/yellow) and unrestrained (pink/green) RMs. The level of hydration of the peptides is similar in each environment with peptides in the restrained RMs being more hydrated than peptides in the unrestrained RMs.

Figure 7 shows snapshots of CHARMM AKA₂ in restrained and unrestrained RMs with the surrounding water and AOT tails after 50 ns of simulation. The peptide in the restrained RM is almost completely hydrated, while the peptide in the unrestrained RM is in contact with AOT aliphatic tails. Tian and Garcia noted similar behavior in their simulations of AKA₄ peptides in RMs.²² They observed significant contact between the nonpolar peptide core and the AOT/water interface as well as some contact with isooctane molecules. This interaction “frees” water molecules bound to the interface and may increase the entropy of the system. The lysine residues, in particular, were either well-hydrated or in contact with the AOT head groups. Similar results were obtained for systems modeled using the GROMOS force field with the exception that, in general, the AKA₂ peptides in the RMs are less hydrated than those for the CHARMM systems. See the Supporting Information for GROMOS data.

Figure 7.

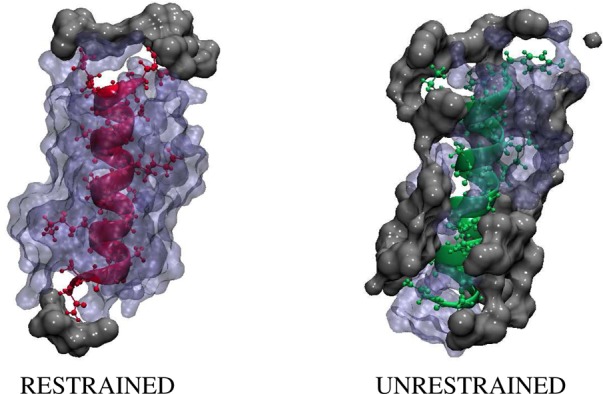
Capped AKA₂ in a restrained (left) and unrestrained (right) RM. The snapshot on the left shows the peptide in pink, and the snapshot on the right shows the peptide in green. Each peptide is shown with the surrounding water molecules in blue and AOT tails groups in gray.

Calculated IR Spectra for AKA₂ Depend on RM Shape Fluctuations

Infrared spectra for the amide I modes of capped and zwitterionic AKA₂ peptides encapsulated in RM were calculated and compared with experimental data measured for capped AKA₂ peptides in RMs of w₀ = 6 at room temperature.¹ Figure 8 shows the normalized spectra. Simulated spectra were computed using a vibrational exciton model, in which the fundamental frequencies (FFs) and couplings are expressed as a function of electric field and van der Waals forces on the atoms of the peptide bonds.⁴¹ In that recently developed approach, the FF for a particular amide I mode is derived from a “map” parametrized as

1

in terms of the components of the electric field, E_iα, and van der Waals force, F_iα, at atom i (which includes the O, C, N, and H atoms of the peptide bond), where ω₀ is a static frequency (which may be taken to be the gas phase value) and c_iα and d_iα are fitting coefficients as a function of the sum over parameters α.

Figure 8.

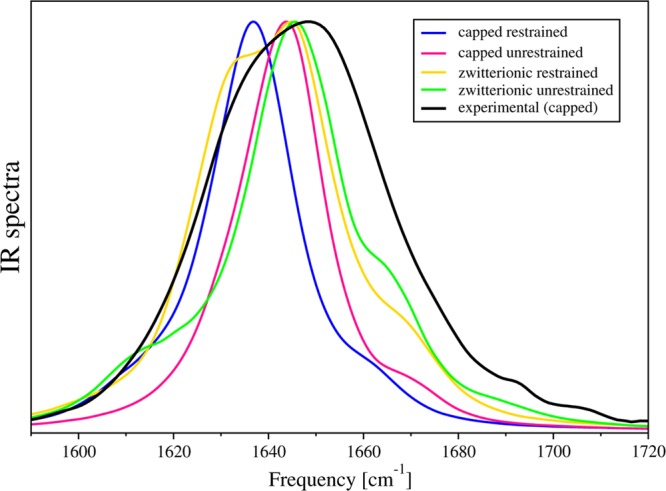
Calculated IR spectra for capped and zwitterionic AKA₂ peptides in restrained and unrestrained reverse micelles, with w₀ = 6 at room temperature, compared with experiment.

All forces were computed using the full interaction between peptide bonds and the surrounding environment, the same forces that inform the molecular dynamics. The proposed maps successfully reproduced experimental data for a set of proteins with a wide range of sizes and secondary structures as well as model peptides in polar and nonpolar solvents. This broad range of applicability is essential for any method that aspires to compute accurate amide I vibrational spectra for peptides in the heterogeneous RM environment such as a RM, that includes polar, nonpolar, and charged domains.⁴¹

The carbonyl stretch makes the primary contribution to the amide I vibration, with minor contributions from the C–N bond stretch. α-Helices typically display a peak at 1655 cm^–1, which shifts to lower frequency with increasing helix length. Several other factors, including hydrogen bonding and solvation, contribute to the peak location. Typically, hydrogen bonding lowers the frequency of bond stretching, and solvated helices may have peaks up to ∼20 cm^–1 lower than nonsolvated helices.⁴²

In our simulations, we observed that systems with more helical structures were associated with red-shifted spectra. We further observed that capped systems exhibited red-shifted spectra when compared with zwitterionic systems. The most helical peptide, capped AKA₂ in a restrained RM, was associated with a main peak at 1637 cm^–1, while the peptide with the least helical content, zwitterionic AKA₂ in an unrestrained RM, produced a major peak with the highest frequency at 1646 cm^–1. In fact, in our simulated spectra the positions of the main peak for all systems, with the exception of capped AKA₂ in a restrained RM, were nearly identical.

Additionally, the two peptides in the restrained RMs were observed to be more hydrated than those in the unrestrained RMs. As a result, the amide I spectra were found to be broader and peaked at lower frequencies, 1637 cm^–1 for the capped AKA₂ and 1645 cm^–1 for the zwitterionic AKA₂.

Other features present in our calculations include additional small peaks, both red- and blue-shifted with respect to the main peaks. To explain the origin of these peaks, we examined the FFs of each peptide bond and included contributions from peptide, water, counterions, and AOT surfactant molecules. Figure 9 shows histograms of FF for each peptide bond, sums of the FFs, and the calculated spectra. We have also constructed new Hamiltonian matrices with modified FFs or couplings. Our analysis demonstrates that the small peak at 1610 cm^–1 for the capped AKA₂ in a restrained RM can be associated with the 18th peptide bond, resulting from strong interactions with counterions. Similarly, the appearance of a small peak at 1613 cm^–1 for zwitterionic AKA₂ in an unrestrained RM resulted from strong interactions of the fourth peptide bond with counterions. For the same system, the peak at 1663 cm^–1 is associated with large couplings of the 13th peptide bond with the nearest peptide bonds. (See Figure 3 in the Supporting Information.) Histograms of the environmentally induced FF shift contributions provide additional insight into the role of the environment in inducing spectral heterogeneity. (See Figure 4 of the Supporting Information).

Figure 9.

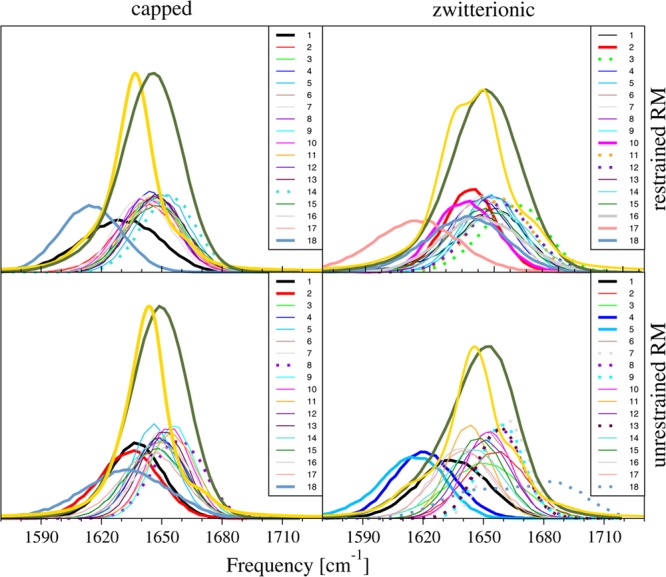
Comparison of histograms of FFs of each peptide bond (low lying histograms), sum of FFs (green lines), and the calculated spectrum (orange lines) for each studied system. Red-shifted FFs are shown as thin lines, and blue-shifted FFs are shown as dotted lines. FFs were scaled by three for clarity.

Orientational Dynamics of Water Confined in RMs Impacted by Peptide Solvation

The orientational dynamics of water confined in RMs has been shown to be qualitatively different than the dynamics of bulk water.^{16,27,43−46} The rotational anisotropy of water displays a single exponential decay for bulk water. However, in an RM environment there are clear signs of stretched exponential and power-law decay resulting from the heterogeneous environment of water molecules under nanoscale confinement,²⁷ as observed in other nanoconfined water systems.^45,47−51 Less is known about the how the presence of peptide in a RM influences the water dynamics, through direct interactions with the peptide, disruption of the water nanopool, and impact on the water–surfactant interface.

The orientational dynamics of the water O–H bond can be described through the autocorrelation function

2

where P₂ is the second Legendre polynomial and u(t) is the unit vector along the O–H bond at time, t. Figure 10 shows C₂(t) reorientational correlation functions for water in six distinct RM environments, including restrained and unrestrained RMs with capped AKA₂ peptide, AKA₂ peptide in a zwitterionic form, and RMs without peptide. Data for the latter system were derived from a previous study.²⁷ Data for RMs in the absence of peptide show faster relaxation than either peptide system. It is likely that this is due to the fact that the water rotational anisotropy decays faster for bulk water, and there is the largest percentage of bulk-like water in the RM with no peptide. Table 2 contains parameters for fits of the rotational anisotropy decay to a piecewise continuous function formed from a short-time stretched exponential decay and long-time power-law decay. These parameters provide further evidence that the rotational anisotropy decay of water is slowed by the presence of peptide.

Figure 10.

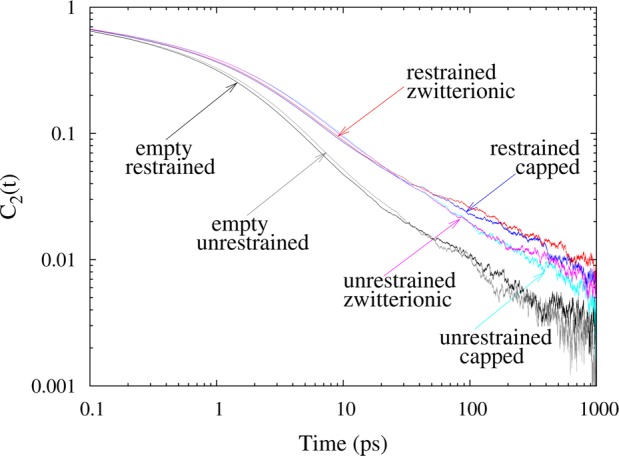
Rotational anisotropy decay autocorrelation functions for restrained and unrestrained RMs with capped AKA₂ peptide, AKA₂ peptide in a zwitterionic form, and RMs without peptide.

Table 2. Parameters for Fits of the Rotational Anisotropy Decay with the Function e^–(t/τ)βH(10 – t) + at^–nH(t – 10), where H(x) is a Heaviside Step Function, for RM Systems with and without AKA₂ Peptides^a.

system	τ	β	a	n
restrained RM	0.772	0.466	0.271	0.739
restrained RM + capped AKA2	1.001	0.409	0.371	0.620
restrained RM + zwitterionic AKA2	1.039	0.409	0.314	0.563
unrestrained RM	0.796	0.448	0.272	0.739
unrestrained RM + capped AKA2	1.156	0.409	0.494	0.711
unrestrained RM + zwitterionic AKA2	1.140	0.409	0.492	0.714

^aTime in picoseconds.

For RMs encapsulating AKA₂ peptide, water in the restrained RM systems shows slightly faster relaxation than water in the unrestrained RM up to 30 ps. This may be due to the fact that the AKA₂ peptides are more hydrated in the restrained RM system than in the unrestrained RM. Peptides in the unrestrained RM are found to be in contact with only half the number of water molecules compared with water in the restrained RM simulations. In the unrestrained RM, there is a corresponding increase in the contact between the peptide and AOT tail groups. However, this observed difference in the rotational anisotropy decay may not be statistically significant. At longer times, the difference in dynamics for these systems is on the order of the noise.

For the AKA₂ peptide solvated in AOT RMs, no significant difference is observed in the rotational anisotropy decay of water interacting with the capped or zwitterionic peptides. This is consistent with the observation that the treatment of the N- and C-termini of the AKA₂ peptide does not dramatically impact interactions of the peptides with the water or surfactant environment.

IV. Conclusions

We have studied the effects of capped versus zwitterionic termini on the secondary structure of AKA₂ peptides encapsulated in spherically restrained and unrestrained RMs. Our results using two force fields demonstrate that capped AKA₂ peptides form more stable helices than zwitterionic AKA₂ peptides. We found that the cap employed on the peptide termini did not significantly alter the interactions between the peptides and their environment. Calculation of the IR spectra of AKA₂ peptides in the CHARMM systems also suggests that our results are in agreement with the work of Mukherjee et al.,¹ with all four systems exhibiting a major peak in the amide I vibrational spectra within a few wavenumbers of the experimental peak. The observed rotational anisotropy decay shows distinct differences in water dynamics induced by the presence of the AKA₂. This difference may be detectable in experiment, providing a means of assessing the differing dynamics of water directly involved in peptide solvation. Such a measurement is far more difficult in a bulk environment.

Overall, our results provide support for the presence of significant fluctuations in the RM structure away from an ideal spherical geometry as well as the importance of surfactant surface fluctuations in facilitating hydrophobic and hydrophilic interactions. The existence and potential significance of such shape fluctuations away from an idealized spherical geometry continue to be debated, with computational predictions forming a consensus view that is only dependent on force field and interpretations of water loading in terms of absolute numbers of water and surfactant molecules in a characteristic RM.

Ultimately, these questions must be resolved by experimental studies that directly assess RM structure and allow for direct, critical comparison of observables with the predictions of simulation studies. Our simulation results demonstrate the amide I vibrational spectral lineshapes as well as the rotational anisotropy decay of water are sensitive to differences in restrained spherical RMs and RMs undergoing significant nonspherical fluctuations. As such, measurement of these experimental observables provides one way to critically assess the structure of RMs, in both the absence and presence of solvated peptide.

Supporting Information Available

Secondary structure progress with respect to time of AKA₂ peptides, in unrestrained and spherically restrained RMs for the GROMOS systems - capped AKA₂ and zwitterionic AKA₂. GROMOS-capped AKA₂ in restrained RM and unrestrained RM. Comparison of calculated spectrum for AKA₂ in unrestrained RM and spectrum calculated after setting four couplings of 13th peptide bond to zero to prove that these couplings cause appearance of small peak. Comparison of histograms of FF shifts caused by protein, water, counterions and AOT molecules. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States