Implications of the apportionment of human genetic diversity for the apportionment of human phenotypic diversity

Abstract

Researchers in many fields have considered the meaning of two results about genetic variation for concepts of “race.” First, at most genetic loci, apportionments of human genetic diversity find that worldwide populations are genetically similar. Second, when multiple genetic loci are examined, it is possible to distinguish people with ancestry from different geographical regions. These two results raise an important question about human phenotypic diversity: To what extent do populations typically differ on phenotypes determined by multiple genetic loci? It might be expected that such phenotypes follow the pattern of similarity observed at individual loci. Alternatively, because they have a multilocus genetic architecture, they might follow the pattern of greater differentiation suggested by multilocus ancestry inference. To address the question, we extend a well-known classification model of Edwards (2003) by adding a selectively neutral quantitative trait. Using the extended model, we show, in line with previous work in quantitative genetics, that regardless of how many genetic loci influence the trait, one neutral trait is approximately as informative about ancestry as a single genetic locus. The results support the relevance of single-locus genetic-diversity partitioning for predictions about phenotypic diversity.

1. Introduction

Going back to Lewontin’s 1972 study of human genetic diversity, many investigators have reported that at typical genetic loci, most of the allelic variation in statistical partitions of human genetic variation is “within,” rather than “between,” populations (e.g. Barbujani et al., 1997; Brown & Armelagos, 2001; Rosenberg et al., 2002, 2003b; Li et al., 2008). Many of these studies presented their results as estimates of F_ST, a quantity that can be interpreted as the proportion of allelic variance—that is, variance in a binary random variable representing the presence or absence of a specific allele—attributable to differences in allele frequencies between populations (Holsinger & Weir, 2009). Estimates of worldwide human F_ST and F_ST-like quantities have ranged from ~0.05 (e.g. Rosenberg et al., 2002) to ~0.15 (e.g. Barbujani et al., 1997), meaning that 5–15% of allelic variance at a representative locus is due to between-population differences in allele frequencies—or, equivalently, that 85–95% lies in the within-population variance component.

In spite of this result, which shows that human groups have similar allele frequencies at most variable loci, it is possible to infer the continental ancestry of individual people using genetic data alone (e.g. Bowcock et al., 1994; Mountain & Cavalli-Sforza, 1997; Rosenberg et al., 2002; Bamshad et al., 2003; Tang et al., 2005). Ancestry inference is performed by pooling information from many loci. Each locus provides only a small amount of information about population membership, but when many loci are used, their information can be combined to distinguish among potential ancestries.

In 2003, A.W.F. Edwards provided a particularly clear explanation of the way in which multiple loci can be used to classify accurately even when each individual locus is only weakly informative (Edwards, 2003). Edwards’ point was not new—it appeared in earlier arguments about allelic-variance partitioning and classification (e.g., Mitton, 1977; Neel, 1981; Smouse et al., 1982)—but he used an accessible model that clarified the result.

What do single-locus variance partitioning and multilocus classification studies lead us to expect about phenotypic differences between human populations? The finding that human groups have similar allele frequencies at most genetic loci has been used to support arguments that most large, genetically-based phenotypic differences between groups are exceptions to the genomic rule (e.g., Goodman, 2000; Brown & Armelagos, 2001; Feldman & Lewontin, 2008). Indeed, single-locus partitioning studies do suggest that human populations will not differ widely on most traits controlled by a single genetic locus. But the fact that classification is possible using many loci seems to suggest that human groups might differ more substantially on traits influenced by many loci. If populations can be distinguished with multilocus genotypes, then it is possible that phenotypes controlled by multilocus genotypes could differ markedly between populations. Should we expect to see larger differences between human populations for traits influenced by many loci than for traits influenced by a single locus?

Here, we extend Edwards’ model—which has already proven to be an effective framework for describing results about allelic-variance partitioning and classification—to study the expected level of between-population difference for a selectively neutral quantitative trait. Other researchers have studied this question in other contexts (e.g. Felsenstein, 1973; Lande, 1976, 1992; Chakraborty & Nei, 1982; Rogers & Harpending, 1983; Whitlock, 1999; Berg & Coop, 2014), but by basing our analysis in Edwards’ model, we explicitly connect questions about trait differences to questions about multilocus ancestry inference. We show that for a random quantitative trait under the extended Edwards model, two groups are not unduly likely to differ on traits that are determined by many loci, even when the loci influencing the trait would provide a sufficient basis for accurate classification. In particular, the expected level of difference between the populations’ mean trait values is, in two senses made more precise below, approximately equal to the magnitude of single-locus genetic difference between the populations. Similarly, a typical multilocus trait contributes approximately as much information for classification as does a single genetic locus.

2. The Edwards Model

Risch et al. (2002, box 1), Edwards (2003), and Tal (2012) have examined related classification models involving accumulations of information across loci; here, we consider the simplest of these models, that of Edwards (2003). We first describe key features of the model, and we then introduce a quantitative trait.

Suppose we have two haploid populations of equal size, labeled A and B. At one genetic locus, the probability that an individual from population A has an allele we label “1” is p, with p ∈ (0, 1/2), and the probability of allele “0” is q = 1 − p. In population B, the allele frequencies are switched: The probability of “1” is q and the probability of “0” is p. Table 1 shows the allele frequencies by population.

Table 1.

The frequencies of the “0” and “1” alleles in each population, with p + q = 1.

Population	Allele
	“0”	“1”
A
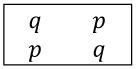
B

We can represent the genotype of an individual at the locus as a random variable L that takes values of 0 and 1, and we can represent population membership of an individual as a random variable M that takes values A and B. Within each population, the allelic variance at the locus—that is, the variance of L—is Var(L|M = A) = Var(L|M = B) = pq. This result follows from the status of L|M as a Bernoulli random variable with probability either p or q.

When not conditioning on population membership, the genotype at the locus is still a Bernoulli random variable, but now, because populations A and B are equal in size, the probability of observing a “1” is 1/2:

$$P(L=1)=P(M=A)P(L=1\mid M=A)+P(M=B)P(L=1\mid M=B)=\frac{1}{2}p+\frac{1}{2}q=\frac{1}{2}[p+(1-p)]=\frac{1}{2}.$$

The total unconditional variance of L is therefore Var(L) = P(L = 0)P(L = 1) = 1/4.

The proportion of the total allelic variance that is “within populations”—that is, the proportion of the total variance that remains after conditioning on an individual’s population membership—is the conditional variance of L given M divided by the total variance of L:

$$\mathit{Var}(L\mid M)/\mathit{Var}(L)=pq/(1/4)=4pq.$$

Because the total allelic variance is the sum of within- and between-population components, the proportion of the total variance in allelic types that is “between populations,” or F_ST, is

$$F_{ST}=(1/4-pq)/(1/4)=1-4pq.$$ (1)

Mimicking estimates for the between-region and between-population proportion of genetic diversity from Lewontin (1972) and subsequent studies, if we assume p < q, then we might take p between 0.3 and 0.4—an interval that produces within-population variance proportions from 0.84 to 0.96—as approximately reflecting differences between human groups at a typical locus.

Suppose we want to classify individuals into populations using the genotype at the locus. That is, we wish to predict population membership M after observing an individual’s allele. If p < q, then the decision rule with the greatest prediction accuracy is to assign individuals with a “0” allele to population A and individuals with allele “1” to population B (Rosenberg et al., 2003a). That is, we assign an individual to the population in which its allele is most common. Misclassification occurs for individuals from population A with a “1” allele and individuals from population B with a “0” allele. The total misclassification probability is

$$P(L=1\mid M=A)P(M=A)+P(L=0\mid M=B)P(M=B)=\frac{1}{2}p+\frac{1}{2}p=p.$$

Thus, if we use a single locus for classification, then the misclassification rate is p.

Suppose now that instead of being limited to one locus, we use k loci to classify. We represent the genotypes of a random individual at the k loci as random variables L₁, …, L_k, denoting the total number of “1” alleles at the loci by the random variable $S={\sum }_{i=1}^k{L}_i$. Assume that for all loci, allele frequencies in each population are the same as at the single locus described above, and that conditional on population membership, alleles at separate loci are independent. In other words, conditional on population membership, the sum S of “1” alleles is the sum of k independent Bernoulli trials—a binomial random variable. For population A, (S|M = A)~ Binomial(k, p), and in population B, (S|M = B)~ Binomial(k, q). Because q > p and q = 1 − p, we set a rule that if S < k/2, then the individual is assigned to population A, and if S > k/2, then the individual is assigned to population B. If S = k/2, then the individual is assigned to population A or B randomly with probability 1/2 for each population. We represent the event that an individual is misclassified on the basis of S with the random variable W_S. If the individual is misclassified, then W_S = 1, and W_S = 0 otherwise.

Following our classification rule, for odd k, the probability that an individual from population B is misclassified into population A is the probability that S < k/2:

$$P(W_S=1\mid M=B)=P(S<k/2\mid M=B)=\sum _{i=0}^{(k-1)/2}\left(\begin{array}{c}k\\ i\end{array}\right)q^i{p}^{k-i}.$$ (2)

For even k, we modify the expression slightly to accommodate the possibility that S = k/2, in which case misclassification occurs with probability 1/2:

$$P(W_S=1\mid M=B)=\frac{1}{2}\left(\begin{array}{c}k\\ k/2\end{array}\right)p^{k/2}{q}^{k/2}+\sum _{i=0}^{k/2-1}\left(\begin{array}{c}k\\ i\end{array}\right)q^i{p}^{k-i}.$$ (3)

Because we have assumed that p = 1 − q, the misclassification probability is the same irrespective of the population from which the individual is drawn, so we can drop the condition on population membership. Moreover, we show in Appendix A that Eq. 2 evaluated at k = 2h + 1, where h is a non-negative integer, is equal to Eq. 3 evaluated at k = 2h + 2. Applying this identity yields an expression for P(W_S = 1) for both odd and even k:

$$P(W_S=1)=\sum _{i=0}^{\lfloor (k-1)/2\rfloor }\left(\begin{array}{c}2\lceil k/2\rceil -1\\ i\end{array}\right)q^i{p}^{2\lceil k/2\rceil -1-i}.$$ (4)

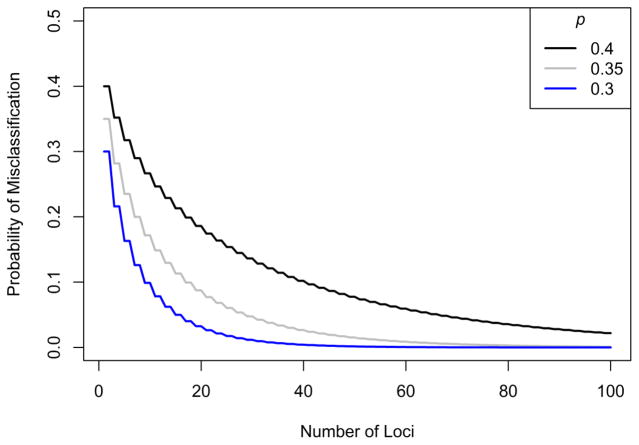
Figure 1 shows the decline in misclassification rates for several values of p, illustrating that the misclassification probability decreases as the number of loci used for classification grows.

Figure 1.

Under the Edwards model, the misclassification rate approaches zero as the number of loci increases, as long as the two source populations differ in their allele frequencies. Misclassification rates are computed from Eq. 4. A similar figure appears in Edwards (2003).

To better understand why the misclassification rate falls as the number of loci increases, we can approximate the distribution of S in each population. By the central limit theorem, as k increases, the distribution of the binomial random variable S in each population approaches a normal distribution. Using the properties of binomial random variables, the expected sum is E(S|M = A) = kp for an individual from population A and E(S|M = B) = kq for an individual from population B. The variance of the sum in each group is Var(S|M) = kpq, and the standard deviation is $\sqrt{\mathit{kpq}}$.

Under the normal approximation, discarding the (1/2)P(S = k/2) term, which is negligible for large k, the probability of misclassifying an individual from population A into population B is the probability that S > k/2. For individuals from population A, the difference between k/2 and the expected value of S in units of the standard deviation of S is

$$\frac{k/2-kp}{\sqrt{\mathit{kpq}}}=\sqrt{k}\frac{q-p}{2\sqrt{pq}}.$$

Eq. 4 is then approximated by

$$P(W_S=1)\approx 1-\mathit{\Phi }\left(\sqrt{k}\frac{q-p}{2\sqrt{pq}}\right),$$ (5)

where Φ is the cumulative distribution function for the standard normal distribution. Φ increases to 1 monotonically as its argument approaches infinity. In fact, the argument need not be too large for Φ to take values close to 1. Φ(c) is the probability that a normal random variable is more than c standard deviations above its expectation. Normal random variables are unlikely to be more than 3 standard deviations above their expectation, Φ(3) ≈ 1 − 10⁻³, and they are less likely still to fall more than 6 standard deviations above their expectation, Φ(6) ≈ 1 − 10⁻⁹. In our case, the argument of Φ grows with $\sqrt{k}$—for example, with p = 0.35, setting k = 90 gives a misclassification rate P(W_S = 1) ≈ 10⁻³, and setting k = 360 gives P(W_S = 1) ≈ 10⁻⁹. As the number of loci k grows large, the misclassification rate approaches 0.

The Edwards model demonstrates that as long as there is a nonzero difference in populations’ allele frequencies and there are enough conditionally independent loci on which to base the classification, it is possible to classify individuals into populations with arbitrarily high accuracy.

3. Adding a quantitative trait

Next, consider a quantitative trait that is completely determined by the alleles at k loci that have the properties described above. The trait is not influenced by variation in the environment, by gene-environment interaction, by gene-gene interaction, or by epigenetic effects. In quantitative genetics terms, its narrow-sense heritability is 1. We assume that each of the k loci contributes equally to the trait. Specifically, at each locus, we label one allele “+” and the other “−”, where we have not yet specified whether the “+” allele is allele “0” or allele “1.” Because each individual’s value for the trait—which we model as the random variable T—is determined entirely by the equal additive effects of the k loci, T is equal to the number of “+” alleles that the individual carries. That is,

$$T=\sum _{i=1}^k{V}_i,$$ (6)

where V_i = 1 if the individual carries a “+” allele at the ith locus and V_i = 0 otherwise. In other words, whereas we counted the number of “1” alleles to build the random variable S—which was useful for classifying individuals into populations—we now count “+” alleles to construct T, which gives the value of a quantitative trait.

Each of our k loci has two alleles, and each allele now has two labels. One label carries information about population membership: as described in Section 2, the allele that is more common in population A is labeled “0”, and the allele that is more common in population B is labeled “1”. The other label tells us about a trait—the allele that leads to larger values of the trait is labeled “+”, and the allele that leads to smaller values of the trait is labeled “−”. We assume that whether an allele is labeled “1” (or “0”) is independent of whether it is labeled “+” (or “−”). Thus, the allele that is more common in population A is as likely to be associated with larger values of the trait as it is to be associated with smaller values. This choice amounts to an assumption that the trait has been selectively neutral during the divergence of populations A and B, that the allele frequencies in the two populations have reached their current status without any influence of the effect of the loci on the trait. We can express the point with the random variable X_i, which equals 0 if the “0” allele is the “+” allele at the ith locus and 1 if the “1” allele is the “+” allele at the ith locus. For each of the k loci, P(X_i = 0) = P(X_i = 1) = 1/2, independently of the other loci. We denote the sum of the X_i as Z,

$$Z=\sum _{i=1}^k{X}_i.$$ (7)

Because each X_i is a Bernoulli random variable with success probability 1/2 and is independent of the other X_i, Z is binomially distributed with k trials and success probability 1/2.

The X_i and the individual’s values for the L_i determine the individual’s values for the V_i, and thus for T. That is, if we know the individual’s set of “0” and “1” alleles and we know which alleles are the “+” alleles, then we can calculate the individual’s value for the trait. In particular,

$$V_i=L_i+(1-2L_i)(1-X_i).$$ (8)

Thus, if L_i = X_i, then V_i = 1, and if L_i ≠ X_i, then V_i = 0. Because T is the sum of the V_i (Eq. 6), we can rewrite $T={\sum }_{i=1}^k{L}_i+(1-2L_i)(1-X_i)$. The relationships between L, X, and V appear in Table 2. Figure 2 shows a schematic of one realization of our model.

Table 2.

The relationships between the random variables L, X, and V.

Situation	L	X	V
Allele is more common in population A and produces smaller T	0	1	0
Allele is more common in population A and produces larger T	0	0	1
Allele is more common in population B and produces smaller T	1	0	0
Allele is more common in population B and produces larger T	1	1	1

Note. L indicates an allele, either 0 or 1. X represents the randomized labeling of the alleles, indicating whether having L = 1 contributes to larger (X = 1) or smaller (X = 0) values of the trait. V indicates whether the individual’s allele contributes to larger (V = 1) or smaller (V = 1) values of the trait. Any one of these variables can be constructed from the other two—if the other two variables have the same value, then the third variable equals 1; otherwise it equals 0.

Figure 2.

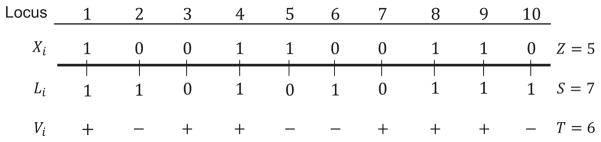
A schematic of one realization of our quantitative trait model with 10 loci. For a given trait, loci are labeled according to whether the “1” or the “0” allele is the “+” allele. These labels are the X_i, and their sum is Z. The X_i are independent Bernoulli random variables with probability 1/2, so Z is a binomial random variable. For every individual, we draw alleles at each locus according to the allele frequencies in the individual’s population—these are the L_i, and their sum is S. The L_i are independent Bernoulli random variables with probability p in population A and q in population B, so S is also binomial in each population. If X_i = L_i, then the individual has a “+” allele at the ith locus (V_i = 1). The number of “+” alleles for an individual is the trait value, T.

4. Properties of the quantitative trait conditional on the labeling of the alleles

We can use this quantitative trait model to study the distribution of group differences for traits. In particular, we can ask how the distribution depends on k. If a trait is highly polygenic, are the populations more likely to differ considerably on the trait than if the trait is determined by a single locus?

Our model contains two randomizations. The first randomization, which we call “labeling,” determines which allele at each locus contributes to larger values of the trait. As mentioned above, independently at each locus, either the “0” or the “1” allele is randomly labeled “+”. Labeling happens once per trait.

In the second randomization, we generate individuals from each population by randomly choosing alleles at each locus according to the allele frequencies in the individual’s population. For example, an individual from population A is generated by drawing “1” alleles with probability p and “0” alleles with probability q, independently at each locus.

We first study properties of the trait conditional on labeling—that is, we study the second randomization conditional on the outcome of the first randomization. More specifically, we examine the distribution, expectation, and variance of the trait value T of an individual, and the misclassification probability of an individual on the basis of T, all conditional on the labels of the alleles being known. These computations tell us how the groups differ on a specific trait with known allelic labels. Later, in Section 5, to learn about how the group differences vary across traits, we study the ways in which these expressions vary across different labelings.

4.1. Distribution of T in each population given the labeling of the alleles

We start by considering the distribution of the trait value T in population A given the labeling. That is, we seek P(T = t|M = A, {X₁, …, X_k} = {x₁, …, x_k}), where T is the sum of the V_i (Eq. 6). Applying Eq. 8 and conditioning on X_i gives either V_i = 1 − L_i if X_i = 0 or V_i = L_i if X_i = 1. Because the L_i are independent and identically distributed in each population, the order of the x_i does not affect the computation. Thus, we can forgo conditioning on the X_i and simply condition on their sum, Z (Eq. 7). For ease of representation, if Z = z, then we order the x_i so that the first z entries are equal to 1 and the remaining k − z entries are equal to 0.

Given that Z = z, we can rewrite T|M, Z as

$$(T\mid M=A,Z=z)=\sum _{i=1}^z(L_i\mid M=A,Z=z)+\sum _{i=z+1}^k[1-(L_i\mid M=A,Z=z)].$$ (9)

We denote the two sums on the right, with the subscript indicating the population (A or B) and the value of X_i for the corresponding values of L_i being summed (1 or 0), by

$$T_{A1}=\sum _{i=1}^z(L_i\mid M=A,Z=z)$$ (10)

$$T_{A0}=\sum _{i=z+1}^k[1-(L_i\mid M=A,Z=z)].$$ (11)

In population A, the first z of the V_i are independent Bernoulli random variables with parameter p. Thus, T_A1~Binomial(z, p). Similarly, T_A0~Binomial(k − z, q).

Viewing T as the sum of two binomial distributions leads to distributions, expectations, and variances of T within each population. Conditional on Z = z and membership in population A, the probability that an individual has T = t is

$$P(T=t\mid M=A,Z=z)=\sum _{l=0}^t\left(\begin{array}{c}z\\ l\end{array}\right)p^l{q}^{z-l}\left(\begin{array}{c}k-z\\ t-l\end{array}\right)p^{k-z-t+l}{q}^{t-l}.$$ (12)

This expression sums the probabilities of the ways that t “+” alleles can be drawn from the z loci for which the “1” allele is the “+” allele and the k − z loci for which the “0” allele is the “+” allele. A useful alternative statement of Eq. 12 is

$$P(T=t\mid M=A,Z=z)=p^{k-z}{q}^z\sum _{l=0}^t\left(\begin{array}{c}z\\ l\end{array}\right)\left(\begin{array}{c}k-z\\ t-l\end{array}\right){\left(\frac{p}{q}\right)}^{2l-t}.$$ (13)

Similarly, transposing the roles of p and q, in population B,

$$P(T=t\mid M=B,Z=z)=p^z{q}^{k-z}\sum _{l=0}^t\left(\begin{array}{c}z\\ l\end{array}\right)\left(\begin{array}{c}k-z\\ t-l\end{array}\right){\left(\frac{q}{p}\right)}^{2l-t}.$$ (14)

Before considering the expectation and variance of T in each population, we need three more facts about the distribution of T in populations A and B (eqs. 15–17). Analogously to Eqs. 9–11, in population B, T can be viewed as the sum T_B1 + T_B0, where T_B1~Binomial(z, q) and T_B0~Binomial(k − z, p). Thus, T_B1 has the same distribution as z − T_A1, and T_B0 has the same distribution as k − z − T_A0. Then T_B0 + T_B1 has the same distribution as k − (T_A0 + T_A1), meaning that

$$P(T=t\mid M=B,Z=z)=P(T=k-t\mid M=A,Z=z).$$ (15)

If Z = k/2, then T_A0~Binomial(k/2, p) and T_A1~Binomial(k/2, q). Similarly, T_B0~Binomial(k/2, q) and T_B1~Binomial(k/2, p). Thus, in both populations, T is the sum of two independent binomial random variables with k/2 trials, one with probability p and one with probability q. The distribution of T is therefore the same in the two populations if Z = k/2:

$$P(T=t\mid M=A,Z=k/2)=P(T=t\mid M=B,Z=k/2).$$ (16)

In combination, Eqs. 15 and 16 guarantee that if z = k/2, then the conditional probability mass function in each population is symmetric around k/2. That is,

$$\begin{array}{l}P(T=t\mid M=A,Z=k/2)=P(T=k-t\mid M=A,Z=k/2)\\ P(T=t\mid M=B,Z=k/2)=P(T=k-t\mid M=B,Z=k/2).\end{array}$$ (17)

The symmetries in Eqs. 15–17 result from our assumption that q = 1 − p, and they assist in our analysis of misclassification rates obtained when using T for classification.

4.2 Expectation and variance of T in each population given the labeling of the alleles

The expectation of T in population A conditional on Z is the sum of the expectations of T_A1 and T_A0 (Eqs. 10, 11), which follow from their status as binomial random variables:

$$E(T\mid M=A,Z=z)=E(T_{A1})+E(T_{A0})=zp+(k-z)q=kq+(p-q)z.$$ (18)

In population B, the expectation of T is

$$E(T\mid M=B,Z=z)=kp+(q-p)z.$$ (19)

Because T_A1 and T_A0 are independent,

$$\mathit{Var}(T\mid M=A,Z=z)=\mathit{Var}(T_{A1})+\mathit{Var}(T_{A0})=\mathit{zpq}+(k-z)pq=\mathit{kpq}.$$

Similarly, Var(T|M = B, Z = z) = kpq. Noticing that z does not appear in the expression, we can remove the condition on Z. The variance ${\sigma }_w^2$ of T in either population is

$${\sigma }_w^2=\mathit{Var}(T\mid M)=\mathit{kpq}.$$ (20)

One convenient summary of the extent to which the two populations differ on the trait is the standardized group difference, D_T. This quantity is the difference between the trait means in the two populations divided by the within-population standard deviation. Conditional on Z = z,

$$\begin{array}{l}(D_T\mid Z=z)=\frac{E(T\mid M=A,Z=z)-E(T\mid M=B,Z=z)}{{\sigma }_w}\\ =\frac{(q-p)(k-2z)}{\sqrt{\mathit{kpq}}}.\end{array}$$ (21)

D_T is an instance of Cohen’s d (Cohen, 1988), a measurement of effect size and a special case of the Mahalanobis distance (Mahalanobis, 1936). Its absolute value is the number of within-population standard deviations separating the population means. For fixed k and z, the value of D_T decreases as p increases from 0 to 1/2, so that D_T is larger for populations with a greater allele frequency difference q − p.

4.3 The total expectation and variance of T given the labeling of the alleles

The expectation of T, removing the condition on population membership, is

$$E(T\mid Z=z)=E_M[E(T\mid M,Z=z)],$$

where the subscript M indicates that the expectation is with respect to randomness in population membership. Each individual has a probability of 1/2 of being from either population. Thus,

$$E(T\mid Z=z)=\frac{E(T\mid M=A,Z=z)}{2}+\frac{E(T\mid M=B,Z=z)}{2}.$$

Using Eqs. 18 and 19 and remembering that p + q = 1 gives

$$E(T\mid Z=z)=\frac{kq+(p-q)z+kp+(q-p)z}{2}=\frac{k}{2}.$$ (22)

This expression does not depend on z, so E(T) = k/2 for all Z.

By the law of total variance, the variance in T can be decomposed into within- and between-population components:

$$\mathit{Var}(T\mid Z=z)=E_M[\mathit{Var}(T\mid M,Z=z)]+{\mathit{Var}}_M[E(T\mid M,Z=z)].$$ (23)

We already have the first term: Var(T|M, Z = z) = kpq (Eq. 20), and because the conditional variance is constant across populations, E_M[Var(T|M, Z = z)] = kpq.

The second term in Eq. 23 is the “between-population” variance of T. Note that

$$E(T\mid M,Z=z)=E(T\mid M=A,Z=z)+[E(T\mid M=B,Z=z)-E(T\mid M=A,Z=z)]I_{M=B},$$

where I_M=B =1 if an individual is in population B and I_M=B = 0 otherwise. Conditional on Z, the only random variable in this expression is I_M=B. I_M=B~Bernoulli(1/2), so Var(I_M=B) = 1/4. Using Eqs. 18 and 19, the between-population variance of T, which we term ${\sigma }_b^2$, is

$$\begin{array}{l}{\sigma }_b^2={\mathit{Var}}_M[E(T\mid M,Z=z)]\\ ={[E(T\mid M=B,Z=z)-E(T\mid M=A,Z=z)]}^2/4\\ ={(k-2z)}^2(1-4pq/4,)\end{array}$$ (24)

and the total variance of T conditional on the labeling of the alleles is then

$$\mathit{Var}(T\mid Z=z)=\mathit{kpq}+{(k-2z)}^2(1-4pq)/4.$$ (25)

In quantitative genetics, Q_ST is a conceptual analogue of F_ST for a quantitative trait. For haploids, it is the proportion of heritable variance in a quantitative trait attributable to genetic differences between populations (Whitlock, 2008). In our case, all the variance of T is heritable, so conditional on Z, we define Q_ST as

$$(Q_{ST}\mid Z=z)=\frac{{\sigma }_b^2}{{\sigma }_w^2+{\sigma }_b^2}=\frac{{[(k-2z)(q-p)]}^2/4}{\mathit{kpq}+{[(k-2z)(q-p)]}^2/4}.$$ (26)

4.4 Probability of misclassification using T given the labeling of the alleles

We represent the event that an individual is misclassified on the basis of its trait value T with the random variable W_T, which equals 1 if the individual is misclassified and 0 otherwise. The probability of misclassifying an individual on the basis of T is thus P(W_T = 1).

We set a classification rule for the trait value T analogous to the rule used for the genotypic statistic S in Section 2. In particular, we classify each individual into the population to whose trait mean the individual’s trait value T is closest. Thus, conditional on Z = z, we classify the individual into population A if

$$\mid T-E(T\mid M=A,Z=z)\mid <\mid T-E(T\mid M=B,Z=z)\mid ,$$ (27)

and into population B if

$$\mid T-E(T\mid M=A,Z=z)\mid >\mid T-E(T\mid M=B,Z=z)\mid .$$ (28)

We randomly classify the individual into either population A or population B, with probability 1/2 for each population, if

$$\mid T-E(T\mid M=A,Z=z)\mid =\mid T-E(T\mid M=B,Z=z)\mid .$$ (29)

We use the properties of the conditional expectation of T to translate this rule into a statement about the distribution of T. By Eq. 22, the two population means of T are symmetric around k/2. Thus, we can translate Eqs. 27–29 into statements about the relationship of T to k/2. In particular, because we assume that p < q, Eqs. 18 and 19 show that if z < k/2, then T > k/2 satisfies Eq. 27, and we classify the individual into population A; T < k/2 satisfies Eq. 28, and we classify the individual into population B; and T = k/2 satisfies Eq. 29, and we randomly classify into either population with probability 1/2. Thus, for z < k/2, the probability of misclassifying an individual from population A into population B is

$$P(W_T=1\mid M=A,Z=z)=P(T<k/2\mid M=A,Z=z)+\frac{1}{2}P(T=k/2\mid M=A,Z=z).$$ (30)

Using the distribution of T in population A (Eq. 13), we have

$$P(W_T=1\mid M=A,Z=z)=\frac{1}{2}\gamma +p^{k-z}{q}^z\sum _{t=0}^{\lceil k/2-1\rceil }\sum _{l=0}^t\left(\begin{array}{c}z\\ l\end{array}\right)\left(\begin{array}{c}k-z\\ t-l\end{array}\right){\left(\frac{p}{q}\right)}^{2l-t},$$ (31)

where γ = P(T = k/2|Z = z) is 0 if k is odd and $p^{k-z}{q}^z{\sum }_{l=0}^{k/2}\left(\begin{array}{c}z\\ l\end{array}\right)\left(\begin{array}{c}k-z\\ k/2-l\end{array}\right){\left(\frac{p}{q}\right)}^{2l-k/2}$ if k is even.

Retaining the assumption that z < k/2, the probability of misclassifying an individual from population B into population A is

$$P(W_T=1\mid M=B,Z=z)=P(T>k/2\mid M=B,Z=z)+\frac{1}{2}P(T=k/2\mid M=B,Z=z).$$ (32)

Because the probability mass function of T in population B is the reflection across k/2 of the probability mass function of T in population A (Eq. 15), the right sides of Eqs. 30 and 32 are equal. Thus, we can use Eq. 31 to calculate the probability of misclassifying an individual from population B on the basis of its trait value when z < k/2.

For z > k/2, applying similar reasoning, the misclassification probability in either population is given by switching the roles of z and k − z in Eq. 31. If z = k/2, then Eq. 31 continues to provide the correct probability of misclassification. Eq. 29 is satisfied for all T if z = k/2, so the misclassification probability is P(W_T = 1|M = A, Z = k/2) = P(W_T = 1|M = B, Z = k/2) = 1/2. To see that Eq. 31 is equal to 1/2 if z = k/2, notice that by the definition of a probability mass function,

$$\begin{array}{l}P(T<k/2\mid M=A,Z=k/2)+P(T=k/2\mid M=A,Z=k/2)+P(T>k/2\mid M=A,Z=k/2)\\ =1.\end{array}$$

By Eq. 17, we can substitute P(T < k/2|M = A, Z = k/2) = P(T > k/2|M = A, Z = k/2) to give 2P(T < k/2|M = A, Z = k/2) + P(T = k/2|M = A, Z = k/2) = 1. Dividing both sides by 2 shows that Eq. 30 is equal to 1/2 if z = k/2. In turn, Eq. 31 is equal to Eq. 30.

We can modify Eq. 31 by replacing z with min(z, k − z}and k − z with max(z, k − z} to get the misclassification probability given Z = z in either population, for any z:

$$P(W_T=1\mid Z=z)=\frac{1}{2}\gamma +p^{max\{z,k-z\}}{q}^{min\{z,k-z\}}\sum _{t=0}^{\lceil k/2-1\rceil }\sum _{l=0}^t\left(\begin{array}{c}min\{z,k-z\}\\ l\end{array}\right)\left(\begin{array}{c}max\{z,k-z\}\\ t-l\end{array}\right){\left(\frac{p}{q}\right)}^{2l-t}.$$ (33)

As we did with P(W_S = 1) (Eq. 5), we can approximate P(W_T = 1|Z = z) using a normal distribution. In population A, if k is large, then T is approximately normal with expectation zp + (k − z)q and variance kpq (Deheuvels et al., 1989, theorem 1.1). The probability of observing a value of T leading to a misclassification—that is, of observing T < k/2 if z < k/2 or T > k/2 if z > k/2—is approximated by

$$P(W_T=1\mid Z=z)\approx 1-\mathit{\Phi }\left[\frac{\mid k-2z\mid (q-p)}{2\sqrt{\mathit{kpq}}}\right].$$ (34)

Because the standard normal cumulative distribution function Φ increases monotonically, the approximation of P(W_T = 1|Z = z) decreases monotonically as z approaches k/2 from either direction. Holding p, q, and k constant, it achieves its upper bound in z if z = k/2 and P(W_T = 1|Z = z) ≈ 1/2. It achieves its lower bound when z = 0 or z = k and P(W_T = 1|Z = z) is approximated by the same expression that approximates P(W_S = 1) (Eq. 5). The approximate misclassification probability is lowest if the k loci all have the same labeling, so that loci with opposite labelings do not “undo” each other’s contributions to separating the populations. In Appendix B, we prove analogous results for the exact misclassification probability.

5. Properties of T across different labelings of the alleles

Conditional on the labelings of the alleles {X₁, X₂, …, X_k}, we have obtained the conditional expectation and variance of T given group membership, the expectation and variance of T in the absence of information on group membership, and the probability of misclassifying an individual on the basis of T. We defined two summaries of group difference—D_T, the standardized difference in group mean trait values (Eq. 21), and Q_ST, the quantitative-trait analogue of F_ST (Eq. 26). The overall expectation of T and the variance of T in each population were constant across labelings of the alleles, and the conditional expectation of T given population membership (Eqs. 18, 19), the variance of T (Eq. 25), D_T (Eq. 21), and Q_ST (Eq. 26) depended only on $Z={\sum }_{i=1}^k{X}_i$, the number of “1” alleles that are labeled as “+” alleles.

In this section, we consider how group differences in the trait vary across labelings of the alleles. That is, we consider the distributions of D_T, Q_ST, and the misclassification rate across different traits T, which can have different values of Z. We address three questions. First, how does D_T change as k, the number of loci that influence the trait, increases? Second, what is the expected proportion of variance in the trait that is accounted for by genetic differences between the populations—that is, what is E(Q_ST)? Third, does the trait become increasingly useful for classification as the number of loci grows, as the genotypic statistic S did?

5.1. Question 1: How does the standardized difference D_T change as k, the number of loci that influence the trait, increases?

Eq. 21 gives the standardized difference D_T conditional on Z = z. Removing the condition on Z gives the random variable

$$D_T=\frac{E(T\mid M=A)-E(T\mid M=B)}{{\sigma }_w}=\frac{(q-p)(k-2Z)}{\sqrt{\mathit{kpq}}}.$$ (35)

D_T is linear in Z. Recall that Z~Binomial(k, 1/2), so E(Z) = k/2 and Var(Z) = k/4. Thus,

$$E(D_T)=0$$ (36)

$$\mathit{Var}(D_T)=\frac{4{(q-p)}^2}{\mathit{kpq}}\mathit{Var}(Z)=\frac{1-4pq}{pq}.$$ (37)

Because E(D_T) = 0,

$$E(D_T^2)=\mathit{Var}(D_T)=\frac{1-4pq}{pq}.$$ (38)

The distribution of D_T across traits comes from solving Eq. 35 for Z, remembering that Z~Binomial(k, 1/2):

$$P(D_T=d)=\frac{1}{2^k}\left(\begin{array}{c}k\\ \frac{k}{2}-\frac{d\sqrt{\mathit{kpq}}}{2(q-p)}\end{array}\right).$$ (39)

Because Z takes values in (0, 1, 2, …, k), D_T takes values in

$$\left\{\frac{-k(q-p)}{\sqrt{\mathit{kpq}}},\frac{(-k+2)(q-p)}{\sqrt{\mathit{kpq}}},\frac{(-k+4)(q-p)}{\sqrt{\mathit{kpq}}},\dots ,\frac{k(q-p)}{\sqrt{\mathit{kpq}}}\right\}.$$

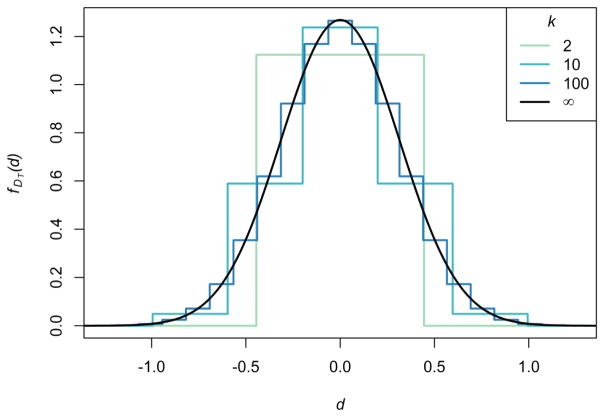
The distribution of D_T is symmetric around 0 because the distribution of Z is symmetric around k/2. Applying the central limit theorem, for large k, the distribution of D_T is approximated by a normal distribution with expectation 0 (Eq. 36) and variance (1 − 4pq)/(pq) (Eq. 37). Figure 3 shows the distribution of D_T for p = 0.35 and several values of k. As seen in the figure, increasing k increases the smoothness of the distribution of D_T and makes larger values of D_T possible, but it does not change the location or spread of the distribution.

Figure 3.

The distribution of the standardized mean group difference D_T for a trait additively determined by k biallelic loci of equal effect. Here, p = 0.35. As the number of loci grows, the distribution approaches a normal distribution with expectation 0 and variance (1 − 4pq)/(pq). The expectation and variance of D_T do not change with k (Eqs. 36, 37). The plot was produced using histograms of the probabilities in Eq. 39, scaled to have total area 1.

What can we conclude from these results? First, the expectation of the difference in population trait means, E(D_T), is zero (Eq. 36). This result reflects the symmetry of the distribution of Z, which, in combination with Eqs. 18 and 19, implies that for a randomly chosen trait, the larger mean value of T is as likely to come from population A as it is to come from population B.

Second, the variance across traits of the standardized mean difference between populations, Var(D_T), does not depend on the number of loci that determine the trait (Eq. 37). If the variance of D_T grew with k, then the probability of observing large absolute values of D_T would also grow with k. Instead, by the central limit theorem, as k increases, the probability of observing absolute values of D_T larger than a positive constant C approaches $P(\mid D_T\mid >C)\approx 2\mathit{\Phi }[-C\sqrt{pq}/(q-p)]$. This value does not depend on k.

Finally, we note that $E(D_T^2)$ is equal to the squared standardized difference in allelic values at a single locus, a quantity we define analogously to D_T (Eq. 21) as

$$D_L=\frac{E(L\mid M=A)-E(L\mid M=B)}{\sqrt{\mathit{Var}(L\mid M)}}.$$

Recall that L is a Bernoulli random variable with probability p in population A and probability q in population B. Plugging in E(L|M = A) = p, E(L|M = B) = q, and $\sqrt{\mathit{Var}(L\mid M)}=\sqrt{pq}$ gives

$$D_L=\frac{p-q}{\sqrt{pq}},$$

and squaring gives

$$D_L^2=\frac{1-4pq}{pq}=E(D_T^2),$$

where $E(D_T^2)$ comes from Eq. 38. Thus, the average squared standardized difference in the population means for the trait, $E(D_T^2)$, is the same as the squared standardized genetic difference between the populations at a single genetic locus, $D_L^2$, regardless of how many loci determine the trait. One answer to question 1, then, is that the expected absolute size of the standardized difference in the two populations’ trait means does not grow as the number of loci influencing the trait increases.

5.2. Question 2: What is the expected proportion of variance in the trait that is accounted for by genetic differences between the populations?

In Eq. 26, we defined Q_ST conditional on Z = z, where Q_ST is, for haploids, the proportion of heritable variance in the trait attributable to genetic differences between the populations. Removing the condition on Z in Eq. 26 gives the random variable

$$Q_{ST}=\frac{{\sigma }_b^2}{{\sigma }_w^2+{\sigma }_b^2}=\frac{{(k-2Z)}^2(1-4pq)/4}{\mathit{kpq}+{(k-2Z)}^2(1-4pq/4)}.$$ (40)

Because $P(Z=z)=\left(\begin{array}{c}k\\ z\end{array}\right)/2^k$, the expectation across traits of Q_ST is

$$E(Q_{ST})=\frac{1}{2^k}\sum _{z=0}^k\frac{{(k-2z)}^2(1-4pq)/4}{\mathit{kpq}+{(k-2z)}^2(1-4pq)/4}\left(\begin{array}{c}k\\ z\end{array}\right).$$ (41)

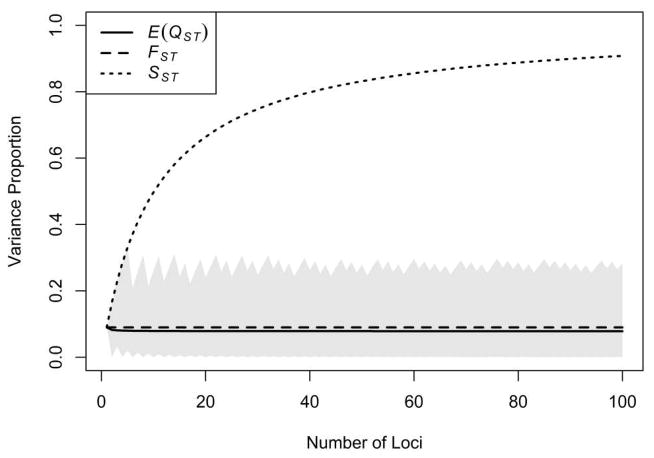
Figure 4 shows E(Q_ST) for p = 0.35 and k ranging from 1 to 100. As seen in the figure, the expected value of Q_ST is nearly constant in k.

Figure 4.

The proportion of variance that is “between groups” in a typical neutral trait, in allelic values at a single locus, and in the genotypic statistic S designed for classification. Here, p = 0.35. Q_ST is the proportion of variance of a neutral trait attributable to differences between groups (Eq. 40). Q_ST varies for different traits according the labeling of alleles, and E(Q_ST) is the expectation of Q_ST across traits (Eq. 41). F_ST is the proportion of allelic variance at a single locus attributable to differences between groups (Eq. 1). We define S_ST analogously to Q_ST and F_ST as the proportion of variance in S, the sum of “1” alleles, attributable to differences between populations: S_ST = Var[E_M(S|M)}/Var(S) = k(1 − 4pq)/[4pq + k(1 − 4pq)]. As the number of loci increases, this quantity grows to 1. By contrast, E(Q_ST) is approximately the same as F_ST, regardless of how many loci influence the trait. Because Q_ST is increasing in |Z − k/2| (Eq. 40), we can obtain quantiles of Q_ST across traits by plugging the corresponding quantiles of the distribution of |Z − k/2| (Eq. B.15) into Eq. 40. The gray region, representing variability in Q_ST, extends from the 5^th to the 95^th percentile.

To obtain more insight into the behavior of Q_ST across different traits, we approximate E(Q_ST) by replacing (k − 2Z)²(1 − 4pq)/4 in Eq. 40 with its expectation. This replacement is justified as a first-order Taylor approximation. If we define a random variable Y = (k − 2Z)²(1 − 4pq)/4, then by Eq. 40,

$$Q_{ST}=\frac{Y}{\mathit{kpq}+Y}=g(Y).$$

Defining μ_Y = E(Y), a first-order Taylor series expansion then gives

$$Q_{ST}=g(Y)\approx g({\mu }_Y)+g^{\prime }({\mu }_Y)(Y-{\mu }_Y),$$

and applying the expectation operator gives

$$E(Q_{ST})=E[g(Y)]\approx g({\mu }_Y)+g^{\prime }({\mu }_Y)E(Y-{\mu }_Y)=g({\mu }_Y).$$

By Eq. 35, ${(k-2Z)}^2(1-4pq)/4=\mathit{kpq}{D}_T^2/4$. By Eq. 38, $E(D_T^2)=(1-4pq)/(pq)$. Therefore,

$$E(Q_{ST})\approx \frac{k(1-4pq)/4}{k(1-4pq)/4+\mathit{kpq}}=1-4pq.$$ (42)

Because Q_ST is a concave function of Y, it follows from Jensen’s inequality—which holds that for a concave function g and a random variable X, E[g(X)] ≤ g[E(X)]—that E(Q_ST) ≤ 1 − 4pq. Thus, the approximation in Eq. 42 is an upper bound on E(Q_ST). In the Edwards model, the proportion of variance in allelic types attributable to differences between the populations, or F_ST, is also 1 − 4pq (Eq. 1), so we have

$$E(Q_{ST})\le F_{ST}.$$ (43)

These results support the idea that for a neutral trait, Q_ST ≈ F_ST, regardless of how many neutral loci influence the trait. The answer to question 2, then, is that we expect the proportion of the variance of a neutral trait attributable to between-population differences to be about the same as the proportion of the allelic variance at a single locus that is attributable to between-population differences.

5.3 Question 3: Does the trait become increasingly useful for classification as the number of loci grows?

We saw that using genotypic data, it is possible to pool information across genetic loci to classify accurately. Can the information about ancestry contained in a large collection of loci be extracted from a neutral trait they influence? To answer this question, we consider the expected misclassification rate across traits influenced by k loci.

The expected misclassification rate across traits is

$$E[P(W_T=1)]=\frac{1}{2^k}\sum _{z=0}^{k}P(W_T=1\mid Z=z)\left(\begin{array}{c}k\\ z\end{array}\right).$$ (44)

Plugging in the expression for P(W_T = 1|Z = z) from Eq. 33 gives

$$E[P(W_T=1)]=\frac{1}{2^k}\sum _{z=0}^k\left(\begin{array}{c}k\\ z\end{array}\right)\left[\frac{1}{2}\gamma +p^{max\{z,k-z\}}{q}^{min\{z,k-z\}}\sum _{t=0}^{\lceil k/2-1\rceil }\sum _{l=0}^t\left(\begin{array}{c}min\{z,k-2\}\\ l\end{array}\right)\left(\begin{array}{c}max\{z,k-z\}\\ t-l\end{array}\right){\left(\frac{p}{q}\right)}^{2l-t}\right],$$ (45)

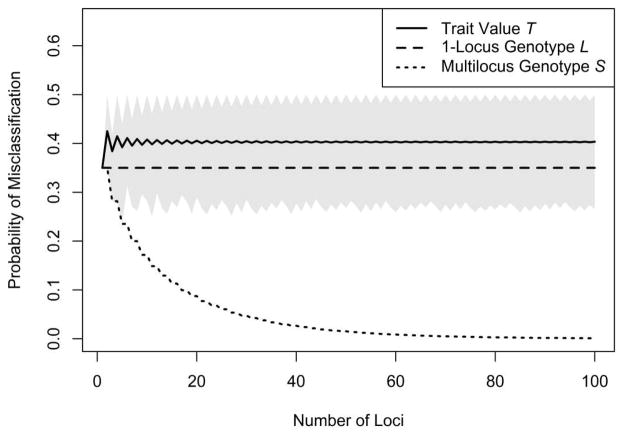
where γ = P(T = k/2|Z = z). Figure 5 shows the expected misclassification rate across traits when p = 0.35, with the misclassification rate obtained using S, the sum of the individual’s “1” alleles (Eq. 4), for comparison. In the figure, the expected misclassification rate obtained using T, the value of the neutral trait, does not systematically decrease as k increases.

Figure 5.

Expected misclassification rates obtained when using T, the individual’s value for a neutral trait (Eq. 45). These values are shown with misclassification rates obtained when using L, the individual’s genotype at a single locus (p), and S, the multilocus sum of the individual’s “1” alleles (Eq. 2). Here, p = 0.35. When one uses S to classify, the misclassification rate declines as the number of loci increases. When the neutral trait—constructed from the same alleles as S, but with different labelings—is used instead, the expected misclassification rate stays approximately the same as when a single genetic locus is used, regardless of how many loci influence the trait. Traits vary in classification accuracy depending on the labeling of alleles, and the gray region indicates this variability. Because the misclassification rate using T decreases monotonically with |Z − k/2| (Appendix B, Theorem 1), we can obtain quantiles of the distribution of the misclassification rate across traits by plugging values of z corresponding to quantiles of |Z − k/2| (Eq. B.15) into Eq. 33. The gray region extends from the 5^th to the 95^th percentile.

In Section 2, considering the genotypic statistic S, we showed that the normal approximation of the misclassification rate P(W_S = 1) (Eq. 5) approaches zero as k increases. We now show that in contrast, the normal approximation to the expected misclassification rate across traits E[P(W_T = 1)] is at least as large as the corresponding approximate misclassification rate from a single locus, regardless of the number of loci k that affect the trait.

For large k, the misclassification probability on the basis of the trait obeys

$$1-P(W_T=1)\approx \mathit{\Phi }\left[\frac{\mid k-2Z\mid (q-p)}{2\sqrt{\mathit{kpq}}}\right],$$

where Φ is the standard normal distribution function (Eq. 34, removing the condition on Z). Taking the expectation across traits of both sides gives

$$1-E[P(W_T=1)]\approx E\left(\mathit{\Phi }\left[\frac{\mid k-2Z\mid (q-p)}{2\sqrt{\mathit{kpq}}}\right]\right).$$

On the right side, the argument to Φ is nonnegative. Φ(x) is concave for x > 0 because for x > 0, the standard normal density Φ′(x) is strictly decreasing in x, implying that Φ″(x) < 0. Applying Jensen’s inequality gives

$$1-E[P(W_T=1)]\approx E\left(\mathit{\Phi }\left[\frac{\mid k-2Z\mid (q-p)}{2\sqrt{\mathit{kpq}}}\right]\right)\le \mathit{\Phi }\left[\frac{E(\mid k-2Z\mid )(q-p)}{2\sqrt{\mathit{kpq}}}\right].$$ (46)

E(|k − 2Z|) = 2E(|k/2 − Z|), twice the mean absolute deviation of Z. For all random variables, by Jensen’s inequality, the mean absolute deviation is no larger than the standard deviation. The standard deviation of Z is $\sqrt{k}/2$. Replacing E(|k − 2Z|) with $2\sqrt{\mathit{Var}(Z)}=\sqrt{k}$ therefore does not decrease the value on the right side of Eq. 46, and

$$1-E[P(W_T=1)]\approx E\left(\mathit{\Phi }\left[\frac{\mid k-2Z\mid (q-p)}{2\sqrt{\mathit{kpq}}}\right]\right)\le \mathit{\Phi }\left(\frac{q-p}{2\sqrt{pq}}\right).$$

The lower bound on the approximate expected misclassification rate is then

$$E[P(W_T=1)]\approx 1-E\left(\mathit{\Phi }\left[\frac{\mid k-2Z\mid (q-p)}{2\sqrt{\mathit{kpq}}}\right]\right)\ge 1-\mathit{\Phi }\left(\frac{q-p}{2\sqrt{pq}}\right).$$ (47)

The approximation of the expected trait-based misclassification rate is no smaller than the normal approximation of the genetic misclassification rate with one locus (Eq. 5). Thus, the answer to question 3 is that unlike the probability of misclassification obtained when using genotypes, the expected misclassification rate for a neutral trait does not decrease as k increases.

6. Discussion

Population-genetic studies have found that even if differences between populations are small at each locus, accurate classification of individuals into source populations is possible when many loci are considered. Our results extend an important model for the demonstration of this result by examining the distribution of population differences in quantitative traits. Specifically, we examined the situation in which the k loci of the Edwards model additively determine the value of a neutral trait. We found that such traits differ between populations to about the same degree as do individual genetic loci, in that the expected proportion of variance in the trait attributable to genetic differences between populations (Eq. 41) is approximately the same as, and no larger than, the single-locus proportion of allelic variance attributable to between-population differences (Eqs. 1, 42, 43). Unlike multilocus genotypes, multilocus neutral traits do not become more useful for classification as the number of underlying loci increases (Eq. 47). For accurate classification, many traits are required. These results (Table 3) emphasize that for neutral, genetically controlled traits, phenotypic-diversity partitioning typically reflects single-locus genetic-diversity partitioning.

Table 3.

Three questions about selectively neutral, polygenic phenotypes and their answers under the extended Edwards model.

Question	Answer	References
1: How does the standardized difference in population means for the trait (DT) change as k, the number of loci influencing the trait, increases?	As k grows, the typical absolute size of DT does not change, but the distribution of DT approaches normality.	Eq. 38, Figure 3.
2: What is the expected proportion of variance in the trait that is accounted for by genetic differences between the populations, E(QST)?	It is approximately equal to, and no larger than, the proportion of allelic variance at a single locus attributable to genetic differences, FST.	Eqs. 42, 43, Figure 4.
3: Does the trait become increasingly useful for classification as the number of loci grows?	No.	Eq. 46, Figure 5.

Why are the results for a selectively neutral quantitative trait so different from the results for multilocus genetic classification? The power of multilocus classification comes from the aggregation of information across loci—an individual from population A is more likely to have a “1” allele not just at one locus but at all of them. Small differences in allele frequency at each locus accumulate to separate the populations clearly. But when we assume that these differences determine a trait that has not been under selection, we impede the accumulation of information across loci. Suppose we have a single locus at which the allele that is more common in population A contributes to larger values of the trait. The influence of this locus on the trait gives us a hint about population membership; that hint, however, is likely to be masked by the influence of another locus at which the allele more common in population A reduces trait values.

Although we have used a simple haploid model, our results are similar to conclusions from other models with different assumptions. The result that the expected proportion of variance in a trait attributable to between-group differences is approximately the proportion of allelic variance attributable to between-group differences (Eqs. 1, 42) is related to previous work in population and quantitative genetics arguing that in several contexts, both haploid and diploid, Q_ST for selectively neutral traits is on average equal to F_ST (e.g. Felsenstein, 1973, 1986; Rogers & Harpending, 1983; Lande, 1992; Spitze, 1993; Lynch & Spitze, 1994; Whitlock, 1999; Berg & Coop, 2014). We use this close analogy between our analysis and previous work to discuss how relaxation of our model’s assumptions might affect our results.

In our model, the genetic architecture of the trait is additive, with no interactions between genes and no dominance. In the presence of dominance and epistasis—that is, gene-gene interaction—Q_ST tends to be somewhat smaller than F_ST (Whitlock, 2008). Thus, modifying our model by adding dominance and epistasis would not likely affect our main claim that the partition of neutral phenotypic diversity mirrors the single-locus partition of genetic diversity.

To keep our model simple, we considered haploids rather than diploids. For diploids, the analysis would proceed similarly, but because diploids have two alleles at each locus, comparable information for distinguishing populations is achieved in a diploid model with half as many loci as in a haploid model. A slightly modified expression for Q_ST in diploids takes this difference into account (Whitlock, 2008, Leinonen et al., 2013).

Another assumption is that the trait is entirely genetically determined. In our model, the environment either does not affect the trait, or individuals in a population live in identical environments, at least in relation to aspects of the environment that could affect the trait. If the trait is influenced by environmental variation, then environmental differences between populations can either cause or erase large group differences in the trait, regardless of genetic differentiation or selection history (Pujol et al., 2008).

Finally, we assumed that the trait has not been under selection. The behavior of Q_ST under divergent selection is a major source of interest in Q_ST. When a trait has been under divergent selection in groups under consideration—that is, when the selective pressure on the trait has varied in strength or direction across groups—Q_ST tends to exceed F_ST, and when the trait has been under uniform selection, Q_ST tends to be smaller than F_ST (Whitlock, 2008).

Considering the phenomena that affect Q_ST and F_ST can help us make sense of past work on human phenotypic variation. For example, in Relethford’s (2002) study of worldwide variation in craniometric traits and skin color, the proportion of variance in craniometric traits attributable to between-population differences was roughly equal to the proportion of allelic variance at a single locus attributable to between-population differences. This finding accords with the results for our extension of the Edwards model, and it is consistent with a hypothesis that selection on many craniometric traits has been weak or absent.

In the same groups studied by Relethford (2002), the proportion of variation in skin color attributable to between-population differences was much larger. When confronted by trait differences between groups that are much larger than genetic differences at typical loci, we have recourse to several possible explanations (Whitlock, 2008; Leinonen et al., 2013). First, the trait differences might stem from an unlikely realization of drift. Second, the trait differences might be due to environmental differences between the groups. Third, the trait differences might be due to differences in selection operating on the groups’ ancestors. Fourth, our measurements may be incorrect in a way that magnifies group differences. These possibilities are not mutually exclusive, nor are they exhaustive. Concluding definitively in favor of any of these explanations requires more investigation. For skin pigmentation, genetic evidence supports natural selection as part of the explanation of group differences (Berg & Coop, 2014).

The finding that genomic analyses enable ancestry inference has led many authors to consider the relevance of both single-locus genetic-diversity partitioning and multilocus classification for philosophical ideas of “race” (e.g. Glasgow, 2003; Andreasen, 2004; Kitcher, 2007; Gannett, 2010; Sesardic, 2010; Hardimon, 2012; Hochman, 2013; Kaplan & Winther, 2014; Spencer, 2014; Kopec, forthcoming; Ludwig, forthcoming; Donovan, forthcoming; Spencer, forthcoming). Our results contribute to these discussions by clarifying the phenotypic consequences of single-locus genetic diversity partitioning and multilocus classification results. Both sets of results are valid, and they are mutually compatible, but they have different implications and uses (Neel, 1981; Rosenberg, 2011; Barbujani et al., 2013; Winther, 2014). Multilocus methods allow us to detect genome-wide patterns of variation and to investigate the ancestry of individual people. But it is single-locus allelic-variance partitioning that informs our expectations about selectively neutral phenotypic diversity. In particular, population genetics and quantitative genetics lead us to expect that differences between human populations in neutral phenotypes will mirror differences between human populations at single neutral loci.

Highlights.

• We extend a simple model for studying genetic differences between groups.

• We study selectively neutral traits controlled by k genetic loci.

• Traits are about as informative about group membership as single genetic loci.

• The expected size of the between-group trait difference does not increase with k.

Appendix A

In this appendix, we prove that Eq. 2 evaluated at k = 2h + 1 with h a non-negative integer is equal to Eq. 3 evaluated at k = 2h + 2. That is, we show that for odd k ≥ 1 and q = 1 − p, with 0 < p,q < 1.

$$\sum _{i=0}^{(k-1)/2}\left(\begin{array}{c}k\\ i\end{array}\right)p^i{q}^{k-i}=\frac{1}{2}\left(\begin{array}{c}k+1\\ \frac{k+1}{2}\end{array}\right)p^{(k+1)/2}{q}^{(k+1)/2}+\sum _{i=0}^{(k-1)/2}\left(\begin{array}{c}k+1\\ i\end{array}\right)p^i{q}^{k+1-i}.$$ (A.1)

Because k is odd, we write k = 2h + 1, with h ≥ 0 an integer. Because q ≠ 0, we let u = p/q, so q = 1/(u + 1). The desired identity is then equivalent to

$$(u+1)\sum _{i=0}^h\left(\begin{array}{c}2h+1\\ i\end{array}\right)u^i=\frac{1}{2}\left(\begin{array}{c}2h+2\\ h+1\end{array}\right)u^{h+1}+\sum _{i=0}^h\left(\begin{array}{c}2h+2\\ i\end{array}\right)u^i.$$

Applying the binomial identity $\left(\begin{array}{c}2h+1\\ i\end{array}\right)=\left[1-\frac{i}{2h+2}\right]\left(\begin{array}{c}2h+2\\ i\end{array}\right)$, we obtain

$$\sum _{i=0}^h\left[u\left(1-\frac{i}{2h+2}\right)-\frac{i}{2h+2}\right]\left(\begin{array}{c}2h+2\\ i\end{array}\right)u^i=\frac{1}{2}\left(\begin{array}{c}2h+2\\ h+1\end{array}\right)u^{h+1}.$$

Next, noting that $\frac{i}{2h+2}\left(\begin{array}{c}2h+2\\ i\end{array}\right)=\left(\begin{array}{c}2h+1\\ i-1\end{array}\right)$, Eq. A.1 is equivalent to

$$u+\sum _{i=1}^h\left[\left(\left(\begin{array}{c}2h+2\\ i\end{array}\right)-\left(\begin{array}{c}2h+1\\ i-1\end{array}\right)\right)u^{i+1}-\left(\begin{array}{c}2h+1\\ i-1\end{array}\right)u^i\right]=\frac{1}{2}\left(\begin{array}{c}2h+2\\ h+1\end{array}\right)u^{h+1}.$$ (A.2)

The sum telescopes: by Pascal’s rule, the $\left(\left(\begin{array}{c}2h+2\\ i\end{array}\right)-\left(\begin{array}{c}2h+1\\ i-1\end{array}\right)\right)u^{i+1}$ term with index i is canceled by the $-\left(\begin{array}{c}2h+1\\ (i+1)-1\end{array}\right)u^{(i+1)}$ term with index i + 1. Thus, the left-hand side of Eq. A.2 evaluates to

$$u+\left[-u+\left(\left(\begin{array}{c}2h+2\\ h\end{array}\right)-\left(\begin{array}{c}2h+1\\ h-1\end{array}\right)\right)u^{h+1}\right]=\left(\left(\begin{array}{c}2h+2\\ h\end{array}\right)-\left(\begin{array}{c}2h+1\\ h-1\end{array}\right)\right)u^{h+1}.$$

Applying Pascal’s rule twice more, $\left(\begin{array}{c}2h+2\\ h\end{array}\right)-\left(\begin{array}{c}2h+1\\ h\end{array}\right)=\left(\begin{array}{c}2h+1\\ h\end{array}\right)$ and $\left(\begin{array}{c}2h+1\\ h\end{array}\right)+\left(\begin{array}{c}2h+1\\ h+1\end{array}\right)=\left(\begin{array}{c}2h+2\\ h+1\end{array}\right)$; because $\left(\begin{array}{c}2h+1\\ h\end{array}\right)=\left(\begin{array}{c}2h+1\\ h+1\end{array}\right)$, the left-hand side of Eq. A.2 reduces to $\frac{1}{2}\left(\begin{array}{c}2h+2\\ h+1\end{array}\right)u^{h+1}$, completing the proof of Eq. A.2 and hence of Eq. A.1.

Appendix B

In this appendix, we show that the conditional probability of misclassifying an individual on the basis of its trait value, P(W_T = 1|Z = z), increases as z gets closer to k/2. We introduce and prove three claims used to obtain the result. We then give upper and lower bounds on P(W_T = 1|Z = z) in z, and we outline a method for obtaining quantiles of P(W_T = 1).

Theorem 1

Define P(W_T = 1|Z = z)as in Eq. 33 and fix k ≥ 1 an integer. For integers z₁ and z₂ in {0,1, …, k}, if |z₁ − k/2| > |z₂ − k/2|, then P(W_T = 1|Z = z₁) < P(W_T = 1|Z = z₂).

B.1. Claim 1: For even k, P(W_T = 1|M = A,Z = k/2) = 1/2

This claim has been shown in the main text, but we restate the proof for completeness.

Proof of Claim 1

For even k, the claim follows from the classification rule in the main text (Eqs. 27–29). By Eqs. 18 and 19, if Z = k/2, then Eq. 29 holds for all T, and we classify each individual randomly into either population, each with probability 1/2.

B.2. Claim 2: For odd k, P(W_T = 1|M = A,Z = (k − 1)/2) < 1/2

We start by introducing two lemmas.

Lemma 1 (Samuels, 1965, eq. 15)

Let Y be a sum of independent Bernoulli random variables with probabilities that are not necessarily identical, and let p₁ be the smallest probability associated with any of these Bernoulli trials. If y < E(Y) + p₁, then P(Y = y − 1) < P(Y = y).

Lemma 2

Let R be a random variable taking values in {0,1, …, 2h} for an integer h ≥ 1. Assume that for each r in {0,1, …, 2h},

$$P(R=r)=P(R=2h-r),$$ (B.1)

and that

$$0<P(R=0)<P(R=1)<\cdots <P(R=h).$$ (B.2)

Let B_q be an independent Bernoulli random variable with parameter q > 1/2, and let p = 1 − q. Then for l ∈ {0,1, …, h},

$$P(R+B_q=l)<P(R+B_q=2h+1-l).$$ (B.3)

Proof of Lemma 2

For l ∈ {1, …, h}, probabilities for the sum R + B_q satisfy

$$P(R+B_q=l)=P(R=l)p+P(R=l-1)q$$ (B.4)

$$P(R+B_q=2h+1-l)=P(R=2h+1-l)p+P(R=2h-1)q.$$ (B.5)

Note that Eqs. B.4 and B.5 also hold for l = 0 because P(R = −1) = P(R = 2h + 1) = 0. Because of the symmetry of the distribution of R (Eq. B.1), Eq. B.5 is equivalent to

$$P(R+B_q=2h+1-l)=P(R=l-1)p+P(R=l)q.$$

Because q > p, Eq. B.3 is then equivalent to

$$P(R=l-1)<P(R=l).$$

This last inequality is true for l ∈ {1, …, h} by the assumption in Eq. B.2 and, for l = 0, by the fact that P(R = −1) = 0.

Proof of Claim 2

In population A, for h a positive integer, the random variable (T|M = A,Z = h,k = 2h), including the extra condition on k to indicate the number of loci contributing to the trait, satisfies the hypotheses of Lemma 2. The symmetry in Eq. B.1 comes from Eq. 17, and the monotonically increasing probabilities in Eq. B.2 come from applying Lemma 1 to the independent Bernoulli trials that sum to produce the random variable (Eqs. 9–11) and noting that P(T = 0|M = A,Z = h,k = 2h) = p^hq^h > 0.

We can view B_q as an additional locus with X = 0, meaning that the probability in population A that the locus increases the trait value T is q (Table 1). The sum (T|M = A,Z = h,k = 2h) + B_q is therefore equal in distribution to (T|M = A,Z = h,k = 2h + 1). Applying Lemma 2 with (T|M = A,Z = h,k = 2h + 1) as R + B_q gives, for l ∈ {0,1, …, (k − 1)/2},

$$P(T=l\mid M=A,Z=(k-1)/2)<P(T=k-l\mid M=A,Z=(k-1)/2).$$ (B.6)

Eq. B.6 guarantees that

$$\sum _{l=0}^{(k-1)/2}P(T=l\mid M=A,Z=(k-1)/2)<\sum _{l=(k+1)/2}^{k}P(T=l\mid M=A,Z=(k-1)/2),$$

meaning that

$$P(T\le (k-1)/2\mid M=A,Z=(k-1)/2)<P(T\ge (k+1)/2\mid M=A,Z=(k-1)/2).$$ (B.7)

Applying Eq. 30 and noting P(T ≤ (k − 1)/2) + P(T ≥ (k + 1)/2) = 1, for odd k ≥ 3,

$$P(W_T=1\mid M=A,Z=(k-1)/2)<1/2.$$ (B.8)

Because Lemma 2 assumes h ≥ 1, our argument applies to odd k ≥ 3. If k = 1, then Eq. B.8 holds because q > p.

B.3. Claim 3: If z ≤ k/2 − 1, then P(W_T = 1|M = A,Z = z) < P(W_T = 1|M = A,Z = z + 1)

To prove this claim, we use a lemma.

Lemma 3

Consider a random variable R = R₁ + R₂ that is the sum of two independent binomial random variables, R₁ with an integer z ≤ k/2 − 1 trials and probability p and R₂ with k − z − 1 trials and probability q. That is, R₁~Binomial(z,p), and independently, R₂~Binomial(k − z − 1,q). Define two independent random variables, B_q~Bernoulli(q) and B_p~Bernoulli(p) with q > p. Then for 0 ≤ j ≤ k/2,

$$P(R+B_q=j)<P(R+B_p=j).$$ (B.9)

Proof of Lemma 3

For 1 ≤ j ≤ k/2, the random variables R + B_q and R + B_p satisfy

$$\begin{array}{l}P(R+B_q=j)=P(R=j)p+P(R=j-1)q\\ P(R+B_p=j)=P(R=j)q+P(R=j-1)p.\end{array}$$

For j = 0, these equations follow from the fact that P(R = −1) = 0. Eq. B.9 therefore holds if

$$P(R=j)p+P(R=j-1)q<P(R=j)q+P(R=j-1)p.$$

Because q > p, the inequality is satisfied if

$$P(R=j-1)<P(R=j).$$ (B.10)

R is the sum of k − 1 independent Bernoulli random variables. Lemma 1 guarantees that Eq. B.10 is satisfied if j < E(R) + p Because z ≤ k/2 − 1 and q > p,

$$k/2=(p+q)k/2<(z+1)p+(k-z-1)q=E(R)+p.$$

Thus, Eq. B.10 is satisfied for j ≤ k/2, which shows that Eq. B.9 holds for j ≤ k/2.

Proof of Claim 3

The random variable (T|M = A,Z = z), which, with k loci, is the sum of z ≤ k/2 − 1 independent Bernoulli trials with probability p and k − z independent Bernoulli trials with probability q, has the properties required for R + B_q in Lemma 3. Similarly, (T|M = A,Z = z + 1) has the properties of R + B_p. Applying Lemma 3, for z ≤ k/2 − 1 and t ≤ k/2,

$$P(T=t\mid M=A,Z=z)<P(T=t\mid M=A,Z=z+1).$$

It follows that

$$\begin{array}{l}P(T<k/2\mid M=A,Z=z)+P(T=k/2\mid M=A,Z=z)/2\\ <P(T<k/2\mid M=A,Z=z+1)+P(T=k/2\mid M=A,Z=z+1)/2.\end{array}$$

Applying Eq. 30 to this last inequality gives, for z ≤ k/2 − 1,

$$P(W_T=1\mid M=A,Z=z)<P(W_T=1\mid M=A,Z=z+1),$$ (B.11)

demonstrating the desired result.

B.4. Completing the proof of Theorem 1: both populations and all z

Claims 1–3 prove Theorem 1 for population A and z₁,z₂ ≤ k/2. If Z = k/2, then P(W_T = 1|M = A,Z = z) = 1/2) (Claim 1); for odd k, if Z = (k − 1)/2, then P(W_T = 1|M = A,Z = z) < 1/2) (Claim 2); and as Z decreases from k/2 − 1, P(W_T = 1|M = A,Z = z) decreases (Claim 3). We have thus proven that for z₁,z₂ ∈ {0,1, …, ⌊k/2⌋}, if z₁ < z₂, then

$$P(W_T=1\mid M=A,Z=z_1)<P(W_T=1\mid M=A,Z=z_2).$$ (B.12)

It remains to examine z > k/2 and to remove the condition on M.

By Eq. 33, the misclassification probability on the basis of T does not depend on population membership, so we can drop the condition on M = A in Eq. B.12. That is, for z₁,z₂ ∈ {0,1, …, ⌊k/2⌋}, if z₁ < z₂, we now have

$$P(W_T=1\mid Z=z_1)<P(W_T=1\mid Z=z_2).$$ (B.13)

Further, Eq. 33 shows that P(W_T = 1|Z = z) = P(W_T = 1|Z = k − z), so that Eq. B.13 holds for z₁,z₂ ∈ {0,1, …, k} with min{z₁,k − z₁} < min{z₂,k − z₂}. But min{z₁,k − z₁} < min{z₂,k − z₂} if and only if |z₁ − k/2| > |z₂ − k/2|, completing the proof of Theorem 1.

B.5. Applying Theorem 1

By Theorem 1, the upper bound in z of P(W_T = 1|Z = z), achieved when z = k/2, is (Section B.1)

$$P(W_T=1\mid Z=z)\le 1/2.$$

The lower bound in z of P(W_T = 1|Z = z), achieved when when z = 0 or z = k, is

$$P(W_T=1\mid Z=z)\ge P(W_S=1),$$

taking P(W_S = 1) from Eq. 4. The lower bound is calculated using z = 0 or z = k in Eq. 33.

Because P(W_T = 1|Z = z) decreases with |z − k/2|, quantiles of the distribution of P(W_T = 1) are obtained by identifying the corresponding quantiles of |Z − k/2|. We define J = |Z − k/2|. If k is even, then J takes values in {0,1, …, k/2}; if k is odd, then J takes values in {1/2,3/2, …, k/2}.

Because Z~Binomial(k, 1,2),

$$P(J=j)=\{\begin{array}{ll}\frac{1}{2^k}\left(\begin{array}{c}k\\ k/2\end{array}\right),\hfill & j=0\hfill \\ \frac{1}{2^{k-1}}\left(\begin{array}{c}k\\ k/2-j\end{array}\right),\hfill & j\ne 0\hfill \end{array}$$ (B.14)

The cumulative distribution function of J is

$$F_J(j)=\sum _{i=0}^{j}P(J=i).$$

The qth quantile of J is

$$F_J^{-1}(q)=min\{j:F_J(j)\ge q\}.$$ (B.15)

The two values of z corresponding to the qth quantile of J are $k/2-F_J^{-1}(q)$ and $k/2+F_J^{-1}(q)$. Plugging either of these values into Eq. 33 gives the qth quantile of P(W_T = 1).