Significance
The rate at which ecosystems recover from disturbance can greatly influence their resilience to environmental change. We used more than a decade of satellite data to model how the extraordinarily biodiverse shrublands of South Africa recover following fire and how recovery rates vary with temperature and precipitation across the region. We found that climate strongly affects how quickly plant communities can recover after fire. We also used global climate models to project ecosystem recovery into the future and found that warmer winter temperatures will likely speed up postfire recovery unless precipitation declines as temperature increases (as some models project).
Keywords: hierarchical Bayesian, ecology, fire, climate, remote sensing
Abstract
Conservation of biodiversity and natural resources in a changing climate requires understanding what controls ecosystem resilience to disturbance. This understanding is especially important in the fire-prone Mediterranean systems of the world. The fire frequency in these systems is sensitive to climate, and recent climate change has resulted in more frequent fires over the last few decades. However, the sensitivity of postfire recovery and biomass/fuel load accumulation to climate is less well understood than fire frequency despite its importance in driving the fire regime. In this study, we develop a hierarchical statistical framework to model postfire ecosystem recovery using satellite-derived observations of vegetation as a function of stand age, topography, and climate. In the Cape Floristic Region (CFR) of South Africa, a fire-prone biodiversity hotspot, we found strong postfire recovery gradients associated with climate resulting in faster recovery in regions with higher soil fertility, minimum July (winter) temperature, and mean January (summer) precipitation. Projections using an ensemble of 11 downscaled Coupled Model Intercomparison Project Phase 5 (CMIP5) general circulation models (GCMs) suggest that warmer winter temperatures in 2080–2100 will encourage faster postfire recovery across the region, which could further increase fire frequency due to faster fuel accumulation. However, some models project decreasing precipitation in the western CFR, which would slow recovery rates there, likely reducing fire frequency through lack of fuel and potentially driving local biome shifts from fynbos shrubland to nonburning semidesert vegetation. This simple yet powerful approach to making inferences from large, remotely sensed datasets has potential for wide application to modeling ecosystem resilience in disturbance-prone ecosystems globally.
In many ecosystems, climate change will exert its most powerful impacts via disturbance, such as outbreaks of forest pests (1), species invasions (2), and fire (3). A key feature of ecosystems’ response to disturbance is the recovery time, the time required for the ecosystem to return to a state similar to its state before disturbance [called “engineering resilience” by Peterson et al. (4)]. Rapid recovery from disturbance is associated with high resilience—that is, the ability of the system to return reliably to its previous state (5). Slow recovery can signal an approaching catastrophic jump to an alternative state (6) or, given frequent disturbance, chronically lower function (7).
Fire is one of the most widespread and important forms of disturbance globally, occurring as an important feature in more than 50% of the world’s terrestrial ecosystems (8). However, the risk of climate change is difficult to assess because fires are not well represented in global ecosystem models (9). There is growing evidence of increased fire frequency, severity, and/or size in many regions, due in large part to warming and incidence of drought (3, 10–13). In many regions of the world and especially Mediterranean climate systems, the frequency and severity of wildfire is expected to continue to increase in the coming decades due to warmer and drier weather conditions (14, 15), although some areas may actually see a decrease in frequency due to slower fuel accumulation (16). Accordingly, resilience to disturbance by fire will strongly influence the response of these regions to climate change and is central to management; in the western United States, South Africa, and elsewhere, postfire resilience is a focus of land management agencies (9).
Despite the critical role of resilience to disturbance (and especially to fire) in the response of ecosystems to climate change, few studies have attempted to quantify and predict patterns of resilience or to understand the climatic controls on postfire recovery across a biome. Equally importantly, there has been virtually no research at large scales most relevant to ecosystem regime shifts and management (17). The key reasons are logistical: it is difficult to measure postdisturbance recovery over relevant time frames (years to decades) and spatial scales (10s to 1,000s of square kilometers).
The necessary data and tools are now, however, available. We have multidecadal, continuous global measurements from satellites including Moderate Resolution Imaging Spectroradiometer (MODIS) and LANDSAT that can be used to measure key ecosystem properties through time (18). High-resolution historical weather data are also now increasingly available (19, 20), as are decades of spatially detailed fire records (3, 10). In this paper, we develop a relatively simple yet powerful computational approach to make regional-scale inferences and predictions of ecosystem resilience in response to projected climate change. By incorporating millions of pixels from satellite imagery over the last 15 y, for the first time to our knowledge, it is possible to quantify broad-scale patterns in ecosystem recovery and identify regional climatic gradients in postfire ecosystem dynamics. With relatively simple parametric models fit in a hierarchical Bayesian (HB) framework, we can use large environmental datasets to explain these patterns in terms of climatic variation and predict the effects of climate change on postfire resilience.
Remotely sensed vegetation indices have a long tradition in vegetation monitoring (21–25). Remotely sensed data are commonly used to assess various attributes of wildfires including locations of active fires, fire severity, and identification of burned areas (see ref. 26 for an excellent review of various tools and metrics). The majority of these studies use remotely sensed data to monitor fire characteristics rather than postfire recovery. Even fewer studies have attempted to use biophysical data to model postdisturbance recovery rates. For example, Röder et al. (27) used 20 LANDSAT scenes to assess postfire recovery in Spain with simple linear regression to quantify the increase in vegetation cover as a function of time since fire. However, no attempt was made to quantitatively estimate the relationship between explanatory variables or construct a predictive model. In another study, Schroeder, et al. (28) classified forest regrowth into four categories (little to no, slow, moderate, and fast) using field data and then used LANDSAT imagery and a regression tree approach to identify environmental covariates of the recovery rates. However, this method required all pixels to be binned into the four classes before analysis and was capable only of making coarse categorical predictions for a fixed time period. Other similar studies have used various methods to quantify recovery, including object-based image analysis (29), linear regression (30, 31), spatially binning regions and comparing with unburned areas (32), and log-normal regression (33), but none of these methods were able to incorporate environmental covariates directly into the postfire recovery model or make quantitative recovery predictions.
In this study, we develop an HB model that uses climate and topographical parameters to predict postfire biomass accumulation across the fynbos (Mediterranean shrubland) biome (34) in the Cape Floristic Region (CFR) of South Africa (Fig. S1). The CFR alone has over nine thousand vascular plant species, two-thirds of which are endemic to the region (representing nearly half of the 20,000 vascular plant species in all of southern Africa) and is one of the most biodiverse regions globally (35). The extraordinary biodiversity and speciation rates in combination with the large proportion of transformed habitats have led to the region’s high conservation priority (36). Fire, which has a typical return time of 10–13 y in the system (37), is recognized as one of the most important factors in developing and maintaining such extraordinary biodiversity (38), and therefore, it is critical that we understand the climatic controls on the fire regime and postfire recovery in this system.
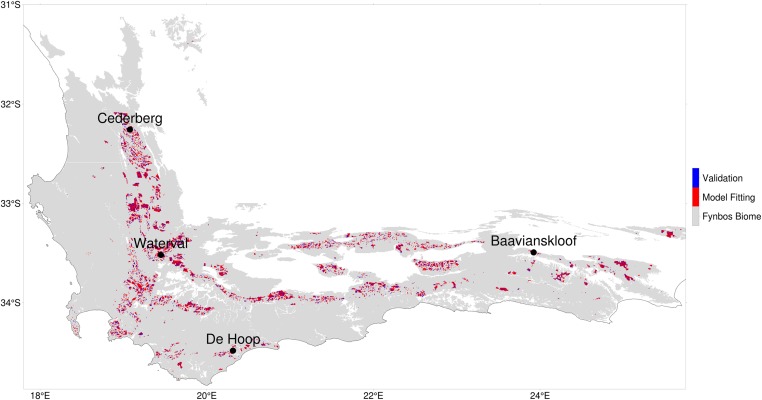
Fig. S1.
Illustration of the pixels included in this analysis. The red and blue pixels have associated fire data and were used in fitting and validation, respectively. The model was used to predict the recovery parameters and postfire NDVI trajectory in the light gray region, which includes the full fynbos biome in the CFR. Predictions are shown for areas that have been transformed (e.g., for agriculture), but these areas were not used in model fitting. The fitted recovery curves for the four labeled locations are shown in Fig. 1.
Our approach draws on detailed fire history records from the region, a 10-y archive of biweekly MODIS satellite imagery, high-resolution climate and topographical data (Fig. S2), and a hierarchical model. In fynbos, there is a strong relationship between biomass and the Normalized Difference Vegetation Index (NDVI) (39), so despite its low spectral resolution compared with modern hyperspectral sensors, for long-term continuous monitoring of large spatial domains, it remains extremely useful. The model was evaluated using 25% holdout cross-validation and comparison with a 40-y history of observed fire events. We also used an ensemble of 11 Coupled Model Intercomparison Project Phase 5 (CMIP5) general circulation models downscaled to the region to predict future change in postfire recovery rates.
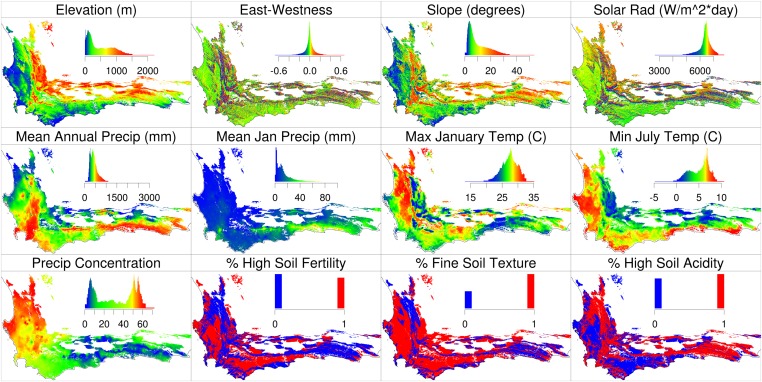
Fig. S2.
Maps of the environmental variables for the region included in this analysis. The histogram inset in each panel shows the distribution of each variable across the region. East-westness is an index quantifying east and west aspect, normalized by slope. Precip concentration is a metric of the seasonality of rainfall and ranges from 0 (equal rainfall in all months) to 100 (all rainfall in a single month). East-westness is a unitless index that ranges from −1 to 1 and accounts for the effects of slope. See SI Materials and Methods for data sources and complete descriptions of each variable.
Results
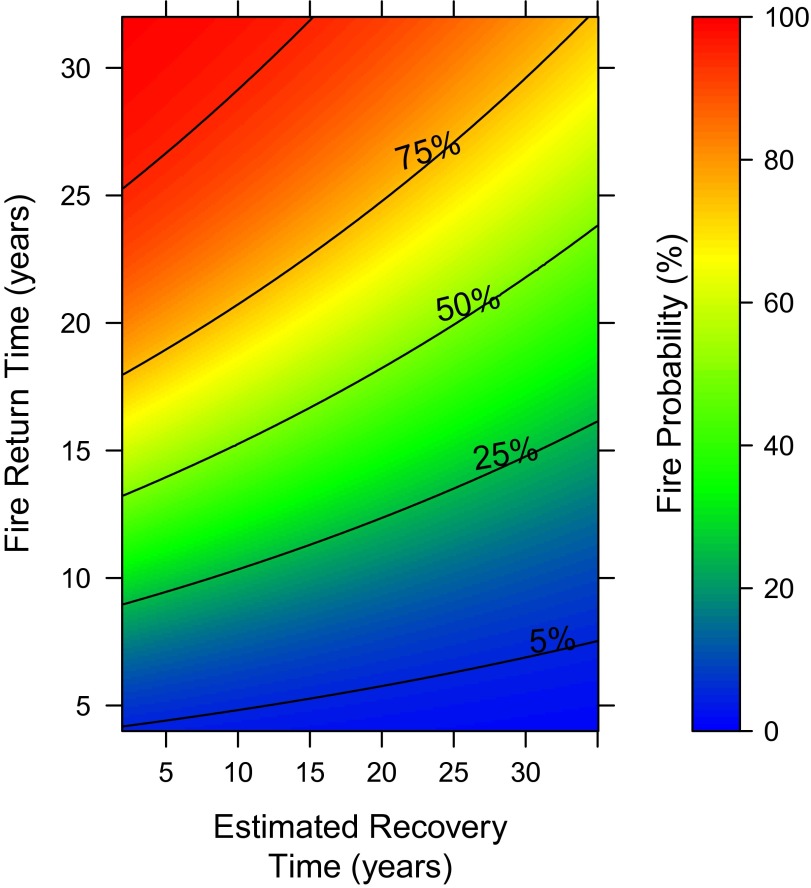
The full model, which included climate, topography, and soil, had a lower deviance information criterion score (DIC; mean deviance: 3,104,349; effective number of parameters pD: 14,608; DIC: 3,089,741) compared with a model with only topography and soil (mean deviance: 3,136,752; pD: 15,656; DIC: 3,121,097, DIC = 31,356), indicating extremely strong support (40) for the hypothesis that climate is a key predictor of the postfire NDVI trajectory in this system (model code available in Dataset S1). The mean predicted and observed NDVI values for four fires across the region illustrate how the model is able to capture the spatial variability observed in postfire NDVI (Fig. 1; locations shown in Fig. S1). To assess the predictive performance across different post fire ages, the R2 between the predicted and observed median annual values were calculated for various ages (e.g., 0–2 y, 1–3 y, etc.) for every location and time step in the validation dataset. The model can predict approximately half () of the variation in NDVI between 2 and 10 y following fire (which decreases slightly in older areas; Fig. S3). Furthermore, there is strong support [ Akaike information criterion (AIC) = 229] for a relationship between the estimated recovery time and observed fire return intervals in this system (SI Materials and Methods), suggesting that recovery time can be used to estimate mean fire return intervals given environmental conditions.
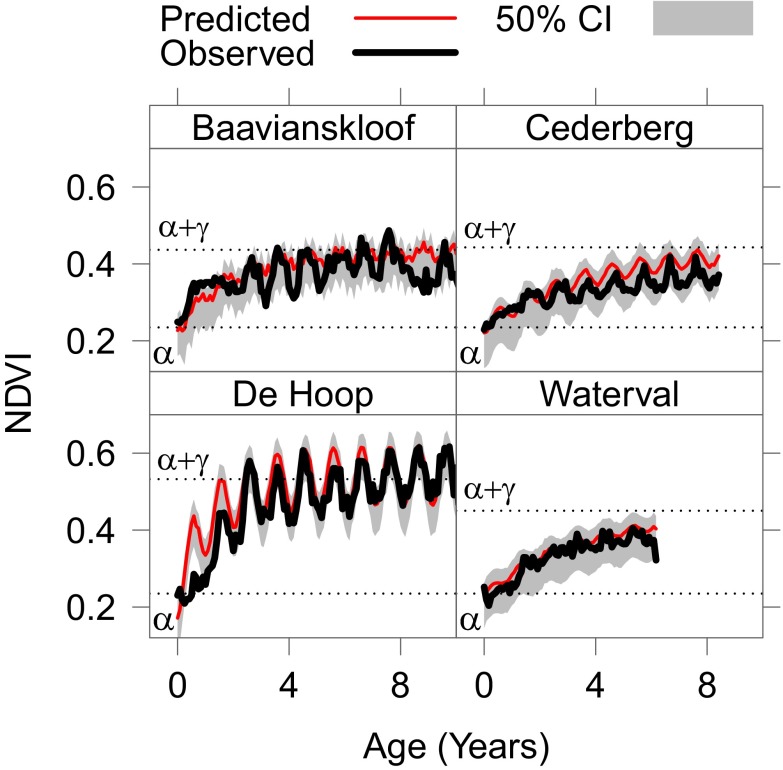
Fig. 1.
Predicted and observed postfire recoveries for four regions across the CFR (see Fig. S1 for locations). The heavy black lines are the mean observed NDVI values for all validation pixels from a single fire in each region. The red lines represent the mean predicted value (Eq. 3). The horizontal dotted lines illustrate the estimated initial (α) and upper asymptote () of postfire NDVI. The shaded areas represent the 50% highest posterior density (HPD) credible intervals (CIs) of the predicted values. Note that the predicted values were estimated using the fitted model (Table S1) and environmental data for each validation pixel as specified in the model and not fit directly to the observed data plotted here.
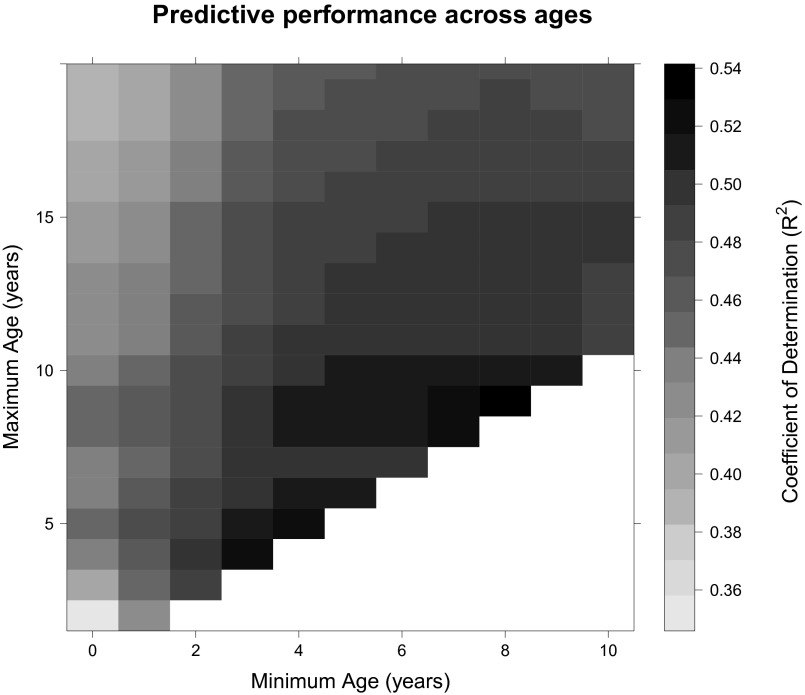
Fig. S3.
The coefficient of determination () between the median annual predicted and observed values in the validation data set for various age windows. The x axis represents the start of the age window and the y axis the end. For example, the lower left corner indicates that the model predictions had an of 0.36 in pixels between 0 and 2 y of age.
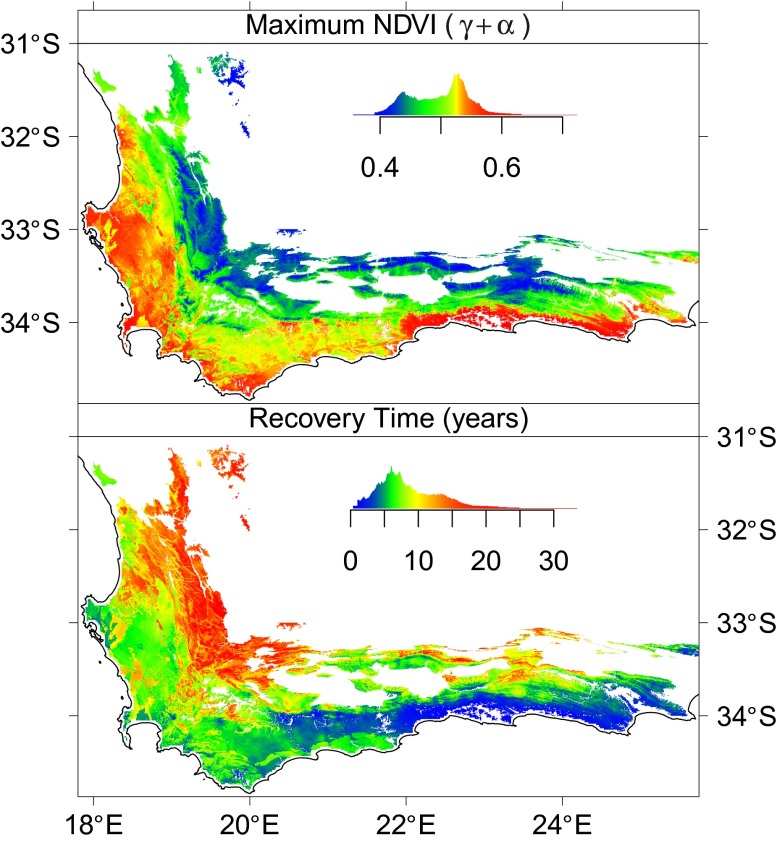
Spatial Variability in Postfire Recovery.
Estimated recovery times ranged from to 25 y, depending on the environmental conditions (Fig. 2). The regression coefficients shown in Table S1 represent the association between each predictor (climate, topography, and soil) and the recovery parameters. Previous work has shown that satellite derived NDVI is significantly correlated with biomass in fynbos (39), so these parameters can be used to infer how climate affects various aspects of postfire biomass accumulation across the region. The γ parameter, which represents the maximum increase in NDVI from the initial postfire value (α) to the asymptotic value (α + γ), is positively correlated with mean January (midsummer) rainfall and minimum temperatures in July (midwinter). In contrast, γ is negatively correlated with maximum January temperature. These relationships suggest that the potential maximum NDVI (and, therefore, maximum biomass) is sensitive to the temperature and precipitation extremes in the region, with less biomass accumulation in parts of the region with hot, dry summers (Fig. 2). Furthermore, NDVI increase (γ) is also positively associated with fine soil texture which has an important influence on soil nutrients, water holding capacity, and plant water availability (41–44).
Fig. 2.
Median posterior values of maximum NDVI (, unitless) and recovery time (years for NDVI to return to prefire levels; Eq. 10). (Inset) Histogram of the values across the region and serves as a color key to the map in each panel. Fig. S1 shows the pixels used in model fitting and validation. Note that maximum NDVI is the modeled asymptotic maximum predicted due to the climate, topography, and soil across the region. Predictions were made for all areas in the fynbos biome including those currently transformed (e.g., for agriculture), whereas white areas are outside the fynbos biome.
Table S1.
Posterior medians and 95% CIs of regression coefficients from the full model
| Covariate | A | γ | λ |
| Intercept | −3.9 (−3.98, −3.82)* | −1.46 (−1.52, −1.4)* | 0.99 (0.74, 1.22)* |
| Elevation (m) | −0.09 (−0.11, −0.07)* | −0.11 (−0.12, −0.09)* | 0.12 (0.07, 0.17)* |
| East-westness | −0.03 (−0.04, -0.02)* | 0.03 (0.02, 0.04)* | 0.05 (0.02, 0.08)* |
| Slope (°) | −0.42 (−0.43, -0.4)* | 0.02 (0.01, 0.03)* | −0.05 (−0.09, −0.01)* |
| Solar rad () | −0.01 (−0.02, 0) | −0.02 (−0.03, −0.01)* | 0.12 (0.08, 0.16)* |
| Mean annual precipitation (mm) | 0.16 (0.14, 0.18)* | 0.01 (0, 0.03) | 0.08 (−0.01, 0.15) |
| Mean January precipitation (mm) | −0.31 (−0.33, −0.29)* | 0.06 (0.05, 0.08)* | −0.38 (−0.53, −0.29)* |
| Maximum January temperature (°C) | 0.14 (0.12, 0.15)* | −0.02 (−0.03, −0.01)* | 0.12 (0.06, 0.16)* |
| Minimum July temperature (°C) | 0.01 (−0.01, 0.03) | 0.07 (0.05, 0.08)* | −0.22 (−0.27, −0.17)* |
| Precipitation concentration | −0.41 (−0.43, −0.39)* | 0.03 (0.02, 0.05)* | 0.14 (0.08, 0.2)* |
| % high soil fertility | 0.03 (−0.06, 0.11) | −0.09 (−0.15, −0.02)* | −0.6 (−0.87, −0.31)* |
| % fine soil texture | 0.07 (0.04, 0.09)* | 0.08 (0.06, 0.1)* | 0.2 (0.11, 0.28)* |
| % high soil acidity | 0.2 (0.12, 0.28)* | −0.05 (−0.11, 0.01) | −0.16 (−0.4, 0.08) |
A, amplitude of the sine wave reflecting the magnitude of the seasonality; γ, potential maximum increase in the NDVI (given enough time to recover after fire); λ, recovery rate (larger values indicating slower recovery).*95% HPD intervals do not overlap 0.
The recovery rate (λ; which indicates more rapid recovery with smaller values) was sensitive to midsummer precipitation and precipitation concentration but not mean annual precipitation (Table S1). This result suggests that the growth of young and recovering plants through the first few years following fire is limited by warm season moisture availability, as has been observed in detailed studies of individual plants (43, 45, 46) and population level analyses (47). The association with summer precipitation may also be driven by increased seedling mortality in drier microsites as observed by Midgley (45) or alternatively by differences in species composition and community functional traits across the gradient in recovery time. For example, there is some evidence for higher frequency of resprouting shrubs in wetter areas (48), which could lead to faster postfire recovery of biomass observed from satellite. Recovery rate (λ) is also strongly associated with soil fertility, with faster recovery occurring in more nutrient-rich soils (Table S1).
The potential maximum NDVI () and recovery rate (λ) have similar (but inverted) spatial patterns indicating lower peak NDVI values and slower recovery (larger λ) in interior arid regions (e.g., Cederberg and Waterval) compared with wetter areas along the coast and in the eastern portion of the region with aseasonal rainfall (e.g., de Hoop and Baviaanskloof; Figs. 1 and 2). The spatial pattern of maximum NDVI () shows the overall effect of elevation is less pronounced than the coastal-interior gradient (Fig. 2). The most arid parts of the region (near 20°E, 33°S) have estimated maximum NDVI () values near 0.4, indicating that the aridity limits biomass below the levels found in wetter areas.
The seasonal amplitude (A) is negatively associated with elevation, slope, and mean January (midsummer) precipitation, but positively associated with soil acidity, maximum January temperature, and mean annual precipitation (Table S1). The seasonality of precipitation (SI Materials and Methods) is also an important influence on A, with less seasonal variability in parts of the region with more seasonal concentration of rainfall. The counter intuitive relationship is likely driven by differences in species composition and functional traits across the region. The most important traits that would lead to a seasonal variation in NDVI are deciduous leaves or an annual life cycle, which are more common in parts of the region with aseasonal rainfall (primarily in the east) (49). Model output including maps of λ, γ, A, and the recovery time are available at dx.doi.org/10.6084/m9.figshare.1420575.
Climate Projections.
The climate models forecast that the region will consistently warm in the coming century but precipitation is much less certain, reflecting the climatological complexity in precipitation across the region. For example, the 2081–2100 RCP8.5 changes (multimodel regional mean SD) for January maximum temperature (), and July temperature () are relatively smooth across the region, with higher values in the inland regions (Fig. S4). However, the predictions for mean annual precipitation ( mm), mean January precipitation ( mm), and precipitation seasonality () have large spatial and intermodel variability (Fig. S4). In general, the western part of the region is likely to experience decreased mean annual and January precipitation, whereas there may be an increase in winter rainfall in the east.
Fig. S4.
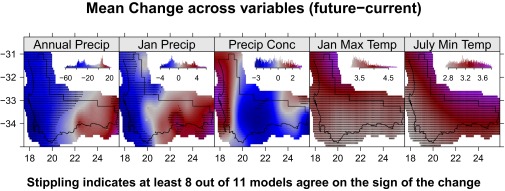
Multimodel mean projected change in annual precipitation, January precipitation, precipitation concentration, January maximum temperature, and July minimum temperature from 11 downscaled CMIP5 GCMs for the period 2081–2100 and scenario RCP8.5. Stippling indicates at least 8 of 11 models agree on the sign of the change.
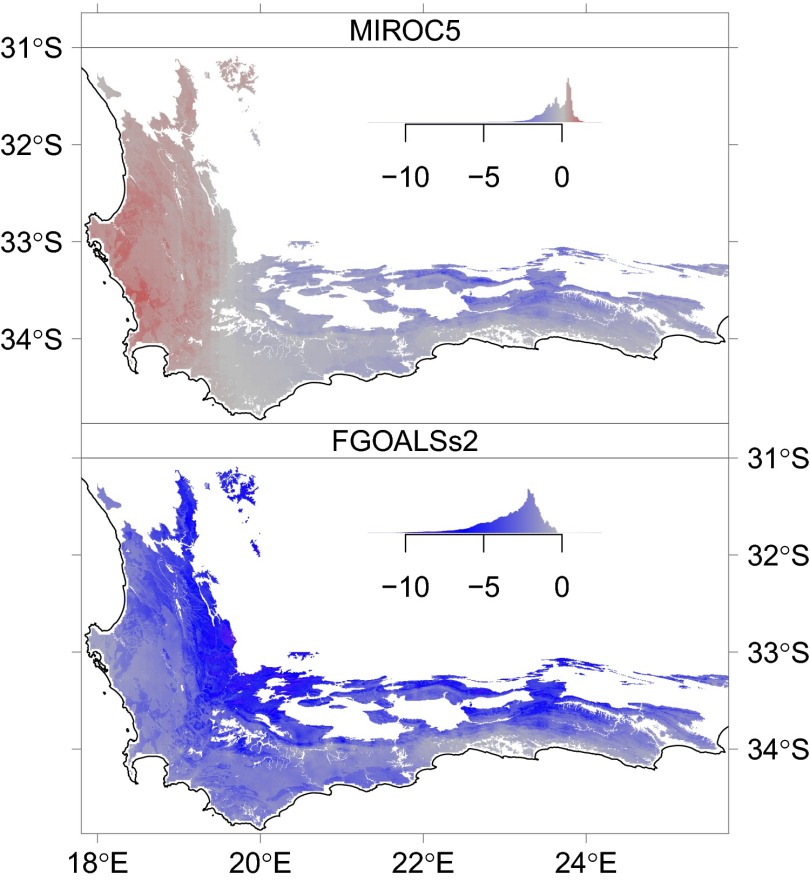
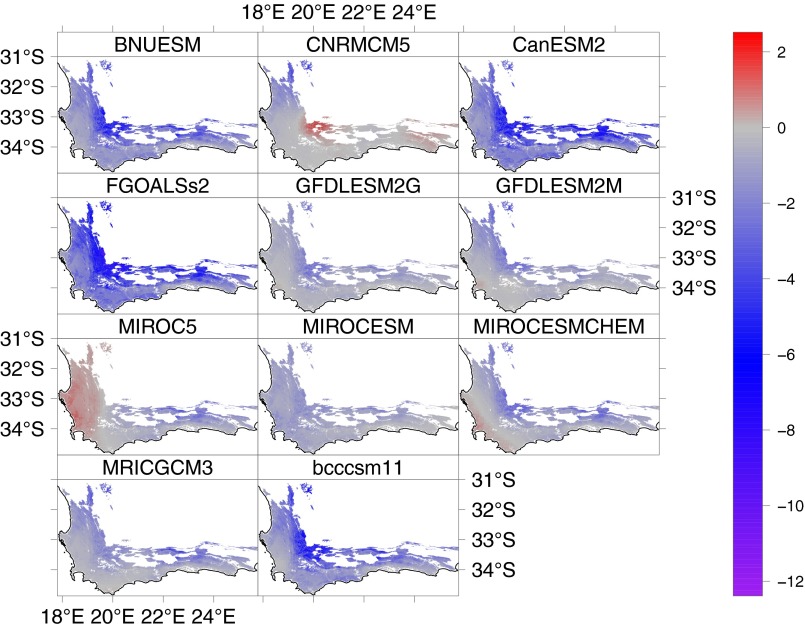
Multimodel mean projections of postfire recovery time show little change ( y), but predictions vary widely between models and across the region (Fig. 3). Overall, most show decreasing (faster) recovery time driven primarily by warmer winter temperatures (Fig. S5). However, precipitation is paramount in this system and the high uncertainty in projected precipitation change for this region translates to large intermodel variability even in the sign of the projected postfire recovery rates. Some models (e.g., MIROC5, GFDL-ESM2M) show regional gradients with slowing recovery in the west (driven by decreased precipitation) and faster recovery in the east, while others (e.g., FGOALSs2) result in faster recovery times ( y) across the region by as much as −12.4 y (Fig. 3).
Fig. 3.
Median posterior value of predicted change in recovery time (years) under two downscaled CMIP5 general circulation models (FGOALSs2 and MIROC5) with scenario RCP8.5 averaged over 2080–2100. Negative values indicate faster postfire recovery, whereas positive values indicate slower recovery. See Fig. S5 for all 11 models.
Fig. S5.
Median posterior value of predicted change in recovery time with future climate change (RCP8.5, 2080–2100) for 11 downscaled CMIP5 GCMs.
SI Materials and Methods
Fire Data.
Fire boundaries from protected areas in the region were compiled by the CapeNature management organization (65). The boundaries consist of polygons representing the burned areas and several attributes including date and cause of fire, if known (66). These locations were typically mapped by direct observation and have high spatial accuracy within the reserves (67). However, CapeNature reserves cover only a small fraction of the study area, so a satellite burned area product was used to identify fires outside the reserves. The MODIS/Terra+Aqua Burned Area Monthly L3 Global SIN Grid V005 (MCD45A1) product attempts to map the approximate day of the fire and extent of the burned area with a spatial resolution of 500 m (68). We recently evaluated this product for use in this region (67) and found it has relatively high omission errors (varying from 40.1% to 80.8% over different years), but low errors of commission (varying from 8.1% to 19.1% over different years). In this study, only pixels with fire history are used for analysis, so it is more important to avoid false positives than to identify every burned area in the region. These validation results indicate that the MCD45A1 dataset is a useful product despite the high errors of omission.
The MCD45A1 data were downloaded in GeoTIFF format from the University of Maryland (e4ftl01.cr.usgs.gov/MOTA/MCD45A1.051/) and subset to the CFR. Only burned areas larger than five pixels ( km2) with a MCD45A1 pixel quality assurance equal to 1 were retained for the remaining analysis to minimize the probability of false positives associated with partially burned pixels or geolocation error. See ref. 69 for a description of the detection algorithm and quality assurance methodology. The CapeNature fire data were then rasterized and combined with the MCD45A1 data from outside the reserves to create a single gridded fire data set with 500-m resolution. Any spatial bias in the fire detection rates (e.g., false negatives) that are associated with particular environmental characteristics (such as particular soil characteristics) could introduce some bias into the fitted model. By combining two types of fire data (human and satellite observed), we hope to minimize any spatial biases in the fire detection probabilities. The following information was also compiled for each pixel in the combined dataset: distance to fire edge, area burned (to capture subpixel burning in the CapeNature data set), fire date, and whether the pixel had burned more than once during 1990–2010. Pixels that burned less than 95%, were within 500 m of a fire edge, or were within 1 km of the coast were removed to reduce the influence of mapping errors and heterogeneous fire edges. These thresholds were selected to remove the most error-prone classes of observations while retaining as many high-quality observations as possible for model fitting and validation. The burned areas from these two sources were subset to include only fires that occurred between 1990 and 2011. This process produced a dataset containing 2,364 unique fires (of which 61% were identified by the MCD45A1 dataset) containing km2 of burned area.
Satellite Vegetation Index.
We used the NDVI to quantify aboveground plant biomass as it recovers following the fire. Although similar studies have used other metrics such as the normalized burn ratio (NBR) to assess fire severity and short-term (months to years) recovery (70), vegetation indices such as NDVI are more appropriate for long-term estimates of vegetation biomass recovery (71) and are known to be a useful proxy for biomass in this system (39).
The complete 10-y record (2000–2010) for tiles h19v12 and h20v12 were downloaded in Hierarchical Data Format (HDF-EOS) from the USGS (e4ftl01.cr.usgs.gov/MOLT/MOD13A1.005/). The tiles were then mosaiced, clipped to the CFR (Fig. S1), and reprojected to the same 500-m grid as the fire data using the MODIS Reprojection Tool (https://lpdaac.usgs.gov/tools/modis_reprojection_tool).
Climate and Topographical Data.
Long-term (1950–2000) mean climate data for the region were extracted from the South African Atlas of Agrohydrology and Climatology (61), including mean minimum July (winter) temperature (tmin07), mean maximum January (summer) temperature (tmax01), mean annual precipitation (map), and mean January precipitation (mmp01). We also included Markham’s precipitation concentration, which ranges from 0%, indicating equal rainfall throughout the year, to 100%, indicating all precipitation falls in a single month (pptconc) (72). The climate data were downscaled from the original 1-min ( 1.55 × 1.85 km) resolution to the 0.5-km resolution of the MODIS data using a bicubic interpolation.
Soil texture, fertility, and pH were extracted from a spatial dataset on soils developed to model species distribution in the region (73). The soil data were derived from a 1:250,000 scale vector geological map that was reclassified into edaphic fertility, texture, and pH. This classified map was then rasterized to 500-m resolution, keeping the proportion of each cell within various high/low fertility/texture/pH classes. The rasterized data used here indicate the percentage of high vs. low fertility/texture/pH soil in the pixel. The majority of soils across the region are derived from the quartzitic sandstones of the Table Mountain Group and are sandy, acidic, and infertile (74). However, there are some locations (see % high soil fertility panel in Fig. S2) with soils derived from shales of the Bokkeveld Group that have relatively fertile soils (74). For example, cells with a value of one for fertility contain only high-fertility soil derived from shales, whereas cells with a value of zero may contain only soils derived from nutrient-poor quartzitic bedrock. Interestingly, there is some evidence that several soil nutrients (Ca, K, P, Fe, and Zn) are transported into the region as dust blown from the more arid interior of South Africa during significant wind events (75).
Topographical data including elevation and slope were estimated using the 30-m digital elevation model (DEM) from the ASTER project (asterweb.jpl.nasa.gov/gdem.asp). The DEM was also used to estimate daily potential solar radiation (in the absence of clouds) by summing the incoming direct and diffuse radiation at 15-min intervals, taking into account the solar elevation and azimuth and the slope, aspect, and surrounding topography using the GRASS GIS r.sun program (76). These daily values were then averaged over a year to get the mean annual potential solar radiation for each pixel (rad_ave). The index was used to quantify east-westness and accounts for the decreased significance of aspect as slope goes to zero. This index (eastwest) varies from −1 to 1 (tending toward 0 in flat areas) and is a convenient way to account for varying slopes when including aspect in regression models (77). The index is a useful metric of north-southness but is highly correlated with the average potential solar radiation and is not included in this analysis.
The environmental data were selected to avoid strongly correlated variables (no two variables had correlations greater than 0.7 as suggested in ref. 78).
Climate Projections.
A suite of 11 CMIP5 general circulation models (GCMs) for two future scenarios (RCP4.5 and RCP8.5) were downscaled to monthly time series at station locations across the CFR for the CORDEX project (79) and accessed through the Climate Information Portal at the University of Cape Town (cip.csag.uct.ac.za/webclient2/app/). These data were aggregated across months/years into climatological means for three time periods (1960–2000, 2046–2065, and 2081–2100). The anomalies (future–current) for both future periods values were then interpolated using ordinary kriging from the point locations to the full modeling grid (Fig. S4). These interpolated anomolies were then added to the original high resolution data (see above), and the biomass recovery model was used to predict ecosystem recovery parameters under the projected climate for each model-scenerio-time triple.
Model Fitting and Computational Notes.
The data were prepared using a collection of custom R code that download the data, conduct the spatial processing using GRASS (76) and R (80), collate the various data sources, prepare the final data structures for the model, run the model on a computer cluster, and summarize and plot the output. The model itself was specified in the BUGS language and fit using JAGS software (81). Four parallel chains of the model were run in adaptive mode for 1,000 iterations to optimize sampling, followed by another 5,000 iterations to allow convergence. Following convergence, 10,000 posterior samples were drawn, and every 10th sample was retained to reduce autocorrelation. Convergence was assessed using the BGR diagnostic (82) and visual inspection of the chains. Credible intervals were constructed using the highest posterior density (HPD) approach (83). All variables were significant predictors of at least one of the three recovery parameters (A, γ, λ).
To assess whether including the climate variables in the model improves the complexity-penalized model fit, the model was run with and without the climate variables. These two models were compared using the (DIC) (40). Model evaluation was accomplished with cross-validation. A random subset of 75% of the pixels was selected and used for model fitting (Fig. S1). The posterior distributions of all model parameters and environmental covariates were used to predict NDVI in the remaining 25% of the pixels for each time step. The predictive performance of the model was assessed using the coefficient of determination (R2) between the predicted and observed data in the validation pixels. The model chains were run in parallel on a cluster of Xeon E5530 2.4GHz CPUs and required 5 d to complete the model fitting.
The lower predictive performance in the first 2 y following fire (Fig. S3) is probably due to variability in substrate (i.e., soil and geology, shadowing, estimated by α) or errors in the exact fire date as recorded in the field reports. Wildfires in fynbos often burn for several days but are assigned a single date (the date of detection) in the database. The decreased performance in older areas is probably due to differences in species composition and vegetation structure across the region. For example, stands of Protea nitida can accumulate over 20 kg/m2 of biomass, whereas areas dominated by cape reeds (Restionaceae) will rarely accumulate more than 1 kg/m2 (39). These differences will become increasingly apparent as the stand ages and thus the model does a poorer job of predicting NDVI in older sites. However, given that mean fire return times across the region are 10–20 y and the incidence of short interval ( 6 y) fires are increasing (66), the model performs best when it matters most: the critical 5- to 15-y period after fire.
Corroboration with Observed Fire Data.
In addition to validating the observed NDVI trajectories, we also compared the recovery times to the observed fire intervals across the region. To make the comparison, we gridded the fire data polygons to the MODIS 500-m grid and extracted all observed fire return intervals for each pixel in the model. These observed intervals were then regressed in a survival model framework with the modeled fire recovery time. Any pixel with at least one observed fire will have two censored observations (from before beginning of record to the first fire, and then from the last fire to the end of the record) in addition to any complete intervals between two observed fires. Therefore, in this dataset, the number of censored observations greatly overwhelms the observed intervals. The censored observations were dealt with in two ways: (i) The date of initial monitoring of fires in each reserve was not recorded, so it is unknown when to begin counting the censored intervals before the first observed fire. However, after a fire is recorded for a location, it is less likely that future fires will be missed (due to staggered inclusion of reserves into the fire monitoring program since the 1950s). Because the probability of missing fires is much higher in the early part of the record, only the censored observations from the last fire to the end of the record were included. It is possible to model the timing of the prior fire (10), but this was beyond the scope of this analysis. (ii) After discarding the intervals at the beginning of the record, there were still nearly four times as many censored observations as complete observations. To reduce the influence of the censored observations, they were given a weight of 0.25, whereas the complete observations were weighted at 0.75 (leading to approximately equal influence of observed and censored intervals in the model fitting). Two models, one with a constant hazard function and one with recovery time as a covariate, were fit using the survreg function from the Survival package in R and compared using the AIC.
Discussion
Much of the focus in the remote sensing literature has been on mapping and monitoring ecosystem patterns (50–52) rather than understanding ecosystem processes and building predictive models of spatiotemporal dynamics (53). In this study, we used millions of satellite observations collected over the last two decades to identify recovery gradients in postfire ecosystem dynamics. By breaking ecosystem recovery into distinct but complementary components and quantifying the role of climate, soil, and other topographical variables, we also gain the ability to forecast how the ecosystem may respond to future climate change. Despite its relative simplicity and ease of interpretation, the model performed well in cross-validation, explaining 50% of the variation in the held-out data.
We found that postfire recovery rate varies dramatically across the region and is significantly associated with climatic gradients (Table S1). Additionally, we found that the estimated postfire recovery times were a useful predictor of fire return intervals using a separate survival analysis (SI Materials and Methods and Fig. 4). Recovery time ranges from only a few years on the warmer mesic coast to more than three decades in the arid interior where fynbos shrubland transitions into desert vegetation (Fig. 2). Eastern coastal regions have the shortest recovery times despite accumulating more biomass (large γ) due to fast recovery rates (). In contrast, vegetation in the more arid west requires decades to recover to prefire conditions even though the maximum NDVI tends to be smaller ().
Fig. 4.
Fire return time distributions estimated from a survival model fit with observed fire return times (SI Materials and Methods) and the satellite-derived estimated recovery times described in this study (Fig. 2). This relationship corroborates the utility of the satellite-derived recovery times as a useful proxy for fire return intervals in this system. Colors indicate the cumulative probability of observing a given fire return interval (y axis) given the satellite-derived postfire recovery time estimated in this study (x axis).
Warmer winter temperatures in the future are expected to accelerate postfire recovery across the region, which could further increase fire frequency due to faster fuel accumulation (Fig. 3 and Fig. S5). Warmer conditions are known to increase short-term fire risk in the region (10), but the impact of climate change on fuel load accumulation rates had not been previously quantified. This knowledge gap is important, because climate affects fire regimes through its influence on fuel loads as well as burning conditions.
This study is limited to recovery of ecosystem-level above-ground biomass, which cannot account for changes in functional or phylogenetic community structure. There are likely to be additional ecological impacts of shorter fire return times according to the regeneration strategies and dispersal capabilities of the constituent species (54, 55). For example, some fynbos species require up to 10 y following fire before successfully reproducing (56), which in combination with more frequent fires leads to the aptly named interval squeeze (57). More frequent fires encouraged by both high-risk weather (10) and faster postfire biomass accumulation could lead to significant shifts in community composition by eliminating long-lived, nonsprouting shrubs (as observed experimentally) (58).
However, moisture availability is extremely important in this region and the climate models exhibit large variability in projected precipitation (Fig. S4). Several climate models project a decrease in precipitation in the western CFR, which would lead to slower recovery rates there and faster recovery in the eastern part of the region (e.g., MIROC5 in Fig. 3). This outcome would likely lead to reduced fire frequency in the west due to lack of fuel despite higher temperatures and more frequent high-risk fire weather and could lead to a biome conversion from fynbos to semidesert vegetation in strongly affected areas.
Understanding the spatiotemporal variability of the fire regime and ecosystem resilience is critical to successfully manage and conserve floral biodiversity in this system. For example, land managers in the region currently attempt to maintain intervals between fires long enough for 50% of the “individuals in a population of the slowest-maturing of the obligate reseeding species to have flowered and developed seed for at least three successive seasons” (59, 60). In combination with field observations, this modeling framework could be further developed to account for the phylogenetic and functional composition of plant communities to give a more comprehensive perspective on the relationship between climate and ecological resilience in this system.
Materials and Methods
Data.
Long-term (1950–2000) mean climate data (61) for the region were extracted, and topographical parameters were calculated using the 30-m digital elevation model (DEM) from the ASTER project (asterweb.jpl.nasa.gov/gdem.asp) and aggregated to the 500-m grid.
Fire occurrence data include fire boundaries mapped by reserve managers extending back to the 1950s (10) and the remotely sensed burned area product derived from the MODIS satellite sensor. The historical burned area polygons were then used to resolve the postfire age of each pixel in each time step during the MODIS era, with postfire ages ranging from 0 to 59 y. This, in combination with the climate data described above, allowed us to extract the multidecadal climate signal from a single decade of satellite observations. For example, imagine we know from the field data that a pixel burned in both 1980 and 2008. The NDVI observations for that pixel (which are limited to post-2000 MODIS) would start at postfire age 20, continue to 28, and then reset back to age zero (due to the fire in 2008) and increase again until the end of the record. By comparing these postfire trajectories with climate rather than weather, we can arrange the data in terms of age rather than date and have a record of recovery extending back decades before the satellite data are available.
Locations with no NDVI observations from the first 3 y, or with fewer than 3 y of data, were removed resulting in 16,700 pixels across the region, each with 225 bimonthly observations of NDVI through time (totaling 3.7 million observations of individual pixels) from the MODIS 500-m resolution 16-d gridded NDVI product (MOD13A1). Furthermore, there were 1.4 million NDVI observations from over 3,000 km2 greater than 10 y old and 375,000 observations from 850 km2 greater than 20 y old. This space-for-time substitution extended the ability of the model to infer recovery trajectories much longer than the duration of the MODIS data. See SI Materials and Methods for a more detailed description of data sources and processing.
Model Design.
The postfire NDVI trajectory is modeled as a simple parametric function of the environmental variables mentioned above in a HB model. The first level of the model fits the trajectory of observed NDVI values as a function defined in Eqs. 1–3. The second level regresses each parameter against the environmental variables, providing a link between climate and the shape of the postfire recovery trajectory (Eq. 4). The model was completed by specifying vague prior distributions on the model hyperparameters (Eqs. 5–9). This approach accomplishes several tasks in a single coherent framework. For learning about environmental controls on resilience, the parameters of primary interest are the regression coefficients between the environment and the three recovery function parameters. The model provides full posterior distributions for all model parameters and avoids complications introduced by stringing together several disparate models in an ad hoc fashion (e.g., one model to describe the postfire trajectory of NDVI through time and another to relate the trajectories to environmental variables). This approach ensures that uncertainty inherent in each level of the model is propagated through to the posterior distributions (62).
The postfire NDVI trajectory is approximated by an exponential function that increases to an asymptote similar to the curve described by Dìaz-Delgado and Pons (63). We extended this function by adding (i) a sinusoidal component to capture the seasonality, (ii) a term (ϕ) to adjust the curve for month of fire, and (iii) a term (α) that allows spatial variation in NDVI immediately following fire (Eq. 3). Let index space (), index time (2000–2010 with 225 16-d intervals), indicates the month of the previous fire, and index the environmental covariates including an intercept.
| [1] |
| [2] |
| [3] |
The spatial recovery parameters (α, γ, λ, and A) are assumed to be constant for each location (i) and do not vary through time (although the model could be extended to include time-varying parameters). The terms of this equation can be interpreted as follows: α represents the initial postfire NDVI. Because various regions have different postfire reflectance (due to soil, topography, and other factors), this term accounts for this spatial variability in the observed NDVI immediately postfire. See ref. 64 for discussion on the impact of different soil types across the region on remotely sensed data. The term defines the asymptotic upper limit of the curve and thus represents the potential maximum NDVI of the pixel (given enough time to recover after fire). The parameter λ is the exponential term that describes the recovery rate, A describes the amplitude of the sine wave and reflects the magnitude of the seasonality in that location, and ϕ adjusts for month-of-fire (m). The month-of-fire must be taken into account because the fires occurred throughout the year, so age 0 can occur at any phase of the seasonal cycle. Using fixes January at ϕ and allows the subsequent months to increase by . The term sets the seasonal frequency to be one year. Fig. 1 provides an example fit of this function to observed data.
The P environmental variables (soil, climate, topography, etc.; Fig. S2) are used to explain the variation in the spatial recovery parameters , , and . These parameters are fit as independent variables in multivariate regressions with the matrix of environmental variables X, an I × P matrix with , , and as vectors of length P
| [4] |
The NDVI immediately after fire can vary due to soil reflectance, exposed bedrock, and other factors that are not easily explained using climate or topography. Our uncertainty in the value of this parameter was represented in the model with a relatively vague prior on the α term
| [5] |
| [6] |
The priors on each of the regression terms ( and ) were selected to be sufficiently noninformative to let the data drive the posterior distributions
| [7] |
| [8] |
| [9] |
The parameters can be used to estimate the postfire recovery time () by calculating the time until the predicted curve approaches (33). This process is sensitive to the threshold (especially for larger values of λ which increase gradually to the asymptote) but serves as a useful relative metric to compare the recovery trajectories across the region. Here we define to be when the exponential component of the model equals . Therefore, solving for , we have
| [10] |
Supplementary Material
Acknowledgments
This work was supported by NASA headquarters under NASA Earth and Space Science Fellowship Program Grant NNX09AN82H and a Yale Climate & Energy Postdoctoral fellowship (to A.M.W.), as well as National Science Foundation (NSF) Grants OISE-0623341, DEB-0516320, and DEB-1046328 (to J.A.S.) and NSF Grant DEB-1045985 (to A.M.L.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: Fire recovery parameters (maps) are available via figshare at dx.doi.org/10.6084/m9.figshare.1420575.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1416710112/-/DCSupplemental.
References
- 1.Haynes KJ, Allstadt AJ, Klimetzek D. Forest defoliator outbreaks under climate change: Effects on the frequency and severity of outbreaks of five pine insect pests. Glob Change Biol. 2014;20(6):2004–2018. doi: 10.1111/gcb.12506. [DOI] [PubMed] [Google Scholar]
- 2.Chambers JC, et al. Resilience to stress and disturbance, and resistance to bromus tectorum l. invasion in cold desert shrublands of western North America. Ecosystems (N Y) 2014;17(2):360–375. [Google Scholar]
- 3.Westerling AL, Hidalgo HG, Cayan DR, Swetnam TW. Warming and earlier spring increase western U.S. forest wildfire activity. Science. 2006;313(5789):940–943. doi: 10.1126/science.1128834. [DOI] [PubMed] [Google Scholar]
- 4.Peterson G, Allen CR, Holling CS. Ecological resilience, biodiversity, and scale. Ecosystems (N Y) 1998;1(1):6–18. [Google Scholar]
- 5.Côté IM, Darling ES. Rethinking ecosystem resilience in the face of climate change. PLoS Biol. 2010;8(7):e1000438. doi: 10.1371/journal.pbio.1000438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Scheffer M, Carpenter S, Foley J, Folke C, Walker B. 2001. Catastrophic shifts in ecosystems RID f-2386-2011. Nature 413(6856):591–596. [DOI] [PubMed]
- 7.Mumby PJ, Hastings A, Edwards HJ. Thresholds and the resilience of Caribbean coral reefs. Nature. 2007;450(7166):98–101. doi: 10.1038/nature06252. [DOI] [PubMed] [Google Scholar]
- 8.Shlisky A, Alencar AAC, Nolasco MM, Curran LM. 2009. Tropical Fire Ecology. (Springer, Berlin), pp 65–83.
- 9.Bowman DMJS, et al. Fire in the Earth system. Science. 2009;324(5926):481–484. doi: 10.1126/science.1163886. [DOI] [PubMed] [Google Scholar]
- 10.Wilson AM, Latimer AM, Silander JA, Gelfand AE, de Klerk H. A Hierarchical Bayesian model of wildfire in a mediterranean biodiversity hotspot: Implications of weather variability and global circulation. Ecol Modell. 2010;221(1):106–112. [Google Scholar]
- 11.Pausas JG. Changes in fire and climate in the eastern Iberian peninsula (Mediterranean basin) Clim Change. 2004;63(3):337–350. [Google Scholar]
- 12.Seidl R, Schelhaas M, Lexer M. Unraveling the drivers of intensifying forest disturbance regimes in Europe. Glob Change Biol. 2011;17(9):2842–2852. [Google Scholar]
- 13.Aldersley A, Murray SJ, Cornell SE. Global and regional analysis of climate and human drivers of wildfire. Sci Total Environ. 2011;409(18):3472–3481. doi: 10.1016/j.scitotenv.2011.05.032. [DOI] [PubMed] [Google Scholar]
- 14.Gitay H, Brown S, Easterling W, Jallow B. Climate Change 2001: Impacts, Adaptation, and Vulnerability: Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge Univ Press; Cambridge, UK: 2001. [Google Scholar]
- 15.IPCC-WGI 2013. Climate Change 2013: The Physical Science Basis. Annex i: Atlas of Global and Regional Climate Projections: Final Draft Underlying Scientific-Technical Assessment (WMO, Geneva)
- 16.Batllori E, Parisien MA, Krawchuk MA, Moritz MA. Climate change-induced shifts in fire for Mediterranean ecosystems. Glob Ecol Biogeogr. 2013;22(10):1118–1129. [Google Scholar]
- 17.Mace G. Global change: Ecology must evolve. Nature. 2013;503(7475):191–192. doi: 10.1038/503191a. [DOI] [PubMed] [Google Scholar]
- 18.Kennedy RE, et al. Bringing an ecological view of change to LANDSAT-based remote sensing. Front Ecol Environ. 2014;12(6):339–346. [Google Scholar]
- 19.Hijmans RJ, et al. Very high resolution interpolated climate surfaces for global land areas. Int J Climatol. 2005;25(15):1965–1978. [Google Scholar]
- 20.Wilson AM, Silander JA. Estimating uncertainty in daily weather interpolations: A Bayesian framework for developing climate surfaces. Int J Climatol. 2014;34(8):2573–2584. [Google Scholar]
- 21.Townshend JR, Goff TE, Tucker CJ. Multitemporal dimensionality of images of normalized difference vegetation index at continental scales. IEEE Trans Geosci Rem Sens. 1985;GE-23(6):888–895. [Google Scholar]
- 22.Tucker CJ. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens Environ. 1979;8(2):127–150. [Google Scholar]
- 23.Curran P. Multispectral remote sensing of vegetation amount. Prog Phys Geogr. 1980;4(3):315–341. [Google Scholar]
- 24.Zhao M, Running S, Heinsch FA, Nemani R. 2011. Land Remote Sensing and Global Environmental Change, Remote Sensing and Digital Image Processing, eds Ramachandran B, Justice CO, Abrams MJ (Springer, New York), pp 635–660.
- 25.Huete A, et al. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens Environ. 2002;83(1-2):195–213. [Google Scholar]
- 26.Lentile LB, et al. Remote sensing techniques to assess active fire characteristics and post-fire effects. Int J Wildland Fire. 2006;15(3):319–345. [Google Scholar]
- 27.Roder A, Hill J, Duguy B, Alloza J, Vallejo R. Using long time series of landsat data to monitor fire events and post-fire dynamics and identify driving factors. a case study in the ayora region (eastern Spain) Remote Sens Environ. 2008;112(1):259–273. [Google Scholar]
- 28.Schroeder T, Cohen W, Yang Z. Patterns of forest regrowth following clearcutting in western oregon as determined from a LANDSAT time-series. For Ecol Manage. 2007;243(2-3):259–273. [Google Scholar]
- 29.Mitri GH, Gitas IZ. Mapping post-fire forest regeneration and vegetation recovery using a combination of very high spatial resolution and hyperspectral satellite imagery. Int J Appl Earth Obs Geoinf. 2013;20:60–66. [Google Scholar]
- 30.Hernández Clemente R, Navarro Cerrillo RM, Gitas IZ. Monitoring post-fire regeneration in mediterranean ecosystems by employing multitemporal satellite imagery. Int J Wildland Fire. 2009;18(6):648–658. [Google Scholar]
- 31.van Leeuwen WJD. Monitoring the effects of forest restoration treatments on post-fire vegetation recovery with MODIS multitemporal data. Sensors (Basel Switzerland) 2008;8(3):2017–2042. doi: 10.3390/s8032017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hope A, Albers N, Bart R. Characterizing post-fire recovery of fynbos vegetation in the western cape region of south africa using MODIS data. Int J Remote Sens. 2012;33(4):979–999. [Google Scholar]
- 33.Gouveia C, DaCamara C, Trigo R. Post-fire vegetation recovery in Portugal based on spot/vegetation data. Nat Hazards Earth Syst Sci. 2010;10:673–684. [Google Scholar]
- 34.Cowling RM, Richardson DM, Paterson-Jones C. 1995. Fynbos: South Africa’s Unique Floral Kingdom (Fernwood Press, Vlaeberg, South Africa)
- 35.Manning J, Goldblatt P. 2012. Plants of the Greater Cape Floristic Region, Strelitzia (South African National Biodiversity Institute, Pretoria, South Africa), Vol 1.
- 36.Forest F, et al. Preserving the evolutionary potential of floras in biodiversity hotspots. Nature. 2007;445(7129):757–760. doi: 10.1038/nature05587. [DOI] [PubMed] [Google Scholar]
- 37.Van Wilgen BW, et al. Fire management in Mediterranean climate shrublands: A case study from the Cape Fynbos, South Africa. J Appl Ecol. 2010;47(3):631–638. [Google Scholar]
- 38.Cowling RM, Pressey RL. Rapid plant diversification: Planning for an evolutionary future. Proc Natl Acad Sci USA. 2001;98(10):5452–5457. doi: 10.1073/pnas.101093498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wilson AM, Silander JA, Gelfand A, Glenn JH. Scaling up: Linking field data and remote sensing with a hierarchical model. Int J Geogr Inf Sci. 2011;25(3):509–521. [Google Scholar]
- 40.Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A. Bayesian measures of model complexity and fit. J R Stat Soc Series B Stat Methodol. 2002;64(4):583–639. [Google Scholar]
- 41.Newman BD, et al. Ecohydrology of water-limited environments: A scientific vision. Water Resour Res. 2006;42(6):W06302. [Google Scholar]
- 42.Mustart P, Cowling R. Effects of soil and seed characteristics on seed germination and their possible roles in determining field emergence patterns of four agulhas plain (south africa) proteaceae. Can J Bot. 1993;71(10):1363–1368. [Google Scholar]
- 43.Lechmere-Oertel R, Cowling R. Abiotic determinants of the fynbos/succulent karoo boundary, south africa. J Veg Sci. 2001;12(1):75–80. [Google Scholar]
- 44.Vereecken H, Maes J, Feyen J, Darius P. Estimating the soil moisture retention characteristic from texture, bulk density, and carbon content. Soil Sci. 1989;148(6):389–403. [Google Scholar]
- 45.Midgley JJ. Mortality of cape proteaceae seedlings during their first summer. South African Forestry J. 1988;145:9–12. [Google Scholar]
- 46.Bond WJ. Fire survival of cape proteaceae-influence of fire season and seed predators. Plant Ecol. 1983;56(2):65–74. [Google Scholar]
- 47.Merow C, et al. On using integral projection models to generate demographically driven predictions of species’ distributions: Development and validation using sparse data. Ecography. 2014;37(12):1167–1183. [Google Scholar]
- 48.Vlok JHJ, Yeaton RI. The effect of short fire cycles on the cover and density of understorey sprouting species in south african mountain fynbos. Divers Distrib. 2000;6(5):233–242. [Google Scholar]
- 49.Campbell BM, Werger MJA. 1988. Plant form in the mountains of the Cape, South Africa. J Ecol 76(3):637–653.
- 50.Beck P, Atzberger C, Hogda K, Johansen B, Skidmore A. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens Environ. 2006;100(3):321–334. [Google Scholar]
- 51.Ahl D, et al. Monitoring spring canopy phenology of a deciduous broadleaf forest using MODIS. Remote Sens Environ. 2006;104(1):88–95. [Google Scholar]
- 52.Zhang XY, et al. Monitoring vegetation phenology using MODIS. Remote Sens Environ. 2003;84(3):471–475. [Google Scholar]
- 53.Batt RD, Carpenter SR, Cole JJ, Pace ML, Johnson RA. Changes in ecosystem resilience detected in automated measures of ecosystem metabolism during a whole-lake manipulation. Proc Natl Acad Sci USA. 2013;110(43):17398–17403. doi: 10.1073/pnas.1316721110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Buhk C, Meyn A, Jentsch A. The challenge of plant regeneration after fire in the mediterranean basin: Scientific gaps in our knowledge on plant strategies and evolution of traits. Plant Ecol. 2007;192(1):1–19. [Google Scholar]
- 55.Thuiller W, Slingsby JA, Privett SDJ, Cowling RM. Stochastic species turnover and stable coexistence in a species-rich, fire-prone plant community. PLoS ONE. 2007;2(9):e938. doi: 10.1371/journal.pone.0000938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kruger FJ, Bigalke RC. 1984. Ecological Effects of Fire in South African Ecosystems, Ecological Studies, eds Booysen PV, Tainton NM (Springer, Berlin), Vol 48, pp 67–114.
- 57.Bradstock R, Williams R, Gill A. Flammable Australia: Fire Regimes, Biodiversity and Ecosystems in a Changing World. Csiro Publishing; Clayton, VIC, Australia: 2012. [Google Scholar]
- 58.van Wilgen BW. 1981. Some effects of fire frequency on fynbos plant community composition and structure at Jonkershoek, Stellenbosch. South African Forestry J 118(1):42–55.
- 59.Kruger FJ, Lamb A. 1979. Conservation of the Kogelberg State Forest. Preliminary Assessment of the Effects of Management From 1967 to 1978 (Jonkershoek Forestry Research Centre, Stellenbosch, South Africa)
- 60.Forsyth G, van Wilgen B. 2008. The recent fire history of the Table Mountain National Park, and implications for fire management. Koedoe: African Protected Area Conserv Sci 50(1):3–9.
- 61.Schulze RE. 2007. The South African Atlas of Agrohydrology and Climatology (Water Research Commission, Pretoria, South Africa)
- 62.Clark JS. Models for Ecological Data: An Introduction. Princeton Univ Press; Princeton: 2007. [Google Scholar]
- 63.Diaz-Delgado R, Pons X. Spatial patterns of forest fires in Catalonia (NE of spain) along the period 1975–1995: Analysis of vegetation recovery after fire. For Ecol Manage. 2001;147(1):67–74. [Google Scholar]
- 64.DeKlerk H. A pragmatic assessment of the usefulness of the MODIS (terra and aqua) 1-km active fire (MOD14a2 and MYD14a2) products for mapping fires in the fynbos biome. Int J Wildland Fire. 2008;17(2):166–178. [Google Scholar]
- 65.Province WC. 2000. Western Cape Nature Conservation Laws amendment act, 2000 (no. 3 of 2000)
- 66.Forsyth GG, van Wilgen BW. 2007. An Analysis of the Fire History Records From Protected Areas in the Western Cape (CSIR, Stellenbosch, South Africa)
- 67.De Klerk H, Wilson AM, Steenkamp K. Evaluation of satellite-derived burned area products for the fynbos, a Mediterranean shrubland. Int J Wildland Fire. 2012;21(1):36–47. [Google Scholar]
- 68.Roy D, Boschetti L, Justice C, Ju J. The collection 5 MODIS burned area product–global evaluation by comparison with the MODIS active fire product. Remote Sens Environ. 2008;112(9):3690–3707. [Google Scholar]
- 69.Roy D, Boschetti L. 2008. MODIS Collection 5 Burned Area Product (MCD45) User’s Guide v1.1 (South Dakota State Univ, Brookings, SD)
- 70.Escuin S, Navarro R, Fernandez P. Fire severity assessment by using NBR (normalized burn ratio) and NDVI (normalized difference vegetation index) derived from LANDSAT TM/ETM images. Int J Remote Sens. 2008;29(4):1053–1073. [Google Scholar]
- 71.Epting J, Verbyla D. Landscape-level interactions of prefire vegetation, burn severity, and postfire vegetation over a 16-year period in interior Alaska. Can J For Res. 2005;35(6):1367–1377. [Google Scholar]
- 72.Markham CG. 1970. Seasonality of precipitation in the United States. Ann Assoc Am Geograph 60(3):593–597.
- 73.Latimer AM, Wu S, Gelfand AE, Silander JA., Jr Building statistical models to analyze species distributions. Ecol Appl. 2006;16(1):33–50. doi: 10.1890/04-0609. [DOI] [PubMed] [Google Scholar]
- 74.Cowling RM. The occurrence of C3 and C4 grasses in fynbos and allied shrublands in the south eastern Cape, South Africa. Oecologia. 1983;58(1):121–127. doi: 10.1007/BF00384551. [DOI] [PubMed] [Google Scholar]
- 75.Soderberg K, Compton JS. 2007. Dust as a nutrient source for fynbos ecosystems, South Africa. Ecosystems 10(4):550–561.
- 76.Neteler M, Bowman MH, Landa M, Metz M. GRASS GIS: A multi-purpose open source GIS. Environ Model Softw. 2012;31:124–130. [Google Scholar]
- 77.Sherman R, Mullen R, Haomin L, Zhendong F, Yi W. Spatial patterns of plant diversity and communities in alpine ecosystems of the Hengduan mountains, Northwest Yunnan, China. J Plant Ecol. 2008;1(2):117–136. [Google Scholar]
- 78.Dormann CF, et al. 2013. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 36(1):027–046.
- 79.Kalognomou EA, et al. A diagnostic evaluation of precipitation in CORDEX models over southern Africa. J Clim. 2013;26(23):9477–9506. [Google Scholar]
- 80. R Development Core Team (2011) R: A Language and Environment for Statistical Computing (R Development Core Team, Vienna)
- 81.Plummer M. 2011 JAGS (just another Gibbs sampler) open-source, cross-platform engine for the BUGS language. Available at sourceforge.net/projects/mcmc-jags/. Accessed July 15, 2011.
- 82.Brooks S, Gelman A. General methods for monitoring convergence of iterative simulations. J Comput Graph Stat. 1998;7(4):434–455. [Google Scholar]
- 83.Wright D. A note on the construction of highest posterior density intervals. Appl Stat. 1986;35(1):49–53. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.