GABA-mediated repulsive coupling between circadian clock neurons in the SCN encodes seasonal time

Significance

How animals track the seasons has long been a mystery. We found a mechanism that explains how day length is encoded within the neuronal network of suprachiasmatic nucleus (SCN). Using an integrated approach combining experiments and modeling, we find evidence for changes in the coupling in the SCN that divides the clock oscillations into two clusters as a function of day length. We show that asymmetric distribution of intracellular chloride across the SCN causes this coupling change. Blocking GABA or chloride import erases the oscillator organization formed by day-length entrainment. These demonstrate that coupling through GABA is a key ingredient of day-length encoding in the SCN.

Abstract

The mammalian suprachiasmatic nucleus (SCN) forms not only the master circadian clock but also a seasonal clock. This neural network of ∼10,000 circadian oscillators encodes season-dependent day-length changes through a largely unknown mechanism. We show that region-intrinsic changes in the SCN fine-tune the degree of network synchrony and reorganize the phase relationship among circadian oscillators to represent day length. We measure oscillations of the clock gene Bmal1, at single-cell and regional levels in cultured SCN explanted from animals raised under short or long days. Coupling estimation using the Kuramoto framework reveals that the network has couplings that can be both phase-attractive (synchronizing) and -repulsive (desynchronizing). The phase gap between the dorsal and ventral regions increases and the overall period of the SCN shortens with longer day length. We find that one of the underlying physiological mechanisms is the modulation of the intracellular chloride concentration, which can adjust the strength and polarity of the ionotropic GABA_A-mediated synaptic input. We show that increasing day-length changes the pattern of chloride transporter expression, yielding more excitatory GABA synaptic input, and that blocking GABA_A signaling or the chloride transporter disrupts the unique phase and period organization induced by the day length. We test the consequences of this tunable GABA coupling in the context of excitation–inhibition balance through detailed realistic modeling. These results indicate that the network encoding of seasonal time is controlled by modulation of intracellular chloride, which determines the phase relationship among and period difference between the dorsal and ventral SCN.

The physiological and behavioral rhythms of all life on earth are bound to the Earth’s rotational cycle of ∼24 h. This fundamental rhythm is also affected by the planet’s slanted rotational axis, which causes seasonal variations in the length of the day. How life has adapted to anticipate this yearly rhythm is still debated.

The suprachiasmatic nucleus (SCN), the central circadian (∼24 h) pacemaker in mammals, consists of ∼10,000 “clock” neurons. These single-cell clocks maintain endogenous rhythms by autoregulatory feedback loops of genes including period (Per) and brain and muscle Arnt-like 1 (Bmal1) (1). Although it was speculated that seasonal rhythms might be encoded in a single cell (2), single-cell oscillations remain similar regardless of the seasonal time that the SCN tissue encodes (3). Seasonal timing is thus proposed to be encoded in the network of the SCN (4–7) through spatial reorganization of the relative phases of clocks within individual cells (8–10). Subsets of SCN clocks form phase clusters (11) that map approximately to dorsal (shell, D-SCN) and ventral (core, V-SCN) regions of the SCN. When measured through a luciferase reporter monitoring oscillations in the Bmal1 gene, the D-SCN and V-SCN clusters show a phase gap, with the D-SCN leading the V-SCN. Although the D-SCN/V-SCN cluster structure is preserved across a moderate range of day length (8–16 h) (12), the phase gap increases with increasing day length (13). The mechanism for this phase gap remains unknown.

Previous studies explain robust circadian timekeeping by in-phase synchronization of the SCN (14, 15), analogous to the classical phase model of Kuramoto (16). This in-phase state, however, is insufficient to explain the day length-dependent phase gap that is stably seen experimentally (12, 13). According to the phase model, a phase gap can result from the difference in period between the D-SCN and the V-SCN; a larger phase gap emerges when the difference in period of the D-SCN and V-SCN increases. Recent techniques have been proposed to estimate the coupling of biological oscillators from their time-course data using the Kuramoto formalism (17, 18). Using these techniques, we discover the phase clusters emerge through balancing of phase-repulsion (increasing the phase gap) and phase-attraction (decreasing the phase gap) in the SCN. This network motif is also predicted to decrease the period of the SCN as a whole as the phase gap increases, something we observe experimentally.

One difference between the D-SCN and V-SCN is through the effects of the ionotropic γ-aminobutyric acid receptor (GABA_A) (19–21). Contrary to the convention that the GABAergic inputs are hyperpolarizing, high intracellular chloride concentration in some SCN neurons can cause GABA to depolarize the cells (20). We find that the effects of the phase-repulsive coupling disappear after pharmacological blockade of GABA_A, by a surgical cut that severs physical connections between the clusters or by the chloride importer blocker, which decreases intracellular chloride and reverts the polarity of GABA_A signaling back to its normal inhibitory state. One explanation for this, which we test here, is that there is a day length-dependent increase of the relative expression of the neuronal chloride importer (Nkcc1) vs. the exporter (Kcc2), in line with the recent finding of increased excitation by GABA under LD (22). However, how increasing intracellular chloride concentration leads to phase attractive or repulsive coupling remains a mystery.

To answer how increasing intracellular chloride concentration leads to phase attractive or repulsive coupling, we appeal to detailed physiological modeling of the SCN. In a companion paper, we argue that GABA signaling normally has little effect on the SCN molecular clock (23). However, if GABA excites the D-SCN, a tonic signal is released that synchronizes the molecular clock in the D-SCN and can desynchronize and diminish oscillations the V-SCN, as well as increase this phase gap between the D-SCN and V-SCN. Here we show simulations that the day length-mediated increases in excitatory GABA in the D-SCN cause a shortening of the period in the D-SCN and a weakening of the synchronizing signal from the V-SCN, both of which increase the phase gap. We validate that these effects have a similar effect on the coupling in the Kuramoto framework as estimated from the experimental data, validating chloride’s role in coding day length.

Results

Representation of Entrained Day Length in the SCN by Network Interactions.

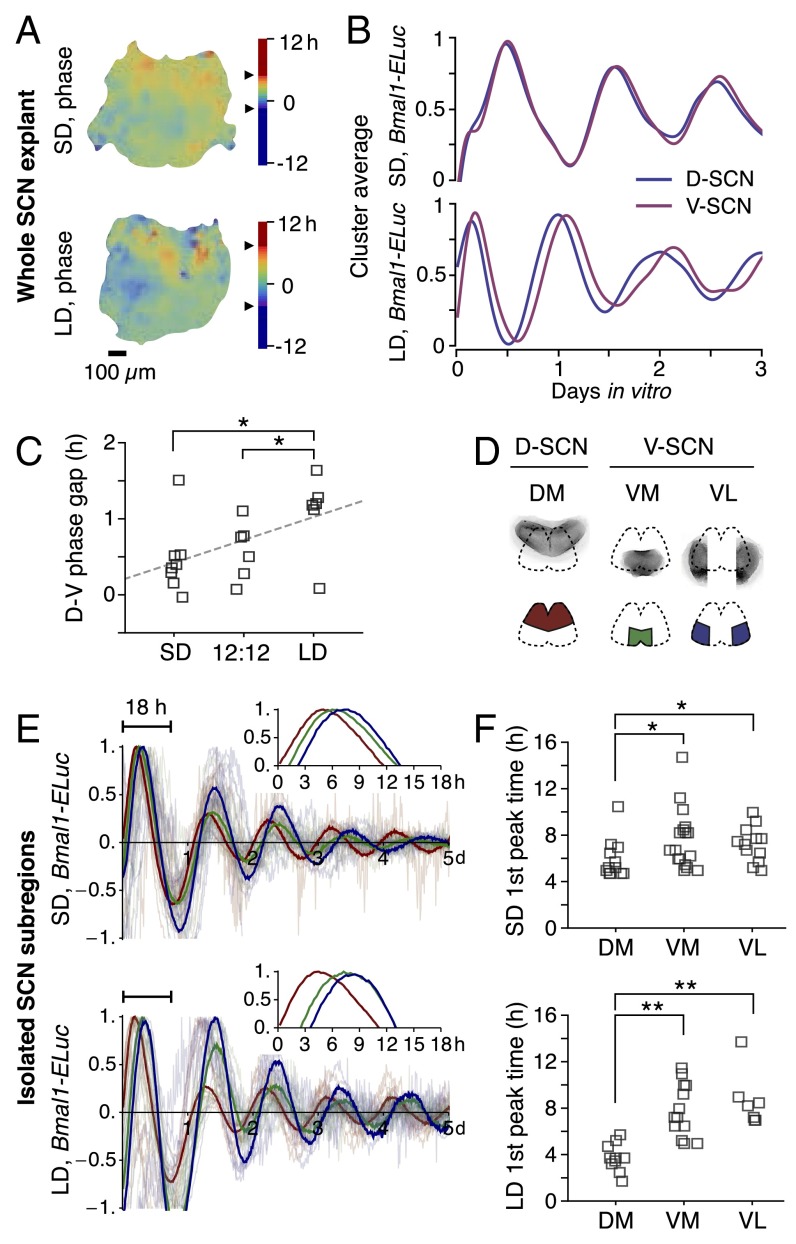
To determine how day length is internally represented, we performed time-lapse imaging of single-cell bioluminescent Bmal1 reporter activity (Bmal1-ELuc) in SCN explants from mice previously entrained under long-day (16:8 h light:dark; LD) and short-day (8:16 h light:dark; SD) light-dark cycles. After 30 or more days in the light cycle (6), mice developed changes in the free-run period under constant darkness (DD) (LD: 23.59 ± 0.05 h, mean ± SEM, n = 13; SD: 23.97 ± 0.04 h, n = 10; P = 0.00002, Student’s t test; SI Appendix, Fig. S1). The period of the Bmal1-ELuc reporter oscillation in the SCN changes similarly to the change in behavioral period after day-length entrainment (12), similar to Per1 GFP rhythms in cultured SCNs after perinatal photoperiodic imprinting (24). Bioluminescence imaging revealed that the phase distribution of the cellular Bmal1-ELuc oscillations in the SCN becomes narrower after SD and wider after LD entrainment (Fig. 1 A and B). The D-SCN and V-SCN (D-V) phase gap increased linearly with increasing day length from SD to LD (Spearman’s ρ = 0.045, P < 0.05) and the increase was significant (SD vs. LD and 12:12 vs. LD, P < 0.05; Welch’s t test, SD SCN explants n = 8; 12:12 n = 6; LD n = 6) (Fig. 1C).

Fig. 1.

Day length reorganizes the phases of Bmal1 oscillations. The length of day regulates synchrony of the peak phases of circadian Bmal1 promoter activities in the SCN. (A) SD entrainment induces a narrow phase distribution on a coronal plane of the SCN (Upper), whereas LD widens the phase gap between the dorsal (D-SCN) and the ventral subregion clusters (V-SCN) (Lower). The arrows on the scale bar indicate SD (1σ) of the period distribution. (B) The cluster averages of the detrended Bmal1-ELuc oscillations show a narrow phase gap between D-SCN and V-SCN under SD (Upper) and a wider phase gap under LD (Lower). (C) The D-SCN and V-SCN (D-V) phase gap in the first day in culture increases nearly linearly with day length across SCNs (*P < 0.05; Welch’s t test). The dashed line indicates the linear fit and horizontal variation is for illustration only. (D) The isolated SCN microsection (onigiri section) of the dorsomedial (DM, red) subregion approximates D-SCN and ventromedial (VM, green) and ventrolateral (VL, blue) subregions together approximate V-SCN (Upper) as diagrammatically illustrated and color-coded (Lower) for E. The bilateral VL microsections were put immediately next to each other in actual culture. Ensemble averages (thick line) of detrended, normalized Bmal1-ELuc oscillations in the isolated SCN subregions are presented against plots of all samples (half transparent) from SD (Upper) and LD (Lower) entrainments. The relative phase distribution is retained in the isolated subregions in the first day in culture (Inset: ensemble average for first 18 h). (F) The phase gap as a median peak time difference between DM and VM also increases with day length (*P < 0.05; **P < 0.01; Mann–Whitney U test). See SI Appendix, Fig. S2 for RT-qPCR measurement of mRNA levels in D- and V-SCN.

The initial phase distribution was latently retained in cultures of isolated SCN subregions [dorsomedial (DM), ventromedial (VM), and ventrolateral (VL) “onigiri” sections] (Fig. 1D) targeted to dissect phase clusters (12). In the isolated SCN subregions, the first-day peak times (acrophases) of DM, VM, and VL were similar in the SD-entrained group (Fig. 1E, Upper; SD: DM n = 12, VM n = 17, VL n = 12), whereas a wider phase gap was seen between the DM and ventral subregions (VM and VL) in the LD-entrained group (Fig. 1E, Lower; LD: DM n = 12, VM n = 13, VL n = 11). The intact SCN explant maintained the phase gap throughout culture (Fig. 1B), better than the isolated subregions, an effect likely due to coupling (Fig. 1E), although the phase gap in the intact SCN did increase with time. The peak time difference in the isolated subregion culture was significantly wider in the LD-entrained group than in the SD group (both DM-VM and DM-VL comparisons, LD: P < 0.01, SD: P < 0.05; Mann–Whitney U test) (Fig. 1F).

Phase Model-Based Analysis Suggests Phase-Repulsive Coupling in the SCN.

Circadian Bmal1-ELuc oscillations in SCN neurons can be approximated using the phase equations proposed by Kuramoto (12, 16), which assume that the dynamics of individual oscillators are close to limit cycles, that coupling between cells is weak, and that the coupling only depends on the difference in phase between the oscillators. In this model, the instantaneous angular frequency of individual oscillators (dθ_i/dt) is linearly related to its interaction with other oscillators, and estimating coupling coefficients (K_ij) is essentially a multiple linear regression problem between the dynamics of an oscillator (dθ_i/dt) and the coupling terms [sin(θ_j − θ_i)] (Materials and Methods). Assuming only positive coupling (K_ij > 0) would cause the oscillators to all come into phase (16). This all-attraction model, however, fit the data poorly (R² = 0.55 ± 0.03, n = 15), as did a model with all repulsive coupling (K_ij < 0) (R² = 0.56 ± 0.03, n = 15). When the coupling coefficients were allowed to have both signs, the goodness of fit greatly improved (R² = 0.98 ± 0.01, n = 15), suggesting that all-attractive or all-repulsive coupling assumptions for the model are insufficient for describing the observed oscillations.

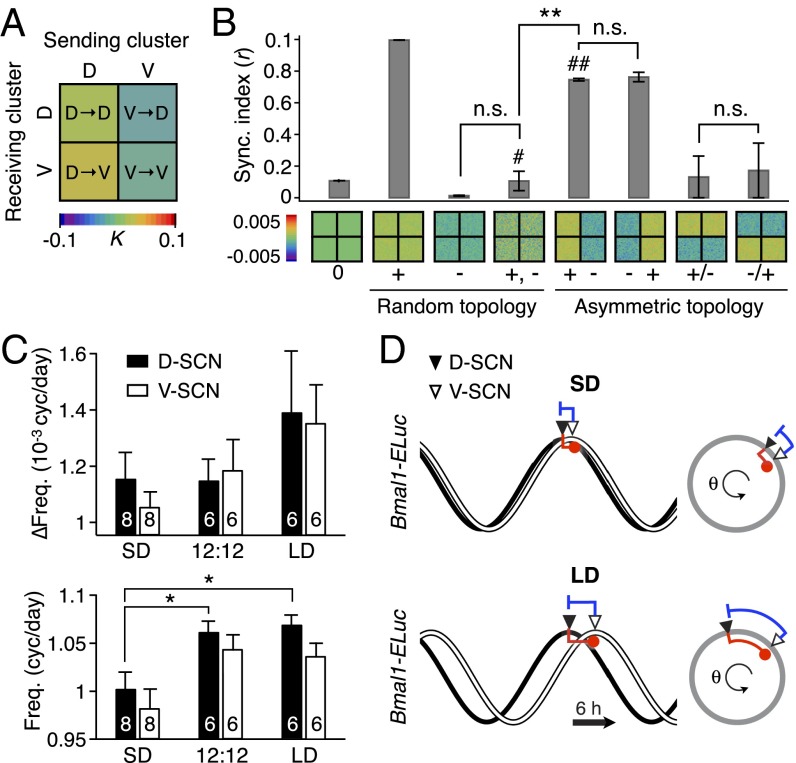
We next ask what the coupling estimation tells us about the typical behavior of the SCN oscillators in each subregion. Averaging the couplings within the D-SCN and V-SCN, which gives us the average impact of one region on the average oscillation in the other, we see that the V-to-D-SCN coupling is predicted to be the opposite of the D-to-V-SCN coupling (Fig. 2A). We simulated many other possible mixtures of repulsive and attractive couplings and found that the asymmetric structure, seen in our estimated coupling coefficients, promotes a metastable state (25) with partial synchrony (marked with #, Fig. 2B). Furthermore, a stable phase gap (attained by an intrinsic period difference between the D-SCN and V-SCN) with this coupling makes both subregions oscillate faster (∆Freq > 0 in all counts; Fig. 2C, Upper) in a day length-dependent manner (Fig. 2C, Lower).

Fig. 2.

Dynamics of SCN oscillators imply asymmetrically distributed repulsive and attractive phase couplings. (A) The phase-model–based estimation of coupling finds a network motif of phase-repulsive coupling (blue) from V- to D-SCN and phase-attractive coupling (red) from D- to V-SCN in the cross-sample mean (SEM ≤0.002, n = 6 12:12 SCNs). (B) Surrogate models under various coupling schemes show that partial synchronization emerges under the asymmetric attractive (+)–repulsive (−) coupling motif (marked with ##) found in A, whereas desynchronization ensues under a randomly distributed, structureless (marked with #) 50:50 mixture of attractive and repulsive couplings (**P < 0.001, Student’s t test for triplicates; details in SI Appendix, Fig. S3). The synchronization index (order parameter, r) measures the degree of synchronization at simulated day 30 (0 for complete desynchronization and 1 for complete synchronization). (C) Estimated shifts in the intrinsic frequency due to the coupling effects (Upper) and average intrinsic frequency in each subregion (Lower). (*P < 0.05, Student’s t test; number of explants indicated on the bar graph.) Note an increasing trend of the coupling contribution by day length in the D-SCN. (D) A two-oscillator phase model explains the day length-modulated phase gap (Fig. 1A) with an asymmetric “push” from V- and “pull” from D-SCN as a consequence of the coupling modulation, which can be explained by both coupling strength and intrinsic frequency (SI Appendix, Fig. S4).

Dynamics of the Oscillator Network with Asymmetric and Tunable Couplings.

We constructed a two-oscillator phase model of asymmetrically coupled fast and slow oscillators that represent the D-SCN and V-SCN clusters respectively. As estimated from the experimental data, the fast oscillating D-SCN receives phase-repulsive coupling from the slow oscillating V-SCN and the V-SCN receives phase-attractive coupling from the D-SCN (Eq. 4 and Materials and Methods). A stable phase gap exists in this model and can be adjusted by varying the relative coupling strengths (Fig. 2D and Materials and Methods). Under LD, when the D-SCN leads the V-SCN in phase, the larger phase gap translates as a stronger repulsive coupling that further increases the phase gap by pushing the D-SCN faster. At the same time, a weak attractive coupling on the V-SCN also speeds up the V-SCN to decrease the phase gap and both clusters reach a stable state with a faster oscillation than when uncoupled. This speeding up of both the dorsal and ventral SCN is similar to the period-shortening aftereffect seen under DD after first being exposed to a long photoperiod (12, 26). The network encoding can be modified by adjusting the strength of the repulsive coupling on the D-SCN (Fig. 3D) or, equivalently, by changing the D-SCN’s period of oscillation (SI Appendix, Fig. S4).

Fig. 3.

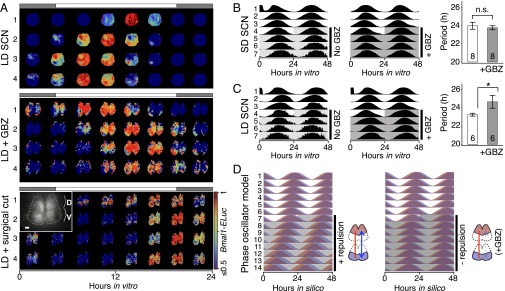
GABA_A inhibition disturbs the phase and period organization caused by long or short day length. (A) Time-lapse images of normalized Bmal1-ELuc oscillations in the LD-entrained SCNs are shown for every 3 h, color-coded to indicate the peak expression with dark red and lower-than-50% expression with dark blue (color bar on the bottom right). The clear D-V cluster formation and the short oscillation period can be seen in the control LD-entrained SCN (Upper). Application of the GABA_A blocker gabazine (GBZ) lengthens the free-running period in culture while making the cluster separation less clear (Middle). Similarly, physical separation by a surgical cut (Inset) lengthens the free-running period in the LD SCN (Lower). (Scale bar, 100 µm.) (B and C) The effect on the free-running period is observed consistently in a larger number of samples through whole-field luminometry using a photomultiplier tube. GBZ has no effect on the SD SCN culture (B) but in the LD SCN culture (C) GBZ increases the period (*P < 0.05, Student’s t test; n indicated in the bar graph). (D) The asymmetric repulsive coupling model can explain the phase and period organization under LD entrainment. With increased repulsive coupling in the D-SCN, the phase gap between D- and V- SCNs increases and the free-running period becomes shorter, as seen in the LD SCN. The light or dark shade indicates the region of vehicle or drug application. Simulation parameters are described in Materials and Methods and SI Appendix, Table S2.

Although conceptually simple, this model replicates various photic entrainment behaviors by adjusting the repulsive coupling strength between the D-SCN and the V-SCN (SI Appendix, Fig. S7), suggesting that modulation of the D-SCN may hold the key to the encoding of day length.

GABAergic Connections Mediate Phase-Repulsive Coupling.

GABA, the most predominantly expressed neurotransmitter in the SCN, can have both inhibitory and excitatory effects (19, 20), making it difficult to interpret its role in terms of circadian synchronization (14, 20, 27, 28). Because the same GABAergic signal can have opposite effects depending on the intracellular chloride concentration in downstream cells (19), we tested GABA as a physiological source of the phase-repulsive coupling using a GABA_A blocker, gabazine (GBZ, 10 µM). GBZ immediately removed the short-period aftereffect in the cultured SCN from LD-entrained animals (Fig. 3A, Middle). The neuronal connection that mediated day-length encoding was likely to be synaptic because the surgical separation of the dorsal and ventral SCN also removed aftereffects (Fig. 3A, Lower). The effect of GBZ on period was not significant in the SD-entrained SCN (Fig. 3B) but it was in the LD-entrained SCN (P < 0.05, Student’s t test; Fig. 3C). The phase model predicted period lengthening and the narrowing of the phase gap after removal of the repulsive coupling as under GBZ treatment (Fig. 3D). Because GABA can work as a desynchronizing agent (28), blocking it with GBZ slightly increases the period (12) and the synchronization index compared with the control (SI Appendix, Fig. S5), making it a strong candidate for the source of the repulsive coupling.

Day-Length Modulation of GABA_A Connection by Adjustment of Chloride Homeostasis.

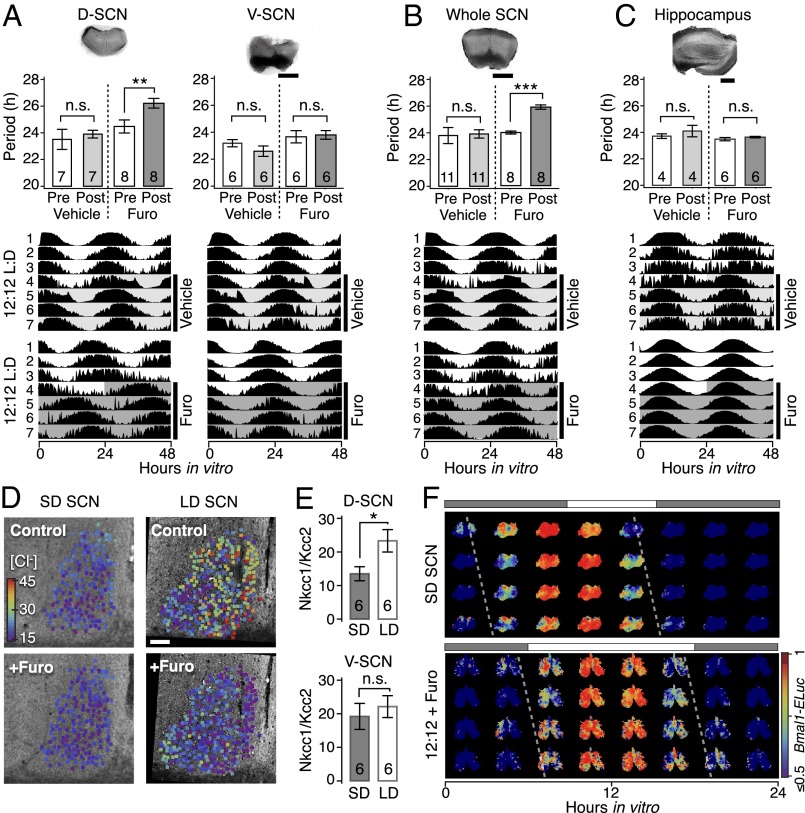
Because the modulation of the D-SCN period was found to be a hallmark of day-length encoding, we sought pharmacological agents that specifically modulate dorsal SCN oscillations. We reasoned that preferential GABA excitation in the D-SCN (19) could contribute to the speed of the Bmal1 oscillation frequency. The GABA excitation is caused by enhanced expression of the neuronal chloride importer Nkcc1 compared with chloride exporters, especially Kcc2 (29), leading to increased intracellular chloride and reversing the polarity of a cell’s response to GABA from inhibition to excitation in the SCN (20, 30). In isolated SCN subregion cultures, chronic application of the chloride importer inhibitor furosemide (Furo, 30 µM) increased the period of Bmal1-ELuc oscillations in the D-SCN, but not in the V-SCN, compared with the control condition before drug application (P < 0.01, paired t test; Fig. 4A). The same was seen when Furo was applied at the beginning of the culture. Coapplication of GBZ prevented this effect, suggesting that the period lengthening is GABA_A-mediated and a consequence of GABA excitation under high intracellular chloride concentration in the D-SCN (SI Appendix, Fig. S6). In the whole SCN, Furo caused a period lengthening similar to that seen in the D-SCN, suggesting that the V-SCN follows the D-SCN and also slows down its oscillation, causing the whole SCN to lengthen its period (Fig. 4B). No such effect was seen when Furo was applied to the hippocampus (Fig. 4C), which harbors a circadian clock but has no known role in seasonal timekeeping.

Fig. 4.

Intracellular chloride concentration and the period organization of the SCN relate to day-length entrainment. A potential mechanism for the D-V asymmetry in the repulsive coupling lies in GABA’s dual roles of excitation and inhibition, regulated by intracellular chloride concentration. (A) The chloride transporter blocker furosemide (Furo) preferentially increases the period of Bmal1-ELuc oscillations in the isolated D-SCN microsection only, entrained under 12:12 h light:dark (L:D) cycles. Representative pictures of cultured explants (Upper), statistics across explants (Middle), and representative Bmal1-ELuc activity double-plots from the explants (Lower; light shade indicates vehicle application and dark shade indicates Furo application) are presented (**P < 0.01, ***P < 0.001; paired t test; n indicated in the bar graph). A parallel experiment was performed for Furo and GBZ application from beginning of culture (SI Appendix, Fig. S6). (B) Consistent with the repulsive coupling model, the slowed oscillation in the D-SCN induces a slow-down of the whole SCN section under application of Furo. (C) This effect is specific to the SCN, because a similar treatment in the hippocampus does not show period dependence on Furo. The shade indicates the region of drug application. (Scale bar, 500 µm.) (D) MQAE imaging of a unilateral SCN shows higher intracellular chloride in LD SCN (Upper Right) compared with SD SCN (Upper Left), which is decreased by application of Furo (Lower Right). (Scale bar, 100 µm.) (E) LD entrainment also causes relative up-regulation of the neuronal chloride importer (Nkcc1) transcripts compared with the chloride exporter (Kcc2) transcripts significantly in the D-SCN (Upper) and not in the V-SCN (Lower; *P < 0.05, paired t test; see also SI Appendix, Fig. S9.) (F) As a proof-of-concept, an equinox (12:12)-entrained SCN in culture is shown to mimic the lengthened free-running period of the SD entrained SCN under application of Furo.

The corresponding relative bias of intracellular chloride concentration between the D-SCN and V-SCN was observed in our measurement by N-(ethoxycarbonylmethyl)-6-methoxyquinolinium bromide (MQAE) fluorescence. The chloride concentration was found to increase across the SCN after LD entrainment (Fig. 4D, Left) but was decreased by Furo preferentially in the D-SCN (Fig. 4D, Right and SI Appendix, Fig. S8 D–I). At the transcript level, expression of all chloride transporters was up-regulated under LD compared with SD (SI Appendix, Fig. S9 E, G, and H). However, in the D-SCN, LD increased the relative expression ratio between the neuronal chloride importer Nkcc1 and the chloride exporter Kcc2 (grand averages of six time points; P <0.05, paired t test), whereas the increase was not significant in the V-SCN (Fig. 4E). In contrast to Kcc2, although the LD entrainment up-regulated the absolute amount of transcripts, the change in the expression ratio between Nkcc1 and Kcc1 was not significant (SI Appendix, Fig. S9I). Kcc2 is critical for developmental E_GABA shift in neurons and are expressed in nonarginine vasopressin (AVP) neurons in the SCN (31). Another chloride exporter, Kcc1, is also neuronally expressed but, unlike Kcc2, is involved in osmotic cell volume regulation (31, 32).

If indeed the intracellular chloride concentration modulates the SCN network to encode the day length, the low intracellular chloride condition caused by chloride importer blockade should switch a normal equinox (12:12 h light:dark)-entrained SCN into an SD-entrained SCN. Consistent with this prediction, we found that application of Furo in the equinox (12:12)-entrained SCN narrowed the internal phase gap and lengthened the period of Bmal1-ELuc oscillations in the entire explant, like what was seen in the SD-entrained SCN (Fig. 4F). These results suggest that modulation of chloride homeostasis can be a modus operandi for day-length encoding in the SCN.

Realistic Simulation Reveals the Mechanism of Day-Length Encoding.

In a parallel study (23), we developed a multicellular and multiscale SCN model (“realistic” model) comprising detailed electrophysiology (33), the biochemistry of intracellular circadian timekeeping (34), as well as coupling through GABA and vasoactive intestinal polypeptide (VIP). This model tracks the billions of action potentials and GABA postsynaptic currents in the SCN each day as well as over 1,000 chemical reactions in each of over 1,000 cells that generate timekeeping. The model used our measurements of intracellular chloride levels throughout the SCN, allowing for detailed study of the physiology of SCN coupling (see Materials and Methods and Fig. 6B for modeling schematics). By modulating the degree of GABA excitation in the D-SCN, as determined by our chloride measurements, and the intrinsic periods in the cells of D-SCN, we found that the realistic model also predicted the increasing phase gap with increasing day length (Fig. 5 A and B). Not only did the phase distribution increase with increasing photoperiod, but as seen in Fig. 1 the D-SCN was advanced from the V-SCN.

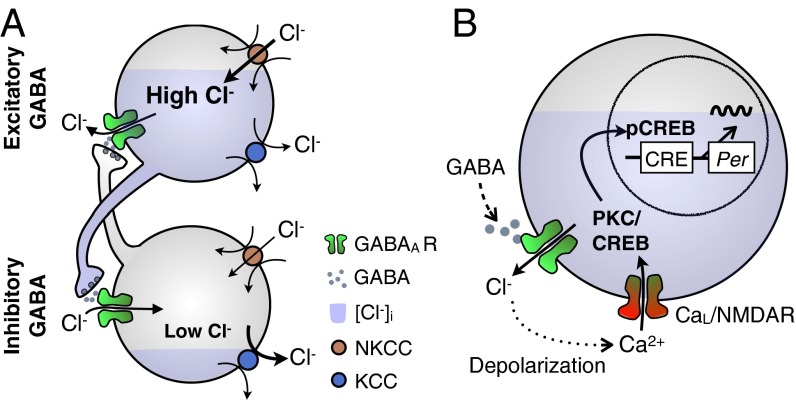
Fig. 6.

Model of day-length encoding by regulation of chloride homeostasis. (A) The GABA can introduce asymmetry in the SCN network coupling by the biased distribution of intracellular chloride, which can make GABA excitatory (Upper) or inhibitory (Lower), driven by relative activation of chloride importers (NKCC) vs. chloride exporters (KCC). (B) The GABA excitation under high intracellular chloride influences the clock gene expression cycle through excitation–transcription coupling (21) and helps organize the overall phase distribution of Bmal1 oscillations in SCN neurons, as the realistic model simulates.

Fig. 5.

The realistic multiscale SCN model reproduces day length-dependent reorganization of phases. (A) A multiscale, multicellular SCN simulation that models both electrophysiology and gene expression in each neuron faithfully reproduces emergent separation of phases between D- and V-SCN subregional oscillators under simulated LD, which is minimal under simulated SD. (B) The phase separation is replotted as the averages of the Bmal1 transcript levels in D-SCN and V-SCN subregional clusters. (C) The estimated mean phase coupling coefficients (K) from the simulation recovers the asymmetric coupling motif with a repulsive coupling from D-SCN to V-SCN (Left), which disappears when GABA coupling is removed from the model parameter (Right) (SEM ≤0.001, n = 3 simulated SCNs). (D) The realistic model predicts both the shortened dorsal period owing to increased GABA excitation during LD and the lengthened period in cultured SCN during GBZ application (GABA KO) as consequences of the change in E/I ratio.

We estimated the coupling effects from (dθ_i/dt) and the coupling terms [(sin(θ_j − θ_i)] of the simulated data by a similar procedure as the experimental data (Materials and Methods). Averaging the estimated coupling coefficients over each subregion, we found the same phase-attractive and -repulsive network structure and SEMs (Fig. 5C, Left) as found from the data (Fig. 2A). Interestingly, when GABA was removed from our simulation, leaving only VIP, all coupling was switched to attractive (Fig. 5C, Right). This implicates GABA as the source of the repulsive coupling.

We next explored the role of excitatory GABA in the D-SCN. In our companion paper (23), we demonstrate that increasing the excitatory effects of GABA in the D-SCN leads to a larger phase distribution in the SCN. This also shortens the period of the coupled SCN (Fig. 5D). Blocking GABA, or switching GABA to be all-inhibitory, lengthens the period (Fig. 5D), which matches the experiments presented in Figs. 3 and 4. Using the experimentally measured chloride levels for an equinox 12:12 light:dark cycle (from ref. 23) also shows a longer period than would be with more excitatory GABA as found in long photoperiods. Surprisingly, switching all GABA to excitatory also lengthened the period (Fig. 5D), which argues that GABA must act both in an excitatory and inhibitory way to encode photoperiod, similar to the both attractive and repulsive coupling estimated in (Fig. 2A).

So, why would excitatory GABA in the D-SCN lead to a shorter period in the SCN? The explanation suggested by the model can be seen when VIP signaling is removed, leaving just the coupling effects of GABA (SI Appendix, Fig. S10). DeWoskin et al. (23) report that under normal conditions of inhibitory GABA, GABA has little affect on synchronizing the SCN. However, when GABA’s effects become excitatory in the D-SCN, these cells become depolarized and send a tonic GABA signal (see Fig. 6 for schematics). This signal synchronizes the D-SCN and desynchronizes the V-SCN. Synchronized rhythms in the SCN are known to have larger amplitudes and shorter periods (e.g., see ref. 35) and the D-SCN decreases its period from 23.62 h to 23.3 h as the fraction of excited cells in the D-SCN increases from 40 to 80% [simulations shown in companion paper (23)]. Moreover, the V-SCN receives a tonic GABA signal at an earlier phase from the phase-advanced D-SCN, which, based on both experimental and simulated phase-response curves (PRCs) (23), will delay the V-SCN. Thus, the V-SCN delays, increasing the phase gap between the D-SCN and the V-SCN (SI Appendix, Fig. S10). In summary, excitatory GABA in the D-SCN speeds up the D-SCN and slows the V-SCN.

If the D-SCN is phase-advanced from the V-SCN, experimental and simulated PRCs both predict that the effect of VIP, which is released from the V-SCN, will delay the D-SCN, and lengthen its period, in an effort to match its phase to that of the V-SCN. However, if the V-SCN is less synchronized and has a lower-amplitude rhythm, as would happen in the presence of excitatory GABA, this VIP signal would become more diffuse, and the period-lengthening effect of the V-SCN on the D-SCN would diminish. Our real-time quantitative PCR (RT-qPCR) data (SI Appendix, Fig. S2) suggest this because during long photoperiods VIP transcripts in the V-SCN are present in significant amounts at all phases, matching this hypothesis. Thus, excitatory GABA in the D-SCN diminishes the period lengthening effects of VIP on the D-SCN, further speeding up the period.

Discussion

In this paper, we propose asymmetrical repulsive coupling as an essential network mechanism that enables day-length encoding in the SCN. This type of coupling has been proposed previously, with the fundamental idea of phase repulsion implicit in the morning–evening oscillator interpretation of behavioral splitting under LL (26, 36). Similarly, internal desynchronization has been modeled as two oscillators for sleep–wake cycles that are mutually repulsive of one other (37). Various scenarios with asymmetric coupling between two nonidentical oscillators have also been considered using Pittendrigh–Pavlidis equations, which showed that a stable, but not antiphasic, phase gap is possible when the positive (attractive) and negative (repulsive) coupling have much different strengths (38).

Our results point to modulation of GABA polarity as the underlying physiological mechanism of tunable coupling (21, 22) that is responsible for day-length encoding via the phase gap between SCN oscillators (6). Although GABA is the most abundant and ubiquitous neurotransmitter in the SCN, reports on its role for synchronization have been mixed. In neonatal preparations, it is a synchronizer (14) or plays an unclear role (27), but in mature animals (>3 wk old) it can be a desynchronizer (28) (SI Appendix, Fig. S5) or can have both effects depending on the relative phase difference between SCN subregions (13). This is in contrast with VIP, which works as a synchronizer in the SCN (39) and plays a coherent role in the phase reorganization after entrainment under varied day lengths (13). GABA’s role in the SCN has been difficult to assess. Its polarity can switch from inhibition to excitation depending on time of the day (40) or the subregion of the SCN (19) through modulation of intracellular chloride (41). Chloride transporters can switch the GABA-response polarity (20) and are expressed in a region-specific manner in the SCN (33) (Figs. 4E and 6A).

Theoretically, we find two ways to increase the phase gap between the D-SCN and V-SCN. First, the difference in intrinsic period between these two regions could be increased. Additionally, the attractive coupling between the regions, likely mediated by VIP signaling from the V-SCN, could be reduced. Our results point to both mechanisms working to modulate the phase gap. Excitatory GABA in the D-SCN causes greater synchrony and a shorter period in the D-SCN. It causes the opposite effect on the V-SCN, which releases the attractive pull of VIP.

This is consistent with the higher synchrony in firing rate rhythms in the D-SCN under LD (7) and dispersed phases in the V-SCN (5) seen experimentally. The weaker effective repulsive coupling in the SD-entrained SCN is also consistent with higher synchrony (4) and molecular rhythmicity (42). The model predicts that VIP provides the attractive coupling and that its removal markedly compromises the balance between the two asymmetric couplings. GABA’s action is complex because it depends on the intracellular chloride concentration, a fact that has caused a great deal of confusion and debate in the literature (for example, see refs. 19, 20, and 40). Our experimental results, however, suggest that the modulation of GABA response through the reorganization of chloride homeostasis makes a potent physiological pathway for day-length encoding. This interpretation is in line with the finding that the GABA-mediated excitatory input increases with the day length (22), given the increase of the chloride importer over the exporter after LD entrainment. It is also notable that the short-period light–dark cycles of 22 h induce little change in methylation of clock genes but do affect other genes including chloride transporters (ref. 43; accession nos. GSE54124 and GSE54021).

In LD- and SD-entrained SCNs, we find little difference in the amount of Bmal1 and Per2 transcripts, whereas LD up-regulates transcripts of chloride transporters (Nkcc1, Kcc1, and Kcc2), their regulator (Wnk3), and major neuropeptides of the SCN (Avp and Vip) (SI Appendix, Fig. S9). We also find that the neuronal “with no lysine” kinase (Wnk3) is up-regulated in the D-SCN under LD (SI Appendix, Fig. S9F), because it increases the activity of NKCC1 and inhibits KCC1 and KCC2 (32).

Synchronization is a powerful mechanism for bringing order out of a number of neurons. However, if all neurons are locked in the same state, they are unable to process diverse and complex information. The brain is, therefore, often observed to be in the metastable state between complete synchrony and desynchrony that generates spontaneously formed patterns such as, for example, those seen in ocular dominance columns (25). This metastable network state in the SCN is programmable by the seasonal day length and persists on a timescale much longer than the circadian timescale (44). The clock neurons in the SCN also exhibit spatiotemporal patterns in the oscillatory clock gene expressions (13, 45). Metastability in the brain clock was noticed even in the early days of circadian biology and has long been thought to be relevant for encoding seasonal rhythms (26). Our study identifies an active force resisting complete synchronization as a mechanism for metastability in the SCN, which enables a richer encoding of day-length information. Because of these findings, we believe that the SCN potentially makes a powerful platform to study the brain’s metastable states.

Materials and Methods

Day-Length Entrainment of Bmal1-ELuc Transgenic Mice.

We used Bmal1-Eluc luciferase reporter mice, generated by Nakajima (46), on a C57BL/6J background (SLC Japan) carrying a heterozygous transgene at an age around postnatal 60–90 d. Animal experiment protocols were approved by the Animal Research Committees of Hiroshima University and RIKEN Brain Science Institute. Conditions for breeding and day-length entrainment were identical to those in our previous study (12). Animals were housed in individual cages with light controlled by a computer. The control day-length condition was defined by the equinox light–dark ratio (12:12 h light:dark, L:D). The seasonal day-length conditions simulated summer and winter conditions approximately at the latitude of 45°N. In the SD paradigm, the light phase lasted for 8 h and the dark phase for 16 h (8:16 L:D), and in the LD paradigm the light phase lasted for 16 h (16:8 L:D). Day-length entrainment was performed for minimum of 30 d before sampling (6). Control and monitoring of the light conditions and general locomotor activities were done with a white light-emitting diode and a periinfrared sensor through an Arduino microprocessor (SmartProjects). The breeding room was maintained at 25 °C at all times but inside the individual breeding chamber the ambient temperature fluctuated slightly with the animal’s body temperature. This fluctuation was not exogenous and hence not a temperature cue for entrainment. Each chamber had a fan that generated constant environmental noise.

Continuous Bioluminescence Monitoring of SCN Explant Culture.

Slice culture, imaging, and photomultiplier luminometry were performed as described previously (12). Briefly, brains were isolated between 1600–2000 hours under dim light (<40 lx) after carefully dissecting optic nerves and coronally sliced at 250-µm thickness on a Microslicer (DSK) in ice-cold HBSS. SCNs were closely trimmed immediately. All SCN slices were taken from the midposterior (MP) section of the SCN, defined as the region immediately posterior to the sudden breakpoint in the spatial distribution of phase clusters along the anterior–posterior axis, where the distribution becomes from mediolateral to dorsoventral (12). Each trimmed SCN explant was cultured on a membrane (Millicell-CM; Millpore) in a 35-mm dish containing 1 mL of Dulbecco’s Modified Eagle Medium (Sigma) supplemented with B27 (Gibco/Invitrogen), penicillin–streptomycin (25 U/mL–25 µg/mL; Nacalai Tesque), and 100 µM beetle luciferin (Promega). To prevent evaporation, each dish was sealed airtight with vacuum grease. Stock aliquots of 10 mM gabazine (Sigma) in sterile distilled water and 30 mM furosemide (Sigma) in DMSO were added to the 1-mL medium immediately before recording (1:1,000 dilution). The slice culture was maintained at 37 °C (effective around the culture dish) and imaged continuously using three independent systems: a commercial incubator-microscope system (LV200, Olympus; Orca C4742-80–12AG, Hamamatsu; and a 40× objective, N.A. 0.6 LUCPlan FLN, Olympus), a custom-built upright imaging system around a Nikon FN1 microscope (Orca R2 CCD camera or ImagEM1K EM-CCD camera, Hamamatsu; a 20× objective or a 10× objective, and a relay lens, Nikon), and a custom-built microscope-free imaging system (Hamamatsu Orca R2 directly coupled to a Nikon 20× objective and a Tokai Hit microincubator chamber). Parts of recordings published previously were reanalyzed for coupling estimation (12). Binning was set to 4 × 4 and the exposure time was 15 min. For continuous bioluminescence monitoring of the whole culture dish, we used a 24-dish-on-a-wheel photomultiplier system (LM-2400; Hamamatsu) that counts photons for 1 min every 15 min, per dish.

Subregional Isolation (Onigiri Section) of the SCN Explant.

SCN explants from the MP section were microdissected into the dorsomedial (DM or D) region and the ventral region (V), which was further dissected into ventromedial (VM), and ventrolateral (VL) regions. This scheme of microdissection was as previously described (onigiri sectioning, ref. 12). Sectioning was rapidly performed on explants after transferring onto the culture membrane. The DM region was a V-shaped area from the dorsal tip of the explant extending to the ventral tip of the third ventricle where the bilateral SCNs join. The cut region was transferred on the blade to a separate dish. The sectioning and transfer took about 30 s. The dishes were immediately sealed with vacuum grease and incubated at 37 °C.

Measurement of Intracellular Free Chloride Concentration.

We estimated the chloride concentration using quenching of MQAE (Molecular Probes) fluorescence by chloride. The MP sections of the SCN sliced at 100- to 150-µm thickness were transferred to culture membranes and incubated in culture medium containing 2 mM MQAE for 1–2 h at 37 °C in the dark. After washing and a brief incubation in artificial cerebrospinal fluid (ACSF; 124 NaCl, 3 KCl, 1.2 CaCl₂, 2.8 MgCl₂, 25 NaHCO₃, 1.2 NaH₂PO₄, 10 d-glucose, and 10 Hepes, in millimolar, pH 7.4, with NaOH), fluorescence images were scanned at room temperature (23–25 °C) in z axis stacks on either a confocal microscope (FV1000; Olympus) under 405-nm excitation over 425–480 nm or a two-photon microscope (A1R; Nikon) under mode-locked 750-nm excitation over a 400- to 492-nm emission window. After imaging in ACSF (135 mM external chloride), the maximal fluorescence (F₀) was determined by scanning the sample after incubation in 0 mM chloride standard (0 KCl, 140 K-gluconate, 10 Na-gluonate, 10 Hepes, in millimolar, pH 7.4, with KOH) and ionophores nigericin (100 µM; Invitrogen) and tributyltin chloride (100 µM; Sigma). To determine the intracellular chloride concentration, we used the Stern–Volmer relation, $\left[{\text{Cl}}^{-}\right]=K_{\text{SV}}^{-1}\left(F_0/F-1\right)$, and calibrated using known chloride concentrations at 10, 20, 30, and 40 mM by adjusting concentrations of KCl and K-gluconate of the 0 mM standard (SI Appendix, Fig. S8). Owing to bleaching, not all chloride standards were used at the same time in one experiment. The Stern–Volmer constant (K_SV) was estimated to be 13 M⁻¹ in aqueous solution (SI Appendix, Fig. S8 A–C) but was variable across the SCN samples in situ (10–25 M⁻¹) owing to cellular exclusion and fluorescence bleaching of the MQAE dye. Images before and after drug treatments or chloride standards were flattened through z-stack averaging on ImageJ (NIH) and automatically aligned using the imregister function on MATLAB (The MathWorks). Regions-of-interest (ROIs) were manually selected to cover the round neuronal cell soma while avoiding areas around blood vessels. ROI fluorescence averages and center-of-mass positions were exported and sorted by center-of-mass position (SI Appendix, Fig. S8F) in Mathematica (Wolfram Research). The consistency of coronal slice plane between SD and LD comparison groups was confirmed by comparable spatial AVP expression patterns in the post hoc immunofluorescence images (SI Appendix, Fig. S11), produced with a polyclonal AVP antibody (1:1,000 dilution, Chemicon/Millipore) following the protocol described earlier (12).

Quantification of Chloride Transporter Transcripts by RT-qPCR.

LD- and SP-entrained SCN samples were taken from six to eight animals after decapitation under dim light (<40 lx) in 4-h time bins throughout a day (24 h) with an average of three independent samplings for each targeted time bin. The MP sections of the SCNs prepared at 300- to 350-µm thickness were trimmed in RNAlater ICE solution (Life Technologies) to remove the optic chiasm and hypothalamic regions surrounding the SCN and dissected into D-SCN and V-SCN microsections. The exact sampling time was determined as the time that a slice was put into the RNAlater ICE solution. After dissection, samples were quickly transferred to 50 µL PicoPure extraction buffer (Life Technologies) and chilled in liquid nitrogen before being stored at −80 °C. RNA purification was performed using a PicoPure kit (10-µL elution) or an ENZA total RNA kit (20-µL elution; Omega Bio-Tek). Total RNA from samples per one time point was for D-SCN, 572 ± 31 ng (n = 50, SD and LD pooled; mean ± SEM) and for V-SCN, 384 ± 19 ng (n = 49), quantified using a spectrophotometer (NanoDrop; Thermo Scientific). The RNA quality assessed by RNA integrity number was 8.83 ± 0.17, estimated with 2100 BioAnalyzer NanoChip (Agilent Technologies) from randomly selected samples. After an RNA purity check, cDNA was synthesized with random primers. RT-qPCR was performed in three technical replicates using the cDNA equivalent of 7.5 ng mRNA in a 20-µL volume with SYBR Green DNA binding dye on 7900HT and StepOnePlus (all Applied Biosystems). The reaction steps were 50 °C for 2 min, 95 °C for 10 min, and 40–45 cycles at 95 °C for 15 s and 60 °C for 1 min. PCR efficiencies of the primers were evaluated on SCN samples using six dilution standards in triplicates. Two reference genes (Actb and Gapdh) were used for standardization (47). Estimated Ct values were exported and analyzed on Mathematica. We used the PCR efficiency (1 for 100%) and Ct values for quantification without weighting using the formula

$$\frac{{\left(1+\text{PCR}\hspace{0.17em}{\text{efficiency}}_{\mathit{Actb}}\right)}^{{\text{Ct}}_{Actb}}+{\left(1+\text{PCR}\hspace{0.17em}{\text{efficiency}}_{\mathit{Gapdh}}\right)}^{{\text{Ct}}_{Gapdh}}}{2{\left(1+\text{PCR}\hspace{0.17em}{\text{efficiency}}_{\mathrm{sample}}\right)}^{{\text{Ct}}_{\text{sample}}}}$$

and validated the formula using two dilutions of the cDNA template (7.5 ng vs. 15 ng) in select samples. The sequences of the forward and reverse primers are listed in SI Appendix, Table S1. All measurements were made on technical triplicates.

Analysis of Time-Lapse Bioluminescence Imaging Data.

Two methods were used for image preprocessing. In the ROI-based method, square pixels (15.4 × 15.4 µm²) containing bioluminescent cells were manually selected on ImageJ and the mean luminosity and position of the ROIs were exported for subsequent period and phase analyses in Mathematica. In the grid-based method, we first removed outliers from the raw images and performed convolution with a single-cell-sized homogeneous kernel and reduced the image size such that the kernel size corresponded to one pixel, effectively mapping the images to ROI averages over all areas. The pixels in those preprocessed images were selected by a brightness criterion (12), sorted, and analyzed in Mathematica.

Phase-Oscillator Model and Fitting of the Model to Data.

In the phase-oscillator model-based approach, we assumed that the network of SCN neurons functions as a system of weakly coupled oscillators, as in other studies (12, 14). This led to a generalization to the canonical phase model (48), which describes the temporal evolution of the phase θ_i of the i-th oscillator with period τ_i as

$$\frac{d{\theta }_i}{dt}=\frac{2\pi }{{\tau }_i}+{\displaystyle \sum _{i=1}^N{H}_{ij}({\theta }_j-{\theta }_i+{\phi }_{ij})}.$$ [1]

We assumed that the interaction function H_ij is dominated by its first Fourier mode. We also assumed that the phase delay φ_ij is vanishingly small compared with the circadian period. Therefore, the model was simplified to the Kuramoto model (16):

$$\frac{d{\theta }_i}{dt}=\frac{2\pi }{{\tau }_i}+{\displaystyle \sum _{i=1}^N{K}_{ij}\sin ({\theta }_j-{\theta }_i)}.$$ [2]

Given our phase data {θ_i(t)} for individual oscillators, we can find K_ij that minimizes the sum of squared error (SSE) (see also ref. 18):

$$SSE={\Vert \left(d{\mathit{\theta }}_i\left(t\right)/dt-{\langle d{\mathit{\theta }}_i\left(t\right)/dt\rangle }_t\right)-{\displaystyle \sum _{j=0}^N{K}_{ij}\left(\sin \left({\mathit{\theta }}_j\left(t\right)-{\mathit{\theta }}_i\left(t\right)\right)-{\langle \sin \left({\mathit{\theta }}_j\left(t\right)-{\mathit{\theta }}_i\left(t\right)\right)\rangle }_t\right)}\Vert }_2^2,$$ [3]

where <x>_t represents a time average of x. Note that we subtracted time-independent parts and only used the fluctuations in the data. In the cases for negative or positive-only coefficients, we combined this SSE minimization with the corresponding constraint.

In all cases, we had more cells than the length of the data, making our regression an ill-posed problem, particularly in the unconstrained estimation of negative and positive couplings. Inspired by the observation that couplings in the SCN are sparse (49, 50), that is, only a small number of K_ij’s are nonzero, we used simultaneous minimization of the L₁ norm $\Vert K_{ij}{\Vert }_1={\displaystyle {\sum }_{j=1}^N\left|K_{ij}\right|}$ for each i, which is known to efficiently recover the sparse coefficient matrix (51). By testing with simulated data in Fig. 2B and SI Appendix, Fig. S2, we found that this procedure reduces the magnitude of the estimated couplings but maintains the sign of the couplings with significance. We also carried out 10-fold cross-validation. For constrained and unconstrained cases, we used the convex optimization package CVX (52) and the glmnet package (53) in some unconstrained cases. All of the estimation procedures were performed in MATLAB 2012a.

For the simulated data used in Fig. 5, we were not limited by a small number of time points. Therefore, we skipped the L1 norm minimization, performed a linear regression as described in the text, and verified that it gave results consistent with that found in Fig. 2. The longer and more stable simulated data also allowed us to do the proper protophase-to-phase transformation (18), which was done by extracting the protophases via a Hilbert transform (where the first and last data points of the simulation were not included) during one cycle for each of the oscillators individually, and combining them into one probability density function.

A Two-Oscillator Model for Day-Length Encoding.

The coupling estimation inspired us to reduce Eq. 2 for the SCN network into two phase-oscillators, the dorsal (θ_D) and the ventral (θ_V) with respective intrinsic frequencies ${\mathit{\omega }}_D$ and ${\mathit{\omega }}_V$, which are related to the period τ by ω = 2π/τ:

$$\begin{array}{l}\frac{d{\mathit{\theta }}_D}{dt}={\mathit{\omega }}_D-K_{VD}\sin \left({\mathit{\theta }}_V-{\mathit{\theta }}_D\right)\\ \frac{d{\mathit{\theta }}_V}{dt}={\mathit{\omega }}_V+K_{DV}\sin \left({\mathit{\theta }}_D-{\mathit{\theta }}_V\right),\end{array}$$ [4]

where K_VD > 0 and K_DV > 0 indicate the coupling contributions from V to D and from D to V, respectively. K_VD is preceded by a minus sign to represent repulsive coupling. Eqs. 4 are more easily analyzed by rewriting the variables in terms of averages and differences: that is, phases as $\overline{\mathit{\theta }}=\left({\mathit{\theta }}_V+{\mathit{\theta }}_D\right)/2$ and $\mathrm{\Delta }\mathit{\theta }={\mathit{\theta }}_V-{\mathit{\theta }}_D$, frequencies as $\overline{\mathit{\omega }}=\left({\mathit{\omega }}_V+{\mathit{\omega }}_D\right)/2$ and $\mathrm{\Delta }\mathit{\omega }={\mathit{\omega }}_V-{\mathit{\omega }}_D$, and coupling constants as $\overline{K}=\left(K_{\mathrm{V}\mathrm{D}}+K_{\mathrm{D}\mathrm{V}}\right)/2$ and $\mathrm{\Delta }K=K_{DV}-K_{VD}$. If the phase gap is small, that is, both oscillators operate in a state close to synchrony, we can approximate $\sin \mathrm{\Delta }\mathit{\theta }\sim \mathrm{\Delta }\mathit{\theta }$ and write

$$\begin{array}{l}\frac{d\mathrm{\Delta }\mathit{\theta }}{dt}=\mathrm{\Delta }\mathit{\omega }-\mathrm{\Delta }K\cdot \mathrm{\Delta }\mathit{\theta }\\ \frac{d\mathit{\theta }}{dt}=\overline{\mathit{\omega }}-\overline{\mathit{K}}\cdot \mathrm{\Delta }\mathit{\theta }.\end{array}$$ [5]

The oscillators maintain a stable phase gap $\widetilde{\mathrm{\Delta }\mathit{\theta }}=\mathrm{\Delta }\mathit{\omega }/\mathrm{\Delta }K$ when $d\mathrm{\Delta }\mathit{\theta }/dt$ = 0 and an effective frequency $\tilde{\mathit{\omega }}=\overline{\mathit{\omega }}-\overline{K}\cdot \widetilde{\mathrm{\Delta }\mathit{\theta }}=\tilde{\mathit{\omega }}-\mathrm{\Delta }\mathit{\omega }\overline{K}/\mathrm{\Delta }K$. External light input can be modeled to influence the average phase of the oscillator system (d$\mathit{\theta }$/dt) so that Eq. 5 becomes

$$\frac{d\mathit{\theta }}{dt}=\overline{\mathit{\omega }}-\overline{\mathit{K}}\cdot \mathrm{\Delta }\mathit{\theta }+I\left({\mathit{\varphi }}_{\mathrm{light}}-\overline{\mathit{\theta }}\right).$$ [6]

Parameters for simulating consequences of various light inputs (SI Appendix, Fig. S7) are a_D = 0.267 rad/h (τ_D = 23.5 h), ω_V = 0.256 rad/h (τ_V = 24.5 h), K_VD = 0.001 h⁻¹, and K_DV = 0.01 h⁻¹. For rhythmic light input I = 0.01 h⁻¹, and for constant conditions I(${\mathit{\varphi }}_{\mathrm{light}}-\overline{\mathit{\theta }}$) = 0 rad/h, with other parameters unchanged for DD and ω_D = 0.242 rad/h (τ_D = 26 h) for LL (SI Appendix, Table S2).

Realistic Multiscale, Multicellular SCN Model.

Detailed simulations of SCN signaling were performed using a multiscale, multicellular SCN model, developed and given in full detail in refs. 23 and 35. Briefly, the model simulates a network of 1,024 SCN neurons. Each neuron contains a biochemical model, based on mass action kinetics, of the negative feedback loops regulating clock gene expression (34). Additionally, the electrical activities of each neuron are also simulated, down to the timescale of individual action potentials, using a conductance-based model of SCN electrophysiology (33). These two models are coupled bidirectionally within each cell; the molecular clock phase controls two potassium channel conductances (g_KCa and g_K-leak) leading to circadian variation in the resting membrane voltage and electrical activity of the cell. In the other direction, calcium from the electrophysiology model affects VIP release and can directly lead to activation of Per transcription as in ref. 35. Model cells in the network are coupled by VIP (some to all connectivity) as in ref. 35, and through GABA_A signaling (10% random connectivity), modified from ref. 54 to match the strength and timing of GABAergic currents in the SCN (54, 55) (g_syn = 0.5, V_T = −20 mV, K_P = 3.0). The model enabled us to evaluate the overall network effect of differentially distributed chloride concentrations in single cells by varying the E_GABA for different cells in the network (−32 mV for GABA-excited and −80 mV for GABA-inhibited cells, respectively). All other electrophysiology parameters were unchanged between the two populations and as in ref. 23. SD SCN simulations used all original parameters as in ref. 23, with 40% of cells excited by GABA. For the LD SCN simulation, all molecular clock parameters were scaled to 102% of their original values in the 40% of SCN cells in the dorsal shell; ventral SCN parameters were unchanged. This led to effective intrinsic periods of 23.7 h in the dorsal and 24.2 h in the ventral SCN.

Statistics.

For significance tests, we first checked the datasets for normality and equal variance and when the two criteria were met we used Student's t test; when variance was unequal, we used Welch’s t test. For nonnormal data, we used Mann–Whiney u test. For linear correlation of ordinal data (day lengths), we used Spearman’s ρ. All statistical tests were performed in Mathematica 9 and MATLAB 2012.