Consequences of clonality for sexual fitness: Clonal expansion enhances fitness under spatially restricted dispersal

Abstract

Clonality is a pervasive feature of sessile organisms, but this form of asexual reproduction is thought to interfere with sexual fitness via the movement of gametes among the modules that comprise the clone. This within-clone movement of gametes is expected to reduce sexual fitness via mate limitation of male reproductive success and, in some cases, via the production of highly inbred (i.e., self-fertilized) offspring. However, clonality also results in the spatial expansion of the genetic individual (i.e., genet), and this should decrease distances gametes and sexually produced offspring must travel to avoid competing with other gametes and offspring from the same clone. The extent to which any negative effects of clonality on mating success might be offset by the positive effects of spatial expansion is poorly understood. Here, we develop spatially explicit models in which fitness was determined by the success of genets through their male and female sex functions. Our results indicate that clonality serves to increase sexual fitness when it is associated with the outward expansion of the genet. Our models further reveal that the main fitness benefit of clonal expansion might occur through the dispersal of offspring over a wider area compared with nonclonal phenotypes. We conclude that, instead of interfering with sexual reproduction, clonal expansion should often serve to enhance sexual fitness.

Modular growth, clonality, and hermaphroditism are widespread features of sessile organisms. Sessile organisms might benefit from modularity and the spatial expansion of the individual via enhanced resource capture, and thereby improved growth and survival (1–3). However, growth and survival are only two of the key components of an organism’s life history, and the third, reproduction, is the one that is most intimately linked to fitness. Indeed, during reproduction, the growth of a modular hermaphrodite might interfere with its success as a parent. In particular, it has been argued that the production of numerous partially or fully autonomous clonal modules (i.e., ramets) should interfere with mating success because there is a nonzero chance that sperm (or pollen) will encounter the receptive tissues associated with the female function of the same genetic individual (i.e., the genet). All else being equal, the larger the clone, the greater the chance that this kind of mating interference should occur (4, 5). The negative effects of such intraclonal mating is expected to occur through reductions in the number of offspring sired on other genets (i.e., outcross siring success, corresponding with the fitness of individuals via their male function) and, in self-compatible organisms, through inbreeding depression (i.e., a reduction in offspring fitness, with negative effects on the fitness of individuals through their female function; e.g., ref. 5). However, these forms of mating interference are simply by-products of attaining a larger size and are not exclusively associated with clonality (6). Moreover, several emerging studies on the sexual fitness of self-compatible clonal plants have revealed high outcrossing rates (e.g., refs. 7–9) and presumably therefore no negative fitness impacts arising from the “intrusion of clonal growth” (4) on sexual fitness.

Because mating in plants typically involves near neighbors, whether or not clonality interferes with mating should depend on how clonal growth affects the spatial relations of ramets from different genets (5, 10–12). The growth forms of clonal plants range from compact with closely aggregated ramets (a so-called “phalanx” growth form) to laterally spreading with loosely aggregated ramets (a “guerrilla” growth form; ref. 13). These different growth forms are likely to differ in the degree to which they can compete or resist competition, and the degree to which they can sample the environment (14–16) and “forage” for resources (17, 18). In addition, by affecting the extent of genet intermingling and the proximity to mating partners, clonal growth forms should also affect the degree to which clonal growth interferes with plant mating and sexual fitness (12).

Evidence for the interference of clonal growth on plant mating patterns and sexual fitness is mixed. Some studies have indicated that clonality increases selfing rates (refs. 4 and 19; and see ref. 20) and reduces pollen export (4, 21). However, many of these studies were conducted on plants with a phalanx growth form and/or used indirect proxies to measure selfing and pollen export. A detailed study that partitioned selfing into its specific components [the movement of self pollen: (i) within flowers; (ii) between flowers within branches; (iii) between branches within ramets; and (iv) between ramets] found that between-ramet pollen movement accounted for only one-third of selfing by a plant with intermingled genets (19). More recent studies have shown that outcrossing rates can be substantial if clones are intermingled (7, 8, 22). However, in general, patterns of clonal intermingling and its effects on mating patterns remain poorly understood.

In addition to the indirect effects of clonality on sexual fitness via its effects on mating patterns, clonality might also directly interfere with sexual fitness if investment in clonal reproduction reduces the amount of resources available for investment in sexual reproduction. Trade-offs between sexual reproduction and clonal growth have received considerable attention (reviewed in ref. 5). Again, evidence that trade-offs affect sexual fitness is mixed, and some studies conducted at the level of entire genets have found negligible resource costs of clonality (23, 24). However, manipulative and artificial selection studies conducted at the level of individual ramets and at the whole-genet level have shown that these trade-offs can occur, with clonal investment incurring substantial reductions in seed production (25, 26). Indeed, depending on the currency used to evaluate the costs of sexual and clonal reproduction, direct 1:1 trade-offs between sexual and clonal offspring have been found (27).

The above discussion clearly indicates that the fitness implications of clonal expansion can vary, at least in part through the effects that clonal expansion might have on the probability that pollen exchange occurs within vs. between clones. Moreover, the only attempt to model the mating implications of clonal expansion indicated that, instead of incurring a mating penalty, clonal expansion might often increase sexual fitness (28). However, that model was not spatially explicit and the potential mating costs of clonality are expected to arise from spatial associations among ramets during mating. This occurs because pollen dispersal for both wind- and animal-pollinated plants is typically strongly leptokurtic, with the majority of pollen dispersed to neighboring individuals (29). Short pollen dispersal distances are also a problem for nonclonal plants and can result in the transfer of pollen between inflorescences within plants or between flowers within an inflorescence (30), with the same negative fitness consequences as between-ramet pollen transfer for clonal plants. Moreover, the outward growth of a genet should generally decrease intergenet distances, increasing the likelihood that pollen dispersal “shadows” overlap with the locations of other genets (11). All else being equal, pollen grains from clonal plants should therefore have higher encounter rates with other genets than pollen from nonclonal plants.

Regardless of how clonal expansion affects mating patterns, any outward spread of genets might be favored during seed dispersal and recruitment. As for pollen dispersal, seed dispersal is often strongly leptokurtic (29, 31). Accordingly, greater spatial dispersion of reproductive modules in clonal compared with nonclonal plants should increase the area encompassed by seed dispersal shadows, reducing competition among seeds from the same genet for recruitment opportunities (i.e., local resource competition; ref. 32). Patterns of pollen and seed dispersal have been shown to affect selection on allocations to pollen and seed production (33). Similarly, we expect that selection on the investment in clonal expansion will depend on how clonality affects patterns of seed and pollen dispersal, and therefore sexual fitness.

Here, we develop a spatially explicit invasion analysis and stochastic simulations to evaluate the consequences of clonal expansion for sexual fitness. Our main objective was to evaluate the circumstances under which clonal propagation can be favored over increased size (and therefore reproductive output) of the main shoot. We assumed that clonal investment incurs a cost that trades off directly with reproductive investment (e.g., ref. 27). In the models, we explored the effects of (i) the degree to which clones were spatially intermingled, (ii) pollen and seed dispersal distances, and (iii) the penalty to selfing from inbreeding depression. We show that, even if the production of additional ramets reduces total reproductive output, clonal phenotypes are often favored, especially under spatially restricted dispersal of pollen or seeds. Clonality therefore appears to be advantageous under limited mate availability and competition among seeds to become established.

Materials and Methods

Spatially Explicit Invasion Analysis.

We considered an infinitely large population of plants that each occupied a single unit of space in one dimension (i.e., there were r plants per unit linear distance r). Each resident plant in the population had a fixed budget for investment in clonal growth (G) vs. sexual reproduction (1 − G). Investment in clonality therefore yielded a direct trade-off with the production of pollen and seeds compared with nonclonal phenotypes. We further assumed that generations were nonoverlapping and that clonal expansion was a linear function of investment in growth (i.e., n = k_gG, where k_g is a constant that determines the number of shoots per clone, n). Following Dorken and Van Drunen (28), we set k_g = 10. This constrained allocations of G to range between 0.2 and 0.9 for clonal phenotypes; a value of G = 0.1 corresponded to a nonclonal individual with a total of n = 1 ramet per genet and a value of G = 1.0 corresponded with a nonreproductive individual (i.e., a vegetative clone; this phenotype was not considered in the analysis).

Reproductive budgets were further divided between allocations to male (a) and female (1 − a) functions, which represented allocations to pollen and seeds, respectively. We assumed that seed (s) and pollen allocations (p) per genet were linear functions of a, such that s = (1 – a)(1 – G) and p = a(1 – G). All individuals in the population shared the same sex-allocation strategy with a = 0.5, and therefore s = p. We considered a rare mutant phenotype allocating Ĝ (0.1 ≤ Ĝ ≤ 0.9, yielding $\widehat{n}={\mathrm{k}}_{\text{g}}\widehat{G}$ ramets per genet) resources to clonal expansion and with equal allocations to seed and pollen production (i.e., $\widehat{s}=\widehat{p}$). These reproductive allocations were divided equally among ramets, such that the seed and pollen production per ramet were given by s/n = p/n for resident phenotypes, or $\widehat{s}/\widehat{n}\hspace{0.17em}=\hspace{0.17em}\widehat{p}/\widehat{n}$ for the mutant phenotype.

Because dispersal of seeds and pollen tends to be strongly leptokurtic, sibling seeds will often compete with one another during germination and establishment (i.e., the growth and survival of individuals from early life stages to adulthood). Similarly, pollen grains from the same plant will compete locally for access to ovules. Following Fromhage and Kokko (33), we assumed that these forms of competition reduce the fitness of plants through their male and female sex functions in a spatially explicit manner. Accordingly, pollen and seed dispersal distances were determined using probability density functions for pollen D_p(r) and seeds D_s(r) with average dispersal distances d_p and d_s, respectively. Here, we used a Gaussian distribution to describe pollen and seed dispersal as follows:

$$D_{\mathrm{p}}\left(r\right)=\hspace{0.17em}\frac{e^{-r/\pi d_{\mathrm{p}}^2}}{\pi d_{\mathrm{p}}},\hspace{1em}{D}_{\mathrm{s}}\left(r\right)=\hspace{0.17em}\frac{2e^{-r/\pi d_{\mathrm{s}}^2}}{\pi d_{\mathrm{s}}}.$$ [1a,b]

We constrained pollen and seed dispersal such that d_s = d_p and explored three average dispersal distance values. For restricted dispersal, d_s = d_p = 0.25, or one-quarter of the distance between genets. Intermediate dispersal was characterized as d_s = d_p = 1 (i.e., one-half of pollen and seeds were dispersed as far as the next genet in the population), whereas long-distance dispersal was set at d_s = d_p = 5 (i.e., one-half of pollen and seeds were dispersed five times further than the next genet). Resident and mutant phenotypes were assumed to have equal average dispersal distances.

The n ramets comprising a clone were evenly spaced over a total distance b. We chose three values of b to correspond with different clonal growth forms, and therefore, the intermingling of ramets of different clones. First, we used b = 0.1 to represent a phalanx growth strategy. Under this value of b, the ramets of clonal phenotypes were aggregated together, with the outermost ramet on one side of a genet 10 times closer to the ramet on the other side of the genet than it was to other genets in the population. Second, we used b = 5.0 to represent a guerrilla strategy. Under this value, some ramets were always further away from clone mates than they were to ramets from other genets. We also used b = 1.0 to represent an intermediate condition. Under this value, only the outermost ramet was intermingled with other genets. Values of b were equal for both resident and mutant strategies for a given parameter set. For a focal plant investing $\widehat{G}$ resources in growth (yielding n > 1 ramets), we assumed that the proportion of selfed seeds for a resident phenotype (γ) was a function of the pollen production per shoot, pollen dispersal between shoots within clones, and the degree to which a mutant phenotype was intermingled with other shoots, determined by the value b. In particular, self-fertilization within and between ramets in a genet was proportional to the ratio of self-pollen (σ) vs. allopollen (α, the contribution of pollen from other individuals in the population) at the site of the focal genet:

$$\sigma =p{D}_{\mathrm{p}}\left(0\right)+\frac{2p}{n}{\displaystyle \sum }_{i=1}^{n-1}(n-i)D_{\mathrm{p}}\left(\frac{ib}{n}\right),$$ [2]

$$\alpha ={\displaystyle \sum }_{i=0}^{n-1}{\displaystyle \sum }_{j=1}^{\infty }p{D}_{\mathrm{p}}\left(j-\frac{ib}{n}\right).$$ [3]

The proportion of selfed seeds was therefore: γ = σ/(σ + α). The proportion of selfed seeds for a mutant phenotype ($\widehat{\gamma }$) was calculated using the same approach, substituting the mutant allocation pattern ($\widehat{G}$).

Pollen and seed dispersal were affected by the spatial dispersion of ramets within a mutant clonal phenotype; i.e., we assumed that pollen and seeds were dispersed from ramets, not from the center of the genet. Thus, assuming no pollen loss due to self-fertilization within a ramet, the outgoing pollen (O_p) and seeds (O_s) from each ramet within the genet for a resident phenotype were as follows:

$$O_{\mathrm{p}}=\frac{m}{n}{\displaystyle \sum }_{i=0}^{n-1}{D}_{\mathrm{p}}\left(r-\frac{ib}{n}\right),\hspace{0.17em}{O}_{\mathrm{s}}=\frac{f}{n}{\displaystyle \sum }_{i=0}^{n-1}{D}_{\mathrm{s}}\left(r-\frac{ib}{n}\right),$$ [4a,b]

where total pollen production was given by m = p, and total seed production was given by $f=s\left(1-k_s\gamma \right)$, and where k_s represents the proportion of selfed seeds that are not viable. In other words, k_s is the magnitude of inbreeding depression. Analogous expressions for a mutant phenotype (${\widehat{O}}_p$, ${\widehat{O}}_s$, $\widehat{m}$, $\widehat{f}$) were found by substituting $\widehat{G}$ for G.

Once dispersed, seeds competed against $f\left(r_2-r_1\right)$ seeds dispersed from resident genets located between distances r₁ and r₂ from the focal genet. If we consider a focal genet with either a resident (G) or a mutant phenotype ($\widehat{G}$), its success through seed production depended on the ratio of outgoing seeds produced to the total number of seeds produced in the population against which it competed. A similar argument applies to success through outgoing pollen. Therefore, for a focal genet with the resident phenotype, postdispersal pollen success (v_p) and seed success (v_s) were given by the following: v_p = O_p/(O_p + m) and v_s = O_s/(O_s + f). For a mutant phenotype, pollen success (${\widehat{v}}_{\mathrm{p}}$) and seed success (${\widehat{v}}_{\mathrm{s}}$) were given by the following: ${\widehat{v}}_{\mathrm{p}}={\widehat{O}}_{\mathrm{p}}/\left({\widehat{O}}_{\mathrm{p}}+m\right)$ and ${\widehat{\mathrm{v}}}_{\mathrm{s}}={\widehat{O}}_{\mathrm{s}}/\left({\widehat{O}}_{\mathrm{s}}+f\right)$.

Given these expressions, the distance-dependent absolute seed fitness per genet for the resident phenotype was as follows: $F_{\mathrm{s}}={{\displaystyle \int }}_0^{\infty }{v}_{\mathrm{s}}\hspace{0.17em}\mathrm{d}\mathrm{r}.$ Similarly, for a genet with the mutant phenotype seed fitness was as follows: $\widehat{F_{\mathrm{s}}}={{\displaystyle \int }}_0^{\infty }{\widehat{v}}_{\mathrm{s}}\hspace{0.17em}\mathrm{d}\mathrm{r}$. The absolute fitness of a genet through its pollen was a function of its outcross siring success, the seeds sired via selfing, and reductions to siring success via selfing due to inbreeding depression (in runs for which k_s > 0). Thus, the pollen fitness for a resident phenotype was $F_{\mathrm{p}}={\gamma }_{\mathrm{s}}\left(1-k_{\mathrm{s}}\right)F_{\mathrm{s}}+\left(1-k_{\mathrm{s}}\gamma \right){{\displaystyle \int }}_0^{\infty }{v}_{\mathrm{p}}\hspace{0.17em}\mathrm{d}\mathrm{r}$, and for a mutant phenotype was $\widehat{F_{\mathrm{p}}}={\widehat{\gamma }}_{\mathrm{s}}\left(1-k_{\mathrm{s}}\right)\widehat{F_{\mathrm{s}}}+\left(1-k_{\mathrm{s}}\gamma \right){{\displaystyle \int }}_0^{\infty }{\widehat{v}}_{\mathrm{p}}\hspace{0.17em}\mathrm{d}\mathrm{r}$.

The overall fitness of the focal phenotype (resident or mutant) was the average of the relative fitnesses (compared with the resident phenotype) through seed and pollen production:

$$W=\frac{F_{\mathrm{s}}+\hspace{0.17em}{F}_{\mathrm{p}}\hspace{0.17em}}{F_{\mathrm{s}}+\hspace{0.17em}{F}_{\mathrm{p}}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\widehat{W}=\frac{\widehat{F_{\mathrm{s}}}+\hspace{0.17em}{\widehat{F}}_{\mathrm{p}}}{F_{\mathrm{s}}+\hspace{0.17em}{F}_{\mathrm{p}}}.$$ [5a,b]

Therefore, a resident strategy has total fitness of W = 1. Mutant strategies with fitness below the resident strategy (i.e., $\widehat{W}$ < W) will not be able to invade the population, whereas strategies conferring fitness above the resident value will invade ($\widehat{W}$ > W). Evolutionary stability of resource allocation strategies to G were evaluated using pairwise invasion analysis (ref. 34; e.g., ref. 35).

Stochastic Simulations.

Populations were initialized with 100 genets randomly placed along a one-dimensional lattice with 10⁷ cells. The lattice was scaled such that its total length was 1.0. One ramet from each genet was placed at a location chosen at random from a uniform distribution. Each genet was randomly assigned an allocation to clonal expansion (G) vs. reproduction (1 – G) with 0.1 ≤ G ≤ 0.9 (in increments of 0.1). As for the invasion analysis, allocations to G determined the number of ramets per clone (n), with n = G × 10. For clonal phenotypes with n > 1 ramets, additional ramets were evenly spaced on one side of the central ramet using distance intervals determined by the clonal aggregation variable b. To avoid edge effects, the edges of the lattice were wrapped; seed or pollen dispersing beyond the population limits reentered the population on the other side (i.e., the population was ring-shaped).

As described for the invasion analysis above, we assumed three intensities of inbreeding depression, with values for the inviability of selfed seeds (k_s) of 0, 0.5, and 1.0. Accordingly, the probability of selfed seeds germinating at each site was also scaled by 1 − k_s. We evaluated the effects of clonal intermingling on the evolution of G using the clonal aggregation variable b. On average, given the length of the lattice and the number of genets within it, the average intergenet distance was 0.005 units. We used b = 0.0005 for runs simulating a phalanx growth form. Although genets were randomly spaced in the lattice, this value typically ensured that ramets did not overlap with those from other genets. For runs simulating a guerrilla growth form, we used b = 0.025, corresponding with extensive intermingling of ramets with those from other genets. We also used the intermediate b = 0.005, corresponding with some intermingling for clonal phenotypes; for n > 1, the outermost ramet was typically intermingled with other genets.

As for the invasion analysis described above, we assumed that the allocation to sexual reproduction (1 − G) for each genet was further divided between allocations to male (a) and female function (1 − a), such that a = 0.5 and genets had equal pollen [P = a(1 − G)] and seed production [S = (1 − a)(1 − G); i.e., P = S]. Every ramet within a genet shared the same value of G, but total resources were shared equally among ramets. For example, a genet with G = 0.5 has five ramets, each with a total of 0.1 units to allocate toward sexual reproduction. Alternatively, a genet with G = 0.1 comprised one ramet with 0.9 units to allocate to sexual reproduction.

Simulations were stochastic in that (i) genets were randomly located in the lattice; (ii) mating events were determined by randomly identifying a pollen source from all possible pollen donors, scaled by a Gaussian probability density function of pollen dispersal (see details below) from each source; (iii) selecting 100 seeds at random to occupy one of 100 germination sites, chosen at random from a uniform distribution, with the probability of seed selection scaled by a Gaussian probability density function that described the dispersal of seeds from each ramet (see details below). Generations were nonoverlapping, so for each time step 100 new germination sites were randomly chosen, with the pollen and seed donors for each site found using the procedure described above.

The probability density functions used to identify pollen and seed sources during mating and seed dispersal were similar to those used in the invasion analysis described above. Specifically, for a ramet within a genet with phenotype i, the density of pollen (P) at a distance r from the source ramet was given by $P_{\mathrm{i}}=(p_{\mathrm{i}}/n_{\mathrm{i}})D_{\mathrm{p}}\left(r\right)$ and seed densities (S) for each were $S_{\mathrm{i}}=(s_{\mathrm{i}}/n_{\mathrm{i}})D_{\mathrm{s}}\left(r\right)$, where D_s(r) and D_p(r) are as defined in Eq. 1a,b above. Because the spatial scale of the simulations was different from that used in the invasion analysis, values of d_p and d_s were different from those used above. Average dispersal values were chosen to be directly analogous to the invasion analysis, such that restricted dispersal was set at one-quarter of the average intergenet distance (i.e., 0.005 units) at d_s = d_p = 0.00125 units, intermediate dispersal was d_s = d_p = 0.005 (i.e., equal to the average intergenet distance), and long-distance dispersal was d_s = d_p = 0.025 (i.e., five times the average intergenet distance). The next generation of plants were selected based on (i) the dispersal of seeds into 100 randomly chosen sites and (ii) the realized value of k_s for each seed (for seeds generated by selfing, the seed was inviable with probability k_s). If the seed was inviable, new seed and pollen donors were chosen for the germination site until the site was filled. Seedlings in the next generation had a 50:50 chance of inheriting the G allocation patterns from either their mother or father, or they could also express a G phenotype not possessed by either of its parents with a probability of 0.001 (i.e., mutation was allowed to occur and mutants could take on any value of G between 0.1 and 0.9). For genets with values of G ≥ 0.2, additional ramets were added immediately upon seedling formation in the population and offset by the interval b. This new complement of genets formed the parental generation for the next generation of plants.

For each parameter combination (b, k_s, d_s, and d_p), simulations were run for 200 generations by which time we saw no systematic changes in average values of G. Because G values were heritable and because the probability of a genet with a given value of G was determined by the relative fitness of the different clonal phenotypes in the previous generation, values of G evolved over time and for the majority of runs converged on a narrow range of values. Runs were each replicated five times to evaluate whether the populations converged on the same value of G for a given set of parameter combinations. Simulations were coded and run in R (R Core Team 2014). All code is available in Dataset S1.

Results

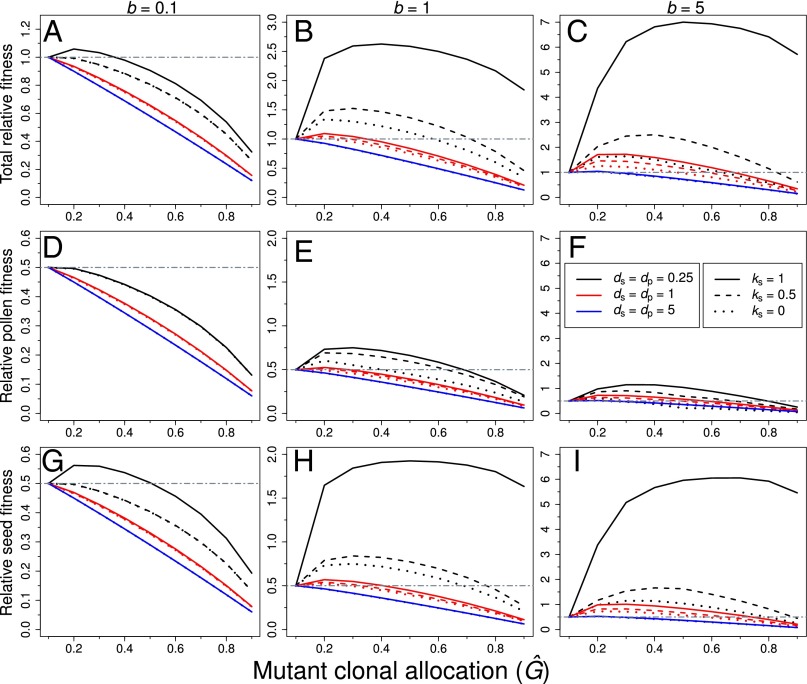
Even though allocations to clonal growth directly reduced allocations to sexual reproduction, investment in clonal growth increased sexual fitness under a wide range of values affecting the dispersal distances of pollen and seeds, the intermingling of genets, and the magnitude of inbreeding depression (Fig. 1). Although our results were consistent with expectations that clonality can interfere with mating success (i.e., phenotypes with more ramets tended to have lower fitness through male function than nonclonal phenotypes; Fig. 2 D–F), allocations to clonal growth were driven largely by the effects of clonal expansion on the successful dispersal of seeds, not pollen (Fig. 2). In particular, clonal phenotypes often had an advantage over nonclonal phenotypes via the dispersal of seeds, particularly when dispersal was spatially restricted and clones were spatially intermingled (Fig. 2 G–I).

Fig. 1.

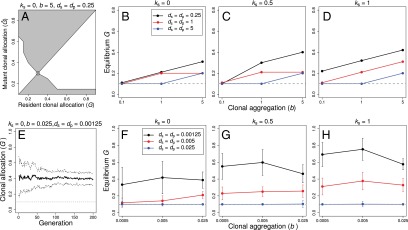
Summary of invasion analysis and stochastic simulation results showing obtained equilibrium values of allocation to clonal growth G for the indicated values of the clonal clumping variable b, the dispersal distances for pollen (d_p) and seeds (d_s), and the magnitude of inbreeding depression (k_s). An example pairwise invasion plot (PIP) is shown for the indicated values of b, d_p, d_s, and k_s (A). PIPs indicate the combinations of Ĝ vs. G for which mutant allocations to Ĝ are associated with higher (white areas of the PIP) or lower fitness (gray areas of the PIP) than the resident value of G. The intersection of the white and gray areas (marked with a circle) indicates the value of G for which the mutant and resident values of G are equal (i.e., the equilibrium value of G). A similar example from the stochastic simulations indicating the evolutionary trajectory of G (± 1 SD) values is shown for the analogous values of b, d_p, d_s, and k_s as in A (E). In the absence of inbreeding depression (k_s = 0), clonal allocations were low (or zero) unless dispersal distances of pollen and seeds were low and/or clones were spread out spatially (b ≥ 1) (B and F). Allocations to clonal growth (G) were higher under spatially restricted pollen and seed dispersal (d_p = d_s = 0.25 in the invasion analysis; d_p = d_s ≤ 0.005 in the simulations) under intermediate values of inbreeding depression (k_s = 0.5) in comparison with results obtained in the absence of inbreeding depression (C and G). When selfed seeds were inviable (k_s = 1), allocations to clonal growth were higher again, especially under spatially restricted pollen and seed dispersal (D and H). Note that the minimum value of G was 0.1 (i.e., genets were constrained to have at least n = 1 ramets; indicated with a dashed line).

Fig. 2.

Summary of the fitness of mutant phenotypes relative to a resident nonclonal phenotype for the full range of Ĝ values considered in the invasion analysis. Panels indicate the total fitness (via both pollen and seeds, i.e., W) (A–C), male fitness only (i.e., via pollen) (D–F), and female fitness (i.e., via seeds) (G–I) under k_s = 1 (solid lines), k_s = 0.5 (dashed lines), and k_s = 0 (dotted lines); colors refer to the average dispersal distances of pollen and seeds: d_s = d_p = 0.25 (black), d_s = d_p = 1 (red), and d_s = d_p = 5 (blue). When clonal growth was associated with a phalanx growth form (b = 0.1), clonal phenotypes had lower fitness than nonclonal phenotypes (i.e., W_{Ĝ = 0.1} > W_{Ĝ > 0.1}) unless selfed seeds were inviable (k_s = 1) and the dispersal of pollen and seeds was spatially restricted (i.e., d_s = d_p = 0.25) (A). When clonal growth occurred via the outward expansion of the genet (i.e., b ≥ 1), clonal phenotypes often had higher fitness than nonclonal phenotypes (i.e., W_{Ĝ = 0.1} < W_{Ĝ > 0.1}), particularly under spatially restricted dispersal of pollen and seeds (i.e., d_s = d_p ≤ 1) and under higher values of inbreeding depression (i.e., k_s ≥ 0.5) (B and C). Unless clonal growth was associated with guerrilla growth forms (i.e., b = 5), clonal phenotypes usually had lower fitness through male function (pollen) than nonclonal phenotypes (D–F). By contrast, clonal growth was often associated with greater fitness through seeds, particularly when clonal growth was associated with the outward growth of the genet (i.e., b ≥ 1) and when the dispersal of seeds was spatially restricted (i.e., d_s ≤ 1) (G–I). Note that the scale of the y axis differs with the value of b and whether total fitness or only its male or female components are depicted.

The invasion analysis and stochastic simulations yielded largely concordant results, with increased allocations to clonal growth (G) under spatially restricted dispersal (compare black lines in Fig. 1 B–D and F–H) and higher magnitudes of inbreeding depression (compare values of G as k_s increases from 0 to 1 in Fig. 1 B–D and F–H). However, for most combinations of b, k_s, d_s, and d_p, equilibrium allocations to G were higher in the simulations than the invasion analysis. Moreover, unlike the invasion analysis, we observed no clear trend for increased allocations to G under greater clonal intermingling (Fig. 1 F–H) and there were no combinations of inbreeding depression and intermingling that yielded values of G > 0.1 under broad dispersal of pollen and seeds (the blue lines in Fig. 1 F–H always tracked the minimum value of G).

Examination of the invasion analysis indicated that clonal expansion ameliorated the negative effects of restricted movement of pollen and seeds via reduced selfing rates (Fig. 3) and increasing seed fitness (Fig. 2 G–I) when clonal growth was associated with the occupation of more space (i.e., when b = 1 corresponding with the outward growth of genets and the intermingling of genets when b = 5). In particular, under spatially restricted dispersal, fitness gained through the dispersal of pollen was greater for clonal phenotypes, particularly under b ≥ 1 (Fig. 2 D–F). This more effective dispersal of pollen when clonal growth was associated with the outward expansion of the genet reduced the total amount of selfing experienced by clonal phenotypes (Fig. 3 C and E). Lower selfing combined with the dispersal of seeds over a greater area gave clonal phenotypes a substantial advantage over nonclonal phenotypes in the competition for recruitment sites, particularly when dispersal was spatially restricted (Fig. 2). As dispersal distances increased, advantages to clonal expansion declined; selfing rates were low (Fig. 3 A, C, and E) and seed fitness was highest for nonclonal phenotypes when d_s and d_p were high (Fig. 2 A–C).

Fig. 3.

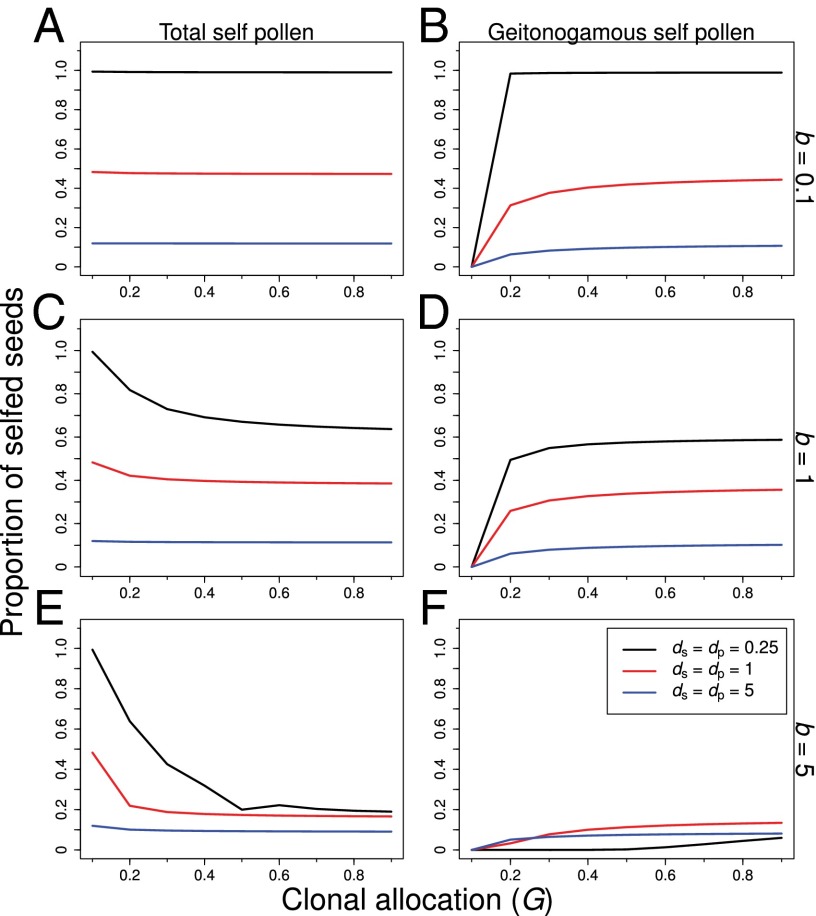
Summary of calculated values of γ, the proportion of selfed seeds, as a function of the allocation to clonal growth (G) for the indicated values of the clonal clumping variable b, and the dispersal distances for pollen (d_P) (A, C, and E). B, D, and F show the contribution of interramet geitonogamous pollen transfer to total selfing. The total proportion of selfed seeds was nearly constant with clone size for plants with a phalanx strategy (b = 0.1) (A) but declined with clone size when clonality was associated with the spatial expansion of the genet (i.e., b ≥ 1) (C and E). Spatially restricted dispersal was associated with higher selfing rates but stronger reductions in selfing as clones became larger (black lines in all panels). Interramet geitonogamy declined with the magnitude of b, such that greater intermingling of clones was associated with reduced geitonogamous selfing (B, D, and F). When clones were strongly intermingled (i.e., b = 5), interramet geitonogamy contributed little to overall selfing, particularly under spatially restricted pollen dispersal (F).

In addition to the effects of pollen and seed dispersal distances, clonal growth strategies affected equilibrium values of G in the invasion analysis. For example, guerrilla growth forms were associated with greater overall pollen (Fig. 2F) and seed fitness (Fig. 2I), and reduced selfing, mainly via very low contributions of interramet self-pollination (Fig. 3F). By contrast, phalanx growth forms were rarely favored over nonclonal phenotypes except under spatially restricted pollen and seed dispersal combined with higher magnitudes of inbreeding depression (black point in Fig. 1D at b = 0.1). The lower fitness of clonal phenotypes under phalanx growth appeared to be driven by their high selfing rates, which occurred almost entirely via interramet self-pollination (Fig. 3B). Because allocations to clonality reduced total reproductive output via trade-offs between clonal growth and sexual reproduction, high selfing by phalanx growth forms generally reduced the fitness of clonal vs. nonclonal phenotypes unless there was a high premium on the successful dispersal of seeds (i.e., under k_s = 1; Fig. 2G).

Because patterns of selfing varied for phenotypes with different allocations to G (Fig. 3), the magnitude of inbreeding depression influenced the equilibrium allocation to clonal growth. For example, when genets were intermingled clonal growth was associated with reduced selfing rates (Fig. 3E). This effect was particularly strong when dispersal distances of pollen were low (black lines in Fig. 3 C and E). By contrast, clonal growth had little effect on selfing rates under broad dispersal of pollen (blue lines in Fig. 3 C and E). Accordingly, we found contrasting effects of the magnitude of inbreeding depression on equilibrium allocations to clonal growth under the different values of seed and pollen dispersal considered here; high inbreeding depression was generally associated with higher equilibrium values of G, particularly under spatially restricted dispersal, but low inbreeding depression was associated with low (or no) allocation to clonal growth, particularly under broad dispersal.

Discussion

Here, we show that, despite a direct trade-off between allocations to clonal growth and sexual reproduction, investment in clonal growth can be favored by selection acting on sexual fitness. The majority of studies on the effects of clonal growth on sexual fitness have focused on the potential for mating interference via interramet pollen exchange (i.e., interramet geitonogamy, where geitonogamy refers to the movement of self-pollen between flowers on the same plant; e.g., refs. 4, 19, and 36). Our results, however, indicate that the major influence of clonality on sexual fitness occurred via its effects on the successful dispersal of seeds, not pollen. Clonality increases the area over which seeds can be dispersed, reducing the probability that siblings compete with one another in the next generation. Under some conditions (i.e., the intermingling of genets combined with spatially restricted pollen dispersal), clonality also promoted the fitness of plants through their male function. Again, this occurred because clonal phenotypes dispersed their pollen over a larger area than nonclonal phenotypes, yielding a siring advantage to clonal plants. In general, therefore, our results point to the importance of spatial expansion in the avoidance of dispersal limitation to the sites of mating and seed recruitment.

We found that the subdivision of reproductive effort among spatially separated ramets reduced selfing rates, yielding further advantages to clonal phenotypes. This finding is generally consistent with empirical observations of the effects of clonal growth on selfing; guerrilla growth forms are usually associated with higher outcrossing rates than plants with phalanx growth. In particular, selfing rates have been observed to decrease with the diversity of neighboring clones [e.g., Decodon verticillatus (19); Zostera marina (22)] indicating that the spatial intermingling of genets can increase pollen transfer between clones. Similarly, when ramets of the clonal shrub Vaccinium myrtillus were highly intermingled with other genets, they had lower selfing rates than ramets that were less intermingled (7). However, our results also suggest that intermingling per se is not required for clones to experience enhanced mating success (i.e., clonality was often favored under b = 1.0, which corresponded with spatially distributed clonal growth but minimal intermingling of genets). If the dispersal of pollen is spatially restricted, the outward growth of clones brings ramets into closer proximity with other genets, increasing mating opportunities for clonal phenotypes, particularly for peripheral ramets. Along these lines, Wang et al. (37) showed for the distylous, clonal aquatic plant Nymphoides peltata that fruit production at the edge of a large genet was much higher than in its middle where ramets were further away from genets of the other morph.

A major assumption of our models was that the production of seeds and pollen trades off against allocations to clonal growth. Under this assumption, selfing rates decreased with genet size when clones were highly intermingled (Fig. 3E). However, a study of a highly intermingled stand of the bamboo Sasa veitchii var. hirsuta showed that selfing rates were independent of genet size (38). On one hand, this might reflect broad pollen dispersal in S. veitchii; under broad dispersal, we expect only a weak association between clone size and selfing rates (Fig. 3). On the other hand, this discrepancy might reflect our assumption of a direct trade-off between allocations to clonal growth vs. sexual reproduction: in our model, the production of pollen by, and therefore the density of self-pollen around, the ramets of clonal phenotypes was lower than for nonclonal phenotypes. In natural populations, however, direct trade-offs between clonal growth and pollen production might not occur, for example because clonal propagules and pollen require different resources (ref. 27; see also ref. 23). Indeed, clonality might more strongly trade-off against investment in female sex function than male sex function (27, 39). If this is generally true and trade-offs between clonal growth and pollen production are usually weak, we predict that this should have two contrasting effects on the fitness of clones via their pollen production. First, selfing rates might be independent of clone size in highly intermingled patches of plants [as was found for Sasa veitchii (38)] or positively associated with clone size in less intermingled patches. Second, because under these conditions total pollen production would be substantially greater in large vs. small clones, total siring success should also be higher in larger clones, particularly in intermingled patches (and see ref. 28). Although siring success was also evaluated in the study of Sasa veitchii, as discussed by Matsuo et al. (38), the results are not conclusive because only a spatially restricted subset of the population was evaluated. Studies that contribute to our understanding of how clonal growth trades off against pollen vs. seed production are needed to help clarify the extent to which our assumptions of trade-offs should be modified.

Our models predict that clonality should be most strongly favored under spatially restricted dispersal of pollen and seeds. In terms of pollen dispersal, many clonal plants do indeed appear to have highly restricted pollen dispersal distances regardless of whether pollen dispersal occurs via wind pollination [e.g., Typha latifolia (40)] or insect pollination [e.g., Glechoma hederacea (41)]. For these plants, which can generally be characterized as having guerrilla growth forms (42–44), strong outward growth via the production of rhizomes should usually be associated with extensive intermingling of genets, enhancing the dispersal of pollen to other genets. In general therefore, we predict that, among closely related plants, pollen dispersal distances should be inversely related to the capacity for the outward spread of genets and the spatial intermingling of clones. Although this is a general expectation, not all clonal plants have spatially restricted pollen dispersal. The phalanx marine grass Posidonia australis has outcrossing rates close to 1 and pollen dispersal distances larger than mean clone sizes (9). In this species, hydrophilous pollination appears to be an effective vector for completely outcrossed offspring despite its phalanx growth form. However, clonality is an ancestral feature of seagrasses and may reflect an evolutionary constraint and/or its evolutionary maintenance because it aids in other key aspects of plant growth and survival (e.g., anchorage to the substrate; ref. 45). Similarly, Vandepitte et al. (8) found that neither the distance between ramets of different genets nor the distance to the genet center significantly affected fruiting success or seed production in a population of lily of the valley (Convallaria majalis). They concluded that pollen dispersal distances were sufficiently high to mitigate local mate scarcity despite extensive clonal growth. By contrast, however, clonal intermingling has been shown to be associated with reduced mating costs of clonal expansion in other plants (7, 38). Therefore, whether the two exceptions mentioned above really are exceptions to the pattern we predict here or more generally reflect mating patterns in clonal plants will be revealed as more studies of the mating patterns of clonal plants are conducted.

Although the major effect of clonal growth on sexual fitness considered in the literature to date has involved the concept of mating interference, our models reveal that clonal growth has its strongest effects on sexual fitness after mating. Under a broad range of assumptions of the distances over which clones spread, the magnitude of inbreeding depression, and dispersal distances, the seed fitness of clonal phenotypes was higher than that for nonclonal phenotypes. The models therefore predict that clonality will often be favored via its positive effects on fitness because, all else being equal, clonal plants disperse their seeds over a wider area than nonclonal plants, yielding a seed shadow advantage. We further predict that clonality will be most strongly favored when average seed dispersal distances are low. This expectation was partially evaluated by Eriksson (46) who tested the “escape” hypothesis for clonal plants (in this context, escape refers to the enhanced survival of seedlings that disperse away from their maternal parent and thereby avoid competing with an already-established individual). In particular, he evaluated whether clonality was associated with high dispersal ability of seeds, which might be favored if (and contrary to our expectations) clonality interferes with the recruitment of seeds. However, the results of his comparative analysis were inconsistent with the escape hypothesis. Instead, he argued that clonal growth forms might be more evolutionarily labile than seed dispersal traits (and see ref. 47). Therefore, the extent and manner of clonal growth might evolve in response to a plants ability to disperse its seeds (46). As predicted for pollen dispersal, therefore, among closely related plants we expect that seed dispersal distances and the capacity for the outward spread of genets will be inversely related.

Few studies have assessed the effects of clonal growth on fitness through both male and female functions, and among those that have (20, 48, 49) none has investigated postdispersal seed fitness. Similarly, several studies have evaluated associations between components of sexual fitness and genet size or the intermingling of genets in natural populations (e.g., refs. 7 and 38). However, inferring whether these associations reflect causal patterns or are driven by some unmeasured confounding variables is not straightforward. For example, trade-offs between allocation to clonal growth and sexual reproduction might be masked in natural populations when there is heterogeneity in resource availability allowing plants in high-resource patches to have high investment in both clonal growth and sexual reproduction (50). Therefore, ideally, one would use an experimental approach in which artificial populations are created with varying genet sizes and degrees of intermingling. Recently, Zeng et al. (51) set up such experimental arrays for the presumably self-incompatible, clonal herb Coreopsis lanceolata. They found, as expected, that seed set increased with the degree of intermingling.

Clonal intermingling, commonly associated with guerrilla growth forms, appears to promote mating and seed fitness in clonal plants. In addition, the guerrilla strategy enables the exploitation of heterogeneously distributed resources (52) and the rapid occupation of space under low density (53). By contrast, our results indicate that phalanx growth forms are disfavored by selection acting through sexual reproduction (and see ref. 4). We expect, therefore, that the maintenance of phalanx strategies reflects evolutionary constraints on the mechanisms by which plants can achieve larger size and/or selection acting through other components of the life history (i.e., survival and growth). For example, caespitose grasses, the epitome of the phalanx growth form, are nonrhizomatous and new ramets arise from within the sheath of the subtending leaf; these plants have no mechanism that could result in clonal intermingling. A phalanx growth form, however, has the advantage that it enables the consolidation, retention, and monopolization of resources at a site (53, 54). Moreover, for plants capable of plastic adjustments to traits regulating the spatial spread of clones, the expression of phalanx growth forms enables the exploitation of locally abundant resources (refs. 17 and 53; e.g., ref. 18). Clearly, more research is needed to establish under which circumstances these potential benefits of a phalanx growth form outweigh the costs of reduced pollen and seed dispersal.

Clonality is thought to increase selfing via the movement of pollen among ramets (5). Although our results indicate that large clones did indeed have higher rates of interramet self-pollination than smaller clones, total selfing was generally lower in clonal vs. nonclonal phenotypes. This result mirrors that of a recent study by Liao and Harder (55), who showed that the subdivision of reproductive display onto three ramets vs. a single large inflorescence reduced total selfing. Similarly, an analysis of the European flora found that selfing is significantly less frequent among clonal species (29% of 423 species) than among nonclonal species (47% of 388 species; ref. 56). These findings are inconsistent with previous assertions that clonality, combined with its effect on selfing rates, should affect selection on self-incompatibility systems (57, 58); as clones increase in size, selfing rates, it was argued, should increase, affecting patterns of selection on the mating system and self-incompatibility in particular. However, a metaanalysis of 36 clonal species found no significant association between compatibility status and clonal growth form (58). Moreover, our results, and those from Liao and Harder (55), indicate that no such association should occur; these two studies show that clonality affects the mode of self-pollination (i.e., whether selfing occurs via transfer of pollen within flowers, ramets, or genets; e.g., ref. 19) but can have weaker effects on total selfing rates (Fig. 3 A and C; figure 2A from ref. 55), and rather than increasing self-pollen transfer, selfing rates might decrease with clone size in comparison with nonclonal phenotypes with the same reproductive investment. Therefore, contrary to previous assertions in the literature, our results indicate that clonality should not influence the evolution of self-incompatibility.

We assumed that pollen movement was independent of other mating events involving a particular plant and, therefore, that there was no pollen discounting. This assumption is particularly suitable for plants with abiotic modes of pollination for which the pollen used in selfing within a clone should have negligible effects on the size and volume of a plant’s pollen cloud (59). However, for animal-pollinated plants, the mode of self-pollination can have substantial effects on the magnitude of pollen discounting (6) and, therefore, fitness gains via pollen. Our results indicate that clones with more widely spaced ramets have lower interramet self-pollination and higher fitness through pollen, particularly if average pollen-dispersal distances are low relative to the distance between genets (and see ref. 55). Selfing in clones with phalanx growth forms, however, was almost entirely due to interramet self-pollination, with the potential for substantial pollen discounting (Fig. 3B). Mating success in clonal plants with phalanx growth forms should therefore be enhanced by mechanisms that reduce the magnitude of pollen discounting (e.g., wind pollination and/or synchronized dichogamy; ref. 55). By contrast, our results indicate that guerrilla growth is an effective strategy for reducing interramet self-pollination and improving fitness through male function under spatially restricted pollen movement (and see ref. 55). By extension, therefore, guerrilla growth should benefit plants under “mate finding” (12), i.e., in populations in which fewer plants are potential mating partners (e.g., plants with separate sex phenotypes as in the females and males of dioecious plants, or short- and long-styled plants of heterostylous plants).

It is well established that, as plants increase in size, the probability of pollen exchange within the plant increases (6). What is less clear is how the manner by which plants achieve increased size should affect mating patterns. Increases to the number of ramets in a genet is analogous to the growth of a nonclonal plant. On a nonclonal plant, however, the growth occurs all in the same place, and there is less scope for the intermingling of reproductive modules among plants. In clonal plants, the situation is very different; each ramet is capable of an independent existence, ramets may be placed some distance away from the other ramets of the same genet, and in some species clonal growth is associated with mechanisms that enable the dispersal of daughter ramets over substantial distances (e.g., ref. 60). The question, therefore, is not what are the mating consequences of increased size but are the consequences of increased size different for clonal vs. nonclonal plants? The answer, based on the results of our study, is that, compared with nonclonal plants, plant growth via clonal expansion can result in decreased selfing rates (and see ref. 55). Perhaps more importantly, however, our results show that, for plants subject to dispersal limitation, clonal expansion might increase the probability of the successful dispersal of pollen and seeds. Because evolutionary adjustments to clonal growth forms might be more labile than evolutionary changes to the mechanisms of dispersal (46, 47), clonal growth might often evolve as a mechanism to alleviate the spatially restricted movement of pollen and seeds.