Preventing clonal evolutionary processes in cancer: Insights from mathematical models

Abstract

Clonal evolutionary processes can drive pathogenesis in human diseases, with cancer being a prominent example. To prevent or treat cancer, mechanisms that can potentially interfere with clonal evolutionary processes need to be understood better. Mathematical modeling is an important research tool that plays an ever-increasing role in cancer research. This paper discusses how mathematical models can be useful to gain insights into mechanisms that can prevent disease initiation, help analyze treatment responses, and aid in the design of treatment strategies to combat the emergence of drug-resistant cells. The discussion will be done in the context of specific examples. Among defense mechanisms, we explore how replicative limits and cellular senescence induced by telomere shortening can influence the emergence and evolution of tumors. Among treatment approaches, we consider the targeted treatment of chronic lymphocytic leukemia (CLL) with tyrosine kinase inhibitors. We illustrate how basic evolutionary mathematical models have the potential to make patient-specific predictions about disease and treatment outcome, and argue that evolutionary models could become important clinical tools in the field of personalized medicine.

Clonal evolutionary processes can be instrumental to the development of human disease and the response to treatment. A good example where this observation applies is cancer (1). Although different cancers are biologically distinct, a common principle is the escape of cells from mechanisms that ensure healthy tissue homeostasis, which is driven by the clonal evolution of cells. Cancer arises through the sequential accumulation of mutations that allow for uncontrolled cell proliferation. The end point of this evolution is typically the generation of cells that have gained the ability to migrate to and grow in sites different from the tissue of origin, which results in the formation of metastases. The selection of increasingly advantageous mutants is a key factor that drives the emergence and progression of disease (2).

Mathematical models have been useful to study the clonal evolution of cells in the context of disease initiation, progression, and treatment (3). The use of mathematical models has become a rather large field of research, and many types of questions have been investigated, which can be broadly divided into the following categories:

• i)Mathematical models can be applied to epidemiological data that document cancer incidence to investigate in vivo evolutionary processes. For example, the mathematical analysis of age-incidence curves has provided key insights into the number of rate-limiting steps that occur during carcinogenesis, which has implications for understanding the genetic and epigenetic pathways involved in tumor formation (4).
• ii)Mathematical models of in vivo clonal evolutionary processes can be formulated to interpret experimental and clinical data or to test different hypotheses to explain observed phenomena. An example is the question about the relevance of genetically unstable cells that are found in various cancers and are characterized by elevated mutation rates (5). It has been debated whether genetic instability is required for the accumulation of multiple mutations in cells or whether clonal expansion processes in the absence of instability are sufficient to achieve this goal (6). Mathematical models comparing disease development in the presence and absence of genetic instability have been useful to address this question (7, 8). Such approaches are applicable to the interpretation of many other complex phenomena in cancer (e.g., phenomena discussed in refs. 9–12).
• iii)Another use of mathematical models is the estimation of crucial kinetic parameters by applying those models to experimental and clinical data. This parameterization can be done during the natural growth phase of a tumor to calculate division and death rates of cells (13), as well as during responses to specific therapies (14, 15).

To understand better how cancer emerges, how it can be prevented, and how it can be successfully treated, we need to gain more insights into mechanisms that prevent clonal expansion and evolution. Clonal expansion and the initiation of disease can be prevented by host defense mechanisms, such as immune responses (16), inhibition of angiogenesis (17), and the presence of replicative limits in cells (18). Once a cancer has overcome such defense mechanisms, further expansion and evolution can be prevented by a variety of treatment approaches. In this paper, we will show how mathematical models can be useful for improving our understanding of (i) natural defense mechanisms against clonal evolution and the initiation of disease and (ii) therapy approaches to block continued growth of tumors. We will do so by discussing a collection of studies from our own group. Among defense mechanisms against clonal evolution, we will consider the role of replicative limits and cellular senescence. In the context of therapies, we will consider targeted treatment approaches against chronic lymphocytic leukemia (CLL) and discuss how mathematical models can be used to design treatment strategies to prevent the emergence of resistant cell clones that lead to disease relapse.

Clonal Evolution and Replicative Senescence

Biological Background.

Normal somatic cells lose the ability to divide after a limited number of divisions. This phenomenon, known as replicative senescence, is dependent on telomere shortening during cell division (19). Telomeres are repetitive noncoding DNA sequences that cap both ends of linear chromosomes. They play a protective role by preventing the DNA damage response machinery from interpreting the natural chromosome ends as dsDNA breaks (19). In cells that naturally lack telomere length maintenance pathways, the inability of conventional polymerases to replicate DNA fully results in a net loss of telomere sequences during cell division (19). If telomeres become critically short, they lose their protective properties and send cells into a terminal state of arrest (replicative senescence) or cause cell death (20). In stem cells and germ cells, telomere shortening is offset by the action of telomerase, an enzyme that extends telomere length (20).

Replicative senescence might have evolved as a tumor suppressor pathway that prevents cells from becoming immortal. If a cell and its progeny undergo uncontrolled proliferation, replication limits protect against cancer by limiting the size of the clonal population. Furthermore, because mutations typically occur during cell division, limiting the possible number of divisions reduces the probability of acquiring multiple mutations, which, according to the multihit theory of carcinogenesis, is necessary for the full progression toward malignancy.

Multiple lines of evidence support the role of replicative senescence as an important barrier to tumor progression. First, essentially all human cancers acquire mechanisms to maintain telomere length, most often through high levels of telomerase expression (90%) (21) and less frequently through the alternative telomere lengthening (ALT) pathway (10%) (22). There is also evidence of senescence in premalignant stages of tumor progression. In humans, senescent cells have been identified in benign skin lesions, neurofibromas, and benign lesions of the prostate (reviewed in 18). Senescence response in vivo after oncogenic activation has been observed in mice, where tumors initiated by the endogenous expression of the oncogene ras showed an abundance of senescent cells in premalignant lesions in the lung but no signs of cellular senescence in lung adenocarcinomas (23). Together, these findings support an emerging consensus for the role of replicative senescence as a potent tumor suppressor mechanism.

Senescent cells accumulate with age in vivo, and numerous studies describe an inverse correlation between telomere length and age (24). There is also evidence that senescent cells contribute to a host of age-related degenerative pathologies (25). Senescent cells express a senescence-associated secretory phenotype (SASP) (reviewed in 26), which entails the secretion of numerous proinflammatory agents that can cause local and possible systemic chronic inflammation (an important contributor to most age-related diseases). Telomere shortening in adult stem cells can also limit the regenerative potential of stem cell pools (18). In blood, for example, the progressive shortening of telomere length in stem cells may limit hematopoietic regeneration (27). Current understanding points to replicative senescence as a contributor to aging, but aging itself is a complex multifactorial process that also depends on multiple factors independent of telomere shortening (28). Laboratory mice, for example, have notoriously long telomeres, but their life span is comparable to the life span of other rodent species (29).

It is important to mention that SASP and the accumulation of senescent cells can contribute to chronic inflammation and the creation of microenvironments that are permissive to cancer progression, which, in turn might fuel the occurrence of cancer in late life (26). However, in the context of reproductive-age humans, replicative senescence is primarily understood as both a cancer-protecting and proaging mechanism. At the heart of this antagonistically pleiotropic nature of replicative senescence lie two opposing objectives: (i) the replication capacity of cells (defined as the telomere-mediated maximum number of cell divisions possible) should be large enough to allow for the necessary number of cell divisions required to perform the tasks of normal tissue function and regeneration necessary for life, and (ii) the replication capacity should be small enough to be effective at suppressing excessive abnormal cell proliferation and tumor development. This last observation underscores the necessity of understanding the process of cellular senescence from a quantitative perspective.

There are numerous mathematical models that explore telomere dynamics in relation to replicative senescence and cancer (e.g., 30–32). In the next sections, we discuss three models that explore replicative limits in different contexts: (i) as a possible evolutionary force behind commonly observed features of cell lineages, (ii) as a mechanism acting against precancerous nonneoplastic mutations, and (iii) as a mechanism to curtail the clonal expansion of cells.

Tissue Architecture and Cellular Replication Limits.

Replication limits should allow for enough cell divisions to maintain tissue homeostasis and regeneration after an injury while, at the same time, keeping cells’ replication capacity as small as possible to protect against cancer. In this respect, the precise manner in which a tissue organizes the cell division labor has an impact on its ability to fulfill these two objectives. Most self-renewing tissues are organized into cell lineages, in which the highly differentiated mature cells are the end products of orderly tissue-specific sequences of divisions that originate in stem cells (33). Quantitative modeling can help elucidate how different architectural characteristics of a cell lineage—the number of intermediate cell compartments, the self-renewal capabilities of cells, and cell division rates—affect the replication capacity of a cell population. Here, we describe a mathematical model that defines an optimal tissue architecture that minimizes the replication capacity of dividing cells, and thus cancer risk.

Fig. 1A introduces a variant of a widely proposed model of a cell lineage (33, 34). Stem cells S represent the starting point of the lineage. Downstream from stem cells are intermediate cell types, often termed progenitors or transit-amplifying cells ($X_0,\dots ,X_k$ in Fig. 1A). If a stem cell divides, each daughter cell remains in the stem cell compartment with probability $p_s$ or proceeds to the $X_0$ compartment with probability $1-p_s$. Similarly, if a cell in compartment j (hereafter called a j-type cell) divides, each daughter cell will remain in the j compartment with probability $p_j$ or differentiate into a $\left(j+1\right)$-type cell with probability $1-p_j$. The end products of the cell lineage are fully differentiated cells D, which cannot divide any further and die at a certain rate d. The division rates are r for stem cells and $v_j$ for a j-type cell. To model telomere shortening, a number called its replication capacity is associated with every cell. When a nonstem cell divides, the replication capacity of the daughter cells will be one unit less than the replication capacity of the parent cell. Because adult stem cells express enough telomerase to offset, at least partially, the shortening of telomeres during cell division, when a stem divides, the replication capacity of the offspring is assumed to be ε (where $\epsilon <1$).

Fig. 1.

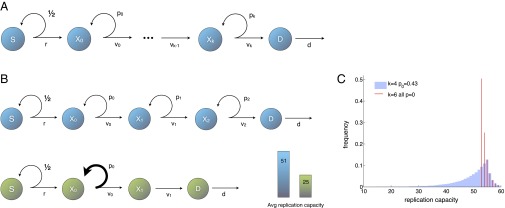
(A) Lineage begins with stem cells S; progresses through a sequence of transit-amplifying stages ($X_0,\dots ,X_k$); and ends with differentiated cells D, which are postmitotic and die at a certain rate d. Cells in stage $X_j$ divide at rate $v_j$, producing two $X_j$ cells with probability $p_j<0.5$ or two $X_{j+1}$ cells with probability $1-p_j$. The stem cell’s division rate is r. (B) Two alternative architectures for the same target number of intermediate cell divisions. For the cell lineage in blue $\left(k=2,p_0=p_1=p_2=0.341\right)$, the resulting average replication capacity of dividing cells is 51. An optimal cell lineage is depicted in green $\left(k=1,p_0=0.485,p_1=0\right)$. In both cell lineages, $rS=50$, $\rho =60$, and all $v=1$. The average replication capacity of dividing cells is minimized by a tissue architecture in which, at most, one intermediate cell type has self-renewal capabilities and the number of transit-amplifying stages is kept as small as possible (a discussion is provided in the main text). (C) Distribution of the replication of capacity of dividing cells for two alternative architectures that produce the same number of transit-amplifying divisions. In both cases $v_j=1$ for all j, the replication capacity of stem cells is $\rho =60$, and the influx of cells from the stem cell compartment is $rS=50$. Red lines illustrate $k=6$ and all $p_j=0$. Blue bars illustrate $k=4$, $p_0=0.43$, and all other $p_j=0$.

When the tissue is at homeostasis, the self-renewal probabilities and division rates of each cell type can be considered constant and the model can be used to find an optimal cell lineage architecture that protects against cancer by minimizing the replication capacity of dividing cells. This problem, however, is not sufficiently constrained. In particular, the number of differentiated cells at homeostasis, D, and their death rate, d, depend on other biological considerations, such as organismal physiology, which lie outside the scope of the optimization problem. Thus, the outflow of differentiated cells $\left(dD\right)$ is considered as a fundamental fixed quantity of the system. With this constraint, the model is implemented as a stochastic agent-based model and as a deterministic model that considers the equilibrium number of cells in each compartment. The first result, as reported in a study by Rodriguez-Brenes et al. (35), is that a cell lineage architecture concerned exclusively with minimizing cancer risk should have exactly one stem cell. In practice, a stem cell compartment consisting of a single cell could be extremely fragile, and thus the actual number of stem cells in a lineage is likely influenced by other factors that promote robustness in the system. More broadly, this result suggests that the number of stem cells per lineage should be very small [e.g., in the colon epithelium, there are 15–20 (36) or fewer (34) stem cells per crypt].

The result that the number of stem cells should be small to protect against cancer is intuitive. Even if adult stem cells do not have sufficient telomerase to prevent telomere shortening associated with continuous cell division, they possess a replication capacity that far exceeds the replication capacity of nonstem cells. The replication capacity of stem cells is difficult to measure and is likely tissue-specific. However, although subject to a degree of uncertainty, measurements on the average division rates make some estimates possible. Stem cells in the colon crypt, for example, are estimated to divide more than 5,000 times in a life span of 80 y (34), and, based on the midpoint from measurements taken from several studies, hematopoietic stem cells have been estimated to divide roughly 960 times during the same time period (37). Thus, the likely large replication capacity of stem cells suggests that in tumors initiating in telomerase-positive stem cells, even if telomere length continues to shorten, replicative senescence is unlikely to act as a significant barrier to tumor progression. Instead, a quantitative analysis suggests that replicative senescence might only be efficient at protecting against oncogenic mutations that originate in nonstem cells. This observation, however, does not imply that all tumors have a stem cell origin. For example, although a substantial portion of leukemias are thought to be initiated in hematopoietic stem cells (e.g., 38, 39), progenitor cell populations have been identified as targets for tumor initiation in several types of acute myeloid leukemias (40, 41). Progenitor cells as possible cells of origin in cancer have also been identified in solid tumors, including glioblastoma, medulloblastoma, prostate cancer, basal cell carcinoma, and basal-like breast cancer (reviewed in 42). Moreover, cells with a limited proliferative potential can escape replication limits by activating telomerase. Frequent somatic mutations that activate the core promoter of telomerase have been identified in multiple types of cancers, including, among others, melanomas (71%), hepatocellular carcinomas (59%), primary glioblastomas (83%), and urothelial cancer (43–46).

To study how replication limits and tissue architecture protect against mutations originating in nonstem cells, the number of stem cell divisions per unit of time $\left(rS\right)$ and the number of cell deaths per unit of time $\left(dD\right)$ are held fixed. We then ask: How do the number of intermediate cell compartments, the self-renewal probabilities, and the cell division rates affect the replication capacity of dividing cells? At homeostasis, $dD-rS$ equals the number of intermediate cell divisions per unit of time; thus, the system in Fig. 1A is constrained by the equation ${\displaystyle \sum v_j{X}_j}=dD-rS$. The key insight is to realize that the same number of intermediate cell divisions can be realized by multiple architectures [e.g., the same transit-amplifying output may be reached by a lineage with smaller self-renewal probabilities and a larger number of compartments or by a lineage with larger self-renewal probabilities and fewer compartments; figure 2 of ref. 35]. However, two different architectures that produce the same target number of divisions can produce radically different distributions in the replication capacity of the cell population (Fig. 1B).

Because most mutations occur during cell division, from the point of view of replication limits, an optimal architecture to protect against cancer is one that minimizes the expected replication capacity of dividing cells. Using this definition, the main results in the study by Rodriguez-Brenes et al. (35) follow. In an optimal tissue architecture, there can be self-renewal in at most one intermediate cell compartment and the number of compartments should be kept as small as possible. If there is self-renewal in one compartment, it should be in the first one $\left(X_0\right)$. This same compartment, $X_0,$ should have the slowest division rate. Note that there may be a lower limit to the number of intermediate compartments. First, having only one intermediate compartment may lead to too many cells, exhausting their replication capacity and making it impossible for the lineage to reach the target number of divisions. Second, every fork in the differentiation pathway adds a compartment to a lineage. Thus, there is a minimum number of compartments when different types of mature cells arise from the same kind of stem cell (e.g., in the hematopoietic system). Fig. 1C depicts two alternative architectures with the same number of transit-amplifying cell divisions.

In an optimal tissue architecture to protect against cancer, the less differentiated cells have a larger rate of self-renewal and a slower cell division rate. These types of dynamics have been repeatedly observed in cell lineages, suggesting that they may have evolved to decrease cancer risk. A discussion on how these ideas relate to neural tissue and the hematopoietic system is included in the study by Rodriguez-Brenes et al. (35). The analysis of the model also underscores the importance of understanding the precise mechanism used to accomplish transit-amplifying behavior. In particular, it is often unclear whether transit-amplifying behavior is produced by a cell program that allows for a fixed number of divisions in progenitor cells or by some degree of self-renewal. A cell program that calls for a fixed number of divisions would be represented in the framework of Fig. 1A as a lineage with numerous intermediate compartments and no self-renewal. By contrast, through a self-renewal mechanism, the cell’s decision to differentiate would be independent of the number of previous divisions and would be determined instead by the current state of the cell’s microenvironment. However, these two strategies can result in dramatically different distributions of cell replication capacity. Finally, the fact that some of the features that characterize an optimal architecture are present in various tissues suggests that they might have evolved to minimize cancer risk. This observation, however, does not mean that tissues must follow all aspects that define an optimal architecture, because other evolutionary forces unrelated to cancer risk can also play a role in determining the architectures of specific tissues.

Replication Limits in Precancerous Mutations.

Dozens of cancer-associated mutations have been repeatedly identified in healthy individuals. For example, monoclonal B-cell lymphocytosis (MBL), which resembles CLL, is found in 4% of the population over the age of 40 y (47). All cases of CLL seem to arise from MBL, although the majority of MBL cases do not give rise to proliferative disorders (47). In another example, the t(14;18) translocation between the BCL2 gene on chromosome 18 and the Ig heavy chain on chromosome 14 occurs in ∼90% of follicular lymphomas (FLs) and is considered a hallmark of the disease (48). However, it is also found in 30–60% of healthy individuals (49), and no clear link between its presence and the later development of FL has been established (50). Longitudinal studies of both t(14;18) and MBL suggest that these abnormalities persist for long periods of time in some individuals and are transient, completely disappearing, in others (51, 52).

A cell lineage model based on the concepts of fitness in evolutionary theory and replication limits proposes that the transient and persistent nature of the phenotypes observed in t(14;18) and MBL could depend on the stage in the differentiation pathway where the mutation originates (53). The model distinguishes between three cell types: stem, progenitors, and differentiated cells (Fig. 2A). At homeostasis, the basic cell dynamics are the same as in the previously discussed model: Stem cells produce, on average, one stem cell per cell division, allowing them to maintain their own numbers through self-replication, whereas the self-renewal potential of progenitors is more limited and, by itself, insufficient to sustain a constant population size. Upon cell division, the replication capacity decreases by 1 in progenitors and by ε in stem cells (Fig. 2B).

Fig. 2.

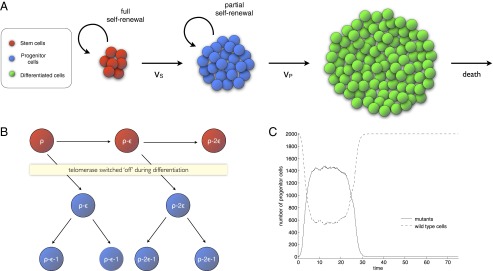
(A) Cell lineage model. Cells are divided into three compartments: stem cells, progenitor cells, and differentiated cells. Stem cells have a full capacity to self-renew and maintain their own number through self-replication. Progenitors have only a limited capacity to self-renew. The final products are the fully differentiated cells, which die at a certain rate. (B) Replication capacity of cells decreases upon cell division. Adult stem cells express telomerase, which at least partially offsets the shortening of telomere length that occurs when a cell divides. As a consequence, the loss in replication capacity of stem cells $\left(\epsilon <1\right)$ is smaller than the loss that occurs in progenitors (equal to 1 in the figure). (C) Dynamics of a mutant clone originating in a progenitor cell. At time $t=0$, a mutation originates in a progenitor. The number of mutants first steadily increases and then remains very close to a constant level (partial fixation occurs). As the replication capacity of the mutants is gradually exhausted, their numbers drop and the mutant clone eventually goes extinct.

Because the mutations considered are nonneoplastic, each population is assumed to be constant and the mutation dynamics are modeled based on the Moran process (54). In the Moran process, the fitness of WT cells is set equal to 1 and the fitness of mutants is set to r, where $r<1$, $r=1$, and $r>1$ correspond to disadvantageous, neutral, and advantageous mutations, respectively. Although mutant fitness can be context-dependent and can change over time in some settings (10), there are currently no data that show such effects for the mutants under consideration; hence, this possibility is not included in the model. At each time step, we select two random cells: one for reproduction and one for elimination. In the context of the model’s stem cell dynamics, cell replication corresponds to reproduction and differentiation corresponds to elimination, with the caveat that if a cell exhausts its replication capacity, it is no longer eligible for reproduction. The Moran process suggests that replication limits have little effect on mutant dynamics in the stem cell compartment. Even if cell division slightly diminishes the replication capacity of stem cells, the loss is probably too small to have a significant effect. Take again the example of the colon epithelium; here, stem cells might be capable of as many as 5,000 divisions (34) and the number of stem cells is small [15–20 (36) or fewer (34) per crypt]. For a neutral mutant in a population of size N, the mean time to fixation is on the order of N time steps (55). Hence, in a small stem cell compartment, the large replication capacity of stem cells is unlikely to hinder a mutant’s ability to colonize the entire compartment.

In the progenitor population, self-replication cannot occur during every Moran step; doing so would imply that progenitors have a full capacity to self-renew, and the influx of cells from the stem cell compartment would cause uncontrolled growth. Instead, at regular time intervals, the progenitor reproduction step is skipped and a stem cell is randomly chosen for division to replenish the progenitor population. The following dynamics ensue. A sufficiently advantageous mutant originating in a progenitor will have a certain probability of partially colonizing its compartment. If this colonization occurs, the mutant clone will remain as a near-constant fraction of the entire population. However, unless mutants manage to escape replicative senescence, partial fixation will be transient, and the mutants will eventually be driven to extinction through the exhaustion of their replicative capacity (Fig. 2C). Note that fixation is only partial in this case because there is a constant reseeding of WT cells from the stem cell compartment.

The level and probability of reaching partial fixation can be estimated with great accuracy in terms of the equilibrium number of progenitors, their self-renewal probability, and mutant fitness. These estimates allow us to quantify the protection that replication limits offer against nonneoplastic mutations by comparing the probabilities of acquiring a second mutation in the absence and presence of replicative limits. The following example is included in a study by Rodriguez-Brenes et al. (53). Consider a progenitor cell population of 2,000 cells with a self-renewal probability of 0.44, a mutant fitness of 1.5 (compared with a fitness of 1 for WT cells), and a mutation rate per gene per cell division of ${10}^{-7}$. In this case, having a maximum replication capacity of 50 cell divisions [a value commonly used for human somatic cells (56)] reduces the chances that a mutant will acquire a second mutation by at least 93% within the first year. After 10 y without replication limits, the probability of a second mutation appearing in the mutant lineage is ∼0.25. In contrast to replication limits, the probability would be less than 0.0022, more than a 100-fold decrease.

In sum, quantitative modeling suggests that if a sufficiently advantageous nonneoplastic mutation originates in stem cells, long-term persistence of the mutants is likely, and this long-term persistence poses a significant risk of cancer progression. If the mutation arises downstream, such as in progenitor cells, the mutant presence is likely to be transient and the risk of disease significantly lower. These insights could shed light into the dynamics of cancer-associated mutations in healthy individuals and, in particular, into the existence of the transient and persistent phenotypes observed in t(14;18) and MBL (51, 52). Finally, the model suggests that telomere length can be used to distinguish between mutations that carry an increased risk of cancer development and those mutations that do not. This hypothesis can be experimentally tested by following cohorts of healthy people who harbor these mutations longitudinally and measuring average telomere length both in the aberrant cells and in the normal cells of these individuals. According to the model, in patients in whom the mutation is transient, the telomeres of aberrant cells should be smaller than the telomeres of the normal cells, and this difference becomes amplified over time. In patients in whom the mutation is persistent, there should be no significant difference between the telomere length of normal and aberrant cells. If such longitudinal studies confirm this hypothesis, then a single blood test could potentially determine the risk posed by cancer-associated mutation in individual patients.

Replicative Limits in a Growing Clonal Cell Population.

Although clonal expansion can occur in normal tissue [e.g., during the transition to marked oligoclonality in the hematopoietic system with age (57)], the clonal expansion of abnormal cells is also a hallmark of cancer. Here, we concentrate on clonal expansion in cancer, particularly on the effectiveness of replication limits at protecting against an abnormally growing clonal cell population. In the simplest assessment, a cell with replication capacity N is theoretically capable of spanning a colony of $2^N$ cells. If we consider as an example the replication capacity of human embryonic fibroblasts, which, on average, are able to divide ∼50 times in cell culture (56), then a single cell would be capable of spanning a population of $2^{50}$ cells, which is far greater than the number of cells in a human body. The previous example however, does not take into account that unlike cells stimulated to grow in a controlled medium, cancer cells in the human body grow in an environment with multiple levels of protection against excessive cell proliferation, and are thus potentially subject to high levels of cell death. If we take into account cell death and stochasticity in cell division, it becomes apparent that knowing the replication capacity of the cell that initiates abnormal growth is not, by itself, sufficient to assess the effectiveness of replicative limits in controlling the size of a clone. It is necessary to understand the distributions of the number of cells, how they depend on the balance between cell division and death, and the probability of escaping replication senescence through telomerase activation.

This analysis can be done by assuming cancer cells stochastically divide and die independent of each other at exponentially distributed times. The distribution of the maximum size of a clone spawned by a single cell depends on the replication capacity of the founder cell and the ratio between the rates of cell division and death. Population sizes are compared against two benchmarks: ${10}^9$ cells, a common level for the clinical detection of solid tumors (58), and ${10}^{12}$ cells, an order of magnitude where several types of cancers reach a lethal burden (59). The results from the model suggest that replicative senescence acts as a potent tumor suppressor pathway when the imbalance between birth and death in tumor cells is moderate or low (high death-to-birth ratio). Conversely, replicative limits might be ineffective as a tumor suppressor mechanism when abnormal cell proliferation is not accompanied by elevated rates of mortality in abnormal cells. Thus, in practice, replicative senescence might be efficient as a cancer-protecting mechanism only when it works in tandem with other factors that contribute to cell death in tumor cells. The immune system, for example, can contribute to the death of abnormal cells during the elimination and equilibrium phases of cancer immunoediting (16).

This work also highlights the importance of understanding quantitatively the population dynamics of clones restricted by replicative limits to assess the effectiveness of therapies aimed at inducing senescence in cancer cells. Telomeres and telomerase have long been identified as potential targets for cancer therapy (60). In particular, several telomerase inhibitors aimed at triggering telomere-initiated senescence or apoptosis in cancer cells have been developed (60, 61). One potential drawback of this approach is that the replication capacity of target cells must first be exhausted before senescence or apoptosis takes place (60). Indeed, if the replication capacity of cancer cells is large enough, the tumor could still progress to harmful or even lethal levels before the effects of telomerase inhibition take place. Thus, antitelomerase strategies could be ineffective as a sole treatment against cancer. Instead, this argument suggests that telomerase inhibition could work best in conjunction with a conventional cancer therapy, such as chemotherapy or radiation, that produces high levels of mortality in cancer cells.

Clonal Evolution and the Response to Cancer Treatments

When tumor cells escape natural defense mechanisms and grow uncontrolled, the ensuing expansion processes can be countered by specific drug treatments. In this context, clonal evolution plays an important role determining tumor responses to treatment. Recent treatment approaches involve the specific targeting of molecular defects in cells that are responsible for driving uncontrolled cell growth. Consequently, such targeted therapies are characterized by fewer side effects than traditional chemotherapy approaches. The treatment of chronic myeloid leukemia with the tyrosine kinase inhibitor imatinib, and with subsequently developed targeted inhibitors, was the first major success. Recently, new tyrosine kinase inhibitors have emerged in the treatment of CLL, the most common leukemia in adults. Examples are the drugs ibrutinib and idelalisib, which act in a similar fashion (62). To illustrate how the understanding of clonal evolutionary processes can be useful from a clinical point of view, we discuss CLL treatment with ibrutinib (63) and the evolutionary dynamics of ibritinib-resistant cells.

Although the state of the disease is assessed by analyzing CLL cells in the blood, the majority of the tumor cells reside in tissues, which include the lymph nodes, spleen, and bone marrow. Tumor cells are released into the blood, but homing mechanisms ensure that they traffick back toward the tissue sites. In the tissue, the appropriate microenvironment allows the cells to divide, driving disease progression (64). Upon initiation of ibrutinib therapy, a lymphocytosis phase is observed, during which the number of CLL cells in the blood increases, reaches a peak, and subsequently declines (65). In the long term, the absolute lymphocyte count in the blood stabilizes at a level that, in some cases, may be higher than in healthy individuals. The lymphocytosis phase occurs because ibrutinib disrupts the interactions between CLL cells and their microenvironment, leading to redistribution of the cells from the tissue into the blood. Kinetic analysis, however, indicates that the cells redistributing from tissue to blood represent only a relatively small fraction of the total tissue disease burden, and that the majority of the tissue-resident CLL cells die in response to this therapy (15).

Recent data indicate that the disease relapses in a few patients despite continuous ibrutinib therapy. Such relapse cases are thought to be caused by the emergence of drug-resistant cells, and specific point mutations have been identified in such patients that confer resistance to ibrutinib (66). A very important question is for how long ibrutinib therapy can maintain control of CLL and at what time disease relapse can be expected. Answering this question requires an understanding of the evolutionary dynamics of drug-resistant cells, and mathematical models have been crucial in this endeavor (67). To describe the exponential growth of CLL cells before treatment, and their decline during treatment, we consider a stochastic linear birth–death process. CLL cells are assumed to divide in tissues with a probability L, and they die with a probability D. During cell division, there is a probability μ that the cell receives a mutation that confers resistance to ibrutinib. Before treatment, $L>D$; that is, the probability of cell division is larger than the probability of cell death, resulting in clonal expansion. The cell population is allowed to grow in the model up to a defined size N. When this size is reached, treatment is started in the model. During treatment, it is assumed that $D>L$; that is, the probability of cell death is larger than the probability of cell division, resulting in an exponential decline of the tumor cell population. Data indicate that cell division is largely shut off by ibrutinib (68), such that death is the dominant dynamic process that occurs. The principles of this modeling approach are illustrated in Fig. 3A.

Fig. 3.

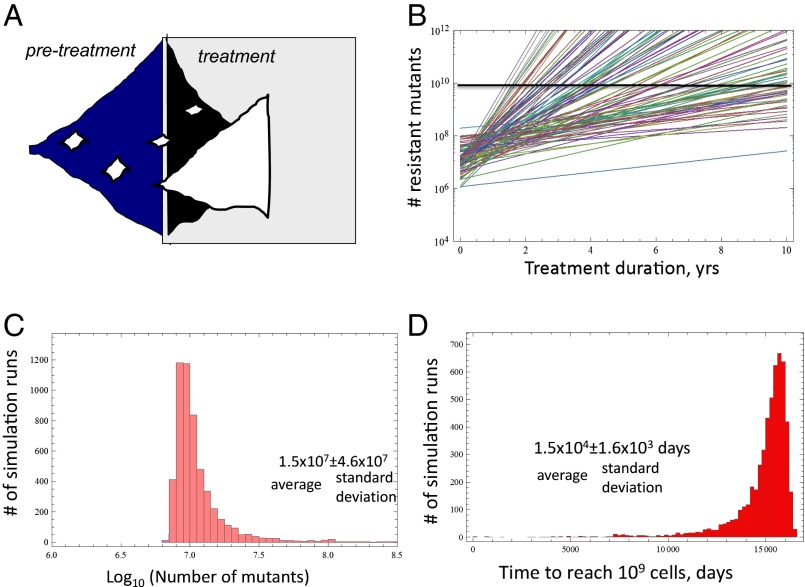
(A) Principles of the stochastic birth–death model. If the division rate is larger than the death rate, exponential growth of the tumor occurs. The number of cells is allowed to grow up to a defined size, N, when treatment is initiated. During treatment, the death rate is larger than the division rate, leading to exponential decline. Resistant mutants are depicted in white, and can, in principle, emerge either before or during treatment. If resistant mutants are present during treatment, they are selected. (B) Average number of resistant mutants over time during treatment. Each line represents the average growth of resistant cells for a given parameter combination. Different parameter combinations (mostly differences in the division and death rate of cells) lead to very different growth rates of resistant mutants, resulting in different predicted average relapse times. (C) Variation in the predicted number of mutants at size N when treatment is initiated, among repeated runs of the stochastic process. This measure is highly variable, with the SD being an order of magnitude larger than the mean. (D) Variation in the predicted time to relapse among repeated runs of the stochastic process. This measure is much less variable, with the SD being an order of magnitude lower than the mean. Relapse is defined by the number of resistant cells reaching ${10}^9$ cells, when regrowth is likely observable. In C and D, the y axis indicates the frequency among all computer simulations.

From a mathematical modeling point of view, an important aspect of this system is that all parameters that determine the dynamics in this model can be measured, and have been measured to a certain extent. The rates of cell division and cell death before treatment have been measured in patients by the administration of deuterated “heavy” water (13). Uptake, and subsequent dilution, of the label by cells in vivo allows these kinetic parameters to be calculated. The total number of CLL cells in the tissues upon the start of therapy has been estimated from radiological studies (15), in which the volume of the lymph nodes and spleen was measured from computed tomography scan images. The death rates of cells during therapy have been calculated by fitting a two-compartment mathematical model to data that document absolute lymphocyte counts during the lymphocytosis phase in the blood (15). Because resistance mutations are generated by straightforward point mutations, it can be assumed that resistance is generated with a rate of $\mu ={10}^{-8}$ to ${10}^{-9}$ per cell division.

When the model is parameterized, some important insights can be obtained (67), such as whether resistance is more likely to evolve before or after therapy. Within the measured parameter regions, the model strongly suggests that resistant mutants are almost certain to exist before treatment is initiated. In such a scenario, the time until disease relapse is observed is determined by how many resistant mutants exist at the start of therapy, and how fast these cells grow toward levels at which they can contribute to a renewed rise in the overall lymphocyte counts. Based on the limited parameters estimated so far, model predictions suggest that the time until relapse can be highly variable among patients, driven by variation in the division and death rates of the resistant cells during therapy. For different parameter sets within the measured ranges, the model can be used to predict the time course of resistant mutant growth, as shown in Fig. 3B. Different parameter combinations within the observed ranges can give rise to very different growth dynamics.

Now, let us turn to the growth prediction for an individual patient (i.e., for one parameter set). For a given set of measured parameters, the modeling framework can predict the average growth dynamics and the average time of relapse (i.e., the average over many realizations of the stochastic process). Because the dynamics are stochastic, however, there is a certain degree of variation from one computer simulation to the other. Whether the predicted average time of disease relapse for a given patient can be useful clinically depends on the degree of variation in the outcomes of the stochastic simulations. If the relapse time is predicted to be highly variable for a given parameter set, then the average timing is of limited use. On the other hand, if the degree of variation is relatively small, then the average relapse time predicted by the model could be a reliable predictor of the patient’s relapse time. According to the model, the number of mutants predicted to be present at the start of treatment is highly variable, with an SD that is one order of magnitude larger than the mean (Fig. 3C). Importantly, however, the predicted time until disease relapse is characterized by only limited variability, with an SD that is one order of magnitude smaller than the mean (Fig. 3D). The reason is that the timing of disease relapse depends on the logarithm of the number of mutants at the start of treatment, which reduces variation. Therefore, the average time of disease relapse that is predicted to occur for a given parameter combination (i.e., for a given patient) can be a clinically useful measure to estimate how long the drug can maintain control of the tumor.

So far, only limited parameter estimates and data that document disease relapse exist, and more such data are needed to test the predictive power of the calculations discussed here. This work, however, has shown that, in principle, an evolutionary model can be parameterized with patient-specific measurements, and that this model could allow us to make personalized predictions about the duration for which ibrutinib can maintain control of CLL. For cases where control is predicted to be short, the effectiveness of different strategies to combat drug resistance can be calculated, such as various drug combinations. Hence, the study of clonal evolutionary processes could allow the generation of clinically useful tools in the area of personalized medicine or precision medicine.

Conclusions

This review has demonstrated with a few select examples how the understanding of clonal evolutionary processes through mathematical modeling can be useful to provide biologically and clinically important insights into the determinants of disease progression and into the treatment responses of cancers. Such evolutionary models can be used to interpret biological observations, to generate new hypotheses, to estimate crucial parameters from experimental or clinical data, and to make predictions. An exciting application of evolutionary models is the generation of patient-specific predictions, which, when tested and validated, could become a new tool in the clinic that can help make decisions about patient management and treatment approaches. In this review, we illustrated these applications with two specific examples: Evolutionary models were used to suggest new methods to determine whether MBL is likely to progress to CLL in individual patients. In the context of targeted therapies, mathematical models have been developed to calculate patient-specific outcomes of ibrutinib treatment. To develop these approaches further, close collaborations between mathematical biologists, experimentalists, and clinicians will be crucial to test and validate model predictions further.