Episodic Memory Does Not Add Up: Verbatim-Gist Superposition Predicts Violations of the Additive Law of Probability

Abstract

Fuzzy-trace theory’s assumptions about memory representation are cognitive examples of the familiar superposition property of physical quantum systems. When those assumptions are implemented in a formal quantum model (QEMc), they predict that episodic memory will violate the additive law of probability: If memory is tested for a partition of an item’s possible episodic states, the individual probabilities of remembering the item as belonging to each state must sum to more than 1. We detected this phenomenon using two standard designs, item false memory and source false memory. The quantum implementation of fuzzy-trace theory also predicts that violations of the additive law will vary in strength as a function of reliance on gist memory. That prediction, too, was confirmed via a series of manipulations (e.g., semantic relatedness, testing delay) that are thought to increase gist reliance. Surprisingly, an analysis of the underlying structure of violations of the additive law revealed that as a general rule, increases in remembering correct episodic states do not produce commensurate reductions in remembering incorrect states.

Historically, an enduring feature of judgment-and-decision-making research has been the availability of pre-existing normative models for human reasoning. Specifically, the axioms of formal logic and classical probability theory have long been implemented in such research as prescriptive benchmarks against which reasoning is gauged. As decades of experimentation in the heuristics and biases tradition have shown, reasoning routinely violates the most basic axioms. Examples of decision making tasks that exhibit such violations include various forms of preference, such as intertemporal choice (e.g., Killen, 2009; Scholten & Read, 2010) and choices among risky prospects (e.g., Tversky & Fox, 1995). Examples of judgment tasks that exhibit such violations include probability judgment (e.g., Rottenstreich & Tversky, 1997; Tversky & Kahneman, 1983) and frequency judgment (e.g., Fiedler, Unkelbach, & Freytag, 2009), with the literature on probability judgment being quite extensive (see Pothos & Busemeyer, 2013; Busemeyer, Pothos, Franco, & Trueblood, 2011). Owing to the availability of a normative model, such violations have deep psychological significance, inasmuch as they demonstrate that reasoning is neither logical nor rational, in a formal sense.

Memory research, in contrast, has not drawn upon formal logic or classical probability theory as a normative framework. For that reason, experiments that assess whether memory conforms to axiomatic criteria of logic and rationality have been rare (for an exception, see Hicks, Marsh, & Cook, 2005). We have argued, however, that experiments of that ilk can answer fundamental theoretical and empirical questions about memory (Brainerd, Holliday, Nakamura, & Reyna, 2014; Brainerd, Reyna, & Aydin, 2010). On the theoretical side, they can deliver tests of competing principles of representation and retrieval, principles that differ in their predictions as to whether memory data will align with particular axioms. On the empirical side, whether our memories are distorted in specific ways can be shown to turn on whether memory follows certain axioms.

These issues are elaborated in the first section, below. There, we consider one of the central axioms of classical probability, the additive law, which specifies that the probabilities of the components of any partition of a set of possible events must sum to 1. We note some known violations of this law in human judgment and discuss what the general significance of parallel violations in the domain of episodic memory would be. As theoretical motivation for the latter, we show that nonadditivity of episodic memories is predicted by a quantum probability model that implements a memory representation principle (superposition of verbatim and gist traces) and a retrieval principle (description dependency). The model has been used to explain false memory phenomena and can identify conditions that should influence observed levels of nonadditivity. Experiments are then reported that evaluated those predictions using two types of designs, item false memory and source false memory.

Superposition and Additive Probability

Measuring Violations of the Additive Law

Suppose that some set S of events has been partitioned into i subsets; that is, the subsets S₁, S₂, …, S_i are mutually exclusive and exhaustive. Suppose that the sampling probabilities of these subsets are known to be p₁, p₂, …, p_i; that is, the probability of selecting an event from S₁ on a random draw is p₁, the probability of selecting an event from S₂ is p₂, and so on. Although individual sampling probabilities are free to vary over the unit interval, the additive law constrains the possible values that can be observed for the components of the partition such that p₁ + p₂ + … + p_i = 1 must be satisfied. For instance, imagine that S is an urn containing a large quantity of marbles, whose partition is S₁ = white marbles, S₂ = red marbles, and S₃ = blue marbles. If the sampling probabilities of the white and red subsets are known to be .35 and .45, respectively, then by the additive law, the sampling probability of the blue subset must be .20.

However, when subjects make probability judgments about partitions of sets of real-life events, those judgments fail to obey the additive law. Instead, the judged probabilities of the subsets are normally subadditive (p₁ + p₂ + … + p_i ≥ 1; e.g., Redelmeier, Koehler, Liberman, & Tversky, 1995), although they are occasionally superadditive (p₁ + p₂ + … + p_i ≤ 1; e.g., Macchi, Osherson, & Krantz, 1999). In an early illustration of subadditivity, Redelmeier et al. presented the case history of a hospitalized patient to physicians and asked different groups of them to estimate the probability of one of the following outcomes: (a) The patient dies during the current hospitalization; (b) the patient is discharged alive, but dies within 1 year; (c) the patient is discharged alive and lives more than 1 but less than 10 years; or (d) the patient is discharged alive and lives 10 years or more. Note that these four outcomes are mutually exclusive and exhaustive with respect to patient mortality. Thus, the additive law applies—so that the actual objective probabilities of these outcomes, based on mortality statistics for patients with this history, must sum to one. However, Redelmeier et al. found that physicians’ probability estimates summed to much more than one, 1.64 to be precise. This pattern is not restricted to high-stakes risky events—such as death, gambling, stock market investment, and so forth—because judgments about partitions of more prosaic events are also subadditive.

The psychological significance of subadditive probability judgments is both simple and fundamental: As a general rule, people perceive the probabilities of real-life events to be higher than their objective probabilities; they believe that events are more likely to happen than they are. An important consequence is that this can lead to a number of distortions in life-altering decisions. For instance, people may fail to take appropriate risks because they perceive the chances of a negative outcome to be higher than they are, or conversely, they may take inappropriate risks because they perceive the chances of a positive outcome to be higher than they are.

Turning to memory, our concern in this article lies with whether episodic memory also violates the additive law of probability and with the psychological significance of such an outcome. To illustrate this possibility, consider two familiar paradigms that figure in hundreds of prior experiments, false memory for items and false memory for sources (e.g., Hicks & Starns, 2002; Tse & Neely, 2004). In a typical item false memory experiment, subjects encode some target items (e.g., a word list), and then test cues of three types are administered: old targets (O; e.g., sofa; true memory measures), new-similar items (NS; e.g., couch; false memory measures), and new-dissimilar items (ND; e.g., ocean; controls for guessing and response bias). Subjects make a single episodic judgment about each of these types of cues: Is it old (O?)? In a typical source false memory experiment, on the other hand, subjects encode target items that are presented in one of two distinct contexts (e.g., List 1 or List 2), and then test cues of three types are administered—namely, targets from the first context (L1), targets from the second context (L2), and new-dissimilar items (ND). Subjects make one or both of two episodic judgments about each type of cue. First, they decide whether it is an old target (usually called an item judgment), and if the response is “old,” they decide which context it appeared in (usually called a source judgment). The true memory index is the rate at which correct contexts are selected for L1 and L2 cues that are recognized as old, the false memory index is the rate at which incorrect contexts are selected for the same cues. Both can be corrected for bias using the rate at which the two contexts are selected for ND cues that are recognized as old.

Consider some simple variants of the memory tests in these two paradigms, variants that are capable of detecting violations of additive probability but that, to the best of our knowledge, have not been studied. In the item design, suppose that the three types of test cues are factorially crossed with three types of judgments: Is it old (O?); is it new-similar (NS?); or is it new-dissimilar (ND?). In other words, for each test cue, subjects are simply asked to decide whether it belongs to one of the three possible episodic states of the design. In the research reported below, to rule out the possibility that subjects’ decisions might be influenced by assumptions about the proportions of O, NS, and ND cues on memory tests, they were informed that test lists contained the same number of each type of cue. For any cue, these episodic states form a partition because the states are mutually exclusive (a cue cannot belong to more than one of them) and exhaustive (a cue must belong to one of them). If episodic memory obeys the additive law, the total probability of remembering a cue as belonging to these three states will be p(O?) + p(NS?) + p(ND?) = 1.

With respect to the source design, suppose that the three types of test cues are factorially crossed with three types of judgments: Is it an old item from List 1 (L1?); is it an old item from List 2 (L2?); or is it a new item (ND?). As in the modified item design, then, subjects are merely asked to decide whether each test cue belongs to one of the possible episodic states, and in the research reported below, they were informed that the test list contained the same number of each type of cue. As in the item design, the episodic states in the source design form a partition because a cue must belong to one of them and cannot belong to more than one. Hence, if episodic memory obeys the additive law, the total probability of remembering a cue as being a List 1 target or a List 2 target or new will be p(L1?) + p(L2?) + p(ND?) = 1.

If the additive law is violated in these paradigms, the psychological significance of such a finding is that people over-remember or under-remember the events of their lives, depending on whether the violations are in a subadditive or superadditive direction. If the probabilities are subadditive, some event that, based on our experience with it, belongs to episodic state E_i and does not belong to other plausible states E_j and E_k will not only be remembered as belonging to E_i at statistically reliable levels but will also be remembered as belonging to E_j and/or E_k at statistically reliable levels. (Statistical reliability is determined in the conventional way using performance on ND cues to correct for guessing and bias, normally by computing signal detection indices.). It might be thought that false memory phenomena somehow guarantee subadditivity in item designs because NS cues are being remembered as O, at reliable levels. That does not follow, however, because the probability of remembering NS cues as NS may decrease in proportion to the tendency to remember them as O, preserving additivity. Similarly, it might be thought that false memories in source designs somehow guarantee subadditivity because L1 cues are remembered as being L2 and conversely, at reliable levels. Again, that does not follow because the probability of remembering L1 cues as L1 may decrease in proportion to the tendency to remember them as L2 and the probability of remembering L2 cues as L2 may decrease in proportion to the tendency to remember then as L1, preserving additivity.

On the other hand, memory probabilities might be superadditive, which would mean that people systematically under-remember the events of their lives. Thus, some event that, based on our experience with it, belongs to an episodic state E_i and does not belong to other plausible states E_j and E_k will be remembered as belonging to E_i at statistically reliable levels but will be remembered as belonging to E_j and/or E_k at levels that are below what would be expected by chance.

Predicting Violations of the Additive Law in Item and Source Designs

Beyond the significance of violations of the additive law for whether we over- or under-remember experience, there is a firm theoretical basis for studying such phenomena. It turns out that violations are forecast by representation and retrieval principles that have often been used to explain false memory errors, fuzzy-trace theory’s (FTT) notions of parallel, dissociated storage and retrieval of verbatim and gist traces (e.g., Brainerd & Reyna, 2005). According to these ideas, as events are encoded subjects store dissociated verbatim and gist traces of them in parallel. On subsequent memory tests or reasoning problems, verbatim and gist traces are accessed in a parallel, dissociated fashion. A number of effects that are predicted by these assumptions, including some counterintuitive ones, have been reported in the false memory literature (for a review, see Brainerd & Reyna, 2005) and in the judgment-and-decision-making literature (for a review, see Reyna & Brainerd, 2011). On a memory probe, performance can be based on retrieval of verbatim traces or gist traces or both or neither, and even though the two types of traces are stored for the same event, they generate different response patterns over different memory probes for the same test cue.

For instance, consider the target cue sofa, along with the probes O? and NS? FTT assumes that the traces that are retrieved are determined by the test cue, rather than by the probe that is administered in connection with the cue (Brainerd, Gomes, & Moran, 2014). If sofa produces verbatim retrieval, regardless of whether it also produces gist retrieval, it is unambiguously identified as being a target, yielding responses to O? and NS? that are mutually consistent—accept and reject, respectively. If sofa produces gist retrieval without verbatim retrieval, it is unambiguously identified as being either a target or a related distractor, but gist is indeterminate with respect to which it is. In this situation, FTT posits that subjects’ perceptions of sofa‘s episodic state are different for different probes, and their responses are governed by a principle that Brainerd et al. (2010) referred to as description dependency: Sofa is perceived to be a target when the probe asks if it is a target (O?) and such probes are accepted, but it is perceived to be a related distractor when the probe asks if it is a related distractor (NS?) and such probes are also accepted. Note that each of these responses, by itself, is consistent with the information that has been retrieved from memory. It is only when the two responses are considered as a pair that an inconsistency emerges.

In recent work quantum probability (QP) models, parallel dissociated processing of verbatim and gist traces has been discussed as a cognitive instance of the superposition property of physical quantum systems (Brainerd, Holliday, et al., 2014; Brainerd, Wang, & Reyna, 2013; Busemeyer & Bruza, 2012). It is equivalent to saying that the two types of traces are superposed in memory, in much the same way that the vertical and horizontal components of electron spin are superposed (Gerlach & Stern, 1922). Consequently, the aforementioned assumptions about memory representation and retrieval can be modeled with the QP formalism, and when such a model is in place, it can be analyzed to derive principled, axiomatic predictions about episodic memory. Based on earlier proposals by Brainerd et al. (2013; see related proposals by Busemeyer & Bruza, 2012; Trueblood & Hemmer, under review; Denolf & Lambert-Mogiliansky, under review; see the Appendix for a discussion), we developed such a model, called quantum episodic memory (QEM), for the item and source paradigms. When the simplest version of this model (QEMc), which implements the assumption of compatibility of memory test probes, was analyzed, it predicted that memory judgments would violate the additive law in both paradigms and that violations would be in a subadditive direction. The details of QEMc are relegated to the Appendix. Here, we present its main features and predictions in intuitive language.

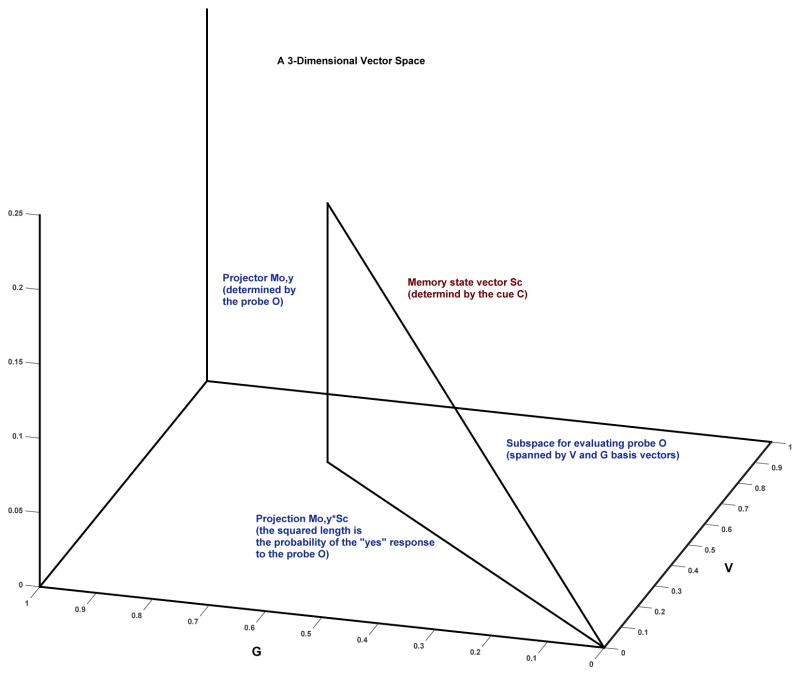
As in QP models of other cognitive tasks (e.g., Nelson, Kitto, Galea, McEvoy, & Bruza, 2013; Bruza, Wang, & Busemeyer, 2015; Pothos & Busemeyer, 2013; Wang, Busemeyer, Atmanspacher, & Pothos, 2013), QEMc uses vector spaces to capture FTT’s distinctions. The memory vector space for item false memory experiments, which is illustrated in Figure 1, is generated by three orthonormal basis vectors |V〉, |G〉, and |N〉. (The vector space can be arbitrarily high-dimensional, but for simplicity of illustration, a three-dimensional space is used in the illustration.) For any test cue C, |V〉 is a verbatim vector that matches its surface form, |G〉 is a gist vector that matches its semantic/relational content, and |N〉, is a vector that does not match either the cue’s surface form or its semantic/relational content. The cue induces a perceived memory state, S_C, which QEMc represents as a vector |S_C〉 in the memory space, where |S_C〉 is a superposition of the three basis vectors: |S_C〉 = v_C|V〉 + g_C|G〉 + n_C|N〉. In this expression, v_C, g_C, and n_C are probability amplitudes (scalars, weighting parameters) that represent the respective strengths of the three types of traces. By the axioms of QP, the probabilities of verbatim, gist, or nonmatching traces being retrieved for C are obtained by squaring the corresponding probability amplitudes, so that those probabilities are |v_C |², |g_C|², and |n_C|², respectively. Because these are the only possible outcomes in this memory space, the additive law must be satisfied when their squared probability amplitudes are summed: |v_C|² + |g_C|² + |n_C|² = 1.

Figure 1.

The quantum probability representation of fuzzy-trace theory’s principles of parallel, dissociated storage and retrieval of verbatim and gist traces. The vector space can be arbitrarily high-dimensional—as in vector spaces for feature matching models—although for simplicity of illustration, a simple three-dimensional vectors space is used in this example.

It turns out that QEMc predicts that regardless of whether C is an O, NS, or ND item and regardless of what the empirical values of |v_C|², |g_C|², and |n_C|² may be, the total probability of remembering it as belonging to each of these states will exceed 1; that is, subadditivity is a fundamental property of episodic memory under verbatim-gist superposition. This is shown for each type of cue in the upper half of Table 1, where QEMc’s expressions for accepting O?, NS?, and ND? probes, respectively, for each type of cue are displayed. First, note that for each type of cue i, its total acceptance probability over the three episodic states, is always of the form |v_i|² +|g_i|² +|g_i|²+|n_i|² = 1+ |g_i|² ≥ 1, where the values of the individual terms fall somewhere in the unit interval and reflect the magnitudes of the contributions of verbatim traces, gist traces, and nonmatching traces, respectively. Thus, subadditivity is predicted a priori, without fitting the model to data or estimating its parameters. Second, note that the reason QEMc predicts subadditivity is that |g_i|² appears twice in each total probability expression.¹ Regardless of what the values of v_i, g_i, and n_i may be, this forces subadditivity mathematically because |v_C|² + |g_C|² + |n_C|² = 1. Third, the reason that |g_i|² appears twice in each total probability expression derives from FTT’s principles of representation and retrieval (Brainerd et al., 2013): According to those principles: (a) An O cue will be perceived as O on O? probes (first line of Table 1) but as NS on NS? probes (second line) if the cue retrieves its gist trace but not its verbatim trace; (b) an NS cue will be perceived as O on O? probes (fifth line of Table 1) but as NS on NS? probes (sixth line) if the cue retrieves the gist trace of a related target but not its verbatim trace; and (c) an ND cue will be perceived as O on O? probes (ninth line of Table 1) but as NS on NS? probes (tenth line) if the cue retrieves the gist trace of a related target but not its verbatim trace.²

Table 1.

Subadditivity of Episodic Memory as Predicted by the Quantum Model of Fuzzy-Trace Theory in False Memory and Source-Monitoring Experiments

Memory judgment	Trace vector
	|V〉	|G〉	|N〉	Vector sum
1. Item false memory experiment
Cue = target
O?	|vO|2	|gO|2	0	|vO|2 + |gO|2
NS?	0	|gO|2	0	|gO|2
ND?	0	0	|nO|2	|nO|2
Total memory probability	|vO|2 +|gO|2 +|gO|2 + |nO|2 > 1
Cue = New-Similar
O?	|vns|2	|gns|2	0	|vns|2 + |gns|2
NS?	0	|gns|2	0	|gns|2
ND?	0	0	|nns|2	|nns|2
Total memory probability	|vns|2 +|gns|2 +|gns|2 + |nns|2 > 1
Cue = New-dissimilar
O?	|vnd|2	|gnd|2	0	|vnd|2 + |gnd|2
NS?	0	|gnd|2	0	|gnd|2
ND?	0	0	|nnd|2	|nnd|2
Total memory probability	|vnd|2 +|gnd|2 +|gnd|2 + |nnd|2 > 1
2. Source false memory experiment
Cue = List 1target
List 1?	|vL1-1|2	|gL1|2	0	|vL1-1|2 +|gL1|2
List 2?	|vL1-2|2	|gL1|2	0	|vL1-2|2 +|gL1|2
New?	0	0	|nL1|2	|nL1|2
Total memory probability	|vL1-1|2+|vL1-2|2+|g L1|2 +|g L1|2 + |nL1|2 > 1
Cue = List 2 target
List 1?	|vL2-1|2	|gL2|2	0	|vL2-1|2+|gL2|2
List 2?	|vL2-2|2	|gL2|2	0	|vL2-2|2+|gL2|2
New?	0	0	|nL2|2	|nL2|2
Total memory probability	|vL2-1|2+|vL2-2|2+| gL2|2 +| gL2|2 + |nL2|2 > 1

Note. |V〉, |G〉, and |N〉 are unit-length vectors for verbatim, gist, and nonmatching traces, respectively, which form an orthonormal basis in a three-dimensional space where memory judgments are made in false memory and source-monitoring experiments. In both types of experiments, the v_c, g_c, and n_c parameters are scalars that multiply the |V〉, |G〉, and |N〉 vectors, respectively, giving the magnitudes of these vectors, subject to the constraint that |v_c|² +|g_c|² + |n_c|² = 1 for the item false memory paradigm and |v_c-1|² +|v_c-2|² +|g_c|² + |n_c|² = 1 for the source false memory paradigm.

Psychologically, the v_c, g_c, and n_c parameters correspond to the strength/accessibility of verbatim, gist, and nonmatching traces, respectively, for the test cue c. The subscript c runs over O (old), NS (newsimilar), and ND (new-dissimilar) cues in false memory experiments, and in general, the scalars have different values for the three types of cues. The subscript c runs over L₁ (List 1), L₂ (List 2), and ND (newdissimilar) cues in source-monitoring experiments designs, and in general, the scalars have different values for the three types of cues.

According to the QEMc implementation of FTT, the additive law will be violated by all three types of cues, not just by targets, because the model’s total probability expression has the same form for NS and ND cues as for O cues. Another important prediction is that the amount of subadditivity that is observed for any cue will be directly proportional to the strength of gist traces because it is the gist retrieval term |g_i|² that causes subadditivity in the first place. (Subadditivity is also inversely proportional to the strengths of verbatim and nonmatching traces because the value of |g_i|² is jointly constrained by the values of |v_i|² and |n_i|².) That opens an attractive avenue for experimentation on the model. In the false memory literature, a number of manipulations have been studied that are intended to strengthen gist memory relative to verbatim memory, such as the presentation of several targets that share the same meaning and administration of delayed memory tests (for a review, see Brainerd & Reyna, 2005). QEMc makes the straightforward prediction that such manipulations ought to increase observed levels of subadditivity. Therefore, some well-known examples were included in the experiments that are reported later.

Finally, returning to the modified source paradigm, subadditivity is also predicted there, for the same reasons that it is predicted for the item paradigm. The QEMc model for source designs is the same as the item model, except that there are now two verbatim trace vectors, |V₁〉 and |V₂〉 (see Appendix). That is because O items have been presented in two distinct contexts, which means that the vector space for source memory is generated by the four orthonormal basis vectors, |V₁〉, |V₂〉, |G〉, and |N〉. For any cue C, the expression for its perceived memory state, which is a superposition of these vectors, is S_C = v_C1|V₁〉 + v_C2|V₂〉 + g_C|G〉 + n_C|N〉. As before, the probability amplitudes v_C1, v_C2, g_C, and n_C represent the strengths of the corresponding verbatim, gist, and nonmatching traces, and these parameters are subject to the constraint that |v_C1|² + |v_C2|² + |g_C|² +|n_C|² = 1.

The additive law of probability can be tested for this design by summing the individual probabilities of remembering a cue as belonging to each of the three mutually exclusive and exhaustive episodic states; that is, using the metric p(L1?) + p(L2?) + p(ND?). According to QEMc, this sum is given by |v_C1|² + |v_C2|² +|g_C|² +|g_C|² +|n_C|² = 1 +|g_C|² ≥ 1. Thus, subadditivity is predicted for the source paradigm and for the same reason as before: The gist term contributes twice to the total probability expression—so that as long as gist memory is involved, subadditivity is predicted. The psychological reasons for that are also the same as before, as can be seen in the lower half of Table 1.

Models that Do Not Predict Violations of the Additive Law

QEMc’s predictions about violations of the additive law, specifically subadditivity, are not common among memory models. Indeed, true (parameter-free, a priori) predictions that memory will violate this law do not follow from some classical models that are well known to readers. This includes what, historically, has been the most influential model of item recognition, the one-process signal detection model (e.g., Glanzer & Adams, 1990) and what, historically, has been the most influential model of source recognition, Batchelder and Riefer’s (1990) source-monitoring model. We briefly describe each of these models before considering an important interpretive point,, which is that QEMc’s predictions about violations of the additive law should be not be equated with recent studies of disjunction fallacies in false memory for items and sources.

Signal Detection Model

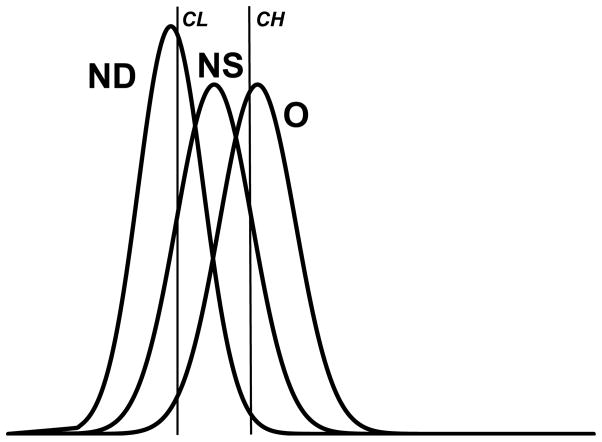
Taking the item design first, the signal detection model represents the memory information in simple item recognition experiments, in which only O and ND test cues are administered, as a pair of Gaussian distributions of familiarity values—one for O and one for ND (the O and ND distributions in Figure 2). In an item false memory experiment in which NS test cues are also administered, a third Gaussian distribution is added (the NS distribution in Figure 2). When a target cue is presented for test, the subject samples a familiarity value from the O distribution and generates a response by setting a decision criterion along the strength axis. Because the mean strength of the O distribution is greater than the mean strength of the NS distribution, different decision criteria will be needed, depending on whether only O cues, only NS cues, or neither can be accepted,

Figure 2.

Signal detection representation of memory information in the item false memory paradigm. O, NS, and ND are Gaussian distributions of familiarity values for old cues, new-similar cues, and newdissimilar cues, respectively. C_H and C_L are decision criteria. C_H is the sole decision criterion on O? probes, for O, NS, and ND cues. C_L is the sole decision criterion for all three types of cues on ND? probes. However, both C_H and C_L are used for all three types of cues on NS? probes.

If the probe is O?, the subject sets a “strong” decision criterion, C_H in Figure 2, and responds affirmatively if the sampled familiarity value equals or exceeds that criterion. The probability density of such a value is given by the cumulative Gausssian probability integral φ_O,CH, which runs from C_H to +∞ in the O distribution. If the probe is NS?, the subject sets a “strong” decision criterion and a “weak” decision criterion, C_L and C_H in Figure 2, and responds affirmatively if the sampled value equals or exceeds C_L but falls below C_H. The probability density of such a value is given by the cumulative probability integral φ_O,CL-CH, which runs from C_L to C_H in the O distribution. Last, if the probe is ND?, the subject sets a single “weak” decision criterion, C_L in Figure 2, and responds affirmatively if the sampled value falls below that criterion. The probability density of such a value is given by the cumulative probability integral φ_O,CL, which runs from −∞ to C_L in the O distribution. Thus, the total probability p(O?|O) + p(NS? |O) + p(ND?|O) is the sum of the three cumulative probability integrals. It is easy to see that this sum is just the cumulative probability density from −∞ to +∞ of the O distribution, which is 1 by the definition of a probability distribution. It is also easy to see that parallel demonstrations can be given for NS and ND cues, using cumulative probability integrals for the NS and ND distributions, so that the model predicts that p(O?|NS) + p(NS? |NS) + p(ND? |NS) and p(O?|ND) + p(NS? |ND) + p(ND? |ND) will satisfy the additive law, too.

Although this standard model predicts that all three types of cues will satisfy the additive law, ad hoc adjustments are possible that will accommodate violations in either the subadditive or superadditive direction. In particular, suppose that two “strong” criteria are permitted, one for O? probes and one for NS? probes, and that two “weak” criteria are permitted, one for NS? probes and one for ND? probes. Now, the model can accommodate additivity, subadditivity, and superadditivity, but at the cost of not being able to predict any of these patterns.

Source-Monitoring Model

Turning to the source design, Batchelder and Riefer’s (1990) source model postulates five processes to account for performance: (a) a detect-old process that identifies whether a cue is old (parameter D₁ for List 1 targets and parameter D₂ for List 2 targets); (b) a source memory process that operates when cues are detected to be old and identifies them as belonging to List 1 or List 2 (parameter d₁ for List 1 and parameter d₂ for List 2), (c) a guessing process that operates when cues are detected to be old and attributes them to List 1 or List 2 when the source memory process fails to identify their source (with probability g), (d) a second guessing process that operates when cues are not detected to be old and attributes them to the old and new states (with probabilities b and 1-b, respectively), and (e) a third guessing process that decides whether items that have been guessed to be old belong to List 1 or List 2 (with probability a). This model’s expressions for acceptance of L1?, L2?, and ND? probes, for L1, L2, and ND cues appear in Table 2.

Table 2.

Additivity of Source-Monitoring Judgments as Predicted by Batchelder and Riefer’s (1990) Model of Source Memory

Cue/probe	Model expression
Cue: List 1 target
L1?	D1d1 + D1(1-d1)g + (1-D1)ba
L2?	D1(1-d1)g + (1-D1)ba
ND?	1 - D1 - (1-D1)(1-b)
Cue: List 2 target
L1?	D2(1-d2)g + (1-D2)ba
L2?	D2d2 + D2(1-d2)g + (1-D2)ba
ND?	1 - D2 - (1-D2)(1-b)
Cue: Distractor
L1?	ba
L2?	ba
ND?	1 - b

Algebraic manipulation of the expressions in Table 2 for each cue shows that this model does not make determinant predictions of subadditivity, additivity, or superadditivity for the present source false memory paradigm. Instead, like the adjusted signal detection model, it can account for any of these patterns post hoc when its parameters have certain values, but it does not predict any of them. For ND cues (last three lines of Table 2), the sum of the probabilities of accepting the three probes is 1 + b(2a − 1), from which it is apparent that whether this sum is subadditive, additive, or superadditive depends on whether parameter a is greater than, equal to, or less than .5. For L1 and L2 cues, the model does not make determinant predictions either. In each instance, the sum of the probabilities of accepting the three probes is 1 + D_i[d_i + 2(1−d_i)g − 1] + (1−D_i)b(2a − 1). From this, it is clear that whether the sum is subadditive, additive, or superadditive depends on whether the empirical values of the d_i + 2(1−d_i)g − 1 term and the (2a − 1) term are positive, zero, or negative. The latter term will be positive, zero, or negative accordingly as the parameter a is greater than, equal to, or less than .5. Whether the former term is positive, zero, or negative depends on the empirical values of d_i and g. For instance, it is easy to see that if d_i is held constant at .3, this term will be negative when g < .61, zero when g = .61, and positive when g > .61.

Disjunction Fallacies in Item and Source Memory

QEMc’s parameter-free predictions about violations of the additive law should not be conflated with another nonadditivity phenomenon in item and source memory—namely, disjunction fallacies. Disjunction fallacies were originally studied in probability judgment by Tversky and Kohler (1994). They refer to situations in which subjects make probability judgments about (a) two or more mutually exclusive events (the probability of dying from cancer; the probability of dying from heart disease) versus (b) an equivalent disjunctive event (the probability of dying from either cancer or heart disease). The axioms of probability theory say that the sum of the probabilities of two mutually exclusive events must equal the probability of their disjunction. Usually, this equality does not hold, with the sum of the nondisjunctive probabilities typically being greater than the disjunctive probability (subadditivity) but sometimes being smaller (superadditivity; see Fox, Ratner, & Lieb, 2005).

Recently, memory analogues of disjunction fallacies have been studied with both item and source memory, using the conjoint-recognition paradigm and a multinomial model that is defined over that paradigm. In the item version of the paradigm (Brainerd et al., 2010), subjects respond to three probes about test cues, two nondisjunctive probes (Is it a target? Is it a related distractor?) and a disjunctive probe (Is it either a target or a related distractor?). In the source version of the paradigm (Brainerd, Reyna, Holliday, & Nakamura, 2012), subjects also respond to two nondisjunctive probes (Was it presented on List 1? Was it presented on List 2?) and a disjunctive probe (Was it presented on either List 1 or List 2?). In either version, the sum of the probabilities of accepting the two mutually exclusive probes should equal the probability of accepting the disjunctive probe. Instead, subadditivity has predominated. Brainerd et al. (2010), Brainerd, Gomes, et al. (2014) found that the conjoint recognition model and a related model (dual recollection) were able to fit such data for item false memory, and Brainerd et al. (2012) found that the conjoint recognition model was able to fit such data for source false memory. More recently, Kellen, Singmann, and Klauer (2014) found that the two-high-threshold source memory (2HTSM) model was also able to fit such data for source false memory.

The research that we report in the present article differs from this prior work in two key ways, one empirical and the other theoretical. The empirical difference is that tests of disjunction fallacies are not tests of the additive law. Tests of the additive law ask whether the empirical probabilities of events that partition a sampling space sum to 1, whereas tests of disjunction fallacies ask whether two logically equivalent probabilities are also equal empirically. The fact that the latter tests reveal disjunction fallacies does not mean that the former tests will reveal violations of the additive law for either item or source false memory. As Brained, Holliday, et al. (2014) pointed out, disjunction fallacies may occur simply because disjunctive probes are less effective retrieval cues than nondisjunctive probes. This feature is absent from tests of the additive law, as described earlier, because all probes are nondisjunctive.

The theoretical difference between the present research and prior work on disjunction fallacies is that whereas true predictions were not tested in prior work, they are tested in the present research. For all three types of cues in item and source designs, we saw that QEMc makes true (i.e., parameter-free, a priori) predictions that the additive law will be violated in the subadditive direction. In contrast, the models that have been fit to the data of disjunction fallacy experiments do not make parameter-free predictions, and like the adjusted signal detection model and the 1HTSM model, they allow the relation between disjunctive and nondisjunctive probabilities to be additive, subadditive, or superadditive, depending on the empirical values of their parameters. With the conjoint recognition and dual recollection models, the specific relation that is observed depends on the values of their bias/guessing parameters (see Brainerd et al., 2010, 2012; Brainerd, Gomes, et al., 2014). With 2HTSM, the specific relation that is observed depends on the values of its bias/guessing parameters and its memory parameters (see Kellen et al., 2014).

Finally, although these alternative models do not make true predictions about the additive law, there is an important conceptual similarity between QEMc and two of the models (conjoint recognition and dual recollection) at the level of the psychological processes that foment subadditivity. In QEMc, we saw that subadditivity in item and source false memory should increase as its gist parameter increases and/or its verbatim parameter decreases. The conjoint recognition and dual recollection models also contain verbatim and gist parameters, and when their equations are analyzed, they, too, expect that item and source false memory will move in a subadditive direction as gist parameters increase and/or verbatim parameters decrease. Differently, the 2HTSM model predicts that source memory will move in a subadditive direction when the values of its source guessing parameters move in opposite directions.

Experiment 1: Item False Memory

To our knowledge, the question of whether memory judgments about a specific type of cue (say, O) are additive over a partition of its possible episodic states has not been directly evaluated. Therefore, we conducted a large-scale evaluation, using a basic type of false memory design that involved Deese/Roediger/McDermott (DRM) lists (cf. Gallo, 2010). In standard versions of this design, subjects study a series of such lists, are then administered a series of test cues consisting of O, NS, and ND items, and finally, they respond to O? probes for all of those cues. In our design, in order to evaluate the additive law, the three types of test cues were factorially crossed with O?, NS?, and ND? probes.

We know that QEMc predicts that episodic memory will violate the additive law in a particular way (subadditivity rather than superadditivity) and that there is a specific process mechanism for that prediction—namely, superposition of verbatim and gist memories. Because the gist component of the superposition is what ostensibly forces nonadditivity, QEMc expects that nonadditivity will be more pronounced in conditions that increase reliance on gist memory. We attempted to generate converging evidence on this principle by including three manipulations that have been used in several prior experiments to manipulate reliance on gist memory (see Brainerd & Reyna, 2005): (a) O cues versus NS cues, (b) O and NS cues versus ND cues, and (c) whether or not a cue on a delayed test had been previously tested.

Concerning a, the first manipulation takes advantage of the simple fact that the ratio of gist to verbatim retrieval should be higher for critical distractors than for O cues. That is because critical distractor cues (e.g., chair) match DRM lists’ semantic content better than any single target (e.g., couch) owing to the way these lists are constructed (see Barnhardt, Choi, Gerkens, & Smith, 2006), and critical distractor cues do not match the surface structure of any of the targets. Concerning b, ND cues obviously provide a poorer match to DRM lists’ semantic content than either targets or critical distractors do and, hence, violations of additivity should be less marked for ND cues. Concerning c, this manipulation takes advantage of the fact that at over time, memory for targets’ surface structure becomes inaccessible more rapidly than memory for their semantic content (Kintsch, Welsch, Schmalhofer, & Zimny, 1990), and that this difference can be amplified by prior testing. Specifically, although prior memory tests help to preserve access to both verbatim and gist memories over time, the gist-preservation effect is substantially larger and the spread between the two preservation effects is larger for NS cues than for O cues (Bouwmeester & Verkoeijen, 2011; Brainerd & Reyna, 1996), which is presumably because the meaning content but not the surface form of NS cues was presented. In any case, it follows that on delayed tests, reliance on gist memory should be greater for cues that have been previously tested than for cues that have not been.

Method

Subjects

The subjects were 260 undergraduates who participated to fulfill a course requirement.

Materials and Procedure

The target materials were 24 DRM lists drawn from the Roediger, Watson, McDermott, and Gallo (2001) pool of 55 lists. Each list contains 15 semantically-related words (e.g., table, sit, legs, seat, couch, desk, recliner, sofa, wood, cushion, swivel, stool, sitting, rocking, bench) that are forward associates of an unpresented word (chair) that is usually called the critical distractor or critical lure. Norms for true recall, false recall, true recognition, and false recognition for these 55 lists are reported in Roediger et al. For the present experiment, we chose the 24 lists that produced the highest levels of false recognition of critical distractors. These lists supplied the items that were presented during the study phase, and they also supplied the O and NS cues for the immediate and 1-week delayed memory tests.

The experiment consisted of two sessions—an initial one, in which all of the lists were presented for study and an immediate memory test for half of the lists was administered, and a 1-week delayed session, in which a memory test for all of the lists was administered. During the study phase, the first 6 words from each of the 24 lists were presented, for total of 144 items. (For example, the presented words for the chair list were table, sit, legs, seat, couch, and desk.). During the first session, following general memory instructions, each subject studied all 24 lists, with the individual lists being presented in random order. Presentation was visual, on a computer screen, at a 2.5-s rate with an 8-s pause following each 6-word DRM list. Just prior to presentation, the subject was informed that he or she would be viewing a series of 24 short word lists and that a memory test would be administered after all of the lists had been presented. Next, the 24 lists were presented in random order. Presentation began with the phrase “first list” appearing in the center of the screen. The six words of the first list were then presented. After the 8-s pause following the first list, the phrase “next list” appeared in the center of the screen, followed by the six words of the next list. The procedure of list presentation alternating with 8-s pauses continued until all 24 lists had been presented.

After the lists had been presented, the subject read a page of instructions, which explained that the cues on the upcoming test would consist of words that they had just seen in the presented lists (O), unpresented words whose meanings were similar to those of the presented lists (NS), and words that were unrelated to the presented lists (ND). Subjects were told that 1/3 of the test cues would be O, 1/3 would be NS, and 1/3 would be ND. Illustrations of each type of cue were provided in the instructions, which also explained that the subject would be answer one of three types of questions about each test cue: (a) Is it old word that you saw on one of the lists (O?)? (b) Is it a new word whose meaning is similar to one of the lists (NS?)? (c) Is it a new word whose meaning is not similar to any of the lists (ND?)? The three questions were illustrated with further example words.

Following instructions the subject responded to a 72-item self-paced visual recognition test for 12 (randomly selected) of the 24 DRM lists, with testing of the other 12 being delayed for 1 week. The composition of the 72 test cues was as follows: (a) 24 O cues (2 per list, randomly selected), (b) 24 NS cues (12 the critical distractors for the tested lists and 1 other related distractor for each list), (c) 24 ND cues. With respect to category b, it is common in DRM research to include other related distractors as well as critical distractors as NS cues on test lists (e.g., Brainerd et al., 2010). The standard method of generating other related distractors for a DRM list is to select them from among list words that are not presented for study. In our case, because we presented DRM lists that consisted of 6 words apiece, a related distractor for each list was obtained by selecting one of the unpresented words from positions 7–15 of that list (e.g., sofa or stool for the chair list). As also traditional in this type of research, the ND cues were obtained by randomly sampling words from positions 1–6 from unpresented lists in the Roediger et al. (2001) pool. The three types of episodic probes were factorially varied over the 24 targets, the 12 critical distractors, the 12 related distractors, and the 24 unrelated distractors.

A delayed memory test was administered 1-week later. The delayed test consisted of a total of 144 test cues administered in random order and was composed of two subtests. One subtest was simply a repetition of the immediate test; that is, the same O, NS, and ND cues, with the same probes for each cue. The other was for the 12 DRM lists that had not been tested 1-week earlier. That subtest was also composted of 72 cues: (a) 24 O cues (2 per previously untested list, randomly selected), (b) 24 NS cues (the critical distractors for the previously untested lists and a related distractor for each previously untested list), (c) 24 new ND cues. As before, the ND cues were drawn from words in positions 1–6 of unpresented lists in the Roediger et al. (2001) pool. Also as before, the three types of episodic probes were factorially varied over the 24 targets, the 12 critical distractors, the 12 related distractors, and the 24 unrelated distractors. At the start of the delayed session, the subject read a page of detailed instructions that reminded him/her of the word lists that had been presented a week earlier and explained that the purpose of the session was to respond to another memory test like the one that had been administered a week earlier. As on the immediate test, the instructions explained that the cues on the test would consist of words that they had seen in the presented lists, unpresented words whose meanings were similar to those of the presented lists, unpresented words that were unrelated to the presented lists, and 1/3 of the test cues would be each of these types. Illustrations of each type of cue were again provided, and the instructions again explained the three types of questions that the subject would be answer. Following these instructions, the subject responded to the probes for the 96 text cues, using the same self-procedure as before.

Results

Descriptive statistics for the various Cue X Probe combinations appear in Table 3, for the immediate condition and the two delayed conditions (previously untested vs. previously tested). We report the results for the immediate and delayed tests separately.

Table 3.

Acceptance Probabilities in Experiment 1(SDs in Parentheses)

Test cue	Memory judgment
	O?	NS?	ND?	Sum
Immediate test
O	.53(.19)	.43(.19)	.26(.16)	1.22
NS
Critical	.55(.31)	.60(.26)	.21(.22)	1.36
Related	.28(.21)	.54(.18)	.41(.21)	1.23
ND	.17(.18)	.34(.22)	.62(.19)	1.13
Delayed test – previously tested cues
O	.49(.17)	.50(.19)	.35(.18)	1.33
NS
Critical	.55(.28)	.57(.26)	.23(.22)	1.36
Related	.48(.22)	.49(.19)	.44(.20)	1.42
ND	.28(.20)	.38(.23)	.58(.25)	1.21
Delayed test – previously untested cues
O	.33(.19)	.36(.21)	.56(.22)	1.25
NS
Critical	.38(.28)	.44(.27)	.48(.30)	1.30
Related	.34(.22)	.29(.19)	.62(.25)	1.25
ND	.23(.21)	.33(.24)	.68(.22)	1.11

Note. O = old words from DRM lists, NS = new but similar words (DRM critical distractors or related distractors), and ND = new unrelated words.

Immediate Test

In our design, test cues for targets, critical distractors, related distractors, and unrelated distractors were administered for half the DRM lists at the end of Session 1. The relevant descriptive statistics are displayed at the top of Table 3, with the statistic that was used to test the additive law appearing in the sum column on the far right. It can be seen that all of the values in the sum column fell out in accordance with QEMc’s predictions inasmuch as all were subadditive. At a finer-grained level, they also fell out in accordance with the notion that subadditivity increases in proportion to gist reliance: Subadditivity was more marked for critical distractors than for any of the other three types of cues, and it was more marked for targets and related distractors than for unrelated distractors.

Initially, we conducted a one-way analysis of variance (ANOVA) of the sum values for the four types of cues, which produced a highly reliable effect, F (3, 780) = 29.18, MSE = .08, partial η² = .10, p < .0001. Follow-up analyses (paired-samples t tests) revealed that the level of subadditivity was higher for critical distractors than for any of the other three types of cues, as expected on theoretical grounds. The mean value of the three test statistics was t (260) = 5.92, p < .0001).. In addition, subadditivity was higher for targets than for unrelated distractors, t (260) = 4.40, p < .0001, and higher for related distractors than for unrelated distractors, t (260) = 4.69, p < .0001, but did not differ for targets versus related distractors. The ordering of the sum values, then, was the same as the likely order of reliance on gist memory.

Although some of the sum values differed reliably, the question remains as to whether all of them were reliability greater than zero, as QEMc predicts. To test that hypothesis, we computed a one-sample t test for each of the four types of cues, using 1 as the predicted value of the sum index. The tests showed that the observed value was greater than the predicted value for targets, t (260) = 13.15, p < .0001, for critical distractors, t (260) = 13.40, p < .0001, for related distractors, t (260) = 11.83, p < .0001, and for unrelated distractors, t (260) = 6.42, p < .0001. Thus, all four types of cues failed to obey the additive law.

Next, what about violations of the additive law among individual subjects? There are two general scenarios that could produce the above findings. According to one, which is what QEMc would expect, most subjects’ sum values conform to the p(O?) + p(NS?) + p(ND?) > 1 rule—it is the modal pattern, in other words. According to the second scenario, however, there are two groups of subjects, with most subjects’ exhibiting additivity but a minority exhibiting extreme subadditivity. Although both scenarios can produce the above group results, they would obviously lead to different theoretical interpretations. Therefore, we examined the sum values of individual subjects for all four types of cues and simply counted the numbers of values that satisfied the p(O?) + p(NS?) + p(ND?) > 1 rule. The rules favored the first scenario, in which most values conform to this rule. The numbers of subjects (out of 260) whose sum values followed the rule were 200 (p < .0001 by a sign test), 174 (p < .0001 by a sign test), 180 (p < .0001 by a sign test), and 148 (p < .02 by a sign test), for targets, critical distractors, related distractors, and unrelated distractors, respectively. Hence, regardless of cue, more than half of the sum values satisfied the rule.

One-Week Delayed Tests

Of the original 260 subjects, 40 failed to return for the delayed test, for an attrition rate of 15%. On the delayed test, all of the test cues that had appeared on the immediate test were readministered with the same probe questions as before. In addition, the delayed test included cues for targets, critical distractors, related distractors, and unrelated distractors for the 12 DRM lists that were not tested during Session 1. Thus, all 24 lists were included on the delayed test, with half them having been previously tested and half not have been previously tested. The relevant descriptive statistics for previously tested and untested lists are displayed at the top of Table 3, with sum statistic again appearing in the far right. It can be seen that all eight of the sum values were subadditive, as QEMc predicts. Note that these data are consistent with the notion that prior memory tests selectively preserve gist memories: The mean sum value was greater for previously tested cues that for previously untested ones.

First, we computed a 2 (previously tested vs. untested) X 4 (cue: target, critical distractor, related distractor, unrelated distractor) of the sum values. This produce a main effect for prior testing, F (1, 219) = 36.97, MSE = .13, partial η² = .14, and a main effect for cue, F (3, 219) = 48.28, MSE = .06, partial η² = .18, p < .0001. The mean sum value was higher for previously tested than for previously untested cues, of course. With respect to the ordering of the sum values for the four types of cues, mean values were lower for unrelated distractors than for targets, t (219) = 7.55, p < .0001, for critical distractors, t (219) = 7.16, p < .0001, and for related distractors, t (219) = 8.99, p < .0001. In addition, the mean sum for targets was lower than the mean sum for related distractors, t (219) = 3.10, p < .002, but targets did not differ from critical distractors and critical distractors did not differ from related distractors. In addition the ANOVA produced a small Prior Text X Cue interaction, F (3, 219) = 3.10, MSE = .08, partial η² = .01, p < .03. The reason was that the sum statistics for targets versus related distractors only differed reliably for previously tested cues.

Turning to the question of whether all of the sum values were reliably greater than 1, as QEMc predicts, they were. For previously tested cues, one-sample t tests produced rejections of the null hypothesis that p(O?) + p(NS?) + p(ND?) ≤ 1 for targets, t (218) = 18.31, p < .0001, for critical distractors, t (219) = 12.52, p < .0001, for related distractors, t (219) = 18.42, p < .0001, and for unrelated distractors, t (219) = 10.51, p < .0001. The results were similar for previously untested cues. One-sample t tests produced rejections of the null hypothesis that p(O?) + p(NS?) + p(ND?) ≤ 1 for targets, t (219) = 14.48, p < .0001, for critical distractors, t (219) = 10.61, p < .0001, for related distractors, t (219) = 13.02, p < .0001, and for unrelated distractors, t (219) = 4.97, p < .0001. Hence, regardless of whether cues had been tested a week earlier, all four types of cues failed to obey the additive law.

However, as we saw, this does not mean that violation of the additive law was the modal pattern at the level of individual subjects. Therefore, we again examined the sum values of individual subjects for all four types of cues and counted the numbers of values that satisfied the p(O?) + p(NS?) + p(ND?) > 1 rule, doing so separately for previously tested versus untested cues. The results again showed that most sum values conformed to this rule. The numbers of subjects (out of 220) whose sum values followed the rule for previously tested cues were 200 for targets (p < .0001 by a sign test), 156 for critical distractors (p < .0001 by a sign test), 186 for related distractors (p < .0001 by a sign test), and 167 for unrelated distractors (p < .0001 by a sign test). The numbers of subjects whose sum values followed the rule for previously untested cues were 173 for targets (p < .0001 by a sign test), 145 for critical distractors (p < .0001 by a sign test), 168 for related distractors (p < .0001 by a sign test), and 126 for unrelated distractors (p < .03 by a sign test). As before, then, more than half of the sum values satisfied the rule for all cues.

Summary

The additive law was violated everywhere—in every condition in which it was possible to evaluate it. This was true at the level of individual subjects, as well as at the level of mean values of the sum index. Additional findings were consistent with the hypothesis that such violations result from reliance on gist memory because sum values were more subadditive in conditions in which gist reliance should have been greater. For instance, on the immediate test, subadditivity was more marked for cues whose meaning content had been encoded during the study phase (targets, critical distractors, and related distractors) than for cues whose meaning content had not been encoded (unrelated distractors), and subadditivity was more marked for critical distractors than for other types of cues. On the delayed test, subadditivity was again more marked for cues whose meaning content had been encoded during the study phase than for cues whose meaning content had not been encoded, and it was also more marked for cues that had been tested a week earlier than for cues that had not been tested.

Although the predicted violations of the additive law were confirmed everywhere, there was one feature of the data that is inconsistent with QEMc. It can be seen in Table 1 that the model imposes constraints on the relative magnitude of p(O?) and p(NS?), such that the latter cannot be larger than the former for any of the types of test cues. In Table 3, however, there are four cells in which paired-samples t tests showed that p(NS?) was reliably larger than p(O?): in the immediate test cell for related distractors and in the immediate, delayed-untested, and delayed-tested cells for unrelated distractors. The likely reason is a phenomenon that has been studied in the false memory literature and is termed recollection rejection (e.g., Brainerd & Reyna, 2005) or recall-to-reject (e.g., Gallo, 2004). The phenomenon in question is that test cues, whether distractors or targets, can sometimes retrieve verbatim traces of related targets, as when the cue salad retrieves a verbatim trace of soup, and this causes subjects to classify the cue as NS rather than O or ND.

This effect can be easily incorporated into QEMc by switching to a four-dimensional vector space that includes a second verbatim vector. (Recall that the vector space for source false memory is four-dimensional, with two verbatim vectors; see Appendix.) For any given cue i = O, NS, or ND, the two verbatim vectors are |V_i〉, the vector for the cue’s verbatim trace, and |V_i,r〉, the vector for the verbatim trace of a related cue. QEMc’s item false memory expressions (upper half of Table 1) are then revised in a minimal way: The NS? expression for O, NS, and ND becomes |v_i,r|² + |g_i|². Now, the relation between p(O?) and p(NS?) is unconstrained because it will depend on the relative magnitude of |v_i|² and |v_i,r|², but parameter-free subadditivity predictions are preserved because the total probability expression for each cue is |v_i|² + |v_i,r|² + |g_i|² + |g_i|² + |n_i,r|² = 1 + |g_i|².

Experiment 2: False Memory for Source

Next, we investigated whether the additive law is also violated in source designs, as QEMc anticipates. We implemented the same procedure of administering separate probes for the members of an exhaustive set of mutually exclusive episodic states in an otherwise standard source-monitoring design (e.g., cf. Kurilla & Westerman, 2010). Subjects studied two lists of words that were accompanied by distinctive contextual details, followed by a recognition test containing three types of cues: targets from List 1 (L1), targets from List 2 (L2), and new items (ND). On the recognition test, three types of probes that formed a partition of these cues’ possible episodic states (L1?, L2?, and ND?) were factorially crossed with the three types of cues.

The focal prediction, of course, is that source memory will violate the additive law everywhere and will follow the p(L1?) + p(L2?) + p (ND?) ≥ 1 rule instead. In addition, as in Experiment 1, we included manipulations that were designed to test the hypothesis that gist processing strengthens this pattern. There were three in all. The most direct and obvious one was categorization. In the false memory literature, a common method of enhancing memory for semantic gist (cf. Brainerd & Reyna, 2007; Gallo, 2004; Howe, 2006, 2008; Smith, Gerkens, Pierce, & Choi, 2002) is to present lists that contain exemplars of some familiar taxonomic categories (e.g., animal, food, furniture, and vehicle names). That method was used in the present experiment, with eight exemplars from each of 12 taxonomic categories being distributed over the two study lists. The lists also contained other targets that were unrelated to each other and that did not belong to any of the taxonomic categories. Naturally, the expectation was that violations of the additive law would be less marked for these unrelated targets than for category exemplars because reliance on gist processing would be more pronounced for category exemplars.

The second manipulation, which was more subtle, was whether, for each of the 12 taxonomic categories, its 8 exemplars appeared together in a single block on one of the lists or appeared in 2 blocks of 4 exemplars, with one block on List 1 and one block on List 2. The logic behind this manipulation is straightforward. Prior source-monitoring studies show that when multiple targets on lists share salient meanings, subjects are apt to process test cues’ semantic gist as a basis for source judgments (Arndt, 2012). For example, suppose that List 1 words are printed in red, List 2 words are printed in blue, and all the exemplars of the furniture category appear on List 1. Subjects can make accurate source judgments about a test cue such as desk by simply remembering that the furniture words were on first (red) list. This form of gist processing is a very efficient method of enhancing source accuracy, as it is easier to remember that furniture words appeared on List 1 than it is to retrieve criterial contextual details for desk. However, this can also impair source discrimination if the focal meaning originated from both sources (e.g., bed, couch, desk, and table appeared on List 1 and chair, dresser, loveseat, sofa appeared on List 2).

As mentioned in connection with the first manipulation, we assumed that the presence of blocks of meaning-sharing targets on study lists would increase gist processing for test cues that were category exemplars, ensuring robust violations of the additive law. With respect to the second manipulation, those violations should be even more marked for categories that were exemplified on both lists than for categories that were exemplified on only one list. The reason is simple. In the present design, the additive law is evaluated for a given cue by the sum p(L1?) + p(L2?) + p(ND?). If all the furniture exemplars appear on List 1, gist processing with the test cue desk will produce good source discrimination (p(L1?) > p(L2?)), but if half the exemplars, including desk, appear on List 1 and half appear on List 2, gist processing will selectively elevate p(L2?). If p(L1?) and p(ND?) remain roughly constant, p(L1?) + p(L2?) + p(ND?) will be larger for two-block category exemplars than for one-block category exemplars.

The final manipulation was list order, and it also grows out of the results of some recent source-monitoring experiments that focused on the relative contributions of verbatim and gist memory to performance (Brainerd, Holliday, et al., 2014; Brainerd et al., 2012). In those experiments, multinomial models and other techniques were used to measure how verbatim and gist processing on source tests varied as function of selected factors. One factor that had consistent effects was list order: Verbatim memory for target cues was always better and tended to override the effects of other manipulations when cues had appeared on List 2 as compared to List 1. That verbatim memory would be superior for List 2 targets was not surprising theoretically because previous research had suggested that verbatim memory is quite sensitive to retroactive interference (Barnhardt et al., 2006). In the present experiment, this translates into predictions about violations of the additive law—explicitly, that they will be less marked for List 2 targets, owing to greater reliance on verbatim memory, and consequently, this will reduce the effectiveness the first two manipulations.

Method

Subjects

The subjects were 70 undergraduates who participated to fulfill a course requirement.

Materials and Procedure

The words on the study and test lists were drawn from production norms for Van Overschelde, Rawson, & Dunlosky’s (2004) revision of the Battig and Montague (1969) categorized word pools. The Van Overschelde et al. norms contain word pools for 70 common taxonomic categories. The items that were selected from these norms for inclusion on the study and test lists that were administered to individual subjects came from the first eight frequency positions for each category. The study lists that were generated for individual subjects consisted of two types of targets: (a) words from multiple-exemplar categories and (b) words from single exemplar categories. Concerning a, if a target such as drums, for instance, were from a multiple-exemplar category, seven other targets from that category (clarinet, flute, guitar, piano, saxophone, trumpet, violin) would also appear on the study lists. However, if a target such as salt were from a single-exemplar category, no other target from that category (e.g., no other seasoning) would appear on either list.

The subjects studied two lists of words, presented at a 2.5 sec rate. There was a 10 sec pause between lists, with each word appearing in 50 point font in the center of a computer screen. The subjects were told that the lists were completely different; that no word would appear on List 2 that appeared on List 1 and vice versa. As usual in source-monitoring designs, different contextual details accompanied the two lists. The words on List 1 were printed in a different distinctive font (e.g., Broadway, Niagara, Script) against a different background color (e.g., white, pink, blue) than the words on List 2. Each list began with an opening buffer of three unrelated words and ended with a closing buffer of three words. The list itself—that is, the words that were presented between the opening and closing buffers—was composed of 54 items. List 1 consisted of 8 exemplars of each of four taxonomic categories (e.g., sports, trees), for a total of 32 words, plus 4 exemplars of each of two taxonomic categories (e.g., cities, furniture) for a total of 8 words, plus 14 words that were exemplars of single-exemplar categories. The latter 14 words were unrelated to each other and were not members of any of the 12 multiple-exemplar categories. List 2 consisted of 8 exemplars of each of four taxonomic categories that had not appeared on List 1 (e.g., metals, relatives), for a total of 32 words, plus the remaining 4 exemplars of the two taxonomic categories for which 4 exemplars appeared on List 1 (e.g., cities, furniture) for a total of 8 words, plus 14 words that were exemplars of single-exemplar categories. Similar to List 1, the latter 14 words were unrelated to each other and were not members of any of the 12 multiple-exemplar categories.

The study lists were followed by test instructions, which reiterated that the two lists had not shared any words, explained that the memory test would present three types of cues (L1, L2, and ND), and explained that exactly one-third of the test cues would be of each type. The instructions stated that the subject would be asked to make one of three types of judgments about each cue—I saw it on the first list (L1?), I saw it on the second list (L2?), or I did not see it on either list (ND?)—so that the probability that any of these judgments would be correct by chance was always one-third. The instructions contained examples of hypothetical list words, of the three types of cues, of the three types of judgments, and of correct answers for each Cue X Judgment combination. The test list that was administered to individual subjects consisted of the following cues: (a) 3 targets from each of the 4 one-block List 1 multiple-exemplar categories (12 cues in all); (b) 3 targets from each of the 4 two-block List 1 multiple-exemplar categories (12 cues in all); (c) 12 of the 14 single-exemplar targets from List 1; (d) 18 unpresented words that were arbitrarily designated as List 1 unrelated distractors; (e) 3 targets from each of the 4 one-block List 2 multiple-exemplar categories (12 cues in all); (f) 3 targets from each of the 4 two-block List 2 multiple-exemplar categories (12 cues in all); (g) 12 of the 14 single-exemplar targets from List 2; (h) a further 18 unpresented words that were arbitrarily designated as List 2 unrelated distractors. Thus, the test list was composed of 108 cues, with 8 groups of cues (a–h). The cues in each group were factorially crossed with the three types of probes (L1? L2? ND?), so that each type of probe question was administered for the same number of cues in each group. Concerning the unrelated distractors in groups d and h, these 36 cues were selected from of the remaining Van Overschelde et al. (2004) categories by randomly sampling 18 of those categories and then randomly sampling 2 exemplars from frequency positions 1–8 of each category.

Following instructions, the subject responded to a self-paced visual recognition test on which The 108 Cue X Probe combinations were presented in random order. Subjects simply agreed or disagreed with each probe, accordingly as they though it was true of false for the indicated cue.

Results

Descriptive statistics for the various Cue X Probe combinations appear in Table 4, with the sum statistic that is used to evaluate the additive law appearing in the far right column. The major results that stand out in Table 4 are that, as in Experiment 1, the additive law was violated everywhere it was possible to test it, and it was always violated in a subadditive direction. Another clear result is that violations of additivity were always less pronounced for target cues for which verbatim memories were presumably stronger: The mean value of the sum statistic for the three types of target cues (one-block multiple-exemplar, two-block multiple-exemplar, single-exemplar) was 1.15 for List 2 versus 1.38 for List 1. Further, the prediction that violations of additivity would be more robust for multiple-exemplar categories (stronger gist memory) than for single-exemplar categories (weaker gist memory) was born out at a general level because the overall average of the sum statistic was 1.30 for multiple-exemplar categories versus 1.20 for single-exemplar categories. However, this pattern depended on whether strong verbatim memories were competing with gist memories as it was only evident for List 1 targets.

Table 4.

Acceptance Probabilities in Experiment 2 (SDs in Parentheses)

Test cue	Memory Judgment
	L1?	L2?	ND?	Sum
List 1
Targets:
Multiple exemplar–List 1	.73(.22)	.41(.27)	.24(.22)	1.38
Multiple exemplar-both lists	.69(.25)	.67(.22)	.18(.20)	1.54
Single exemplar	.60(.24)	.40(.28)	.23(.24)	1.23
Distractors	.18 (.18)	.17(.19)	.73(.26)	1.08
List 2
Targets:
Multiple exemplar–List 2	.21(.26)	.65(.25)	.27(.25)	1.13
Multiple exemplar-both lists	.29(.30)	.66(.27)	.18(.20)	1.13
Single exemplar	.33(.29)	.60(.29)	.25(.27)	1.18
Distractors	.16(.21)	.16(.17)	.72(.26)	1.07

Note. L1? = presented on the first list, L2? = presented on the second list, ND? = not presented.

First, we conducted a 2 (list: 1 vs. 2) X 4 (cue: one-block multiple-exemplar categories, two-block multiple exemplar categories, single-exemplar categories, unrelated distractors) ANOVA of the sum values. This produced main effects for list, F (1, 69) = 34.65, MSE = .14, partial η² = .33, p < .0001, and for cue, F (3, 207) = 12.32, MSE = .14, partial η² = .15, p < .0001. It also produced a List X Cue interaction, F (3, 207) = 9.13, MSE = .13, partial η² = .11, p < .0001. As mentioned, the list main effect was due to the fact that the average value of the sum statistic was larger on List 1 than on List 2. The cue main effect was due to the fact that the average value of the sum statistic was larger for targets from multiple-exemplar categories than for targets from single-exemplar categories or for distractors. Post hoc analysis of the List X Cue interaction revealed that the sum statistics for multiple-exemplar categories were strongly affected by which list a cue appeared on. Specifically, post hoc tests showed that the sum value was greater on List 1 that on List 2 for targets from one-block multiple-exemplar categories (t(69) = 6.36, p < .0001) and two-block multiple-exemplar categories (t(69) = 4.49, p < .0001), but not for targets from single-exemplar categories (t(69) = .79) or distractors (t(69) = .20).

As also mentioned, variability in sum values as a function of the strengths of gist memories was different for List 1 than for List 2, and in fact, such variability was confined to List 1 cues. For List 1 cues, post hoc analysis of the List X Cue interaction revealed that (a) the sum value was smaller for unrelated distractors than for any of the three types of targets (mean t(69) = 5.45, p < .0001), (b) the sum value was smaller for targets from single-exemplary categories than for either of the types of targets from multiple-exemplar categories (mean t(69) = 3.53, p < .005), and (c) the sum value was smaller for targets from multiple-exemplar categories that only appeared on List 1 than for targets from multiple-exemplar categories that appeared on both lists (t(69) = 2.39, p < .01). All of these findings are congruent with earlier QEMc predictions: The first shows that additivity was more strongly violated by targets than by distractors, the second that additivity was more strongly violated by targets for which strong gist memories were available, and the third that additivity was more strongly violated when strong gist memories were not associated with a single source.

None of these patterns was detected for List 2 cues, as can be seen by inspecting the small differences between cues types in the sum column of Table 4. In this experiment, then, it seemed that when strong verbatim memories were available for cues, that fact trumped the effects that would otherwise have been produced by differences in the strengths of gist memories.

Next, although all 8 of the sum values in Table 4 are > 1, that does not establish that any of them are reliably so. Therefore, we computed one-sample t tests for these sums, using a predicted value of 1 as the null hypothesis. For List 1, this null hypothesis was rejected for targets from one-block multiple-exemplar categories (t(69) = 11.14, p < .0001), targets from two-block multiple-exemplar categories (t(69) = 8.37, p < .0001), targets from single-exemplar categories (t(69) = 4.83, p < .0001), and distractors (t(69) = 2.41, p < .01). For List 2, the same null hypothesis was rejected for targets from one-block multiple-exemplar categories (t(69) = 2.82, p < .003), targets from two-block multiple-exemplar categories (t(69) = 3.30, p < .001), targets from single-exemplar categories (t(69) = 2.86, p < .003), and distractors (t(69) = 1.94, p < .03). Therefore, notwithstanding the less marked violations of the additivity on List 2, four types of cues failed to obey the additive law on both lists.

Finally, what about individual subjects? Is p(L1?) + p(L2?) + p(ND?) > 1 the modal pattern, or do most subjects’ exhibit additivity while a minority exhibit extreme subadditivity? To answer that question, we examined the sum values of individual subjects for all four types of cues and simply counted the numbers of values that satisfied the p(L1?) + p(L2?) + p(ND?) > 1 rule. For List 1, the numbers of subjects (out of 70) whose sum values followed the rule were 57 (p < .0001 by a sign test) for one-block multiple-exemplar categories, 53 for two-block multiple-exemplar categories (p < .0001 by a sign test), 43 for single-exemplar categories (p < .04 by a sign test), and 36 for distractors (n.s.). For List 2, however, where, as we saw, the mean values of the sum statistic were much smaller than for List 1, the numbers of subjects (out of 70) whose sum values followed the rule were 32 for one-block multiple-exemplar categories, 33 for two-block multiple-exemplar categories, 33 for single-exemplar categories, and 32 for distractors. None of the latter values was reliably above .5, of course.

Summary

Source memory tests focus on a more precise, verbatim type of content than the tests in item false memory experiments, inasmuch as accuracy depends on retrieving contextual details that are arbitrarily mapped with individual targets. Nevertheless, the results of Experiment 2 resembled those of Experiment 1 when it came to (a) whether the probabilities of remembering cues as belonging to the members of a partition of their possible episodic states violate the additive law, (b) whether variability in the robustness of those violations is connected to variability in the relative strengths of verbatim and gist memories, and (c) whether those violations are in a subadditive or superadditive direction.

General Discussion

QEMc is a quantum probability implementation of FTT’s principles of parallel dissociated storage and retrieval of verbatim and gist traces. Unlike some other models, it predicts a priori that episodic memory will violate the additive law of probability—that the observed probabilities of remembering a cue as belonging to the members of a partition of its possible episodic states (e.g., O, NS, ND) will not sum to 1 but, instead, will exceed 1. For instance, this pattern is anticipated for two common types of memory experiments, false memory for items and for sources. In both instances, the reasons are connected to the notion that gist processing can support memory for incompatible members of a partition—remembering a cue as being both O and NS in item designs or as being both L1 and L2 in source designs—whereas verbatim processing does not. Specifically, as discussed in the Appendix and as illustrated in Figure 1, QEMc represents a cue’s perceived episodic state as a vector |S_C〉, which is the sum of the three basis vectors v_C|V〉, g_C|G〉, and n_C|N〉 in item experiments and the sum of the four basis vectors v_C1|V₁〉, v_C2|V₂〉, g_C|G〉, and n_C|N〉 in source experiments. Quantum probability rules require that the squared values of the scalars that multiply the vectors in each expression (whatever those values may be) must sum to unity; that is, |v_C|² + |g_C|² + |n_C|² = 1 and |v_C1|² + |v_C2|² + |g_C|² + |n_C|² = 1, which is just a mathematical way of saying that on a memory test, a cue will retrieve information from the three types of traces (V, G, N).

However, the model’s expressions (Table 1) for the total probability that cue C_i will then be remembered as belonging to any of its possible episodic states are |v_Ci|² +|g_Ci|² +|g_Ci|²+|n_Ci|² = 1+ |g_Ci|² ≥ 1 for item memory and |v_Ci1|² + |v_Ci2|² +|g_Ci|² +|g_Ci|²+|n_Ci|² = 1+ |g_Ci|² ≥ 1 for source memory. The origin of these expressions is theoretical rather than mathematical because they follow from FTT’s assumption that gist processing can cause O, NS, and ND cues to all be remembered as both O and NS in item designs and can cause L1, L2, and ND cues to all be remembered as both L1 and L2 in source designs. It is the fact that for theoretical reasons, |g_Ci|² must appear twice in total memory probability expressions that forces subadditivity. Consequently, two other straightforward predictions are that total memory probability will become progressively more subadditive as reliance on gist processing increases (i.e., as |g_Ci|² increases relative to |v_Ci|², |v_Ci1|², or |v_Ci2|²) and progressively less so as reliance on verbatim processing increases (i.e., as |v_Ci|², |v_Ci1|², or |v_Ci2|² increase relative to |g_Ci|²). Theoretically, such results can be produced by manipulations that directly increase |g_Ci|² by enhancing gist processing or by manipulations that indirectly increase |g_Ci|² by impairing verbatim processing (List 1 targets vs. List 2 targets in Experiment 2).

As the memory literature does not contain systematic tests of the additive law, we evaluated such predictions using item and source designs. Both used standard procedures that can be found in prior studies, with one key exception: On memory tests, the usual types of test cues were factorially crossed with probes that formed a partition of the cues’ possible episodic states (O, NS, or ND in item false memory and L1, L2, or ND in source false memory). Across experiments, there was consistent confirmation of QEMc’s prediction that total memory probabilities are subadditive rather than additive. Twelve such probabilities could be computed in Experiment 1, and 8 could be computed Experiment 2. All were reliably greater than one. Within experiments, variations in subadditivity were congruent with the notion that it increases in proportion to the level of gist processing and decreases in proportion to the level of verbatim processing. To illustrate that idea, subadditivity was always more marked for critical distractors than for other types of cues in Experiment 1, and subadditivity was more marked for targets and related distractors than for unrelated distractors. As further illustrations, subadditivity was more marked in Experiment 2 for targets for which strong gist memories had been stored (targets from multiple-exemplar categories) when verbatim memory was weak (List 1), although not when it was strong (List 2).

To conclude, we return to the psychological significance of the fact that episodic memory violates the additive law, and that it is subadditive instead. Beyond the important fact that QEMc can predict this a priori, we saw that, psychologically, it means that we over-remember events because we remember them as belonging to too many episodic states. Concretely, when discussing what you had for lunch, you may correctly remember drinking a Coke (O? probe) and incorrectly remember not drinking a Coke (NS? probe), or when discussing when you last ate a hamburger, you may correctly say that it was at lunch yesterday (L1? probe) and incorrectly say that it was at dinner (L2? probe). We conclude this article by considering two points that delve more deeply into the theoretical meaning of the maxim that we over-remember experience. The first is the exact form that over-remembering takes, which turns out to be a pattern of very conservative compensatory relations between correct and incorrect episodic states. The second is that conservative compensation between correct and incorrect episodic states accounts for a classic but counterintuitive finding about false memory, which is that levels of true and false memory are often found to be uncorrelated.

Conservative Compensation

The additive law implies close titration among the probabilities of remembering an item as belonging to the various members of a partition of its possible episodic states; increases in one are balanced by decreases in others. For instance, recall that in Experiment 1 (also in Experiment 2) there was a chance probability of 1/3 that a given probe (O?, NS?, ND?) was correct for a given cue, and thus, there was an objective, quantitative definition of learning—namely, increases above 1/3 in acceptance rates for correct states and decreases below 1/3 in acceptance rates for incorrect states. Suppose that the subjects had been assigned to three conditions: (a) control; (b) no-study + three-cue test; and (c) one-item study + three-cue test. The control condition is just the procedure for Experiment 1. In condition b, subjects do not study any targets, but simply respond to a test that consists of one O cue (e.g., seat), one NS cue (e.g., chair), and one ND cue (e.g., sweet). They receive the same memory test instructions as the controls, including the fact that the probability that any given test cue is an O, NS, or ND item is 1/3. The test cues are then administered, with O?, NS?, and ND? probes being factorially varied over cues and subjects. Condition c is identical to condition b, except that subjects receive a one-item study list on which the target cue (seat) appears, just before the memory test. We know how the control data will turn out (Table 3), but what about conditions b and c?

In the no-study condition, subjects have nothing to go on other than the baseline probabilities, and hence, the average acceptance probabilities over subjects should be roughly p(O?) = p(NS?) = p(ND?) = 1/3, for targets, critical distractors, related distractors, and unrelated distractors. Thus, the additive law is satisfied. In the one-item study condition, the memory test is administered immediately after seat is studied, and hence, we should find: (a) p(O?) = 1 and p(NS?) = p(ND?) = 0 for seat; (b) p(NS?) = 1 and p(O?) = p(ND?) = 0 for chair; and (c) p(ND?) = 1 and p(O?) = p(NS?) = 0 for sweet. Again, the additive law is satisfied, and it is because there have been precise tradeoffs, relative to the no-study condition, between increases in memory for correct states versus decreases in memory for incorrect states. The key point that as a principle of episodic memory, the additive law requires that increases in true memory for correct episodic states be compensated by commensurate reductions in false memory for incorrect states.

Unlike the one-item study condition, we know that in the control condition, p(O?) for targets, p(NS?) for critical and related distractors, and p(ND?) for unrelated distractors will all be far from unity. However, the additive law may still be satisfied because, as we just saw, this turns on whether learning produces compensatory adjustments between acceptance rates for correct versus incorrect episodic states. On the one hand, the study list clearly produced learning of correct episodic states for all cues because p(O?) for targets, p(NS?) for critical and related distractors, and p(ND?) for unrelated distractors were well above the 1/3 baseline. However, the additive law was not satisfied because the degree of compensation in memory for incorrect states was conservative. A dramatic feature of this pattern is that in our experiments, the relation between increases in memory for correct states and decreases in memory for incorrect states was completely noncompensatory in most instances.

For targets, restricting attention to the immediate test and the delayed test for previously tested items, where p(O?) was much higher than baseline, it can be seen in Table 3 that there were no compensating decreases in memory for incorrect states. The average value of p(O?) was .51, while the average value of p(ND?), .31, was not reliably below baseline, and the average value of p(NS?), .47, was well above it. For critical distractors, p(NS?) was well above baseline in all three testing conditions (M = .54), but similar to targets, there were no compensating decreases in memory for the two incorrect states: The average value of p(ND?), .31, was not reliably below baseline, while the average value of p(O?), .49, was well above it. The picture was similar for related distractors. p(NS?) was well above baseline (M = .44), but there were no compensating decreases in memory for the two incorrect states: The average value of p(O?), .37, was not reliably different than baseline, while the average value of p(ND?), .49, was well above it. Unrelated distractors were the only cues that displayed any evidence of compensatory tradeoffs for correct versus incorrect states. p(ND?) was well above baseline (M = .64) and p(O?) was well below baseline (M = .23), but compensation was still conservative because p(NS?) was not reliably below baseline (M = .35).

Conservative compensation was also present in the source-monitoring experiment, but it was somewhat less marked. For List 1 targets, the picture was similar to that for O and NS cues in the false memory experiment. p(L1?) was well above the 1/3 baseline (M = .67), but p(L2?) was also well above baseline (M = .49). However, p(ND?) exhibited compensation because it was reliably below baseline (M = .22). Compensation was better for L2 targets and best of all for unrelated distractors (as in Experiment 1). For L2 targets, p(L2?) was much higher than baseline (M = .64), p(L1?) was slightly below baseline (M = .28), and p(ND?) was substantially below baseline (M = .23). For unrelated distractors, p(ND?) was much higher than baseline (M = .73), p(L1?) was substantially below baseline (M = .17), and p(L2?) was also substantially below baseline (M = .17). Nevertheless, compensation was still conservative for L2 targets and for unrelated distractors because, it will be remembered, p(L1?) + p(L2?) + p(ND?) > 1 for both types of cues.

One can summarize the overall pattern of compensation among episodic states in three statements. First, increases in memory for correct states and decreases memory for incorrect states are not symmetrical. Second, on the contrary, there were instances in both experiments in which memory for an incorrect state actually increased as memory for a cue’s correct state increased. Third, the extent to which the relation between memory for correct and incorrect states was noncompensatory was correlated with the likelihood that subjects were relying on gist memories, which can be exemplified by three features of the data.

One is that compensation was less conservative in the source experiment than in the item experiment. The memory test had more of a gist slant in the item experiment, where all probes involved item memory, than in the source experiment, where 1/3 involved item memory. A second illustration is that compensation was least conservative for unrelated distractors. Naturally, unrelated distractors are poorer retrieval cues for gist memories than either targets or related distractors. A third illustration is that with targets and related distractors, compensation between correct and incorrect episodic states was never observed when there was a good chance that subjects would rely on gist memories (i.e., with target, critical distractor, and related distractor cues in Experiment 1 and with L1 cues in Experiment 2).

How Conservative Compensation Explains True-False Memory Independence

Finally, an instructive by-product of conservative compensation is that it accounts for a classic but perplexing finding in the false memory literature—namely, that the relation between true and false memory is not what is expected by common sense and many memory theories. In that literature, true memory and false memory refer to memory for different cues, as distinct from remembering correct and incorrect states for the same cue. Also, the exact content of true and false memory differs for item experiments versus source experiments. In a traditional item design, as we know, only O? probes are administered, so that true memories are target hits and false memories are false alarms to related distractors. Note that both involve item memory. In the most commonly used source design in the false memory literature, only L1? probes are administered. That design is the Loftus (1975; Loftus, Miller, & Burns, 1978) misinformation paradigm, which emulates the forms of suggestive questioning that are prominent features of police interviews and interrogations of witnesses. The two encoding contexts are L1 = observing a series of events that may have legal implications, such as a video of an automobile accident, and L2 = responding to questions about those events, some of which state that events were observed that were not. Memory tests follow and as in police investigations, the focus is squarely on memory for observed events. Two types of probes have been used on such tests. Originally, as in our Experiment 1, Loftus (1975) administered separate accept-reject probes for observed and suggested events, with correct acceptances of L1 events being the true memory measure and incorrect acceptances of L2 suggestions being the false memory measure. In later experiments, multiple-choice probes were administered that pitted observed events against suggested ones (e.g., “Did you see a Yield sign or a Stop sign in the video?”). Here, the true memory measure is the acceptance rate for the L1 choice relative to its acceptance rate in probes that pit it against a distractor event (e.g., “Did you see a Yield sign or a Slow sign in the video?”), whereas the false memory measure is the acceptance rate for the L2 choice relative to its acceptance rate in probes that pit it against a distractor event (e.g., “Did you see a Stop sign or a Slow sign in the video?”). Regardless of which measures are used, the true and false memory measures involve source memory rather than item memory.

We have powerful expectations, which are grounded in commonsense beliefs about how experience must affect memory, that there should be strong negative correlations between true and false memory (Brainerd & Reyna, 2005). Objectively, experience is symmetrical in the information it conveys about correct and incorrect episodic states; that is, as it specifies items’ correct states (true memory), it automatically specifies their incorrect states (false memory). These symmetrical effects are completely transparent when, as in our experiments, correct and incorrect states form a partition because such states are logically incompatible. For instance, logically, a test cue cannot be a distractor if it is a target or a target if it is a distractor because an item cannot be both presented and not presented. Intuitively, then, it would seem that better memory for items’ correct states should mean better memory for their incorrect states because, strictly speaking, they are the same thing. It follows that in traditional item and source designs, measures of true and false memory ought to exhibit strong negative correlations. For instance, in an item design in which desk but no other article of furniture appears on the study list, it is objectively established that desk is O while table, sofa, chair, and so forth are NS. If our intuition is correct, then, levels of false acceptance of O? for table, sofa, and chair (false memory measures) will drop as correct acceptance of O? for desk (true memory measure) rises. Similarly, in a misinformation design in which Yield sign appears in the video and Stop sign appears during the question period, it is objectively established that Yield sign is L1 and Stop sign is L2. Again, if our intuition is correct, levels of false acceptance of L1? for Stop sign will drop as levels of correct acceptance of L1? for Yield sign rise.

These are not the modal patterns in the literature, however. It has long been known that when correlations between subjects’ rates of true and false memory are computed, the modal pattern is that the correlations are not reliable (e.g., Brainerd & Reyna, 1996, 2005; Reyna & Kiernan, 1994). Although modest negative correlations have occasionally been reported for certain materials (e.g., Roediger et al., 2001), so have modest positive correlations for the same materials (e.g., Brainerd, Reyna, & Forrest, 2002). These points are well illustrated by the data of our experiments. For L1 probes In Experiment 2, the mean correlation between acceptance rates for L1 cues (true memory) and L2 cues (false memory) was −.08, and for L2 probes, the mean correlation between acceptance rates for L2 cues (true memory) and L1 cues (false memory) was −.03. Neither was reliable, of course. In Experiment 1, the correlation between O? acceptance rates for targets and related distractors was not reliable, while there was a small but reliable positive correlation between O? acceptance rates for targets and critical distractors. Like the larger literature, then, the data of our experiments are at odds with the intuitive expectation of robust negative correlations.

The reason why our intuition is wrong is obscured by conventional item and misinformation designs, but it is revealed by the pattern of conservative compensation that emerged in our designs. As we just saw, robust negative correlations have been predicted in conventional designs because it is thought that experience drives down memory for a cue’s incorrect episodic states as it drives up memory for its correct state, regardless of whether the cue is a true or false memory item. However, that assumption is untestable in conventional designs because (a) only memory for the correct state is measured for true memory items and (b) only memory for one incorrect state is measured for false memory items. In our experiments, memory for correct and incorrect states was measured for all items, and the assumption proved to be false. Following the study list in Experiment 1, p(O?) for targets (true memory items) and p(NS?) for critical and related distractors (false memory items) had all increased to well above baseline. However, there were no complementary decreases in p(O?) for critical and related distractors, which would have been needed to produce negative correlations between p(O?) for targets versus p(O?) for critical and related distractors. Thus, although knowing that a critical or a related distractor is NS is logically the same thing as knowing that it is not O?, episodic memory does not see it that way.

Much the same conclusion follows from the compensation analysis of Experiment 2. On the one hand, following the two study lists, the two true memory measures, p(L1?) for L1 targets and p(L2?) for L2 targets, were both well above baseline, so that their correct states could be remembered at reliable levels. Again, however, what would be needed to confirm our intuition of robust negative correlations between p(L1?) for L1 targets versus L2 targets and between p(L2?) for L2 targets versus L1 targets are complementary decreases in p(L1?) for L2 targets and p(L2?) for L1 targets. As in Experiment 1, that is precisely what did not happen. One of the false memory measures, p(L2?) for L1 targets, actually increased to well above baseline, while the other, p(L1?) for L2 targets, decreased by only a small amount.

Much has been written in the false memory literature about the surprising lack of strong negative correlations between true and false memory. Actually, this was one of the key findings that the supplied the impetus for dual-trace accounts of false memory, such as fuzzy-trace theory (Brainerd & Reyna, 2005). Without delving into the wider evidence for such theories, or for other explanations, our data suggest that the general reason for the lack of correlation is that the manner in which episodic memory learns from experience is only partly logical. The logical part is that experience, in the form of the study lists in memory experiments, always increases true memory for correct episodic states. Further, it is not necessary for items to be directly experienced for this improvement to occur because in Experiment 1, p(NS?) was far above baseline for critical and related distractors, and in both experiments, p(ND?) was far above baseline for unrelated distractors. On the other hand, the illogical part is that the same experience does not produce commensurate decreases in false memory for incorrect states. Sometimes it produces decreases that lag behind increases in true memory for correct states (e.g., L2 targets in Experiment 2 and unrelated distractors in both experiments). At other times, it produces no decreases, and sometimes, it even increases false memory for incorrect states (e.g., L1 targets in Experiment 2 and critical and related distractors in Experiment 1). In short, although, logically, the effects of experience are symmetrical when it comes to the identifying correct and incorrect episodic states, their memory counterparts are dissociated.

Highlights.

• Quantum models can implement fuzzy-trace theory’s verbatim-gist distinction.

• Models predict that memory will violate the additive law of probability.

• Additivity violations are detected in item and source false memory experiments.

• Additivity violations are directly proportional to reliance on gist memory.

Appendix: Quantum Episodic Memory (QEM)

We describe a QP formalization of FTT, specifically a model that assumes compatibility of memory measures. The model makes principled, parameter-free, a priori predictions about violations of the additive law in the direction of subadditivity in experiments on item false memory and source false memory. The data sets to which the model is applied in this paper are posted at http://www.human.cornell.edu/hd/brainerd/research.cfm. FTT has previously been formalized using variants of multinomial processing models and signal detection models, which are based on classical probability rules (see Brainerd, Gomes, et al., 2014). Those models were able to account for many false memory phenomena, including a subadditivity phenomenon that is described in the text (memory disjunction fallacies). However, as also noted in the text, those models do not make true (parameter-free, a priori) subadditivity predictions, and instead, they only account for such phenomena ex post facto by fitting the models to data using parameter values estimated from the data. The same is true of another multinomial model that was mentioned in the text, which has been used to account for memory disjunction fallacies (Kellen et al., 2014).

FTT can be formalized with QP, owing to the fact that there is a natural affinity between QP’s principles and FTT’s assumptions about memory (Brainerd et al., 2013; Wang et al., 2013). For instance, the notion of parallel, dissociated storage and retrieval of verbatim and gist traces is a cognitive instantiation of the superposition property of physical quantum systems. Crucially, the present QP model of FTT predicts violations of the additive law in an a priori manner, based on quantum principles, rather than accounting for them ex post facto. This is a significant theoretical advance, relative to prior work on nonadditivity in memory. Moreover, the QP model of FTT relies on the same quantum principles that have been used to explain a variety of other puzzling cognitive phenomena (for reviews, see Busemeyer & Bruza, 2012; Bruza et al., 2015; Busemeyer & Wang, 2015; Pothos & Busemeyer, 2013; Wang et al., 2013).

The QP implementation of FTT is quite simple inasmuch as it uses a single psychological state (the memory state) for any memory test cue to generate different contextualized probability distributions under different memory probe conditions. Its core features, called quantum episodic memory (QEM), were sketched in Brainerd et al (2013). To make determinant predictions about specific paradigms, QEM is used to construct specific FTT models for those paradigms. Those models can be specified for either incompatible or compatible memory measures (e.g., the O? and NS? probes in Experiment 1). In QP, compatibility means that two measures can be taken simultaneously and their order of administration does not affect their observed probabilities (Busemeyer & Bruza, 2012; Wang & Busemeyer, 2013; Wang, Solloway, Shiffrin, & Busemeyer, 2014; Bruza et al., 2015). Whether the probes that are administered on memory tests are compatible or not is an empirical question (Busemeyer & Wang, 2014). This can be evaluated in at least three ways: (a) The prediction that the order of probe administration should not affect acceptance probabilities if the probes are compatible can be tested (Busemeyer & Wang, 2014; Wang & Busemeyer, 2013); (b) the prediction that violations of the additive law should always be in a subadditive direction if the probes are compatible can be tested (Busemeyer & Bruza, 2012; Busemeyer & Trueblood, 2010; Brainerd et al., 2013); and (c) tests of the comparative fit of compatible versus incompatible models to data can be computed. Some initial work along these lines has recently been conducted (Trueblood & Hammer, under review; Denolf & Lambert-Mogiliansky, under review), but so far, the results are inconclusive. Thus, the data that are necessary to decide between compatibility and incompatibility do not currently exist.

Therefore, it is reasonable to begin with models that predict simpler data, in the sense of predictions a and b, and to move to models that predict more complex data when this is forced by new theories or findings. Mathematically, this is the version of QEM with a compatibility assumption. Crucially, compatibility version suffices to make parameter-free, a priori predictions about violations of the additive law for both item false memory and source false memory, thereby making the model highly falsifiable. To highlight the model’s compatibility assumption, we label this version of QEM as QEMc and the version with the incompatibility assumption as QEMi.

As shown below, QEMc predicts a surprising pattern in false item and source memory: Memory judgments about individual events will not be additive over an exhaustive set of mutually exclusive episodic states and, instead, will be subadditive. The model also predicts that observed levels of subadditivity will covary with the strengths of gist traces that are retrieved on memory tests. We demonstrate this for item false memory (Experiment 1) first. Then, we briefly demonstrate the same points for source false memory.

The QEMc Model for Item False Memory

The basic methodology, of which there are numerous examples in the memory literature, runs as follows. Subjects encode a set of memory targets, most often a word list, after which they respond to a recognition test composed of three types of test cues: old (target) cues (O; e.g., sofa); new-similar cues (NS; e.g., couch); and new-dissimilar cues (ND; e.g., ocean). NS cues share salient features of targets and serve as false memory measures, whereas ND cues do not and serve as guessing/bias indexes. In the standard design, subjects make just one type of judgment about each type of cue—namely, they decide whether it is old (O?). In the novel design that we used, the three types of cues were factorially crossed with three types of probes that partitioned the set of all possible episodic states that a cue could belong to: O?; new-similar (NS?); and new-dissimilar (ND?). These states are obviously exhaustive and mutually exclusive because, logically, a cue must belong to one of them and cannot belong to more than one of them.

Similar to QP models of judgment and decision making (Busemeyer & Bruza, 2012), QEMc implements FTT’s memory principles in vector spaces, in which the probabilities of making different types of memory responses are measured with projection operations. The FTT vector space for false item memory experiments, which is illustrated in Figure 1, is three-dimensional and is generated by the trio of unit length basis vectors |V〉, |G〉, and |N〉. (It is important to note that the vector space can be arbitrarily high-dimensional, although for simplicity of illustration, a three-dimensional vector space is used in Figure 1.) These vectors represent verbatim, gist, and nonmatching traces, respectively. In other words, they are representations of episodic traces that, respectively, match a cue’s surface form, match its semantic/relational content, or do not match either. When a test cue C is presented to a subject, it induces a perceived memory state, S_C. QEMc represents this memory state as a vector in the three-dimensional space that is a superposition of the three basis vectors:

$$\mid S_C\rangle =v_C·\mid V\rangle +g_C·\mid G\rangle +n_C·\mid N\rangle .$$ (A1)

This memory state vector is subject to the mathematical constraint |v_C|² + |g_C|² + |n_C|² = 1, and the subscript C denotes the specific test cue, which can be O, NS, or ND. The parameters v_C, g_C, and n_C are scalars that multiply the respective memory vectors, and psychologically, they represent the strengths of the three types of traces. (Technically, they are “probability amplitudes” of accepting the O?, NS?, and ND? probes, respectively.)

Conceptually, as discussed in Brainerd et al. (2013), the superposition state in Equation A1 captures the fuzziness and uncertainty that is associated with memory judgments. Note that the subscript C indicates that a distinct memory state vector is generated for each of the three types of cues, with corresponding amplitudes v_C, g_C, and n_C, where C = O, NS, or ND. In other words, the memory state vector depends on the specific test cue that is presented, which means that v_C, g_C, and n_C have different values for O, NS, and ND cues. For instance, based on prior FTT research (see Brainerd & Reyna, 2005), O cues are better retrieval cues than ND cues for both verbatim and gist traces (so that v_C and g_C are larger for O than for ND cues), and NS cues are better retrieval cues than ND cues for both verbatim and gist traces (so that v_C and g_C are larger for NS than for ND cues).

When a cue C is presented and before a probe question is posed, the cue’s perceived episodic state can be O, NS, or ND with probabilities |v_C |², |g_C|², and |n_C|², respectively. Based on the axioms of QP, these probabilities must sum to 1 because these possible states are mutually exclusive and exhaustive. This constraint has psychological meaning: It captures subjects’ knowledge (which is reiterated to them in the instructions that they receive) that C must belong to exactly one of the three states, so that information from the |V〉, |G〉, and |N〉 basis vectors is retrieved on memory tests. In addition, a cue’s perceived episodic state can be an uncertain one in which the subject remembers C as being “either O or NS” (a disjunction, e.g., Brainerd et al., 2013) with probability |v_C |² + |g_C|². This also has psychological meaning: It captures the common experience of knowing that something about C is old but of being unsure whether it is actually a target or a new item that preserves salient features of a target, such as membership in a taxonomic category.

As indicated, O, NS, and ND cues were factorially crossed with O?, NS?, and ND? probes in our experiment, with the subject accepting or rejecting each probe. According to QP, the probability of accepting a probe can be interpreted as projecting the memory state to the subspace used to evaluate the probe question in the vector space, as illustrated in Figure 1. The projectors that generate the probabilities of accepting a probe are denoted M_{O, y}, M_{NS, y}, and M_{ND, y}, respectively. Each of these projectors is a diagonal matrix. The matrices are M_{O, y} = diag[1,1,0], M_{NS, y} = diag[0,1,0], and M_{ND, y} = diag[0,0,1]. In other words, the M_{O, y} matrix picks out the |V〉 and |G〉 vectors of Equation A1, the M_{NS, y} matrix picks out the G vector, and the M_{ND, y} matrix picks out the N vector. All of this is translated into the response probabilities that are given for O, NS, and ND cues in Table 1 of the article. Here, it is worth emphasizing that in QEMc, the cue elicits the memory state, and the probe determines the projector used to answer the question.

In our item false memory design, empirical tests of the additive law can be obtained for each of the three cues by summing the individual probabilities of remembering it as belonging to each of the mutually exclusive and exhaustive episodic states; that is, by finding the total probability that a cue is remembered as being an O, NS, or ND item. QEMc predicts that this sum must be subadditive, p(O?) + p(NS?) + p(ND?) > 1 for all three cues, as long as there is some gist memory. (Importantly, note that the model predicts that this pattern will extend to events that are not directly experienced.) That prediction falls out as follows. Under QP axioms, the probability of accepting an O? probe for cue C (C can be O, NS, or ND) is the squared magnitude of the projection that is obtained by projecting the memory state S_C to the subspace spanned by the V and G trace vectors (because matching of either verbatim information or gist information or both would support acceptance of an O? probe): ||M_O,y|S_C〉||²=|v_C|²+|g_C|². This is illustrated in Figure 1. As shown there, the V, G, and N axes are the three vectors spanning the three-dimensional memory vector space. The subspace for accepting O? probes is the plane spanned by the vectors |V〉 and |G〉. The red line is the memory state vector that is elicited by the cue C, which has a value (a coordinate or “probability amplitude”) on each of the three basis vectors (the V, G, and N axes). Those values are the scalars v_C, g_C, and n_C. The probability of accepting O? probes is obtained by first projecting the memory state S_C to the subspace for evaluating O? as “accept” and then taking the square of the magnitude (or more generally, of the length) of that projection.

Similarly, the probability of accepting NS? probes for cue C is ||M_NS,y|S_C〉||² = |g_C|², and the probability of accepting ND probes is ||M_ND,y|S_C〉||² = |n_C|². In these two cases, in Figure 1, the subspaces for evaluating the “accept” answer to NS? probes and the “accept” answer to ND? probes are the one-dimensional rays G and N, respectively. The probability of accepting NS? probes is obtained by squaring the magnitude of the projection of the memory state vector to the ray G, and the probability of accepting ND? probes is obtained by squaring the magnitude of the projection of the memory state vector to the ray N.

Then, for a cue C, the sum of the probability of accepting all three probes equals |v_C|² +|g_C|² +|g_C|² +|n_C|² = 1+|g_C|² ≥1. Thus, QEMc predicts violations of the additive rule of classical probability theory, specifically, subadditivity. In addition, the model predicts that the greater the reliance on gist traces in making memory judgments (i.e., the larger the value of |g_C|²), the larger the subadditivity effect will be. This means that manipulations that increase the strength of gist traces relative to verbatim traces or that simply encourage gist retrieval on memory tests should also increase observed levels of subadditivity. Some manipulations of that sort were included in our experiments.

Before we describe the QEMc model for source false memory paradigm, we note, for the sake of completeness, that QEMc also predicts another subadditivity phenomenon that is described in the text, disjunction fallacies. It is easy to see that the sum of the probabilities of accepting each of the mutually exclusive events (O? and NS?) equals |v_C|² +|g_C|² +|g_C|². However, when directly judging the disjunction of these vents (O or NS?), the acceptance probability under QEMc is |v|² + |g|², as explained earlier. Obviously, that probability is smaller than the sum of the nondisjunctive probabilities: |v_C|² +|g_C|² <|v_C|² +|g_C|² +|g_C|². Thus, this other memory subadditivity phenomenon is also predicted a prior by QEMc.

The QEMc Model for Source False Memory

Next, we briefly generalize the preceding results to our modified source false memory procedure. In the conventional procedure, as mentioned, subjects first encode two (or more) sets of memory targets, with each set being accompanied by distinctive contextual cues. For instance, as in the research that we report, the targets are often presented as two word lists, with the words on one list being presented in fonts/colors/positions that differ from the fonts/colors/positions in which the words on the other list are presented. After encoding the two sets of targets, subjects respond to a recognition test composed of three types of test cues: old (target) cues from List 1 (L1; e.g., potato); old cues from List 2 (L2; e.g., baseball); and new-dissimilar cues (ND; e.g., crown). Subjects first make an old-new (item) recognition decision about a cue. Next, they make a source judgment (L1 or L2?) about this cue only if it is recognized as old. In the novel design that we used, similar to our false memory design, the three types of test cues were factorially crossed with three types of source probes that partitioned the set of possible episodic states that a cue could belong to: (a) the cue was presented on List 1(L1?); (b) the cue was presented on List 2 (L2?); and (c) the cue was not presented (ND?). As in the item false memory design, these states are obviously exhaustive and mutually exclusive.

The details of the QEMc model for this design are the same as for the item false memory design, except for one feature: There are two verbatim memory vectors, |V₁〉 and |V₂〉, which accommodate the fact that targets are presented in two distinct contexts rather than one. Thus, the vector space for the source design is generated by the quartet of unit length basis vectors, |V₁〉, |V₂〉, |G〉, and |N〉, which represent List 1 verbatim traces, List 2 verbatim traces, gist traces, and nonmatching traces, respectively. As before, a test cue C induces a perceived memory state, S_C, which the model represents as a vector in the four-dimensional space that is a superposition of the four memory vectors:

$$\mid S_C\rangle =v_{C1}·\mid V_1\rangle +v_{C2}·\mid V_2\rangle +g_C·\mid G\rangle +n_C·\mid N\rangle .$$ (A2)

As in Equation A1, Equation A2 is subject to the constraint that |v_C1|² + |v_C2|² +|g_C|² +|n_C|² = 1, which reflects subjects’ knowledge that a cue must be from List 1, or from List 2, or new. The subscript C runs over L1, L2, and ND test cues. The scalars in Equation 2 have the same psychological meaning as before (i.e., they capture the strengths of the traces).

Empirically, the additive law of probability can be tested for this source design by summing the individual probabilities of remembering a cue as belonging to each of the three mutually exclusive and exhaustive episodic states; that is, by finding the total probability that a cue is remembered as being an L1, L2, or ND item. As before, the model predicts that this sum must be subadditive as long as gist memory is involved, that p(L1?) + p(L2?) + p(ND?) will be > 1. This can be seen as follows. Suppose that an item is presented as a test cue. The probabilities of accepting each of the three probes are determined, once again, by projecting the perceived memory state to the subspace that is spanned by the trace vectors that are picked out by the probe. The relevant projectors for accepting the three probes L1?, L2?, and ND? are M_{L1, y} = diag[1,0,1,0], M_{L2, y} = diag[0,1,1,0], and M_{ND, y} = diag[0,0, 0,1], respectively. In other words, the M_{L1, y} diagonal picks out the |V₁ 〉and |G〉 vectors of Equation A2, the M_{L2, y} diagonal picks out the |V₂ 〉and |G 〉vectors, and the M_{ND, y} diagonal picks out the |N 〉vector. Therefore, the model says that the sum of the individual probabilities of accepting the individual probes for the test cue C is

$${\mid v_{C1}\mid }^2+{\mid v_{C2}\mid }^2+{\mid g_C\mid }^2+{\mid g_C\mid }^2+{\mid n_C\mid }^2=1+{\mid g_C\mid }^2\ge 1.$$

From this, it is clear that memory is predicted to violate additive probability in source as well as in item false memory. Note that the QP model for the source design also predicts that the greater the reliance on gist traces, the larger the subadditivity effect will be.