Individual Differences and Fitting Methods for the Two-Choice Diffusion Model of Decision Making

Abstract

Methods of fitting the diffusion model were examined with a focus on what the model can tell us about individual differences. Diffusion model parameters were obtained from the fits to data from two experiments and consistency of parameter values, individual differences, and practice effects were examined using different numbers of observations from each subject. Two issues were examined, first, what sizes of differences between groups can be obtained to distinguish between groups and second, what sizes of differences would be needed to find individual subjects that had a deficit relative to a control group. The parameter values from the experiments provided ranges that were used in a simulation study to examine recovery of individual differences. This study used several diffusion model fitting programs, fitting methods, and published packages. In a second simulation study, 64 sets of simulated data from each of 48 sets of parameter values (spanning the range of typical values obtained from fits to data) were fit with the different methods and biases and standard deviations in recovered model parameters were compared across methods. Finally, in a third simulation study, a comparison between a standard chi-square method and a hierarchical Bayesian method was performed. The results from these studies can be used as a starting point for selecting fitting methods and as a basis for understanding the strengths and weaknesses of using diffusion model analyses to examine individual differences in clinical, neuropsychological, and educational testing.

Research using simple two-choice tasks to examine cognition and decision making has had a long history in psychology. The most successful current models of decision making are sequential sampling models, which assume that decisions are based on the accumulation of evidence from a stimulus, with moment-to-moment fluctuations in the evidence that are largely responsible for errors and for the spread in the distributions of response times (RTs). During the accumulation process, the amount of evidence needed to choose between alternatives is determined by response criteria, one criterion for each of the choices. The time taken to make a decision and which alternative is chosen are jointly determined by the rate at which evidence accumulates (drift rate) and the settings of the response criteria or boundaries. This article will focus on one of the more popular of these models, the diffusion model (Ratcliff, 1978; Ratcliff & McKoon, 2008).

The aim of these models is to provide an understanding of the basic cognitive processes that underlie simple decision making. One of the key advantages of the models is to separate the settings of the criteria (which determine speed-accuracy tradeoffs) from the quality of the evidence obtained from a stimulus and also from the duration of other processes. This provides the basis for another key advantage and that is the ability to examine differences in these aspects of processing in different subject populations. For example, studies have examined reversible changes in normal individuals such as sleep-deprived individuals (Ratcliff & Van Dongen, 2009) and hypoglycemic individuals (Geddes, et al., 2010), as well as decision making in children (Ratcliff, Love et al., 2012). The model allows examination of decision making in various clinical populations such as aphasic individuals, (Ratcliff, Perea, et al. 2004), adults and children with ADHD (Mulder et al., 2010; Karalunas & Huang-Pollock, 2013), individuals with dyslexia (Zeguers et al., 2011), and individuals with anxiety or depression (White et al., 2009, 2010a, 2010b). The model has also been used to examine decision processes in neurophysiology with single-cell recording methods (Ratcliff, Cherian, & Segraves, 2003; Gold & Shadlen, 2007), EEG signals (Ratcliff, Philiastides, & Sajda, 2009), and fMRI methods (Mulder, van Maanen, & Forstmann, in press).

Some applications of the diffusion model have produced new interpretations of differences between subject groups. In the domain of aging, in many tasks there is little difference between older adults and young adults in accuracy but a large difference in RT, with older adults slower than young adults. This suggests a deficit when using RT measures but no deficit when using accuracy measures. Application of the diffusion model showed that there were small or negligible differences in drift rates between older and young adults which explains the lack of differences in accuracy. Increases in boundary settings and nondecision time (the duration of processes other than the decision process) with age explains the differences in RTs. There is also the opposite dissociation with IQ related to drift rate but not boundary setting or nondecision time. Such patterns of results and new interpretations provide strong support for this approach to understanding simple decision making (McKoon & Ratcliff, 2012, 2013; Ratcliff, Thapar, & McKoon, 2001; 2003; 2004; 2010; 2011; Schmiedek et al., 2007; Spaniol, Madden, & Voss, 2006).

In a number of these latter studies examining aging, individual differences across subjects in model parameters show strong external validity by correlating with, for example, IQ. This illustrates a third potential advantage of the models and that is to provide individual difference measures and perhaps even the possibility of determining whether an individual is different from a group (i.e., has a deficit relative to a comparison group).

One large domain for potential application of the model is in the domains of clinical research, educational research, and neuropsychological testing. The highest bar is that the model might contribute to diagnoses of cognitive impairments in individuals. The aim would be to compare a possibly impaired individual to a matched group of normal individuals. In the model, this means that normal ranges of drift rates, criteria, and nondecision times must be estimated and the standard deviations (SD's) across individuals calculated in order to determine whether and how far an individual is outside the normal range.

This model-based approach contrasts with standard neuropsychological and educational testing approaches. In these, often performance is measured on several different tasks, often with relatively few trials on each task, and then the results are averaged into a single indicator of some ability, such as working memory or speed of processing. From the point of view of cognitive modeling, multi-task tests represent a compendium of disparate processes that may share some common features. If processing components differ across the tasks, they might be averaged out. This neuropsychological testing approach is advantageous for many uses, especially when deficits are large, but in other situations, it may be more important to understand deficits in the components of processing with a model-based approach.

Neuropsychological and educational testing approaches often measure speed of processing and label it a basic “ability”. Given that it deals with the speed with which cognitive processes proceed one would expect that modern modeling of decision making and RT would be used or evaluated in this approach. However, it is hard to find neuropsychological or educational tests that come from cognitive modeling research more recent than the 1980's. For example, a recent edited book, “Information processing speed in clinical populations” (DeLuca & Kalmar, 2008) makes no reference to modeling RTs and a review article of intelligence and speed of processing (Sheppard, 2008) likewise makes no reference to modeling approaches. Given this disconnect between theory and applications, models that deal with speed and accuracy in rapid decision making are a natural domain to explore.

In this article we examine an number of practical issues that arise in fitting the diffusion model to data.

1. Using data from two experiments, we examine effects of numbers of observations and practice effects on both the mean values of model parameters and the variability in them across subjects. This is done by dividing the data into subgroups and fitting the model to each. This analysis provides the basis to determine how large differences in model parameters have to be in order to determine whether a single individual falls outside the normal range.

2. Simulated data were generated from the diffusion model with ranges of parameters similar to those from the experiments to examine recovery of individual differences in model parameters. The different fitting methods were applied to them and the correlations between the recovered parameters and the ones used to generate the simulated data were compared.

3. 64 sets of simulated data were generated from each of 48 sets of parameters representing the two designs with several different sets of numbers of observations. The different fitting methods were applied and means and SD's in recovered parameter values were obtained. These showed whether there were systematic biases in recovered parameter values and how variable estimates were from the different methods.

4. A hierarchical Bayesian fitting application was evaluated and compared with a standard method.

It is important to examine practice effects and we did this using the experimental data (this also provides a modest test-retest evaluation of model parameters). If performance changes radically over the first tens or few hundreds of trials, and the changes are not consistent across individuals, then the data from two choice tasks with model analyses may be of limited use when only a small amount of testing time is available as occurs with neuropsychological testing batteries. The experiments presented below used a homogeneous group of undergraduates (with some possibly not particularly motivated) and so provide results for undergraduates as well as a demonstration of how to conduct such studies with other populations.

It is important to distinguish between different sources of variability relevant to applications of the diffusion model. Variability across subjects in the parameters of the model from the fits to each subject's data (SD's) can be used to determine if a parameter value for an individual is significantly different from the values for the group. Standard errors across subjects can be used to determine whether a parameter for one group differs significantly from the parameter for another group. These standard errors represent the variability in the group means and they can be made smaller by increasing the number of subjects in the group.

There is also sampling variability in the model parameters, that is, given the number of observations, how close are the parameters recovered to the parameter values that generated the data. For example, if the diffusion model was used to generate simulated data, the parameters recovered from the simulated data would be more variable if there were 100 simulated observations compared with 1000 observations. In typical applications of the diffusion model, this source of variability is typically 3 to 5 times smaller than the variability due to differences among individuals for 45 min. of data collection. Because individual differences produce larger variability in model parameters than sampling variability, significant correlations can be obtained with variables such as IQ, even when there are relatively small numbers of observations. However, when trying to detect whether an individual falls outside the normal range of the model parameters, both high power and low variability in parameter estimates are needed.

For all such applications of the model just discussed we need to understand how large are SD's in individual differences across subjects as well as SD's in model parameters as a function of number of observations in the sample. Also, SD's differ as a function of the values of the parameters, for example, a small boundary separation has smaller SD than a large boundary separation.

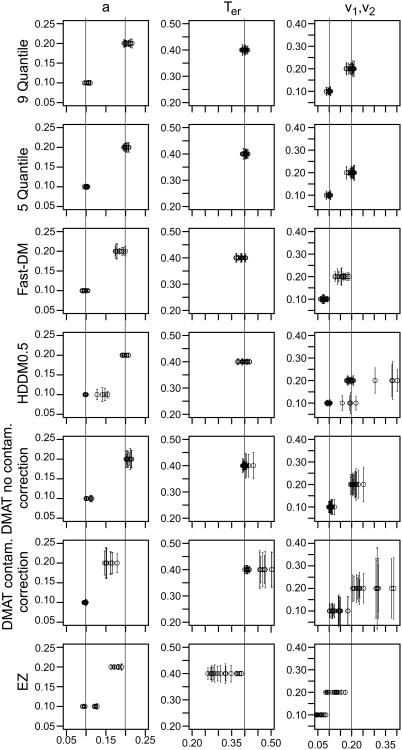
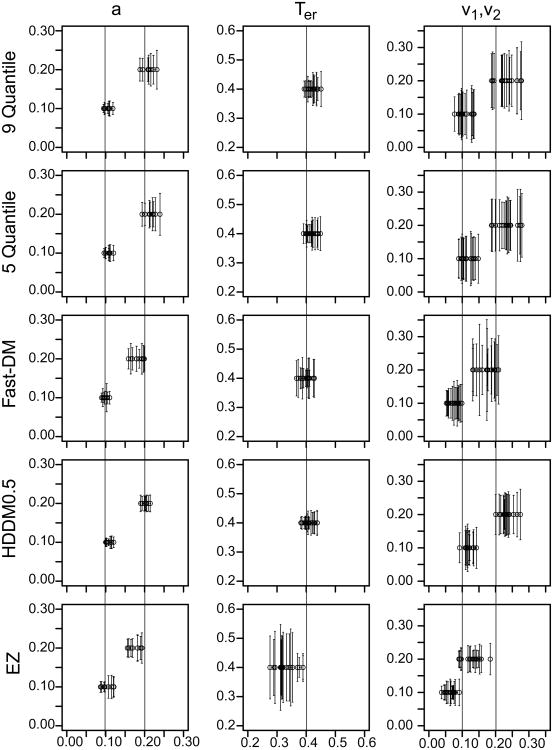
Following the experimental study, we tested a number of methods for obtaining parameter estimates from two-choice data. The first three were our locally-developed programs: two chi-square methods using binned data and a maximum likelihood method (MLH) (Ratcliff & Tuerlinckx, 2002). The other five were from recently developed diffusion-model fitting packages, DMAT, with and without correction for contaminant RTs using the mixed default method (Vandekerckhove & Tuerlinckx, 2007, 2008), fast-dm (Voss & Voss, 2007, 2008), the non-hierarchical HDDM (Wiecki, Sofer, & Frank, 2013), and EZ (Wagenmakers, van der Maas, & Grasman, 2007). In addition, we tested a hierarchical model from the HDDM package with a more limited set of simulated data.

For Simulation Study 1, the aim was to determine how well each method performed in recovering individual differences, that is, providing the correct ordering of parameters across individuals. A method might produce estimates that are biased away from the true values, those from which the simulated data were generated, but if the ordering is correct, then it can be used as a measure of individual differences. For examining differences among individuals and the relationship of such differences to clinical or educational tests, a more accurate order would be more important than accurate recovery of true values.

We used the best-fitting parameter values from fits to the two experiments to generate simulated data using the designs from the two experiments. For each experiment, different studies used different numbers of observations and each study was performed with and without contaminants (assumed to be random delays added to the decision time, see later). For each parameter, its value for each simulated data set was drawn from a normal distribution with the mean and SD from the parameter values from the fits to Experiment 1 or Experiment 2. Each combination of parameters produced a data set for each simulated subject.

For Simulation Study 2, the aim was to determine how well each method recovered the true values of the parameters. The fitting methods were evaluated by how much their estimates were biased away from the true values and the variability in these estimates. The combinations of parameter values were chosen to be representative of what is typically observed in real experiments, 16 such combinations for the numerosity design and 32 for the lexical decision design. For both simulation studies, data were simulated for 64 subjects, each with and without outlier RTs, for numbers of observations ranging per condition from 40 to 1000.

For Simulation Study 3, we tested the nine-quantile chi-square against a hierarchical Bayesian fitting method. Hierarchical methods have been demonstrated to be superior to standard methods when there are low numbers of observations per subject and this study examined the degree to which this is true with the existing package.

The results of the simulation studies are intended to provide methodological guidelines: which methods of fitting the diffusion model provide the correct ordering of the model's parameters and therefore can be used to determine individual differences for correlational analyses; which methods provide values that are not biased away from the true values and therefore can be used to test differences between groups of individuals; and how many subjects for how many numbers of observations does it take to produce sufficiently useful estimates of parameters. If the design of an experiment is substantially different from the numerosity and lexical decision designs, in terms of number of conditions, numbers of observations, accuracy or RT levels, and so on, then the studies here can show how to perform the evaluation needed. Recommendations are presented at the end of the General Discussion section.

The Diffusion Model

In the diffusion model, two-choice decisions are made when information accumulated from a starting point, z, reaches one of the two response criteria, or boundaries, a and 0 (see Figure 1). The drift rate of the accumulation process, v determined by the quality of the information extracted from the stimulus in perceptual tasks and the degree to which a test item matches memory in memory and lexical decision tasks. It is usually assumed that the value of v cannot change during the accumulation of information (see Ratcliff, 2002, p286 for example of mimicking between drift rate ramping on and a constant drift rate). The mean time taken by nondecision processes is labeled T_er. In separating drift rates, criteria, and nondecision times, the model decomposes accuracy and RTs for correct and error responses into individual components of processing. It explains how the components determine all aspects of data, including mean RTs for correct and error responses, the shapes and locations of RT distributions, the relative speeds of correct and error responses, and the probabilities with which the two choices are made.

Figure 1.

An illustration of the diffusion model and the logic of fitting the model to data. The top panel shows the diffusion model with sample paths and correct and error RT distributions. The middle panel shows the components that contribute to the nondecision time. The bottom panel shows a schematic of how RT and accuracy data are mapped into diffusion model parameters. Only the main parameters that have been used in examining individual differences are shown, but all the other model parameters are also estimated.

The model includes three sources of across-trial variability: variability in drift rate, variability in the starting point of the accumulation process (which is equivalent to variability in the criteria settings for low to moderate values), and variability in the time taken by nondecision processes. Variability in drift rate expresses the idea that the evidence subjects obtain from nominally equivalent stimuli differs in quality from trial to trial. Variability in starting point expresses the idea that subjects cannot hold their criteria constant from one trial to the next, and variability in nondecision components from one trial to the next expresses the idea that processes of encoding etc. do not take exactly the same time across trials. Across-trial variability in drift rate is normally distributed with SD η, across trial variability in starting point is uniformly distributed with range s_z, and across trial variability in the nondecision component is uniformly distributed with range s_t. (Ratcliff, 1978, 2013, showed that the precise forms of these distributions are not critical.)

Subjects sometimes make responses that are spurious in that they do not reflect the processes of interest but instead are due to, for example, distraction, lack of attention, or concern for lunch. We describe the assumptions for such contaminant responses later. Subjects also sometimes make fast guesses with short RTs (e.g., between 0 and 200 ms). Experimentally these can be minimized by adding a delay (1-2 sec.) between the response and the next test item with a message saying “too fast” if the response is shorter than say 200 ms. The HDDM package for fitting the model, discussed below, assumes a contaminant distribution that has a minimum value of zero and this can accommodate a small proportion of fast guesses. Other methods for eliminating them are excluding all responses below some cutoff value (e.g. 200 ms) or excluding all responses that occur before accuracy begins to rise above chance (this latter method is formally implemented in the DMAT package discussed below). Another way of looking for fast guesses, or any kinds of guesses, is to include in the design of the experiment, a condition with high accuracy. The proportion of errors in this condition would be an upper limit on the proportion of guesses.

When the model is fit to data, all of its parameters are estimated simultaneously for all the conditions in an experiment. The model is tightly constrained in several ways. The most powerful is the requirement that the model fit the right-skewed shape of RT distributions (Ratcliff, 1978, 2002; Ratcliff & McKoon, 2008; Ratcliff et al., 1999). Another is the requirement that differences in the data between conditions that vary in difficulty must be captured by changes in only one parameter of the model, drift rate. Boundary settings and nondecision time do not change as a function of difficulty; doing so would require that subjects know the level of difficulty before the start of information accumulation.

The assumption that drift rates change little as a function of boundary settings has been verified in experiments to date. An exception is a recent study by Starns, Ratcliff, and McKoon (2012; see also Rae et al., 2014) who found that if subjects are given extreme speed instructions (to respond in a recognition memory task in under 600 ms), then drift rates are lower than with accuracy instructions. This is likely because subjects limit stimulus or memory processing in order to respond quickly; something that they do not otherwise do.

There have been hints in the literature that nondecision time can change as a function of either changes in difficulty or changes between boundary settings. In a few experiments, fits of the model have been modestly better with small differences in nondecision time between speed and accuracy instructions (e.g., Ratcliff & Smith, 2004, p348; Ratcliff, 2006); however, in most other experiments, the difference has been relatively small (Ratcliff & McKoon, 2008, p895).

One of the most important functions of the diffusion model is that it maps RT and accuracy onto common underlying components of processing, drift rates, boundary settings, and nondecision time, which allows direct comparisons between tasks and conditions that might show the effects of independent variables in different ways. For example, a study by McKoon and Ratcliff (2012) examined associations between the two words of pairs that were studied for recognition memory. Memory was tested in two ways: either subjects were asked whether two words had appeared in the same pair at study or they were asked whether a single word had been studied. In the latter case, a single word was preceded in the test list by the other word of the same pair (“primed”) or by some other studied word (“unprimed”). For priming, the effects of independent variables showed up mainly in RTs whereas for pair recognition, they showed up mainly in accuracy. McKoon and Ratcliff found that age, IQ, and the semantic relatedness of the words of a pair all affected drift rates in the same ways for the two tasks, from which they concluded that priming and pair recognition depend on the same associative information in memory. This conclusion would not have been possible without the model.

Another important function of the model is that it allows direct comparisons between groups of subjects. For example, older adults are generally slower than younger adults and show larger differences among conditions. For pair recognition, for example, older adults' RTs for same-pair tests might be 1200 ms and for different-pair tests, 1400. For young adults, RTs might be 1000 ms and 1100. Ratcliff et al. (2011) found that the differences in performance between older and younger subjects were due to differences in all three components of the model: drift rates, boundary settings, and nondecision times. This contrasts with item recognition in which older adults (60-74 year olds) show little difference in drift rates compared with young adults.

Methods for Fitting the Diffusion Model to Data

The methods used most commonly have been the maximum likelihood method (MLH) (Ratcliff & Tuerlinckx, 2002) and three binned methods: the chi-square (Ratcliff & Tuerlinckx, 2002) method, the multinomial likelihood ratio chi-square (G² method), and the quantile maximum likelihood method (Heathcote, Brown, & Mewhort, 2002). The latter two methods are nearly identical, so we do not discuss the quantile maximum likelihood method further.

In all of these methods, from some RT (either a single RT for the MLH method or a quantile for a binned method) and the model parameters, the predicted probability density is computed. The expression for the cumulative density is (with ξ drift rate and ζ starting point):

$$G(t,\xi ,\zeta )=P(\xi ,\zeta )-\frac{\pi s^2}{a^2}{e}^{-(\zeta \xi /s^2)}\times {\sum }_{k=1}^{\infty }\frac{2k\mathit{sin}(k\pi \zeta /a)e^{-\frac{1}{2}({\xi }^2/s^2+{\pi }^2{k}^2{s}^2/a^2)t}}{({\xi }^2/s^2+{\pi }^2{k}^2{s}^2/a^2)}$$

The expression for the response proportion for the choice is

$$P(\xi ,\zeta )=(e^{-(2\xi a/s^2)}-e^{-(2\xi \zeta /s^2)})/(e^{-(2\xi a/s^2)}-1)$$

These equations must be integrated over the distributions of drift rate, starting point, and nondecision time (τ):

$$G(t,v,z)={\int }_{(T_{er}-s_t/2)}^{(T_{er}+s_t/2)}\left({\int }_{(z-s_z/2)}^{(z+s_z/2)}\right({\int }_{-\infty }^{\infty }G(t-\tau ,\xi ,\zeta )N(\xi ;v,\eta )U(\zeta ;z,s_z)U(\tau ;T_{er,}{s}_t))d\xi d\zeta d\tau$$

where

$$N(\xi ;v,\eta )=\frac{1}{\sqrt{2\pi {\eta }^2}}{e}^{-\left(\frac{{(v-\xi )}^2}{2{\eta }^2}\right)}$$

and

$$U(x;a,s)=\frac{1}{s},a-\frac{s}{2}<x<a+\frac{s}{2}$$

To obtain the probability density from the cumulative density, F(t_i), at a time, t_i, the value of F(t_i) and the value for that time plus an increment, F(t_i+dt) is computed, where dt is small (e.g., .00001 ms). Then using f(t)=(F(t+dt)-F(t))/dt, the predicted probability density at t_i is obtained.

For the MLH method, the predicted probability density (f(t_i)) for each RT (t_i) for each correct and error response is computed and the product over all densities for all the RTs t_i is the likelihood (L=Пf(t_i)). To obtain the maximum likelihood parameter estimates, the value of the likelihood is maximized by adjusting parameter values using a function minimization routine. However, because products of densities can become very large or very small, numerical problems occur and so it is standard instead to maximize the log likelihood, i.e., the sum of the logs of the densities (summing logs of the values is the same as the log of the product of the values, log(ab)=log(a)+log(b)). Summing the logs of the predicted probability densities for all the RTs gives the log likelihood and minimizing minus the log likelihood produces the same parameter values as maximizing the likelihood.

Minus log likelihood can be minimized using a variety of software routines and we use the robust SIMPLEX routine (Nelder & Mead, 1965). This routine takes starting values for each parameter, calculates the value of the function to be minimized, then changes the values of the parameters (usually one at a time) to reduce minus log likelihood. This process is repeated until either the parameters do not change from one iteration to the next by more than some small amount or the value to be minimized does not change by more than some small amount.

For the chi-square method, the chi-square value is minimized using the SIMPLEX minimization routine, typically with RTs divided into either 5 or 9 quantiles. For 5 quantiles, the data entered into the minimization routine for each experimental condition are the .1, .3, .5, .7, and .9 quantile RTs for correct and error responses and the corresponding accuracy values. For 9 quantiles, the .1, .2, .3, …, and .9 quantiles are used. The quantile RTs and parameter values of the model are used to generate the predicted cumulative probabilities of a response by that quantile RT. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For the chi-square computation, these are the expected values, to be compared to the observed proportions of responses between the quantiles (i.e., for the 5-quantile method, the proportions between 0, .1, .3, .5, .7, .9, and 1.0, which are .1, .2, .2, .2, .2, and .1, and for the 9-quantile method, the proportions between quantiles and outside them, which are all .1). These proportions are multiplied by the number of observations to give the expected frequencies and summing over (Observed-Expected)²/Expected for all conditions gives a single chi-square value to be minimized. The SIMPLEX routine then adjusts parameter values to minimize the chi-square value.

For the G² method, G² = 2 Σ N p_i ln(p_i/π_i). This statistic is equal to twice the difference between the maximum possible log likelihood and the log likelihood predicted by the model (because ln(p/π)=ln(p)-ln(π)). Every time we have used this method (with several hundred observations per subject) and compared results to the chi-square method, we have found almost identical parameter estimates. This is because the chi-square approximates the multinomial likelihood statistic (see Jeffreys, 1961, p. 197); both are distributed as a chi-square random variable. We fit all the data for each subject in Experiments 1 and 2 and found that boundary separation, nondecision time, and drift rates correlated between the two methods greater than .986 for Experiment 1 and greater than .958 for Experiment 2. The across-trial variability parameters correlated greater than .930 for Experiment 1 and greater than .855 for Experiment 2. These correlations show that for the relatively large numbers of observations in Experiments 1 and 2, the estimates are equivalent. When we reduced the numbers of observations, for example to 40, there were some failures such that the two methods did not produce the same values, but we have not pursued this further.

We only applied the chi-square method to the data from Experiments 1 and 2 but we applied all the methods to the simulation studies. We assumed that every observed RT distribution has contaminants and their probability is p_o, the same probability for all experimental conditions for a subject. The contaminants are assumed to come from a uniform distribution with a range determined by the maximum and the minimum RTs in each experimental condition so that the model fit is a mixture of contaminants and responses from the diffusion process. In generating simulated data from this mixture, contaminants are assumed to involve a delay in processing (but not random guessing). Thus the contaminant assumption in generating simulated data is not the same as in fitting the data. However, the assumption of a uniform distribution of contaminants in all conditions gave successful recovery of the parameters of the diffusion process and the proportion of contaminants (Ratcliff & Tuerlinckx, 2002). In the General Discussion, we examine contaminants further.

Fitting the model with the chi-square and G² methods is much faster in terms of computer time than the MLH method, especially for large numbers of observations. For example, for Experiments 1 and 2, for each experimental condition, the 5-quantile chi-square required five evaluations of the diffusion model cumulative density for correct responses and five evaluations for error responses, no matter how many observations there were per condition. For the MLH method, the density function must be evaluated for each RT, which means hundreds or thousands of evaluations for each condition (with two evaluations of the cumulative distributions function to produce the density function for each RT). For the studies below, we used the chi-square method because it is what we have been using and because the results would be similar if we used, for example, G² (see above). As a check, we have fit exact predictions for the accuracy values and quantile RTs with the chi-square method and the model parameters used to generate the predictions are recovered to within 1%. (Note that our home grown fitting programs were handed off to the second author who implemented batch scripts for fitting with one version to avoid the possibility of tuning the programs specific to the data set).

In addition to the chi-square and MLH methods, we tested four diffusion-model fitting packages that are available in the public domain: DMAT (Vandekerckhove & Tuerlinckx, 2007, 2008), fast-dm (Voss & Voss, 2007, 2008), HDDM (Wiecki, Sofer, & Frank, 2013), and EZ (Wagenmakers, et al., 2007). The DMAT, fast-dm, and HDDM packages can all fit all the conditions of an experiment and both correct and error responses simultaneously, but the EZ method fits only one condition at a time and only correct RTs or only error RTs. For each method, we used the most straightforward default method and options. The aim was to reproduce what a user might employ in fitting. Simulated data used in the studies used here will be available as a supplement.

The data input to the DMAT package are the RTs and choice probabilities for each quantile of the data, where the number of quantiles is defined by the user (values of the bin limits can also be specified by the user). The values of the model parameters that best generate the quantile data are determined by minimizing a chi-square or G² statistic. The package also allows the user to choose to implement a mixture model for slow contaminants and an exponentially weighted moving average method to eliminate fast outliers (Vandekerckhove & Tuerlinckx, 2007). In the applications below, DMAT was applied both with (using the “Mixed Model” option) and without contaminant correction.

Note that DMAT was designed to be used with data with large numbers of observations per condition (hundreds) and was not tuned for smaller numbers and will likely not produce meaningful estimates for numbers of observations per condition in the tens. It also provides warning messages when there may be problems with the fit. Often in published applications, these are ignored. We operate like the normal user and provide what the package produces, ignoring the warning messages. But then we report the number of them for one of the studies.

Fast-dm uses a Kolmogorov-Smirnov (KS) statistic in which the whole cumulative RT distributions for correct and error responses are generated and then compared with the cumulative for the data. The model parameters are adjusted until the deviation between the two is minimized. Fast-dm, instead of using the expressions in Equations 1-5, solves the partial differential equation (the Fokker-Planck backward equation, Ratcliff, 1978; Ratcliff & Smith, 2004) numerically, which is very fast. It might be possible to use numerical solutions like this for other packages or for the chi-square or MLH methods, but we have not investigated this (but see discussions by Diederich and Busemeyer, 2003, and Smith, 2000). The fast-dm method is robust to contaminants, as demonstrated later.

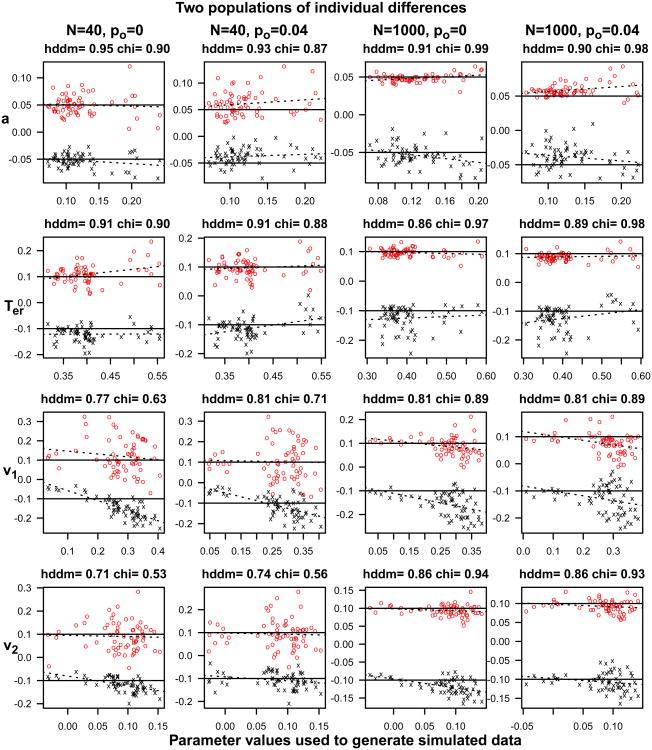
HDDM uses a Bayesian method that essentially combines a likelihood function with prior distributions over parameters. The prior distributions for boundary separation and nondecision time are Gamma distributed, drift rate and starting point are normally distributed, across trial variability in drift rate and nondecision time are half normals, and across trial variability in starting point is beta distributed (see Wiecki et al., 2013) and we used these informative priors in our fits. We used the package to fit the data from each subject individually in the same way as for the other methods. The default settings in HDDM were used, including a 20 sample burn-in, and 1800 samples for the estimation. The proportion of contaminants were estimated and not fixed in the model.

HDDM can also be fit using a hierarchical model in which model parameters are assumed to be drawn from distributions and the parameters of those distributions are estimated along with the parameters for each individual subject. This means that extreme values of parameters that might be produced because of noise in the data are constrained to be less extreme through the distributions over the group of subjects. For the first two simulation studies, we examined separate fits to individual subjects. We also compared parameters recovered from the hierarchical method with those recovered from the chi-square method. As for individual fits, we used a 20 sample burn-in, and 1800 samples for the estimation.

The EZ method (Wagenmakers et al., 2007) is based on a restricted diffusion model; there is no across-trial variability in any of the model parameters, the starting point is set midway between the two boundaries, there is no allowance for contaminant responses, and as mentioned above, it can be applied only to correct RTs or only to error RTs, for only one condition of an experiment at a time. Without across-trial variability, it cannot account for relations between correct and error RTs. With the starting point midway between the boundaries, it produces biased parameter estimates if the true starting point is not midway. It also predicts that RTs for correct and error responses will be the same, something that is known to be incorrect for the vast majority of experiments. Without allowance for contaminants, it produces quite biased estimates of parameter values (unless there are no contaminants in the data; see Ratcliff, 2008).

Wagenmakers et al. (2007) derived expressions to relate the mean RT for a condition, the variability in the mean, and the accuracy for that condition to boundary settings, nondecision time, and drift rate for that condition. Essentially, this transforms three statistics of data into three model parameters. This means that the model cannot be falsified on the basis of accuracy, mean RT, or variance in RT. The model does make predictions about RT distributions, the same predictions as the standard model and so it is easily possible to evaluate how well EZ fits RT distributions. In our applications of the EZ method, we fit only correct responses. For error responses, the RT means and the variance in them are much more variable (because there are few observations) making parameter estimates less reliable than for correct responses.

van Ravenzwaaij and Oberauer (2009) compared the EZ method to the fast-dm and DMAT methods by generating simulated data and using these methods to fit the model to the simulated data. They found that EZ and DMAT were better at recovering parameter values and that EZ was the preferred method when the goal was to recover individual differences in parameter values. We extend their results by comparing these three methods with the other methods described above, by explicitly introducing contaminants into simulated data, and by including conditions in which the starting point is not equidistant from the boundaries (a requirement for the EZ method).

When faced with a very low number of observations either because existing data sets are being used or it is not possible to collect many observations per subject, it might be tempting to simply pool the observations (e.g., Menz et al., 2012) if group differences, not individual differences are the focus. This is an incorrect way of grouping data. This is easy to see: if there are only two subjects with distributions that are well separated, then the combination will be bimodal. A better way of combining subjects is to compute quantiles of the distribution and then average them (Ratcliff, 1979). An even better way would be to use hierarchical modeling using the HDDM package.

Refinements of the Chi-square Fitting Method

Over the last several years, we have added refinements to the chi-square method. When there are fewer data points than the number of quantiles, then a median split is used to form two bins, each with probability .5. However, if the median is outside the range of the .3 to .7 quantiles for correct responses, then we use a single value of chi-square ((O-E)²/E, where O is the observed number of observations and E is the expected value from the model) for that condition and add this to the sum of the rest of the values for all the conditions and quantiles. This is because when there are low numbers of errors in conditions with high accuracy, some of the error RTs can be spurious and (we assume) not from the decision process used in performing the task.

Sometimes, accommodating very slow error responses with lower numbers of observations leads to estimates of across-trial variability in drift rate that can be a lot larger than they should be and along with this drift rates can be several times larger than they should be. This problem can be limited by placing upper and lower bounds on across-trial variability in drift rates (e.g., 0.3 and 0.08). The bounds might be determined by examining the ranges of the variability parameter values from similar experiments with larger numbers of observations. For fits for the simulation studies below with low numbers of observations, the value of the across trial variability in drift parameter was often estimated to be at the upper or lower bound for our programs that implemented these limits.

Experiments 1 and 2

The numerosity task for Experiment 1 and the lexical decision task for Experiment 2 were chosen because they are representative of commonly used experimental designs for practical applications. Numerosity discrimination has been used in examining numerosity abilities for a variety of populations and lexical decision has been used in studies of aphasia and Alzheimer's disease. The design of the numerosity experiment is the same as that frequently used with perceptual tasks including brightness, letter, motion, number, and length discrimination (Ratcliff, 2014; Ratcliff & Rouder, 1998; Ratcliff et al, 2001, 2003; Thapar, Ratcliff, & McKoon, 2003, Smith & Ratcliff, 2009; Smith, Ratcliff, & Wolfgang, 2004). The design of the lexical decision experiment is the same as that used with many memory tasks (e.g., Ratcliff, Gomez, & McKoon, 2004; Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff, Thapar & McKoon, 2004, 2010).

In Experiment 1, on each trial, a 10×10 array was filled with spaces, and between 31 and 70 asterisks were placed in the array in random positions. Subjects decided whether the number of asterisks was large (greater than 50) or small (less than 51). This range of the number of asterisks produces a range of levels of difficulty from very easy to very difficult.

In Experiment 2, on each trial, a string of letters was presented and subjects decided whether it was a word or not. There were three levels of difficulty for the words: words that occur in English with high frequency, low frequency, or very low frequency. The difficulty of the nonwords was not varied.

For both experiments, we examined practice effects by grouping the trials into earlier versus later blocks. We also examined the number of trials that are needed to estimate the diffusion model's parameters with reasonably small standard errors (SE's). Ideally, the estimated parameters for early trials would be consistent with those for later trials and the estimates from relatively small numbers of trials would be consistent with those from larger numbers. If so, the model could be used for the limited test durations that occur in applied domains.

In the numerosity discrimination experiments, subjects started the task immediately after the instructions with no prior practice. In the lexical decision task, subjects were given 30 practice trials before starting the real experiment. This means that we can look at practice effects from the beginning of testing in the numerosity discrimination task, and after a very modest amount of practice in the lexical decision task.

Method

Undergraduates at Ohio State University participated in the experiments for course credit, 63 in Experiment 1 and 61 in Experiment 2, each for one 45 min. session (data are archival and were collected in 2005). For both experiments, stimuli were displayed on a PC screen and responses were collected from the keyboard.

Numerosity discrimination

On each trial, the asterisks were placed in random positions in the 10×10 array. Subjects were asked to press the “/” key if the number of displayed asterisks was larger than 50 and the “z” key if the number was smaller than 51 and they were asked to respond as quickly and accurately as possible. If a response was correct, the word “correct” was presented for 500 ms, the screen was cleared, and the next array of asterisks was presented after 400 ms. If a response was incorrect, the word “error” was displayed for 500 ms, the screen was cleared, and the next array of asterisks was presented 400 ms later. If a response was shorter than 280 ms, the words “TOO FAST” were presented for 500 ms after a correct response or after the error message for an incorrect response. There were 30 blocks of 40 trials each with all the numbers of asterisks between 31 and 70 presented once in each block.

Lexical Decision

Words were selected from a pool of 800 words with Kucera-Francis frequencies higher than 78, a pool of 800 words with frequencies of 4 and 5, and a pool of 741 words with frequencies 0 or 1 (Ratcliff, Gomez, & McKoon, 2004). There was a pool of 2341 nonwords, all pronounceable in English. There were 70 blocks of trials with each block containing 30 letter strings: 5 high frequency words, 5 low frequency words, 5 very low frequency words, and 15 nonwords. Subjects were asked to respond quickly and accurately, pressing the “/” key if a letter string was a word and the ‘z’ key if it was not. Correct responses were followed by a 150 ms blank screen and then the next response. Incorrect responses were followed by “ERROR” for 750 ms, a blank screen for 150 ms, and then the next test item.

Results for Experiment 1

Responses shorter than 250 ms and longer than 3500 ms were excluded from the analyses (less than 0.8% of the data). The data for numbers of asterisks less than 51 were collapsed with numbers greater than 50 and they were then grouped into two conditions, easy (numbers 31-40 and 61-70) and difficult (41-50 and 51-60). Averaging over all the trials of the experiment, accuracy for the easy condition was .89 (for individual subjects, the highest accuracy was .98 and the lowest .69), mean RT for correct responses was 627 ms, and mean RT for errors was 687 ms. For the difficult condition, accuracy was .68 (for individual subjects, the highest accuracy was .78 and the lowest .57), mean RT for correct responses was 664 ms, and mean RT for errors was 721 ms.

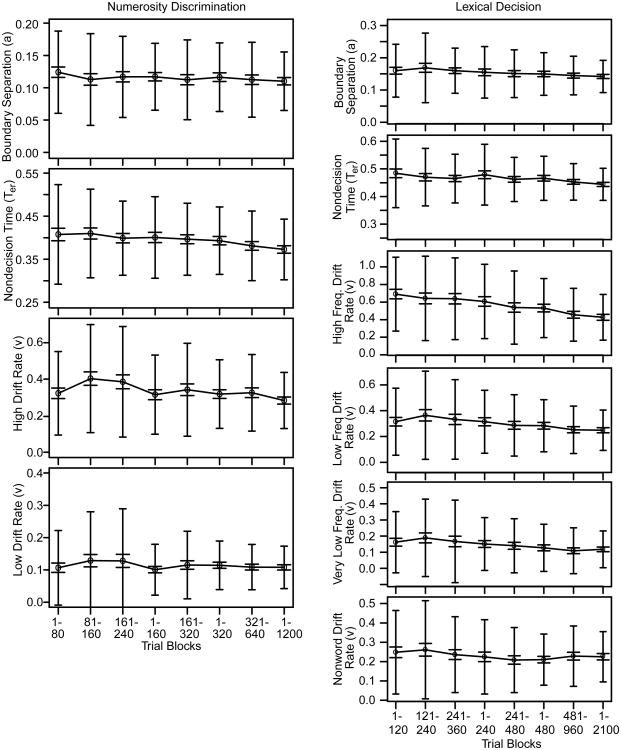
To examine practice effects and the number of trials needed for the diffusion model's parameters to have small SD's, eight groups of data were constructed: trials 1-80, trials 81-160, trials 161-240, trials 1-160, trials 161-320, trials 1-320, trials 321-640, and trials 1-1200. We fit the model to the data with the chi-square method with 9 quantiles. The model fit well, as we detail after presenting results for this experiment and for Experiment 2.

For each of the eight groups of data, Figure 2 plots the mean values over subjects of the parameters that best fit the accuracy and RT data. The means are shown for nondecision time, boundary separation, and two drift rates, one for the easy condition and one for the difficult condition. The wider error bars represent 2 SD's from the mean and the narrower ones, 2 SE's. The means and SD's are also shown in Table 1.

Figure 2.

Plots of the mean values of model parameters across subjects along with the SD's and SE's across subjects for several divisions of the data from Experiments 1 and 2 (the numerosity discrimination and lexical decision tasks respectively). The larger error bars are 2 SD confidence intervals in model parameters and the smaller error bars are 2 SE confidence intervals.

Table 1. Mean Parameter Values and SD's Across Subjects for the Numerosity Discrimination Experiment.

	Trial group	a	Ter	η	sz	p0	st	vE	vD	χ2
Mean	1-80	0.126	0.409	0.171	0.050	0.010	0.161	0.321	0.106	25.1
	81-160	0.114	0.411	0.157	0.051	0.006	0.158	0.401	0.128	22.2
	161-240	0.118	0.400	0.138	0.051	0.009	0.172	0.383	0.127	24.5
	1-160	0.119	0.402	0.162	0.050	0.007	0.161	0.314	0.100	29.6
	161-320	0.114	0.398	0.145	0.051	0.009	0.171	0.340	0.115	33.0
	1-320	0.118	0.395	0.155	0.053	0.008	0.182	0.317	0.114	34.1
	321-640	0.114	0.382	0.145	0.063	0.008	0.174	0.324	0.108	34.6
	1-1200	0.112	0.374	0.126	0.064	0.007	0.180	0.282	0.107	50.4
SD	1-80	0.032	0.058	0.076	0.036	0.023	0.087	0.113	0.058	10.5
	81-160	0.036	0.052	0.073	0.037	0.015	0.091	0.147	0.076	10.6
	161-240	0.032	0.043	0.070	0.043	0.018	0.080	0.150	0.081	11.4
	1-160	0.026	0.047	0.075	0.036	0.019	0.078	0.107	0.039	11.0
	161-320	0.031	0.042	0.078	0.034	0.021	0.076	0.126	0.052	15.0
	1-320	0.027	0.039	0.067	0.031	0.018	0.064	0.093	0.038	13.1
	321-640	0.029	0.041	0.061	0.027	0.015	0.058	0.104	0.035	12.0
	1-1200	0.023	0.035	0.047	0.021	0.011	0.049	0.076	0.033	20.7
Mean	Simulation Parameters	0.11	0.375	0.13	0.06		0.16	0.30	0.10
SD		0.03	0.05	0.08	0.01		0.10	0.10	0.05
Mean	Hierarchical simulation parameters: two subject groups	0.20	0.53	0.13	0.06		0.16	0.10	0.00
SD		0.02	0.03	0.08	0.01		0.10	0.05	0.025

Note. a=boundary separation, z=starting point, T_er=nondecision component of response time, η =standard deviation in drift across trials, s_z=range of the distribution of starting point (z), s_t = range of the distribution of nondecision times, v_E and v_D are the drift rates for the easy and difficult conditions respectively, and χ² is the chi-square goodness of fit measure. For the data, the number of degrees of freedom for the fits to data was 30 and the critical value of chi-square at the .05 level was 43.8. In the simulations, the drift rates were correlated. The same random number was used to generate both drift rates with half the value added to the lower drift rate. The following were lower limits on parameter values: a, 0.07; η, 0.02; T_er, 0.25; s_t, 0.04, and an upper limit on s_z of 0.9a. Separate sets of simulations were conducted with p_o 0 or 0.04.

When the values of the parameters estimated from the first 80 trials (the 1-80 group) were compared to the values estimated from all 1200 trials (the 1-1200 group), there were modest differences. The estimated values from all the trials were only slightly lower than for the early trials for boundary separation, nondecision time, and drift rate for the easy condition. For boundary separation, nondecision time, and drift rates, the SD's and SE's were smaller by one half to two thirds for all the trials than for 80 trials. Results were similar for the 1-160 group and the 1-320 group but with smaller differences. In general, for this subject population (undergraduates) and this task, there is little difference in the parameter values estimated from the first few trials and those estimated from the whole session.

Figure 2 and Table 1 also show further divisions of the data that allow examination of practice effects over the first few blocks of trials. There were small declines in nondecision time and boundary separation from the first block to later blocks. Drift rates for the easy condition were higher for the 81-160 and 161-240 groups than for the 1-80 and 1-160 groups respectively, but these were probably spurious because with lower numbers of observations, there are very few errors and this leads to inflated drift rate estimates. As the amount of data increases, the number of errors increases and so drift rate estimates decrease because the larger numbers of errors allows them to be estimated with more accuracy. The overall decrease in SE's across the groups also reflects increasingly larger numbers of errors. These same trends occur for the difficult condition but with smaller differences.

The SD's across subjects in the estimated parameter values (the larger error bars in Figure 2) allow examination of power for detecting differences between an individual and our population of subjects. College students are likely to provide the best performance of any population of subjects because they are likely to have the shortest nondecision times and highest drift rates (and perhaps the narrowest boundary settings, although these vary with task and with instructions that emphasize speed over accuracy or accuracy over speed). To identify an individual as different from our student population, his or her value for any of the parameters would have to lie at least one SD outside the 2 SD confidence interval for the students (e.g., Cumming & Finch, 2005). One SD outside a 2 SD confidence interval gives about 6% false negatives and 6% false positives. One SD outside 2 SD's for nondecision time is about 500 ms and one SD outside 2 SD for boundary separation is about 0.18. Values of boundary separation and nondecision time larger than these values are often found with older adults which means it is possible to detect age differences through the model parameters. However, it is unlikely that subjects with deficits could be distinguished from the students on the basis of drift rates. This is because the bottom of the two SD range extends to zero or almost to zero and 1 SD lower than this is below zero (i.e., even a drift rate of zero representing chance performance would not be far enough outside the confidence intervals).

In contrast, the model parameters can be used to detect differences between different subject groups. Because standard errors decrease and hence power increases with the number of observations (subjects), even quite small differences can be discriminated. For example, 2 SE's in drift rates in Figure 2 for the easy condition with 1200 observations is about 0.02. This means differences as small at 0.03 could be detected for the population, number of observations, and conditions in Experiment 1 (the SE's can be found from the SD's in Tables 1 and 2 by dividing the SD by the square root of the number of subjects). Thus, there is power to detect even small differences in parameter values between the different groups.

Table 2. Mean Parameter Values and SD's Across Subjects for the Lexical Decision Experiment.

	Trial group	a	Ter	η	sz	p0	st	z	vH	vL	vV	vN	χ2
Mean	1-120	0.153	0.476	0.133	0.038	0.001	0.171	0.081	0.660	0.271	0.159	-0.240	43.0
	121-240	0.162	0.462	0.150	0.042	0.002	0.175	0.085	0.626	0.323	0.186	-0.259	41.2
	241-360	0.153	0.457	0.122	0.062	0.003	0.153	0.081	0.618	0.290	0.165	-0.233	36.7
	1-240	0.148	0.471	0.139	0.040	0.003	0.182	0.075	0.581	0.272	0.147	-0.219	63.3
	241-480	0.144	0.454	0.125	0.051	0.002	0.173	0.083	0.516	0.244	0.135	-0.204	61.0
	1-480	0.143	0.458	0.132	0.045	0.001	0.193	0.083	0.502	0.237	0.122	-0.201	82.3
	481-960	0.138	0.445	0.144	0.054	0.002	0.167	0.076	0.431	0.206	0.104	-0.221	83.2
	1-2100	0.135	0.436	0.123	0.066	0.002	0.178	0.080	0.399	0.203	0.114	-0.216	158.
SD	1-120	0.041	0.062	0.052	0.037	0.003	0.078	0.028	0.185	0.113	0.087	0.092	20.7
	121-240	0.054	0.052	0.057	0.039	0.006	0.084	0.040	0.176	0.150	0.114	0.100	18.2
	241-360	0.035	0.044	0.045	0.039	0.009	0.084	0.039	0.176	0.136	0.122	0.068	14.0
	1-240	0.040	0.055	0.055	0.036	0.011	0.070	0.028	0.175	0.101	0.077	0.073	20.4
	241-480	0.037	0.040	0.048	0.040	0.005	0.071	0.027	0.164	0.099	0.080	0.055	24.1
	1-480	0.033	0.040	0.047	0.033	0.001	0.059	0.028	0.141	0.087	0.070	0.047	26.1
	481-960	0.030	0.033	0.049	0.030	0.006	0.062	0.024	0.106	0.078	0.069	0.052	25.0
	1-2100	0.025	0.029	0.036	0.025	0.003	0.049	0.023	0.096	0.063	0.052	0.041	51.5
Mean	Simulation parameters	0.14	0.44	0.115	0.04		0.17	0.080	0.38	0.19	0.11	-0.20
SD		0.04	0.04	0.06	0.02		0.06	0.002	0.06	0.06	0.06	0.06

Note. a=boundary separation, z=starting point, T_er=nondecision component of response time, η =standard deviation in drift across trials, s_z=range of the distribution of starting point (z), s_t = range of the distribution of nondecision times, v_H, v_L, v_V, and v_N are the drift rates for high, low, and very low frequency words and for nonwords respectively, and χ² is the chi-square goodness of fit measure. The number of degrees of freedom for the fits to data was 65 and the critical value of chi-square at the .05 level was 84.8. In the simulations, the drift rates were not correlated. The following were lower limits on parameter values: a, 0.07; η, 0.02; T_er, 0.25; s_t, 0.04, s_z, 1.8 the distance from the starting point to the nearest boundary. Separate sets of simulations were conducted with p_o 0 or 0.04. Each drift rate had the same random number added to it so if a subject had a high drift rate in one condition they had a high drift rate in the other conditions.

Results for Experiment 2

RTs shorter than 300 ms and longer than 4000 ms were excluded (about 2.7% of the data) from data analyses.

For the data for all the trials, for the high-, low-, very-low frequency words, and nonwords, accuracy was .95, .84, .72, and .89 respectively, mean RTs for correct responses were 609, 714, 767, and 730 ms respectively, and mean RTs for errors were 600, 735, 777, and 792 ms respectively. The minimum and maximum values of accuracy across subjects were 1.0 and .88, .96 and .57, .88 and .45, and .98 and .79 for the high-, low-, very-low frequency words, and nonwords respectively.

To examine practice effects and the number of trials needed for the diffusion model's parameters to have small SD's, eight groups of data were constructed: trials 1-120, 121-240, 241-360, 1-240, 241-480, 1-480, 481-960, and 1-2100. Figure 2 shows the means across subjects of the best-fitting parameter values. The wider error bars represent 2 SD's from the mean and the narrower ones, 2 SE's. The means and SD's are also given in Table 2.

Compared to Experiment 1, there is more variability in the estimates of the parameters and this is true even though there were more observations. There are two reasons for this: a larger range of individual differences and more variability because the starting point was estimated from the data; it was not fixed at z=a/2 as it was for Experiment 1.

There were only modest differences between the estimates for the first 120 trials and the estimates from all 2100 trials, mirroring the results from Experiment 1. The estimates from all the trials were only slightly lower than for the early trials for boundary separation and nondecision time, and the estimates were a little higher for drift rates for the low and very low frequency words and nonwords. The estimate for high frequency words was considerably higher due to no error responses for many of the subjects in the first few trials in that condition (leading to spuriously higher estimates). For all six parameters, the SD's and SE's were smaller with all the trials by up to half the value. The pattern of results was similar for all the parameters for the 1-240 group and the 1-480 group, but with reduced differences and smaller SD's and SE's relative to the 1-120 group.

The trends in model parameters as a function of practice (Figure 2 and Table 2) are similar to those from Experiment 1 but with slightly larger differences. Results show that there were small declines in nondecision time and boundary separation from the first block to later blocks. Drift rates for the high-frequency condition are higher for the 1-120, 121-240, and 241-360 groups and are higher than the drift rate for all the data. Also, the drift rates for the 121-240, and 241-360 low frequency groups are higher than the drift rate for all the data. For each of these conditions, 2 SE error bars do not overlap with those for all the data. This is because there are relatively few errors (and zero for some subjects) in these conditions, i.e., for a group with 120 observations, 60 are from word categories and of these, 20 are from each of the three frequency classes and so with a 5% error rate, there will often be zero errors. As discussed earlier, this leads to inflated estimates of drift rates. Two SE error bars for nondecision times and boundary separation for the 1-120, 121-240, and 241-360 groups do not overlap with the 2 SE error bars for all the data (trials 1-2100). But generally, the practice effects are relatively small (especially compared to individual differences).

Following the discussion for Experiment 1, the results of this experiment show that an individual subject could be identified as having a deficit relative to our undergraduate subjects if boundary separation was 1 SD above the 2 SD confidence limit, which, for parameters from fits to all the data, is 0.21. For nondecision time, the value would be 530 ms. Two SD's below the means for drift rate were near zero for all conditions except for high frequency words. Therefore, differences between an individual and the undergraduate group could not be detected unless his or her drift rates were near zero (and there was a relatively large number of trials).

In contrast to detecting differences between an individual and the undergraduates, the SE's on the model parameters have enough power to detect even quite small differences between groups of subjects just as in Experiment 1.

Last blocks of trials

We also examined parameters from fits of the model to the last three blocks of trials, blocks of 80 trials for the numerosity experiment and 120 trials for the lexical decision experiment. This was done as a check to see if there were practice or fatigue effects at the end of the sessions. Boundary separation and nondecision times were a little larger than those for the fit to all the data (by less than .005 and 20 ms respectively) and drift rates were similar to the fits for the first three trial groups in Tables 1 and 2 (i.e., a little larger than those for fits to all the data). These results show that there are no dramatic differences between model parameters estimated from the last few blocks of trials and the first few blocks of trials.

The results of these two experiments are consistent with other studies that have used the diffusion model to examine practice effects. Petrov, Van Horn, and Ratcliff (2011), Ratcliff, Thapar, and McKoon (2006), and Dutilh, Vandekerckhove, Tuerlinckx, and Wagenmakers (2009) all found that boundary separation becomes smaller and nondecision time shorter with increasing amounts of practice but that there is little change in drift rates. These changes are largest between sessions.

Across-trial variability parameters

For both experiments, the across-trial variability parameters were relatively poorly estimated (Ratcliff & Tuerlinckx, 2002). The means of across-trial variability in drift rate, starting point, and nondecision time minus 2 SD's either include zero or are close to it. In fitting the model to the data for Experiments 1 and 2, we constrained the across-trial variability in drift rate to be in the range that has been observed in other applications of the model to similar experiments. If it were not constrained in this way, one SD in across-trial variability in drift rate would be 2/3 the drift rate. Generally, differences in the across-trial variability parameters between individuals or between populations cannot be determined without quite large numbers of observations.

Goodness of fit

Tables 1 and 2 show chi-square goodness-of-fit values for Experiments 1 and 2 using the chi-square method with 9 bins per distribution. Chi-square goodness of fit values are often used to assess how well diffusion models (and other two-choice models) fit data. Because the bins are determined by the data, that is, by the values of the RT quantiles, the statistic we calculate is not, strictly speaking, a chi-square. However, the statistic approaches a chi-square asymptotically (e.g., Jeffreys, 1961), and when the standard chi-square is compared to the chi-square based on quantiles, little difference is found between them (Fific, Little, Nosofsky, 2010).

In fitting the model to data, there are two constraints that a fitting method tries to satisfy. First, it needs to adjust the model parameters to adjust proportions (probability mass) across the bins between quantiles within each condition to match the proportions between the quantile RTs in the data. The second is to adjust parameters to move proportions so that the proportion of correct responses between data and predictions match and the proportion of error responses match.

For each of our data sets, using 5 quantile RTs, there were 12 bins (6 for correct responses and 6 for errors) in each experimental condition and the total probability mass in each condition summed to 1.0, reducing the number of degrees of freedom to 11. For a total of k experimental conditions and a model with m parameters, the number of degrees of freedom in the fit was therefore df = k(12 - 1) - m. For Experiment 1, the number of degrees of freedom was 14 and for Experiment 2, the number was 33. With 9 quantiles, there are 20 bins with 19 degrees of freedom per condition. Thus, for Experiment 1, the number of degrees of freedom was 30 and for Experiment 2, the number was 65.

Ratcliff, Thapar, Gomez, and McKoon (2004) examined the effect of moving a .1 probability mass from one quantile bin (so the .2 probability mass became .1) to another adjacent quantile bin (so the .2 probability mass became .3). They found that the increment to the chi-square for N=100, the increment was 13.3 (over half the critical value of 22.4) and for N=1000, the increment was 133 (five times the critical value). These increments mean that even relatively small systematic misses in the proportions are accompanied by large increases in the chi-square, especially as the number of observations increases.

The mean values of the chi-square for the lowest numbers of observations for the two experiments (the first three lines in Tables 1 and 2) are smaller than the mean chi-square from the chi-square distribution. If the data were generated from a chi-square distribution, the mean chi-square would be the number of degrees of freedom. This means that the model is overfitting the data, i.e., the model is producing fits that are accommodating random variations in the data from variability due to small numbers of observations. For all the data from Experiments 1 and 2, the mean values of the chi-square are 50 and 158 respectively, with critical values of 44 and 85. These represent a better estimate of how well the model is fitting the data because the number of observations is large and variations in the data that occur with small numbers of observations are minimized with a thousand observations or more as in these fits. For many data sets from a number of experiments, we have found that with numbers of observations per subject like the ones in the experiments here, the mean values of chi-square over subjects are typically between the critical value and twice the critical value. Thus, the quality of the fits for Experiments 1 and 2 are about the same as for previous experiments (e.g., Ratcliff, Thapar, & McKoon, 2003, 2004, 2010, 2011).

Power analyses for Experiments 1 and 2

Table 3 shows simple power analysis calculations using the means of the parameter values estimated from the data. We used SD's rounded up or down based on those from Tables 1 and 2, values that would correspond to a moderate number of observations, around several hundred. We assumed normal distributions of the populations (the distributions of parameter values across individuals are usually reasonably symmetric, e.g., Ratcliff et al., 2010).

Table 3. Power analyses showing the value of the parameter needed to detect a score outside the normal range 90% and 95% of the time.

Task	Parameter	Parameter value	SD in parameter value	Parameter for 90% correct	Parameter for 95% correct	SD in parameter value	Parameter for 90% correct	Parameter for 95% correct
Numerosity	a	0.110	0.030	0.187	0.208	0.045	0.225	0.258
	Ter	0.400	0.045	0.515	0.548	0.068	0.573	0.622
	vD	0.110	0.035	0.020	0	0.053	0	0
Lexical ecision	a	0.150	0.040	0.253	0.282	0.060	0.304	0.347
	Ter	0.450	0.040	0.553	0.582	0.060	0.604	0.647
	vH	0.460	0.122	0.147	0.058	0.183	0	0
	vN	0.200	0.050	0.072	0.036	0.075	0.008	0

Note. Parameter refers to the population parameter value, SD is the standard deviation in the population parameter value. a is boundary separation, T_er is nondecision component of response time, v_H, and v_N are the drift rates for high frequency words and for nonwords respectively. v_L and v_V (drift rates for low and very low frequency words) were not included because there was no value greater than 0 for either 90% or 95% correct detection.

To perform a power analysis, we needed an alternative hypothesis. We assumed another population (e.g., for which the subjects had deficits) and estimated the value of the mean to obtain 90% and 95% correct classification of individuals. Boundary separations were assumed to be larger, their nondecision times were assumed to be longer, and drift rates were assumed to be lower. In each case, the SD in the model parameters for this population was assumed to be the same as for the non-deficit population (i.e., the undergraduates in our experiments).

Given the means for the non-deficit population and the SD's for both, we found means for the deficit population so that a score selected from either distribution would be classified correctly 90% of the time and another set of means that would produce a 95% correct classification. Results are shown in Table 3 columns 5 and 6. We also did the same analyses with SD's for both groups 1.5 times larger than those in column 4 of Table 3 and these are shown in columns 7 and 8.

Results showed that for boundary separation and nondecision time, the differences between the values for the deficit population and the undergraduate population for 90 and 95% classification accuracy were large, but only as large as differences that have been found in previous studies with older adults. This means that these parameters are in the range that might be useful for classifying individuals. For example, for 90% correct classification with the smaller of the two SD's, the means for nondecision time and boundary separation are about the same as those for older adults (Ratcliff et al., 2001, 2004, 2010).

However, for drift rates, the classification would be much more difficult. Few of the conditions had drift rates that would separate the population with deficits from the undergraduate population. For the easy condition in numerosity and the low- and very-low frequency word conditions in lexical decision, the values of the drift rates to provide correct classification were negative, and so these conditions are not shown in Table 3. For drift rates for the difficult condition in the numerosity design and high-frequency words and nonwords in the lexical decision design, the drift rates to achieve 90% correct classification were low enough that performance would be near, but not quite at chance (except for high frequency words in lexical decision).

But for 95% correct classification and for the larger values of the SD in drift rates across subjects, performance would be near chance in a condition to detect a deficit. This suggests that the range of individual differences in drift rates in these tasks is so large that individuals with a deficit would have a large overlap with the normal range. This analysis is based on each parameter separately and shows that drift rates in single conditions are likely not to be useful detecting deficits in these tasks and designs. However, it may be possible to use multivariate methods to improve classification with combinations of several parameters (e.g., drift rates, boundary separation, and nondecision time) and, if subjects were tested on multiple tasks, combinations of measures across tasks might also improve classification.

Correlations Among Parameters

If estimates of the model's parameters from small numbers of observations correlate positively with estimates from large numbers, then small numbers can still be used to examine individual differences such as whether model parameters are correlated with measures such as IQ, reading measures, depression scores, etc.

The correlations in Table 4 show the consistency of parameter estimates across the various groupings of trials and numbers of observations for Experiments 1 and 2. For each parameter, the table shows the correlations between that parameter as estimated for the different groups of trials and that parameter as estimated from all the data.

Table 4. Correlations between model parameters for fits to small numbers of trials with model parameters from fits to all the trials.

Task	Trial block	a	Ter	v1	v2	v3	v4
Numerosity	1-80	0.278	0.675	0.247	0.292
	81-160	0.735	0.578	0.304	0.304
	161-240	0.687	0.532	0.260	0.306
	1-160	0.617	0.718	0.377	0.404
	161-320	0.773	0.628	0.546	0.438
	1-320	0.733	0.783	0.538	0.467
	321-640	0.877	0.852	0.725	0.543
Lexical Decision	1-120	0.704	0.515	0.357	0.526	0.474	0.467
	121-240	0.715	0.487	0.347	0.568	0.476	0.497
	241-360	0.809	0.670	0.359	0.584	0.654	0.447
	1-240	0.795	0.597	0.424	0.625	0.611	0.438
	241-480	0.871	0.760	0.363	0.609	0.731	0.394
	1-480	0.860	0.777	0.525	0.711	0.730	0.485
	481-960	0.889	0.802	0.408	0.722	0.844	0.473

Note: v₁=v_E and v₂=v_D for numerosity (v_E and v_D are the drift rates for the easy and difficult conditions respectively), and v₁=v_H, v₂=v_L, v₃=v_V, and v₄=v_N for lexical decision (v_H, v_L, v_V, and v_N are the drift rates for high, low, and very low frequency words and for nonwords respectively). a is boundary separation and T_er is nondecision component of response time.

As would be expected, the correlations increase as the number of trials increases. For boundary separation and nondecision time, the correlations are strong even with smaller numbers of trials, mostly above .5 for both tasks (except the 1-80 group for numerosity). The correlations for drift rates are lower, ranging from around .25 for smaller numbers of observations to over .5 for larger groups for Experiment 1 and from around .35 for smaller numbers of observations to over .7 for the larger groups for Experiment 2. There was one unexpected result: in Experiment 2, correlations for drift rates for nonwords are below those for low- and very-low-frequency words even though there were more observations for the nonwords. We have no explanation for this.

The conclusion from these correlations is that consistency in parameter values is good from small to large numbers of observations for boundary separation and nondecision time but not drift rates. Thus, if the aim is to examine differences among individuals or populations, this can be done for nondecision time and boundary separation with smaller numbers but more observations would be needed for drift rates.

Summary for Experiments 1 and 2

The data from Experiments 1 and 2 show that there is enough power in the numbers of observations provided by a 20- or 25-min. session of around 200-300 trials to give estimates of boundary separation and nondecision time that are sufficiently precise to detect differences between populations of subjects and to study individual differences. However, something different would be needed for drift rates, for example, a different task with a smaller range of drift rates, or multivariate methods that combine several model parameters.

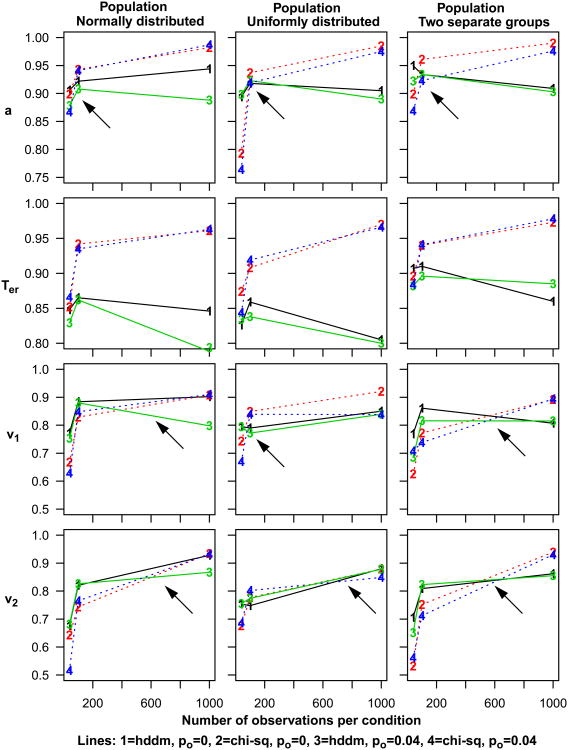
Simulation Study 1

For this study, we generated simulated data for 64 subjects and evaluated how well each of the eight methods for fitting the diffusion model reproduced the ordering of the values of the parameters across subjects. Simulated data were generated using the random walk approximation (Tuerlinckx, Maris, Ratcliff, & De Boeck, 2001). If the fitted values are strongly correlated with the generating values, then the fitted values can be used to investigate correlations between parameters of the model and subject variables such as age or IQ.

We simulated the data using the values of the diffusion model's parameters that best fit the data from Experiments 1 and 2. For Experiment 1, numerosity, the simulations were performed with 40, 100, and 1000 observations for each condition (easy and difficult). For Experiment 2, lexical decision, the simulations were performed either with 20 observations for each of the word conditions (high-, low-, and very-low-frequency) and 60 for the nonwords, or 200 for each of the word conditions and 600 for nonwords.

The values of the drift rates for the conditions were perfectly correlated. For the numerosity design, a random number was added to the easy condition drift rate and half the same random number was added to the smaller drift rate for each subject. For the lexical decision design, the same random number was added to each drift rate.

For each of the numbers of observations, data were simulated for the 64 subjects, once with 4% contaminant RTs and once without contaminants. For each subject, the value of each parameter was drawn randomly from a normal distribution for which the mean and SD across subjects (bottom of Tables 1 and 2) were rounded versions of those from Experiments 1 and 2. The contaminant RTs were obtained by adding a delay randomly selected from a uniform distribution with range 2000 ms (see Ratcliff & Tuerlinckx, 2002).

For the model to be fit successfully, it is best to have at least one condition with enough errors to provide a modest estimate of the RT distribution for errors. For numerosity, the drift rate for the difficult condition was low enough that there were enough errors for the simulations with the lowest number of observations (usually greater than 6) to constrain fitting the model. Similarly, for lexical decision, the drift rates were low enough for the low- and very-low frequency words to provide enough errors to constrain the model fitting.

For some of the 64 simulated subjects, the combinations of parameter values were not like those typically observed in practice. For example, large across-trial variability in nondecision time occurred with small nondecision time. However, we did not try to assess the plausibility of the various combinations; instead we let them vary independently to provide a wide range of combinations.

The metric for evaluating the fitting methods for this study was the correlation between the recovered parameter values and the parameter values that were used to generate the simulated data. We focus on the boundary separation, nondecision time, and drift rate parameters, parameters that have been used in understanding the effects of, for example, aging, development, and sleep deprivation, on performance. Generally, because the across-trial variability parameters are not well estimated, significant differences in them between individuals or groups are usually not obtained.

Results

For each of the eight fitting methods, Tables 5 and S1 show the correlations between the recovered values and the values used to generate the data for each simulated subject. For the numerosity design, Table 5 shows correlations for drift rates for the easy and difficult conditions for 1000, 100, and 40 observations per condition for 0% and 4% contaminants. Table S1 shows them for lexical decision for high-, low-, and very-low frequency words and nonwords, for 200 observations per word condition and 600 for nonwords, and for 20 observations per word condition and 60 for nonwords, each with and without contaminants.

Table 5. Correlations between parameters used to generate simulated data and recovered parameters for 8 fitting methods and three sets of numbers of observations for the numerosity discrimination design.

		N=1000, 1000				N=100, 100				N=40, 40
	Method	a	Ter	v1	v2	a	Ter	v1	v2	a	Ter	v1	v2
0% contaminants	HDDM	0.991	0.972	0.952	0.960	0.782	0.877	0.356	0.571	0.426	0.791	-0.129	0.154
	Fast-dm	0.971	0.971	0.932	0.926	0.893	0.910	0.843	0.774	0.878	0.851	0.573	0.605
	DMATout	0.913	0.888	0.810	0.921	0.755	0.808	0.265	0.591	0.493	0.719	-0.041	0.366
	DMATno	0.980	0.957	0.902	0.916	0.798	0.854	0.586	0.651	0.379	0.650	0.091	0.337
	MLH	0.987	0.977	0.937	0.894	0.954	0.923	0.835	0.647	0.923	0.890	0.743	0.665
	Chi9q	0.982	0.961	0.908	0.934	0.943	0.942	0.829	0.743	0.899	0.852	0.668	0.643
	Chi5q	0.979	0.961	0.921	0.951	0.948	0.917	0.822	0.746	0.899	0.871	0.650	0.636
	EZ	0.976	0.928	0.926	0.929	0.896	0.804	0.866	0.798	0.821	0.745	0.741	0.670
4% contaminants	HDDM	0.667	0.939	0.602	0.752	-0.126	0.880	0.181	0.360	0.478	0.790	0.089	0.332
	Fast-dm	0.946	0.968	0.786	0.838	0.876	0.859	0.783	0.684	0.873	0.847	0.629	0.546
	DMATout	0.930	0.930	0.674	0.838	0.525	0.771	0.221	0.494	0.352	0.666	-0.026	0.471
	DMATno	0.862	0.941	0.649	0.745	0.619	0.765	0.597	0.626	0.333	0.626	0.115	0.405
	MLH	0.975	0.975	0.844	0.830	0.894	0.872	0.755	0.636	0.763	0.862	0.599	0.613
	Chi9q	0.987	0.963	0.910	0.932	0.941	0.935	0.848	0.765	0.867	0.866	0.629	0.516
	Chi5q	0.967	0.938	0.854	0.903	0.930	0.907	0.807	0.786	0.835	0.858	0.691	0.594
	EZ	0.804	0.760	0.766	0.849	0.675	0.640	0.814	0.778	0.643	0.575	0.611	0.623

Note: DMATout was the DMAT method with contaminant correction, DMATno was the DMAT method with no contaminant correction, MLH was the maximum likelihood method, chi9q and chi5q were the chi-square methods with 9 and 5 quantiles respecitvely. a is boundary separation, T_er is nondecision component of response time, v₁ and v₂ are the drift rates for the easy and difficult conditions respectively.

Because the EZ method can fit only a single condition at a time, we fit it separately for correct responses for each condition of each experiment and then averaged the values of boundary separation and nondecision time.

For the numerosity design, for the simulation with 1000 observations per condition and no contaminant RTs, all of the fitting methods produced parameter values that were highly correlated with the generating values, above .9. With only 40 or 100 observations, fast-dm, MLH, the two chi-square methods, and EZ had correlations above .6, but HDDM and DMAT did considerably worse, with correlations dropping nearly to zero when there were only 40 observations per condition. The low DMAT correlations for low numbers of observations are expected because DMAT does not use error RTs to constrain parameter estimates when the number of errors is less than 11.

With 4% contaminant RTs and 1000 observations per condition, the two chi-square methods and the MLH method produced correlations of greater than .83 for all four parameters, fast-dm produced correlations above .78, and EZ produced correlations above .76. DMAT (with and without correction for contaminants) produced correlations above .86 for boundary separation and nondecision time, but the correlations for drift rates dropped substantially to around .6. HDDM produced correlations for boundary separation of .67, for nondecision time .94, and drift rates, .60 and .75. In each of these cases, the correlations were lower than when there were no contaminants.

With 4% contaminant RTs, for 100 and 40 observations per condition, the two chi-square methods and the MLH method produced correlations greater than .63, fast-dm produced correlations above .54, and EZ produced correlations above .57. For HDDM and the two versions of DMAT some correlations were near zero.

To summarize, the MLH method, the two chi-square methods, and fast-dm were a little superior to the EZ method because they produced higher correlations between recovered parameter values and values used to generate simulated data across all combinations of numbers of observations and did so whether there were contaminants or not. These methods all produced higher correlations than the two DMAT versions and HDDM, each of which produced some correlations near zero.

For the lexical decision design, the correlation results mirror those for the numerosity design with one exception: HDDM's correlations were competitive and often exceeded the correlations for the chi-square and MLH methods (see the supplement).

Fixing across-trial variability parameters

The EZ diffusion method assumes no across-trial variability in model parameters. This would be equivalent to fixing these across-trial variability parameters at zero in the other model fitting methods. By fixing across-trial variability parameters, the model might avoid some of the instability produced when model parameters trade off and become extreme when the number of observations is small. This may be part of the reason the EZ method performs quite well in the simulations presented above and in van Ravenzwaaij and Oberauer (2009).

Rather than fixing these across-trial variability parameters at zero, we fit the model to group data and then fixed these parameters at the values from the group fits for the two chi-square methods for all the combinations used in the numerosity and lexical decision designs as in Tables 5 and S1. We found that in almost every case, the correlations for boundary separation, nondecision time, and drift rates were lower than for the chi-square method presented in Tables 5 and S1, namely, with the range of parameter values restricted but free to vary over a plausible range. Thus, fixing the across-trial variability parameter values at their group means did not improve recovery of the parameter values. (We see a similar issue later with the hierarchical diffusion model in which across trial variability parameters are set to the same value across subjects).

Summary

Overall, the MLH, both chi-square methods, and fast-dm methods were robust to contaminants in the data and low numbers of observations. The correlations between recovered parameter values and generating values were moderate to high.

EZ performed somewhat worse, especially with contaminants (Ratcliff, 2008). It would perform even more poorly if some subjects had contaminants and others did not. However, the correlations in Tables 5 and S1 are not that much worse than for the other methods, and so we conclude that EZ might serve as a useful exploratory tool for examining individual differences.

DMAT did not perform as well as MLH, both chi-square methods, fast-dm, and EZ. One reason is that it does not use error responses when the number of observations is less than 11. If the tricks outlined in the earlier section were implemented, (e.g., using the median RT to construct two bins when the number of observation is low, excluding error conditions when the data appear spurious, and restricting the ranges of across-trial variability parameters), DMAT without contaminant correction for fast contaminants but with the correction for slow contaminants should perform equivalently to the two chi-square methods.

One striking difference between the results of the numerosity and lexical decision experiments is the behavior of the HDDM method. For numerosity, HDDM performed relatively poorly but in lexical decision, it performed at the top of the list. This may be because of the additional constraint imposed by having four conditions (i.e., four drift rates) in the lexical decision design instead of the two for the numerosity design.

Finally, Figure 3 shows sample correlations for two fitting methods, the chi-square method and the EZ method. The recovered values are plotted against the generating values for the numerosity design with 40 and 1000 observations per condition. We chose the examples presented in Figure 3 to illustrate what correlations of the sizes presented in Tables 5 and S1 look like and to illustrate biased parameter recovery but with a high correlation (e.g., the EZ method with 4% contaminants N=1000).

Figure 3.

Plots of parameter values recovered from fitting the diffusion model to simulated data from Simulation Study 1 plotted against the model parameters used to generate the simulated data. Plots are for boundary separation, nondecision time, and the highest drift rate for the numerosity design with 1000 observations and with 40 observations per condition. The different columns are for the chi-square method with 9 quantiles and the EZ method with either 0 or 4% contaminants. The correlations are shown in the top right corner of each plot and the diagonal line has slope 1 and intercept zero.

Simulation Study 2

In Simulation Study 1, we examined whether the eight fitting methods produced the same ordering of parameter values across subjects as the ordering that was used to generate the simulated data and we did this irrespective of whether the fitted values were biased away from the generating values. In this study, we looked at the accuracy of the fitting methods. For each set of parameter values, described below, we generated 64 sets of simulated data and fit the model to them for each of the methods.

The first question was whether and how much the means of the recovered values deviate from the generating values. If the bias for one parameter is consistent across combinations of all the other parameters, then there are few if any negative consequences (e.g., it would not matter if all the boundary separation parameters were estimated to be 80% of the true value; they would all line up the in the same way). If the bias varies as a function of the values of the other parameters, then it is necessary to assess how large the degree of bias is and do so for different numbers of observations. If bias is reduced as the number of observations increases, then the number of observations appropriate for a specific application must be determined.

The second question was how tightly the recovered parameter values cluster around their mean, that is, what are their SD's. It is especially important to examine this when the number of observations is low in order to detect whether there is sufficient power to test empirical hypotheses.

If the mean of the recovered values is unbiased, then the better estimation methods are those that produce smaller SD's. When the mean is biased, its SD might be smaller than when the mean is unbiased. Sometimes an application may be better served by a biased mean with a smaller SD than an unbiased mean with a larger SD or vice versa (unless the bias changed with the value of the parameter as we see for the EZ method below).

To examine bias and variability in recovered parameters, we simulated data for the numerosity and lexical decision designs using the values of the parameters shown in Table 6. These are representative of the ranges of mean values over subjects that were obtained in Experiments 1 and 2 and in other published sets of data (e.g., Matzke & Wagenmakers, 2009; Ratcliff, 2013). For boundary separation, there were two values: 0.1 is a little more than might be obtained under speed instructions (0.08 would be the smallest) and 0.2 is a little less than might be obtained for older adults (0.25 might be the largest). Nondecision time and across-trial variability in it were held constant across the simulations because nondecision time is simply an additive constant to RTs and variability in nondecision time has effects mainly on the leading edge of the RT distribution (Ratcliff, Gomez, & McKoon, 2004).

Table 6. Parameter values used in simulations to examine accuracy and bias in parameter recovery.

Simulation	a	Ter	η	sz	st	z/a	v1	v2	v3	po
Set 1	0.1	0.4	0.1	0.02	0.15	0.5	0.2	0.1		0.00
	0.2		0.2	0.06						0.04
				0.08
Set 2	0.1	0.4	0.1	0.02	0.15	0.3	0.2	0.1	-0.2	0.00
	0.2		0.2	0.06		0.5				0.04
				0.08		0.7

Note. The parameter sets are produced by the combinations of the parameters, a, η, z/a, and p_o. The combinations involving s_z depend on the values of a and z/a. For parameter set 1, when a is 0.1, s_z is 0.02 or 0.06, when a is 0.2, s_z is 0.02 or 0.08. For parameter set 2, for all combinations of the other parameters, one set has s_z=0.02. When z/a=0.5 and a=0.1, one parameter set has s_z=0.08 and when z/a=0.5 and a=0.2, another parameter set has s_z=0.08. When z/a=0.3 or z/a=0.7, the only value of s_z is 0.02.

Across-trial variability in drift rate had two values and across-trial variability in starting point had two or three values (the larger value differed depending on the boundary separation). The proportion of contaminants was set at zero or .04.

For numerosity, the drift rate for the easy condition was (v=0.2) and for the difficult condition it was (v=0.1). The larger value of drift rate was lower than that in the experimental data in order to produce errors in most of the combinations of parameter values. There were two values of across-trial variability in drift rate, η=0.1 and 0.2. In this design, the starting point is symmetric between the two conditions because large responses to large stimuli are grouped with small responses to small stimuli (thus z=a/2). The range of across-trial variability in starting point is limited by the boundaries. When a was 0.1, the values of s_z were 0.02 and 0.06 and when a was 0.2, the values were 0.06 and 0.08. Altogether, there were 16 combinations of parameter values.

For lexical decision, there were three conditions: one with a relatively high value of drift rate (v=0.2, high-frequency words), one with a lower value (v=0.1 low-frequency words), and one with a negative value (v=-0.2, nonwords). (We did not use a fourth condition as in Experiment 2 and Simulation Study 1 in order to reduce the time it took to fit the simulated data; for some methods, this saved a day of computation time.) In this design, the starting point, z, is a free parameter so it is fit along with the other parameters. In some experiments, the proportion of choices is manipulated and this produces a bias in starting point (Leite & Ratcliff, 2011; Ratcliff, 1985). To represent such manipulations, we used three values of z: halfway between the boundaries, z/a=.5, closer to one of the boundaries z/a=.3, and closer to the other boundary, z/a=.7. Across-trial variability in starting point was the same as for the numerosity simulation, 0.02 and 0.06 when a was 0.1 and 0.06 and 0.08 when a was 0.2. Boundary separation, across-trial variability in drift rate, and proportion of contaminants had the same values as in the numerosity simulation. The total number of combinations was 32.

For each of the combinations of parameter values for the two designs, 64 sets of simulated data were generated. For the numerosity design with two conditions, data sets had 40 observations per condition, 100 observations per condition, and 1000 observations per condition. One thousand per condition would be about the number for a 50 min. session of data collection. For the lexical decision design, data sets had 30 observations for two conditions and 60 for the third, and 300 observations for two conditions and 600 for the third. A total of 1200 observations is about the number for a 35 min. session.

Our implementation of the MLH method was not efficient and very slow (it would have taken several weeks for 64 sets of fits with large numbers of observations in the two studies). To rewrite it to be efficient would have taken considerable effort. Also, parameter recovery differed little between the chi-square method and the MLH method in the first simulation study, so the results for this study should be similar to those for Study 1. For these reasons, we did not test the MLH method in this study.

Results

Tables of the means of the best-fitting parameters and their SD's for all 48 combinations of parameter values and all seven fitting methods are given in the online data supplement. Figures 4 and 5 show, in a concise way, how well the fitting methods recovered the values of the generating parameters for the numerosity design. Figure 4 shows the results for 1000 observations per condition for the 16 parameter combinations for the numerosity design and Figure 5 shows them for 40 observations per condition.

Figure 4.

Plots of boundary separation, nondecision time, and two drift rates for the numerosity design with 1000 observations per condition in Simulation Study 2. Each row shows a different fitting method. On the x-axis is plotted the mean of the parameter values and on the y-axis, in a horizontal row at the value of the parameter used to generate the simulated data is plotted 1 SD error bars. The thin vertical line represents the values used to generate the simulated data. Movement away from the vertical line on the x-axis represents bias in the recovered parameter values and a large spread of the error bars represents high variability in the recovered parameter values. There are two values of boundary separation and two values of drift rate, hence the two vertical lines and the vertical separation of the points.

Figure 5.

The same plot as in Figure 4, but for the numerosity design with 40 observations per condition in Simulation Study 2. The DMAT results had SD's that overlapped zero and so are not shown.

Each panel in the figures shows the results for one parameter for one fitting method. The x- and y-axes represent the parameter's possible values and the vertical line on the x-axis is the value used for generating the data. The circles plot the means of the recovered values across the 64 sets of simulated data, one mean for each of the 16 combinations of the generating parameters. The means form a horizontal line at the generating value and one SD distance above and below the line is shown by the error bars. Plotting the results in this way makes the results easy to grasp visually, a necessity because there is a total of 36 panels in the two figures (with 48 more in the lexical design in the supplement). Consider two examples.

First, for the values of v₁ and v₂ recovered by the 9-quantile chi-square method (the top right panel in Figure 4), the vertical lines show the generating values, 0.1 and 0.2. For both, the 16 dots, one for each combination of parameters, lie almost entirely on top of each other, which means that they vary little across the combinations of parameters. They also lie on top of the generating value, which means that they are not systematically biased away from it. The variability in each of the 16 means (one SD error bars in the y-direction) is small; the one SD error bars cluster tightly around their means.

Second, consider the HDDM method for large numbers of observations in the fourth row of Figure 4. Many of the means are clustered more tightly around the generating mean than for the chi-square example. However, for both boundary separation and drift rates, there are a few outliers that have means up to twice as large as the values used to generate the 64 sets of simulated data (the points are shifted to the right of the lines). These also have quite large standard deviations (large error bars). This occurred in both the numerosity and lexical designs (see the Supplementary Figure S1) and were primarily from conditions with the small value of boundary separation and 4% contaminants. These deviations are not due to just a few extreme values, but they occur because of misses in many of the values for fits to the 64 simulated data sets. Thus, for a few parameter combinations, HDDM produces large biases in boundary separation and drift rates. However, for simulations with the low number of observations, HDDM shows less bias and smaller SDs than the other methods (Figure 5 and S2).

For the simulations with 1000 observations per condition, the chi-square methods and fast-dm did well, with modest biases with both larger and smaller numbers of observations. The EZ method produced biased values of parameters, especially when there were contaminants. Estimated drift rates were as low as half their generating value and nondecision times were as low as 250 ms instead of 400 ms. The SD's in the EZ parameter estimates are small, so the EZ model provides highly consistent estimates of the parameter values but these can be very wrong. DMAT without contaminant correction produced relatively unbiased values, but with SD's larger than the best methods. DMAT performed poorly relative to the other methods with contaminant correction.

For the simulations with 40 observations per condition, means of the parameters were generally farther from their true values than for the results with 1000 observations per condition and the SD's were larger. The chi-square methods produced parameter values that were biased toward larger values than the true values and fast-DM produced values that were biased toward smaller values. HDDM produced smaller biases and smaller SD's than the chi-square and fast-dm methods for values of boundary separation and nondecision time. The HDDM estimates of drift rates were biased to values larger than the true values (the biases were similar to those for the chi-square method) and the SD's were somewhat smaller than those for the chi-square and fast-dm methods. EZ's recovered values were again far from the true values. For DMAT, recovered parameter values were off the scale of those shown in the figures and plus and minus 1 SD included zero and extended outside the ranges shown in the figures for some combinations of parameters. For this reason, DMAT results were not plotted in Figure 5 and it is not possible to recommend DMAT when the number of observations is small. This is not a criticism of DMAT because it was never designed to work with this few observations.

For the best methods, the results for low numbers of observations showed that the boundary separation is quite well estimated for the 0.1 value (the SD's are quite small) but for the 0.2 value, some of the SD's are quite large (relative to, for example, individual differences, see Ratcliff et al., 2010). For drift rates, the SD's were particularly large: a plus or minus 2 SD confidence interval in the drift rate with a true value 0.2 often included zero. Also, 1 SD confidence intervals in nondecision time for the chi-square, fast-dm and HDDM methods have about a 100 ms range.

After the first draft of this article, we contacted Thomas Wiecki about the anomalous results for HDDM for the large number of observations. He suggested fixing the proportion of contaminants to 0.05 plus a longer burn-in (1500 trials). This improved the parameter recovery as is shown in Figure S6, but there are still biases in parameter estimates. These biases occur in the cases in which there are no contaminants in the simulated data. The larger boundary separation is underestimated and in the fits without longer burn-in, drift rates are underestimated. With these fixes, the results do not show the large deviations as in the first version. However, the recovered parameters have somewhat larger variability in many cases than the other methods illustrated in Figure 4.

We also tried fixing the proportion of contaminants at 0.0 and 0.02 with the longer burn-in. For recovery with the proportion of contaminants 0.02, some of the recovered mean drift rates (over the 64 simulated data sets) were 1.5 times the true value used to generate the simulated data. For the proportion of contaminants 0.0, some of the recovered mean drift rates were 2 times the true value. Thus, there is a problem that is largely fixed with the longer burn-in and with the proportion of contaminants fixed at 0.05. However, the puzzle is that this problem does not arise with lower numbers of observations.

Short Outlier RTs

Ratcliff and Tuerlinckx (2002) found that short outliers caused serious problems for maximum likelihood fitting methods. The reason is that in order to compute a likelihood for a short RT, there has to be probability density at that point. This means that the estimate of nondecision time has to be below that shortest RT if there is no across-trial variability in nondecision time, and if there is across-trial variability, then T_er-s_t/2 has to be smaller than the shortest RT. This produces extreme biases in parameter estimates. In contrast, quantile-based methods are robust to a small percentage of short outliers. For DMAT, contaminant correction methods did not work well; however, it is robust when the number of short outliers is small because it is quantile (or bin) based. Note that the MLH method without a contaminant model is even less robust (Ratcliff & Tuerlinckx, 2002).

We examined the effects of short outliers on the fast-dm and HDDM packages using simulations with a subset of parameters from the simulations above. Fast-dm does not have an outlier or contaminant model, but the Kolmogorov-Smirnov statistic used to evaluate it is robust to a few outliers. HDDM implements the same outlier model as in Ratcliff and Tuerlinckx but sets a lower limit at 0 instead of the minimum RT as Ratcliff and Tuerlinckx did. We now examine how well these methods worked in the face of short outliers.

We performed two studies with a relatively large number of short outliers (occasionally many more than this number can be obtained with uncooperative subjects). In the first, we used the first 4 combinations of parameter values in both the numerosity and lexical decision simulations and randomly replaced 5% of the RTs with a RT of 50 ms. In the second, we replaced the fastest 5% of responses with 50 ms. The latter would have no effect on quantile methods and the former would affect parameter estimates only modestly (because 5% of RTs, some of which are long, are replaced with shorter ones). We used three sets of numbers of observations for the numerosity design and two for the lexical decision design with 64 sets of simulated data for each of the combinations of parameters (just as for Simulation Study 2). The results were only minimally different for the two designs, so we present only the summary of both studies together.

For HDDM, boundary separation was underestimated by up to 15%. Nondecision time was overestimated by up to 60 ms over the 400 ms true value except when boundary separation was 0.2 and there were 1000 observations per condition; in this case, the estimate was too large by about 100 ms. Drift rates were overestimated with 40 observations per condition by up to 50% (estimates of 0.149 and 0.292 instead of 0.1 and 0.2) and they were underestimated by up to 25% with 1000 observations (estimates of 0.084 and 0.163 instead of 0.1 and 0.2).

For fast-dm, there was underestimation of boundary separation by up to 15% and generally underestimation of nondecision time by up to 30 ms (though in some cases there was overestimation by up to 20 ms). Drift rates were underestimated for all but one case by up to 25% (0.073 and 0.146 instead of 0.1 and 0.2). These results show that fast-dm and HDDM are not very robust to 5% short outliers.

The fact that fast-dm and HDDM were not robust to 5% short outliers means that more than a very small proportion of short outliers is likely to be a problem. It is important that experimenters examine data and exclude non-cooperative subjects and/or short outliers. If short outliers are eliminated either experimentally or by eliminating responses or non-cooperative subjects, then we do not have to worry about problems with fast-dm and HDDM. In contrast, the quantile based methods have the benefit of being robust for a few percent (under 10%) short outliers and so parameter estimates are not affected even if these outliers are not eliminated.

The supplementary information provides a discussion of DMAT warning messages that flag potential poor fits or suspect parameter estimates. If one is using DMAT, then these should be taken seriously and reported. Two variants of the EZ method are also evaluated and discussed in the supplement using simulated data from the numerosity and lexical decision designs. The conclusion is that neither can be recommended.

Simulation Study 3: A Hierarchical Bayesian Diffusion Model

Hierarchical models assume that the values of parameters for individual subjects come from a distribution of values across some group of subjects. Individuals' values and the group values are estimated simultaneously; the group sits hierarchically above the individuals. To the degree that the subjects are similar to each other, variability in the group will be estimated to be small and this will constrain the individuals' parameters to be closer to the mean. The method allows an individual to be distinguished from the group if there are enough data and the difference between individual and group is large enough (see Farrell & Ludwig 2008; Vandekerckhove, Tuerlinckx, & Lee, 2011; Vandekerckhove, Verheyen, & Tuerlinckx, 2010; Wiecki, Sofer, & Frank, 2013).

Hierarchical Bayesian methods for fitting the diffusion model have been developed by Vandekerckhove, Tuerlinckx, and Lee (2011) and Wiecki, Sofer, and Frank (2013). The latter authors have made available a hierarchical package within HDDM. In their implementation, the parameter values for the group are drawn from specific distributions: normal for drift rates and nondecision times and Gamma for boundary separation.

Hierarchical methods have an advantage over non-hierarchical methods in that they can be used when the number of observations per condition is small, as small as the number of parameters in a model plus 1 (we briefly describe results from an example and present the full results in the supplement), but there are also other advantages and disadvantages. One is that the distributions of parameters assumed for the group (e.g. normal or Gamma) may not be their true distributions and so estimates of parameters can be biased. This is not a problem for non-hierarchical methods for which the parameter values of a group are simply averages of the individuals' values. Another advantage or disadvantage, especially with low numbers of observations, is that the estimates of parameters for individuals can be pulled toward the values for the group; this is termed “shrinkage.” This is an advantage when extreme parameter estimates are due to variability arising from small numbers of observations (Efron & Morris, 1977) and the hierarchical method pulls them back towards the true values. This could be a disadvantage when the aim is to identify sub-groups of individuals within a group, for example, when individuals with a deficit are mixed with individuals without deficits and shrinkage pulls the estimates toward the mean for the whole group. As we see below, except for very small numbers per condition, these issues are not problems with this diffusion model application.

In HDDM, across-trial variability in drift rates, nondecision time, and starting point and the proportion of contaminants are set the same for every subject. This is because with small numbers of observations, the differences produced by different values of these parameters in the function being minimized are small relative to variability in the data and Wiecki et al. (2013, p.3) suggest that this might lead to spurious results. In the simulations here, we allowed differences in across-trial variability among subjects in the simulated data as in real data, which results in misspecification in the HDDM hierarchical fitting method.

For Simulation Study 3, we compared the HDDM to the 9-quantile chi-square method using the numerosity design (two conditions differing in difficulty) with 40, 100, or 1000 observations per condition with no contaminants or 4% contaminants and 64 subjects. With a number of observations as large as 1000, hierarchical and non-hierarchical methods usually produce similar estimated parameters (e.g., Farrell & Ludwig, 2008). We used the same method of producing combinations of parameters as in Simulation Study 1, where the parameter values for each simulated subject were drawn from a normal distribution centered on a parameter's mean. For each combination, we simulated 64 subjects and fit their data by the two methods under three different distributions of parameters across subjects. We present one example with 54 of the subjects with one set of parameter values drawn from normal distributions and the other 10 with values drawn from normal distributions with larger boundaries and nondecision time and lower drift rates than for the other 54 subjects. This was to simulate two populations that might represent a normal and impaired group. If there is shrinkage, we would see an inability to discriminate the two populations. We also examined two other examples that are presented in detail in the supplement, one with normal distributions of parameters and one with uniform distributions of parameters.

Simulated subjects were drawn from two well-separated populations. For 54 of the 64 subjects, we used the means from the fourth row from the bottom of Table 1 and for the other 10 subjects, we used values from the second to last row of Table 1. SD's in the parameter values were from the last row of Table 1 (the SD's in the third row are from the other two simulations presented in the supplement).

The means of the generating parameters over subjects for the two groups were 0.11 and 0.20 for boundary separation, 375 ms and 530 ms for nondecision times, 0.3 and 0.1 for the easy condition and 0.1 and 0.0 for the difficult condition. These are large differences between the two groups, but not out of line with differences in age and IQ (e.g., the 54 subjects might come from a high IQ young adult group and the 10 subjects might come from a low IQ older adult group, Ratcliff et al., 2010).

Figure 6 shows the recovered values of the two drift rates, boundary separation, and nondecision time for the two methods for 40 observations per condition and 1000 observations per condition for the two methods (we use the results for the 100 observations condition later). We present the plots in a different way from the other plots to highlight the issue of shrinkage of the parameters (regression to the mean).

Figure 6.

Plots of the recovered values of parameters from the hierarchical fitting method and for the chi-square method for the numerosity design with parameters drawn from two distributions for 40 and 100 observations per condition and for 0 and 4% contaminants. Plotted on the y-axis are the recovered parameter values minus the values used to generate the simulated data (i.e., the residuals) offset by the amount represented by the thick horizontal lines. The circles are for the chi-square method and the crosses are for the hierarchical method. The dashed lines are regression lines for the two methods (shrinkage of model parameters results in a negative slope). The numbers at the top of each plot are the correlations between the recovered values and those used to generate the simulated data for the two methods.

Plotted on the x-axis are the values of the parameters from which the simulated data were generated. Plotted on the y-axis are the recovered values minus the value used to generate the simulated data (i.e., the plots show the residuals). If there is no shrinkage, the plots will be horizontal, but if there is shrinkage, the lines will have negative slope. Figure 6 shows the results from the hierarchical method and chi-square methods. To separate the values for the two methods, they were offset by adding a constant for the chi-square method (the circles in the figure) and subtracting a constant for the hierarchical method (the x's in the figure). Any other biases in the recovered values will be seen as systematic deviations between the points and the offsets between the dotted regression lines and the offset shown by the horizontal solid lines. The residual vertical spread in the recovered parameter values can be used to compute the SD in the recovered parameter values. The correlations between the recovered values of the parameters (not the residuals) and the values used to generate the simulated data are shown in the headings of the panel.

For both the chi-square and HDDM methods, the recovered parameters for the two groups of simulated subjects were as well separated in the recovered parameters as they were in the generating values, i.e., the two groups were visually separate. For boundary separation and nondecision time, there are groups of 10 points at the right ends of the plots and for drift rate they are at the left ends of the plots.

We noted earlier the concern that the HDDM method would lead to shrinkage, pulling the recovered values for individual subjects toward the values for the group. If this was extreme, the parameters for the two groups of subjects would merge so they could not be discriminated and the hierarchical method would not be useful for applications in which discrepant individuals were to be identified. However, for these simulations this did not occur and the groups were separated. There was some shrinkage particularly in the higher drift rate condition (also in Figures S3 and S4), the dashed line has negative slope, but this does not seem to affect the ordering of the drift rates and does not cause the two groups to merge.

For 40 observations per condition, the correlations between the recovered model parameters (boundary separation, nondecision time, and drift rates) and the parameters used to generate the simulated data are higher than for the chi-square method which shows that HDDM provides superior parameter recovery for all the parameters. But for 1000 observations per condition, the chi-square method provides the higher correlations and better parameter recovery.

Summary of the Hierarchical Model Results

Figure 7 plots the correlations between the best-fitting recovered values and the true values for boundary separation, nondecision time, and the two drift rates as a function of the number of observations. The first column shows the correlations from the case when the distributions of the parameters for the group were assumed normal, the second column for when they were assumed uniform, and the third column for when the distributions were assumed to be normal and the simulated subjects came from two groups with different mean values of each parameter for the two groups. For Figures S3, S4, and 6, we reported results for 40 and 1000 observations per condition; here we include the correlations for 100 observations per condition.

Figure 7.

Plots of correlations between the recovered values of parameters and the values used to generate the simulated data as a function of the number of observations for the three distributions in hierarchical modeling study for the two methods, and for simulated data with 0% and 4% contaminants. The oblique arrows represent the approximate average number of observations at which the correlation for the chi-square method becomes larger than that for the hierarchical method.

The figure shows approximate cross-over points between the two methods, that is, the points at which correlations switch from having higher values for the HDDM method to higher values for the chi-square method. The oblique arrows in the figure point to the cross-over points. For boundary separation, the cross-over is somewhere around 100 observations per condition, for drift rates, the cross-over is several hundred observations, but for nondecision time, there is no cross-over and the chi-square method produces higher correlations for all sample sizes. These conclusions about the points at which the cross-overs occur are qualified by having only three numbers of observations per distribution type. However, the important finding is a qualitative one, that the correlations do cross-over.

In all these simulations with the hierarchical model (HDDM) used here, the model is misspecified because it assumes all the across trial variability parameters and the proportion of contaminants have the same value across subjects. This misspecification explains why the standard chi-square method outperforms the hierarchical method for larger numbers of observations. If this misspecification were eliminated by fitting a hierarchical model with all parameters free to differ, the hierarchical model may well outperform standard methods in all situations.

More generally, for educational or neuropsychological testing, if the hypothesis involves drift rates (evidence from the stimulus or memory), and there are a low number of observations (on the order of 100 or 200), then this implementation of hierarchical method would be the superior method. But if there were larger numbers of observations, and all parameters were of interest, then standard methods might be just as good or even superior. It is important to note however that shrinkage is likely not to be a problem in identifying subjects with deficits in hierarchical HDDM in the design studied here (with the caveat that results may differ in different designs).

In the supplement, we present results from the hierarchical model fit to simulated data with five observations for each of the easy and hard conditions in the numeracy design for the three distributions across subjects (this was suggested by Joachim Vandekerckhove). Results showed extreme shrinkage in model parameters, especially drift rates. But the correlations in model parameters between the recovered parameter values and ones used to generate the data were high for some of the model parameters.

Using very few observations has been a selling point of hierarchical models, and this set of simulations shows what happens with the diffusion model with very few observations. As noted earlier, if all that was available was a few trials with no practice, then results would be suspect because performance could change radically over 10 or 20 trials with practice and warm up effects. Note, this is not an issue with the hierarchical model, it is a problem with the data, i.e., the hierarchical model would not solve the problem of a very few trials. A method of avoiding this problem is to test subjects on a different two-choice task for a few minutes with the same response keys (e.g., lexical decision if the target task was a memory task).

General Discussion

The studies in this article were designed to examine how well parameters can be recovered when the diffusion model is applied to data of the kinds that might be obtained from studies in practical domains such as neuropsychological, clinical, and educational testing. With both experiments and simulations, we explored under what circumstances differences between individuals and groups can be detected and under what circumstances differences between groups can be detected. We also used simulation studies to examine the ability of various fitting methods to recover individual differences and parameter values.

Experiments 1 and 2 provided estimates of the parameters for individual undergraduate subjects for a numerosity discrimination task and a lexical decision task. We used the parameters from fitting all the data and subsets of the data to examine power. Results showed that differences in nondecision time and boundary separation might be large enough to detect discrepant individuals, but individual differences in drift rates were so large that drift rates would have to be near zero for most of the conditions to detect that an individual was discrepant. The wide range of drift rates is a result of the wide range of performance of undergraduates in these experiments.

We also examined whether the recovered parameters changed with practice from early to late blocks of data and from smaller numbers of observations to larger numbers. Moving from a few observations (80 or 120) to a large number (over 1000) changes the SD's in individual differences by about a factor of 2. The SD's in model parameters for each fit decrease approximately with the square root of the number of observations. But the SD's across subjects (in Tables 1 and 2 and Figure 2) decrease less because the SD's represent both individual differences, which are not reduced by increasing the number of observations, and variability in model parameter estimates, which is reduced by increasing the number of observations.

In the Simulation Study 1, simulated data were generated with a random selection of parameter values from the ranges seen in the two experiments. Then the various fitting methods were applied to those simulated data and correlations between the recovered parameter values and generating values were used to examine how well the methods recovered individual differences. We found that the two chi-square methods, fast-dm, and the maximum likelihood methods produced the highest correlations for the simulations that differed in the number of observations and the presence or absence of contaminants. HDDM was the best performing with low numbers of observations, but produced some poor correlations for larger numbers of observations. DMAT performed less well than the other methods when there were low numbers of observations (because it does not use error RTs when the number is less than 11) and it performed poorly when the contaminant correction methods were used. The EZ method was competitive with the other methods when there were no contaminants, but with contaminants, correlations were lower.

The correlations in Simulation Study 1 show the upper limit on correlations with the range of individual differences observed in the two experiments. For experiments with different designs, the results from this study could be used as a guideline if the designs were not too different, otherwise a new study would be needed. For the better of the fitting methods, if there are a couple of hundred observations and two conditions (with starting point symmetric between the two boundaries), as in the numerosity design, correlations between recovered model parameters and those used to generate the data were generally above .9 for boundary separation and nondecision time and above .75 for drift rates, even in the worst case with 4% contaminants. For the lexical design, even with only 120 observations, correlations for boundary separation and nondecision time were above .85 and for drift rates above .6. These values are large enough so that with 10-15 minutes of data collection, SD's in model parameters will be low enough so that any relationships between other measures (IQ, reading or numeracy ability measures, etc.) will be able to be detected.

We have performed experimental studies with similar designs that have produced large individual differences and correlations in the .5 to .6 range across tasks in model parameters (McKoon & Ratcliff, 2012, 2013; Ratcliff, et al., 2010, 2011; Ratcliff, Thompson, & McKoon, in press). These reinforce the claim above that with larger numbers of observations, recovery of model parameters is good enough (i.e., the relative order as reflected in high correlations) to produce strong meaningful relationships (correlations) even between different tasks.

The results from Simulation Study 2 show the means and SD's in model parameters recovered from 64 sets of simulated data with the same parameter values for a number of different parameter sets for two designs with five different numbers of observations. These show the biases in model parameters (i.e., bias from the generating value) and the SD in the recovered parameter values. Results showed that with large numbers of observations, model parameters were recovered by the better methods with low bias and low SD's. Some of the methods (DMAT with contaminant correction, EZ, and HDDM) had discrepant values for some parameter combinations. Some of the methods that were better performing for individual differences produced consistent biases in model parameters, and these differed as a function of the parameter values. For example, fast-dm for the lexical design with the large numbers of observations had boundary separation vary between .15 and .2 when the value used to generate the simulated data was .2 (most of the methods have these kinds of biases). At the same time, some of the drift rates had a bias to low values (e.g., for nonwords, the correct value was .2 and the recovered values ranged from .1 to .2. The problem that this raises is that if the other model parameters differ, as in the simulations in Figures 4 and 5, especially by a large amount, no observed difference in boundary separation between two groups of subjects might reflect a real difference or vice versa.

For low numbers of observations, HDDM provided better parameter recovery than the other methods and did not show the discrepant values that occurred with the larger number of observations. The other methods showed similar biases as with large numbers of observations and as before, the DMAT method was not competitive. EZ showed some extreme biases with 4% contaminants.

We performed comparisons between the chi-square method and the hierarchical method for three populations of individual differences on model parameters and for three different numbers of observations. We used normally and uniformly distributed populations (presented in the supplement) and a population with two subpopulations (representing a normal group and a group with deficits in the main model parameters). For low numbers of observations, the hierarchical model outperformed the chi-square method, but when there were a large number of observations, the chi-square method outperformed the hierarchical method. This is because the HDDM implementation of the hierarchical method assumed that the across trial variability parameters and proportion of contaminants were the same across subjects whereas the simulated data were generated with differences across subjects (as in real data).

We had two initial main concerns with the hierarchical model. First, when the distribution of model parameters was not the same as the distribution assumed by the hierarchical model, individual differences may be compressed or distorted. In fact, this did not happen and the simulations with two populations showed good separation of the two groups. Second, the recovered parameters might be drawn to the mean (termed shrinkage). But this was not a problem even with only 40 observations per condition. Drift rates showed some shrinkage, but they were well separated and the ordering was maintained.

We then performed simulations with 5 observations per condition with the hierarchical model. With this few observations, none of the other methods would have produced anything meaningful. Individual differences in boundary separation and nondecision time were recovered to some degree, but there was extreme shrinkage in drift rates (the model tended to recover values of drift rates that differed little from the mean). With two populations, estimates of nondecision time shrunk but the drift rates for the two populations were better recovered. With this few observations, there are other problems, especially in clinical or neuropsychological populations and experiments with so few observations would likely produce nothing meaningful. Besides the problems with poor parameter estimation, the first few dozen trials may involve understanding instructions and learning how to perform the task, and even after this, practice and warm up effects would likely distort the results.

Contaminants and Outliers

There are two kinds of contaminants in the tasks to which the diffusion model is usually applied, fast guesses and slow responses. Slow responses can just involve a delay in processing or could be guesses. In some paradigms, it is easy to see if there is a moderate proportion of fast random guesses if there is an easy condition in which accuracy is at ceiling. If accuracy in that condition is 98% correct, then no more than two percent of the responses could be guesses. It might be assumed that the proportion of guesses differs as a function of experimental condition (for example, with more guesses for difficult conditions), but such an assumption is rarely made.

Another way to eliminate fast guesses from data for some paradigms is to exclude responses that occur before the point at which accuracy starts to rise above chance (this is similar to the fast error correction method in the DMAT package). In our laboratory, we use such a cutoff, but if a subject has more than a few fast guesses, we usually treat them as non-cooperative (with the instructions) and eliminate them from the experiment. This occurs sometimes with undergraduates participating for course credit but rarely for paid subjects. We reduce such non-cooperation experimentally by presenting a message, for example for 1-2 seconds, saying “too fast” if the RT is less than 200 ms. Often subjects that are fast guessing are trying to get out of the experiment quickly, and the delay seems to produce regular responding.

Slow outliers that are not guesses can be the result of a moment's inattention, a scratch of the head, an interruption from a cell phone call, etc. A problem with such outliers is that some will not lie outside the normal range, e.g., those with a short delay and a fast decision process (that is why they are called contaminants rather than outliers). For fitting the model to data, it is assumed that processes with these delays can be represented by a uniform distribution that has a range from the minimum and maximum RT. Therefore RTs are a mixture of this uniform distribution and regular diffusion process responses. Ratcliff and Tuerlinckx (2002) generated simulated data with a random delay added to some small proportion of RTs produced from the diffusion model and showed that the mixture model recovered model parameters and the proportion of contaminants well. In an experiment with sleep-deprived adults, Ratcliff & Van Dongen (2009) found that under sleep deprivation, a moderately high proportion of responses for a few subjects were random guesses (because conditions with high accuracy in non-sleep deprived conditions dropped from say 97% correct to 85% correct in the sleep deprived condition). They modeled this case with a proportion of random choices with RTs represented by a uniform distribution with a range from the minimum and maximum RT.

The HDDM method, the fast-dm method, and the chi-square methods are quite robust to slow contaminants. Parameter recovery with 4% contaminants is good and the effects of a very few fast outliers are minimal. When there are 5% fast outliers, the recovered parameter values do not differ much from the parameter values used to simulate the other 95% of the data for the chi-square methods, but there are modest deviations of model parameters for fast-dm and HDDM. DMAT is less robust to slow contaminants and it performed more poorly than the other methods on most of the simulations from studies 1 and 2 above. The EZ method is not robust to slow contaminants (Ratcliff, 2008) and, because it is based on the SD in RTs, it is also not robust to fast contaminants.

Biases, Parameter Tradeoffs, and Over-Fitting

When applying a fitting method to data to uncover differences between individuals, success means that the recovered values are not biased away from their true values or are at least equivalently biased across subjects and conditions. For example, if the estimate of boundary separation were underestimated by the same amount for all subjects in an experiment, say by 20%, then questions about individual differences can be answered in the same way as if the parameter was unbiased. However, if the bias changed from one subject to another as a function of the other model parameters (or other things such as the proportion of contaminants) then systematic biases in estimation might be interpreted as individual differences. This would become important to investigate if parameter estimates were being used as an index of, for example, cognitive deficits.

One important problem with fitting any model with low numbers of observations is that the relatively high variability in data will lead to overfitting. Because model parameters are adjusted to get as close to the data as possible, extra high or low values of accuracy or RTs will be accommodated by some combination of extra high or low values of the parameters. For example, Ratcliff & Tuerlinckx (2002, Figure 7) examined the correlations among model parameters when one RT quantile was high by chance. Results showed that several model parameters were adjusted in fitting to accommodate the misfit in the data. This resulted in model parameters covarying with each other; across trial variability in drift rate, boundary separation, and drift rate correlated between .35 and .66. Such overfitting is signaled by low values of chi-square relative to the significance level (as, for example, for the first three trial groups with low numbers of observations in Tables 1 and 2). However, usually these tradeoffs are much smaller in magnitude than differences in parameter values across individuals.

The results reported here show in some cases less than perfect parameter recovery. This is in contrast to a view implied by Jones and Dzhafarov (2014). In their article, they argue that if the forms of the across trial variability distributions are unconstrained, then the models can exactly match any form of response proportions and RT distributions, hence rendering evidence accumulation models unfalsifiable. Smith, Ratcliff, and McKoon (2014) pointed out that this argument is based on making within-trial variability in the accumulation process zero and hence misrepresenting the stochastic diffusion model as a deterministic process.

Jones and Dzhafarov's (2014) argument then boils down to using a mapping between velocity, distance, and time. In a deterministic model, if every process travels the same fixed distance (from the starting point to the boundary), then every response time can be converted into a velocity (drift rate) by velocity=distance/time thus producing a one-to-one mapping between drift rates and RTs. To account for errors with such a deterministic model, it is necessary to assume complex bimodal distributions of drift, consisting of two unequally sized, asymmetric lobes (the probability mass in each corresponding to the proportion of responses of each type, see Figure 2 of Smith et al., 2014). Every different RT arises from a different value of drift and the drifts for correct responses and errors have opposite signs, because the only way the model can produce errors is when the sign of the drift is wrong. Because response probabilities and RT distributions vary from condition to condition, a different bimodal distribution of drift is needed for every condition of the experiment. The resulting model is complex and has some highly unintuitive properties. As stimuli become more discriminable and the task becomes easier, the asymmetry of the distribution of drift and the separation between its positive and negative lobes increases. To account for the finding that repeated presentation of the same stimulus can lead to different responses, the model needs to assume that the sign of the drift can vary from one presentation of the stimulus to the next and that the magnitude of the difference between drifts leading to correct responses and those leading to errors increases as the task becomes easier (i.e., error drift rates become more strongly negative).

In the standard diffusion model, mean drift rates are assumed to come from a unimodal distribution as they would if drift arises from summed evidence as in memory models (e.g., Murdock, 1982). Furthermore, in a few cases, neurophysiological data might address the distributions of drift rates. For example, single-trial EEG measures are consistent with unimodal distributions rather than bimodal distributions preferred by Jones and Dzhafarov (see Figure 2 D and E, Ratcliff, Philiastides, & Sajda, 2009).

Individual Differences

Experiments 1 and 2 provided estimates of model parameters and individual differences in them as a function of the number of observations used in model fitting. Figure 2 (and Tables 1 and 2) show that the SD's in the parameter values for boundary separation and nondecision time decrease by less than a factor of 2 going from 80 to 1200 observations or from 120 to 2100 observations. Drift rate SD's decreased by about a factor of 2. This can be attributed to a decrease in the SD in model parameters with more accurate recovery from the greater number of observations. Figures 5 and S2 show the SD's in model parameters for the lowest numbers of observations for simulated experiments similar to Experiments 1 and 2. The SD's in boundary separation and nondecision time even for the lowest numbers of observations in the simulations are less than the SD's for parameters recovered for fits to all the data in each experiment. Therefore, the SD's in model parameters from variability in data given the number of observations is smaller than the individual differences in model parameters. (Even if the SD in estimation were the same value as the SD in individual differences, the ceiling on the correlation would be reduced from 1 to only .72.)

To examine individual differences in model parameters across subjects, the choice of method (fast-dm, HDDM, chi-square) is not critical unless the method produces a few spurious results (e.g., HDDM, Figures 4 and S1). The loss in precision (larger SD) due to a less efficient but more robust fitting method could be easily outweighed by collecting data from more subjects. However, in most situations, the difference in results between an experiment with 40 and 50 subjects or 100 and 120 subjects will be not be large.

The conclusions are different for the task of attempting to identify individuals that may show a deficit relative to the normal range of processing. In these experiments, quite large differences between the individual and the population would be needed in boundary separation and nondecision time, differences as large as the mean difference between young and old adults (e.g., Ratcliff et al., 2010). Usually we would expect deficits to occur in drift rates, for example, poorer memory or perceptual processing for an individual relative to a control group. Results from Experiments 1 and 2 showed that drift rates would have to be near zero for a deficit to be detectable in these two tasks. There is one caveat to this and that is to collect data from a control group that has the same motivation as the experimental group. All the undergraduates in Experiments 1 and 2 are not guaranteed to be highly motivated and it is quite possible that some of the lower-performing subjects were non-cooperative at least on a proportion of trials. However, the data and model fits from the numeracy task in Ratcliff et al. (2010) produced similar results so the results here are probably typical of those that might be obtained from this task. Therefore, for detecting deficits, it is important to collect as many trials as possible given constraints of accessibility to the population and testing time (e.g., patients of some kind) and to use the best fitting methods, i.e., those with the lowest SD's and that do not produce spurious results.

In Experiments 1 and 2, differences in model parameters between the first few trials and all the data and also practice effects in model parameters from test block to test block were small. There is no guarantee that such results will be obtained for other populations. Undergraduate students probably adapt to a new task about as quickly as any group. Therefore, practice and training effects would have to be examined for any neuropsychological, clinical or educational population and an appropriate control group, especially if there is a limit on the number of observations that can be collected.

In some applications such as using emotional or threat words, or applications involving specific psycholinguistic constructions in text processing, there may be limitations on the number of critical materials that are available. In such applications, these critical materials are embedded in much longer lists of filler materials and there is usually no constraint on the number of trials from these fillers. (Often they are used to reduce the proportion of trials with critical materials and/or disguise the hypothesis.) Fitting the diffusion model simultaneously to the critical materials plus the filler materials increases the power on the critical materials (see McKoon & Ratcliff, 1986, 1992, 2012, 2013; Ratcliff, 2008; White, Ratcliff, Vasey, and McKoon 2009, 2010a, 2010b) because boundary settings and nondecision times are largely determined by the larger number of filler materials. This is an important methodological advantage in such applications (see the supplement for details).

There are some other features of the fitting methods that should be mentioned. First, HDDM has an application in which drift rate can be made a function of, for example, a brain measure such as EEG, fMRI, or some eye tracking measure. In this, drift rate is assumed to be a function of, for example, a EEG regressor and if the function is linear, the method allows the slope of drift rate versus the regressor to be estimated. Second, there are other Bayesian diffusion model tools, specifically a WinBUGS implementation in Vandekerckhove, Tuerlinckx, and Lee (2011) and a JAGS implementation in Wabersich and Vandekerckhove (2014). These allow diffusion model fitting to be implemented with minimal programming, but they do not provide a point and click interface. Third, the latest version of fast-dm has implemented both chi-square and maximum likelihood estimation methods, but this was made available after the simulations and fitting were done.

Recommendations for Software to use in Diffusion Model Fitting

When the number of observations is large, most of the methods produce parameter estimates that are reasonable. The exceptions are the EZ method that can be extremely biased in the presence of contaminants (though it is useful for exploration), DMAT with the default contaminant correction method, and HDDM fit to separate subjects with large numbers of observations and few conditions (though this package is still under development and upgrades appear regularly). With smaller numbers of observations, the quantile methods and fast-dm were reasonably robust, but HDDM was a little better. We found that the hierarchical diffusion method performed very well, and is the method of choice when the number of observations is small. But we would not recommend blindly applying any method to experiments with just a few dozen observations because the data may not be reliable enough because of start up issues, the potential for spurious observations, and practice effects. In general, for any application of the diffusion model, the quality of the data needs to be evaluated.