Computational models in the age of large datasets

Abstract

Technological advances in experimental neuroscience are generating vast quantities of data, from the dynamics of single molecules to the structure and activity patterns of large networks of neurons. How do we make sense of these voluminous, complex, disparate and often incomplete data? How do we find general principles in the morass of detail? Computational models are invaluable and necessary in this task and yield insights that cannot otherwise be obtained. However, building and interpreting good computational models is a substantial challenge, especially so in the era of large datasets. Fitting detailed models to experimental data is difficult and often requires onerous assumptions, while more loosely constrained conceptual models that explore broad hypotheses and principles can yield more useful insights.

Introduction

By nature, experimental biologists collect and revere data, including the myriad details that characterize the particular system they are studying. At the same time, as the onslaught of data increases, it is clear that we need tools that allow us to crisply extract understanding from the data that we can now generate. How do we find the general principles hiding among the details? And how do we understand which details are critical features of a process, and which details can be approximated or ignored while still permitting insight into an important biological question? Intelligent model building coupled to disciplined data analyses will be required to progress from data collection to understanding.

Computational models differ in their objectives, limitations and requirements. Conceptual models examine the consequences of broad assumptions. These kinds of models are useful for conducting rigorous thought experiments: one might ask how noise impacts latency in a forced choice between multiple alternatives [1], or how network topology determines the fusion and rivalry of visual percepts [2]. While conceptual models must be constrained by data in the sense that they cannot violate known facts about the world, they do not strive to assimilate or reproduce detailed experimental measurements. Phenomenological data-driven models aim to capture details of empirically observed data in a parsimonious way. For example, reduced models of single neurons [3,4] can often capture the behavior of neurons, but with simplified dynamics and few parameters. These kinds of models are useful for understanding ‘higher level’ functions of a neural system, be it a dendrite, a neuron or a neural circuit [5**] that, in the appropriate context, are independent of low-level details. Used carefully, they can tell us biologically relevant things about how nervous systems work without needing to constrain large numbers of parameters. Detailed data-driven or “realistic” models attempt to assimilate as much experimental data as are available and account for detailed observations at the same time. Successful examples might include detailed structural models of ion channels that capture voltage-sensing and channel gating [6], or carefully parameterized models of biochemical signaling cascades underlying long-term potentiation [7]. With notable exceptions, models of this kind are often the least satisfying, as they can be most compromised by what hasn’t been measured or characterized [8**].

How should we approach computational modelling in the era of ‘big data’? The non-linear and dynamic nature of biological systems is a key obstacle for building detailed models [8**,9**] even when large amounts of data are available. For example, even well-characterized neural circuits such as crustacean CPGs that have full connectivity diagrams have not, to date, been successfully modelled in a level of detail that incorporates all of what is known about the synaptic physiology, intrinsic properties and circuit architecture [10]. As a consequence, there is still a big role for conceptual models that tell investigators what kinds of processes may underlie the data [11], or, more importantly, what potential mechanisms one should rule out [12,13*].

Relating data to models

The Hodgkin-Huxley [14] model stands almost alone in its level of impact and in the way it achieved a more-or-less complete fit of the data. In hindsight their success came from extraordinarily good biological intuition about how action potentials are generated and a clever choice of experimental preparation. Their model revealed fundamental principles of how a ubiquitous phenomenon – the spike, or action potential – resulted from few processes, namely two voltage-dependent membrane currents mediated by separate ionic species.

By contrast, the success of subsequent attempts to fit and model the biophysics of more complex neuronal conductances, neurons and circuits has been less dramatic – although insight into the roles of specific currents in neuronal dynamics has certainly been achieved [6,14,15,16*,17,18]. Understanding why this is the case requires investigators to step back and view the problem in a general setting. Biological systems are assembled from many component enzymes, signaling molecules and cellular structures. Modelling these components and their interactions produces complex nonlinear dynamical systems with multiple parameters for each component. For example, even if one specifies quite rigidly the desired output of a neuronal network, the underlying parameters that can give rise to these properties is weakly constrained as multiple solutions to neuronal and network dynamics are found [19,20]. Subsequent work, informed by this general finding, explored families of models with parameters scattered over plausible ranges [21,22,23,24*]. Although these studies abandoned the idea of finding unique fits to data, they nonetheless revealed important principles about how specific combinations of conductances contribute to neuronal and network behavior [22,23], and how temperature-robust neuronal function might emerge in cold-blooded animals that experience significant changes in temperature [21,24*].

There are fundamental reasons why it is challenging to fit large numbers of parameters in biological models [9**,25]. First, the models are typically nonlinear, so the relation between the parameters and the output can be complicated and many-valued. Averages of measured parameters can give rise to non-observed behavior [26] and models can be exquisitely sensitive to measured parameters [27,28,29,30]. The value of averaging as a means of combating experimental noise might thus be obviated by the possibility that the average values are not valid parameter combinations themselves. Second, biological systems have degenerate pathways and components, meaning that properties and functions of structurally distinct components overlap. While this confers robustness to the systems themselves, it means that models can be remarkably insensitive to many combinations of parameters [5**,21,22,23,27,29,30,31]. This ‘sloppy’ property of biological systems is well-documented in systems biology [8**] and neuroscientists may benefit from a wider appreciation of the tribulations and successes of model building in this sister field [32].

Sloppiness (Figure 1) means that models with large numbers of parameters exhibit relatively few sensitive directions in local regions of parameter space, although these directions are not generically aligned with parameter axes. Instead, the sensitive (and insensitive) directions are comprised of mixtures of parameters (Figure 1c), meaning that performance of a detailed model will be severely compromised by poor measurement, or ignorance of even a single parameter [8**]. A recent, elegant modelling study of oculomotor integration [5**] revealed a handful of sensitive directions in the high-dimensional parameter space of a complex neuronal circuit model (Figure 1d). The model permitted fresh insight into the trade-offs between structural and functional properties of a circuit and did so by constraining model behavior rather than measured parameters. As this study illustrates, useful insight into circuit function can be obtained from phenomenological matching of the overall model behavior to experimental data, provided the non-sloppy, or ‘stiff’, parameter combinations are identified [33].

Figure 1.

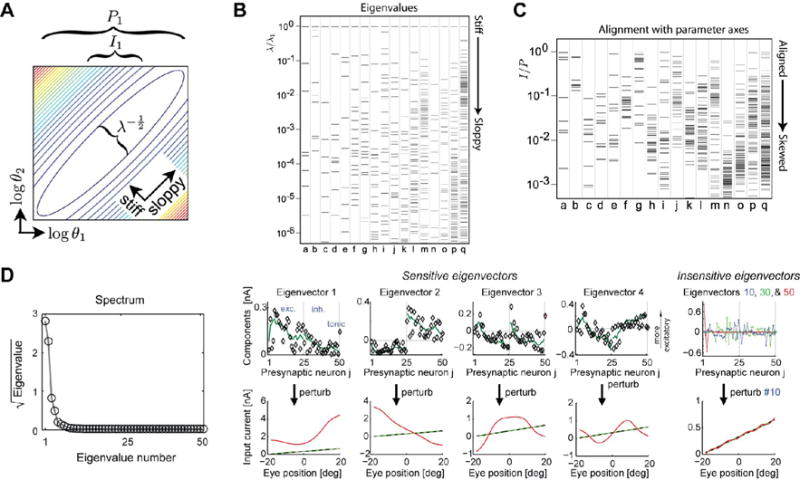
In high-dimensional biological models there are often many parameter combinations that can co-vary without significant effect on the behavior of the model, known as sloppy parameter combinations [8**]. (A) Elliptical level sets in the deviation of model output from a nominal value (computed from the Hessian, or second derivative) shows a direction in which parameter variation does not change model behavior (sloppy direction) and an orthogonal direction in which the model is sensitive (stiff). The major and minor axes of these ellipses (and thus the relative sensitivity to the stiff/sloppy directions) are determined by the eigenvalues, λ_i, and the projections of these onto the parameter axes (θ₁, θ₂) parameter axes are denoted by P₁ and I₁, respectively. (B) Eigenvalues computed for 17 different systems biology models [8**], including detailed models of circadian transcriptional circuits and yeast metabolism (a–q) are spread evenly across many orders of magnitude. Only the first few eigenvectors have significant effects on the behavior of the model, thus only a few parameter directions determine model behavior. (C) The alignment of the ‘error ellipsoids’ I/P relative to model parameters shows that most eigenvectors tend to be composed of many underlying parameters (tend to be skewed). Thus, while there are relatively few stiff directions in parameter space that change model behavior, these directions usually have contributions from many experimentally measurable parameters. (D, left) A computational model of an oculomotor circuit [5**] shows similar sensitivity to only four or five parameter combinations (D, right) to the systems biology models (A–C). The sensitive directions, projected onto the underlying parameter axes (presynaptic input weights) have substantial contributions from all parameters. Figures (A–C) reproduced from [8**], (D) Reproduced from [5**].

A third reason for the difficulty of the ‘fitting problem’ arises because biological systems are intrinsically variable [34]. This variability is well-appreciated in the context of single neuron parameters, where neurons with highly stereotyped properties exhibit surprisingly large variability in their membrane conductance expression [20,35,36,37,38]. High variability is present wherever one looks, whether it is the synaptic connectivity of well-defined neural circuits [39,40,41,42] or the behavior of entire animals [43]. As a consequence, the number of valid, distinct parameter sets – should they be accessible – can equal the number of biological repeats of an experiment. This kind of variability is not noise; it represents genuinely different parameter combinations that the biological system has found. For this reason, understanding the regulatory logic of the nervous system is of fundamental importance [44**].

In an age when increasingly voluminous and complex datasets are demanding interpretation, these fundamental model-fitting problems are sobering. However, there are direct means of taming these difficulties by exploiting the resolution and high-dimensionality of the data themselves. An elegant analysis of the requirements for fitting a multicompartment model [31] showed that if one could access, at high temporal resolution, the membrane voltage of each compartment in a neuron, then one can recover the densities of multiple voltage-gated conductances – providing the identity and kinetics of the conductances are known. At the time this study was published, such measurements seemed impractical. Nearly ten years later, we are on the verge of being able to make such measurements thanks to new molecular tools and improved microscopy.

Advances in statistical methods and fitting algorithms are accompanying advances in data collection. Many of these exploit fast computers and numerical methods such as Monte Carlo sampling to solve complex statistical inference problems, such as inferring synaptic inputs from noisy physiological traces [45,46*]. Knowledge of the general properties of the system permits ill-posed problems to be regularized, allowing noisy or incomplete data to yield informative measurements [47*,48]. Statistical inference has other important roles aside from making biological parameter values accessible. Oftentimes, inference can be performed in a way that incorporates important assumptions – such as the presence of interneuronal connections in a network – thus embedding a modelling question in the data analysis task. Such statistical modelling approaches can yield valuable hidden information, such as how common noise sources may explain population activity in the retina [49**] and how the statistics of complex multiunit activity can encode aversive and appetitive taste [50,51*](Figure 2).

Figure 2.

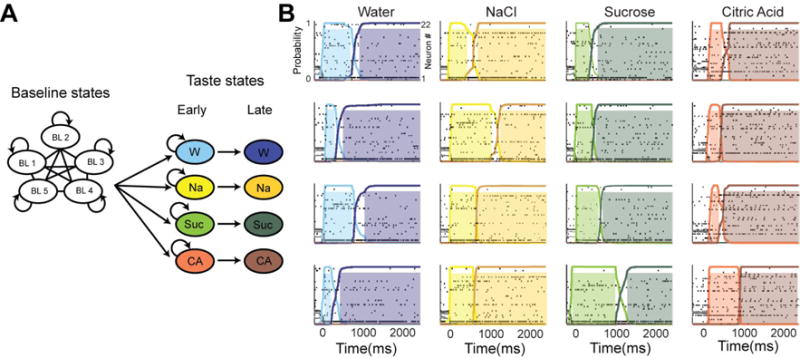
A Markov Models describing the statistics of transitions in multiunit network activity in sensory (taste) cortex [50,51*] during delivery of one of four tastes (water – W, salt – Na, sugar – Suc, acid – CA). (A) Baseline activity before tastes were presented was disorganized: all transitions are possible. After taste presentation the networks entered one state in a probabilistic way, determined by the stimulus. Each state is characterized by distinct combinations of neural firing patterns (raster plots in (B)). The network can remain in the early state or advance to the late state. (B) Spiking data across four trials illustrates how the same network of neurons leaves a baseline state to enter an early state, which entirely depends on the stimulus, then advances to the late state after a certain amount of time. Each color represents a state that can be distinguished from all other states by the network firing activity. Thus given only spiking data the taste stimulus can be inferred based on the state of the network. An important feature of this statistical model is that the variable latencies of discrimination ‘decision’ events is evident, something that is lost if activity is averaged over trials. Figure reproduced from [50].

Alternative strategies for fitting data, including evolutionary algorithms [52,53] and dynamic state estimation [29] have also been developed to exploit multiple, time-series measurements. In spite of the sophistication of current data analysis techniques and the increasing richness and quality of data, any model that is constrained by data is only as sound as the necessary assumptions upon which it rests: even incorrect models can fit the data.

Conceptual models as tools for explaining data and asking “what if?”

The mammalian prefrontal cortex (PFC) is one of the most complex and mysterious structures in neuroscience. Single-unit activity from tens to hundreds of neurons reveals a diverse and puzzling array of activity profiles during behavioral tasks, with no obvious relation to external variables. Faced with a snapshot of data from a miniscule and only loosely identified population of neurons, a recent study was nonetheless successful in shedding light on how behavioral output can be represented in this brain region [54**](Figure 3). The role of the computational model in this study was not to fit and explain the data in painstaking detail – far too many unknowns exist for this to be practical even if the fitting problem could be solved. Instead, the authors appealed to the general properties of an abstract, recurrent neural network to explain ‘how’ such a structure could represent the external world in its internal state. In spite of the gulf between the unknown and complex properties of the PFC and the simpler and more abstract nature of the model, a striking agreement was evident in the way population activity evolved during a decision.

Figure 3.

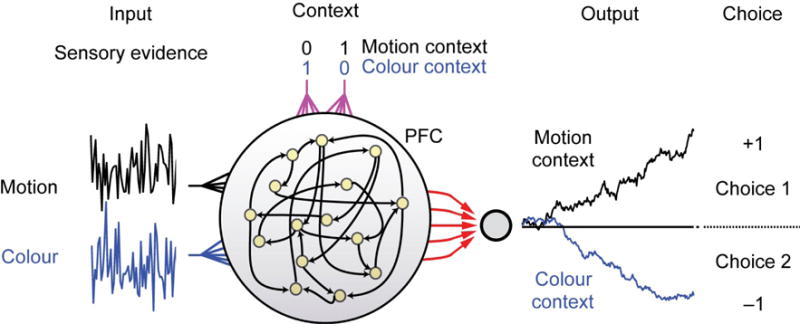
A conceptual/phenomenological model [66] of recurrent networks such as the pre-frontal cortex (PFC) can account for the observed data even when precise understanding of the underlying, anatomy and detailed mechanisms is lacking. The experimental task involves a monkey looking at moving, colored dots and reporting the perceived direction of movement, or the color, depending on a context cue. Here, the same physiological data regarding the color and motion are fed into the network, along with a context cue, and the model reliably selects the correct choice. Thus without knowing the precise molecular/network mechanisms of the PFC the authors were still able to postulate how such a network might work and create testable hypotheses. Figure reproduced from [54**].

Similarly, a wealth of neurophysiological and behavioral data is emerging from models of motor sequence learning and navigation. For example, the brain structures involved in bird song learning are still being mapped and characterized. Nonetheless, deep insights into the nature of reinforcement learning [55] and temporal sequence learning [56**] have emerged from modelling studies that focused on conceptual, rather than detailed features of experimental data. Similarly, the power of C elegans in linking circuit dynamics to behavior was recently demonstrated in a combined experimental and modelling study of chemotaxis [57*]. Notably, this study used phenomenological models to characterize single neuron dynamics that informed a behavioral model of active sensing.

Conceptual models are not confined to ‘high level’ neurophysiological phenomena such as decision making and learning. Low level, mechanistic phenomena such as how protein synthesis impinges on synaptic plasticity can be studied using computational models without attempting to parameterize every molecule involved. A recent study by O’Donnell and Sejnowski [58*] shows that memory generalization can emerge from diffusion of plasticity proteins in dendritic trees. Similarly, a coarse model of activity dependent ion channel regulation has recently helped explain physiologically important expression patterns in the mRNA of ion channels in identified neurons, while accounting for cell-to-cell variability [44**,59]. Building more realistic and detailed molecular models is becoming more feasible as imaging and subcellular biochemistry are providing more data to constrain these models [60], but there will always be a role for conceptual models – especially in gaining intuition and in situations where data-fitting is impractical for reasons we have already discussed.

A skeptic might worry that conceptual models can be adjusted ad-hoc, or post-hoc, to agree with data and thus be consistent with any finding. If this were the case, conceptual models would only make vacuous statements about the world and not generate new understanding. However, many conceptual models can be falsified, and can stimulate important, fruitful research programs in experimental neuroscience. For example, the oscillatory interference model of grid cell formation was proposed very soon after the discovery of grid cells [61]. The power of the oscillatory interference model was that it used a simple mechanism – interference – and combined it with a well-documented phenomenon – theta oscillations – to account for a puzzling observation. However, recent work [62*], motivated by tension between this model and a rival theory, the continuous attractor model [63], found compelling evidence for the latter. It is important to note how much has been learned in the wake of these modelling attempts, irrespective of whether they are correct. Deeper understanding of intrinsic cellular properties, network dynamics and robustness of alternative coding schemes [64] have all descended from simple conceptual models.

Exploring an artificial model universe comes with its own risks. If exploration is done without reality-checking assumptions, it is easy to fall into the trap of building irrelevant models. There are infinitely many models consistent with any one piece of experimental data, so it is important to avoid just-so explanations that can arise when a model spuriously matches an observed phenomenon. Well-conceived models rest on underlying principles that ensure the model does not only work under idiosyncratic circumstances. Sometimes this can be done formally; for example, physiological models of central pattern generating neurons and networks can be reduced to the underlying family of dynamical systems, permitting an understanding of intrinsic neuronal dynamics and network interactions that is model-independent [4,65]. In other cases, strong biological intuition and close contact with the experimentalist, or experimental preparation can combat fragile or spurious modelling results.

All experimentalists have, on occasion, seen a piece of new data and said, “Of course!” There is a sense of recognition that comes from seeing the answer to a previously puzzling question. The best computational models are equally illuminating: an idea or a principle is revealed and recognized as part of the path to understanding a biological conundrum. Principled model building will be ever more important in the era of big data, as it is only principled model construction and evaluation that will allow us to understand which details are important for what functions of the brain.

• Computational models will prove increasingly useful for understanding large datasets

• Substantial challenges exist for fitting detailed models to data

• Conceptual and phenomenological models are often more useful than detailed models