Abstract
Objective
Medical coma is an anesthetic-induced state of brain inactivation, manifest in the electroencephalogram by burst suppression. Feedback control can be used to regulate burst suppression, however, previous designs have not been robust. Robust control design is critical under real-world operating conditions, subject to substantial pharmacokinetic and pharmacodynamic parameter uncertainty and unpredictable external disturbances. We sought to develop a robust closed-loop anesthesia delivery (CLAD) system to control medical coma.
Approach
We developed a robust CLAD system to control the burst suppression probability (BSP). We developed a novel BSP tracking algorithm based on realistic models of propofol pharmacokinetics and pharmacodynamics. We also developed a practical method for estimating patient-specific pharmacodynamics parameters. Finally, we synthesized a robust proportional integral controller. Using a factorial design spanning patient age, mass, height, and gender, we tested whether the system performed within clinically acceptable limits. Throughout all experiments we subjected the system to disturbances, simulating treatment of refractory status epilepticus in a real-world intensive care unit environment.
Main results
In 5400 simulations, CLAD behavior remained within specifications. Transient behavior after a step in target BSP from 0.2 to 0.8 exhibited a rise time (the median (min, max)) of 1.4 [1.1, 1.9] min; settling time, 7.8 [4.2, 9.0] min; and percent overshoot of 9.6 [2.3, 10.8]%. Under steady state conditions the CLAD system exhibited a median error of 0.1 [−0.5, 0.9]%; inaccuracy of 1.8 [0.9, 3.4]%; oscillation index of 1.8 [0.9, 3.4]%; and maximum instantaneous propofol dose of 4.3 [2.1, 10.5] mg kg−1. The maximum hourly propofol dose was 4.3 [2.1, 10.3] mg kg−1 h−1. Performance fell within clinically acceptable limits for all measures.
Significance
A CLAD system designed using robust control theory achieves clinically acceptable performance in the presence of realistic unmodeled disturbances and in spite of realistic model uncertainty, while maintaining infusion rates within acceptable safety limits.
Keywords: control, burst suppression, medical coma, anesthesia, electroencephalogram
1. Introduction
Medical coma is a brain state characterized by profound reductions in metabolic demand, blood flow, and neuronal activity. It can be reversibly induced by administering anesthetics or by cooling the brain [1–3]. Therapeutic uses of medical coma include cerebral protection during cardiac surgery with complete circulatory arrest [4, 4–8], induced by deep hypothermia and inhaled anesthetics; reduction of intracranial pressure after traumatic brain injury, induced by intravenous administration of barbiturate anesthetics [9]; and termination of refractory status epilepticus (RSE), a condition of unrelenting seizures, induced by intravenous anesthetics such as propofol and midazolam [10–14].
Burst suppression is a qualitative change in the dynamics of neuronal activity that marks the onset of medical coma. The state of burst suppression is named for its appearance in noninvasive/scalp electroencephalogram (EEG) recordings, in which periods of high voltage EEG activity are interrupted at semi-regular intervals by periods of low-voltage EEG activity (suppressions) [15, 16]; see figure 1. The probability at any given moment that brain activity is suppressed, the burst suppression probability (BSP), relates monotonically to the degree of cerebral suppression. For example, increasing the anesthetic infusion rate systematically increases the BSP [17–20]. Consequently, induction of medical coma is performed under the guidance of continuous electroencephalography (cEEG) monitoring, titrating the strength of the inducing stimulus to achieve and maintain a target level of burst suppression.
Figure 1.
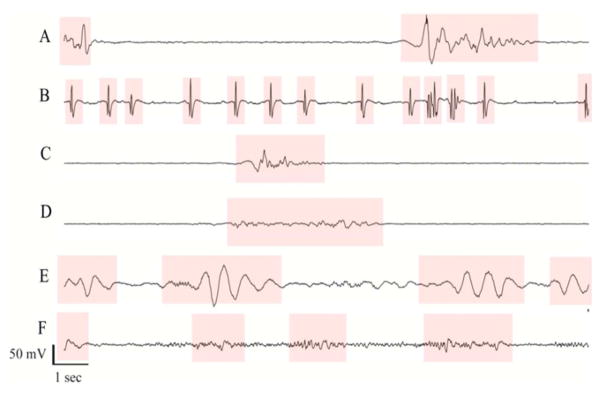
Electroencephalogram samples from six different patients undergoing pharmacologically induced burst suppression as treatment for refractory status epilepticus. In each case burst suppression depth was controlled manually by nursing staff adjusting the rate of propofol anesthetic infusions, according to standard clinical practice. Bursts are highlighted in pink, while suppression periods are not highlighted. The approximate burst suppression probability (BSP) values for these examples, given as percentages (100% = complete suppression, 0% = no suppression) are (A) 68%, (B) 55%, (C) 83%, (D) 70%, (E) 39%. Only case (C) is within 5% of the clinical target value, which in all cases was 80%.
In the case of RSE, no universally agreed upon guidelines exist for the optimal target levels or duration of medical coma. In practice, intensive care physicians agree upon a target level of burst suppression and aim to maintain this target level for 24–48 h at a time, periodically lifting the patient gradually out of coma, and re-inducing burst suppression to repeat the cycle if seizures recur [14]. This management is performed under the guidance of cEEG displated at the bedside, intermittently hand-adjusting the anesthetic infusion rate to keep near target level [14, 21–23]. This current practice pattern is not ideal, because the medical staff who act, in effect, as anesthesiologists and clinical electroencephalographers, typically lack specialized training in either EEG or anesthesiology, and the numerous other demands of providing intensive care unit (ICU) care do not allow for constant monitoring of the EEG and adjustment of the anesthetic infusion rate.
A better strategy would be to develop a closed-loop anesthesia delivery (CLAD) system that monitors the depth of burst suppression quantitatively and in real time and continually adjusts the anesthetic infusion rate automatically, without the need for constant human supervision. Such a system could in principle provide tighter control, avoiding the morbidities associated with both over- dosing and under-dosing of anesthetics that are common in ICU care [24–26]. Outside the practice of medicine, closed-loop control technology is ubiquitous, and rooted on a mature foundation of both theory and a wealth of practical experience.
While CLAD systems have been a subject of research for over 60 years [27–31], they have had minimal impact on the practice of medicine. Two categories of reasons for this situation are commonly cited.
-
Concerns about sensor reliability: the most widely used brain monitor, the bispectral index (BIS) monitor, has not proved sufficiently reliable for measuring the depth of anesthesia, because it assumes the same numerical index indicates the same brain state across all anesthetics. Moreover, BIS is based on a proprietary algorithm and is thus cannot be manipulated from first principles. Finally, the BIS algorithm has been empirically observed to operate in a nonlinear fashion with a variable time delay ranging from 15 to 55 s [32, 33]. Such behavior creates the risk for undesirable oscillations and instability when incorporated into feedback loops. Recent alternatives to BIS have been reported to overcome some of these difficulties [34–36].
Automatic monitoring of burst suppression depth is a problem with a substantially higher ‘signal to noise ratio’ than the problem of inferring the depth of lighter stages of general anesthesia. That is, from a signal processing point of view, the essential EEG changes associated with burst suppression, namely a periodic change in EEG signal power, are extremely reliable. Effective algorithms for tracking the depth of burst suppression in real time have been developed [18–20, 37], and we present further refinements in this work. Consequently, sensor reliability is easily ensured, and control of burst suppression can be considered an ideal starting point for developing robust CLAD systems.
Concerns about patient safety: patients’ responses to drugs vary considerably. This variation includes differences in both parmacokinetics (PK, the rates of drug distribution and elimination), and differences in pharmacodynamics (PD, drug effect as a function of dose). PK/ PD differences stem from several factors, including patient demographics (e.g. age, weight, gender, height), underlying medical conditions (e.g. kidney or liver dysfunction), and anesthetic interactions with other drugs [14, 35, 38–43]. This variability implies that population-based PK/PD models are often crude approximations to the true PK/PD parameters of individual patients. Controllers must therefore be designed to perform robustly in the face of model error. Furthermore, surgical operating rooms and ICUs are fundamentally noisy environments [44–46], with unpredictable internal stimuli (e.g. changes in medical condition) and external stimuli (e.g. painful procedures or new medications) that change the underlying state of the patient and their responsiveness to medication. These internal and external stimuli continually act as disturbances and noise in the feedback loop that must be accounted for in the controller design to avoid inducing unpredictable, dangerous behavior of the CLAD system. Most work to date has failed to deal directly with these safety concerns. Dumont [35] has recently pointed out that robust control theory, developed over the last several decades, provides fundamental techniques to address these issues rigorously.
Several CLAD system designs for managing medical coma have previously been proposed and tested in computer simulations and animal models [17, 37, 47]. Early controllers were based on ad hoc designs, and, reported average rather than individualized results, and considered only constant target levels of anesthesia without investigating controller behavior in response to changes in target burst suppression ratio (BSR) values [17]. Recent work by our group has focused on providing rigorous approaches to the initial signal processing [18–20, 37], and has explored a variety of principled controller design methods, including proportional integral (PI), linear quadratic regulator (LQR), and model predictive control (MPC) controller designs. However, to date, no work on CLAD design for medical coma has explicitly dealt with the problem of ensuring robust performance under real-world operating conditions.
In this work we introduce several innovations that prepare the way for real-world implementation of a robust CLAD system for automatic control of medical coma in the ICU environment. These include an improved real-time algorithm for monitoring burst suppression depth; a safe method for estimating PD parameters in critically ill patients; and a controller design that ensures robust control in the face of within- and between-patient PK–PD variability. We verify these results with thorough and realistic Monte Carlo simulations. Our results confirm that the integrated system performs safely under realistic operating conditions, including the presence of estimation error, input disturbances, set point changes, and model uncertainty.
2. Theory and Methods
2.1. Observations
The amplitude and frequency characteristics of burst suppression EEG recordings can vary substantially between patients. However, for the purpose of tracking the depth of burst suppression, we will regard the EEG as a sequence of binary observations. We write nt ∈ {0, 1}, t = 0, 1, … for the sequence of observations, with nt = 0 indicating a sample within a burst period and nt = 1 indicating a sample within a suppression period. In prior work, we described an algorithm for detecting the onset and offset of bursts in EEG signals and outputting a binary signal, and validated the algorithm on a broad set of EEG recordings from critically ill patients undergoing burst suppression treatment. Our burst suppression segmentation algorithm identifies bursts and suppressions in human EEG recordings with a performance comparable to human experts [20]. We have also successfully used this algorithm previously in two sets of burst suppression CLAD control experiments in animals [37, 48]. In the remainder of this work we therefore treat the binary observations as given.
2.2. Pharmacokinetics
Pharmacokinetic (PK) models (figure 2(A)) describe the time-dependent absorption, distribution, and elimination of drugs in the body. Propofol is the most widely used anesthetic for induction of burst suppression for treatment of RSE [14, 21, 49–51]. Our CLAD system is based on the human PK model of propofol developed by Schnider [41, 52–54]. Schnider’s model contains three body compartments connected to a central compartment. The central compartment represents blood. Diffusion of propofol between the central compartment i and each peripheral compartment j occurs at a rate kij. Mean PK values across patients depend on body mass, age, sex, and height, as shown in table 1. The table also includes published estimates of the uncertainty in these parameters arising from inter-patient variability.
Figure 2.
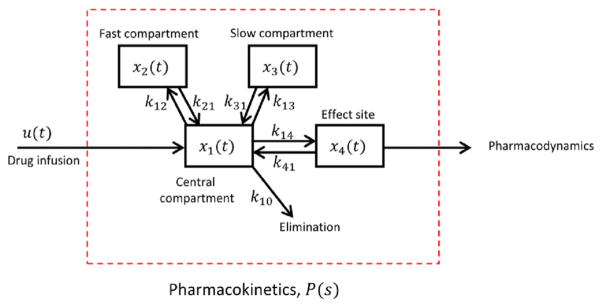
Schnider model for propofol pharmacokinetics.
Table 1.
Schnider model for propofol pharmacokinetics (PK). Vi, volume of body compartment i; CLi, drug clearance for compartment i; kij, rate constant for drug transport from compartment i into compartment j. LBM, lean body mass. LBM is calculated according to the James formula as: males: LBM (1.10 × weight(kg)) −128 × (weight2/(100 × height(m))2), females: (1.07 × weight(kg)) −148 × (weight2/(100 × height(m))2).
| Parameter | Value/Equation | CoV | Units |
|---|---|---|---|
| V1 | 4.27 | 4.04 | L |
| V2 | 18.9–0.391 (age-53) | 1 | L |
| V3 | 238 | 14.35 | L |
| CL1 | 1.89 + 0.0456 (mass-77)−0.068 (LBM-59) + 0.0264 (height-177) | 10.05 | L/min |
| CL2 | 1.29–0.024 (age-53) | 1 | L/min |
| CL3 | 0.836 | 11.79 | L/min |
| k10 | CL1/V1 | — | min-1 |
| k12 | CL2/V1 | — | min-1 |
| k21 | CL2/V2 | — | min-1 |
| k13 | CL3/V1 | — | min-1 |
| k31 | CL3/V3 | — | min-1 |
| k14 | 0.456 | — | min-1 |
| k41 | 0.456 | — | min-1 |
Mathematically the Schnider PK model is a four-dimensional linear dynanmical system. We represent this system in discrete time for purposes of computer implementation, taking as a time increment Δ = 1 s. Bursts and suppressions nearly always last >0.5 s [20, 55], thus this choice for Δ is small enough to ensure that each observation can be assigned uniquely to either the burst or suppression state. The state model for drug concentrations is
| (1) |
where xt = (x1t, x2t, x3t, x4t)′ represents the drug concentrations in the four body compartments of the Schnider model, ut is the rate of propofol infusion, and
| (2) |
| (3) |
The indices for the drug concentration variables in these equations are x1t for the central compartment, x2t and x3t for the ‘fast’ and ‘slow’ peripheral compartments, respectively (so called because the diffusion rates k12,, k21 are faster than for k13, k31), and x4t is the drug concentration in the brain, also called the effect site compartment. Note from table 1 that the rate constants are conventionally determined as ratios between a compartment volume and a clearance rate, except in the case of the effect site, for which the value is given directly [41, 54].
2.3. Pharmacodynamics
To relate the effect site concentration to the binary EEG observations, we next introduce a pharmacodynamic (PD) model (figure 3). The effect of interest is the depth of burst suppression as a function of the effect site concentration of propofol. In clinical practice burst suppression depth is described in terms of the number of visually identified bursts present in a 10 s window. A quantitative measure of burst suppression depth sometimes used in experimental settings is the BSR, defined as the fraction of the time within a moving time window that the EEG is in the suppressed state [55, 56]. However, the BSR lacks a direct relationship with the underlying pharmacokinetics, requires a fairly large time window (e.g. 60 s) to produce stable estimates, and lacks a rigorous statistical foundation [18, 19]. Instead, we use the BSP, a statistically rigorous measure of burst suppression depth [18]. We have used the BSP in our prior CLAD work for medical coma [37, 48].
Figure 3.
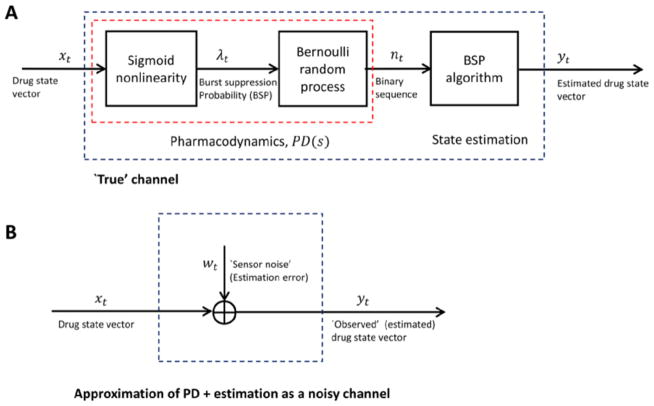
Block diagram for propofol pharmacodynamic model and state estimation (A) the drug concentration state vector xt enters the sigmoid nonlinearity, where the fourth element (effect site concentration, x4t) is transformed by the sigmoid nonlinearity (Hill equation) into the burst suppression probability, λt (BSP). The BSP is a time-varying rate in a Bernoulli process that gives rise to the observed binary data nt. Although the pharmacodynamic model and state estimation procedures are nonlinear, the resulting input-output relationship is approximately linear (see figures 4 and 9). In the method used to design a robust controller for this system, we view the estimated state as a noisy observation of the true state (B).
In the BSP estimation algorithm that we develop in the next section, we view the binary observations as sequence of random variables produced by a Bernoulli process with a time-varying rate, λt. Our PD model thus needs to relate the underlying effect site concentration x4t to the suppression rate λt.
A parametric form for λt = λt(x4t) must satisfy two contstraints. First, low doses of propofol do not cause burst suppression, thus λt(x4t) should remain close to zero at low effect site concentrations. Second, λt should saturate at high concentrations of propofol. To satisfy both constraints, we adopt as our PD model the Hill sigmoid function
| (4) |
where C is the effect site concentration at which BSP = 0.5, and γ controls the steepness of the sigmoid.
2.4. State estimation
We have developed PK and PD models that relate the rate of propofol infusion to the sequence of binary observations derived from burst suppression EEG data. Here we present a recursive Bayesian algorithm to estimate the BSP from binary observations. Given the instantaneous suppression rate λt, the probability of observing a suppression in any given small interval Δ is given by the conditional intensity function in discrete time as
| (5) |
Note that up to order o(Δ), the observation model is simply the likelihood function for a single observation point process model on small interval data. From here on we assume Δ is small enough that the o(Δ) term can be safely ignored.
Whereas drug concentration values are strictly positive, it will be mathematically advantageous to work with quantities that can take on positive and negative values. Consequently we take the logarithm zt = log(xt). Taking logarithms of both sides of the discretized PK equation (1) we obtain:
| (6) |
In this expression, wt = (w1t, w2t, w4t, w4t)′ is an i.i.d. sequence wt ~ N(0, W), W = Iσ2, and zt = (z1t, z2t, z4t, z4t)′
In the appendix, we derive from expressions (5) and (6) a set of alternating prediction and update steps. The complete set of prediction and update equations is:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
where à is defined in equations (35)–(37). Hereafter we refer to these equations collectively as the BSP algorithm.
2.5. Robust feedback controller design
The recursive state estimation algorithm described above provides a real-time estimate of drug concentration states at each time step. We now design a controller that takes as feedback the estimated state and outputs at each time the appropriate infusion rate to keep the BSP near a target value [57]. In contrast with our previous work on CLAD control of BSP, here we explicitly design our controller within the framework of robust control theory.
A general block diagram for robust CLAD system design is shown in figure 3. In discussing controller design, we will use lower case letters for time-domain quantities, e.g. d = d (t), and upper case letters for the corresponding frequency-domain quantities, e.g. D = D(s) for Laplace-transformed quantities or D = D(iω)) for Fourier-transfored quantities. The arguments of Laplace or Fourier transfors will be omitted where needed to simplify notation.
The general system contains two components: the process, which represents the patient pharmacokinetics (PK) and consists of a nominal model P(s) plus uncertainty ΔP(s) (explained further below); and the controller, consisting of the feedback block C(s) and the feedforward block F(s). The inputs under our control are the target signal R(s), describing the desired BSP trajectory, and the drug infusion rate, U(s). We observe the signal Y(s), which represents the estimates produced by the BSP algorithm of the propofol concentrations in the various compartments of the body.
State observations are subject to uncertainty, which we model as arising from three sources. First, load disturbances D(s), such as noxious environmental stimuli or changes in pharmacokinetic parameters, are modeled as entering the system by combining additively with the infused drug. Load disturbances act effectively as an unobservable internal random source or sink of propofol, thereby causing the depth of burst suppression to drift away from the value predicted by the pharmacokinetic model. Second, the Schnider PK model, P(s), is a population-based approximation to an individual patient’s pharamacokinetics. We call P(s) the nominal PK model. We represent the true underlying PK model for any given patient as P′(s) = P (s) + ΔP(s), where ΔP(s) represents the degree of uncertainty associated with the nominal model allowed for in our controller design. Finally, the state observations Y(s) resulting from the recursive estimation procedure will have some amount of error, such that they do not precisely match the true underlying concentration state X(s). We represent this error for the purposes of controller design as an additive measurement noise, Y (s) = X (s) + N (s).
The system inputs (R, D, N) are related to the system outputs (X, Y, U) by the following three equations, derived from inspection of the block diagram in figure 3.
| (14) |
where
| (15) |
The closed-loop transfer functions S(s) and T(s) are called the sensitivity and complementary sentitivity functions, respectively. They play fundamental roles in the theory of robust control. Robust control system design techniques are often called ‘loop shaping’ methods, because they achieve robustness by influencing the shapes of the T(s) and S(s) functions. Good command following and disturbance rejection can be guaranteed by keeping the sensitivity function S(s) small. Insensitivity of the controller to measurement noise and PK modeling and avoidance of excessive controller responses to commands can be guaranteed by keeping T(s) small. However, it is impossible to keep both S(s) and T(s) small at all frequencies because S (s) + T (s) = 1. Consequently, robust controller design must trade off between the sensitivity and complementary sensitivity functions. This is possible in practice because reference signals and disturbances generally occur at low frequencies, whereas sensor noise and unmodeled dynamics tend to be concentrated at high frequencies. The appropriate tradeoff is thus to make S (jω) small at low frequencies and T (jω) small at high frequencies. The design strategy used herein achieves these aims, as will be seen below.
Many control paradigms are available, including proportional-integral-derivative, LQR, and MPC frameworks used in previous animal experiments by our group [37, 48], as well as nonlinear and adaptive methods. In the present work we employ a standard PI controller. We choose a PI design because of the rich body of theoretical work and practical experience using this paradigm to control real-world systems, and because of its mathematical simplicity [35, 57, 58]. A PI controller has the following standard form:
The last term is a first-order lowpass filter applied to the measurement signal. In our experiments we set Tf to 10 s, which empirically achieves a good trade off between load disturbance rejection (better with low values) and noise rejection (better with high values of Tf). The other parameters in the PI controller K and Ti are set by solving a constrained optimization problem. As the objective function for our controller design optimization problem we use the integrated absolute error value in response to a unit step load disturbance d acting on the closed-loop system. The non-convex PI controller design optimization problem that we solve can be written as
| (16) |
where ωs and ωt are peak frequencies for S (iω) and T (iω), respectively. The Ms and Mt criteria are known to determine closed loop robustness in the face of model (PK) uncertainty/ variation, disturbances, nonlinearities, and measurement noise, as described in [57]. The maximum allowed values for the sentitivity and complementary sensitivity functions, Ms and Mt, are chosen to achieve pre-specified performance criteria. Values known to give generally good robustness are between 1.2 and 2. For our experiments we set Ms = Mt = 1.4. This choice yields a phase margin of 41.8° and gain margin of 3.5. To solve this optimization problem, we use the software developed and made freely available by Garpinger and colleagues [58].
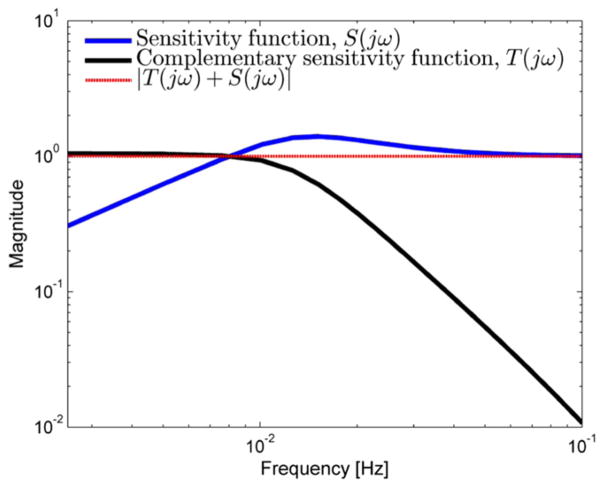
Figure 5 shows examples of Bode plots of the sensitivity function S (jω) and complementary sensitivity function T (jω) automatically synthesized by solving the optimization problem just described. Their sum is also shown, demonstrating the constraint that |T(jω) + S (jω)| = 1. These functions successfully trade off to meet the qualitative design criteria outlined previously: T(jω) ≈ 1 and S(jω) ≈ 0 at low frequencies, as is required to ensure good command following and load disturbance rejection. At higher frequencies, T(jω) ≈ 0 and S(jω) ≈ 1, as required for attenuation of responses to sensor noise, control sensitivity minimization, and robustness to PK uncertainty.
Figure 5.
Bode plots for the magnitude of the sensitivity function |S (iω)| and complementary sensitivity function T (iω) that result from the controller design optimization procedure, for a typical patient (60 year old, 70 kg, 175 cm male).
2.6. Identification of model parameter values
2.6.1. Pharmacokinetic parameters
For state estimation and controller design we use the Schnider PK model, adjusted for patient mass, age, sex, and height [41]. The Schnider PK model is denoted P(s) (figure 4). As mentioned above, because P(s) is based on population values, we call it the nominal model. The true (unobserved) PK model, P′(s) for any given patient may deviate from the nominal model, sometimes substantially. In our control system block diagram figure 4, the difference between the nominal and true model was denoted ΔP(s) = P′(s) − P (s).
Figure 4.
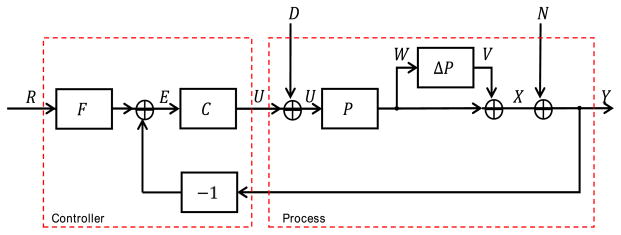
Block diagram of the process model and robust controller. Symbol meanings are as follows: R, reference signal (effect site concentration corresponding to the target BSP value); E, error signal (target minus estimated effect site concentration); C, controller; U, control signal (propofol infusion rate); D, disturbance signal; Ubar, the input to the process dynamics, consisting of the control signal plus the unknown disturbance signal; ΔP, plant error term, representing the discrepancy between the nominal model and the true PK dynamics model; W, the input to the plant error term; V, output of the plant error term; X, true pharmacokinetic state of the patient, consisting of the drug concentrations in each body compartment; N, estimation error, represented here as additive observation noise; Y, observed PK state of the patient, obtained by the BSP algorithm.
To simulate PK between-patient parameter variability we use published estimates of the coefficients of variation (CV) [41]. These CV values are given on an exponential scale. For the ith subject the model for each parameter (θi) is written as
| (17) |
where θμ is the population mean and ηi is the deviation from the mean for the ith subject, and deviations are assumed to be normally distributed with zero mean and variance σ2. The variance of the log-normal distribution is expressed in terms of the CV [59],
| (18) |
Rearranging, we obtain
| (19) |
The mean (μLN) and variance ( ) of these log-normally distributed parameters θi are then given by
| (20) |
| (21) |
To generate PK values for individual patients in the computer simulations described herein, we first transform the desired log-normal distribution into the equivalent normal distributions. The mean and variance of the corresponding normal distribution are then given by
| (22) |
| (23) |
Figure 6 illustrates the degree of uncertainty in the Bode plot and step response for a patient 60 year old male with weight 75 kg and height 175 cm.
Figure 6.
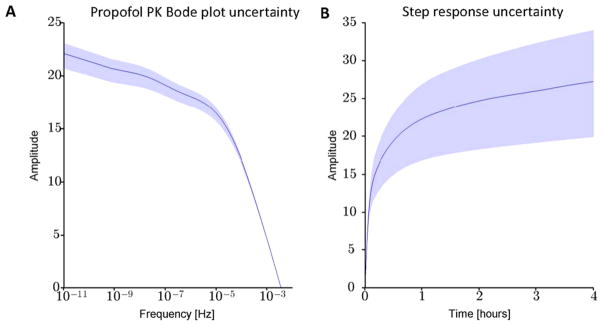
Examples of Bode (A) and step response (B) plots. For this example, the simulated patient was 60 year old male with weight 75 kg and height 175 cm. Solid blue lines correspond to the nominal (population-based) model for this patients demographics, calculated from the Schnider PK equations (table 1). Shading indicates the maximum and minimum values obtained from 1000 simulations in which PK values were generated by the random sampling process described in the main text.
2.6.2. Pharmacodynamic parameters
In this section we explain how we chose the true values for the PD parameters used in the Monte Carlo simulations described below. These parameter values are used to simulate patient data, but are treated as unobservable and thus are not available to use in designing the state estimator or controller. In the next section we present a procedure for estimating these parameters for state estimation and control.
The serum concentration of propofol required to cause the onset of burst suppression falls in most surgical patients within the range 4.25–5.4 μg ml−1 [60]. At steady state, the effect site propofol concentration is equal to the serum concentration. In the ICU environment propofol pharmacodynamics may be altered substantially by the presence of other drugs with similar mechanisms of action [43, 61, 62]. In particular, in the treatment of RSE the benzodiazepine midazolam is often infused at a constant rate while propofol is adjusted to achieve the desired depth of burst suppression. Like propfol, midazolam exerts its primary effect by binding to GABAA receptors in the brain. Consequently, smaller propofol effect site concentrations are required to reach any given level of burst suppression in the presence of midazolam, and this will alter the values of γ and C such that the Hill sigmoid curve may be left-shifted and/or steeper than it would be for propofol used in isolation.
Infusion rates of 100–200 mg h−1 often suffice to induce light levels of burst suppression in ICU patients undergoing treatment for RSE (BSP = 0.4), and deep levels cab be in induced at rates 200–300 mg h−1 (authors’ unpublished observations). These observations suggest approximate ranges for the pharmacodynamic parameters. Assuming for illustration a 60 year old female who weighs 70 kg and with a height of 175 cm, the steady state effect site concentrations obtained by solving the Schnider PK model during steady state propofol infusions of 100, 200 and 300 mg h−1 are 3.4, 6.9, and 10.3 μg ml−1, respectively. The values of γ and C can be calculated from pairs of steady state BSP measurements at two different concentrations, (b0, c0) and (b1, c1), using formulas derived from the Hill equation:
| (24) |
Assuming steady state BSP values of 0.4, 0.95 for rates of 100, 200 mg h−1, respecitively, yields γ = 4.8, C = 3.7, whereas assuming that these BSP values are reached for propofol infusion rates of 200 and 300 mg h−1 yields γ = 8.3, C = 10.2. These considerations yield approximate ranges for γ of 3.0–8.3 (unitless parameter), and for C, 3.7–7.2 μg ml−1. In our simulations we henceforth assume that the correct (but unknown) values are γ = 6.6 and C = 5.5, corresponding to steady state BSP values of 0.4 and 0.95 achieved at propofol infusion rates of 150 and 250 mg h−1, respectively.
2.6.3. Estimated pharmacodynamic parameters
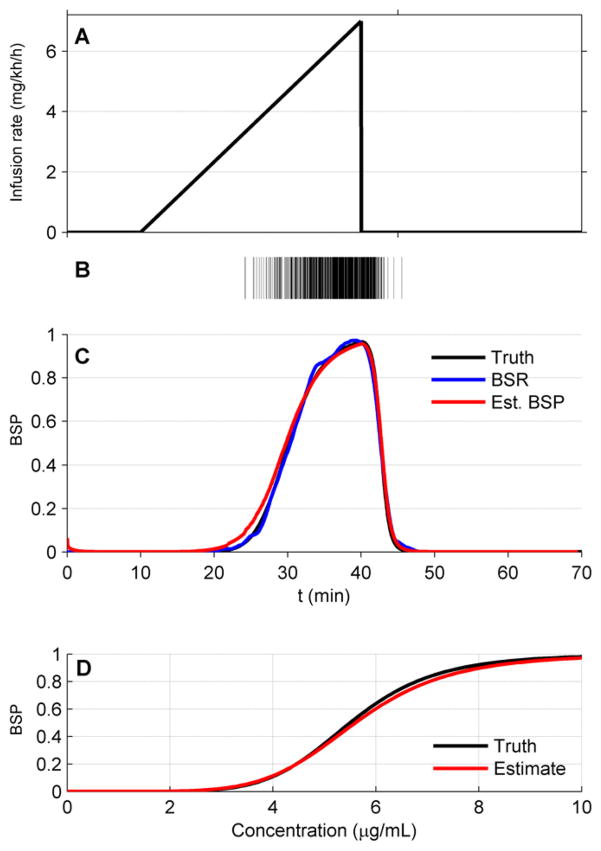
Due to the wide between-patient variation that can be expected in practice, the PD values C and γ must be estimated on a case-by-case basis. To accomplish this estimation we use a two-step process. First, we take the patient through a two-step infusion sequence termed the ‘ramp-drop’ maneuver (figure 7). At the beginning of each experiment propofol is infused at a rate near the minimum required to induce burst suppresion. Then, in the ramp part of the maneuver, the rate of infusion is gradually increased in a linear fashion to induce progressively deeper levels of burst suppression. While doing this, we monitor the depth of burst suppression by calculting the BSR, defined as the fraction of EEG spent in suppression within a time window. In general, BSR estimation requires several consecutive seconds or minutes of binary data, so it cannot be used to track rapid transition in burst suppression depth. However, BSR is suitable for tracking burst supression during slowly changing conditions such as those used in the ramp-drop procedure. In our procedure the BSR is estimated using 60 s intervals with overlap and averaged by a moving average filter with data points for 60 s. The ramping is stopped upon exceding a maximum target value of BSP = 0.9. At this point, the ‘drop’ part of the maneuver is excecuted, in which the infusion rate is abruptly decreased back to the starting value, and the level of burst suppression is allowed to drift back to the baseline value. In practice, if a patient is already in burst suppression when CLAD operation begins, burst suppression can be lightened to an acceptable low level, e.g. BSP = 0.2, then gradually ramped to the maximum BSP value.
Figure 7.
Illustration of the ramp-drop experiment performed before commencement of control, used to estimate the pharmacodynamics parameters γ and C of the Hill equation. The propofol infusion rate is linearly increased over a period of 20 min (A), and the resulting EEG signal is automatically segmented to yield a binary observation sequence (B). The binary data and infusion history are used to estimate parameter values for γ̂ and Ĉ such that the BSR (blue), estimated without reference to the Hill equation, provides a close match to the BSP tracing (red) estimated by the BSP algorithm, which does depend on the Hill equation parameter values. Both curves agree well with the true BSP value (black). (C) Example of the match between the true PD curve (Hill equation) based on the values γ and C (black), and the PD curve based on the estimated values γ̂ and Ĉ (red).
From the binary data that results from this ramp-drop experiment, we perform the following calculations in order to estimate the patient’s pharmacodynamic parameters, γ and C. Given candidate values for γ and C, the infusion history, the observed binary data, and the nominal PK model, we can plug all of these into the BSP algorithm to generate a candidate time series for the propofol effect site concentration x̂4t, and in turn a candidate BSP time series, λ̂t, which can be compared with the ‘observed’ BSR. The candidate PD parameters are subsequently improved using an iterative nonlinear least squares procedure to minimize the objective function
| (25) |
For this optimization we use the Nelder–Mead simplex algorithm [63] implemented in Matlab (Natick, MA).
2.6.4. External disturbances
The PK+PD model predicts that holding the propofol infusion rate constant should eventually result in a constant BSP value. In practice, however, the BSP exhibits slow random drift. The disturbance signal in the block diagram shown in figure 4 represents this drift as the effect of a random signal added to the infusion rate. We model the disturbance signal as a modified first-order autoregressive (AR(1)) process, dt = φdt−1 + σnt, where nt is a sequence of independent standard normal random variables. The autocorrelation function and standard deviation for dt are
| (26) |
We choose φ to make the autocorrelation function decay by 90% over 30 min or 1800 samples. That is, using at the sampling rate of Δ = 1 s−1 used in our simulations, φ = exp(log(0.1) 1800). Empirically, the magnitude of random fluctuations in the BSP at steady state is generally <30% (authors’ unpublished observations). Therefore we conservatively allow the magnitude of fluctuations in the model disturbance signal to be up to 50% of the steady state infusion rate needed to maintain a constant BSP. To this end, we set the standard deviation of of the disturbance SD(dt) signal to 1/4 the steady state infusion rate u0 by choosing , and we clip the maximum disturbance values at 1/2 the steady state infusion rate. That is, let the , be a candidate update value for the disturbance. Then
| (27) |
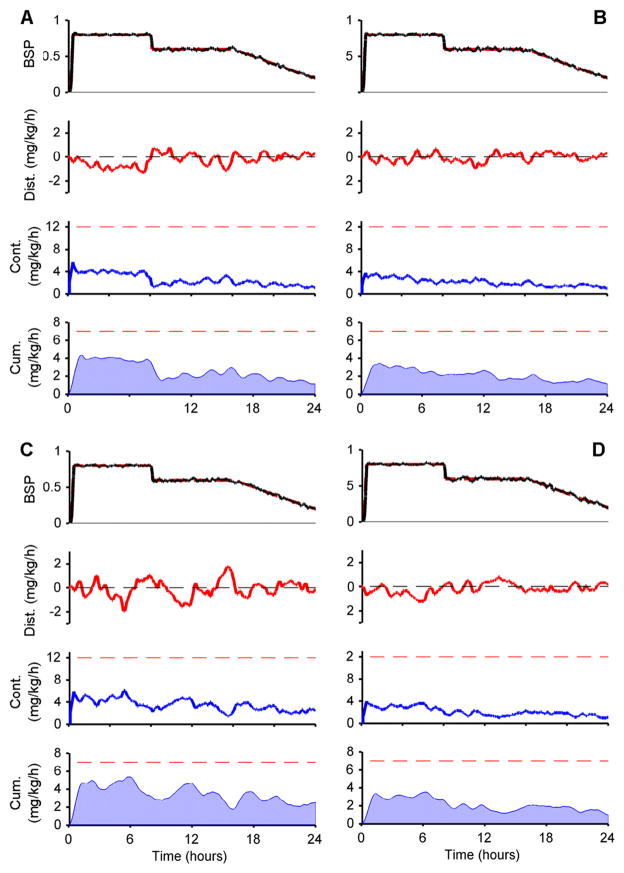
As an example, for a 60 year old male, who is 75 kg and 200 cm tall, the steady state infusion rates needed to maintain BSP values of 0.8, 0.6, and 0.2 are approximately 2.34, 2.01, and 1.54 mg kg−1 h−1, respectively, and we set the maximum magnitude of the disturbance signal at these points to 1.17, 1.01, and 0.77 mg kg−1 h−1. Examples are shown in figure 10 as illustrations for experiments described in section 3.4.1.
Figure 10.
Examples of 24 h simulations of CLAD-assisted treatment for refractory status epilepticus in (A) a 40 year old, 50 kg, 150 cm tall female, (B) a 60 year old, 75 kg, 175 cm tall male, (C) a 40 year old, 100 kg, 150 cm tall female, and (D) an 80 year old, 100 kg, 200 cm tall male. In each case the target BSP level (top panel, red dashed line) is increased from zero to 80% over 10 min, held for 8 h, reduced over 10 min to 60%, held for another 8 h, then tapered gradually over 8 h to 0.2. The patient PK dynamics are subject to a continuous stochastic load disturbance (dist., red curve). The robut controller adjusts the infusion rage continuously (cont., blue curve) without exceeding the maximum allowed rate (12 mg kg−1 h−1, red dashed line). The cumulative dose over the preceding hour (cum., shaded blue curve) also stays within the safety limit (red dashed line).
2.6.5. Signals to test estimator performance
To test the performance of the recursive state estimation algorithm we run the estimator while driving the PK model with a random infusion signal, ut. We model ut as a constant rate u0 plus a randomly varying signal. We set u0 equal to the steady state infusion needed to produce BSP = 0.8. For the random component we use the same model described in the previous section for the disturbance signal model, except that we allow maximum fluctuations that are twice as large. This choice allows us to thoroughly explore the full dynamic range of the recursive estimator.
2.6.6. Observation noise
The true concentration state, xt = (x1t, x2t, x3t, x4t)′ is an unobservable quantity. We view the discrepancy between the recursive estimate inferred from the binary observations by the BSP algorithm, yt, and the true state xt, as high frequency observation noise, nt = yt − xt (figure 3(B)), or in Laplace transform notation, N (s) = Y (s) − X (s) (figure 4). We describe methods for evaluating the validity of this additive observation noise model in the next section.
2.7. Evaluation of system performance
We use a factorial experimental design based on four patient characteristics to test each component of our system over a full range of clinical conditions. The characteristics are mass, divided into groups of 50, 75, and 100 kg; age, divided into groups patients aged 40, 60, and 80 years old; sex; and height, divided into groups 150, 175, and 200 cm tall. Taking all combinations of these divisions creates 3 × 3 × 2 × 3 = 54 distinct groups. For each group, and for each performance measure described below, we performed 100 experiments. In all experiments the true PK and PD parameters are treated as unobserved quantities. The true PK values are randomly generated as described in section 2.6.1. The true PD parameters are set in all experiments to γ = 6.6 and C = 5.5, as explained in section 2.6.2.
Except where otherwise specified, we summarize the results for each set of 100 experiments in terms of the median, minimum, and maximum value of the relevant performance metric.
In the following subsections we describe methods for evaluating performance of give metrics to quantify transient and steady state behavior of the fully integrated closed-loop system. We also specify values for these performance metrics that constitute clinically acceptable close-loop controller performance.
2.7.1. Controller transient performance specifications
To characterize transient responses of the closed-loop system we calculate the rise time, settling time, and percent overshoot. We also specify minimum clinically acceptable values for these transient controller performance statistics.
Rise time: we require the initial rise time, defined as the time taken to reach 90% of the target value after a step command, to be under 5 min. This specification is reasonable in ICU care, as times taken to reach burst suppression under manual control (standard practice) are usually substantially longer. For measuring rise time we use a step command to take the system from BSP = 0.2 up to BSP = 0.8, which is a typical set point for treatment of RSE.
Percent overshoot: the CLAD system must produce a percent overshoot in response to a step input of less than 15% (1.2 BSP units), to protect the patient against overdosing.
Settling time: the system must settle after a step command and remain (in the absence of disturbances) within ± 5% of the target value within less than 15 min. This requirement is again well within the limits of current medical practice.
2.7.2. Controller steady state performance specifications
To characterize steady state performance of the CLAD system we calculate the bias, inaccuracy, divergence, and wobble statistics [64, 65]. These statistics are based on the relative performance error (PE), defined for time sample t of patient i as the difference between the measured suppression rate λ̂i (t) and the constant target rate λ* expressed as a fraction of the target rate
In the following descriptions we leave off the i subscripts in order to reduce clutter in the notation. We also specify minimum clinically acceptable values for these steady state controller performance statistics.
- Bias (median PI): measures any systematic deviation of the BSP from the target value. The bias is calculated as the median percent (%) error
- Inaccuracy (median absolute PI): measures the median value of the error magnitude, with units of percentage (%)
- Wobble: measures the total within-patient variability of the error over time, expressed as a percentage (%). This statistic reflects the CLAD system’s ability to maintain a stable depth of burst suppression by quantifying oscillations around the target burst suppression depth λ*,
The median values in these expressions are calculated across steady state measurements. We also compute the median and interquartile ranges across all experiments within a given MASH group to summarize the overall performance of the CLAD system.
3. Results
In this section we present performance and robustness results for each stage of the CLAD system design and testing process, including the ramp-drop procedure for PD parameter estimation, the Bayesian recursive state estimator, and the final integrated closed-loop control system under simulated ICU operating conditions. We present the evaluation of each component with an illustrative case, followed by a summary of performance statistics across the 54 conditions in our factorial experimental design. All experiments are based on Monte Carlo simulation of the PK parameters and external disturbances, as described sections 2.6.1 and 2.6.4.
3.1. Pharmacodynamic parameter estimation
3.1.1. Illustrative case
The ramp-drop experiment (section 2.6.3) allows us to estimate the unobservable PD paraemters C and γ from the binary EEG observations. For illustration, consider a 60 year old male with weight 75 kg and height 175 cm. To simulate clinical conditions, we characterize the patient’s response to propofol by a set of unobservable PK and PD parameters. We take the nominal PK values from the Schnider model equations (table 1). We generate the true (but unobservable) PK parameters by random perturbation of the nominal Schnider model values as described in section 2.6.1. The true and nominal PK parameter values k10, k12, k21, k13, k31, keo in this example are, respectively,
| True values: | 0.4206, 0.2478, 0.0688, 0.1725, 0.0031, 0.4560 |
| Nominal values: | 0.4091, 0.2628, 0.0694, 0.1958, 0.0035, 0.4560; |
where the units are min−1. In this and all subsequent experiments we assume that the true PD values are γ = 6.6 and C = 5.5 (section 2.6.2).
Figure 7 shows the results of running the ramp-drop experiment in this example case. The parameters estimated by the ramp-drop procedure are γest = 6.0835 and Cest = 5.431. As shown in the next sections, these values are close enough to the true values to allow accurate state estimation and robust feedback control.
3.2. Performance across patient characteristics
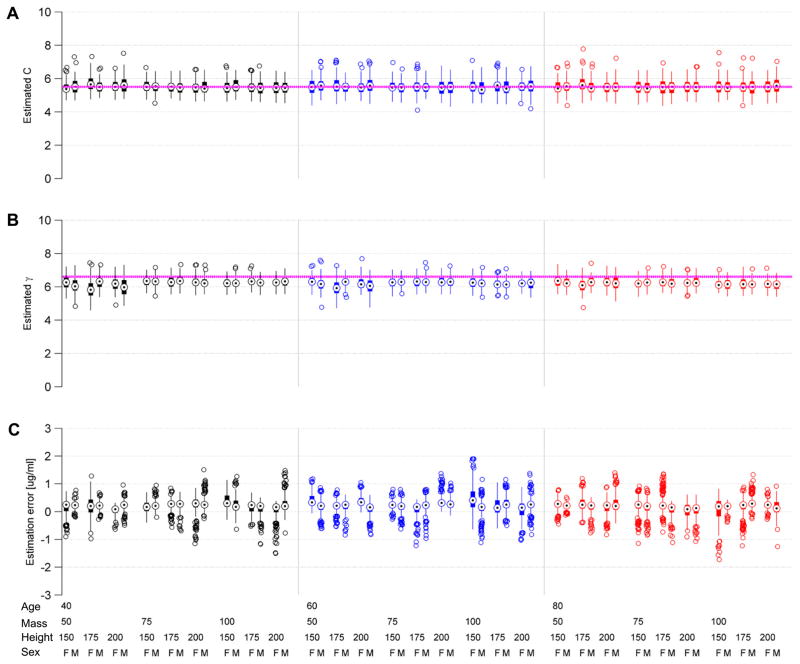
Figure 8 shows results for the ramp-drop PD parameter estimation from 5,400 simulated experiments, following the factorial experimental design described in section 2.7. In all experiments we set the true value for γ and C as γ = 6.6 and C = 5.5, respectively. Parameters in the nominal PK models were set equal to the population values given by the Schnider propofol PK model (table 1). True (unobserved) OK values were generated by random perturbation of the nominal model (see section 2.6.1).
Figure 8.
Box plots for factorial estimation experiments. Each experiment consists of 100 repetitions for each of 54 combinations of patient age (40, 60, 80 years), mass (50, 75, 100 kg), height (150, 175, 200 cm) and sex (male, M; female, F). Color groupings indicate patient ages. The top panels show results of the ramp-drop experiments for estimating the pharmacodynamic parameters C (A) and γ (B). The true parameter values C = 5.5 and γ = 6.6 used to generate the observations are indicated by pink dashed horizontal lines. The bottom panel (C) shows testing results for the state estimator. The results are expressed as the true minus the estimated effect site concentration. The estimated values for C and γ from the ramp-drop experiments were used in these experiments.
The global median and range (minimum, maximum) of the estimated values across all 5400 experiments were, for γ, 6.2 [4.6, 7.8], and for C 5.5 [4.1, 7.8]. Note that some of the variation in parameter estimates is attributable to mismatch of the nominal PK model with the true PK values, and may hence be ‘helpful’. These experiments suggest that the ramp-drop estimation procedure yields reasonably accurate estimates of the true parameters.
3.3. State estimation
3.3.1. Illustration
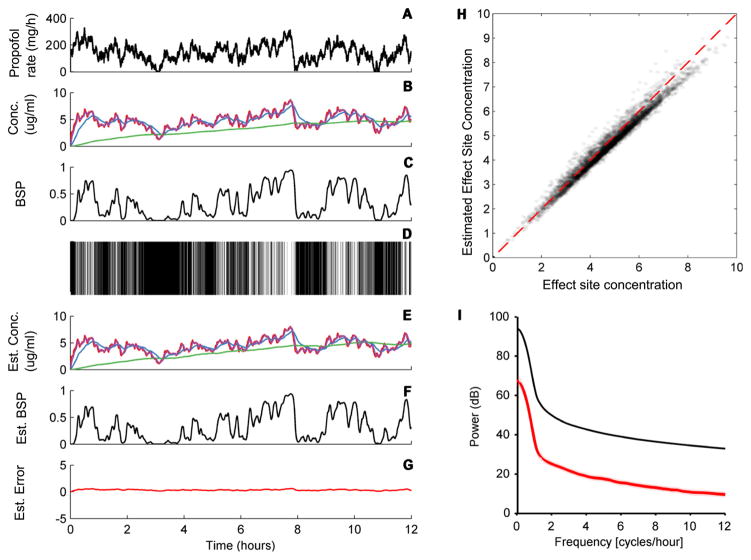
Continuing with the example from section 3.1.1, we next evaluated performance of the recursive state estimation algorithm. Figure 9 shows a 12 h simulation for the patient from section 3.1.1, in which propofol is infused with a randomly varying rate, generated as described in section 2.6.5. In the case shown, the estimated four-compartment drug concentrations closely match the true concentrations, yielding a small average observation error. A scatter scatter plot derived from repeated simulations with the same mass, age, sex, and height parameters demonstrates that the system behaves essentially linearly over all relevant concentrations. A regression fit to the data has a slope of 0.9786[95%CI: 0.9770, 0.9802] and intercept −0.2092 [−0.2267, −0.1916]; while the median estimation error and 95% quantile range for all error values across all conditions is −0.3991[−1.1217, 0.2442]. Thus, while there is some tendency to systematically underestimate the true value, the discrepancy is small. Finally, direct comparison between the power spectrum of the signal (effect site concentration) and the noise (estimation error) demonstrates excellent quality of the estimated signal over all relevant frequencies. This example suggests that the recursive Bayesian state estimate behaves, to a very good approximation, as linear observations of the signal in the presence of additive high frequency noise, with high signal to noise ratio, and is thus a suitable control signal.
Figure 9.
Estimation error of the BSP algorithm. The panels show an example of a randomly varying infusion rate (A), the resulting four-compartment drug concentrations (state) (B), burst suppression probability (BSP) (C), the resulting binary observations (D), the estimated state (E), the estimated BSP (F), and the discrepancy between the estimated and actual BSP, which is considered observation noise (G). (H) Effect site concentration values sampled every 5 min for 100 simulations like the one shows are plotted against the estimated values, demonstrating that the estimates are consistently accurate with minimal bias over the range of clinically relevant effect site concentrations, despite underlying uncertainty about the PK parameters and imperfect accuracy in the PD parameter estimation routine. (I) Power spectral density for the driving signal (black line) relative to the observation noise/estimation error power spectrum. The signal is well above the noise ratio at all relevant frequencies.
3.3.2. Performance across patient characteristics
Figure 8 shows the results of repeating the state estimation experiment from the previous section 100 times for each of 54 conditions, following the factorial experimental design described in section 2.7. We summarize performance results using box plots and showing the median, maximum, and minimum estimation error for each of the 54 conditions in the factorial design. Across all conditions the effect site concentration estimation error is tightly concentrated near zero.
3.4. Robust control
3.4.1. Illustration
Expanding on our example from section 3.1.1, we now demonstrate the ability of the final CLAD system to maintain target BSP levels for 24 h in four different simulated patients (figure 10). In these experiments we simulated the end-to-end operation of the CLAD controller in the ICU environment.
In each case we first ran the ramp drop ramp-drop experiment to estimated PD parameters, then synthesized the recursive estimator and controller using the estimated PD values and nominal (Schnider) PK values. We then simulated 24 h of control. Target values in each experiment consisted of, first, a 15 min long transition period in which the patient is brought from a state just prior to burst suppression, BSP = 0, to a deep state of burst suppression, BSP = 0.8. After maintaining this target for 8 h, we decreased the target value over 10 min to a lower depth of burst suppression, BSP = 0.6, as may be done if the treating physician decides that a lower dose of anesthetic is needed to reduce cardiovascular side effects. After maintaining this target for 8 h, we slowly taper the target BSP values over a period of 8 h to minimize the risk of rebound seizures.
In each experiment we again generate the true (but unobservable) PK model by perturbing the nominal (Schnider) model as described in section 2.6.1 to simulate PK uncertainty. We set the true (but also unobservable) PD parameters equal to γ = 6.6 and C = 5.5. For the recursive state estimator, we use the nominal PK values and the PD values estimated from the ramp-drop procedure. Finally, throughout each experiment we subject the CLAD system to a stochastic input disturbance with maximum amplitude equal to 50% of the infusion rate necessary to maintain steady state, as described in section 2.6.4. The presence of PK and PD parameter uncertainty and load disturbances in these experiments allowed us to evaluate whether the integrated CLAD system met transient and steady state performance specifications robustly.
Despite the uncertainties/errors in the PK and PD parameters, the robust CLAD controller maintains tight control of burst suppression throughout the 24 h period, both in steady state and during transitions. The controller simultaneously makes two types of adjustments to attain this level of control. First, the controller gradually reduces the long-term average infusion rate as drug accumulates in the patient’s slow compartment, effectively becoming a internal source of accumulated propofol. Second, the controller continually makes short-term adjustments to combat the load disturbance, increasing the propofol rate in response to negative load disturbances, and decreasing the rate in response to positive load disturbances.
The CLAD controller consistently maintains propofol infusion rates within the prescribed safety limits, never exceeding 12 mg kg−1 h−1, and always maintaining the maximum hourly cumulative propofol rate below 7 mg kg−1. The excellent performance seen in this example case holds generally, as demonstrated by the experiments described next.
3.4.2. Performance across patient characteristics
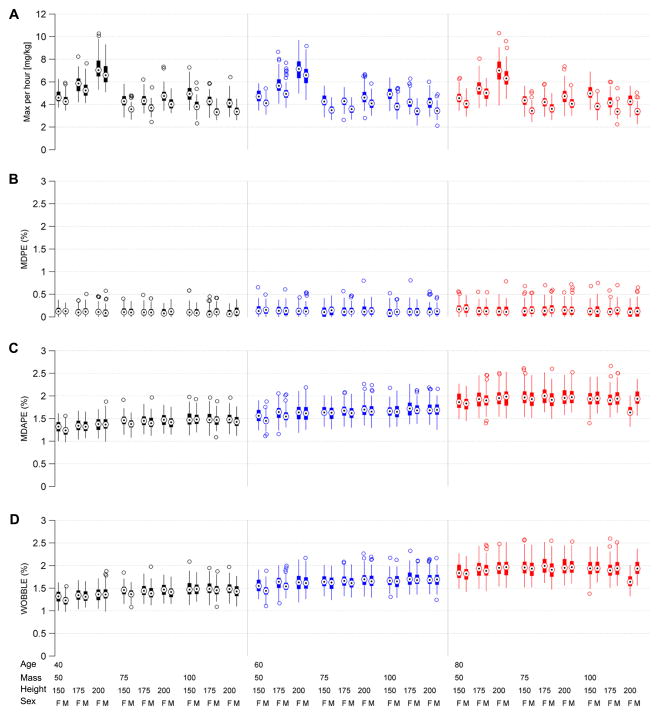
Box plots in figure 11 summarize the steady state performance results for the 5,400 experiments performed using our factorial design. All steady state performance measures were within specification (bias, accuracy, and wobble <5%) across all 54 MASH conditions. Global median (minimum, maximum) values across all experiments were, bias (MDPE) 0.1 [−0.5, 0.9]%; accuracy (MDAPE) 1.8 [0.9, 3.4]%; and oscillation index (‘wobble’) of 1.8 [0.9, 3.4]%.
Figure 11.
Steady state performance statistics for the CLAD system, including bias (median performance error, MDPE), inaccuracy (median absolute performance error, MDAPE), and oscillation index (WOBBLE). These values are obtained by repeating the experiment illustrated in figure 8 one hundred times for each of 54 patient demographic conditions, which vary according to a factorial design by patient mass, age, sex, and height. In these box plots, circles with central dots show median values, vertical lines show the upper and lower 95% parameter bounds, and empty circles show outliers. In all cases performance is within specification.
The median (min, max) value for the maximum cumulative propofol dose in any given hour was 4.3 [2.1, 10.3]. The number that exceeded the pre-specified clinical limit (7 mg kg−1 h−1) was 5.1% (275/4500). These rare cases were almost entirely in the tallest patients, and all occurred during periods when the BSP target was high, at 0.8. In clinical practice these cases would trigger an alert to the medical team. A typical physician response in such a case would be to either lower the target BSP if medically safe, or to add or increase the rate of another drug such as midazolam, thereby reducing the dose of propofol required to maintain the target BSP level. Note that in the latter case it might be necessary to re-estimate the propofol PD parameters used in the CLAD controller after the second drug reached steady state.
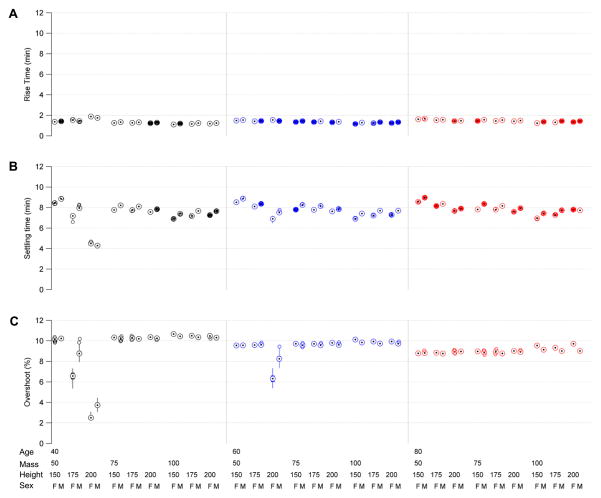
We performed a second set of 5,400 experiments using the same factorial design to investigate transient responses to a step command. We omitted load disturbances were omitted for these experiments. For each repetition we measured the rise time, percent overshoot, and settling time, in response to a step command chosen to drive the system from a BSP of 0 to 50/60 ≈ 83%, which is approximately the level typically targeted in treatment of RSE. Figure 12 summarizes the performance statistics. All transient performance measures were within specification (rise time <5 min, % overshoot <15%) across all 54 MASH conditions. The global median (minimum, maximum) values across all experiments were, for rise time 1.4 [1.1, 1.9] min; settling time, 7.8 [4.2, 9.0] min; and percent overshoot 9.6 [2.3, 10.8]%.
Figure 12.
Transient response performance statistics for the CLAD system, including rise time, settling time, and percent overshoot in response to a step command to bring the BSP from 0 to 80%. These values are obtained by repeating the experiment illustrated in figure 8 one hundred times for each of 54 patient demographic conditions, which vary according to a factorial design by patient mass, age, sex, and height. In these box plots, circles with central dots show median values, vertical lines show the upper and lower 95% parameter bounds, and empty circles show outliers. In all cases performance is within specification.
The results for the steady state and transient performance simulations indicate that the integrated CLAD system, including the ramp-drop PD estimation procedure, recursive Bayesian state estimation, and the robust PI controller design, is robust across and performs safely under the operating conditions approximating an ICU environment. We conclude that good closed-loop performance can be achieved by identifying a nominal PK/PD model using published population PK parameter values and safely estimated patient-specific PD (sigmoid) parameter values, in combination with well-established robust controller design methodology.
4. Discussion
We have developed a robust feedback control system for medical coma. The system maintains the brain state of a critically ill patient near a target depth of burst suppression by using EEG-based feedback to provide moment-by-moment adjustments to the rate of an infused anesthetic drug. Under conditions simulating realistic pharmacokinetic and phamarcodynamic uncertainty, our CLAD system accurately and robustly controlled burst suppression across a broad range of patient mass, age, height, and gender parameters. The system achieved clinically acceptable steady state performance across all patient conditions, with a maximium bias of <1%, maximum inaccuracy <4%, and maximum oscillation index of <4%. Transient responses were likewise clinically acceptable, with maximum rise time <2 min, maximum percent overshoot <11%, and setting time <10 min. All of these values fall well within clinically acceptable limits.
4.1. Relation to prior CLAD research
Our work builds on a growing body of research dating back to the 1950s aimed at regulating brain states during anesthesia [66, 67]. Open loop or ‘target controlled infusion’ systems enjoy widespread use outside the United States [53, 68, 69]. Several prototype closed-loop systems for general anesthesia have been tested in pilot studies [27–31, 66, 67, 70–73]. Systems developed to date have relied on a variety of computed EEG features, including wavelet coefficients [72], median spectral frequency [74], BIS [27, 28, 75–77], and signal entropy [78]. Some of these derived EEG signals have recently come under criticism for being unphysiological and for being unreliable indicators of depth of anesthesia [36, 79–81]. Consequently the the EEG correlates of general anesthesia remains an area of active research. By contrast, burst suppression is a well-defined, ‘high signal to noise ratio’ EEG pattern, which is reliably quantifiable in ICU patients [18–20].
In this work we introduced three new innovations, namely, an ICU-safe method for obtaining patient-specific estimates of pharmacodynamic parameters; an improved method for tracking the depth of burst suppression; and a controller design procedure that is explicitly formulated to be robust in the presence of disturbances, estimation noise, and PK parameter uncertainty.
4.2. State estimation for tracking burst suppression depth
Our CLAD framework pairs a four-dimensional recursive state estimator with an optimal PI controller. The recursive estimation algorithm is a critical factor underlying our controller’s ability to acheive good transient performance in response to set point changes. By incorporating a full four-dimensional dynamical model of propofol pharmacokinetics, and updating the full state vector x(t) = (x1(t), x2(t), x3(t), x4(t)) at each time step, our estimator produced estimates which accurately tracked the effects of the time-varying drug infusion rate. The ability of the estimator to tightly track the effect site concentration x4(t) with negligible lag largely accounts for the fact that the PI controller is able to achieve rise time, percent overshoot, and settling time that are all well within clinically acceptable limits.
An improvement of the BSP estimation algorithm presented herein over a previous design [37] is that the current version employs a sigmoidal function (Hill equation) to capture patient pharmacodynamics. The logistic link function used in previous work λt = (1 − exp(−x4t)/(1 + exp(−x4t) has a maximum slope at an effect site concentration of x4t = 0. However, low concentrations of propofol generally induce sedation without causing burst suppression. By contrast, the sigmoid link function, , is nearly equal to zero up to a positive ‘takeoff point’ which can be matched to an individual patient’s onset of burst suppression. The sigmoid equation provides a more flexible and realistic model for burst suppression pharmacodynamics.
In this work we also presented a ‘ramp-drop’ infusion experiment to allow safe estimation of the sigmoid PD parameters in critically ill patients. This procedure involves a gradual increase in the rate of anesthetic to reveal the steady state level of burst suppression as a function of effect site concentration. Because this ramp maneuver involves only gradual increases in anesthetic infusion rate, there is ample time for a supervising clinician to respond to any adverse effects that may develop. This procedure can thus be safely performed in critically ill patients. By allowing accurate estimation of patient-specific sigmoid parameters, the ramp-drop procedure enhances the tracking ability of the state estimator. In the subsequent ‘drop’ part of the procedure, we reduce the propofol infusion rate and allow the patient to drift out of burst suppression. This maneuver is also generally safe in critically ill patients. Indeed shutting off anesthetic infusions is routinely performed in ICU patients to allow reliable neurological examinations.
Unlike previous work in animals, we have not attempted to estimate patient-specific PK parameters in this work. This is because safety considerations preclude the type of dynamic manipulation of infusion rates needed for full PK model identification. Consequently we set the PK parameters to their demographic-adjusted population values. Robust controller design techniques compensate for the resulting uncertainty about patient-specific PK parameter values.
Because of the excellent tracking performance of the recrusive BSP estimation procedure, we were also able to demonstrate that the highly nonlinear transformation x4(t) → y(t) (i.e. x4(t) = effect site concentration → binary signal → nonlinear recursive Bayesian estimate = y(t)) is well approximated by a a simple additive noise model, y(t) ≈ x4(t) + n(t), where the estimation error or ‘noise’ n(t) is high-frequency noise which is spectrally well-separated from the effect site concentration dynamics at low/clinically relevant frequencies. In turn, this feature allows the entire PK–PD model to be treated mathematically within the framework of stochastic linear dynamical systems, a necessary condition for the application of robust control system design methodology.
4.3. Robustness
Many previous studies have addressed closed-loop control of anesthesia [27–30]. However, most have approached the tuning of control algorithms empirically, without using rigorous techniques that explicitly account for uncertainties in pharmacokinetic and pharmacodynamics parameters, state estimation error, and external disturbances. As argued in [35], this lack of rigor strongly contributes to the general resistance of the medical community at large to closed-loop control devices in anesthesia and other domains. In turn, it is likely that for widespread adoption to occur, any CLAD system will need to pass through a certification process that will include robust performance criteria.
Previous work on closed-loop control of burst suppression has likewise not taken advantage of explicit robust controller design techniques [37, 47], leaving the work open to concerns about safety of operation under real-world ICU operating conditions.
In the present work we have closed this gap, by formulating the design of the controller component of our CLAD system as the solution to a well studied optimization problem. For our PI controller optimization we used a robust loop shaping procedure designed to achieve good performance while explicitly allowing for PK modeling error, estimation error, and load disturbances. Our design method is automatic, requiring no empirical or hand-tuning of parameters. The simulations presented herein demonstrate that it is possible to design safe and reliable CLAD systems for robust control of medical coma.
4.4. Limitations
Our primary motivation for the present work is the need for safety in the face of PK and PD variability in the ICU population. We have addressed this challenge by formulating our CLAD system within a robust control framework, by choosing PD parameters for our simulations that reflect the lower propofol requirements of ICU patients, by introducing a safe and practical method for estimating individualized PD models, and by performing extensive Monte Carlo sampling over possible PK parameters. Nevertheless, despite these efforts, caution will be necessary when moving to human testing. In particular, it is conceivable that for some critically ill patients the Schnider PK model will be so inaccurate that our design may not be able to compensate. Therefore in human pilot studies several additional safety measures, not discussed in the present work, will be necessary. These include hard limits to drug infusion rates, alerts that sound in case of out-of-range BSP values, and a manual override function that allows a human operator to take over at any time.
A second limitation is related to the ramp-drop procedure which we have proposed for estimating patient-specific PD parameters. In some patients this procedure might lead to seizure recurrence. Nevertheless, as described above, this procedure will generally be safe, and at minimum will not increase risk beyond current practices, for three reasons. First, in clinical practice the induction of burst suppression and titration to target BSP levels typically takes longer than the proposed ramp-drop procedure (unpublished observations). Overall we expect that our system will allow not only tighter control, but also more reliable and more rapid attainment of therapeutic BSP targets. Second, because the ramp maneuver involves only gradual increases in anesthetic infusion rate, there is sufficient time for a supervising clinician to respond to any adverse effects that may develop. Finally, after attainment of target levels, current practice is to periodically reduce or discontinue propofol to allow neurological assessments and to assess for seizure recurrence. This routine procedure provides a natural window in which to perform the ramp-drop experiment and to begin control in patients not recruited immediately at the time of diagnosis and initiation of treatment. An alternative approach would be to start with a reasonable initial population-based PD model, and to update the model adaptively based on discrepancies between the predicted and observed BSP. This approach presents additional challenges for ensuring stability of the controller design, but ultimately may provide greater safety and ease of use. We are exploring the issue of adaptive estimation in the loop currently.
A final limitation is that the PD model estimated by the ramp-drop procedure could be invalidated in case rates of other burst suppression maintenance medications (e.g. midazolam) other than propofol are changed. This limitation is addressed in part by the robustness of the controller design. However, for initial human pilot studies, we will require that either no changes to maintenance medications during the operation of the controller, or that in case of a change, the ramp-drop procedure will be repeated to estimate a new PD model before resuming control. As mentioned in the previous paragraph, future research on in-the-loop adaptive PK/PD estimation may eventually remove the need for these precautions.
4.5. Advantages and potential clinical benefits over current practice
Medical coma for the treatment of RSE and severe intracranial hypertension following traumatic brain injury must often be maintained for days at a time. Under current practice, medical personell monitor the EEG and adjust anesthetic rates manually. Practical realities and limited resources dicatate that the majority of this anesthesiologists’ and clinical-neurophysiologists’ task falls to staff who lack expertise in either clinical EEG analysis or in anesthesiology. Moreover, staff necessarily perform manual monitoring and anesthetic adjustments only intermittently. Consequently, levels of burst suppression in practice often drift out of target range. Automated control of burst suppression holds promise as a more efficient and reliable means to regulate medical coma in the these critically ill patients.
Our results show how it is possible to develop a robust CLAD system to manage medical coma in critically ill patients. Using the methods presented herein, we can construct a CLAD system with proven stability and clinically acceptable transient and steady state performance. This can be done in the face of PK and PD values that fall within a clinically realistic range of uncertainty. By using a carefully designed dose-response experiment, we can safely compensate for additional pharmacodynamic variation introduced by the presence of organ system dysfunction and concurrent medications. By using robust control design techniques and statistically principled EEG processing methods, the resulting control system can be made safe and reliable.
This CLAD design framework paves the way for clinical investigation of the hypothesis that automated regulation of burst suppression can provide tighter adherence to therapeutic target depths of medical coma, while using less anesthetic and subjecting the patient to fewer large changes in anesthetic infusion rates. In turn, with reduced anesthetic doses it is reasonable to expect reduced ICU lengths of stay, fewer morbidities, and potentially better outcomes (e.g. more rapid resolution of RSE).
Appendix. Derivation of the BSP algorithm
In this section we derive the update and prediction equations of the BSP algorithm (equations (8)–(14)). The BSP equations represent a recursive Bayesian inference procedure for estimating the burst suppression probability (BSP) from the binary observations.
Recall from (5) that the probability of observing a suppression in any small interval Δ is given by the conditional intensity function in discrete time as
In addition, in equation (6) we expressed the PK dynamics of the log-transformed state vector zt = log(xt) as
where wt = (w1t, w2t, w3t, w4t)′ is an i.i.d. sequence wt ~ N(0, W), W = Iσ2, and zt = (z1t, z2t, z3t, z4t)′.
Next, denote the binary sequence of data observed so far by , and the history of the state variable as . Then using Bayes rule and noting that nt depends on the history only through the current value of zt, we can write the posterior distribution as
| (28) |
The second term in the numerator is the Bernoulli observation model given above and in equation (5), expressed in terms of zt instead of xt (equivalent because the transformation xt = exp(zt) is invertible). The first term in the numerator can be written using the Chapman–Kolmogorov equation and the Markov structure of the state model as
| (29) |
The term p(zt|zt−1) comes from the prior model (6), and the second term is the posterior density from the previous time step. Hence substituting (29) and (5) into (28) yields the recursion
| (30) |
Evaluating (30) is difficult, because the prior (state dyanmics model) (6) is nonlinear and the observation model is binomial rather than Gaussian. Therefore we make two approximations: (1) a linear approximation to the prior at each time step, which allows us to approximate the prediction density as Gaussian; (2) a Gaussian approximation to the update equation (posterior), at each time step.
Denote the mean and covariance matrix of the posterior by
| (31) |
| (32) |
and similarly for the mean and covariance matrix of the one step prediction density write
| (33) |
| (34) |
Linearizing the prior (6) around the posterior mean from the previous step we have
with
| (35) |
where for i = 1,
| (36) |
and for i = 2, 3, 4
| (37) |
Using this approximation the prediction density will be approximately Gaussian, and the approximate prediction mean and covariance are
| (38) |
| (39) |
Next we introduce a Gaussian approximation to the posterior distribution (30):
| (40) |
The first expression approximates the Chapman–Kolmogorov integral as a Gaussian centered at the one step prediction estimate, and the second line approximates the entire function as a Gaussian density with parameters zt|t and Wt|t, which remain to be determined. To find these parameters, we first take the log of both sides to get
| (41) |
where R is a constant that does not depend on zt. Differentiating with respect to zt gives
| (42) |
Substituting zt = zt|t−1 gives
| (43) |
Solving for zt|t gives the posterior mean state update equation
| (44) |
Diffentiating (42) again and once more setting zt = zt|t−1 gives the posterior variance equation,
| (45) |
Working out the derivatives and substituting yields the expressions for the prediction and update equations.
Contributor Information
M Brandon Westover, Email: mwestover@mgh.harvard.edu.
Emery N Brown, Email: enb@neurostat.mit.edu.
References
- 1.Stecker MM, et al. Deep hypothermic circulatory arrest: I. Effects of cooling on electroencephalogram and evoked potentials. Ann Thoracic Surg. 2001;71:14–21. doi: 10.1016/s0003-4975(00)01592-7. [DOI] [PubMed] [Google Scholar]
- 2.Brown EN, Lydic R, Schiff ND. General anesthesia, sleep, and coma. New England J Med. 2010;363:2638–50. doi: 10.1056/NEJMra0808281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brain Trauma Foundation. The American Association of Neurological Surgeons. The Joint Section on Neurotrauma and Critical Care . The use of barbiturates in the control of intracranial hypertension. J Neurotrauma. 1996;13:711–4. [Google Scholar]
- 4.Lima B, et al. Results of proximal arch replacement using deep hypothermia for circulatory arrest: is moderate hypothermia really justifiable? Am Surgeon. 2011;77:1438–44. [PMC free article] [PubMed] [Google Scholar]
- 5.Weiss AJ, et al. A propensity score-matched comparison of deep versus mild hypothermia during thoracoabdominal aortic surgery. J Thoracic Cardiovascular Surg. 2012;143:186–93. doi: 10.1016/j.jtcvs.2011.07.020. [DOI] [PubMed] [Google Scholar]
- 6.Englum BR, Andersen ND, Husain AM, Mathew JP, Hughes GC. Degree of hypothermia in aortic arch surgery-optimal temperature for cerebral and spinal protection: deep hypothermia remains the gold standard in the absence of randomized data. Ann Cardiothoracic Surg. 2013;2:184–93. doi: 10.3978/j.issn.2225-319X.2013.03.01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Coselli JS, et al. Determination of brain temperatures for safe circulatory arrest during cardiovascular operation. Ann Thoracic Surg. 1988;45:638–42. doi: 10.1016/s0003-4975(10)64766-2. [DOI] [PubMed] [Google Scholar]
- 8.Bavaria JE, et al. New paradigms and improved results for the surgical treatment of acute type a dissection. Ann Surg. 2001;234:336–42. doi: 10.1097/00000658-200109000-00007. discussion 342–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brain Trauma Foundation, American Association of Neurological Surgeons, Congress of Neurological Surgeons, Joint Section on Neurotrauma and Critical Care, AANS/CNS. Bratton SL, et al. Guidelines for the management of severe traumatic brain injury. XI. Anesthetics, analgesics, and sedatives. J Neurotrauma. 2007;24(Suppl 1):S71–76. doi: 10.1089/neu.2007.9985. [DOI] [PubMed] [Google Scholar]
- 10.Costello DJ, Cole AJ. Treatment of acute seizures and status epilepticus. J Intensive Care Med. 2007;22:319–47. doi: 10.1177/0885066607307506. [DOI] [PubMed] [Google Scholar]
- 11.Arif H, Hirsch LJ. Treatment of status epilepticus. Semin Neurology. 2008;28:342–54. doi: 10.1055/s-2008-1079339. [DOI] [PubMed] [Google Scholar]
- 12.Pang T, Hirsch LJ. Treatment of convulsive and nonconvulsive status epilepticus. Curr Treat Options Neurology. 2005;7:247–59. doi: 10.1007/s11940-005-0035-x. [DOI] [PubMed] [Google Scholar]
- 13.Claassen J, Hirsch LJ, Mayer SA. Treatment of status epilepticus: a survey of neurologists. J Neurological Sci. 2003;211:37–41. doi: 10.1016/s0022-510x(03)00036-4. [DOI] [PubMed] [Google Scholar]
- 14.Shorvon S, Ferlisi M. The treatment of super-refractory status epilepticus: a critical review of available therapies and a clinical treatment protocol. Brain: J Neurology. 2011;134:2802–18. doi: 10.1093/brain/awr215. [DOI] [PubMed] [Google Scholar]
- 15.Niedermeyer E. The burst-suppression electroencephalogram. Am J Electroneurodiagn Technol. 2009;49:333–41. [PubMed] [Google Scholar]
- 16.Swank RL, Watson CW. Effects of barbiturates and ether on spontaneous electrical activity of dog brain. J Neurophysiol. 1949;12:137–60. doi: 10.1152/jn.1949.12.2.137. [DOI] [PubMed] [Google Scholar]
- 17.Vijn PC, Sneyd JR. I.v. anaesthesia and EEG burst suppression in rats: bolus injections and closed-loop infusions. Br J Anaesthesia. 1998;81:415–21. doi: 10.1093/bja/81.3.415. [DOI] [PubMed] [Google Scholar]
- 18.Chemali JJ, Wong KFK, Solt K, Brown EN. A state-space model of the burst suppression ratio. Conf Proc: Annual Int Conf of the IEEE Engineering in Medicine and Biology Society. 2011:1431–4. doi: 10.1109/IEMBS.2011.6090354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chemali J, Ching S, Purdon PL, Solt K, Brown EN. Burst suppression probability algorithms: state-space methods for tracking EEG burst suppression. J Neural Eng. 2013;10:056017. doi: 10.1088/1741-2560/10/5/056017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Westover MB, Ching S, Shafi MM, Cash SS, Brown EN. Real-time segmentation and tracking of brain metabolic state in ICU EEG recordings of burst suppression. Proc of the Ann Int IEEE Conf Engineering in Medicine and Biology Society. 2013:7108–11. doi: 10.1109/EMBC.2013.6611196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Parviainen I, Uusaro A, Kälviäinen R, Mervaala E, Ruokonen E. Propofol in the treatment of refractory status epilepticus. Intensive Care Med. 2006;32:1075–9. doi: 10.1007/s00134-006-0154-1. [DOI] [PubMed] [Google Scholar]
- 22.Rossetti AO, Logroscino G, Bromfield EB. Refractory status epilepticus: effect of treatment aggressiveness on prognosis. Arch Neurology. 2005;62:1698–702. doi: 10.1001/archneur.62.11.1698. [DOI] [PubMed] [Google Scholar]
- 23.Krishnamurthy KB, Drislane FW. Depth of EEG suppression and outcome in barbiturate anesthetic treatment for refractory status epilepticus. Epilepsia. 1999;40:759–62. doi: 10.1111/j.1528-1157.1999.tb00775.x. [DOI] [PubMed] [Google Scholar]
- 24.McCollam JS, O’Neil MG, Norcross ED, Byrne TK, Reeves ST. Continuous infusions of lorazepam, midazolam, and propofol for sedation of the critically ill surgery trauma patient: a prospective, randomized comparison. Crit Care Med. 1999;27:2454–8. doi: 10.1097/00003246-199911000-00022. [DOI] [PubMed] [Google Scholar]
- 25.Jackson DL, Proudfoot CW, Cann KF, Walsh TS. The incidence of sub-optimal sedation in the ICU: a systematic review. Crit Care. 2009;27:R204. doi: 10.1186/cc8212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Payen JF, et al. Current practices in sedation and analgesia for mechanically ventilated critically ill patients: a prospective multicenter patient-based study. Anesthesiology. 2007;106:687–95. doi: 10.1097/01.anes.0000264747.09017.da. quiz 891–892. [DOI] [PubMed] [Google Scholar]
- 27.Absalom AR, Sutcliffe N, Kenny GN. Closed-loop control of anesthesia using bispectral index: performance assessment in patients undergoing major orthopedic surgery under combined general and regional anesthesia. Anesthesiology. 2002;96:67–73. doi: 10.1097/00000542-200201000-00017. [DOI] [PubMed] [Google Scholar]
- 28.Struys MM, et al. Comparison of closed-loop controlled administration of propofol using bispectral index as the controlled variable versus ‘standard practice’ controlled administration. Anesthesiology. 2001;95:6–17. doi: 10.1097/00000542-200107000-00007. [DOI] [PubMed] [Google Scholar]
- 29.Liu N, et al. Titration of propofol for anesthetic induction and maintenance guided by the bispectral index: closed-loop versus manual control: a prospective, randomized, multicenter study. Anesthesiology. 2006;104:686–95. doi: 10.1097/00000542-200604000-00012. [DOI] [PubMed] [Google Scholar]
- 30.Puri GD, Kumar B, Aveek J. Closed-loop anaesthesia delivery system (CLADS) using bispectral index: a performance assessment study. Anaesthesia Intensive Care. 2007;35:357–62. doi: 10.1177/0310057X0703500306. [DOI] [PubMed] [Google Scholar]
- 31.West N, et al. Robust closed-loop control of induction and maintenance of propofol anesthesia in children. Paediatric Anaesthesia. 2013;23:712–9. doi: 10.1111/pan.12183. [DOI] [PubMed] [Google Scholar]
- 32.Pilge S, et al. Time delay of index calculation: analysis of cerebral state, bispectral, and narcotrend indices. Anesthesiology. 2006;104:488–94. doi: 10.1097/00000542-200603000-00016. [DOI] [PubMed] [Google Scholar]
- 33.Zanner R, Pilge S, Kochs EF, Kreuzer M, Schneider G. Time delay of electroencephalogram index calculation: analysis of cerebral state, bispectral, and narcotrend indices using perioperatively recorded electroencephalographic signals. Br J Anaesthesia. 2009;103:394–9. doi: 10.1093/bja/aep198. [DOI] [PubMed] [Google Scholar]
- 34.Zikov T, Bibian S, Dumont GA, Huzmezan M, Ries CR. Quantifying cortical activity during general anesthesia using wavelet analysis. IEEE Trans Bio-Med Eng. 2006;53:617–32. doi: 10.1109/TBME.2006.870255. [DOI] [PubMed] [Google Scholar]
- 35.Dumont GA, Martinez A, Ansermino JM. Robust control of depth of anesthesia. Int J Adapt Control Signal Process. 2009;23:435–54. [Google Scholar]
- 36.Purdon PL, et al. Electroencephalogram signatures of loss and recovery of consciousness from propofol. Proc Natl Acad Sci USA. 2013;110:E1142–1151. doi: 10.1073/pnas.1221180110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shanechi MM, Chemali JJ, Liberman M, Solt K, Brown EN. A brain-machine interface for control of medically-induced coma. PLoS Comput Biol. 2013;9:e1003284. doi: 10.1371/journal.pcbi.1003284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Weinert CR, Calvin AD. Epidemiology of sedation and sedation adequacy for mechanically ventilated patients in a medical and surgical intensive care unit. Crit Care Med. 2007;35:393–401. doi: 10.1097/01.CCM.0000254339.18639.1D. [DOI] [PubMed] [Google Scholar]
- 39.Coppens M, et al. Study of the time course of the clinical effect of propofol compared with the time course of the predicted effect-site concentration: performance of three pharmacokinetic-dynamic models. Br J Anaesthesia. 2010;104:452–8. doi: 10.1093/bja/aeq028. [DOI] [PubMed] [Google Scholar]
- 40.Schnider TW, Gentilini A, Wymann R. Feedback controlled anesthesia: can the computer replace the anesthesiologist? Acta Anaesthesiologica Belgica. 2001;52:201–4. [PubMed] [Google Scholar]
- 41.Schnider TW, et al. The influence of method of administration and covariates on the pharmacokinetics of propofol in adult volunteers. Anesthesiology. 1998;88:1170–82. doi: 10.1097/00000542-199805000-00006. [DOI] [PubMed] [Google Scholar]
- 42.Lichtenbelt BJ, et al. Propofol reduces the distribution and clearance of midazolam. Anesthesia Analgesia. 2010;110:1597–606. doi: 10.1213/ANE.0b013e3181da91bb. [DOI] [PubMed] [Google Scholar]
- 43.Hamaoka N, et al. Propofol decreases the clearance of midazolam by inhibiting CYP3a4: an in vivo and in vitro study. Clin Pharmacology Therapeutics. 1999;66:110–7. doi: 10.1053/cp.1999.v66.100038001. [DOI] [PubMed] [Google Scholar]
- 44.Tatum WO, Dworetzky BA, Schomer DL. Artifact and recording concepts in EEG. J Clin Neurophysiol: Official Publ Am Electroencephalographic Soc. 2011;28:252–63. doi: 10.1097/WNP.0b013e31821c3c93. [DOI] [PubMed] [Google Scholar]
- 45.Friedman D, Claassen J, Hirsch LJ. Continuous electroencephalogram monitoring in the intensive care unit. Anesthesia Analgesia. 2009;109:506–23. doi: 10.1213/ane.0b013e3181a9d8b5. [DOI] [PubMed] [Google Scholar]
- 46.Wittman JJ, Jr, Hirsch LJ. Continuous electroencephalogram monitoring in the critically ill. Neurocritical Care. 2005;2:330–41. doi: 10.1385/ncc:2:3:330. [DOI] [PubMed] [Google Scholar]
- 47.Ching S, et al. Real-time closed-loop control in a rodent model of medically induced coma using burst suppression. Anesthesiology. 2013;119:848–60. doi: 10.1097/ALN.0b013e31829d4ab4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ching S, et al. Real-time closed-loop control in a rodent model of medically induced coma using burst suppression. Anesthesiology. 2013;119:848–60. doi: 10.1097/ALN.0b013e31829d4ab4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rossetti AO. Which anesthetic should be used in the treatment of refractory status epilepticus? Epilepsia. 2007;48(Suppl 8):52–55. doi: 10.1111/j.1528-1167.2007.01350.x. [DOI] [PubMed] [Google Scholar]
- 50.Hwang WS, Gwak HM, Seo DW. Propofol infusion syndrome in refractory status epilepticus. J Epilepsy Res. 2013;3:21–27. doi: 10.14581/jer.13004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rossetti AO, Reichhart MD, Schaller MD, Despland PA, Bogousslavsky J. Propofol treatment of refractory status epilepticus: a study of 31 episodes. Epilepsia. 2004;45:757–63. doi: 10.1111/j.0013-9580.2004.01904.x. [DOI] [PubMed] [Google Scholar]
- 52.Schnider TW, et al. The influence of age on propofol pharmacodynamics. Anesthesiology. 1999;90:1502–16. doi: 10.1097/00000542-199906000-00003. [DOI] [PubMed] [Google Scholar]
- 53.Schnider T, Minto C. Pharmacokinetic models of propofol for TCI. Anaesthesia. 2008;63:206. doi: 10.1111/j.1365-2044.2007.05419_1.x. author reply 206207. [DOI] [PubMed] [Google Scholar]
- 54.Absalom AR, Mani V, De Smet T, Struys MMRF. Pharmacokinetic models for propofol-defining and illuminating the devil in the detail. Br J Anaesthesia. 2009;103:26–37. doi: 10.1093/bja/aep143. [DOI] [PubMed] [Google Scholar]
- 55.Rampil IJ. A primer for EEG signal processing in anesthesia. Anesthesiology. 1998;89:980–1002. doi: 10.1097/00000542-199810000-00023. [DOI] [PubMed] [Google Scholar]
- 56.Rampil IJ, Laster MJ. No correlation between quantitative electroencephalographic measurements and movement response to noxious stimuli during isoflurane anesthesia in rats. Anesthesiology. 1992;77:920–5. doi: 10.1097/00000542-199211000-00014. [DOI] [PubMed] [Google Scholar]
- 57.Åström KJ, Hägglund T. Advanced PID Control. Instrumentation, Systems and Automation Society; Research Triangle Park, NC: 2006. ( http://lup.lub.lu.se/record/535630) [Google Scholar]
- 58.Garpinger O, Hagglund T. A software tool for robust PID design. Proc 17th IFAC World Congress.2008. [Google Scholar]
- 59.Rowland M. Clinical Pharmacokinetics and Pharmacodynamics: Concepts and Applications. 4. Philadelphia: LWW; 2010. [Google Scholar]
- 60.Pilge S, Jordan D, Kreuzer M, Kochs EF, Schneider G. Burst suppression-MAC and burst suppression-CP50 as measures of cerebral effects of anaesthetics. Br J Anaesthesia. 2014;112:1067–74. doi: 10.1093/bja/aeu016. [DOI] [PubMed] [Google Scholar]
- 61.Hendrickx JFA, Eger EI, Sonner JM, Shafer SL. Is synergy the rule? a review of anesthetic interactions producing hypnosis and immobility. Anesthesia Analgesia. 2008;107:494–506. doi: 10.1213/ane.0b013e31817b859e. [DOI] [PubMed] [Google Scholar]
- 62.McClune S, McKay AC, Wright PM, Patterson CC, Clarke RS. Synergistic interaction between midazolam and propofol. Br J Anaesthesia. 1992;69:240–5. doi: 10.1093/bja/69.3.240. [DOI] [PubMed] [Google Scholar]
- 63.Lagarias J, Reeds J, Wright M, Wright P. Convergence properties of the Nelder–Mead simplex method in low dimensions. SIAM J Optim. 1998;9:112–47. [Google Scholar]
- 64.Varvel JR, Donoho DL, Shafer SL. Measuring the predictive performance of computer-controlled infusion pumps. J Pharmacokinetics Biopharmaceutics. 1992;20:63–94. doi: 10.1007/BF01143186. [DOI] [PubMed] [Google Scholar]
- 65.Struys MMRF, et al. Performance evaluation of two published closed-loop control systems using bispectral index monitoring: a simulation study. Anesthesiology. 2004;100:640–7. doi: 10.1097/00000542-200403000-00026. [DOI] [PubMed] [Google Scholar]
- 66.Bickford RG. Automatic electroencephalographic control of general anesthesia. Electroencephalogr Clin Neurophysiol. 1950;2:93–96. doi: 10.1016/0013-4694(51)90058-2. [DOI] [PubMed] [Google Scholar]
- 67.Mayo CW, Bickford RG, Faulconer A. Electroencephalographically controlled anesthesia in abdominal surgery. J Am Med Assoc. 1950;144:1081–3. doi: 10.1001/jama.1950.02920130033008. [DOI] [PubMed] [Google Scholar]
- 68.Breslin DS, Mirakhur RK, Reid JE, Kyle A. Manual versus target-controlled infusions of propofol. Anaesthesia. 2004;59:1059–63. doi: 10.1111/j.1365-2044.2004.03870.x. [DOI] [PubMed] [Google Scholar]
- 69.Guarracino F, et al. Target controlled infusion: Tci. Minerva Anestesiologica. 2005;71:335–7. [PubMed] [Google Scholar]
- 70.Schwilden H, Stoeckel H. Closed-loop feedback controlled administration of alfentanil during alfentanil-nitrous oxide anaesthesia. Br J Anaesthesia. 1993;70:389–93. doi: 10.1093/bja/70.4.389. [DOI] [PubMed] [Google Scholar]
- 71.Gentilini A, et al. Modeling and closed-loop control of hypnosis by means of bispectral index (BIS) with isoflurane. IEEE Trans Biomed Eng. 2001;48:874–89. doi: 10.1109/10.936364. [DOI] [PubMed] [Google Scholar]
- 72.Hahn JO, Dumont GA, Ansermino J. Robust closed-loop control of propofol administration using WAVCNS index as the controlled variable. Proc of the Ann Int IEEE Conf Engineering in Medicine and Biology Society. 2010:6038–41. doi: 10.1109/IEMBS.2010.5627609. [DOI] [PubMed] [Google Scholar]
- 73.Hahn JO, Dumont GA, Ansermino JM. Closed-loop anesthetic drug concentration estimation using clinical-effect feedback. IEEE Trans Biomed Eng. 2011;58:3–6. doi: 10.1109/TBME.2010.2076811. [DOI] [PubMed] [Google Scholar]
- 74.Schwilden H, Stoeckel H, Schüttler J. Closed-loop feedback control of propofol anaesthesia by quantitative EEG analysis in humans. Br J Anaesthesia. 1989;62:290–6. doi: 10.1093/bja/62.3.290. [DOI] [PubMed] [Google Scholar]
- 75.Liu N, et al. Titration of propofol for anesthetic induction and maintenance guided by the bispectral index: closed-loop versus manual control: a prospective, randomized, multicenter study. Anesthesiology. 2006;104:686–95. doi: 10.1097/00000542-200604000-00012. [DOI] [PubMed] [Google Scholar]
- 76.Reboso JA, Méndez JA, Reboso HJ, León AM. Design and implementation of a closed-loop control system for infusion of propofol guided by bispectral index (BIS) Acta Anaesthesiologica Scand. 2012;56:1032–41. doi: 10.1111/j.1399-6576.2012.02738.x. [DOI] [PubMed] [Google Scholar]
- 77.De Smet T, et al. The accuracy and clinical feasibility of a new bayesian-based closed-loop control system for propofol administration using the bispectral index as a controlled variable. Anesthesia Analgesia. 2008;107:1200–10. doi: 10.1213/ane.0b013e31817bd1a6. [DOI] [PubMed] [Google Scholar]
- 78.Liu N, et al. Feasibility of closed-loop titration of propofol and remifentanil guided by the spectral m-entropy monitor. Anesthesiology. 2012;116:286–95. doi: 10.1097/ALN.0b013e318242ad4f. [DOI] [PubMed] [Google Scholar]
- 79.Nasraway SA, Jr, Wu EC, Kelleher RM, Yasuda CM, Donnelly AM. How reliable is the bispectral index in critically ill patients? a prospective, comparative, single-blinded observer study. Crit Care Med. 2002;30:1483–7. doi: 10.1097/00003246-200207000-00014. [DOI] [PubMed] [Google Scholar]
- 80.Avidan MS, et al. Prevention of intraoperative awareness in a high-risk surgical population. New England J Med. 2011;365:591–600. doi: 10.1056/NEJMoa1100403. [DOI] [PubMed] [Google Scholar]
- 81.Whitlock EL, et al. Relationship between bispectral index values and volatile anesthetic concentrations during the maintenance phase of anesthesia in the b-unaware trial. Anesthesiology. 2011;115:1209–18. doi: 10.1097/ALN.0b013e3182395dcb. [DOI] [PMC free article] [PubMed] [Google Scholar]