Early Foundations for Mathematics Learning and Their Relations to Learning Disabilities

Abstract

Children’s quantitative competencies upon entry into school can have lifelong consequences. Children who start behind generally stay behind, and mathematical skills at school completion influence employment prospects and wages in adulthood. I review the current debate over whether early quantitative learning is supported by (a) an inherent system for representing approximate magnitudes, (b) an attentional-control system that enables explicit processing of quantitative symbols, such as Arabic numerals, or (c) the logical problem-solving abilities that facilitate learning of the relations among numerals. Studies of children with mathematical learning disabilities and difficulties have suggested that each of these competencies may be involved, but to different degrees and at different points in the learning process. Clarifying how and when these competencies facilitate early quantitative learning and developing interventions to address their impact on children have the potential to yield substantial benefits for individuals and for society.

I am certain that professionals and the lay public would agree that the long-term consequences of illiteracy are socially and personally devastating. The National Assessment of Adult Literacy revealed that 14% of adults in the United States have difficulty identifying basic ideas in short, simple texts, and, indeed, these individuals have difficulty completing high school and remaining gainfully employed (Baer, Kutner, Sabatini, & White, 2009). I am just as certain that these same people would be much less concerned about the long-term consequences of innumeracy, which is understandable in some respects: Illiteracy is likely to have broader effects than innumeracy on most individuals’ lives. In other respects, however, we should be just as concerned about innumeracy as we are about illiteracy, because innumeracy is more common—22% of adults in the United States are innumerate (e.g., they would have difficulty computing a 10% tip)—and because the quantitative demands of living in modern economies have been increasing steadily (Hudson, Price, & Gross, 2009).

Adults’ functional numeracy is gauged by their skill at solving simple word problems that require whole-number arithmetic, fractions, simple algebra, and measurement. Performance on these tests predicts employability and wages in adulthood, controlling for other factors (Bynner, 1997; Rivera-Batiz, 1992). No doubt there are many reasons why some people are functionally innumerate when they leave school, and identifying these reasons and developing ways to address them have the potential to yield substantial benefits for individuals and society. Over the past two decades, researchers have been searching for these reasons (Butterworth, Varma, & Laurillard, 2011; Jordan, Hanich, & Kaplan, 2003; Mazzocco, Feigenson, & Halberda, 2011a; Swanson, Jerman, & Zheng, 2008) and developing interventions to address them (Clements, Sarama, Spitler, Lange, & Wolfe, 2011; Fuchs et al., in press).

Much of this research has focused on children with mathematical learning disabilities (MLD) and persistently lower mathematics achievement than would be expected on the basis of intelligence, working memory, and reading ability (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Murphy, Mazzocco, Hanich, & Early, 2007). Children who consistently score at or below the 10th percentile on mathematics achievement tests and have intelligence scores above the 15th percentile (as a group, they are typically between the 30th and 35th percentiles) are typically categorized as having MLD, and in recent studies, children scoring between the 11th and the 25th percentiles as having low mathematics achievement. Children with MLD tend to have below-average scores on intelligence tests and substantial working memory deficits (i.e., poor attentional control). The intelligence of children with low mathematics achievement is average, although they may have subtle deficits in attentional control (Geary, Hoard, Nugent, & Bailey, 2012). Children in both groups show persistent deficits or developmental delays in mathematical areas that are critical for achieving numeracy in adulthood.

Early Sources of Learning Difficulties in Mathematics

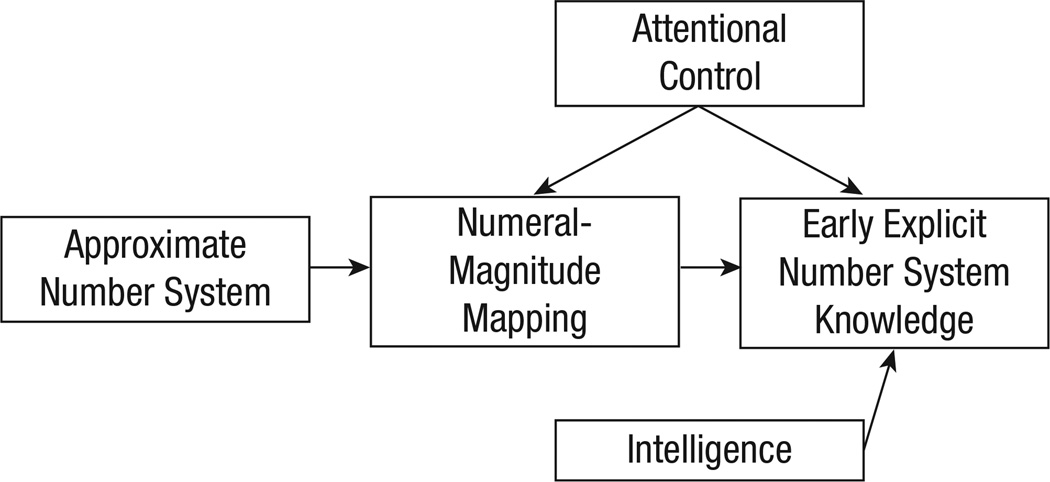
I focus on difficulties that emerge before children enter school, because most children who start behind in mathematics stay behind throughout schooling (Duncan et al., 2007) and thus are at risk for later innumeracy. Unfortunately, there has been little research on the relation between quantitative development before entry into schooling and later deficits found in children with MLD and low mathematics achievement. Fortunately, research has examined infants’ and preschool children’s quantitative development and how older children with MLD or low mathematics achievement perform on similar tasks. The combination of these two research areas allows for inferences about the most fundamental deficits that might underlie MLD and low mathematics achievement and provides a roadmap for studies of preschool precursors of later learning difficulties, as summarized in Figure 1.

Fig. 1.

The beginning of children’s mathematical learning. The initial step toward learning mathematics may be based on an intuitive sense of the approximate magnitude of collections of items. The first abstract mathematical symbols that children learn are number words and Arabic numerals, which in turn acquire meaning when mapped onto this number sense. The critical next step is an explicit understanding of the relations among numerals.

Attentional focus and intelligence

Children who have a better ability to maintain effortful attentional control and focus—including a better ability to ignore irrelevant internal distractions (e.g., something “popping” into mind) and external distractions (e.g., another child)—learn more quickly than their less attentive peers (Clark, Pritchard, & Woodward, 2010; Engle, Kane, & Tuholski, 1999), especially in evolutionarily novel areas (Geary, 2005), such as formal mathematics. Attentional control manifests as the ability to maintain goal-relevant information in mind while processing other information, as measured by working memory tests, and as the ability to stay focused and organized in classroom settings. Attentional control and intelligence are related, but they make independent contributions to the learning of mathematics. The key component of intelligence is facility at understanding abstract information, which includes the highly logical and systematic relations among numerals and the procedures that can be used to operate on them.

The approximate number system

Many species have an inherent sense of quantity that is dependent on part of the parietal cortex called the intraparietal sulcus (Dehaene, Piazza, Pinel, & Cohen, 2003); their behavior indicates that they implicitly discriminate between smaller and larger collections of objects, such as food items (Feigenson, Dehaene, & Spelke, 2004). Current debate revolves around whether the mechanisms that enable these discriminations are composed of one or two discrete systems—one for representing exact quantities of sets of three or four items and the other for representing approximate quantities of larger sets—or simply one approximate system that provides precise representations for smaller collections. For ease of discussion, I assume that there is one system. I also note that attention is required to apprehend quantity, but because this is a built-in, evolved system, it is automatically allocated to numerosity, and thus effortful controlled attention is not necessary for apprehending quantity processed by the approximate system.

The ease of discriminating smaller quantities from larger ones varies according to the ratio of their elements. Infants can reliably discriminate between sets that differ by a ratio of 2:1 (an 8-item set vs. a 16-item set; Xu & Spelke, 2000), whereas adults can discriminate between sets that differ by a ratio of 10:11 (Halberda & Feigenson, 2008). The extent to which these changes are driven by maturation of the brain systems that support the approximate number system, by experience, or, most likely, by some combination of the two is not known. Whatever the reason, developmental delays in the fine-tuning of this system will result in a poor intuitive sense of quantity, which may potentially slow children’s early learning of the meaning of number words and Arabic numerals.

Several recent studies have suggested that children with MLD, but not their peers with low mathematics achievement, may have less precise representations of magnitude in the approximate number system (Mazzocco et al., 2011a; Piazza et al., 2010), although this deficit is not always found (Iuculano, Tang, Hall, & Butterworth, 2008; Rousselle & Noël, 2007). This effectively means that MLD children’s representations of adjacent magnitudes overlap more than those of their typically achieving peers; children in the latter group easily discriminate a set of five objects from a set of six objects, whereas children with MLD respond to these sets as if they were the same. Piazza et al. (2010) found that the fidelity of the approximate number system of 10-year-old children with MLD was about the same as that of typically achieving 5-year-olds matched on intelligence. The next step is to determine if preschool children with less fidelity in the approximate number system are at heightened risk for MLD when they enter school; one preliminary study has suggested that they are (Mazzocco, Feigenson, & Halberda, 2011b).

Mapping symbols to magnitudes

The basic symbols of early formal mathematics, number words and Arabic numerals, have meaning only if they are associated with the quantities they represent, and children’s early number sense may provide the foundation for these associations. How children map number words and numerals onto their sense of magnitude is not fully understood, but at the very least, it requires attentional focus and engagement of areas of the prefrontal cortex (Nieder, 2009; Noël, 2009). Controlled attention is necessary because number words and numerals are evolutionarily meaningless symbols and acquire their initial, rudimentary meaning when mapped onto children’s intuitive sense of magnitude. I suspect that intelligence is not particularly important at this stage, because children do not yet need to know the systematic relations among numerals, only to associate numerals with quantities represented by the approximate magnitude system. On this view, this early step involves at least three potential sources of risk for later MLD or low mathematics achievement: the approximate number system (as discussed above), the attentional-control system, and the white matter connections that link them. The last source includes connections among the prefrontal attentional-control systems, the intraparietal sulcus, the systems that process numerals and number words, and the hippocampus (for long-term memory formation; Cho et al., 2012).

Rousselle and Noël (2007) found that second graders with MLD had an intact approximate number system but were slower than their peers at accessing the quantities associated with Arabic numerals, suggesting a mapping deficit. These children were of average intelligence, but their attentional focus was not independently assessed. The children with MLD in the Mazzocco et al. (2011a) study showed less precision in the approximate number system and had difficulties with mapping number words into magnitudes represented by this system. Attentional control and other factors contributed to these children’s mapping deficit but not to their approximate-number-system deficit. Many children with low mathematics achievement are also slower than typically achieving children at mapping numerals to quantities (Geary, Hoard, & Nugent, 2012), but the extent to which this disadvantage is due to subtle deficits in attentional control or, perhaps, to the integrity of the connections between the prefrontal control systems and the intraparietal sulcus remains to be determined.

Creating an explicit number system

Coming to understand the meaning of specific number words and Arabic numerals—knowing their cardinal value—is an important and challenging step in learning mathematics. The emergence of an explicit understanding of the logical structure of the number system is an even more critical step. One of the first indicators that children are coming to understand the relations among numbers is their ability to explicitly order relative magnitudes. This is not simply reciting the string of counting words, but rather knowing that 9 is one more than 8, for instance, and that magnitudes can be systematically ordered on a number line.

An unresolved issue concerns the extent to which children’s intuitive number sense and other implicit quantitative knowledge (e.g., knowledge that adding an item to a set increases set size) are necessary for mathematics learning, once children have used this intuitive knowledge to scaffold their early learning of number words and numerals. It seems likely that aspects of children’s mathematical learning become at least partially disengaged from their early intuitive number sense, because the reach of inherent quantitative knowledge is quite limited in comparison with the expansive reach of formal mathematics. Of course, people continue to use their number sense in many contexts after childhood—the question here is whether it is important for learning formal mathematics. I suspect that effortful attentional control and intelligence are relatively more important for understanding and processing the explicit relations among numerals and in other mathematical domains.

Indeed, Bugden and Ansari (2011) found that the fluency with which first and second graders automatically mapped numerals onto quantities was uncorrelated with the children’s ability to explicitly compare the magnitudes of two numerals. The latter predicted mathematics achievement, but the fluency of automatic mapping did not (see Lyons & Beilock, 2011). Huttenlocher, Jordan, and Levine (1994) found that preschoolers’ ability to develop a mental model of a hidden collection of items and to perform additions and subtractions on this collection was related to intelligence. In another study, a modest disadvantage in intelligence seen among children with MLD (mean IQ = 96 vs. 107 for typically achieving children) partially mediated their delayed number-line learning in first grade, but a substantial deficit in attentional control was the primary mediator of their poor performance in second grade (Geary, Hoard, Nugent, & Byrd-Craven, 2008). The intelligence of children with low mathematics achievement (mean IQ = 101) was lower than that of their typically achieving peers, but the attentional control of the two groups did not differ. The number-line performance of the children with low mathematics achievement lagged behind that of the typically achieving children in first grade, but by second grade, these low-achieving children had caught up.

It appears that once the logical structure of the number line is understood, intelligence is not as important for number-line performance as the ability to focus attention during the actual online, so to speak, placements of the numerals. In this case, the delays seen in children with MLD were related to intelligence and attentional control, but to different degrees at different points during learning. Later in development, many of the quantitative deficits of children with MLD and low mathematics achievement are independent of intelligence and attentional control, but it is unclear whether early deficits in, say, attentional control result in delays in initial quantitative learning that then cascade into more severe problems.

Conclusions and Future Directions

The quantitative competencies that students bring into adulthood will influence their employability, wages, and skill at negotiating many now-routine activities. Preparation for these demands begins before formal schooling, and many children who are not prepared at the outset are at a disadvantage thereafter (Duncan et al., 2007). Insights into the mechanisms that facilitate children’s early quantitative learning are critical to the development of interventions that put at-risk children on the path to numeracy. These mechanisms may include an inherent sense of magnitude, fluent mapping of basic mathematical symbols onto this intuitive number sense, and the ability to explicitly operate on these symbols and understand the logical relations among them. It may be that these mechanisms vary in importance, depending on where children are in the learning process, and that they vary in the extent to which they contribute to the learning difficulties of different children.

Children’s intuitive number sense may have an evolved basis, but it changes substantially over the course of development, suggesting some degree of malleability (Halberda & Feigenson, 2008). Likewise, the importance of attentional control and logical problem solving does not mean that children with deficits in these areas cannot learn mathematics. It does suggest, however, that explicit, direct instruction of core numerical relations may be particularly important for these children (Gersten et al., 2008; also Clements et al., 2011; Fuchs et al., in press). These are just the first steps toward numeracy, but without them, the long-term prospects of many children will be dimmed.