The Role of Hydroxyl Channel in Defining Selected Physicochemical Peculiarities Exhibited by Hydroxyapatite

Abstract

Mysteries surrounding the most important mineral for the vertebrate biology, hydroxyapatite, are many. Perhaps the Greek root of its name, απαταo, meaning ‘to deceive’ and given to its mineral form by the early gem collectors who confused it with more precious stones, is still applicable today, though in a different connotation, descriptive of a number of physicochemical peculiarities exhibited by it. Comparable to water as the epitome of peculiarities in the realm of liquids, hydroxyapatite can serve as a paradigm for peculiarities in the world of solids. Ten of the peculiar properties of hydroxyapatite are sketched in this review piece, ranging from (i) the crystal lattice flexibility to (ii) notorious surface layer instability to (iii) finite piezoelectricity, pyroelectricity and conductivity to protons to (iv) accelerated growth and improved osteoconductivity in the electromagnetic fields to (v) high nucleation rate at low supersaturations and low crystal growth rate at high supersaturations to (vi) higher bioactivity and resorbability of biological apatite compared to the synthetic ones, and beyond. An attempt has been made to explain this array of curious characteristics by referring to a particular element of the crystal structure of hydroxyapatite: the hydroxyl ion channel extending in the direction of the c-axis, through a crystallographic column created by the overlapping calcium ion triangles.

Graphical abstract

1. Introduction

Figuration of structure-property relationships is engrained in the heart of materials science, but it has suffered immensely in the recent past. The demands for practicality and applicability in natural sciences have taken their toll. No longer is the mainstream materials scientist interested in paralleling practical findings with fundamental insights. Rather, the former is given priority over the latter. As a result, methods for synthesis of materials with exciting properties multiply, though only rarely followed by their developers' eagerness to comprehend the physicochemical bases of the structural forms adopted by the materials and linking those with the characteristic types of behavior displayed by them. In this work, a major turnabout has been taken and an attempt made to look back at one of the key structural features of a material that is of a particular interest to bone biology and correlate it with some of the experimentally observed oddities displayed by it and collected over the past century.

The compound that is the subject of this review is hydroxyapatite (HAp): Ca₁₀(PO₄)₆(OH)₂. It is a hydroxylated form of apatite, Ca₁₀(PO₄)₆(F, Cl, OH)_2, the most abundant phosphorus-bearing mineral on Earth, findable in igneous, sedimentary and metamorphic rocks alike¹. In its calcium-deficient and partially carbonated form, representable as (Ca,Z)₁₀(PO₄,Y)₆(OH,X)₂ [Z = Na⁺, Mg²⁺, K⁺, Sr²⁺, etc., Y = CO₃^2-, HPO₄^2-, and X = Cl^-, F^-], it acts as the sole mineral component of bone. Its role in this complex and multifunctional organ is to impart solid compressive properties to elastic but weak collagen fibers and thus participate in a synergy thanks to which deficiencies of both the soft and the hard components of bone alone become effectively canceled out.

HAp, interestingly, is a compound that can appeal to the curiosity of chemists owing to its broad range of peculiar properties just about as much as water can. Like water, exhibiting so many extraordinary properties in the realm of fluids, from (i) its highest surface tension among all liquids except mercury to (ii) its density being highest in the liquid, not the solid state, at 4°C and 1 bar, to (iii) its extremely low vapor pressure and an incredibly high boiling point compared to the neighboring hydrides in the Periodic Table to (iv) its being one of the rare carbonless liquids at room temperature to (v) its being an almost universal solvent, HAp abounds with unexpected features that reveal themselves to the studious and inquisitive research eyes. Perhaps due to Nature's finding utility in peculiarity, both of these compounds, water and HAp, have been chosen as central ingredients of the molecular machinery of life.

But, like most ceramics, HAp is difficult to work with. It cannot be easily processed into any particle size or shape, as metals can, nor can it be easily functionalized with therapeutic ligands, as polymers, silica or gold can. It is also very unattractive to a casual observer - pale, fragile, not very conductive to electricity or vibration as well as inexpensive, without really displaying many appealing characteristics at the first sight. Although in the mineral form it can be easily confused with more precious stones, ranging from beryl to amethyst to olivine, a drop of lime juice is enough to start dissolving it, the reason for which A. G. Werner named it in 1786 using the Greek word αпαταO, meaning ‘to deceive’ or ‘to mislead’². On top of this, it is highly defective in its most natural and functional, bioactive and osteoconductive state. Yet, in spite of all of this, it is the material evolutionarily selected to build the bases of our biophysical structures with, yielding yet another glimpse into the wonders of natural creation whereby perfection is found almost exclusively in imperfection.

The central aim of this review piece, elaborated in Section 3, is to elucidate the idea that a particular structural feature of HAp, known as the hydroxyl ion channel, running straight through the center of the basal plane of its hexagonal lattice and parallel to the c-axis, is partially responsible for an array of its extraordinary characteristics. The preceding Section 2, which follows next, presents the compilation of unusual properties exhibited by this strange member of the biomineral family: unappealing at first, to those who spend enough time examining it, it may come to reveal semantic signs that extend across the world of atoms and molecules and into the spheres of our psyches, our social lives and beyond.

2. Peculiarities of HAp

2.1. Crystal lattice flexibility

HAp has the capacity to undergo enormous lattice distortion as it accommodates cations and anions that differ in size from Ca²⁺ and PO₄^3-, respectively. Approximately one-fifth of Ca²⁺ ions in biological HAp are substituted with cationic impurities and, for example, substitution of Ca²⁺ with Mg²⁺ reduces the lattice constant c by 0.33 % and increases the lattice constant a by 0.1 %³, which itself is enough to produce significant lattice disturbances and increase the solubility of the compound^4,5. The more frequent incorporation of CO₃^2- ions in the hexagonal channel of the apatite structure (A-type HAp) leads to an increase in the lattice parameter a and a markedly lesser decrease in the parameter c in comparison with the stoichiometric Hap⁶. In contrast, the parameter a decreases while c increases with a partial substitution of PO₄^3- by smaller CO₃^2- ions (B-type HAp)⁷.

These changes in crystal lattice parameters often induce changes in crystallinity, thermal stability, morphology, solubility and other physicochemical and biological properties of the material⁸. Charge neutrality principle also implies the formation of structural defects in order to accommodate foreign ions. The extraordinary stoichiometric flexibility of the compound manifests itself in accommodating such defects, as Ca/P molar ratio, equaling 1.67 for pure HAp, can drop down to 1.3 without the breaking of the crystallographic symmetry: P6_3/m. The crystal structure of stoichiometric HAp is, in fact, monoclinic (P2_1/b)⁹, but due to foreign ion inclusion, vacancy formation and Ca²⁺ depletion it becomes hexagonal (P6_3/m)¹⁰ for more disordered biological HAp. The same transition to a crystallographic state of lower symmetry is observed following annealing at temperatures higher than 207°C. This polymorphic transition is reversible and the hexagonal symmetry transforms back to the monoclinic at temperatures lower than 204°C in the cooling regime¹¹.

Though the capacity to incorporate foreign ions may not be as large as that typifying silicate glasses, the lattice flexibility of HAp is large enough to accommodate a half of all the elements of the Periodic Table¹¹, in almost any valence state, from SiO₄^4- to As⁵⁺. It is thanks to this effect of lattice flexibility that bone can act as the mineral reservoir of the body and the storage for toxic elements and thus fulfill two of its essential physiological roles. Despite this flexibility, the driving force for crystallization is still sufficiently high to drive out most of the organic molecules present at the moment of precipitation and limit the loading capacity of the compound to mostly the amount that could be adsorbed on the surface. This surface layer of the drug bound by weak forces to the particle predisposes HAp to exhibit burst release and prevents it from being used as a sustained release platform in the dispersed form. Powder compaction and drug capturing within the pores is an approach that overcomes this deficiency of HAp^13,14,15,16, but limits the use of such composites to application as solid blocks. Although entrapment of fluorophores has been reported for glassy, silicate calcium phosphates prepared in an amorphous form in Igepal-based reverse micelles and stabilized with citric acid¹¹, the compound naturally present in bone where it coats HAp crystals at 0.5 molecules/nm² and prevents their coalescence in the collagen matrix¹¹, it appears that loading HAp with organics in any amount greater than that present in nacre or tooth enamel (< 3 wt%) via intercalation is not possible. The intracrystalline loading also appears to be theoretically possible only for sufficiently small molecules, such as glycine, the smallest amino acid, in the amount ranging from 1 – 3 wt%, depending on the concentration of paired cationic and OH^- vacancies in the material¹¹.

2.2. Surface layer instability

Surface layer instability, another one of the key properties of HAp, is of vital importance in ensuring the timely resorption of this compound during in vivo remodeling in spite of its sparsely soluble nature. Dissolution of biological HAp, for example, yields twice higher Ca²⁺ concentrations in the supernatant compared to the theoretically more soluble, commercial β-tricalcium phosphate (β-TCP)²⁰ and this effect is predominantly due to the highly mobile surface layer whose composition and structure are constantly fluctuating in response to the fluctuant physicochemical conditions of the fluid at the interface. As a result, the surface of HAp, particularly in dynamic environments, such as the biological ones, can be imagined to be in a state of constant phase transition.

Although the exact mechanism of phase transformations in calcium phosphates has not been fully elucidated yet, it has been traditionally held that solution-mediated, dissolution/reprecipitation mechanism constitutes the dominant one^21,22. This was elegantly proven by the noticed acceleration of phase transformations by stirring and their slowing down by substituting water with nonpolar solvents²³ and later supported by the ability of organic adsorbates, such as alendronate sodium, to extend the phase transformation timescale from minutes to days²⁴. The complementary mechanism, on the other hand, similar in nature to the martensitic/austenitic transition involving bulk lattice rearrangements, is still the subject of debate. Namely, although transitions solely in the interiors of compact calcium phosphate blocks have been observed, it is usually the surface that changes the phase composition to fit the chemical and energy demands of the local environment. Thus, for example, the core of dicalcium phosphate monohydrate (DCPM, a.k.a. brushite) implants transformed to HAp even while the surface retained the DCPM composition²⁵, though such reports are a rarity in the literature and a far more prevalent scenario involves the surface transformation in the direction of the most stable phase under the given chemical conditions, which most often serves to protect the bulk from premature dissolution. DCP blocks implanted as bone substitutes would thus undergo restructuring of the surface until the most stable phase under physiological conditions, HAp, is present on it. It is for this reason that it has been held that the solubility of calcium phosphates does not conform to the solubility product, just as much as experimentally determined solubilities cannot be readily converted to bioresorption rates²⁶.

Interestingly, this constant restructuring involving periodic dissolution and reprecipitation of surface ions could provide a counterforce against the low surface charge that facilitates aggregation. Namely, ξ-potential of HAp is almost always below +- 15 mV, which is the lower threshold for colloidal instability²⁷. On the other hand, the observed surface charge fluctuations during the aging of HAp precipitates in the solution²⁸, along with frequent swings from the positive to the negative values and vice versa, have been suggestive of constant restructuring of the surface, which may have the capacity to partially compensate for the low surface charge. This has enabled HAp particles in suspension to be comparatively stable in phosphate buffer saline ([H_xPO₄^x-3] = 11.8 mM and the overall salt concentration ∼ 150 mM), undergoing virtually no ‘salting out’ effect²⁹. The central practical downside of this constant restructuring of the surface, however, is the impossibility of chemical functionalization of the surface since the continuously dissolving and reprecipitating surface ions would ensure the rapid release of the ligand to the environment. HAp, otherwise, does have a plenty of attributes that justify its use as a drug delivery vehicle, with the central one of them being the capability of launching the endosomal escape of drugs owing to dissolution in the moderately acidic interior of the late endosome (pH 4.5 – 5.5)³⁰ before this intracellular compartment transitions into the enzymatically permeated lysosome that would degrade macromolecular drugs had they been retained by the particle by then³¹. This has been linked to the great effectiveness of this compound in gene delivery^32,33, second to none in the realm of non-viral transfection agents³⁴. Despite all of these pros, however, the instability of the surface, along with the resistance to drug loading via transcrystalline entrapment, has greatly limited the use of HAp in targeted and sustained drug delivery.

2.3. Multiphasic particle composition

So we see that despite its sparse solubility in water, equaling only 0.3 mg/dm³ at 25°C for K_sp of 117.3, HAp has a very unstable surface which undergoes constant restructuring and prevents stable chemical functionalization achievable for some other ceramics, predominantly covalent ones, such as alumina³⁵, titania³⁶ or zirconia³⁷. On the other hand, a constant engagement in the exchange of ionic species across the interface with the solution has allowed HAp to be used as an efficient industrial sorbent^38,39. This surface instability, along with the relatively high specific surface area of the compound, has also contributed to the facileness with which HAp accommodates foreign ions and acts as a mineral reservoir for the body.

In spite of the long-time use of HAp as an adsorbent in waste removal industry^40,41,42 and in chromatographic columns for electrophoretic separation of a variety of biological entities, including proteins^43,44, nucleic acids⁴⁵ and even microorganisms⁴⁶, all thanks to the surface alternation of highly charged divalent calcium and trivalent phosphate ions capable of interacting with both positively and negatively charged functional groups in biomolecules and binding them in zwitterionic forms⁴⁷, constant dissolution and reprecipitation of surface ions stands as an obstacle to their binding ligands stably. Such swift surface rearrangements are, on one hand, responsible for the fact that no grain boundary segregation of ionic species has ever been observed in HAp⁴⁸, suggesting that, perhaps with the help of structural defects, whose concentration is directly proportional to the diffusivity of ions through the lattice, foreign ions comparatively easily diffuse across the particle-solution interface and into the bulk. On the other hand, however, the constant exchange of ions with the solution creates conditions for the formation of surface calcium phosphate phases different in composition and structure from those comprising the core of the particle. As a result, a HAp particle in contact with a pH 6 solution might form a protective DCP layer on its surface that would considerably slow down its dissolution and the reverse effect might happen to a DCP particle in contact with a pH 7 solution. A single-phase particle could thus undergo a partial internal phase transition upon immersion into the solution, yielding multiphasic and possibly even surface-gradient particle compositions. This effect is the direct consequence of the unstable surface layers that undergo constant rearrangement in contact with the solution or body fluids to find the most energetically favorable composition for the given chemical conditions of the local environment.

It is worth mentioning here that HAp is only one of a dozen existing calcium orthophosphate phases, which together cover a broad range of solubility values, as illustrated in Table 1. Combinations with more soluble phases and the possibility of achieving time-controlled solidification of as-precipitated gels enables its use as a component of self-setting pastes with an immense therapeutic potential as bone grafts⁴⁹. In such a form, despite their ceramic nature, calcium phosphates are typified by excellent viscous flow properties, the reason for which they are added to polymers to facilitate their injectability^50,51 rather than vice versa, as common sense would expect, in analogy with the emulsifying properties of calcium phosphate nanoparticles naturally present in milk⁵² and utilized in Pickering emulsions⁵³.

Table 1.

Main calcium phosphate phases, along with their chemical formulas, space group symmetries, solubility product values (K_sp) and solubilities at 25°C and pH 7.4^{54,55,56,57,58}.

Phase	Chemical formula	Space group	pKsp	Solubility (mg/dm3)
MCPA*	Ca(H2PO4)2	Triclinic P1̄	1.14	17 · 103
MCPM*	Ca(H2PO4)2·H2O	Triclinic P1̄	1.14	18 · 103
DCPD*	CaHPO4·2H2O	Monoclinic Ia	6.6	88
DCPA*	CaHPO4	Triclinic P1̄	7.0	48
β-CPP*	Ca2P2O7	Tetragonal P41	18.5	7.6
ACP*	Ca3(PO4)2·nH2O	/	25	0.8
α-TCP*	Ca3(PO4)2	Monoclinic P21/a	25.5	2.5
β-TCP*	Ca3(PO4)2	Rhombohedral R3cH	29.5	0.5
TTCP*	Ca4(PO4)2O	Monoclinic P21	37.5	0.7
OAp*	Ca10(PO4)6O	Hexagonal P63/m	69	8.7
CDHAp*	Ca10−x(HPO4)x(PO4)6−x(OH)2−x (0 < x < 1)	Hexagonal P63/m	85	9.4
OCP*	Ca8H2(PO4)6·5H2O	Triclinic P1̄	97.4	8.1
HAp*	Ca10(PO4)6(OH)2	Hexagonal P63/m	117.3	0.3
FAp*	Ca10(PO4)6F2	Hexagonal P63/m	120	0.2

^*MCPA = monocalcium phosphate anhydrous; MCPM = monocalcium phosphate monohydrate; DCPD = dicalcium phosphate dihydrate, a.k.a. brushite; DCPA = dicalcium phosphate anhydrous, a.k.a. monetite; CPP = calcium pyrophosphate; ACP = amorphous calcium phosphate (data pertain to the phase obtainable at pH 9 – 11); TCP = tricalcium phosphate; TTCP = tetracalcium phosphate; OAp = oxyapatite; CDHAp = calcium-deficient hydroxyapatite; OCP = octacalcium phosphate; HAp = hydroxyapatite; FAp = fluoroapatite.

2.4. Finite piezoelectricity, pyroelectricity and conductivity to protons

Both of the main components of bone, collagen and HAp, exhibit piezoelectricity⁵⁹. In the case of collagen, it is presumably due to charge separation under shear, the process in which HAp plays a facilitative role by restricting access to water for collagen and distributing load across large spatial scales so as to enable a large number of collagen molecules to deform locally⁶⁰. In the case of HAp, piezoelectricity is due to the polarization of OH^- groups confined to the channel formed by the overlapping hexagonal calcium atoms (Ca2). It appears to be the sole property of the inherently disordered, nonstoichiometric P6_3/m HAp and not of its pure, monoclinic, P2_1/b counterpart⁶¹. The order of magnitude of the piezoelectric response of HAp, with the piezoelectric coefficient, D = 16 pC/N⁶², is lower than that exhibited by lead zirconate titanate (PZT), but higher than that of aluminum nitride and in about the same range as that of polyvinylidene fluoride and zinc oxide^63,64. In addition, HAp thin films exhibit the ferroelectric nature of polarization, with remnant polarization being approximately one-fourth of the value of PZT films⁶⁵. Although nanocrystalline HAp is predominantly polar, its polycrystalline nature in bone and mostly elsewhere is the reason why this piezoelectric effect becomes averaged over the three dimensions, resulting in minor values along its favored direction, perpendicular to the basal plane and parallel to the OH^- channel. HAp is also a pyroelectric material, being able to generate electrical charge as a function of the rate of temperature change and characterized by the pyroelectric coefficient, p_i = 12 μC/m²K. It is also an efficient proton conductor with the potential to be used in energy conversion devices⁶⁶. The proton conduction is directly causative of spontaneous polarization observed in these materials⁶⁷.

2.5. Accelerated growth and improved osteoconductivity in the electromagnetic field

The polarizability of HAp explains its responsiveness to electric and magnetic fields in the context of its application as a biomaterial for bone regeneration. For example, sintered and electrically polarized HAp with the total stored charge density of 3.9 μC/cm² proved to be able to enhance the osteobonding and osteoconducting abilities when implanted in the cortical bone of the femoral diaphysis in white rabbits⁶⁸. Then, a metacarpal fracture in goats healed much faster in the presence of static magnetic field stimulation (800 G/cm²) and the healing process was paralleled by an increase in preferential alignment and crystallinity of HAp crystals in bone⁶⁹. Cobalt-doped HAp also facilitated the regeneration of mandibular osteoporotic bones in rats⁷⁰. Even outside the biomedical context, the effects of external fields on the habit of crystal growth of HAp have been observed. Thus, the growth of HAp was accelerated when it was grown on polarized HAp substrates and slowed down when grown on non-polarized HAp⁷¹. To verify that the effect was due to the existence of lattice channels populated by OH^- ions, annealing of the substrates was paired with dehydration under low water vapor content, the result of which was tricalcium phosphate, not HAp, but the difference between the growth on polarized and non-polarized substrates was, expectedly, none. The presence of the static magnetic field of 0.1 T was also shown to increase the precipitation rate of HAp by accelerating the phase transformations along steps defined by the Ostwald-Lussac rule, predominantly DCP → OCP → HAp⁷².

2.6. The fastest growing face in enamel HAp grows considerably slower in bone HAp

Growing fast in the world of crystals does not pay off, given that either minimization of the surface eminence of crystalline faces or their complete disappearance entails their overly fast growth. In contrast, the slowest growing faces tend to be the most prominent ones on the crystal surface⁷³. This is illustrated in Fig.1, where two HAp crystals of geological origin are shown: one with the exposed (001) face by cutting and the other one with diagonal (011) and (101) faces instead of (001), the result of the sole directional growth of (001). An example among apatites of biomineral origin comes from the tooth enamel, where HAp grows almost uniaxially in the [001] direction, leading to the comparatively minor presence of basal, (001) faces in comparison with the prismatic, (hk0) ones in the final crystal forms⁷⁴. The growth of HAp platelets (30 × 20 × 2 nm⁷⁵) in bone, however, proceeds in a very different manner. Namely, their growth in [001] direction is not considerably faster than that along [010] direction, which is atypical for most hexagonal close packed symmetries, given that the growth along the central axis of (001) plane is usually the most favorable. This difference can be explained by the fact that the crystals of HAp in enamel and bone grow in two vastly different conditions. Elongated HAp crystals in enamel grow without the direct involvement of cells, in a comparatively hydrophobic and gelatinous amelogenin matrix, and are therefore free to grow according to their elementary crystallographic propensities, that is, primarily along the c-axis⁷⁶. Still, that the enamel matrix proteins do not merely block (hk0) faces so as to foster the uniaxial growth of the basal plane, as the dominant model of amelogenesis assumes⁷⁷, but directly participate in the growth of the (001) face, producing crystals with the aspect ratios of up to 10⁴ as the result, is suggested by the presence, not disappearance, of this face in HAp crystals comprising mature enamel. In contrast, HAp platelets in bone grow in a highly hydrophilic environment, with the direct involvement of bone cells that alternately deposit and resorb the solid material, so the crystals do not get to effectively grow equally much on average along their most favorable axis of growth, the c-axis. This versatility in terms of crystal orientation and growth adds another type of crystallographic flexibility to the crystal lattice one – i.e., symmetry preservation under considerable lattice compression or expansion caused by ionic substitutions and defects - mentioned earlier.

Fig.1.

Two HAp crystals of mineralogical origin: one with the exposed (001) face (left) and the other one with the (001) face being overgrown by the (011) and (101) planes as the result of its preferred growth on the account of the stagnation of the adjacent planes (right). Reprinted with permission from Ref.78.

2.7. An ultrahigh nucleation rate even at extremely low supersaturations and an ultralow crystal growth rate even at extremely high supersaturations

Nanosize is the natural form of existence of HAp particles⁷⁹. In bone and in intertubular dentin, HAp particles are nanosized (< 100 nm in length by convention) along all three dimensions, whereas in enamel they are nanosized in the two directions that define their diameter and microsized in their height. Most precipitation protocols performable in the lab likewise yield HAp nanoparticles. This means that, unlike what is the case with most other materials, an experimenter has to try hard not to obtain HAp in a nanoparticulate form. Which is precisely the consequence of an ultrahigh nucleation rate even at extremely low supersaturations. This phenomenon coincides with the complex precipitation mechanism starting with the formation of amorphous, ∼ 1 nm sized solid units colloquially called Posner's clusters⁸⁰, which undergo aggregation and recrystallization over the early course of the ripening time⁸¹. Depending on the extent of aggregation and compactness achieved in the process, the high nucleation rate need not be an obstacle for the formation of larger crystals, which will, however, always be composed of aggregates of distinct nanosized growth units in the absence of thermal treatments and extensive recrystallization that they bring about. HAp also has a relatively low interfacial energy in aqueous environments⁸², especially when the surface of the material is terminated by OH^- groups⁸³, which additionally contributes to its propensity to remain stable in the form of nanoparticles and resist uncontrolled growth.

Another remarkable feature of this material, following in step the high nucleation rate in its favoring the adoption of nanostructured forms, is a considerably low crystal growth rate even under relatively high supersaturations^84,85,86. For example, the step kinetic coefficient, a reciprocal measure of the resistance to crystallization at the surface step⁸⁷, was measured to be around 4 × 10^-5 cm/s, which is by 3 - 4 orders of magnitude lower than the value attributed to most inorganic crystals and in about the same range as protein crystals⁸⁸. The slow motion of elementary steps on the crystal surface can be both a puzzling and a logical observation in view of the rather high mobility of ionic species comprising the hydrated surface layers of HAp. For, while high surface ion mobility can be translated to high step propagation rate, under the conditions of intense hydration, as is the case with HAp, it can also provide conditions for the constant dissolution of the steps, which, as such, propagate back and forth, by alternately advancing and retreating. There are other reasons too, involving most importantly the complex, multistage growth mechanism with the initial precipitation of Posner's clusters and their subsequent aggregation and structural rearrangement followed by an increase in size, compactness and crystallinity⁸¹, all the while obeying the Ostwald-Lussac principle which dictates that, in the absence of kinetic factors, the least thermodynamically stable phases (i.e., the most soluble and having the lowest interfacial energy) are the first to form before transforming sequentially to the most stable one⁸⁹, which is HAp in alkaline solutions (> pH 6.8 at 37°C) and DCP in the acidic ones (< pH 6.8 at 37°C). By bearing resemblance to the growth of protein and viral crystals through chirality selection and orientation fitting, the low crystal growth rate of HAp, involving not ions, but amorphous nanoparticulate precursors, is sometimes compared to that of these biologics⁹⁰. Despite the low crystal growth rate, crystallinity of HAp precipitated under physiological conditions is remarkably low⁹¹, the reason being the amorphous precursors that only partly crystallize as the growth proceeds. Slow crystal growth in ordinary crystals produces relatively smooth surfaces, but this is not so in HAp where both the leading edges and terraces in-between the surface steps exhibit a highly irregular profile at the atomic scale⁹². As the result, unlike DCP, which dissolves by a combined volume diffusion and surface reaction mechanism⁹³, the dissolution of HAp follows the polynucleation mechanism⁹⁴ and is greatly hindered for atomically smooth, step- and pit-free HAp crystals⁹⁵. The crystallization process mediated by amorphous precursors is responsible for yet another peculiarity exhibited by HAp upon nucleation: the inversely proportional dependence of the nucleation rate on supersaturation, as indicated by the linear increase of the nucleation lag time with pH in range of 6.8 – 7.6⁹⁶. Finally, in the presence of kinetic factors, which abound in the biological milieus, and a high content of impurities, this already low, multistage growth rate can be prolonged indefinitely and take unexpected crystallographic turns, which is why it has been said that there is no direct correspondence between maturity and crystallinity in biological HAp⁹⁷. This effect certainly contributes to the structural versatility of this compound, the versatility which we have barely begun to translate into a functional one and harness as such⁹⁸.

2.8. A higher bioactivity and resorbability of biological HAp compared to the synthetic one

As the result of high carbonate content, calcium deficiency and topographic irregularities on the atomic scale, bioactivity, osteoconductivity and resorbability of biological HAp is higher than of its synthetic analog. The carbonate content of biological HAp, varying anywhere between 2 and 8 wt%, has a particularly large effect on its higher solubility and bioresorbability compared to the synthetic one. Interestingly, whereas synthetic carbonated HAp is usually the A-type (CO₃^2- → OH^-) when prepared by annealing at high temperatures (owing to the high mobility of OH^- groups) and B-type (CO₃^2- → PO₄^3-) when it is precipitated at the room temperature⁹⁹, biological HAp is a mixed A and B type^100,101. This suggests a vastly different formation mechanism of biomineralized HAp compared to the synthetic processes usually run in the lab. The surface energy and interaction potential of biological HAp was also measured to be 1.6 and 2.5 times higher, respectively, compared to pure synthetic HAp, indicating a considerably higher surface heterogeneity and a greater conduciveness to protein adhesion and cell binding¹⁰². Multiple substitutions and defects in biological HAp are certainly the key to explaining its superior biological activity over its synthetic, pure and defect-free HAp counterpart^103,104.

2.9. Ultrahigh sensitivity to variations in the environmental conditions

Precipitation of HAp, especially at low supersaturations, when it bears resemblance to the biological formation pathway, is extraordinarily sensitive to the subtlest changes in the conditions. The reaction routes leading to HAp as the final phase in a long chain of transformations, frequently proceeding in concert with the Ostwald-Lussac rule^105,106,107, are subject to change depending on even the mildest modifications of the initial experimental conditions. For example, formation pathways and properties of HAp are greatly sensitive to the amount and nature of impurities. Impurities create condensation centers for the primary particle formation during crystallization of synthetic HAp and calcium phosphates in general appear to be sensitive to impurities in concentrations of less than 10^-6 % (0.01 ppm)¹⁰⁸. Texture, porosity and chemical content of the reaction vessel also drastically affect the level of critical supersaturation¹⁰⁹. For example, nucleation of HAp will proceed at a considerably lower supersaturation level in borosilicate vessels than in plastic ones, as the result of leaching of silicate ions and of more polar container walls that reduce the energy barrier for nucleation. Tadashi Kokubo, the inventor of the dubiously thorough method for evaluating the bioactivity of a solid compound by immersing it in simulated body fluid (SBF) and looking for the signs of HAp deposition on its surface¹¹⁰, consequently suggested discarding any plastic bottles with visible scratches and never reusing them for storing SBF¹¹¹, a metastable solution with supersaturation per growth unit equaling 19.5 with respect to HAp. The kinetics of HAp dissolution is also strongly influenced by the presence of impurities released into the solution during the reaction¹¹². Solutions particularly prone to exhibit this sensitivity lie in the middle of the metastability zone, between the levels of saturation and critical supersaturation. In this supersaturation window, kinetic effects, such as the presence of an organic matrix, exert the finest level of control over the microstructure and hierarchical superstructure of HAp precipitates¹¹³. As a result, there is a multitude of possible stoichiometries and phase combinations that could appear in the final products of the precipitation reaction depending on the subtlest changes in synthesis conditions^114,115 and some of them, such as the acidic and biosoluble transitory calcium phosphate phases, found exclusively in pathological calcification deposits, may be all but ideal components of HAp designed for specific biomedical applications. This versatility of reaction outcomes depending on variations in the experimental conditions becomes even more magnified when various preparation methods are introduced in the comparison. This is why different methods to synthesize HAp led to materials that vastly differed in crystalline order and properties, with the most notable difference being found in the diffusivity across the hydroxyl ion channel, which spanned two orders of magnitude, ranging from ultralow for the ordered, monoclinic samples prepared by solid state synthesis at 1100°C to ultrahigh for the disordered, hexagonal samples prepared by room temperature precipitation¹¹⁶. Tracing this journey of ions across the channel running through the center of triple hexagons that define the crystal structure of HAp takes us to the elaboration of its properties, the subject of the next section.

3. The role of hydroxyl ion channel

The question framing this opinion piece is this: what if there is a single structural detail that could explain all these peculiar phenomena demonstrated by the protean nature of HAp? Our fancy is limitless, we know, and, though unsupported by direct computational analyses, it has been set out to play in the following paragraphs. But let us look first at the crystal structure model of HAp.

3.1. The place for hydroxyl in the crystal lattice of HAp

Although its first chemical composition analyses in the mineral form date back to 1788^117,118 and the first synthesis to 1851¹¹⁹, HAp was first detected as the bone mineral phase in 1926¹²⁰. In 1930, four years later, in two simultaneously published independent studies, its crystal structure was determined^121,122. Pure HAp crystallizes in monoclinic, P2_1/b space group symmetry, with 88 atoms per unit cell and Ca₂₀(PO₄)₁₂(OH)₄ stoichiometry, but presents a rarity even in the lab, let alone in Nature, where it virtually never occurs in such a form. For, any precipitation under atmospheric conditions leads to the inclusion of carbonate ions, which necessitate charge compensation and, thus, lead to vacancies, deformations of the lattice and adoption of hexagonal, P6_3/m space group symmetry, with 44 atoms per unit cell and Ca₁₀(PO₄)₆(OH)₂ stoichiometry, whereas solid state processing at elevated temperatures, higher than 207°C, produces the same transition to hexagonal symmetry. When it comes to pure HAp, the structural difference between the two phases boils down to the ordered, head-to-tail arrangement of OH^- groups located in the center of every other Ca2 triangle in the monoclinic, low-temperature symmetry and disordered arrangement of OH^- groups where the head-to-tail and tail-to-head arrangements alternate throughout the channel in the hexagonal, high-temperature symmetry. The monoclinic-to-hexagonal transition at elevated temperatures is thus paralleled by a curious phenomenon: namely, thermal energy during annealing converts a more ordered OH^- channel structure to a more disordered one. As a result, the hexagonal phase is higher in energy than the monoclinic phase by a rather small amount of 22 meV per unit cell¹²³ and the transition between the two, typified by a relatively low transition enthalpy of 130 J/mol¹²⁴, is initiated by the rotation and reorientation of OH^- dipoles^125,126 and may proceed by the subsequent progressive twinning of the monoclinic, pseudo-hexagonal lattice until the hexagonal symmetry is reached¹²⁷. Note that both the occupational and the orientational order of OH^- ions becomes perturbed by this transition from the state of higher, P2_1/b space group symmetry to the state of lower, P6_3/m one, leading to a greater diffusivity of OH^- species along the channel and a higher potential for restructuring of the material under the demands of the local biological environment. The hexagonal form is, thus, the one favored by the biological systems, in part because it allows for an easier exchange of OH^- groups⁷⁸ with ions such as F^-, Cl^- and CO₃^2-, which brings about an increased level of structural disorder utilizable during the incessantly ongoing process of bone remodeling. The symmetry elements present in the rather disordered biological HAp include six-fold rotation axis parallel to the c-axis, a ½ translation along the c-axis and a mirror plane perpendicular to the screw axis and the c-axis. The theoretical lattice parameters are a = 9.418 Å and c = 6.884 Å for P6_3/m (b = 2a, α = 120° for P2_1/b). However, depending on the preparation method and that particularly when wet, room temperature syntheses are involved, the lattice parameters a and c could be found anywhere in the ranges 9.41 – 9.44 Å and 6.84 – 6.94 Å, respectively, for the P6_3/m space group.

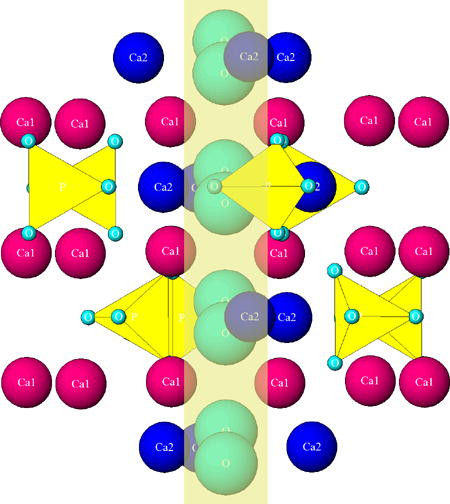
The unit cell formula of hexagonal HAp, Ca₁₀(PO₄)₆(OH)₂, can be more precisely given as Ca1₄Ca2₆(PO₄)₆(OH)₂, where Ca1 denotes columnar calcium ions and Ca2 denotes the hexagonal ones¹²⁸. Columnar calcium ions are named so because they are arranged in columns that uninterruptedly traverse the lattice, while hexagonal ones outline hexagons when projected on the basal plane. Such an etymology conceals a mild misnomer because the columnar Ca atoms also create a hexagon when viewed down the c-axis, just as hexagonal Ca atoms do. The difference between the two hexagons projected on the basal plane is that the one created by columnar Ca atoms is wider and accommodates in its center the hexagon created by the hexagonal ones. As seen from Fig.2, the outer hexagon created by the columnar Ca atoms outlines the edges of the P6_3/m unit cell, while the six hexagonal Ca atoms form a series of overlapping inner hexagons. While all six hexagonal Ca atoms occupy the interior of the P6_3/m unit cell, columnar Ca atoms are positioned in the six corners of the two basal planes and the six corners of the equatorial mirror plane in-between them, yielding eighteen Ca1 atoms within the unit cell but only four per unit cell (each of the six basal plane atoms is shared with five neighboring unit cells, while each of the six atoms on the mirror plane is shared with two adjacent cells). Each inner hexagon is formed by two overlapping Ca2 triangles positioned parallel to the basal plane at z = 1/4 and z = 3/4 and at a 60° angle with respect to each other (Fig.3a). Each of the six PO₄^3- tetrahedra populating the interior of the hexagonal unit cell is positioned between the pairs of Ca²⁺ ions in the outer hexagon when viewed down the c-axis, with three of them lying on the Ca2 triangle plane at z = 1/4 and the other three lying on the Ca2 triangle plane at z = 3/4. Furthermore, one of the four oxygen atoms of each of the PO₄^3- tetrahedra is found just outside of the edge of the outer hexagon, which is compensated by the intrusion of an oxygen from tetrahedra positioned on planes below and above (z = ± 1/2). PO₄^3- tetrahedra, 2.6 Å in radius, are arranged so as to form hexagonal close packing (ABABA) and given their size-wise dominance over the crystal structure, Ca²⁺ ions, 1.06 Å in radius, could be visualized as merely filling the holes between them. These holes come in two sizes and both form long columns in the direction of the c-axis. While smaller holes can accommodate ions ≤ 0.225r in radius (r being the radius of a PO₄^3- tetrahedron), which is too small to fit Ca²⁺, larger holes provide enough room for Ca²⁺, given that they can accommodate ions ≤ 0.41r in radius (∼ 1.1 Å), and are filled with Ca atoms¹²⁹. Each site at which a Ca1 atom is located lies in-between two parallel PO₄^3- sheets, A and B, and is coordinated by nine oxygen atoms from three PO₄^3- tetrahedra on top and three more at the bottom. The Ca1 site is also called “octahedral” because the six PO₄^3- groups it is coordinated to outline the corners of a regular octahedron together with Ca1. Ca1 atoms are, thus, found in columns, perpendicular to the PO₄^3- sheets and parallel to the c-axis, with the Ca1/OH^- ratio of 2:1. Ca2 atoms, on the other hand, lie in the same plane as PO₄^3- tetrahedra and reside inside the holes formed by the oxygen atoms of the tetrahedra that line the c-axis channel. Ca2 ions are engaged in a seven-fold coordination with six oxygen ions belonging to five different PO₄^3- tetrahedra and an OH^- group¹³⁰. Arranged in a series of triangles lying parallel to the basal plane, Ca2 atoms outline the boundaries of the OH^- channel extending through the center of the crystal structure, perpendicularly to the basal plane.

Fig.2.

A view of a stoichiometric HAp crystal down the c, [001] axis, showing an OH group (small green circle) in its center, surrounded by hexagonal (blue circles) and columnar (purple circles) Ca atoms and phosphate tetrahedra: each green pyramid is a P⁵⁺ ion and four red circles in its corners are four O^2- ions. Notice the misrepresentation though: O^2- ions are not the smallest ions in the lattice, as it is being shown here, but, in fact, the largest, occupying most space in it. As parts of the PO₄ sublattice, they determine the stacking order of the unit cell. All other ions could be imagined as if merely occupying interstices created by oxygen atoms.

Fig.3.

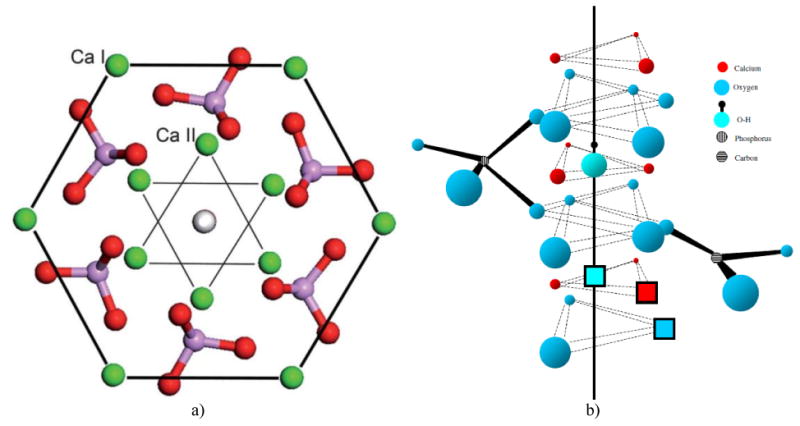
(a) A view of the hexagonal unit cell of HAp when projected down the c, [001] axis. Three parallel hexagons with columnar calcium atoms (Ca1) on their corners, positioned at the two basal planes (z = 0 and z = 1) and at the equatorial mirror plane in-between them (z = 1/2), define the geometric form of the unit cell, while hexagonal calcium atoms (Ca2) form a pair of inner triangles (z = 1/4 and z = 3/4) positioned at a 60° angle with respect to each other. Six PO₄ tetrahedra occupying the interior of the unit cell are distributed in such a way so that three of them lie on the Ca2 triangle plane at z = 1/4 and three of them lie on the Ca2 triangle plane at z = ¾, themselves forming triangles at the 60° angle with respect to the in-plane Ca2 triangles and with respect to one another. Reprinted with permission from Ref.144. (b) The effect of phosphate-to-carbonate substitution on the creation of paired vacancies at adjacent Ca2 and hydroxyl group sites. The solid line represents the axis of the OH^- channel formed by the series of overlapping calcium triangles and running perpendicular to the basal plane of the hexagonal unit cell. Reprinted with permission from Ref.145.

The OH^- groups are, thus, lined up along the c-axis, being positioned inside the overlapping triangles formed by hexagonal Ca²⁺ ions, with the average distance of 2.5 Å between them. The triangles are stacked on top of one another in the direction of the c-axis, with each neighboring triangle being rotated by 60° with respect to the triangle below it and the triangle above it, and the line connecting all the OH^- groups in a stacked array of unit cells runs straight through their center, with both oxygen and hydrogen of the OH^- lying on the c-axis in the higher, monoclinic symmetry (Fig.3b). Being inherently disordered as a part of P6_3/m symmetry, however, oxygen atoms of the hydroxyl are equally likely found either slightly above or slightly below the plane of the calcium triangles (Fig.4a) and the same applies to their halide ion substitutes. Moreover, there is no energetic preference as to whether the hydrogen atom of the OH^- group is to point upwards or downwards with respect to the c-axis and, as the result, each OH^- ion has a 50 % probability of being in one state or another. Compared to other ionic groups in the lattice, particularly PO₄^3-, the OH^- groups have a considerable freedom of movement along the Ca2 channel circa 3 Å in diameter. To be more precise, the diameter of the channel varies across the unit cell, being widest in its center and on the basal plane (z = 0, z = 1/2, 2.85 Å) and narrowest at the two midpoints between the basal planes and the center of the unit cell, lying in-plane with the Ca2 triangles (z = 1/4, z = 3/4, 2.73 Å)¹³¹. For this reason, the channel could be better visualized as a continuous array of ovoid cavities than as a hollow cylinder (Fig.4b).

Fig.4.

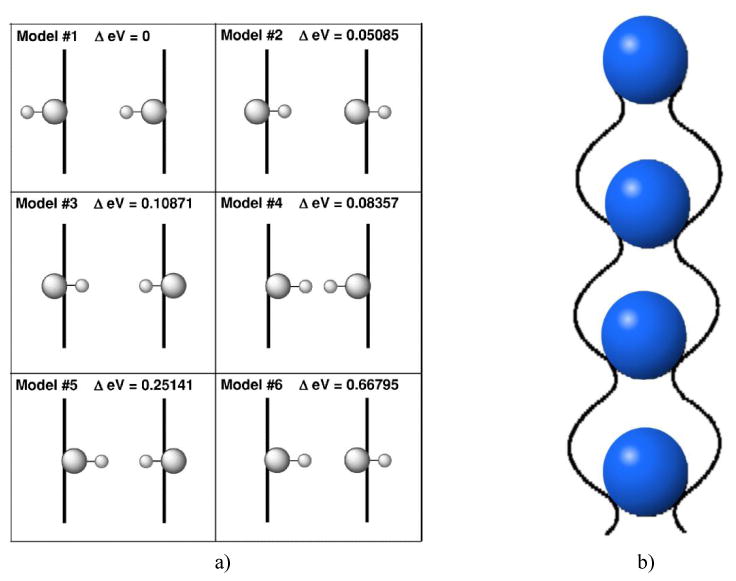
(a) The result of an ab initio calculation of the band gap deviation from the lowest energy configuration depending on the different orientation of OH^- groups with respect to the two Ca2 triplet planes (two vertical lines in each subfigure). Reprinted with permission from Ref.150. (b) A sketched view of the ordered channel structure, with al OH^- groups pointing in the same direction, as seen in P2_1/b apatite space group.

As could be seen from Fig.4b, there is not enough room in the lattice to accommodate two OH^- groups pointing towards each other (^-OH--- ---HO^-) in the adjacent calcium triangles without producing significant lattice distortion and the loss of higher, monoclinic symmetry. For this reason, the OH^- groups in the channel must either be arranged in an ‘ordered column’ fashion, i.e. as OH^- OH^- OH^- OH^-… along the c-axis, or in ‘disordered column’ fashion, implying the reversal of the direction from OH^- OH^- OH^- OH^-… to HO^- HO^- HO^- HO^-… and back at various places. While the former, head-to-tail arrangement is seen in stoichiometrically pure, monoclinic HAp, the latter, disordered arrangement is seen in biological, intrinsically impure, defective and hexagonal HAp. The reorientation of a single OH^- group from the ordered OH^- OH^- OH^- configuration to a disordered OH^- HO^- OH^- one also seems to be followed by the tilting of the flipped OH^- group by ∼ 20 – 40° from the [001] direction to decrease the unfavorably short distance between the two protons and the two oxygens of the adjacent OH^- groups¹³². This entails widening of one edge of the Ca2 triangle accommodating the reoriented OH^- group and subsequent tilting of PO₄^3- tetrahedra adjacent to the channel by 2.4°, whereby the symmetric distribution of the electron density of O^2- atoms bound to P⁵⁺ ions becomes restored¹³³. The disorder initiated in the channel thus extends to the neighboring regions of the lattice. Note, however, that even in the ordered channel structure there is no correlation between the orientations of OH^- groups in neighboring channels in the absence of a polarization-inducing electric field.

So we see that both the two different types of calcium atoms and the phosphate groups outline hexagons when viewed down the [001] axis, while the OH^- groups occupy a central place by creating a vertical line that spans across the interiors of all these three hexagons. The attempt to translate this structural centrality into a property-wise one presents the central aim of this discourse.

3.2. Effects on resorbability, surface composition variability and trends in crystal growth/dissolution of HAp

The higher bioactivity and osteoclastic resorption rate of biological HAp compared to the synthetic is owing to less than 50 % of OH^- positions being filled. This is a direct consequence of the comparatively large amount of impurities accommodated by biological HAp. These impurities are the cause of structural defects, which are directly proportional to ion diffusivity and solubility of the compound in spite of its having a high melting point and allowing virtually no diffusion of Ca²⁺ and PO₄^3- ions at room temperature and in the pure state¹³⁴. More specifically, as shown in Fig.3b, substitution of trivalent phosphate for bivalent carbonate induces the formation of one Ca2 vacancy per PO₄^3- → CO₃^2- substitution as the result of charge compensation, which, on the other hand, entails the creation of a vacancy at the OH^- ion site. The content of OH^- in HAp isolated from the human cortical bone was estimated to an even lower level than ½ of the theoretical: only 20 % of that present in synthetic and stoichiometric HAp¹³⁵. The degree of hydroxylation, greatly dependent on age, weight and the overall health of the donor, was measured to be 45 – 65 % of the stoichiometric in chicken and mouse cortical tibia bone¹³⁶. The incomplete hydroxylation of the bone mineral is the reason why it is often being insisted that it must be called apatite rather than HAp, even though apatite, technically, is a term reserved exclusively for the apatite group of minerals and not for any single member of this group¹³⁷. Nevertheless, the OH^- ion content in biological HAp is still sufficient to affect the properties of the material and, although bone apatite is often considered virtually dehydroxylated^138,139, the aqueous environment in which it forms necessitates the incorporation of this ion (note that even lunar apatite was found to contain up to 8 % of the channel ion sites occupied by OH^-140, which, if released in its entirety, would be enough to cover the surface of the Moon with a one-meter-deep ocean¹⁴¹). Studies that reported undetectable amounts of OH^- ions in the bone mineral, relying predominantly on solid state NMR and other dry methods, could have been done on dehydrated apatite samples and could be thus seen as an implicit evidence of the pronounced diffusivity of OH^- groups intrinsic to the structure of this material. Namely, the amorphous surface of biological apatite is known to comprise large amounts of trapped water¹⁴², which has been hypothesized to even have a directional effect on the crystal growth of this compound¹⁴³. Its prompt dehydration outside of its natural, aqueous milieu might be envisaged to draw the threads of OH^- groups to the surface via osmosis if the ion channel is structurally loose enough to allow for this effect to take place.

Vacancies created by only partially filled OH^- ion sites in the central channel have, in fact, an essential role by allowing room for the direction-dependent mobility of OH^- groups, their mobile O^2- substitutes and Ca2 ions, thus facilitating restructuring of the crystals during bone remodeling orchestrated by the mutually antagonistic bone-building cells, osteoblasts and bone-resorbing cells, osteoclasts. Also, paired with vacancies at the adjacent Ca2 sites, they appear to be able to entrap modest amounts of small organic molecules, such as glycine¹⁴⁶, as mentioned in section 2.1, suggesting a wholly unexplored avenue in the utilization of the OH^- channel, which would be replicating the molecular trapping functionality of zeolites or clathrates in highly defective, nonstoichiometric HAp. In addition, the missing OH stretch and libration bands have suggested that the structural binding of OH^- groups in biological HAp must be weak or almost nonexistent¹⁴⁷, which is the result of inherently disordered OH content in regard to both its location and orientation and which obviously facilitates structural reorganization during bone remodeling due to a lower entropic cost. This inherent disorder may be responsible for the existence of a multitude of energetically acceptable ion channel configurations and might even be the key to explaining the weaker mechanical properties of HAp when compared to other apatites¹⁴⁸. Substituting OH^- with F^- reduces this disorder by restricting the number of possible channel ion configurations, but only to a certain extent, after which the rigidity of the channel structure starts to take hold, resulting in the increased proneness to cracking and the overall weakening of the material¹⁴⁹.

The role of OH^- ions in enhancing solubility of the surface layer and the ease of its restructuring, having immense biological repercussions during bone remodeling, can be tentatively supported by the effects of their substitution with fluoride and other halide ions. The size, the electronegativity and the orientation of these ionic substitutes plays a vital role in determining the number and strength of primary bonds, which, in turn, shifts the ionic-covalent equilibrium extending through the entire crystal structure. Larger ions lying farther from the Ca2 triplet plane, thus, have a greater number of bonds whose strength is weaker on average. Such is the case with relatively large Br^- ions that lie in-between the two parallel calcium triplet planes. Smaller Cl^- displays a minor offset from the calcium triplet plane, while even smaller F^- is positioned right on the plane, exhibiting consequently the strongest bonding. Because of its intrinsic polarity, OH^- has multiple ways of positioning, typically exhibiting a small offset from the plane, like Cl^-. Orientation of the OH^- ions in the channel can also have a profound effect on the bonding strength¹⁵⁰. This is illustrated in Fig.4a, where the results of the theoretical band gap prediction based on an ab initio, density-functional-theory-based computational model are shown: depending on the orientation of the two OH^- groups per unit cell with respect to the Ca2 triplet plane, the deviation from the lowest energy configuration can vary from 0 – 15 % (i.e., 0 – 0.66795 eV for the band gap estimated at 4.71 eV). Another way in which halide substitutes, such as F^- and Cl^-, modify the structure and properties of HAp is by promoting hydrogen bonding between neighboring OH^- dipoles in the channel^151,152. These bonds have otherwise not been observed in pure HAp due to a large distance between adjacent OH^- groups^153,154, limiting hydrogen bonding only to that between OH^- groups and the nearest oxygen atoms belonging to PO₄^3- groups¹⁵⁵.

Then, OH^- group exchange is known to proceed much faster than the exchange of surface phosphate or calciumions¹⁵⁶. This is even more facilitated as the result of the deformation of the Ca2 hexagon outlining the edges of the OH^- ion channel when it is being exposed on the surface¹⁵⁷ (Fig.5). The protonation of OH^- groups and their release into the solution is promptly followed by the release of Ca2 ions, which endows the surface with a net negative charge and increases the rate of binding of electrostatically attracted integrins and other adhesion proteins that precede bone cell attachment^158,159. Relatively light Ca²⁺ ions are, in fact, flexibly arranged within the lattice, the result of which is proneness to display Ca²⁺ vacancies, whereas heavier PO₄^3- groups are practically those that define the hexagonal structure of the crystal, given that the atomic arrangement of all calcium orthophosphates is built around the network of PO₄^3- groups that provide stability to the structure¹⁶⁰. With PO₄^3- network being more resistant to restructuring and dissolution in the solid phase and with heavier H_xPO₃^x-3 ions spending effectively more time on a surface than lighter and more diffusible Ca²⁺ ions (the same effect explains the negative charge of neutral surfaces in water, as OH^- groups spend more time on them on average that more mobile protons), the surface carries a negative charge, which, as it turns out (Fig.6), facilitates the crystal growth and remodeling¹⁶¹. For, unlike cations, which are generally more hydrated than anions and have a greater tendency to reside in the bulk aqueous medium, bigger anions tend to be specifically adsorbed, affecting the crystal habit to a greater degree than cations¹⁶² and leading to the most commonly negative charge of surfaces in water¹⁶³. At the same time, during dissolution events bulkier anions tend to be retained on the surface longer than cations, as exemplified by silver iodide, which preferentially releases smaller and more mobile Ag⁺ ions and retains heavier and less mobile I^-. Consequently, although the solubility product (a_Ag+a_I-) for AgI equals 10^-16, the point of zero charge is found not at pAg 8, but at pAg 5.5 (pI 10.5)¹⁶⁴. An NMR study of nanocrystalline HAp has indeed demonstrated the presence of circa 1 nm thick, amorphous surface layer predominantly populated by hydrogen phosphate ions, contrasting in composition and structure the crystalline and electrically neutral HAp core¹⁶⁵. And because of the more extensive adsorption of H_xPO₄^x-3 species onto the growing particle surface and their greater retention during dissolution, Ca/P molar ratios in the equilibrium solution were measured to be as high as 25 despite the stoichiometric composition of the precipitate¹⁶⁶. Low Ca/P molar ratios, naturally brought about by the binding of free Ca²⁺ by phosphorylated proteins in the bone matrix, have, for example, been shown to be critical for promoting controlled growth of HAp on amelogenin-functionalized surfaces¹⁶⁷. This is in agreement with calcium triphosphate (Ca/P = 0.333) being the composition of pre-nucleation clusters during the formation of HAp from supersaturated solutions¹⁶⁸. The transformation of these pre-critical nucleation clusters to stable HAp particles is accompanied by a gradual increase in Ca/P molar ratio from 0.333 to 1 – 1.5 for the amorphous particles and the short-lived OCP transient (if present) to 1.67 for stoichiometric HAp, indicating that the growth rate is highest when phosphate groups are dominant at the interface between the solid phase and the solution. Also, though this is highly dependent on the atomic scale roughness, on surface irregularities and on the exact groups that terminate the crystal faces, atomistic simulations of most (hk0) faces - e.g. the preferentially exposed (010) – have displayed an excess of Ca²⁺ ions, which is supposed to endow them with the positive surface charge. In contrast, the prominence of OH^- and PO₄^3- groups endows (001) faces with the negative surface charge¹⁶⁹, which is supposed to additionally foster their growth along [001] axis in light of low Ca/P molar ratios as the central condition for crystal growth. This preferential direction of growth is additionally reinforced by the presence of Ca²⁺-chelating agents, such as EDTA or citric acid, which constrict the growth along the a-axis and extend the crystals along their c-axis¹⁷⁰. The less pronounced growth of the bone mineral crystals along the latter direction than expected from these considerations might be explained by the lower surface energy of (001) faces compared to the prismatic ones: 1 J/m² for (001) vs. 1.7 J/m² for (010)¹⁷¹ and twice more for (100)¹⁷². Growth along the axes perpendicular to high energy planes, of course, minimizes their surface prominence and thus stabilizes the crystal by lowering its surface energy, the result of which is the plate-shaped morphology of HAp crystals in bone. The reports in the literature have not, however, reached agreement over the surface energy difference between the crystal faces of HAp, primarily because of a variety of ways the surfaces could be terminated. Recent surface modeling studies have, thus, arrived at contradictory findings with respect to the idea that (001) faces should be the least energetic: according to some of them, OH^--terminated (010) faces should, in fact, be the most stable on HAp surface and (001) faces the least¹⁷³. From the biological angle, the growth along the c-axis is also partially mitigated by the (001) faces being aligned along the collagen fibril axis and placed in direct contact with the fibrils¹⁷⁴, where they are constricted and partly shielded from the inflow of ionic growth units. Conversely, the fact that the turnover of HAp platelets via resorption by the lactic-acid-secreting osteoclasts is easiest on (hk0) planes abundant in alkaline Ca²⁺ ions and threads of easily dissolvable OH^- groups explains the orientation of their c-axis in the direction of the long axis of the collagen fibers in the intrafibrillar region of bone and the exposition of (hk0) faces to the surface of the fibers (Fig.7). In turn, (001) faces are the least prominent ones in enamel rods, but most exposed to the environment of the oral cavity, so as to minimize the dissolution of the mineral that does not get regenerated by cells during the lifetime of the organism and for which solubility is an undesired propensity. And indeed, the solubility of (001), the smallest habit face on hexagonal HAp crystals, was both theoretically predicted and experimentally determined to be less than the one of (100)¹⁷⁵, the dominant face in bone and enamel crystals alike, with the only difference that it is shielded from the environment in enamel and exposed to the cellular milieu in bone, along with other (hk0) faces. Therefore, it can be speculated that threads of OH^- groups extending along the c-axis of the unit cell, facilitating rapid OH^- ion exchange between the surface and the solution, are the key to endowing the material with comparative surface instability and ‘liveliness’ that their biological environment utilizes oh so well. In support of this idea comes the observed increase in the thickness of the mobile, defective and intensely hydrated surface layer in more soluble forms of HAp, such as Mg-substituted one¹⁷⁶. To that end, the concentration of OH^- groups emerging from the central c-axis channel to (001) faces as the result of their migration between two hydrated c-planes (20 % of bone is water and the water sheath enfolding collagen molecules provides an essential enthalpic contribution to its structural stability¹⁷⁷) must be considerable and, if the entire exposed channels thereof along (hk0) faces are added to the picture, yielded is a material stiff and sturdy, yet flexible enough to undergo constant remodeling over the course of the lifetime of bone, with the annual turnover rate averaging at 3 % for cortical bone and 25 % for the lighter, more porous and vascularized cancellous bone¹⁷⁸.

Fig.5.

Results of an interatomic potential study showing the structural rearrangement of (001) faces on HAp surface (left and right of the diagram) as the result of free energy minimization requirements. Even though the unit cells adjacent to the surface appear to be perfectly hexagonal, while the channels closer to the surface assume a distorted hexagonal geometry, the simulation has suggested the deformation of the OH^- channel outlined by Ca2 atoms, extending together with a short-range interaction between the surfaces over the distance of several unit cells into the bulk of the material.

Fig.6.

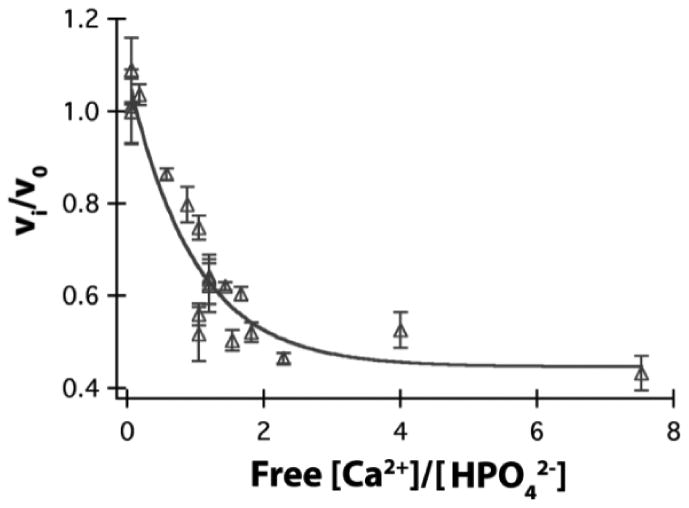
Surface step propagation velocity (v_i/v₀) as a measure of the crystal growth rate for HAp increases exponentially when the concentration of free H_xPO₄^x-3 ions dominates over the concentration of free Ca²⁺ ions.

Fig.7.

The reigning model of the packing of polycrystalline HAp platelets inside of the parallel arrays of collagen fibrils in bone¹⁷⁹: (a) HAp particles initially nucleate and grow within the gaps between N- and C-termini of collagen molecules in fibrils, but (b) either in the later stages of mineralization or in separate events they grow into the intermolecular spaces within fibrils, so that effectively between 30 and 70 % of HAp is found external to the fibrils¹⁸⁰. Despite the polycrystalline nature of the particles, the c-axis is predominantly oriented in parallel with the long axis of the fibers.

The rapidly rearranging surface layer of HAp, of which more has been said in sections 2.2 and 2.3, is also heavily hydrated¹⁸¹ and is not to be confused with the Stern layer of transiently adsorbed counter-ionic solutes since it is, strictly speaking, a part of the crystal and not the solution, even though it belongs to an entropic transition zone between the two. This surface layer hydration must have a considerable effect on the migration of constituent OH^- groups in and out of the channel, to and from the surface, on the length scale of a couple of unit cells extending down the c-axis from a (001) face. Generically speaking, dissolution of HAp proceeds with the first step being the acidic neutralization of channel OH^- groups and their release in form of water. As the result, HAp is sparsely soluble at the physiological pH and its solubility increases approximately tenfold with every unit decrease in pH, equaling 6.8 mg/dm³ at pH 7, 4.8 g/dm³ at pH 4 and 88 g/dm³ at pH 3 (all in pure water at 20°C)¹⁸², the point below which the compound becomes practically fully soluble. The release of OH^- groups induces charge instability of the calcium column and opening up of the channel. This can be the starting point for two different processes: continued dissolution via release of Ca²⁺ ions or accommodation of foreign ions into the lattice, the process in which, as we see, the OH^- channel plays an equally critical role¹⁸³. This role, holding the key to the extraordinary ionic substitution capacity of HAp, can be also evident from the fact that other calcium phosphate phases, such as DCP or OCP, do not tend to incorporate impurity ions despite containing water in their crystal lattices¹⁸⁴. After the release of OH^- ions, migration of Ca2 ions out of the channel and into the solution is the next step in the sequence of dissolution events^185,186, which leaves a highly negatively charged, PO₄^3--rich layer at the solid interface. This greater diffusivity of Ca2 ions compared to Ca1 ones explains their being the primary sites for cationic substitution; only at higher weight contents of the foreign ion do Ca1 ions begin to cede their places to the oncoming ions¹⁸⁷. The PO₄^3--rich layer exposed by the release of Ca2 ions is the next to dissolve due to water penetration and destabilization of the cross-linked network of PO₄^3- tetrahedra. For this reason it is said that HAp undergoes incongruent dissolution¹⁸⁸, in a sense that the Ca/P ratio in the supernatant (Ca/P = 2) is higher than the stoichiometric (Ca/P = 1.67)¹⁸⁹ during the dissolution of HAp, whereas as the result of the acidic nature of DCP the trend is the opposite during the dissolution of this more soluble calcium phosphate phase (Ca/P < 0.5)¹⁹⁰. The sequential dissolution of different ionic species also predisposes the supernatant to exhibit the occasionally observed periodic fluctuations in Ca/P ratio and pH over the course of dissolution or ripening of the precipitate¹⁹¹. Additives and substitutions can alter the dissolution process, e.g., by binding the exposed Ca2 ions, as is the case with citrate ions¹⁹², the inhibitors of the dissolution of HAp¹⁹³, or by restricting the primary ion channel, as is the case following OH^- → F^- substitution whereby fluoroapatite, the least soluble apatite, forms. Namely, F^- and OH^- ions are of similar size and identical charge, which facilitates easy substitution (ionic radii equal 110 pm for OH^-, 119 pm for F^-, 167 pm for Cl^- and 182 pm for Br^-). Fluoride forms a particularly strong ionic bond with the surrounding Ca²⁺ ions in part because of being positioned right on the Ca2 triplet plane and in part in analogy with CsF, a compound that forms the strongest ionic bond by involving the most electropositive nonradioactive atom of the Periodic Table, Cs (0.79 in dimensionless Pauling units), and the most electronegative one, F (3.98 in Pauling units). Of course, when it comes to CsF crystals, the discrepancy in size of the ions prevents their close packing and diminishes the bond strength, so that other halides, such as NaF, KF and NaCl, outweigh them in the solid form in terms of the bond strength. This, however, is not the case with fluoroapatite, where both the packing factor and the electronegativity factor favor the residence of F^- ions in the OH^- channel. As the result of the stronger bonding to Ca2 ions, substitution of OH^- with F^- contracts the lattice spacing a¹⁹⁴ and thus limits the diameter of the channel, reducing the mobility of the OH^- ion, while it also expands the c-axis, increasing the length of the channel. Both of these effects, causing the lattice expansion in the [001] direction and contraction in [hk0] ones, respectively, reduce the solubility of the compound through the hampered movement of OH^- groups along the channel. In contrast, substitution of Ca²⁺ with Mg²⁺, as mentioned in Section 2.1, increases the channel diameter and contracts it in length, enabling an easier escape of the OH^- ion and, as a result, increasing the solubility of the compound. A similar effect is achieved by the incorporation of Co²⁺ ions in place of Ca²⁺, being the result of the expansion of HAp lattice in [100] and [010] directions and contraction along the c-axis¹⁹⁵, evidenced by the reduction of the aspect ratio and increase in the sphericity of HAp crystallites accompanying this substitution^196,197. Likewise, the introduction of divalent carbonate ions induces the formation of Ca2 vacancies, which additionally contributes to decreased confinement of OH^- groups in the channel and fosters their migration to and from the surface, facilitating the dissolution and cell-guided restructuring processes.

3.3. Hydroxyl ion channel as the route to polarization, proton conduction and susceptibility to electromagnetic radiation

Spontaneous polarization of OH^- ions in the c-axis channel is responsible for both the piezoelectric and the pyroelectric effect exhibited by HAp. As shown in Fig.8, different arrangements of OH^- dipoles in the channel created by the overlapping Ca2 triangles are possible, resulting in either ferroelectric or anti-ferroelectric ordering and justifying the envisioning of polarized HAp lattice as an array of parallel 1D ferroelectric nanowires embedded in a dielectric matrix composed of Ca²⁺ and PO₄^3- groups¹⁹⁸. And if this polarization has been shown to accelerate the crystal growth, while the increased disorder in the OH^- channel increases solubility and facilitates particle restructuring, then there are also grounds to correlate the surface layer instability that typifies HAp and the difficulty of inducing the growth of singlets past the nanosize range with the structure of the OH^- channel. For example, it is conceivable that the rapid exchange of OH^- groups between the solution and the particle surface, along with the partial penetration of protons contributing to internal hydration and disordering of the channel structure, plays an important role in destabilizing the surface and disfavoring the rapid particle growth via a classical mechanism that involves the attachment of individual ions, not amorphous clusters, onto a growing particle. In turn, the rapidity of nucleation at low supersaturations may be due to a relatively low energy barrier standing in the way of the transition of a large concentration of pre-nucleated clusters to their spontaneous growth via coalescence into stable particles. The pivotal role OH^- groups play in conducting the coalescence of Posner's clusters into amorphous particles later to be transformed into crystalline platelets could be tentatively inferred from the fact that one Ca²⁺ ion and two OH^- groups constitute the difference between the stoichiometry of an anhydrous Posner's cluster, Ca₉(PO4)₆, and that of a hexagonal HAp unit cell, Ca₁₀(PO₄)₆(OH)₂. With the external Ca²⁺ ions, all of which are thought to be hexagonal, Ca2 ones, initially acting as bridges between the organic surface and the anchored clusters, in analogy with Ca²⁺ immobilizing DNA by being sandwiched between two phosphate groups, one from a DNA molecule and another one from a zwitterionic derivative of phosphatidylcholine¹⁹⁹, and OH^- drawing a thread in-between them that defines the central axis of the six-fold symmetry of the apatite hexagon and enables precise localization of adjacent clusters, obtained are the conditions for the unprecedented, virtually defect-free aggregative growth at ambient temperatures.

Fig.8.

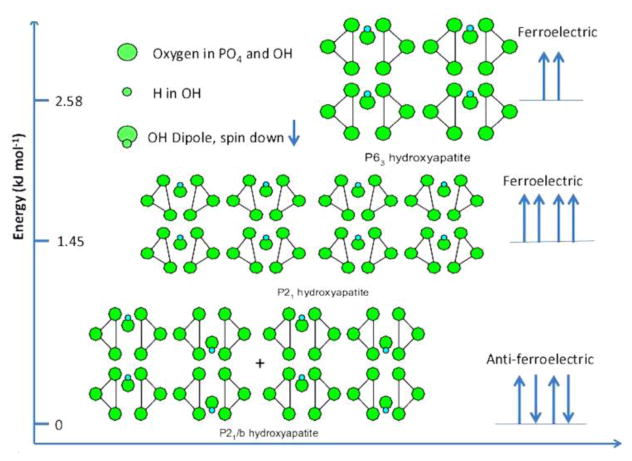
Energy levels corresponding to different arrangements of OH^- groups inside the c-axis channel for different lattice space groups: P6₃ ferroelectric, P2₁ ferroelectric and P2_1/b anti-ferroelectric. Reprinted with permission from Ref.65.

The brick-and-mortar model of growth, according to which the growth occurs through aggregation of small clusters whose structurally unstable, mortar-resembling surface swiftly rearranges itself when in contact with the growing crystal so as to enable a seamless blend with it, is thus favored overall, but with definite limitations. Namely, while the coalescence of clusters may proceed fast when the cluster size is sufficiently small, regardless of supersaturation (hence the high nucleation rate at low supersaturations), it may be hindered at larger sizes, which is when the surface instability brought about by the diffusion of OH^- groups across the particle/solution interface can induce the opposite effect, effectively slowing down the growth instead of facilitating it (hence the low crystal growth rate at high supersaturations). Note that the OH^- groups emerging on the particle surface from the c-axis channel are also causative of the intense hydration of ionic growth units in the Stern layer, which presents an additional barrier that prevents the fast growth of HAp crystals even under high supersaturations, given that dehydration is most frequently the kinetic step with the largest energy barrier in the growth unit transfer from the solution to the solid surface²⁰⁰. An inverse effect is seen during the dissolution of HAp: namely, even when the initial crystals are coarse and polydispersed, the particle size and morphology often evolve towards the monodispersed and the nanosized, with the high surface area unexpectedly stabilizing the further dissolution²⁰¹, again presumably owing to the highly mobile and hydrated interfacial layer, the outcome of the rapid exchange of OH^- ions between the channel and the solution. Dehydration effects involving the channel OH^- ion migration across the interface are also thought to be responsible for another peculiar effect exhibited by some HAp precipitates, which is the unexpected reduction in the particle size following calcination at up to 750°C, in spite of the evident increase in crystallinity^202,203. In any case, the exposition of OH^- groups necessitates major surface reconstructions in search of stability⁸³ and their dynamic interaction with the aqueous environment makes the surface reconstruction processes perpetually fluctuant.

The ability to transmit protons across the OH^- channel makes HAp a good proton conductor too, with a potential to be used in H⁺-conducting fuel cells and chemical sensors²⁰⁴. The proton diffusion path, proceeding straight through the OH^- channel in a sinusoidal fashion and being accompanied by the reorientation of the OH^- ions, is depicted in Fig.9. This proton conduction is directly responsible for the polarization of the compound²⁰⁵ and for its responding to electrical and magnetic fields with accelerated growth and enhanced bone formation. The high surface ion mobility, originating predominantly from the diffusion of OH^- groups along the c-axis channel and intense local hydration that it brings about, is also thought to be responsible for the higher electrical conductivity exhibited by HAp than theoretically predicted by assuming the transport of charges across a fixed lattice. The band gap associated with HAp, 4.51 eV, is consequently lower than that of apatites with a more compact and constrained channel structure, including fluoroapatites (5.47 eV), bromoapatites (4.71 eV) and chloroapatites (5.27 eV)¹⁵⁰. Interestingly, the diffusion path of protons through HAp lattice bears resemblance to that taken by O^2- diffusing along the c-axis of the hexagonal, apatitic ionic conductor La₅(Si_3-xMg_x)O₁₃ (x = 0 – 0.15)²⁰⁶. However, though the diffusion direction may be the same, the involvement of OH^- ions, whose reorientation accompanies the transfer of a proton from one OH^- group to another¹³³, makes the transport mechanism profoundly different in comparison with that present in La₅(Si_3-xMg_x)O₁₃. The same transport mechanism applies to conductivity of HAp to O^2- ions too, which becomes particularly pronounced in B-type HAp²⁰⁷, in which larger PO₄^3- groups are partially substituted by smaller CO₃^2- ones, causing the moderate widening of the channel and increased diffusivity of ions through it. Finally, the frequently noted positive effect of external fields on the biological response to HAp implants in the literature is the sole result of reorientation of OH^- dipoles in these fields, an effect whose complexity needs to be explored in far more detail before it could be utilized for therapeutic purposes.

Fig.9.

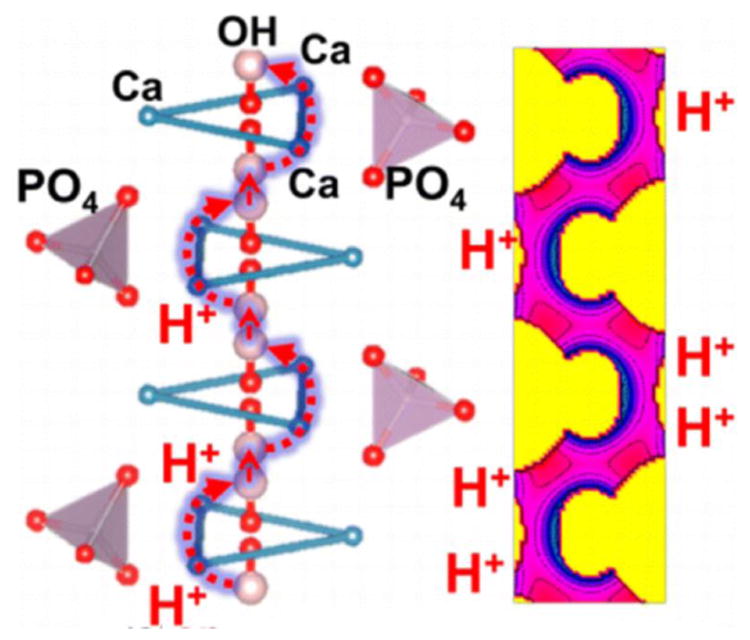
The sinusoidal proton diffusion path through the OH^- channel of HAp lattice. Reprinted with permission from Ref.208.

3.4. Hydroxyl ion channel, one of many structural features that, together, define physicochemical peculiarities of HAp

In the end, it would be overly simplistic to say that OH^- ion channel is the only structural element responsible for the broad range of peculiarities exhibited by HAp. The complex interaction involving all the ionic groups must take an equal part in defining the properties for which Nature selected it through the evolution as the indispensable ingredient of vertebrate skeleton. The discourse provided herein should act as an incentive for more detailed explorations of the structure-property relationships with a particular emphasis on this central channel and ions residing in and diffusing through it. The future studies on this literal structural centerpiece of HAp structure will benefit from in situ high-resolution spectroscopic, diffractometric and microscopic techniques, though with definite limitations: complementary techniques, such as small-angle X-ray scattering and Fourier-transform infrared spectroscopy, for example, oftentimes give incompatible information about the crystal size and structure parameters²⁰⁹, alongside having remained largely inconclusive about the state of hydroxylation of the lattice, while HAp particles have disintegrated during transmission electron microscopic analyses into CaO, volatile P₂O₅ and water under high beam currents²⁹, whose optimization entails an inescapable tradeoff in contrast and resolution. Also, since for half a century now X-ray diffraction and neutron scattering studies have not been able to reach an agreement over the precise location of OH^- groups in the channel^210,211 nor distinguish between their different orientations, e.g., between the ordered monoclinic configuration and the disordered hexagonal one, molecular dynamics simulations will need to step forth to compensate for such critical experimental limitations¹³². The rather limited spectroscopic, diffractometric and microscopic studies will also need to be coupled to the traditional methods of analytical chemistry, which have also benefitted in the meantime from the availability of more precise instrumentation. In any case, combinatorial analytical techniques are hoped to derive new paths in our understanding of this exciting structural detail of the most essential mineral in vertebrate biology. Only the future will tell how many insights relevant for the fundamental understanding of materials and for continuing to harness the untapped biomedical potentials existing within this unique biomineral will be derived by those who will proceed to play with this fine watery thread that runs through the center of its crystal symmetry.

4. Conclusions and perspectives

We were taken on a journey to meet a myriad of interesting features of HAp, the biomineral that constitutes the foundations of our biological makeup. The purpose of this review study was twofold: firstly, to compile physicochemical peculiarities exhibited by HAp, and, secondly, to engage in an effort to explain them by referring to the hydroxyl ion channel as an essential crystallographic element of this compound. We have seen that the spontaneous polarization of HAp, the increased solubility, resorption rate and bioactivity of biological apatite as well as the precise crystallographic orientation of apatite platelets in bone may all have their roots in the column of hydroxyl ions extending in the direction of the c-axis of HAp crystals, through a crystallographic column created by the overlapping calcium ion triangles. Still, what this review has aimed at is to provide only a glimpse at a remarkable structural feature of a crystalline structure that is, unexplainably, evolutionarily favored over others and assuring the readers that there are reasons for which it should be studied in more detail.

Ideally, therefore, the impact of this study is to be the stimulation of a greater interest in examining the relationships between the hydroxyl ion channel extending across the longest axis of the crystal structure of HAp and the properties of this compound in both simple chemical environments and more complex, biological niches. Unfortunately, as already insinuated in section 3.4, the level of sophistication of the current state-of-the-art microscopic and spectrometric techniques is not adequate for visualizing this channel and quantifying interatomic potentials in and around it, let alone solving the finest symmetry perturbations on its scale under dynamic conditions. We have just begun to visualize the ripening of nanoclusters during crystal growth in real time and there is a long way before the dynamic surface restructuring that differs the ion channel from the rest of the lattice will be observable using atomic-resolution imaging techniques. Although combinatorial techniques - such as microbeam X-ray diffraction and small-angle scattering paired with electron microscopy²¹² - are capable of discerning the deposition of Posner's clusters onto growing HAp crystals in real time, any ideas about the precise structural transformations taking place on the atomic scale upon the coalescence of amorphous precursors and their recrystallization have so far emerged strictly from theorizing. To compensate for these definitive deficiencies of experimental methods, computational analyses have justifiably stepped in, yet shortcomings of theirs, stemming from a range of approximations applied to enable mathematical solvability, are equally substantial. Continued examination of the effects of the hydroxyl ion channel on the properties of HAp will undoubtedly resemble the digging of a tunnel from two opposite sides, hoping that the hollows will eventually meet in the middle. And each time they do, a new line, like that running through the center of the crystal that was the subject of this study, will have been drawn, perhaps to remind us on a grander scale of things of the infinitude of applicative and inspirational analogies latent in the structure of this magnificent material.

Highlight.

Physicochemical peculiarities of hydroxyapatite are explained referring to its essential crystallographic feature: hydroxyl channel passing through the center of P6_3/m hexagons.