Proton dose calculation on scatter-corrected CBCT image: Feasibility study for adaptive proton therapy

Abstract

Purpose:

To demonstrate the feasibility of proton dose calculation on scatter-corrected cone-beam computed tomographic (CBCT) images for the purpose of adaptive proton therapy.

Methods:

CBCT projection images were acquired from anthropomorphic phantoms and a prostate patient using an on-board imaging system of an Elekta infinity linear accelerator. Two previously introduced techniques were used to correct the scattered x-rays in the raw projection images: uniform scatter correction (CBCT_us) and a priori CT-based scatter correction (CBCT_ap). CBCT images were reconstructed using a standard FDK algorithm and GPU-based reconstruction toolkit. Soft tissue ROI-based HU shifting was used to improve HU accuracy of the uncorrected CBCT images and CBCT_us, while no HU change was applied to the CBCT_ap. The degree of equivalence of the corrected CBCT images with respect to the reference CT image (CT_ref) was evaluated by using angular profiles of water equivalent path length (WEPL) and passively scattered proton treatment plans. The CBCT_ap was further evaluated in more realistic scenarios such as rectal filling and weight loss to assess the effect of mismatched prior information on the corrected images.

Results:

The uncorrected CBCT and CBCT_us images demonstrated substantial WEPL discrepancies (7.3 ± 5.3 mm and 11.1 ± 6.6 mm, respectively) with respect to the CT_ref, while the CBCT_ap images showed substantially reduced WEPL errors (2.4 ± 2.0 mm). Similarly, the CBCT_ap-based treatment plans demonstrated a high pass rate (96.0% ± 2.5% in 2 mm/2% criteria) in a 3D gamma analysis.

Conclusions:

A priori CT-based scatter correction technique was shown to be promising for adaptive proton therapy, as it achieved equivalent proton dose distributions and water equivalent path lengths compared to those of a reference CT in a selection of anthropomorphic phantoms.

1. INTRODUCTION

Dose calculation for dose delivery verification and treatment planning based on daily volumetric imaging is an essential part of adaptive radiation therapy (ART).¹ Since radiotherapy patients undergo fractionated treatments, the patient’s body is prone to daily setup error and changes in anatomy such as deformation, tumor shrinkage, and weight loss. Therefore, dose evaluation using volumetric imaging is important in dose adaptation and quality assurance. Several studies using various imaging modalities such as computed tomography (CT)-on-rails² and MV CT³ were demonstrated to be useful for ART.

Cone-beam CT (CBCT) imaging integrated with a medical linear accelerator is a competitive option for ART.⁴ However, the image quality and especially HU accuracy of the CBCT are known to be inferior to that of helical CT mainly due to scattered x-rays.⁵ Previous studies proposed various methods to correct those artifacts using analytical methods,⁶ Monte Carlo simulations,⁷ and experimental techniques.⁸ It has been reported that photon dose calculation discrepancy caused by CBCT HU error can reach up to 11% without any scatter correction and can be reduced to <1% with scatter correction.⁹

As a similar concept to ART, adaptive proton therapy (APT) was introduced.¹⁰ Although APT is not yet widespread due to the limited deployment of volumetric imaging systems at proton centers, dose adaptation of proton treatments promises improved target coverage and normal tissue sparing.¹¹ Daily volumetric imaging with CBCT is a good candidate for APT as well as for image-guided proton therapy. However, there have been few studies on CBCT imaging for APT.^12,13

It is expected that the HU accuracy of CBCT is more crucial in APT than it is in ART, because small HU differences may cause range errors and absolute dose errors, which will in turn lead to reduced integrity of the dose calculation.¹⁴ To date, no study has demonstrated proton dose calculation or treatment planning on either raw or scatter-corrected CBCT images.

This study aims to investigate the feasibility of proton treatment planning on CBCT images. To improve the HU accuracy of the CBCT images, two previously introduced scatter correction methods were investigated. Water equivalent path lengths (WEPLs) and proton dose distributions were evaluated for the CBCT images of phantoms and compared with reference helical CT images.

2. MATERIALS AND METHODS

2.A. Image acquisition

Imaging studies were carried out with three different phantoms: an electron density CT phantom (Model 467; Gammex Inc, Middleton, WI), an anthropomorphic head/thorax phantom (Phantom Patient; The Phantom Laboratory, New York, NY), and an anthropomorphic abdomen/pelvis phantom (The Phantom Laboratory, New York, NY). The reference CT for treatment planning (CT_ref) image was acquired using a helical CT system (LightSpeed16; GE Healthcare, Milwaukee, WI) following standard clinical settings of our institution (140 kVp, 1.25 mm slice width, and 0.7–1.0 mm pixel size). The phantoms were set up in a linear accelerator treatment room and underwent CBCT imaging with an on-board cone-beam system (Elekta Synergy XVI; Elekta Oncology Systems, Atlanta, GA). Two combinations (high and low) of tube current (mA) and exposure time (ms) were tested for each phantom study except the electron density CT phantom. The CBCT acquisition parameters are summarized in Table I. The original projections had a resolution of 1024 by 1024 with a spacing of 0.4 mm. To speed up the processing, they were resampled into 512 by 512 images.

TABLE I.

Acquisition parameters for CBCT scans.

Subjects	Tube voltage (kVp)	Tube current (mA)	Exposure time (ms)	Bowtie filter	Panel position/ collimator	Number of projections
Electron density CT phantom	120	25	40	Yes	M15	654
Head phantom	100	10	10, 20	No	S20	343
Thorax phantom	120	40, 64	40	Yes	M20	342
Abdomen phantom	120	40, 64	40	Yes	M20	346
Pelvis phantom	120	40, 64	40	Yes	M20	346
Prostate patient	120	64	40	Yes	M15	325

Note: M15 and M20 = middle panel positions (offset detector; half fan) with 15 and 20 cm collimator size; S20 = small panel position (centered detector; full fan) with 20 cm collimator.

2.B. Image reconstruction

The projection images were reconstructed with a spacing of 1 mm in each coordinate direction using in-house software based on an open source toolkit (RTK, reconstruction tool kit).¹⁵ In the reconstruction process, standard FDK algorithm with typical ramp filters (Hann and HannY filters with a cut frequency of 5.0) was used. The RTK-based CBCT reconstruction provided floating-point voxel intensities (μ_CB). Then, the HU value for the CBCT image was calculated from the μ_CB as follows:

$${\displaystyle {\mathrm{HU}}_{\mathrm{CBCT}}={\mu }_{\mathrm{CB}}\times 65536-1024.}$$ (1)

The above equation is the equation to convert CBCT values from RTK-based reconstruction into HU.

A median filter with a window size of 3 pixels in superior–inferior direction was then used to reduce random noises. Finally, voxel values outside the body were overridden with a zero density using a skin contour automatically produced by a commercial software package (MIM 6.3.7; MIM Software, Cleveland, OH), which was also done with the CT_ref. If no scatter correction is applied, the CBCT image generated via the above procedure is denoted as “CBCT_raw” hereafter.

2.C. Uniform scatter correction of a CBCT image

The uniform scatter correction proposed by Boellaard et al.¹⁶ assumes that the scattered radiation is uniformly distributed across the projection field. The scatter constant is estimated by multiplying the averaged projection signal of the body region by a scatter-to-primary ratio (SPR). The maximum SPR value was set to 0.5 and was automatically adjusted to yield only positive values of the scatter-corrected intensities over each projection. The constant was then subtracted from each projection image to constitute a corrected projection image. Reconstruction was performed as described in Sec. 2.B to generate a uniform scatter-corrected CBCT image, denoted as “CBCT_us” hereafter.

2.D. Soft-tissue-based HU shifting

Due to differences in software processing, CBCT_raw and CBCT_us are expected to have substantially different HU values compared to CT_ref. To calibrate intensities in these CBCT images, HU values were linearly shifted, based on soft tissue intensities sampled from a peripheral region of each image. This method is similar to the method of Richter et al.¹⁷ except that they used a multiple material-based look-up table (LUT). The simpler calibration, i.e., soft-tissue based shifting, was preferred in this study since a multiple material LUT is more easily affected by spatially varying scatter signals in our phantom images.

2.E. A priori CT-based CBCT scatter correction

The a priori CT-based scatter correction method proposed by Niu et al.¹⁸ was also benchmarked in this study. The procedures of the method are briefly summarized as follows:

• (1)Reconstruct a CBCT image using raw cone-beam projections.
• (2)Register the corresponding plan CT image to the CBCT_raw using deformable image registration (DIR).
• (3)Generate primary-beam projections from the deformed plan CT by using the Beer’s law and Joseph’s algorithm.¹⁹
• (4)Rescale measured projections from CBCT to match the primary-beam projections according to a predefined CT-CBCT calibration relationship.
• (5)Estimate scatter maps by subtracting the primary-beam projections from the rescaled raw projections and by applying smoothing operations.
• (6)Generate scatter-corrected projections by subtracting the scatter maps from the raw projections.
• (7)Reconstruct the volumetric image using the scatter-corrected projections.

Detailed descriptions of this method can be found in Refs. 18 and 20. For deformable registration for step 2, we used the Plastimatch software with mutual information-based optimization.²¹ Prior to the forward projection (step 3), the HU values of the deformed CT are mapped to floating-point values using the inverse of Eq. (1). This guarantees that identical HU values can be reproduced if reconstruction is performed.

After the scatter-corrected projections were prepared, the final reconstruction was performed as described in Sec. 2.B to generate a priori CT-based scatter-corrected CBCT image, denoted as “CBCT_ap” hereafter.

2.E.1. Calibration of projection intensity between CBCT and plan CT

An important part of the a priori scatter correction technique is to find the calibration relationship between the CT forward projections and the raw CBCT images (step 4). Where Niu et al.¹⁸ obtained the calibration formula using fan-beam CBCT acquisitions that require specially designed hardware, we utilized an empirical model to determine the CBCT calibration factor without such hardware.

Similar to Niu et al. study,¹⁸ we assume that the scatter-corrected intensity in a cone-beam projection can be formulated as follows:

$${\displaystyle I_{\mathrm{corr}}=\mathrm{CF}\times I_{\mathrm{raw}}-I_{\mathrm{sca}},}$$ (2)

$${\displaystyle I_{\mathrm{sca}}=f(\mathrm{CF}\times I_{\mathrm{raw}}-I_{\mathrm{pri}}),}$$ (3)

where I_corr is the scatter-corrected intensity, I_sca is the estimated scatter map, I_raw is the original projection intensity, CF is the calibration factor for I_raw, I_pri is the intensity from the forward projections of the planning CT, and f is a smoothing function such as a 2D median or a Gaussian filter. The CF is required to rescale I_raw to an intensity level that matches I_pri so that I_corr will provide accurate HU values after reconstruction. In other words, with properly rescaled I_raw, the reconstructed HU value of CBCT_ap is mainly determined by I_pri.

The projection intensity (I_raw) is linearly correlated with the exposure current-time product (mAs) applied during the CBCT scan. Therefore, we assume that a reference mAs (mAs_ref) exists that allows for the best HU accuracy of CBCT_ap without any intensity rescaling (CF = 1.0). To empirically determine mAs_ref, a pelvis phantom was scanned with a diagnostic CT and multiple CBCT images acquired at different mAs values. The CBCT_ap images for each mAs were reconstructed without intensity rescaling of I_raw, and mAs_ref was determined by assessing HU accuracy of the reconstructed CBCT_ap with respect to the diagnostic CT image.

For a specific mAs setting, the calibration factor is a function of mAs as follows:

$${\displaystyle \mathrm{CF}=\frac{{\mathrm{mAs}}_{\mathrm{ref}}}{\mathrm{mAs}}.}$$ (4)

In this study, mAs_ref was determined to be 2.56 mAs (64 mA/40 ms). Once determined, mAs_ref remained constant for all CBCT_ap reconstructions in this study.

2.F. Calculation of WEPL

WEPL is an important factor that determines proton range in the proton pencil beam algorithm.²² If equivalent WEPL values are calculated for CT_ref and CBCT images, we assume an approximate equivalence between the proton dose distributions. In this study, WEPL was calculated using uniform step-based ray tracing²³ in conjunction with proton stopping power ratio approximation²⁴ as follows:

$${\displaystyle \mathrm{WEPL}=\sum _{i=1}^N{t}_m\left(i\right)\times \mathrm{RSP}\left({\overline{\mathrm{HU}}}_i\right),}$$ (5)

where N is the number of steps along the ray, t_m(i) is the physical length of i-th step in heterogeneous medium, ${\overline{\mathrm{HU}}}_i$ is the mean HU value (or HU_CBCT value in a CBCT case) of the voxels in i-th step, RSP is the relative proton stopping power as a function of HU as defined by Schneider et al.²⁵ The RSP table was imported from our treatment planning system (XiO; Elekta CMS, St. Louis, MO). The same HU to RSP conversion was applied for all CT and CBCT data analyzed in this study.

To comprehensively investigate the proton range equivalence between CT_ref and CBCT images, an angular WEPL profile containing 360 equiangular WEPLs centered at a selected point was introduced. Five middle and peripheral points (middle, superior-left, superior–anterior, inferior–posterior, and inferior-right) from different image slices were selected and analyzed for each volumetric image. It should be noted that the CT_ref images were rigidly registered to the corresponding CBCT_raw images prior to the comparison.

In addition to the angular WEPL profiles, 2D WEPL maps were also calculated for graphical demonstration. The grid size was set to be 1 mm and parallel beams targeting the middle of the phantom were simulated.

2.G. Treatment planning study

Representative clinical target volumes (CTVs) and organs at risk were delineated on the CT_ref images and copied to the corresponding CBCT images. Mock proton treatment plans based on double scattered spread-out Bragg peak (SOBP) beams were made by the XiO treatment planning system with a fast pencil beam algorithm.²⁶ In total, four treatment plans were simulated on the CT and CBCT images of the phantoms as follows: (1) a single posterior-oblique field for a brain target with a diameter of 30 mm in the head phantom; (2) two fields (right and anterior) for a middle-lung target with a diameter of 40 mm in the thorax phantom; (3) a single anterior field for a mediastinum target with a diameter of 40 mm in the thorax phantom; (4) a single lateral field for a prostate target with a volume of 73.2 cm³ in the pelvis phantom. Prescription doses to the CTVs were 60 Gy/30 fractions, 48 Gy/4 fractions, 48 Gy/4 fractions, and 75.6 Gy/48 fractions for the brain, middle-lung, mediastinum, and prostate plans, respectively.

Calculated dose distributions on the CBCT images with or without scatter correction were compared to the dose distributions of the CT_ref plans using 3D gamma analysis.²⁷ In the gamma analysis, a threshold dose value was set to 10% of the prescription dose and the dose difference criterion was defined as percentage of the prescription dose. All plans were calculated with the same HU to RSP calibration.

2.H. Feasibility tests on practical cases

Unlike the simple uniform scatter correction, a priori CT-based correction involves some preprocessing techniques such as DIR and air-pocket removal. Even though the validations for those techniques were already carried out in the previous study,²⁰ we also validated them for some complex cases in our experimental framework. This validation aimed to prove that the CBCT_ap is still feasible when there are obvious anatomical changes at some time points between CT and CBCT scans. To address this issue, four practical situations were simulated using the pelvic phantom as listed below:

• (1)Filled rectum: A rectum was empty in a CT scan and became filled in a CBCT scan.
• (2)Empty rectum: A rectum was filled with water in a CT scan and became empty in a CBCT scan.
• (3)Weight gain: A bolus and rectal filling was not applied during a CT scan and applied in a CBCT scan.
• (4)Weight loss: A bolus with 1 cm thickness and a filled rectum were applied during a CT scan and removed in a CBCT scan.

For the above cases, the air-pocket removal technique proposed by Niu et al.²⁰ was applied to account for high-contrast geometry mismatching in the rectal cavities. Briefly, the procedure consists of the following steps: cavity segmentation using intensity threshold for both CT_ref and CBCT_raw, filling cavities with surrounding soft-tissue intensity values, DIR, and creating new cavities on the deformed CT using the segmentation mask from CBCT_raw.

Additional validation was performed to investigate whether DIR inaccuracy will affect the quality of CBCT_ap. This was done to ensure that high precision DIR is not a prerequisite to implement CBCT_ap. This test was done by applying translational offsets to the CT_ref image after the DIR process. The tested offsets ranged from 1 to 3 mm along a single axis (left–right) or all (x, y, z) axis. It was expected that the following “misaligned” forward projections would affect the accuracy of the scatter-map estimation in some degree. Finally, a feasibility test was also performed on a prostate patient’s image set (IRB Approval No. 2010P-002050) using a mock proton treatment plan.

3. RESULTS

3.A. Improvement in HU accuracy

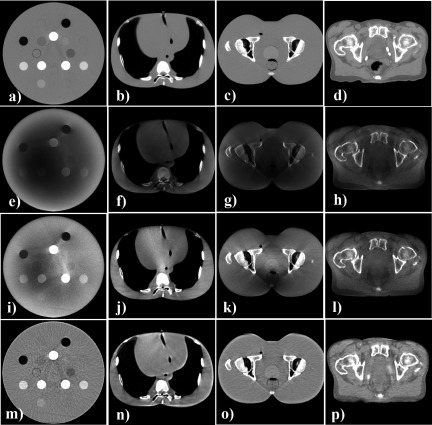
Figure 1 shows the image quality comparison of the CT_ref and CBCT images (with and without correction) of the phantoms and the patient. Without any scatter corrections, the cupping artifact (darker regions in the middle of the images) was observed in the CBCT_raw images. As seen in the CBCT_us images, the uniform scatter correction technique mitigated this artifact and improved contrast in some high HU regions. However, residual shading artifacts and abnormally brightened regions were still found within the images due to the inaccurate scatter model. In contrast, the CBCT_ap images were more effective in removing these artifacts and improving HU accuracy. Table II summarizes the HU values measured in each insert of the electron density CT phantom.

FIG. 1.

Axial views of the CT_ref and CBCT images of three phantoms and a patient. Display window is [1000–200] for all images. [(a)–(d)] CT_ref images; [(e)–(h)] uncorrected CBCT images; [(i)–(l)] CBCT_us images; [(m)–(p)] CBCT_ap images. The CBCT_ap demonstrated comparable HU accuracy and uniformity to the CT_ref, while the CBCT_raw and CBCT_us showed shading artifacts and image heterogeneities.

TABLE II.

HU comparison between CT_ref and CBCT images of the electron density CT phantom.

	HU value (mean ± SD)
Material insert	CTref	CBCTrawa,b	CBCTusa,b	CBCTapa
Solid water	7 ± 7	0 ± 12	0 ± 16	17 ± 17
Lung (LN-300)	−685 ± 9	−259 ± 7	−533 ± 16	−700 ± 19
Inner bone	199 ± 8	27 ± 16	72 ± 13	211 ± 21
Solid water	8 ± 6	−97 ± 13	−101 ± 17	10 ± 24
Liver	74 ± 8	−128 ± 14	−73 ± 14	74 ± 20
Bone	202 ± 7	−111 ± 19	−60 ± 24	214 ± 24
Lung (LN-450)	−494 ± 11	−242 ± 8	−408 ± 13	−506 ± 30
Solid water	5 ± 9	−66 ± 12	−94 ± 15	1 ± 24
Cortical bone	1065 ± 18	16 ± 13	504 ± 32	1071 ± 43
Brain	38 ± 7	−81 ± 6	17 ± 17	51 ± 35
Adipose	−83 ± 8	−112 ± 6	−48 ± 18	−99 ± 22
CB2-50%	717 ± 12	−43 ± 10	377 ± 25	714 ± 31
Solid water	9 ± 9	−253 ± 6	−167 ± 21	14 ± 28
CB2-30%	403 ± 8	−269 ± 8	−112 ± 17	410 ± 35
True water	2 ± 8	−321 ± 8	−319 ± 15	14 ± 34
Breast	−36 ± 7	−242 ± 13	−222 ± 21	−31 ± 32

^aHU for CBCT was custom defined according to Eq. (1).

^bHU values were shifted with respect to a nominal HU value (0 HU) of solid water; SD = one standard deviation.

3.B. WEPL comparison

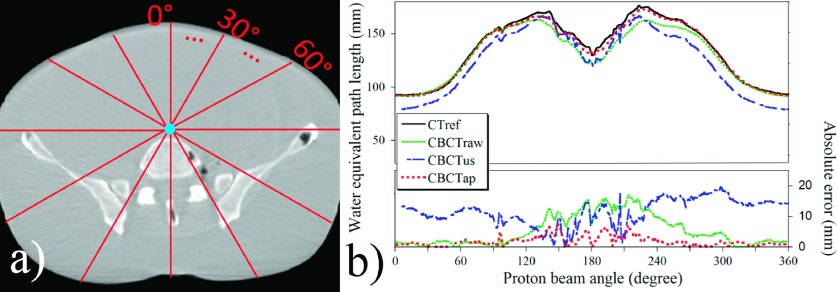
Figure 2 demonstrates the concept of the angular WEPL profile and an example data set generated based on a middle point of the abdomen phantom image. In Fig. 2(b), the x-axis shows the proton beam angle and the y-axis indicates either the WEPL value (upper graph) or the WEPL error with respect to the WEPL from CT_ref (lower graph).

FIG. 2.

Angular WEPL profile to a middle point of the abdominal phantom. (a) An illustration of the simulated beam angles on the CBCT_ap image. (b) An overlap graph of the WEPL profiles acquired from the CT_ref, CBCT_raw, CBCT_us, and CBCT_ap images.

The calculated WEPL error between the CT_ref and CBCT images for 1800 angular WEPLs of each phantom image is summarized in Table III.

TABLE III.

The WEPL errors between the CT_ref and CBCT images measured in five angular WEPL profiles for each image.

	Absolute error (mean ± SD, mm)			Absolute error (mean ± SD, %)a
Phantom	CBCTraw	CBCTus	CBCTap	CBCTraw	CBCTus	CBCTap
Head (L)	12.4 ± 9.4	3.6 ± 3.7	1.5 ± 2.0	14.3 ± 5.6	5.1 ± 4.7	1.9 ± 2.4
Head (H)	10.4 ± 8.0	4.6 ± 5.3	1.3 ± 1.8	11.9 ± 4.8	5.6 ± 5.1	1.8 ± 2.1
Thorax (L)	6.6 ± 3.5	6.6 ± 6.4	3.3 ± 2.6	8.3 ± 5.7	7.6 ± 7.4	3.6 ± 3.0
Thorax (H)	6.1 ± 3.4	7.8 ± 6.7	3.0 ± 2.4	7.5 ± 4.9	9.2 ± 8.6	3.4 ± 2.8
Abdomen (L)	5.0 ± 4.9	22.4 ± 9.4	2.2 ± 1.4	3.5 ± 2.4	19.3 ± 6.4	1.9 ± 1.0
Abdomen (H)	5.0 ± 4.9	14.6 ± 7.0	2.0 ± 1.7	3.5 ± 2.4	13.1 ± 5.4	1.7 ± 1.3
Pelvis (L)	6.8 ± 4.4	12.8 ± 6.7	2.8 ± 1.9	6.2 ± 4.4	12.1 ± 8.2	2.2 ± 1.4
Pelvis (H)	5.8 ± 4.3	16.4 ± 7.6	2.8 ± 1.9	5.2 ± 4.4	15.2 ± 9	2.2 ± 1.4
Overall	7.3 ± 5.3	11.1 ± 6.6	2.4 ± 2.0	7.6 ± 4.3	10.9 ± 6.9	2.3 ± 1.9

^aPercentage error relative to the WEPL of CT_ref; H = high mAs; L = low mAs; SD = one standard deviation.

Substantial WEPL error was observed in the CBCT_raw images (overall absolute error: 7.3 ± 5.3 mm). The CBCT_us was found to be not effective or even worse than CBCT_raw to reduce such errors (overall absolute error: 11.1 ± 6.6 mm). It should be noted that the results of the CBCT_raw and CBCT_us would be even worse if the soft-tissue-based HU shifting was not used. In contrast, the errors were substantially reduced in the CBCT_ap images (overall absolute error: 2.4 ± 2.0 mm). The quality of the CBCT_ap was maintained comparably in the different mAs cases. Figure 3 shows the 2D WEPL difference maps calculated for the pelvic and thorax phantoms. Similar to the angular WEPL results, substantial reduction of WEPL discrepancy from the CT_ref images was demonstrated in the CBCT_ap images.

FIG. 3.

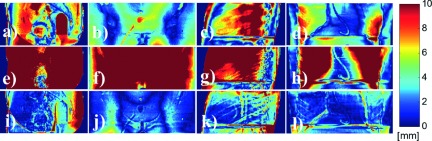
2D proton WEPL difference maps (absolute) calculated between the CT_ref and CBCT images. The WEPL comparison was performed at the phantom midplane perpendicular to the incident beam. Difference shown between [(a)–(d)] CT_ref and CBCT_raw; [(e)–(h)] CT_ref and CBCT_us; [(i)–(l)] CT_ref and CBCT_ap. Columns 1 and 2: lateral and anterior beam simulations on a pelvis phantom; columns 3 and 4: lateral and anterior beam simulations on a thorax phantom.

3.C. Plan comparison

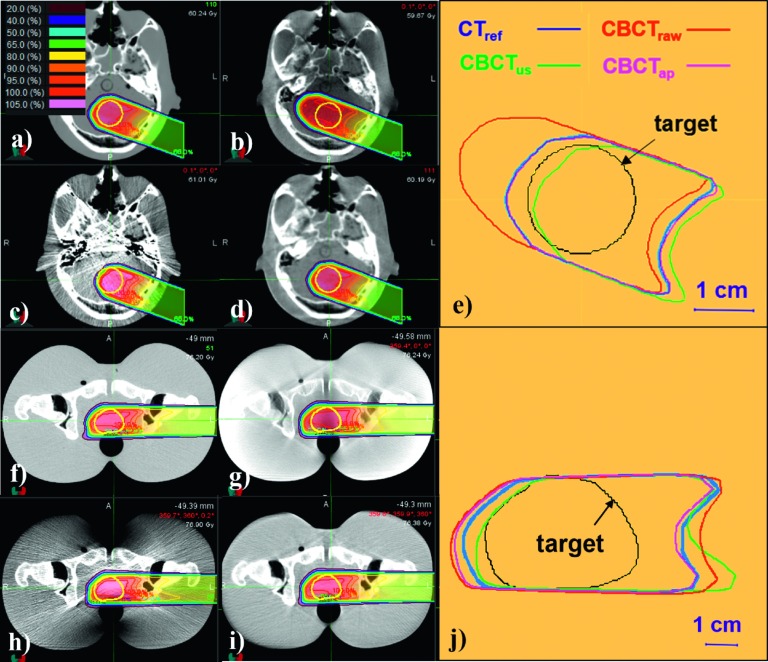
Figure 4 shows proton treatment planning results for the CT_ref and CBCT images with and without correction. The dose distributions of CBCT_ap plans were found to be comparable to those of the CT_ref-based plans while the CBCT_raw and CBCT_us plans showed substantial discrepancies from the ground truth. As seen in Figs. 4(e) and 4(j), isodose line shifts of CBCT_ap were about 1 mm for the head phantom and about 3–4 mm for the pelvis phantom. Even though the shifts could vary depending on beam incident angles and target positions, the observed differences are in-line with the WEPL differences recorded in Table III.

FIG. 4.

Isodose lines of proton treatment plans simulated images of the head (upper) and pelvis (lower) phantoms. [(a) and (f)] CT_ref plans; [(b) and (g)] CBCT_raw plans; [(c) and (h)] CBCT_us plans; [(d) and (i)] CBCT_ap plans; [(e) and (j)] 90% isodose lines of each calculation overlaid with the target.

The result of a 3D gamma evaluation is summarized in Table IV. The CBCT_ap plans showed substantially higher gamma pass rates (mean value of 96.0% ± 2.5% with 2 mm/2% criteria) compared to the CBCT_raw and CBCT_us plans (mean values of 83.9% ± 5.1% and 78.2% ± 12.8%, respectively).

TABLE IV.

The 3D gamma analysis result for proton treatment plans on the phantoms. The numbers represent the percentages of voxels passing the gamma evaluation.

	Gamma criteria: 3 mm/3%			Gamma criteria: 2 mm/2%
Plan	CBCTraw	CBCTus	CBCTap	CBCTraw	CBCTus	CBCTap
Head	85.6	87.7	99.5	78.6	78.1	98.1
Thorax (lung)	84.4	69.0	98.6	79.9	58.6	93.0
Thorax (mediastinum)	96.4	97.5	99.7	91.6	94.4	98.8
Pelvis	94.8	92.4	98.4	85.5	81.7	94.3
Overall	90.3 ± 5.3	86.7 ± 10.8	99.0 ± 0.6	83.9 ± 5.1	78.2 ± 12.8	96.0 ± 2.5

3.D. Feasibility of CBCT_ap for complex cases

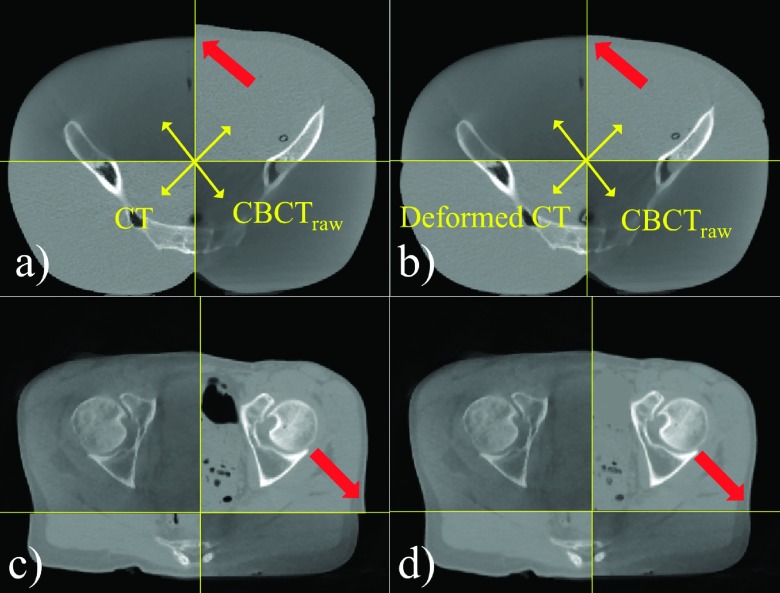
Figure 5 illustrates examples of DIR results for a complex case (the pelvis phantom with weight loss) and a real patient. To qualitatively review the DIR results, the following criteria were considered: (1) bone structure matching; (2) continuity of external skin boundary; (3) shape and size matching of air pockets. It was demonstrated that the mutual information-based DIR engine in conjunction with air-pocket removal used in this study could generate reasonably deformed CT images for challenging cases such as these.

FIG. 5.

Examples of deformable image registration results for a weight loss case [(a) and (b)] and a real patient [(c) and (d)]. Soft-tissue mismatching was observed in rigidly registered CT images [see arrows in (a) and (c)]. Improved continuity could be achieved after the deformable image registration [see arrows in (b) and (d)].

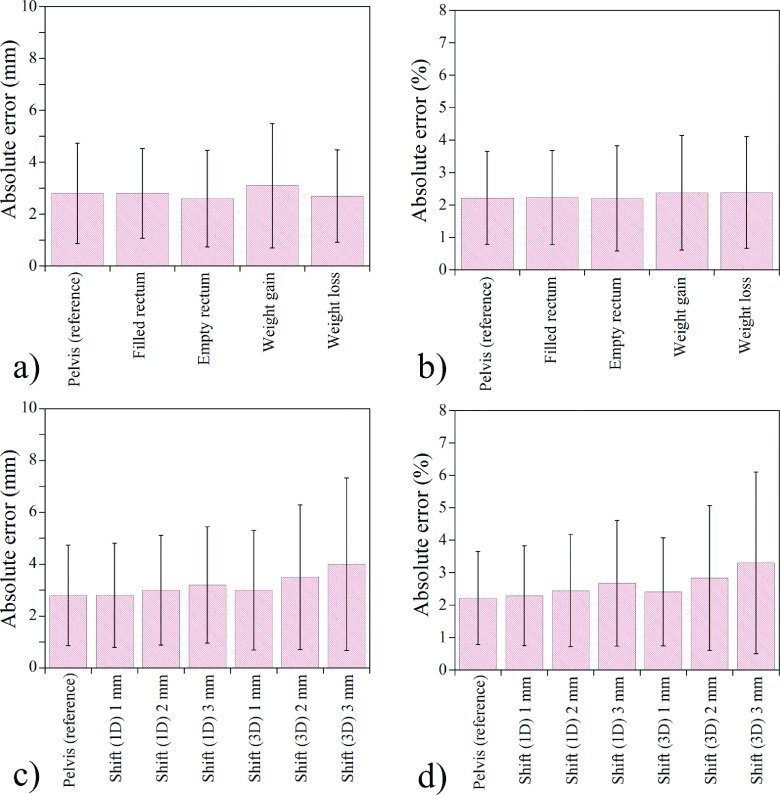
Figure 6 shows the angular WEPL results of the complex and misregistration cases. The a priori CT-based scatter correction still performed well in such complex situations [Figs. 6(a) and 6(b)]. Regarding the misregistration cases, it was indicated that the registration error up to 2 mm in each direction did not make more than 1% additional error in the WEPL calculation [Fig. 6(d)].

FIG. 6.

The WEPL errors between the CT_ref and CBCT_ap images in special cases. [(a) and (b)] absolute error (in mm and percentage, respectively) in the situations of anatomic changes between CT and CBCT scans; [(c) and (d)] absolute error (in mm and percentage, respectively) for the cases of misregistration of a priori image. The result demonstrates the feasibility of CBCT_ap in a practical application of APT. The error bars represent one standard deviation.

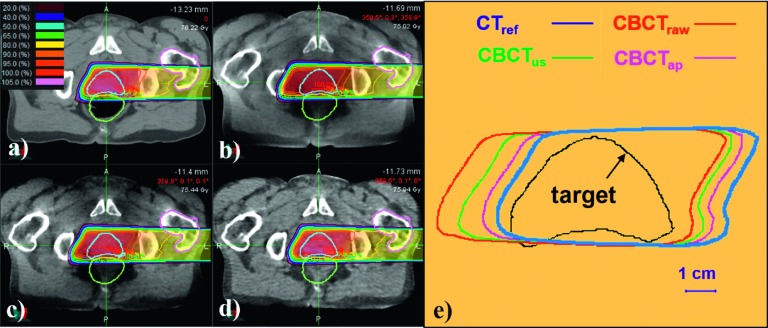
Figure 7 compares the results of the proton treatment planning on the patient’s CT/CBCT images. In agreement with the above results, the CBCT_ap plan demonstrated the most reasonable dose distributions when compared to the CT_ref plan. As seen in Fig. 7(e), the 90% isodose line of CBCT_ap was shifted by less than 5 mm from that of the CT_ref over the proximal and distal fall-off regions. However, it should be noted that the dose distributions in a real patient’s CBCT image could be affected not only by HU accuracy but also by image deformation and anatomic changes that might occur between the acquisitions of the CT and CBCT images.

FIG. 7.

Dose distributions of a proton treatment plan simulated on a patient’s image sets. (a) CT_ref-based plan; (b) CBCT_raw plan; (c) CBCT_us plan; (d) CBCT_ap plan; (e) 90% isodose lines of each calculation overlaid with the target.

4. DISCUSSION

In this phantom study, we investigated the feasibility of proton dose calculation on a daily CBCT image with scatter correction techniques. To the best of our knowledge, this study is the first to demonstrate reliable proton dose calculations on CBCT images.

This study focused on comprehensive phantom validation to investigate the feasibility of CBCT-based proton dose calculation. Similar validation studies had been already performed for photon dose calculation.^18,20 However, we believe it necessary for this to be independently conducted since the residual HU errors after the scatter correction would have different effects on proton dose calculations compared to photon cases. Moreover, this validation cannot be done in real patient images, as there would be no ground truth of CT_ref to compare with daily CBCT images unless CT and CBCT images are acquired at the same patient setup as pointed out by Landry et al.¹²

Recently, Landry et al.^12,13 investigated the feasibility of proton dose calculations on a virtual CT image using deformable image registration between plan CT and daily CBCT images. Even though they demonstrated a promising WEPL error (2% error of the proton range), they encountered residual DIR errors of 2–3 mm which potentially degrade the effectiveness of their approach. Several studies had reported uncertainties of DIR between CT and CBCT images.^28,29 Therefore, the feasibility of DIR-based proton dose recalculation might be limited to the regions with small deformations such as head and neck. Compared to their approach, the CBCT_ap used in this study is more robust for such residual registration errors, as this method uses the prior information to estimate only low frequency errors. Thus, small high frequency errors stemming from the misregistration can be suppressed.^18,20 An additional complication for DIR-based dose calculations is the appearance or disappearance of air pockets in either the CT or CBCT in the esophagus, bowels, or rectum that are difficult for DIR.

One of the assumptions of this study is that the accuracy of proton dose calculation is proportional to the HU accuracy of the CBCT image. It has been reported that the proton dose calculation relying only on the RSP translated from CT-HU leads to proton range uncertainties, which supports the need of stoichiometric calibration procedure and Monte Carlo simulation.^30,31 However, due to the time and cost efficiency, the HU-RSP calibration is widely used in clinical settings, together with a proper range margin (e.g., 3.5% of range uncertainty suggested by Paganetti³²). As long as the HU-RSP calibration is used in the TPS, the importance of improving HU accuracy in CT/CBCT imaging is crucially important.

Unexpectedly, the overall performance of CBCT_us for the proton dose calculation was not satisfactory even though the HU accuracy and contrast were partially improved. This can be explained in part by the overcorrected regions and residual heterogeneities of the CBCT_us images due to its uniform distribution scatter model. Even though these artifacts can be mitigated by using optimized parameters such as individualized scatter-to-primary ratio,³³ we demonstrated that the feasibility of proton dose calculation on CBCT images varies according to which scatter correction strategy is used.

For the implementation of CBCT_ap, we introduced a simpler CT-CBCT HU calibration method, as opposed to the original one proposed by Niu et al.^18,20 Since our method no longer requires any special hardware, it will potentially allow the a priori CT-based scatter correction technique to be easily used in any institution. It should be noted that the reference mAs value (mAs_ref) for the CF may need to be determined specifically for an individual CBCT system.

One limitation of this research is that the projection data used in this study are acquired with limited options. Understanding the effect of different CBCT systems, number of projections, bowtie filters, or kVp on the proton dose calculation accuracy will require additional work. A validation study for a cohort patient case is planned in our institution. This study will begin with brain cancer cases where the ground truth will be relatively reliable due to less interfractional motion and deformation. Another limitation is the computation time needed to generate CBCT_ap images. This includes initial CBCT_raw acquisition, preprocessing of CT_ref, and correcting projection images. Although we substantially reduced the computation time from the original method by using a c++ implementation with GPU-based RTK modules, ∼6 min was still required to generate a full CBCT_ap image set assuming ∼360 projections. However, this issue will not affect the utility of this method for offline adaptive verification.

The impact of patient size on the HU accuracy of the CBCT_ap was not addressed in this study due to the limited size of the available phantoms. As a patient size increases, more beam hardening effect is expected since lower-energy photons are filtered from the polychromatic beam.³⁴ However, Niu et al.¹⁸ demonstrated that the majority of beam-hardening effects are low-frequency components that can be estimated together with the scatter signal, and removed during the correction process. Therefore, we believe that patient size will not substantially degrade the HU accuracy of the CBCT_ap as long as the a priori information (i.e., HU of CT_ref) is still valid regardless of patient size. Further studies with phantoms are required to investigate the patient size effect.

Even though the CBCT_ap demonstrated a promising result for proton treatment planning, there is still some room for improvement. As presented in Table III, the residual range error of 1.8%–3.6% should be accounted for when this technique is used for an APT application. Therefore, the current status of the technique might benefit those cases where the detected range errors are beyond such the residual errors. More studies need to be done to reduce the uncertainty of our method. Use of the beam hardening correction is expected to remove residual shading artifacts near high-density objects.³⁵ Moreover, iterative reconstruction techniques rather than standard FDK might also be used to improve the spatial resolution and to lower the noise level with even fewer projections.³⁶

5. CONCLUSIONS

This study investigated the feasibility of proton dose calculation for dose verification and treatment planning based on daily CBCT images. It was demonstrated that the scatter-induced shading artifact leads to severe proton range errors in dose calculation on an uncorrected CBCT image. A simple uniform scatter-corrected CBCT was found to be inappropriate for the proton dose calculation due to similar dose calculation errors compared to the reference. An a priori CT-based scatter-corrected CBCT was shown to be promising, as it achieved equivalent proton dose distributions and water equivalent path lengths compared to those of the reference CT.